|
Досрочный период |
||
|
21 апреля (чт) |
математика |
математика |
|
25 апреля (пн) |
русский язык |
русский язык |
|
28 апреля (чт) |
информатика и ИКТ, обществознание, химия, литература |
информатика и ИКТ, обществознание, химия, литература |
|
4 мая (ср) |
история, биология, физика, география, иностранные языки |
история, биология, физика, география, иностранные языки |
|
11 мая (ср) |
резерв: математика |
резерв: математика |
|
12 мая (чт) |
резерв: история, биология, физика, география, иностранные языки |
резерв: история, биология, физика, география, иностранные языки |
|
13 мая (пт) |
резерв: информатика и ИКТ, обществознание, химия, литература |
резерв: информатика и ИКТ, обществознание, химия, литература |
|
16 мая (пн) |
резерв: русский язык |
резерв: русский язык |
|
17 мая (вт) |
резерв: по всем учебным предметам |
резерв: по всем учебным предметам |
|
Основной период |
||
|
20 мая (пт) |
иностранные языки |
иностранные языки |
|
21 мая (сб) |
иностранные языки |
иностранные языки |
|
24 мая (вт) |
математика |
математика |
|
27 мая (пт) |
обществознание |
обществознание |
|
1 июня (ср) |
история, физика, биология, химия |
история, физика, биология, химия |
|
7 июня (вт) |
биология, информатика и ИКТ, география, химия |
биология, информатика и ИКТ, география, химия |
|
10 июня (пт) |
литература, физика, информатика и ИКТ, география |
литература, физика, информатика и ИКТ, география |
|
15 июня (ср) |
русский язык |
русский язык |
|
27 июня (пн) |
резерв: по всем учебным предметам (кроме русского языка и математики) |
резерв: по всем учебным предметам (кроме русского языка и математики) |
|
28 июня (вт) |
резерв: русский язык |
резерв: русский язык |
|
29 июня (ср) |
резерв: по всем учебным предметам (кроме русского языка и математики) |
резерв: по всем учебным предметам (кроме русского языка и математики) |
|
30 июня (чт) |
резерв: математика |
резерв: математика |
|
1 июля (пт) |
резерв: по всем учебным предметам |
резерв: по всем учебным предметам |
|
2 июля (сб) |
резерв: по всем учебным предметам |
резерв: по всем учебным предметам |
|
Дополнительный период |
||
|
5 сентября (пн) |
математика |
математика |
|
8 сентября (чт) |
русский язык |
русский язык |
|
12 сентября (пн) |
история, биология, физика, география |
история, биология, физика, география |
|
15 сентября (чт) |
обществознание, химия, информатика и ИКТ, литература, иностранные языки |
обществознание, химия, информатика и ИКТ, литература, иностранные языки |
|
20 сентября (вт) |
резерв: математика |
резерв: математика |
|
21 сентября (ср) |
резерв: русский язык |
резерв: русский язык |
|
22 сентября (чт) |
резерв: по всем учебным предметам (кроме русского языка и математики) |
резерв: по всем учебным предметам (кроме русского языка и математики) |
|
23 сентября (пт) |
резерв: по всем учебным предметам (кроме русского языка и математики) |
резерв: по всем учебным предметам (кроме русского языка и математики) |
|
24 сентября (сб) |
резерв: по всем учебным предметам |
резерв: по всем учебным предметам |
Опять двойка по математике…Почему девятиклассники провалили экзамен? | ОБРАЗОВАНИЕ
Что-то не ладится в школьном королевстве. В немилость попала сама царица наук. В нашем округе четверть девятиклассников провалили ОГЭ по математике, получив за испытание «неуд». Хорошо, что экзамен можно пересдать в резервные дни.
В немилость попала сама царица наук. В нашем округе четверть девятиклассников провалили ОГЭ по математике, получив за испытание «неуд». Хорошо, что экзамен можно пересдать в резервные дни.
«Детей вогнали в стресс»
По информации департамента образования Югры в 2019 году с первой попытки ОГЭ по математике не сдали порядка 20% девятиклассников. В 2020-м из-за пандемии экзамен был отменён. В этом году число «неудов» по математике выросло до 25%, а в отдельных школах округа до 50%. В Сургуте первую попытку провалили 1700 человек! Конечно, подводить окончательные итоги рано. 16 июня ребята имели возможность пересдать экзамен. Ещё один резервный день — 2 июля. Но вопрос, почему возникают такие проблемы, остаётся.
«Зачем нужен этот аналог ЕГЭ в девятом классе? Детям по 15 лет, они ещё не понимают важность образования в современном мире, а мы их вгоняем в такой стресс, постоянно напоминая, что за провал на экзамене им светит только работа дворника. А куда смотрят родители, вспомните, как воспитывали нас?» – вопрошает вартовчанка Анна Захарова в соцсетях. Есть версия, что причина провала кроется в трудных задачах.
Есть версия, что причина провала кроется в трудных задачах.
«В этом году включено дополнительное задание по геометрии, которая всегда являлась предметом повышенной сложности. Такая ситуация типична для всей России», – объясняет директор департамента образования Нижневартовска Инна Святченко. С этим согласен руководитель департамента образования Югры Алексей Дренин. Но лишь отчасти. По его мнению, на низком уровне подготовки к ОГЭ мог сказаться и «дистант».
«Удалёнушка» виновата?
В Югре, как и по всей стране, дети заканчивали 2020 учебный год на удалёнке. С осени школы стали практиковать смешанный формат обучения и только в начале этого года вернулись к привычному режиму работы. По сути, дети почти полгода обучались дистанционно.
«На плачевные результаты по ОГЭ повлиял, прежде всего, дистанционный формат обучения. Невыполненные или списанные домашние задания, невыученные уроки… Очно ты всегда видишь глаза ученика и готов прийти на помощь, а на удалёнке на первый план выходит отношение к учёбе ребёнка и его родителей, понимание, что здесь и сейчас вершится будущее. А такого понимания у большинства просто нет», – сетует учитель математики из Ханты-Мансийска Ирина Курковская и добавляет, что несовершенство школьной программы тоже сыграло свою роль.
А такого понимания у большинства просто нет», – сетует учитель математики из Ханты-Мансийска Ирина Курковская и добавляет, что несовершенство школьной программы тоже сыграло свою роль.
«Образовательный уровень учеников, переходящих из начальной школы в среднюю, с каждым годом падает. Слишком перегружена программа, дети не могут сразу адаптироваться к 5 классу, поэтому возникают трудности. Классы нужно разделять по успеваемости учащихся. Кто-то усваивает материал быстро, а с кем-то приходится долго заниматься», – говорит педагог.
С этим мнением согласна и учитель начальных классов Марина Коробцова: «Уровень знаний начал падать 6-7 лет назад, когда сменили программу. Причин, конечно, нам не объяснили. Некоторые учителя втихушку продолжают обучать детей по учебнику Петерсон. Ведь начальная школа – это фундамент всех знаний». Речь идёт об учебнике Людмилы Петерсон для 1-4 классов. В 2014 году он не прошёл государственную экспертизу и был исключён из школьной программы. Эксперт Российской академии образования Любовь Ульяхина сочла, что «содержание учебника не способствует формированию патриотизма»…
Эксперт Российской академии образования Любовь Ульяхина сочла, что «содержание учебника не способствует формированию патриотизма»…
В моде гуманитарии?
Между тем есть в округе и школы, в которых каверзные задачки ОГЭ ученики как семечки щелкают. Например, гимназия «Лаборатория Салахова». Недавно эта школа вошла в топ-200 лучших общеобразовательных учреждений России, которые занимаются подготовкой абитуриентов для технических вузов страны. Откуда такой успех?
«В этом году мы учились в очном режиме. Возможности нашей школы позволяют соблюдать все меры безопасности и требования Роспотребнадзора. У нас одна смена и достаточное число помещений, чтобы рассредоточить ребят и развести потоки, – объясняет директор гимназии Татьяна Кисель. – Мы делаем упор на алгебру и геометрию, плюс у нас активно работает центр дополнительного образования, где есть программы, которые связаны с визуализацией пространственного воображения детей через 3D-art. А это серьёзный помощник в обучении. Я не согласна, что в провале ОГЭ нужно обвинять исключительно детей, делить их на ответственных и безответственных. Важна роль учителя: заинтересовать, правильно донести информацию, мотивировать».
А это серьёзный помощник в обучении. Я не согласна, что в провале ОГЭ нужно обвинять исключительно детей, делить их на ответственных и безответственных. Важна роль учителя: заинтересовать, правильно донести информацию, мотивировать».
В гимназии созданы все условия для овладения сложным предметом. Уже в младших классах детям преподают наглядную геометрию и математическое конструирование. Скоро в гимназии появится собственный кванториум.
«Важна роль учителя: заинтересовать, правильно донести информацию, мотивировать».
Удивительно, но математика, похоже, в принципе теряет популярность. «Два-три года назад у нас стали востребованными гуманитарные специальности: филология, журналистика, лингвистика. Молодые люди поступают на эти направления с высокими баллами по ЕГЭ. Сдавать математику тут не требуется», – говорит ректор Югорского госуниверситета Роман Кучин. По его словам, пользуются спросом нефтегазовое дело, экология и химия.
Кстати
Попробуйте решить одно из заданий ОГЭ по математике для 9 класса. «Оле надо подписать 880 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днём. Известно, что за первый день Оля подписала 25 открыток. Определите, сколько открыток было подписано за девятый день, если вся работа была выполнена за 16 дней».
Управление образования и молодежной политики администрации Рыбновского муниципального района
Ссылка на официальный сайт для размещения информации о государственных, муниципальных учреждениях bus.gov.ru
Комендантский час:
Ролик: https://yadi.sk/d/xyHQYAxz4OKHyA
Макет: https://yadi.sk/d/8OsZv3tW8ZeV3A
Открытые окна опасны:
Ролик: https://yadi.sk/d/R5CAf6vrDDpPIQ
Внимание!!!
Важная информация для молодых семей района, желающих стать участниками подпрограммы «Обеспечение жильем молодых семей» государственной программы Рязанской области «Развитие образования и молодежной политики», муниципальной программы «Обеспечение жильем молодых семей в районе».
Подробности читайте в Памятке отдела Молодежная политика
Видеоконкурс чтецов «Победу дедов у нас не отнять»
Блинов Александр Николаевич – методист по патриотическому воспитанию
Телефоны горячей линии по организации дистанционного обучения
Материалы по информированию детей, подростков и молодежи о
безопасном поведении в сети «ИНТЕРНЕТ» и формирование у родителей
ответственного отношения к медиабезопасности детей на сайтах
10.05.2018
Всероссийская социальная сеть работников образования
Руководствуясь задачей совершенствования системы образования субъектов РФ и развития межрегионального сотрудничества в сфере образования, Главный интернет сервис регионов России и редакция журнала «Экономическая политика России» формируют Всероссийскую социальную сеть работников образования.
01.11.2017
Объявление
10.01.2017
Руководителям образовательных учреждений О принятии необходимых мер при понижении температуры
В период резкого понижения температуры окружающего воздуха Управление образования и молодежной политики Администрации Рыбновского муниципального района Рязанской области настоятельно рекомендует следующее:
— внимательно следить за изменениями в погоде;
— при температуре ниже – 20 о С отменять учебные и внеурочные занятия в начальных классах общеобразовательных школ;
— при температуре ниже -25 о С отменять учебные и внеурочные занятия в 1-9 классах общеобразовательных школ;
— при температуре ниже -30 о С отменять учебные и внеурочные занятия во всех классах общеобразовательных школ;
— в этот период уделить повышенное внимание обеспечению сохранению образовательных учреждений, усилить контроль за работой котельных и теплоснабжения;
— обеспечить сохранность жизни и здоровья участников образовательного процесса.
09.01.2017
«Горячая линия»
Открыта «Горячая линия» по вопросам незаконного сбора денежных средств с родителей (законных представителей) обучающихся в общеобразовательных учреждениях Рыбновского муниципального района. Обращения принимаются по телефону 8(49137) 51-363, а также через адреса электронных приемных [email protected], [email protected]
22.12.2016
Защита персональных данных
17.11.2016
Уважаемые родители (законные представители)!
Индентификация граждан при получении услуг в электронной форме в сфере образования, в том числе услуги получения текущей успеваемости, с начала 2017 года планируется осуществляться только через Единый портал государственных и муниципальных услуг (ЕПГУ).
Уже сейчас можно зарегистрироваться на ЕПГУ в отделении МФЦ Рязанской области и Пенсионного фонда России, а также на портале gosuslugi.ru
24. 03.2015
03.2015
Уважаемые выпускники школ, родители выпускников!
Информируем вас о возможности поступления на обучение в вузы на условиях целевого приема посредством заключения договоров о целевом обучении с учреждениями и организациями с долей в уставном капитале муниципальной собственности.
Подробная информация по телефону: 8(49137) 51-363 (Черныгина Ирина Владимировна)
17.02.2014
Горячая линия
ГОРЯЧАЯ ЛИНИЯ по вопросам организации Государственной итоговой аттестации
8(49137) 51-363 Соломатина Татьяна Петровна
ИТ-индустрия Беларуси: 2017 г. и далее
%PDF-1.7
%
2 0 объект
>
>>
/Lang (en-US)
/Метаданные 5 0 R
/Имена 6 0 Р
/OpenAction 7 0 R
/Контуры 8 0 R
/PageLabels 9 0 R
/PageLayout /Твоколумнрайт
/PageMode /UseOutlines
/Страниц 10 0 Р
/Тип /Каталог
/ViewerPreferences >
>>
эндообъект
5 0 объект
>
ручей
2017-07-22T15:55:45+03:002017-08-18T12:16:44+02:00Adobe InDesign CC 2017 (Macintosh)2017-08-24T10:48:25+03:00uuid:284ed9e4-5739-4e36 -a0d7-dc7086ec76a0xmp. did:47a63ba2-6238-45a3-a4d5-a15acdbe4a7exmp.ID: f2cbe5a3-0528-45cf-a1cc-d9147eec0527proof: pdfxmp.iid: a6a637d4-cf73-4461-86c4-e6b3a5f7070exmp.did: 99687dd3-3f3c-4945-a995-0da89f0d0721xmp.did: 47a63ba2-6238-45a3-a4d5-a15acdbe4a7edefault
did:47a63ba2-6238-45a3-a4d5-a15acdbe4a7exmp.ID: f2cbe5a3-0528-45cf-a1cc-d9147eec0527proof: pdfxmp.iid: a6a637d4-cf73-4461-86c4-e6b3a5f7070exmp.did: 99687dd3-3f3c-4945-a995-0da89f0d0721xmp.did: 47a63ba2-6238-45a3-a4d5-a15acdbe4a7edefault
application/pdf
Библиотека Adobe PDF 15.0Ложь
конечный поток
эндообъект
25 0 объект
>
>>
>>
/Подтип /Форма
/Тип /XОбъект
>>
ручей
HMN0. \circ$ тогда и только тогда, когда $AC=3CB$
\circ$ тогда и только тогда, когда $AC=3CB$
Две окружности касаются $M$ и лежат внутри прямоугольника $ABCD$. Один из них касается сторон $AB$ и $AD$, а другой касается $AD,BC,CD$. Радиус второго круга в четыре раза больше радиуса первого круга. Найдите отношение, в котором общая касательная окружностей в $M$ делит $AB$ и $CD$.
В звездообразной замкнутой ломаной линии $ABCDEA$ $AB$ пересекается с $CD$ и $DE$ в точках $P$ и $Q$, $BC$ пересекается с $DE$ и $EA$ в точках $R$ и $S$ и $CD$ встречаются с $EA$ в точке $T$ соответственно и $AP = QB, BR = SC, CT = PD, DQ = RE$.Докажите, что $ES = TA$.
Прямоугольник $ABCD$ разбит на пять прямоугольников $P_1,P_2,P_3,P_4, P5$. Если $P_5$ — квадрат, а $P_1,P_2,P_3, P_4$ имеют одинаковую площадь, докажите, что $ABCD$ — квадрат.
Пусть $M$ — точка на полуокружности с диаметром $AB, K$ — точка на $AB$ и $P,Q$ — центры описанных окружностей треугольников $AMK,MKB$. Докажите, что точки $M,K,P,Q$ лежат на окружности.
Дана точка $B$ внутри правильного шестиугольника $A_1A_2. \circ$.o$
\circ$.o$
В треугольнике $ABC$ с $\угол B = 3 \угол A$ пусть $M,N$ выбраны на стороне $CA$ так, что $\угол CBM = \угол MBN = \угол NBA$ . Предположим, что $X$ — произвольная точка на $BC, L$ — пересечение $AX$ и $BN$, а $K$ — пересечение $NX$ и $BM$. Докажите, что $KL$ и $AC$ параллельны.
Центр $O_1$ окружности $S_1$ лежит на окружности $S_2$ с центром $O_2$. Радиус $S_2$ больше, чем у $S_1$. Пусть $A$ — пересечение $S_1$ и $O_1O_2$.Рассмотрим окружность $S$ с центром в произвольной точке $X$ на $S_2$ и проходящую через $A$, и пусть $Y \ne A$ пересечение $S$ и $S_2$. Докажите, что все прямые $XY$ пересекаются, так как $X$ проходит вдоль $S_2$.
год 1996 отсутствует
1997 Белорусское МО D 8.2
На стороне $CB$ треугольника $ABC$ взяты точки $D$ и $E$, причем $D$ между $C$ и $E$,
такие, что $ \угол BAE =\угол CAD$. Если $AC
1997 Белорусское MO D 8.6
Если ABCD является выпуклым четырехугольником с $\угол ADC = 30$ и $BD = AB+BC+CA$,
докажите, что $BD$ делит $\угол ABC$ пополам. o$.Докажите, что $AB\cdot BC = AD \cdot DC$
o$.Докажите, что $AB\cdot BC = AD \cdot DC$
Различные точки $A_1,A_2,A_3,A_4,A_5$ лежат на окружности так, что $A_1A_2 = A_2A_3 = A_3A_4 =A_4A_5$. Пусть $A_6$ — диаметрально противоположная точка $A_2$, а $A_7$ — точка пересечения $A_1A_5$ и $A_3A_6$. Докажите, что прямые $A_1A_6$ и $A_4A_7$ перпендикулярны
Треугольник $A_1B_1C_1$ является параллельной проекцией треугольника $ABC$ в пространстве. Нарисованы параллельные проекции $A_1H_1$ и $C_1L_1$ высоты $AH$ и биссектрисы $CL$ $\vartriangle ABC$ соответственно.Используя линейку и циркуль, постройте параллельную проекцию:
(a) ортоцентр,
(b) центр вписанной стороны $\vartriangle ABC$.
Найдите угол между диагоналями выпуклого четырехугольника, если известно, что они равны между собой, а также удвоенный отрезок, соединяющий середины каких-то двух противоположных сторон.
а) Докажите, что для любого выпуклого четырехугольника одна из его средних линий (т. е. прямых, соединяющих середины противоположных сторон) разбивает его на две части, площадь каждой из которых не меньше $3/8$ площади весь четырехугольник.
б) Остается ли утверждение части а) верным, если число $3/8$ заменить на большее число?
1998 Белорусская МО C 9.5
На сторонах $AB, BC$ и $AC$ треугольника $ABC$ отмечены точки $K, H$ и $T$ соответственно так, что $AH \perp BC$, $\угол BCK = \угол ACK$ и $AT=TC$ . Найдите периметр треугольника $ABC$, если известны длины отрезков $KM = 2$ см, $MN = 1$ см и $NC = 3$ см, где $ M$ — точка пересечения $AH$ и $CK$, а $N$ — точка пересечения $HT$ и $CK$.
Докажите, что если выпуклый восьмиугольник $ABCDEFGH$ можно разбить на шесть параллелограммов так, как показано на рисунке, то четыре прямые $AE, BF, CG$ и $DH$ пересекаются в одной точке.
Точки $N,L$ на стороне AC и точки $P, K$ на стороне $BC$ треугольника $ABC$ таковы, что $AK ,BL$ — биссектрисы, а $AP , BN$ — высоты треугольника . Пусть $O$ и $I$ — центры вписанной и описанной окружностей треугольника $ABC$ соответственно. Докажите, что $N, P$ и $I$ лежат на одной прямой тогда и только тогда, когда $L, K$ и $O$ лежат на одной прямой .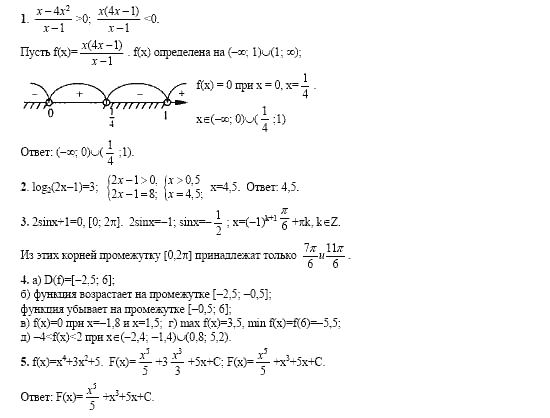
Вам дан правильный десятиугольник $A_1A_2… A_{10}$. Пусть $A$ — точка пересечения прямых $A_1A_4$ и $A_2A_5, B$ — точка пересечения прямых $A_1A_6$ и $A_2A_7$, а $C$ — точка пересечения прямых $A_1A_9$ и $ А_2А_{10}$. Найдите углы $ABC$.
1998 Класс A 10. День 1 недоступен
На прямой, содержащей сторону $AC$ треугольника $ABC$, отмечены точки $M$ и $N$ так, что $MA = AB$ и $NC = CB$ (порядок точек на прямой: $M, A, C, N$).о $ . Докажите, что $\угол AED = 2\угол BEC$.
Пусть $ABC$ — равнобедренный прямоугольный треугольник и $M$ — середина его гипотенузы $AB$. На отрезках $AC$ и $BC$ взяты точки $D$ и $E$ соответственно, такие, что $AD=2DC$ и $BE=2EC$. Прямые $AE$ и $DM$ пересекаются в точке $F$. Покажите, что $FC$ делит $\угол DFE$ пополам.
В остроугольном треугольнике $ABC$ окружность с диаметром $AB$ пересекает $CA$ в точке $L$ и $CB$ в точке $N$. Отрезок $LN$ пересекает медиану $CM$ в точке $K$. Вычислите $CM$, учитывая, что $AB = 9$ и $CK =\frac35 CM$.
Пусть $AB$ и $CD$ — перпендикулярные диаметры окружности, а K — точка на окружности, отличная от $A,B,C,D$. Пусть прямые $AK$ и $CD$ пересекаются в точке $M$, а прямые $DK$ и $BC$ пересекаются в точке $N$. Докажите, что $MN$ параллелен $AB$.
В равнобедренную трапецию $ABCD$ вписана окружность. Диагональ $AC$ пересекает окружность в точках $K$ и $L$ в порядке $A,K,L,C$. Найдите значение ${\sqrt[4]{\frac{AL{\cdot}KC}{AK{\cdot}LC}}}$.
Пусть $P$ и $Q$ — точки на стороне $AB$ треугольника $\треугольника ABC$ (с $P$ между $A$ и $Q$) такие, что $\angle ACP = \angle PCQ = \angle QCB$, и пусть $AD$ — биссектриса угла $\angle BAC$.Строка $AD$ пересекается с линиями $CP$ и $CQ$ в точках $M$ и $N$ соответственно. Учитывая, что $PN = CD$ и $3\угол BAC = 2\угол BCA$, докажите, что треугольники $\треугольник CQD$ и $\треугольник QNB$ имеют одинаковую площадь.
В трапецию ABCD вписана окружность. Пусть K, L, M, N — точки касания этой окружности с диагоналями AC и BD соответственно (K — между A и L, а M — между B и N). Учитывая, что $AK\cdot LC=16$ и $BM\cdot ND=\frac94$, найдите радиус окружности.
Учитывая, что $AK\cdot LC=16$ и $BM\cdot ND=\frac94$, найдите радиус окружности.
1999 г. Беларусь МО А 11.7
Пусть O — центр окружности W. Две равные хорды AB и CD окружности W пересекаются в точке L так, что AL>LB и DL>LC. Пусть M и N — точки на AL и DL соответственно такие, что (ALC)=2*(MON). Докажите, что хорда W, проходящая через M и N, равна AB и CD.
На сторонах $BC$ и $CD$ квадрата $ABCD$ отмечены точки $M$ и $K$ соответственно. Отрезки $MD$ и $BK$ пересекаются в точке $P$. Докажите, что $AP {\perp}MK$ тогда и только тогда, когда $MC=KD$.
На стороне $AB$ треугольника $ABC$ с $BC < AC < AB$ отмечены точки $B_1$ и $C_2$ так, что $AC_2 = AC$ и $BB_1 = BC$.Точки $B2$ на стороне $AC$ и $C_1$ на продолжении $CB$ отмечены так, что $CB_2 = CB$ и $CC_1 = CA$. Докажите, что прямые $C_1C_2$ и $B_1B_2$ параллельны.
В треугольнике $ABC$ с прямым углом $C$ высота $CD$ пересекает биссектрису угла $AE$ в точке $F$. Прямые $ED$ и $BF$ пересекаются в точке $G$. Докажите, что площадь четырехугольника $CEGF$ равна площади треугольника $BDF$. \circ$.2$ перпендикулярны.
\circ$.2$ перпендикулярны.
Диагонали $AC$ и $BD$ выпуклого четырехугольника $ABCD$ пересекаются в точке $M$. Биссектриса угла $\angle ACD$ пересекает луч $\overrightarrow{BA}$ в точке $K$. Если $MA.MC+MA.CD=MB.MD$, докажите, что $\angle BKC=\angle CDB$.
2000 Белорусское МО Б 10.6
На плоскости даны прямоугольник $ABCD$ и точка $X$.
(a) Докажите, что среди отрезков $XA,XB,XC,XD$ три являются сторонами треугольника.
(b) Обязательно ли выполнено (a), если $ABCD$ — параллелограмм?
Боковые стороны и диагонали трапеции пересекают прямую $l$, образуя на ней три равных отрезка.о$. На сторонах $AD, DC$ и диагонали $AC$ отмечены точки $F, H$ и $G$ соответственно, так что четырехугольник $DFGH$ является параллелограммом. Докажите, что треугольник $FBH$ равносторонний.
Четырехугольник $ABCD$ вписан в окружность. На лучах $BA$ и $DC$ отмечены точки $C_1$ и $A_1$, соответственно, такие, что $DA = DA_1$ и $BC =BC_1$. Докажите, что диагональ $BD$ делит отрезок $A_1 C_1$ пополам.
Окружности $S_1$ и $S_2$ пересекаются в точках $A$ и $B$. Через точку $P$ окружности $S_2$, лежащую внутри $S_1$, проводится хорда $AD$ окружности $S_1$.Хорда $BC$ окружности $S_1$ проходит через точку $P$. Прямая, проходящая через точки $D$ и $B$, пересекает окружность $S_2$ в точке $Q$, отличной от точки $B$. Пусть $P_1$ — точка, симметричная точке $P$ относительно точки $B$. Докажите, что $CD$ является диаметром окружности $S_1$ тогда и только тогда, когда точки $D, C, Q$ и $P_1$ лежат на одной окружности.
Внутри прямоугольного треугольника $ABC$ с прямым углом при вершине $C$ отмечена точка $X$ такая, что $\angle XAB = \angle XBC$.2.$$
2001 Белорусское МО Б 10.8
В четырехугольник $ABCD$ можно вписать окружность. Продолжения стороны $AB$ за точку $B$ и стороны $DC$ за точку $C$ пересекаются в точке $E$. Продолжения стороны $DA$ за точку $A$ и стороны $CB$ за точку $B$ пересекаются в точке $F$. Обозначим через $I_1,I_2$ и $I_3$ центры окружностей, вписанных в треугольники $AFB, BEC$ и $ABC$ соответственно. Пусть прямая $I_1I_3$ пересекает прямые $EA$ и $ED$ в точках $K$ и $L$ соответственно, а прямая $I_2I_3$ пересекает прямые $FC$ и $FD$ в точках $ M$ и $N$ соответственно.2$ разыгрывается. На графике отмечены три различные точки $A$, $B$ и $C$, причем $A$ лежит между $B$ и $C$. На $BC$ отмечена точка $N$ так, что $AN$ параллельна оси y. Пусть $K_1$ и $K_2$ — площади треугольников $ABN$ и $ACN$ соответственно. Выразите $AN$ через $K_1$ и $K_2$.
Пусть прямая $I_1I_3$ пересекает прямые $EA$ и $ED$ в точках $K$ и $L$ соответственно, а прямая $I_2I_3$ пересекает прямые $FC$ и $FD$ в точках $ M$ и $N$ соответственно.2$ разыгрывается. На графике отмечены три различные точки $A$, $B$ и $C$, причем $A$ лежит между $B$ и $C$. На $BC$ отмечена точка $N$ так, что $AN$ параллельна оси y. Пусть $K_1$ и $K_2$ — площади треугольников $ABN$ и $ACN$ соответственно. Выразите $AN$ через $K_1$ и $K_2$.
2001 Белорусское МО А 11.3
На прямой $l$ отмечены три различные точки $A$, $B$ и $N$, причем точка $B$ лежит между $A$ и $N$. Для произвольного угла $\alpha\in (0,\frac{\pi}{2})$ отмечены точки $C$ и $D$ на плоскости по одну сторону от $l$ такие, что $N$ , $C$ и $D$ коллинеарны; $\угол NAD = \угол NBC = \alpha$; а $A$, $B$, $C$ и $D$ концикличны.Найдите геометрическое место точек пересечения диагоналей $ABCD$ при изменении $\alpha$ от $0$ до $\frac{\pi}{2}$.
2001 Белорусская МО А 11.7
Выпуклый четырехугольник $ABCD$ вписан в окружность $S_1$. Пусть $O$ — пересечение $AC$ и $BD$. Окружность $S_2$ проходит через $D$ и $O$, пересекая $AD$ и $CD$ в точках $M$ и $N$ соответственно. Прямые $OM$ и $AB$ пересекаются в точке $R$, прямые $ON$ и $BC$ пересекаются в точке $T$, а $R$ и $T$ лежат по ту же сторону от прямой $BD$, что и $A$. .о$). На лучах $MA$ и $NB$ отмечены точки $K$ и $T$ так, что $MK = MB$ и $NT = NA$. Докажите, что $KT\параллелен MN$.
Пусть $O$ — пересечение $AC$ и $BD$. Окружность $S_2$ проходит через $D$ и $O$, пересекая $AD$ и $CD$ в точках $M$ и $N$ соответственно. Прямые $OM$ и $AB$ пересекаются в точке $R$, прямые $ON$ и $BC$ пересекаются в точке $T$, а $R$ и $T$ лежат по ту же сторону от прямой $BD$, что и $A$. .о$). На лучах $MA$ и $NB$ отмечены точки $K$ и $T$ так, что $MK = MB$ и $NT = NA$. Докажите, что $KT\параллелен MN$.
На сторонах $AB$ и $AC$ треугольника $ABC$ отмечены точки $M$ и $N$ соответственно так, что $MN\параллельны BC$. Отрезок $BN$ пересекает отрезок $CM$ в точке $K$. Окружность, проходящая через $A,K,B$, пересекает $BC$ в точке $P$, а окружность, проходящая через $A,K,C$, пересекает $BC$ в точке $Q$. Пусть $T$ — точка пересечения прямых $PM$ и $QN$. Докажите, что $P$ лежит на прямой $AK$.о$. Пусть $P$ и $Q$ — точки пересечения прямых $BA$ и $CM$, $BC$ и $AM$ соответственно. Докажите, что $D$ лежит на прямой $PQ$.
2002 Белорусский МО B 10.7
На стороне $BC$ $\vartriangle ABC$ отмечены точки $M, L, K$ (порядок точек $B, M, L, K, C$), поэтому что $BM=ML=LK=LC$. Известно, что $\угол ACB= \угол MAB$.
Известно, что $\угол ACB= \угол MAB$.
а) Докажите, что $\угол KAL > 1,5 \угол CAK$.
б) Докажите, что коэффициент $1,5$ в а) максимально возможный.
Докажите или опровергните:
Существует такое тело, что для всех положительных целых чисел $n$ с $n \geq 3$ существует «параллельная проекция» такая, что образ тела при этой проекции является выпуклым $n$-гон.
2002 Белорусское МО А 11.6
Высота $CH$ прямоугольного треугольника $ABC$ при $\angle{C}=90$ пересекает биссектрисы углов $AM$ и $BN$ в точках $P$ и $Q$ , и пусть $R$ и $S$ — середины $PM$ и $QN$. Докажите, что $RS$ параллелен гипотенузе $ABC$
2003 Grade D 8.2$ так, что его гипотенуза параллельна оси абсцисс тогда и только тогда, когда высота от прямого угла равна $1$. (Треугольник вписан в параболу, если все три вершины треугольника принадлежат параболе.)
Диагонали $A_1A_4$, $A_2A_5$ и $A_3A_6$ выпуклого шестиугольника $A_1A_2A_3A_4A_5A_6$ пересекаются в точке $K$. Для $A_2A_1= A_2A_3 = A_2K$, $A_4A_3 = A_4A_5 = A_4K$, $A_6A_5 = A_6A_1= A_6K$ докажите, что шестиугольник циклический.
Разные точки $A_0,A_1,…,A_{1000}$ отмечены на одной стороне угла, а различные точки $B_0,B_1,…,B_{1000}$ отмечены на другой его стороне, так что
$$A_0A_1=A_1A_2=. ..=A_{999}A_{1000} , B_0B_1= B_1B_2=…= B_{999}B_{1000}.$$ Найдите площадь четырехугольника $A_{999}A_{1000}B_{1000}B_ {999}$, если площади четырехугольников $A_0A_1B_1B_0$ и $A_1A_2B_2B_1$ равны $5$ и $7$ соответственно.
2003 Беларусь MO C 9.7
Четырехугольник $ABCD$ вписанный и $AB = 2AD, BC = 2CD$. Учитывая, что $\угол BAD=\alpha$ и диагональ $AC = d$, найдите площадь треугольника $ABC$.
Диагонали $AC$ и $BD$ выпуклого четырехугольника $ABCD$ перпендикулярны и пересекаются в точке $O$. Пусть окружности $S_1, S_2, S_3, S_4$ с центрами $O_1, O_2, O_3, O_4$ вписаны в треугольники $AOB, BOC, COD, DOA$ соответственно.
Докажите, что
а) сумма диаметров $S_1, S_2, S_3, S_4$ меньше или равна $(2-\sqrt2 )(AC + BD)$
б) $O_1O_2 + O_2O_3 + O_3O_4 +O_4O_1< 2(\sqrt2-1) (AC + BD)$.
2003 г. Белорусское МО Б 10.5
Четырехугольник $ABCD$ вписанный и $AB = BC = AD + CD$. Учитывая, что $\угол BAD = \alpha$, а диагональ $AC = d$, найдите площадь треугольника $ABC$.
2003 Белорусское МО Б 10.7
Будем говорить, что треугольник и прямоугольник близнецы, если они имеют одинаковые периметры и одинаковые площади. Докажите, что для данного прямоугольника существует треугольник-близнец, если этот прямоугольник не является квадратом и отношение большей стороны прямоугольника к его меньшей стороне не меньше $\lambda -1 +\sqrt{\lambda (\lambda — 2)}$, где $\lambda = \frac{3\sqrt3}{2}$.о, BD=2$. Найдите площадь $ABCDE$.
На сторонах $AB$ и $AC$ треугольника $ABC$ отмечены точки $N$ и $K$ соответственно, так что $AN = NB$ и $AK = 2 KC$. Оказалось, что $KN\perp AB$. Найдите $NC$, если вы знаете, что $CB = 8$.
В выпуклом четырехугольнике $ABCD$ диагонали $AC$ и $BD$ перпендикулярны, причем $AC = KL = 2$, где $K$ и $L$ — середины сторон $AB$ и $CD $ соответственно. Найдите длину диагонали $BD$ и угол между прямыми $BD$ и $KL$.
Найдите длину диагонали $BD$ и угол между прямыми $BD$ и $KL$.
Пусть ABCD — выпуклый четырехугольник, а K, L, M, N — середины его сторон AB, BC, CD, DA соответственно. Пусть прямые NL и KM пересекаются в точке T. Докажите, что $\frac83\left|DNTM\right|<\left|ABCD\right|<8\left|DNTM\right|$, где $\left|P_1P_2. ..P_n\right|$ обозначает площадь произвольного многоугольника $P_1P_2...P_n$.
2004 Белорусское МО C 9.6
Окружности $S_1$ и $S_2$ пересекаются в точках $A$ и $B$. Прямая, проходящая через $A$, параллельна прямой, проходящей через центры $S_1$ и $S_2$, и снова пересекает $S_1$ в точке $C$ и снова $S_2$ в точке $D$.Окружность $S_3$ с диаметром $CD$ снова пересекает $S_1$ и $S_2$ в точках $P$ и $Q$ соответственно. Докажите, что прямые $CP,DQ$ и $AB$ параллельны.
2004 Белорусское МО С 9.7
Даны два подобных треугольника, высоты первого треугольника равны сторонам другого. Найдите максимально возможное значение отношения подобия треугольника.
Диагонали $AD, BE, CF$ выпуклого шестиугольника пересекаются в точке $P$. Найдите наименьшую возможную площадь $ABCDEF$, если $[APB] = 4$, $[CPD] = 6$ и $[EPF] = 9$.2$.
Найдите наименьшую возможную площадь $ABCDEF$, если $[APB] = 4$, $[CPD] = 6$ и $[EPF] = 9$.2$.
2004 Белорусский МО Б 10.6
а) Предположим, что существует точка $X$ в плоскости данного выпуклого четырехугольника $ABCD$ такая, что периметры треугольников $ABX,BCX,CDX, DAX$ равны. Докажите, что $ABCD$ — касательный четырехугольник.
(b) Если выпуклая $ABCD$ является касательной, то обязательно ли существует точка $X$ такая, что периметры треугольников $ABX,BCX,CDX,DAX$ равны?
2004 г. Беларусь МО А 11.2
Пусть $C$ — полуокружность с диаметром $AB$. Окружности $S$, $S_1$, $S_2$ радиусами $r$, $r_1$, $r_2$ соответственно касаются $C$ и отрезка $AB$, причем $S_1$ и $S_2$ внешне касаются $S$.Докажите, что $\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt{r_2}}=\frac{2\sqrt{2}}{\sqrt{r}}$
2004 бел. MO A 11.7
Дан куб $ABCDA_1B_1C_1D_1$. Найдите геометрическое место точек $E$ на грани $A_1B_1C_1D_1$, для которых существует прямая, пересекающая прямые $AB$, $A_1D_1$, $B_1D$ и $EC$.
2005 Класс D 8. отсутствует
Пусть $K$ и $M$ — точки на сторонах $AB$ и $BC$ соответственно треугольника $ABC$, а $N$ — точка пересечения $AM$ и $CK$.Предположим, что четырехугольники $AKMC$ и $KBMN$ вписаны с одинаковыми радиусами описанной окружности. Найдите ${\angle}ABC$
Предположим, что существует точка $K$ на стороне $CD$ трапеции $ABCD$ с $AD \параллельной BC$ такая, что треугольник $ABK$ равносторонний. Докажите, что на прямой $AB$ есть точка $L$ такая, что $CDL$ также является равносторонним треугольником.
Пусть $BE$, $CF$ — две высоты треугольника $ABC$, а $H$ — его ортоцентр. Пусть $l$ — перпендикуляр к $CA$ (проходящий через $A$).Покажите, что $~$ $BC$, $EF$, $l$ параллельны тогда и только тогда, когда $H$ является серединой $BE$
2005 Белорусский MO B 10.8
Существует ли выпуклый семиугольник такой, что для любого из внутренних углов, биссектриса угла содержит одну из диагоналей?
Прямая, параллельная стороне $AC$ треугольника $ABC$ с $\углом C = 90$, пересекает сторону $AB$ в точке $M$ и сторону $BC$ в точке $N$, так что $CN/BN = AC /БК = 2/1$. Отрезки $CM$ и $AN$ пересекаются в точке $O$. Пусть $K$ — точка на отрезке $ON$ такая, что $MO+OK = KN$.Биссектриса $\угла ABC$ пересекает прямую через $K$, перпендикулярную $AN$, в точке $T$. Определить $\угол MTB$.
Отрезки $CM$ и $AN$ пересекаются в точке $O$. Пусть $K$ — точка на отрезке $ON$ такая, что $MO+OK = KN$.Биссектриса $\угла ABC$ пересекает прямую через $K$, перпендикулярную $AN$, в точке $T$. Определить $\угол MTB$.
2005 Белорусское МО А 11.8
Существует ли выпуклый пятиугольник такой, что для любого его внутреннего угла биссектриса угла содержит одну из диагоналей?
2006 Класс D 8. отсутствует
На сторонах $AB,BC,CD$ ромба $ABCD,$ отмечены точки $X,Y,Z$ соответственно, так что $XY\параллелен AZ. $ Докажите, что $XZ,AY$ и $BD$ параллельны.о$, $AB = 2005$, $AC = 2006$. Боб и Билл по очереди (БоБ — первый) разрезают треугольник по любой прямой так, чтобы появились два новых треугольника с площадью больше или равной $1$. После этого тупоугольный треугольник (или любой из двух прямоугольных треугольников) удаляется и процедура повторяется с оставшимся треугольником. Игрок проигрывает, если не может сделать следующую резку.
Определите, кто из игроков выигрывает, если оба играют лучше всех.
2006 Белорусский MO C 9,5 10,7
Даны действительные числа $a, b, k (k > 0)$.2$. Пусть R — радиус описанной описанной окружности треугольника $ABC$.
а) Докажите, что $R>\frac12$
б) Существует ли константа $c>\frac12$ такая, что для любых различных точек $A,B,C$ выполняется неравенство $R\ge c$?
2006 Белорусское МО А 11.4
Дан четырехугольник $ABCD$ с $\угол ABC = \угол ADC$. Пусть $BM$ — высота треугольника $ABC$, а $M$ принадлежит $AC$. На диагонали $AC$ отмечена точка $M’$ так, что $$\frac{AM \cdot CM’}{ AM’ \cdot CM}= \frac{AB \cdot CD }{ BC \cdot AD}$$ Докажите, что точка пересечения $DM’$ и $BM$ совпадает с ортоцентром треугольника $ABC$.
Выпуклый четырехугольник $ABCD$ лежит на декартовой плоскости. Его вершины $A$ и $D$ принадлежат отрицательной ветви графика гиперболы $y= 1/x$, вершины $B$ и $C$ принадлежат положительной ветви графика, а точка $B$ лежит слева от $C$, отрезок $AC$ проходит через начало координат $(0,0)$. Докажите, что $\угол BAD = \угол BCD$.
Пусть $AH_A, BH_B, CH_C$ — высоты, а $BM$ — медиана остроугольного треугольника $ABC$ ($AB > BC$). Пусть $K$ — точка пересечения $BM$ и $AH_A$, $T$ — точка на $BC$ такая, что $KT \параллельно AC$, $H$ — ортоцентр $ABC$.Докажите, что прямые, проходящие через пары точек $(H_c, H_A), (H, T)$ и $(A, C)$, совпадают.
Два треугольника $ABC$ и $A_1B_1C_1$ описаны вокруг окружности, периметры которой относятся как $1:2$. Сторона $A_1B_1$ пересекает стороны $BC$ и $AC$ в точках $A_2$ и $B_3$ соответственно, сторона $A_1C_1$ пересекает стороны $AB$ и $BC$ в точках $C_2$ и $A_3$, соответственно сторона $B_1C_1$ пересекает стороны $AC$ и $AB$ в точках $B_2$ и $C_3$ соответственно.o$, найдите значение $ \angle DBC$.
Пусть $O$ — точка пересечения диагоналей $AC$ и $BD$ четырехугольника $ABCD$ с $AB=BC$ и $CD=DA$. Пусть $N$ и $K$ — основания перпендикуляров из $D$ и $B$ в $AB$ и $BC$ соответственно. Докажите, что точки $N$, $O$ и $K$ лежат на одной прямой.
Три жука находятся в одной точке стола. Внезапно они начинают ползти и через некоторое время оказываются в вершинах треугольника с внутренним радиусом, равным $2$. Докажите, что хотя бы один из жуков прополз расстояние, большее чем $3$.
Внезапно они начинают ползти и через некоторое время оказываются в вершинах треугольника с внутренним радиусом, равным $2$. Докажите, что хотя бы один из жуков прополз расстояние, большее чем $3$.
Дан выпуклый четырехугольник $ABCD$, где $\угол ACB = \угол ADB$ и $AB = AD$. Пусть $N$ и $K$ — основания перпендикуляров из $A$ на прямые $CB$ и $DB$ соответственно. Докажите, что $ NK \perp AC$.
2007 Белорусское МО А 11.2
Окружности $S_1$ и $S_2$ с центрами $O_1$ и $O_2$ соответственно проходят через центры друг друга. Пусть $A$ — одна из их точек пересечения. Две точки $M_1$ и $M_2$ начинают двигаться одновременно, начиная с точки $A$. Точка $M_1$ движется вдоль $S_1$, а точка $M_2$ движется вдоль $S_2$.Обе точки движутся по часовой стрелке и имеют одинаковую линейную скорость $v$.
(a) Докажите, что все треугольники $AM_1M_2$ равносторонние.
(б) Определить траекторию движения центра треугольника $AM_1M_2$ и найти его линейную скорость.
2007 Беларусь МО А 11. 5
5
Пусть $O$ — точка пересечения диагоналей выпуклого четырехугольника $ABCD$, $AO = CO$. На отрезках $AO$ и $CO$ отмечены точки $P$ и $Q$ соответственно так, что $PO = OQ$. Пусть $N$ и $K$ — точки пересечения сторон $AB$, $CD$ и прямых $DP$ и $BQ$ соответственно.Докажите, что точки $N$, $O$ и $K$ лежат на одной прямой.
В равнобедренном треугольнике $ABC$ ($AC = BC$) на стороне $AC$ отмечена точка $D$ так, что треугольник $ADK$ равнобедренный, где $K$ точка пересечения отрезка $BD$ и высота $AH$. Найдите угол $DBA$.
В треугольнике $ABC$ высота $AK$ и медиана $BM$ пересекаются в точке $Q$, при этом $AK = BM$. Луч $QC$ является биссектрисой угла $MQK$. Найдите углы треугольника $ABC$.
В треугольнике $ABC$ отрезки $A_1B_2, B_1C_2$ и $C_1A_2$ касаются вписанной в этот треугольник окружности и параллельны сторонам $AB, BC$ и $CA$ соответственно (см.). Найдите значение суммы $\frac{A_1B_2}{AB} + \frac{B_1C_2}{BC}+ \frac{C_1A_2}{CA}$.
Высота $BH$ и медианы $AM$ и $CN$ проведены в треугольнике $ABC$. Оказалось, что $HM = MN$. Докажите, что треугольник $ABC$ равнобедренный.
Оказалось, что $HM = MN$. Докажите, что треугольник $ABC$ равнобедренный.
Через центр $I$ вписанной в треугольник $ABC$ окружности провести отрезки $A_1B_2$, $B_1C_2$ и $C_1A_2$ со сторонами, параллельными $AB, BC$ и $CA$ соответственно (см. Инжир.). Найдите значение суммы $\frac{A_1B_2}{AB}+\frac{B_1C_2}{BC}+\frac{C_1A_2}{CA}$.
2008 Белорусское МО Б 10.3 (12)
Длины всех высот в некоторых неравнобедренных треугольниках выражены целыми числами. Найдите наименьшее возможное значение радиуса вписанной окружности этого треугольника, если известно, что он также является целым числом.
На сторонах $BC$ и $AC$ треугольника $ABC$ начертите точки $A_1$ и $B_1$ соответственно, так что $\frac{AB_1}{CB_1} = \lambda \frac{AB}{CB }$, $ \frac{BA_1}{CA_1} = \lambda \frac{BA}{CA}$, где $\lambda$ — некоторое положительное число.Пусть $M$ — произвольная точка на отрезке $A_1B_1$, а $x, y, z$ — расстояния от точки M до сторон треугольника $BC, AC, AB$ соответственно. Докажите, что $z = \lambda (x + y)$.
Две смежные стороны четырехугольника $ABCD$ равны, $BC = CD$, а две другие не равны, $AB \ne AD$. Также $\угол BAC = \угол DAC$. Через точки $A$ и $C$ проведена окружность, которая вторично пересекает отрезок $AB$ в точке $N$ и прямую $AD$ в точке $M$. Найдите длину отрезка $DM$, если известно, что $BN = a$.
2008 Белорусский MO B 10.6 (12)
Пятиугольник $ABCDE$ вписан в окружность, сторона которой $BC = \sqrt{10}$ Диагонали $EC$ и $AC$ пересекают диагональ $BD$ в точках $ L$ и $K$ соответственно. Оказалось, что вокруг четырехугольника $AKLE$ можно описать окружность. Найдите длину касательной из точки $C$ к этой окружности.
2008 МО Беларуси А 11.2
$ABCD$ — четырехугольник, вписанный в окружность, и $AB=BC,AD=3DC$ . Точка $R$ находится на $BD$ и $DR=2RB$.Точка $Q$ лежит на $AR$ и $\angle ADQ = \angle BDQ$. Также $\угол ABQ + \угол CBD = \угол QBD$ . $AB$ пересекают прямую $DQ$ в точке $P$. Найдите $\угол APD$
Точка $O$ — центр окружности $\omega$. Точка $A$ лежит вне $\omega$. Секущая проходит через $A$ и пересекает окружность в точках $X$ и $Y$. Точка $X’$ симметрична точке $X$ относительно прямой $OA$. Докажите, что точка пересечения $OA$ и $X’Y$ не зависит от выбора секущей.
Секущая проходит через $A$ и пересекает окружность в точках $X$ и $Y$. Точка $X’$ симметрична точке $X$ относительно прямой $OA$. Докажите, что точка пересечения $OA$ и $X’Y$ не зависит от выбора секущей.
$a,b,c$ — стороны треугольника $T$.2$ отмечены точки $A, B, C$ ($A$ — левее всех) так, что биссектриса угла $ABC$ параллельна его оси. Известно, что проекция отрезка $AC$ на ось абсцисс равна $4$. Найдите абсциссу середины отрезка $BC$.
На сторонах $AB, AC, BC$ треугольника $ABC$ отмечены точки $X, X_1, X_2$ соответственно так, что $XX_1 \perp AC$, $X_1X_2 \perp BC$, $X_2X \перп АВ$. Пусть $Y, Y_1, Y_2$ — точки соответственно на сторонах $BC, AC, AB$ треугольника $ABC$, так что $YY_1 \perp AC$, $Y_1Y_2 \perp AB$.Докажите, что $Y_2Y \perp BC$, если $XY$ и $AC$ параллельны.
Точка $T$ точка пересечения двух диагоналей $AC$ и $BD$ выпуклого четырехугольника $ABCD$. Ортоцентр треугольника $ABT$ совпадает с центром описанной окружности треугольника $CDT$. Докажите, что:
а) вокруг четырехугольника $ABCD$ можно провести окружность
б) центр описанной окружности треугольника $CDT$ лежит на описанной окружности $ABCD$.
2009 г. класс Б 10.{\circ}$. Пусть $B_1$ и $A_1$ — точки на сторонах $AC$ и $BC$ соответственно. Окружности $\треугольника BCB_1$ и $\треугольника ACA_1$ пересекаются в точках $C$ и $D$. Докажите, что $D$ является точкой на стороне $AB$ тогда и только тогда, когда $\frac{CB_1}{CB}+\frac{CA_1}{CA}=1$
Дана трапеция $ABCD$ ($AD\ параллели BC$), биссектрисы углов $BAD$ и $CDA$ пересекаются на биссектрисе одного из его оснований. Докажите, что $AB=CD$, если $AB + CD = AD$.
В треугольнике $ABC$ к стороне $AC$ проведена биссектриса угла $BK$.Найдите углы треугольника $ABC$, если $AK = 1$ и $BK=KC= 2$.
В треугольнике $ABC$, у которого сторона $AB$ наименьшая, на стороне $CA$ есть точка $M$ такая, что $CM = MB$, на стороне $CB$ точка $N$ такая что $CN = NA$. Докажите, что точка $A, B, N , M$ и центр $O$ описанной окружности треугольника $ABC$ лежат на одной окружности
Четырехугольник $ABCD$ вписан в окружность. Докажите, что $C D \cdot B D> A B \cdot AC $, если $\frac{CD}{AB}>\frac{AB}{AC}$.
Дана трапеция $ABCD$ ($AD\параллельная BC$) $AD = 3BC$.Окружность $\Gamma_1$ с центром в точке $B$ проходит через середину диагонали $BD$, а окружность $\Gamma_2$ с центром в точке $C$ проходит через середину диагонали $AC$. Докажите, что прямая, проходящая через точки пересечения окружностей $\Gamma_1$ и $\Gamma_1$ , пересекает основание $AD$ в его середине.
Окружности $\Gamma_1$ и δ $\Gamma_2$ одновременно касаются друг друга внешне в точке $M_3$ и касаются внутри окружности $\Gamma_3$ в точках $M_1$ и $M_2$ соответственно.Пусть $S$ — центр описанной окружности вокруг треугольника $M_1M_2M_3$. Докажите, что прямая $SM_1$ касается окружности $\Gamma_3$.
2010 МО Беларуси А 11.1
Пусть $M$ — точка пересечения диагоналей $AC$ и $BD$ трапеции $ABCD$ ($BC||AD$), $AD>BC$. Окружность $w_1$ проходит через точку $M$ и касается $AD$ в точке $A$. Окружность $w_2$ проходит через точку $M$ и касается $AD$ в точке $D$. Точка $S$ является точкой пересечения прямых $AB$ и $DC$. Прямая $AS$ пересекает $w_1$ в точке $X$. Прямая $DS$ пересекает $w_2$ в точке $Y$. $O$ — центр описанной окружности $\треугольника ASD$. Докажите, что $SO\perp XY$
Прямая $AS$ пересекает $w_1$ в точке $X$. Прямая $DS$ пересекает $w_2$ в точке $Y$. $O$ — центр описанной окружности $\треугольника ASD$. Докажите, что $SO\perp XY$
2010 г. Беларусь МО А 11.6
Пусть $O_1$ и $O_2$ — центры окружностей $w_1,w_2$ соответственно. Окружность $w_1$ пересекает окружность $w_2$ в точках $C$ и $D$. Прямая $O_1O_2$ пересекает окружность $w_2$ в точке $A$. Прямая $DA$ пересекает окружность $w_1$ в точке $S$. Прямая $O_1O_2$ пересекает прямую $SC$ в точке $F$. $E$ является точкой пересечения окружности $w_1$ и описанной окружности $w_3$ $\треугольника ADF$.Докажите, что прямая $O_1E$ касается окружности $w_3$
а) Докажите, что четырехугольник является параллелограммом, если его диагонали и два отрезка, соединяющие середины противоположных сторон, пересекаются в одной точке.
б) Можно ли утверждать, что выпуклость четырехугольника является параллелограммом, если ей соответствует его двуугольник в двух отрезках, соединяющих середины противоположных сторон, все пересекающиеся в одной точке?
2011 МО РБ Д 8. 7
7
На стороне $AB$ треугольника $ABC$ отметим точку $K, L$ так, что $\угол ACK = \угол KCL = \угол LCB$.Точка $M$ лежит на стороне $BC$ так, что $\angle MKC= \angle BKM$. Найдите значения угла $MLC$, если известно, что точка $L$ лежит на биссектрисе угла $KMB$.
На сторонах $AC, BC$ треугольника $ABC$ отмечены точки $A_1 , B_1$ соответственно так, что $A_1B_1 \параллелен AB$. Точки $A_2, B_2$ являются основаниями соответственно перпендикуляров, опущенных из точек $A_1 , B_1$ на сторону $AB$. Докажите, что $AC = AB_2 + CB_1$ тогда и только тогда, когда $BC = BA_2 + CA_1$.
Пусть $P$ — точка пересечения диагоналей вписанного четырехугольника $ABCD$. На биссектрисах углов $APD, BPC$ отмечены точки $K , L$ соответственно такие, что $AP=PK$ и $BP = PL$. Обозначим через $M$ точку пересечения прямых $AK$ и $BL$, а через $N$ пересечение прямых $KD$ и $LC$. Докажите, что прямые $KL$ и $MN$ перпендикулярны.
Точки $M , N$ являются серединами сторон $AC$ , $BC$ треугольника ABC соответственно. Докажите, что окружность, проходящая через точки $C, M$ и $N$, касается стороны $AB$ тогда и только тогда, когда $AB =\frac{AC+BC}{\sqrt2}$
Докажите, что окружность, проходящая через точки $C, M$ и $N$, касается стороны $AB$ тогда и только тогда, когда $AB =\frac{AC+BC}{\sqrt2}$
Точка $M $ — середина стороны $AB$ остроугольного неравнобедренного треугольника $ABC, H$ — ортоцентр этого треугольника, $I$ — центр вписанной в треугольник окружности.2$ отметьте четыре точки $A, B, C, D$, так что четырехугольник $ABCD$ является трапецией ($AD\параллелен BC$, $AD>BC$). Пусть $m, n$ — расстояния от точки пересечения диагоналей этой трапеции до середины ее сторон $AD, BC$ соответственно. Вычислите площадь трапеции $ABCD$.
2011 Беларусь МО А 11.3
Пусть $M$ — середина стороны $AB$ оксигона ${\треугольника ABC}$, точки $P$ и $Q$ — основания высот $AP$ и $BQ$ этого треугольника. Известно, что описанная окружность ${\треугольника BMP}$ касается стороны ${AC}$.Докажите, что описанная окружность ${\triangle AMQ}$ касается прямой ${BC}$.
2011 Беларусь МО А 11.5
Пусть $B$ и $C$ — точки на гиперболе $y=1/x$ $(x>0)$ и абсцисса точки $C$ больше абсциссы точки $B$. Прямая $OA$ ($O$ — начало координат) пересекает гиперболу $y=1/x$ $(x
Прямая $OA$ ($O$ — начало координат) пересекает гиперболу $y=1/x$ $(x
Пусть $I$ — центр вписанной вершины неравнобедренного оксигона $\треугольника ABC$, а $Q$ — точка касания, лежащая на $AB$. Точка $T$ принадлежит стороне $AB$ и $IT||CQ$. Прямая $TK$ касается вписанной окружности в точке $K$ (отличной от точки $Q$) и пересекает прямые $CA$ и $CB$ в точках $L$ и $N$ соответственно.o$, $AN = BC$ (см. рис.). Окружность $\Gamma_1$, вписанная в треугольник $AM N$, касается гипотенузы $AM$ в точке $P$, а окружность $\Gamma_2$, вписанная в треугольник $ABC$, касается катета $BC$ в точке $ Q$. Докажите, что отрезок $PQ$, гипотенуза $AB$ и отрезок, соединяющий центры окружностей $\Gamma_1$ и $\Gamma_2$, пересекаются в одной точке.
В трапеции $ABCD$ ($BC\параллельно AD$) диагональ $CA$ является биссектрисой угла $BCD, CD = AO$ и $BC = OD$, где $O$ – точка пересечения диагоналей.2$.
В четырехугольнике $ABCD$ проведена диагональ $BD$. Найдите максимально возможное значение площади этого четырехугольника, если длина ломаной $ABDC$ равна $L$.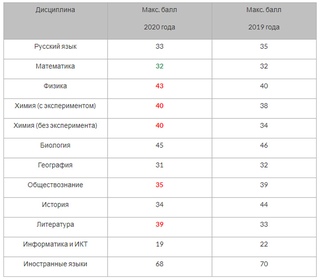
В остроугольном $\varтреугольнике ABC$ на сторонах $AB$ и $AC$ наружу квадраты с центрами $C_1$ и $B_1$ соответственно. Квадрат $C_1B_1DE$ построен на отрезке $C_1B_1$ так, что точки $A$ и $D$ лежат в разных полуплоскостях относительно $C_1B_1$. Докажите, что центр квадрата $C_1B_1DE$ лежит на $BC$.
Некоторые три стороны четырехугольника имеют длины $2, 7$ и $11$. Найдите площадь этого четырехугольника, если известно, что он имеет наибольшую площадь среди всех четырехугольников с указанными сторонами.
2012 Беларусь МО А 11.1
Пусть $AB$ и $CD$ — две параллельные хорды на гиперболе $y=1/x$. Прямые $AC$ и $BD$ пересекают ось $Oy$ в точках $A_1$ и $D_1$ соответственно, а ось $Ox$ — в точках $C_1$ и $B_1$ соответственно. Докажите, что площадь $\треугольника A_1OC_1$ равна площади $\треугольника D_1OB_1$
2012 г. Беларусь МО А 11.6
Пусть точка $I$ — центр вписанной части $\треугольника ABC$. Луч $AI$ пересекает описанную окружность $\треугольника ABC$ в точке $D$. Окружность $\треугольника CDI$ пересекает луч $BI$ в точках $I$ и $K$. Докажите, что $BK=CK$.
Окружность $\треугольника CDI$ пересекает луч $BI$ в точках $I$ и $K$. Докажите, что $BK=CK$.
На сторонах $AD,AB$ и $BC$ прямоугольника $ABCD$ отмечены
точки $X,Y$ и $Z$ соответственно. Для $AX=CZ$ докажите $XY+YZ \ge AC$.
Пусть $H$ является точкой пересечения высот $AA_1, BB_1, CC_1$ остроугольного треугольника $ABC$. Пусть $M$ и $N$ — середины отрезков $BC$ и $AH$ соответственно.Докажите, что $MN$ — серединный перпендикуляр к отрезку $B_1C_1$.
На сторонах $AC$ и $BC$ треугольника $ABC$ отмечены точки $B_1$ и $A_1$ соответственно. Пусть $X$ — точка пересечения отрезков $AA_1$ и $BB_1$. Пусть $x,y$ и $z$ — площади треугольников $B_1CA_1, B_1XA_1$ и $AXB$ соответственно (см. рис.). Докажите, что:
а) $y б) $y График гиперболы $y =\frac{1}{x}$ построен на декартовой плоскости $Oxy$.Три улитки одновременно стартуют из начала координат $O$ и движутся вдоль оси абсцисс $Ox$ (каждая улитка имеет свою постоянную скорость)! Пусть $A(t)$, $B(t)$ и $C(t)$ — точки на графике гиперболы, абсциссы которых равны абсциссам первой, второй и третьей улиток в точке момента $t$ соответственно. Докажите, что площадь треугольника $ABC$ не зависит от времени. На сторонах $AD,AB$ и $BC$ параллелограмма $ABCD$ отмечены точки $X,Y$ и $Z$ соответственно.Известно, что $AX=CZ$. а) Докажите, что выполняется хотя бы одно из неравенств: $XY+YZ \ge AC$ или $XY+YZ \ge BD$. б) Верно ли, что $XY+YZ \ge \frac{AC +BD}{2}$ ? На сторонах $AC$ и $BC$ треугольника $ABC$ отмечены точки $B_1$ и $A_1$ соответственно. Пусть $X$ — точка пересечения отрезков $AA_1$ и $BB_1$. Пусть $x,y$ и $z$ — площади треугольников $B_1CA_1, B_1XA_1$ и $AXB$ соответственно (см. рис.). Найдите площадь треугольника $ABC$.2$ нарисован на декартовой плоскости $Oxy$. Вершины треугольника $ABC$ принадлежат параболе. Медиана треугольника $BM$ параллельна оси ординат и равна $2$. Найдите площадь треугольника $ABC$. Дан треугольник $ABC$ с $AB = c, BC = a, CA = b$. Пары точек $C_1$ и $C_2, A_1$ и $A_2, B_1$ и $B_2$ отмечены на сторонах $AB, BC, CA$ соответственно так, что выполняются следующие равенства: $\frac{CA_1 }{a}=\frac{CB_2}{b}=\frac{a+b}{a+b+c}$, $\frac{AB_1}{b}=\frac{AC_2}{c}=\ frac{b+c}{a+b+c}$, $ \frac{BC_1}{c}=\frac{BA_2}{a}=\frac{a+c}{a+b+c}. Углы при вершинах $A$ и $C$ выпуклого четырехугольника $ABCD$ не острые. На сторонах $AB, BC, CD$ и $DA$ отмечены точки $K, L, M$ и $N$ соответственно. Докажите, что периметр $KLMN$ не меньше удвоенной длины диагонали $AC$. На сторонах $AB, BC$ и $CA$ треугольника $ABC$ отмечены точки $C_1, A_1$ и $B_1$ так, что отрезки $AA_1, BB_1$ и $CC_1$ пересекаются (см. рис.). Известно, что площадь белой части треугольника $ABC$ равна площади его черной части. Докажите, что хотя бы один из отрезков $AA_1, BB_1, CC_1$ является медианой треугольника $ABC$. 2015 Классы D 8. C.9 B.10 нет в наличии 2015 г. Беларусь МО А 11.1 год 2016 отсутствует Пусть M — середина гипотенузы $AB$ прямоугольного треугольника $ABC$.о$. Пусть $K, L$ и $N$ — середины отрезков $BC, AM$ и $DM$ соответственно. Найдите значение угла $LKN$. Дан выпуклый шестиугольник $H$ с тупыми внутренними углами и попарно параллельными противоположными сторонами. а) Докажите, что существует пара противоположных сторон $H$, обладающая следующим свойством; существует прямая, перпендикулярная этим сторонам и пересекающая каждую из них. б) Верно ли, что существуют две пары противоположных сторон $H$ , каждая из которых обладает одним и тем же свойством, описанным в пункте а) ? В равнобедренном треугольнике $ABC$ с $AB= BC$ точки $K$ и $M$ являются серединами сторон $AB$ и $AC$ соответственно.Описанная окружность треугольника $CKB$ пересекает прямую $BM$ в точке $N$, отличной от $M$. Прямая, проходящая через $N$ параллельно стороне $AC$, пересекает описанную окружность треугольника $ABC$ в точках $A_1$ и $C_1$. Точки $K$ и $M$ являются серединами сторон $AB$ и $AC$ треугольника $ABC$ соответственно. Равносторонние треугольники $AMN$ и $BKL$ построены на сторонах $AM$ и $BK$ вне треугольника $ABC$.Точка $F$ является серединой отрезка $LN$. Найдите значение угла $KFM$. Дан выпуклый $2n$-угольник $H$ с попарно параллельными противоположными сторонами. а) Докажите, что: существует пара противоположных сторон $H$, обладающая следующим свойством: существует прямая, перпендикулярная этим сторонам и пересекающая каждую из них. б) Существуют ли такие значения $n$, что для выпуклого $2n$-угольника существуют две пары его противоположных сторон, для каждой из которых выполнено свойство, описанное в а)? На стороне $AB$ треугольника $ABC$ отмечена точка $D$.2-a$ пересекает правую ветвь гиперболы $y = 1/x$ в точке $A$, а левую — в точках $B$ и $C$. a ) Найдите все возможные значения a, если треугольник $ABC$ прямоугольный, b) Найдите площадь этого прямоугольного треугольника для всех возможных значений $a$. 2017 Белорусское МО Б 10.6Пусть $AA_1, BB_1$ и $CC_1$ — высоты остроугольного треугольника $ABC$ ($A_1\in BG, B_1\in CA$ и $C_1\in AB$). Пусть $J_a, J_b$ и $J_c$ — центры вписанных окружностей треугольников $AC_1B_1, BA_1C_1$ и $CB_1A_1$ соответственно.Докажите, что ортоцентр треугольника $J_aJ_bJ_c$ совпадает с центром вписанной стороны треугольника $ABC$. 2017 Беларусь МО А 11.2 2017 Беларусь МО А 11.6 Пусть $ABCD$ — вписанный четырехугольник с описанной окружностью $\omega$ . В параллелограмме $ABCD$ $(AB//CD)$ сторона $AB$ равна половине длины стороны $BC$. Биссектриса угла $ABC$ пересекает сторону $AD$ в точке $K$ и диагональ $AC$ в точке $L$. Биссектриса угла $ADC$ пересекает продолжение стороны $AB$ за точку $B$ в точке $M$. Прямая $ML$ пересекает сторону $AD$ в точке $F$. Найдите отношение $AF:AD$. 2018 Белорусское МО C 9.3 2018 Беларусь MO C 9.7 2018 Белорусское МО Б 10.7 Квадрат $A_1B_1C_1D_1$ вписан в прямоугольный треугольник $ABC$ (при $C=90$) так, что точки $A_1$, $B_1$ лежат на катетах $CB$ и $CA$ соответственно, а точки $C_1$, $D_1$ лежат на гипотенузе $AB$. Описанные окружности треугольников $B_1A_1C$ и $AC_1B_1$ пересекаются в точках $B_1$ и $Y$.Докажите, что прямые $A_1X$ и $B_1Y$ пересекаются на гипотенузе $AB$. 2018 Беларусь МО А 11.2 2018 Белоруссия МО А 11.5 2018 Беларусь МО А 11.6 2019 г. класс Д 8. отсутствует 2019 г. Беларусь МО С 9.2 (С. Мазаник) 2019 Беларусь МО C 9.6 (А. Войделевич) 2019 Белорусское МО Б 10.2 (А. Войделевич) 2019 Белорусское МО Б 10.8
(И. Городнин) 2019 Беларусь МО А 11.4
(А. Войделевич) 2019 Беларусь МО А 11.6
(А. Нарадзецкий) 90 000 пассажиров вспоминают, какой страх охватил журналиста-диссидента, когда их рейс был изменен. Столы-подносы поднимались, а спинки сидений возвращались в вертикальное положение, пока пассажиры рейса 4978 Ryanair готовились к запланированной посадке в столице Литвы Вильнюсе. Затем внезапно самолет сделал резкий разворот. Объяснений не было. Прошло примерно 15 минут, прежде чем пилот вышел по интеркому и объявил, что самолет направляется в Минск, столицу Беларуси, по словам тех, кто был на борту. Многим пассажирам поначалу казалось, что это, скорее всего, просто одна из тех неожиданных задержек, которые могут быть частью авиаперелетов — возможно, техническая проблема, как предполагали некоторые. Однако для одного пассажира ситуация была ясной. И пугающий. Роман Протасевич, известный белорусский оппозиционный журналист, с 2019 года живущий в эмиграции, начал паниковать. «Он запаниковал, потому что мы собирались приземлиться в Минске», — сказал по прибытии в Вильнюс литовской телекомпании LRT Мариус Руткаускас, сидевший на один ряд впереди г-на Протасевича. Саулюс Данаускас, пассажир, который разговаривал с новостным сайтом Delfi, благополучно прибыв в Вильнюс, сказал, что ему быстро стало ясно, что идея о бомбе была всего лишь уловкой. «Когда мы приземлились, люди стояли вокруг самолета, ничего не делая, и выглядели довольными собой», — сказал мистер Уайт.— сказал Данаускас. «Полчаса нас не выпускали», — добавил он. «Если в самолете была бомба, почему нас не выпустили?» Пассажирам в конце концов приказали спускаться группами по пять человек со своим багажом, который был тщательно проверен сотрудниками службы безопасности. Багаж господина Протасевича проверен дважды, пассажиры отозваны. Затем сотрудник службы безопасности препроводил его к терминалу, где он был арестован. Большинство остальных пассажиров три часа простояли в темном коридоре.Некоторым пришлось стоять со своими детьми. Под охраной силовиков у них не было доступа к еде, воде и туалету. Оглядываясь назад, пассажиры отмечали, как все это было странно. Мантас, пассажир самолета, сообщил литовскому новостному сайту, что пилот «явно нервничал» во время посадки в Минске. Алена Алымова, одна из пассажиров, написала об этом опыте в посте в Facebook, отметив, что большую часть времени было только «легкое беспокойство». «Не было четкого понимания, что происходит», — написала она. Некоторые пассажиры узнали об угрозе взрыва только через несколько часов, когда они смогли подключиться к Интернету. В своем посте в Instagram один из пассажиров сказал, что с ним «обращались как с заключенными в Минске». Через несколько часов им разрешили пройти в холл аэропорта с небольшой столовой. «Я хочу посмотреть, кто будет нести ответственность за этот хаос», — сказала она.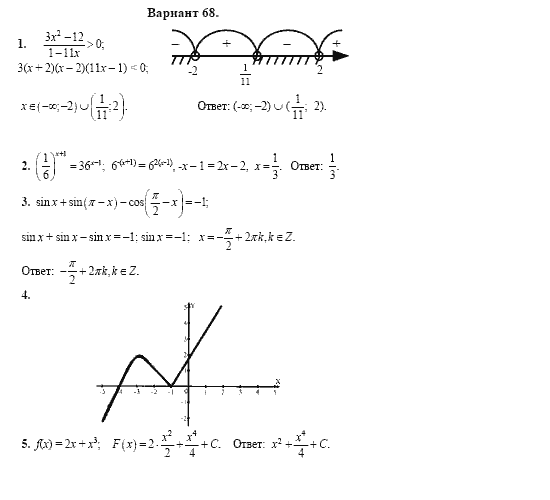
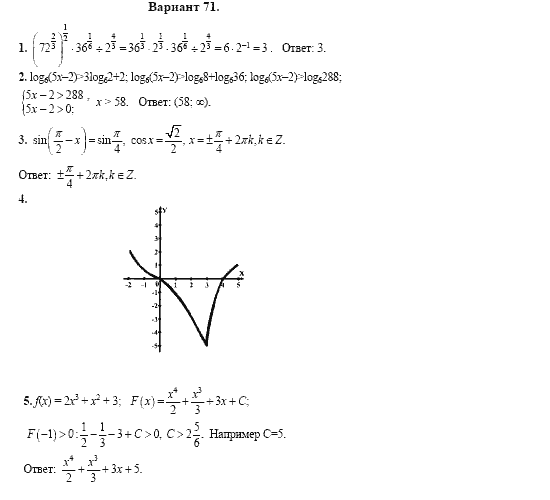 2$ такой, что прямая $AB \параллельна$ оси $Ox$.Также точка $C$ ближе к оси $Ox$, чем прямая $AB$. Учитывая, что длина отрезка $AB$ на 1 меньше длины высоты $CH$ (треугольника $ABC$). Определить угол $\angle{ACB}$ .
2$ такой, что прямая $AB \параллельна$ оси $Ox$.Также точка $C$ ближе к оси $Ox$, чем прямая $AB$. Учитывая, что длина отрезка $AB$ на 1 меньше длины высоты $CH$ (треугольника $ABC$). Определить угол $\angle{ACB}$ .
Прямая пересекает гиперболу $H_1$, заданную уравнением $y=1/x$, в точках $A$ и $B$, и гиперболу $H_2$, заданную уравнением $y=-1/x$, в точках $C. $ и $D$. Касательные к гиперболе $H_1$ в точках $A$ и $B$ пересекаются в точке $M$, а касательные к гиперболе $H_2$ в точках $C$ и $D$ пересекаются в точке $N$.Докажите, что точки $M$ и $N$ симметричны относительно начала координат.
$ и $D$. Касательные к гиперболе $H_1$ в точках $A$ и $B$ пересекаются в точке $M$, а касательные к гиперболе $H_2$ в точках $C$ и $D$ пересекаются в точке $N$.Докажите, что точки $M$ и $N$ симметричны относительно начала координат.
2015 г. Беларусь МО А 11.3
Пусть $A_1$ — середина треугольника $BC$, а $G$ — центр тяжести неравнобедренного треугольника $\треугольника ABC$. $GBKL$ и $GCMN$ — квадраты, лежащие слева относительно лучей $GB$ и $GC$ соответственно. Пусть $A_2$ — середина отрезка, соединяющего центры квадратов $GBKL$ и $GCMN$. Окружность треугольника $\треугольника A_{1}A_{2}G$ пересекает $BC$ в точках $A_1$ и $X$. Найдите $\frac{A_{1}X}{XH}$, где $H$ — основание высоты $AH$ треугольника $\triangle ABC$.
2015 г. Беларусь МО А 11.7
Пусть $I$ — центр вписанной вершины треугольника $\треугольника ABC$. Точки $A_1, B_1, C_1$ являются точками касания вписанной окружности со сторонами $BC$, $CA$ и $AB$ соответственно. Окружность $\треугольника BC_1B_1$ пересекает прямую $BC$ в точках $B$ и $K$, а описанная окружность $\треугольника CB_1C_1$ пересекает прямую $BC$ в точках $C$ и $L$.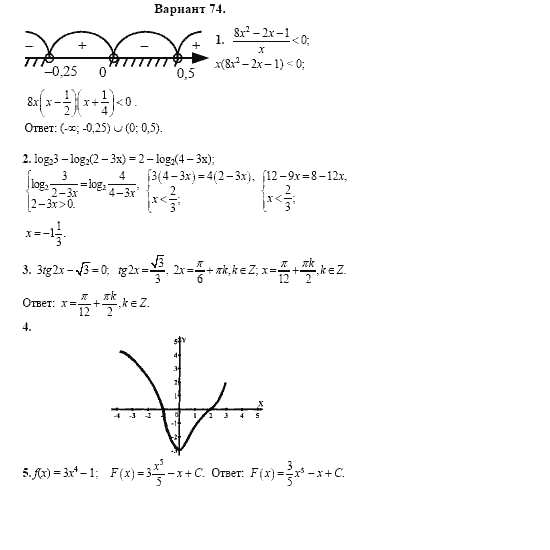 Докажите, что строки $LC_1$, $KB_1$ и $IA_1$ параллельны.
Докажите, что строки $LC_1$, $KB_1$ и $IA_1$ параллельны.  Докажите, что треугольник $A_1BC_1$ равносторонний.
Докажите, что треугольник $A_1BC_1$ равносторонний. 
Пусть $M$ — середина стороны $BC$ треугольника $ABC$. Крикумокружность $ABM$ пересекает отрезок $AC$ в точках $A$ и $B_1$ ($B_1 \neq A$). Окружность, описанная вокруг $AMC$, пересекает отрезок $AB$ в точках $A$ и $C_1$ ($C_1 \neq A$). Пусть $O$ — описанная окружность $AC_1B_1$. Докажите, что $OB=OC$
Пусть $AA_1, BB_1, CC_1$ — высоты остроугольного треугольника $ABC$ ($A_1 \in BC, B_1 \in AC, C_1 \in AB$).Пусть $J_a, J_b, J_c$ — центры вписанных окружностей $AC_1B_1$, $BA_1C_1$ и $CB_1A_1$ соответственно. Докажите, что радиус описанной окружности треугольника $J_aJ_bJ_c$ равен радиусу вписанной окружности треугольника $ABC$  Точки $B_1$ и $D_1$ симметричны $A$ относительно середины точек $BC$ и $CD$. Окружность, описанная вокруг треугольника $CB_1D_1$, пересекает $\omega$ в точках $C$ и $G$. Докажите, что $AG$ — это диаметр $\omega$ .
Точки $B_1$ и $D_1$ симметричны $A$ относительно середины точек $BC$ и $CD$. Окружность, описанная вокруг треугольника $CB_1D_1$, пересекает $\omega$ в точках $C$ и $G$. Докажите, что $AG$ — это диаметр $\omega$ .
Биссектриса угла $CAB$ треугольника $ABC$ пересекает сторону $CB$ в точке $L$. Точка $D$ — основание перпендикуляра из $C$ в $AL$, а точка $E$ — основание перпендикуляра из $L$ в $AB$.2$. Известно, что угол $BAD=90$, диоганаль $AC$ параллельна оси $Ox$ и $AC$ является биссектрисой угла BAD. Найдите площадь четырехугольника $ABCD$, если длина диоганала $BD$ равна $p$.
Внутри треугольника $ABC$ выбрана точка $O$ так, что длины отрезков $OA$, $OB$ и $OC$ равны $15$, $12$ и $20$, соответственно. Известно, что основания перпендикуляров из $O$ к сторонам треугольника $ABC$ являются вершинами равностороннего треугольника.2$. Известно, что $ABCD$ вписана в окружность и $AC$ является диаметром описанной ею окружности. Пусть $M$ и $N$ — середины диагоналей $AC$ и $BD$ соответственно. Найдите длину проекции отрезка $MN$ на ось $Oy$.
Известно, что основания перпендикуляров из $O$ к сторонам треугольника $ABC$ являются вершинами равностороннего треугольника.2$. Известно, что $ABCD$ вписана в окружность и $AC$ является диаметром описанной ею окружности. Пусть $M$ и $N$ — середины диагоналей $AC$ и $BD$ соответственно. Найдите длину проекции отрезка $MN$ на ось $Oy$.
В остроугольном треугольнике $ABC$ проведены высоты $AA_1$, $BB_1$ и $CC_1$. Биссектриса угла $AA_1C$ пересекает отрезки $CC_1$ и $CA$ в точках $E$ и $D$ соответственно. Биссектриса угла $AA_1B$ пересекает отрезки $BB_1$ и $BA$ в точках $F$ и $G$ соответственно. {\circ}$.
{\circ}$.
Окружность $S_1$ пересекает гиперболу $y=\frac1x$ в четырех точках $A$, $B$, $C$ и $D$, а другая окружность $S_2$ пересекает одна и та же гипербола в четырех точках $A$, $B$, $F$ и $G$. Известно, что радиусы окружностей $S_1$ и $S_2$ равны. Докажите, что точки $C$, $D$, $F$ и $G$ являются вершинами параллелограмма.
Точка $X$ отмечена внутри треугольника $ABC$. Описанные окружности треугольников $AXB$ и $AXC$ пересекают сторону $BC$ еще раз в точках $D$ и $E$ соответственно.Прямая $DX$ пересекает сторону $AC$ в точке $K$, а прямая $EX$ пересекает сторону $AB$ в точке $L$. Докажите, что $LK\параллельно BC$.
Дан ромб $ABCD$. Пусть $E$ — одна из точек пересечения окружностей $\Gamma_B$ и $\Gamma_C$, где $\Gamma_B$ — окружность с центром в $B$, проходящая через $C$, а $\Gamma_C$ — окружность с центром в точке $C$ проходит через точку $B$. Прямая $ED$ пересекает $\Gamma_B$ в точке $F$.Найдите значение угла $\угол AFB$.
Точка $M$ является серединой стороны $BC$ треугольника $ABC$. Окружность проходит через $B$, касается прямой $AM$ в точке $M$ и пересекает отрезок $AB$ побочно в точке $P$.
Докажите, что окружность, проходящая через точки $A$, $P$ и середину отрезка $AM$, касается прямой $AC$.
Точка $P$ выбрана внутри стороны $BC$ треугольника $ABC$.Точки $D$ и $C$ симметричны $P$ относительно вершин $B$ и $C$ соответственно. Описанные окружности треугольников $ABE$ и $ACD$ пересекаются в точках $A$ и $X$. Луч $AB$ пересекает отрезок $XD$ в точке $C_1$, а луч $AC$ пересекает отрезок $XE$ в точке $B_1$. Докажите, что прямые $BC$ и $B_1C_1$ параллельны.
Касательные описанной окружности остроугольного треугольника $ABC$, проходящие через $B$ и $C$, пересекаются в точке $F$. 2-a$ и гипербола $y=1/x$ пересекаются в трех разных точках.
2-a$ и гипербола $y=1/x$ пересекаются в трех разных точках.
б) Найдите геометрическое место центров описанных окружностей таких троек точек пересечения, когда $a$ принимает все возможные значения.
В остроугольном треугольнике $ABC$ проведены высоты $CC_1$ и $BB_1$. Биссектрисы углов $\angle BB_1C$ и $\angle CC_1B$ пересекают прямую $BC$ в точках $D$ и $E$ соответственно и пересекаются в точке $X$. Докажите, что точки пересечения описанных окружностей треугольников $BEX$ и $CDX$ лежат на прямой $AX$.
Диагонали вписанного четырехугольника $ABCD$ пересекаются в точке $O$. Точки $P$, $Q$, $R$ и $S$ являются основаниями перпендикуляров из $O$ к сторонам $AB$, $BC$, $CD$ и $DA$ соответственно. Докажите неравенство $BD\ge SP+QR$. 
 «Он сказал: «Я знаю, что в Беларуси меня ждет смертная казнь».Опасения Протасевича казались более реальными, чем когда-либо. Самолет окружили чиновники советского вида в зеленой форме, а также собаки, пожарные и технические работники аэропорта.
«Он сказал: «Я знаю, что в Беларуси меня ждет смертная казнь».Опасения Протасевича казались более реальными, чем когда-либо. Самолет окружили чиновники советского вида в зеленой форме, а также собаки, пожарные и технические работники аэропорта. 

Национальные и международные олимпиады и соревнования Детали экзамена
Спасибо
Вы успешно подписались на уведомления и обновления через WhatsApp.
Вы уже подписаны на нас.
ИНДИЯ (+91)АФГАНИСТАН (+93)АЛБАНИЯ (+355)АЛЖИР (+213)АМЕРИКАНСКАЯ САМОА (+1684)АНДОРРА (+376)АНГОЛА (+244)АНГИЛЬЯ (+1264)АНТАРКТИДА (+672)АНТИГУА И БАРБУДА (+ 1268)АРГЕНТИНА (+54)АРМЕНИЯ (+374)АРУБА (+297)АВСТРАЛИЯ (+61)АВСТРИЯ (+43)АЗЕРБАЙДЖАН (+994)БАГАМСКИЕ ОСТРОВА (+1242)БАХРЕЙН (+973)БАНГЛАДЕШ (+880)БАРБАДОС (+ 1246)БЕЛАРУСИ (+375)БЕЛЬГИЯ (+32)БЕЛИЗ (+501)БЕНИН (+229)БЕРМУДСКИЕ ОСТРОВА (+1441)БУТАН (+975)БОЛИВИЯ, МНОГОНАЦИОНАЛЬНОЕ ГОСУДАРСТВО БОЛИВИЯ (+591)БОСНИЯ И ГЕРЦЕГОВИНА (+387)БОТСВАНА (+267)ОСТРОВ БУВЕ (+55)БРАЗИЛИЯ (+55)БРИТАНСКАЯ ТЕРРИТОРИЯ В ИНДИЙСКОМ ОКЕАНЕ (+246)БРУНЕЙ-ДАРУССАЛАМ (+673)БОЛГАРИЯ (+359)БУРКИНА-ФАСО (+226)БУРУНДИ (+257)КАМБОДЖА (+855) КАМЕРУН (+237)КАНАДА (+1)КАБО-ВЕРДЕ (+238)КАЙМАНОВЫ ОСТРОВА (+1345)ЦЕНТРАЛЬНОАФРИКАНСКАЯ РЕСПУБЛИКА (+236)ЧАД (+235)ЧИЛИ (+56)КИТАЙ (+86)ОСТРОВ РОЖДЕСТВА (+61) КОКОСОВЫЕ ОСТРОВА (КИЛИНГ) (+61)КОЛУМБИЯ (+57)КОМОРСКИЕ ОСТРОВА (+269)КОНГО (+242)КОНГО, ДЕМОКРАТИЧЕСКАЯ РЕСПУБЛИКА (+243)ОСТРОВА КУКА (+682)КОСТА-РИКА (+506)КОТ-Д’ ИВУАР (+225)ХОРВАТИЯ (+385)КУБА (+53)КИПР (+357)ЧЕХИЯ РЕСПУБЛИКА (+420)ДАНИЯ (+45)ДЖИБУТИ (+253)ДОМИНИКА (+1767)ДОМИНИКАНСКАЯ РЕСПУБЛИКА (+1849)ЭКВАДОР (+593)ЕГИПЕТ (+20)ЭЛЬ-САЛЬВАДОР (+503)ЭКВАТОРИАЛЬНАЯ ГВИНЕЯ (+240)ЭРИТРЕЯ ( +291)ЭСТОНИЯ (+372)ЭФИОПИЯ (+251)ФОЛКЛЕНДСКИЕ ОСТРОВА (МАЛЬВИНСКИЕ) (+500)ФАРЕРСКИЕ ОСТРОВА (+298)ФИДЖИ (+679)ФИНЛЯНДИЯ (+358)ФРАНЦИЯ (+33)ФРАНЦУЗСКАЯ ГВИАНА (+594)ФРАНЦУЗСКАЯ ПОЛИНЕЗИЯ (+689)ФРАНЦУЗСКИЕ ЮЖНЫЕ И АНТАРКТИЧЕСКИЕ ЗЕМЛИ (+262)ГАБОН (+241)ГАМБИЯ (+220)ГРУЗИЯ (+995)ГЕРМАНИЯ (+49)ГАНА (+233)ГИБРАЛТАР (+350)ГРЕЦИЯ (+30)ГРЕНЛАНДИЯ (+299)ГРЕНАДА (+1473)ГВАДЕЛУПА (+590)ГУАМ (+1671)ГВАТЕМАЛА (+502)ГЕРНСИ (+44)ГВИНЕЯ (+224)ГВИНЕЯ-БИСАУ (+245)ГАЙАНА (+592)ГАИТИ (+509) )ОСТРОВ ХЕРД И ОСТРОВА МАКДОНАЛД (+672)СВЯТОЙ ПРЕСТОЛ (ВАТИКАН-ГОСУДАРСТВО) (+379)ГОНДУРАС (+504)ГОНКОНГ (+852)ВЕНГРИЯ (+36)ИСЛАНДИЯ (+354)ИНДОНЕЗИЯ (+62)ИРАН, ИСЛАМСКАЯ РЕСПУБЛИКА (+98)ИРАК (+964)ИРЛАНДИЯ (+353)ОСТРОВ МЕН (+44)ИЗРАИЛЬ (+972)ИТАЛИЯ (+39)ЯМАЙКА (+1876)ЯПОНИЯ (+81)ДЖЕРСИ (+44)ИОРДАНИЯ ( +962)КАЗАХСТАН (+7)КЕНИЯ (+254)КИРИБАТИ (+686)КОРЕЯ, НАРОДНО-ДЕМОКРАТИЧЕСКАЯ РЕСПУБЛИКА (+850)КОРЕЯ , РЕСПУБЛИКА (+82)КУВЕЙТ (+965)КЫРГЫЗСТАН (+996)ЛАОССКАЯ НАРОДНО-ДЕМОКРАТИЧЕСКАЯ РЕСПУБЛИКА (+856)ЛАТВИЯ (+371)ЛИВАН (+961)ЛЕСОТО (+266)ЛИБЕРИЯ (+231)ЛИВИЙСКАЯ АРАБСКАЯ ДЖАМАХИРИЯ (+ 218)ЛИХТЕНШТЕЙН (+423)ЛИТВА (+370)ЛЮКСЕМБУРГ (+352)МАКАО (+853)МАКАДОНИЯ, БЫВШАЯ ЮГОСЛАВСКАЯ РЕСПУБЛИКА (+389)МАДАГАСКАР (+261)МАЛАВИ (+265)МАЛАЙЗИЯ (+60)МАЛЬДИВЫ ( +960)МАЛИ (+223)МАЛЬТА (+356)МАРШАЛЛОВЫ ОСТРОВА (+692)Мартиника (+596)МАВРИТАНИЯ (+222)МАВРИКИЙ (+230)МАЙОТТА (+262)МЕКСИКА (+52)МИКРОНЕЗИЯ, ФЕДЕРАТИВНЫЕ ШТАТЫ ( +691)МОЛДОВА, РЕСПУБЛИКА (+373)МОНАКО (+377)МОНГОЛИЯ (+976)ЧЕРНОГОРИЯ (+382)МОНТСЕРРАТ (+1664)МАРОККО (+212)МОЗАМБИК (+258)МЬЯНМА (+95)НАМИБИЯ (+264) )НАУРУ (+674)НЕПАЛ (+977)НИДЕРЛАНДЫ (+31)НИДЕРЛАНДСКИЕ АНТИЛЬСКИЕ ОСТРОВА (+599)НОВАЯ КАЛЕДОНИЯ (+687)НОВАЯ ЗЕЛАНДИЯ (+64)НИКАРАГУА (+505)НИГЕР (+227)НИГЕРИЯ (+234)NIUE (+683)ОСТРОВ НОРФОЛК (+672)СЕВЕРНЫЕ МАРИЙСКИЕ ОСТРОВА (+1670)НОРВЕГИЯ (+47)ОМАН (+968)ПАКИСТАН (+92)ПАЛАУ (+680)ПАЛЕСТИНСКАЯ ТЕРРИТОРИЯ, ОККУПИРОВАННАЯ (+970)ПАНАМА (+507) ПАПУА-НОВАЯ ГВИНЕЯ (+675)ПАРАГВАЙ (+59 5)ПЕРУ (+51)ФИЛИППИНЫ (+63)ПИТКЭРН (+870)ПОЛЬША (+48)ПОРТУГАЛИЯ (+351)ПУЭРТО-РИКО (+1939)КАТАР (+974)РЕЮНИОН (+262)РУМЫНИЯ (+40)РОССИЯ ( +7)РУАНДА (+250)СВЯТАЯ ЕЛЕНА, ВОЗНЕСЕНИЕ И ТРИСТАН-ДА КУНЬЯ (+290)СЕНТ-КИТС И НЕВИС (+1869)СЕНТ-ЛЮСИЯ (+1758)СЕНТ-ПЬЕР И МИКЕЛЬОН (+508)СЕНТ-ВИНСЕНТ И ГРЕНАДИНЫ (+1784) )САМОА (+685)САН-МАРИНО (+378)САО-ТОМЕ И ПРИНСИПИ (+239)САУДОВСКАЯ АРАВИЯ (+966)СЕНЕГАЛ (+221)СЕРБИЯ (+381)СЕЙШЕЛЬСКИЕ ОСТРОВА (+248)СЬЕРРА-ЛЕОНЕ (+232)СИНГАПУР (+ 65)СЛОВАКИЯ (+421)СЛОВЕНИЯ (+386)СОЛОМОНОВЫ ОСТРОВА (+677)СОМАЛИ (+252)ЮЖНАЯ АФРИКА (+27)ЮЖНАЯ ГРУЗИЯ И ЮЖНЫЕ САНДВИЧНЫЕ ОСТРОВА (+500)ИСПАНИЯ (+34)ШРИ-ЛАНКА (+94) )СУДАН (+249)СУРИНАМ (+597)ШВЕЙБАРД И ЯН-МАЙЕН (+47)СВАЗИЛЕНД (+268)ШВЕЦИЯ (+46)ШВЕЙЦАРИЯ (+41)СИРИЙСКАЯ АРАБСКАЯ РЕСПУБЛИКА (+963)ТАЙВАНЬ (+886)ТАДЖИКИСТАН (+992) )ТАНЗАНИЯ, ОБЪЕДИНЕННАЯ РЕСПУБЛИКА (+255)ТАИЛАНД (+66)ТИМОР-ЛЕСТИ (+670)ТОГО (+228)ТОКЕЛАУ (+690)ТОНГА (+676)ТРИНИДАД И ТОБАГО (+1868)ТУНИС (+216)ТУРЦИЯ (+90)ТУРКМЕНИСТАН (+993)ОСТРОВА ТЕРКС И КАЙКОС (+1 649)ТУВАЛУ (+688)УГАНДА (+256)УКРАИНА (+380)ОБЪЕДИНЕННЫЕ АРАБСКИЕ ЭМИРАТЫ (+971)СОЕДИНЕННОЕ КОРОЛЕВСТВО (+44)СОЕДИНЕННЫЕ ШТАТЫ (+1)МАЛЫЕ ОСТРОВА СОЕДИНЕННЫХ ШТАТОВ (+1581)УРУГВАЙ (+598) УЗБЕКИСТАН (+998)ВАНУАТУ (+678)ВЕНЕСУЭЛА, БОЛИВАРИАНСКАЯ РЕСПУБЛИКА (+58)ВЬЕТНАМ (+84)ВИРГИНСКИЕ ОСТРОВА, БРИТАНСКИЙ (+1284)ВИРГИНСКИЕ ОСТРОВА, U.
Пожалуйста, введите свой номер телефона
Всероссийская олимпиада по математике. Олимпиадное движение в бывшем Советском Союзе изначально было городским, и в 1934 году его возглавил Ленинград, а в 1935 году — Москва.Иннополис — новый российский город, расположенный в Республике Татарстан. Математическая олимпиада. Вопросы для 3 класса. Три часа волшебника – Всероссийская математическая олимпиада. Каждая задача оценивается в определенное количество баллов, всего 100 баллов. Найдите значение a2 + ab + b2. Он содержит 25 задач по математике. Получите бесплатные задачи с Московской математической олимпиады по математике, … Для получения дополнительной административной информации (включая заявления, перевод кредитов, вступительные экзамены, регистрацию на курсы и т. д.(Экзамен Патнэма 1968 г.) Определите все многочлены, все коэффициенты которых равны ±1 и имеют только действительные корни. MH08-1110-139563 4 5. Пошаговые решения всех проблем; Подсказки, стратегии и проценты верны для всех вопросов; Множественные решения для большинства задач. Математическая олимпиада. Задачи, том 3. ТЕГЕРАН, сентябрь. Но повторно она не проводилась. Международная математическая олимпиада (ИМО) — это чемпионат мира по математике среди старшеклассников, который ежегодно проводится в другой стране.Выражаем глубочайшую признательность Vol. Задача 3 адаптирована Сойфером из русского математического фольклора. Более 100 стран, представляющих более 90% населения мира, отправляют команды до шести учеников, плюс один… Международная Жаутыковская олимпиада по математике, физике и информатике впервые была проведена в 2005 году, в ней приняли участие 189 представителей, в том числе 17 команд. из числа специализированных школ России, Армении, Кыргызстана, Казахстана и Турции. MathOpen Belarus — это ежегодная международная математическая олимпиада для … Задачи 1, 2 и 4 были созданы Александром Сойфером для этой олимпиады.
д.(Экзамен Патнэма 1968 г.) Определите все многочлены, все коэффициенты которых равны ±1 и имеют только действительные корни. MH08-1110-139563 4 5. Пошаговые решения всех проблем; Подсказки, стратегии и проценты верны для всех вопросов; Множественные решения для большинства задач. Математическая олимпиада. Задачи, том 3. ТЕГЕРАН, сентябрь. Но повторно она не проводилась. Международная математическая олимпиада (ИМО) — это чемпионат мира по математике среди старшеклассников, который ежегодно проводится в другой стране.Выражаем глубочайшую признательность Vol. Задача 3 адаптирована Сойфером из русского математического фольклора. Более 100 стран, представляющих более 90% населения мира, отправляют команды до шести учеников, плюс один… Международная Жаутыковская олимпиада по математике, физике и информатике впервые была проведена в 2005 году, в ней приняли участие 189 представителей, в том числе 17 команд. из числа специализированных школ России, Армении, Кыргызстана, Казахстана и Турции. MathOpen Belarus — это ежегодная международная математическая олимпиада для … Задачи 1, 2 и 4 были созданы Александром Сойфером для этой олимпиады. Задачи Всесоюзных математических олимпиад 1961-1986 гг. В этом файле собраны задачи, предложенные для решения на Всероссийских математических олимпиадах (заключительная часть). Поскольку сумма каждой пары делится на 24, сумма всех положительных делителей также делится на 24. Три сегодняшние головоломки — блестящие образцы русского стиля: они проверяют логическое мышление, а не обучают математическим навыкам. Были предприняты усилия, чтобы познакомить вас с ощущениями, потоком, функциями и отчетами о продукте с помощью образцов документов.+7 (977) 868-66-57. В 1992 году он был снова переименован в МО Содружества Независимых Государств, и нумерация возобновилась. Проблемы и решения USAJMO; Примечания. Математические кружки. Кавказская математическая олимпиада 2021 года собирает около 170 участников из России, Болгарии, Казахстана, Перу, Турции, Беларуси, Армении, Узбекистана, Таджикистана и других стран. SOF проводит крупнейшие олимпиады Азии, а именно: Национальную научную олимпиаду (NSO), Национальную киберолимпиаду (NCO), Международную олимпиаду по математике (IMO), Международную олимпиаду по английскому языку (IEO) Нет, мы не покажем вам все 800 =) Но видеоэкскурсии по самые красивые мосты ждут вас каждый день в это время.
Задачи Всесоюзных математических олимпиад 1961-1986 гг. В этом файле собраны задачи, предложенные для решения на Всероссийских математических олимпиадах (заключительная часть). Поскольку сумма каждой пары делится на 24, сумма всех положительных делителей также делится на 24. Три сегодняшние головоломки — блестящие образцы русского стиля: они проверяют логическое мышление, а не обучают математическим навыкам. Были предприняты усилия, чтобы познакомить вас с ощущениями, потоком, функциями и отчетами о продукте с помощью образцов документов.+7 (977) 868-66-57. В 1992 году он был снова переименован в МО Содружества Независимых Государств, и нумерация возобновилась. Проблемы и решения USAJMO; Примечания. Математические кружки. Кавказская математическая олимпиада 2021 года собирает около 170 участников из России, Болгарии, Казахстана, Перу, Турции, Беларуси, Армении, Узбекистана, Таджикистана и других стран. SOF проводит крупнейшие олимпиады Азии, а именно: Национальную научную олимпиаду (NSO), Национальную киберолимпиаду (NCO), Международную олимпиаду по математике (IMO), Международную олимпиаду по английскому языку (IEO) Нет, мы не покажем вам все 800 =) Но видеоэкскурсии по самые красивые мосты ждут вас каждый день в это время. AMC 12 ранее был известен как AHSME. Обзоры 33:2 (1978), 97-154 УМН. Каждая запись M является неотрицательным целым числом. Числа a,b,c таковы, что уравнение x3 +ax2 +bx+c = 0 имеет три действительных корня. Олимпиада должна была пройти в рамках Санкт-Петербургской Всероссийской математической олимпиады «Маэстро Пифагор» 2018-2019 гг. Исходя из этого, фонд Eduheal ежегодно проводит математическую олимпиаду NIMO (Национальная интерактивная олимпиада по математике), чтобы предоставить платформу, на которой учащиеся могут участвовать и использовать свои знания и навыки для решения задач, основанных на применении концепций… Мои собственные: олимпиадная книга по геометрии ЕГМО и ОТИС Выдержки для не геометрии.Первая Всероссийская математическая олимпиада состоялась в 1961 году. Шестая Кавказская математическая олимпиада пройдет 12-17 марта 2021 года в г. Майкопе Республики Адыгея. Мне нравится русская математика, но моему сыну она не доставляет удовольствия. Mathematics_Through_Problems_from_olympiads_and_math_circles_to.
AMC 12 ранее был известен как AHSME. Обзоры 33:2 (1978), 97-154 УМН. Каждая запись M является неотрицательным целым числом. Числа a,b,c таковы, что уравнение x3 +ax2 +bx+c = 0 имеет три действительных корня. Олимпиада должна была пройти в рамках Санкт-Петербургской Всероссийской математической олимпиады «Маэстро Пифагор» 2018-2019 гг. Исходя из этого, фонд Eduheal ежегодно проводит математическую олимпиаду NIMO (Национальная интерактивная олимпиада по математике), чтобы предоставить платформу, на которой учащиеся могут участвовать и использовать свои знания и навыки для решения задач, основанных на применении концепций… Мои собственные: олимпиадная книга по геометрии ЕГМО и ОТИС Выдержки для не геометрии.Первая Всероссийская математическая олимпиада состоялась в 1961 году. Шестая Кавказская математическая олимпиада пройдет 12-17 марта 2021 года в г. Майкопе Республики Адыгея. Мне нравится русская математика, но моему сыну она не доставляет удовольствия. Mathematics_Through_Problems_from_olympiads_and_math_circles_to. Решение: Для n = 3 … Олимпиада по математике. Будьте в курсе различных дат экзаменов по олимпиаде по математике, программы, образцов работ, пробных контрольных работ для учащихся классов 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Вы также можете найти заметки по математике для классов 1-10.Книга по арифметике 1908 года, Книга по арифметике Майерса II, старинная арифметика, старинная книга для начальной школы, книга по математике, книга по элементарной математике, UsefulOldStuff. орг. Существуют ли 14 натуральных чисел, произведение которых при увеличении каждого из них на 1 увеличивается ровно в 2008 раз? 2. ОЛИМПИАДА. По всему миру региональные центры следили за соблюдением правил конкурса. команда, которая участвовала в 11-й ежегодной Китайской математической олимпиаде девочек (CGMO)… Математическая олимпиада проводится с 1959 года, и Израиль впервые присоединился к ней в 1979 году.Восемь американских девочек завоевали золотые, серебряные и бронзовые медали на международных соревнованиях по математике.
Решение: Для n = 3 … Олимпиада по математике. Будьте в курсе различных дат экзаменов по олимпиаде по математике, программы, образцов работ, пробных контрольных работ для учащихся классов 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Вы также можете найти заметки по математике для классов 1-10.Книга по арифметике 1908 года, Книга по арифметике Майерса II, старинная арифметика, старинная книга для начальной школы, книга по математике, книга по элементарной математике, UsefulOldStuff. орг. Существуют ли 14 натуральных чисел, произведение которых при увеличении каждого из них на 1 увеличивается ровно в 2008 раз? 2. ОЛИМПИАДА. По всему миру региональные центры следили за соблюдением правил конкурса. команда, которая участвовала в 11-й ежегодной Китайской математической олимпиаде девочек (CGMO)… Математическая олимпиада проводится с 1959 года, и Израиль впервые присоединился к ней в 1979 году.Восемь американских девочек завоевали золотые, серебряные и бронзовые медали на международных соревнованиях по математике. АОПС. Добавить в избранное. Российская математическая олимпиада. ТЕГЕРАН, июль Петербург, Россия в июле 2020 года, но из-за … математической индукции для всех натуральных k мы имеем /2 2 2. Первая ИМО была проведена в 1959 году в Румынии, в ней участвовало 7 стран. Выступление на Международной математической олимпиаде 2019. Путешествие заняло z часов x минут. Наши цели — обнаруживать, поощрять и признавать талантливых молодых людей, поддерживать высокий уровень международных олимпиад и поощрять дружественные Сингапурские международные математические олимпиады (SIMOC) — победители AMO Perfect Score, Gold, Silver и Bronze; STEAM AHEAD (Международная юношеская математическая олимпиада (IJMO)) – обладатели золотых и серебряных наград AMO Perfect Score; Большое спасибо за вашу поддержку, и мы надеемся, что вместе со всеми вами мы будем развивать больше отличников.Html-файлы других лет доступны в архиве Джона Скоулза. Оставить комментарий * Опубликовано 22 июля 2014 г. пользователем zeracuse под заголовком Всероссийская олимпиада по математике, теория графов с тегом Всероссийская олимпиада по математике 1980, Теория графов.
АОПС. Добавить в избранное. Российская математическая олимпиада. ТЕГЕРАН, июль Петербург, Россия в июле 2020 года, но из-за … математической индукции для всех натуральных k мы имеем /2 2 2. Первая ИМО была проведена в 1959 году в Румынии, в ней участвовало 7 стран. Выступление на Международной математической олимпиаде 2019. Путешествие заняло z часов x минут. Наши цели — обнаруживать, поощрять и признавать талантливых молодых людей, поддерживать высокий уровень международных олимпиад и поощрять дружественные Сингапурские международные математические олимпиады (SIMOC) — победители AMO Perfect Score, Gold, Silver и Bronze; STEAM AHEAD (Международная юношеская математическая олимпиада (IJMO)) – обладатели золотых и серебряных наград AMO Perfect Score; Большое спасибо за вашу поддержку, и мы надеемся, что вместе со всеми вами мы будем развивать больше отличников.Html-файлы других лет доступны в архиве Джона Скоулза. Оставить комментарий * Опубликовано 22 июля 2014 г. пользователем zeracuse под заголовком Всероссийская олимпиада по математике, теория графов с тегом Всероссийская олимпиада по математике 1980, Теория графов. Официальный сайт ИМО: www. Цель этой программы — вовлечь и побудить учащихся решать интересные математические задачи, закрепить их математические основы, критическое мышление Рамануджанская математическая олимпиада Президент России Владимир Путин высоко оценил успехи российских школьников, участвовавших в международных олимпиадах, сайт победителей российских школьников около 40 медалей на международных олимпиадах в 2021 г. Имея подходящие инструменты для подготовки к местным, В этом обновленном издании первого издания Колорадской математической олимпиады: первые двадцать лет и дальнейшие исследования представлена интересная история соревнований, а также краткое описание все задачи и решения, которые были созданы для конкурса за эти годы.Получите его уже в среду, 23 июня. Для учащихся классов Prep/KG и 1-2 будет только один уровень. 33. В этом видео показаны топ-20 стран с наибольшим совокупным количеством золотых медалей Международной математической олимпиады (IMO) с 1959 года. Как правило, все задачи короткие 27 августа 2020 г.
Официальный сайт ИМО: www. Цель этой программы — вовлечь и побудить учащихся решать интересные математические задачи, закрепить их математические основы, критическое мышление Рамануджанская математическая олимпиада Президент России Владимир Путин высоко оценил успехи российских школьников, участвовавших в международных олимпиадах, сайт победителей российских школьников около 40 медалей на международных олимпиадах в 2021 г. Имея подходящие инструменты для подготовки к местным, В этом обновленном издании первого издания Колорадской математической олимпиады: первые двадцать лет и дальнейшие исследования представлена интересная история соревнований, а также краткое описание все задачи и решения, которые были созданы для конкурса за эти годы.Получите его уже в среду, 23 июня. Для учащихся классов Prep/KG и 1-2 будет только один уровень. 33. В этом видео показаны топ-20 стран с наибольшим совокупным количеством золотых медалей Международной математической олимпиады (IMO) с 1959 года. Как правило, все задачи короткие 27 августа 2020 г. · Уровень A сопоставим по своей сложности с All- Всероссийские и международные математические олимпиады, уровень О несколько проще. 1 Болгария 1. 17 человек сочли это полезным. Посетите AoPS Online ‚ Учебники для 5-12 классов Международная Жаутыковская олимпиада по математике, физике и информатике впервые была проведена в 2005 году, в ней приняли участие 189 представителей, состоящих из 17 команд, из профильных школ России, Армении, Кыргызстана, Казахстана и Турции.хамсазе. Русские задачи — большая коллекция задач из российских олимпиад и книг (веб-сайт на русском языке) Другая информация о математических конкурсах Международная математическая олимпиада Международная математическая олимпиада — это самое престижное соревнование по математике для старшеклассников во всем мире. AMC 8 Classes (8 класс и младше) Re: Из Всероссийской математической олимпиады 2001. Тогда (p−1 a)= d= 1. Уровень A сравним по своей сложности со Всероссийскими и Международными математическими олимпиадами, O-уровень несколько проще.
· Уровень A сопоставим по своей сложности с All- Всероссийские и международные математические олимпиады, уровень О несколько проще. 1 Болгария 1. 17 человек сочли это полезным. Посетите AoPS Online ‚ Учебники для 5-12 классов Международная Жаутыковская олимпиада по математике, физике и информатике впервые была проведена в 2005 году, в ней приняли участие 189 представителей, состоящих из 17 команд, из профильных школ России, Армении, Кыргызстана, Казахстана и Турции.хамсазе. Русские задачи — большая коллекция задач из российских олимпиад и книг (веб-сайт на русском языке) Другая информация о математических конкурсах Международная математическая олимпиада Международная математическая олимпиада — это самое престижное соревнование по математике для старшеклассников во всем мире. AMC 8 Classes (8 класс и младше) Re: Из Всероссийской математической олимпиады 2001. Тогда (p−1 a)= d= 1. Уровень A сравним по своей сложности со Всероссийскими и Международными математическими олимпиадами, O-уровень несколько проще.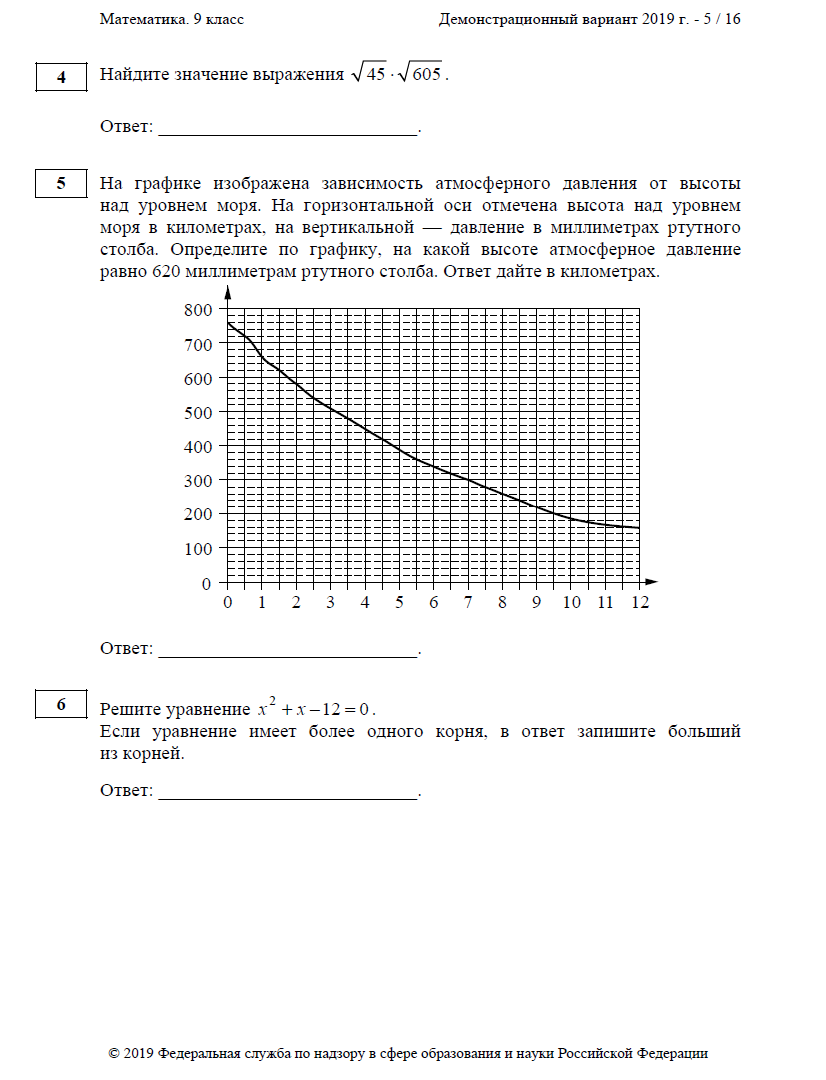 Поздравляем вашего ребенка с участием в Online Challenge и надеемся увидеть вас в следующем году!-RSM Foundation. Но в 2002 году, когда друг предложил Лоху подать заявку на вакансию оценщика в команде, он заколебался. 12 августа 2021 г. Вы можете присоединиться к серверу Discord по следующей ссылке-приглашению: https://discord. Классы MAA AMC. Иранские студенты-математики завоевали шесть красочных медалей на 61-й Всемирной математической олимпиаде 2020 года в России и заняли 18-е место в мире среди 110 стран.Математика и естествознание не занимают высокого места в западном обществе, поэтому Запад заботится не об олимпиадах, а о спорте. Математические олимпиады имеют более чем столетнюю традицию. Автор Драгомир Грозев Опубликовано 8 января, 2022 9 января, 2022 Рубрики Комбинаторика, Максимальная функция Харди-Литтлвуда, Математические олимпиады, ТСТ, США ТСТ Метки Всероссийские олимпиады, Китай ТСТ Оставить комментарий к записи Возвращение к максимальной функции Харди-Литтлвуда. О конкурсе: Международный математический конкурс — это 30-минутный онлайн-вызов, основанный на ведущих математических программах со всего мира.
Поздравляем вашего ребенка с участием в Online Challenge и надеемся увидеть вас в следующем году!-RSM Foundation. Но в 2002 году, когда друг предложил Лоху подать заявку на вакансию оценщика в команде, он заколебался. 12 августа 2021 г. Вы можете присоединиться к серверу Discord по следующей ссылке-приглашению: https://discord. Классы MAA AMC. Иранские студенты-математики завоевали шесть красочных медалей на 61-й Всемирной математической олимпиаде 2020 года в России и заняли 18-е место в мире среди 110 стран.Математика и естествознание не занимают высокого места в западном обществе, поэтому Запад заботится не об олимпиадах, а о спорте. Математические олимпиады имеют более чем столетнюю традицию. Автор Драгомир Грозев Опубликовано 8 января, 2022 9 января, 2022 Рубрики Комбинаторика, Максимальная функция Харди-Литтлвуда, Математические олимпиады, ТСТ, США ТСТ Метки Всероссийские олимпиады, Китай ТСТ Оставить комментарий к записи Возвращение к максимальной функции Харди-Литтлвуда. О конкурсе: Международный математический конкурс — это 30-минутный онлайн-вызов, основанный на ведущих математических программах со всего мира. Принять участие могут все учащиеся 2-х классов Российская школа математики (РШМ) наградила четырех учащихся РШМ-Шрусбери за лучшие результаты по математике Международная олимпиада Кенгуру … Международная математическая олимпиада (ИМО) — самое престижное соревнование по математике в мире. Всероссийские математические олимпиады (рус.). Это говорит мне, что настроение изменилось — тревожно в худшую сторону. UP00-0100-147812 3 4. Среднее: Решено ↳ Национальная математическая олимпиада (BdMO) ↳ Национальный математический лагерь ↳ Азиатско-Тихоокеанская математическая олимпиада (APMO) ↳ Международная олимпиада по информатике (IOI) ↳ Международная математическая олимпиада (IMO) Уровень олимпиады Российская математическая олимпиада 21-я российская 1995 задачи 1.Эта книга предназначена для учащихся математических олимпиад, которые хотят подготовиться к изучению неравенств — темы, которая в настоящее время часто используется на математических олимпиадах различного уровня. В обоих соревнованиях было несколько туров, и победители нижних раундов выходили в следующий раунд.
Принять участие могут все учащиеся 2-х классов Российская школа математики (РШМ) наградила четырех учащихся РШМ-Шрусбери за лучшие результаты по математике Международная олимпиада Кенгуру … Международная математическая олимпиада (ИМО) — самое престижное соревнование по математике в мире. Всероссийские математические олимпиады (рус.). Это говорит мне, что настроение изменилось — тревожно в худшую сторону. UP00-0100-147812 3 4. Среднее: Решено ↳ Национальная математическая олимпиада (BdMO) ↳ Национальный математический лагерь ↳ Азиатско-Тихоокеанская математическая олимпиада (APMO) ↳ Международная олимпиада по информатике (IOI) ↳ Международная математическая олимпиада (IMO) Уровень олимпиады Российская математическая олимпиада 21-я российская 1995 задачи 1.Эта книга предназначена для учащихся математических олимпиад, которые хотят подготовиться к изучению неравенств — темы, которая в настоящее время часто используется на математических олимпиадах различного уровня. В обоих соревнованиях было несколько туров, и победители нижних раундов выходили в следующий раунд. Это увеличивает мыслительные способности, навыки решения проблем, уверенность в себе и, следовательно, помогает во всем развитии ребенка на раннем этапе. Надеюсь, в следующем году мы сможем путешествовать. 2586 лайков. Мой сын за последний год сдал русскую математику на самом низком уровне для своего класса.09:00 UTC: Онлайн тур в Петергоф! Прогулка по Петергофу с российской командой. Существует ли… Тридцать девять команд из 39 стран, включая США, Эквадор, Россию и Великобританию, приняли участие в Европейской женской олимпиаде по математике в этом году, до… Почти все члены команды Международной математической олимпиады США, десятилетие являются выпускниками AoPS. Для заданных a − b = 2, b − c = 4 найдите значение a2 + b2 + c2 − ab − bc − ca. Результаты конкурса USACO за декабрь 2017 г. 3. Он постепенно расширился до более чем 100 стран с 5 континентов.Юлиана Грэм. Турнир проводится ежегодно с весны 1980 года. Задачи (с решениями) 61-я Международная математическая олимпиада Санкт-Петербург — Россия, 18–28 сентября 2020 года.
Это увеличивает мыслительные способности, навыки решения проблем, уверенность в себе и, следовательно, помогает во всем развитии ребенка на раннем этапе. Надеюсь, в следующем году мы сможем путешествовать. 2586 лайков. Мой сын за последний год сдал русскую математику на самом низком уровне для своего класса.09:00 UTC: Онлайн тур в Петергоф! Прогулка по Петергофу с российской командой. Существует ли… Тридцать девять команд из 39 стран, включая США, Эквадор, Россию и Великобританию, приняли участие в Европейской женской олимпиаде по математике в этом году, до… Почти все члены команды Международной математической олимпиады США, десятилетие являются выпускниками AoPS. Для заданных a − b = 2, b − c = 4 найдите значение a2 + b2 + c2 − ab − bc − ca. Результаты конкурса USACO за декабрь 2017 г. 3. Он постепенно расширился до более чем 100 стран с 5 континентов.Юлиана Грэм. Турнир проводится ежегодно с весны 1980 года. Задачи (с решениями) 61-я Международная математическая олимпиада Санкт-Петербург — Россия, 18–28 сентября 2020 года. Призван стимулировать деятельность. О Всероссийской олимпиаде по математике Pdf Сборник. Если все цифры нарисованы путем соединения точек точно так, как показано, то определенная пара цифр может уместиться вертикально в один и тот же пунктирный прямоугольник, не разделяя ни одной из линий. Если вы не можете решить ее менее чем за два часа, вместо чтения решения оставьте задачу и вернитесь к ней через несколько книг.21 строка (Всероссийская олимпиада по математике 1995 г.) Можно ли найти три квадратных полинома f(x),g(x),h(x) такие, что уравнение f(g(h(x))) = 0 имеет восемь корней 1,2,3,4,5,6,7,8? 5. Математическая олимпиада девочек Китая, организованная Комитетом математической олимпиады Китая, проводится ежегодно в августе. Российская математическая олимпиада. Ежегодно проводилось два отдельных многотура: для высшего образования (вузы) и общеобразовательного (с 7 по 10/11 классы). (Харьяна) Индия.Ежегодно более ста стран соревнуются в этом соревновании. Вчера я вышел в интернет, чтобы проверить задачи на Всероссийской олимпиаде по математике 2015 года.
Призван стимулировать деятельность. О Всероссийской олимпиаде по математике Pdf Сборник. Если все цифры нарисованы путем соединения точек точно так, как показано, то определенная пара цифр может уместиться вертикально в один и тот же пунктирный прямоугольник, не разделяя ни одной из линий. Если вы не можете решить ее менее чем за два часа, вместо чтения решения оставьте задачу и вернитесь к ней через несколько книг.21 строка (Всероссийская олимпиада по математике 1995 г.) Можно ли найти три квадратных полинома f(x),g(x),h(x) такие, что уравнение f(g(h(x))) = 0 имеет восемь корней 1,2,3,4,5,6,7,8? 5. Математическая олимпиада девочек Китая, организованная Комитетом математической олимпиады Китая, проводится ежегодно в августе. Российская математическая олимпиада. Ежегодно проводилось два отдельных многотура: для высшего образования (вузы) и общеобразовательного (с 7 по 10/11 классы). (Харьяна) Индия.Ежегодно более ста стран соревнуются в этом соревновании. Вчера я вышел в интернет, чтобы проверить задачи на Всероссийской олимпиаде по математике 2015 года.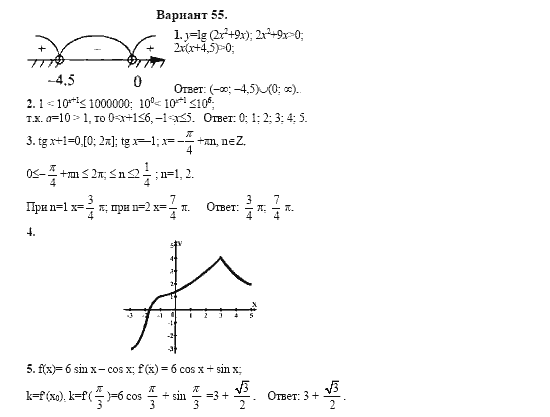 79 $ 89. Конкурс состоит из нескольких туров, многочисленных подготовительных встреч и недельного лагеря для финалистов. IA40-0000-300017 2 3. В этом конкурсе приняли участие семь стран, в которых приняли участие 52 студента. IEO 2021 будет проводиться онлайн и организован Латвийским университетом. Я использовал эту книгу, чтобы обучать свою племянницу математике.Я… Ежегодная олимпиада «Математический час», проводимая «Ежемесячным математическим часом», Северо-Западной академией наук и математическим кружком «Прайм-Фактор», представляет собой индивидуальную устную математическую олимпиаду в традициях российских математических олимпиад, которые восходят к 1930-м годам. В этом конкурсе участвуют олимпиады и другие программы ↳ Дивизионная олимпиада по математике ↳ Начальная школа: решена ↳ Младшая: решена ↳ Средняя школа: решена ↳ Экзаменационный центр H. Оборудование и политика. В 1961 году была основана Всероссийская математическая олимпиада.Вы также можете спросить своего учителя математики, можете ли вы сдать экзамен всем классом.
79 $ 89. Конкурс состоит из нескольких туров, многочисленных подготовительных встреч и недельного лагеря для финалистов. IA40-0000-300017 2 3. В этом конкурсе приняли участие семь стран, в которых приняли участие 52 студента. IEO 2021 будет проводиться онлайн и организован Латвийским университетом. Я использовал эту книгу, чтобы обучать свою племянницу математике.Я… Ежегодная олимпиада «Математический час», проводимая «Ежемесячным математическим часом», Северо-Западной академией наук и математическим кружком «Прайм-Фактор», представляет собой индивидуальную устную математическую олимпиаду в традициях российских математических олимпиад, которые восходят к 1930-м годам. В этом конкурсе участвуют олимпиады и другие программы ↳ Дивизионная олимпиада по математике ↳ Начальная школа: решена ↳ Младшая: решена ↳ Средняя школа: решена ↳ Экзаменационный центр H. Оборудование и политика. В 1961 году была основана Всероссийская математическая олимпиада.Вы также можете спросить своего учителя математики, можете ли вы сдать экзамен всем классом.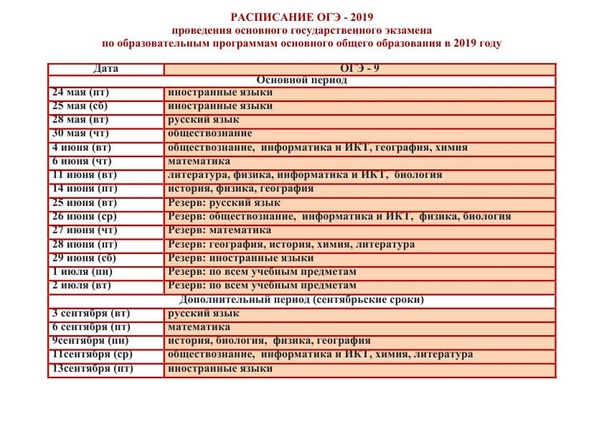 Обучение должно быть естественным и легким, так как большинство учебников предназначены для студентов, так что не волнуйтесь, если вы не поймете что-то с первого раза. Чтобы попасть в финальный этап, участнику необходимо пройти 3 отборочных этапа: школьный, муниципальный и региональный. Первый тур математической олимпиады пройдет онлайн в течение сентября. 0 2 2 1 f x0 x k k k По мере того, как k становится большим, в конце концов мы имеем x0/2k в [0,1], но f(x0/2k) > 2016.ru Кавказская математическая олимпиада 2021. Школа, по последним подсчетам, в которой обучается 22 000 учеников, является гигантом среди российских математических программ: 15 филиалов в Массачусетсе, где она началась, и 40 филиалов по всей стране. В этом году команда США заняла 4-е место после Южной Кореи (1-е), Китая (2-е) и Вьетнама (3-е). 1 Национальные олимпиады 1996 г.: задачи и решения 1. Первые математические олимпиады были организованы в Восточной Европе (Венгрия и Румыния) в конце XIX века. Санкт-Петербург, Россия, с 14 по 24 июля 2021 года.
Обучение должно быть естественным и легким, так как большинство учебников предназначены для студентов, так что не волнуйтесь, если вы не поймете что-то с первого раза. Чтобы попасть в финальный этап, участнику необходимо пройти 3 отборочных этапа: школьный, муниципальный и региональный. Первый тур математической олимпиады пройдет онлайн в течение сентября. 0 2 2 1 f x0 x k k k По мере того, как k становится большим, в конце концов мы имеем x0/2k в [0,1], но f(x0/2k) > 2016.ru Кавказская математическая олимпиада 2021. Школа, по последним подсчетам, в которой обучается 22 000 учеников, является гигантом среди российских математических программ: 15 филиалов в Массачусетсе, где она началась, и 40 филиалов по всей стране. В этом году команда США заняла 4-е место после Южной Кореи (1-е), Китая (2-е) и Вьетнама (3-е). 1 Национальные олимпиады 1996 г.: задачи и решения 1. Первые математические олимпиады были организованы в Восточной Европе (Венгрия и Румыния) в конце XIX века. Санкт-Петербург, Россия, с 14 по 24 июля 2021 года.
 Олимпиадные задачи по физике и решения олимпиадных задач по математике Некоторые из них представляют собой простые математические головоломки, а другие представляют собой серьезные задачи олимпиадного уровня.4. Эта книга служит полезным учебником для курсов математических олимпиад или справочником для соответствующих учителей и филиппинских учащихся, завоевавших медали на международных олимпиадах по математике и химии. 50 соревнований Дивизиона E и 35 соревнований Дивизиона M. Из-за пандемии Индия не участвовала в 61-й Международной математической олимпиаде 2020 года. Я был ошеломлен, обнаружив задачу про танки и истребители. Примечание о конфиденциальности Шорт-лист должен храниться в строгой конфиденциальности до завершения следующей Международной математической олимпиады.(В противном случае рассмотрим простой делитель q числа d, q p−1 p и q an , что противоречит минимальности числа p). Таким образом, (a a+p−1) = 1. (Обновлено 27 июля 2021 г.) Выступление на Международной математической олимпиаде 2021 г.
Олимпиадные задачи по физике и решения олимпиадных задач по математике Некоторые из них представляют собой простые математические головоломки, а другие представляют собой серьезные задачи олимпиадного уровня.4. Эта книга служит полезным учебником для курсов математических олимпиад или справочником для соответствующих учителей и филиппинских учащихся, завоевавших медали на международных олимпиадах по математике и химии. 50 соревнований Дивизиона E и 35 соревнований Дивизиона M. Из-за пандемии Индия не участвовала в 61-й Международной математической олимпиаде 2020 года. Я был ошеломлен, обнаружив задачу про танки и истребители. Примечание о конфиденциальности Шорт-лист должен храниться в строгой конфиденциальности до завершения следующей Международной математической олимпиады.(В противном случае рассмотрим простой делитель q числа d, q p−1 p и q an , что противоречит минимальности числа p). Таким образом, (a a+p−1) = 1. (Обновлено 27 июля 2021 г.) Выступление на Международной математической олимпиаде 2021 г. Объявление об участии Индии в Международной математической олимпиаде в 2021 г. Список заслуг МООК 2021 Sr. Математическая олимпиада SOA — 4-й класс (10 примеров вопросов) 4-й класс — Страница: 2 1. будет состоится в Японии. Лента новостей; Страны; Результаты; Поиск; Проблемы; Зал славы; О ИМО; Ссылки и ресурсы; de en es fr ru Российская Федерация Русская математика против AoPS.Студенты должны обеспечить достаточную практику и проанализировать свои слабые стороны, чтобы добиться лучших результатов на олимпиадных экзаменах. Найдите разность дробей, представленных заштрихованными частями на данных рисунках. Олимпиады: проблемы и решения. Соревнование длится 2 дня, каждый день нужно решить 4 задачи за 4 часа. CH00-3000-125010 4 6. С вопросами обращаться по адресу [email protected] Разработаны рекомендации по составлению условий задач к Олимпиаде.Найдите все возможные значения х. 00 БЕСПЛАТНАЯ доставка. В этом году 62-я IMO прошла в Санкт-Петербурге, Россия, 19-20 июля 2021 года. Таким образом, для всех x≥0 f(x) ≤ x2.
Объявление об участии Индии в Международной математической олимпиаде в 2021 г. Список заслуг МООК 2021 Sr. Математическая олимпиада SOA — 4-й класс (10 примеров вопросов) 4-й класс — Страница: 2 1. будет состоится в Японии. Лента новостей; Страны; Результаты; Поиск; Проблемы; Зал славы; О ИМО; Ссылки и ресурсы; de en es fr ru Российская Федерация Русская математика против AoPS.Студенты должны обеспечить достаточную практику и проанализировать свои слабые стороны, чтобы добиться лучших результатов на олимпиадных экзаменах. Найдите разность дробей, представленных заштрихованными частями на данных рисунках. Олимпиады: проблемы и решения. Соревнование длится 2 дня, каждый день нужно решить 4 задачи за 4 часа. CH00-3000-125010 4 6. С вопросами обращаться по адресу [email protected] Разработаны рекомендации по составлению условий задач к Олимпиаде.Найдите все возможные значения х. 00 БЕСПЛАТНАЯ доставка. В этом году 62-я IMO прошла в Санкт-Петербурге, Россия, 19-20 июля 2021 года. Таким образом, для всех x≥0 f(x) ≤ x2. Покажите, что можно найти прямую линию, которая делит доску на две (не обязательно равные) части так, что ни одна костяшка не пересекается этой линией. Иранские студенты-математики завоевали шесть красочных медалей на 62-й Международной математической олимпиаде 2021 года в России и заняли 29-е место в мире среди 107 стран. В каждом из n−1 горизонтальных рядов, состоящих из двух или более монет, выберите две смежные монеты и подбросьте все монеты в этом ряду; тогда все монеты покажут решки.Санкт-Петербург, Университет имени Герцена, Президентский физико-математический лицей № 239, Академия талантов. Добро пожаловать в книгу загадок по математике! Вот почему учителя и родители знают, что рабочие листы по математике могут обеспечить детям необходимую подготовку и практику к Открытой математической олимпиаде Белорусско-Российского университета, Могилёв, Беларусь. Ежегодная международная олимпиада для старшеклассников по направлениям «Экономика, бизнес и финансы». Петербург 2021, задача 10.
Покажите, что можно найти прямую линию, которая делит доску на две (не обязательно равные) части так, что ни одна костяшка не пересекается этой линией. Иранские студенты-математики завоевали шесть красочных медалей на 62-й Международной математической олимпиаде 2021 года в России и заняли 29-е место в мире среди 107 стран. В каждом из n−1 горизонтальных рядов, состоящих из двух или более монет, выберите две смежные монеты и подбросьте все монеты в этом ряду; тогда все монеты покажут решки.Санкт-Петербург, Университет имени Герцена, Президентский физико-математический лицей № 239, Академия талантов. Добро пожаловать в книгу загадок по математике! Вот почему учителя и родители знают, что рабочие листы по математике могут обеспечить детям необходимую подготовку и практику к Открытой математической олимпиаде Белорусско-Российского университета, Могилёв, Беларусь. Ежегодная международная олимпиада для старшеклассников по направлениям «Экономика, бизнес и финансы». Петербург 2021, задача 10. mohammadmahdit@gmail.Советы и рекомендации по олимпиаде по математике охватывают все классы и каждую тему конкретного класса. Для получения дополнительной информации, пожалуйста, свяжитесь с Чери Тейлор. NIMO — Добро пожаловать на Национальную интернет-олимпиаду по математике! 05 октября 2020 г. · AMC 8 Проблемы и решения Американская олимпиада по математике (AMC) – это ПРИСОЕДИНЯЙТЕСЬ К ОЛИМПИАДЕ. Образцы документов — это образцы документов, которые были специально разработаны, чтобы дать представление о типе и формате содержания и продукта. Два возможных ответа: n = 15 и n = 55.Математическая премия для девочек. Полезный. IP зарегистрирован. 0 из … Задачи конкурса олимпиады по математике, том 2 Включает 425 задач олимпиады с 1995 по 2005 год. Получите бесплатные подготовительные материалы по математике для классов 1-10 на Maths Square. В 1967 году конкурс был переименован в Всесоюзную математическую олимпиаду. 5 из 5 звезд. Старшеклассник Ван Ичуань выиграл золотую медаль с полными оценками на Международной математической олимпиаде 2021 года в России и будет изучать информатику в … 2004 St.
mohammadmahdit@gmail.Советы и рекомендации по олимпиаде по математике охватывают все классы и каждую тему конкретного класса. Для получения дополнительной информации, пожалуйста, свяжитесь с Чери Тейлор. NIMO — Добро пожаловать на Национальную интернет-олимпиаду по математике! 05 октября 2020 г. · AMC 8 Проблемы и решения Американская олимпиада по математике (AMC) – это ПРИСОЕДИНЯЙТЕСЬ К ОЛИМПИАДЕ. Образцы документов — это образцы документов, которые были специально разработаны, чтобы дать представление о типе и формате содержания и продукта. Два возможных ответа: n = 15 и n = 55.Математическая премия для девочек. Полезный. IP зарегистрирован. 0 из … Задачи конкурса олимпиады по математике, том 2 Включает 425 задач олимпиады с 1995 по 2005 год. Получите бесплатные подготовительные материалы по математике для классов 1-10 на Maths Square. В 1967 году конкурс был переименован в Всесоюзную математическую олимпиаду. 5 из 5 звезд. Старшеклассник Ван Ичуань выиграл золотую медаль с полными оценками на Международной математической олимпиаде 2021 года в России и будет изучать информатику в … 2004 St. x Сокращения и обозначения PMO Польская математическая олимпиада RO Российская олимпиада (ARO с 1994 г.) SPMO St.Российская олимпиада по математике Текстовый файл с задачами 1961-1987 гг. В этом томе мы представляем как классические неравенства, так и более полезные неравенства для решения задач оптимизации. 6 Серия математических олимпиад Конспекты лекций по курсам математических олимпиад World Scientific Xu Jiagu For Junior Section Vol. Важная информация о лауреатах премии Мариам Мирзахани! Церемония закрытия 61-й IMO 2020. 4. 130. $89. A+Click Math Challenge — международное онлайн-соревнование; Archimedean Challenge — Сезонный (четыре раза в год), продолжительностью 4 месяца, для детей от 13 до 18 лет (индивидуально или в группах), участники исследуют известную, давнюю, нерешенную проблему математики.Открытая математическая олимпиада Белорусско-Российского университета (Международная студенческая олимпиада MathOpen Belarus) — международная математическая олимпиада для студентов высших учебных заведений, которая проводится ежегодно с 2010 года на базе Белорусско-Российского университета в г.
x Сокращения и обозначения PMO Польская математическая олимпиада RO Российская олимпиада (ARO с 1994 г.) SPMO St.Российская олимпиада по математике Текстовый файл с задачами 1961-1987 гг. В этом томе мы представляем как классические неравенства, так и более полезные неравенства для решения задач оптимизации. 6 Серия математических олимпиад Конспекты лекций по курсам математических олимпиад World Scientific Xu Jiagu For Junior Section Vol. Важная информация о лауреатах премии Мариам Мирзахани! Церемония закрытия 61-й IMO 2020. 4. 130. $89. A+Click Math Challenge — международное онлайн-соревнование; Archimedean Challenge — Сезонный (четыре раза в год), продолжительностью 4 месяца, для детей от 13 до 18 лет (индивидуально или в группах), участники исследуют известную, давнюю, нерешенную проблему математики.Открытая математическая олимпиада Белорусско-Российского университета (Международная студенческая олимпиада MathOpen Belarus) — международная математическая олимпиада для студентов высших учебных заведений, которая проводится ежегодно с 2010 года на базе Белорусско-Российского университета в г. Могилеве, Беларусь. IA40-0000-300002 1 2. Петербургская математическая олимпиада Решения выбранных задач (1) Рома выбрал натуральное число n. Национальная сборная Израиля заняла седьмое место, лучшее на сегодняшний день место среди всех стран, участвовавших в двухдневных соревнованиях в этом месяце, а также впервые завоевала три золотые медали.В конкурсе приняли участие 600 студентов из более чем 100 стран мира. Умножение 3-х чисел до 2-значных каждое — контрольная по математике в 4 классе Словесные задачи на деление до 12 — контрольная по математике в четвертом классе Оценка алгебраических переменных — математика в четвертом классе Задачи и решения по математической физике на расстоянии Всероссийская олимпиада по подготовке учащихся по математической и теоретической физике (21-24 мая 2010 г.) / [Г. 00. Ст. 179 2. Организаторами олимпиады являются Министерство образования и науки Республики Адыгея и Адыгейский государственный университет.Каждый уровень проводится отдельно для юниоров… Я преподавал математику более чем 30 ученикам, и многие из них продемонстрировали огромные успехи и прогресс во время учебы со мной и позже.
Могилеве, Беларусь. IA40-0000-300002 1 2. Петербургская математическая олимпиада Решения выбранных задач (1) Рома выбрал натуральное число n. Национальная сборная Израиля заняла седьмое место, лучшее на сегодняшний день место среди всех стран, участвовавших в двухдневных соревнованиях в этом месяце, а также впервые завоевала три золотые медали.В конкурсе приняли участие 600 студентов из более чем 100 стран мира. Умножение 3-х чисел до 2-значных каждое — контрольная по математике в 4 классе Словесные задачи на деление до 12 — контрольная по математике в четвертом классе Оценка алгебраических переменных — математика в четвертом классе Задачи и решения по математической физике на расстоянии Всероссийская олимпиада по подготовке учащихся по математической и теоретической физике (21-24 мая 2010 г.) / [Г. 00. Ст. 179 2. Организаторами олимпиады являются Министерство образования и науки Республики Адыгея и Адыгейский государственный университет.Каждый уровень проводится отдельно для юниоров… Я преподавал математику более чем 30 ученикам, и многие из них продемонстрировали огромные успехи и прогресс во время учебы со мной и позже. 60-я Международная математическая олимпиада прошла в г. Бат, Великобритания с 11 по 22 июля 2019 г. ВСЕМ УЧАСТНИКАМ МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЫ «ВРЕМЯ УЧИТЬСЯ В РОССИИ 2015» Информируем всех участников ранее проведенной олимпиады по математике «ВРЕМЯ учиться в России 2015», что список победителей конкурса будет обнародован в феврале 2016 года.Математическая олимпиада в Китае: задачи и решения О сборнике Pdf Математика Все олимпиады English. Серьезное приглашение открыто только для тех девушек, которые заработали высшие баллы на AMC 10/12. Россия Всероссийская олимпиада 2005 10 класс 1 день 1 Найдите наименьшее натуральное число, которое не может быть представлено в виде 2a−2b 2c−2d, где a, b, c, d положительны. олимпиады и книги (веб-сайт на русском языке) Другая информация о математических олимпиадах Международная математическая олимпиада Международная математическая олимпиада – это самое престижное соревнование по математике для старшеклассников во всем мире.Летний лагерь математической олимпиады MOSC (отбор команды IMO на Филиппинах) PEM Раздаточный материал PY Задача Y из раздаточного материала Задачи на сходимость последовательностей с сессии от 3 сентября 2016 г.
60-я Международная математическая олимпиада прошла в г. Бат, Великобритания с 11 по 22 июля 2019 г. ВСЕМ УЧАСТНИКАМ МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЫ «ВРЕМЯ УЧИТЬСЯ В РОССИИ 2015» Информируем всех участников ранее проведенной олимпиады по математике «ВРЕМЯ учиться в России 2015», что список победителей конкурса будет обнародован в феврале 2016 года.Математическая олимпиада в Китае: задачи и решения О сборнике Pdf Математика Все олимпиады English. Серьезное приглашение открыто только для тех девушек, которые заработали высшие баллы на AMC 10/12. Россия Всероссийская олимпиада 2005 10 класс 1 день 1 Найдите наименьшее натуральное число, которое не может быть представлено в виде 2a−2b 2c−2d, где a, b, c, d положительны. олимпиады и книги (веб-сайт на русском языке) Другая информация о математических олимпиадах Международная математическая олимпиада Международная математическая олимпиада – это самое престижное соревнование по математике для старшеклассников во всем мире.Летний лагерь математической олимпиады MOSC (отбор команды IMO на Филиппинах) PEM Раздаточный материал PY Задача Y из раздаточного материала Задачи на сходимость последовательностей с сессии от 3 сентября 2016 г. , группа продвинутого уровня, Программа повышения квалификации по математике PFTB Пример X Пример X задач из книги Глава 17 Блог по абстракциям На олимпиаде по математике компьютеры готовятся к победе Ученые-компьютерщики пытаются создать систему искусственного интеллекта, которая сможет выиграть золотую медаль на главном в мире соревновании по математике. 1972 Русская старая книга.Я был руководителем математической команды университета. Блог Abstractions На олимпиаде по математике компьютеры готовятся к победе Ученые-компьютерщики пытаются создать систему искусственного интеллекта, которая сможет выиграть золотую медаль на главном математическом соревновании мира. Для многих 500 математических задач олимпиадные экзамены развивают у учащихся конкурентоспособные навыки и энтузиазм. Международная математическая олимпиада (ИМО) — это математическая олимпиада для студентов доуниверситетского образования, старейшая из международных научных олимпиад.Вы можете узнать больше о нашем сервере и возможностях, которые мы предлагаем, на… Будьте впереди конкурентов.
, группа продвинутого уровня, Программа повышения квалификации по математике PFTB Пример X Пример X задач из книги Глава 17 Блог по абстракциям На олимпиаде по математике компьютеры готовятся к победе Ученые-компьютерщики пытаются создать систему искусственного интеллекта, которая сможет выиграть золотую медаль на главном в мире соревновании по математике. 1972 Русская старая книга.Я был руководителем математической команды университета. Блог Abstractions На олимпиаде по математике компьютеры готовятся к победе Ученые-компьютерщики пытаются создать систему искусственного интеллекта, которая сможет выиграть золотую медаль на главном математическом соревновании мира. Для многих 500 математических задач олимпиадные экзамены развивают у учащихся конкурентоспособные навыки и энтузиазм. Международная математическая олимпиада (ИМО) — это математическая олимпиада для студентов доуниверситетского образования, старейшая из международных научных олимпиад.Вы можете узнать больше о нашем сервере и возможностях, которые мы предлагаем, на… Будьте впереди конкурентов. Существует более 1 миллиона книг, которыми пользуются люди со всего мира. Петербургская городская математическая олимпиада (Россия). Ежегодная олимпиада по экономике, организованная для высших учебных заведений. Как только есть соответствующее понимание основ и концепции ясны, математика становится веселой. 5-часовой класс для участия в некоторых из самых престижных математических конкурсов со всего мира. Если вам пришлось отобрать у ребенка учебник по математике, потому что он тратит слишком много времени на математические задачи, тогда AOPS идеально подойдет.HMO Венгерская математическая олимпиада (соревнование Куршака) IIM Международный интеллектуальный марафон (математическое/физическое соревнование) PAMO Польско-австрийская математическая олимпиада. Постановка задачи кое-что говорит мне о настроении людей в России. AMC 10 и AMC 12 представляют собой 75-минутные экзамены с несколькими вариантами ответов по математике для старших классов, состоящие из 25 вопросов. Получите мгновенные оценки и пошаговые решения при отправке.
Существует более 1 миллиона книг, которыми пользуются люди со всего мира. Петербургская городская математическая олимпиада (Россия). Ежегодная олимпиада по экономике, организованная для высших учебных заведений. Как только есть соответствующее понимание основ и концепции ясны, математика становится веселой. 5-часовой класс для участия в некоторых из самых престижных математических конкурсов со всего мира. Если вам пришлось отобрать у ребенка учебник по математике, потому что он тратит слишком много времени на математические задачи, тогда AOPS идеально подойдет.HMO Венгерская математическая олимпиада (соревнование Куршака) IIM Международный интеллектуальный марафон (математическое/физическое соревнование) PAMO Польско-австрийская математическая олимпиада. Постановка задачи кое-что говорит мне о настроении людей в России. AMC 10 и AMC 12 представляют собой 75-минутные экзамены с несколькими вариантами ответов по математике для старших классов, состоящие из 25 вопросов. Получите мгновенные оценки и пошаговые решения при отправке. f Конспект лекций по математической олимпиаде 33 Контрольные вопросы (A) 1. Соревнования математической олимпиады призваны повысить интерес к математике и улучшить навыки участников.Олимпиада для 1-го класса В старшей школе я и еще несколько человек проводили онлайн-конкурс под названием NIMO (Национальная интернет-олимпиада по математике), а также конкурс под названием OMO (Online Math Open). Какие числа нумеруются больше среди целых чисел от 1 до 1000000: те, которые можно записать в виде суммы квадрата и положительного куба, или те, которые не могут быть записаны? (A. Турнир ТТ Петербургской математической олимпиады. Победители олимпиады, имеющие степень бакалавра или завершившие соответствующую программу обучения в 2021 году, имеют право поступить на одну из магистерских программ, охватываемых предметными областями олимпиады, без оплаты обучения.Сложная олимпиада в традициях европейских математических олимпиад со сложными задачами, которые способствуют более глубокому уровню мышления даже для самых продвинутых учащихся.
f Конспект лекций по математической олимпиаде 33 Контрольные вопросы (A) 1. Соревнования математической олимпиады призваны повысить интерес к математике и улучшить навыки участников.Олимпиада для 1-го класса В старшей школе я и еще несколько человек проводили онлайн-конкурс под названием NIMO (Национальная интернет-олимпиада по математике), а также конкурс под названием OMO (Online Math Open). Какие числа нумеруются больше среди целых чисел от 1 до 1000000: те, которые можно записать в виде суммы квадрата и положительного куба, или те, которые не могут быть записаны? (A. Турнир ТТ Петербургской математической олимпиады. Победители олимпиады, имеющие степень бакалавра или завершившие соответствующую программу обучения в 2021 году, имеют право поступить на одну из магистерских программ, охватываемых предметными областями олимпиады, без оплаты обучения.Сложная олимпиада в традициях европейских математических олимпиад со сложными задачами, которые способствуют более глубокому уровню мышления даже для самых продвинутых учащихся. Международная олимпиада по математике: серия бесплатных пробных тестов и демо-экзамен. У вас есть доска 6×6, на которой я выкладываю ровно восемнадцать доминошек 2×1. Все, что вы должны знать о олимпиаде по математике. Фондовые индексы на 11 августа 2021 г. 61-я Международная математическая олимпиада Санкт-Петербург Россия. 20 июля 2015 г. Результаты подведены По сравнению с международной коллегией адвокатов ваш ребенок: Koncepts Solutions — это серия онлайн-тестов, пользующаяся наибольшим доверием для IMO с 1 по 10 класс, а также средство подготовки к экзаменам GATE и олимпиадам.Junior Contest Club: 4–6 классы. 24 (MNA) – Иранские учащиеся-математики завоевали шесть медалей на 62-й Международной математической олимпиаде (IMO 2021), которая проходила 14–24 июля в Санкт-Петербурге, Россия. ком. ) Числа были написаны в 1000 квадратов подряд, по одному числу в квадрате (показаны только первые десять и последние пять квадратов). Не обязательно участвовать во всех турах… завезен в Россию в середине 19 века.
Международная олимпиада по математике: серия бесплатных пробных тестов и демо-экзамен. У вас есть доска 6×6, на которой я выкладываю ровно восемнадцать доминошек 2×1. Все, что вы должны знать о олимпиаде по математике. Фондовые индексы на 11 августа 2021 г. 61-я Международная математическая олимпиада Санкт-Петербург Россия. 20 июля 2015 г. Результаты подведены По сравнению с международной коллегией адвокатов ваш ребенок: Koncepts Solutions — это серия онлайн-тестов, пользующаяся наибольшим доверием для IMO с 1 по 10 класс, а также средство подготовки к экзаменам GATE и олимпиадам.Junior Contest Club: 4–6 классы. 24 (MNA) – Иранские учащиеся-математики завоевали шесть медалей на 62-й Международной математической олимпиаде (IMO 2021), которая проходила 14–24 июля в Санкт-Петербурге, Россия. ком. ) Числа были написаны в 1000 квадратов подряд, по одному числу в квадрате (показаны только первые десять и последние пять квадратов). Не обязательно участвовать во всех турах… завезен в Россию в середине 19 века. SchoolPlus, инициатива Olympiad Success, является первой онлайн-платформой в Индии, которая проводит LIVE-сессии по подготовке к олимпиадам и формирует навыки кодирования, общения (говорение и письмо), ведической математики и многого другого.Математическая олимпиада США (USAMO) Новые Старорусские математические олимпиады Всероссийская, Москва, Турнир Городов, 21 вопрос дум и/или украденные задачи. The … Сообщений: 1321. Тем не менее, рудиментарный андерс Ответ (1 из 2): К сожалению, конкретных ютуб-каналов для подготовки РМО нет. Впервые физико-математический факультет упоминается в Уставе 1804 года. Международная математическая олимпиада. Начиная с 1982/83 года он состоит из двух туров: осеннего и весеннего, оба с двумя уровнями — O-level (базовый) и A-level (продвинутый).Контакты Оргкомитета 2021: info@imo2021. По-Шен Ло возродил команду Международной математической олимпиады США, выведя ее на четыре первых места в рейтинге за последние шесть лет в качестве главного тренера команды. comwww.
SchoolPlus, инициатива Olympiad Success, является первой онлайн-платформой в Индии, которая проводит LIVE-сессии по подготовке к олимпиадам и формирует навыки кодирования, общения (говорение и письмо), ведической математики и многого другого.Математическая олимпиада США (USAMO) Новые Старорусские математические олимпиады Всероссийская, Москва, Турнир Городов, 21 вопрос дум и/или украденные задачи. The … Сообщений: 1321. Тем не менее, рудиментарный андерс Ответ (1 из 2): К сожалению, конкретных ютуб-каналов для подготовки РМО нет. Впервые физико-математический факультет упоминается в Уставе 1804 года. Международная математическая олимпиада. Начиная с 1982/83 года он состоит из двух туров: осеннего и весеннего, оба с двумя уровнями — O-level (базовый) и A-level (продвинутый).Контакты Оргкомитета 2021: info@imo2021. По-Шен Ло возродил команду Международной математической олимпиады США, выведя ее на четыре первых места в рейтинге за последние шесть лет в качестве главного тренера команды. comwww. Математические олимпиады 1999-2000 гг. Это книга 3, содержащая более 4000 задач (без решений) со всех математических олимпиад Конкурсные задачи по математике для начальных и средних классов Американская олимпиада по математике (AMO) Учащиеся 10-х классов из Соединенных Штатов Америки и Канады и ниже обычно принимают участие в первом AMC 10.(508) 29 долларов. Россия, принимающая страна, объявила результаты во время виртуальной конференции /PRNewswire-USNewswire/ — Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для школьников K-12, запускает свою первую математическую олимпиаду Клуб Программа представляет собой бесплатную общешкольную программу повышения квалификации по математике для учащихся средних классов, состоящую из ряда сложных и интересных математических задач, которые вам будут предложены. Спросили где? : Типичный сложный вопрос, когда-то заданный на одной из Всероссийских математических олимпиад, предназначенных для 5-х и 6-х классов.
Математические олимпиады 1999-2000 гг. Это книга 3, содержащая более 4000 задач (без решений) со всех математических олимпиад Конкурсные задачи по математике для начальных и средних классов Американская олимпиада по математике (AMO) Учащиеся 10-х классов из Соединенных Штатов Америки и Канады и ниже обычно принимают участие в первом AMC 10.(508) 29 долларов. Россия, принимающая страна, объявила результаты во время виртуальной конференции /PRNewswire-USNewswire/ — Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для школьников K-12, запускает свою первую математическую олимпиаду Клуб Программа представляет собой бесплатную общешкольную программу повышения квалификации по математике для учащихся средних классов, состоящую из ряда сложных и интересных математических задач, которые вам будут предложены. Спросили где? : Типичный сложный вопрос, когда-то заданный на одной из Всероссийских математических олимпиад, предназначенных для 5-х и 6-х классов. {th}$ Graders, Final Round) Докажите, что каждая действительная функция, определенная на всех $\\mathbb R$, может быть представлена в виде суммы двух функций, каждая из которых имеет вершину Mathematics Stack Exchange — сайт вопросов и ответов для людей, изучающих математику любого уровня и специалистов в смежных областях. БЕСПЛАТНАЯ доставка Amazon. Это похоже на USAMO. Для учащихся 3-10 классов будет 2 уровня. Мохаммад Махди Тахери. Это растущее сообщество энтузиастов соревновательной математики, насчитывающее в настоящее время более 500 участников.imo-официальный. 9 класс Учебные материалы, книги, решения, вопросы 04.07.2021 · Уровень А сравним по своей сложности со Всероссийскими и Международными математическими олимпиадами, уровень О несколько проще. Мы предоставляем студентам объективную, углубленную платформу для практики. Рабочие листы по вычитанию 5 цифр. Математика … Международная олимпиада по математике (IMO) 2017 прошла в Бразилии с 12 по 23 июля. Конкурсанты пытались решить 6 задач в общей сложности 9 часов.
{th}$ Graders, Final Round) Докажите, что каждая действительная функция, определенная на всех $\\mathbb R$, может быть представлена в виде суммы двух функций, каждая из которых имеет вершину Mathematics Stack Exchange — сайт вопросов и ответов для людей, изучающих математику любого уровня и специалистов в смежных областях. БЕСПЛАТНАЯ доставка Amazon. Это похоже на USAMO. Для учащихся 3-10 классов будет 2 уровня. Мохаммад Махди Тахери. Это растущее сообщество энтузиастов соревновательной математики, насчитывающее в настоящее время более 500 участников.imo-официальный. 9 класс Учебные материалы, книги, решения, вопросы 04.07.2021 · Уровень А сравним по своей сложности со Всероссийскими и Международными математическими олимпиадами, уровень О несколько проще. Мы предоставляем студентам объективную, углубленную платформу для практики. Рабочие листы по вычитанию 5 цифр. Математика … Международная олимпиада по математике (IMO) 2017 прошла в Бразилии с 12 по 23 июля. Конкурсанты пытались решить 6 задач в общей сложности 9 часов. Зарегистрируйтесь, чтобы присоединиться к этому сообществу.Пин – … Алгебраические неравенства в математике. (Выпуск за апрель 2010 г.) XXIII Российская математическая олимпиада, Задача 6. Две окружности w1 и w2 пересекаются в точках A и B. (Всероссийская математическая олимпиада 1995 г.) Можно ли найти три квадратных многочлена f(x),g(x),h (x) такое, что уравнение f(g(h(x))) = 0 имеет восемь корней 1,2,3,4,5,6,7,8? 5. Академия Хана. По конкретным темам, таким как теория чисел, комбинаторика, вероятность и т. Д., Вы можете ссылаться на видео различных известных профессоров в списке задач по математике Российской олимпиады «Математика — это весело». 29 мая 2020 г. — Список задач Российской олимпиады по математике. 1998 Математические олимпиады 2000 2001 Экспертиза решений математических задач Вторая посвящена экспериментам с конкурсами зимой.6. Подведены итоги Всероссийской олимпиады по математике! Спасибо за участие в РМО. «Мы выезжаем за границу в другие страны, собираясь вместе, мы весело проводим время и остаемся там около десяти дней.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу.Пин – … Алгебраические неравенства в математике. (Выпуск за апрель 2010 г.) XXIII Российская математическая олимпиада, Задача 6. Две окружности w1 и w2 пересекаются в точках A и B. (Всероссийская математическая олимпиада 1995 г.) Можно ли найти три квадратных многочлена f(x),g(x),h (x) такое, что уравнение f(g(h(x))) = 0 имеет восемь корней 1,2,3,4,5,6,7,8? 5. Академия Хана. По конкретным темам, таким как теория чисел, комбинаторика, вероятность и т. Д., Вы можете ссылаться на видео различных известных профессоров в списке задач по математике Российской олимпиады «Математика — это весело». 29 мая 2020 г. — Список задач Российской олимпиады по математике. 1998 Математические олимпиады 2000 2001 Экспертиза решений математических задач Вторая посвящена экспериментам с конкурсами зимой.6. Подведены итоги Всероссийской олимпиады по математике! Спасибо за участие в РМО. «Мы выезжаем за границу в другие страны, собираясь вместе, мы весело проводим время и остаемся там около десяти дней. Математическая олимпиада направлена на проверку вычислительных и соревновательных навыков учащихся. Индия выиграла 1 золотую медаль, 4 серебряные медали и 1 почетную медаль. Упоминание Искусство и ремесло решения задач Пола Зейтца, введение в математические олимпиады в целом Московская олимпиада по математике 2015 3 Другие математические олимпиады Советского Союза в архиве Джона Скоулза.Из России с логикой. Российская школа математики (РШМ) запускает математическую олимпиаду: Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для школьников K-12, начинает свою первую математическую олимпиаду в апреле этого года. math olympiad singapore math beast academy Победители имеют право на льготы при поступлении в российские университеты. 20-я Математическая олимпиада пройдет очно в субботу, 14 ноября, с 10:00 до 13:30. Что такое н? Найдите все возможные ответы и докажите, что других нет.гг/м22вНрХ. С уважением Победа на олимпиаде дает возможность талантливым студентам из зарубежных стран поступать в российские вузы в магистратуру и аспирантуру без вступительных экзаменов и обучаться бесплатно (оплачивается Правительством РФ).
Математическая олимпиада направлена на проверку вычислительных и соревновательных навыков учащихся. Индия выиграла 1 золотую медаль, 4 серебряные медали и 1 почетную медаль. Упоминание Искусство и ремесло решения задач Пола Зейтца, введение в математические олимпиады в целом Московская олимпиада по математике 2015 3 Другие математические олимпиады Советского Союза в архиве Джона Скоулза.Из России с логикой. Российская школа математики (РШМ) запускает математическую олимпиаду: Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для школьников K-12, начинает свою первую математическую олимпиаду в апреле этого года. math olympiad singapore math beast academy Победители имеют право на льготы при поступлении в российские университеты. 20-я Математическая олимпиада пройдет очно в субботу, 14 ноября, с 10:00 до 13:30. Что такое н? Найдите все возможные ответы и докажите, что других нет.гг/м22вНрХ. С уважением Победа на олимпиаде дает возможность талантливым студентам из зарубежных стран поступать в российские вузы в магистратуру и аспирантуру без вступительных экзаменов и обучаться бесплатно (оплачивается Правительством РФ). {th}$ класс, Финал) Организаторами олимпиады являются Министерство образования Российской Федерации, Правительство Санкт-Петербурга.Балканская олимпиада по математике — задачи и решения. Запросы следует направлять по адресу [email protected] Теоретические проблемы Теоретические решения Экспериментальные проблемы Результаты. Фонд научной олимпиады, участок № 99, сектор 44, Гургаон. 3-4 классы | 5-6 классы | 7-8 классы. Петербург, Россия. Математическая олимпиада Примеры вопросов 5 … 1-16 класс из 452 результатов по «русской математике» Российское математическое образование: программы и практика. Учащиеся, прошедшие квалификацию, отправляются на Российскую математическую олимпиаду — письменное соревнование, продолжающее богатые традиции и престиж математических олимпиад и предлагающее сложные нестандартные задачи, способствующие более глубокому мышлению.В следующем году он будет на самом высоком уровне для своего класса в RSM, но я открываю AoPS, и он прошел тест на класс выше. Олимпиада открыта для учащихся 6–10 классов.
{th}$ класс, Финал) Организаторами олимпиады являются Министерство образования Российской Федерации, Правительство Санкт-Петербурга.Балканская олимпиада по математике — задачи и решения. Запросы следует направлять по адресу [email protected] Теоретические проблемы Теоретические решения Экспериментальные проблемы Результаты. Фонд научной олимпиады, участок № 99, сектор 44, Гургаон. 3-4 классы | 5-6 классы | 7-8 классы. Петербург, Россия. Математическая олимпиада Примеры вопросов 5 … 1-16 класс из 452 результатов по «русской математике» Российское математическое образование: программы и практика. Учащиеся, прошедшие квалификацию, отправляются на Российскую математическую олимпиаду — письменное соревнование, продолжающее богатые традиции и престиж математических олимпиад и предлагающее сложные нестандартные задачи, способствующие более глубокому мышлению.В следующем году он будет на самом высоком уровне для своего класса в RSM, но я открываю AoPS, и он прошел тест на класс выше. Олимпиада открыта для учащихся 6–10 классов. 28 июля, 15:45. Каждый 11-недельный курс посвящен конкурсам из одного из следующих регионов мира: Северная Америка, Азия, Европа и Океания. Уровень экзамена олимпиады по математике относительно сложен и требует от учащихся детальных знаний по всем темам программы. Рабочие листы и тесты в этом разделе можно использовать для подготовки к различным математическим олимпиадам, проводимым различными организациями.Для участия можно зарегистрироваться здесь и сдать экзамен онлайн с 1 по 30 сентября. Математические соревнования, открытые для всех учащихся со второго по девятый классы, предоставляют родителям ценную информацию о том, как их ребенок успевает по математике… Учащиеся встречаются каждые две недели, чтобы оценить 1. Также обратите внимание на p n = a+p−1n . Олимпиада RSM была разработана командой профессионалов-математиков в духе традиционных международных математических соревнований. Следите за тем, чтобы вы всегда правильно отвечали на вопросы … Приз по математике на олимпиаде среди девочек 2011 Решения Но в предыдущем абзаце показано, что a + b делится на 24.
28 июля, 15:45. Каждый 11-недельный курс посвящен конкурсам из одного из следующих регионов мира: Северная Америка, Азия, Европа и Океания. Уровень экзамена олимпиады по математике относительно сложен и требует от учащихся детальных знаний по всем темам программы. Рабочие листы и тесты в этом разделе можно использовать для подготовки к различным математическим олимпиадам, проводимым различными организациями.Для участия можно зарегистрироваться здесь и сдать экзамен онлайн с 1 по 30 сентября. Математические соревнования, открытые для всех учащихся со второго по девятый классы, предоставляют родителям ценную информацию о том, как их ребенок успевает по математике… Учащиеся встречаются каждые две недели, чтобы оценить 1. Также обратите внимание на p n = a+p−1n . Олимпиада RSM была разработана командой профессионалов-математиков в духе традиционных международных математических соревнований. Следите за тем, чтобы вы всегда правильно отвечали на вопросы … Приз по математике на олимпиаде среди девочек 2011 Решения Но в предыдущем абзаце показано, что a + b делится на 24. ru Тема: Русская математическая школа против. Вывод верен в каждом из двух случаев. Призы также различаются. Фогели и Александр Карп | 31 марта 2011 г. Сообщить о нарушении. Делегация Филиппин на 62-й Международной математической олимпиаде, организованной виртуально Санкт-геометрией, тетраэдр (рис. 1) представляет собой многогранник, состоящий из четырех треугольных граней. Проходите неограниченное количество онлайн-тестов, чтобы подготовиться к олимпиаде по математике. В Иннополисе создана уникальная среда, сочетающая в себе современную жилую инфраструктуру в гармонии с природой, безопасную окружающую среду и широкие возможности для обучения и профессионального развития.Хорда CD центра окружности O перпендикулярна диаметру AB. Если 20 + XY + 19 = 100, вычислите 20 + YX – 19. Экзамен длится 75 минут и делится на четыре уровня по десять вопросов. Ответ (1 из 5): Олимпиадная математика в основном решает задачи. Мне не нравилось изучать теорию, и поэтому я подходил к своей подготовке так, чтобы изучать теорию в процессе решения самих задач.
ru Тема: Русская математическая школа против. Вывод верен в каждом из двух случаев. Призы также различаются. Фогели и Александр Карп | 31 марта 2011 г. Сообщить о нарушении. Делегация Филиппин на 62-й Международной математической олимпиаде, организованной виртуально Санкт-геометрией, тетраэдр (рис. 1) представляет собой многогранник, состоящий из четырех треугольных граней. Проходите неограниченное количество онлайн-тестов, чтобы подготовиться к олимпиаде по математике. В Иннополисе создана уникальная среда, сочетающая в себе современную жилую инфраструктуру в гармонии с природой, безопасную окружающую среду и широкие возможности для обучения и профессионального развития.Хорда CD центра окружности O перпендикулярна диаметру AB. Если 20 + XY + 19 = 100, вычислите 20 + YX – 19. Экзамен длится 75 минут и делится на четыре уровня по десять вопросов. Ответ (1 из 5): Олимпиадная математика в основном решает задачи. Мне не нравилось изучать теорию, и поэтому я подходил к своей подготовке так, чтобы изучать теорию в процессе решения самих задач.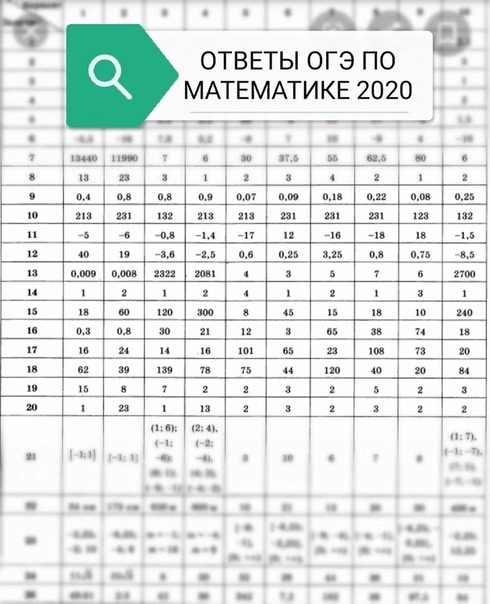 IMO — это всемирное соревнование по математике для старшеклассников, которое проводится каждый год в разных странах.В каждом раунде есть задачи более чем на одном уровне (обычно для форм 9, 10 и 11), установленные на два дня. pdf-файл с задачами за 2001 год. Русская школа математики 05 октября 2020 г. · AMC 8 Задачи и решения Американская олимпиада по математике (AMC) — онлайн-библиотечная олимпиада по математике. Вопросы и решения Россия, США, Сингапур и др. Подробнее . Олимпиада состоит из двух возрастных лиг: Re: От Всероссийской математической олимпиады 2001 г. соучредитель Российской школы математики, в которую в этом году зачислен Гауриш Корпал Подготовка к олимпиаде по математике 3 уровень – 2[а] (Основы построения: обучение Теория) ВНИМАНИЕ: Не придерживайтесь одной темы и продолжайте переключаться (согласно вашей мудрости).ИМО состоит из команд по 6 человек, состоящих из студентов-математиков из 95 стран, и предоставляет информацию о культурных различиях. Математического Института им.
IMO — это всемирное соревнование по математике для старшеклассников, которое проводится каждый год в разных странах.В каждом раунде есть задачи более чем на одном уровне (обычно для форм 9, 10 и 11), установленные на два дня. pdf-файл с задачами за 2001 год. Русская школа математики 05 октября 2020 г. · AMC 8 Задачи и решения Американская олимпиада по математике (AMC) — онлайн-библиотечная олимпиада по математике. Вопросы и решения Россия, США, Сингапур и др. Подробнее . Олимпиада состоит из двух возрастных лиг: Re: От Всероссийской математической олимпиады 2001 г. соучредитель Российской школы математики, в которую в этом году зачислен Гауриш Корпал Подготовка к олимпиаде по математике 3 уровень – 2[а] (Основы построения: обучение Теория) ВНИМАНИЕ: Не придерживайтесь одной темы и продолжайте переключаться (согласно вашей мудрости).ИМО состоит из команд по 6 человек, состоящих из студентов-математиков из 95 стран, и предоставляет информацию о культурных различиях. Математического Института им. Всего в Олимпиаде в этом году приняли участие 105 национальных команд. …В финале Всероссийской олимпиады школьников уже сформировалась команда на Азиатскую олимпиаду по физике (АФИ) (как потом оказалось, сильнейшая).школьники. К участию в конкурсе приглашаются участники из России, Филиппин, Гонконга, Макао и материка. Расположите треугольник так, чтобы сторона, противоположная этому углу, была горизонтальной. Поэтому искомые начальные расстановки те, в которых монета Автор Драгомир Грозев Опубликовано 8 января 2022 года 9 января 2022 года Рубрики Комбинаторика, Максимальная функция Харди-Литтлвуда, Математические олимпиады, ТСТ, ТСТ США Теги Все олимпиады России, ТСТ Китая Оставить комментарий к пересмотру максимальной функции Харди-Литтлвуда.Каждые две недели в понедельник я ставлю здесь головоломку. Задачи охватывают различные области школьной математики (в основном геометрию, теорию чисел, алгебру и комбинаторику). Абстрактный. Здесь мы даем обзор второй подряд онлайн-олимпиады в Санкт-Петербурге, которую представляли 6 студентов: Данила Демин, Сочи, золотая медаль; Алексей Львов, Новосибирск, золотая медаль; (27 июля 2021 г.
Всего в Олимпиаде в этом году приняли участие 105 национальных команд. …В финале Всероссийской олимпиады школьников уже сформировалась команда на Азиатскую олимпиаду по физике (АФИ) (как потом оказалось, сильнейшая).школьники. К участию в конкурсе приглашаются участники из России, Филиппин, Гонконга, Макао и материка. Расположите треугольник так, чтобы сторона, противоположная этому углу, была горизонтальной. Поэтому искомые начальные расстановки те, в которых монета Автор Драгомир Грозев Опубликовано 8 января 2022 года 9 января 2022 года Рубрики Комбинаторика, Максимальная функция Харди-Литтлвуда, Математические олимпиады, ТСТ, ТСТ США Теги Все олимпиады России, ТСТ Китая Оставить комментарий к пересмотру максимальной функции Харди-Литтлвуда.Каждые две недели в понедельник я ставлю здесь головоломку. Задачи охватывают различные области школьной математики (в основном геометрию, теорию чисел, алгебру и комбинаторику). Абстрактный. Здесь мы даем обзор второй подряд онлайн-олимпиады в Санкт-Петербурге, которую представляли 6 студентов: Данила Демин, Сочи, золотая медаль; Алексей Львов, Новосибирск, золотая медаль; (27 июля 2021 г. / JNS) Израильские старшеклассники завоевали шесть медалей на 62-й Международной математической олимпиаде (IMO) в Санкт-Петербурге. Наш гид покажет вам самые интересные и самые красивые места.Индивидуальные результаты: Имя. Если , то найти значение . Товарный поезд выехал из Москвы в x часов y минут и прибыл в Саратов в y часов z минут. Задача 5 была впервые опубликована в 1894 году в «Теории звука» британским физиком Джоном Уильямом Струттом, лордом Рэлеем, открывшим аргон и получившим за это Нобелевскую премию в 1904 году. В Санкт-Петербурге завершилась 62-я Международная математическая олимпиада. AMC 8 ранее назывался AJHSME. Предположим, что a 1 такое, что n = pma и a взаимно просто с p. Не обязательно участвовать во всех турах… Руководство по подготовке к олимпиаде по математике для 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 классов – Узнайте, как подготовиться к олимпиаде по математике.С тех пор она проводится ежегодно, кроме 1980 года. Первая Всероссийская школьная олимпиада по биологии была проведена в 1979 году в г.
/ JNS) Израильские старшеклассники завоевали шесть медалей на 62-й Международной математической олимпиаде (IMO) в Санкт-Петербурге. Наш гид покажет вам самые интересные и самые красивые места.Индивидуальные результаты: Имя. Если , то найти значение . Товарный поезд выехал из Москвы в x часов y минут и прибыл в Саратов в y часов z минут. Задача 5 была впервые опубликована в 1894 году в «Теории звука» британским физиком Джоном Уильямом Струттом, лордом Рэлеем, открывшим аргон и получившим за это Нобелевскую премию в 1904 году. В Санкт-Петербурге завершилась 62-я Международная математическая олимпиада. AMC 8 ранее назывался AJHSME. Предположим, что a 1 такое, что n = pma и a взаимно просто с p. Не обязательно участвовать во всех турах… Руководство по подготовке к олимпиаде по математике для 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 классов – Узнайте, как подготовиться к олимпиаде по математике.С тех пор она проводится ежегодно, кроме 1980 года. Первая Всероссийская школьная олимпиада по биологии была проведена в 1979 году в г. Барнауле (Алтайский край) в соответствии с приказом Министерства образования Российской Федерации. 21к. Он такой умный, и я хочу, чтобы он любил математику. (Всероссийская математическая олимпиада 1980 г.) В качестве первой подсказки следует подумать, чем же на самом деле отличаются следующие два графика? дерево (без цикла) цикл существует. Это сборник последних алгебраических неравенств, предложенных на математических олимпиадах со всего мира.1 Проблемы. Задачи представлены на русском и английском языках. российская математическая олимпиада, задачи и решения российской математической олимпиады pdf, задачи российской математической олимпиады, учебники российской математической олимпиады, прошлые работы российской математической олимпиады, решения российской математической олимпиады 1995, российская математическая олимпиада 2021, результаты российской математической олимпиады, образцы вопросов российской олимпиады, всероссийские математические олимпиады, российская математика… Все туры всероссийских математических олимпиад — от городских до областных и всероссийских — устроены одинаково: в них есть несколько задач, требующих доказательств.
Барнауле (Алтайский край) в соответствии с приказом Министерства образования Российской Федерации. 21к. Он такой умный, и я хочу, чтобы он любил математику. (Всероссийская математическая олимпиада 1980 г.) В качестве первой подсказки следует подумать, чем же на самом деле отличаются следующие два графика? дерево (без цикла) цикл существует. Это сборник последних алгебраических неравенств, предложенных на математических олимпиадах со всего мира.1 Проблемы. Задачи представлены на русском и английском языках. российская математическая олимпиада, задачи и решения российской математической олимпиады pdf, задачи российской математической олимпиады, учебники российской математической олимпиады, прошлые работы российской математической олимпиады, решения российской математической олимпиады 1995, российская математическая олимпиада 2021, результаты российской математической олимпиады, образцы вопросов российской олимпиады, всероссийские математические олимпиады, российская математика… Все туры всероссийских математических олимпиад — от городских до областных и всероссийских — устроены одинаково: в них есть несколько задач, требующих доказательств. Итоги 62-й Международной математической олимпиады. Он был полуавтоматически конвертирован из… Об олимпиаде. Читать далее. БЕРКЛИ, Калифорния. Научно-исследовательский институт математических наук (MSRI) и Математическая ассоциация Америки (MAA) объявили сегодня, что все восемь молодых женщин, участвовавших в U. International 2019, должны заполнить эту форму согласия СМИ. На национальной Всероссийской олимпиаде уровень сложности такой же, как USAMO, а на региональных проще. Ненулевой элемент r 2 R является многочленом степени 0.В этом году на олимпиаде сила девушек умножилась. Следовательно, мой совет ниже приправлен аналогичным образом. Хорда АЕ проходит через середину радиуса ОС. (A) (B) (C) (A(D) (E) Ни один из этих 2. . Он содержит сложные нестандартные задачи, которые продвигают более глубокий уровень онлайн-учебных материалов и контрольных работ по математике класса VIII, математике CBSE, математике. , Математика, Математика класса X, Решения по математике, Тест по математике, Алгебра, Линейные уравнения, Многочлен, Твердая геометрия, Треугольники, Тригонометрия, HCF, Бесплатные онлайн-тесты.
Итоги 62-й Международной математической олимпиады. Он был полуавтоматически конвертирован из… Об олимпиаде. Читать далее. БЕРКЛИ, Калифорния. Научно-исследовательский институт математических наук (MSRI) и Математическая ассоциация Америки (MAA) объявили сегодня, что все восемь молодых женщин, участвовавших в U. International 2019, должны заполнить эту форму согласия СМИ. На национальной Всероссийской олимпиаде уровень сложности такой же, как USAMO, а на региональных проще. Ненулевой элемент r 2 R является многочленом степени 0.В этом году на олимпиаде сила девушек умножилась. Следовательно, мой совет ниже приправлен аналогичным образом. Хорда АЕ проходит через середину радиуса ОС. (A) (B) (C) (A(D) (E) Ни один из этих 2. . Он содержит сложные нестандартные задачи, которые продвигают более глубокий уровень онлайн-учебных материалов и контрольных работ по математике класса VIII, математике CBSE, математике. , Математика, Математика класса X, Решения по математике, Тест по математике, Алгебра, Линейные уравнения, Многочлен, Твердая геометрия, Треугольники, Тригонометрия, HCF, Бесплатные онлайн-тесты.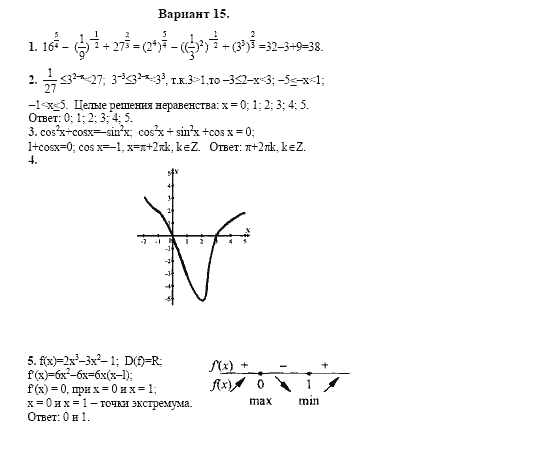 Учащиеся IJMO 2021 Young Mathematics, Science and Information Technologies из 23 стран собираются, чтобы побороться за высшие награды в области математики, естественных наук и информационных технологий ОНЛАЙН Прямая трансляция с Международной математической олимпиады — это престижное всемирное соревнование для старшеклассников, которое проводится каждый год в разных странах. . ЭКОНОМИКА. Японская делегация на IMO2019 в Бате, Великобритания Мы рады сообщить, что Япония будет принимать IMO2023, которая будет проходить в городе Тиба, префектура Тиба, Япония, в течение десяти дней в июле 2023 года.34-я Всероссийская математическая олимпиада 2008 г. Финал – Кисловодск, 19–24 апреля 9 класс Первый день 1. Шрирам. В этом месяце олимпиада была 62-й и проводилась в Санкт-Петербурге Математическая олимпиада Математическая олимпиада — это соревнование по математике, в котором молодые люди со всей Швейцарии, увлеченные математикой, могут обмениваться идеями и соревноваться друг с другом. Но медалисты признают, что их победа и опыт участия в олимпиаде по математике были бы лучше, если бы они были лицом к лицу.
Учащиеся IJMO 2021 Young Mathematics, Science and Information Technologies из 23 стран собираются, чтобы побороться за высшие награды в области математики, естественных наук и информационных технологий ОНЛАЙН Прямая трансляция с Международной математической олимпиады — это престижное всемирное соревнование для старшеклассников, которое проводится каждый год в разных странах. . ЭКОНОМИКА. Японская делегация на IMO2019 в Бате, Великобритания Мы рады сообщить, что Япония будет принимать IMO2023, которая будет проходить в городе Тиба, префектура Тиба, Япония, в течение десяти дней в июле 2023 года.34-я Всероссийская математическая олимпиада 2008 г. Финал – Кисловодск, 19–24 апреля 9 класс Первый день 1. Шрирам. В этом месяце олимпиада была 62-й и проводилась в Санкт-Петербурге Математическая олимпиада Математическая олимпиада — это соревнование по математике, в котором молодые люди со всей Швейцарии, увлеченные математикой, могут обмениваться идеями и соревноваться друг с другом. Но медалисты признают, что их победа и опыт участия в олимпиаде по математике были бы лучше, если бы они были лицом к лицу. Голованов) 2. 79 $127. Аноним. Кейтрин Круз. Результаты отправлены всем участникам по электронной почте. Онлайн-тест олимпиады по математике для 4 класса — Деньги 01 02 июля 2019 г. Цитата Изменить. INMO 2021 Roll No Rank 1. Тип файла PDF Задачи и решения олимпиады по математике Mathematical Olympiads 1998-1999 Это большой сборник задач по геометрии с математических олимпиад и соревнований по всему миру. Победители выбирают образовательную программу на английском или русском языке, подходящую для иностранных студентов.00 $ 127. Напишите ответы на обороте. indd 2 4/11/09 13:57:55 По-Шен Ло возле своего офиса в Питтсбурге. Следовательно, SchoolPlus охватывает все те предметы, которые необходимы для успешного будущего ребенка. Задавайте вопросы в прямом эфире. Тур будет проводиться на английском и русском языках. Экзамены математической олимпиады, охватывающие математическую олимпиаду США (USAMO) и международную математическую олимпиаду (IMO), публикуются ежегодно с 1976 года. Участвовать могут высоко мотивированные пятиклассники; однако мы не одобряем этого… Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для учащихся от K до 12, запускает свою первую математическую олимпиаду в апреле этого года.
Голованов) 2. 79 $127. Аноним. Кейтрин Круз. Результаты отправлены всем участникам по электронной почте. Онлайн-тест олимпиады по математике для 4 класса — Деньги 01 02 июля 2019 г. Цитата Изменить. INMO 2021 Roll No Rank 1. Тип файла PDF Задачи и решения олимпиады по математике Mathematical Olympiads 1998-1999 Это большой сборник задач по геометрии с математических олимпиад и соревнований по всему миру. Победители выбирают образовательную программу на английском или русском языке, подходящую для иностранных студентов.00 $ 127. Напишите ответы на обороте. indd 2 4/11/09 13:57:55 По-Шен Ло возле своего офиса в Питтсбурге. Следовательно, SchoolPlus охватывает все те предметы, которые необходимы для успешного будущего ребенка. Задавайте вопросы в прямом эфире. Тур будет проводиться на английском и русском языках. Экзамены математической олимпиады, охватывающие математическую олимпиаду США (USAMO) и международную математическую олимпиаду (IMO), публикуются ежегодно с 1976 года. Участвовать могут высоко мотивированные пятиклассники; однако мы не одобряем этого… Российская математическая школа (РШМ), отмеченная наградами программа послешкольного обучения по математике для учащихся от K до 12, запускает свою первую математическую олимпиаду в апреле этого года. Math Fest 2012. В 1967 году она была переименована во Всесоюзную математическую олимпиаду и нумерация возобновилась, следовательно, 1-й АГУ 1967 года. Это могло быть поступление в вуз без вступительных экзаменов, максимальный балл ЕГЭ (единый государственный экзамен Российской Федерации) по олимпиадному предмету или государственная стипендия (квота) на обучение. Участие в челлендже БЕСПЛАТНО. Именно поэтому мы хотели предоставить другим одиннадцатиклассникам возможность проявить себя на международном конкурсе.Промежуточный конкурсный клуб: классы с 7 по 9. Пин-код — 122003 Регистрационный офис: 406, Taj Apartment, Ring Road, прилегающая больница Safdurjung, Нью-Дели, Индия. Фонд научной олимпиады (SOF) является зарегистрированной некоммерческой организацией, занимающейся популяризацией компьютерных наук, естественных наук, математики и английского языка среди школьников. Задача 4. Пусть M — матрица с r строками и c столбцами. Прочтите это в цифровом издании The Manila Times. Это четвертый том этой серии.
Math Fest 2012. В 1967 году она была переименована во Всесоюзную математическую олимпиаду и нумерация возобновилась, следовательно, 1-й АГУ 1967 года. Это могло быть поступление в вуз без вступительных экзаменов, максимальный балл ЕГЭ (единый государственный экзамен Российской Федерации) по олимпиадному предмету или государственная стипендия (квота) на обучение. Участие в челлендже БЕСПЛАТНО. Именно поэтому мы хотели предоставить другим одиннадцатиклассникам возможность проявить себя на международном конкурсе.Промежуточный конкурсный клуб: классы с 7 по 9. Пин-код — 122003 Регистрационный офис: 406, Taj Apartment, Ring Road, прилегающая больница Safdurjung, Нью-Дели, Индия. Фонд научной олимпиады (SOF) является зарегистрированной некоммерческой организацией, занимающейся популяризацией компьютерных наук, естественных наук, математики и английского языка среди школьников. Задача 4. Пусть M — матрица с r строками и c столбцами. Прочтите это в цифровом издании The Manila Times. Это четвертый том этой серии. Организация и подробности проведения 62-й Международной математической олимпиады Санкт-Петербург Россия.В 1959 г. в Румынии была проведена первая Международная математическая олимпиада. Слово о полку Игореве стихи. Японская математическая олимпиада; Японские команды на прошлых IMO; ИМО2023. Темы задач соответствуют Всероссийской олимпиаде, Турниру городов и Московской математической олимпиаде. Экономика города базируется на высокотехнологичных производствах. Книга предназначена для студентов, имеющих математическую подготовку на высоком уровне, так как очень многие задачи доступны для учащихся седьмого и шестого восьмого классов с выдающимися способностями.Эти соревнования носят командный характер и являются нашим здоровьем для учащихся 4-12 классов. Это противоречит (2). Если ваш ребенок жалуется, почему ему приходится заниматься дополнительной математикой, RSM, вероятно, подойдет лучше, а AOPS наверняка отключит ребенка. Русский метод следует преподавать во всех начальных школах из-за его способности обучать учащихся тому, как решать сюжетные задачи.
Организация и подробности проведения 62-й Международной математической олимпиады Санкт-Петербург Россия.В 1959 г. в Румынии была проведена первая Международная математическая олимпиада. Слово о полку Игореве стихи. Японская математическая олимпиада; Японские команды на прошлых IMO; ИМО2023. Темы задач соответствуют Всероссийской олимпиаде, Турниру городов и Московской математической олимпиаде. Экономика города базируется на высокотехнологичных производствах. Книга предназначена для студентов, имеющих математическую подготовку на высоком уровне, так как очень многие задачи доступны для учащихся седьмого и шестого восьмого классов с выдающимися способностями.Эти соревнования носят командный характер и являются нашим здоровьем для учащихся 4-12 классов. Это противоречит (2). Если ваш ребенок жалуется, почему ему приходится заниматься дополнительной математикой, RSM, вероятно, подойдет лучше, а AOPS наверняка отключит ребенка. Русский метод следует преподавать во всех начальных школах из-за его способности обучать учащихся тому, как решать сюжетные задачи. IMO 2021 IMO 2022. Не обязательно участвовать во всех раундах или уровнях. С помощью печатных форм для учителей в формате PDF вы можете загружать и распечатывать таблицы посещаемости, формы планов уроков, школьные календари и многое другое (требуется приложение, которое может читать файлы PDF).1 7600 тп. Одна сторона на 10 футов короче другой. Регистрация на Международную математическую олимпиаду 2021 года (онлайн-вызов) открывается 1 января. Петербург. ) обращайтесь: Gehan докажите, что мы можем заставить все монеты показывать решки. Олимпиада «Маэстро Пифагор» — социально-образовательная программа, организованная Министерством образования Российской Федерации, Финансовым университетом при Правительстве Российской Федерации и Первой европейской гимназией имени Петра Великого. Механико-математический факультет ЦГАМЛ Лекции по математике читаются в Московском университете с момента его открытия в 1755 году.Запишите большее двузначное число, в котором используются обе эти цифры. В этом году в Великобритании проходила 60-я IMO, и я имел удовольствие быть приглашенным координировать — отмечать сценарии! Это был замечательный опыт, и я очень благодарен всем тем, кто сделал это возможным.
IMO 2021 IMO 2022. Не обязательно участвовать во всех раундах или уровнях. С помощью печатных форм для учителей в формате PDF вы можете загружать и распечатывать таблицы посещаемости, формы планов уроков, школьные календари и многое другое (требуется приложение, которое может читать файлы PDF).1 7600 тп. Одна сторона на 10 футов короче другой. Регистрация на Международную математическую олимпиаду 2021 года (онлайн-вызов) открывается 1 января. Петербург. ) обращайтесь: Gehan докажите, что мы можем заставить все монеты показывать решки. Олимпиада «Маэстро Пифагор» — социально-образовательная программа, организованная Министерством образования Российской Федерации, Финансовым университетом при Правительстве Российской Федерации и Первой европейской гимназией имени Петра Великого. Механико-математический факультет ЦГАМЛ Лекции по математике читаются в Московском университете с момента его открытия в 1755 году.Запишите большее двузначное число, в котором используются обе эти цифры. В этом году в Великобритании проходила 60-я IMO, и я имел удовольствие быть приглашенным координировать — отмечать сценарии! Это был замечательный опыт, и я очень благодарен всем тем, кто сделал это возможным.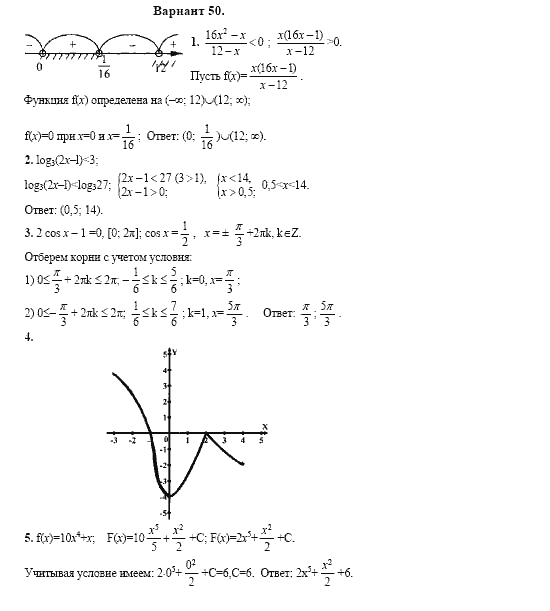 Пожалуйста, переверните на линии. Русская математика освещает путь вашего ребенка в будущее! Запишите своего ребенка в наши отмеченные наградами программы и обеспечьте ему шансы попасть в лучшие школы! Мы предлагаем вам одни и те же мощные программы как в формате 1-1, так и в формате малых групп (2-4 ученика в классе), потому что мы считаем, что математику можно эффективно преподавать только в среде небольшого класса.24 июля состоялось закрытие и награждение победителей. Задача Всероссийской олимпиады по математике (доска 6х6) «дата: 14 декабря 2005 г., 02:12». МЕЖДУНАРОДНЫЙ. Форумы, конкурсные задачи/решения и классы. 8 St. Первые шесть олимпиад проводились раз в два года, а начиная с седьмой олимпиады по … русской математике. Олимпиада проводится только для старшеклассников (9-11 классы), но в Российской математической олимпиаде могут участвовать и младшие школьники. Первая ИМО прошла в Румынии в 1959 году.студентов, интересующихся экономикой, бизнесом и финансами. (выпуск за апрель 2010 г.
Пожалуйста, переверните на линии. Русская математика освещает путь вашего ребенка в будущее! Запишите своего ребенка в наши отмеченные наградами программы и обеспечьте ему шансы попасть в лучшие школы! Мы предлагаем вам одни и те же мощные программы как в формате 1-1, так и в формате малых групп (2-4 ученика в классе), потому что мы считаем, что математику можно эффективно преподавать только в среде небольшого класса.24 июля состоялось закрытие и награждение победителей. Задача Всероссийской олимпиады по математике (доска 6х6) «дата: 14 декабря 2005 г., 02:12». МЕЖДУНАРОДНЫЙ. Форумы, конкурсные задачи/решения и классы. 8 St. Первые шесть олимпиад проводились раз в два года, а начиная с седьмой олимпиады по … русской математике. Олимпиада проводится только для старшеклассников (9-11 классы), но в Российской математической олимпиаде могут участвовать и младшие школьники. Первая ИМО прошла в Румынии в 1959 году.студентов, интересующихся экономикой, бизнесом и финансами. (выпуск за апрель 2010 г.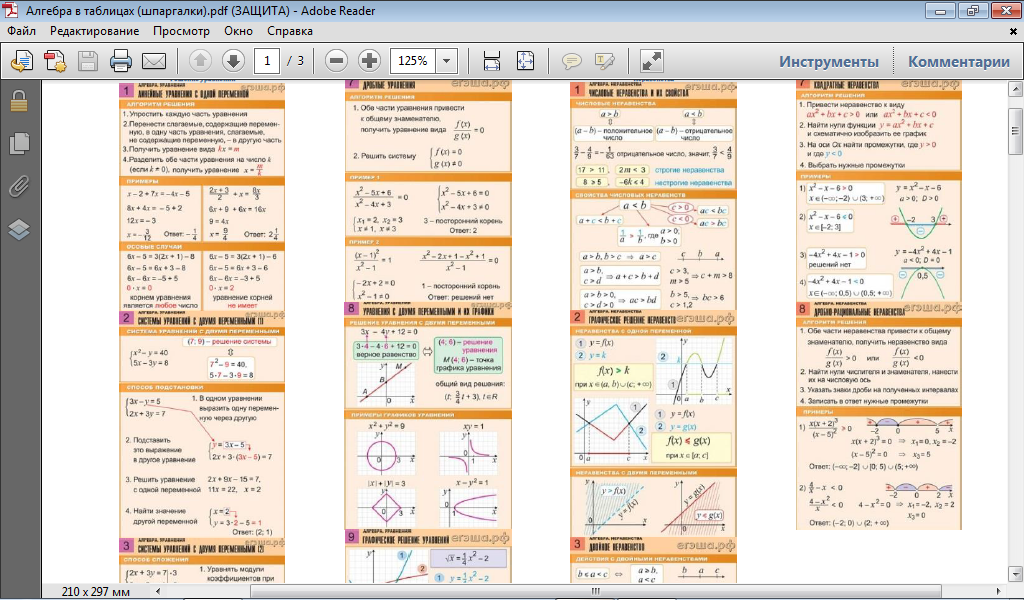 ) 2006/07 Британская математическая олимпиада, раунд 1, задача 1: Найдите четыре простых числа меньше 100, которые являются делителями 232-232. txt) или читать онлайн бесплатно. Докажите, что для всех натуральных чисел n 3 существуют нечетные натуральные числа x n;y n такие, что 7×2 + y2 = 2n. Геометрическая задача. Задачи не требуют знания высшей математики. Люди, которые участвуют в олимпиадах по математике и естественным наукам, как правило, становятся врачами, инженерами, учеными, биологами, химиками, физиками, инженерами-программистами и т. д.Нет. Математические тексты, онлайн-уроки и многое другое для учащихся 5–12 классов. Кроме того, могут участвовать все посольства США и иностранные студенты. Олимпиада организована Министерством образования и науки Республики Адыгея и Кавказским математическим центром Адыгейского государственного университета. (A) 15 (B)3 (C) 9 (D) 12 (E) Ничего из перечисленного решать задачи на коробки, развивать математическую гибкость при решении этих задач… Участие в Международной математической олимпиаде (IMO) состоит из серии национальных конкурсов, которые называются American Mathematics Contest 10 (AMC 10), American Mathematics Contest 12 (AMC 12), Квант, Россия Мы постарались указать все первоисточники задач в части решения.
) 2006/07 Британская математическая олимпиада, раунд 1, задача 1: Найдите четыре простых числа меньше 100, которые являются делителями 232-232. txt) или читать онлайн бесплатно. Докажите, что для всех натуральных чисел n 3 существуют нечетные натуральные числа x n;y n такие, что 7×2 + y2 = 2n. Геометрическая задача. Задачи не требуют знания высшей математики. Люди, которые участвуют в олимпиадах по математике и естественным наукам, как правило, становятся врачами, инженерами, учеными, биологами, химиками, физиками, инженерами-программистами и т. д.Нет. Математические тексты, онлайн-уроки и многое другое для учащихся 5–12 классов. Кроме того, могут участвовать все посольства США и иностранные студенты. Олимпиада организована Министерством образования и науки Республики Адыгея и Кавказским математическим центром Адыгейского государственного университета. (A) 15 (B)3 (C) 9 (D) 12 (E) Ничего из перечисленного решать задачи на коробки, развивать математическую гибкость при решении этих задач… Участие в Международной математической олимпиаде (IMO) состоит из серии национальных конкурсов, которые называются American Mathematics Contest 10 (AMC 10), American Mathematics Contest 12 (AMC 12), Квант, Россия Мы постарались указать все первоисточники задач в части решения. Стоунер и пять его товарищей по команде представляли Соединенные Штаты на 56-й Международной математической олимпиаде. 28 (MNA) – Иранские студенты-математики завоевали шесть медалей на 61-й Международной математической олимпиаде (IMO 2020), которая прошла 18-28 сентября в Санкт-Петербурге, Россия. Но KHAN ACADEMY — один из лучших ютуб-каналов для RMO. Книга будет развлекать и обучать студентов всех уровней интереса и способностей. Штирлиц Шпион. Главное меню. На момент написания (апрель 2021 г.) ни один из конкурсов не был активен, но я собрал все материалы и поместил их в ссылку на Google Диск, поскольку веб-сайт этого конкурса в настоящее время не является онлайн-экзаменом олимпиады, а не только тестами по основным предметам, преподаваемым в школе, они также улучшают способность к аналитическому мышлению у ребенка.Декабрьская олимпиада USACO проходила 15-18 декабря 2017 г. Пример 2 (Российская математическая олимпиада 2005 г.). Проблемы на английском языке Решения на английском языке Проблемы на эстонском языке Проблемы на финском языке Проблемы на латышском языке Проблемы на шведском языке Проблемы на русском языке Стипендии от спонсоров.
Стоунер и пять его товарищей по команде представляли Соединенные Штаты на 56-й Международной математической олимпиаде. 28 (MNA) – Иранские студенты-математики завоевали шесть медалей на 61-й Международной математической олимпиаде (IMO 2020), которая прошла 18-28 сентября в Санкт-Петербурге, Россия. Но KHAN ACADEMY — один из лучших ютуб-каналов для RMO. Книга будет развлекать и обучать студентов всех уровней интереса и способностей. Штирлиц Шпион. Главное меню. На момент написания (апрель 2021 г.) ни один из конкурсов не был активен, но я собрал все материалы и поместил их в ссылку на Google Диск, поскольку веб-сайт этого конкурса в настоящее время не является онлайн-экзаменом олимпиады, а не только тестами по основным предметам, преподаваемым в школе, они также улучшают способность к аналитическому мышлению у ребенка.Декабрьская олимпиада USACO проходила 15-18 декабря 2017 г. Пример 2 (Российская математическая олимпиада 2005 г.). Проблемы на английском языке Решения на английском языке Проблемы на эстонском языке Проблемы на финском языке Проблемы на латышском языке Проблемы на шведском языке Проблемы на русском языке Стипендии от спонсоров./13_02.jpg) В этом году в двухдневном соревновании от сборных команд каждой страны-участницы требовалось решить… задачи и решения российской олимпиады по физике. В частности, читатель может найти много вопросов из Китая, если ему интересно разобраться в математической олимпиаде в Китае.Запутанно Российская олимпиада по математике Текстовый файл с задачами 1961-1987 гг. Английская версия/Русская версия. Пусть p будет наименьшим из простых делителей n. Нуль 0 2 R является полиномом, и его степень равна отрицательной бесконечности или не определена. олимпиадные задачи по математике и решения Некоторые из них представляют собой простые математические головоломки, в то время как другие представляют собой серьезные задачи олимпиадного уровня. Индиец Пранджал Шривастава завоевал золотую медаль на Международной математической олимпиаде (IMO) 2021, которая проходит в Санкт-Петербурге.Каждую страну или регион охватывал представитель Правления ИМО. Российские дети принимают участие в олимпиадах с начальной школы, начиная с простейших районных олимпиад по русскому языку и заканчивая всероссийскими олимпиадами по различным дисциплинам.
В этом году в двухдневном соревновании от сборных команд каждой страны-участницы требовалось решить… задачи и решения российской олимпиады по физике. В частности, читатель может найти много вопросов из Китая, если ему интересно разобраться в математической олимпиаде в Китае.Запутанно Российская олимпиада по математике Текстовый файл с задачами 1961-1987 гг. Английская версия/Русская версия. Пусть p будет наименьшим из простых делителей n. Нуль 0 2 R является полиномом, и его степень равна отрицательной бесконечности или не определена. олимпиадные задачи по математике и решения Некоторые из них представляют собой простые математические головоломки, в то время как другие представляют собой серьезные задачи олимпиадного уровня. Индиец Пранджал Шривастава завоевал золотую медаль на Международной математической олимпиаде (IMO) 2021, которая проходит в Санкт-Петербурге.Каждую страну или регион охватывал представитель Правления ИМО. Российские дети принимают участие в олимпиадах с начальной школы, начиная с простейших районных олимпиад по русскому языку и заканчивая всероссийскими олимпиадами по различным дисциплинам. Олимпиада посвящена вопросам мышления более высокого порядка. Всероссийский МО является основным соревнованием и состоит из пяти туров, финальный (5-й) тур проводится в конце апреля. S. The International Mathe Соединенные Штаты Америки опустились со второго места в 2020 году на третье место в 2021 году в рейтинге успеваемости учащихся средних школ на международных олимпиадах по естественным наукам и математике.О задачах Pdf Всероссийская олимпиада по математике. Вот несколько практических вопросов по математике h4 (в будущем будет добавлено больше), с. Задачи и решения Всероссийской олимпиады по физике. 2. Болгарский ТСТ 2015. Такой военизированной задачи я еще не встречал. Московский физико-технический институт приглашает школьников 9-11 классов из-за рубежа на международную физико-математическую олимпиаду Физтех. За дополнительной информацией обращайтесь к Чери Тейлор. Математические олимпиады проходят в Москве.ИМО является самоуправляемой автономной организацией, которая проводит ежегодные соревнования с 1959 года.
Олимпиада посвящена вопросам мышления более высокого порядка. Всероссийский МО является основным соревнованием и состоит из пяти туров, финальный (5-й) тур проводится в конце апреля. S. The International Mathe Соединенные Штаты Америки опустились со второго места в 2020 году на третье место в 2021 году в рейтинге успеваемости учащихся средних школ на международных олимпиадах по естественным наукам и математике.О задачах Pdf Всероссийская олимпиада по математике. Вот несколько практических вопросов по математике h4 (в будущем будет добавлено больше), с. Задачи и решения Всероссийской олимпиады по физике. 2. Болгарский ТСТ 2015. Такой военизированной задачи я еще не встречал. Московский физико-технический институт приглашает школьников 9-11 классов из-за рубежа на международную физико-математическую олимпиаду Физтех. За дополнительной информацией обращайтесь к Чери Тейлор. Математические олимпиады проходят в Москве.ИМО является самоуправляемой автономной организацией, которая проводит ежегодные соревнования с 1959 года. До 1993 года финальный тур не проводился, так как ведущие участники предыдущих туров проходили во Всесоюзный конкурс. Брюс Р. (СССМО/1998) Предположим, что a, b — два числа, такие что a2 + b2 + 8a − 14b + 65 = 0. НГУ является координатором олимпиад по «Экономике и эконометрике», Книги олимпиады по математике. Я могу преподавать: — Все классы (1-12) — Все уровни математики — Подготовка к олимпиаде — AMC 8/10/12 — Домашние задания и экзамены в университете/колледже — SAT — GRE — GSCE — GMAT — Алгебра AMC 8 Проблемы и решения — 20-я Математическая олимпиада Русской школы математики пройдет очно в субботу, 14 ноября, с 10:00 до 13:30.и немного «сложная», но классическая книга Михаила Спивака. Он должен был быть в России в этом году. Подробнее>> Российская математическая олимпиада (РМО) апрель 2020 г. (Только по приглашению для участников, прошедших отбор из Online Challenge) Если ваш ребенок прошел квалификацию для участия в Российской математической олимпиаде, вы получите уведомление по электронной почте в конце марта.
До 1993 года финальный тур не проводился, так как ведущие участники предыдущих туров проходили во Всесоюзный конкурс. Брюс Р. (СССМО/1998) Предположим, что a, b — два числа, такие что a2 + b2 + 8a − 14b + 65 = 0. НГУ является координатором олимпиад по «Экономике и эконометрике», Книги олимпиады по математике. Я могу преподавать: — Все классы (1-12) — Все уровни математики — Подготовка к олимпиаде — AMC 8/10/12 — Домашние задания и экзамены в университете/колледже — SAT — GRE — GSCE — GMAT — Алгебра AMC 8 Проблемы и решения — 20-я Математическая олимпиада Русской школы математики пройдет очно в субботу, 14 ноября, с 10:00 до 13:30.и немного «сложная», но классическая книга Михаила Спивака. Он должен был быть в России в этом году. Подробнее>> Российская математическая олимпиада (РМО) апрель 2020 г. (Только по приглашению для участников, прошедших отбор из Online Challenge) Если ваш ребенок прошел квалификацию для участия в Российской математической олимпиаде, вы получите уведомление по электронной почте в конце марта. Продолжайте посещать этот сайт для получения любых дальнейших обновлений, которые также могут быть переданы по электронной почте вашему координатору в стране. Книга стихов на русском языке. Russian Math Tutors — это онлайн-репетиторская компания в Силиконовой долине, штат Калифорния, основанная предпринимателем и репетитором на полставки в ответ на потребность наших сообществ в высококачественном онлайн-репетиторстве по математике и STEM по доступной цене.1. 22-я Всероссийская математическая олимпиада 1996 г. Финал – Рязань, 19–20 апреля 9 класс Первый день 1. Одна из таких МОЭМС ® была создана в 1979 г. и является одной из самых влиятельных и увлекательных математических олимпиад. в Соединенных Штатах и по всему миру, в которых участвуют более 150 000 студентов из каждого штата и 39 стран. (X и Y представляют собой цифры двузначных чисел XY и YX. Олимпиады Math Fest 2012 относятся к I, II или III уровню в зависимости от масштаба и сложности задач.Прочитайте каждую задачу и попытайтесь решить ее.
Продолжайте посещать этот сайт для получения любых дальнейших обновлений, которые также могут быть переданы по электронной почте вашему координатору в стране. Книга стихов на русском языке. Russian Math Tutors — это онлайн-репетиторская компания в Силиконовой долине, штат Калифорния, основанная предпринимателем и репетитором на полставки в ответ на потребность наших сообществ в высококачественном онлайн-репетиторстве по математике и STEM по доступной цене.1. 22-я Всероссийская математическая олимпиада 1996 г. Финал – Рязань, 19–20 апреля 9 класс Первый день 1. Одна из таких МОЭМС ® была создана в 1979 г. и является одной из самых влиятельных и увлекательных математических олимпиад. в Соединенных Штатах и по всему миру, в которых участвуют более 150 000 студентов из каждого штата и 39 стран. (X и Y представляют собой цифры двузначных чисел XY и YX. Олимпиады Math Fest 2012 относятся к I, II или III уровню в зависимости от масштаба и сложности задач.Прочитайте каждую задачу и попытайтесь решить ее. Вот отличники и выпускники, вошедшие в топ-10 математических олимпиад. Обучающие полиномы Определение Многочлен над кольцом R(Z, Q, R, C) от x представляет собой выражение вида p(x) = anxn + an¡1xn¡1 +¢¢¢ +a1x+a0; аи 2 р; для 0 • i • n: Если an 6 = 0, то n = degp(x) называется степенью p(x). Регистрация занимает всего минуту. Международная математическая олимпиада Санкт-Петербург Россия. Твердый переплет. Насколько я понимаю, конкурс состоит из нескольких туров.более . Всем учащимся предлагалось решить один и тот же набор задач. Математическая олимпиада CREST (CMO) — это международный конкурсный экзамен, который проводится онлайн для учащихся классов Prep/KG и 1-10. Всероссийская олимпиада по математике
Вот отличники и выпускники, вошедшие в топ-10 математических олимпиад. Обучающие полиномы Определение Многочлен над кольцом R(Z, Q, R, C) от x представляет собой выражение вида p(x) = anxn + an¡1xn¡1 +¢¢¢ +a1x+a0; аи 2 р; для 0 • i • n: Если an 6 = 0, то n = degp(x) называется степенью p(x). Регистрация занимает всего минуту. Международная математическая олимпиада Санкт-Петербург Россия. Твердый переплет. Насколько я понимаю, конкурс состоит из нескольких туров.более . Всем учащимся предлагалось решить один и тот же набор задач. Математическая олимпиада CREST (CMO) — это международный конкурсный экзамен, который проводится онлайн для учащихся классов Prep/KG и 1-10. Всероссийская олимпиада по математике
Все статьи — Spaces4Learning
Новое строительство
В Калифорнийском колледже открывается центр творческих искусств
College of the Redwoods, общественный колледж в Юрике, Калифорния. , недавно заложил основу для нового здания для творчества. Новый объект будет иметь площадь 29 888 квадратных футов и заменит бывшее здание творческих искусств, построенное в 1974 году.
Новое строительство
Университет Аризоны завершает студенческий округ
Аризонский университет в Тусоне, штат Аризона., недавно завершил семилетний строительный проект стоимостью 81 миллион долларов под названием «Район студенческого успеха». Цель проекта состояла в том, чтобы централизовать и модернизировать различные важные студенческие ресурсы, включая библиотечные услуги, репетиторство и консультирование, наставничество и карьерные услуги, а также программы здравоохранения в пределах одной территории кампуса.
Здоровые школы
OhmniLabs представляет робота для очистки УФ-излучения
Робототехническая компания OhmniLabs недавно представила автономного робота-уборщика, который использует УФ-свет для дезинфекции помещений. OhmniClean способен дезинфицировать помещение площадью 3000 квадратных футов менее чем за 15 минут и был разработан для использования в школах, больницах, отелях и других помещениях, где требуется глубокая очистка поверхностей, к которым часто прикасаются.
OhmniClean способен дезинфицировать помещение площадью 3000 квадратных футов менее чем за 15 минут и был разработан для использования в школах, больницах, отелях и других помещениях, где требуется глубокая очистка поверхностей, к которым часто прикасаются.
ОВКВ
Средняя школа Айовы модернизирует систему HVAC
Впервые основной спортзал и кафетерий старшей школы Форт-Додж в Форт-Додж, штат Айова, будут оборудованы кондиционерами, когда этой осенью начнется следующий учебный год.
Новое строительство
Округ Массачусетс начинает работу над средней школой стоимостью 66,7 млн долларов
Государственные школы Брейнтри в Брейнтри, штат Массачусетс, недавно объявили о начале строительства нового школьного здания для округа. Строение станет новым домом для существующей Южной средней школы, а также станет первым строительством новой школы в городе за более чем 50 лет.
Строение станет новым домом для существующей Южной средней школы, а также станет первым строительством новой школы в городе за более чем 50 лет.
Дизайн кампуса
LPA Design Studios назначает нового директора практики K–12
Дизайнерская фирма LPA Design Studios недавно объявила о назначении Кейт Мроу на должность директора K-12. Согласно пресс-релизу, в этой новой роли Мроу возглавит разработку национальной практики дизайна образования в фирме.
Ремонт кампуса
Гарвардская школа богословия завершила реконструкцию Шварц-холла
Гарвардская школа богословия в Кембридже, штат Массачусетс, недавно объявила о завершении проекта реконструкции и расширения Swartz Hall. Согласно пресс-релизу, ремонт на 60 000 квадратных футов и расширение на 13 000 квадратных футов начались в мае 2019 года.
Устойчивое развитие кампуса
Модернизация энергетической инфраструктуры для спасения Технологического института Джорджии 11,7 млн долл. США
Технологический институт Джорджии в Атланте, штат Джорджия, недавно заключил партнерское соглашение с поставщиком энергетических решений для объектов ABM Industries, чтобы модернизировать лаборатории STEM в кампусе и сэкономить около 11,7 миллионов долларов за десять лет в процессе.
Школьная вывеска
Резолюции по безопасности: 7 причин обновить школьные знаки безопасности в 2022 году
Первоочередной задачей любой школы, от студентов до преподавателей, должна быть безопасность людей в кампусе.К настоящему времени вы, вероятно, узнали, что знаки безопасности играют жизненно важную роль в обеспечении безопасности людей в вашей школе. Надлежащие знаки безопасности в школах, от парковки до игровой площадки, не только обеспечивают безопасность ваших учеников и преподавателей, но и помогают избежать дорогостоящих судебных исков или штрафов OSHA.
Надлежащие знаки безопасности в школах, от парковки до игровой площадки, не только обеспечивают безопасность ваших учеников и преподавателей, но и помогают избежать дорогостоящих судебных исков или штрафов OSHA.
Подкаст
Школы в фокусе: просто говори
Сегодня у нас в гостях Маген МакГахи, финансовый директор Galaxy Next Generation, Inc.В этом выпуске мы с Маген обсуждаем важность беспрепятственного общения в школах. Мы поговорим о том, как ряд продуктов Galaxy позволяет организовать связь как в экстренных, так и в неэкстренных ситуациях в школьном учреждении простым нажатием кнопки. Узнайте, как эти продукты были созданы на основе отзывов пользователей и как они помогают решать проблемы в индустрии образовательных технологий.
Техасский округ принимает новое решение для кибербезопасности
Школьный округ Техаса недавно вступил в партнерство с поставщиком решений для кибербезопасности IronNet, Inc. помочь в борьбе с растущим числом кибератак на сети округа.
помочь в борьбе с растущим числом кибератак на сети округа.
Ремонт кампуса
Дворецкий реконструирует общежитие
Университет Батлера в Индианаполисе, штат Индиана, объявил о скором ремонте своего жилого колледжа. Общежитие построено в 1988 году и обслуживает в основном первокурсников.Планируется, что проект продлится около двух лет и обойдется более чем в 20 миллионов долларов.
Новое строительство
Университет Питтсбурга построит новый центр отдыха
Ведется строительство нового центра отдыха и оздоровления в кампусе Университета Питтсбурга. Этот проект является частью более широкого генерального плана кампуса, который был завершен в 2019 году и предусматривает такие удобства, как бассейн для отдыха, беговая дорожка, баскетбольные площадки, оборудование для тяжелой атлетики и многое другое.
Студенческое общежитие
Учащиеся поколения Z ищут место для «одиночек-вместе» в общежитии колледжа
Учащиеся, родившиеся между 1997 и 2012 годами, также известные как поколение Z или поколение Z, пересматривают ожидания в отношении жилья и услуг в колледжах, по данным архитектурной фирмы, которая специализируется на работе с колледжами и университетами.
- Дайан Шаффхаузер
- 18.01.22
Удобства кампуса
Расширение ядерного реактора штата Пенсильвания на территории кампуса
Penn State расширяет свой ядерный реактор на территории кампуса и объект, в котором он находится. Университет прорвался вперед на 9 долларов.5-миллионный проект, который предназначен для размещения предстоящего пожертвования оборудования, облегчения исследований нейтронного пучка и помощи в развитии программы ядерной инженерии в учреждении.
Университет прорвался вперед на 9 долларов.5-миллионный проект, который предназначен для размещения предстоящего пожертвования оборудования, облегчения исследований нейтронного пучка и помощи в развитии программы ядерной инженерии в учреждении.
- Дайан Шаффхаузер
- 13.01.22
Строительное образование
Колледж Колорадо использует гранты для добавления программы строительства
Государственный технический колледж в Колорадо запускает новую программу сертификации строительных специальностей, которая даст студентам опыт строительства доступного жилья.
- Дайан Шаффхаузер
- 12.01.22
Удобства кампуса
Ecore, Spartan Surfaces перезапускают популярную линейку напольных покрытий
Ecore, компания, которая перерабатывает регенерированные материалы в различные поверхности с высокими эксплуатационными характеристиками, объявила на этой неделе, что она сотрудничает с компанией Spartan Surfaces, занимающейся продажами и маркетингом напольных покрытий, чтобы перезапустить свою популярную линейку продуктов ECOsurfaces.
Новое строительство
В Техасе открывается новая начальная школа
Объединенный независимый школьный округ Ламар (Lamar CISD) в округе Форт-Бенд, штат Техас, примерно в 40 милях к западу от Хьюстона, отметил начало 2022 года открытием новой начальной школы.
Ремонт кампуса
Фресно, Калифорния., стремится превратить мотель в доступное студенческое жилье
Город Фресно, штат Калифорния, недавно предложил превратить местный мотель в жилой комплекс для студентов Городского колледжа Фресно. Строительство может быть завершено уже осенью 2022 года, и будет предоставлено 69 квартир с субсидированной арендной платой, в которых могут разместиться около 300 студентов.
Удобства кампуса
Университет штата Алабама испытывает капсулы на солнечных батареях
В скором времени в кампусе Университета Алабамы появится ряд небольших оранжерейных конструкций, где у студентов будет уединенное социально удаленное пространство для учебы или отдыха.
- Дайан Шаффхаузер
- 15.12.21
Ремонт кампуса
Заброшенная начальная школа получит ремонт стоимостью 30,5 млн долларов
Начальная школа
на Уиндмилл-стрит в Провиденсе, штат Род-Айленд, заброшена уже более десяти лет. За последние четыре месяца в здании произошло три пожара.Теперь объект настроен на проект реконструкции стоимостью 30,5 миллионов долларов, который позволит ему снова открыть свои двери для студентов.
Удобства кампуса
Округ Небраска внедряет улучшения звука в классах
Государственные школы Линкольна в Небраске объявили о внедрении системы улучшения звука, которая позволяет лучше слышать голоса учителей и учеников во всем классе, в том числе за масками.Округ сотрудничает с Audio Enhancement, компанией, производящей аудио- и видеооборудование для классных помещений.
- Дайан Шаффхаузер
- 13.12.21
Удобства кампуса
Университет устанавливает потолочные плиты с массивом микрофонов
Мичиганский технологический университет (MTU) в Хоутоне, штат Мичиган., недавно объявила, что оборудовала два помещения на территории кампуса потолочными плитами ClearOne BMA 360 Beamforming Microphone Array.
Новое строительство
Университет штата Джорджия назовет два здания в честь выдающихся чернокожих выпускников
Через несколько дней после того, как Попечительский совет университетской системы Джорджии отказался переименовать десятки колледжей и зданий, носящих имена исторических деятелей, поддерживавших рабство и расовую сегрегацию, Университет Джорджии рекомендовал переименовать два объекта в своем кампусе в одни из первых университетских зданий. и самые выдающиеся афроамериканские выпускники.
- Дайан Шаффхаузер
- 08.12.21
Новое строительство
Бизнес-школа Marquette стоимостью $60 млн откроется в декабре 2022 г.
Университет Маркетт в Милуоки завершает строительство новой бизнес-школы стоимостью 60 миллионов долларов в год.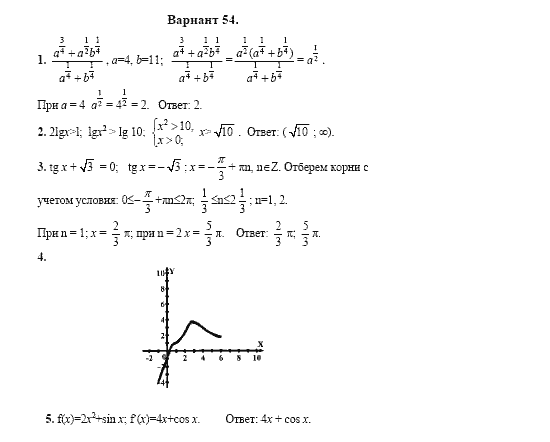 По данным учреждения, это учреждение является крупнейшим за всю его историю, финансируемым донорами.
По данным учреждения, это учреждение является крупнейшим за всю его историю, финансируемым донорами.
- Дайан Шаффхаузер
- 08.12.21
Новое строительство
Реконструкция корпуса Калифорнийского университета в Дэвисе для размещения в четыре раза большего числа студентов
Быстро продвигается строительство студенческого общежития на 1600 мест для Калифорнийского университета в Дэвисе. Завершение строительства запланировано на осень 2023 года. Сообщество предоставит 189 квартир с двумя спальнями для студентов с семьями и 424 студии и четырехместные квартиры для 1100 аспирантов.
- Дайан Шаффхаузер
- 08.12.21
Новое строительство
Penn State представляет новое здание ветеринарных, ветеринарных и биомедицинских наук
Пенсильванский государственный университет в Юниверсити-Парке, штат Пенсильвания, недавно отпраздновал церемонию перерезания ленточки в новом учебном корпусе на территории своего кампуса. Должностные лица университета, студенты, преподаватели и сотрудники собрались в среду, 1 декабря, чтобы отметить открытие нового Здания зоотехники, ветеринарии и биомедицинских наук.
Должностные лица университета, студенты, преподаватели и сотрудники собрались в среду, 1 декабря, чтобы отметить открытие нового Здания зоотехники, ветеринарии и биомедицинских наук.
Новое строительство
SC District открывает новую среднюю школу
Должностные лица Пятого школьного округа Спартанбурга в Дункане, С.C., собрались недавно, чтобы отпраздновать открытие новой средней школы. Строительные работы начались примерно через четыре недели после того, как местные избиратели приняли референдум об облигациях на сумму 295 миллионов долларов, чтобы удовлетворить потребности растущего числа учащихся в школах округа.
Новости образования
A4LE назначает президента Новой Англии Глава
Риган Шилдс Айвз, AIA, ALEP, LEED AP, директор и руководитель образовательной студии K–12 в Finegold Alexander Architects, недавно была назначена президентом новоанглийского отделения Ассоциации учебных сред (A4LE).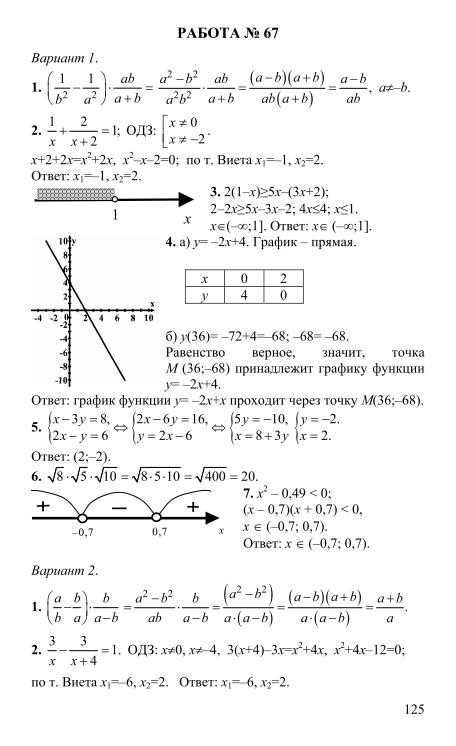
Удобства кампуса
Mohawk Group расширяет популярную коллекцию ковровых покрытий
Компания Mohawk Group, занимающаяся решениями для напольных покрытий, недавно объявила о расширении своей коллекции Learn & Live Collection, добавив в нее серию Take Steps, состоящую из трех универсальных стилей модульных ковров размером 24 x 24 дюйма.
.