Самостоятельные и контрольные работы по алгебре 7 класс
Самостоятельная работа по теме А — 7
«Прямоугольная система координат на плоскости»
1 вариант 2 вариант
1. Постройте в координатной плоскости прямую, проходящую через точки
С( — 4 ; 3 ) и Е ( 3 ; — 1 ) А ( 3 ; 4 ) и В ( — 5 ; — 1 )
Найдите координаты точек, в которых эта прямая пересекает ось Ох и ось Оу.
2. Постройте в координатной плоскости точки
А ( — 2 ; — 1,5 ), В ( — 3,5 ; 0 ), С ( — 2 ; 1,5), А ( 3,5 ; 4 ), В ( 0 ; 6 ), С ( — 3,5 ; 4),
Е ( 2; 1,5 ), К ( 3,5 ; 0 ) , М ( 2 ; — 1,5 ) Е ( — 3,5; — 4 ), К ( 0 ; — 6 ) , М ( 3,5 ; — 4 )
Соедините эти точки последовательно отрезками так, чтобы получился многоугольник. Запишите координаты точек пересечения с осью
Оу прямых СЕ и АМ. Ох прямых СЕ и АМ.
Самостоятельная работа по теме А — 7
«Прямоугольная система координат на плоскости»
1 вариант 2 вариант
1. Постройте в координатной плоскости прямую, проходящую через точки
Постройте в координатной плоскости прямую, проходящую через точки
С( — 4 ; 3 ) и Е ( 3 ; — 1 ) А ( 3 ; 4 ) и В ( — 5 ; — 1 )
Найдите координаты точек, в которых эта прямая пересекает ось Ох и ось Оу.
2. Постройте в координатной плоскости точки
А ( — 2 ; — 1,5 ), В ( — 3,5 ; 0 ), С ( — 2 ; 1,5), А ( 3,5 ; 4 ), В ( 0 ; 6 ), С ( — 3,5 ; 4),
Е ( 2; 1,5 ), К ( 3,5 ; 0 ) , М ( 2 ; — 1,5 ) Е ( — 3,5; — 4 ), К ( 0 ; — 6 ) , М ( 3,5 ; — 4 )
Соедините эти точки последовательно отрезками так, чтобы получился многоугольник. Запишите координаты точек пересечения с осью
Оу прямых СЕ и АМ. Ох прямых СЕ и АМ.
Самостоятельная работа по теме А — 7
«Прямоугольная система координат на плоскости»
1 вариант 2 вариант
1. Постройте в координатной плоскости прямую, проходящую через точки
С( — 4 ; 3 ) и Е ( 3 ; — 1 ) А ( 3 ; 4 ) и В ( — 5 ; — 1 )
Найдите координаты точек, в которых эта прямая пересекает ось Ох и ось Оу.
2. Постройте в координатной плоскости точки
А ( — 2 ; — 1,5 ), В ( — 3,5 ; 0 ), С ( — 2 ; 1,5), А ( 3,5 ; 4 ), В ( 0 ; 6 ), С ( — 3,5 ; 4),
Е ( 2; 1,5 ), К ( 3,5 ; 0 ) , М ( 2 ; — 1,5 ) Е ( — 3,5; — 4 ), К ( 0 ; — 6 ) , М ( 3,5 ; — 4 )
Соедините эти точки последовательно отрезками так, чтобы получился многоугольник. Запишите координаты точек пересечения с осью
Оу прямых СЕ и АМ. Ох прямых СЕ и АМ.
Самостоятельная работа по теме А — 7
«Прямоугольная система координат на плоскости»
1 вариант 2 вариант
1. Постройте в координатной плоскости прямую, проходящую через точки
С( — 4 ; 3 ) и Е ( 3 ; — 1 ) А ( 3 ; 4 ) и В ( — 5 ; — 1 )
Найдите координаты точек, в которых эта прямая пересекает ось Ох и ось Оу.
2. Постройте в координатной плоскости точки
А ( — 2 ; — 1,5 ), В ( — 3,5 ; 0 ), С ( — 2 ; 1,5), А ( 3,5 ; 4 ), В ( 0 ; 6 ), С ( — 3,5 ; 4),
Е ( 2; 1,5 ), К ( 3,5 ; 0 ) , М ( 2 ; — 1,5 ) Е ( — 3,5; — 4 ), К ( 0 ; — 6 ) , М ( 3,5 ; — 4 )
Соедините эти точки последовательно отрезками так, чтобы получился многоугольник. Запишите координаты точек пересечения с осью
Запишите координаты точек пересечения с осью
Оу прямых СЕ и АМ. Ох прямых СЕ и АМ.
Самостоятельная работа по алгебре. 7 класс. Тема: Сумма и разность кубов
САМОСТОЯТЕЛЬНАЯ РАБОТА ПО АЛГЕБРЕ
7 КЛАСС
ТЕМА: СУММА И РАЗНОСТЬ КУБОВ
Целью проведения тематической самостоятельной работы является закрепление практических навыков учащихся полученных ими при изучении этой темы. На выполнение одного варианта отводится 15 — 20 минут. В целях самопроверки можно сравнить полученные результаты с приведенными здесь верными ответами.
ВАРИАНТ 1
1. Разложите на множители:
а) p3 − t3; б) 8 + х3; в) 125 + у3.
Ответ:
а) (p − t)(p2 + pt + t2)
б) (2 + х)(4 − 2х2 + х2)
в) (5 + у)(25 − 5у + у2)
2. Представьте в виде произведения:
Представьте в виде произведения:
а) m3 − n6; б) a9 + b9.
Ответ:
а) (m − n2)(m2 + mn2 + n4)
б) (a3 + b3)(a6 − a3b3 + b6) = (a + b)(a2 − ab + b2)(a6 − a3b3 + b6)
3. Разложите на множители:
а) 0,001х3 − 8у3; б) 27а3 − 125b3.
Ответ:
а) (0,1х − 2у)(0,01х2 + 0,2ху + 4у2)
б) (3a − 5b)(9a2 + 15ab + 25b2)
ВАРИАНТ 2
1. Разложите на множители:
а) m3 + n3; б) 64 + у3; в) 8 − m3.
Ответ:
а) (m + n)(m2 − mn + n2)
б) (4 + у)(16 − 4у + у2)
в) (2 − m)(4 + 2m + m2)
2. Представьте в виде произведения:
Представьте в виде произведения:
а) с3 − d9; б) a6 + b6.
Ответ:
а) (c − d3)(c2 + cd3 + d6)
б) (a2 + b2)(a4 − a2b2 + b4)
3. Разложите на множители:
а) 0,008а3 − 64b3; б) 1000х3 − у6.
Ответ:
а) (0,2a − 4b)(0,04a2 + 0,8ab + 16b2)
б) (10х − у2)(100х2 + 10ху2 + у4)
Самостоятельная работа по алгебре. 7 класс. Тема: «Решение уравнений». Вариант 1
{module Адаптивный блок Адсенс в начале статьи}
САМОСТОЯТЕЛЬНАЯ РАБОТА ПО АЛГЕБРЕ
7 КЛАСС
ТЕМА: РЕШЕНИЕ УРАВНЕНИЙ
ВАРИАНТ 1
(уровень соответствует обязательным программным требованиям)
1.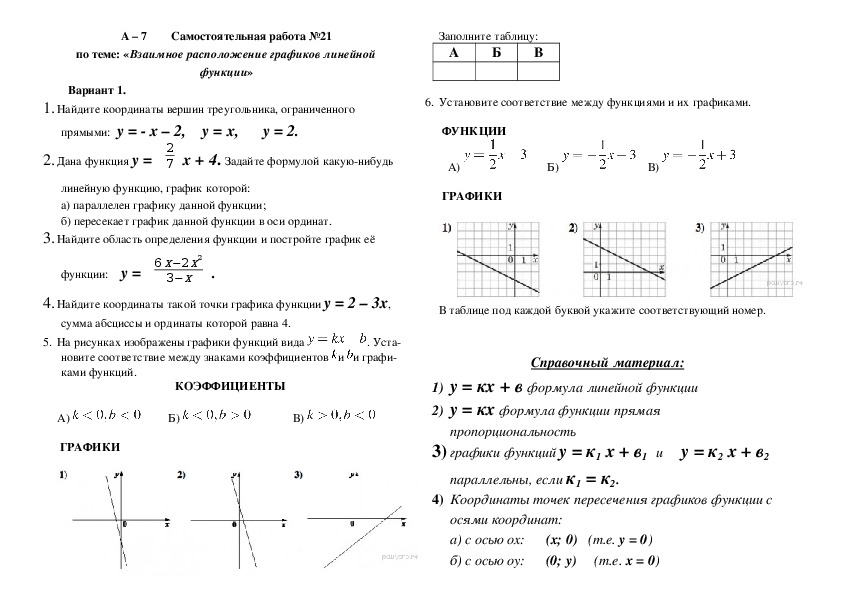 Решите уравнения:
Решите уравнения:
а) 6х − 12 = 4х – 8
Решение:
Для решения данного уравнения, необходимо перенести слагаемые содержащие переменную в одну часть уравнения, а слагаемые без переменных — в другую. Не забывайте, что при переносе слагаемого из одной части уравнения в другую, знак меняется на противоположный:
6х − 4х = 12 − 8
2х = 4
х = 2
Ответ: 2. /самостоятельная работа по алгебре 7 класс /
б)
Решение: Выразим переменную х, разделив правую часть уравнения на 2/3:
х = 18 ÷ 2/3
х = 18 · 3/2
х = 54/2 = 27
Ответ: 27.
в) (2х − 5) − (3х − 7) = 4
Решение: При решении данного уравнения для начала упростим левую часть, раскрыв скобки:
2х − 5 − 3х + 7 = 4
− х + 2 = 4
− х = 4 − 2 = 2
х = − 2
Ответ: − 2.
г) 5(х − 1,2) − 3х = 2
Решение: Раскроем скобки в уравнении.
5х − 6 − 3х = 2
Приведем подобные слагаемые с переменной в левой части уравнения:
2х − 6 = 2
Оставим слагаемые с переменной в левой части уравнения, а слагаемые без переменной соберем в правой части уравнения:
2х = 2 + 6
2х = 8
х = 4
Ответ: 4.
2. При каком значении у равны значения выражений:
1,8у − 2 и 0,6у + 4 ?
Решение: Для ответа на вопрос уравняем эти два выражения и решим полученное уравнение:
1,8у − 2 = 0,6у + 4
Перенесем все слагаемые, содержащие переменную, в левую часть уравнения, а слагаемые без переменной — в правую:
1,8у − 0,6у = 4 + 2
1,2у = 6
у = 6 ÷ 1,2
у = 5
Ответ: 5.
{module Адаптивный блок Адсенс в конце статьи}
Самостоятельные и контрольные работы по алгебре -7 класс.
 Глазков Ю.А.
Глазков Ю.А.
Данное пособие полностью соответствует федеральному государственному образовательному стандарту (второго поколения). Пособие является необходимым дополнением к школьному учебнику Ю.Н. Макарычева и др. «Алгебра. 7 класс» (издательство «Просвещение»), рекомендованному Министерством образования и науки Российской Федерации и включенному в Федеральный перечень учебников. Сборник содержит тексты 33 самостоятельных и 10 контрольных работ для формирования знаний, умений и навыков учащихся, предусмотренных программой курса алгебры 7 класса, и текущего контроля результатов обучения. Каждый текст самостоятельной и контрольной работы представлен в 4 равной трудности вариантах. В сборник включены также ответы к заданиям, рекомендации по подсчету баллов и выставлению отметок. Планируемое время выполнения каждой самостоятельной работы — 30 минут, каждой контрольной работы — 40 минут. Регулярное выполнение самостоятельных и контрольных работ поможет школьникам освоить программный материал и получать своевременно информацию о полноте его усвоения. Книга адресована учителям математики 7 класса и школьникам.
Книга адресована учителям математики 7 класса и школьникам.
СОДЕРЖАНИЕ
Предисловие 6
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
Самостоятельная работа 1.
Числовые выражения. Выражения с переменными 9
Самостоятельная работа 2. Сравнение значений выражений.
Свойства действий над числами 12
Самостоятельная работа 3.
Тождества. Тождественные преобразования выражений 15
Самостоятельная работа 4.
Уравнение и его корни 18
Самостоятельная работа 5.
Линейное уравнение с одной переменной 21
Самостоятельная работа 6.
Решение задач с помощью уравнений 24
Самостоятельная работа 7.
Что такое функция. Вычисление значений функций по формуле. График функции 30
Самостоятельная работа 8.
Прямая пропорциональность 34
Самостоятельная работа 9.
Линейная функция и ее график 39
Самостоятельная работа 10.
Взаимное расположение графиков линейных функций 43
Самостоятельная работа 11.
Определение степени с натуральным показателем 48
Самостоятельная работа 12.
Умножение и деление степеней 51
Самостоятельная работа 13.
Возведение в степень произведения и степени 54
Самостоятельная работа 14.
Одночлен и его стандартный вид 56
Самостоятельная работа 15.
Умножение одночленов. Возведение в степень 59
Самостоятельная работа 16.
Функции у = х2 и у = х3 и их графики 62
Самостоятельная работа 17.
Многочлен и его стандартный вид 69
Самостоятельная работа 18.
Сложение и вычитание многочленов 72
Самостоятельная работа 19.
Умножение одночлена на многочлен 76
Самостоятельная работа 20.
Вынесение общего множителя за скобки 80
Самостоятельная работа 21.
Умножение многочлена на многочлен 83
Самостоятельная работа 22. Разложение многочлена на множители способом группировки 86
Самостоятельная работа 23. Возведение в квадрат и куб суммы и разности двух выражений 89
Самостоятельная работа 24.
Разложение на множители с помощью формул квадрата суммы и квадрата разности. Умножение разности двух выражений на их сумму 92
Самостоятельная работа 25.
Разложение разности квадратов на множители 95
Самостоятельная работа 26.
Разложение на множители суммы и разности кубов 99
Самостоятельная работа 27.
Преобразование целого выражения в многочлен 103
Самостоятельная работа 28.
Применение различных способов для разложения на множители 107
Самостоятельная работа 29.
Линейное уравнение с двумя переменными.
График линейного уравнения с двумя переменными 110
Самостоятельная работа 30. Системы линейных уравнений с двумя переменными. Способ подстановки 114
Самостоятельная работа 31.
Способ сложения. Решение задач с помощью систем уравнений 119
Самостоятельная работа 32.
Статистические характеристики 124
Самостоятельная работа 33.
Итоговое повторение курса алгебры 7-го класса . 128
КОНТРОЛЬНЫЕ РАБОТЫ
Контрольная работа № 1.
Выражения. Тождественные преобразования выражений 132
Контрольная работа № 2.
Уравнения. Решение задач с помощью уравнений 136
Контрольная работа № 3.
Функции и графики. Линейная функция 141
Контрольная работа № 4.
Степень. Одночлен. Функции у-х2, у-х3 144
Контрольная работа № 5.
Многочлены 148
Контрольная работа № 6.
Умножение многочлена на многочлен. Разложение многочленов на множители методом группировки 152
Контрольная работа № 7.
Формула квадрата суммы, квадрата разности, разности квадратов 156
Контрольная работа № 8. Формулы суммы и разности кубов. Преобразование целых выражений 161
Контрольная работа № 9.
Решение систем линейных уравнений с двумя переменными. Решение задач с помощью систем линейных уравнений 165
Контрольная работа №10.
Итоговая 171
Ответы 175
Ответы к самостоятельным работам 175
Ответы к контрольным работам 185
Сборник содержит тексты 33 самостоятельных и 10 контрольных работ (в 4 вариантах каждая) по курсу алгебры 7 класса (Алгебра: Учеб. для 7 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, СБ. Суворова; Под. ред. СЛ. Теляковского. М.: Просвещение, 2014).
ред. СЛ. Теляковского. М.: Просвещение, 2014).
Во всех работах используются задания трех форм: с выбором ответа (задания А1, А2, A3), с кратким ответом (В1), с развернутым ответом (С1).
Для записи ответов рекомендуем учащимся использовать таблицы из двух строк и 4 столбцов:
Размер ячеек — 1 х 1 см. Такие таблицы ученики должны подготовить дома накануне урока выполнения самостоятельной работы. Прикладывая к таблице ученика свою таблицу ответов, учитель может в течение 10 минут проверить 25 работ учащихся.
Решение задачи С1 ученик записывает на том же листе ответов.
Инструкции для учащихся по выполнению работы просты.
ГДЗ решебник по алгебре 7 класс Александрова Самостоятельные работы Мнемозина
Алгебра 7 класс
Тип пособия: Самостоятельные работы
Авторы: Александрова
Издательство: «Мнемозина»
Помимо получения предметных знаний, школа воспитывает и множество других важных навыков. И одним из главных является умение работать самостоятельно. Но в тех случаях, когда учитель объявляет проведение контрольной или самостоятельной работы в классе, многие школьники, даже обладающие высоким уровнем знаний, испытывают самый настоящий стресс. Они не могут сосредоточиться на работе в первую очередь из-за волнения. А если речь идёт о такой сложнейшей науке, как алгебра, то проблема может приобрести серьёзный характер. Именно для того, чтобы ученик смог подготовиться к любой проверке знаний, разработан профессиональный помощник – виртуальный консультант юного математика «ГДЗ по алгебре, 7 класс Александрова Самостоятельные работы(Мнемозина)».
Но в тех случаях, когда учитель объявляет проведение контрольной или самостоятельной работы в классе, многие школьники, даже обладающие высоким уровнем знаний, испытывают самый настоящий стресс. Они не могут сосредоточиться на работе в первую очередь из-за волнения. А если речь идёт о такой сложнейшей науке, как алгебра, то проблема может приобрести серьёзный характер. Именно для того, чтобы ученик смог подготовиться к любой проверке знаний, разработан профессиональный помощник – виртуальный консультант юного математика «ГДЗ по алгебре, 7 класс Александрова Самостоятельные работы(Мнемозина)».
Осваиваем науку с тетрадью Александрова
Безусловно, многие элементы математики необходимы семикласснику при знакомстве с курсом алгебры. Но большинство новых тем настолько серьёзны, что каждая из них могла бы стать отдельной наукой. А ведь школьникам приходится работать параллельно и с другими предметами, некоторые из которых не менее сложны – геометрией и физикой. В результате ученики испытывают острый дефицит времени. Зачастую нет свободных минут на работу со всеми домашними заданиями, не говоря уже о полноценном отдыхе. А ведь отдых для любого человека, тем более в столь юном возрасте, не менее важен, чем весь комплекс знаний. Поэтому так важна любая возможность ускорить подготовку к урокам, но при этом поддерживать высокий уровень получаемых знаний. И в этой сложной задаче отличным советником становится «ГДЗ по алгебре, 7 класс Александрова Л.А. Самостоятельные работы(Мнемозина)».
В результате ученики испытывают острый дефицит времени. Зачастую нет свободных минут на работу со всеми домашними заданиями, не говоря уже о полноценном отдыхе. А ведь отдых для любого человека, тем более в столь юном возрасте, не менее важен, чем весь комплекс знаний. Поэтому так важна любая возможность ускорить подготовку к урокам, но при этом поддерживать высокий уровень получаемых знаний. И в этой сложной задаче отличным советником становится «ГДЗ по алгебре, 7 класс Александрова Л.А. Самостоятельные работы(Мнемозина)».
Немного о пособии
Автор предлагает семикласснику проработать все темы основного учебника текущего учебного года:
- Что такое математические модели.
- Линейное уравнение.
- Таблица степеней.
- Метод подстановки.
- Системы уравнений с двумя переменными.
В решебнике ученик найдёт не просто готовые ответы, но и подробное разъяснение всего алгоритма выполнения аналогичных заданий.
Что представляет собой ГДЗ
Порядок изложения материала в решебнике структурирован в соответствии с тематикой основного учебника алгебры для седьмого класса. О содержании:
- 43 тематических самостоятельных работы;
- итоговая работа по всем изученным разделам;
- понятное объяснение к каждой задаче.
Пособие принесёт пользу и в следующем учебном году, когда возникнет необходимость повторить ранее изученные темы.
Похожие ГДЗ Алгебра 7 класс
Самостоятельная работа 1. Числовые выражения: Вариант 1
Самостоятельная работа по математике 7 класс Многочлены
Тест по теме: «Сложение и вычитание многочленов»
Часть 1 (Общая)
1.Найдите сумму многочленов: -4а3+3 и 3а3+8
а) -7а3+11 б) а3+11 в) -а3+11 г) а3-11
2. Найдите разность многочленов: 4х2+8х и 2х2-6х+4
Найдите разность многочленов: 4х2+8х и 2х2-6х+4
а) 2х2+2х+4 б) -2х2-14х+4 в) 6х2 +14х-4 г) 2х2+14х-4
3.Упростите выражение: (2а2+4а)+(-а2+а)-(2а2+3а-2)
а) -а2+8а-2 б) 3а2+8а-2 в) 3а2+2а+2 г) -а2+2а+2
4.Решите уравнение: 3а3-(3а3 -4а)-(4а+2)=10
а) а= -1 б) а= 12 в)уравнение не имеет корней г)а- любое число
5. Решить уравнение: (4х2-2)-(3х+4)=4х2
а)х=2 б) х= -2 в)х=0,5 г)х= -0,5
6.Вместо * запишите такой многочлен, чтобы образовалось тождество:
19а4-17а2в+в3-(*)=20 а4+5а2в
а)а4 +22а2в+ в3 б) -а4 -22а2в+ в3 в) -а4 +22а2в+ в3 г) а4 +12а2в- в3
|
Часть 2 Вариант 1
а) ; б) .
а) ; б) .
а) ; б) .
а) ; б) .
и найдите его значение при . |
Часть 2 Вариант 2
а) ; б).
а) ; б) .
а) ; б) .
а) ; б) .
и найдите его значение при . |
Ответы
Вариант 1
-
а) ;
б) .
-
а) ;
б) .
-
а)
1,5;
б)
.
-
а) ;
б) ).
-
.
Вариант 2
-
а) ;
б) .
-
а) ;
б) .
-
а)
;
б)
.
-
а) ;
б) .
-
.
Системы линейных уравнений
Линейное уравнение представляет собой уравнение для линии .
Линейное уравнение не всегда имеет форму y = 3,5 − 0,5x ,
Также может быть как y = 0,5(7 − x)
Или как у + 0,5х = 3,5
Или как у + 0,5х — 3,5 = 0 и больше.
(Примечание: это все одно и то же линейное уравнение!)
Система линейных уравнений — это когда у нас есть два или более линейных уравнения , работающих вместе.
Пример: Вот два линейных уравнения:
Вместе они составляют систему линейных уравнений.
Можете ли вы сами определить значения x и y ? (Просто попробуйте, поиграйте с ними немного.)
Давайте попробуем построить и решить реальный пример:
Пример: Вы против Лошади
Это гонка!
Вы можете пробежать 0,2 км каждую минуту.
Лошадь может бегать 0.5 км каждую минуту. Но чтобы оседлать лошадь, нужно 6 минут.
Как далеко ты уедешь, прежде чем тебя настигнет лошадь?
Мы можем составить два уравнения ( d = расстояние в км, t = время в минутах)
- Каждую минуту вы бежите со скоростью 0,2 км, поэтому d = 0,2t
- Лошадь бежит со скоростью 0,5 км в минуту, но мы уменьшаем ее время на 6: d = 0,5(t−6)
Итак, у нас есть система уравнений ( линейных ):
Решим на графике:
Видишь, как лошадь стартует через 6 минут, а потом бежит быстрее?
Кажется, тебя поймают через 10 минут… у вас всего 2 км.
В следующий раз беги быстрее.
Итак, теперь вы знаете, что такое система линейных уравнений.
Продолжаем узнавать о них больше….
Решение
Способов решения линейных уравнений может быть много!
Давайте посмотрим на другой пример:
Пример: Решите эти два уравнения:
На этом графике показаны два уравнения:
Наша задача — найти пересечение двух линий.
Ну, мы видим, где они пересекаются, так что это уже решено графически.
А теперь давайте решим ее по алгебре!
Хммм… как это решить? Способов может быть много! В этом случае в обоих уравнениях есть «y», поэтому давайте попробуем вычесть все второе уравнение из первого:
х + у — (-3х + у) = 6 — 2
Теперь упростим:
х + у + 3х — у = 6 — 2
4x = 4
х = 1
Итак, теперь мы знаем, что линии пересекаются в точке x=1 .
И мы можем найти соответствующее значение y , используя любое из двух исходных уравнений (потому что мы знаем, что они имеют одно и то же значение при x=1). Используем первый (второй можете попробовать сами):
х + у = 6
1 + у = 6
г = 5
И решение:
х = 1 и у = 5
И график показывает, что мы правы!
Линейные уравнения
В линейных уравнениях допускаются только простые переменные. № x 2 , y 3 , √x и т. д. :
д. :
Линейный и нелинейный
Размеры
| A Линейное уравнение может быть двухмерным… (например, x и y ) |
||
| … или в 3-х измерениях … (делает самолет) |
||
| … или 4 размера … | ||
| … или больше! |
Общие переменные
Чтобы уравнения «работали вместе», они используют одну или несколько переменных:
Система уравнений содержит два или более уравнений в одну или несколько переменных
Многие переменные
Таким образом, система уравнений может иметь многих уравнений и многих переменных.
Пример: 3 уравнения с 3 переменными
| 2x | + | г | — | 2з | = | 3 |
| х | — | г | — | с | = | 0 |
| х | + | г | + | 3з | = | 12 |
Может быть любая комбинация:
- 2 уравнения с 3 переменными,
- 6 уравнений с 4 переменными,
- 9000 уравнений с 567 переменными,
- и т.д.
Решения
Когда количество уравнений равно тем же , что и количество переменных, то вероятно будут решением. Не гарантировано, но вероятно.
На самом деле возможны только три случая:
- № раствор
- Один раствор
- Бесконечное множество решений
Когда нет решения уравнения называются «несовместимыми» .
Один или бесконечно много решений называются «непротиворечивыми»
Вот диаграмма для 2 уравнения с 2 переменными :
Независимый
«Независимая» означает, что каждое уравнение дает новую информацию.
В противном случае они «Зависимые» .
Также называется «линейная независимость» и «линейная зависимость».
Пример:
Эти уравнения «зависимы» , потому что они на самом деле то же самое уравнение , просто умноженное на 2.
Итак, второе уравнение не дало новой информации .
Где уравнения верны
Весь фокус в том, чтобы найти, где все уравнений верны одновременно .
Правда? Что это значит?
Пример: Вы против Лошади
Строка «you» истинна по всей своей длине (но больше нигде).
В любом месте этой строки d равно 0.2т
- при t=5 и d=1 уравнение верно
- при t=5 и d=3 уравнение не верно (верно ли d = 0,2t? Нет, так как 3 = 0,2×5 неверно )
Точно так же линия «лошадь» также истинна по всей своей длине (но больше нигде).
Но только в точке, где они пересекают (при t=10, d=2), они оба истинны .
Значит, они должны быть верными одновременно …
… поэтому некоторые люди называют их «Одновременными линейными уравнениями»
Решить с помощью алгебры
Обычно для их решения используется алгебра.
Вот пример «Лошадь», решенный с помощью алгебры:
Пример: Вы против Лошади
Система уравнений:
В данном случае проще всего приравнять их друг к другу:
д = 0. 2t = 0,5(t−6)
2t = 0,5(t−6)
Начните с :0,2t = 0,5(t − 6)
Расширение 0,5(т-6) :0,2т = 0,5т — 3
Вычесть 0,5t с обеих сторон: −0,3t = −3
Разделите обе части на −0,3 :t = −3/−0,3 = 10 минут
Теперь мы знаем , когда тебя поймают!
Зная t , мы можем вычислить d :d = 0,2t = 0,2×10 = 2 км
И наше решение:
t = 10 минут и d = 2 км
Алгебра против графиков
Зачем использовать алгебру, если графики так просты? Потому что:
Более 2 переменных не могут быть решены с помощью простого графика.
Итак, алгебра приходит на помощь двумя популярными методами:
- Решение подстановкой
- Решение методом исключения
Мы увидим каждый, с примерами в 2-х переменных и в 3-х переменных. Вот так…
Решение подстановкой
Вот шаги:
- Напишите одно из уравнений в стиле «переменная =.
 ..»
..» - Заменить (т.е. заменить) эту переменную в другом уравнении (уравнениях).
- Решить другое уравнение(я)
- (Повторите при необходимости)
Вот пример с 2 уравнения с 2 переменными :
Пример:
Мы можем начать с любого уравнения и любой переменной .
Используем второе уравнение и переменную «y» (выглядит простейшим уравнением).
Напишите одно из уравнений в стиле «переменная = …»:
Мы можем вычесть x из обеих частей x + y = 8, чтобы получить y = 8 − x . Теперь наши уравнения выглядят так:
Теперь замените «y» на «8 − x» в другом уравнении:
- 3x + 2 (8 − x) = 19
- у = 8 — х
Решите, используя обычные методы алгебры:
Расширить 2(8−x) :
- 3x + 16 − 2x = 19
- у = 8 — х
Тогда 3x−2x = x :
И, наконец, 19−16=3
Теперь, когда мы знаем, что такое x , мы можем представить это в уравнении y = 8 − x :
И ответ:
х = 3
у = 5
Примечание: поскольку является решением, уравнения «непротиворечивы»
Проверка: почему бы вам не проверить, работает ли x = 3 и y = 5 в обоих уравнениях?
Решение методом замены: 3 уравнения с 3 переменными
ОК! Давайте перейдем к более длинному примеру : 3 уравнения с 3 переменными .
Это не сложно сделать… просто долго !
Пример:
- х + г = 6
- г — 3г = 7
- 2х + у + 3z = 15
Мы должны аккуратно выстроить переменные, иначе мы можем потерять представление о том, что мы делаем:
| х | + | с | = | 6 | |||||
| — | 3 года | + | с | = | 7 | ||||
| 2x | + | г | + | 3з | = | 15 |
Мы можем начать с любого уравнения и любой переменной. Давайте используем первое уравнение и переменную «x».
Давайте используем первое уравнение и переменную «x».
Запишите одно из уравнений в стиле «переменная =…»:
| х | = | 6 — я | |||||||
| — | 3 года | + | с | = | 7 | ||||
| 2x | + | г | + | 3з | = | 15 | |||
Теперь замените «x» на «6 − z» в других уравнениях:
(К счастью, есть только одно уравнение с x в нем)
| х | = | 6 — я | ||||||||
| — | 3 года | + | с | = | 7 | |||||
| 2 (6-з) | + | г | + | 3з | = | 15 | ||||
Решите, используя обычные методы алгебры:
2(6−z) + y + 3z = 15 упрощается до y + z = 3 :
| х | = | 6 — я | |||||||
| — | 3 года | + | с | = | 7 | ||||
| г | + | с | = | 3 | |||||
Хорошо. Мы добились некоторого прогресса, но еще не все.
Мы добились некоторого прогресса, но еще не все.
Теперь повторите процесс , но только для двух последних уравнений.
Запишите одно из уравнений в стиле «переменная =…»:
Выберем последнее уравнение и переменную z:
| х | = | 6 — я | |||||||
| — | 3 года | + | с | = | 7 | ||||
| з | = | 3 − у | |||||||
Теперь замените «z» на «3 − y» в другом уравнении:
| х | = | 6 — я | |||||||
| — | 3 года | + | 3 − у | = | 7 | ||||
| с | = | 3 − у | |||||||
Решите, используя обычные методы алгебры:
−3y + (3−y) = 7 упрощается до −4y = 4 , или, другими словами, y = −1
| х | = | 6 — я | |||||||
| г | = | −1 | |||||||
| с | = | 3 − у | |||||||
Почти готово!
Зная, что y = −1 , мы можем вычислить, что z = 3−y = 4 :
| х | = | 6 — я | |||||||
| г | = | −1 | |||||||
| з | = | 4 | |||||||
Зная, что z = 4 , мы можем вычислить, что x = 6−z = 2 :
| х | = | 2 | |||||||
| г | = | −1 | |||||||
| с | = | 4 |
И ответ:
х = 2
у = −1
z = 4
Проверка: пожалуйста, проверьте это сами.
Мы можем использовать этот метод для 4 или более уравнений и переменных… просто повторяйте одни и те же шаги снова и снова, пока не решите.
Вывод: Замена работает хорошо, но требует много времени.
Решение методом исключения
Ликвидация может быть быстрее… но должна быть аккуратной.
«Устранить» означает удалить : этот метод работает путем удаления переменных до тех пор, пока не останется только одна.
Идея в том, что мы можем смело :
- умножить уравнение на константу (кроме нуля),
- добавить (или вычесть) уравнение из другого уравнения
Как в этих примерах:
ПОЧЕМУ мы можем складывать уравнения друг с другом?
Представьте себе два очень простых уравнения:
х — 5 = 3
5 = 5
Мы можем добавить «5 = 5» к «x − 5 = 3»:
х — 5 + 5 = 3 + 5
х = 8
Попробуйте сами, но используйте 5 = 3+2 в качестве второго уравнения
Он по-прежнему будет работать нормально, потому что обе стороны равны (для этого и нужен =!)
Мы также можем поменять местами уравнения, чтобы первое могло стать вторым и т. д., если это поможет.
д., если это поможет.
ОК, время для полного примера. Давайте используем 2 уравнения с 2 переменными пример из предыдущего:
Пример:
Очень важно поддерживать порядок:
| 3x | + | 2 года | = | 19 | |||
| х | + | г | = | 8 |
Сейчас … наша цель состоит в том, чтобы исключить переменную из уравнения.
Сначала мы видим, что есть «2y» и «y», так что давайте поработаем над этим.
Умножить второе уравнение на 2:
| 3x | + | 2 года | = | 19 | |||
| 2 х | + | 2 г | = | 16 |
Вычесть второе уравнение из первого уравнения:
| х | = | 3 | |||||
| 2x | + | 2 года | = | 16 |
Ура! Теперь мы знаем, что такое х!
Далее мы видим, что второе уравнение имеет «2x», поэтому давайте уменьшим его вдвое, а затем вычтем «x»:
Умножьте второго уравнения на ½ (т. е. разделить на 2):
е. разделить на 2):
| х | = | 3 | |||||
| х | + | г | = | 8 |
Вычесть первое уравнение из второго уравнения:
| х | = | 3 | |||||
| г | = | 5 |
Готово!
И ответ:
х = 3 и у = 5
А вот и график:
Синяя линия показывает, где 3x + 2y = 19 верно
Красная линия показывает, где x + y = 8 верно
При x=3, y=5 (где линии пересекаются) они оба верны. Ответ: .
Ответ: .
Вот еще пример:
Пример:
- 2х — у = 4
- 6х — 3у = 3
Аккуратно разложить:
| 2x | — | г | = | 4 | |||
| 6x | — | 3 года | = | 3 |
Умножьте первое уравнение на 3:
| 6x | — | 3 года | = | 12 | |||
| 6x | — | 3 года | = | 3 |
Вычесть второе уравнение из первого уравнения:
| 0 | — | 0 | = | 9 | |||
| 6x | — | 3 года | = | 3 |
0 − 0 = 9 ???
Что здесь происходит?
Проще говоря, решения нет.
| На самом деле это параллельные линии: |
И наконец:
Пример:
- 2х — у = 4
- 6х — 3у = 12
Аккуратно:
| 2x | — | г | = | 4 | |||
| 6x | — | 3 года | = | 12 |
Умножьте первое уравнение на 3:
| 6x | — | 3 года | = | 12 | |||
| 6x | — | 3 года | = | 12 |
Вычесть второе уравнение из первого уравнения:
| 0 | — | 0 | = | 0 | |||
| 6x | — | 3 года | = | 3 |
0 − 0 = 0
Что ж, это действительно ПРАВДА! Ноль действительно равен нулю. ..
..
… потому что это одно и то же уравнение …
… так что существует бесконечное количество решений
| Это одна и та же строка: |
Итак, мы рассмотрели пример каждого из трех возможных случаев:
- № раствор
- Один раствор
- Бесконечное множество решений
Решение методом исключения: 3 уравнения с 3 переменными
Прежде чем мы начнем со следующего примера, давайте посмотрим на улучшенный способ выполнения действий.
Следуйте этому методу, и мы с меньшей вероятностью допустим ошибку.
Прежде всего, удалите переменные в порядке :
- Сначала исключить x с (из уравнений 2 и 3, по порядку)
- затем исключить y (из уравнения 3)
Вот как мы их устраняем:
Получим вот такую »форму треугольника»:
Теперь начните снизу и выполните резервное копирование (так называемая «обратная замена»)
(поместите z , чтобы найти y , затем z и y , чтобы найти x
3 ):
И мы решили:
ТАКЖЕ, мы обнаружим, что легче выполнить некоторые расчетов в уме или на бумаге, чем всегда работать в рамках системы уравнений:
Пример:
- х + у + г = 6
- 2г + 5г = -4
- 2x + 5y — z = 27
Аккуратно написано:
| х | + | г | + | с | = | 6 | |||
| 2 года | + | 5з | = | −4 | |||||
| 2x | + | 5 лет | — | с | = | 27 |
Сначала исключите x из 2-го и 3-го уравнения.
Во втором уравнении нет x… переходим к третьему уравнению:
Вычтите 2 раза 1-е уравнение из 3-го уравнения (просто сделайте это в уме или на бумаге):
И получаем:
| х | + | г | + | с | = | 6 | |||
| 2 года | + | 5з | = | −4 | |||||
| 3 года | — | 3з | = | 15 |
Затем исключите и из 3-го уравнения.
Мы могли бы вычесть 1½ раза 2-е уравнение из 3-го уравнения (потому что 1½ умножить на 2 равно 3) …
… но мы можем избежать дробей , если мы:
- умножить 3-е уравнение на 2 и
- умножить второе уравнение на 3
и потом делаем вычитание… вот так:
И получаем:
| х | + | г | + | с | = | 6 | |||
| 2 года | + | 5з | = | −4 | |||||
| з | = | −2 |
Теперь у нас есть «треугольная форма»!
Теперь вернитесь снова «обратно-заменив»:
Мы знаем z , поэтому 2y+5z=−4 становится 2y−10=−4 , затем 2y=6 , поэтому y=3 :
| х | + | г | + | с | = | 6 | |||
| г | = | 3 | |||||||
| с | = | −2 |
Тогда x+y+z=6 становится x+3−2=6 , поэтому x=6−3+2=5
| х | = | 5 | |||||||
| г | = | 3 | |||||||
| с | = | −2 |
И ответ:
х = 5
у = 3
z = −2
Чек: проверьте сами.
Общая консультация
Как только вы привыкнете к методу исключения, он станет проще, чем замена, потому что вы просто выполняете шаги, и ответы появляются.
Но иногда Замена может дать более быстрый результат.
- Замена часто проще для небольших случаев (например, 2 уравнения, а иногда и 3 уравнения)
- Устранение проще для больших ящиков
И всегда стоит сначала просмотреть уравнения, чтобы увидеть, нет ли простого пути … так что опыт помогает.
7 реальных математических стратегий | Edutopia
Раньше математика сводилась к механическому заучиванию и написанию уравнений с карандаша на бумаге, оторванных от реального мира, но все больше и больше учителей осознают важность установления практических и релевантных связей в математике.
Мы спросили нашу аудиторию преподавателей: как вы используете реальный мир для обучения математике? Мы собрали некоторые из самых интересных ответов о том, как учителя связывают математику с повседневной жизнью своих учеников.
Математическая стена реального мира
Саманта Баумгарднер, учительница начальной школы Вудро Петти в Тафте, штат Техас, чтобы заставить своих пятиклассников задуматься о математике в своей жизни и предотвратить неизбежную жалобу на то, что «мы никогда не будем использовать это в реальном мире». , пусть они принесут общий предмет и напишут на карточке три его отношения к математике. Эти объекты образуют реальную математическую стену класса.
Savannah Olkowski
Учащиеся приносят предметы, чтобы повесить их на стену, с описанием того, как они связаны с математикой.
Интересное правило: после того, как что-то размещено на стене, этот предмет нельзя принести снова, что побуждает учащихся мыслить нестандартно, чтобы проводить математические связи в реальном мире. Учащиеся приносят такие предметы, как игральные карты, формы для кексов, протоколы софтбола и рецепты печенья. Один студент принес пипетку с лекарством и в качестве пояснения написал: «Пипетка с лекарством помогает вам измерять количество воды, а также помогает вам готовить стейк».
Саванна Олковски
Саманта Баумгарднер и ее ученики и их настоящая математическая стена.
Аудит школьного водоснабжения
Криста Данлоп-Шеппард
Учащиеся измеряют расход воды из крана в классе.
В государственной школе North Agincourt Jr. в Скарборо, Канада, Криста Данлоп-Шеппард, двуязычный учитель и учитель домашней школы для 1–6 классов, предлагает своим ученикам провести проверку воды дома и в школе. Ее ученики обладают широким диапазоном математических способностей: в одном классе у нее есть ученики с ограниченными возможностями обучения, одаренные ученики и ученики без диагнозов, но нуждающиеся в дополнительной поддержке.Изменяя пилотный проект, созданный Департаментом образования зоопарка Торонто, учащиеся складывают, вычитают, находят средние значения и измеряют жидкости — например, скорость потока во всех фонтанах, туалетах и писсуарах — для измерения количества воды, используемой их школой в день.
Они также опрашивают сторожей, чтобы выяснить, сколько воды они ежедневно расходуют при мытье полов, и проводят онлайн-исследования, чтобы выяснить, сколько воды расходует посудомоечная машина в столовой. Закончив, учащиеся предлагают школе способы экономии — например, собирать дождевую воду в бочку для полива растений или мыть кисти в ведре вместо использования проточной воды.В июне учащиеся повторяют аудит воды и смотрят, принесли ли изменения, которые они внесли, изменения.
Закончив, учащиеся предлагают школе способы экономии — например, собирать дождевую воду в бочку для полива растений или мыть кисти в ведре вместо использования проточной воды.В июне учащиеся повторяют аудит воды и смотрят, принесли ли изменения, которые они внесли, изменения.
Разыгрывание сценариев ресторана
Нет ничего плохого в том, чтобы использовать деньги для обучения отрицательным и положительным числам или пиццу для введения дробей, но Джастин Уэллетт, преподаватель международного бакалавриата третьего-пятого классов в Сучжоуской Сингапурской международной школе в Китае, делает эти упражнения на незабываемый шаг вперед. внесение меню, чтобы учащиеся могли разыграть реалистичные сценарии ресторана.Голландский ужин и чаевые укрепляют сложение, вычитание, десятичные дроби и проценты, говорит Уэллетт.
Если вам нужен хороший ресурс: Уэллетт использовала этот бесплатный план урока о вымышленной забегаловке под названием «Ресторан Сафари».
Джастин Уэллетт
Ученики Джастина Уэллетта практикуют математику на распечатках из вымышленного ресторана «Сафари».
Интеграция математики в английский язык и историю
Установление математических связей в реальном мире может происходить и за пределами урока математики.
Читая книгу Эли Визеля « Ночь », учащиеся 12-го класса региональной средней школы Киттатинни в Хэмптон-Тауншип, штат Нью-Джерси, подсчитывают сумму в 11 миллионов пенсов, чтобы представить себе влияние жизней, потерянных во время Холокоста. Эшли Свордс, преподаватель английского языка в ресурсном центре для 9-12 классов, использует пенни, потому что они маленькие и их много, и они позволяют ей реконтекстуализировать знакомый, повседневный предмет.
Учащиеся выполняют другие расчеты, чтобы усилить влияние уроков — например, на школьном футбольном поле они сами определяют объем Мечей, а затем вычисляют, сколько футбольных полей потребовалось бы, чтобы похоронить 11 миллионов жертв Холокоста, если бы каждый из них был Мечи размером с меч и были зарыты в могилы глубиной 10 футов.Предположения варьировались от двух до 20 футбольных полей, и в конце концов студенты пришли к выводу, что потребуется около 343 футбольных полей.
Мечи знали, что этот урок удался, когда группа из шести пожилых людей взволновалась после его завершения и осознала масштабы смертей во Второй мировой войне.
Мишель Пауэрс
Эшли Суордс и ее ученики измеряют футбольное поле в рамках расследования Холокоста по роману Эли Визеля «Ночь».
Математические рецепты
Рецепты были, пожалуй, самой популярной идеей среди учителей начальных классов, которые откликнулись на нашу просьбу о реальных примерах математики.Например, учительница пятого класса Габи Санфилиппо из Медоу-Ридж в Орланд-парке, штат Иллинойс, попросила своих учеников записать один-два способа использования математики вне класса во время весенних каникул, и более половины ее учеников написали, что они практиковали используя измерения и дроби при выпечке и приготовлении пищи со своими семьями.
Габи Санфилиппо
Один из учеников Габи Санфилиппо изменяет количество ингредиентов, необходимых для бруки – брауни-печенья – чтобы практиковать дроби.
В классе учащиеся практикуют деление вдвое, втрое или вчетверо рецептов в зависимости от того, для скольких людей они готовят или пекут. Большинство учителей на самом деле не готовят в классе, но часто ученики готовят дома, чтобы практиковать свои новые навыки.
Другой педагог, Элизабет Иган из независимого школьного округа Бастроп в Техасе, приносит тостер, чтобы печь на уроке. Она обучает слабовидящих, от новорожденных до 22-летних, используя рецепты, напечатанные крупным шрифтом, шрифтом Брайля или аудио, чтобы показать реальное применение сложения и вычитания дробей.
Иган распечатывает рецепты на 129 процентов для своих учеников с плохим зрением или преобразует текст в шрифт Брайля с помощью программного обеспечения для транскрипции Брайля, а затем распечатывает их на принтере Брайля. Она приобрела Stir It Up — кулинарную книгу, написанную как шрифтом Брайля, так и печатным шрифтом, что облегчает семьям и учителям помощь ученикам, не овладевшим тактильным языком. Студенты могут использовать электронные увеличительные стекла, такие как Pebble и Ruby. Для аудио Иган записывает, как она читает рецепты, пользуется помощью сверстников или родителей или использует приложение Seeing AI, которое может сканировать и читать рецепты вслух.
Студенты могут использовать электронные увеличительные стекла, такие как Pebble и Ruby. Для аудио Иган записывает, как она читает рецепты, пользуется помощью сверстников или родителей или использует приложение Seeing AI, которое может сканировать и читать рецепты вслух.
Элизабет Иган
Элизабет Иган печет в доме одной из своих учениц вместе с родителями. Ученица Игана умножила количество ингредиентов на четыре, чтобы приготовить завтрак для своей семьи.
Экскурсия в продуктовый магазин
Многие учителя связывают математику с покупками продуктов в реальном мире. Второклассникам Леанны Агкаойли в начальной школе имени Джозефа Дж. Ферна в Гонолулу, Гавайи, поручено приготовить здоровую еду для своей семьи с бюджетом в 20 долларов. Во время экскурсии в продуктовый магазин учащиеся учатся складывать и вычитать однозначные и двузначные целые числа, а в процессе узнают о деньгах и составлении бюджета.
Агкаойли говорит, что в следующем году проведет тренировочный забег в классе, отметив, что в первый раз некоторым ученикам было трудно найти ингредиенты.
График любимых оберток для конфет на Хэллоуин
После Хэллоуина Дотти Райт Берзинс, учительница государственной школы на пенсии, попросила своих учеников принести обертки от своих любимых хэллоуинских конфет. Затем в зависимости от возраста ученики построили графики, показывающие их любимые конфеты.
Дети младшего возраста строили гистограммы конфет в натуральную величину, отмечая оси x и y малярной лентой на полу и используя обертки для изображения батончиков.Учащиеся старшего возраста строили итоговые таблицы и бумажные графики, следили за рекламой, отслеживали, какие бренды рекламируют больше, брали интервью у сверстников о своих любимых конфетах, делали прогнозы и создавали сценарии «что, если» — например, что, если цена на шоколад увеличится — как эта переменная повлияет график?
7 советов по обучению математике в любом классе с помощью Nearpod
1 июля 2021 г.Кейт Роскиоли
Nearpod делает преподавание математики увлекательным для учащихся, одновременно продвигая математический дискурс и предоставляя учителям формирующие данные. Успеваемость по математике в США продолжает вызывать все большую озабоченность. Согласно Национальной оценке образовательного прогресса, 2019 г., только 41% наших 4-х классов, 34% наших 8-х классов и 24% наших 12-классников набрали или превышают уровень знаний по математике. Доступные ресурсы часто слишком сосредоточены только на охвате стандартов и содержании, отсутствует преднамеренность в отношении учебного опыта. С Nearpod вы можете использовать интерактивные видеоролики, интерактивные уроки на основе слайдов и игровые задания для увлекательного учебного процесса.
Успеваемость по математике в США продолжает вызывать все большую озабоченность. Согласно Национальной оценке образовательного прогресса, 2019 г., только 41% наших 4-х классов, 34% наших 8-х классов и 24% наших 12-классников набрали или превышают уровень знаний по математике. Доступные ресурсы часто слишком сосредоточены только на охвате стандартов и содержании, отсутствует преднамеренность в отношении учебного опыта. С Nearpod вы можете использовать интерактивные видеоролики, интерактивные уроки на основе слайдов и игровые задания для увлекательного учебного процесса.
В этой статье рассказывается о 7 стратегиях использования Nearpod для обучения математике. Стратегии включают в себя советы по привлечению учащихся с помощью различных мероприятий Nearpod, таких как интеграция Time to Climb и FlipGrid, а также предложения для учителей по сбору формирующих данных о своих учениках, чтобы дифференцировать обучение и адаптироваться на основе неправильных представлений учащихся.
1. Использовать урок в темпе ученика как самостоятельную работу
Использовать урок в темпе ученика как самостоятельную работу
Традиционно вы можете подумать об использовании Nearpod в качестве инструмента для презентаций.Тем не менее, вы можете назначить урок в индивидуальном темпе как самостоятельную работу, чтобы предоставить дополнительные возможности для практики, игр и сбора данных для формативного оценивания. В режиме Live to Student-Paced учителя могут переключаться между режимами Live и Student-Paced для гибкого обучения, чтобы поддерживать дифференциацию в соответствии с потребностями учащихся. Эта увлекательная независимая деятельность может позволить учащимся получить немедленную обратную связь по таким действиям, как сопоставление, решение проблемы на слайде «Нарисуй», объяснить свое мышление с помощью Open-Ended или бросить вызов своим одноклассникам с помощью Time to Climb.Чтобы узнать больше о других способах использования уроков в индивидуальном темпе, ознакомьтесь с этой записью в блоге.
2. Сбор данных в режиме реального времени для формативной оценки учащихся на протяжении всего урока
Сбор данных в режиме реального времени для формативной оценки учащихся на протяжении всего урока
Формирующее оценивание — ценный инструмент для учителей. Это позволяет учителям сразу увидеть, что ученики знают и какие у них могут быть неправильные представления о немедленном решении проблем. Nearpod эффективно собирает данные в режиме реального времени с помощью различных действий, когда учитель может просматривать все ответы учеников на одном экране.Например, предположим, что учащиеся создают модель умножения на слайде Draw It. В этом случае учитель может видеть, какие стратегии используют учащиеся, и устранять любые ошибки, которые могут быть у учащегося или группы учащихся, прежде чем двигаться дальше. Вы также можете использовать Collaborate Board для обмена студенческой работой, которая позволяет учащимся просматривать, обсуждать и критиковать ответы своих сверстников.
3. Напишите о математике, используя открытые вопросы
Учащимся нужна возможность поделиться своими мыслями о математике в безопасной среде. Использование открытых вопросов в Nearpod позволяет учащимся печатать или озвучивать свои мысли, не делясь ими со всем классом. Кроме того, открытые вопросы позволяют учащимся, которые не хотят говорить вслух, иметь возможность быть услышанными. Вы также можете прикрепить справочные материалы к действиям Nearpod, таким как «Нарисуй», «Открытые вопросы» или «Опросы», чтобы способствовать независимому мышлению.
Использование открытых вопросов в Nearpod позволяет учащимся печатать или озвучивать свои мысли, не делясь ими со всем классом. Кроме того, открытые вопросы позволяют учащимся, которые не хотят говорить вслух, иметь возможность быть услышанными. Вы также можете прикрепить справочные материалы к действиям Nearpod, таким как «Нарисуй», «Открытые вопросы» или «Опросы», чтобы способствовать независимому мышлению.
4.
Начните урок с игровых заданий
Вместо того, чтобы заканчивать урок «Время подняться», чтобы посмотреть, чему научились учащиеся, начните урок со сбора данных о том, что учащиеся помнят о концепции, чтобы дифференцировать инструкции на день.Учащимся нравится Time to Climb, и начало урока с увлекательного занятия поможет поддерживать высокий уровень энергии на протяжении всего урока.
Drag & Drop — еще один инструмент геймификации Nearpod, который учителя могут добавлять в начале или в конце урока. С помощью этого упражнения учащиеся могут классифицировать, маркировать и упорядочивать элементы или изображения.
5. Встроить Flipgrid, чтобы учащиеся могли делиться своей работой
Flipgrid — это отличный способ увидеть работы учащихся и попросить их объяснить свои мысли.Nearpod позволяет легко встроить Flipgrid в любой урок. Вы можете поделиться проблемой со студентами, поделиться их мыслями и смоделировать их стратегию, записывая себя и загружая ее в сетку. Как учитель, вы можете просматривать все видео и выделять стратегии для класса. Студенты также могут просматривать стратегии других и устанавливать связи между различными представлениями. Обмен связями обеспечивает отличную основу для обсуждения и позитивного сообщества по изучению математики.
6. Начните урок с разговора по номерам
Числовые беседы — идеальная разминка, и их можно адаптировать для любого уровня подготовки. Nearpod позволяет учащимся поделиться своей стратегией, в то время как в традиционном числовом общении только горстка учащихся может поделиться своим мнением. Кроме того, Nearpod позволяет учащимся решить задачу с низким уровнем риска и предоставить учителю формирующие данные о стратегиях. Например, учитель может использовать 5 х 25 в качестве числа. Затем учащиеся могут поделиться своей стратегией решения проблемы, используя слайды «Нарисуй» или открытое задание.Затем учитель может продемонстрировать стратегии, а учащиеся могут устно объяснить классу свои мысли.
Кроме того, Nearpod позволяет учащимся решить задачу с низким уровнем риска и предоставить учителю формирующие данные о стратегиях. Например, учитель может использовать 5 х 25 в качестве числа. Затем учащиеся могут поделиться своей стратегией решения проблемы, используя слайды «Нарисуй» или открытое задание.Затем учитель может продемонстрировать стратегии, а учащиеся могут устно объяснить классу свои мысли.
7. Дублирование слайда без рисования для моделирования решения задач с использованием аннотаций Live Teacher
Если вы когда-либо давали учащимся задачу для решения по определенному шаблону, сделайте ее слайдом «Нарисуй», а затем изо всех сил пытаетесь поддержать учащихся, моделируя стратегию, которую ученики не разделяли, затем продублируйте слайд «Нарисуй» как слайд с содержанием! В качестве слайда с содержимым вы можете использовать аннотацию Live Teacher для рисования на слайде.Ваши рисунки сразу же появятся на экранах учащихся, чтобы они могли увидеть и обсудить стратегию, которая могла отсутствовать в примерах ваших учеников. Обратите внимание, что функция Live Teacher Annotation доступна только для пользователей Premium Plus.
Обратите внимание, что функция Live Teacher Annotation доступна только для пользователей Premium Plus.
Nearpod — отличный инструмент для повышения вовлеченности, общения и успеваемости на уроках математики. Вы можете легко взять свои существующие презентации, загрузить их в Nearpod и внести небольшие изменения, которые обеспечат мгновенный доступ к математическому мышлению ваших учеников.Зарегистрируйтесь в Nearpod сегодня и попробуйте один из советов со своими учениками!
Кейт — специалист по математике первого уровня в Северной Вирджинии. Ей нравится помогать учителям интегрировать технологии в уроки, чтобы ученики могли по-настоящему погрузиться в изучение математики.
12 Объединение похожих терминов Действия, которые качают
Объединение одинаковых терминов — очень важная тема в математике в 7-м и 8-м классах. Нам, учителям, часто кажется настолько интуитивным, что термины должны быть одинаковыми, чтобы их можно было комбинировать. Однако по какой-то причине многим учащимся требуется много повторений, чтобы действительно усвоить эту концепцию. Даже несмотря на то, что мы можем учить объединению одних и тех же терминов по отдельности в течение дня или двух, это проявляется снова и снова, включенное во многие другие математические концепции, которые мы изучаем в средней школе. Итак, я хочу убедиться, что мои ученики получают необходимую им практику, рассредоточенную в течение всего года. Вот 12 упражнений, которые я использую в течение года, чтобы дать студентам много практики, сочетая похожие термины.
Однако по какой-то причине многим учащимся требуется много повторений, чтобы действительно усвоить эту концепцию. Даже несмотря на то, что мы можем учить объединению одних и тех же терминов по отдельности в течение дня или двух, это проявляется снова и снова, включенное во многие другие математические концепции, которые мы изучаем в средней школе. Итак, я хочу убедиться, что мои ученики получают необходимую им практику, рассредоточенную в течение всего года. Вот 12 упражнений, которые я использую в течение года, чтобы дать студентам много практики, сочетая похожие термины.
Если подумать, учащимся приходится комбинировать подобные термины, когда они занимаются многими другими делами.Например, вам нужно комбинировать одинаковые термины при преобразовании уравнения в форму пересечения наклона. Кроме того, вы должны использовать его, когда решаете уравнения. Этот навык настолько фундаментален. В свою очередь, мы должны убедиться, что студенты действительно понимают это. Приведенные ниже действия делают объединение похожих терминов увлекательным занятием. Эти упражнения отлично подходят в качестве начальных практических занятий или позже в качестве циклического обзора.
Эти упражнения отлично подходят в качестве начальных практических занятий или позже в качестве циклического обзора.
Комбинирование похожих терминов Лабиринты
Кубики пенопласта
Крестики-нолики с партнерами
Объединение похожих терминов Uno
Интерактивная сортировка блокнотов
Нравится Термин Захватчики
Распределение собственности и комбинирование подобных терминов Карточки с заданиями
Опасность за объединение похожих терминов
Комбинирование похожих терминов Игра на выбывание
Дудл-заметки
Объединение похожих терминов Kahoot
Миниатюрная бумажная цепочка
Давайте познакомимся с деятельностью
Эти задания различаются по типу и времени их использования в классе.Вы обнаружите, что список содержит задания для начала урока или для повторения. Некоторые задания учащиеся могут выполнять самостоятельно, а другие должны выполняться всем классом. Продолжайте читать, чтобы узнать больше о каждом из них и найти упражнения, которые подходят именно вашему классу.
В моем классе мы используем лабиринты почти каждый день. Учащиеся входят в комнату, берут свой лабиринт и приступают к работе. Часто я использую лабиринт, объединяющий похожие термины в начале года, а затем я использую его снова в конце года.Если вы выждете несколько месяцев между использованием, дети этого не запомнят. В этих трех лабиринтах учащиеся увидят разные переменные и даже некоторые отрицательные целые числа. Если вы хотите что-то, что вы можете распечатать и пойти, то эти лабиринты как раз то, что вам нужно.
Хотите еще больше математических лабиринтов? Каждый месяц мы отправляем БЕСПЛАТНЫЙ математический лабиринт для средней школы прямо на почту членов клуба «Лабиринт месяца». Зарегистрируйтесь сегодня и начните работу с бесплатным лабиринтом целых чисел исключительно для членов клуба!
Присоединяйтесь к клубу «Лабиринт месяца» здесь.
Это задание от My Math Imagination требует небольшой подготовки. Вам понадобятся маленькие пенопластовые кубики, а затем вы напишете на них разные термины. Студенты следуют некоторым простым правилам, чтобы играть в игру, сочетающую одинаковые термины (в ее блоге есть пошаговые инструкции). Когда я использую эту идею, я делаю несколько раундов со всем классом.
Студенты следуют некоторым простым правилам, чтобы играть в игру, сочетающую одинаковые термины (в ее блоге есть пошаговые инструкции). Когда я использую эту идею, я делаю несколько раундов со всем классом.
Вы можете найти пенопластовые кубики, идеально подходящие для этого занятия, на сайте Oriental Trading. У них есть набор действительно маленьких кубиков, 1 см, по низкой цене или, если вы хотите разориться, у них есть большие.У меня не было пустых кубов, но я нашел несколько квадратных дюймовых плиток, лежащих вокруг. Они действительно хорошо работали, когда их вытягивали из миски, а не катали. Итак, даже если у вас нет пенопластовых кубиков, возможно, у вас есть что-то еще, что вы не используете, что может подойти для этого занятия. Одним из преимуществ этого занятия является то, что после того, как вы его сделали, вы можете легко использовать его в качестве губки в течение всего года.
В моем классе очень распространена работа с партнерами. Я предлагаю учащимся работать с назначенным им партнером, случайно сгенерированным партнером и иногда с партнером по своему выбору.Эта игра «Объединение похожих терминов в крестики-нолики» — отличный способ побудить учащихся говорить с партнерами о комбинировании похожих терминов. Эта доска для игры в крестики-нолики имеет размер 5 на 5 вместо 3 на 3, поэтому ученики должны собрать 5 карт подряд, чтобы выиграть. Совет профессионала: моделирование того, как вы хотите, чтобы они играли в игру, является ключевым. Таким образом, совместная игра (или даже половина раунда) с упором на язык, который должны использовать студенты, имеет большое значение.
Я предлагаю учащимся работать с назначенным им партнером, случайно сгенерированным партнером и иногда с партнером по своему выбору.Эта игра «Объединение похожих терминов в крестики-нолики» — отличный способ побудить учащихся говорить с партнерами о комбинировании похожих терминов. Эта доска для игры в крестики-нолики имеет размер 5 на 5 вместо 3 на 3, поэтому ученики должны собрать 5 карт подряд, чтобы выиграть. Совет профессионала: моделирование того, как вы хотите, чтобы они играли в игру, является ключевым. Таким образом, совместная игра (или даже половина раунда) с упором на язык, который должны использовать студенты, имеет большое значение.
Вместе со своим партнером каждый учащийся может играть за x или o.Учащиеся ходят по очереди, но оба ученика все равно упрощают все выражения в игре. Учащиеся, чья очередь, выбирают квадрат. Затем оба ученика упрощают выражение, комбинируя одинаковые термины. Если человек, которому пришла очередь, делает это правильно, то он получает квадрат. Когда они ошибаются, а другой человек делает это правильно, они «крадут» квадрат. Эта игра дает хорошую математическую практику, разбавленную весельем.
Когда они ошибаются, а другой человек делает это правильно, они «крадут» квадрат. Эта игра дает хорошую математическую практику, разбавленную весельем.
В моем классе мы много работаем в напарниках. Я считаю, что партнерские игры эффективны и вовлекают учащихся.Эта игра «Комбинируя похожие термины Uno» — это весело, и учащиеся могут легко освоить ее, если у них есть опыт игры в карточную игру UNO. Как и в других перечисленных выше упражнениях, я бы поиграл в эту игру со всем классом, по крайней мере, одну или две руки, чтобы ученики видели, что делать.
Сообщение в блоге, связанное с этой игрой, содержит пошаговые инструкции. Эта игра занимает около 5-15 минут, чтобы играть. Я использовал эту игру для быстрых финишеров, когда работал с группой отстающих учеников.
Что мне нравится в этом интерактивном упражнении по сортировке тетрадей от Math Equals Love, так это то, что оно показывает учащимся, как буквально сочетать одинаковые термины.Они на самом деле разрезают выражение и соединяют похожие термины. Учащиеся не видят, как такие термины, как 2x и -5y, являются отдельными и что переменные соответствуют коэффициентам. Вы можете использовать это задание в интерактивной записной книжке или как отдельное задание. Мы записываем его в свои тетради, чтобы мы могли обратиться к нему позже.
Учащиеся не видят, как такие термины, как 2x и -5y, являются отдельными и что переменные соответствуют коэффициентам. Вы можете использовать это задание в интерактивной записной книжке или как отдельное задание. Мы записываем его в свои тетради, чтобы мы могли обратиться к нему позже.
Мы делаем одно вместе всем классом, и я прошу учеников поделиться своими мыслями, пока мы работаем над ним. Затем я предлагаю им работать с партнерами, но каждый ученик отвечает за выполнение своей работы.Это дает учащимся возможность рассказать о том, что они делают, но они должны думать и принимать решения о том, как выполнить каждый пример.
Кто не любит возвращаться к игре Space Invaders? Эта игра Like Term Invaders от XP Math дает учащимся интерактивный способ понять, что только x могут сочетаться с x. Кроме того, они видят множество переменных и комбинаций. Я люблю такие игры, потому что они закрепляют концепцию, а дети даже не осознают, что учатся.Другая идея состоит в том, чтобы вы, как учитель, играли с ними. Мои ученики ЛЮБЯТ бросать вызов учителю. Не бойтесь немного повеселиться с ними.
Мои ученики ЛЮБЯТ бросать вызов учителю. Не бойтесь немного повеселиться с ними.
Не знаю, где бы я был без карточек заданий. Они такие универсальные. В большинстве модулей я предлагаю учащимся заполнять карточки с заданиями вместе с партнером. Кроме того, я всегда помещаю ответы на обратную сторону карточек. Это дает учащимся возможность исправить свои ошибки. Некоторые учителя беспокоятся о том, чтобы выбор ответов был так легко доступен, но я считаю, что чем более немедленная обратная связь, тем больше влияние.
Этот конкретный набор карточек с заданиями содержит несколько карточек для комбинирования таких терминов, свойств распределения и выражений факторинга. Они дают студентам много разных взглядов на эти навыки.
Эта игра «Опасность, объединяющая подобные термины» бесплатна, и в ней есть много практических задач для детей. Когда мы играем в Jeopardy, ученики работают индивидуально. Я считаю, что вам нужно, чтобы каждый ученик решил каждую задачу. Если вы не попросите каждого из них решить задачу, то Jeopardy может стать большой тратой времени, когда ученики на самом деле не занимаются математикой.Мне нравится разнообразие вопросов в этой опасной игре. Эта игра не займет много времени, и вы, возможно, захотите иметь ее в своем заднем кармане. Иногда у вас есть несколько минут, и вам нужна губка. Ну, этот идеально подходит для такого рода деятельности.
Если вы не попросите каждого из них решить задачу, то Jeopardy может стать большой тратой времени, когда ученики на самом деле не занимаются математикой.Мне нравится разнообразие вопросов в этой опасной игре. Эта игра не займет много времени, и вы, возможно, захотите иметь ее в своем заднем кармане. Иногда у вас есть несколько минут, и вам нужна губка. Ну, этот идеально подходит для такого рода деятельности.
Несколько лет назад я создал игру в PowerPoint для своих занятий. Я решил назвать его Нокаутом. В этой игре учащиеся выбирают призрака Pac-Man, а затем им показывают вопрос. Позже я узнал, что студенты действительно выбивались из колеи, когда выбирали вопросы, за которые давали не просто баллы, а «бонусы».Некоторые из бонусов дают им дополнительные очки, в то время как другие на самом деле плохие, и они теряют очки. Удивительно, но мои ученики любят терять очки. Они думают, что это очень смешно. Они действительно входят в игру и вовлечены. Каждый ученик отвечает на все вопросы. Я предлагаю им написать свои ответы на своих досках, но они также могут использовать бумажное руководство, чтобы показать свою работу.
Я предлагаю им написать свои ответы на своих досках, но они также могут использовать бумажное руководство, чтобы показать свою работу.
Игра на выбывание «Комбинируя похожие термины» включает в себя простые выражения. Если ваши ученики находятся на базовом уровне, эта игра подойдет им.Он также может служить обзором для более продвинутых студентов. Кроме того, поскольку эта тема не очень сложна, это занятие не займет много времени. Вы можете закончить его за 15 минут.
Если вы не знакомы с Doodle Notes, вы можете прочитать о них здесь. Они дают учащимся другой взгляд на объединение подобных терминов. Мне нравится использовать этот конкретный набор каракулей от Math Giraffe на 3-й или 5-й день работы с комбинированием похожих терминов. Волшебство этого типа заметок заключается в том, что ученики могут написать то, что они знают.Вы не хотите просто сделать еще один набор заметок, которые ученики копируют. Позвольте учащимся показать вам, что они знают о переменных и что делает термины похожими или нет.
Может быть, вы ищете игру для всего класса, которая собирает данные. Kahoot отслеживает, как каждый человек и как весь класс справляется с каждым вопросом. Это хорошо работает в качестве формирующего оценивания в конце урока.
В этой игре Kahoot «Комбинируя похожие термины» 10 вопросов, и они довольно простые.Кроме того, существует множество игр Kahoo, в которых используются слова, созданные учителями. Если эта конкретная игра не соответствует вашим потребностям, вы всегда можете поискать, и вы найдете множество возможных игр Kahoot по этой теме.
Бумажные цепочки — это очень весело. Эта игра «Комбинируя похожие термины в бумажной цепочке» короткая и может быть завершена за 10–15 минут. Что мне действительно нравится, так это то, что ученики должны сначала расставить выражения и ответы по порядку. Это действительно показывает вам, если они получают это или не очень быстро.С помощью этой цепочки вы можете распечатать копию каждого учащегося на бумаге разного цвета, а затем попросить их соединить их. Повесьте цепочку в классе или за дверью. Это не занимает много времени, и студенты гордятся своей работой.
Вы можете БЕСПЛАТНО загрузить эту бумажную цепочку вместе с 4 другими играми и заданиями по математике для средней школы, нажав здесь:
Получите БЕСПЛАТНУЮ цепочку заданий «Комбинируй похожие термины»
Попробуйте одну вещь…
Ищете ли вы практику, дополнительную практику, домашнюю работу, звонарей, заключительные или повторные задания, в этом списке есть что-то, что вы можете взять с собой в класс.Вы можете включить их в работу всего класса, работу с партнером или самостоятельную практику. Когда дело доходит до объединения подобных терминов, кажется, что у студентов никогда не будет достаточно практики. Они должны быть потрясающими в этом навыке на долгие годы. Пусть они видят это по-разному и укрепляют его в течение года.
Спасибо за прочтение! До скорого.
Родственные
Horizons Pre-Algebra and Algebra 1
Horizons Pre-Algebra входит в мой TopPicks. Horizons Algebra 1 настолько похож на Pre-Algebra , что я решил объединить их обзоры в один. Тем не менее, Algebra I не попал в мой список лучших, потому что его немного сложнее использовать, чем Pre-Algebra .
В обоих курсах используется традиционный подход, который также включает некоторое использование манипулятивных методов — больше в Pre-Algebra , чем в Algebra 1 . Каждый курс состоит из трех компонентов: руководства для учителя, рабочего текста для учащихся и книги Tests and Resources .Они продаются бокс-сетом.
Уроки следуют общепринятому формату: презентация новой концепции, управляемая практика (называемая «классная работа» в тексте для учащихся), затем самостоятельная практика. В руководствах для учителей есть советы по обучению, в которых выделяются моменты, которые учитель может объяснить. Во многих случаях презентация новой концепции достаточно хорошо объясняется в студенческом тексте, так что никакого обучения не требуется. Иногда концепции и навыки преподаются только из руководства учителя. Среди них использование плиток алгебры в обоих курсах.В Pre-Algebra среди других тем, которые преподаются только из руководства для учителя, есть такие, как использование компаса и транспортира для построения круговой диаграммы, использование карточек с десятичными дробями и использование научного калькулятора.
Урок презентации новых концепций относительно краток. Введение в студенческом тексте редко помогает учащемуся попрактиковаться в решении проблем. Управляемая практика или классная работа предназначены для этой цели. Ожидается, что в этот момент учитель будет работать со студентами.В Pre-Algebra многие учащиеся смогут самостоятельно работать с новой концептуальной презентацией и классной работой. Алгебра 1 , с другой стороны, кажется, что требуется больше обучения и помощи для работы в классе, прежде чем учащиеся смогут работать самостоятельно. Это означает, что родитель или учитель должны ознакомиться с материалом до урока.
Пособия учителя полезны. В них перечислены концепции, цели и необходимые материалы, а также советы по обучению.Созданные для занятий в классе, они упоминают такие вещи, как учащиеся, работающие над доской, или учащиеся, объясняющие проблемы для класса. Тем не менее, эти курсы могут хорошо подойти для домашнего обучения. В идеале родитель, работающий с одним ребенком, будет использовать советы по обучению, чтобы провести урок с конкретными примерами и объяснениями. Эти курсы, вероятно, лучше всего подойдут большинству учащихся, обучающихся на дому, при использовании комбинации некоторых уроков, которые преподаются, и других, проводимых независимо, в зависимости от содержания и советов по обучению. Pre-Algebra с большей вероятностью подойдет для самостоятельного изучения, чем Algebra 1 .
«Оценка готовности» и ключи к ответам находятся в начале руководства для учителя. Шестнадцать тестов и четыре экзамена включены в книгу Tests and Resources для каждого курса. и тестовые страницы с ответами, надпечатанными, чтобы они служили вашими ключами для ответов.80 дополнительных рабочих листов находятся в книге Test and Resources для каждого курса, и некоторые из них могут также использоваться как тесты.
Студенческие рабочие тексты очень красиво напечатаны в полноцветном режиме. Количество действий и проблем, которые нужно решить, не кажется огромным по сравнению с некоторыми текстами, которые изобилуют проблемами. Однако для решения некоторых задач Horizon потребуется некоторое время. Например, одна задача на с. 170 в Предварительная алгебра инструктирует студента «Найти среднее значение, медиану, моду и диапазон. Затем нарисуйте гистограмму и график «ящик с усами». Футбольный счет в одну из суббот был 14, 0, 7, 26, 13, 27, 36, 37, 24, 7, 7, 31, 20, 19, 24, 27, 17, 10, 31, 24, 24, 27, 41. , 34, 16, 13.Частые словесные задачи помогают учащимся понять практическое применение того, что они изучают. Так что есть много работы без страниц, которые кажутся загроможденными проблемами.
Каждый десятый урок курса Pre-Algebra включает интервью с христианином, который использует навыки предварительной алгебры в своей карьере. В Algebra 1, каждый десятый урок посвящен спорту, хобби или деятельности, такой как футбол, сбор средств и парки развлечений. Словесные задачи в этом уроке и некоторых последующих уроках основываются на интервью или теме.Кроме того, на каждом десятом уроке учащимся предоставляется набор вопросов в стандартизированном формате теста с несколькими вариантами ответов, чтобы помочь им с навыками подготовки к тесту.
Для обоих курсов учащиеся должны иметь научный калькулятор, цветные карандаши и миллиметровую бумагу. (Три страницы миллиметровки включены в конце учебника Pre-Algebra для учащихся.)
Обратите внимание, что Alpha Omega идентифицирует Pre-Algebra как курс седьмого класса, а Algebra 1 как курс восьмого класса.Их также можно использовать для восьмого и девятого классов соответственно.
Pre-Algebra
Это сложный курс. Хотя в нем рассматриваются основы сложения, вычитания, умножения, деления и теории чисел, он быстро переходит к числам со знаком, показателям степени, разложению на множители, квадратным корням и порядку операций. Он продолжается через работу с дробями, десятичными знаками и процентами, включая много практического применения. Большое внимание уделяется графикам, вероятности и статистике.Геометрия охватывает периметр, площадь и объем, а также такие темы, как конгруэнтные треугольники и сетки объемных фигур (двумерные представления трехмерных объектов, как если бы они были раскрыты и уложены плоско), линии, углы, графические точки на плоскости. координатная плоскость и форма пересечения наклона. Он даже вводит тригонометрию. Понятия алгебры, изучаемые в этом курсе, включают сложение, вычитание, умножение и деление многочленов, включая факторинг. Преподаются и другие темы, такие как метрическая система и измерения.
Пособие для учителя полезно. В нем перечислены концепции, цели и необходимые материалы, но наиболее полезными являются советы по обучению. Разработанный для работы в классе, он упоминает такие вещи, как учащиеся, работающие над доской, или учащиеся, объясняющие проблемы для класса. Тем не менее, этот курс хорошо подойдет для домашнего обучения. В идеале родитель, работающий с одним ребенком, будет использовать советы по обучению, чтобы провести урок с более конкретными примерами и объяснениями, а также с дополнительными темами, упомянутыми выше.
В дополнение к предметам, упомянутым ранее, которые необходимы для обоих курсов, учащимся потребуются транспортир, линейка и один кубик. Другие предметы, такие как блоки, ножницы, лента, праздничная шляпа и монеты, используются редко и могут быть импровизированными заменителями.
Хотя время от времени используются и другие простые манипуляции, наиболее важными манипуляциями для развития понятий являются плитки алгебры. Они напечатаны в полном цвете в книге «Тесты и ресурсы», и их необходимо вырезать.Я рекомендую вам заламинировать их для удобства обращения. Плитки алгебры учат понятиям алгебры, используя метод «построения прямоугольника», аналогичный тому, что преподается в Math-U-See . Лично мне очень нравится использовать это визуальное представление для алгебры, чтобы помочь учащимся действительно понять, что происходит, когда они манипулируют уравнениями.
В этой книге также есть «полоски с формулами», которые нужно раздавать учащимся для использования на некоторых уроках. В них переформулированы некоторые основные формулы, например, для нахождения площади круга или эквиваленты измерений, такие как 1 миля = 5280 футов и эквиваленты в британских метрических единицах.Есть 24 таких полоски, которые можно использовать на разных уроках, и формулы иногда повторяются более чем на одной полоске. Причина представления формул таким образом, а не в учебнике, заключается в том, что полоски иногда используются с викторинами и экзаменами, когда учащемуся было бы нецелесообразно иметь доступ к тексту. Конечно, учащимся необходимо запомнить некоторые формулы. В руководстве для учителя указано, какие формулы не указаны в тестах ACT/SAT (и, следовательно, не указаны на полосках с формулами) и должны быть выучены наизусть.
Карточки с дробями и десятичными дробями используются в ряде уроков, но их необходимо приобретать отдельно. Некоторым студентам не нужно будет их использовать, и они могут их пропустить. Их использование указано в руководстве для учителя, поэтому учащиеся не заметят их отсутствия, если будут работать самостоятельно.
Текст явно написан для христианской аудитории со многими ссылками на церковь, пасторов, евангельское магическое шоу, дизайн рубашек для молодежного ретрита, миссионеров и других мероприятий, связанных с церковью.
Алгебра 1
Как и Предварительная алгебра, Алгебра 1 начинается с обзора основных тем, таких как абсолютное значение, показатели степени, корни, радикалы, порядок операций, разложение на множители и простые числа. Он проходит через стандартные темы алгебры для первого года обучения, включая различные стратегии решения уравнений, построение графиков линейных уравнений, решение и построение графиков линейных неравенств, работу с системами уравнений, квадратными уравнениями, рациональными выражениями и радикалами.Он охватывает проблемы смеси и движения, отношения и скорости. Он также вводит функции относительно рано в курс и обучает дискриминантам ближе к концу.
Этот курс, вероятно, более сложен в использовании, чем другие, популярные среди школьников, потому что в большинстве случаев родители или учителя должны помогать учащимся работать в начале каждого урока, чтобы изучить новые понятия. Это кажется более сложным, чем в Pre-Algebra , вероятно, потому, что преподаваемые концепции более сложны.
Множество текстовых задач помогают учащимся понять, как некоторые понятия и навыки, которые они изучают, могут применяться в реальной жизни. Большинство текстовых задач основаны на теме каждого модуля (например, футбол, футбол, сбор средств, зимние Олимпийские игры), которые могут хорошо работать, если учащиеся заинтересованы в теме, но могут быть помехой, если нет.