Сферы физика 9 класс: «Сферы» УМК «Физика. 9 класс»

«Сферы» УМК «Физика. 9 класс»

Учебник Данный учебник продолжает линию учебно-методических комплектов «Сферы» по физике. Издание подготовлено в соответствии с Федеральным государственным… Подробнее	Электронное приложение Электронное приложение к учебнику является составной частью учебно-методического комплекта и значительно расширяет содержание учебника за счёт… Подробнее
Тетрадь-тренажёр Тетрадь-тренажёр является составной частью учебно-методического комплекта «Физика. 9 класс» линии «Сферы». В данном пособии содержатся задания для… Подробнее	Тетрадь-практикум Пособие является составной частью учебно-методического комплекта «Физика. 9 класс» линии «Сферы». В данном пособии представлены лабораторные… Подробнее
Тетрадь-экзаменатор Тетрадь-экзаменатор входит в учебно-методический комплект «Физика. 9 класс» линии «Сферы». Пособие предназначено для проверки знаний учащихся по… Подробнее	Задачник Задачник является составной частью учебно-методического комплекта «Физика» для 9 класса линии УМК «Сферы». В пособии содержатся задачи по всем темам… Подробнее
Поурочное тематическое планирование Данное пособие сопровождает учебно-методический комплект «Физика» линии «Сферы». В пособии содержится поурочное тематическое планирование,… Подробнее	Поурочные методические рекомендации Пособие входит состав учебно-методического комплекса «Физика» линии «Сферы». В пособии содержатся поурочные методические рекомендации, разработанные… Подробнее
Программы общеобразовательных учреждений для 7-9 классов Данное пособие сопровождает учебно-методический комплект «Физика» линии «Сферы». В нём содержатся программы, разработанные группой авторов на основе… Подробнее	Рабочие программы Рабочая программа по физике для 7–9 классов разработана к учебно-методическим комплексам линии «Сферы» издательства «Просвещение». Программа… Подробнее
Конструктор уроков Конструктор уроков по физике — электронное приложение, позволяющее легко и быстро формировать увлекательные уроки по физике, наполненные… Подробнее

ГДЗ по Физике за 9 класс Тетрадь-практикум Сферы Артеменков Д.

А., Белага В.В.

Физика 9 класс
Артеменков Д.А.
тетрадь-практикум

Авторы: Артеменков Д.А., Белага В.В., Воронцова Н.И.

«ГДЗ по физике 9 класс тетрадь-практикум Артеменков, Белага, Воронцова (Просвещение)» позволит старшеклассникам чувствовать себя свободнее на классных часах по этой дисциплине. Справится с возросшей школьной нагрузкой молодым людям поможет онлайн-решебник, ведь он:

• развивает самостоятельность и независимость от помощи извне;
• прошел проверку федерального государственного образовательного стандарта;
• составлен максимально удобно для пользователя и представлен в онлайн-формате, имеет постраничную навигацию для быстрого доступа к нужному номеру упражнения.

Сборник верных ответов позволит без проблем понять все разделы учебно-методического комплекта. Ребята быстро забудут про свои прошлые неудачи, успеваемость станет стабильно положительной. Пособие превратится в лучшего товарища для каждого ученика, желающего досконально освоить техническую науку.

Как решебник тетради-практикума по физике для 9 класса от Артеменкова повышает мотивацию учеников

ГДЗ помогают ребятам чаще посещать классные часы. Как это происходит? Давайте разберёмся с истинными причинами прогула занятий. Чаще всего, это плохая подготовка к уроку или отсутствие таковой в принципе. Из-за этого ребенок подросткового возраста принимает решение пропустить занятие, чтобы не заработать неудовлетворительные баллы.

Решебник позволит сделать подготовительное мероприятие более оперативным и результативным. Благодаря этому факту школьник не захочет «прогуливать» классные часы, так как пожелает заработать положительную оценку за домашнюю работу, выполненную под присмотром онлайн-самоучителя. Таким элементарным способом решается «вселенская» проблема посещаемости уроков.

Характеристика процесса обучения по физике в девятом классе

В этом году молодые люди освоят следующие темы из учебно-методического комплекта:

• почему прямолинейное движение считается инструментом кинематики, что изучает данный физический раздел;
• о чем гласит закон всемирного тяготения, каково ускорение свободного падения;
• как по окружности движется тело с постоянной по модулю скоростью.

«ГДЗ к тетради-практикуму по физике за 9 класс Артеменков Д. А., Белага В. В., Воронцова Н. И. (Просвещение)» направит девятиклассников к положительным оценкам. Успеваемость улучшится в долгосрочной перспективе, а в самом ученике проснется интерес к этой увлекательной науке.

ГДЗ по физике для 9 класса на 5.fun

ГДЗ по физике для 9 класса на 5. fun

• • Физика 9 класс

  • Авторы:
    Л. Э. Генденштейн, А. Б. Кайдалов, В. Б. Кожевников

  • Издательство:

    Мнемозина 2010

• • Физика 9 класс
    Сборник задач

  • Авторы:
    Лукашик В. И., Иванова Е.В.

  • Издательство:

    Просвещение 2016

• • Физика 9 класс
    Сборник задач

  • Автор:
    А.В. Перышкин

  • Издательство:

    Экзамен 2015

• • Физика 9 класс

  • Авторы:
    Кикоин И. К., Кикоин А.К.

  • Издательство:

    Просвещение 1999

• • Физика 9 класс

  • Автор:
    А.В. Перышкин

  • Издательства:

    Экзамен, Дрофа 2014-2020

• • Физика 9 класс
    Классический курс

  • Авторы:
    Громов С. В., Родина Н.А., Белага В.В., Ломаченков И.А., Панебратцев Ю.А.

  • Издательство:

    Просвещение 2018

• • Физика 9 класс
    Задачник

  • Авторы:
    Л. Э. Генденштейн, Л. А. Кирик, И. М. Гельфгат, И. Ю. Ненашев

  • Издательство:

    Мнемозина 2010

• • Физика 9 класс
    Рабочая тетрадь

  • Авторы:
    Гутник Е. М., Власова И. Г.

  • Издательство:

    Дрофа 2016

• • Физика 9 класс
    Архимед

  • Автор:
    Кабардин О.Ф.

  • Издательство:

    Просвещение 2017

• • Физика 9 класс
    Дидактические материалы

  • Авторы:
    Марон А. Е., Марон Е.А.

  • Издательство:

    Дрофа 2016

• • Физика 9 класс
    Самостоятельные и контрольные работы

  • Авторы:
    Марон А.Е., Марон Е.А.

  • Издательство:

    Дрофа

• • Физика 9 класс

  • Авторы:
    Грачев А. В., Погожев В.А., Боков П.Ю.

  • Издательство:

    Вентана-граф 2016

• • Физика 9 класс
    Рабочая тетрадь

  • Авторы:
    Грачев А.В., Погожев В.А., Боков П.Ю.

  • Издательство:

    Вентана-граф 2017

• • Физика 9 класс
    Тесты

  • Автор:
    Слепнева Н. И.

  • Издательство:

    Дрофа 2016

• • Физика 9 класс
    Лабораторные работы

  • Авторы:
    Филонович Н.В., Восканян А.Г.

  • Издательство:

    Дрофа 2018

• • Физика 9 класс
    Сборник вопросов и задач

  • Авторы:
    Марон А. Е., Марон Е.А., Позойский С.В.

  • Издательство:

    Дрофа 2018

• • Физика 9 класс
    Контрольно-измерительные материалы (КИМ)

  • Автор:
    Лозовенко С.В.

  • Издательство:

    ВАКО 2016

• • Физика 9 класс
    Рабочая тетрадь

  • Авторы:
    Касьянов В. А., Дмитриева В.Ф.

  • Издательство:

    Дрофа 2017

• • Физика 9 класс
    Рабочая тетрадь УМК

  • Авторы:
    Минькова Р.Д., Иванова В.В.

  • Издательство:

    Экзамен 2017

• • Физика 9 класс
    Рабочая тетрадь

  • Авторы:
    Пурышева Н. С., Важеевская Н.Е., Чаругин В.М.

  • Издательство:

    Дрофа 2017

• • Физика 9 класс
    Проверочные и контрольные работы

  • Авторы:
    Пурышева Н.С., Лебедева О.В.

  • Издательство:

    Дрофа 2015

• • Физика 9 класс

  • Авторы:
    Пурышева Н. С., Важеевская Н.Е., Чаругин В.М.

  • Издательство:

    Дрофа 2017

• • Физика 9 класс
    Сферы

  • Авторы:
    Белага В.В., Ломаченков И.А., Панебратцев Ю.А.

  • Издательство:

    Просвещение 2017

• • Физика 9 класс
    Тетрадь для лабораторных работ

  • Авторы:
    Генденштейн Л. Э., Орлов В.А.

  • Издательство:

    Мнемозина 2017

• • Физика 9 класс
    Самостоятельные работы

  • Авторы:
    Генденштейн Л.Э., Орлов В.А., Никифоров Г.Г.

  • Издательство:

    Мнемозина 2017

• • Физика 9 класс
    Тематические контрольные работы

  • Авторы:
    Генденштейн Л. Э., Кошкина А.В.

  • Издательство:

    Мнемозина 2014

• • Физика 9 класс
    Рабочая тетрадь УМК

  • Автор:
    Перышкин А.В.

  • Издательство:

    Экзамен 2017

• • Физика 9 класс
    Алгоритм успеха

  • Авторы:
    Хижнякова Л. С., Синявина А.А.

  • Издательство:

    Вентана-граф 2019

• • Физика 9 класс
    Рабочая тетрадь Алгоритм успеха

  • Авторы:
    Хижнякова Л.С., Синявина А.А., Холина С.А.

  • Издательство:

    Вентана-граф 2014

• • Физика 9 класс
    Рабочая тетрадь Архимед

  • Автор:
    Кабардина С. И.

  • Издательство:

    Просвещение 2018

• • Физика 9 класс
    Задачник Сферы

  • Авторы:
    Артеменков Д.А., Ломаченков И.А., Панебратцев Ю.А.

  • Издательство:

    Просвещение 2016

• • Физика 9 класс
    Тетрадь-практикум Сферы

  • Авторы:
    Артеменков Д. А., Белага В.В., Воронцова Н.И.

  • Издательство:

    Просвещение 2016

• • Физика 9 класс
    Тетрадь-тренажёр Сферы

  • Авторы:
    Артеменков Д.А., Белага В.В., Воронцова Н.И.

  • Издательство:

    Просвещение 2016

• • Физика 9 класс
    Тетрадь-экзаменатор Сферы

  • Автор:
    Жумаев В. В.

  • Издательство:

    Просвещение 2018

• • Физика 9 класс

  • Авторы:
    Исаченкова Л.А., Сокольский А.А., Захаревич Е. В.

  • Издательство:

    Народная асвета 2019

• • Физика 9 класс

  • Авторы:
    Генденштейн Л. Э., Булатова А.А., Корнильев И.Н., Кошкина А.В.

  • Издательство:

    Бином 2017

Часто ищут

• • Русский язык 9 класс
    Рабочая тетрадь Академический школьный учебник

  • Авторы:
    Загоровская О.В., Чаплыгина Э.Н

  • Издательство:

    Просвещение 2014

• • Английский язык 9 класс

  • Авторы:
    В. П. Кузовлев, Н.П. Лапа, Э.Ш. Перегудова

  • Издательство:

    Просвещение 2015

• • Биология 9 класс
    Живой организм

  • Авторы:
    Сапин М.Р., Сонин Н.И.

  • Издательство:

    Дрофа 2014

• • Английский язык 9 класс
    Happy English

  • Авторы:
    К. И. Кауфман, М.Ю. Кауфман

  • Издательство:

    Титул 2015

• • Русский язык 9 класс
    Алгоритм успеха

  • Авторы:
    Шмелев А.Д., Флоренская С.Н., Митюрев С.Н.

  • Издательство:

    Вентана-граф 2016

• • Черчение 9 класс

  • Автор:
    В. Н. Виноградов

  • Издательство:

    Национальный институт образования 2014

• • Английский язык 9 класс
    Рабочая тетрадь Spotlight

  • Авторы:
    В. Эванс, Д. Дули, О. Подоляко, Ю.Е. Ваулина

  • Издательство:

    Просвещение 2016

• • Русский язык 9 класс

  • Авторы:
    М. М. Разумовская, С.И. Львова, В.И. Капинос, В.В. Львов

  • Издательство:

    Дрофа 2015-2020

• • Геометрия 9 класс
    Дидактические материалы Алгоритм успеха

  • Авторы:
    Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С.

  • Издательства:

    Просвещение, Вентана-граф 2017-2021

Урок «Небесная сфера. Системы небесных координат. Подвижная карта звездного неба» (физика 9 класс)

ФИЗИКА 9

Тема: Небесная сфера. Системы небесных координат. Подвижная карта звездного неба.

Задачи: ввести основные понятия :небесная сфера, экваториальной и горизонтальной системы координат; способствовать развитию мышления, речи; продолжить развитие взглядов уч-ся на мироздание

Ход урока

1. Орг. момент.

2. Изучение нового материала

Небесная сфера — это воображаемая сферическая поверхность произвольного радиуса, в центре которой находится наблюдатель.

Небесные тела проектируются на небесную сферу.

Из-за малых размеров Земли, в сравнении с расстояниями до звезд, наблюдателей, расположенных в разных местах земной поверхности, можно считать находящимися в центре небесной сферы.

В действительности никакой материальной сферы, окружающей Землю, в природе не существует.

Небесные тела движутся в беспредельном мировом пространстве на самых различных расстояниях от Земли. Эти расстояния невообразимо велики, наше зрение не в состоянии их оценить, поэтому человеку все небесные тела представляются одинаково удаленными.

За год Солнце описывает большой круг на фоне звёздного неба. Годичный путь Солнца по небесной сфере называется эклиптикой. Перемещаясь по эклиптике, Солнце в равноденственных точках дважды пересекает небесный экватор. Это бывает 21 марта и 23 сентября.

Точка небесной сферы, которая остается неподвижной при суточном движении звезд, условно называется северным полюсом мира. Противоположная точка небесной сферы называется южным полюсом мира. Жители северного полушария его не видят, т. к. он находится под горизонтом. Отвесная линия, проходящая через наблюдателя, пересекает небо над головой в точке зенита и в диаметрально противоположной точке, называемой надиром.

Элементы небесной сферы

Отвесная линия — линия, проходящая через наблюдателя и центр Земли.

Зенит и Надир — точки, образованные при пересечении отвесной линии и небесной сферы.

Истинный (математический) горизонт — большой круг небесной сферы перпендикулярный отвесной линии, асателен к поверхности Земли. Делит небесную сферу на видимую и скрытую половины.

Полуденная линия — линия, соединяющая точки юга и севера истинного горизонта.

Суточное вращение небесной сферы — видимое движение светил, происходящее из-за вращения Земли вокруг своей оси.

Ось мира — ось, вокруг которой происходит суточное вращение небесной сферы. Ось мира параллельна оси вращения Земли и совпадает с ней только на полюсах Земли.

Полюса мира (северный и южный) — точки пересечения оси мира и небесной сферы.

Небесный экватор — большой круг небесной сферы перпендикулярный оси мира. Делит небесную сферу на северную и южную половины. Пересекает истинный горизонт в точках востока и запада.

Небесный меридиан — большой круг небесной сферы, проходящий через точки зенит, надир, полюса мира, север и юг. Делит небесную сферу на восточную и западную половины.

Круги склонения — дуги окружностей, соединяющие полюса мира.

Круги высоты — дуги окружностей, соединяющие точки зенит и надир.

Эклиптика — большой круг небесной сферы, по которому проходит видимое годовое движение Солнца. Пересекает небесный экватор под углом 23,50 в точках весеннего и осеннего равновесия.

Системы небесных координат

Системы небесных координат используются в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере.

В астрономии применяют несколько систем небесных координат, удобных для решения различных научных и практических задач. При этом используются известные плоскости, круги и точки небесной сферы.

В зависимости от стоящей задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальные системы координат. Реже — эклиптическая, галактическая и другие.

1. Горизонтальная система небесных координат

В горизонтальной системе небесных координат основным кругом служит математический, или истинный, горизонт, а координатой, аналогичной географической широте, — высота светила (над горизонтом) h.

Высота светила отсчитывается от плоскости горизонта со знаком «плюс» в видимом полушарии небесной сферы и со знаком «минус» — в невидимом, под горизонтом; таким образом, высоты, так же как и широты на Земле, могут принимать значения от + 90 до — 90°.

Круг небесной сферы, на котором все точки имеют равные высоты, аналогичный географической параллели, называется альмукантаратом.

Взамен высоты в астрономии часто используется зенитное расстояние z = 90°—h. Геометрически зенитное расстояние z представляет собой угол между направлениями на зенит и на объект; оно всегда положительно и принимает значения в пределах от 0 (для точки зенита) до 180° (для точки надира).

Аналогом географической долготы в горизонтальной системе координат служит азимут, представляющий собой двугранный угол между плоскостью вертикала, проходящего через зенит и рассматриваемую точку, и плоскостью небесного меридиана.

Поскольку обе указанные плоскости перпендикулярны плоскости математического горизонта, мерой двугранного угла может служить соответствующий угол между их следами в горизонтальной плоскости (альфа).

В геодезии принято отсчитывать азимуты от направления на точку севера по часовой стрелке (через точки востока, юга и запада) от 0 до 360°. В астрономии азимуты отсчитываются в том же направлении, однако часто начиная от точки юга. Тем самым астрономические и геодезические азимуты отличаются друг от друга на 180°, поэтому важно при решении той или иной задачи на небесной сфере выявить, с каким именно азимутом приходится иметь дело.

Частным случаем понятия «азимут» служат долго применявшиеся в мореплавании и метеорологии румбы. В морской навигации окружность горизонта делилась на 32 румба; в метеорологии— на 16. Направления на север, восток, юг и запад называют главными румбами. Остальные направления называются по имени главных, например: северо-запад или юго-восток, соответственно, между севером и западом, югом и востоком. Еще более дробные румбы именуют так: румб между севером и северо-западом называют северо-северо-западом; между востоком и юго-востоком — восток-юго-восток и т.д. Таким образом, румб является округленным значением азимута.

2. Экваториальная система небесных координат

В экваториальной системе небесных координат исходной плоскостью служит небесный экватор. Координатой, аналогичной географической широте на Земле, в этом случае является склонение светила, угол между направлением на объект и плоскостью небесного экватора.

Склонение отсчитывается по так называемому часовому кругу от плоскости небесного экватора со знаком «плюс» в северном полушарии небесной сферы и со знаком «минус» — в южном; оно может принимать значения в пределах от + 90 до — 90 °. Геометрическим местом точек с равными склонениями является суточная параллель.

Другая координата в экваториальной системе прямое восхождение (альфа). Прямым восхождением  светила называется угловое расстояние, отсчитываемое вдоль небесного экватора от точки весеннего равноденствия до круга склонений, проходящего через данное светило. Прямое восхождение отсчитывается в сторону востока от 0° до 360° (или от 0  до 24 ).

3. ПКЗН

4. Итог. Дома

Что нового ждет школы в 2022 году: 10 главных изменений и прогнозов — ukraina-novosti

Что нового ждет школы в 2022 году

С 1 сентября пятиклассники будут учиться по-новому

Новая украинская школа теперь будет не только для начинающих. Реформа вводится в базовой школе – для 5 классов.

К теме Конец учебного года в 2022: когда школьники уйдут на летние каникулы и кто будет учиться в июне

Для этого нужно сделать несколько шагов. Прежде всего, каждое учебное заведение на основе типовой программы должно утвердить собственную образовательную программу до начала учебного года. Она должна содержать выбранные школой модельные учебные программы.

Или это могут быть другие, утвержденные МОН, или даже разработанная в самой школе и одобренная на педсовете программа. Среди предложенных вариантов есть отраслевые интегрированные курсы, а есть и такие, которые объединяют предметы различных отраслей, например, «Робототехника» (информатика, физика, математика, природоведение, география, биология, технологии).

Пока ученики будут учиться по-новому в базовой школе, заранее начнется работа по внедрению старшей профильной школы. На 2022 запланировали утверждение Госстандарта профильного среднего образования.

Оценки будут, но по новому принципу

Пятиклассникам обещают в первом семестре постепенный переход от уровневого (начальный, средний, достаточный и высокий уровень) к бальному оцениванию, а формировальное оценивание будет оставаться столь же важным.

Например, проверку тетрадей МОН советует не связывать с оцениванием, а вместо этого делать короткие письменные комментарии. Хотя рекомендации, как оценивать учеников в 5 классах, уже есть, но над оцениванием в базовой школе еще будут работать.

Ученики ежедневно будут заниматься спортом

Пятиклассников ожидает 31 час учебной нагрузки в неделю (вместе с физкультурой). Хотя еще 20 лет назад, согласно типовым учебным планам, она составляла лишь 26 часов в неделю.

Но нормы постепенно изменились, на что нередко сетуют родители учеников. Сейчас больше всего изменилось количество учебных часов математики (на 5 часов) и украинского языка (на 3,5 часа).

По физкультуре, предусмотрено три занятия в неделю. Но в два других дня тоже должна быть организована двигательная активность:

• утренняя гимнастика,
• физкультминутки во время уроков,
• активные перерывы,
• часы здоровья,
• челенджи,
• флешмобы,
• мини-соревнования во время уроков.

Такие новации предусмотрены приказом МОН и Минмолодьспорт, который вступил в силу 1 января 2022 года. Он вводит в действие Концепцию развития ежедневного спорта в учебных заведениях.

«Всеукраинскую школу онлайн» расширят

По результатам национального опроса, ВШО заняла 5 место среди наиболее успешных проектов за 30 лет Независимости. ПУ МОН планируют расширить такую модель обучения на другие сферы образования.

По словам первого заместителя министра образования и науки, предлагают сделать аналогичную платформу для высшего образования. Значительное количество украинских университетов уже разработали собственные онлайн платформы.

Что же относительно самой ВШО, в этом году будут размещены дополнительные образовательные материалы на платформе и курсы для учителей, также возьмутся за подготовку уроков для начальной школы.

В школах появятся Интерны

Учителя, которые впервые приходят в школу, будут иметь в течение года наставников, как утверждает Положение о педагогической интернатуре. Они будут консультировать, посещать уроки, помогать при необходимости в подготовке к занятиям.

Также учителя надеются, что до начала нового учебного года проведут повышения квалификации для тех, кто будет учить 5 классы по программе НУШ.

А вот сертификация в этом году вновь будет касаться учителей начальной школы. Ее смогут пройти до 2,5 тысячи человек. Регистрировать желающих будут 4 – 17 апреля.

Учебники будут иметь электронные приложения

Чтобы понять, чего ожидать, обычно изучают опыт пилотных школ. Однако учителя, работавшие по новой программе, говорят о тревогах. В основном речь шла о проблемах с обеспечением учебниками и методической литературой для учителей, которая какой-то период была только в электронном виде.

Чтобы этого не произошло в будущем, Рада приняла закон по совершенствованию научно-методического обеспечения образования и качества учебной литературы. Он вступит в силу в июле 2022 года. Учебники сначала будут проходить экспертизу и получать разрешение МОН, а уже потом будут участвовать в конкурсе.

Этот процесс также сделают прозрачным – экспертные заключения с названиями издания и именами экспертов будут обнародовать на официальных сайтах. В этом году планируют издать учебники для 5 и 9 классов.

А еще теперь будут разрабатывать интерактивные электронные приложения, с которыми удобно будет работать во время дистанционного обучения. На 2022 год запланировано разработать критерии их оценивания.

Будут заботиться о безопасности школ

В 2022 году должны обновить и модернизировать пожарные системы в школах. К тому же, сложнее всего позаботиться о безопасных условиях для обучения и преподавания, конечно, в прифронтовой зоне.

Поэтому активно внедрять положения Декларации о безопасности школ — это политическое обязательство по защите во время вооруженных конфликтов, которое взяли на себя уже 111 государств, в том числе и Украина.

Для учителей разработают обучающий онлайн-курс на эту тему. Позаботятся о раннем предупреждении и эвакуации участников образовательного процесса в случае нападения или риска нападения на учебное заведение, об алгоритме восстановления школы в случае повреждения.

Каждому учителю по ноутбуку

Цифровизация образования – это направление во время пандемии стало очень актуальным. В МОН обещают до конца года обеспечить каждого учителя ноутбуком. Интернет проведен уже во все школы, но не везде он скоростной, поэтому «не тянет» дистанционные уроки. За 2022 год планируется все школы подсоединить именно к скоростному интернету.

Если говорить глобально, именно в этом году должны утвердить стратегию цифровой трансформации образования и науки. В частности, планируют оснащать школы компьютерным, мультимедийным и STEM-оборудованием.

А учителям будут предлагать курсы по цифровым навыкам. В 2022 планируется создать несколько важных онлайн-платформ. На одной будет информация обо всех Олимпиадах от школьного до всеукраинского уровня. На другой – все предложения для повышения квалификации учителей.

PISA во второй раз и последствия пандемии

В международном исследовании качества образования PISA-2022 Украина примет участие с 4 апреля по 20 мая. Как всегда, будут оценивать компетентности 15-летних учеников. На этот раз в фокусе внимания будет математика, а дополнительной отраслью — креативное мышление. Результаты представят в декабре 2023 года.

По словам первого заместителя министра образования и науки Андрея Витренко, МОН ожидает, что эти результаты частично смогут продемонстрировать влияние пандемии на обучение.

Добавим, что за последний раз проанализировали более 1000 онлайн-уроков педагогов разных регионов. Рассматривали формы преподавания материала, контроля и взаимодействия с учениками. А последний опрос среди учеников и родителей дал такие результаты: три четверти респондентов довольны его качеством.

Ученики будут иметь при необходимости шесть уровней поддержки

Инклюзивная помощь отныне более структурирована и имеет шесть уровней оказания поддержки. С 1 января заработали соответствующие изменения в постановления Кабмина по организации инклюзивного обучения.

В частности, сотрудничество школ и ИРЦ должно расти, теперь они составляют одну команду сопровождения ребенка. А для учителей готовят методические рекомендации по преподаванию учебных предметов для детей с ООП.

Объем сферы CBSE Class 9 Mathematics Notes with Examples

Объем сферы

Объем сферы

Чтобы найти объем сферы, рассмотрим следующий эксперимент.

Возьмем две сферы разного радиуса и емкость, достаточно большую, чтобы в нее можно было поместить каждую из сфер по одной. Также возьмем большое корыто, в которое мы сможем поместить контейнер.Затем наполните контейнер до краев водой, как показано на рисунке (1) ниже. Теперь аккуратно поместите одну из сфер в контейнер. Часть воды из контейнера будет переливаться в желоб, в котором она хранится, как показано на рисунке (2) ниже.

Осторожно вылейте воду из желоба в мерный цилиндр (градуированный цилиндрический кувшин) и измерьте количество вытекшей воды, как показано на рисунке (3).

Предположим, что радиус погруженной сферы равен r, тогда объем переливной воды равен πr ³ .

Еще раз повторите процедуру, сделанную только что, с другим размером сферы. Найдите радиус R этой сферы и вычислите πr ³

Опять же, это значение почти равно мере объема воды, вытесненной (переполненной) сферой.

Следовательно, объем сферы равен π, умноженному на куб ее радиуса. Это наводит нас на мысль, что Объем сферы = πr ³ .

Где r — радиус сферы.

Так как полушарие является половиной сферы, то

Объем полушария = πr ³ .

Где r — радиус сферы.

Пример 1: Найдите объем футбольного мяча радиусом 7 см.

Решение: Ясно, что футбольный мяч имеет форму сферы с радиусом 7 см.

Мы это знаем,

Объем сферы = πr ³ .
Итак, объем футбольного мяча = πr ³ .

                                           =    ×  × (7 см) ³ .
                                           

                                      =    × 22 × 1 см × 7 см × 7 см.

                                      = 1437,33 см ³ .

Следовательно, объем футбольного мяча = 1437,33 см ³ .

Пример 2: Найдите объем чаши радиусом 7 см.

Решение: Чаша имеет форму полусферы. Полусфера имеет радиус 7 см.

Мы это знаем,

Объем полушария = πr ³ .

Итак, объем полушария =   πr ³ .

                                             =   ×  × (7 см) ³ .

                                              = ×  × 7 см × 7 см × 7 см.

                                              =  × 22 × 1 см × 7 см × 7 см.

                                               = 718.66 см ³ .

Следовательно, объем полушария равен 718,66 см ³ .

RD Sharma Решения класса 9 Глава 21 Площадь поверхности и объем A Sphere

RD Sharma Решения класса 9 Глава 21 Площадь поверхности и объем A Sphere

RD Sharma Solutions Class 9 Глава 21 Площадь поверхности и объем сферы Ex 21.

1

Вопрос 1.
Найдите площадь поверхности сферы радиусом.
(i) 10,5 см
(ii) 5.6 см
(iii) 14 см
Решение:
В сфере,
(i) Радиус (r) = 10,5 см
Площадь поверхности = 4πr ²

Вопрос 2.
Найдите площадь поверхности сферы диаметром
(i) 14 см
(ii) 21 см
(iii) 3,5 см
Решение:
(i) Диаметр сферы = 14 см
Радиус (r ) = \(\frac { 14 }{ 2 }\) = 7 см

Вопрос 3.
Найдите площадь полной поверхности полусферы и сплошной полусферы радиусом 10 см каждая. [Используйте π = 3.14]
Решение:
(i) Радиус полушария = 10 см
∴ Общая площадь поверхности полушария = 2πr ²
= 2 x 3,14 x 10 x 10 см ²
= 6028 см 9 2 ) Общая площадь твердой полусферы
= 3πr ² = 3 x 3,14 x 10 x 10 см ²
= 942 см ²

Вопрос 4.
Площадь поверхности сферы в 5544 см ² , найдите диаметр.
Решение:
Пусть r — радиус сферы, тогда площадь поверхности = 4πr ²

Вопрос 5.
Чаша полусферическая из латуни, внутренний диаметр 10,5см. Узнать стоимость лужения изнутри из расчета 4 рубля за 100 см ² . [NCERT]
Решение:
Внутренний диаметр полусферической чаши = 10,5 см

Вопрос 6.
Купол здания имеет форму полусферы. Его радиус составляет 63 дм. Найдите стоимость его покраски из расчета 2 рубля за кв.м.
Решение:
Радиус купола (полусферический) = 63 дм
Площадь криволинейной поверхности

Вопрос 7.
Предполагая, что Земля представляет собой сферу радиусом 6370 км, сколько квадратных километров составляет площадь суши, если три четверти земной поверхности покрыты водой?
Решение:
Радиус земли (сферы) = 6370 км
Вода на земле = \(\frac { 3 }{ 4 }\) % общей площади

Вопрос 8.
Цилиндр одинаковой высоты и радиуса расположен на вершине полусферы. Найдите площадь криволинейной поверхности фигуры, если длина фигуры равна 7 см.
Решение:
Общая высота сформированной фигуры = 7 см

Вопрос 9.
Диаметр Луны составляет примерно одну четвертую диаметра Земли. Найдите отношение площадей их поверхностей.
Решение:
Диаметр Луны = \(\frac { 1 }{ 4 }\) диаметра Земли
Пусть радиус Земли = r км
Тогда радиус Луны = \(\frac { 1 }{ 4 }\) r км
Теперь площадь поверхности земли = 4πr ²

Вопрос 10.
Требуется покраска полусферического купола здания. Если окружность основания купола 17,6 м, найдите стоимость его покраски, учитывая стоимость покраски 5 руб. за 100 см ² .[NCERT]
Решение:
Окружность основания купола (r) = 17,6 м

Вопрос 11.
Деревянная игрушка в виде конуса, увенчанного полусферой. Диаметр основания конуса 16 см, высота 15 см. Узнайте стоимость покраски игрушки из расчета 7 ₹ за 100 см ² .
Решение:
Диаметр игрушки = 16 см
Радиус (r) = \(\frac { 16 }{ 2 }\) = 8 см
Высота конической части (h) = 15 см

Вопрос 12.
Резервуар для хранения состоит из круглого цилиндра с полусферой, примыкающей к обоим концам. Если внешний диаметр цилиндра 1,4 м, а длина 8 м, найдите стоимость покраски его снаружи из расчета 10 ₹ за м ² .
Решение:
Диаметр резервуара = 1,4 м
∴ Радиус (r) = \(\frac { 1,4 }{ 2 }\) м = 0,7 м
и высота цилиндрической части = 8 м

Вопрос 13.
Передняя составная стена дома украшена деревянными шарами диаметром 21 см, поставленными на небольшие подставки, как показано на рисунке.Для этой цели используются восемь таких сфер, которые должны быть окрашены в серебристый цвет. Каждая опора представляет собой цилиндр радиусом 1,5 см и высотой 7 см и должна быть окрашена в черный цвет. Найдите стоимость необходимой краски, если серебряная краска стоит 25 пайз за см ² , а черная краска стоит 5 пайсов за см ² . [NCERT]

Решение:
Диаметр каждой сферы = 21 см
∴ Радиус (R) = \(\frac { 21 }{ 2 }\) см
Радиус каждого цилиндра (r) = 1,5 см
и высота ( h) = 7 см

Теперь площадь поверхности одной сферы = 4πR ²

RD Sharma Solutions, класс 9, глава 21, площадь поверхности и объем сферы, пример 21.2

Вопрос 1.
Найдите объем сферы, радиус которой равен
(i) 2 см
(ii) 3,5 см
(iii) 10,5 см
Решение:
(i) Радиус сферы (r) = 2 см

Вопрос 2.
Найдите объем сферы, диаметр которой
(i) 14 см
(ii) 3,5 дм
(iii) 2,1 м
Решение:
(i) Диаметр сферы = 14 см

Вопрос 3.
Полусферический резервуар имеет внутренний радиус 2,8 м. Найдите его вместимость в литрах.
Решение:
Радиус полусферического резервуара (r) = 2,8 м

Вопрос 4.
Чаша полусферическая изготовлена ​​из стали толщиной 0,25 см. Внутренний радиус чаши 5 см.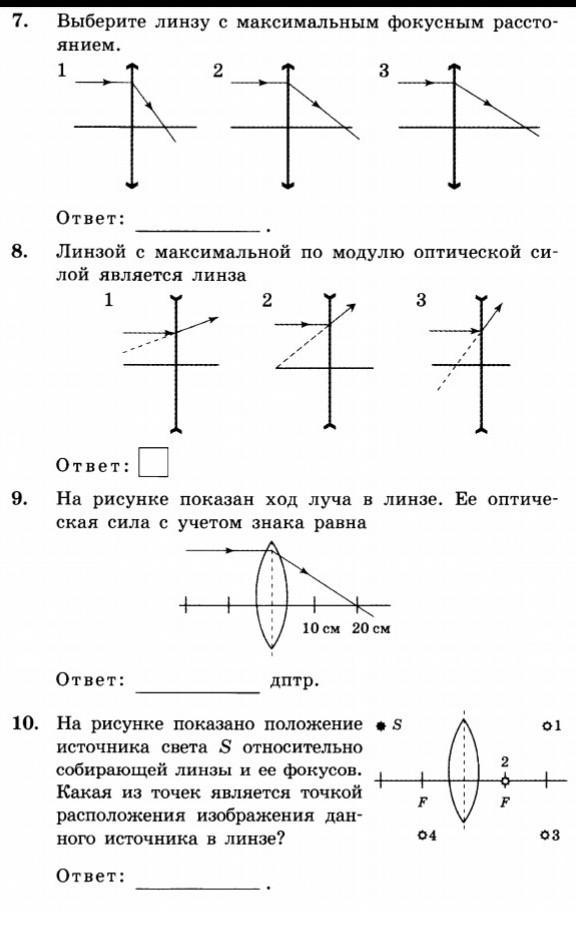 Найдите объем стали, израсходованной на изготовление чаши.
Решение:
Толщина стали = 0,25 см = \(\frac { 1 }{ 4 }\)см
Внутренний радиус полусферической чаши (r) = 5 см
∴ Внешний радиус (R) = 5 + 0,25 = 5,25 см
∴ Объем использованной стали = \(\frac { 1 }{ 4 }\)π(R ³ – r ³ )

Вопрос 5.
Сколько пуль можно сделать из свинцового куба, длина ребра которого 22 см, а диаметр каждой пули 2 см?
Решение:
Ребро куба (r) = 22 см
∴ Объем = a ³ = (22) ³ см ³
= 22 x 22 x 22 = 10648 см ^{3 4 Диаметр пули = 2 см}

Вопрос 6.
У лавочника есть ладду радиусом 5 см. Сколько ладду радиусом 2,5 см можно сделать из одного и того же материала?
Решение:
Радиус большего ладду (R) = 5 см

Вопрос 7.
Сферический свинцовый шар диаметром 3 см расплавляют и переплавляют в три сферических шара. Если диаметры двух шаров равны \(\frac { 3 }{ 2 }\) см и 2 см, найдите диаметр третьего шара.
Решение:
Диаметр сферического свинцового шара = 3 см

Вопрос 8.
Шар радиусом 5 см погружен в воду, наполненную в цилиндре, уровень воды поднимается на \(\frac { 5}{ 3 }\) см. Найдите радиус цилиндра.
Решение:
Радиус сферы (r1) = 5 см

Уровень воды поднимается в цилиндре после погружения в него сферы
∴ Высота уровня воды = \(\frac { 5 }{ 3 }\) см
Пусть r — радиус цилиндра, тогда объем воды = объем сферы

Вопрос 9.
Если радиус сферы увеличить вдвое, каково отношение объемов первой сферы к объему второй сферы?
Решение:
Пусть r2 будет радиусом данной сферы
, тогда объем = \(\frac { 4 }{ 3 }\) πr ³
Путем удвоения радиуса радиус новой сферы = 2r

Вопрос 10.
Сосуд в виде полусферической чаши наполнен водой. Его содержимое выливается в правильный круговой цилиндр. Внутренние радиусы чаши и цилиндра равны 3.5 см и 7 см соответственно. Найдите высоту, на которую поднимется вода в цилиндре.
Решение:
Радиус полусферической чаши (r) = 3,5 см

Вопрос 11.
Цилиндр, высота которого составляет две трети его диаметра, имеет такой же объем, как и шар радиусом 4 см. Вычислите радиус основания цилиндра.
Решение:
Радиус сферы (r) = 4 см

Вопрос 12.
Сосуд в виде полусферической чаши наполнен водой.Содержимое выливается в цилиндр. Внутренние радиусы чаши и цилиндра соответственно 6 см и 4 см. Найдите высоту воды в цилиндре.
Решение:
Радиус полусферической чаши (r) = 6 см

Вопрос 13.
Диаметр медного шара 18 см. Сфера расплавляется и вытягивается в длинную проволоку однородного круглого сечения. Если длина провода 108 м, найдите его диаметр.
Решение:
Диаметр медного шара = 18 см

Вопрос 14.
Диаметр шара 6 см. Его расплавляют и вытягивают в проволоку диаметром 0,2 см. Найдите длину провода.
Решение:
Диаметр сферы = 6 см

Вопрос 15.
Радиусы внутренней и внешней поверхностей полой сферической оболочки равны 3 см и 5 см соответственно. Если его расплавить и перелить в твердый цилиндр высотой 2 \(\frac { 2 }{ 3 }\) см. Найдите диаметр цилиндра.
Решение:
Внутренний радиус полой сферической оболочки (r) = 3 см
и внешний радиус (R) = 5 см

Вопрос 16.
Свинцовая полусфера радиусом 7 см брошена в прямоугольный конус высотой 49 см. Найдите радиус основания.
Решение:
Радиус полушария (r) = 7 см

Вопрос 17.
Полая сфера с внутренним и внешним радиусами 2 см и 4 см соответственно переплавлена ​​в конус с радиусом основания 4 см. Найдите высоту и наклонную высоту конуса.
Решение:
Внутренний радиус полой сферы (r) = 2 см
и внешний радиус (R) = 4 см
∴ Объем используемого металла

Вопрос 18.
Металлическая сфера радиусом 10,5 см расплавлена ​​и переплавлена ​​в маленькие конусы радиусом 3,5 см и высотой 3 см каждый. Найдите, сколько конусов получилось.
Решение:
Радиус металлического шара (R) = 10,5 см

Вопрос 19.
Конус и полусфера имеют равные основания и равные объемы. Найдите отношение их высот.
Решение:
Пусть r — радиус, а h — высота конуса, полусфера

Вопрос 20.
Самая большая сфера вырезана из куба со стороной 10.5 см. Найдите объем шара.
Решение:
Если вырезать из куба наибольшую сферу, диаметр сферы = 10,5

Вопрос 21.
Куб со стороной 4 см содержит шар, касающийся его сторон. Найдите объем промежутка между ними.
Решение:
Сторона куба = 4 см
∴ Объем = (сторона) ³ = 4x4x4 = 64 см ³
Диаметр самой большой сферы, касающейся ее сторон = 4 см

Вопрос 22.
Полусферический резервуар изготовлен из листа железа толщиной 1 см.Если внутренний радиус равен 1 м, то найдите объем железа, использованного для изготовления резервуара. (NCERT)
Решение:
Толщина полусферического резервуара = 1 см
Внутренний радиус (r) = 1 м = 100 см

Вопрос 23.
Капсула с лекарством имеет форму сферы диаметром 3,5 мм. Сколько лекарства (в мм3) необходимо для наполнения этой капсулы? (NCERT)
Решение:
Диаметр сферической капсулы лекарства = 3,5 мм

Вопрос 24.
Диаметр Луны составляет примерно одну четвертую диаметра Земли.Какую часть объема Земли составляет объем Луны? (NCERT)
Решение:

Вопрос 25.
Конус и полусфера имеют равные основания и равные объемы. Найдите отношение их высот.
Решение:
Пусть r — радиус конуса и полусферы, а h — высота конуса, тогда

Вопрос 26.
Цилиндрическая ванна радиусом 16 см содержит воду на глубину 30 см. В ванну опустили сферический железный шар, в результате чего уровень воды поднялся на 9 см.Каков радиус мяча?
Решение:
Радиус цилиндрической ванны (r) = 16 см
Высота воды в ней (h) = 30 см

Вопрос 27.
Цилиндр радиусом 12 см содержит воду на глубину 20 см. В цилиндр опустили сферический железный шар, в результате чего уровень воды поднялся на 6,75 см. Найдите радиус шара. (Используйте π = 22/7).
Решение:
Радиус цилиндра (r) = 12 см
Глубина воды в нем (h) = 20 см
При падении мяча уровень воды поднялся на 6.75 см

Вопрос 28.
В цилиндрической банке радиусом 6 см находится масло. В масло погружены железные шарики радиусом 1,5 см каждый. Сколько сфер необходимо, чтобы поднять уровень масла на два сантиметра?
Решение:
Радиус цилиндрической банки (r) = 6 см
Уровень масла в ней (h) = 2 см

Вопрос 29.
Мерная банка с внутренним диаметром 10 см частично заполнена водой. В него брошены четыре равных сферических шарика диаметром 2 см каждый и они полностью тонут в воде.Как изменится уровень воды в банке?
Решение:
Диаметр мерной банки = 10 см

Теперь после качания мяча в воде в банке Пусть объем воды поднялся, на h см

Вопрос 30.
Конус, полусфера и цилиндр стоят на равных основаниях и имеют одинаковую высоту. Докажите, что их объемы относятся как 1 : 2:3.
Решение:
∵ Основания и высоты полушария конуса и цилиндра равны
Пусть r — радиус, а h — их высоты

Вопрос 31.
Цилиндрическая ванна радиусом 12 см содержит воду на глубину 20 см. В ванну опускают шарик сферической формы, уровень воды поднимается на 6,75 см. Каков радиус мяча?
Решение:
Радиус цилиндрической ванны (r) = 12 см
Глубина воды в ней (h) = 20 см
При падении в нее сферического шара вода поднялась на 6,75 см

Вопрос 32.
Шар, цилиндр и конус имеют одинаковый диаметр. Высота цилиндра, а также конуса равны диаметру сферы.Найдите отношение их объемов.
Решение:
Диаметр шара, цилиндра и конуса равны
Пусть каждый диаметр = 2r
Тогда радиус каждого = r
Высота цилиндра = диаметр = 2r
и высота конуса = 2r
Теперь объем шара = \(\frac { 4 }{ 3 }\)πr ³
Объем цилиндра = πr ² ч

Площадь поверхности и объем сферы класса 9 RD Sharma Solutions VSAQS

Вопрос 1.
Найдите площадь поверхности сферы радиусом 14 см.
Решение:
Радиус сферы (r) = 14 см
∴ Площадь поверхности = 4πr ² = 4 x \(\frac { 22 }{ 7 }\) x 14 x 14 см ²
= 2464 см ³

Вопрос 2.
Найдите полную поверхность afea полушария радиусом 10 см.
Решение:
Радиус полушария (r) = 10 см
∴ Общая площадь поверхности = 3πr ²

Вопрос 3.
Найдите радиус сферы, площадь поверхности которой 154 см ² .
Решение:
Площадь поверхности сферы = 154 см ²

Вопрос 4.
Полая сфера, в которой цирковой мотоциклист выполняет свои трюки, имеет диаметр 7 м. Найдите площадь, доступную мотоциклисту для езды.
Решение:
Диаметр полой сферы = 7 м

Вопрос 5.
Найдите объем шара, площадь поверхности которого 154 см ² .
Решение:
Площадь поверхности сферы = 154 см ²

Вопрос 6.
Сколько сферических пуль можно сделать из сплошного свинцового куба с ребром 44 см, каждая пуля имеет диаметр 4 см?
Решение:
Ребро сплошного куба = 44 см
∴ Объем = a ² = (44) ² см ²
= 44 × 44 × 44 см ³
Диаметр сферической пули = 4 см

Вопрос 7.
Если сфера радиуса 2r имеет тот же объем, что и конус с круглым основанием радиуса r, то найдите высоту конуса.
Решение:
Радиус сферы (R) = 2r

Вопрос 8.
Если из полого шара внутреннего и внешнего диаметров 4 см и 8 см соответственно слился конус с диаметром основания 8 см, то найти высоту конуса.
Решение:
Внутренний диаметр полой сферы = 4 см
∴ Внутренний радиус = \(\frac { 4 }{ 2 }\) = 2 см
Аналогично внешний радиус (R) = \(\frac { 8 }{ 2 }\) = 4 см
∴ Объем расплава, использованный в полой сфере

Вопрос 9.
Площадь поверхности сферы радиусом 5 см в пять раз больше площади криволинейной поверхности конуса радиусом 4 см. Найдите высоту конуса.
Решение:
Радиус сферы (r) = 5 см
∴ Площадь поверхности = 4πr ²
= 4π x 5 x 5 = 100π см ²
Радиус конуса (r ₁ 90 )1 = 22 см

Вопрос 10.
Если шар вписан в куб, найдите отношение объема куба к объему шара.
Решение:
Пусть ребро куба = a
Тогда его объем = a ³
∵ Сфера вписана в куб
∴ Диаметр сферы = a

RD Sharma Solutions Class 9 Глава 21 Площади поверхности и объем сферы MCQS

Отметьте правильный вариант в каждом из следующих вопросов:
Вопрос 1.
В сфере количество граней
(а) 1
(б) 2
(в) 3
(г) 4
Решение:
Количество граней сферы равно 1 (а)

Вопрос 2.
Полная площадь поверхности полусферы радиуса r равна
(а) πr ²
(б) 2πr ²
(в) 3πr ²
(г) 904 4π1 2 909 :
Полная площадь поверхности полушария 37πr ² (c)

Вопрос 3.
Отношение общей площади поверхности сферы и полусферы одного радиуса равно
(а) 2 : 1
(б) 3 : 2
(в) 4 : 1
(г) 4 : 3
Решение:
Общая площадь поверхности сферы = 4πr ²
и общая площадь поверхности полушария = 3 м ²
∴ Отношение 4πr ² : 3πr ^{2 903 903} 403

Вопрос 4.
Шар и куб имеют одинаковую высоту. Отношение их объемов равно
(а) 3 : 4
(б) 21 : 11
(в) 4 : 3
(г) 11 : 21
Решение:
Пусть r — высота сферы и куба

Вопрос 5.
От куба со стороной 6 см отрезается самый большой шар. Объем шара будет
(a) 27π см ³
(b) 36π см ³
(c) 108π см ³
(d) 12π см ³
Решение куба: = 6 см
∴ Диаметр отрезанной от него сферы = 6 см

Вопрос 6.
Цилиндрический стержень, высота которого в 8 раз превышает его радиус, расплавляют и переплавляют в сферические шары того же радиуса. Количество шаров будет
(а) 4
(б) 3
(в) 6
(г) 8
Решение:
Пусть r — радиус цилиндрического стержня = r
Тогда его высота (h) = 8r
Объем = πr ² h = πr ² x 8r = 8πr ³
Радиус сферического шара = r

Вопрос 7.
Если отношение объемов двух сфер 1 : 8, то отношение площадей их поверхностей
(а) 1 : 2
(б) 1 : 4
(в) 1 : 8
(г) ) 1 : 16
Решение:
Пусть r ₁ и r ₂ радиусы двух сфер

Вопрос 8.
Если площадь поверхности шара 144π м ² , то его объем (в м3) равен
(a) 288π
(b) 316π
(c) 300π
(d) 188π
Решение:
Площадь поверхности сфера = 144π м ²
Пусть r будет радиусом, тогда
4πr ² = 144π

Вопрос 9.
Если из твердого шара радиусом 10 см слепить 8 сферических твердых шаров одинакового радиуса, то площадь поверхности каждого шара (в кв. см) равна
(а) 100π
(б) 75π
( в) 60π
(d) 50π
Решение:
Радиус сферы (r) = 10 см

Вопрос 10.
Если сфера вписана в куб, то отношение объема сферы к объему куба равно
(а) π : 2
(б) π : 3
(в) π : 4
(г ) π : 6
Решение:
Пусть сторона куба = a
Тогда объем куба = a ³
Диаметр вписанной сферы = a

Вопрос 11.
Если твердый шар радиуса r расплавить и отлить в виде твердого конуса высотой r, то радиус основания конуса равен
(a) 2r
(b) 3r
(c ) r
(d) 4r
Решение:
Радиус сферы = r

Вопрос 12.
Шар помещают внутрь прямоугольного цилиндра так, чтобы он касался верхней, нижней и боковой поверхностей цилиндра. Если радиус сферы равен r, то объем цилиндра равен

Решение:
Радиус сферы = r

Вопрос 13.
Отношение объема сферы к объему описанного ею прямого кругового цилиндра равно
(а) 2 : 1
(б) 1 : 1
(в) 2 : 3
(г) 1 : 2
Решение:
Пусть r будет радиусом сферы, тогда 4
Объем = \(\frac { 4 }{ 3 }\)πr ³
Диаметр описанного цилиндра = 2r
∴ Радиус = r
и высота ( з) = 2р

Вопрос 14.
Конус и полусфера имеют равные основания и равные объемы, отношение их высот равно
(а) 1 : 2
(б) 2 : 1
(в) 4 : 1
(г) \(\sqrt { 2 } \) : 1
Решение:
Пусть радиус полусферы и конуса равен r

Вопрос 15.
Конус, полусфера и цилиндр стоят на равных основаниях и имеют одинаковую высоту. Отношение их объемов
(а) 1 : 2 : 3
(б) 2 : 1 : 3
(в) 2 : 3 : 1
(г) 3 : 2 : 1
Раствор:
∵ Основания конус, полусфера и цилиндр одинаковы
Пусть радиус каждого = r
и высота каждого = r

RD Sharma Решения класса 9 Глава 21 Площадь поверхности и объем A Sphere Ex 21.1

Решения RD Sharma класса 9

Учебник по физике: Закон Кулона

Взаимодействие между заряженными объектами представляет собой бесконтактную силу, действующую на некотором расстоянии друг от друга. Заряд, заряд и расстояние. Каждое электрическое взаимодействие включает в себя силу, которая подчеркивает важность этих трех переменных.Будь то пластиковая трубка для гольфа, притягивающая кусочки бумаги, два одинаково заряженных шарика, отталкивающиеся, или заряженная пластина из пенополистирола, взаимодействующая с электронами в куске алюминия, всегда есть два заряда и расстояние между ними как три критические переменные, влияющие на прочность. взаимодействия. В этом разделе урока 3 мы рассмотрим важность этих трех переменных.

Сила как вектор Количество

Электрическая сила, как и все силы, обычно выражается в единицах Ньютон.Будучи силой, сила электрического взаимодействия является векторной величиной, имеющей как величину, так и направление. Направление электрической силы зависит от того, заряжены ли заряженные объекты одинаковым или противоположным зарядом, а также от их пространственной ориентации. Зная тип заряда на двух объектах, направление силы на любой из них можно определить с небольшими рассуждениями. На приведенной ниже диаграмме объекты A и B имеют одинаковый заряд, из-за чего они отталкиваются друг от друга.Таким образом, сила на объекте А направлена ​​влево (от В), а сила на объекте В направлена ​​вправо (от А). С другой стороны, объекты C и D имеют противоположный заряд, поэтому они притягиваются друг к другу. Таким образом, сила на объекте C направлена ​​вправо (к объекту D), а сила на объекте D направлена ​​влево (к объекту C). Когда дело доходит до вектора электрической силы, возможно, лучший способ определить его направление — это применить фундаментальные правила взаимодействия зарядов (противоположности притягиваются, а подобные отталкиваются), используя небольшие рассуждения.

Электрическая сила также имеет величину или силу. Как и для большинства типов сил, существует множество факторов, влияющих на величину электрической силы. Два шара с одинаковым зарядом будут отталкивать друг друга, и силу их отталкивания можно изменить, изменив три переменные. Во-первых, на силу отталкивания будет влиять количество заряда одного из шаров. Чем сильнее заряжен воздушный шар, тем больше сила отталкивания.Во-вторых, количество заряда второго шара будет влиять на силу отталкивания. Аккуратно потрите два шарика шерстью животных, и они немного оттолкнутся. Энергично потрите два шарика, чтобы придать им обоим больше заряда, и они сильно отталкиваются. Наконец, расстояние между двумя шарами будет иметь значительное и заметное влияние на силу отталкивания. Электрическая сила наиболее сильна, когда воздушные шары находятся ближе всего друг к другу. Уменьшение разделительного расстояния увеличивает силу.Говорят, что величина силы и расстояние между двумя шарами обратно пропорциональны .

Уравнение закона Кулона

Количественное выражение влияния этих трех переменных на электрическую силу известно как закон Кулона. Закон Кулона гласит, что электрическая сила между двумя заряженными объектами прямо пропорциональна произведению количества заряда на объектах и ​​обратно пропорциональна квадрату расстояния между двумя объектами. В форме уравнения закон Кулона можно сформулировать как

.

, где Q ₁ представляет количество заряда на объекте 1 (в кулонах), Q ₂ представляет количество заряда на объекте 2 (в кулонах), а d представляет собой расстояние между два объекта (в метрах). Символ k представляет собой константу пропорциональности, известную как константа закона Кулона. Значение этой константы зависит от среды, в которую погружены заряженные объекты.В случае воздуха значение составляет примерно 9,0 x 10 ⁹ Н • м ² / C ² . Если заряженные объекты присутствуют в воде, значение k может быть уменьшено в 80 раз. Стоит отметить, что единицы k таковы, что при подстановке в уравнение единицы на заряд (кулоны) и единицы расстояния (метры) будут отменены, оставив Ньютон в качестве единицы силы.

Уравнение закона Кулона обеспечивает точное описание силы между двумя объектами, когда объекты действуют как точечных зарядов . Заряженный проводящий шар взаимодействует с другими заряженными объектами так, как если бы весь его заряд был сосредоточен в его центре. Хотя заряд равномерно распределен по поверхности сферы, центр заряда можно считать центром сферы. Сфера действует как точечный заряд с избыточным зарядом, расположенным в ее центре. Поскольку закон Кулона применим к точечным зарядам, расстояние d в уравнении есть расстояние между центрами заряда обоих объектов (а не расстояние между их ближайшими поверхностями).

Символы Q ₁ и Q ₂ в уравнении закона Кулона представляют количество заряда на двух взаимодействующих объектах. Поскольку объект может быть заряжен положительно или отрицательно, эти величины часто выражаются как значения «+» или «-». Знак заряда просто показывает, имеет ли объект избыток электронов (отрицательно заряженный объект) или недостаток электронов (положительно заряженный объект).Может возникнуть соблазн использовать знаки «+» и «-» при расчете силы. Хотя эта практика не рекомендуется, в этом, безусловно, нет никакого вреда. При использовании знаков «+» и «-» при расчете силы результатом будет то, что значение «-» для силы является признаком силы притяжения, а значение «+» для силы означает силу отталкивания. Математически значение силы будет положительным, когда Q ₁ и Q ₂ имеют одинаковый заряд — либо оба «+», либо оба «-».И значение силы будет отрицательным, когда Q ₁ и Q ₂ имеют противоположный заряд — один «+», а другой «-». Это согласуется с концепцией о том, что противоположно заряженные объекты взаимодействуют притягивающе, а заряженные объекты отталкиваются. В конце концов, если вы мыслите концептуально (а не просто математически), вы вполне сможете определить природу силы — притягивающей или отталкивающей — без использования знаков «+» и «-» в уравнении.

Расчеты по закону Кулона

В курсах физики закон Кулона часто используется в качестве своего рода алгебраического рецепта для решения задач по физике. Здесь показаны три таких примера.

Это не самая сложная математическая задача, которую можно было выбрать. Он определенно не был выбран из-за его математической строгости. Используемая здесь стратегия решения проблем может показаться ненужной, учитывая простоту данных значений. Тем не менее, эта стратегия будет использоваться, чтобы проиллюстрировать ее полезность для любой проблемы закона Кулона.

Первым шагом стратегии является идентификация и перечисление известной информации в переменной форме.Здесь мы знаем заряды двух объектов (Q ₁ и Q ₂ ) и расстояние между ними (d). Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае задача запрашивает информацию о силе. Таким образом, F _{Избрать} является неизвестной величиной. Результаты первых двух шагов представлены в таблице ниже.

Следующий и последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.

F _{избранный} = k • Q ₁ • Q ₂ / d ²

F _Elect = (9,0 x 10 ⁹ Н•м ² /C ² ) • (1,00 C) • (1,00 C) / (1,00 м) ²

F _{избранный} = 9,0 x 10 ⁹ N

Сила отталкивания двух зарядов +1,00 Кулон, находящихся на расстоянии 1,00 м друг от друга, составляет 9 миллиардов ньютонов. Это невероятно большая сила, по величине сравнимая с весом более 2000 реактивных лайнеров.

Эта проблема была выбрана в первую очередь из-за ее концептуального сообщения. Объекты просто не приобретают зарядов порядка 1,00 кулона. На самом деле более вероятные значения Q порядка 10 ^-9 или, возможно, 10 ^-6 кулонов. По этой причине перед кулоновской единицей заряда часто используется греческий префикс. Заряд часто выражается в микрокулонах (мкКл) и нанокулонах (нКл). Если в задаче указан заряд в этих единицах, рекомендуется сначала преобразовать в кулоны перед подстановкой в ​​уравнение закона Кулона.Следующие единицы эквивалентности помогут в таких преобразованиях.

1 Кулон = 10 ⁶ микроКулон

 1 Кулон = 10 ⁹ наноКулон

Стратегия решения проблем, использованная в примере А, включала три шага:

1. Определите и перечислите известную информацию в переменной форме.
2. Перечислите неизвестную (или желаемую) информацию в переменной форме.
3. Подставьте известные значения в уравнение закона Кулона и, используя соответствующие алгебраические шаги, найдите неизвестную информацию.(В некоторых случаях и для некоторых учащихся может быть проще сначала выполнить алгебраические вычисления с использованием переменных, а затем выполнить подстановку в качестве последнего шага.)

Эта же стратегия решения проблем демонстрируется в Примере B ниже.

В задаче указано значение Q ₁ и Q ₂ . Поскольку эти значения выражены в единицах нанокулонов (нКл), необходимо выполнить преобразование в кулоны. В задаче также указывается разделительное расстояние (d). Поскольку расстояние указывается в сантиметрах (см), необходимо также выполнить преобразование в метры. Эти преобразования необходимы, поскольку единицами заряда и расстояния в постоянной Кулона являются кулоны и метры.Неизвестной величиной является электрическая сила (F). Результаты первых двух шагов представлены в таблице ниже.

Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации.Эта замена и алгебра показаны ниже.

F _{избранный} = k • Q ₁ • Q ₂ / d ²

F _{избранный} = (9,0 x 10 ⁹ Н•м ² /C ² ) • (6,25 x 10 ^-9 C) • (6,25 x 10 ^{-4 C)17 (/9004,6) м) 2}

F _{избранный} = 9,23 x 10 ^-7 N

Обратите внимание, что перед подстановкой в ​​уравнение закона Кулона знак «-» был удален из значений Q ₁ и Q ₂ .Как упоминалось выше, использование знаков «+» и «-» в уравнении приведет к положительному значению силы, если Q ₁ и Q ₂ заряжены одинаково, и к отрицательному значению силы, если Q ₁ и Q ₂ заряжены противоположно. Полученные в результате знаки «+» и «-» на F означают, является ли сила притягательной (значение «-» F) или отталкивающей (значение «+» F).

В задаче указано значение Q ₁ и Q ₂ . Поскольку эти значения выражены в микрокулонах (мкКл), будет выполнено преобразование в кулоны. В задаче также указывается электрическая сила (F). Неизвестной величиной является разделительное расстояние (d). Результаты первых двух шагов представлены в таблице ниже.

Как упоминалось выше, использование знаков «+» и «-» необязательно. Однако, если они используются, то они должны использоваться последовательно для значений Q и значений F. Их использование в уравнении показано в этой задаче.

Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации. В этом случае алгебра выполняется первой, а подстановка выполняется последней. Эта алгебра и замена показаны ниже.

F _{избранный} = k • Q ₁ • Q ₂ / d ²

d ² • F _{избранный} = k • Q ₁ • Q ₂

d ² = k • Q ₁ • Q ₂ / F _{избранный}

d = SQRT(k • Q ₁ • Q ₂ ) / F _{избранный}

д = SQRT [(9.0 x 10 ⁹ Н•м ² /C ² ) • (-8,21 x 10 ^-6 C) • (+3,37 x 10 ^-6 C) / (-0,0626 N)]

d = Кв. [ +3,98 м ² ]

d = +1,99 м

Сравнение электрических и гравитационных сил

Электрическая сила и гравитационная сила — две неконтактные силы, обсуждаемые в учебнике «Класс физики».Уравнение закона Кулона для электрической силы очень похоже на уравнение Ньютона для всемирного тяготения.

Эти два уравнения имеют очень похожую форму. Оба уравнения показывают обратную квадратичную зависимость между силой и разделяющим расстоянием. И оба уравнения показывают, что сила пропорциональна произведению величины, вызывающей силу, — заряда в случае электрической силы и массы в случае гравитационной силы. Тем не менее, между этими двумя силами есть некоторые поразительные различия.Во-первых, сравнение констант пропорциональности — k и G — показывает, что константа закона Кулона (k) значительно больше, чем ньютоновская постоянная всемирного тяготения (G). Следовательно, единица заряда будет притягивать единицу заряда со значительно большей силой, чем единица массы притягивает единицу массы. Во-вторых, гравитационные силы действуют только притягивающе; электрические силы могут быть как притягивающими, так и отталкивающими.

Зависимость обратного квадрата между силой и расстоянием, вплетенная в уравнение, является общей для обеих бесконтактных сил.Эта взаимосвязь подчеркивает важность разделяющего расстояния, когда речь идет об электрическом взаимодействии между заряженными объектами. Этому посвящен следующий раздел Урока 3.

Мы хотели бы предложить…

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного закона Кулона.Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный закон Кулона позволяет учащимся исследовать влияние заряда и разделяющего расстояния на величину электрической силы между двумя заряженными объектами.

Проверьте свое понимание

Используйте свое понимание, чтобы ответить на следующие вопросы. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.

1. Q в уравнении закона Кулона означает _____.

а. масса заряженного объекта	б. # избыточных электронов на объекте
в. ток заряженного объекта	д. расстояние между заряженными объектами
эл.заряд заряженного объекта

2. Символ d в уравнении закона Кулона обозначает расстояние от ___.

а. от А до В	б. от А до Д	в.от В до С	д. Б-Д
эл. С-D	ф. от А до G	г. от В до F	ч. С до Е

3.Определить электрическую силу притяжения между двумя шарами с отдельными зарядами +3,5 х 10 ^-8 Кл и -2,9 х 10 ^-8 Кл при расстоянии 0,65 м друг от друга.

4. Определить электрическую силу притяжения между двумя шариками, заряженными противоположным типом заряда, но одинаковым количеством заряда. Заряд на воздушных шарах составляет 6,0 x 10 ^-7 Кл, и расстояние между ними равно 0.50 м.

5. Джоанна натерла шарик шерстью, чтобы придать ему заряд -1,0 x 10 ^-6 Кл. Затем она приобрела пластиковую трубку для гольфа с зарядом +4,0 x 10 ^-6 Кл, локализованным в данной точке. должность. Она держит место заряда на пластиковой трубке для гольфа на расстоянии 50,0 см над баллоном. Определить электрическую силу притяжения между трубкой для гольфа и шариком.

6. Баллон с зарядом 4,0 мкКл держат на расстоянии 0,70 м от второго баллона с таким же зарядом. Вычислите величину силы отталкивания.

7. На каком расстоянии друг от друга должны находиться два заряда в 1,00 мкК, чтобы сила отталкивания между ними была эквивалентна весу (на Земле) 1.00 кг массы?

Четыре сферы Земли – определение, подсистемы Земли и часто задаваемые вопросы

Все, что есть на Земле, можно разделить на основные подсистемы: вода, воздух, живые существа и земля. Они называются сферами. Чтобы быть более точным, они известны как:

В следующем сегменте студенты получат более точное представление о каждой из подсистем и о том, как сферы Земли взаимодействуют друг с другом?

Как сферы взаимодействуют друг с другом: подсистемы Земли

1. Гидросфера

Гидросфера Земли — это общий термин для каждого водоема, такого как океаны, озера, реки, влага и подземные водоносные горизонты. Это может быть любое состояние воды – твердое, жидкое и газообразное. Эксперты предполагают, что вся гидросфера составляет около 1,3 миллиарда кубических километров.

Океаны составляют более 97% воды на Земле, а оставшаяся часть приходится на пресную воду. Опять же из этой пресноводной части две трети остаются замороженными в горах и полюсах. Вы должны отметить, что хотя вода покрывает значительную часть планеты, она удерживает только 0,023% массы Земли.

Окружающая среда нашей Земли не статична, поэтому вода изменяет свою форму в соответствии с различными стадиями гидрологического цикла.Во-первых, вода собирается за счет дождей; затем она уходит под землю, снова поднимается в виде родников и впадает в реки, озера, моря и т. д. Также из этих ручьев испаряется вода, и круговорот продолжается.

2. Атмосфера

Земная атмосфера включает в себя все газы на Земле, удерживаемые ее гравитационным притяжением. Воздух содержит 97% азота, 21% кислорода, а левая часть включает углекислый газ, аргон и другие газы.

Атмосферу можно разделить на четыре различные зоны, а именно: тропосферу, стратосферу, мезосферу и термосферу.

Тропосфера состоит из трех четвертей атмосферной массы и имеет расстояние от 8 до 14,5 километров.

Выше тропосферы лежит стратосфера, которая находится на расстоянии 50 километров над поверхностью Земли.

Мезосфера поднимается на 85 километров над планетой.

Находится на расстоянии 600 километров от поверхности Земли.

3. Биосфера

Биосфера состоит из всех живых существ, начиная от животных, растений и заканчивая одноклеточными организмами.Можно также сказать, что биосфера состоит из биомов. Теперь, если вам интересно, что подразумевается под биомами, вот ответ —

Биом — это сообщество, где вместе обитают животные и растения одной природы, например, пустыня и коралловый риф.

Животные и растения, обитающие на суше, особенно наземная жизнь, имеют зону от 3 до 30 метров. Далее, водная жизнь существует примерно на 200 метров ниже уровня моря.

Однако интересным фактом является то, что некоторые организмы могут жить за пределами этих диапазонов расстояний.Например, немногие птицы могут летать на расстоянии более 7000 метров от поверхности Земли. Кроме того, микроорганизмы могут выжить и вдали от этих уровней.

Знаете ли вы?

В Марианской впадине на глубине ниже 6000 метров обитает марианский улитка.

1. Литосфера

Литосфера, также называемая геосферой, охватывает горные породы Земли. Например, валуны горы Эверест, лава горы Килауэа на Гавайях, пески Майами-Бич и т. д.считаются компонентами литосферы.

Кроме того, эту подсистему Земли можно разделить на 12 значительных и несколько второстепенных плит. Они следующие:

1. EURASIAN

5. Cocos

JUAN de Fuca

6. североамериканских

7. Caribbean

12. SCOTIA

15. 9119

Эти тектонические плиты находятся в постоянном движении, и результат трения между ними приводит к образованию гор, вулканов, землетрясений , и т. д.

Далее приступим к тому, как все сферы взаимодействуют друг с другом.

Как сферы Земли взаимодействуют друг с другом?

Все четыре сферы имеют свою индивидуальность, но взаимодействуют друг с другом. Научные исследования показывают, что если происходит событие в одной подсистеме, оно влияет и на другие. На Земле возможны многие типы взаимодействий, и некоторые из них — между любой из подсистем и событием.

На приведенном выше рисунке вы можете видеть двусторонние стрелки, которые обозначают последствия и причины взаимодействий, применимых в обоих направлениях.Например, извержение вулкана оказывает прямое и косвенное воздействие на атмосферу, гидросферу и биосферу.

Знаете ли вы?

Извержение вулкана Сент-Хеленс в Вашингтоне произошло 18 мая 1980 года и оказало воздействие на окружающую среду. Это помогло исследователям глубже вникнуть в вопрос о воздействии на разные подсистемы Земли.

Помимо взаимодействия событий и сфер, некоторые взаимодействия происходят только между сферами. Они происходят в виде цепных реакций.Вот пример:

Вулкан >> Литосфера >> Атмосфера >> гидросфера >> биосфера

На приведенном выше изображении и реакции видно, что вулкан — это событие, высвобождающее значительное количество необработанного материала. Эти материалы (как ядра) помогают в формировании капель воды. После извержения вулкана количество осадков увеличивается. Это помогает облегчить рост растений.

Помимо этого взаимодействия могут иметь место и некоторые сложные.Посмотрите на пример:

После извержения вулкана выделяется огромное количество диоксида серы, который смешивается с водой, образуя сернистую и серную кислоты. Эти кислоты попадают на Землю с осадками и оказывают неблагоприятное воздействие на рост растений. Это также снижает уровень pH в воде, влияя на рост зоопланктона и фитопланктона. Более того, если фотосинтез будет происходить в меньшей степени, концентрация углекислого газа увеличится, что приведет к глобальному потеплению.

Приведенное выше обсуждение, должно быть, прояснило ваши представления о том, как сферы Земли взаимодействуют друг с другом.Чтобы узнать больше о таких темах, загрузите приложение Vedantu сегодня и получите доступ к онлайн-руководствам и учебным материалам.

Изучение четырех сфер Земли — определение, подсистемы Земли и часто задаваемые вопросы

Вы можете начать изучение четырех сфер Земли — определение, подсистемы Земли и часто задаваемые вопросы на онлайн-платформе обучения Vedantu. Мы делаем процесс обучения гладким и легким для всех студентов, предоставляя вам надежный учебный ресурс, курируемый экспертами в предметной области на простом языке.Ниже приведены несколько советов, которым вы можете следовать при изучении Четырех сфер Земли: определение, подсистемы Земли и часто задаваемые вопросы: данные в учебнике упражнения и попытайтесь ответить на них. Это поможет вам проверить свои знания и проверить, все ли вы поняли о земных подсистемах или нет.

Важность изучения четырех сфер Земли – определение, подсистемы Земли и часто задаваемые вопросы

Четыре сферы Земли – определение, подсистемы Земли и часто задаваемые вопросы – одна из самых важных тем физики.Ниже приведены причины, по которым вам следует изучить эту важнейшую концепцию: существа на планете.

Объем сферы

А

сфера

это множество точек в пространстве, находящихся на заданном расстоянии

р

от центра.

То

объем

из

3

-мерное твердое тело — это объем пространства, которое оно занимает.Объем измеряется в кубических единицах (

в

3

,

футов

3

,

см

3

,

м

3

, и так далее). Перед вычислением объема убедитесь, что все измерения приведены в одних и тех же единицах измерения.

Громкость

В

сферы составляет четыре трети, умноженное на пи, умноженное на радиус в кубе.

В

знак равно

4

3

π

р

3

Объем полушария составляет половину объема связанной с ним сферы.

Примечание


:

Объем шара

2

/

3

объема цилиндра с таким же радиусом и высотой, равной диаметру.

Пример:

Найдите объем шара. Округлите до ближайшего кубического метра.

Решение

Формула объема шара такова.

В

знак равно

4

3

π

р

3

Из рисунка радиус сферы равен

8

м.

Заменять

8

за

р

в формуле.

В

знак равно

4

3

π

(

8

)

3

Упрощать.

В

знак равно

4

3

π

(

512

)

≈

2145

Следовательно, объем шара примерно

2145

м

3

.

Братья Гоял Электричество и магнетизм-1 Класс-9 ICSE Physics Ch-10

Братья Гоял Электричество и магнетизм-1 Класс-9 ICSE Physics Ch-10. Мы предоставляем пошаговые ответы на упражнения, субъективные Goyal Brothers Электричество и магнетизм-1 и методы сохранения ресурсов, класс 9 ICSE Physics Ch-10, посетите официальный веб-сайт CISCE  для получения подробной информации о ICSE Board Class-9 Physics .

Электричество и магнетизм братьев Гоял-1 Класс-9 ICSE Physics Ch-10

-: Выберите тему: —

Часть I Упражнение 1

Практические задачи

Раздел II. Упражнение 2. Целевые вопросы

Раздел II. Упражнение 2. Субъективные вопросы

Часть I Упражнение 1

Электричество и магнетизм братьев Гоял-1 Класс-9 ICSE Physics Ch-10

Вопрос 1.
Имеются положительно заряженная сфера A и отрицательно заряженная сфера B, так что они находятся в электрическом контакте с помощью медного провода. Ответьте на следующие вопросы :

(a)  Какая сфера находится под более высоким потенциалом до электрического контакта на основе соглашения?
(b)  Какая сфера имеет более низкий потенциал до электрического контакта на основе соглашения?
(c)  В каком направлении течет обычный ток?
(d)  В каком направлении течет электронный ток?
(e)  Каков потенциал сфер после электрического контакта?

Ответ:
Сфера А заряжена положительно, а сфера В — отрицательно.
Обе сферы A и B находятся в электрическом контакте с помощью медного провода.

(a)  Условно принято, что положительно заряженная сфера A находится под более высоким потенциалом до электрического контакта.
(b)  Условно говоря, отрицательно заряженная сфера B имеет более низкий потенциал до электрического контакта.
(c) Обычный ток течет из сферы A в сферу B i. е. от тела с более высоким потенциалом к ​​телу с более низким потенциалом.
(d) Электронный ток-цветок из сферы B в сферу A i.е. от тела с более низким потенциалом к ​​телу с более высоким потенциалом.
(e)  После электрического контакта обе сферы будут иметь одинаковый потенциал.

Вопрос 2.

(a)  Что вы понимаете под термином электрический потенциал?
(b)  Определите электрический потенциал с точки зрения затраченной энергии.
(c)  Укажите единицу электрического потенциала и дайте ее определение.

Ответ:
(a) Электрический потенциал : Количество работы, совершаемой при перемещении единичного положительного заряда из бесконечности в заданную точку электрического поля, называется электрическим потенциалом.
(b) Электрический потенциал :  Количество энергии, затраченное на перемещение единичного положительного заряда из бесконечности в заданную точку электрического поля, называется электрическим потенциалом.
(c) Вольт – это единица измерения электрического потенциала в системе СИ.
Один вольт :  Когда один кулон заряда переносится из бесконечности в данную точку электрического поля, так что совершается работа, равная одному джоулю, тогда говорят, что электрический потенциал равен одному вольту.
ИЛИ
Электрический потенциал считается равным одному вольту, если при перемещении заряда в один кулон из бесконечности в данную точку электрического поля совершается работа в один джоуль.

Вопрос 3.

(a)  Что вы понимаете под термином количество электрического заряда?
(b) Укажите единицу электрического заряда в СИ и дайте ей определение.
(c)  Сколько электронов составляет единицу электрического заряда в системе СИ?

Ответ:

(a) Количество электрического заряда : Количество зарядов (электронов), которые дрейфуют от более низкого потенциала к более высокому, называется количеством заряда.
(b) Единицей электрического заряда в СИ является кулон (C).
Один кулон :  Количество электрического заряда, которое осаждает 0,00118 г серебра на катоде при прохождении через нитрат серебра, называется одним кулоном.
(c)  6,25 × 10 ¹⁸  электроны составляют одну единицу (IC) электрического заряда в системе СИ.

Вопрос 4.

(a)  Что вы понимаете под термином электрический ток?
(b)  Укажите и определите единицу измерения электрического тока в системе СИ.
(c)  Укажите связь между электрическим током; число электронов, движущихся по цепи, и время в секундах.

Ответ:
(a) Электрический ток :  Скорость потока электрического заряда в электрической цепи называется электрическим током.
(b) Ампер (А) — единица измерения электрического тока в системе СИ.
Один ампер :  Когда заряд в один кулон проходит через электрическую цепь за одну секунду, то говорят, что электрический ток, протекающий по цепи, равен амперу.
(c)  Если Q представляет собой заряд (в кулонах), протекающий через проводник за время t (в секундах), так что по проводнику протекает ток I, то
Скорость потока заряда = Q/t
Мы знаем скорость потока заряда = I = Электрический ток.
⇒ I = Q/t

Вопрос 5.
Как протекает электрический ток в (i) твердых телах, (ii) жидких веществах?
Ответ:
(i) Поток электрического тока в твердых телах:  В твердых телах положительные заряды связаны с атомными ядрами.Поскольку ядра плотно упакованы и тесно удерживаются межатомными силами, положительные заряды не могут дрейфовать.
С другой стороны, отрицательные заряды (электроны) не удерживаются прочно. Таким образом, когда применяется разность потенциалов, какой бы малой она ни была, они начинают дрейфовать от более низкого потенциала к более высокому.
Непрерывный дрейф электронов через тело твердого проводника составляет ток.
(ii) Поток электрического тока в жидкостях:  В жидкости электроны не движутся.Однако, когда отрицательно заряженный и положительно заряженный электроды помещаются в жидкость, создается электрическое поле.
Под действием электрического поля положительно заряженные ионы мигрируют к отрицательно заряженному электроду и наоборот.
На катоде положительно заряженные ионы присоединяют электроны. На аноде отрицательно заряженные ионы теряют столько же электронов.
Таким образом, в некотором смысле количество электронов, отдаваемых катодом, равно количеству электронов, принятых анодом.Подводя итог, можно сказать, что одновременное движение и выброс положительных и отрицательных ионов в противоположных направлениях составляет ток в жидкостях.

Вопрос 6.

(a)  Определите термин разность потенциалов.
(b)  Как разность потенциалов связана с проделанной работой и количеством заряда?

Ответ:
(a) Разность потенциалов: Количество работы, совершаемой при перемещении единичного положительного заряда из одной точки в другую в электрическом поле, называется разностью потенциалов.
(b)  Если Q = заряд, перемещающийся из одной точки в другую в электрическом поле.
Вт = Работа, совершенная для перемещения заряда Q из одной точки в другую.
В = разность потенциалов между двумя точками.
Тогда работа, совершаемая при перемещении Q единиц заряда = Вт
Работа, совершаемая при перемещении одной единицы заряда = W/Q
Но работа, совершаемая при перемещении одной единицы заряда = Разность потенциалов = V
⇒ V = W/Q

Практические задачи

Электричество и магнетизм братьев Гоял-1 Класс-9 ICSE Physics Ch-10

Практические задачи 1

Вопрос 1.
Заряд 5000 Кл проходит через электрическую цепь за 2 часа 30 минут. Вычислите величину тока в цепи.
Ответ:

Вопрос 2.
Заряд 8860 Кл протекает по электрической цепи за 2 мин 40 с. Вычислите величину тока в цепи.
Ответ:

Практические задачи 2

Вопрос 1.
Аккумулятор может обеспечить заряд 25 × 10 ⁴ Кл.Если ток потребляется от батареи в размере 2,5 А, рассчитайте время, за которое батарея полностью разрядится.
Ответ:

Читать дальше 👇 Нажмите на номер страницы, указанный ниже 👇

Численные задачи — Класс 9 Физика — ClassNotes

Числовые задачи

5.1 Найти силу притяжения двух сфер массой 1000 кг каждая. Расстояние между центрами сфер равно 0.5 м.

                                                                               (2,67 × 10 ^{— 4 N) N}

Решение:         Масса = m ₁ = m ₂ = 1000 кг

Расстояние между центрами = d = 0,5 м

Гравитационная постоянная = G = 6,673 × 10 ^-11 Нм ² кг ^-2

                              Гравитационная сила = F = ?

F = Gm ₁ m ₂ /d ²

                                                                        F = 6.673 * (10) ^-11 * 1000*1000/(0,5) ²

                                                        = 6,673 * (10) ^-11 * (10) ⁶ /0,25

= 6,673 * (10) ^-5 /0,25

= 26,692 * (10) ^-5

= 2,67 × 10 ^-4 Н

5.2 Сила гравитации между двумя одинаковыми свинцовыми сферами, находящимися на расстоянии 1 м друг от друга, равна 0,006673 Н.Найдите их массы. (по 10 000 кг)

Решение:         Гравитационная сила = F = 0,006673 Н

Гравитационная постоянная = G = 6,673 × 10 ^-11 Нм ² кг ^-2

                              Расстояние между грузами = d = 1 м

Масса = m ₁ = m ₂ =?

F = Gm ₁ m ₂ /d ²

F = M ² / D ^{2 2} (пусть M ₁ = M ₂ = M)

м ² = F*d ² /G

м ² = 0.006673 * (1) ^-3 / 6,673*(10) ^-11

Извлечение квадратного корня с обеих сторон

                                  = 10 ⁸

м = 10 ⁴ = 10000 кг каждый

Следовательно, масса каждого свинцового шара равна 10000 кг.

5.3 Найдите ускорение свободного падения на поверхности Марса. Масса Марса равна 6.42 × 10 ²³ кг и его радиус 3370 км.

Решение:         Масса Марса = M _м = 6,42 × 10 ²³ кг

Радиус Марса = R _м = 3370 км = 3370 × 1000 м = 3,37 × 10 ⁸ м

Ускорение свободного падения поверхности Марса = g _м =?

г _м = G мм/об ² м

               или                   г _м = 6.673 × 10 ^-11 × 6,42*10 ²³ / (3,37*10 ⁶ ) ²

                                             = 6,673*10 ^-11 * 6,42*10 ²³ / 11,307 90,357

= 42,84/11,357 = 3,77 м ^-2

5.4 Ускорение свободного падения на поверхности Луны составляет 1,62 мс ^-2 . Радиус Луны 1740 км. Найдите массу Луны.

Решение:         Ускорение свободного падения = g _м = 1.62 мс ^-2

Радиус Луны = R _м = 1740 км = 1740 × 1000 м = 1,74 × 10 ⁶ м

Масса Луны = M _m = ?

г _м = GMm/R ² м

               или            M _m =g _m *R ² m/ G  

М _м = 1,62*(1,74*10 ⁶ ) ² /6,673*10 ^-11

= 4,86*10 ¹² *10 ¹¹ /6.673

М _м = 7,35 × 10 ²² кг

5.5 Рассчитайте значение g на высоте 3600 км над поверхностью Земли. (4,0 мс ^-2 )

Решение:         Высота = h = 3600 км = 3600 × 1000 м = 3,6 × 10 ⁶ м

Масса Земли = M _e = 6.0 × 10 ²⁴ кг

Ускорение свободного падения = g _ч =?

г _ч = GMe/(R+ч) ²

г _ч = 6,673 × 10 ^-11 × 6,0*10 ²⁴ /(6,4*10 ⁶ +3,6*10 ^{6 7} ) ^{2 2}

= 6.673 × 10 ^-11 × 6,0 * 10 ²⁴ / (10 / 12 ⁶ ) ²

= 6,673 × 10 ^-11 × 6.0*10 ²⁴ /(100*10 ¹² )

= 6.673 × 10 ^-11 × 6,0 × 10 ¹⁰ = 40 × 10 ^-1 = 4,0 мс ^-2

5.6 Найдите значение g от Земли на геостационарном спутнике. Радиус геостационарной орбиты составляет 48700 км. (0,17 мс ^-2 )

Решение:         Радиус = R = 48700 × 1000 м = 4.87 × 10 ⁷ м

Гравитационное ускорение = g =?

г = GMe/R

                              г = 6,673 × 10 ^-11 × 6,0*10 ²⁴ /(4,87*10 ^{7 9004 9 9004 1 )}

= 6,673 × 10 ^-11 × 6,0*10 ²⁴ /(23,17*10 ¹⁴ ) ²

= 4,0038/23,717

= 0,17 мс ^-2

5.7 Значение g равно 4,0 мс ^-2 на расстоянии 10000 км от центра Земли. Найдите массу Земли. (5,99 × 10 ²⁴ кг)

Решение:      Гравитационное ускорение = g = 4,0 мс ^-2

                              Радиус Земли = R _e = 10000 км = 10000 × 1000 м = 10 ⁷ м

Масса Земли = M _e =?

M _e = гР ² /G

М _и = 4.0*(10 ⁷ ) ² / 6,673*10 ^-11

= 0,599 × 10 ²⁵ кг = 5,99 × 10 ²⁴ кг

5.8 На какой высоте значение g станет вчетверо больше, чем на поверхности Земли? (Радиус одной Земли)

Решение:         Масса Земли = M _e = 6,0 × 10 ²⁴ кг

Радиус Земли = R _e = 6.4 × 10 ⁶ м

Гравитационное ускорение = g _ч = g = × 10 мс ^-2 = 2,5 мс ^-2

                              Высота над поверхностью Земли = h =?

г _ч = GMe/(R+ч) ²

               или        (R + h) ² = GMe/г _ч

               Извлечение квадратного корня с обеих сторон

или     √(R+h) ² = √GM _e /g _ч

               или        R + h = √G GM _e /g _h

               или        h = √GM _e /g _h – R

или        h = √6.673*10 ^-11 *6,0*10 ²⁴ /2,5 – 6,4*10 ⁶   – 6,4 × 10 ⁶

= √40,038*10 ¹³ */2,5 – 6,4*10 ⁶

                                    = √16*10 ¹³ м ² – 6,4*10 ⁶

                            = -6,0 × 10 ⁶ м

Поскольку высота всегда принимается положительной, поэтому

ч = 6,0 × 10 ⁶ м = один радиус Земли

5.9 На высоте 850 км над Землей запущен полярный спутник. Найдите его орбитальную скорость.

Решение:         Высота = h = 850 км = 850 × 1000 м = 0,85 × 10 ⁶ м

Орбитальная скорость = v _o =?

v _или = √GM _e /R+h

v _o = √6,673*10 ^-11 * 6.0*10 ²⁴ /6,4*10 ⁶ + 0,85*10 ⁶ =

                             = √40,038*10 ¹³ /7,25*10 ⁶

= √5,55*10 ⁷

                            = 7,431 × 10 ³ = 7431 мс ^-1

5.10 Связь запущена на высоте 42000 км над Землей. Найдите его орбитальную скорость. (2876 мс ^-1 )

Решение:         Высота = h = 42000 км = 42000 × 1000 м = 42 × 10 ⁶ м

Орбитальная скорость = v _o =?

v _или = √GM _e /R+h

v _o = √6.673*10 ^-11 * 6,0*10 ²⁴ / 6,4*10 ⁶ +42*10 ⁶  

= √40,038*10 ¹³ /48,4*10 ⁶

                        = √400,38*10 ¹² /48,4*10 ⁶

                          = √8,27*10 ⁶

                         = 2,876 × 10 ³ = 2876 мс ^-1

.