9 класс примеры алгебра: ГДЗ по алгебре 9 класс с ответами онлайн и бесплатно

Содержание

Урок 41. примеры комбинаторных задач — Алгебра — 9 класс

Конспект

Комбинаторные задачи – это задачи, в которых необходимо составить комбинации каких-либо элементов из заданного набора по определённым условиям и (или) подсчитать количество получившихся комбинаций.

Комбинаторика – раздел математики, который занимается решением комбинаторных задач.

При решении комбинаторных задач можно воспользоваться:
• методом перебора;
• деревом возможных вариантов;
• комбинаторным правилом умножения.

Рассмотрим эти способы на примерах.

Задача 1
В магазине детских игрушек Маше понравились четыре мягких игрушки: мишка, енот, лиса и белка. Мама разрешила взять только две из них. Сколько существует вариантов выбора игрушек у Маши?

Решение
Переберём все возможные варианты выбора двух игрушек.

Сначала составим все варианты, в которых одной из игрушек будет мишка. Получим три варианта:
мишка и енот
мишка и лиса
мишка и белка

Теперь составим все варианты, в которых не будет мишки, но будет енот.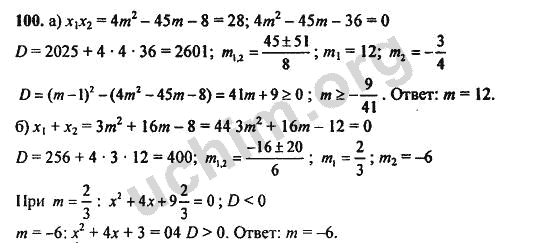 Получим ещё два варианта:
енот и лиса
енот и белка

Наконец составим все варианты, в которых не будет ни мишки, ни енота, но будет лиса. Такой вариант остался только один:
лиса и белка

Других вариантов выбора игрушек не осталось. Значит, у Маши всего 6 вариантов выбора игрушек.

Ответ: 6 вариантов.

Мы решили задачу методом перебора.

Задача 2
Петя, Коля и Вася решили съесть мороженое. У мальчиков было одно клубничное, одно шоколадное, одно малиновое и одно вишнёвое мороженое. Сколько вариантов выбора мороженого было у мальчиков?

Решение
Решим эту задачу с помощью дерева возможных вариантов. Обозначим клубничное мороженое буковой «к», шоколадное – «ш», малиновое – «м», вишнёвое – «в».
Поскольку мы учтём все возможные варианты, то нам всё равно, в каком порядке мальчики будут выбирать мороженое. Сначала проиллюстрируем все возможные варианты выбора Пети:

Теперь для каждого из вариантов выбора Пети проиллюстрируем все возможные варианты выбора Коли:

И наконец, для каждого из вариантов выбора Пети и Коли проиллюстрируем все возможные варианты выбора Васи:

Мы перебрали все возможные варианты.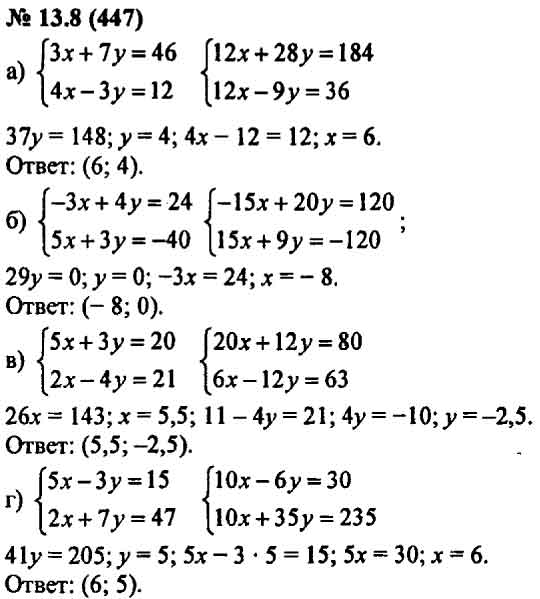 Полученная схема и называется деревом возможных вариантов. Осталось определить количество этих вариантов. Для этого нужно посчитать количество вариантов в последней строке. Получилось 24 варианта.

Ответ: 24 варианта.

Мы решили задачу с помощью дерева возможных вариантов.

Эту же задачу можно решить, не изображая схему.

Решение
Будем рассуждать следующим образом. Поскольку мы учтём все возможные варианты, то нам всё равно, в каком порядке мальчики будут выбирать мороженое.

Пусть Петя выбирает мороженое первым. У него есть 4 варианта выбора.

Если Коля выбирает вторым, то у него останется 3 варианта для каждого выбора Пети. То есть всего вариантов выбора Пети и Коли будет 4 • 3.

У Васи останется по 2 варианта для каждого из выборов Пети и Коли. Значит, всего вариантов будет 4 • 3 • 2 = 24.

Ответ: 24 варианта.

Мы решили задачу с помощью комбинаторного правила умножения. Сформулируем его для общего случая.

Пусть из некоторого набора элементов нужно выбрать последовательно k элементов. И пусть первый элемент можно выбрать n₁ способами, затем второй – n₂ способами из оставшихся, и т. д. Тогда количество способов, которыми могут быть выбраны все k элементов, равно n₁ • n₂ • … • n_k.

Решим ещё одну задачу.

Задача 3
Марина, Вера и Лена решили купить по воздушному шару. У продавца было 7 шаров разных цветов: зелёный, красный, розовый, жёлтый, оранжевый, фиолетовый и синий. Сколько вариантов выбора шаров есть у девочек, учитывая, что Марина не любит зелёный цвет и не купила бы себе такой воздушный шар?

Решение
Для решения задачи воспользуемся комбинаторным правилом умножения.

Поскольку у Марины есть предпочтения по цвету шара, начнём выбор с неё. У Марины всего 6 вариантов выбора шара. Вера может выбрать любой из оставшихся шаров, т. е. у неё тоже 6 вариантов выбора шара. Тогда у Лены остаётся 5 вариантов выбора.

Используя комбинаторное правило умножения получаем, что всего вариантов выбора шаров у девочек было 6 • 6 • 5 = 180.

Ответ: 180 вариантов.

Открытый урок по алгебре на тему «Примеры комбинаторных задач» (9 класс)

МБОУ МАНЬКОВО – БЕРЕЗОВСКАЯ СОШ

ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ

ПРИМЕРЫ КОМБИНАТОРНЫХ ЗАДАЧ

Класс: 9

Учитель: Н. В. Горелова

15.02.2019 год

Открытый урок по математике в 9 классе

Тема: Примеры комбинаторных задач.

Место урока: 1 (первый из 2 Глава 5 «Элементы комбинаторики и теории вероятности»).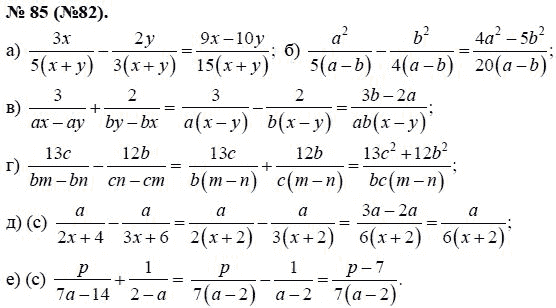

Тип урока: урок «открытия новых знаний».

Цель урока: создать условия для изучения нового понятия «комбинаторика», комбинаторной задачи, способов их решения.

Задачи:

— познакомить обучающихся с понятием «комбинаторика», комбинаторные задачи, способами решения комбинаторных задач;

— формировать навыки применения комбинаторных задач при решении простейших упражнений;

— развивать математическое мышление и логику;

— развивать самоконтроль и взаимоконтроль, опыт общения при работе в парах;

— воспитывать навыки коммутативности в работе, умение слушать другого, уважение к мнению товарища;

— воспитывать у обучающихся такие нравственные качества, как настойчивость, аккуратность, инициативность, точность, самостоятельность, активность.

Планируемые результаты УУД

Личностные: формирование коммуникативной компетентности в общении со сверстниками, умение ясно, четко излагать свои мысли в устной и письменной речи.

Познавательные: формируют познавательную цель, выражают смысл ситуации с помощью различных примеров, делают предположения об информации, необходимой для решения упражнений.

Регулятивные: самостоятельно формулируют познавательную цель и строят свои действия в соответствие с ней, умеют анализировать, делать выводы: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Коммуникативные: высказывают свою точку зрения, умеют слушать и вступать в диалог.

Основные понятия, изучаемые на уроке: комбинаторика, комбинаторные задачи, способы решения комбинаторных задач: перебор возможных вариантов, дерево возможных вариантов.

Ход урока

Организационный момент

Учитель: Добрый день, ребята! Сегодня на уроке у нас присутствуют гости. Я хочу пожелать вам хорошей, продуктивной работы, и чтобы каждый из вас для себя сделал хотя бы небольшое, но открытие.

Итак, проверьте готовность к уроку. Мы сегодня будем работать не только по учебнику, но и с карточками. Они у вас на парте.

Постановка проблемы, цели урока, определение задач

Сегодня утром у меня возникла проблема. Мне нужно было найти некоторую информацию на компьютере. На нем стоит пароль, мне его говорили, но я забыла последние 2 цифры. Что делать? Подскажите, может есть выход, какую пару чисел можно набрать? А сколько мне таких пар необходимо перебрать, чтобы найти походящий?

(ответы учащихся)

Конечно, можно долго подбирать такую пару цифр. Чтобы точно ответить на эти вопросы, существует такая наука, которая нам в этом поможет. А как она называется, предлагаю решить небольшой ребус.

Работа в парах: Разгадывание ребуса

Возьмите карточку красного цвета (учащиеся отгадывают ребус)

Это слово – КОМБИНАТОРИКА (СЛАЙД 1)

Итак, на уроке мы будем говорить о науке комбинаторике, рассмотрим примеры комбинаторных задач. Какова тема нашего урока?

Правильно, запишите в рабочих тетрадях число, классная работа, тему: «Примеры комбинаторных задач».

Как вы думаете, какова цель нашего урока?

(изучить новое понятие «Комбинаторика»)

Что бы достигнуть цели, давайте обозначим для себя задачи на урок. В этом нам помогут начальные слова:

Познакомиться с наукой …….;

Рассмотреть примеры ………..;

Научиться ……………………..;

Закрепить ………………………

Итак, мы узнали тему, поставили цель, определились с задачами, чтобы достичь эту цель. Движемся вперед!

Мотивация к учебной деятельности:

Посмотрите на портрет на доске. Это римский философ и поэт СЕНЕКА ЛЮЦИЙ АННЕЙ, прочтите его высказывание.

«Учимся не для школы, а для жизни».

Эти слова я хочу взять эпиграфом к нашему уроку. Как вы думаете, почему?

(ответы обучающихся)

Так как при изучении какой — либо темы, нового материала вы иногда спрашиваете: « А зачем она нужна?», «Может ли она чем – то помочь в реальной жизни?»

Попытаемся понять, а нужны ли комбинаторные задачи в жизни? И начнем мы с игры «Верите ли вы, что …» (КАРТОЧКИ ГОЛУБОГО ЦВЕТА)

Я услышала ваши мнения и в конце урока мы вернемся к этим вопросам.

Историческая страничка

Итак, что же такое комбинаторика? Внимание на экран. Ознакомьтесь с данной информацией.

(Показ слайдов: обучающиеся читают текст, знакомятся с историей возникновения комбинаторики, возможные сферы применения комбинаторных задач).

Что вы можете сказать о науке комбинаторике, как вы понимаете это слово?

(составление каких – либо комбинаций из данного набора).

Открытие нового знания

Скажите, вам приходилось делать выбор, что – то подсчитывать? В каких ситуациях? (с кем сидеть за партой, с кем сесть за праздничный стол, выбрать украшение, прическу, наряд, куда сходить погулять на выходные)

То есть, можно сделать вывод, что мы всегда делаем какой – то выбор в нашей повседневной жизни.

Сделаем и сейчас выбор.

Светлана Николаевна предложила вам участвовать в соревновании по шахматам, но только двоим из всех мальчиков. Сколько существует вариантов выбора такой пары? Давайте составим такие пары. 1 человек у доски, остальные в тетради. А Даша Воронкова сделает свой выбор, она выберет, кто пойдет к доске (составляем комбинации возможных вариантов).

О, А, В, Е, И1, И2.

ОА, ОВ, ОЕ, ОИ1, ОИ2

АВ, АЕ, АИ1, АИ2

ВЕ, ВИ1, ВИ2

ЕИ1, ЕИ2

И1, И2.

Мы составляли пары, перебирая все возможные варианты. Такой способ решения комбинаторной задачи называется перебор возможных вариантов.

Это не единственный способ решения, другой вариант решения называется дерево возможных вариантов. Посмотрите в учебник, с. 184, рис 80. Здесь изображена схема этого способа решения комбинаторной задачи. В чем он заключается?

Решим эту же задачу деревом возможных вариантов.

Кирилл Буряченко сделает выбор, кто пойдет к доске. Остальные в тетради.

Мини – итог: что же такое комбинаторика, как решить комбинаторную задачу?

Мы справились с работой, пришло время отдохнуть.

Физминутка (упражнения, связанные с темой урока)
Закрепление полученных знаний

Немного расслабились, пришло время следующей работы. Работа по учебнику.

Выполнение № 714 (выбор обучающегося, кто пойдет к доске)

Выполнение № 715 (выбор обучающегося, кто пойдет к доске).

Рефлексия

Мы с вами решили комбинаторные задачи двумя способами, я предлагаю вам применить эти способы при решении еще одной задачи.

Каждый из нас хочет быть в жизни востребованным, представьте, что вам представилась возможность открыть школьный буфет. Вам предстоит сделать рекламу своему заведению: на листах ватмана выполните дерево возможных вариантов меню продукции, которое вы хотите предложить покупателям (можно оформить способом перебора возможных вариантов).

(работа в группах – 3 – 5 минут. Защита – 1 человек от группы)

Подведение итога

Видим, что навыки решения комбинаторных задач в дальнейшем помогут вам творить, думать смело, оригинально. И я предлагаю вернуться к нашей игре «Верите ли вы, что….» и заново ответить на вопросы.

Так может ли комбинаторика помочь в реальной жизни? В чем? Я рада слышать ваши ответы.

Домашнее задание

П. 30

1 вариант № 716

2 вариант № 717

,+М+ ,,,+, ,,,+то+

е = и е = и

«Не для школы мы учимся, а для жизни мы учимся»

Познакомиться с наукой …….;

Рассмотреть примеры ………..;

Научиться ……………………..;

Закрепить ………………………

Алгебра 9 класс — Образовательная онлайн-платформа МЭО

Описание

Интерактивный онлайн-учебник «Алгебра 9 класс» сможет заменить бумажный учебник или дополнить его. Содержание интерактивных курсов соответствует требованиям федеральных государственных образовательных стандартов (ФГОС).

Онлайн-уроки построены таким образом, что перед изучением новой темы, предлагается повторить и закрепить ранее изученный материал Алгебра 8 класса.

Онлайн-уроки подходят для самостоятельного изучения. Ребенок познакомится с теорией, проверит полученные знания с помощью онлайн-тренажеров и интерактивных заданий, подготовится к контрольным и проверочным работам, экзаменам и ОГЭ.

Такой формат занятий поможет разобраться в новой теме или подтянуть знания по предмету. Доступ к онлайн-урокам осуществляется через интернет (24/7). Это позволяет заниматься в дороге и дома, во время соревнований, выездов на олимпиады или в оздоровительный лагерь.

Наш сборник — это способ улучшить успеваемость, начать подготовку к экзаменам, повторить пройденный материал во время каникул.

В качестве одной из составляющей курса, ученикам доступен объемный дополнительный материал, позволяющий углубить имеющиеся знания. Различные типы заданий, представленные в онлайн-курсе — одна из важных составляющих подготовки к будущим экзаменам.

Школьник научится:

работать с математическим текстом;

владеть базовым понятийным аппаратом;

выполнять алгебраические преобразования рациональных, иррациональных и тригонометрических выражений, выражений с рациональными степенями, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;

пользоваться математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;

решать линейные и квадратные уравнения и неравенства, а также приводимые к ним уравнения, неравенства, системы;

применять графические представления для решения и исследования уравнений, неравенств, систем;

применять полученные умения для решения задач из математики, смежных предметов, практики;

пользоваться системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функционально-графические представления для описания и анализа математических задач и реальных зависимостей;

определять члены прогрессий и вычислять сумму членов прогрессии;

пользоваться основными способами представления и анализа статистических данных;

решать задачи на нахождение частоты и вероятности случайных событий;

применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.

n

Интернет-урок 2. Четные и нечетные функции

Занятие 7. Корень n-ой степени

Интернет-урок 1. Определение корня n-ой степени

Интернет-урок 2. Свойства корня n-ой степени

Интернет-урок 3. Преобразование выражений, содержащих корень n-ой степени

Занятие 8. Степень с рациональным показателем

Интернет-урок 1. Определение степени с рациональным показателем

Интернет-урок 2. Свойства степени с рациональным показателем

Интернет-урок 3. Преобразование выражений, содержащих степень c рациональным показателем

Занятие 9. Уравнения с одной переменной

Интернет-урок 1. Целое уравнение и его корни

Интернет-урок 2. Уравнения, приводимые к квадратным

Занятие 10. Тематическая контрольная работа № 3

Занятие 11. Системы уравнений с двумя переменными

Интернет-урок 1.

Системы уравнений 2- й степени

Интернет-урок 2. Решение задач с помощью систем уравнений второй степени

Занятие 12. Арифметическая прогрессия

Интернет-урок 1. Последовательности

Интернет-урок 2. Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии

Интернет-урок 3. Формула суммы n первых членов арифметической прогрессии

Занятие 13. Геометрическая прогрессия

Интернет-урок 1. Определение геометрической прогрессии.Формула n-го члена геометрической прогрессии

Интернет-урок 2. Формула суммы n первых членов геометрической прогрессии

Занятие 14. Тематическая контрольная работа № 4

Занятие 15. Элементы комбинаторики

Интернет-урок 1. Решение комбинаторных задач

Интернет-урок 2. Перестановки

Интернет-урок 3. Размещения

Интернет-урок 4. Сочетания

Занятие 16. Элементы теории вероятностей

Интернет-урок 1. Вероятность случайного события

Интернет-урок 2. Вероятность равновозможных событий

Занятие 17. Статистические исследования

Интернет-урок 1. Статистические характеристики

Интернет-урок 2. Статистические исследования

Занятие 18. Тематическая контрольная работа № 5

Занятие 19. Тригонометрические функции

Интернет-урок 1. Радианная мера угла

Интернет-урок 2. Определения синуса, косинуса, тангенса, котангенса

Занятие 20. Основные тригонометрические формулы

Интернет-урок 1. Соотношения между тригонометрическими функциями одного и того же угла

Занятие 21. Тригонометрические преобразования

Интернет-урок 1. Преобразование тригонометрических выражений

Интернет-урок 2. Значения синуса, косинуса, тангенса и котангенса некоторых углов

Занятие 22. Тематическая контрольная работа № 6

ГДЗ (решебник) Алгебра 9 класс Мерзляк

Алгебра в девятом классе

Для некоторых девятый класс является завершающим, а для кого-то очередной ступенькой в следующий. Однако и в том и в другом случае по итогам года нужно будет сдать экзамены по основным предметам. Один из них — алгебра. Так как эта дисциплина достаточно сложна, то и внимание к ее изучению требуется повышенное. Потому что хоть одна неверно понятая тема может свести на нет весь учебный процесс. В этом году школьникам предстоит ознакомиться со следующими разделами:

Неравенства.
Квадратичная функция.
Элементы прикладной математики.
Числовые последовательности, и т.д.

Помимо этого учеников ждут постоянные проверочные работы и активная подготовка к ГИА, поэтому времени расслабиться просто не остается. Подобный темп может быстро вымотать, и некоторые подростки начинают испытывать затруднения с изучением материала. Чтобы облегчить детям учебу, был разработан решебник «Алгебра 9 класс Мерзляк».

Систематизация информации в решебниках Мерзляка

Сборники, представленные на сайте, последовательно и подробно дают примеры решений на все задания из учебных пособий. В «ГДЗ по Алгебре 9 класс Мерзляк» наглядно представлены всевозможные задачи, в том числе и дополнительные, которые рассчитаны на проверку знаний школьников. Автор постарался представить все в предельно доступной для понимания форме, чтобы у учеников не возникало никаких вопросов, поэтому ко всем номерам приведены самые детальные ответы.

Положительные стороны ГДЗ по алгебре

Испытывая затруднения с алгеброй, учащиеся довольно часто начинают поступать необдуманно и не осмотрительно. Вместо того, чтобы попытаться понять тему, они предпочитают просто скопировать домашку, а это не принесет абсолютно никакой пользы, скорее наоборот. Среди негативных последствий списывания можно отметить:

недополучение реальных знаний;
плохое понимание алгоритмов решений;
невозможность правильно написать контрольные работы.

Поэтому пользоваться ГДЗ все же нужно правильно. Они смогут существенно облегчить учебу и сделать материал более доступным пониманию. Помимо этого школьники грамотно и качественно сделают д/з, а также подтянут свой базовый уровень знаний. Решебники «Алгебра 9 класс Мерзляк» специально разрабатывались для того, чтобы дети смогли восполнить белые пятна в своем образовании.

Факторинг в алгебре

Факторы

Числа имеют коэффициенты:

И выражения (например, x ² +4x+3 ) также имеют множители:

Факторинг

Факторинг (называемый в Великобритании « Факторинг ») — это процесс нахождения факторов :

Факторинг: поиск того, что нужно умножить, чтобы получить выражение.

Это похоже на «разбиение» выражения на произведение более простых выражений.

Пример: коэффициент 2y+6

И 2y, и 6 имеют общий делитель 2:

Таким образом, мы можем разложить все выражение на:

2у+6 = 2(у+3)

Таким образом, 2y+6 «учтено в» 2 и y+3

Факторинг также противоположен расширению:

Общий коэффициент

В предыдущем примере мы видели, что 2y и 6 имеют общий делитель 2

Но для правильной работы нам нужен наибольший общий делитель , включая любые переменные

Пример: коэффициент 3y

² +12y

Во-первых, 3 и 12 имеют общий делитель 3.

Таким образом, мы могли бы иметь:

3г ² +12г = 3(г ² +4г)

Но мы можем лучше!

3y ² и 12y также имеют общую переменную y.

Вместе это составляет 3 года:

3 года ² это 3 года × у
12 лет — это 3 года × 4

Таким образом, мы можем разложить все выражение на:

3 года ² +12 лет = 3 года(у+4)

Проверить: 3y(y+4) = 3y × y + 3y × 4 = 3y ² +12y

Более сложный факторинг

Факторинг может быть сложным!

До сих пор примеры были простыми, но факторизация может быть очень сложной.

Потому что мы должны вычислить , что было умножено на , чтобы получить выражение, которое нам дано!

Это все равно, что пытаться выяснить, какие ингредиенты
вошли в торт, чтобы сделать его таким вкусным.

Это может быть трудно понять!

Опыт помогает

Чем больше опыта, тем проще факторинг.

Пример: Коэффициент

4x ² − 9

Хммм… вроде бы нет общих факторов.

Но знание специальных биномиальных произведений дает нам подсказку, называемую «разностью квадратов» :

Потому что 4x ² равно (2x) ² , а 9 равно (3) ² ,

Итак, имеем:

4x ² − 9 = (2x) ² − (3) ²

И что можно получить по формуле разности квадратов:

(а+б)(а-б) = а ² — б ²

Где a равно 2x, а b равно 3.

Давайте попробуем сделать так:

(2x+3)(2x−3) = (2x) ² − (3) ² = 4x ² − 9

Да!

Таким образом, множители числа 4x ² − 9 равны (2x+3) и (2x−3) :

Ответ: 4x ² − 9 = (2x+3)(2x−3)

Как этому научиться? Получив много практики и зная «Идентичности»!

Запомнить эти личности

Вот список общих «Идентификаций» (включая «разность квадратов» , использованную выше).

Их стоит запомнить, так как они могут упростить факторинг.


а ² − б ²	=	(а+б)(а-б)
а ² + 2аб + б ²	=	(а+б)(а+б)
а ² − 2аб + б ²	=	(а-б)(а-б)
а ³ + б ³	=	(а+б)(а ² −аб+б ² )
а ³ − б ³	=	(а-б)(а ² +аб+б ² )
а ³ +3а ² б+3аб ² +б ³	=	(а+б) ³
а ³ −3а ² b+3ab ² −b ³	=	(а-б) ³

Таких много, но эти самые полезные.

Совет

Обычно лучше использовать факторизованную форму.

При попытке факторинга выполните следующие действия:

«Вынести за скобки» любые общие термины
Посмотрите, подходит ли оно к какой-либо из идентификаций, а также к тому, что вы знаете
Продолжайте, пока не перестанете множить

Существуют также системы компьютерной алгебры (называемые «CAS»), такие как Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce и многие другие, которые хорошо подходят для факторинга.

Дополнительные примеры

Опыт помогает, поэтому вот еще несколько примеров, которые помогут вам на этом пути:

Пример: w

⁴ − 16

Показатель степени 4? Может быть, мы могли бы попробовать показатель степени 2:

w ⁴ − 16 = (w ² ) ² − 4 ²

Да, это разность квадратов

w ⁴ − 16 = (w ² ^{+ 4)(w ² ^{− 4)}}

И «(w ² ^{− 4)» это еще одна разность квадратов}

w ⁴ − 16 = (w ² ^{+ 4)(w ^{+ 2)(w ^{− 2)}}}

Это все, что я могу сделать (если я не использую мнимые числа)

Пример: 3u

⁴ − 24uv ³

Удалить общий делитель «3u»:

3u ⁴ − 24uv ³ = 3u(u ³ − 8v ³ )

Тогда разница кубов:

3u ⁴ − 24uv ³ = 3u(u ³ − (2v) ³ )

= 3u(u−2v)(u ² +2uv+4v ² )

Это все, что я могу сделать.

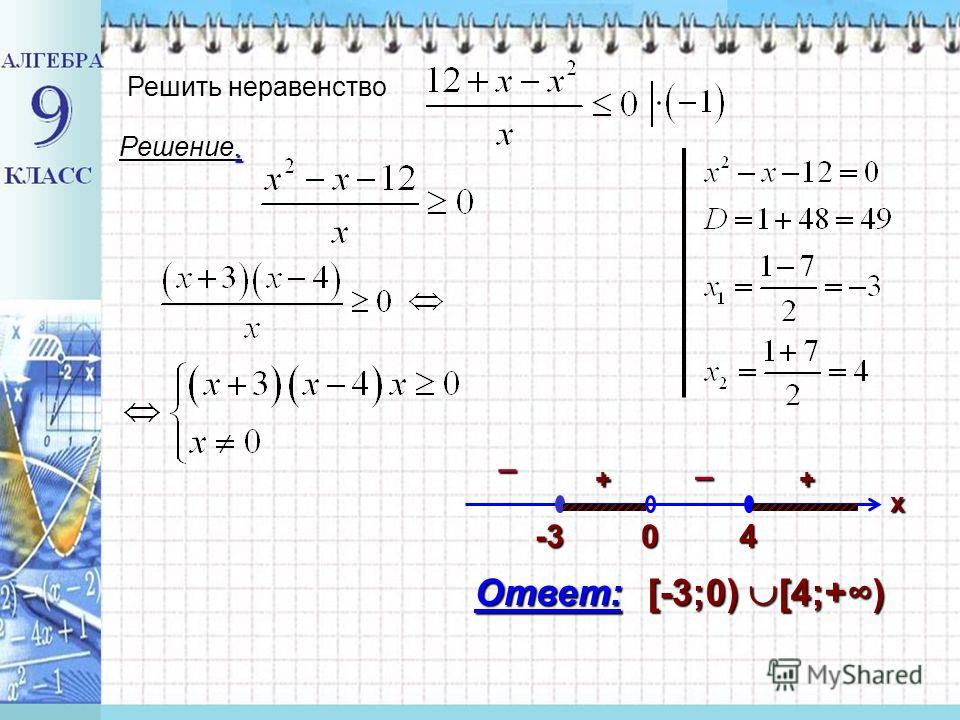
Пример: z

³ − z ² − 9z + 9

Попробуйте разложить на множители первые два и вторые два отдельно:

z ² (z−1) − 9(z−1)

Ничего себе, (z-1) есть на обоих, так что давайте использовать это:

(z ² −9)(z−1)

А z ² −9 есть разность квадратов

(г-3)(г+3)(г-1)

Это все, что я могу сделать.

Теперь получите больше опыта:

20 лучших онлайн-репетиторов 9-го класса по математике рядом со мной

Если вы ищете репетиторство по математике для 9-го класса для своего ученика, свяжитесь с университетскими репетиторами.Мы можем помочь вам связаться с инструктором, который не только является экспертом в своей области, но также квалифицирован и обладает необходимыми навыками, которые могут помочь вашему 9-класснику стремиться делать все возможное. Частные инструкторы доступны как онлайн, так и лично, что дает вам и вашему ученику гибкость и удобство, которые вы ищете. Частное обучение предлагает больше практических и персонализированных подходов, включая ответственность, по сравнению с обучением в одиночку. Если ваш ученик нуждается в руководстве, когда речь идет о таких темах, как числа и операции или даже алгебра, индивидуальная помощь может быть полезной.

Совместная работа с академическим наставником означает, что ваш ученик получает внимание эксперта один на один. В типичном классе у преподавателей обычно есть расписание, которому они должны следовать, когда дело доходит до учебной программы на учебный год. Это оставляет им ограниченное время для вопросов учащихся, которые выходят за рамки основ и могут быть особенно трудными для ученика, которому нужна дополнительная помощь или у которого проблемы с конкретной темой. Выбрав частного инструктора, ваш ученик может получить индивидуальную поддержку по мере развития своих математических навыков, например, понимания анализа данных и вероятности или измерения, а также того, как это может быть связано с геометрией.

Если вашему девятикласснику нужно дополнительное время для работы над чем-то, например, для подробного изучения начальной алгебры, его преподаватель может замедлить учебные занятия и работать с ним только над этим. Если есть тема, в которой ваш ученик преуспевает, он может пропустить ее и перейти к чему-то другому. Потребности вашего ученика диктуют, как проходят учебные занятия, гарантируя, что они будут максимально использовать свое время с инструктором. Их наставник также может найти время, чтобы оценить стиль обучения вашего ученика и найти методы, которые работают для них.Например, если они работают лучше всего, разбивая и объясняя математическую задачу, инструктор может сделать это. Или они могут прочитать лекцию о том, как вероятность используется в реальной жизни, и оставить время для вопросов и заметок. Каждое занятие может быть адаптировано к стилю обучения вашего ученика.

Дать вашему ученику возможность учиться с помощью репетитора по математике в 9-м классе проще, чем вы думаете. Независимо от того, выбираете ли вы репетитора лично или онлайн, у вас будет возможность организовать занятия, когда они лучше всего подходят для вашего ученика.Вы можете выбрать очное обучение и пригласить репетитора к вам домой во второй половине дня или даже встретиться в библиотеке. Онлайн-сеансы используют нашу платформу интерактивного обучения, а также виртуальную доску и другие функции, что упрощает взаимодействие вашего 9-классника со своим инструктором. Если у вас есть подключение к Интернету и компьютер, ноутбук или мобильное устройство, ваш девятиклассник может воспользоваться этой полезной формой обучения.

Как мне найти репетитора по математике для 9-го класса рядом со мной?

Когда вы будете готовы начать, обратитесь к университетским наставникам.Мы можем помочь вашему ученику связаться с репетиторами по математике 9-го класса, которые соответствуют их потребностям, и могут помочь им развить свои навыки таким образом, который соответствует их стилю обучения. Вы можете избежать хлопот, связанных с несовместимостью расписаний, если у вас есть инструктор, который согласовывает занятия с графиком вашего ученика и семейной жизнью. Свяжитесь с одним из наших образовательных консультантов сегодня и узнайте, с чего начать. Мы можем ответить на любые ваши вопросы и даже связать вашего ученика с инструктором уже на следующий день.Позвоните сегодня и узнайте, как частное обучение может помочь вашему ученику достичь своих целей по математике в 9-м классе.

9 способов развития алгебраического мышления в младших классах

Никогда не рано начинать закладывать основы алгебраического мышления для младших школьников, помогая им изучать различные понятия с помощью простых, веселых, но стимулирующих мышление упражнений.

Вот девять способов развить алгебраическое мышление у младших школьников.

Топ 📸 кредит: фантастически четвертый в Instagram

1.Охотники за узорами

Большая часть математики, и особенно алгебры, основана на закономерностях. Помогите юным ученикам начать искать закономерности вокруг себя. Отличное место для поиска — это одежда, которую мы носим. Предложите учащимся объединиться и описать узор в одежде своего партнера, например полосатую рубашку с чередующимися синими и белыми полосами. Попросите учеников нарисовать рубашку, чтобы записать узор.

2. Музей узоров

Предоставьте учащимся манипуляторы, такие как шаблоны, кнопки, клавиши, цветные кубики и т. д.Попросите их создать из этих материалов два узора на своих партах. Одноклассники приходят, чтобы посетить «экспонаты музея узоров», попытаться угадать узоры и рассказать, что будет дальше в последовательности.

3. Повторяющиеся цветовые узоры

Некоторые узоры повторяются, например X, O, X, O, X, O. Раздайте учащимся цветные карандаши и лист бумаги для рисования. Попросите их выбрать два цвета и нарисовать повторяющийся узор из цветных фигур, например, зеленый треугольник, синий круг, зеленый треугольник, синий круг. Сотрудничайте с учащимися и попросите их посмотреть, смогут ли они расширить шаблон своего партнера, нарисовав элемент, который будет следующим.

4. Сопоставьте шаблон

Подружитесь со студентами и дайте им набор мелких предметов и манипуляторов. Попросите одного партнера быть лидером. Ведущий берет несколько предметов и рисует на столе узор, например: копейка, копейка, пятак, копейка, копейка, пятак. Затем второй партнер берет разные предметы и создает соответствующий узор, например: шарик, ключ, пуговица, шарик, ключ, пуговица.Оба шаблона ABC, но из разных материалов. Пусть учащиеся по очереди будут ведущими.

5. Растущие шаблоны чтения вслух

Читать вслух Королевская шахматная доска Дэвида Берча. Король хочет наградить верного мудреца. По настоянию короля мудрец отвечает: «Я прошу только об этом: завтра на первую клетку твоей шахматной доски дай мне одно рисовое зерно; на следующий день за вторую клетку два зернышка риса… и так далее за каждую клетку на шахматной доске. Король соглашается и вскоре усваивает удивительный и ценный урок математических моделей выращивания и смирения, поскольку количество риса быстро становится больше, чем весь рис в мире.

6. Функциональная машина

Функции — большая часть алгебры. Помогите учащимся узнать об этой идее с помощью функциональной машины. Возьмите коробку из-под обуви и вырежьте прорезь с левой стороны и прорезь с правой стороны. Внутри коробки есть набор карточек с цифрами от 0 до 100. Дайте учащемуся еще один набор карточек с одинаковыми номерами.Попросите ученика выбрать число и вставить его слева. Это ввод. Вы сами решаете, какова функция коробки. Это может быть + 2, — 1, как хотите. Допустим, учащийся ставит 4. Вы решили, что ваша функция + 2. 4 + 2 = 6, поэтому возьмите 6 и выдвиньте ее из выходного слота. Попросите трех разных учеников дать вам три разных числа и продолжайте прибавлять 2 к каждому введенному числу. Спросите учащихся, могут ли они угадать функцию машины.

7. Веселый калькулятор

Покажите учащимся, как превратить простой калькулятор в функциональную машину. Допустим, функция равна + 2. Попросите учеников нажать «+», затем «2», затем «=». С этого момента каждый раз, когда учащиеся нажимают «=», их калькулятор будет прибавлять 2 к предыдущему числу. Студенты могут запрограммировать свои калькуляторы с функцией и посмотреть, смогут ли одноклассники угадать ее, просматривая результаты.

8. Таинственные загадки с числами X

В алгебре X часто используется для обозначения неизвестного. Юные ученики могут начать работать с X (или любым другим неизвестным символом) таким образом. Предложите учащимся три числовых предложения, в которых X представляет одно и то же неизвестное, и попросите их выяснить, каково значение X.Представьте его в виде числовой загадки. Дайте три подсказки, чтобы помочь учащимся понять, что такое загадочный X. Например: X + 1 = 3, X + 0 = 2 и 4 – X = 2. Что такое X? (Х равно 2.)

9. Знак равенства = То же, что и

Подчеркните учащимся, что когда они читают числовые предложения, а затем и алгебраические уравнения, знак равенства означает «такой же, как». Маленькие дети часто думают, что «=» означает «ответ». Например, уравнение 4 + 4 = 2 x 4 можно прочитать как «четыре плюс четыре равно 90 534, то же самое, что 90 535 два раза по четыре».Это укрепит идею балансировки уравнений, потому что каждая сторона имеет одинаковое количество. В более простом примере мы могли бы использовать 4 + 4 = 8, говоря: «4 + 4 90 534 — это то же самое 90 535, что и 8». Также попробуйте поставить знак равенства в начале числового предложения, например, 8 = 4 + 4. Это поможет учащимся лучше понять, что на самом деле представляет собой знак равенства.

Как вы развиваете алгебраическое мышление в младших классах? Приходите и поделитесь в нашей группе WeAreTeachers HELPLINE на Facebook.

Кроме того, ознакомьтесь с разделом «Почему нам не следует учить длинное деление с помощью симпатичных мнемоник (и что делать вместо этого)».

Распределительное свойство

: 5 четких примеров использования в классе

Что такое распространяемое свойство ? Также известный как распределительный закон умножения, это одно из наиболее часто используемых свойств в математике.

Когда вы что-то распространяете, вы делите это на части. В математике свойство дистрибутивности помогает упростить сложные задачи, поскольку оно разбивает выражения на сумму или разность двух чисел.

В соответствии с этим принципом умножение суммы двух слагаемых на число даст нам точно такой же результат, как и умножение каждого слагаемого по отдельности на число, а затем их сложение.

Понимание распределительного свойства

Для выражений вида a(b+c) распределительное свойство показывает нам, как решать их на:

Умножение внутри
Сложение продуктов вместе

Что насчет PEMDAS? Что случилось с первой оценкой того, что находится внутри скобок?

Если ваши ученики задаются вопросом, почему вы не следуете тому порядку операций, которому их учили в прошлом, они не ошибаются.

Однако, когда алгебраические выражения имеют круглые скобки, содержащие переменные — количество, которое может измениться в контексте математической задачи, обычно представленное одной буквой — выполнение этой операции невозможно.

Распределительное свойство умножения над сложением

Независимо от того, используете ли вы распределительное свойство или следуете порядку операций, вы получите один и тот же ответ. В первом примере ниже мы просто оцениваем выражение в соответствии с порядком операций, упрощая сначала то, что было в скобках.

Используя закон распределения, мы:

Умножаем или распределяем внешний член на внутренние члены.
Комбинируйте похожие термины.
Решите уравнение.

Давайте используем сценарий из реальной жизни в качестве примера распределительного свойства.

Представьте, что у одной ученицы и двух ее друзей есть по семь ягод клубники и четыре клементина. Сколько всего фруктов у всех трех учеников?

В пакетах для завтрака — или, в скобках — у каждого из них по 7 клубник и 4 клементина.Чтобы узнать общее количество кусочков фруктов, им нужно умножить все это на 3.

Когда вы разбиваете это число, вы умножаете 7 клубник и 4 клементина на 3 учащихся. Итак, у вас получится 21 клубника и 12 клементинов, всего 33 фрукта.

Распределительное свойство умножения над вычитанием

Подобно предыдущей операции, выполнение распределительного свойства с вычитанием следует тем же правилам, за исключением того, что вы находите разность вместо суммы.

Примечание : Не имеет значения, положительная или отрицательная операция. Оставьте то, что в скобках.

Распределительное свойство с переменными

Помните, что мы говорили об алгебраических выражениях и переменных? Распределительное свойство позволяет нам упростить уравнения при работе с неизвестными величинами .

Используя закон распределения с задействованными переменными, мы можем изолировать x :

Умножить или распределить внешний член на внутренние члены.
Комбинируйте похожие термины.
Расположите термины так, чтобы константы и переменные находились по разные стороны от знака равенства.
Решите уравнение и при необходимости упростите его.

Примечание : При изоляции переменных (см. третий шаг) то, что вы делаете с одной стороной, вы должны делать и с другой. Чтобы исключить 12 с левой стороны, вы должны добавить по двенадцать и к левой, и к правой стороне. То же самое касается умножения и деления: чтобы изолировать 90 514 x 90 515, разделите каждую сторону на 4.

Распределительное свойство с показателями степени

Показатель степени — это сокращенная запись, указывающая, сколько раз число умножается само на себя. Когда задействованы круглые скобки и показателей степени, использование распределительного свойства может значительно упростить выражение.

Расширьте уравнение.
Умножьте (распределите) первые числа каждого набора, внешние числа каждого набора, внутренние числа каждого набора и последние числа каждого набора.
Комбинируйте похожие термины.
Решите уравнение и при необходимости упростите его.

Примечание . На втором этапе используйте метод FOIL (первое, внешнее, внутреннее, последнее) для распределения каждого выражения.

Распределительное свойство с дробями

Решение алгебраических выражений с дробями выглядит сложнее, чем есть на самом деле. Выполните шаги, описанные ниже, чтобы увидеть, как это делается.

Надеюсь, этот пошаговый процесс поможет вашим учащимся понять, как и почему свойство дистрибутивности может пригодиться при упрощении дробей и комплексных чисел.

Найдите дроби. Используя свойство распределения, вы в конечном итоге превратите их в целые числа.
Для всех дробей найдите наименьшее общее кратное (НОК) — наименьшее число, в которое могут точно вписаться оба знаменателя. Это позволит вам добавлять дроби.
Умножьте каждый член уравнения на НОК.
Изолировать переменные, добавляющие или вычитающие одинаковые термины по обе стороны от знака равенства.
Комбинируйте похожие термины.
Решите уравнение и при необходимости упростите его.

Примечание : На шагах два и три мы находим НОК и используем его для умножения дробей, чтобы упростить их и избавиться от них. Нужна быстрая переподготовка? См. статью в нашем блоге о том, как умножать дроби.

Разнообразные свойства

Помимо распределительного свойства, существуют и другие широко используемые свойства, такие как ассоциативное свойство и коммутативное свойство.

Давайте посмотрим на ассоциативное свойство:

Ассоциативное свойство относится к группированию элементов вместе.Это правило гласит, что то, как числа (или целые числа) сгруппированы в математической задаче, не изменит результат.

Пример в дополнении:

a + (b +c) = (a + b) + c или 2 + (3 + 4) = (2 + 3) + 4

Пример в умножении:

5×4×2 = (5 x 4) x 2 = 20 x 2 = 40

Это свойство работает с умножением, сложением, вычитанием и делением.

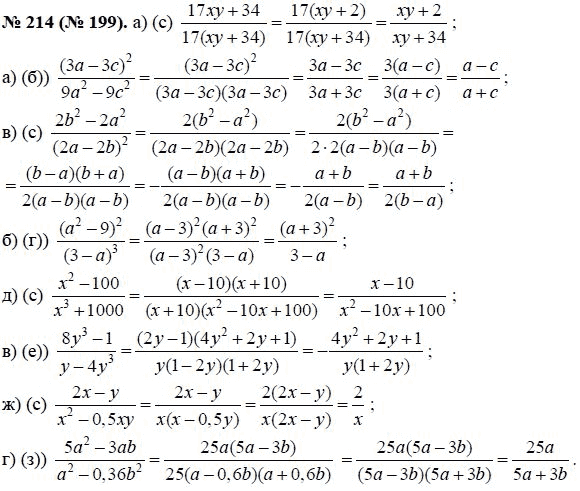
Различные способы изучения распределительной собственности

1.Prodigy

Prodigy — это адаптивная игровая обучающая математическая платформа, которую любят более миллиона учителей и 150 миллионов учащихся по всему миру! Он предлагает материалы, соответствующие учебной программе, по всем основным математическим темам в 1–8 классах, в том числе инструкции:

Использование свойства распределения для раскрытия и решения выражений
Заполнение пропущенных чисел в эквивалентных выражениях с помощью свойства распределения

Использование Prodigy Math Game может помочь учащимся изучать и практиковать математику не только бегло говоря, но и переходя на второй и третий уровни DoK.Ответив на такие вопросы, как приведенный выше, учащиеся получат массу удовольствия, пока будут практиковать распределительное свойство.

Хотите дополнить уроки математики увлекательной игровой платформой для обучения и мощными инструментами для учителей?

Зарегистрируйтесь прямо сейчас, чтобы получить бесплатную учетную запись учителя

2. Словесные задачи

Распределяющее свойство может быть неприменимым к повседневной жизни, но давайте посмотрим на него в действии через некоторые словесные задачи!

У Лиама разносторонний музыкальный вкус. Просматривая музыку на своем телефоне, друзья Лиама находят песни трех разных жанров: поп, металл и кантри.Металлических песен в шесть раз больше, чем поп-песен, и кантри-песен в 11 раз больше, чем поп-песен. Если x представляет собой количество поп-песен, сколько всего песен у Лиама в телефоне? Напишите выражение. Упрощать.

Чтобы получить количество металлических песен, умножьте количество поп-песен на пять — 5x . Чтобы получить количество кантри-песен, умножьте количество поп-песен на 11 — 11x . Поскольку вы знаете, что x — это количество поп-песен, вы можете записать это выражение в следующем виде:

Школьный тренер по футболу снабжает свою команду новой формой: майкой, парой шорт и щитками для голеней. Одна футболка стоит 15 долларов, пара шорт — 11 долларов, а комплект щитков — 8 долларов.

Сколько стоит форма на одного товарища по команде? Напишите выражение и упростите.

Сколько всего будет стоить, если в команде 11 игроков? Напишите выражение и упростите.

3. Массивы

Визуальные или практические манипуляции помогают учащимся разобраться в математике и конкретизировать абстрактные понятия. Они особенно полезны для углубления понимания вашими учащимися свойства распределения.

Используйте предметы, картинки, числа — что угодно! — в строках и столбцах как полезный способ представления математических выражений, таких как 4×5 и 5×9. Взгляните на приведенный ниже пример на Indulgy:

Разбивая выражения на маленькие кусочки, учащиеся могут решать более сложные математические задачи. Вот где распределительная собственность помогает.

Если ребенок не может ответить на 45, используйте массивы меньшего размера и перепишите выражение как 4(3+2) или 4(3)+4(2). Это четыре строки по три плюс четыре строки по два , что равно массиву четыре строки по пять .

Заключительные мысли о свойстве распределения

Поскольку это одно из наиболее часто используемых свойств, важно научиться выполнять и применять свойство распределения. Без него очистка скобок была бы невозможна.

Включая ресурсы EdTech, массивы или математические задачи, учащиеся должны увидеть практическое применение свойства распределения.

Сработал ли один пример более эффективно, чтобы привлечь учащихся и углубить их понимание? Есть только один способ узнать это — попробовать!

Prodigy Math Game — это игровая платформа для обучения математике, которую легко использовать как преподавателям, так и учащимся.В соответствии с учебными планами англоязычного мира ваша бесплатная учетная запись учителя дает вам доступ к инструментам, которые помогают с дифференциацией, мотивацией и оценками.

Зарегистрируйте бесплатную учетную запись

Алгебра TeachersFirst — классы 9–12

Подготовьте своих учеников к успеху с помощью навыков Common Core Math на этом превосходном сайте, представленном Академией Хана. 50 000 уникальных вопросов охватывают концептуальное понимание, беглость процедур и применение в реальном мире. Воспользуйтесь ссылкой «Просмотреть нашу новую общую основную карту», чтобы найти интерактивные математические задачи для классов K-12.В каждом упражнении указано количество навыков и задач, доступных для каждого уровня. Просмотрите пошаговые решения каждой проблемы. Многие задачи даже снабжены видео пояснениями. Консорциум Smarter Balanced Assessment Consortium и Illustrative Mathematics сотрудничают с Khan Academy, чтобы обеспечить строгость материалов и полное соответствие Common Core Standards. Узнайте больше об Академии Хана, рассмотренной здесь. Видео размещаются на YouTube. Если ваш округ блокирует YouTube, они могут быть недоступны для просмотра.

тег(и): сложение (124), углы (51), основание счисления (5), координаты (12), счет (57), данные (128), деление (97), уравнения (119), факторизация (24), дроби (163), функции (51), геометрические фигуры (129), измерение (130), смешанные числа (8), умножение (118), отрицательные числа (11), числовые линии (33), числовой смысл (69), многочлены (21), простые числа (24), вероятность (92), квадратичные вычисления (25), округление (9), квадратные корни (16), статистика (107), вычитание (108), преобразования (11) , векторы (16), целые числа (10)

В классе

Поделитесь этим сайтом на веб-сайте своего класса или в блоге, чтобы учащиеся могли практиковать математические понятия дома.Поделитесь с родителями через веб-сайт вашего класса или информационный бюллетень как отличный ресурс для повторения и закрепления математических концепций. Делитесь действиями на интерактивной доске или проекторе. Используйте проблемы на сайте, чтобы представить новые концепции или просмотреть информацию перед оценкой в конце модуля. Разместите ссылки на уроки на веб-сайте класса или в блоге, чтобы учащиеся могли просмотреть их дома. Предложите учащимся создать свои собственные уроки по образцу этого сайта. Затем предложите учащимся создать блоги, чтобы попрактиковаться в написании своих математических решений.Если вы только начинаете процесс интеграции технологий, предложите учащимся создать блоги, в которых они будут делиться своими знаниями и знаниями с помощью Tumblr, рассмотренные здесь.

Стратегии вмешательства в математику для учащихся, испытывающих затруднения

Стратегии, которые можно использовать во время обучения

Попробуйте этот список математических вмешательств во время урока, так как они могут помочь отдельным учащимся — или даже всему классу! — которые, кажется, застряли на задаче.

Стратегия 6: использование метакогнитивных стратегий

Исследования снова и снова показывают, что если вы можете заставить учащихся критически относиться к их собственному математическому мышлению, у них есть возможность для роста. На первый взгляд может показаться, что проблема заключается в понимании математических понятий, но на самом деле более глубокой проблемой может быть образ мышления учащихся.

Поощряйте учащихся рассказывать свои собственные математические истории. Какой была математика в их семье и на предыдущих уроках? Намеренно привлекайте внимание учащихся не только к математическим понятиям, но и к тому, как они к ним относятся. Попросите учащихся сделать паузу, чтобы подумать о том, что они чувствуют и какие мысли приходят им в голову. Думают ли они о таких мыслях, как «Я никогда этого не получу» или «Я ничего не могу с этим поделать?» Расскажите о способах борьбы с этим мышлением, таких как перерыв, просьба о помощи или мозговой штурм, чтобы попробовать новую стратегию.

Стратегия 7: Вербализация мыслительных процессов

Исследования показывают, что самые успешные математические вмешательства являются явными и систематическими. Один из способов сделать это — вербализовать мыслительные процессы. Другими словами, когда учащиеся думают о том, как решить проблему, попросите их сказать, что они думают вслух. Здесь важно терпеливо и без осуждения слушать, даже если их математический язык неточен или их рассуждения несовершенны. Когда вы услышите весь процесс, это может помочь вам определить, как именно нужно вмешаться.Возможно, они понимают большую идею, но застревают на арифметике. Или, возможно, они понимают, о чем проблема, но отключаются, как только сталкиваются с какой-то ее частью.

Можно и наоборот. Как вы решаете проблему, вербализируете свой мыслительный процесс. Пусть учащиеся увидят шаги, которые вы предпринимаете для решения проблемы, и смоделируйте точный математический язык и рассуждения.

Стратегия 8: Быстрое вытягивание

Быстрое вытягивание — это обучающая стратегия, разработанная Сесилом Д.Мерсер и Сьюзен П. Миллер около 30 лет назад, чтобы помочь учащимся с ограниченными возможностями в обучении решать математические задачи. Буквы Fast Draw являются мнемоникой для шагов:

Найдите то, что вы решаете: Найдите вопросительный знак и подчеркните, что вы пытаетесь решить.
Спросите сами, какая информация дается: Прочтите всю задачу и посмотрите, какая информация уже предоставлена.
Set up уравнение: Напишите уравнение с цифрами и символами в правильном порядке.
Свяжите вниз уравнение: Произнесите вслух, что это за операция и что она означает. Если можете, решите задачу. Это может помочь в рисовании.
Найдите знак. Найдите знак и произнесите его вслух.
Прочтите проблему. Произнесите проблему вслух.
Ответьте на задачу или нарисуйте.
Напишите ответ на задачу.

Вот ресурс Университета Джеймса Мэдисона, который содержит подробную информацию о каждом шаге, а также примеры. Учащиеся, испытывающие затруднения в математике, часто становятся пассивными, когда сталкиваются с текстовыми задачами, и набор Fast Draw предлагает конкретную стратегию, которая может помочь им стать активными и самостоятельно решать текстовые задачи. Стратегия не только помогает повысить успеваемость по математике, но и отношение к математике, особенно для учащихся с ограниченными возможностями обучения.

Стратегия 9: использование нескольких представлений

Множественные представления важны далеко за пределами математического вмешательства. Они помогают учащимся по-разному воспринимать математические понятия и формировать важные обобщения.Однако они могут служить более целенаправленной цели для студента, нуждающегося в адресной помощи. Демонстрация математических представлений различными способами дает учащимся возможность рассмотреть различные ментальные модели, повышая вероятность понимания. Другими словами, это помогает учащимся «видеть» математику, даже если одно представление сбивает их с толку. Упражнение по сортировке карточек из «Стратегия 3: взаимное обучение » — это один из способов, с помощью которого вы можете подготовить конкретные множественные представления для сравнения учащимися.

Даже понятия, которые кажутся вам простыми, могут быть сложными для ваших учеников.Поскольку все люди без нарушений зрения являются визуальными учениками, используйте несколько визуальных представлений, чтобы демистифицировать идеи. Но будьте преднамеренными, в каких представлениях вы показываете. Если представления трудно интерпретировать или они кажутся несвязанными, вы рискуете еще больше запутать учащихся!

***

Хотите разблокировать математические знания для учащихся, которые в этом больше всего нуждаются? Ознакомьтесь с нашими программами вмешательства по математике для учащихся 5–12 классов.