8 класс

Задачи 8 класс геометрия: Геометрия, 8 класс: уроки, тесты, задания

Содержание

Практика. Решение задач 8 класс онлайн-подготовка на Ростелеком Лицей

Центральный и вписанный углы

 

Вспомним определение и свойства центрального и вписанного углов (см. рис. 1): центральный угол – это угол, вершина которого совпадает с центром окружности; вписанный угол – это угол, вершина которого принадлежит окружности.

 

Рис. 1. Центральный угол  и вписанный угол

При этомвписанный угол равен половине градусной меры дуги окружности, на которую он опирается, а центральный угол равен этой дуге:

Одним из следствий является то, что два вписанных угла, опирающихся на одну дугу (или одну хорду), равны друг другу (см. рис. 2).

Рис. 2. Вписанные углы , опирающиеся на одну дугу

 

Угол, вершина которого лежит внутри окружности

 

 

А как обстоит дело с остальными углами, опирающимися на дугу, но вершина которых не лежит ни на окружности, ни в ее центре?

 

Понятно, что в этом случае вершина лежит либо внутри окружности (см. рис. 3), либо снаружи (см. рис. 4).

Рис. 3. Вершина угла лежит внутри окружности

Рис. 4. Вершина угла лежит вне окружности

Рассмотрим случай, когда вершина лежит внутри окружности. Угол  опирается на дугу  (см. рис. 5).

Рис. 5. Угол  опирается на дугу

Интуитивно понятно, что угол больше вписанного, опирающегося на ту же самую дугу. Продлим стороны угла  и  до пересечения с окружностью (см. рис. 6) и попробуем выразить сам угол через величины дуг, на которые разбита окружность.

Рис. 6. Стороны угла  и  продлили до пересечения с окружностью

Наш угол является внешним для треугольника . А раз так, то он равен сумме двух внутренних углов, не смежных с ним (см. рис. 7):

Рис. 7. Угол , являющийся внешним для треугольника , равен сумме двух внутренних углов, не смежных с ним

Но углы  и  уже являются вписанными, а значит, каждый из них равен половине дуги, на которую опирается:

Уберем лишнее с рисунка (см.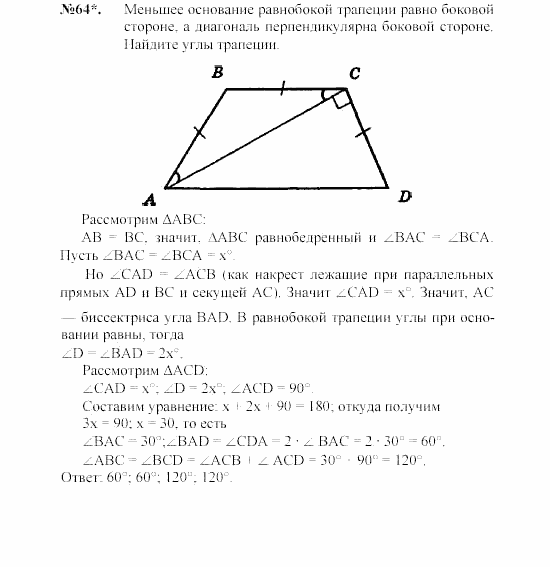 рис. 8).

Рис. 8. Угол  равен полусумме дуг  и

Итак: если через точку внутри окружности проведены две секущие, то угол между ними равен полусумме дуг, на которые опираются сам угол и ему вертикальный.

Легко проверить, что это выполняется и для центрального, и для вписанного углов (как для предельных случаев). Т. е. мы обобщили теорему о центральном и вписанном угле (как раньше обобщили теорему Пифагора теоремой косинусов).

Второй случай, когда вершина угла лежит вне окружности, а стороны угла пересекают эту окружность. Попробуйте самостоятельно изобразить этот случай и выразить величину угла через дуги, на которые окружность поделилась сторонами угла. А решение можно посмотреть ниже.

 

Угол, вершина которого лежит вне окружности

Итак, постановка задачи: через точку, лежащую вне окружности, проходят две секущие (см. рис. 9). Выразить величину угла через полученные дуги окружности.

Рис. 9. Через точку, лежащую вне окружности, проходят две секущие

Посмотрим на две дуги, которые лежат внутри угла : дуги  и . Мы знаем, как выразить через дуги вписанные углы, которые на них опираются. Поэтому попробуем выразить угол  через вписанные углы. Для этого соединим точки  и . Получим два вписанных угла  и  (см. рис. 10).

Рис. 10. Соединили точки  и , получили два вписанных угла  и

Угол  опирается на дугу , угол  опирается на дугу . Эти углы равны половине соответствующих дуг. И при этом исследуемый угол  выражается через эти два угла.

В самом деле, угол  является внешним для треугольника , значит:

Тогда:

Вспомним теперь, что эти углы равны половинам своих дуг:

Таким образом, угол  равен полуразности дуг, заключенных внутри угла.

 

 

Свойство вписанного четырехугольника

 

 

При изучении новых объектов мы обычно формулируем два типа утверждений: свойства (то, что мы всегда можем сказать об этом объекте) и признаки (благодаря чему мы можем узнать именно этот объект).

 

Например: у каждой лошади есть голова. Это свойство лошадей или их необходимый признак. Но назвать признаком наличие головы нельзя: она есть у людей, у собак и т. д.

Умение читать книги – достаточный признак человека (если кто-то умеет читать, то это точно человек). Если признак работает в обе стороны, то он так и называется – необходимым и достаточным. Молния – необходимый и достаточный признак грозы (если гроза, то обязательно есть молния, но если видим молнию, значит, точно гроза).

Итак, ранее мы убедились, что, в отличие от треугольников, далеко не все четырехугольники можно вписать в окружность (и, соответственно, любой четырехугольник можно вписать в окружность). Например, квадрат можно вписать в окружность, а ромб, не являющийся квадратом, нельзя.

Оказалось, что можно сформулировать признаки вписанного и описанного четырехугольников (т. е. то свойство, которым обладают только такие четырехугольники и не обладают остальные).

Свойство вписанного четырехугольника: если четырехугольник вписан в окружность, то суммы противоположных углов в нем равны  (см. рис. 11).

Рис. 11. Если четырехугольник вписан в окружность, то суммы противоположных углов в нем равны

 

Признак вписанного четырехугольника

 

 

Доказать это свойство оказалось несложно (Окружность и многоугольники). Но оно не поможет нам, если мы не докажем, что у любого другого не вписанного четырехугольника суммы противоположных углов не равны . Вспомните пример с лошадью: отсутствие головы точно говорит нам, что данный объект не лошадь, но вот ее наличие еще ничего не говорит.

 

Итак, в свое время мы доказали свойство, а обратное утверждение приняли на веру. Сейчас у нас есть все инструменты, чтобы вернуться и доказать признак вписанного четырехугольника.

Теорема

Если в четырехугольнике сумма противоположных углов равна , то он вписанный (вокруг него можно описать окружность).

Доказательство

Рассмотрим четырехугольник , у которого углы  и  в сумме равны  (см. рис. 12).

Рис. 12. Четырехугольник , где сумма углов  и  равна

Вокруг любого треугольника можно описать окружность. Опишем ее вокруг треугольника  (см. рис. 13) и докажем, что она пройдет обязательно и через точку .

Рис. 13. Вокруг треугольника  описана окружность

Будем доказывать методом от противного. Предположим, что окружность не проходит через точку . Тогда точка  может оказаться внутри или вне окружности.

Рассмотрим случай, когда она находится внутри (см. рис. 13).

Рис. 13. Точка  находится внутри окружности

Продлим стороны до пересечения с окружностью:

Но тогда он больше, чем просто половина дуги :

При этом угол  вписанный и равен половине дуги, на которую опирается:

Если к обеим частям неравенства прибавить равные выражения, то получим эквивалентное неравенство:

Таким образом:

Но это противоречит условию. Таким образом, точка  не может лежать внутри окружности.

Самостоятельно рассмотрите случай, когда точка  лежит вне окружности, и докажите, что это невозможно. Там рассуждения совершенно аналогичны (изменится только знак неравенства).

Доказано.

Итак, равенство суммы противоположных углов  является теперь необходимым и достаточным признаком вписанного четырехугольника.

 

Нахождение значений тригонометрических функций

 

 

Мы с вами успели убедиться, что тригонометрические функции очень удобный инструмент для решения геометрических задач. Во многом это связано с тем, что значение тригонометрической функции зависит только от величины угла и не зависит от типа треугольника.

 

В произвольном треугольнике есть три угла и для каждого угла можно посчитать значение синуса, косинуса, тангенса и котангенса (или указать, что тангенс не определен – для прямого угла).

Мы нашли значения тригонометрических функций для некоторых углов. Обычно их сводят в такую таблицу (см. рис. 15).

Рис. 15. Таблица значений основных тригонометрических функций

Запоминать ее не обязательно (хотя при решении большого количества задач вы это сделаете непроизвольно), лучше помнить, как можно их получить (Тригонометрические функции произвольных углов. Теоремы синусов и косинусов).

Значения разных тригонометрических функций для одного угла связаны между собой основными тригонометрическими тождествами:

Зная значение одной тригонометрической функции угла, можно найти все остальные.

 

Задача 1. Найти неизвестные тригонометрические функции угла, если:

Решение

Можно, конечно, найти угол, зная, что угол лежит в интервале от  до , а его косинус равен  (см. рис. 16).

Рис. 16. Иллюстрация к задаче 1

Зная определение тригонометрической функции (косинус – абсцисса соответствующей точки на окружности) (см. рис. 17), несложно получить, что:

Т. е. .

Рис. 17. Иллюстрация к задаче 1

Но мы рассмотрим общий способ, ведь нам не обязательно «повезет» с табличным значением тригонометрической функции.

Чтобы найти синус, зная, косинус, воспользуемся тождеством, которое их связывает, а именно:

Выразим из него синус:

Мы получили два возможных значения синуса. Как быть? Если бы у нас не было больше никакой информации об угле, то на этом нам бы пришлось остановиться. Действительно, при данном значении косинуса у синуса может быть два значения (вертикальная прямая пересекает окружность в двух точках с противоположными ординатами) (см. рис. 18).

Рис. 18. Иллюстрация к задаче 1

Но у нас есть дополнительная информация: угол лежит в четвертой четверти (см. рис. 19).

Рис. 19. Иллюстрация к задаче 1

В этой четверти у всех точек окружности ордината отрицательная, значит, синус будет иметь знак «минус»:

Осталось найти тангенс и котангенс, зная синус и косинус:

Ответ: .

Обратите внимание: если бы в условии речь шла об угле треугольника, то мы бы сами ограничили величину угла: , и сказали бы, что т. к. его косинус положительный, то угол лежит в первой четверти (тогда и все остальные тригонометрические функции данного угла были бы положительными).

 

Задача 2. Найти неизвестные тригонометрические функции угла, если:

Решение

Мы знаем, что, по определению, синус угла – это ордината соответствующей точки окружности. Видим, что окружность пересекается горизонтальной прямой  в двух точках (см. рис. 20).

Рис. 20. Иллюстрация к задаче 2

Значит, условию  соответствуют два угла:  в первой четверти и  во второй (больше никакой информации об угле, в отличие от предыдущей задачи, нет).

Соответственно, у нас будут два разных значения косинуса. По рисунку видно, что по модулю эти значения равны и отличаются только знаком (см. рис. 21).

Рис. 21. Иллюстрация к задаче 2

Снова воспользуемся основным тригонометрическим тождеством:

Тогда:

В такой постановке мы бы должны были получить и два возможных значения тангенса и котангенса (с точностью до знака). Давайте добавим информацию о величине угла, чтобы получить однозначный ответ: пусть  (или, по-другому, угол находится во второй четверти).

Косинус, который ему соответствует, имеет знак «минус» (т. к. абсциссы точек окружности во второй четверти отрицательные):

Осталось найти тангенс и котангенс:

Ответ: .

 

Теоремы синусов и косинусов

 

 

Кроме непосредственно тригонометрических функций, у нас есть еще два очень мощных инструмента, которые помогают нам находить недостающие элементы треугольников: теорема синусов и теорема косинусов. Вспомним обе теоремы.

 

Теорема синусов: отношение сторон к синусам противолежащих углов постоянно для данного треугольника и равно диаметру описанной окружности:

Возьмем первую часть этого утверждения:

Зная три элемента в этой пропорции, мы можем найти четвертый.

Например, если мы знаем две стороны и один противолежащий угол, то можем найти второй угол:

Или знаем одну сторону и два угла, найдем вторую сторону:

Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

С помощью этой теоремы мы находим третью сторону, если знаем две стороны и угол между ними. Или, зная три стороны, можно найти каждый угол, точнее – его косинус.

Задача 3. Выяснить тип треугольника (остроугольный, прямоугольный, тупоугольный), если его стороны равны:

Решение

Тип треугольника определяется его наибольшим углом, а наибольший угол лежит напротив наибольшей стороны (см. рис. 22). Зная три стороны, мы можем найти угол, используя теорему косинусов.

Рис. 22. Иллюстрация к задаче 3

1. Стороны треугольника равны , значит, наибольший угол лежит напротив стороны . По теореме косинусов имеем:

Выразим косинус:

Косинус положительный, соответствующий ему угол треугольника может быть только острым (у тупых углов косинус отрицательный – соответствующие им точки окружности расположены во второй четверти) (см. рис. 23). Т. е. наибольший угол треугольника острый, остальные тем более острые. Треугольник остроугольный.

Рис. 23. Иллюстрация к задаче 3

Остальные два случая решаются аналогично. Выполните их самостоятельно. У вас должно получиться, что во втором случае косинус наибольшего треугольника равен  (треугольник прямоугольный), а в третьем – косинус угла отрицательный (треугольник тупоугольный).

Ответ: остроугольный, прямоугольный, тупоугольный.

 

Свойство биссектрисы угла треугольника

 

 

Биссектриса делит угол пополам – это ее определение. Но, оказывается, противоположную сторону треугольника она тоже делит всегда не пополам, но в определенном соотношении.

 

Биссектриса  треугольника  делит противоположную сторону на два отрезка. Обозначим их как  и  (см. рис. 24). Углы , и, конечно, .

Рис. 24. Биссектриса  треугольника  делит противоположную сторону на отрезки  и

Кроме того, углы  и  смежные (см. рис. 25):

Рис. 25. Смежные углы  и

Но у таких углов синусы тоже равны (в самом деле, на единичной окружности двум таким углам соответствует одно и то же значение синуса) (см. рис. 26).

Рис. 26. На единичной окружности углам  и  соответствует одно и то же значение синуса

Тогда имеем:

Применим к двум треугольникам теоремы синусов. Для треугольника  имеем:

Для треугольника  имеем:

Но правые части в обеих пропорциях равны, следовательно, равны и левые:

Или:

Таким образом, мы доказали, что биссектриса угла треугольника делит его противоположную сторону на отрезки, пропорциональные прилежащим сторонам. Этот факт сам по себе полезный инструмент, который мы будем использовать для решения различных задач.

 

Решение практической задачи с использованием теоремы синусов

 

 

Задача 4. На горе находится башня, высота которой равна  м. Некоторый предмет  у подножия горы наблюдают сначала с вершины  башни под углом  к горизонту, а потом с ее основания  под углом . Найдите высоту  горы (см. рис. 27).

 

 

Рис. 27. Иллюстрация к задаче 4

Решение.

Рассмотрим прямоугольный треугольник  (см. рис. 28):

Рис. 28. Иллюстрация к задаче 4

Тогда:

Теперь рассмотрим треугольник . В нем мы знаем:

Тогда:

Используем теорему синусов:

 м

Ответ:  м.

Чтобы потренироваться использовать рассмотренные инструменты для решения других задач, используйте наши тренажеры и тесты. Чем больше вы практикуетесь, тем легче вам будет «увидеть», какой инструмент лучше всего применить для решения той или иной задачи и как именно это сделать.

 

Список литературы

  1. Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.

  2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 8 класс. Учебник. – М.: «Просвещение», 2018.

  3. Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия. 8 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

  1. Интернет-портал tmath.ru (Источник)

  2. Интернет-портал cleverstudents.ru (Источник)

  3. Интернет-портал схемо.рф (Источник)

 

Домашнее задание

  1. Доказать, что если в параллелограмм можно вписать окружность и можно описать около него окружность, то этот параллелограмм – квадрат.

  2. Найти угол между лучом  и положительной полуосью , если точка  имеет координаты .

  3. В равнобедренной трапеции меньшее основание равно боковой стороне, большее основание равно  см, а угол при основании равен . Найти периметр трапеции.

 

Тесты по геометрии для 8 класса онлайн



Окружность



  • Прямоугольник. 8 класс


    07. 10.2021
    2020

    Тест для контроля знаний учащихся по теме «Прямоугольник». Геометрия 8 класс.



  • Четырехугольники и их свойства. 8 класс.


    06.11.2020
    2296

    Тест предназначен для проверки теоретических знаний по теме » Четырёхугольники и их свойства.» 8 класс.Тест ориентирован на учебник «Геометрия 7-9 классы » Л.С.Атанасян и др. В тесте 44 вопроса. Для ответа случайным образом выбирается 20 вопросов. 



  • ВПР математика 8 класс


    04.05.2020
    4275
    0

    Назначение ВПР по математике — оценить уровень общеобразовательной подготовки обучающихся 8 класса. 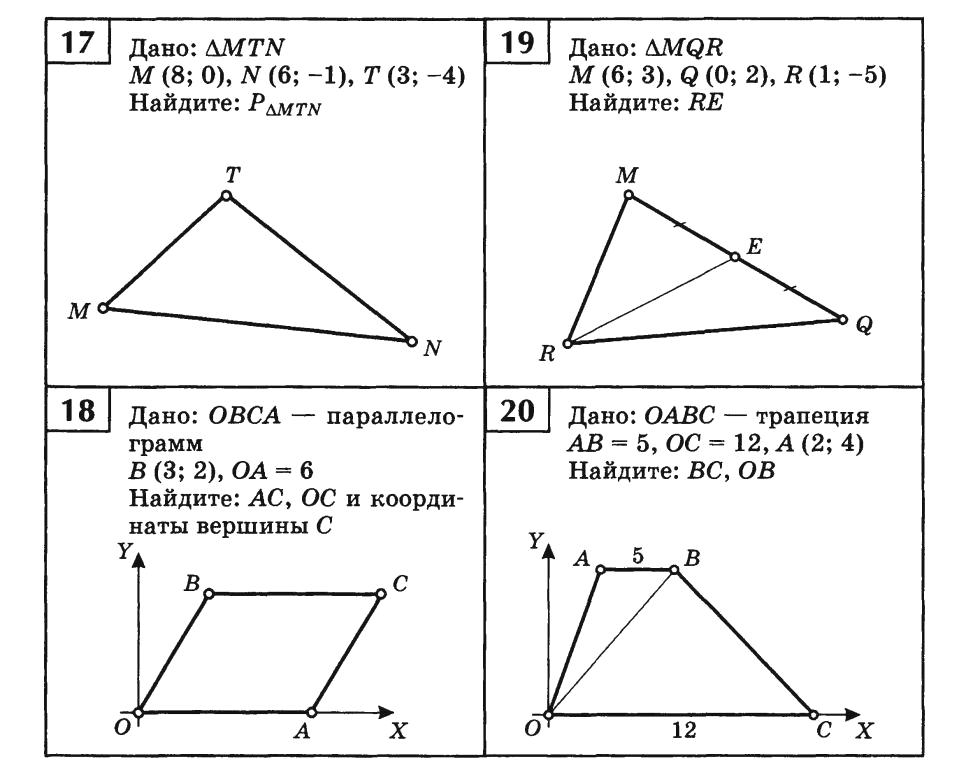В работе 19 заданий. 14 заданий курса алгебре и 5 заданий курса геометрии. Максимальное количество баллов 25.



  • ГЕОМЕТРИЯ выбор верных утверждений 8 класс


    12.04.2021
    4536
    0

    Тест содержит 30 заданий. Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста. Время ОГРАНИЧЕНО 20 минут.



  • ВПР-2020. 8 класс. Математика. Тест 1


    07.02.2020
    6082
    0

    Тест 1 — подготовка к Всероссийской проверочной работе по математике. 8 класс.



  • Итоговый тест 8 класс геометрия ТЕОРИЯ


    08.05.2021
    3394
    0

    Тест содержит 30 заданий. Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.



  • Геометрия 8 класс. Окружность.


    22.04.2020
    227

    Тест по теме: «Окружность». Теоретические вопросы по данной теме.



  • 8 класс Геометрия


    15. 03.2019
    29286

    Данный тест предназначен для определения знания предмета «Геометрия» за курс 8 класса.



  • Входной тест Геометрия 8


    23.07.2020
    189
    0

    Входной тест по геометрии, нацеленный на проверку остаточных знаний по геометрии в начале учебного года, проверяет программу по геометрии 7 класса.



  • Векторы на плоскости Основные понятия.


    31.10.2021
    899
    0

    Тест содержит вопросы на основные определения, связанные с векторами, а также на действия с векторами на плоскости.



  • 8 класс Глава 5 Четырёхугольники ТЕОРИЯ


    09.05.2021
    2527
    0

    Тест содержит 20 заданий. Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.



  • Теорема Пифагора (домашнее задание №1)


    22.11.2021
    368
    0

    Домашнее задание в тестовой форме. В тесте 5 вопросов.
    Система оценивания:
    «5» — 5 верно выполненных заданий (95%)
    «4» — 4 верно выполненных заданий (75%)
    «3» — 3 верно выполненных заданий (55%)
    «2» —  2 и менее верно выполненных заданий (меньше 55%)



  • 8 класс.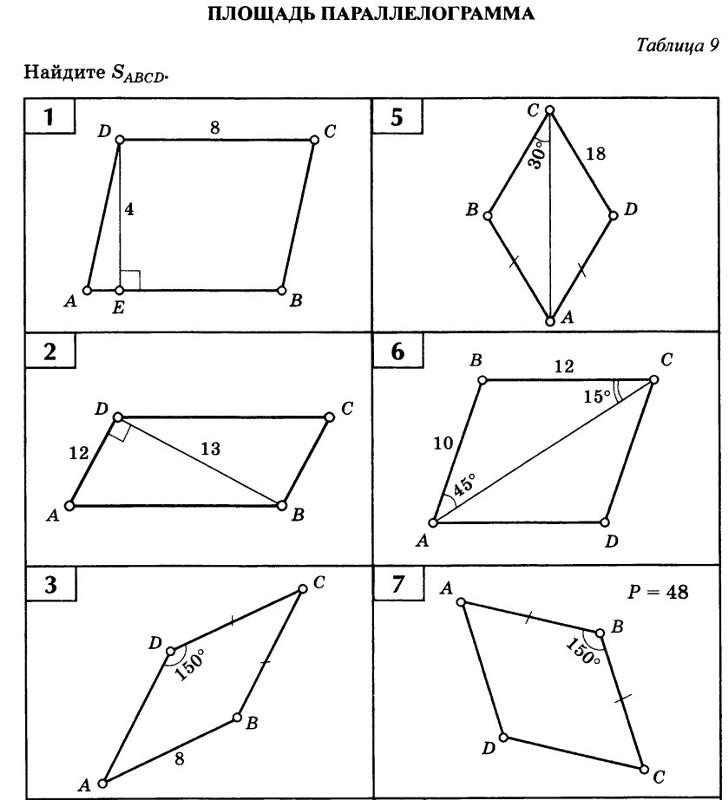

    Геометрия. Соотношения в прямоугольном треугольнике


    04.04.2015
    8537

    Тест предназначен для учащихся 8 классов при отработке навыков решения задач по теме «Соотношения в прямоугольном треугольнике».



  • Площади четырёхугольников. 8 класс.


    07.11.2020
    714
    0

    Тест предназначен для проверки теоретических знаний по теме » Площади  четырёхугольников», 8 класс.Тест ориентирован на учебник «Геометрия 7-9 классы » Л.С.Атанасян и др. В тесте 27 вопросов. Для ответа случайным образом выбирается 15 вопросов. Может быть использован для подготовки к ОГЭ по математике.



  • Тест № 1.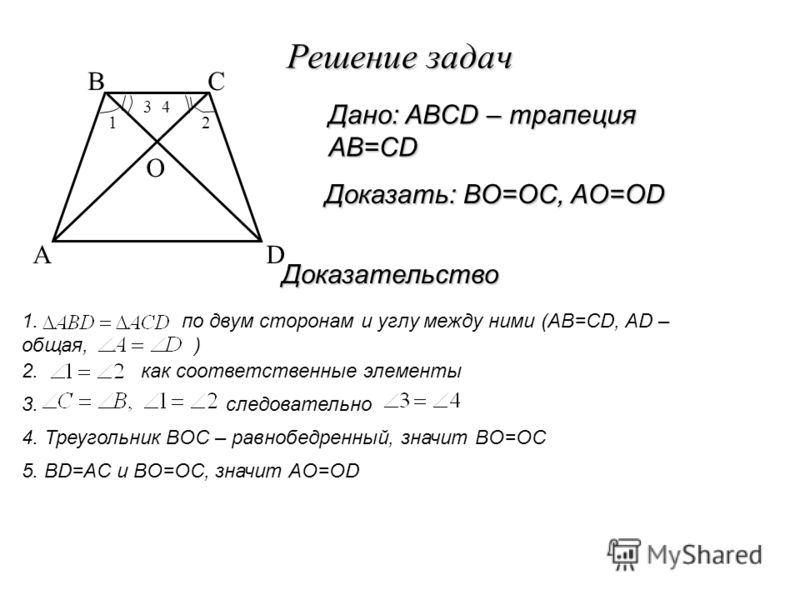

    Тема «Окружность»


    10.09.2022
    4
    0

    Тест представляет собой теоретические вопросы по теме: «Окружность». Тест предназначен для определения предметных результатов учащихся 8 класса по теме.



  • 8 класс. Геометрия. Центральные и вписанные углы.


    25.07.2017
    19686

    Тест предназначен для учащихся 8 классов при отработке навыков решения задач по теме «Центральные и вписанные углы».



  • Определение подобных треугольников. 8 класс


    20.01.2020
    8705
    0

    Самостоятельная работа в форме теста по теме: «Определение подобных треугольников»



  • Итоговая контрольная работа по математике за курс 8 класса.

    8Б класс


    08.05.2020
    275
    0

    Итоговая работа соответствует матералам 8 класса, изучаемым по учебникам Алгебра 8 клаас (Колягин) и Геометрия 8 класс (Ататнасян). 
    Работа содержит 10 заданий (6 по алгебре и 4 по геометрии). На выполнение работы отводится 1час 30 минут.
    Количество прохождений: 1.



  • Итоговый тест 8 класс геометрия ЗАДАЧИ


    09.05.2021
    2100
    0

    Тест содержит 20 заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.



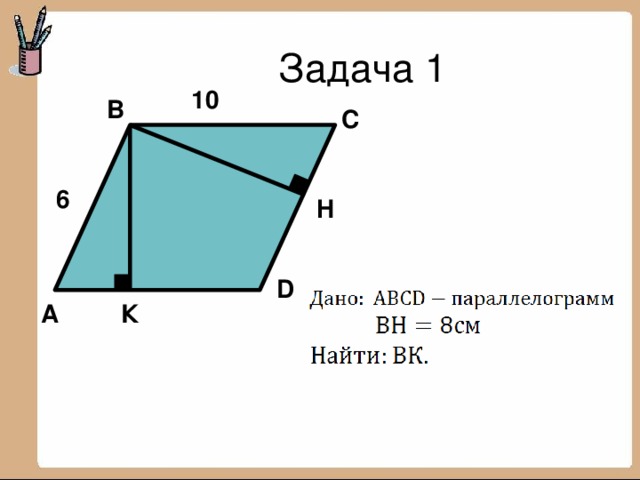
  • Признаки подобия треугольников. 8 класс


    07. 02.2022
    1560

    Тест «Признаки подобия треугольников» состоит из трех вопросов (задач), выпадающих случайным образом из общего списка.
     



  • ВПР-2020. 8 класс. Математика. Тест 2


    13.02.2020
    384
    0

    Тест 2 — подготовка к Всероссийской проверочной работе по математике. 8 класс.



  • Тест по заданию №17 (ОГЭ-2020 по математике) по теме: Решение геометрических задач по теме «Окружность и круг».


    16.02.2020
    865
    0

    Тест содержит десять тестовых заданий по основным прототипам задания №17 (ОГЭ 2020). 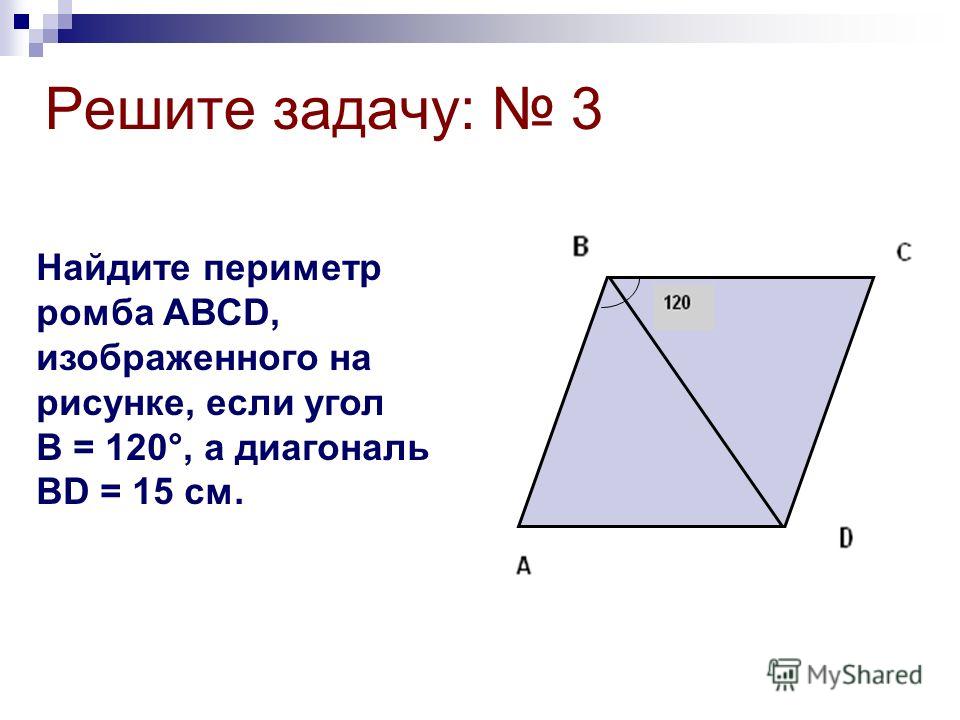К каждому номеру ответом является число (без единиц измерения).



  • ОГЭ 8 класс математика


    29.04.2020
    590
    0

    Вариант ОГЭ математика 2020 год. Содержит 25 демонстрационных вариантов из сборника подготовки к ОГЭ, адаптированных к программе 8 класса.



  • Площадь многоугольника.


    20.02.2021
    38
    0

    Проверочная работа по теме «Площадь многоугольника» предназначена для проверки знаний по указанной теме. Работа составлена на основе прототипов заданий ОГЭ по математике.



  • Формула Пика.

    Задачи на клетчатой бумаге.


    24.11.2021
    77
    0

    Данный тест будет полезен педагогу для проверки знаний по теме «Площади многоугольников» и ребятам для закрепления материала.



  • Практические задачи на тему: «Подобие треугольников».


    03.02.2022
    620
    0

    Тестовые задания, проверяющие умение применять подобие треугольников для решения практических задач.



  • Площадь. 8 класс


    14.12.2019
    12273

    Тест предназначен для повторения темы «Площадь». 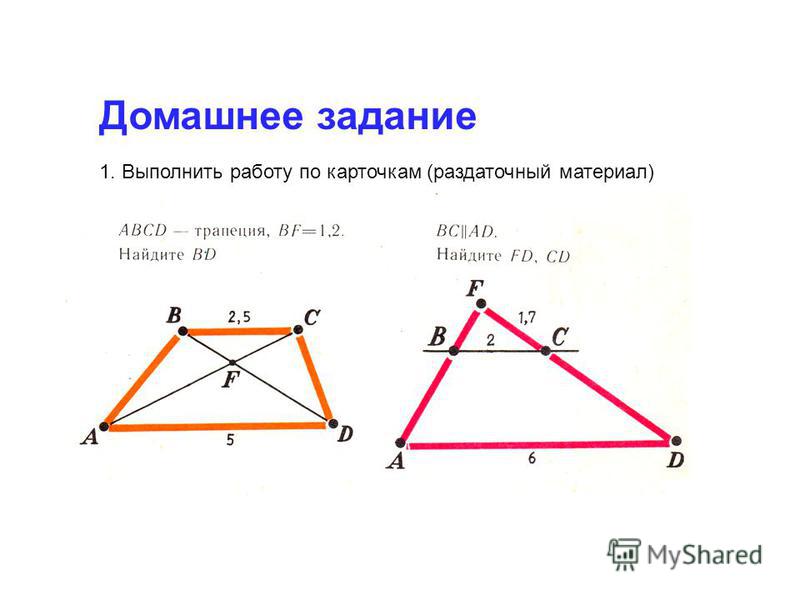Базовый уровень сложности. 5 заданий. Время выполнения 15 минут. 



  • Вписанные и центральные углы. 8 класс. урок 2. Повторение.


    13.04.2020
    140
    0

    Тетс составлен к теме «Вписанные и описанные углы» по учебнику Л.С.Атаносяна геометрия 8 класс.



  • свойство хорд и углов, образованных касательными и хордами


    14.04.2020
    221
    0

    Тест предназначен ддля первичного закрепления на уроке по теме «Свойство хорд окружности». Все задачи решаются устно с последующей самопроверкой



  • СООТНОШЕНИЯ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ.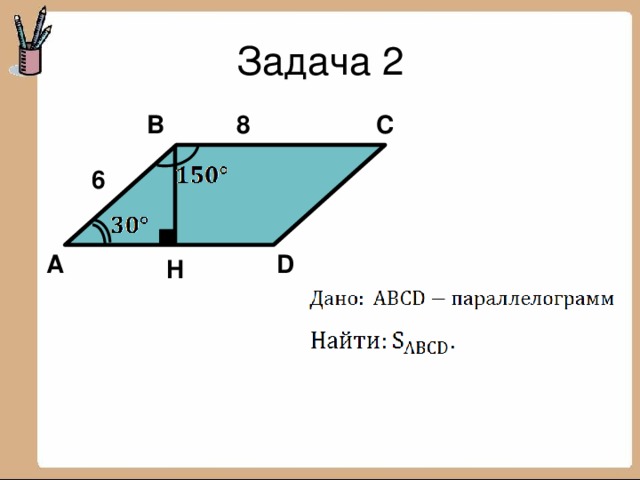

    ТЕОРЕМА ПИФАГОРА


    16.04.2020
    3886
    0

    Тест по темам: «Соотношения в прямоугольном треугольника. Теорема Пифагора» для обучающихся в 8 классе.



  • 8 класс. Центральные и вписанные углы


    20.04.2020
    556
    0

    Для успешного прохождения теста повторите, что такое центральные и вписанные углы, свойства биссектрисы угла. Время прохождения теста — 30 минут.  Удачи!



  • МД «Свойство биссектрисы угла»


    23.04.2020
    739
    0

    Решение задач по готовым чертежам по теме «Биссектриса угла» геометрия 8 класс по учебнику Атоносяна. 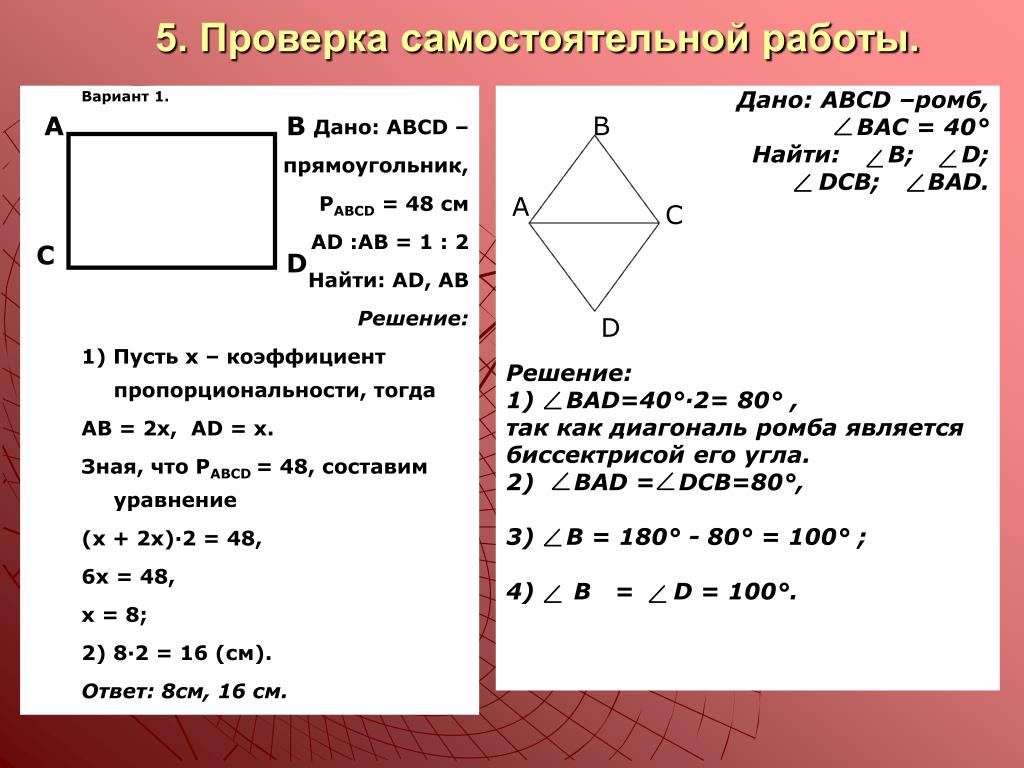Проводится в начале урока «Серединный перпендикуляр»



  • Вариант 2 Свойства биссектрисы угла и серединного перпендикуляра к отрезку


    24.04.2020
    643
    0

    Тест ориентирован на учебник Л.С. Атанасяна и др. «Геометрия. 7 — 9 классы». Направлен на первичный контроль текущего усвоения материала. Задания проверяют понимание новой терминологии, распознавание видов фигур и их свойств. 



  • Площадь многоугольника.


    24.04.2020
    184
    0

    Тест предназначен для проверки знаний  по геометрии по теме «Площадь».



  • Итоговый тест по геометрии, тема: «Решение треугольника, подобные треугольники»


    27. 04.2020
    283
    0

    Проверочный тест к теме «Решение треугольников и подобные треугольники»



  • Центральные и вписанные углы


    29.04.2020
    5680
    0

    Тест позволяет закрепить тему «Центральные и вписанные углы». Тест содержит две задачи из кзаменационных материалов ОГЭ.



  • Центральный и вписанный углы


    11.05.2020
    23
    0

    Тест предназначен для самостоятельной работы с учебником. Задания составлены так, чтобы каждый участник мог в должной мере оценить знания по предмету, причем участвовать можно как группой, так и индивидуально.



  • Промежуточная аттестация


    11.05.2020
    178
    0

    Данный тест предназначен для определения знания предмета «Геометрия» за курс 8 класса.



  • окружность_ геометрия_8класс


    21.05.2020
    539
    0

    Геометрия 8 класс. Тема Окружность. Учебник Атанасяна Л.С. и др. Итоговый тест



  • Центральные и вписанные углы


    24.11.2020
    111
    0

    Тест составлен на основе учебника по геометрии за 8 класс авторы Мерзляк А. Г., Полонский В. Б., Якир М. С.  Параграф девять. Глава один



  • Контрольная работа за І семестр по геометрии 8 класс


    11.12.2020
    14
    0

    Контрольная работа за I семестр по геометрии состоит из 10 заданий.
    с 1 по 6 — тестовые задания (от 1 до 3 правильных),
    с 7 по 8 — установить соответствие,
    9 — расположить в правильной последовательности,
    10 — указать только ответ (число).



  • Неравенство треугольника


    17.12.2020
    61
    0

    Тест предназначен для учащихся средней школы  для проверки уровня знаний по  теме «Неравенство треугольника».



  • Пропорциональные отрезки. Подобные треугольники.


    07.02.2021
    61
    0

    Тест  составлен по вопросам к учебнику А.Г. Мерзляк, В.Б Полонский. В тесте содержатся вопросы о свойстве биссектрисы треугольника, свойстве касательной и секущей, свойстве отрезков пересекающихся хорд.



  • Углы, образованные хордами, секущими и касательными


    14.03.2021
    306
    0

    Тренировочный тест предназначен для учащихся 8-ых классов при отработке навыков решения задач по теме «Углы, образованные хордами, секущими и касательными».



  • Окружность (итоговый тест)


    14. 03.2021
    1872
    0

    Тренировочный тест предназначен для учащихся 8-ых классов при отработке навыков решения задач по теме «Окружность».



  • 8 класс Глава 8 Окружность ТЕОРИЯ


    08.05.2021
    773
    0

    Тест содержит 20 заданий. Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.



  • 8 класс Глава 6 Площадь ТЕОРИЯ


    09.05.2021
    249
    0

    Тест содержит 20 заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.



  • 8 класс Глава 7 Подобные треугольники ТЕОРИЯ


    09.05.2021
    915
    0

    Тест содержит 20 заданий. Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.



  • геометрия к ОГЭ


    09.08.2021
    119
    0

    Данный тест составлен на основе вопросов ОГЭ по теме «Углы» по курсу геометрии 8 класса. Он поможет проверит основные знания.



  • Теорема Пифагора


    10. 11.2021
    113
    0

    Тест по геометрии по теме «Теорема Пифагора» 8 класс по учебнику Погорелова



  • теорема Пифагора


    10.11.2021
    250
    0

    Тест по геометрии 8 класс по учебнику Погорелов по закреплению теорема Пифагора



  • Теорема Пифагора


    10.11.2021
    1269

    тест по геометрии  8 класс , учебник Погорелов , по теме : Теорема Пифагора



  • Тест по теме «Четырехугольники» 8 класс


    25. 11.2021
    66
    0

    Тест предназначен для учащихся 8 класса для проверки и закрепления знаний по теме «Четырехугольники»



  • Теорема Пифагора


    04.12.2021
    1154
    0

    Тест содержит 7 вопросов по геометрии,тема теорема Пифагора, предназначен для учеников 8 класса. В тесте 2 задания с выбором ответа и 5 заданий с вводом числового ответа. Тест содержит простые задачи на умение находить гипотенузу и катет прямоугольного треугольника,по известным 2 сторонам. В нем есть  более сложные задачи с использованием теоремы Пифагора и других формул и теорем геометрии, например, формул площадей и периметра геометрических фигур. В заданиях кроме прямоугольного треугольника надо знать и уметь применять свойства равнобедренного треугольника, прямоугольника, ромба. Вычислять площадь прямоугольника, прямоугольного треугольника, ромба. Уметь вычислять площадь ромба через диагонали.



  • Тест по теме «Соотношения между сторонами и углами прямоугольного треугольника»


    02.02.2022
    1301
    0

    Данный тест проверяет знания по теме «Соотношения между сторонами и углами прямоугольного треугольника», геометрия, 8 класс



  • Викторина о тригонометрии


    21.02.2022
    391
    0

    Викторина о разделе математики, изучающем функции угла: синус, косинус и т.п. В рамках школьной программы.



  • Тест № 2 по теме «Окружность»


    10. 09.2022
    5
    0

    Тест содержит пятнадцать практических заданий по теме «Окружность» и предназначен для определения предметных результатов учащихся 8 класса.

Вопросы и задачи к публичному зачёту по геометрии 8 класс

Вопросы к публичному зачёту по геометрии 8 класс.

Вопрос №1.

1. Определение многоугольника. Вершины, стороны, диагонали и периметр многоугольника. Формула суммы углов выпуклого многоугольника.

2. Определение и свойства параллелограмма.

3. Определение и свойства прямоугольника.

4. Определение и свойства ромба.

5. Определение трапеции. Виды трапеций.

6. Определение подобных треугольников. Признаки подобия треугольников.

7. Синус, косинус и тангенс острого угла прямоугольного треугольника.

8.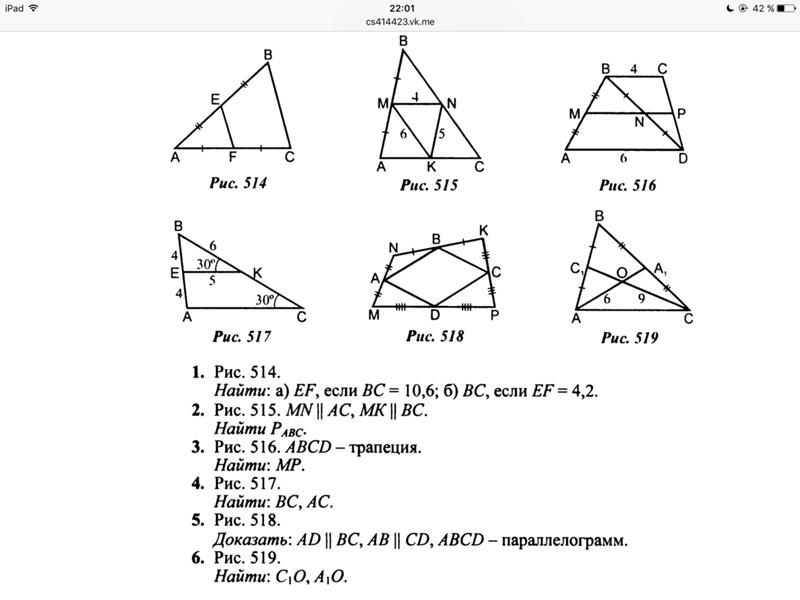 Значение синуса, косинуса и тангенса углов 30 ,45 ,60 .

9. Определение секущей и касательной к окружности.

10. Определение вписанного и центрального углов окружности.

11. Определение серединного перпендикуляра к отрезку. Свойство серединного перпендикуляра.
12. Определение окружности, вписанной в многоугольник. Многоугольник, описанный около окружности.

Свойство описанного четырехугольника.

13. Определение окружности, описанной около многоугольника. Многоугольник, вписанный в окружность. Свойства четырехугольника, вписанного в окружность.

14. Окружность, вписанная в треугольник. Окружность, описанная около треугольника. Нахождение центров этих окружностей.

15. Свойство отрезков пересекающихся хорд.

Вопрос №2.

1. Доказать свойства противоположных сторон и углов параллелограмма.

2. Доказать свойство диагоналей параллелограмма.

3.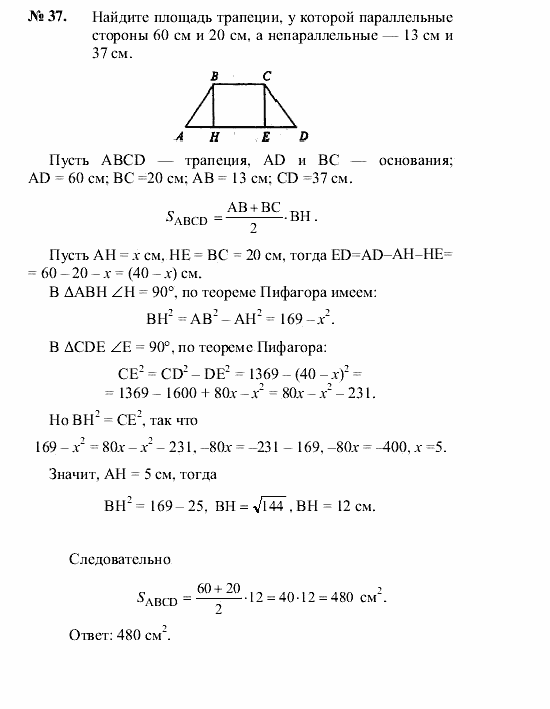 Доказать признак параллелограмма через равенство и параллельность

двух противоположных сторон.

4. Доказать признак параллелограмма (по точке пересечения диагоналей).

5. Свойство углов при основании равнобедренной трапеции.

6. Доказать свойство диагоналей прямоугольника.

7. Доказать свойства диагоналей ромба.

8. Вывод формулы площади треугольника. Следствия. Формула Герона (без доказательства).

9. Доказать теорему Пифагора.

10. Доказать теорему о средней линии треугольника.

11. Доказать свойство отрезков касательных, проведенных к окружности из одной точки.

12. Доказать теорему о вписанном угле (любой частный случай).

13. Доказать свойство биссектрисы угла.

14. Доказать свойство медиан треугольника.

15. Свойство отрезков пересекающихся хорд.

Задачи к публичному зачёту по геометрии 8 класс.

Задача №1.

1. Ра­ди­ус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду AC в точке D и пер­пен­ди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ра­ди­ус

о круж­но­сти равен 5 см.

2 . Про­ек­тор пол­но­стью осве­ща­ет экран A вы­со­той 80 см, рас­по­ло­жен­ный на рас­сто­я­нии 250 см от про­ек­то­ра. На каком наи­мень­шем рас­сто­я­нии (в сан­ти­мет­рах) от про­ек­то­ра нужно рас­по­ло­жить экран B вы­со­той 160 см, чтобы он был пол­но­стью освещён, если на­строй­ки про­ек­то­ра оста­ют­ся не­из­мен­ны­ми?

3. Най­ди­те ве­ли­чи­ну (в гра­ду­сах) впи­сан­но­го угла α, опи­ра­ю­ще­го­ся на хорду  AB, рав­ную ра­ди­у­су окруж­но­сти.

4. Два па­ро­хо­да вышли из порта, сле­дуя один на север, дру­гой на запад. Ско­ро­сти их равны со­от­вет­ствен­но 15 км/ч и 20 км/ч. Какое рас­сто­я­ние (в ки­ло­мет­рах) будет между ними через 2 часа?

5 .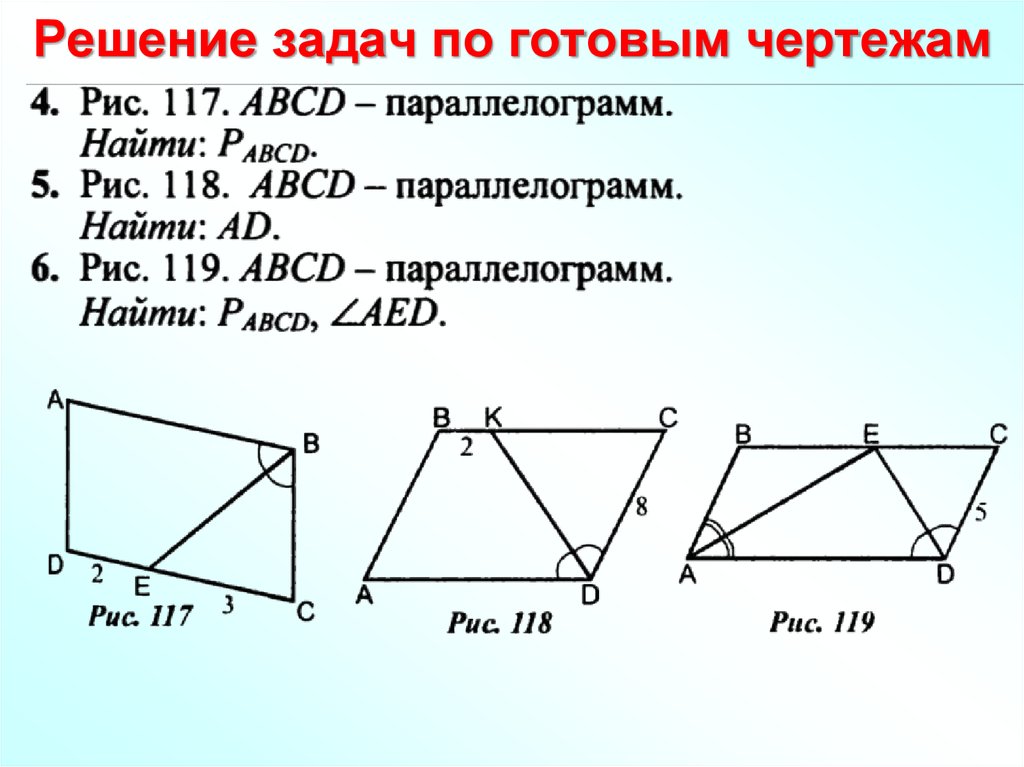 От стол­ба вы­со­той 9 м к дому на­тя­нут про­вод, ко­то­рый кре­пит­ся на вы­со­те 3 м от земли (см. ри­су­нок). Рас­сто­я­ние от дома до стол­ба 8 м. Вы­чис­ли­те длину про­во­да.

6. В рав­но­сто­рон­нем тре­уголь­ни­ке  ABC  ме­ди­а­ны  BK  и  AM  пе­ре­се­ка­ют­ся в точке O. Най­ди­те .

7 . Най­ди­те гра­дус­ную меру ∠MON, если из­вест­но, NP — диа­метр, а гра­дус­ная мера ∠MNP равна 18°.

8. У тре­уголь­ни­ка со сто­ро­на­ми 16 и 2 про­ве­де­ны вы­со­ты к этим сто­ро­нам. Вы­со­та, про­ведённая к пер­вой сто­ро­не, равна 1. Чему равна вы­со­та, про­ведённая ко вто­рой сто­ро­не?

9. В 60 м одна от дру­гой рас­тут две сосны. Вы­со­та одной 31 м, а дру­гой — 6 м. Най­ди­те рас­сто­я­ние (в мет­рах) между их вер­хуш­ка­ми.

10. Че­ло­век ро­стом 1,7 м стоит на рас­сто­я­нии 8 шагов от стол­ба, на ко­то­ром висит фо­нарь. Тень че­ло­ве­ка равна че­ты­рем шагам. На какой вы­со­те (в метрах) рас­по­ло­жен фо­нарь?

1 1. К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO. Най­ди­те ра­ди­ус окруж­но­сти, если AB = 12 см, AO = 13 см.

12. Най­ди­те пе­ри­метр пря­мо­уголь­но­го участ­ка земли, пло­щадь ко­то­ро­го равна 800 м2 и одна сто­ро­на в 2 раза боль­ше дру­гой. Ответ дайте в мет­рах.

13. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 10, а угол, ле­жа­щий на­про­тив него, равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

14. В вы­пук­лом че­ты­рех­уголь­ни­ке ABCD , , , . Най­ди­те угол A. Ответ дайте в гра­ду­сах.

15. Сто­ро­на ромба равна 34, а ост­рый угол равен 60° . Вы­со­та ромба, опу­щен­ная из вер­ши­ны ту­по­го угла, делит сто­ро­ну на два от­рез­ка. Ка­ко­вы длины этих от­рез­ков?

Задача №2.

1. Пе­ри­метр пря­мо­уголь­ни­ка равен 56, а диа­го­наль равна 27. Най­ди­те пло­щадь это пря­мо­уголь­ни­ка.

2 . Най­ди­те угол АСО, если его сто­ро­на СА ка­са­ет­ся окруж­но­сти, О — центр окруж­но­сти, а дуга AD окруж­но­сти, за­ключённая внут­ри этого угла, равна 100°.

3. Пря­мая, па­рал­лель­ная ос­но­ва­ни­ям и тра­пе­ции , про­хо­дит через точку пе­ре­се­че­ния диа­го­на­лей тра­пе­ции и пе­ре­се­ка­ет её бо­ко­вые сто­ро­ны и в точ­ках и со­от­вет­ствен­но. Най­ди­те длину от­рез­ка , если см, см.

4. В тре­уголь­ни­ке АВС углы А и С равны 20° и 60° со­от­вет­ствен­но. Най­ди­те угол между вы­со­той ВН и бис­сек­три­сой BD.

5. Отрезки AB и DC лежат на па­рал­лель­ных прямых, а от­рез­ки AC и BD пе­ре­се­ка­ют­ся в точке M. Най­ди­те MC, если AB = 16, DC = 24, AC = 25 .

6. Окруж­ность с цен­тром на сто­ро­не AC тре­уголь­ни­ка ABC про­хо­дит через вер­ши­ну C и ка­са­ет­ся пря­мой AB в точке B. Най­ди­те AC, если диа­метр окруж­но­сти равен 7,5, а AB = 2.

7. В тре­уголь­ни­ке ABC от­ме­че­ны се­ре­ди­ны M и N сто­рон BC и AC соответственно. Пло­щадь треугольника CNM равна 57.

Най­ди­те пло­щадь четырёхугольника ABMN.

8 . Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окруж­но­сти, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 8.

9. Окруж­ность пе­ре­се­ка­ет сто­ро­ны AB и AC тре­уголь­ни­ка ABC в точ­ках K и P со­от­вет­ствен­но и про­хо­дит через вер­ши­ны B и C. Най­ди­те длину от­рез­ка KP, если AK = 18, а сто­ро­на AC в 1,2 раза боль­ше сто­ро­ны BC.

10. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 8 и 18, а пе­ри­метр равен 56. Най­ди­те пло­щадь тра­пе­ции.

11. На сто­ро­нах угла и на его бис­сек­три­се от­ло­же­ны рав­ные от­рез­ки и . Ве­ли­чи­на угла равна 160°. Опре­де­ли­те ве­ли­чи­ну угла .

12. Окружность про­хо­дит через вер­ши­ны А и С тре­уголь­ни­ка АВС и пе­ре­се­ка­ет его сто­ро­ны АВ и ВС в точ­ках К и Е соответственно. Отрезки АЕ и СК перпендикулярны. Най­ди­те ∠КСВ, если ∠АВС = 20°.

13. Биссектрисы углов A и B па­рал­ле­ло­грам­ма ABCD пе­ре­се­ка­ют­ся в точке K. Най­ди­те пло­щадь параллелограмма, если BC = 19, а рас­сто­я­ние от точки K до сто­ро­ны AB равно 7.

14. Найдите от­но­ше­ние двух сто­рон треугольника, если его медиана, вы­хо­дя­щая из их общей вершины, об­ра­зу­ет с этими сто­ро­на­ми углы в 30° и 90°.

15. Высота тре­уголь­ни­ка разбивает его ос­но­ва­ние на два от­рез­ка с дли­на­ми 8 и 9. Най­ди­те длину этой высоты, если известно, что дру­гая высота тре­уголь­ни­ка делит ее пополам.

Департамент образования штата Орегон: решение задач по математике 3–8 классы: основные навыки: штат Орегон

Перейти к основному содержанию

Официальный сайт штата Орегон.
Учиться
Откуда ты знаешь »
(как определить веб-сайт Oregon.gov)

Официальный сайт штата Орегон »

Поиск

Требование к оценке эффективности на местах

Образцы работ будут более эффективно способствовать обучению учащихся, если они будут систематически интегрированы в учебную программу округа, а также станут частью обучения в классе (то есть в обычном процессе непрерывной оценки и выставления оценок). Например, когда они используются для подведения итогов учебного модуля или расширения представленных концепций, образцы работ могут стать естественной частью занятий в классе и предлагаться много раз в течение учебного года.

Эти примеры рабочих заданий приведены в соответствие с 2011-12 Руководство по подсчету очков для решения математических задач и к Общепринятым государственным стандартам (CCSS).

Местные задания по оценке успеваемости*

* Для 2 класса не требуется оценка успеваемости; задания для 2-го класса предназначены для того, чтобы дать учителям примеры заданий, соответствующих стандартам 2-го класса.

2 класс​

2 класс​

Категория отчетности по баллам (SRC) 1 — ОПЕРАЦИИ И АЛГЕБРАИЧЕСКОЕ МЫШЛЕНИЕ (OA), ЧИСЛА И ОПЕРАЦИИ В ДЕСЯТИЧНОМ СИСТЕМЕ (NBT)
  • Лимонад
  • Счетчик мармеладок
  • Сумма и разница
  • Чудесная тайна денег
  • Загадай число
SRC 2 — ИЗМЕРЕНИЯ И ДАННЫЕ (MD)
  • Требуют внесения изменений
  • Комбинации монет
  • Деньги Тая
  • 33 цента
  • Продажа мрамора
  • Веселые владельцы ранчо
SRC 3 — ГЕОМЕТРИЯ (G)

Shape House

​​​​

3 класс​

3 класс​

Категория отчетности (SRC) 1 — ОПЕРАЦИИ И АЛГЕБРАИЧЕСКОЕ МЫШЛЕНИЕ (OA), ЧИСЛА И ДЕЙСТВИЯ С СЧИСЛЕНИЕМ С СЧИСЛЕНИЕМ (NBT) И ДРОБЯМИ (NF)
  • Ферма дедушки
  • Ферма дедушки (оценка)
  • Трейл Микс
  • Дилемма зоопарка
  • Клубника Ольги
  • Клубника Ольги (оценка)
  • Бумажный маршрут
SRC 2 – ИЗМЕРЕНИЯ И ДАННЫЕ (MD)
  • Зеленая и желтая шина
  • Дом Тары и Брэда
  • Дом Тары и Брэда (оценка)
  • Прогулка с собакой
  • Лента реальности
  • Собачья будка Купера
  • Заштрихованная область
  • Прямоугольники в квадрате

SRC 3 — ГЕОМЕТРИЯ (G)

​​​

4 класс​

4 класс​

Категория представления результатов (SRC) 1 — ОПЕРАЦИИ И АЛГЕБРАИЧЕСКОЕ МЫШЛЕНИЕ (OA), ЧИСЛА И ДЕЙСТВИЯ С СЧИСЛЕНИЕМ С ОСНОВОЙ ДЕСЯТИ (NBT) И ДРОБЯМИ (NF)

SRC 2 — ИЗМЕРЕНИЕ И ДАННЫЕ (MD)

Kyle’s Corral Caper

4 SRC 3 — ГЕОМЕТРИЯ (G)

​

5 класс​

5 класс​

Категория отчетности (SRC) 1 — ОПЕРАЦИИ И АЛГЕБРАИЧЕСКОЕ МЫШЛЕНИЕ (OA), ЧИСЛА И ОПЕРАЦИИ С ДЕСЯТИЧНЫМ ОСНОВАНИЕМ (NBT) И ДРОБЯМИ (NF)
  • Квадраты
  • Семейная пицца Джонс

SRC 2 — ИЗМЕРЕНИЯ И ДАННЫЕ (MD)

SRC 3 — ГЕОМЕТРИЯ (G)

​​

6 класс​

6 класс​

Категория отчетности (SRC) 1 – ОТНОШЕНИЯ И ПРОПОРЦИОНАЛЬНЫЕ ОТНОШЕНИЯ (RP), СИСТЕМА ЧИСЛОВ (NS), ВЫРАЖЕНИЯ И УРАВНЕНИЯ (EE)
  • Мальчики и девочки
  • Раскрашивание куба
  • Поездка Даррена
  • Негерметичный кран
  • Шоу Боба и Сэма Шу
  • Уровень воды
  • Размеры коробки
SRC 2 — ГЕОМЕТРИЯ (G)
  • Квадрат ABCD
  • Одеяло
  • Произведение искусства
SRC 3 – СТАТИСТИКА И ВЕРОЯТНОСТЬ (SP)

Балетный класс

​

7 класс​

7 класс​

Категория отчетности (SRC) 1 – ОТНОШЕНИЯ И ПРОПОРЦИОНАЛЬНЫЕ ОТНОШЕНИЯ (RP), СИСТЕМА ЧИСЕЛ (NS), ВЫРАЖЕНИЯ И УРАВНЕНИЯ (EE)
  • Rent a Truck
  • Лифт Экспресс
  • Результаты Карлоса
SRC 2 — ГЕОМЕТРИЯ (G)
  • Хитрые плитки
  • Пазл с квадратной пиццей
  • Смотри вниз!
SRC 3 — СТАТИСТИКА И ВЕРОЯТНОСТЬ (SP)
  • Tetra Dice
  • Tetra Dice (с очками)
  • Желейные бобы
  • Плитка Алекса
  • 3-значный номер

​

8 класс​

8 класс​

Категория отчетности (SRC) 1 – СИСТЕМА ЧИСЛЕНИЙ (NS), ВЫРАЖЕНИЯ И УРАВНЕНИЯ (EE), ФУНКЦИИ (F)
  • Пакеты с попкорном
  • Счетные стулья
  • Телефон Молли
  • Пройдено или не пройдено
  • Взвешивание мрамора
  • Два растения Джека
  • Пончики в изобилии
  • Закон о классах
  • Цены на рубашки
  • Поездка Портленд-Сиэтл

SRC 2 — ГЕОМЕТРИЯ (G)

SRC 3 — СТАТИСТИКА И ВЕРОЯТНОСТЬ (SP)

Увлечение концертами!

​

. gov

Официальные веб-сайты используют домен .gov

Веб-сайт .gov принадлежит официальной правительственной организации США.

Безопасные веб-сайты .gov используют HTTPS

Значок замка ( ) или https:// означает, что вы безопасно подключились к веб-сайту .gov.

15 заданий по геометрии для вовлечения учащихся всех классов

Если вы оглянетесь в своем классе, то, скорее всего, везде увидите геометрию — в квадратах календаря, длинных шестиугольных карандашах или прямоугольных ковриках.

Геометрия полна важных основополагающих понятий, но не все студенты лучше усваивают ее на лекциях и бесконечных практических задачах. К счастью, ваши планы уроков геометрии легко связать с реальными приложениями! Занятия по геометрии могут дать вашим ученикам практический опыт и вовлечь их в учебный процесс.

Попробуйте эти 15 увлекательных заданий , которые помогут вам преподавать геометрию и сделать из ваших учеников любознательных и увлеченных учеников.

Юные ученики: попробуйте эти интерактивные задания по геометрии

Практические задания — отличный способ познакомить учащихся с такими математическими понятиями, как фигуры и узоры .

Эти увлекательные занятия помогут им изучить свойства 2D- и 3D-фигур в реальном мире и дадут им возможности для обучения, которые заложат основу для дальнейшего обучения.

1. Создавайте трехмерные фигуры с помощью зубочисток и пластилина

Раздайте учащимся зубочистки, пластилин или зефир и предложите им построить трехмерные фигуры, такие как призмы и кубы. Это отличный способ для учащихся понять свойства трехмерных фигур в реальной жизни!

Кроме того, учащиеся могут использовать это задание, чтобы оживить двухмерные фигуры и понять соответствующие понятия, такие как вершины, углы и стороны.

2. Создавайте 2D-фигуры с помощью танграмм

В головоломках Tangram, возникших в Китае и принесенных в Европу в начале 19 века торговыми путями, используются семь плоских геометрических фигур для создания силуэтов. Хотя танграмы обычно делаются из дерева, вы можете сделать наборы для своего класса из цветной плотной бумаги или войлока.

Танграммы — отличный инструмент для учащихся, которым нравится управлять своей работой, и могут помочь юным учащимся понять свойства различных форм. Кроме того, есть много разных шаблонов для учащихся! Дайте им разные узоры и наблюдайте, как шестиугольник, трапеция и четырехугольник превращаются в зайчика, домик или солнце.

3. Создавайте геометрические узоры из блоков узоров

Для учащихся начальной школы частью понимания форм является также понимание геометрических узоров. Блоки шаблонов помогают учащимся создавать шаблоны, практиковать вращение фигур и сортировать различные фигуры.

Создание моделей важно не только для геометрии — это основополагающая концепция критического мышления и анализа, которая может помочь учащимся устанавливать связи между различными концепциями.

4. Решайте геометрические загадки с наборами LEGO

Будь то головоломки или загадки, математические головоломки могут помочь учащимся решить сложные задачи, сделать выводы и углубить свое понимание.

LEGO — отличный многоцелевой инструмент для вашего класса, который может помочь учащимся лучше понять свойства форм. Дайте учащимся описания различных 2D- и 3D-форм (количество сторон, вершин и длина сторон) и попросите их построить правильный объект!

5. Потренируйтесь формировать фигуры с помощью геобордов

Геоборды — это классический геометрический инструмент, который помогает учащимся создавать фигуры с помощью резинок, натянутых на колышки.

Особенно хорошо подходит для кинестетических учащихся. Используйте геоборды, чтобы учащиеся могли создавать различные формы, описывать их свойства и измерять их. Они могут воспроизводить уже знакомые формы или использовать их для изучения новых.

В вашем классе нет геобордов? Без проблем! Предложите учащимся получить доступ к этой цифровой версии на компьютере или планшете.

Старшие классы: развивайте понимание геометрии с помощью различных средств

Когда учащиеся перейдут в старшие классы начальной или средней школы, они начнут больше узнавать о свойствах фигур , а не только об их внешнем виде.

Они начнут использовать геометрические инструменты и смогут более глубоко изучить применение геометрии в реальной жизни. Используйте эти задания с 3 по 5 класс, чтобы приступить к ним весело и совместно!

1. Создание линейных сегментов с геобордами

Возможно, ваши ученики удивятся, узнав, что на уроке математики строка — это не , а . Независимо от того, изучаете ли вы перпендикулярные линии или сегменты линий, используйте геоборды для практического отображения различных концепций.

Когда дело доходит до геометрии, нужно знать много слов, поэтому используйте геоборды, чтобы пополнить новый словарный запас и поощрить математические разговоры в классе.

2. Нарисуйте геометрические идеи с помощью карандаша и бумаги

Иногда написание новых понятий является лучшим способом их запоминания учащимися! Все прямые углы, вершины и линии геометрии особенно хорошо подходят для визуальной среды.

Каждый учащийся может практиковаться в рисовании геометрических фигур от руки и делать наглядные заметки о новых понятиях. Они также смогут попрактиковаться в использовании таких инструментов, как линейки, компасы и транспортиры для измерения углов и длины.

Чтобы получить дополнительные ресурсы, разместите в своем классе опорные схемы или предложите учащимся сделать свои собственные с помощью забавных маркеров и цветной бумаги.

3. Дополните уроки в школе с помощью онлайн-игр

Цифровое игровое обучение сочетает в себе все удовольствие от видеоигры с эффективными результатами обучения, согласованными с учебным планом.

Prodigy Math Game позволяет вам легко управлять обучением учащихся, пока они играют онлайн! Зарегистрируйте бесплатную учетную запись учителя, чтобы отправлять оценки ученикам, пока они исследуют увлекательный фэнтезийный мир. Кроме того, Prodigy позаботится об оценке за вас!

Создайте мою бесплатную учетную запись учителя сейчас

Другие онлайн-инструменты, такие как Geogebra, также могут помочь учащимся одновременно развивать свои навыки работы с компьютером по геометрии и .

4. Практикуйте геометрические понятия с помощью карточек с заданиями

Карточки с заданиями помогают разбивать более сложные идеи и задания на более мелкие и выполнимые части. Это отличный способ помочь учащимся сосредоточиться на одном вопросе за раз, не перегружая себя, независимо от того, работают ли они:

  • С партнером
  • В небольших группах
  • В одиночку во время смены станции

Попробуйте бесплатно Печатные карточки с заданиями по геометрии от учителей Платите учителям или создавайте свои собственные, чтобы получить еще больше возможностей для настройки! Какую бы концепцию геометрии ни изучают учащиеся, для этого есть карточка с заданием.

5. Совершенствуйте навыки с помощью рабочих листов по геометрии

Интернет — прекрасный инструмент, особенно когда дело доходит до поиска рабочих листов по геометрии. Просто зайдите на свой любимый сайт и распечатайте что-нибудь в качестве домашнего задания или для тех, кто раньше всех закончит.

Используйте рабочие листы по геометрии, чтобы учащиеся практиковали концепции на подходящем для них уровне, или используйте Prodigy, чтобы отправить онлайн-задание, над которым они могут работать в школе или дома.

Создайте мою бесплатную учетную запись учителя сейчас

6. Какой формы ваша земля?

В этом умном геометрическом задании учащиеся должны создать фигуру с наибольшей площадью поверхности из предварительно нарезанной нити.

Учащиеся могут использовать геоборд или веревку и гвозди, чтобы сделать свою фигуру. Им придется использовать формулы, которые они уже выучили, для нахождения площади поверхности, или они могут считать квадраты на бумаге с сеткой или на геобордах.

7. Лента Мёбиуса

Это магия? Это геометрия? Ваши ученики будут настолько поражены, что им может быть трудно понять это. Пусть они смоделируют задачу с помощью полосок бумаги и сами увидят, как эта задача о площади поверхности работает в реальной жизни.

Предложите учащимся поиграть со своими лентами Мёбиуса и провести вокруг них линии, разрезать их посередине или поэкспериментировать с различными поворотами, чтобы посмотреть, что получится.

Другие способы разнообразить изучение геометрии в разных классах

1. Организуйте поиск предметов по геометрии

Предложите учащимся искать различные геометрические фигуры в вашем классе. Попросите их найти:

  • Восемь прямых углов
  • Квадратную призму
  • Наибольшее количество кругов

Или что-нибудь еще, что, по вашему мнению, они могли бы искать в вашем классе!

Для получения дополнительной информации попросите учащихся вычислить площадь поверхности фигур, записать свои выводы в математический журнал и описать их свойства самостоятельно или в небольших группах.

2. Сыграйте в геометрическую игру для всего класса. Игра «Опасность»

«Опасность» — это проверенное временем занятие, в котором участвует весь класс. Используйте бесплатный шаблон, чтобы настроить его в соответствии с тем, что вы изучаете в классе, с разными категориями для разных подтем геометрии.

Предложите учащимся идентифицировать фигуры по картинкам или описать свойства фигур и назвать их.

3. Для младших школьников попробуйте форму БИНГО

Для дополнительного сопоставления и определения формы попробуйте классическую игру в классное бинго! Распечатайте наш шаблон карты BINGO и добавьте к каждой из них разные формы.

Либо назовите формы, чтобы помочь учащимся попрактиковаться в их идентификации, либо опишите форму и попросите дать ответ. Выигрывает тот, кто первым заполнит полный ряд!

Помогите своим учащимся получить максимальную отдачу от вашего раздела геометрии

Каждый учащийся вашего раздела геометрии найдет что-то для себя — практические занятия, практические приложения и возможности для увлекательных игр в классе.

Используйте эти 15 заданий, чтобы закрепить ключевые понятия и поддерживать интерес учащихся к процессу обучения. Скоро они станут мастерами геометрии!

Присоединяйтесь к Prodigy Math Game, чтобы узнать больше о способах проведения увлекательных занятий по геометрии в соответствии с учебным планом. Ваша бесплатная учетная запись учителя включает инструменты, которые помогут вам согласовывать вопросы, на которые учащиеся отвечают, когда они играют, с тем, что вы преподаете в классе! Кроме того, всего за несколько кликов вы сможете получать информацию об учащихся и легко различать их.

Создать бесплатную учетную запись учителя

Математика 8 (7/8 класс) — Раздел 2: Геометрия (8.G)

Учащиеся понимают утверждение теоремы Пифагора, например, разлагая квадрат двумя разными способами. Они применяют теорему Пифагора для нахождения расстояний между точками на координатной плоскости, для нахождения длин и для анализа многоугольников. Учащиеся используют идеи о расстоянии и углах, о том, как они ведут себя при перемещении, вращении, отражении и расширении, а также идеи о конгруэнтности и сходстве для описания и анализа двумерных фигур и решения задач. Учащиеся показывают, что сумма углов в треугольнике есть угол, образованный прямой линией, и что различные конфигурации линий порождают подобные треугольники из-за углов, образующихся при пересечении параллельных прямых секущей.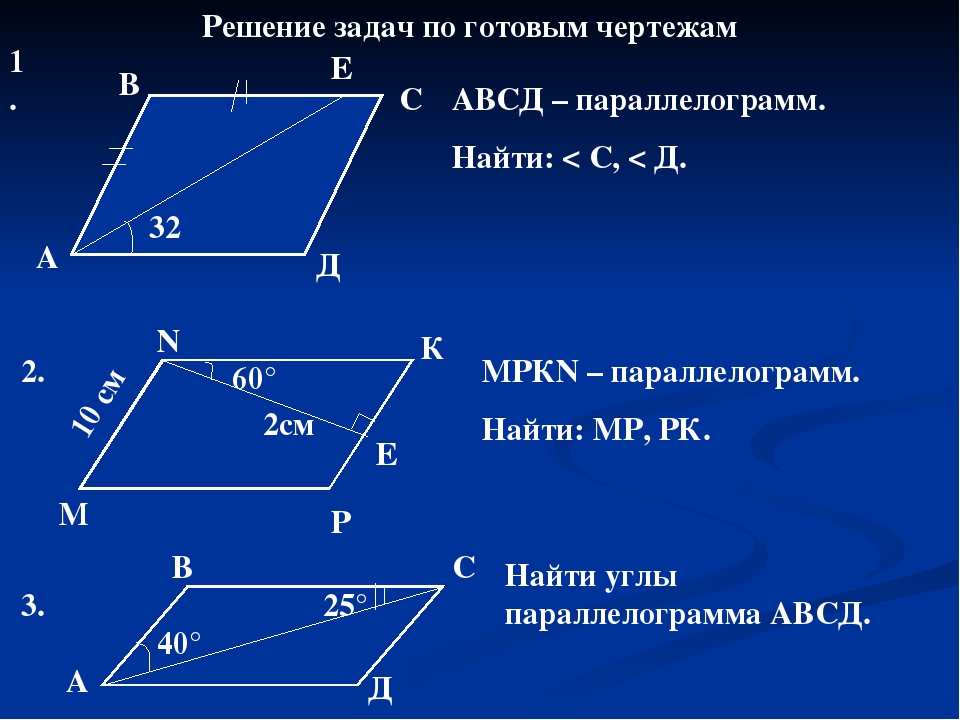

 Что должен знать и уметь мой ребенок?

Учащиеся должны:

Понимать и применять теорему Пифагора.

8.RUS6
Объясните доказательство теоремы Пифагора и ее обратное.

  • Проверка на понимание: Обращение теоремы Пифагора
  • Обзор/перемотка назад: Доказательство теоремы Пифагора Бхаскара

1 Обогащение0287  Применение теоремы Пифагора в математическом контексте | Обратная теорема Пифагора

8.G.B.7
Применение теоремы Пифагора для определения неизвестных длин сторон в прямоугольных треугольниках в реальных и математических задачах в двух и трех измерениях.

  • Проверка на понимание: Теорема Пифагора | Теорема Пифагора в 3D | Словесные задачи по теореме Пифагора | Специальные прямоугольные треугольники
  • Обзор/перемотка назад: Введение в теорему Пифагора
  • Дополнительные задания: Гонки птиц и собак | Бег по футбольному полю

8. RUS8
Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.

  • Проверка на понимание: Расстояние между двумя точками
  • Просмотр/перемотка назад: Формула расстояния
  • Дополнительные задания:  Нахождение равнобедренных треугольников | Прямоугольник на координатной плоскости

Понимание конгруэнтности и подобия с помощью физических моделей, прозрачных пленок или программного обеспечения для геометрии.

8.G.A.1
Экспериментально проверить свойства поворотов, отражений и перемещений (см. нижеследующие вспомогательные стандарты):

  • Проверка на понимание: Свойства жестких преобразований
  • Обзор/перемотка назад: Введение в геометрические преобразования
  • Дополнительные задания: Серебряный прямоугольник оригами

8. G.A.1.A
Линии равны по длине линиям, а их отрезки равны по длине.

  • Проверка на понимание: Свойства жестких трансформаций
  • Просмотр/перемотка назад: Вращение сегмента вокруг исходной точки Пример | Отражение линии через другую линию Пример

8.G.A.1.B
Углы принимают за углы одной меры.

  • Проверка на понимание: Свойства жестких преобразований

8.G.A.1.C
Параллельные прямые превращаются в параллельные прямые.

  • Проверка на понимание: Свойства жестких преобразований

8.G.A.2
Понять, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью вращений , размышления и переводы; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.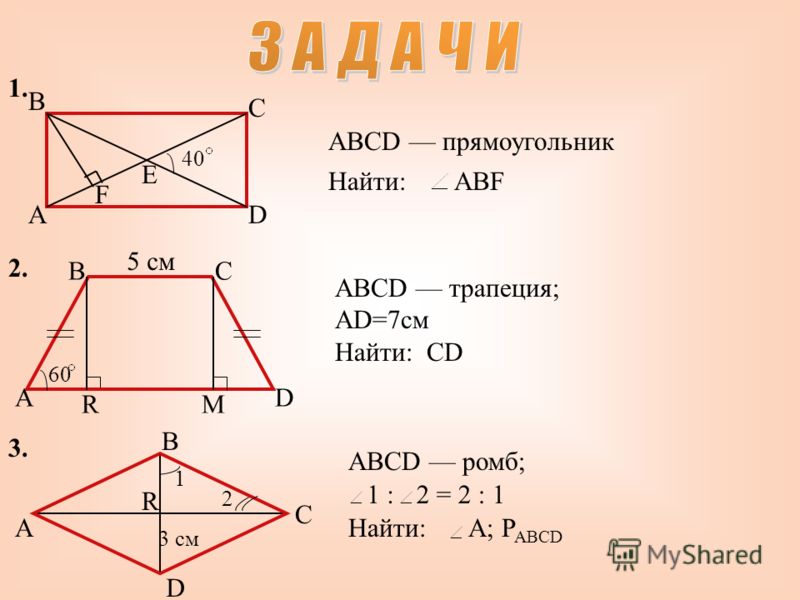

  • Проверка на понимание: Определение преобразований | Конгруэнтность и преобразования
  • Обзор/перемотка назад: Конгруэнтные формы и преобразования | Выполнение последовательностей преобразований
  • Дополнительные задания:  Конгруэнтные прямоугольники | Конгруэнтные сегменты

8.G.A.3
Описать эффект расширения, перемещения, поворота и отражения двухмерных фигур с помощью координат.

  • Проверка на понимание: Выполнение переводов | Выполнение вращений | Perform Reflections
  • Обзор/перемотка назад: Переводы полигонов | Пример поворота полигонов | Пример отражения и сопоставления точек |Расширяющиеся формы: сжатие
  • Задания на расширение:  Соответствие треугольника с координатами | Отражающие отражения

8. G.A.4
Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.

  • Проверка на понимание: Подобие и преобразования
  • Обзор/перемотка назад: Подобные формы и преобразования

8.G.A.5

  • 9 8.G.A.5
  • 9 8.G.A. треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла подобия треугольников. Например, расположите три копии одного и того же треугольника так, чтобы сумма трех углов представляла собой прямую, и приведите аргумент в терминах секущей, почему это так .

    • Проверка на понимание: Практика уравнения с равными углами | Нахождение угловых мер 1 | Нахождение угловых мер 2​
    • Просмотр/перемотка назад: Углы, параллельные линии и сечения | Углы в треугольнике в сумме равны 180 градусам Доказательство
    • Дополнительные задания:  Найти недостающий угол | Конгруэнтность чередующихся внутренних углов посредством поворотов

    Какие некоторые признаки мастерства учащихся?

    • Применяет теорему Пифагора в плоском случае и для нахождения расстояния между двумя точками в системе координат и в трехмерном случае как в математических, так и в реальных многошаговых задачах.
    • Распознает ситуации для применения теоремы Пифагора в многоэтапных задачах.
    • Описывает эффект расширения, перемещения, поворота и отражения двухмерных фигур с координатами и без них, определяет, конгруэнтны или подобны две заданные фигуры посредством одного или нескольких преобразований, и описывает несколько последовательностей преобразований для подтверждения конгруэнтности или сходства двух цифры.

    Инструменты и технологии
    GeoGebra — это динамический математический программный инструмент, который позволяет пользователям изучать геометрию, алгебру, таблицы, графики, статистику и другие области математики в одном простом в использовании пакете. Его можно БЕСПЛАТНО скачать на компьютер или планшет.

    Изучение квадратных корней (Изучение Альберты) Используйте квадраты для визуализации и применения теоремы Пифагора.

    Трансмограф (Шодор) Интерактивный инструмент, позволяющий переводить, отражать и вращать в координатной плоскости.

    alexxlab

    Related Articles

    8 класс

    Английский язык 8 класс гдз несвит: Решебник ⏩ ГДЗ Английский язык 8 класс ⚡ А. Н. Несвит 2016. 8 год обучения

    Содержание Решебник ⏩ ГДЗ Английский язык 8 класс ⚡ А. Н. Несвит 2016. 8 год обученияLessons 1–2. Welcome Back!1 — 7Переклади текстівLessons 1–2. The Age of Information1 — 9Lesson 3. We Are in Fleet Street1 — 7Lessons 4–5. How Do You Get to Know the News?1 — 9Lessons 6–7. What We Read2 — 7Lessons 8–9. […]

    8 класс

    Гдз русский язык 8 класс 2019: ГДЗ Русский Бархударов 8 класс Номер 150

    ГДЗ 8 класс, ответы ко всем учебникам. Восьмикласснику стыдно перекладывать груз учебы на плечи родителей или просить списать у одноклассников. Трудно разобраться с многочисленными предметами – воспользуйтесь готовыми ответами за 8 класс на нашем сайте! Здесь легко найти понятный, хорошо структурированный решебник по русскому языку, химии, физике, математике. В нем не только даны правильные ответы, […]

    8 класс

    Дидактические материалы по геометрии 8 класс бутузов – . 8 . . .., .., ..

    Содержание ГДЗ ЛОЛ по Геометрии за 8 класс, спиши ответ онлайнГДЗ по геометрии для 8 класса на 5.funЧасто ищутГдз по Геометрии 8 класс ГДЗ ЛОЛ по Геометрии за 8 класс, спиши ответ онлайн ☰ ГДЗ 1 КЛАСС Английский язык Русский язык Математика Окружающий мир Литература Информатика Музыка Человек и мир 2 КЛАСС Английский язык Русский […]

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *