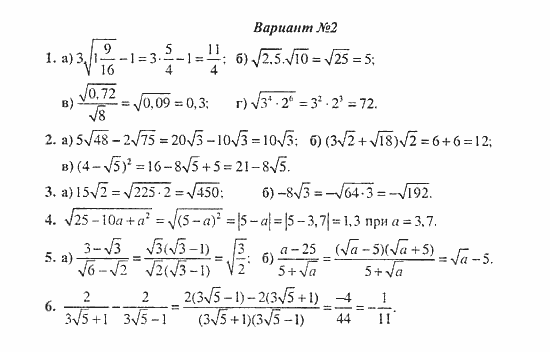ГДЗ Алгебра Александрова 8 класс Самостоятельные Номер Вариант 1 С-35. Рациональные уравнения
Содержание
Авторы:Александрова
Изд-во:Мнемозина
Вид УМК:контрольные и самостоятельные
Серия:под редакцией Мордковича
Смотреть правильно оформленное решениe и ответ на задание Вариант 1 по алгебре 8 класс самостоятельные работы автор(ы) Александрова
Скачать решение
Сообщи об ошибке или поделись идеей💡
Мне не нравится на сайте, измените:Сделайте так, чтобы можно было:Решение неправильно/опечатка
Содержание
Вариант 1Вариант 2Вариант 3Вариант 4
Похожие решебники
по алгебре 8 класс
Учебник
Контрольные
КИМ
Тетрадь
Контрольные
Дидактич.
Тетрадь
Учебник
Учебник
Контрольные
Дидактич.
Контрольные
Тетрадь
Тесты
Дидактич.
Учебник
Учебник
Дидактич.
Дидактич.
Дидактич.
Дидактич.
Контрольные
Контрольные
Тетрадь
Тетрадь
Тетрадь
Учебник
Тесты
Тесты
Тесты
Учебник
Учебник
Учебник
Учебник
Тетрадь
Дидактич.
Дидактич.
КИМ
Контрольные
Контрольные
Тетрадь
Контрольные
Тесты
Тесты
Контрольные
org/Book»>Учебник
org/Book»>Тесты
org/Book»>Тесты
ГДЗ Дорофеев Контрольная работа 4
Админ
Алгебра 8 класс. ГДЗ Дорофеев Контрольная работа 4 «Квадратные уравнения» (2 варианта, три уровня сложности). Решения и ответы на контрольные работы (4 варианта) из пособия для 8 класса (Кузнецова, Минаева, Рослова, Суворова) — М. : Просвещение.
Вернуться к Списку контрольных работ (ОГЛАВЛЕНИЕ).
Алгебра 8 класс. УМК Дорофеев Контрольная работа № 4. Вариант 1
Решения и Ответы на Вариант 1
Контрольная работа № 4. Вариант 2
Решения и Ответы на Вариант 2
Контрольная работа № 4.
Вариант 3
Решения и Ответы на Вариант 3
Контрольная работа № 4. Вариант 4
Решения и Ответы на Вариант 4
Алгебра 8 класс. УМК Дорофеев
Контрольная работа № 4. Вариант 1
Квадратные уравнения (КР Кузнецова)
- Определите, имеет ли корни уравнение 3х2 – 11х + 7 = 0.
- Решите неполное квадратное уравнение: а) 4х2 – 20 = 0; б) 2х + 8х2 = 0.
- Решите уравнение: а) 2х2 – х – 3 = 0; б) х2 – х = 2х – 5.
- Квадратный трёхчлен х2 – 2х – 15 разложите на множители, если это возможно.
- Решите задачу с помощью уравнения: «В прямоугольнике одна сторона на 4 см меньше другой, а его площадь равна 96 см2. Найдите стороны прямоугольника».
- Составьте квадратное уравнение, имеющее корни, равные 2 и –1/2, и преобразуйте его так, чтобы все коэффициенты были целыми числами.
- Найдите все целые значения р, при которых уравнение х2 + рх + 12 = 0 имеет целые корни.
- Решите уравнение х4 – 3х2 –4 = 0.
Дополнительное задание.
*9. Сумма квадратов двух последовательных натуральных чисел на 91 больше их произведения. Найдите эти числа.
Решения и Ответы на Вариант 1
Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ заданий в тетради
Контрольная работа № 4. Вариант 2
Вверх
Решения и Ответы на Вариант 2
Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ заданий в тетради
Контрольная работа № 4. Вариант 3
Вверх
Решения и Ответы на Вариант 3
Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ заданий в тетради
Контрольная работа № 4. Вариант 4
Вверх
Решения и Ответы на Вариант 4
Нажмите на спойлер, чтобы увидеть РЕШЕНИЯ заданий в тетради
Какие умения проверяются:
- определять, имеет ли квадратное уравнение корни и если имеет, то сколько;
- применять формулы корней квадратного уравнения;
- решать неполные квадратные уравнения;
- выполнять разложение на множители квадратного трёхчлена;
- решать текстовые задачи с помощью составления квадратного уравнения;
- решать биквадратные уравнения;
- применять теорему Виета.
Вверх
Алгебра 8 класс. ГДЗ Дорофеев Контрольная работа 4 «Квадратные уравнения» (4 варианта, три уровня сложности). Решения и ответы на контрольные работы из пособия для 8 класса (Кузнецова, Минаева, Рослова, Суворова)
Вернуться к Списку контрольных работ (ОГЛАВЛЕНИЕ).
Просмотров:
63 275
Ответыконтрольные
Академические дисциплины/Математика: 8-й класс
Районный дом
myCherryCreek
- Дом академиков
- Продвинутые академики и GT
- Консультативный
- Искусство
- Аудио/видео производство
- AVID
- Группа
- Хор
- Информатика
- Поддержка английского языка
- Гитара
- Здоровье и благополучие
- Языковые искусства
- Языковые искусства: 6-й класс
- Языковые искусства: 7-й класс
- Языковые искусства: 8-й класс
- Математика
- Математика: 6 класс
- Математика: 7 класс
- Математика: 8 класс
- Оркестр
- Физическая культура
- Наука
- Социальные исследования
- Обществознание: 6 класс
- Обществознание: 7 класс
- Обществознание: 8 класс
- испанский
- КОРЕНЬ
- Службы успеваемости учащихся
- Театральное искусство
Математика 7/8
Учащиеся, успешно завершившие математику 6/7, могут пройти этот двухгодичный сжатый курс, подготовив их к алгебре 1 в 8 классе.
Основное внимание в математике 7/8 будет уделяться решению задач с использованием линейные уравнения и неравенства, использование радикалов и целых показателей, соединение пропорциональных отношений и линий, решение систем линейных уравнений, а также определение, оценка и сравнение функций. В этом курсе будет изучено полное содержание курса «Математика 8» (см. описание курса «Математика 8»). Компактный характер курса потребует, чтобы студенты чувствовали себя комфортно и умело изучали математику в ускоренном темпе.Математика 8
В математике 8 учащиеся начинают серьезное изучение алгебры с изучения линейных функций. Когда их изучение систем счисления относительно завершено, акцент смещается на абстрактное применение их понимания арифметики. Этот контент будет посвящен трем критическим областям, включая (1) формулировку и рассуждение о выражениях и уравнениях, моделирование двумерных данных с помощью линейного уравнения, решение линейных уравнений и работу с системами линейных уравнений; (2) развитие понимания концепции функции и использование функций для описания количественных отношений; и (3) анализ двух- и трехмерного пространства и фигур с использованием расстояния, угла, подобия, конгруэнтности, а также понимания и применения теоремы Пифагора.
Эта работа заложит основу для их успеха в 1 курсе алгебры средней школы.Алгебра 1
Алгебра 1 формализует и расширяет знания учащихся по математике, полученные на курсах Математика 6/7 и Математика 7/8. Основные компоненты обучения включают (1) использование уравнений и неравенств для моделирования реальных величин и манипулирование ими, чтобы выделить интересующие величины, сосредоточив внимание на основных структурах уравнений и неравенств; (2) понимание функции, обозначения функции, а также ограничений домена и диапазона, связанных с функцией; и (3) работа с экспоненциальными и квадратичными функциями через структурную перспективу по сравнению с линейными функциями. Эти концепции закладывают основу для концепций аналитической геометрии и для изучения различных типов функций в Алгебре 2 и других продвинутых курсах. Этот курс эквивалентен курсу алгебры 1, изучаемому в средних школах CCSD.
Основное внимание в математике 7/8 будет уделяться решению задач с использованием линейные уравнения и неравенства, использование радикалов и целых показателей, соединение пропорциональных отношений и линий, решение систем линейных уравнений, а также определение, оценка и сравнение функций. В этом курсе будет изучено полное содержание курса «Математика 8» (см. описание курса «Математика 8»). Компактный характер курса потребует, чтобы студенты чувствовали себя комфортно и умело изучали математику в ускоренном темпе.
Эта работа заложит основу для их успеха в 1 курсе алгебры средней школы.с отличием 8 класс Математика | Центр талантливой молодежи Джона Хопкинса (CTY)
О курсе
Математика 8 класса с отличием
- 6-8 классы
- CTY-уровень
Индивидуальный темп
Этот годовой курс, ориентированный на Common Core, фокусируется на изучении алгебраических манипуляций и графических интерпретаций по мере того, как вы освещаете темы, изучаемые в рамках подготовки к экзамену Honors Algebra I.
Вы освоите такие понятия, как радикалы и экспоненты, линейные уравнения и системы уравнения, функции, конгруэнтность и сходство с помощью увлекательных онлайн-уроков, видеороликов, практических задач и форумов классов. Курс предлагает обширную практику и оценочные оценки, включая проверку навыков, тесты и кумулятивные экзамены. Вы также получите возможность углубиться в приложения и моделирование, работая над творческими проектами. Ваш инструктор будет доступен для поддержки обучения и индивидуальных сеансов повторения для оцениваемых оценок.
Время групповых встреч (по желанию): Среда с 19:00 до 20:00. ET
Обязательство по времени: 3–6 часов в неделю (1 час дополнительного группового занятия, 3–5 часов самостоятельной работы).
Обзор курса
До 9 месяцев доступа
Выберите дату начала
Зарегистрироваться
Тестирование и предварительные условия
7
Проверьте свое право на участие, используя существующие результаты тестов Если у вас нет существующих результатов тестов: Учащиеся должны набрать квалификационные баллы по углубленному тестированию, чтобы иметь право на участие в программах CTY. Зарегистрируйтесь на тестирование. Стоимость обучения
Плата за подачу заявления
Финансовая помощь доступна Мы стремимся служить всем талантливым молодым людям независимо от финансовых обстоятельств. Финансовая помощь предоставляется в зависимости от потребности. Подробнее Технические требования Для прохождения этого курса требуется компьютер с высокоскоростным доступом в Интернет и современный веб-браузер, например Chrome или Firefox. Этот курс использует виртуальный класс для общения преподавателя и студента. Класс работает на стандартных компьютерах с настольным клиентом Zoom, а также на планшетах или портативных устройствах, поддерживающих приложение Zoom Mobile. Записанные встречи можно просматривать только на компьютере с установленным настольным клиентом Zoom. Настольный клиент Zoom и мобильное приложение Zoom можно загрузить бесплатно. Большинство лекций курса можно просматривать на мобильных устройствах, но некоторые задания и тесты необходимо выполнять на настольном или портативном компьютере. Этот курс использует программу прокторинга Respondus LockDown Browser для назначенных оценок. LockDown Browser — это клиентское приложение, которое устанавливается на локальный компьютер. Посетите веб-сайт Respondus, чтобы узнать системные требования. Положения и условияУчащиеся могут взаимодействовать в онлайн-классах и встречах, в которых участвуют сверстники, преподаватели и случайные специальные гости. Курсы могут включать видео из Интернета. Рекомендации или ссылки в конце видео предоставлены организатором видео и не являются рекомендациями CTY. Виртуальные встречи класса могут записываться для просмотра учащимися. После прохождения курса ваши проекты могут быть использованы в качестве иллюстраций для будущих студентов. Наши онлайн-курсы по математике — от начальной до учебной программы колледжа — охватывают широкий круг тем, от алгебры и геометрии до шахмат, криптологии и исчисления AP, и проводятся под руководством опытных инструкторов. Вы будете присоединяться к групповым занятиям с одноклассниками, чтобы не отставать от сложного содержания курса. Если вы ищете чистое математическое развлечение и обогащение, чтобы подняться по математической лестнице и повысить свои награды и академический статус AP (и выше), или подготовиться к математическим соревнованиям, есть курс CTY, который подходит именно вам. Доступны новые курсы повышения квалификации по математике!Изучите наши новые курсы повышения квалификации по математике, в том числе «Экскурсы по предварительной алгебре», «Математическое моделирование» и «Введение в логику и доказательства». Присоединяйтесь к захватывающему миру соревновательной математикиПримите участие в Математическом клубе средней школы или запишитесь на 6 курсов интеллектуальной собственности: Конкурентная математика в средней школе I, Конкурентная математика в средней школе II, Конкурентная математика в средней школе III, Подготовка к соревновательной математике, Конкурентная математика I, Конкурсная математика II. Познакомьтесь с нашими преподавателями математики
|
|---|
Если у вас нет квалификационных баллов, у вас есть несколько различных вариантов тестирования. Мы поможем подобрать правильный вариант для вашей ситуации.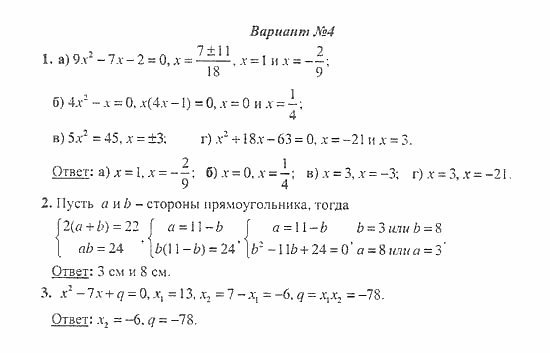
Вы должны иметь возможность общаться с преподавателем по электронной почте. Посетите страницу Технические требования и поддержка для получения более подробной информации.
