|
+ = — =
2 = = , где 5 │3 3 1 2 3 — 1 = — 1 = 2 — 1 = 1 |
|
|
+ = — =
2 = = , где 5 │3 3 1 2 3 — 1 = — 1 = 2 — 1 = 1 |
|
nsportal.ru
Мини справочник по математике для учащихся 5 класса
Мини справочник по математике для учащихся 5 класса может быть истольован как шпаргалка или как справочный матемиал. Справочник состоит из следующих блоков:
1. Свойства натуральных чисел.
2.Алгоритм решения уравнений.
3.Обыкновенные дроби.
4. Формулы.
5.Элементы геометрии.
6. Единицы измерения
Просмотр содержимого документа
«Мини справочник по математике для учащихся 5 класса »
Мини-справочник
по математике
5 класс

Автор
Гартун
Тамара Константиновна
учитель математики
2013 г.

Свойства натуральных чисел
Решение уравнений
Обыкновенные дроби
Свойства сложения:
-
Переместительное а + Ь = Ь + а
-
Сочетательное а + (Ь + с) = (а + Ь) + с
-
а + 0 = 0 + а = а
Свойства вычитания:
-
Вычитание суммы из числа
а — (Ь + с) = а — Ь — с
-
Вычитание числа из суммы
(а + Ь) — с = а + (Ь — с) (а + Ь) — с = (а — с) + Ь
-
а — 0 = а
-
а — а = 0
Свойства умножения:
-
Переместительное а • Ь = Ь • а
-
Сочетательное а • (Ь • с) = (а • Ь) • с
-
Распределительное
(а + Ь) с = ас + Ьс (а — Ь) с = ас — Ьс
-
1 • п = п • 1 = п
-
0 • п = п • 0 = 0
Свойства деления:
-
а : 1 = а
-
а : а = 1
-
0 : а = 0
-
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое
х + а = Ь х = Ь — а
-
Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность
х — а = Ь х = а + Ь
-
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность
Ь — х = а х = Ь — а
-
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель
а • х = Ь х = Ь : а
-
Чтобы найти неизвестное делимое, надо делитель умножить на частное
х : а = Ь х = а • Ь
-
Чтобы найти неизвестный делитель, надо делимое разделить на частное
а : х = Ь х = а : Ь
а Ь а + Ь а Ь
с с с с с
а— Ъ
Формулы
Формула пути
5 = V • 1 V = 5 : 1 1 = 5 : V
Площадь
5 — путь (расстояние)
V — скорость
1 — время
Прямоугольник
5 = а • Ь
5 = а • а = а2
Объём
V = аЬс
V = а3
Ь
а
а
а
с
а
kopilkaurokov.ru
Памятка (формулы по математике 5 класс)
Просмотр содержимого документа
«Памятка (формулы по математике 5 класс)»
-
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое
Х+45=90 45+(Х+12)=90
Х= 90-45 Х+12= 90-45
Х=45 Х+12=45
Х=33
-
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое
Х-45=90 (70-Х)-20=40
Х= 90+45 70-Х=40-20
Х=135 70-Х=20
Х=70-20
Х=50
-
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность
70-Х=30 40-(Х+12)=90
Х= 70-30 Х+12= 90+40
Х=40 Х+12=130
Х=130-12
Х=118
-
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
x·25=50
x=50:25
x=2
-
Чтобы найти неизвестное делимое, нужно частное умножить на делитель
X:2=14
X=14·2
X=28
-
Чтобы найти неизвестный делитель, нужно делимое разделить на частное
28:x=14
X=28:14
X=2
Свойства сложения и вычитания
-
а+b=b+a
-
(a+b)+c=a+b+c=a+c+b=a+(b+c)
-
a-b+c=a+c-b (переставляем вместе со знаками)
-
a+b-c=a-c+b (переставляем вместе со знаками)
-
a-(b+c)= a-b-c (минус перед скобкой меняет знаки на противоположные)
-
a-(b-c)= a-b+c (минус перед скобкой меняет знаки на противоположные)
-
a-b-c=a-(b+c)
-
а-0=а
-
а+0=а
-
а-а=0
-
(a+b)c=ac+bc
-
(a-b)c=ac-bc
Свойства умножения
1.
2.
3.
4.
|
Площадь прямоугольника S=ab Периметр прямоугольника P=2(a+b) |
Объем прямоугольного параллелепипеда V=abc Площадь поверхности прямоугольного параллелепипеда Sпов= 2(ab+bc+ac) Сумма длин всех ребер прямоугольного параллелепипеда l = 4(a+b+c) |
|
Площадь квадрата S=a2 Периметр квадрата P=4a |
Объем куба V=a3 Площадь поверхности куба Sпов= 6a2 Сумма длин всех ребер куба l=12a |
|
Единицы измерения площадей 1га=10 000 1а=100 |
Формула деления с остатком
Формула деления с остатком: n = mk + r, где n — делимое, m — делитель, k — частное, r – остаток.
Формула степени числа
– квадрат числа а
– куб числа а
Формула пути
S=v·t
v=S:t
t=S:v
где S – расстояние, v – скорость, t – время
Формула радиуса
r = 2d, где r – радиус, d – диаметр
Сложение и вычитание обыкновенных дробей
Чтобы из неправильной дроби выделить целую часть, надо:
-
Разделить с остатком числитель на знаменатель;
-
Неполное частное будет целой частью;
-
Остаток от деления (если он есть) дает числитель, а делитель — знаменатель
Чтобы представить смешанное число в виде неправильной дроби, нужно
-
Умножить его целую часть на знаменатель дробной части
-
К полученному произведению прибавить числитель дробной части
-
Записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения
Пример:
Формула среднего арифметического
|
Среднее арифметическое = (сумма чисел) : (количество слагаемых) |
|
Средняя скорость = (весь пройденный путь) : (все время движения) |
|
Сумма чисел = (среднее арифметическое) * (количество чисел) |
Прямой угол – равен 90°
Острый угол – меньше 90°
Тупой угол – больше 90°
Разряды числа
|
Целая часть |
Дробная часть |
|||||||||||||||||||||||
|
Классы |
Миллиарды |
Миллионы |
Тысячи |
единицы |
||||||||||||||||||||
|
разряды |
Сотни |
Десятки |
единицы |
Сотни |
Десятки |
единицы |
Сотни |
Десятки |
единицы |
Сотни |
Десятки |
единицы |
Десятые |
Сотые |
Тысячные |
десятитысячные |
стотысячные |
миллионные |
||||||
|
число |
8 |
7 |
0 |
0 |
5 |
9 |
1 |
3 |
1 |
4 |
, |
1 |
5 |
9 |
6 |
7 |
6 |
|||||||
multiurok.ru
Шпаргалки репетитора по математике. Качайте бесплатно!
Ура, свершилось! Наконец то я собрал свои опорные карточки с теоремами и формулами по планиметрии в единый *.doc файл и выложил его на главную страницу в раздел репетитор по математике — методики. Вы можете скачать его бесплатно и использовать при решении задач. Рекомендую своим ученикам ежедневно просматривать материалы независимо от того, имеются ли соответствующее домашнее задание.
Уважаемые репетиторы по математике, обратите внимание на то, что содержание справочника заточено исключительно под цели итогового повторения при подготовке к ЕГЭ по математике и не включает в себя определения используемых понятий и полные формулировки теорем. Я собрал только те сведения (факты и формулы за 7 — 9 класс), на которых репетитор по математике строит практическую работу с задачами в процессе подготовки к ЕГЭ. Если у ученика возникают проблемы с пониманием самой природы геометрии или просыпается желание совместно с репетитором по математике разобраться во всех хитросплетениях предмета «от А до Я», — требуется совершенно иная и долгая работа по усвоению строгих определений и доказательств с совершенно иными формами заданий и сопроводительными материалами (я работаю с теоретической тетрадью и тетрадью для доказательств).
Шпаргалки репетитора по математике призваны помочь школьнику в самостоятельном поиске решений сложных задач и в перспективе добиться (и ускорить) запоминания используемых математических фактов. Подобные материалы можно использовать в работе со сложными учащимися, которых бесполезно погружать в строгую логику и для которых репетитор по математике лишь «провозглашает» теоремы, а не доказывает их. В таких случаях важно классифицировать факты, собирая их в разделы: «окружность», «площади», «трапеция», «векторы» и т.д.
Пользуйтесь шпаргалками на здоровье. При копировании на другие сайты — поставьте с них, пожалуйста, гиперссылку на мой ресурс. Отдельно отмечу, что 10% представленного в шпаргалках материала не входит в общеобразовательную программу по математике за 7 — 9 класс или рассматривается только как отдельные рядовые задачи к параграфам учебников. При отсутствии хорошего репетитора по математике и проводимой им работы по выделению и повторению теоретического материала, абитуриент к концу 9 класса благополучно забывает большинство фактов. Это является одной из причин возникновения серьезных проблем на ЕГЭ с задачей С4.
Формулы и теоремы сортированы по их фигуральному, смысловому или вычислительному родству. Скачать материалы можно с главной страницы или по прямой ссылке — опорный справочник репетитора по математике. Планиметрия. Подготовка к ЕГЭ.
В каникулы, скорее всего, я завершу работу над аналогичным справочником по стереометрии и выложу его в соответствующий раздел главной страницы. Следите за новостями.
Колпаков А.Н. Репетитор по математике — Москва. Строгино.
Метки:
Справочник репетитора
ankolpakov.ru
| 5-11 классы | Латинский и греческий алфавиты | |
| 7-11 классы | Обозначения и сокращения в математике | |
| 10-11 классы | Справочный материал для подготовки к ЕГЭ | |
| Справочные материалы по математике, алгебре | ||
| 5 класс | Памятка по математике для 5 класса | |
| 6 класс | Памятка по математике для 6 класса | |
| 7 класс | Памятка по математике для 7 класса | |
| 8 класс | Решение квадратных неравенств с помощью параболы new | |
| 7-9 классы | Формулы основной школы | |
| 7-9 классы | Таблица степеней, таблица квадратов | |
| 8-9 классы | Построение графика квадратичной функции | |
| 8-9 классы | Алгоритм решения неравенств методом интервалов | |
| 8-9 классы | Решение квадратных неравенств графическим способом. Образцы решения | |
| 8-9 классы | Решение квадратных неравенств методом интервалов. Образцы решения | |
| 9 класс | Виды преобразований графиков функций | |
| 10 класс | Алгоритм исследования функции с помощью производной | |
| 10 класс | Свойства тригонометрических функций | |
| 10 класс | Таблица значений тригонометрических функций | |
| 10 класc | Тригонометрическая окружность + Формулы приведения | |
| 10 класc | Тригонометрическая окружность + Таблица значений тригонометрических функций | |
| 10 класс | Основные тригонометрические формулы | |
| 10 класс | 50 формул тригонометрии | |
| 10 класс | Решение тригонометрических уравнений | |
| 10 класс | Решение тригонометрических неравенств | |
| 10 класс | Формулы приведения | |
| 10-11 классы | Таблица производных и первообразных | |
| 11 класс | Показательная и логарифмическая функции | |
| 11 класс | Степени и корни. Свойства и графики степенных функций | |
| 11 класс | Важнейшие равносильные преобразования (при решении уравнений и неравенств) | |
| Справочные материалы по геометрии | ||
| 7-9 классы | Основные формулы планиметрии | |
| 8-11 класс | Пифагоровы тройки | |
| 7-9 классы | Треугольники | |
| 7-9 классы | Четырехугольники | |
| 9 класс | Таблица значений тригонометрических функций В.М. Брадиса | |
| 9 класс | Соотношения в правильных многоугольниках | |
| 10-11 классы | Стереометрия | |
semenova-klass.moy.su
❺ Шпаргалки математика
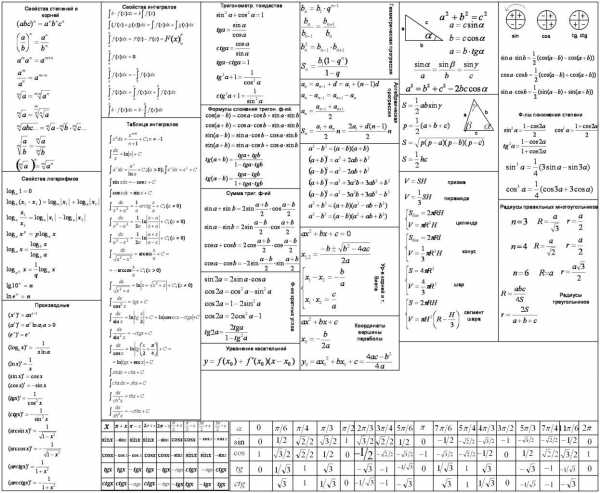
Шпаргалки по математике дают возможность иметь объемный материал под рукой. Причем вся информация представлена в компактных таблицах. Основные формулы и правила можно положить в карман. Не все могут запомнить большое количество формул и правил, и подобное изложение информации позволяет повторять непонятные темы многократно.
Мы предлагаем воспользоваться полезными шпаргалками на разные темы: таблица и свойства интегралов, свойства логарифмов, понятие производных, геометрические и алгебраические прогрессии, сумма тригонометрических функций, функции квадратных углов, радиусы правильный многоугольников и треугольников.
Понравился материал? Загрузка…
otlgdz.online
|
980 + (980 + 50) |
Числовое выражение |
|||||||||||||||||||||||
|
980 + (980 + m) |
Буквенное |
|||||||||||||||||||||||
|
a + b = b + a a + (b + c) = (a + a + 0 = 0 + a = a a – (b + c) = a – (a + b) – c = a + (a + b) – c = (a – a – 0 = a; a – a = 0 |
Переместительное Сочетательное Свойство Свойство Свойство Свойство нуля |
|||||||||||||||||||||||
|
a · b = b · a a · (b · c) = (a · (a + b) · c = a · (a – b) · c = a · 1 · n = n 0 · n = 0 |
Переместительное Сочетательное Распределительное Распределительное |
|||||||||||||||||||||||
|
(a + b)/c = a/c + n/1 = n n/n = 1 0/n = 0 |
Свойство Свойство Свойство Свойство деления |
|||||||||||||||||||||||
|
an a2 a3 |
Число Квадрат Куб числа a |
|||||||||||||||||||||||
|
Таблица квадратов первых 10 |
|||||||||||||||||||||||
|
Таблица кубов первых 10 натуральных |
|||||||||||||||||||||||
|
S = v · t, v = S/t, |
Запись правила с помощью букв – формула |
|||||||||||||||||||||||
|
Обыкновенная дробь 5 – числитель 8 – знаменатель |
||||||||||||||||||||||||
|
Полвина Треть Четверть |
||||||||||||||||||||||||
|
<
> |
Сравнение дробей
Сравнение дробей |
|||||||||||||||||||||||
|
,
, |
Правильная Неправильная дробь |
|||||||||||||||||||||||
|
Сложение дробей с одинаковыми
Вычитание дробей с одинаковыми |
||||||||||||||||||||||||
|
1 |
Смешанное число 1 – целая часть
— дробная часть |
|||||||||||||||||||||||
|
При сложении (и вычитании) чисел |
||||||||||||||||||||||||
|
Десятичная дробь |
||||||||||||||||||||||||
|
3,700 + 2,651 6,351 3,700 – 2,651 1,041 |
Сложение (вычитание) десятичных
1.)Уровнять в этих дробях количество
2.)Записать их друг под другом так,
3.)Выполнить сложение (вычитание), не
4.)Поставить в ответе запятую под |
|||||||||||||||||||||||
|
86,2759 = 86,3 59,7487 = 59,7 |
Округление десятичных дробей
Если первая отброшенная или замененная
Если первая отброшенная или замененная |
|||||||||||||||||||||||
|
1,83
7,32 |
Умножение дроби на натуральное число
1.)Умножить ее на число, не обращая
2.)В полученном произведение отделить |
|||||||||||||||||||||||
|
0,065 · 1000 = 0065 = 65
2,9 · 1000 = 2,900 · |
Умножение десятичной дроби на 10,
В дроби перенести запятую на столько |
|||||||||||||||||||||||
|
4,6 · 0,1 = 0,46 52,7 · 0,01 = 0,527 4837,6 · 0,001 = 4, 8376 |
Умножение числа на 0,1; 0,01; 0,001 и т. д.
То же самое, что разделить число на |
|||||||||||||||||||||||
|
0,254
0,00762 |
Умножение двух десятичных дробей
1.)Выполнить умножение, не обращая
2.)Отделить запятой столько цифр, |
|||||||||||||||||||||||
|
19,2 | 8 | –16 | 2,4 3 2 –3 2 0 |
2,88 | 4 | –0 | 0,72 2 8 –2 8 |
–8 0 |
Деление десятичной дроби на натуральное
1.)Разделить дробь на натуральное
2.)Поставить в частном запятую, когда
Если целая часть меньше делителя, то |
||||||||||||||||||||||
|
96,1 : 10 = 9,61 8,765:100 = 008,765 : 100 = 0,08765 854,9 : 1000 = 0,8549 |
Деление десятичной дроби на 10, 100,
Перенести запятую на столько знаков |
|||||||||||||||||||||||
|
12,096 : 2,24 = 1209,6 : 224 = 5,4
1209,6 | 224 | –1120 | 5,4 89 6 –89 6 0 |
Деление числа на десятичную дробь
1.)В делимом и делителе перенести
2.)После этого выполнить деление на |
|||||||||||||||||||||||
|
45,3 : 0,1 = 453 578,9 : 0,01 = 578,90 : 0,01 = 57890 56,87 : 0,0001 = 56,8700 : 0,0001 = 568700 |
Деление десятичной дроби на 0,1; 0,01;
Перенести в дроби запятую вправо на |
|||||||||||||||||||||||
|
(4,6 + 4,6 + 5,1 + 5,1 + 5,1) : 5 = 4,9 |
Частное от деления суммы чисел на |
|||||||||||||||||||||||
|
часть 0,971 = 0,971 · 100% = 97,1% 39% = 39 : 100 = 0,39 |
1 процент Перевод числа в проценты Перевод процентов в число |
|||||||||||||||||||||||
pedsovet.su