10 класс

Геометрия 10 класс ким – Решебник по Геометрии 10 класс контрольно-измерительные материалы Рурукин А.Н.

Итоговый КИМ по геометрии 10 класс

Пояснительная записка.

Итоговая контрольная работа по геометрии за курс 10 класса составлена в соответствии с учебником: Геометрия, 10-11: учебник для общеобразовательных учреждений. / Атанасян Л.С., Бутузов В.Ф. и др. – М.: Просвещение, 2009 — 2013.

При составлении работы использовались задания следующих пособий:

  1. Геометрия, 10: Карточки для проведения контрольных работ и зачётов / Г.Д. Карташева, Л.Б. Крайнева. – М.: Вербум-М, 2004.

  2. Задачи и упражнения на готовых чертежах. 10-11 кл. Геометрия. / Е.М. Рабинович — М.: Илекса, 2005.

  3. Геометрия. Стереометрия: пособие для подготовки к ЕГЭ. В.А.Смирнов.- М.: МЦНМО, 2011.

  4. Геометрия. 10 класс. Поурочные планы по учебнику Л.С. Атанасяна и др. / Авт.-сост. Г.И. Ковалёва – Волгоград: Учитель, 2004.

Контрольная работа рассчитана на два урока по 40 – 45 минут, содержит 4 разноуровневых варианта: варианты 1 и 2 предназначены менее подготовленным ученикам, варианты 3 и 4 обучающимся на хорошо и отлично. Задача №1 по готовому чертежу на доказательство с применением теоремы о трёх перпендикулярах или обратной ей. К задачам № 2 — № 4 даны ответы.

Цель: проверка умений применять полученные знания по основным темам курса геометрии 10 класса.

  1. ВИД КОНТРОЛЯ – контрольная работа

  1. СОДЕРЖАНИЕ КОНТРОЛЯ:

Проверяются следующие темы:

2.1. Теорема о трёх перпендикулярах.

2.2. Угол между прямой и плоскостью.

2.3. Угол между плоскостями.

2.4. Угол между плоскостями.

  1. ЦЕЛИ КОНТРОЛЯ

обучающийся должен

знать:

  • Основные аксиомы стереометрии;

  • Теоремы стереометрии;

  • Теорему о трёх перпендикулярах;

  • Геометрические тела;

  • Формулы для нахождения площадей поверхностей геометрических тел.

уметь:

  • Применять основные аксиомы стереометрии при решении задач;

  • Применять теорему о ТПП и обратную теорему ТПП при решении задач;

  • Применять формулы ;

  1. СТРУКТУРА КОНТРОЛЬНОЙ РАБОТЫ:

Контрольная работа включает в себя 1 задание по контролируемой теме «Теорема о трёх перпендикулярах.»,1 задание по контролируемой теме «Угол между прямой и плоскостью.», 1 задание по контролируемой теме «Угол между плоскостями», 1 задание по контролируемой теме «Угол между плоскостями.».

  1. КРИТЕРИИ ОЦЕНКИ

На «5» оценивается работа, в которой выполнено 4 задания

На «4» оценивается работа, в которой выполнено 3 задания

На «3» оценивается работа, в которой выполнено 2 задания

На «2» оценивается работа, в которой выполнено 1 задание

Итоговая контрольная работа

по геометрии. 10 кл. (УМК Л.С. Атанасян и др.)

ВАРИАНТ 1.

  1. а Дано: а (АВС),

М АВС – прямоугольный,

С= 90˚

В Доказать: МСВ —

А прямоугольный.

С

  1. АВСDA1B1C1D1 – правильная призма. АВ = 6см, АА1= 8см.

Найти угол между прямыми АА1 и ВС; площадь полной поверхности призмы.

  1. В правильной треугольной пирамиде сторона основания равна 2см, а высота равна 2 см. Найти угол наклона бокового ребра к плоскости основания. Ответ запишите в градусах.

  1. Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом в 120˚ между ними. Наибольшая из площадей боковых граней равна 56 см2. Найти площадь полной поверхности призмы.

Итоговая контрольная работа

по геометрии. 10 кл. (УМК Л.С. Атанасян и др.)

ВАРИАНТ 2.

а

  1. М Дано: ABCD – ромб,

В С АС ВD = О,

а (АВС).

Доказать: МО ВD.

OOOОО

А D

  1. АВСDA1B1C1D1 – правильная призма. Площадь её полной поверхности равна 210 м2, а площадь боковой поверхности 160 м2. Найти сторону основания и высоту призмы.

  1. В правильной четырёхугольной пирамиде со стороной основания 6 см и длиной бокового ребра см найти косинус угла наклона бокового ребра к плоскости основания и площадь боковой поверхности.

  1. Стороны основания прямого параллелепипеда равны 8 см и 15 см и образуют угол в 60˚. Меньшая из площадей диагональных сечений равна 130 см2. Найти площадь полной поверхности параллелепипеда.

Итоговая контрольная работа

по геометрии. 10 кл. (УМК Л.С. Атанасян)

ВАРИАНТ 3.

  1. а Дано: ABCD —

М параллелограмм,

В С а (АВС),

МА АD.

Доказать:

А D ABCD – прямоугольник.

  1. В прямой призме основанием является параллелограмм со сторонами 4 м и 5 м и углом между ними 30˚. Найти площади боковой и полной поверхностей призмы, если её высота равна

7 м.

  1. В правильной четырёхугольной пирамиде РАВСD сторона основания АВ = 10 см, высота РH = 5 см. Найти угол наклона бокового ребра пирамиды к плоскости её основания; площадь сечения, проходящего через высоту и боковое ребро.

  1. Основанием прямой призмы АВСА1В1С1 является равнобедренный треугольник АВС с основанием АС, причём АВ = 6 см, угол В равен 120˚, боковое ребро СС1 = 8 см. Найти площадь сечения А1С1В;

*б) тангенс угла наклона плоскости (А1С1В) к плоскости (АСС1).

Итоговая контрольная работа

по геометрии. 10 кл. (УМК Л.С. Атанасян и др.)

ВАРИАНТ 4.

а Дано: а (АВС),

  1. М MD ВС,

В D – середина ВС.

D Доказать: АВ = АС

А

С

  1. В прямоугольном параллелепипеде длина диагонали 4см, длины его измерений относятся как 1: 2 : 4. Найти площадь полной поверхности параллелепипеда.

  1. В правильной четырёхугольной пирамиде сторона основания равна 4 м, а высота равна 2 м. Найти угол наклона боковой грани к плоскости основания; площадь полной поверхности пирамиды.

  1. Основанием пирамиды МАВСD является прямоугольник АВСD со сторонами АВ = 5 см и AD = 12 см. Боковое ребро МА перпендикулярно к плоскости основания пирамиды и равно 4 см. Найти угол наклона ребра МС к плоскости ABCD. *б) Постройте сечение пирамиды плоскостью, параллельной плоскости основания и проходящей через точку F на ребре МА, MF : FA = 1 : 3. Найдите площадь сечения.

Ответы.

№ задания

Вариант 1

Вариант 2

Вариант 3

Вариант 4

1.

Доказательство основывается

на ТТП или на обратной ТТП.

2.

φ=90˚;

Sполн=264 см2

а=5 м;

h= 8 м

Sбок=126 м2

Sполн=146м2

Sполн=448см2

3.

45˚

cos B = 0,6

Sбок=12 см2

α =60˚

Sсеч = 50 см2

φ=45˚;

Sполн=16( + 1) м2

4.

Sполн= 120 + 7,5 см2

Sполн =460 + 120 см2

Sсеч = 3 см2

tg φ =

arctg ;

Sсеч = 3,75 см2

multiurok.ru

ГДЗ по геометрии для 10 класса контрольно-измерительные материалы Рурукин А.Н.

ГДЗ от Путина

Найти

    • 1 класс

      • Математика
      • Английский язык
      • Русский язык
      • Немецкий язык
      • Информатика
      • Природоведение
      • Основы здоровья
      • Музыка
      • Литература
      • Окружающий мир
      • Человек и мир
    • 2 класс

      • Математика
      • Английский язык
      • Русский язык
      • Немецкий язык
      • Белорусский язык
      • Украинский язык
      • Информатика
      • Природоведение
      • Основы здоровья
      • Музыка
      • Литература
      • Окружающий мир
      • Человек и мир
      • Технология
    • 3 класс

      gdzputina.ru

      КИМ геометрия 10-11 класс

      Контрольно – измерительные материалы

      по геометрии

      11 класс

      Промежуточный контроль

      .

      Пояснительная записка

      Цель: проверка уровня предметной компетентности учащихся 10-11 класса по геометрии, за курс 10-11 класса.

      Форма проведения контрольных работ: письменно, по контрольно-измерительным материалам.

      Контрольные работы по геометрии за курс 10 — 11 класса составлены на основании рабочей программы и УМК:

        1. Атанасян Л.С. Геометрия. 10-11 кл. Учебник/Атанасян Л.С. и др. – М.: 2013, 255с.

        2. Александров А.Д. Геометрия. 10-11 классы/ Александров А.Д., Вернер А.Л., — М.: 2014. -255 с.

        3. Шлыков В.В. Геометрия. 11 кл. – Минск.: 2009, 182с.

        4. Ершова А.П. Самостоятельные и контрольные работы по геометрии/ Ершова А.П., Голобородько В.В. – М.: 2013, 208с.

        5. Саакян С.М. Изучение геометрии 10-11 кл. Книга для учителя. М.: Просвещение, 2010. — 248 с.

        6. Самостоятельные и контрольные работы А.П. Ершова 11 класс. – Москва. ИЛЕКСА – 2013.

        7. Ю.П. Дудницын Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др. «Геометрия 10-11 кл».: М. Просвещение, 2013.

      Контрольные работы для 11 класса составлены по пройденным темам с целью контроля усвоения нового материала и проверки остаточных знаний.

      Запланировано 3 контрольные работы по следующим темам:

      • Контрольная работа №1 «Метод координат в пространстве»

      • Контрольная работа №2 «Цилиндр, конус, шар»

      • Контрольная работа №3 «Объемы тел»

      Контрольные работы №1

      Контрольная работа №1 «Метод координат в пространстве»

      Вариант 1

      1.Даны точки А(-3;1;4), В(1;-5;2), С(-4;6;2), D(2;-4;8).Вычислите расстояние между серединами отрезков АВ и СD.

      2.Известны координаты трех точек А(-1;2;-5), В(3;-1;6) и С(4;5;-7). Определите координаты точки пересечения медиан треугольника АВС.

      3.В кубе АВСDА1В1С1D1 точка М — центр грани ВВ1С1С. Найдите угол между прямыми АМ и DВ1.

      4.Вершины треугольника АВС имеют координаты А(-8;7;-4), В(-6;5;-5) и С(-5;3;-4). Найдите площадь треугольника АВС.

      5*.Точки А(5;-1;2) и В(1;3;-4) симметричны относительно плоскости α. Напишите уравнение этой плоскости.

      Вариант 2

      1.Даны точки А(5;-1;3), В(3;-5;1), С(2;-6;4), D(-4;2;6). Вычислите расстояние между серединами отрезков АВ и СD.

      2.Известны координаты трех точек А(2;-1;7), В(-4;3;-1) и С(-1;4;3). Определите координаты точки пересечения медиан треугольника АВС.

      3.В кубе АВСDА1В1С1D1 точка М — центр грани АА1В1В. Найдите угол между прямыми DМ и С1В.

      4.Вершины треугольника АВС имеют координаты А(-5;2;-3), В(-3;1;-5) и С(-8;6;-3). Найдите площадь треугольника АВС.

      5*.Точки А(-3;4;7) и В(1;-2;3) симметричны относительно плоскости α. Напишите уравнение этой плоскости.

      Контрольная работа №1 «Метод координат»

      №1

      №2

      №3

      №4

      №5

      Вариант 1

      (2;2;-2)

      arccos

      2х-2у+3z-1=0

      Вариант 2

      (-1;2;3)

      arccos

      2х-3у-2z+15=0

      Контрольная работа №2 «Цилиндр, конус, шар»

      Вариант 1

      1.Диаметр основания цилиндра равен 10 см. На расстоянии 3 см от оси цилиндра проведено сечение, параллельное оси и имеющее форму квадрата. Вычислите площадь этого сечения и площадь осевого сечения цилиндра.

      2.Площадь основания конуса равна 15 см2, а площадь боковой поверхности 17 см2. Найдите площадь осевого сечения конуса.

      3.В усеченном конусе радиус меньшего основания равен R, высота h, угол между образующей и большим основанием равен α. Вычислите площадь боковой поверхности конуса.

      4.Сфера касается одной из параллельных плоскостей и пересекает другую плоскость по окружности радиуса r. Найдите радиус сферы, если расстояние между плоскостями равно а.

      5.Сфера, заданная уравнением х2+у2+z2-2х+6у-4z=11, пересечена плоскостью с уравнением х=4. Вычислите площадь сечения и площадь поверхности сферы.

      Вариант 2

      1.Радиус основания цилиндра, осевое сечение которого квадрат, равен 10 см. На расстоянии 8 см от оси цилиндра проведено сечение, параллельное оси. Вычислите площадь этого сечения и площадь осевого сечения цилиндра.

      2.Площадь основания конуса равна 12 см2, а площадь боковой поверхности 13 см2. Найдите площадь осевого сечения конуса.

      3.В усеченном конусе радиус меньшего основания равен R, образующая l, угол между высотой конуса и его образующей равен α. Вычислите площадь боковой поверхности конуса.

      4.Сфера радиуса R касается одной из параллельных плоскостей и пересекает другую плоскость по окружности. Найдите радиус этой окружности, если расстояние между плоскостями равно а.

      5.Сфера, заданная уравнением х2+у2+z2-4х+2у+6z=7, пересечена плоскостью с уравнением у=-3. Вычислите площадь сечения и площадь поверхности сферы.

      Контрольная работа №2 «Цилиндр, конус, шар»

      №1

      №2

      №3

      №4

      №5

      Вариант 1

      64см2 ; 80см2

      8/π см2

      16π; 100π

      Вариант 2

      240см2; 400см2

      5/π см2

      17π; 84π

      Контрольная работа №3

      «Объемы прямого параллелепипеда, прямой призмы и цилиндра»

      Вариант 1

      1.В прямоугольном параллелепипеде диагонали трех граней, выходящих из одной вершины, равны 7см, 8см и 9см. Вычислите объем параллелепипеда.

      2.Площадь большего диагонального сечения правильной шестиугольной призмы равна площади ее основания. Найдите объем призмы, если сторона ее основания равна а.

      3.В основании прямой призмы лежит трапеция. Площади параллельных боковых граней призмы равны S1 и S2, а расстояние между ними равно а. Вычислите объем призмы.

      4.Периметры боковых граней прямоугольного параллелепипеда равны 16см и 24см. Найдите объем параллелепипеда, имеющего наибольшую боковую поверхность.

      5.Прямоугольник с диагональю, равной 2см, вращается вокруг одной из сторон. Вычислите объем тела вращения, если этот объем имеет наибольшее возможное значение.

      Вариант 2

      1.В прямоугольном параллелепипеде диагонали трех граней, выходящих из одной вершины, равны 5см, 7см и 8см. Вычислите объем параллелепипеда.

      2.Площадь меньшего диагонального сечения правильной шестиугольной призмы равна площади ее основания. Найдите объем призмы, если ее высота равна h.

      3.В основании прямой призмы лежит трапеция. Объем призмы равен V.Площади параллельных боковых граней призмы равны S1 и S2. Вычислите расстояние между ними.

      4.Периметры боковых граней прямоугольного параллелепипеда равны 20см и 28см. Найдите объем параллелепипеда, имеющего наибольшую боковую поверхность.

      5.Прямоугольник с диагональю, равной 3см, вращается вокруг одной из сторон. Вычислите объем тела вращения, если этот объем имеет наибольшее возможное значение.

      Контрольная работа №3

      «Объемы прямого параллелепипеда, прямой призмы и цилиндра»

      №1

      №2

      №3

      №4

      №5

      Вариант 1

      48см3

      105см3

      16π см3

      Вариант 2

      20см3

      192см3

      54π см3

      Контрольная работа №3

      «Объемы наклонной призмы, пирамиды, конуса и шара»

      Вариант 1

      1.В основании призмы лежит треугольник, у которого одна сторона равна 2см, а две другие по 3см.Боковое ребро равно 6см и составляет с плоскостью основания угол 60º. Найдите объем призмы.

      2.Сторона основания правильной треугольной пирамиды равна а, боковое ребро равно в. Найдите объем пирамиды.

      3.Радиусы оснований усеченного конуса равны 5см и 20см, образующая равна 17см. Найдите объем усеченного конуса.

      4.Сечение, перпендикулярное диаметру шара, делит этот диаметр в отношении 1:2. Вычислите объем меньшего шарового сегмента, отсекаемого от шара, если площадь поверхности шара равна 144π см2.

      5.В основании пирамиды лежит ромб со стороной а и углов 60º. Одна из боковых граней перпендикулярна основанию, а две соседние с ней грани образуют с основанием двугранные углы по 30º.Найдите объем пирамиды.

      Вариант 2

      1.В основании призмы лежит треугольник, у которого одна сторона равна 6см, а две другие по 5см.Боковое ребро равно 4см и составляет с плоскостью основания угол 45º. Найдите объем призмы.

      2.Сторона основания правильной четырехугольной пирамиды равна а, боковое ребро равно в. Найдите объем пирамиды.

      3.Радиусы оснований усеченного конуса равны 5см и 13см, образующая равна 17см. Найдите объем усеченного конуса.

      4.Сечение, перпендикулярное диаметру шара, делит этот диаметр в отношении 1:3. Площадь поверхности шара равна 144π см2. Вычислите объем большего шарового сегмента, отсекаемого от шара.

      5.В основании пирамиды лежит ромб со стороной а и углов 30º. Одна из боковых граней перпендикулярна основанию, а две соседние с ней грани образуют с основанием двугранные углы по 45º.Найдите объем пирамиды.

      Контрольная работа №3

      «Объемы наклонной призмы, пирамиды, конуса и шара»

      №1

      №2

      №3

      №4

      №5

      Вариант 1

      6см3

      1400π см3

      см3

      Вариант 2

      24см3

      1295π см3

      см3

      Контрольная работа 3. «Объемы многогранников»

      1 Вариант

      1. Основание прямой призмы прямоугольный треугольник с катетами 16 и 4 , объем равен 320. Найти боковую поверхность призмы.

      1. Высота цилиндра равен 8 см, а диагональ осевого сечения 20 см. Найдите объем цилиндра.

      1. Найти объем конуса , если его образующая равна 13, а высота – 5.

      1. Длина окружности сечения, проходящего через центр шара , равна 8π см. Найти объем шара.

      1. Диагональ прямоугольного параллелепипеда равна 6 и образует с боковыми гранями углы 30 с и 45 с . Найдите объем параллелепипеда.

      2 Вариант

      1. Основание прямой призмы прямоугольный треугольник с гипотенузой 10 и катетом 8, объем призмы 240. Найти площадь боковой поверхности.

      1. Радиус цилиндра равен 3 см, а диагональ осевого сечения 15 см. Найдите объем цилиндра.

      1. Найдите объем конуса, если его радиус равен 3, а образующая наклонена к плоскости основания под углом 45с

      2. Сечение шара, удаленное от центра на 3 см, имеет площадь 16 π см 2. Найти объем шара.

      1. Диагональ боковой грани прямоугольного параллелепипеда равна . Диагональ параллелепипеда образует с плоскостью этой грани угол 45 с, а с плоскостью основания — 30 с . Найдите объем параллелепипеда.

      Итоговая контрольная работа

      Вариант 1

      В правильной четырехугольной пирамиде МАВСD сторона основания равна 6, а боковое ребро 5. Найдите:

      1. площадь боковой поверхности пирамиды;

      2. объем пирамиды;

      3. угол наклона боковой грани к плоскости основания;

      4. скалярное произведение векторов ;

      5. площадь описанной около пирамиды сферы;

      6. *угол между ВD и плоскостью DMC.

      Вариант 2

      В правильной четырехугольной пирамиде МАВСD боковое ребро равно 8 и наклонено к плоскости основания под углом 60º. Найдите:

      1. площадь боковой поверхности пирамиды;

      2. объем пирамиды;

      3. угол между противоположными боковыми гранями;

      4. скалярное произведение векторов  , где Е – середина DС;

      5. объем описанного около пирамиды шара;

      6. *угол между боковым ребром АМ и плоскостью DМС.

      2.Зачеты

      Зачет по теме «Векторы в пространстве»

      Вопросы к зачету:

      1. Дайте определение: вектора; коллинеарных векторов; сонаправленных векторов; противоположно направленных векторов; компланарных векторов; произведения вектора на число.

      2. Опишите с помощью чертежа: правило треугольника сложения векторов; правило параллелограмма сложения векторов; правило вычитания векторов; правило параллелепипеда для сложения трех некомпланарных векторов

      3. Сформулируйте: признак компланарности векторов; теорему о разложении вектора по трем некомпланарным векторам.

      Задания для зачета

      Вариант 1.

      1. Верно ли, что векторы, лежащие на боковых ребрах призмы, коллинеарны?

      2. Могут ли три компланарных вектора лежать на трех взаимно перпендикулярных прямых?

      3. Верно ли, что векторы, лежащие на двух прямых, перпендикулярных к третьей, коллинеарны?

      4. Могут ли три вектора, один из которых является суммой двух других, быть некомпланарными?

      5. Точки А и С симметричны относительно плоскости α, а точки В и D симметричны относительно прямой АС. Назовите вектор, равный вектору

      6. Даны ненулевые векторы ,, некомпланарны. Назовите два данных вектора, которые вместе с вектором образуют тройку некомпланарных векторов, если =2.

      7. Назовите вектор, равный + —

      8. В параллелепипеде АВСDА1В1С1D1 назовите вектор, равный — — + .

      Вариант 2.

      1. Верно ли, что векторы, лежащие на боковых ребрах пирамиды, коллинеарны?

      2. Могут ли три некомпланарных вектора лежать на трех параллельных прямых?

      3. Верно ли, что векторы, лежащие в двух параллельных плоскостях, коллинеарны?

      4. Могут ли три вектора, один из которых является разностью двух других, быть некомпланарными?

      5. Точки А и С симметричны относительно плоскости α, а точки В и D симметричны относительно прямой АС. Назовите вектор, равный вектору

      6. Даны ненулевые векторы ,, некомпланарны. Назовите два данных вектора, которые вместе с вектором образуют тройку некомпланарных векторов, если = — 3.

      7. Назовите вектор, равный + —

      8. В параллелепипеде АВСDА1В1С1D1 назовите вектор, равный — — + .

      Зачет по теме «Метод координат в пространстве»

      Вопросы к зачету:

        1. Дайте определение: радиус-вектора точки. Назовите координаты радиус-вектора точки А(а1;а2;а3).

        2. Сформулируйте: правило вычисления координат вектора по координатам его концов.

        3. Запишите формулу: координат середины отрезка; разложения вектора {х;у;z} по координатным векторам; длины вектора; Расстояния между двумя точками.

        4. Дайте определение: скалярного произведения векторов в пространстве.

        5. Запишите формулу: вычисления скалярного произведения двух векторов по их координатам.

        6. Перечислите: виды движений в пространстве и виды симметрии в пространстве.

      Задания для зачета

      Вариант 1.

          1. Может ли вектор с тремя ненулевыми координатами быть параллелен одной из координатных плоскостей?

          2. Дан вектор {-1;2;0}. Назовите координатный вектор, образующий с вектором тупой угол.

          3. Закончите утверждение: «Если две точки симметричны относительно плоскости Охz , то их ординаты…».

          4. Верно ли, что точки симметричны относительно оси Оz , имеют противоположные аппликаты?

          5. Может ли вектор, коллинеарный одному из координатных векторов, иметь ровно одну ненулевую координату?

          6. При зеркальной симметрии куба АВСDА1В1С1D1 относительно одной из плоскостей его симметрии, ребро АА1 отображается на ребро ВА. Назовите плоскость симметрии.

          7. Закончите утверждение: «Если вектор лежит на прямой а, то при параллельном переносе на вектор прямая а…».

          8. Закончите утверждение: «Если при осевой симметрии плоскость отображается на себя, то она перпендикулярна к оси симметрии либо …».

      Вариант 2.

          1. Может ли вектор с тремя ненулевыми координатами быть перпендикулярен к одной из координатных плоскостей?

          2. Дан вектор {-1;2;0}. Назовите координатный вектор, образующий с вектором острый угол.

          3. Закончите утверждение: «Если две точки симметричны относительно оси Оz , то они имеют равные…».

          4. Верно ли, что точки симметричны относительно плоскости Охz , имеют противоположные ординаты?

          5. Может ли вектор, коллинеарный одному из координатных векторов, иметь ровно две ненулевые координаты?

          6. При зеркальной симметрии куба АВСDА1В1С1D1 относительно одной из плоскостей его симметрии, ребро ВВ1 отображается на ребро ВА. Назовите плоскость симметрии.

          7. Закончите утверждение: «Если вектор лежит на прямой, параллельной прямой а, то при параллельном переносе на вектор прямая а…».

          8. Закончите утверждение: «Если при зеркальной симметрии прямая отображается на себя, то она лежит в плоскости симметрии либо …».

      Зачет по теме «Цилиндр. Конус. Шар»

      Вопросы к зачету:

      1. Дайте определение: радиус-вектора точки. Назовите координаты радиус-вектора точки А(а1;а2;а3).

      2. Сформулируйте: правило вычисления координат вектора по координатам его концов.

      3. Запишите формулу: координат середины отрезка; разложения вектора {х;у;z} по координатным векторам; длины вектора; Расстояния между двумя точками.

      4. Дайте определение: скалярного произведения векторов в пространстве.

      5. Запишите формулу: вычисления скалярного произведения двух векторов по их координатам.

      6. Перечислите: виды движений в пространстве и виды симметрии в пространстве.

      Задания для зачета

      Вариант 1.

      1. Может ли вектор с тремя ненулевыми координатами быть параллелен одной из координатных плоскостей?

      2. Дан вектор {-1;2;0}. Назовите координатный вектор, образующий с вектором тупой угол.

      3. Закончите утверждение: «Если две точки симметричны относительно плоскости Охz , то их ординаты…».

      4. Верно ли, что точки симметричны относительно оси Оz , имеют противоположные аппликаты?

      5. Может ли вектор, коллинеарный одному из координатных векторов, иметь ровно одну ненулевую координату?

      6. При зеркальной симметрии куба АВСDА1В1С1D1 относительно одной из плоскостей его симметрии, ребро АА1 отображается на ребро ВА. Назовите плоскость симметрии.

      7. Закончите утверждение: «Если вектор лежит на прямой а, то при параллельном переносе на вектор прямая а…».

      8. Закончите утверждение: «Если при осевой симметрии плоскость отображается на себя, то она перпендикулярна к оси симметрии либо …».

      Вариант 2.

      1. Может ли вектор с тремя ненулевыми координатами быть перпендикуляре к одной из координатных плоскостей?

      2. Дан вектор {-1;2;0}. Назовите координатный вектор, образующий с вектором острый угол.

      3. Закончите утверждение: «Если две точки симметричны относительно оси Оz , то они имеют равные…».

      4. Верно ли, что точки симметричны относительно плоскости Охz , имеют противоположные ординаты?

      5. Может ли вектор, коллинеарный одному из координатных векторов, иметь ровно две ненулевые координаты?

      6. При зеркальной симметрии куба АВСDА1В1С1D1 относительно одной из плоскостей его симметрии, ребро ВВ1 отображается на ребро ВА. Назовите плоскость симметрии.

      7. Закончите утверждение: «Если вектор лежит на прямой, параллельной прямой а, то при параллельном переносе на вектор прямая а…».

      8. Закончите утверждение: «Если при зеркальной симметрии прямая отображается на себя, то она лежит в плоскости симметрии либо …».

      Зачет по теме «Объемы тел»

      Вопросы к зачету:

      Запишите формулу:

      — объема прямоугольного параллелепипеда;

      — объема куба;

      — объема цилиндра;

      — объема конуса;

      — объема пирамиды;

      — объема шара;

      — объема усеченной пирамиды;

      — объема усеченного конуса;

      — площади сферы.

      Задания для зачета

      Вариант 1.

      1. Верно ли, что прямая и наклонная призмы с соответственно равными основаниями могут иметь равные объемы?

      2. Могут ли два цилиндра с равными объемами иметь неравные радиусы?

      3. Основание пирамиды SАВСD – ромб АВСD. Определите, какую часть объема данной пирамиды составляет объем пирамиды SАВD?

      4. Определите, цилиндром, конусом или усеченным конусом является данное тело, если сечение, параллельное основанию и делящее высоту пополам, делит данное тело на два тела с равными объемами.

      5. Верно ли, что отношение высот двух пирамид с равными основаниями равно отношению объемов пирамид?

      6. Может ли плоскость, делящая объем шара пополам, делить поверхность шара на части неравной площади?

      7. Два цилиндра с радиусами r1 и r2 и объемами V1 и V2 имеют равные площади осевых сечений. Сравните V1 и V2 , если r1 > r2.

      Вариант 2.

      1. Верно ли, что правильная и неправильная пирамиды с равными основаниями могут иметь неравные объемы?

      2. Могут ли два шара с равными объемами иметь неравные радиусы?

      3. Основание пирамиды SАВСD – ромб АВСD. Определите, какую часть объема данной пирамиды составляет объем пирамиды SСОD, где О – точка пересечения диагоналей ромба АВСD.

      4. Определите, цилиндром, конусом или усеченным конусом является данное тело, если сечение, параллельное основанию и делящее объем данного тела пополам, проходит через середину его высоты.

      5. Верно ли, что отношение сторон оснований двух правильных треугольных пирамид с равными высотами равно отношению объемов пирамид?

      6. Может ли плоскость, делящая поверхность шара пополам, делить шар на два тела с неравными объемами ?

      7. Два цилиндра с радиусами r1 и r2 и объемами V1 и V2 имеют равные площади осевых сечений. Сравните r1 и r2 , если V1 < V2 .

      infourok.ru

      Календарно-тематическое планирование по геометрии (10 класс) на тему: КИМ 10 кл. Геометрия

      ПРАВИТЕЛЬСТВО САНКТ-ПЕТЕРБУРГА

      КОМИТЕТ ПО ОБРАЗОВАНИЮ

      Государственное бюджетное образовательное учреждение

      Гимназия № 49 Приморского района

      «СОГЛАСОВАНО»

      Заместитель директора

       по учебно-воспитательной работе

      Мелешкевич Е.В.

      «   » августа 2014 г.

      «РАССМОТРЕНО»

      на заседании МО

      учителей математики и информатики

      протокол №1 от «28 » августа 2014г.

      Руководитель МО

                          Сивкова Т.В. 

      «ПРИНЯТО»

      Решением педагогического совета

      Протокол №

      от «   » августа 2014г.

      «УТВЕРЖДАЮ»

      Приказ № 62/1 от « 28» августа 2014 года

      Директор ГБОУ школы № 49

      Приморского района

      Санкт-Петербурга

                                    Семочкина Ф.Ф.

                                                                                                                       

      Система оценочных средств

      по предмету ГЕОМЕТРИЯ

      10  класс

                                                                                        Составитель:

                                                                   Сивкова Татьяна Владимировна,

      учитель математики.

                            г. Санкт-Петербург

                              2014-2015 учебный год

      КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ

      ГЕОМЕТРИЯ

      10 класс  

      Полугодие

      Четверть

      Тема раздела

      Всего часов

      Номер урока

      Контрольная работа

      ПЕРВОЕ

      Первая

      Введение.  Аксиомы стереометрии

      4

      Параллельность прямых и плоскостей

      19

      14

      Контрольная работа №1

      По теме: «Аксиомы стереометрии. Параллельность прямой и плоскости»

      Вторая

      22

      Контрольная работа №2

      по теме:  «Параллельность прямых и плоскостей»

      Перпендикулярность прямых и плоскостей

      17

      ВТОРОЕ

      Третья

      39

      Контрольная работа №3

      по теме: «Перпендикулярность прямых и плоскостей»

      Многогранники

      10

      Четвертая

      50

      Контрольная работа №4

      по теме: «Многогранники»

      Повторение курса 10 класса  

      12

      67-68

      Итоговая контрольная работа

      Рекомендации но оценке знаний и умений учащихся но математике

      Подготовлены с использованием материалов сборника приказов и инструкции Министерства образования Российской Федерации №34 — 35 за 1980г.

      Опираясь на рекомендации, учитель оценивает знания и умения учащихся с учетом их индивидуальных особенностей.

      1. Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
      2. Основными формами проверки знаний и умений учащихся по математике являются письменные работы и устный опрос.

      Основными видами письменных работ являются: упражнения, составления схем и таблиц, текущие письменные самостоятельные (обучающие и проверочные) работы, лабораторные работы, тесты, итоговые контрольные работы и т.п.

      1. При оценке письменных работ  учитель в первую очередь учитывает показанные учащимися знания и умения. Оценка зависит также от наличия и характера погрешностей, допущенных учащимися.
      1. Среди погрешностей выделяются ошибки и недочеты. Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.

      К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в программе основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения: небрежное выполнение чертежа.

      Критерии ошибок:

      1. К   грубым ошибкам относятся ошибки, которые:
      2. — обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; незнание приемов решения задач, рассматриваемых в учебниках, а также вычислительные ошибки, если они не являются опиской;
      • неумение выделить в ответе главное, неумение делать выводы и обобщения, неумение

      пользоваться первоисточниками, учебником и справочниками.

              

                  К не грубым ошибкам относятся:

      • потеря корня или сохранение в ответе постороннего корня: отбрасывание без объяснений одного из них и равнозначные им;

      допущенные в процессе списывания числовых данных (искажения, замена), нарушения в формулировке вопроса (ответа).

                К   недочетам относятся:

      • описки, недостаточность или отсутствие пояснений, обоснований в решениях.
      • небрежное выполнение записей, чертежей, схем, графиков;
      • орфографические ошибки, связанные с написанием математических терминов.

      Контрольная работа 1. Аксиомы стереометрии. Параллельность прямых и плоскостей

      Вариант 1

      1. Прямая c и плоскость а  параллельны прямой b. Определите, может ли прямая c:

      а)        быть параллельной плоскости а;

      б)        пересекать плоскость а;

      в)        лежать в плоскости а.

      1. Докажите, что каждая из двух параллельных прямых не может пересекать каждую из двух скрещивающихся прямых.
      2. Точки А1 и В] лежат в плоскости а, а точки  A2 и В2 — в плоскости b, параллельной плоскости а. Отрезки А1А2 и В1В2 пересекаются в точке С. Найдите A1A2  , если В1В2 = 18 см, В1С = 8 см, СА2 = 5 см.
      3. Точка М не лежит ни на одной из двух скрещивающихся прямых. Докажите, что через эту точку проходит плоскость, параллельная каждой из этих прямых, и притом только одна.

      Контрольная работа 1. Аксиомы стереометрии. Параллельность прямых и плоскостей

      Вариант 2

      1. Прямая c и плоскость а параллельны плоскости р. Определите, может ли прямая c:

      а)        быть параллельной плоскости p;

      б)        пересекать плоскость p;

      в)        лежать в плоскости p.

      1. Докажите, что каждая из двух пересекающихся прямых не может пересекать каждую из двух скрещивающихся прямых.
      2. Точки А1 и В1 лежат в плоскости а, а точки A2 иВ2 — в плоскости p, параллельной плоскости а. Отрезки А1А2 и В1В2 пересекаются в точке С. Найдите В1В2, если А1А2 = 20 см, В1С = 6 см, СА2 = 12 см.
      3. Прямая а и параллельная ей плоскость p не проходят через точку М. Докажите, что через точку М проходит прямая, параллельная прямой а и плоскости p , и притом только одна.

      Контрольная работа 1. Аксиомы стереометрии. Параллельность прямых и плоскостей

      Вариант 1

      1. Прямая c и плоскость а  параллельны прямой b. Определите, может ли прямая c:

      а)        быть параллельной плоскости а;

      б)        пересекать плоскость а;

      в)        лежать в плоскости а.

      1. Докажите, что каждая из двух параллельных прямых не может пересекать каждую из двух скрещивающихся прямых.
      2. Точки А1 и В] лежат в плоскости а, а точки  A2 и В2 — в плоскости b, параллельной плоскости а. Отрезки А1А2 и В1В2 пересекаются в точке С. Найдите A1A2  , если В1В2 = 18 см, В1С = 8 см, СА2 = 5 см.
      3. Точка М не лежит ни на одной из двух скрещивающихся прямых. Докажите, что через эту точку проходит плоскость, параллельная каждой из этих прямых, и притом только одна.

      Контрольная работа 1. Аксиомы стереометрии. Параллельность прямых и плоскостей

      Вариант 2

      1. Прямая c и плоскость а параллельны плоскости р. Определите, может ли прямая c:

      а)        быть параллельной плоскости p;

      б)        пересекать плоскость p;

      в)        лежать в плоскости p.

      1. Докажите, что каждая из двух пересекающихся прямых не может пересекать каждую из двух скрещивающихся прямых.
      2. Точки А1 и В1 лежат в плоскости а, а точки A2 иВ2 — в плоскости p, параллельной плоскости а. Отрезки А1А2 и В1В2 пересекаются в точке С. Найдите В1В2, если А1А2 = 20 см, В1С = 6 см, СА2 = 12 см.
      3. Прямая а и параллельная ей плоскость p не проходят через точку М. Докажите, что через точку М проходит прямая, параллельная прямой а и плоскости p , и притом только одна.

      Контрольная работа 2. Перпендикулярность прямой и плоскости

      Вариант 1

      1.Наклонная, проведенная из точки к плоскости, равна 10 см и образует со своей проекцией на данную плоскость угол 30°. Найдите расстояние от точки до плоскости.

      2. Через вершины А и В треугольника  ∆ABC проведены параллельные прямые АА1 и ВВ1, причем АА1⊥А В и АА1 ⊥ АС. 

      Докажите, что ВВ1⊥ВС.

      3. Точка S не лежит в плоскости прямоугольника ABCD и равноудалена от его вершин. Найдите расстояние от точки S до плоскости прямоугольника, если стороны прямоугольника равны 6 и 8 см, а SA= 13 см.

      4. Вершина А треугольника ∆ABC является основанием перпендикуляра AD к плоскости треугольника. Докажите, что если

      BDA = CDA, то DBC = DCB.

      Контрольная работа 2. Перпендикулярность прямой и плоскости

      Вариант 2

      1. Из точки, удаленной от плоскости на 8 см, к плоскости проведены наклонная и перпендикуляр, угол между которыми равен 60°. Найдите длину наклонной.

      2. Через вершины А и В треугольника ∆ABC проведены прямые АА1и ВВ1, причем АА1 ⊥AB, АА1⊥АС, ВВ1 ⊥AB, ВВ1 ⊥ ВС. Докажите, что ВВ1 I I АА1.

      3. Точка S не лежит в плоскости прямоугольника ABCD и равноудалена от его вершин. Найдите расстояние от точки S до вершин прямоугольника, если расстояние от точки S до плоскости AВС равно 24 см, АВ = 12 см, ВС = 16 см.

      4. Вершина А треугольника ∆ABC является основанием перпендикуляра AD к плоскости треугольника. Докажите, что если

       DBA = DCA, то DBC = DCB.

      Контрольная работа 2. Перпендикулярность прямой и плоскости

      Вариант 1

      1.Наклонная, проведенная из точки к плоскости, равна 10 см и образует со своей проекцией на данную плоскость угол 30°. Найдите расстояние от точки до плоскости.

      2. Через вершины А и В треугольника  ∆ABC проведены параллельные прямые АА1 и ВВ1, причем АА1⊥А В и АА1 ⊥ АС. 

      Докажите, что ВВ1⊥ВС.

      3. Точка S не лежит в плоскости прямоугольника ABCD и равноудалена от его вершин. Найдите расстояние от точки S до плоскости прямоугольника, если стороны прямоугольника равны 6 и 8 см, а SA= 13 см.

      4. Вершина А треугольника ∆ABC является основанием перпендикуляра AD к плоскости треугольника. Докажите, что если

      BDA = CDA, то DBC = DCB.

      Контрольная работа 2. Перпендикулярность прямой и плоскости

      Вариант 2

      1. Из точки, удаленной от плоскости на 8 см, к плоскости проведены наклонная и перпендикуляр, угол между которыми равен 60°. Найдите длину наклонной.

      2. Через вершины А и В треугольника ∆ABC проведены прямые АА1и ВВ1, причем АА1 ⊥AB, АА1⊥АС, ВВ1 ⊥AB, ВВ1 ⊥ ВС. Докажите, что ВВ1 I I АА1.

      3. Точка S не лежит в плоскости прямоугольника ABCD и равноудалена от его вершин. Найдите расстояние от точки S до вершин прямоугольника, если расстояние от точки S до плоскости AВС равно 24 см, АВ = 12 см, ВС = 16 см.

      4. Вершина А треугольника ∆ABC является основанием перпендикуляра AD к плоскости треугольника. Докажите, что если

       DBA = DCA, то DBC = DCB.

      Контрольная работа 3.  Перпендикулярность плоскостей

      Вариант 1

      1. Через вершину К треугольника DKP проведена прямая КМ, перпендикулярная плоскости этого треугольника. Известно, что КМ= 15 см, DP= 12 см, DK = РК= 10 см. Найдите расстояние от точки М до прямой DP.

      2. Точка, удаленная от плоскости квадрата на 8 см, равноудалена от его сторон. Площадь квадрата 144 см2. Найдите расстояние от данной точки до сторон квадрата.

      3. Перпендикулярные плоскости а и p пересекаются по прямой f. Отрезки ОА и ОВ, лежащие в плоскостях а и р соответственно, перпендикулярны прямой I, а их общий конец — точка О — лежит на прямой f. Найдите длины отрезков ОА и ОВ, если АВ = 40 см, а

      ОА : О В = 3 : 4.

      4. Концы отрезков принадлежат двум перпендикулярным плоскостям. Сумма расстояний от концов отрезка до данных плоскостей равна 22 см, а его проекции на плоскости равны 20 и 24 см. Найдите длину отрезка.

      Контрольная работа 3.  Перпендикулярность плоскостей

      Вариант 2

      1. Через вершину А-треугольника КМР проведена прямая КЕ, перпендикулярная плоскости этого треугольника. Известно, что КЕ= 8 см, МР= 2 см, МК = РК. Найдите КМ, если расстояние от

      точки Е до прямой МР равно 2см.

      2. Точка удалена от каждой из сторон квадрата на 13 см. Диагональ квадрата равна 10см. Найдите расстояние от данной точки до плоскости квадрата.

      3. Перпендикулярные плоскости а и p пересекаются по прямой k. Отрезки ОА и ОВ, лежащие в плоскостях а и p соответственно, перпендикулярны прямой k , а их общий конец — точка О — лежит на прямой k. Найдите длину отрезка АВ, если ОА= 20 см,

              а СВ: АВ = 12: 13.

      4. Концы отрезков принадлежат двум перпендикулярным плоскостям. Сумма проекций отрезка на данные плоскости равна 44 см, а его концы удалены от этих плоскостей на 7 и 15 см. Найдите длину отрезка.

      Контрольная работа 3.  Перпендикулярность плоскостей

      Вариант 1

      1. Через вершину К треугольника DKP проведена прямая КМ, перпендикулярная плоскости этого треугольника. Известно, что КМ= 15 см, DP= 12 см, DK = РК= 10 см. Найдите расстояние от точки М до прямой DP.

      2. Точка, удаленная от плоскости квадрата на 8 см, равноудалена от его сторон. Площадь квадрата 144 см2. Найдите расстояние от данной точки до сторон квадрата.

      3. Перпендикулярные плоскости а и p пересекаются по прямой f. Отрезки ОА и ОВ, лежащие в плоскостях а и р соответственно, перпендикулярны прямой I, а их общий конец — точка О — лежит на прямой f. Найдите длины отрезков ОА и ОВ, если АВ = 40 см, а

      ОА : О В = 3 : 4.

      4. Концы отрезков принадлежат двум перпендикулярным плоскостям. Сумма расстояний от концов отрезка до данных плоскостей равна 22 см, а его проекции на плоскости равны 20 и 24 см. Найдите длину отрезка.

      Контрольная работа 3.  Перпендикулярность плоскостей

      Вариант 2

      1. Через вершину А-треугольника КМР проведена прямая КЕ, перпендикулярная плоскости этого треугольника. Известно, что КЕ= 8 см, МР= 2 см, МК = РК. Найдите КМ, если расстояние от   точки Е до прямой МР равно 2см.

      2. Точка удалена от каждой из сторон квадрата на 13 см. Диагональ квадрата равна 10см. Найдите расстояние от данной точки до плоскости квадрата.

      3. Перпендикулярные плоскости а и p пересекаются по прямой k. Отрезки ОА и ОВ, лежащие в плоскостях а и p соответственно, перпендикулярны прямой k , а их общий конец — точка О — лежит на прямой k. Найдите длину отрезка АВ, если ОА= 20 см,

              а СВ: АВ = 12: 13.

      4. Концы отрезков принадлежат двум перпендикулярным плоскостям. Сумма проекций отрезка на данные плоскости равна 44 см, а его концы удалены от этих плоскостей на 7 и 15 см. Найдите длину отрезка.

      Контрольная работа 4. Декартовы координаты и векторы в пространстве

      Вариант 1

      1. Найдите координаты и модуль вектора , если A (5; —1; 3),

             B (2; -2; 4).

      2. Даны векторы {3; 1; -2} и {1; 4; -3}. Найдите | 2 — |.

      3. Даны точки P(1; 0; 2), H ( 1;; 3), К(-1; 0; 3), М (—1; —1; 3). Найдите угол между векторами  и

      4. Найдите скалярное произведение · (— 2), если | | =2,

      | \ =4, а угол между векторами  и    равен 135°.

      5. Дан параллелепипед ABCDA1B1C1D1. Назовите один из векторов, начало и конец которого являются вершинами параллелепипеда, равный:

      а)        + + +        б )  –

      Контрольная работа 4. Декартовы координаты и векторы в пространстве

      Вариант 2

      1. Найдите координаты и модуль вектора , если   А (6; 3; -2),

         В (2; 4; —5).

      2. Даны векторы { 5; —1; 2} и {3; 2; -4}. Найдите |  — |.

      3. Даны точки E(2; 0; 1), M (3; ; 1), F ( 3; 0;-1) , K(3; -1 ;-1 ).

      Найдите угол между векторами  и

      4.Найдите скалярное произведение · (+), если | | =3,

      | \ =2, а угол между векторами  и    равен 150°.

      5. Дан параллелепипед ABCDA1B1C1D1.  Назовите один из векторов, начало и конец которого являются вершинами параллелепипеда, равный:

      а)        + + +        б )  –

      Контрольная работа 4. Декартовы координаты и векторы в пространстве

      Вариант 1

      1. Найдите координаты и модуль вектора , если A (5; —1; 3),

             B (2; -2; 4).

      2. Даны векторы {3; 1; -2} и {1; 4; -3}. Найдите | 2 — |.

      3. Даны точки P(1; 0; 2), H ( 1;; 3), К(-1; 0; 3), М (—1; —1; 3). Найдите угол между векторами  и

      4. Найдите скалярное произведение · (— 2), если | | =2,

      | \ =4, а угол между векторами  и    равен 135°.

      5. Дан параллелепипед ABCDA1B1C1D1. Назовите один из векторов, начало и конец которого являются вершинами параллелепипеда, равный:

      а)        + + +        б )  –

      Контрольная работа 4. Декартовы координаты и векторы в пространстве

      Вариант 2

      1. Найдите координаты и модуль вектора , если   А (6; 3; -2),

         В (2; 4; —5).

      2. Даны векторы { 5; —1; 2} и {3; 2; -4}. Найдите |  — |.

      3. Даны точки E(2; 0; 1), M (3; ; 1), F ( 3; 0;-1) , K(3; -1 ;-1 ).

      Найдите угол между векторами  и

      4.Найдите скалярное произведение · (+), если | | =3,

      | \ =2, а угол между векторами  и    равен 150°.

      5. Дан параллелепипед ABCDA1B1C1D1.  Назовите один из векторов, начало и конец которого являются вершинами параллелепипеда, равный:

      а)        + + +        б )  –

      Контрольная работа 5 (итоговая)

      Вариант 1

      1. Прямоугольник ABCD и треугольник АВМ не лежат в одной плоскости. Точки Е и F— середины отрезков AM и ВМ. Определите вид четырехугольника DEFC.
      2. Из точки к плоскости проведены две наклонные, образующие с данной плоскостью углы 30° и 45°. Найдите расстояние между основаниями наклонных, если большая наклонная равна 2см, а угол между наклонными — прямой.
      3. Точка удалена от каждой из вершин правильного треугольника на 10 см, а от каждой из его сторон — на см. Найдите расстояние от данной точки до плоскости треугольника.
      4. Прямая МА перпендикулярна стороне АВ и диагонали АС ромба ABCD. Найдите угол между плоскостями МАВ и MAD, если диагональ ромба BD равна его стороне.

      Контрольная работа 5 (итоговая)

      Вариант 2

      1. Точка М не лежит в плоскости ромба ABCD. Точки Е и F — середины отрезков MB и МС. Определите вид четырехугольника AEFD.
      2. Из точки к плоскости проведены две наклонные, образующие с данной плоскостью углы 30° и 45°. Найдите расстояние между основаниями наклонных, если проекция меньшей наклонной равна 3 см, а угол между наклонными — прямой.
      3. Точка удалена от каждой из вершин квадрата на см, а от каждой из его сторон — на 5 см. Найдите расстояние от данной точки до плоскости квадрата.
      4. Прямая MB перпендикулярна стороне АВ и высоте ВК ромба ABCD. Найдите угол между плоскостями МАВ и МВС, если точка К — середина стороны AD.

      Контрольная работа 5 (итоговая)

      Вариант 1

      1. Прямоугольник ABCD и треугольник АВМ не лежат в одной плоскости. Точки Е и F— середины отрезков AM и ВМ. Определите вид четырехугольника DEFC.
      2. Из точки к плоскости проведены две наклонные, образующие с данной плоскостью углы 30° и 45°. Найдите расстояние между основаниями наклонных, если большая наклонная равна 2см, а угол между наклонными — прямой.
      3. Точка удалена от каждой из вершин правильного треугольника на 10 см, а от каждой из его сторон — на см. Найдите расстояние от данной точки до плоскости треугольника.
      4. Прямая МА перпендикулярна стороне АВ и диагонали АС ромба ABCD. Найдите угол между плоскостями МАВ и MAD, если диагональ ромба BD равна его стороне.

      Контрольная работа 5 (итоговая)

      Вариант 2

      1. Точка М не лежит в плоскости ромба ABCD. Точки Е и F — середины отрезков MB и МС. Определите вид четырехугольника AEFD.
      2. Из точки к плоскости проведены две наклонные, образующие с данной плоскостью углы 30° и 45°. Найдите расстояние между основаниями наклонных, если проекция меньшей наклонной равна 3 см, а угол между наклонными — прямой.
      3. Точка удалена от каждой из вершин квадрата на см, а от каждой из его сторон — на 5 см. Найдите расстояние от данной точки до плоскости квадрата.
      4. Прямая MB перпендикулярна стороне АВ и высоте ВК ромба ABCD. Найдите угол между плоскостями МАВ и МВС, если точка К — середина стороны AD.

      nsportal.ru

      измерительные материалы по геометрии, 10 класс

      Урок 5. Решение задач на применение аксиом стереометрии.

      Цель урока: закрепить усвоение вопросов теории в процессе решения; проверить уровень подготовленности учащихся путем проведения самостоятельной работы контролирующего характера.

      Самостоятельная работа

      I уровень

      Вариант I

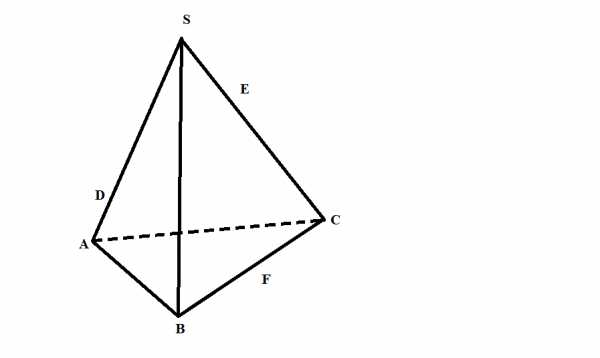
      1. Пользуясь данным рисунком, назовите: а) четыре точки, лежащие в плоскости SAB; б) плоскость, в которой лежит прямая MN; в) прямую, по которой пересекаются плоскости SAC и SBC.

      2. Точка С – общая точка плоскости и . Прямая проходит через точку С. Верно ли, что плоскости и пересекаются по прямой с? Ответ объясните.

      3. Через прямую и точку А можно провести две различные плоскости. Каково взаимное расположение прямой и точки А? Ответ объясните.

      Вариант II

      1. Пользуясь данным рисунком, назовите: а) четыре точки, лежащие в плоскости АВС; б) плоскость, в которой лежит прямая KN; в) прямую, по которой пересекаются плоскости SAC и CAB.

      2. Плоскости и имеют три общие точки. Верно ли, что эти плоскости совпадают? Ответ объясните.

      3. Через А, В и С можно провести две различные плоскости. Каково взаимное расположение точек А, В и С? Ответ объясните.

      II уровень

      Вариант I

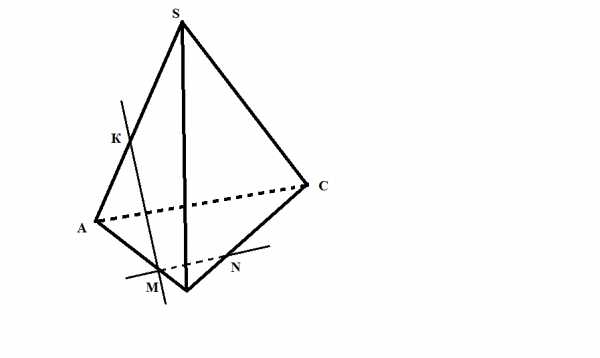
      1. Пользуясь данным рисунком, назовите: а) две плоскости, содержащие прямую DE; б) прямую, по которой пересекаются плоскости AEF и SBC; в) плоскость, которую пересекает прямая SB.

      2. Прямые a, b и c имеют общую точку. Верно ли, что данные прямые лежат в одной плоскости? Ответ объясните.

      3. Плоскости и пересекаются по прямой с. Прямая а лежит в плоскости и пересекает плоскость . Каково взаимное расположение прямых а и с? Ответ объясните.

      Вариант II

      1. Пользуясь данным рисунком, назовите: а) две плоскости, содержащие прямую EF; б) прямую, по которой пересекаются плоскост BDE и SAC; в) плоскость, которую пересекает прямая АС.

      2. Прямые a, b и c попарно пересекаются. Верно ли, что данные прямые лежат в одной плоскости? Ответ объясните.

      3. Плоскости и пересекаются по прямой с. Прямая а лежит в плоскости и пересекает прямую с. Каково взаимное расположение прямой а и плоскости ? Ответ объясните.

      III уровень

      Вариант I

      1. Пользуясь данным рисунком, назовите: а) две плоскости, содержащие прямую В1С; б) прямую, по которой пересекаются плоскости B1CD и AA1D1; в) плоскость, не пересекающуюся с прямой CD;

      2. Четыре прямые попарно пересекаются. Верно ли, что если любые три из них лежат в одной плоскости, то все четыре прямые лежат в одной плоскости? Ответ объясните.

      3. Вершина С плоского четырехугольника ABCD лежит в плоскости , а точки A, B и D не лежат в этой плоскости. Прямые AB и AD пересекают плоскость B1 и D1 соответственно. Каково взаимное расположение точек C, B1 и D1? Ответ объясните.

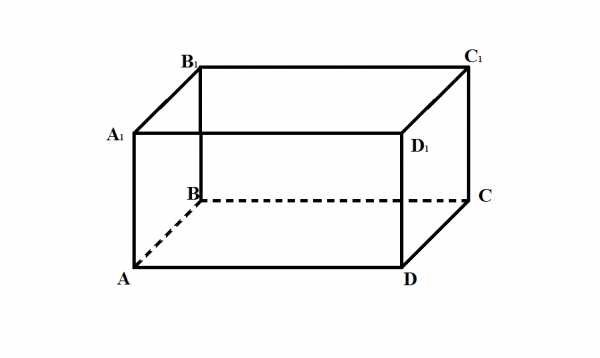
      Вариант II

      1. Пользуясь данным рисунком, назовите: а) две плоскости, содержащие прямую АВ; б) прямую, по которой пересекаются плоскости ADC1 и A1B1B; в) плоскость, не пересекающуюся с прямой BC1.

      2. Три различные плоскости имеют общую точку. Верно ли, что данные имеют общую прямую? Ответ объясните.

      3. Точка D не лежит в плоскости . Прямые a и b проходят через точку D и пересекают плоскость в точках A и B соответственно. Прямая с не проходит через точку D, пересекается с a и b и пересекает плоскость в точке С. Каково взаимное расположение точек A, B и C? Ответ объясните.

      Урок 9.Решение задач по теме «Параллельность прямой и плоскости».

      Цель урока:

      1)обобщить изученный материал;

      2) закрепить навыки применения изученных теорем к решению задач;

      3)воспитывать самостоятельность в выборе способа решения геометрических задач.

      Самостоятельная работа обучающего характера

      (с оказанием индивидуальной дифференцируемой помощи)

      I уровень

      Вариант I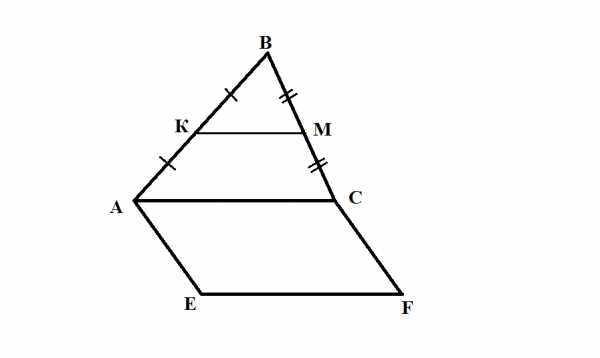

      1. Треугольник АВС и квадрат AEFC не лежат в одной плоскости. Точки К и М – середины отрезков АВ и ВС соответственно.

      а) Докажите, что КМEF.

      б) Найдите КМ, если АЕ=8 см.

      1. Плоскость проходит через основание AD трапеции ABCD. Точки E и F – середины отрезков AB и CD соответственно. Докажите, что EF

      Вариант II

      1. Квадрат ABCD и трапеция KMNL не лежат в одной плоскости. Точки A и D – середины отрезков KM и NL соответственно.

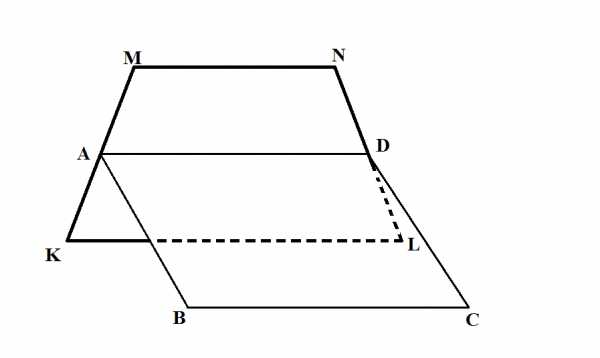
      а) Докажите, что KLBC.

      б) Найдите BC, если KL=10 см, MN=6 см.

      2. Плоскость проходит через сторону AC треугольника ABC. Точка D и E – середины отрезков AB и BC соответственно. Докажите, что DE

      II уровень

      Вариант I

      1. Точки А, В и С не лежат в одной плоскости. Точки E, F, M, K – середины отрезков AB, BC, CD, AD соответственно.

      а) Докажите, что EFMK – параллелограмм.

      б) Найдите периметр EFKM, если AC=6 см, BD=8 см.

      1. Точка A лежит в плоскости , параллельной прямой а. Через точку A проведена прямая b, параллельная прямой а. Докажите, что прямая b лежит в плоскости .

      Вариант II

      1. Точка A не лежит в плоскости треугольника BCD. Точки P, R, S и T – середины отрезков AB, AD, CD и BC соответственно.

      а) Докажите, что PRST – параллелограмм.

      б) Найдите AC, если BD=6 см, а периметр PRST равен 14 см.

      1. Прямые a и b параллельны. Через точку B, лежащую на прямой b, проведена плоскость , параллельная прямой a. Докажите, что плоскость проходит через прямую b.

      III уровень

      Вариант I

      1. Точка M, лежащая вне плоскости ΔABK, соединена с его вершинами, D и E – точка пересечена медиан треугольников MAB и MBK соответственно.

      а) Докажите, что ADEK – трапеция.

      б) Найдите DE, если AK=14 см.

      1. Отрезки AA1, BB1 и CC1 не лежат в одной плоскости и пересекаются в точке O, являющейся серединой каждого из них. Докажите, что прямая AB параллельна плоскости A1CB1.

      Вариант II

      1. Точки A, B, C и D не лежат в одной плоскости. K и M – точки пересечения медиан треугольников ADB и DBC соответственно.

      а) Докажите, что KMǁAC.

      б)Найдите AC, если KM=6 см.

      1. Через точку O – точку пересечения диагоналей параллелограмма ABCD – проведена прямая KM, не лежащая в плоскости ABC, причем O — середина отрезка KM. Докажите, что прямая KB параллельна плоскости AMD.

      Урок 10 Решение задач по теме «Параллельность прямой и плоскости».

      Цели урока:

      1)обобщить материал изученного параграфа

      2) развивать навык применять изученные теоремы к решению задач;

      3)воспитывать самостоятельность в выборе способа решения задач;

      4) контроль знаний учащихся.

      Проверочная самостоятельная работа.

      I уровень

      Вариант I

      1. В ΔABC на стороне AB выбрана точка D, такая, что BD : BA=1:3. Плоскость, параллельная прямой AC и проходящая через точку D, пересекает отрезок BC в точке D1.

      а) Докажите, что ΔDBD1ΔABC.

      б) Найдите AC, если DD1=4 см.

      1. Плоскости и пересекаются по прямой C. Плоскость , параллельная прямой C, пересекает плоскости и по прямым a и b соответственно. Докажите, что aǁ и bǁ.

      Вариант II

      1. Точка D лежит на отрезке AB, причем BD:BA=1:4. Через точку A проведена плоскость , через точку D – отрезок DD1, параллельный . Прямая BD1, пересекает плоскость в точке C.

      А) Докажите подобие Δ DBD1 и ΔABC.

      Б) Найдите DD1, если AC=12 см.

      1. Параллельные прямые a и b лежат в плоскости .Через прямую a проведена плоскость , а через прямую b – плоскость так, что и пересекаются по прямой c. Докажите, что cǁ.

      II уровень

      Вариант I

      1. На стороне AD параллелограмма ABCD выбрана точка A1 так,что DA1=4 см. Плоскость, параллельная диагонали AC, проходит через точку A1 и пересекает сторону CD в точке C1.

      А) Докажите, что ΔC1DA1ΔABC.

      Б) Найдите AC, если BC=10 см, A1C1=6 см.

      1. Докажите, что если каждая из двух пересекающихся плоскостей параллельна данной прямой, то линия их пересечения также параллельна этой прямой.

      Вариант II

      1. На стороне BC параллелограмма ABCD выбрана точка C1 так, что C1B=3 см. Плоскость, параллельная диагонали AC, проходит через точку C1 и пересекает сторону AB в точке A1.

      А) Докажите, что ΔADCΔC1BA1.

      Б) Найдите AD, если A1C1=4 см, AC=12 см.

      1. Точка S не лежит в плоскости параллелограмма ABCD. Докажите, что линия пересечения плоскостей SAB и SCD параллельна плоскости параллелограмма.

      III уровень

      Вариант I

      1. Точка M не лежит в плоскости параллелограмма ABCD. На отрезке AM выбрана точка E так, что ME:EA=2:3.

      А) Постройте точку F – точку пересечения прямой MB с плоскостью CDE.

      Б) Найдите AB, если EF=10 см.

      1. Через прямую a проведена плоскость , а через прямую b – плоскость . Плоскости и пересекаются по прямой c. Докажите, что если c не пересекается с a и b, то aǁb.

      Вариант II

      1. Точка M не лежит на плоскости ромба ABCD. На отрезке BM выбрана точка F так, что MF:FB=1:3.

      А) Постройте точку K – точку пересечения прямой MC с плоскостью AFD.

      Б) Найдите FK, если AD=16 см.

      1. Прямая с не имеет общих точек с плоскостью . Через прямую с проведены плоскости и , пересекающиеся с плоскостью по прямым a и b соответственно. Докажите, что aǁb.

      Урок 14.Решение задач по теме « Параллельность прямых и плоскостей»

      Цель урока:

      1)повторить теорию;

      2)подготовить учащихся к контрольной работе.

      Работа по карточкам.

      Карточка №1 (I уровень)

      №1

      Треугольник ABC и квадрат AEFC не лежат в одной плоскости (см. рисунок). Точки K и M – середины отрезков AB и BC соответственно.

      А) Докажите, что KMǁEF.

      Б) Найдите KM, если AE=8 см.

      №2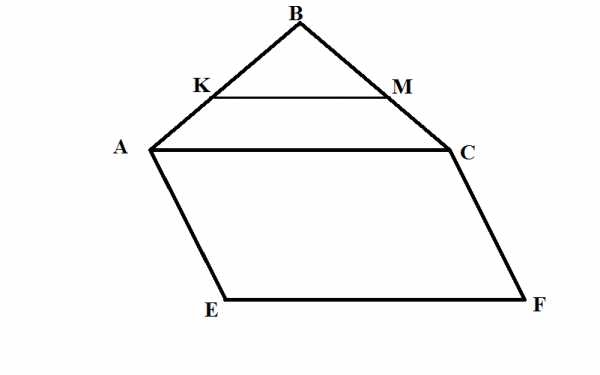

      Плоскость проходит через основание AD трапеции ABCD. Точки E и F – середины отрезков AB и CD соответственно.

      Докажите, что EFǁ.

      №3

      Точки A, B, C и D не лежат в одной плоскости. Среди прямых, проходящих через любые две из данных точек, укажите прямую, которая является скрещивающейся:

      А) с прямой AB;

      Б) с прямой BC.

      Ответ обоснуйте.

      Карточка №2 (II уровень)

      №1

      Точки A, B, C и D не лежат в одной плоскости. Точки E, F, M, K – середины отрезков AB, BC, CD и AD – соответственно.

      А) Докажите, что EFMK – параллелограмм.

      Б) Найдите периметр EFMK, если AC=6 см, BD=8 см.

      №2

      Точка A лежит в плоскости , параллельной прямой a. Через точку А проведена прямая b, параллельная прямой a.

      Докажите, что прямая b лежит в плоскости .

      №3

      Дан куб ABCDA1B1C1D1. Укажите три прямые, проходящие:

      А) через точку D и скрещивающиеся с прямой AB1;

      Б) через точку B1 и скрещивающиеся с прямой A1D.

      Дайте обоснование ответа.

      Карточка №1 (I уровень)

      №1

      Треугольник ABC и квадрат AEFC не лежат в одной плоскости (см. рисунок). Точки K и M – середины отрезков AB и BC соответственно.

      А) Докажите, что KMǁEF.

      Б) Найдите KM, если AE=8 см.

      №2

      Плоскость проходит через основание AD трапеции ABCD. Точки E и F – середины отрезков AB и CD соответственно.

      Докажите, что EFǁ

      №3

      Точки A, B, C, D не лежат в одной плоскости. Среди прямых, проходящих через любые две из данных точек, укажите прямую, которая является скрещивающейся:

      А) с прямой AB;

      Б) с прямой BC.

      Ответ обоснуйте.

      Карточка №3 (III уровень)

      №1

      Точка M, лежащая вне плоскости ΔABC, соединена с его вершинами D и E – точки пересечения медиан треугольников MAB и MBC соответственно.

      А) Докажите, что ADEC – трапеция.

      Б) Найдите DE, если AC=12 см.

      №2

      Отрезки AA1, BB1 и CC1 не лежат в одной плоскости и пересекаются в точке O, являющиеся серединой каждого из них.

      Докажите, что прямая AB параллельна плоскости A1CB1.

      №3

      Дан куб ABCDA1B1C1D1. Укажите в данном кубе количество пар скрещивающихся ребер. Дайте обоснование взаимного расположения для одной из этих пар.

      Урок 15. Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости»

      Цель урока:

      — проконтролировать знания, умения и навыки по данной теме.

      I уровень

      Вариант I

      1. Прямые a и b пересекаются. Прямая c является скрещивающейся с прямой a. Могут ли прямые b и c быть параллельными?

      2. Плоскость проходит через середины боковых сторон AB и CD трапеции ABCD – точки M и N.

      А) Докажите, что ADǁ.

      Б) Найдите BC, если AD=10 см, MN=8 см.

      1. Прямая MA проходит через вершину квадрата ABCD и не лежит в плоскости квадрата.

      А) Докажите, что MA и BC – скрещивающиеся прямые.

      Б) Найдите угол между прямыми MA и BC, если MAD=45.

      Вариант II

      1. Прямые a и b пересекаются. Прямые a и c параллельны. Могут ли прямые b и c быть скрещивающимися?

      2. Плоскость проходит через основание AD трапеции ABCD. M и N – середины боковых сторон трапеции.

      А) Докажите, что MNǁ.

      Б) Найдите AD, если BC=4 см, MN=6 см.

      1. Прямая CD проходит через вершину треугольника ABC и не лежит в плоскости ABC. E и F – середины отрезков AB и BC.

      А) Докажите, что CD и EF – скрещивающиеся прямые.

      Б) Найдите угол между прямыми CD и EF, если DCA=60.

      II уровень

      Вариант I

      1. Прямая a параллельна плоскости , а прямая b пересекает плоскость . Определите, могут ли a и b:

      А) быть параллельными;

      Б) пересекаться;

      В) быть скрещивающимися.

      1. Точка M не лежит в плоскости трапеции ABCD (ADǁBC).

      А) Докажите, что треугольники MAD и MBC имеют параллельные средние линии.

      Б) Найдите длины этих средних линий, если AD:BC=5:3, а средняя линия трапеции равна 16 см.

      1. Через вершину A квадрата ABCD проведена прямая KA, не лежащая в плоскости квадрата.

      А) Докажите, что KA и CD – скрещивающиеся прямые.

      Б) найдите угол между KA и CD, если AKB=850, ABK=450.

      Вариант II

      1. Прямая а параллельна плоскости , а прямая b пересекает плоскость . Определите, могут ли a и b:

      А) быть параллельными;

      Б) пересекаться;

      В) быть скрещивающимися.

      1. Треугольник ABC и трапеция KMNP имеют общую среднюю линию EF, причем KPǁMN, EFǁAC.

      А) Докажите, что ACǁKP.

      Б) Найдите KP и MN, если KP:MN=3:5, AC=16 см.

      1. Точка M не лежит в плоскости ромба ABCD.

      А) Докажите, что MC и AD – скрещивающиеся прямые.

      Б) Найдите угол между MC и AD, если MBC=700, BMC=650.

      III уровень

      Вариант I

      1. Плоскости и пересекаются по прямой l. Прямая a параллельна прямой l и является скрещивающейся с прямой b. Определите, могут ли прямые a и b:

      А) лежать в одной из данных плоскостей;

      Б) лежать в разных плоскостях и ;

      В) просекать плоскости и . В случае утвердительного ответа укажите взаимное расположение прямых a и b.

      1. Плоскость пересекает стороны AB и BC треугольника ABC в точках M и N соответственно, причем AM:MB=3:4, CN:BC=3:7.

      А) Докажите, что ACǁ.

      Б) Найдите AC, если MN=16 см.

      1. Точки A, B, C и D не лежат в одной плоскости. Найдите угол между прямыми AC и BD, если AC=6 см, BD=8 см, а расстояние между серединами отрезков AD и BC равно 5 см.

      Вариант II

      1. Плоскости и пересекаются по прямой l. Прямые a и l пересекаются, а прямые l и b параллельны. Определите, могут ли прямые a и b:

      А) лежать в одной из плоскостей;

      Б) лежать в разных плоскостях и ;

      В) просекать плоскости и . В случае утвердительного ответа укажите взаимное расположение прямых a и b.

      1. Плоскость проходит через сторону AC треугольника ABC. Прямая пересекает стороны AB и BC данного треугольника в точках M и N соответственно, причем BN:NC=2:3, AM:AB=3:5.

      А) Докажите, что MNǁ.

      Б) Найдите MN, если AC=30 см.

      1. Точки A, B, C и D не лежат в одной плоскости. Найдите угол между прямыми AB и CD, если AB=CD=6 см, а расстояние между серединами отрезков AD и BC=3 см.

      Урок 17.Свойства параллельных плоскостей

      Цели урока:

      1)рассмотреть свойства параллельных плоскостей;

      2)сформировать навыки применения изученных свойств параллельных свойств параллельных плоскостей при решение задач.

      Самостоятельная работа

      I уровень

      Вариант I

      1. Через вершины A и C параллелограмма ABCD проведены параллельные прямые A1A и C1C, не лежащие в плоскости параллелограмма.

      Докажите параллельность плоскостей A1AB и C1CD.

      1. Параллельные прямые a и b пересекают одну из двух параллельных плоскостей в точках A1 и B1, а другую в точках A2 и B2 соответственно.

      А) Докажите, что A1B1ǁA2B2.

      Б) Найдите A2A1B1, если A1A2B2=140.

      Вариант II

      1. Через вершины A и C параллелограмма ABCD проведены параллельные прямые A1A и C1C, не лежащие в плоскости параллелограмма.

      Докажите параллельность плоскостей A1AD и C1CB.

      1. Параллельные прямые a и b пересекают одну из двух параллельных плоскостей в точках A1 и B1, а другую в точках A2 и B2 соответственно.

      А) Докажите, что A1B1=A2B2.

      Б) Найдите B1B2A2, если B1A1A=50.

      II уровень

      Вариант I

      1. Параллелограммы ABCD и A1B1CD не лежат в одной плоскости.

      Докажите параллельность плоскостей BCB1 и ADA.

      1. Концы двух пересекающихся отрезков AC и BD лежат на двух параллельных плоскостях, причем расстояние между точками одной плоскости равны.

      А) Докажите, что ABǁCD.

      Б) Один из углов четырехугольника ABCD равен 65.

      Найдите остальные углы.

      Вариант II

      1. Параллелограммы ABCD и ABC1D1 не лежат в одной плоскости. Докажите параллельность плоскостей CBC1 и DAD1.

      2. Концы двух пересекающихся отрезков AC и BD лежат на двух параллельных плоскостях, причем расстояние между точками одной плоскости равны.

      А) Докажите, что ADǁBC.

      Б) Один из углов четырехугольника ABCD равен 130. Найдите остальные углы.

      infourok.ru

      Решебник по геометрии за 10 класс контрольно-измерительные материалы Рурукин А.Н. ФГОС

      gdzguru.com

      решебники

      • 1 класс

        • Математика
        • Английский язык
        • Русский язык
        • Информатика
        • Музыка
        • Литература
        • Окружающий мир
        • Человек и мир
      • 2 класс

        • Математика
        • Английский язык
        • Русский язык
        • Немецкий язык
        • Белорусский язык
        • Информатика
        • Музыка
        • Литература
        • Окружающий мир
        • Человек и мир
        • Технология
      • 3 класс

        • Математика
        • Английский язык
        • Русский язык
        • Немецкий язык
        • Белорусский язык

      gdzguru.com

      Итоговый КИМ по геометрии 10 класс

      Пояснительная записка.

      Итоговая контрольная работа по геометрии за курс 10 класса составлена в соответствии с учебником: Геометрия, 10-11: учебник для общеобразовательных учреждений. / Атанасян Л.С., Бутузов В.Ф. и др. – М.: Просвещение, 2009 — 2013.

      При составлении работы использовались задания следующих пособий:

      1. Геометрия, 10: Карточки для проведения контрольных работ и зачётов / Г.Д. Карташева, Л.Б. Крайнева. – М.: Вербум-М, 2004.

      2. Задачи и упражнения на готовых чертежах. 10-11 кл. Геометрия. / Е.М. Рабинович — М.: Илекса, 2005.

      3. Геометрия. Стереометрия: пособие для подготовки к ЕГЭ. В.А.Смирнов.- М.: МЦНМО, 2011.

      4. Геометрия. 10 класс. Поурочные планы по учебнику Л.С. Атанасяна и др. / Авт.-сост. Г.И. Ковалёва – Волгоград: Учитель, 2004.

      Контрольная работа рассчитана на два урока по 40 – 45 минут, содержит 4 разноуровневых варианта: варианты 1 и 2 предназначены менее подготовленным ученикам, варианты 3 и 4 обучающимся на хорошо и отлично. Задача №1 по готовому чертежу на доказательство с применением теоремы о трёх перпендикулярах или обратной ей. К задачам № 2 — № 4 даны ответы.

      Цель: проверка умений применять полученные знания по основным темам курса геометрии 10 класса.

      1. ВИД КОНТРОЛЯ – контрольная работа

      1. СОДЕРЖАНИЕ КОНТРОЛЯ:

      Проверяются следующие темы:

      2.1. Теорема о трёх перпендикулярах.

      2.2. Угол между прямой и плоскостью.

      2.3. Угол между плоскостями.

      2.4. Угол между плоскостями.

      1. ЦЕЛИ КОНТРОЛЯ

      обучающийся должен

      знать:

      • Основные аксиомы стереометрии;

      • Теоремы стереометрии;

      • Теорему о трёх перпендикулярах;

      • Геометрические тела;

      • Формулы для нахождения площадей поверхностей геометрических тел.

      уметь:

      • Применять основные аксиомы стереометрии при решении задач;

      • Применять теорему о ТПП и обратную теорему ТПП при решении задач;

      • Применять формулы ;

      1. СТРУКТУРА КОНТРОЛЬНОЙ РАБОТЫ:

      Контрольная работа включает в себя 1 задание по контролируемой теме «Теорема о трёх перпендикулярах.»,1 задание по контролируемой теме «Угол между прямой и плоскостью.», 1 задание по контролируемой теме «Угол между плоскостями», 1 задание по контролируемой теме «Угол между плоскостями.».

      1. КРИТЕРИИ ОЦЕНКИ

      На «5» оценивается работа, в которой выполнено 4 задания

      На «4» оценивается работа, в которой выполнено 3 задания

      На «3» оценивается работа, в которой выполнено 2 задания

      На «2» оценивается работа, в которой выполнено 1 задание

      Итоговая контрольная работа

      по геометрии. 10 кл. (УМК Л.С. Атанасян и др.)

      ВАРИАНТ 1.

      1. а Дано: а (АВС),

      М АВС – прямоугольный,

      С= 90˚

      В Доказать: МСВ —

      А прямоугольный.

      С

      1. АВСDA1B1C1D1 – правильная призма. АВ = 6см, АА1= 8см.

      Найти угол между прямыми АА1 и ВС; площадь полной поверхности призмы.

      1. В правильной треугольной пирамиде сторона основания равна 2см, а высота равна 2 см. Найти угол наклона бокового ребра к плоскости основания. Ответ запишите в градусах.

      1. Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом в 120˚ между ними. Наибольшая из площадей боковых граней равна 56 см2. Найти площадь полной поверхности призмы.

      Итоговая контрольная работа

      по геометрии. 10 кл. (УМК Л.С. Атанасян и др.)

      ВАРИАНТ 2.

      а

      1. М Дано: ABCD – ромб,

      В С АС ВD = О,

      а (АВС).

      Доказать: МО ВD.

      OOOОО

      А D

      1. АВСDA1B1C1D1 – правильная призма. Площадь её полной поверхности равна 210 м2, а площадь боковой поверхности 160 м2. Найти сторону основания и высоту призмы.

      1. В правильной четырёхугольной пирамиде со стороной основания 6 см и длиной бокового ребра см найти косинус угла наклона бокового ребра к плоскости основания и площадь боковой поверхности.

      1. Стороны основания прямого параллелепипеда равны 8 см и 15 см и образуют угол в 60˚. Меньшая из площадей диагональных сечений равна 130 см2. Найти площадь полной поверхности параллелепипеда.

      Итоговая контрольная работа

      по геометрии. 10 кл. (УМК Л.С. Атанасян)

      ВАРИАНТ 3.

      1. а Дано: ABCD —

      М параллелограмм,

      В С а (АВС),

      МА АD.

      Доказать:

      А D ABCD – прямоугольник.

      1. В прямой призме основанием является параллелограмм со сторонами 4 м и 5 м и углом между ними 30˚. Найти площади боковой и полной поверхностей призмы, если её высота равна

      7 м.

      1. В правильной четырёхугольной пирамиде РАВСD сторона основания АВ = 10 см, высота РH = 5 см. Найти угол наклона бокового ребра пирамиды к плоскости её основания; площадь сечения, проходящего через высоту и боковое ребро.

      1. Основанием прямой призмы АВСА1В1С1 является равнобедренный треугольник АВС с основанием АС, причём АВ = 6 см, угол В равен 120˚, боковое ребро СС1 = 8 см. Найти площадь сечения А1С1В;

      *б) тангенс угла наклона плоскости (А1С1В) к плоскости (АСС1).

      Итоговая контрольная работа

      по геометрии. 10 кл. (УМК Л.С. Атанасян и др.)

      ВАРИАНТ 4.

      а Дано: а (АВС),

      1. М MD ВС,

      В D – середина ВС.

      D Доказать: АВ = АС

      А

      С

      1. В прямоугольном параллелепипеде длина диагонали 4см, длины его измерений относятся как 1: 2 : 4. Найти площадь полной поверхности параллелепипеда.

      1. В правильной четырёхугольной пирамиде сторона основания равна 4 м, а высота равна 2 м. Найти угол наклона боковой грани к плоскости основания; площадь полной поверхности пирамиды.

      1. Основанием пирамиды МАВСD является прямоугольник АВСD со сторонами АВ = 5 см и AD = 12 см. Боковое ребро МА перпендикулярно к плоскости основания пирамиды и равно 4 см. Найти угол наклона ребра МС к плоскости ABCD. *б) Постройте сечение пирамиды плоскостью, параллельной плоскости основания и проходящей через точку F на ребре МА, MF : FA = 1 : 3. Найдите площадь сечения.

      Ответы.

      № задания

      Вариант 1

      Вариант 2

      Вариант 3

      Вариант 4

      1.

      Доказательство основывается

      на ТТП или на обратной ТТП.

      2.

      φ=90˚;

      Sполн=264 см2

      а=5 м;

      h= 8 м

      Sбок=126 м2

      Sполн=146м2

      Sполн=448см2

      3.

      45˚

      cos B = 0,6

      Sбок=12 см2

      α =60˚

      Sсеч = 50 см2

      φ=45˚;

      Sполн=16( + 1) м2

      4.

      Sполн= 120 + 7,5 см2

      Sполн =460 + 120 см2

      Sсеч = 3 см2

      tg φ =

      arctg ;

      Sсеч = 3,75 см2

      multiurok.ru

    alexxlab

    Related Articles

    10 класс

    Контрольные работы по алгебре профиль 10 класс: Решебник к сборнику контрольных работ по алгебре для 10 класса (авт. Глизбург В. И.). Профильный уровень ОНЛАЙН

    Содержание Решебник к сборнику контрольных работ по алгебре для 10 класса (авт. Глизбург В. И.). Профильный уровень ОНЛАЙНВнимание! Рукопись не проверялась, возможны ошибки!Контрольные работы для 10 класса по учебнику А.ГДЗ по Алгебре за 10 класс контрольные работы Глизбург В.И., Мордкович А.Г.Зачем нужен онлайн-помощник по алгебре за 10 класс контрольные работы ГлизбургАлгебра и начала анализа. 10 […]

    10 класс

    Гдз по алгебре колмогоров 10 класс 2019 год – 10-11

    Содержание ГДЗ решебник по Алгебре 10 класс Колмогоров 2010Гдз вип. Гдз по алгебре 10-11 класс. Колмогоров А.Н.Для того, чтобы увеличить изображение на компьютере- прокручивайте колёсико мыши удерживая клавишу Ctrl.ГДЗ по алгебре для 10 класса А.Н. КолмогоровГдз по Алгебре за 10‐11 класс , авторы А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын ГДЗ решебник по Алгебре 10 класс Колмогоров […]

    10 класс

    Упражнения по русскому языку 10 класс – Упражнения по русскому языку 10-11 класс

    Содержание Материал по русскому языку (10 класс) по теме: ГОТОВИМСЯ К ЭКЗАМЕНАМ Система различных упражнений по русскому языкуИнтересные задания по русскому языку (10 класс)10-11 класс Орфографический тренинг по русскому языку (задание 10 ЕГЭ)Учебно-методический материал по русскому языку (10 класс) на тему: Упражнения и тест по теме «Правописание глаголов. 10 класс»Тест по русскому языку (10 класс) […]

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *