Формулы приведения. Видеоурок. Алгебра 10 Класс
Тема: Тригонометрические функции
Урок: Формулы приведения
Формулы приведения предназначены для того, чтобы привести тригонометрическую функцию произвольного угла к тригонометрической функции наименьшего из углов.
Рассмотрим конкретный пример. Рассмотрим дуги в и, соответственно, (рис. 1).
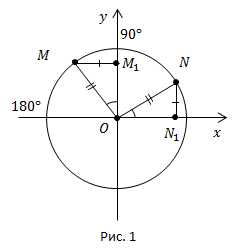
как прямоугольные по гипотенузе и острому углу
Из равенства треугольников следует равенство соответствующих сторон.
Функции большего угла приведены к функциям меньшего угла. В этом суть формул приведения.
Для применения формул приведения тригонометрическую функцию любого угла нужно привести к одному из видов: .
Формул приведения много, но все они подчиняются двум правилам:
Первое правило:
Для аргументов функция меняется на кофункцию, т.е. синус на косинус и наоборот, тангенс на котангенс и наоборот.
Для аргументов функция не меняется.
Примеры на первое правило:
Знак пока не учитываем, он определяется вторым правилом, пока важно понять, в каких случаях функция меняется на кофункцию, а в каких не меняется.
1)
2)
3)
4)
Для аргументов вида наименование функции следует изменить на кофункцию.
5)
6)
7)
8)
Для аргументов вида наименование функции не меняется.
Второе правило (для знака приведенной функции, функции угла ).
1) Считаем угол острым,
2) Определяем четверть и знак в ней приводимой функции (функции слева).
3) Ставим этот знак перед приведенной к углу функцией (функцией справа).
Примечание: Угол может быть любым, острым мы его считаем условно, для применения правила.
Примеры на второе правило:
1)
Рис. 2.
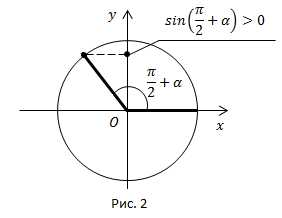
Угол находится во второй четверти. Во второй четверти , ставим знак плюс.
2)
Рис
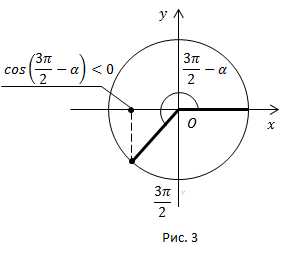
Угол находится в третьей четверти. В третьей четверти ставим знак минус.
3)
Рис. 4.
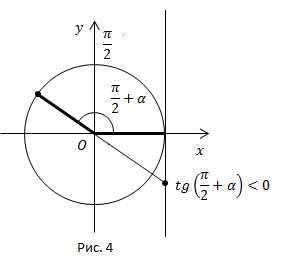
Угол находится во второй четверти. Во второй четверти ставим знак минус.
4)
Рис. 5.
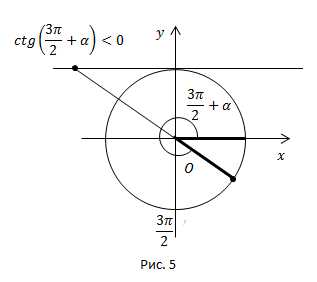
Угол находится в четвёртой четверти. В четвёртой четверти ставим знак минус.
5)
Рис. 6.
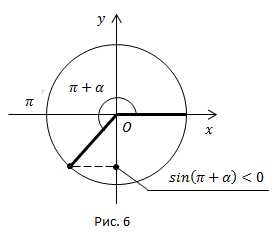
Угол находится в третьей четверти. В третьей четверти ставим знак минус.
6)
Рис. 7.
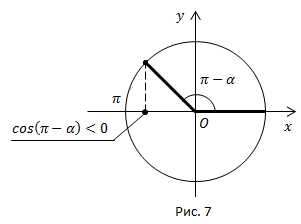
Угол находится во второй четверти, во второй четверти ставим знак минус.
7)
Рис. 8.
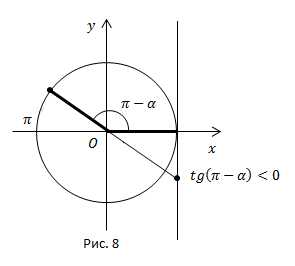
Угол находится во второй четверти. Во второй четверти ставим знак минус.
8)
Рис. 9.
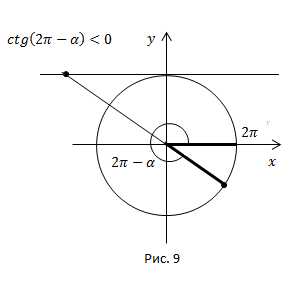
Угол находится в четвёртой четверти. В четвёртой четверти ставим знак минус.
Итак, мы рассмотрели различные примеры применения первого и второго правил формул приведения.
Рассмотрим приемы, облегчающие запоминание формул приведения.
1. «Правило лошади». Глядя на числовую окружность легко ответить на вопрос, меняется ли функция на кофункцию.
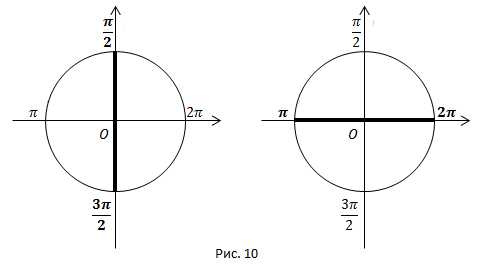
Для аргументов , т.е. аргументов, отложенных от вертикальной оси, на вопрос, меняется ли функция на кофункцию, лошадь, глядя на точки , будет утвердительно кивать – функция меняется на кофункцию (рис. 10) .
Для аргументов , т.е. аргументов, отложенных от горизонтальной оси, лошадь, глядя на точки будет отрицательно мотать головой – функция не меняется (рис. 10) .
2. Используем периодичность и четность.
Вспомним, что наименьший положительный период у тангенса и котангенса равен Это значит, что
Например,
У синуса и косинуса наименьший положительный период равен
Например,
Рассмотрим примеры на использование формул приведения.
1) Вычислить значения всех тригонометрических функций для
Решение (рис. 11).
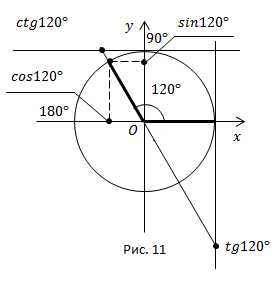
Угол находится во второй четверти, синус в этой четверти положителен, косинус, тангенс и котангенс отрицательны.
2) Вычислить значения всех тригонометрических функций угла
Решение (рис. 12).
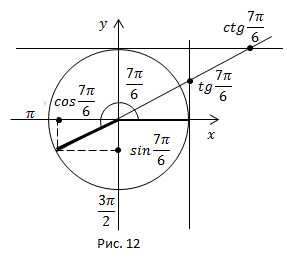
Угол находится в третьей четверти, в третьей четверти синус и косинус отрицательны, тангенс и котангенс положительны.
Мы рассмотрели формулы приведения и пояснили их на конкретных примерах. В дальнейшем мы будем активно использовать формулы приведения для преобразования тригонометрических выражений.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 26.1 – 26.8.
Дополнительные веб-ресурсы
1. Математика (Источник).
2. Интернет-портал Problems.ru (Источник).
3. Образовательный портал для подготовки к экзаменам (Источник).
interneturok.ru
Тригонометрические функции. Алгебра, 10 класс: уроки, тесты, задания.
Вход на портал
Вход на портал
Регистрация
Начало
Поиск по сайту
ТОПы
Учебные заведения
Предметы
Проверочные работы
Обновления
Подписка Я+
Новости
Переменка
Отправить отзыв
- Предметы
- Алгебра
- 10 класс
-
Числовая окружность
-
Синус и косинус. Тангенс и котангенс
-
Тригонометрические функции числового аргумента
-
Тригонометрические функции углового аргумента
-
Свойства функции y = sinx и её график
-
Свойства функции y = cosx и её график
-
Периодичность тригонометрических функций, чётность, нечётность
-
График гармонического колебания (профильный)
-
Функции y = tgx, y = ctgx, их свойства и график
-
Обратные тригонометрические функции (профильный)
Отправить отзыв
Нашёл ошибку?
Сообщи нам!
Copyright © 2019 ООО ЯКласс
Контакты
Пользовательское соглашение
www.yaklass.ru
Один из подходов к изучению тригонометрии в 10-м классе
Разделы:
Математика
Еще в 1905 г. русские читатели могли прочесть в книге Уильяма Джеймса “Психология” его рассуждения о том, “почему зубрение представляет такой дурной способ учения?”
“Знания, приобретенные путем простого зубрения, почти неизбежно забываются совершенно бесследно. Наоборот, умственный материал, набираемый памятью постепенно, день за днем, в связи с различными контекстами, связанный ассоциативно с другими внешними событиями и неоднократно подвергший обсуждению, образует такую систему, вступает в такую связь с остальными сторонами нашего интеллекта, легко возобновляется в памяти массою внешних поводов, что остается надолго прочным приобретением”.
С тех пор прошло более 100 лет, а слова эти поразительно остаются злободневными. В этом каждодневно убеждаешься, занимаясь со школьниками. Массовые пробелы в знаниях настолько велики, что можно утверждать: школьный курс математики в дидактическом и психологическом отношениях – не система, а некое устройство, поощряющее кратковременную память и нисколько не заботиться о памяти долговременной.
Знать школьный курс математики – значит владеть материалом каждого из направлений математики, быть в состоянии актуализировать любое из них в любое время. Чтобы достичь этого, нужно систематически обращаться каждому из них, что порой не всегда возможно из-за сильной загруженности на уроке.
Есть другой путь долговременного запоминания фактов и формул – это опорные сигналы.
Тригонометрия – один из больших разделов школьной математики, изучаемой в курсе геометрии 8, 9 классов и в курсе алгебры 9 класса, алгебры и начал анализа в 10 классе.
Самый большой объем изучаемого материала по тригонометрии приходится на долю 10 класса. Большую часть этого материала из тригонометрии можно изучить и запомнить на тригонометрическом круге (окружность единичного радиуса с центром в начале прямоугольной системы координат). Приложение1.ppt
Это следующие понятия тригонометрии:
- определения синуса, косинуса, тангенса и котангенса угла;
- радианное измерение углов;
- область определения и область значений тригонометрических функций
- значения тригонометрических функций для некоторых значений числового и углового аргумента;
- периодичность тригонометрических функций;
- четность и нечетность тригонометрических функций;
- возрастание и убывание тригонометрических функций;
- формулы приведения;
- значения обратных тригонометрических функций;
- решение простейших тригонометрических уравнений;
- решение простейших неравенств;
- основные формулы тригонометрии.
Рассмотрим изучение этих понятий на тригонометрическом круге.
1) Определение синуса, косинуса, тангенса и котангенса.
После введения понятия тригонометрического круга (окружность единичного радиуса с центром в начале координат), начального радиуса (радиус окружности по направлению оси Ох), угла поворота, учащиеся самостоятельно получают определения для синуса, косинуса, тангенса и котангенса на тригонометрическом круге, используя определения из курса геометрии, то есть, рассматривая прямоугольный треугольник с гипотенузой, равной 1.
Косинусом угла называется абсцисса точки на окружности при повороте начального радиуса на данный угол.
Синусом угла называется ордината точки на окружности при повороте начального радиуса на данный угол.
2) Радианное измерение углов на тригонометрическом круге.
После введения радианной меры угла (1 радиан – это центральный угол, которому соответствует длина дуги, равная длине радиуса окружности), учащиеся делают вывод, что радианное измерение угла – это числовое значение угла поворота на окружности, равное длине соответствующей дуги при повороте начального радиуса на заданный угол. .
Тригонометрический круг разделен на 12 равных частей диаметрами окружности. Зная, что угол радианам, можно определить радианное измерение для углов кратных .
и т.д.
А радианные измерения углов, кратных, получаются аналогично:
3) Область определения и область значений тригонометрических функций.
Будет ли соответствие углов поворота и значений координат точки на окружности функцией?
Каждому углу поворота соответствует единственная точка на окружности, значит данное соответствие – функция.
Получаем функции
На тригонометрическом круге видно, что область определения функций – множество всех действительных чисел, а область значений — .
Введем понятия линий тангенсов и котангенсов на тригонометрическом круге.
1) Пусть Введем вспомогательную прямую, параллельную оси Оу, на которой определяются тангенсы для любого числового аргумента.
2) Аналогично получаем линию котангенсов. Пусть у=1, тогда . Значит, значения котангенса определяются на прямой, параллельной оси Ох.
На тригонометрическом круге без труда можно определить область определения и область значений тригонометрических функций:
для тангенса —
для котангенса —
4) Значения тригонометрических функций на тригонометрическом круге.
Катет , противолежащий углу в равен половине гипотенузы, то есть Другой катет по теореме Пифагора:
Значит по определению синуса, косинуса, тангенса, котангенса можно определить значения для углов кратных или радианам. Значения синуса определяются по оси Оу, косинуса по оси Ох, а значения тангенса и котангенса можно определить по дополнительным осям, параллельным осям Оу и Ох соответственно.
Табличные значения синуса и косинуса расположены на соответствующих осях следующим образом:
Табличные значения тангенса и котангенса —
5) Периодичность тригонометрических функций.
На тригонометрическом круге видно, что значения синуса, косинуса повторяются через каждые радиана, а тангенса и котангенса – через радиан.
6)Четность и нечетность тригонометрических функций.
Это свойство можно получить, сравнивая значения положительных и им противоположных углов поворота тригонометрических функций. Получаем, что
Значит, косинус – четная функция, все остальные функции – нечетные.
7) Возрастание и убывание тригонометрических функций.
По тригонометрическому кругу видно, что функция синус возрастает и убывает
Аналогично рассуждая, получаем промежутки возрастания и убывания функций косинуса, тангенса и котангенса.
8) Формулы приведения.
За угол берем меньшее значение угла на тригонометрическом круге. Все формулы получаются в сравнении значений тригонометрических функций на катетах выделенных прямоугольных треугольников.
Алгоритм применения формул приведения:
1) Определить знак функции при повороте на заданный угол.
При повороте на угол функция сохраняется, при повороте на угол — целое, нечетное число, получается кофункция (
9) Значения обратных тригонометрических функций.
Введем обратные функции для тригонометрических функций, пользуясь определением функции.
Каждому значению синуса, косинуса, тангенса и котангенса на тригонометрическом круге соответствует только одно значение угла поворота. Значит, для функции область определения , область значений — Для функции область определения — , область значений — . Аналогично получаем область определения и область значений обратных функций для косинуса и котангенса.
Алгоритм нахождения значений обратных тригонометрических функций:
1) нахождение на соответствующей оси значения аргумента обратной тригонометрической функции;
2) нахождение угла поворота начального радиуса с учетом области значений обратной тригонометрической функции.
Например:
10) Решение простейших уравнений на тригонометрическом круге.
Чтобы решить уравнение вида , найдем точки на окружности, ординаты которых равны и запишем соответствующие углы с учетом периода функции.
Для уравнения , найдем точки на окружности, абсциссы которых равны и запишем соответствующие углы с учетом периода функции.
Аналогично для уравнений вида Значения определяются на линиях тангенсов и котангенсов и записываются соответствующие углы поворота.
11) Решение неравенств.
Чтобы решить неравенства вида , необходимо найти точки на окружности с ординатой и прочитать соответствующее неравенство против часовой стрелки с учетом периода функции.
Чтобы решить неравенства вида , необходимо найти точки на окружности с абсциссой и прочитать соответствующее неравенство против часовой стрелки с учетом периода функции.
Чтобы решить неравенства вида , необходимо найти точку на линии тангенсов с координатой и прочитать соответствующее неравенство против часовой стрелки с учетом области определения и периода функции.
Аналогично для неравенств с котангенсом.
Необходимо практиковать чтение промежутков на тригонометрическом круге, тогда решения неравенств определяются безошибочно.
12) Основные формулы тригонометрии.
1) Основные тригонометрические тождества.
Очевидны выводы формул которые получаются в прямоугольном треугольнике на тригонометрическом круге.
2) Формулы сложения выводятся с использованием скалярного произведения векторов начального и “конечного” радиусов.
Другие формулы сложения получаются с использованием предыдущей, формул приведения и свойств четности и нечетности тригонометрических функций.
Почти все формулы тригонометрии являются следствиями этих основных формул.
Все понятия и формулы тригонометрии получают сами ученики под четким руководством учителя с помощью тригонометрического круга. В дальнейшем этот “круг” будет служить для них опорным сигналом или внешним фактором для воспроизведения в памяти понятий и формул тригонометрии.
Выводы:
Изучение тригонометрии на тригонометрическом круге способствует:
- выбору оптимального для данного урока стиль общения, организации учебного сотрудничества;
- целевые ориентиры урока становятся личностно значимыми для каждого ученика;
- новой материал опирается на личный опыт действия, мышления, ощущения учащегося;
- урок включает в себя различные формы работы и способы получения и усвоения знаний; присутствуют элементы взаимо- и самообучения; само- и взаимоконтроля;
- имеет место быстрое реагирование на непонимание и ошибку (совместное обсуждение, опоры-подсказки, взаимоконсультации).
18.01.2008
urok.1sept.ru
Открытый урок по алгебре «Формулы тригонометрии», 10 класс
Конспект открытого урока алгебры теме
« Тригонометрические формулы» (10 класс)
Выполнила : учитель математики
МБОУ СОШ р.п. Мухен Кушнарь Л.А.
Урок входит в раздел программы « Тригонометрические формулы». На данный раздел в программе отводится 19 уроков. Урок обобщения проводится в конце изучения темы и предшествует контрольной работе.
Самоанализ урока.
Основная цель данного урока- обобщить полученные по теме знания, закрепить навыки решения простейших примеров по данной теме, подготовиться к контрольной работе. Так как группа сформирована в основном из слабых учащихся, имеющих большие пробелы в знаниях по математике, у них сформировано негативное отношение к урокам математики еще со школы. Поэтому на уроках математике ставится трудная задача вызвать интерес к изучению математики и сформировать познавательную мотивацию к учебной деятельности. Поэтому на уроках необходимо применять различные методы и формы работы. Одной из таких форм и является образец данного урока- форма игры. Такая работа позволяет развивать познавательный интерес к изучению математики.
Средства урока: карточки-задания, тестовые задания, доска, самостоятельная работа, слово учителя.
Разнообразные задания разного уровня сложности позволяют выбрать для себя те задания, которые по силам конкретному учащемуся.
Методы :
-
По организации учебно-познавательной деятельности: устные и письменные ответы учащихся;
-
По характеру управления учебной работой: работа под руководством учителя и учащихся- консультантов;
-
По степени самостоятельности мышления: репродуктивный;
-
Методы стимулирования интереса: игровые моменты, соревновательная атмосфера;
-
Методы стимулирования долга и ответственности: работа в группах, взаимоконтроль, взаимопомощь;
-
Методы контроля и самоконтроля: работа в группах, индивидуальные задания, самооценка и взаимооценка результатов работы.
Формы обучения:
Индивидуальная, групповая, фронтальная.
Цели урока:
-
Закрепить и обобщить знания по теме «Тригонометрические формулы».
-
Развивать познавательный интерес к изучению математики.
-
Активизировать навыки самостоятельной работы.
-
Вырабатывать умение работать в коллективе, воспитывать ответственность, аккуратность.
Ход урока:
-
Оргмомент. Сообщение целей урока. (3 мин)
«Математика уступает свои крепости лишь сильным и смелым». (А.П. Конфорович – автор научно-популярных книг «Математика лабиринта»
«Великая книга природы может быть прочтена только теми, кто знает язык, на котором она написана, и этот язык – математика.» Галилей
Сегодня на уроке мы должны повторить формулы тригонометрии, закрепить все те знания и умения, которые появились у вас при изучении темы.
Для этого вся группа разделится на три бригады. Из числа учащихся назначается координатор(помощник) , который помогает учителю. Каждая бригада выбирает себе командира. ( распределение на бригады проводилось заранее). Наш урок будет состоять из туров. Каждый учащийся выполняет всю работу на уроке на зачетных листах. . За каждый тур вы будете зарабатывать математические: «степы» Заработанные степы зачисляться на счет команды. За урок каждый из вас может получить оценки , которые вы можете выкупить на заработанные деньги. За урок вы можете получить по две оценки: в командном зачете и в личном.
Расценки на оценки:
В личном зачете: В командном зачете:
Оц. «5» -более 6 степов более 25 степов
Оц. «4» -5-6 степов 20-24 степа
Оц. «3» -2-4 степа 16-19 степов
-
1тур: Разминка. (5 мин)
Вопросы к разминке: (1 вопрос – 1 степ)
-
В каких четвертях лежит уголα, если sinα<0? (4,3четв.)
-
Чему равен sin7 π? (0)
-
Какой знак имеет cos150º? (-)
-
В каких пределах находится sinα? (-1≤х≤1) 2 команда
-
cosα>0, в какой четверти расположен угол α? (1,4)
-
Чему равен cos 45 º? ( √2/2)
-
Сколько градусов составляет дуга в π рад? (180°)
-
Чему равен tgα? (sina/cosa)
-
Чему равен ctgα? (cosa/ sina)
-
Сколько радиан составляет 360º? (2П)
11. Что называется углом в 1 радиан?
Ответ: угол в 1 радиан – это такой центральный угол, длина дуги которого равна радиусу окружности. 1радиан ≈ 57º.
12.½ пи
Игорь — Работа координатора: (координатор с объяснением решает пример у доски) (10 мин)
Вычислить:
sin2α, если cosα= ,
,  ‹α‹2π
‹α‹2π
После того, как координатор решит пример, часть записей с доски убирается, и учащиеся самостоятельно восстанавливают пример у себя в зачетных листах.
восстановить запись
2 тур: (10 мин)
-
-
-
-
Игра «Домино» Восстановить формулы 1 чел с бригады в это время проходит конкурс шифровальщиков
-
Конкурс шифровальщиков.
-
-
-
По 1 учащемуся из каждой бригады восстановить формулы тригонометрии Остальные учащиеся принимают участие в конкурсе шифровальщиков.
-
Тур Конкурс шифровальщиков: каждая команда получает задание с 8 примерами, ответы к которым зашифрованы буквами. Из этих букв должны сложить слово. Каждый учащийся решает не менее одного примера. ( один пример-2 степа).
е
к
н
о
с
у
я
—
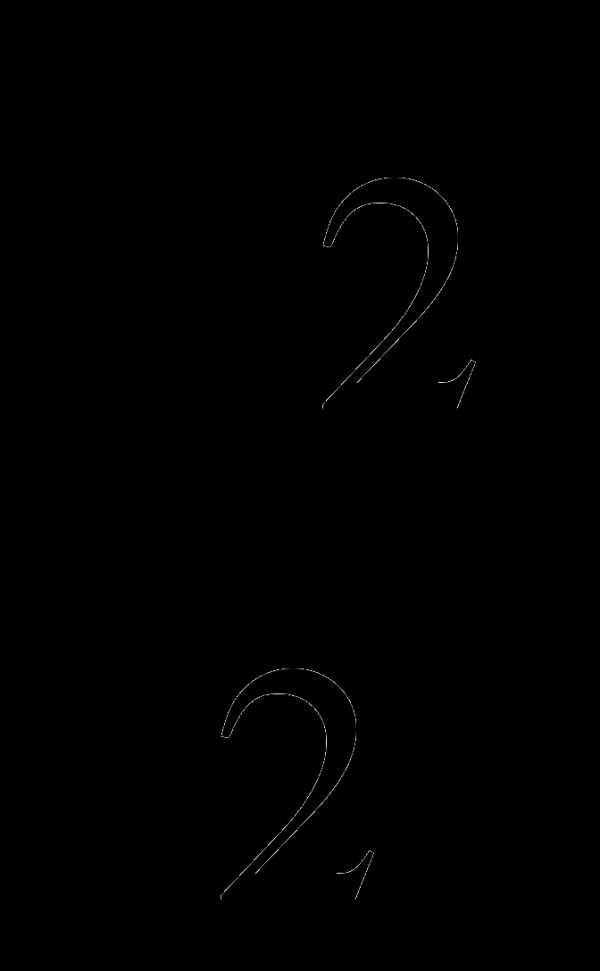
45

—

40
π
1 бригада:
Ответ: косеканс
КООРДИНАТОР, КОСЕКАНС — одна из тригонометрических функций, обозначаемая ( — аргумент) и определяемая формулой
,
1.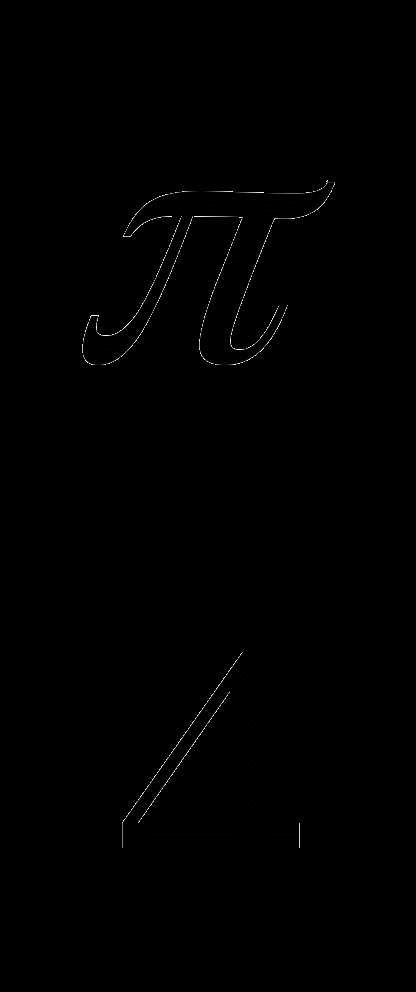 =
=
2.sin(-30º)=
3.cos2 15º- sin2 15º=
4. sin( )=
)=
5. cosα=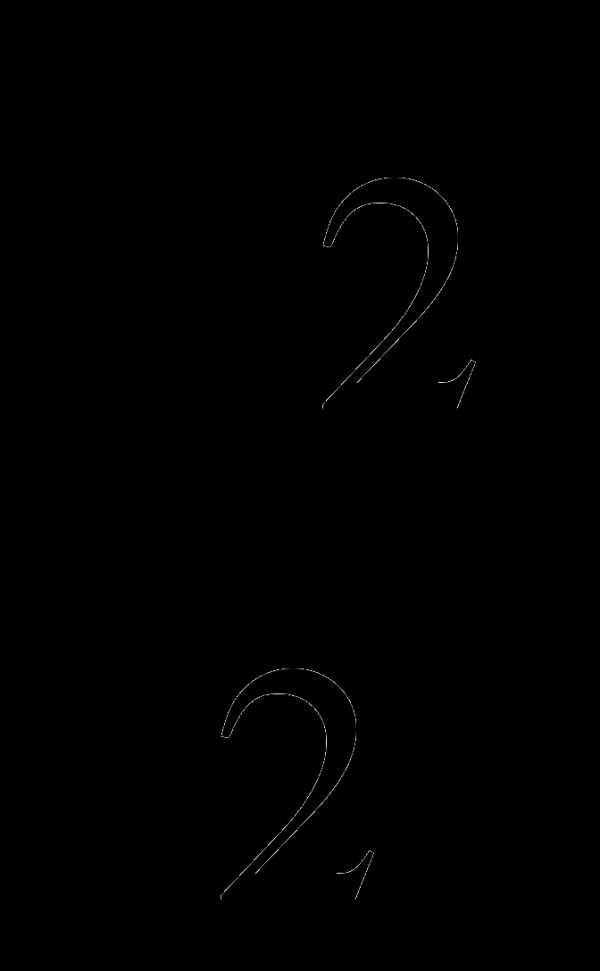 , α=?
, α=?
6. cos =
=
7. 72º=
8. sin =
=
2 бригада:
й
л
м
о
п
т
ф
0
—

18
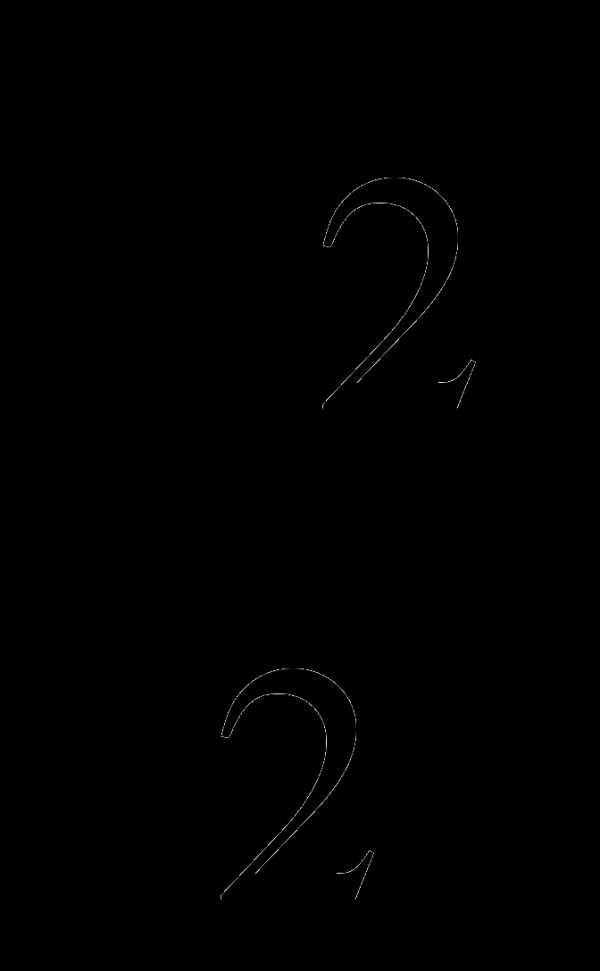

—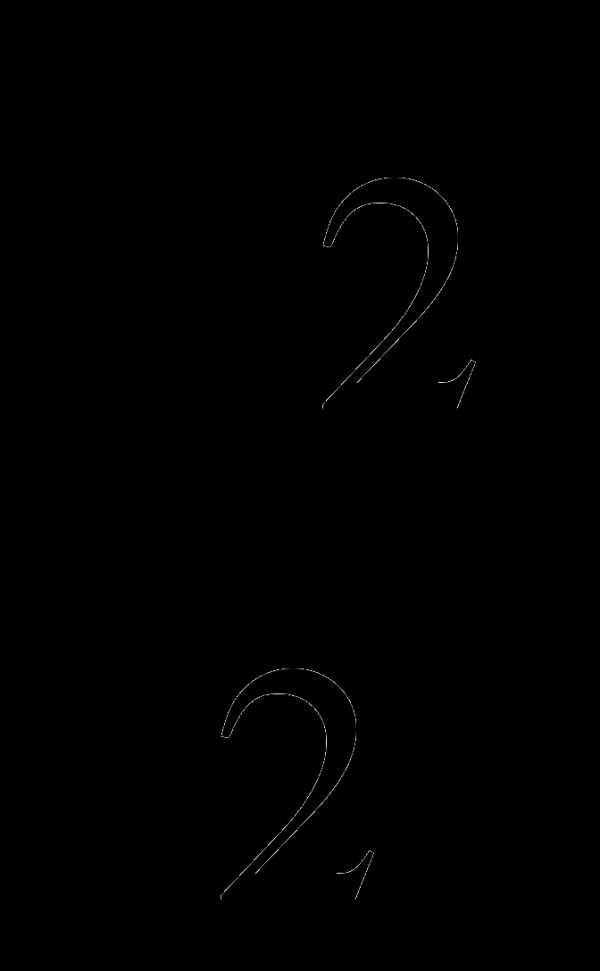
1
Ответ: Птоломей
-
2sin 15º cos15º=
-
cos(π-
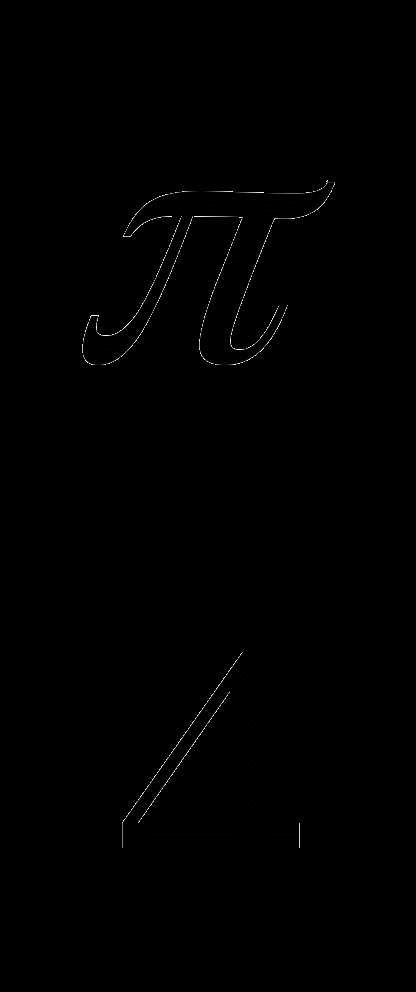 )=
)= -
sin
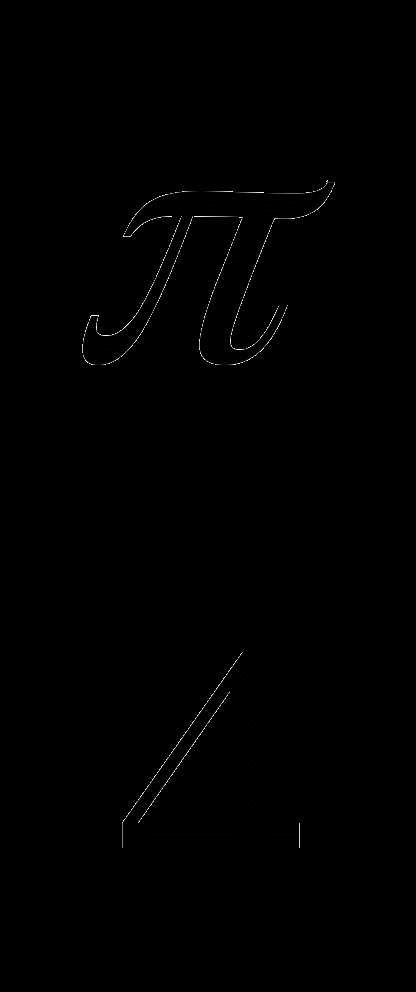 =
= -
60º=
-
cos45º=
-
 =
= -
sin8π=
-
sin(
 π)=
π)=
3 бригада:
к
п
с
т
у
ь
х

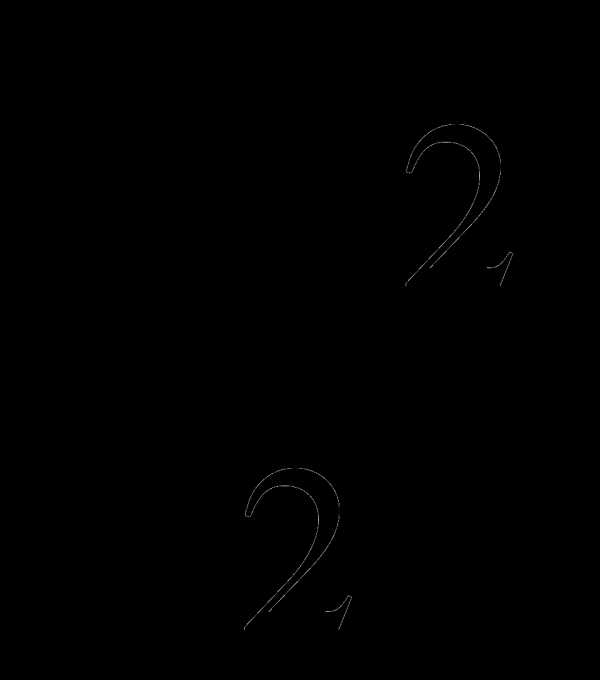
135
1

-1
0
136
О твет: Питискус
твет: Питискус
-
 π=
π=
-
sin
 =
=
-
sin
 =
=
-
cos60º=
-
cos124 π=
-
sin(-45º)=
-
2 sin135º cos135º=
-
sin
 =
=
Та команда, которая первой закончит работу, получает дополнительное задание. ( Кроссворд)
-
тур: карточка 1 Решение индивидуальное и защита 1 примера на доске
-
тур карточка 2 Решение индивидуальное и защита 1 примера на доске
-
тур карточка 3 Решение индивидуальное и защита 1 примера на доске
-
Тур «Тест»
-
Резервный. Тур « Кто вернее?» (10 мин) ( групповая работа) защита одного примера на доске
(Резервное время) Найти; Вычислить; Упростить.
Найти:
а) cosα, если sinα =  ,
,  <α< π
<α< π
б) sinα, если cosα = — ,
,  <α< π
<α< π
в) tgα, если sinα = —  ,
,  < α<2 π
< α<2 π
Вычислить:
а) 2 sin75ºcos75º
б) cos 275º- sin 275º
в) sin cos
cos + sin
+ sin cos
cos
Упростить:
а) 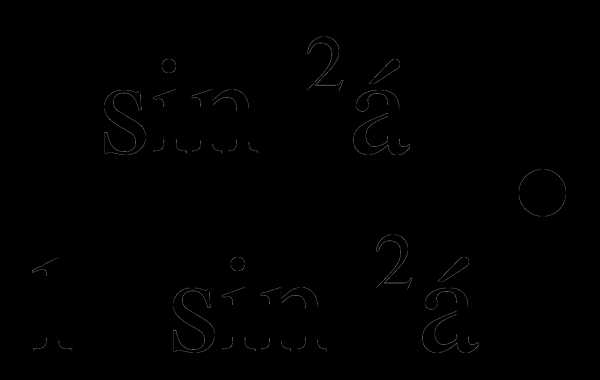 ctg 2α
ctg 2α
б) ( sin α- cosα)2 +( sin α+ cosα) 2 -2
в) 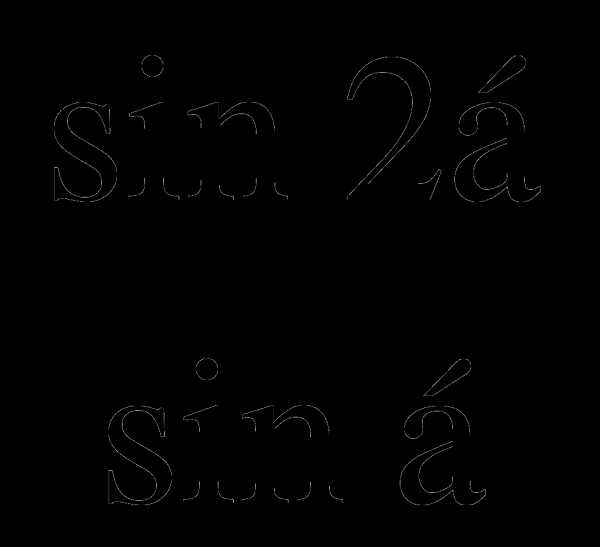
Вывод. Подведение итогов.
Учитель подводит итоги, отмечает работу отдельных учащихся.
Капитаны каждой команд сдают ведомость учета работы каждой команды, и игроки выкупают на заработанные баллы оценки. Каждый учащийся сдают свои листы и учитель проверяет с последующим выставлением оценок.
1. «Восстанови формулы». Один учащийся у интерактивной доски дописывает формулы:
-
tg α =
-
sin2 α +cos2 α = 1
-
1+ tg2 α =
-
sin(-α) = — sin α
-
tg (-α) = — tg α
-
ctg α =
-
tg α∙ ctg α = 1
-
1+ ctg2 α =
-
cos (-α) = cos α
-
ctg (-α) = — ctg α
-
cos2 α = 1- sin2 α
-
sin2 α = 1- cos2 α
-
tg α =
-
ctg α =
Задание
Решение
Ответ
Формулы
1
Упростить выражение:
2
Упростить выражение:
3
Упростить выражение:
Задание
Решение
Ответ
Формулы
1
Вычислить:
Синус суммы
2
Вычислить:
Косинус суммы
3
Вычислить:
Тангенс разности
4
Вычислить:
Зная, что , .
Синус суммы
Задание
Решение
Ответ
Формулы
1
Упростить выражение:
2
Найти , если известно, что , .
ТЕСТ
Задание #1
Вопрос:
Вычисли:
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #2
Вопрос:
Вычисли:
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #3
Вопрос:
Упрости выражение:
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #5
Вопрос:
Упрости выражение:
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #6
Вопрос:
Вычисли:
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #7
Вопрос:
Упрости выражение
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #8
Вопрос:
Вычисли:
Выберите один из 5 вариантов ответа:
1)
2) 1
3)
4) 1/2
5)
Задание #9
Вопрос:
Упрости выражение:
Выберите один из 5 вариантов ответа:
1)
2)
3)
4)
5)
Задание #10
Вопрос:
Вычисли:
Выберите один из 5 вариантов ответа:
1) 2) 3)
4) 5)
Ответы:
1) (1 б.) Верные ответы: 5;
2) (1 б.) Верные ответы: 5;
3) (1 б.) Верные ответы: 1;
5) (1 б.) Верные ответы: 5;
6) (1 б.) Верные ответы: 4;
7) (1 б.) Верные ответы: 2;
8) (1 б.) Верные ответы: 2;
9) (1 б.) Верные ответы: 3;
10) (1 б.) Верные ответы: 1;
КОД 551-542-231
1.тригонометрия
2. косинус
3. ордината
4. тангенс
5. мнемоническое
6 эйлер
ИНДИВИДУАЛЬНЫЙ ЛИСТ УЧЕТА
УЧЕНИКА 10 КЛАССА______________________________
ответы
Карточка 1
Карточка 2
Карточка 3
Тест
Код:
Кроссворд
3 бригада: Конкурс шифровальщиков:
к
п
с
т
у
ь
х

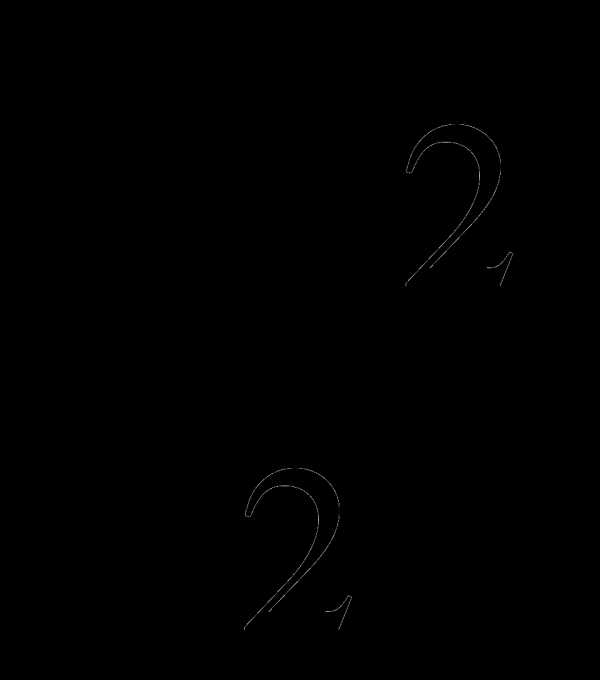
135
1

-1
0
136
-
 π=
π=
-
sin
 =
=
-
sin
 =
=
-
cos60º=
-
cos124 π=
-
sin(-45º)=
-
2 sin135º cos135º=
-
sin
 =
=
2 бригада: Конкурс шифровальщиков:
й
л
м
о
п
т
ф
0
—

18
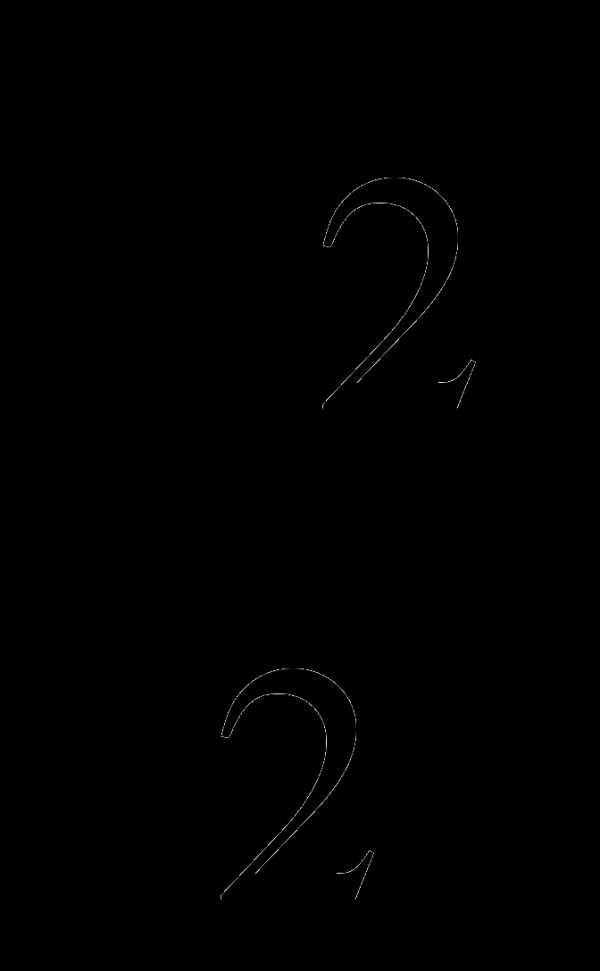

—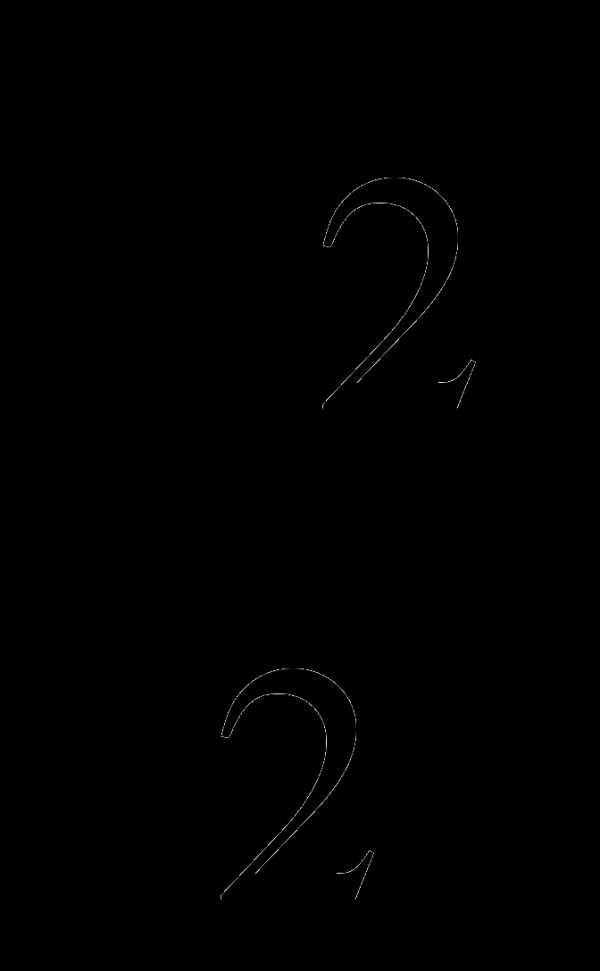
1
1. 2sin 15º cos15º=
2. cos(π-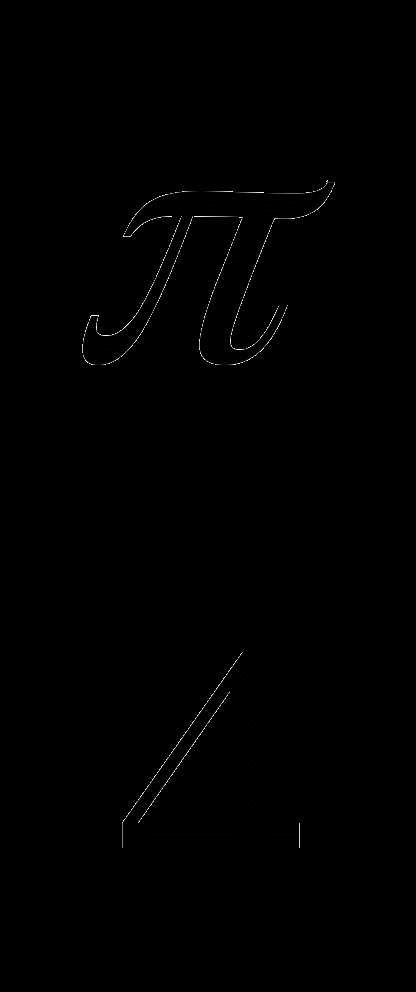 )==
)==
3. sin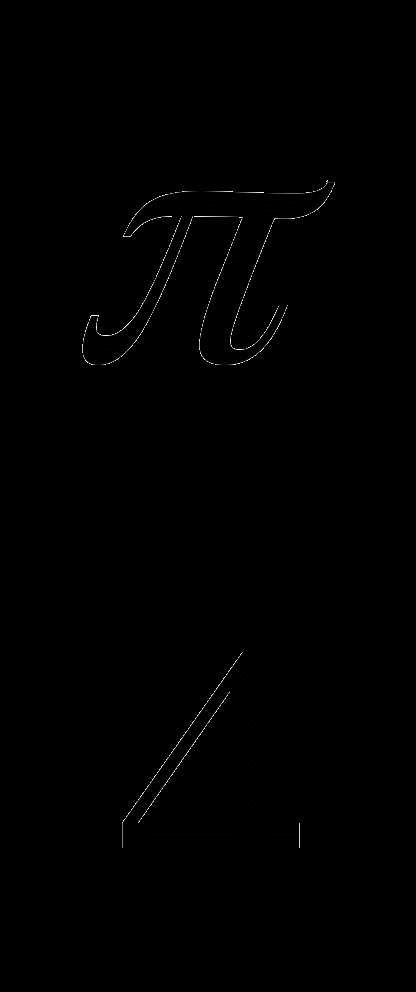 =
=
4. 60º=
5. cos45º=
6.  =
=
7. sin8π=
8. sin( π)=
π)=
1 бригада Конкурс шифровальщиков:
-
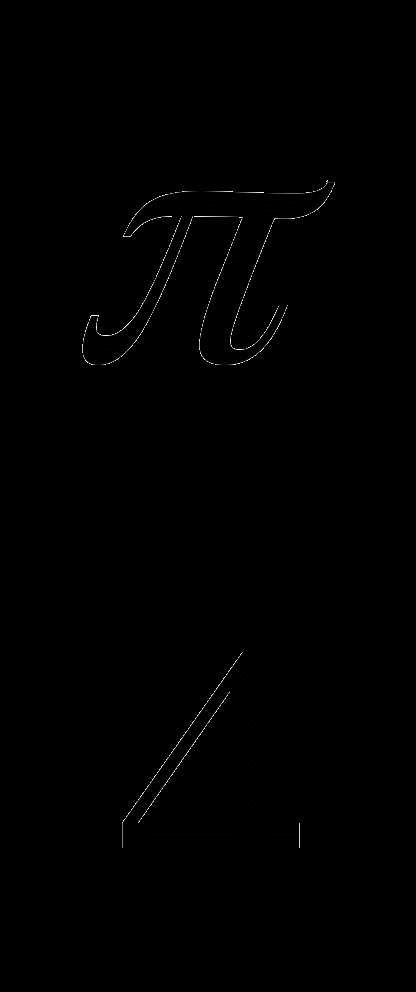 =
=
2. sin(-30º)=
3. cos2 15º- sin2 15º=
4. sin( )=
)=
5. cosα=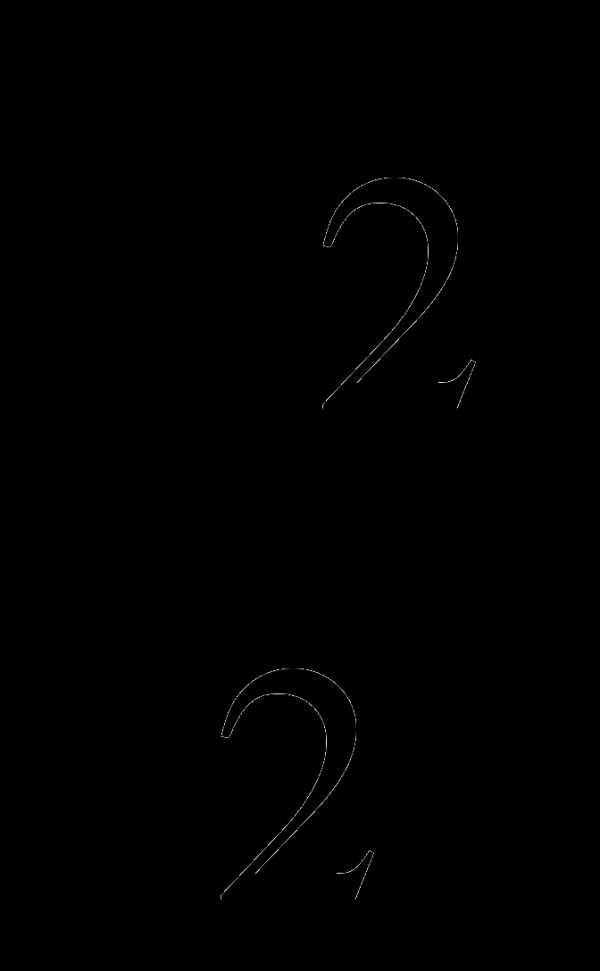 , α=?
, α=?
6. cos =
=
7. 72º=
8. sin =
=
е
к
н
о
с
у
я
—
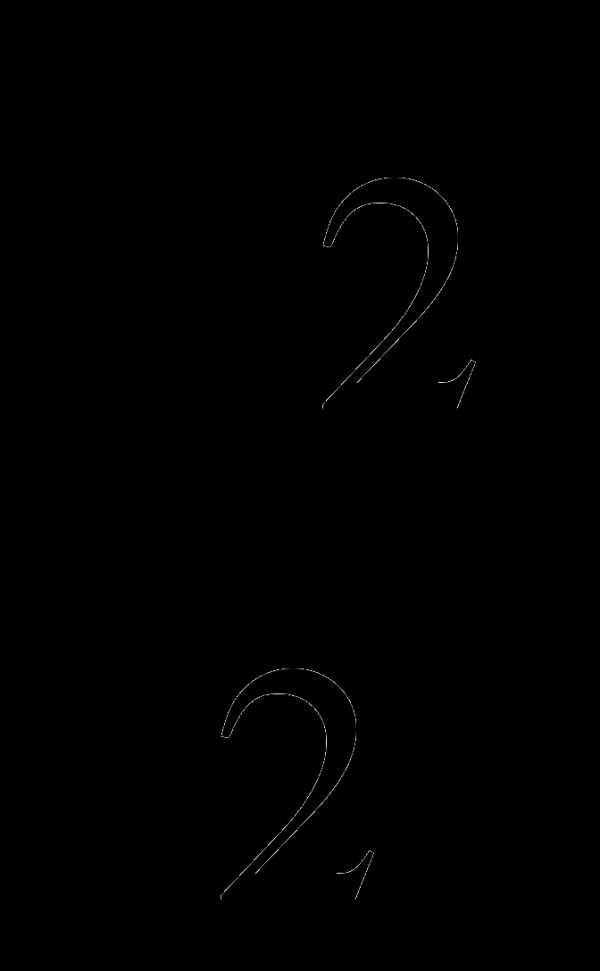
45

—

40
π
infourok.ru
План-конспект урока по алгебре (10 класс) на тему: Конспект урока математики в 10 классе «Различные способы решения тригонометрических уравнений»
Муниципальное бюджетное общеобразовательное учреждение
Бутурлиновская средняя общеобразовательная школа
Бутурлиновского муниципального района Воронежской области
Конспект урока по математике
в 10 классе
«Различные способы решения тригонометрических уравнений».
Подготовила
учитель математики
Коротких Эмма Александровна
2015 год
Цели урока:
Образовательные:
— систематизация знаний учащихся по теме «Методы решения тригонометрических уравнений»;
-углубление знаний по теме;
— формирование умения классифицировать тригонометрические уравнения по методам решений, применять эти методы в новой ситуации.
Развивающие:
– способствовать развитию аналитико-синтетического мышления, внимания;
— содействовать развитию логического, математического мышления учащихся.
Воспитательные:
— развивать у учащихся коммуникативные способности, элементы ораторского искусства;
— способствовать развитию творческой деятельности учащихся, потребности к самообразованию.
Оборудование: экран, проектор, карточки для самостоятельной работы, карточки с проверочной работой «Карусель», интерактивная доска, система опроса и тестирования PrometheanActivExpression, таблицы: «Тригонометрический круг», «Тригонометрия», «Тригонометрические уравнения», индивидуальный справочный материал,индивидуальные оценочные листы; Мордкович А.Г. Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч. 1.Учебник (задачник) для учащихся общеобразовательных учреждений (базовый уровень), — М.: Мнемозина, 2012.
Тип урока: урок обобщения и систематизации знаний
Методы обучения:метод постановки проблемы и метод поиска решений.
Формы организации урока: индивидуальная, фронтальная, групповая.
Педагогические приемы урока:эпиграф, наблюдение, обобщение, общественный смотр знаний, самостоятельная и проверочная работы.
План урока:
- Организационный момент (1 мин).
- Систематизация теоретического материала.
1.Самостоятельная работа: блиц-опрос — контроль знаний по простейшим тригонометрическим уравнениям (система опроса и тестирования Promethean ActivExpression,системное голосование) (8 мин).
2.Повторение: методы решения тригонометрических уравнений (13 мин).
- Проверочная работа (20 мин).
- Итог урока. Рефлексия (2 мин).
- Домашнее задание (1 мин).
Конспект урока
- Организационный момент урока.
Учитель
— Сегодня на уроке мы будем учитьсяприменять различные методыв решении тригонометрических уравнений, которые занимают важное место в математическом анализе. Математика способствует развитию умений анализировать, сопоставлять, творчески мыслить. Правильное решение по-своему красиво, а поиск решения всегда интересен. Эпиграфом нашего урока будут словаМ. И. Калинина:
«Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе».
II. Систематизация теоретического материала
Учитель.
— Посмотрите на уравнения (слайд). Каким способом их можно решить? (постановка проблемы).
Пример 1
Пример 2 cos(x/5)=1
Пример 3. 1 +
Пример 4
Пример 5. Решите уравнение
2sin2(x)+3cos(x)=0
Пример 6.
Пример7.2sin2(x)+3cos(x)=0
Пример 8.
Учащиеся дают разные ответы.
Учитель
— Сравните и сопоставьте эти уравнения. Разбейте их на группы. Какими способами можно решить каждую получившуюся группу уравнений?
Учащиеся
— Решение простейших уравнений: примеры 1,2
— Метод разложения на множители:примеры 3, 4.
— Метод замены переменных: примеры 5 ,6.
— Решение уравнений с помощью применения тригонометрических формул:примеры 7, 8
Учитель
Верно. Все тригонометрические уравнения, как правило, сводятся к простейшим уравнениям, которые мы научились решать с помощью общих формул простейших тригонометрических уравнений, их частных случаев, а также с помощью тригонометрических формул. Обратите внимание на таблицы и справочный материал:
Справочный материал (на рабочем столе учащихся).
Тригонометрические формулы.
Справочный материал (на рабочем столе учащихся).
Тригонометрические уравнения.
С
Учитель:
Проверим ваши умения по решению простейших тригонометрических уравнений.
1. Самостоятельная работа.
Блиц-опрос (проверка — системное голосование)
За правильное решение учащиеся получают балл (самопроверка с последующей записью баллов в оценочный лист)
Оценочный лист
|
Фамилия, имя |
||
|
№ п/п |
Вид работы |
Количество баллов |
|
№ п/п |
Уравнение |
Корни |
|
1 |
нет решений |
|
|
2 |
||
|
3 |
||
|
4 |
||
|
5 |
2. Повторение.
Учитель:
— А сейчас вам предстоит работа в группах. Вы должны представить решение тригонометрического уравнения указанным методомв карточкеи составить алгоритм решения
Учащиеся делятся на группы разной подготовленности. Обсуждают коллективно решение примеров.
Учитель:
Проверка задания: один человек группы произносит алгоритм решения тригонометрического уравнения, сверяясь с решением, предоставленным на слайде(используется материалы курса «Уравнения и неравенства в школьном курсе математики», П.В. Чулков, лекция №5, — М.: Педагогический университет «Первое сентября», 2010)
Слайды
1 группа. Решение простейших уравнений.
Пример 2(слайд)
Решить уравнение:
cos(x/5)=1
Решение:
x/5= ± arccos(1) + 2πk.
x/5=πk
x=5πk
Ответ:5πk,
2 группа. Метод разложения на множители.
Пример 3 (слайд).
Решите уравнение 1 +
Решение. Перепишем уравнение в виде:
1 +
Ответ:
3 группа. Метод замены переменных.
Пример 5 (слайд).
Решите уравнение
Решение. Запишем уравнение в виде откуда
Заметим, что данное уравнение представляет собой квадратное уравнение относительно . Обозначим получим уравнение
корни которого
Получаем два случая:
1) откуда
2)
Ответ:
Учитель.
Методом замены можно решать «однородные тригонометрические» уравнения. Тригонометрическое уравнение называют однородным, если после некоторой замены полученный многочлен от двух переменных составлен из одночленов одинаковой степени. Например:
Слайд
Решите уравнение
Решение. Перепишем уравнение в виде
Получили уравнение, однородное относительно
Рассмотрим два случая:
1) что невозможно, поскольку в этом случае корней нет.
2) тогда разделим обе части уравнения на
Пусть y = tgx. Получим: откуда = .
Осталось решить уравнения tgx = 1 и tgx = .
Ответ:
4группа.
Решение уравнений с помощью применения тригонометрических формул.
Примеры 7 (слайд).
Решить уравнение:
2sin2(x)+3cos(x)=0
Решение:
Воспользуемся тождеством:
sin2(x)+cos2(x)=1
Наше уравнение примет вид:
2-2cos2(x)+3cos(x)=0
2cos2(x)- 3 cos(x) -2 = 0
введем замену t=cos(x): 2t2 -3t — 2 = 0
Решением нашего квадратного уравнения являются корни: t=2 и t=-1/2
Тогда cos(x)=2 и cos(x)=-1/2.
Т.к. косинус не может принимать значения больше единицы, то cos(x)=2 не имеет корней.
Для cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk
Ответ: x= ±2π/3 + 2πk
Учитель:
— При решении тригонометрических уравнений можно использовать универсальную тригонометрическую подстановку на основе
Формул(слайд):
Если то
С помощью универсальной подставки мы можем любое уравнение вида свести к алгебраическому уравнению. Важно при этом помнить, что, делая замену, мы можем потерять те корни исходного уравнения, для которых не определен, то есть значения Их мы должны проверять отдельно.
В следующем примере встречается изначально, поэтому универсальная подстановка не может привести к потере корней указанного вида.
Слайд
Решим уравнение
Решение (учащиеся записывают в тетради)
Сделаем универсальную подстановку , тогда
Таким образом:
а)
б)
Ответ:
Учитель.
В заданиях ЕГЭ встречаются тригонометрические уравнения, решаемые способом отбора корней. Рассмотрим решение такого уравнения (слайд):
Найдите корни уравнения принадлежащие промежутку .
Решение.Корни данного уравнения можно найти из соотношения
откуда получаем, что
Но Тогда
Решим это двойное неравенство:
Полученное неравенство выполнено, если k =
Ответ:
Учитель
- Дифференцированная проверочная работа «Карусель».
Каждому ученику выдается карточка с заданием. Сделав одно задание, ученик передает свою карточку соседу по кругу, вписывая свою фамилию напротив выполненного примера.
Карта №1
|
№ п/п |
Пример |
Ответ |
Фамилия, имя обучающегося |
|
1 |
sin(7x)= 1/2 |
||
|
2 |
3 sin 2(x) + √3sin (x) cos(x) = 0 |
||
|
3 |
cos2(2x) -1 — cos(x) =√3/2 -sin2(2x) |
||
|
4 |
3sin2(3x) + 10 sin(3x)cos(3x) + 3 cos2(3x) =0 |
||
|
5 |
sin(3x)= √3/2. Найти все корни на отрезке [π/2; π ]. |
Карта №2
|
№ п/п |
Пример |
Ответ |
Фамилия, имя обучающегося |
|
1 |
cos(3x)= √3/2 |
||
|
2 |
ctg2(x) + 2ctg(x) + 1 =0 |
||
|
3 |
2 sin2х — 2sin 2х +1 =0 |
||
|
4 |
5 sin2х — 3 sinхcosх — 2 cos2х =0 |
||
|
5 |
sin(2x)= √3/2. Найти все корни на отрезке [0; π ]. |
Карта №3
|
№ п/п |
Пример |
Ответ |
Фамилия, имя обучающегося |
|
1 |
sin(7x)= 1/2 |
||
|
2 |
2 sin2 x – sin x cosx =0 |
||
|
3 |
1- 4 sin 2x + 6 cos2х = 0 |
||
|
4 |
5 sin2 х + sin2х — cos2х =1 |
||
|
5 |
cos(1/2x)= √2/2. Найти все корни на отрезке [0;π]. |
Карта №4
|
№ п/п |
Пример |
Ответ |
Фамилия, имя обучающегося |
|
1 |
ctg(0.5x) = -1.7 |
||
|
2 |
3 cos2х + 2 sin х cos х =0 |
||
|
3 |
2 sin x — 3 cos x = 4 |
||
|
4 |
5 sin2 х + 2 sinхcos х — cos2х =1 |
||
|
5 |
sin(3x)= 1. Найти все корни на отрезке [0;π/2]. |
Карта №5
|
№ п/п |
Пример |
Ответ |
Фамилия, имя обучающегося |
|
1 |
tg(4x) = √3 |
||
|
2 |
4 sin2 х — 2sinх cos х — 4 cos2х =1 |
||
|
3 |
2 sin x — 5 cos x = 3 |
||
|
4 |
6 sin2х — 5 sinх cos х + cos2х =0 |
||
|
5 |
cos(4x)= √2/2. Найти все корни на отрезке [0;π]. |
При проверке работы учитель и ученики-консультанты заполняют таблицу:
|
№ п/п |
Фамилия, имя обучающегося |
Номера выполненных заданий |
Количество баллов |
Оценка |
5. Подведение итогов. Рефлексия.
Учитель: Итак, подведем итоги урока.
Решение тригонометрических уравнений состоит из двух этапов.
Первый — преобразование уравнения для получения его простейшего вида. 2
Второй — решение полученного простейшего тригонометрического уравнения. Существуют основные методы решения уравнений такого вида:
Какие методы решения тригонометрических уравнений мы сегодня повторили?
Ответы учащихся:
- Разложение на множители.
- Метод замены переменной:
— сведение к квадратному уравнению;
— сведение к однородному уравнению;
— универсальная тригонометрическая подстановка.
3.Отбор корней
Учитель
Оцените свою работу по вашим оценочным листам
(дает дополнительные баллы отличившимся ученикам).
Рефлексия.
Учитель
Продолжите фразу:
- Вызвало затруднения задание…
- Самым интересным при работе для меня было…
6. Домашнее задание, инструкция о его выполнении (слайд)
Решить уравнение:
- 2 sin2 x + cos 4 x = 0
- sin4 x + cos4 x = cos22 x + ¼
- sin 2 x = cos x — sin x
- √3 cos x + sin x = 2
№ 23.14 Задачник Алгебра и начала анализа 10 класс, А.Г. Мордкович.
При решении первого уравнения воспользуйтесь формулой понижения степени.
Литература
1. Алексеев А. Тригонометрические подстановки. // Квант. — 1995. — №2. -с. 40 — 42.
2. Гилемханов Р.Г. О преподавании тригонометрии в 10 классе по курсу В //Математика в школе. 2001-№ 6 -с. 26-28.
3. ЕГЭ. Математика 2008.Сборник экзаменационных заданий. Денищева Л.О., Рязановский А.Р., Семёнов П.В. – М., изд-во «Эксмо-Пресс», 2008.
4. Крамор В.С. Тригонометрические функции. — М.: Просвещение, 1979.
5. Мордкович А.Г. Методические проблемы изучения тригонометрии в общеобразовательной. //Математика в школе. 2002 — № 6 — с.32-38.
6. Мордкович А.Г. Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч. 1. Учебник (задачник) для учащихся общеобразовательных учреждений (базовый уровень), — М.: Мнемозина, 2012.
7. Синакевич С.В. Тригонометрические уравнения — М.: Учпедгиз, 1959.
8. Чулков П. В. Уравнения и неравенства в школьном курсе математики. — М.: Педагогический университет «Первое сентября», 2010
Интернет — источники
Сайт «Вся элементарная математика»
http://www.bymath.net/studyguide/tri/sec/tri16.ht
nsportal.ru
План-конспект урока (алгебра, 10 класс) по теме: Урок-обобщение «Методы решения тригонометрических уравнений» 10 класс
Урок-обобщение
Тема: «Общие методы решения тригонометрических уравнений».
Цель:
- образовательные – обеспечить повторение, обобщение и систематизацию материала темы, создать условия контроля усвоения знаний и умений
- развивающие – содействовать развитию у учащихся мыслительных операций: умение анализировать, сравнивать; формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения; отрабатывать навыки самооценивания знаний и умений, выбора задания, соответствующего их уровню развития.
- воспитательные – вырабатывать внимание, самостоятельность при работе на уроке; способствовать формированию активности и настойчивости, максимальной работоспособности.
Задачи:
- развивать умение обобщать, систематизировать, делать вывод;
- активизация самостоятельной деятельности;
- развивать познавательный интерес;
- формирование умения рационально, аккуратно оформлять задание на доске
и в тетради
Тип урока:
- урок обобщения и систематизации знаний
Методы обучения:
- частично-поисковый, проверка уровня знаний, самопроверка, системные обобщения
Формы организации:
- индивидуальна, фронтальная
Приемы:
- обобщения;
- сравнения;
- создание проблемной ситуации;
- самопроверки;
Ход урока:
1.Организационный момент (обеспечить внешнюю обстановку для работы на уроке, психологически настроить учащихся к общению)
Учитель: Здравствуйте, садитесь! Сегодня мы проводим урок-обобщение по теме «Общие методы решения тригонометрических уравнений».
1.2. Проверка готовности учащихся к уроку.
Учитель: Ребята, кто сегодня отсутствует? Все готовы к уроку? Сконцентрируйтесь, начинаем нашу работу!
1.3. Озвучивание целей урока и плана его проведения.
Учитель: Тема нашего урока – решение тригонометрических уравнений.
Цель урока сегодня — рассмотреть общие подходы решения тригонометрических уравнений; закрепить навыки и проверить умение решать тригонометрические уравнения разными способами.
В начале урока мы вспомним основные формулы тригонометрии и их применение для упрощения выражений.
Далее работа будет чередоваться: вспомним формулы решения простейших тригонометрических уравнений, и на их основе посмотрим как происходит выборка корней при решении заданий ЕГЭ в части С1. Вспомним виды тригонометрических уравнений. Решим тригонометрические уравнения по известным алгоритмам, однородные тригонометрические уравнения первого и второго порядка, а также неоднородные уравнения первого порядка. Проведём разноуровневую проверочную работу, задания которой вы будете выбирать самостоятельно, учитывая свои знания, умения и навыки. Проверим решения, и вы выставите себе оценку.
Затем получите домашнее задание и подведем итоги урока. Итак, приступаем.
2. Устная работа.
*На доске заранее подготовлены уравнения. Справа на доске написаны ответы на листках формата А4 на магнитах. Надо правильно расположить их, в соответствии с решением. Ученики выходят по одному и выполняют задание.
Учитель: Задание – используя основные формулы тригонометрии, упростите выражение:
А) (sin a – 1) (sin a + 1) — cos2 a
Б) sin2 a – 1 + cos2 a 0
В) sin2 a + tg a ctg a + cos2 a 2
Г) |1- tg х|
2. Основная часть урока (чередование фронтальной и индивидуальной форм работы с последующей проверкой задания).
2.1 Учитель: Тригонометрические уравнения вызывают наибольшие затруднения в ЕГЭ, в частности, в задании С1, необходимо не только решить уравнение, но и правильно выбрать корни.
Задание №1: Решить уравнение, указать корни, принадлежащие промежутку (-4;4)
*Один из учеников записывает решение уравнения на закрытой доске, отбор корней идет совместно с объяснениями учителя:
Ответ:
2.2 Учитель: Ребята, а теперь вспомним основные методы решения тригонометрических уравнений.
*На экране проецируются основные виды тригонометрических уравнений, методы их решений
|
1. Введение новой переменной. |
2sin2x – 5sinx + 2 = 0. |
Пусть sinx = t, |t|≤1, Имеем: 2t2 – 5t + 2 = 0. Получаем и решаем tg = z, |
|
2. Разложение на множители |
2sinx cos5x – cos5x = 0; |
cos5x (2sinx – 1) = 0. |
|
3. Однородные тригонометрические уравнения. |
I степени a sinx + b cosx = 0, (a,b ≠ 0). |
Разделим на cosx ≠ 0. Получаем ии решаем: a tgx + b = 0; … |
|
II степени a sin2x + b sinx cosx + c cos2x = 0. |
1) если а ≠ 0, разделим на cos2x ≠0 имеем: a tg2x + b tgx + c = 0. 2) если а = 0, то имеем: b sinx cosx + c cos2x =0; разделим на cos2x ≠0 получаем и решаем b tgx + c = 0 |
|
|
4. Неоднородные тригонометрические уравнения. |
Уравнения вида: asinx + bcosx = c где a, b, c – коэффициенты; x – неизвестное. |
Введение вспомогательного угла |
2.3 Учитель: Вспомнив теорию, давайте решим несколько тригонометрических уравнений по известным алгоритмам.
*Задания можно выводить на экран, у меня они были подготовлены на листах формата А3 и крепились к доске на магнитах. Каждое задание выполняется по одному ученику на доске, с объяснением. Первым двоим, не рядом сидящим, при правильном решении и оформлении ставится оценка.
Задание №1.
Решить уравнение sin2 х + 5 sin х — 6 =0.
Учащиеся решают уравнение, вводят замену
sin х = z, ,
решая квадратное уравнение
z2 + 5 z — 6 = 0,
находят
z1 = 1
z2 = -6 (не удовлетворяет условию)
Решением уравнение
sin х = 1
х = π/2 +2 π k, k Z.
Ответ: π/2 +2 π k, k Z.
Учитель: Продолжим решать тригонометрические уравнения, применяя нужный метод.
Задание №2
Решите уравнение 2 sin x+ 3 cos x = 0.
Учащиеся решают уравнение.
2 sin x+ 3 cos x = 0 | : cos x ≠ 0
2 tg x + 3 =0
tg x = -1,5
х= arctg (-1,5) + πk, k Z
х = — arctg 1,5 + πk, k Z
Ответ: — arctg 1,5 + πk, k Z.
Задание №3
Решите уравнение 2 sin2 х — 3 sinх cos х — 5 cos2х =0
Учащиеся решают уравнение
2 sin2 х — 3 sinх cos х — 5 cos2х =0
2 sin2 х — 3 sinх cos х — 5 cos2х =0 | : cos2х ≠ 0
2 tg 2x — 3 tg x — 5 = 0
замена tg x = t
2 t2 – 3 t – 5 =0
t1 = -1; t2 = 2,5
Выполняем обратную замену и решаем уравнения
1) tg х = -1
х = -π/2 + πk , k Z.
2) tg х = 2,5
х = arctg 2,5+ πn, n Z.
Ответ: -π/2 + πk , arctg 2,5+ πn, n, k Z.
Задание №4.
Решить уравнение sin x + cos x = 1
Учащиеся решают уравнение
sin x + cos x = 1 │ :2
Ответ:
3. Самостоятельная работа учащихся с последующей проверкой результатов работы
Учитель: А теперь выберите два уравнения и самостоятельно решите их.
*Работа выполняется под копирку. Оригинальный вариант сдается учителю для проверки и выставления отметки, а второй — остается у учащихся для самопроверки.
На экране проецируется задание.
|
На оценку |
1 вариант |
2 вариант |
|
«3» «4» «5» |
3 sin x+ 5 cos x = 0 5 sin2 х — 3 sinх cos х — 2 cos2х =0 3 cos2х + 2 sin х cos х =0 5 sin2 х + 2 sinх cos х — cos2х =1 2 sin x — 5 cos x = 3 1- 4 sin 2x + 6 cos2х = 0 |
2 cos x+ 3 sin x = 0 6 sin2 х — 5 sinх cos х + cos2х =0 2 sin2 x – sin x cosx =0 4 sin2 х — 2sinх cos х — 4 cos2х =1 2 sin x — 3 cos x = 4 2 sin2 х — 2sin 2х +1 =0 |
Учитель: Ребята, проверьте свое решение с ответами и поставьте оценку.
*Ответы записываются на доске с обратной стороны, пока учащиеся работают. После того, как собраны работы, проводится самопроверка, и учащиеся выставляют себе предварительную оценку.
|
1 вариант |
2 вариант |
|
|
«3» «4» «5» |
— arctg 5/3+ πk, k Z. π/4 + πk; — arctg 0,4 + πn, k, n Z. π/2 + πk; — arctg 1,5 + πn, k, n Z. π/4 + πk; — arctg 0,5 + πn, k, n Z. arctg ( — 1 ± √5) + πk, k Z. π/4 + πk; arctg 7 + πn, k, n Z. |
— arctg 2/3+ πk, k Z. arctg 1/3+ πk; arctg 0,5 + πn, k, n Z. πk; arctg 0,5 + πn, k, n Z. -π/4 + πk; — arctg 5/3 + πn, k, n Z. arctg ( 2 ± √11) + πk, k Z. π/4 + πk; arctg 1/3 + πn, k, n Z. |
4. Учитель: Для закрепления навыков решения тригонометрических уравнений я предлагаю вам выполнить домашнее задание дифференцированного содержания:
*Дифференцированное домашнее задание. Задание выводится на экран, в электронном журнале загружается файлом
Решите уравнения
Оценка «3»:
Оценка «4»:
Оценка «5»:
- Найдите наибольший отрицательный корень уравнения
5. Учитель: Подведем итоги урока. Сегодня на уроке мы вспомнили числовые значения тригонометрических функций, вспомнили формулы решения простейших тригонометрических уравнений, рассмотрели общие подходы решения тригонометрических уравнений, закрепили навыки и проверили умения решать тригонометрические уравнения, познакомились со способом отбора корней при решении тригонометрических уравнений.
Я уверена, что у вас сложилось более полное представление о тригонометрических уравнениях и разнообразии способов их решения, и с решением тригонометрических уравнений большинство из вас справится.
— Что нового узнали на уроке?
— Испытывали ли вы затруднения при выполнении самостоятельной работы?
— Испытывали ли вы затруднения при выборе самостоятельной работы?
— Какие проблемы у вас возникли по окончании урока?
Учитель: Спасибо вам за насыщенную работу на уроке. Я благодарю всех, кто принял активное участие в работе. Урок окончен. До свидания!
nsportal.ru
Методическая разработка (алгебра, 10 класс) по теме: Открытый урок по теме «Решение тригонометрических уравнений»
МОУ СОШ № 3 имени С. А. Красовского
ТЕМА: « РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ».
(Урок алгебры и начала анализа в 10 классе с использованием модульной технологии.)
УЧИТЕЛЬ МАТЕМАТИКИ
МОУ СОШ № 3
ПОДОСЁНОВ А Л..
ПОС МОНИНО – 2009 ГОД
Модульная педагогическая технология конструируется на основе ряда целей. Важнейшими из них являются:
— создание комфортного темпа работы каждого обучающегося;
-определение каждым обучающимся своих возможностей в обучении;
-гибкое построение содержания учебного материала;
-интеграция различных видов и форм обучения.
Самым главным отличием технологии является применение принципа планирования совместной деятельности учителя и обучающегося от начала до конечной учебной цели. Опыт использования такой технологии позволяет сделать вывод, что при обучении создаётся ситуация успеха для обучающихся, которая способствует преодолению страха перед их ответом у доски.
Использование таких занятий помогает осуществлять индивидуальный подход к обучающимся, включать каждого в осознанную учебную деятельность, мотивировать её, успешно решать учебные и коррекционно-развивающие задачи. Эта технология предполагает, необходимое условие формирования навыков самообучения и самоорганизации, что обеспечивает постепенный переход от пассивно-воспринимающей позиции к позиции сотрудничества ученик и учитель. Использование этой технологии способствует достижению основной цели обучения
— саморазвитию обучающихся, поэтому её можно применять как в классах повышенного уровня подготовки, так и в классах КРО.
« УЧИТЬСЯ МОЖНО ТОЛЬКО ВЕСЕЛО… ЧТОБЫ ПЕРЕВАРИВАТЬ ЗНАНИЯ, НАДО ПОГЛОЩАТЬ ИХ С АППЕТИТОМ»
АНАТОЛЬ ФРАНС
ЦЕЛИ УРОКА:
ОБРАЗОВАТЕЛЬНЫЕ – ОБЕСПЕЧИТЬ ПОВТОРЕНИЕ, ОБОБЩЕНИЕ И СИСТЕМАТИЗАЦИЮ МАТЕРИАЛА ТЕМЫ; СОЗДАТЬ УСЛОВИЯ КОНТРОЛЯ УСВОЕНИЯ ЗНАНИЙ И УМЕНИЙ;
РАЗВИВАЮЩИЕ – СПОСОБСТВОВАТЬ ФОРМИРОВАНИЮ УМЕНИЙ ПРИМЕНЯТЬ ПРИЁМЫ: СРАВНЕНИЯ, ОБОБЩЕНИЯ, ВЫДЕЛЕНИЯ ГЛАВНОГО, ПЕРЕНОСА ЗНАНИЙ В НОВУЮ СИТУАЦИЮ, РАЗВИТИЮ МАТЕМАТИЧЕСКОГО КРУГОЗОРА, МЫШЛЕНИЯ И РЕЧИ, ВНИМАНИЯ И ПАМЯТИ;
ВОСПИТАТЕЛЬНЫЕ – СОДЕЙСТВОВАТЬ ВОСПИТАНИЮ ИНТЕРЕСА К МАТЕМАТИКЕ И ЕЁ ПРИЛОЖЕНИЯМ, АКТИВНОСТЬ, МОБИЛЬНОСТЬ, УМЕНИЯ ОБЩАТЬСЯ, ОБЩЕЙ КУЛЬТУРЫ.
ТИП УРОКА:
УРОК ОБОБЩЕНИЯ И СИСТЕМАТИЗАЦИИ ЗНАНИЙ.
МЕТОДЫ ОБУЧЕНИЯ:
ЧАСТИЧНО-ПОИСКОВЫЙ, ТЕСТОВАЯ ПРОВЕРКА УРОВНЯ ЗНАНИЙ, РЕШЕНИЕ ПОЗНАВАТЕЛЬНЫХ ОБОБЩАЮЩИХ ЗАДАЧ, СИСТЕМНЫЕ ОБОБЩЕНИЯ, САМОПРОВЕРКА.
ФОРМЫ ОРГАНИЗАЦИИ ТРУДА: ИНДИВИДУАЛЬНАЯ, ФРОНТАЛЬНАЯ.
ПЛАН УРОКА:
Орг. момент.
Устная работа.
Классификация тригонометрических уравнений.
Решение уравнений с дополнительными заданиями.
Самостоятельная работа.
Домашнее задание.
Итог урока.
ОРГ. МОМЕНТ.
Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом». Давайте будем следовать этому совету писателя, будем активны, внимательны, всё будем делать с удовольствием и большим желанием.
Тема сегодняшнего урока «Решение тригонометрических уравнений». Повторяем, обобщаем, приводим в систему изученные виды, типы, методы и приёмы решения тригонометрических уравнений.
Перед вами задача – показать свои знания и умения по решению тригонометрических уравнений.
Устная работа.
1. Найти ошибки в ответах на предложенные вопросы.
Вопросы
1.Каково будет решение sin x=a, |a| 1?
2.При каком а уравнение sin x=a имеет решение?
3.Какой формулой выражается это решение?
4.В каком промежутке находится arcsin a?
5.В каком промежутке находится значение а?
6.Каким будет решение уравнения sin x=1?
7.Каким будет решение уравнения sin x=-1?
8.Каким будет решение уравнения sinx=0?
9.Чему равно arсsin(-a)?
10.В каком промежутке находится arcctg a?
11.Чему равно arcctg(-a)?
Ответы
1. Нет решения
2. |a|1
3.
4.
5.
6.
7.
8.
9. –arcsin a
10.
11. П – arcctg a
2. Письменно ответьте на вопросы, заменив sinx на cosx, ctgx на tgx.
После ответов, поменяйтесь работами и сверьте с доской, после чего поставьте соответствующую оценку.
Ответы (соs x, tgx)
1. Х = ±arccos a + 2πn, n Z
2. |a|1
3. Х = ±arccos a + 2πn, n Z
4. . [ 0; π ]
5.
6. Х = 2πn, n Z
7. Х = π + 2πn, n Z
8. Х = π/2 + πn, n Z
9. П – arccos a
10.
11. – arctg a
Классификация тригонометрических уравнений.
Системно-обобщающая таблица.
|
ТРИГОНОМЕТРИЧЕСКИЕУРАВНЕНИЯ |
|
Алгебраические уравнения |
Однородные уравнения |
Уравнения, решаемые с помощью разложения на множители |
№ 2,4,6,7,8,11 №1,5,10 №3,9,12
1.Решение алгебраических уравнений заключается в том, что все тригонометрические функции, которые входят в уравнение,
выражают через какую-нибудь одну тригонометрическую функцию, зависящую от одного и того же аргумента.
2.Решение однородных уравнений (уравнения, в которых у всех слагаемых сумма показателей одинакова) и приводимых к ним сводится к решению алгебраических относительно tgx путём деления обеих частей уравнения на cosx≠0 и cos2 x≠0 соответственно.
3. Решение с помощью разложения на множители сводится к решению двух элементарных уравнений.
ЗАДАНИЕ:
Определить тип тригонометрического уравнения:
10. 1 – 3sinx*cosx – 5cos2x = 0
11. 2sin2 2x + 5 sin2x – 3 = 0
12. sin5x + sinx = √2 sin3x
Решение уравнений.
Решение с указанием чёткого алгоритма решения уравнений данного типа.
1. Решить уравнение
Алгоритм:
1. Приведение к однородному уравнению.
2. Деление левой и правой части на Cos2x при условии Cosx0.
3. Решение квадратного уравнения.
4. Подстановка.
5. Решение простейших тригонометрических уравнений.
Ответ:
2. Найти наибольший отрицательный корень уравнения
Алгоритм:
1. Замена переменной.
2. Решение квадратного уравнения.
3. Решение простейших тригонометрических уравнений.
Ответ: Наибольший отрицательный корень
3. Найти сумму корней уравнения принадлежащих промежутку (0;П)
Найдем сумму
Дополнительно: Решить уравнение
Ответ:
ЗАРЯДКА ДЛЯ ГЛАЗ.
Тест. Самостоятельная работа.
Уровень А.
Уровень В.
I вариант
1. Найти наименьший положительный корень уравнения
sinx + sin5x = 0.
А. π/6 Б. π/4
В. π /3 Г. π/2.
II вариант
Найдите наименьший положительный корень уравнения
cosx + cos5x = 0
А. π/6 В. π/4
Б. π/2 Г. π
Домашняя работа.
Домашняя работа выбирается самими обучающимися по уровням.
УРОВЕНЬ А.
УРОВЕНЬ В
VII. Итог урока.
Чем мы занимались сегодня на уроке?
Что за уравнения мы решали?
Какие типы и методы решения мы знаем?
Устная работа по закреплению:
Оценка работы класса.
nsportal.ru