Решебник 10 геометрия: Готовые самост. и контр. по Геометрии 10 класс — Казаков

ГДЗ по Геометрии для 10 класса Латотин Л.А., Чеботаревский Б.Д., Горбунова И.В. на 5

Авторы: Латотин Л.А., Чеботаревский Б.Д., Горбунова И.В..

Издательство:

Образование и воспитание 2020

«ГДЗ по Геометрии для 10 класса Учебник Латотин (Образование и воспитание)» эффективно поможет ученикам старшей школы в изучении одной из главных технических дисциплин школьного курса. Решебник позволит школьникам самостоятельно справиться с выполнением трудного домашнего задания, не прибегая к помощи взрослых. Подростку не придётся ждать пока с работы вернутся родители или освободится учитель, чтобы разобраться в способе решения проблемной задачи. У него под рукой всегда будет надежный вспомогательный ресурс, включающий в себя верные ответы на все номера из учебника. Другие положительные стороны учебно-методического пособия:

• поможет обрести уверенность в себе;
• позволит справиться с возникшими учебными проблемами;
• даст возможность завоевать доверие учителя улучшенными результатами.

К тому же, решебник способствует развитию таких важных навыков у подростка, как самодисциплина и работа над ошибками.

Характеристика процесса изучения геометрии

На занятиях по представленной точной науке школьники смогут подробно разобрать главные свойства и признаки геометрических фигур и параллельных плоскостей. Помимо этого, ребята познакомятся с предметом и основной аксиомой стереометрии.
Стоит отметить, что данный курс содержит в себе, как практические упражнения и задачи, так и теоретические аспекты. Рассмотрим наиболее важные параграфы из учебника: свойства граней и диагоналей параллелепипеда, задачи на построение сечений, правильная и усеченная пирамида.

А, чтобы всецело освоить представленные выше темы и получить твёрдую пятёрку за правильный ответ у доски, школьнику необходимо воспользоваться услугами грамотно составленного вспомогательного ресурса. Здесь ребятам отлично подойдет учебно-методический комплекс «ГДЗ по Геометрии для 10 класса Учебник Латотин Л.А., Чеботаревский Б.Д., Горбунова И.В. (Образование и воспитание)».

Почему стоит выбрать онлайн-решебник по Геометрии для 10 класса Учебник Латотин

Стоит упомянуть и то, что само пособие ГДЗ было размещено в онлайн-формате на популярном интернет-портале. Благодаря этому, молодые люди смогут легко отыскать верный ответ на нужное задание, воспользовавшись интуитивно понятной системой навигации сайта. Ребятам необходимо сделать лишь пару кликов в браузере мобильного телефона или персонального компьютера и нужный интернет-ресурс тут же появится на экране устройства.

Решебник ГДЗ Геометрия 10 класс В. О. Швец, Г. И. Билянин, Г. И. Билянина, 2010 г.. Академический уровень

ГДЗ 10 класс Геометрия

показать обложку

Авторы:  В. О. Швец, Г. И. Билянин, Г. И. Билянина

Год:  2010

Описание:  Академический уровень

Рейтинг: 5. 0Оцените книгу

Самые популярные книги

показать обложку

Авторы:А. Г. Мерзляк, В. Б. Полонский, М. С. Якир, Ю. М. Рабинович

Год:2013

Описание:Сборник задач и контрольных работ

показать обложку

Авторы:В. М. Бойко, И. Л. Дитчук

Год:2017

Описание:Тетрадь для практических работ

показать обложку

Авторы:В. И. Соболь

Год:2015

Описание:Рабочая тетрадь

показать обложку

Авторы:В. Г. Барьяхтар, Ф. Я. Божинова, С. А. Довгий

Год:2015

показать обложку

Авторы:Naomi Simmons

Год:2019

Описание:Family and Friends 4 workbook 2nd edition

показать обложку

Авторы:В. Г. Барьяхтар, Ф. Я. Божинова, Е. А. Кирюхина, С. А. Довгий

Год:2016

2. ✅ ГДЗ ✅
3. ⚡ 10 класс ⚡
4. Геометрия ✍
5. Геометрія (академічний рівень), 10 клас

ГДЗ по геометрии в помощь

Геометрия, также как и алгебра — один из наиболее сложных предметов почти для каждого ученика.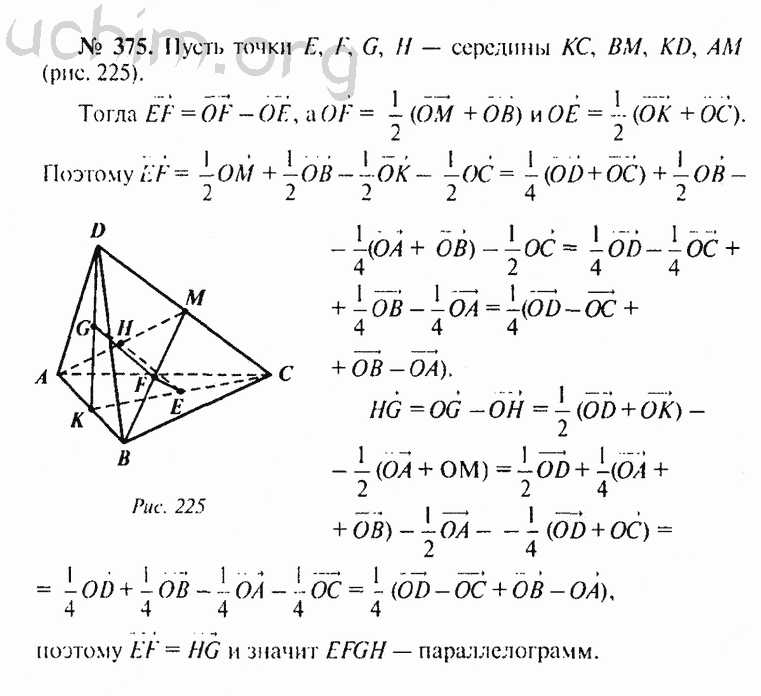 Геометрия неразрывно связана с алгеброй и если Вы отстаете по одной из наук, то и другая будет непонятна. Чтобы наверстать знания и как следует подготовиться к любым контрольным работам, используйте решебник по геометрии за 10 класс Билянина, Билянин, Швец 2010. В нем ученики найдут ответы на каждое задания из школьного учебника.

Сборник ответов — лучший выбор для тех, кто желает улучшить свои знания по геометрии. В любой момент проверяйте свой уровень знаний с помощью нашего сайта. Наличие содержания позволяет быстро найти нужное задание или задачу и сравнить свой ответ с ответом в сборнике. Тренируйтесь самостоятельно решать задачи по геометрии и улучшайте понимание новых тем.

Содержание решебника

Решебник состоит из семи модулей:

• Модуль 1. Систематизация и обобщение фактов и методов планиметрии

• Модуль 2. Вступление к стереометрии

• Модуль 3. Взаимное расположение прямых в пространстве, прямой и плоскости

• Модуль 4. Взаимное расположение плоскостей в пространстве

• Модуль 5. Перпендикулярность прямых и плоскостей в пространстве

• Модуль 6. Углы и расстояния в пространстве

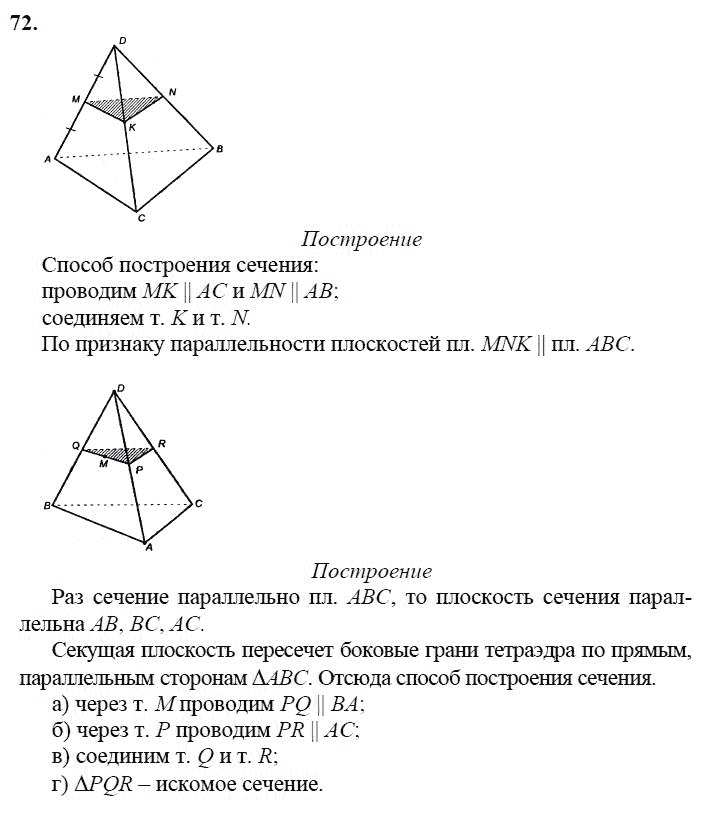
• Модуль 7. Обобщение и систематизация изученного

Геометрия больше не проблема

Используя сборник ответов, Вы без проблем подготовитесь к контрольной или самостоятельной работе. С решебником можно проверить ход решения или найти нужный ответ в любой момент. ГДЗ по геометрии – это незаменимая помощь для учеников, ведь каждый ответ здесь детально проверен, а значит, вероятность ошибки во время списывания исключается.

ГДЗ по геометрии за 10 класс Г. И. Билянина, Г. И. Билянин, В. О. Швец 2010 — это прекрасная дополнительная литература для всех учеников, которым необходимо улучшить знания. Решая с решебником однотипные задачи, школьники понемногу начнут понимать ранее сложный материал, и через время смогут самостоятельно решать задачи. Сборник ответов даст возможность подготовиться к контрольным и самостоятельным работам, а также предстоящему тестовому оцениванию.

ГДЗ по геометрии 10 класс Гусев В.А.

Решебник по учебнику геометрия 10 класс Гусев В.А.

Учебник по геометрии для 10 классов с профильным уровнем изучения предмета написан коллективом авторов под руководством В.А. Гусева, совместно с Е.Д. Куланиным, А.Г. Мякишевым и С.Н. Фединым. Учебник выпущен издательством «Бином. Лаборатория знаний» в 2010 году. Материал учебника полностью соответствует государственным образовательным стандартам по математике для учащихся 10 классов с профильным уровнем изучения предмета. 

Материал учебника начинается с предисловия, в котором авторы знакомят школьника с основными особенностями работы с учебника, а также курса геометрии в целом. Материал учебника разделен на пять глав: планиметрия, параллельные прямые и плоскости, векторы и координаты в пространстве, перпендикулярность прямых и плоскостей в пространстве многогранные углы. В конце пособия приведены решения избранных задач, а также ответы ко всем заданиям курса. В помощь школьнику также приведен сборник основных формул планиметрии.

Отличительная особенность в изложении теоретического материала – это ясность, четкость, а также максимальная строгость. Материал учебника направлен на развитие в школьнике математической культуры мыслей, авторы учебника считают, что нельзя научиться хорошо решать задачи, без знания теоретического материала, поэтому в учебнике, как теоретический, так и практический материал представлен в большом объеме.

Каждая глава начинается художественным эпиграфом по теме, который призван заинтересовать школьников, а заканчивается разделом «Пора, передохнуть», в котором вниманию школьника предлагаются различные математические анекдоты. Такой подход к составлению учебника направлен на то, чтобы изучение проходило в более оживленной атмосфере. В конце каждого параграфа приведены упражнения для закрепления пройденного материала, наиболее трудные задачи в нем отмечены звездочкой, а те задачи, над которыми нарисован символ звездочка в кружке, имеют решение в разделе «Решение избранных задач». В конце главы размещено резюме по её материалов, которое помогает сгруппировать и обобщить пройденный материал.

В конце учебника размещен предметный указатель, который облегчает ориентирование по учебнику. Учебник является прекрасным пособие подготовки к выпускным и вступительным экзаменам в ВУЗы, как математического, так и не математического профиля.

‎Решатель геометрии ² — калькулятор в App Store

Рассчитайте объем, площадь поверхности и периметр геометрических фигур с помощью этого отмеченного наградами калькулятора геометрии! Быстрый решатель треугольников и помощник по тригонометрии.

Нужна помощь по геометрии? Решатель геометрии сертифицирован учителями и награжден профессионалами.
Мы являемся сертифицированным приложением Educational App Store и заняли 11-е место в категории «Математика» в «Мобильном обучении в действии»!

У детей урок геометрии, и родители должны проверить домашнюю работу. Что ж, большинство родителей уже не имеют ни малейшего представления о теоремах и формулах, которые они изучали в школе. Независимо от того, родитель вы или ребенок, теперь в вашем распоряжении помощник по геометрии!

Геометрия также имеет множество практических применений в повседневной жизни, таких как измерение окружности, площади и объема, когда вам нужно что-то построить или создать. Например, вы должны рассчитать периметр своего двора, чтобы определить, сколько ограждений вам нужно, или вычислить площадь поверхности ваших стен, чтобы определить, сколько краски вам нужно.

Вам лучше скачать это приложение!
Простой и удобный помощник в выполнении домашних заданий, который проверяет ваши решения! Решите периметр, площадь, поверхность или объем различных геометрических фигур с помощью этого калькулятора геометрии.

Калькулятор периметра и поверхности для 2D фигур:
— квадрат,
— прямоугольник,
— круг,
— эллипс,
— треугольник,
— трапеция,
— параллелограмм,
— тригонометрия,
— равносторонний треугольник,
— равнобедренный треугольник,
— прямоугольный треугольник,
— круговой сегмент,
— круговой сектор,
— кольцевой сектор,
— эллиптический сегмент,
— кольцо,
— квадратичная функция,
— кубическая функция,
— ромб,
— вписанная и описанная окружность треугольника
— салинон,
— парабола,
— крест,
— прямоугольник со скругленными углами,
— шестерня,
— сердце,
— перемычка,
— прямоугольник,
— форма дома,
— воздушный змей,
— прямоугольный воздушный змей,
— половинчатый воздушный змей и многие другие. ..

Калькулятор площади и объема для трехмерных фигур:
— конус,
— усеченный конус,
— пирамида,
— сфера,
— куб,
— цилиндр,
— тор,
— прямоугольная призма,
— прямоугольная призма,
— усеченная пирамида,
— бочонок,
— асимметричный бочонок,
— трапециевидная призма,
— параллелограммная призма,
— клин,
— эллиптический конус,
— тетраэдр,
— октаэдр,

5 — додекаэдр ,

— косой цилиндр,
— косая призма,
— косой конус,
— косой усеченный конус,
— усеченный эллиптический конус,
— треугольная призма,
— усеченная,
— правая призма,
— сферический сектор,
— сферический сектор ,
— сферический сегмент,
— сферический клин,
— эллипсоид,
— тор,
— призма,
— эллиптический цилиндр,
— эллиптический параболоид,
— призма с правильным основанием,
— полый цилиндр,
— прямоугольная труба ,
— арка (мост),
— косокубовидная,
— клиновидно-кубовидная,
— антипризма,
— капсула,
— бак — цилиндрический сегмент,
— бак — сегмент капсулы,
— полусфера,
— косоугольная призма,
— кубовидный разрез,
— резервуар с усеченными конусами,
— цилиндрический сектор,
— конический сектор и многие другие. ..

Вопросы? Отправьте электронное письмо: [email protected] Сертификат
Educational App Store: https://www.educationalappstore.com/app/geometry-solver
Мобильное обучение в действии: https://bestonlineuniversities.com/favorite-mobile- обучающие приложения/

Треугольники, прямоугольники и теорема Пифагора — Элементарная алгебра

Цели обучения

К концу этого раздела вы сможете:

• Решение приложений с использованием свойств треугольников
• Используйте теорему Пифагора
• Решайте приложения, используя свойства прямоугольника

Решайте приложения, используя свойства треугольников

В этом разделе мы будем использовать некоторые распространенные геометрические формулы.Мы адаптируем нашу стратегию решения задач, чтобы мы могли решать геометрические задачи. Геометрическая формула назовет переменные и даст нам уравнение для решения. Кроме того, поскольку все эти приложения будут включать в себя те или иные формы, большинство людей считают полезным нарисовать фигуру и пометить ее с помощью заданной информации. Мы включим это в первый шаг стратегии решения задач для геометрических приложений.

Решить геометрические задачи.

1. Прочтите задачу и убедитесь, что все слова и идеи понятны.Нарисуйте рисунок и подпишите его с помощью данной информации.
2. Определите , что мы ищем.
3. Пометьте то, что мы ищем, выбрав переменную для ее представления.
4. Переведите в уравнение, написав соответствующую формулу или модель для данной ситуации. Замените предоставленную информацию.
5. Решите уравнение, используя хорошие методы алгебры.
6. Проверьте ответ, подставив его обратно в уравнение, решенное на шаге 5, и убедившись, что он имеет смысл в контексте задачи.
7. Ответьте на вопрос полным предложением.

Мы начнем приложения по геометрии со свойств треугольников. Давайте рассмотрим некоторые основные факты о треугольниках. Треугольники имеют три стороны и три внутренних угла. Обычно каждая сторона помечается строчной буквой, соответствующей прописной букве противоположной вершины.

Множественное число слова вершина равно вершин . Все треугольники имеют три вершины.Треугольники называются по их вершинам: треугольник на (рисунке) называется

.

Треугольник ABC имеет вершины A, B и C. Длины сторон равны a, b и c.

Три угла треугольника связаны особым образом. Сумма их мер равна Обратите внимание, что мы читаем как «мера угла А». Итак, в (рисунок),

Поскольку периметр фигуры равен длине ее границы, периметр фигуры равен сумме длин трех ее сторон.

Чтобы найти площадь треугольника, нам нужно знать его основание и высоту. Высота — это линия, соединяющая основание с противоположной вершиной и образующая с основанием угол. Нарисуем снова, а теперь покажем высоту, х . См. (Рисунок).

Формула площади: где b — основание, а h — высота.

Свойства треугольника

Для

Угловые меры:

• Сумма углов треугольника равна

Периметр:

• Периметр равен сумме длин сторон треугольника.

Район:

• Площадь треугольника равна половине произведения основания на высоту.

Два угла треугольника равны 55 и 82 градусам. Найдите величину третьего угла.

Два угла треугольника равны 31 и 128 градусам. Найдите величину третьего угла.

Два угла треугольника равны 49 и 75 градусов. Найдите величину третьего угла.

Периметр треугольного сада равен 24 футам. Длины двух сторон четыре фута и девять футов. Какой длины третья сторона?

Периметр треугольного сада составляет 48 футов. Длины двух сторон 18 футов и 22 фута. Какой длины третья сторона?

Длина двух сторон треугольного окна составляет семь футов и пять футов. Периметр 18 футов. Какой длины третья сторона?

Площадь треугольного окна церкви 90 квадратных метров.Основание окна 15 метров. Какая высота окна?

Площадь треугольной картины составляет 126 квадратных дюймов. База 18 дюймов. Какова высота?

Треугольная дверь палатки имеет площадь 15 квадратных футов. Высота пять футов. Что такое база?

Свойства треугольника, которые мы использовали до сих пор, применимы ко всем треугольникам. Теперь мы рассмотрим один конкретный тип треугольника — прямоугольный треугольник. Прямоугольный треугольник имеет один угол, который мы обычно обозначаем квадратиком в углу.

Прямоугольный треугольник

Прямоугольный треугольник имеет один угол, вершина которого часто обозначается квадратом.

Размер одного угла прямоугольного треугольника Чему равен третий угол?

Размер одного угла прямоугольного треугольника Чему равен другой меньший угол?

Размер одного угла прямоугольного треугольника Чему равен другой меньший угол?

В примерах, которые мы видели до сих пор, мы могли нарисовать фигуру и подписать ее сразу после прочтения задачи.В следующем примере нам нужно будет определить один угол через другой. Мы будем ждать рисования фигуры, пока не напишем выражения для всех искомых углов.

Размер одного угла прямоугольного треугольника на 20 градусов больше, чем размер наименьшего угла. Найдите меры всех трех углов.

Размер одного угла прямоугольного треугольника на 50° больше, чем размер наименьшего угла. Найдите меры всех трех углов.

Размер одного угла прямоугольного треугольника на 30° больше, чем размер наименьшего угла.Найдите меры всех трех углов.

Используйте теорему Пифагора

Мы узнали, как соотносятся меры углов треугольника. Теперь мы узнаем, как длины сторон связаны друг с другом. Важное свойство, описывающее соотношение между длинами трех сторон прямоугольного треугольника, называется теоремой Пифагора. Эта теорема использовалась во всем мире с древних времен. Он назван в честь греческого философа и математика Пифагора, жившего около 500 г. до н.э.

Прежде чем мы сформулируем теорему Пифагора, нам нужно ввести некоторые термины для сторон треугольника. Помните, что прямоугольный треугольник имеет угол, отмеченный маленьким квадратом в углу. Сторона треугольника, противоположная углу, называется гипотенузой , а каждая из других сторон называется катетом .

Теорема Пифагора говорит, как длины трех сторон прямоугольного треугольника соотносятся друг с другом. Он гласит, что в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.В символах мы говорим: в любом прямоугольном треугольнике, где длины катетов и длина гипотенузы.

Запишите формулу в каждом упражнении и произносите ее вслух, когда пишете, это может помочь вам запомнить теорему Пифагора.

Теорема Пифагора

В любом прямоугольном треугольнике

где a и b длины катетов, c длина гипотенузы.

Чтобы решить упражнения, использующие теорему Пифагора, нам нужно найти квадратные корни.Мы использовали обозначение и определение:

Если то за

Например, мы обнаружили, что 5, потому что

Поскольку теорема Пифагора содержит переменные, которые возводятся в квадрат, для определения длины стороны прямоугольного треугольника нам придется использовать квадратные корни.

Используйте теорему Пифагора, чтобы найти длину гипотенузы, показанной ниже.

Используйте теорему Пифагора, чтобы найти длину гипотенузы в треугольнике, показанном ниже.

Используйте теорему Пифагора, чтобы найти длину гипотенузы в треугольнике, показанном ниже.

Используйте теорему Пифагора, чтобы найти длину ноги, показанной ниже.

Используйте теорему Пифагора, чтобы найти длину катета в треугольнике, показанном ниже.

Используйте теорему Пифагора, чтобы найти длину катета в треугольнике, показанном ниже.

Джон устанавливает основание 13-футовой лестницы в пяти футах от стены своего дома, как показано ниже. Насколько далеко вверх по стене поднимается лестница?

Рэнди хочет прикрепить 17-футовую гирлянду к верхней части 15-футовой мачты своей парусной лодки, как показано ниже. На каком расстоянии от основания мачты он должен прикрепить конец световой нити?

Решение приложений с использованием свойств прямоугольника

Возможно, вы уже знакомы со свойствами прямоугольников. У прямоугольников четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Мы обозначаем одну сторону прямоугольника как длину, L , а смежную сторону как ширину, W .

Расстояние вокруг этого прямоугольника равно или Это периметр, P , прямоугольника.

Как насчет площади прямоугольника? Представьте себе прямоугольный ковер размером 2 фута в длину и 3 фута в ширину. Его площадь составляет 6 квадратных метров. На рисунке шесть квадратов.

Площадь равна длине, умноженной на ширину.

Формула площади прямоугольника:

Свойства прямоугольников

Прямоугольники имеют четыре стороны и четыре прямых угла.

Длины противоположных сторон равны.

Периметр прямоугольника равен сумме удвоенной длины и удвоенной ширины.

Площадь прямоугольника равна произведению длины на ширину.

Длина прямоугольника 32 метра, а ширина 20 метров.Что такое периметр?

Длина прямоугольника 120 ярдов, а ширина 50 ярдов. Что такое периметр?

Длина прямоугольника 62 фута, а ширина 48 футов. Что такое периметр?

Площадь прямоугольной комнаты 168 квадратных футов. Длина 14 футов. Какова ширина?

Площадь прямоугольника 598 квадратных футов. Длина 23 метра. Какова ширина?

Ширина прямоугольника 21 метр.Площадь 609 квадратных метров. Какова длина?

Найдите длину прямоугольника с периметром 50 дм и шириной 10 дм.

Найдите длину прямоугольника с периметром 80 и шириной 25.

Найдите длину прямоугольника с периметром 30 и шириной 6.

Мы решали задачи, в которых были заданы длина или ширина, а также периметр или площадь; теперь мы научимся решать задачи, в которых ширина определяется через длину.Мы будем ждать, чтобы нарисовать фигуру, пока не напишем выражение для ширины, чтобы мы могли пометить одну сторону этим выражением.

Ширина прямоугольника на два фута меньше его длины. Периметр 52 метра. Найдите длину и ширину.

Ширина прямоугольника на семь метров меньше длины. Периметр 58 метров. Найдите длину и ширину.

Длина прямоугольника на восемь футов больше его ширины. Периметр 60 футов.Найдите длину и ширину.

Длина прямоугольника на четыре сантиметра больше его ширины более чем в два раза. Периметр 32 сантиметра. Найдите длину и ширину.

Длина прямоугольника в восемь раз больше его ширины. Периметр равен 64. Найдите длину и ширину.

Ширина прямоугольника в шесть раз меньше его длины. Периметр равен 18. Найдите длину и ширину.

Периметр прямоугольного бассейна составляет 150 футов.Длина на 15 футов больше ширины. Найдите длину и ширину.

Периметр прямоугольного бассейна составляет 200 футов. Длина на 40 футов больше ширины. Найдите длину и ширину.

Длина прямоугольного сада на 30 ярдов больше его ширины. Периметр 300 метров. Найдите длину и ширину.

Практика делает совершенным

Решение приложений с использованием свойств треугольника

В следующих упражнениях решите, используя свойства треугольника.

Два угла треугольника равны 26 и 98 градусов. Найдите величину третьего угла.

Два угла треугольника равны 61 и 84 градусам. Найдите величину третьего угла.

Два угла треугольника равны 105 и 31 градусу. Найдите величину третьего угла.

Два угла треугольника равны 47 и 72 градуса. Найдите величину третьего угла.

Периметр треугольного бассейна равен 36 ярдам.Длины двух сторон 10 ярдов и 15 ярдов. Какой длины третья сторона?

Треугольный двор имеет периметр 120 метров. Длины двух сторон 30 метров и 50 метров. Какой длины третья сторона?

Если стороны треугольника 6 и 9 футов, а периметр равен 23 футам, то какой длины третья сторона?

Если стороны треугольника 14 см и 18 см, а периметр равен 49 см, то какой длины третья сторона?

Треугольный флаг имеет основание 1 фут и высоту 1. 5 футов. Какова его площадь?

Треугольное окно имеет основание восемь футов и высоту шесть футов. Какова его площадь?

Чему равно основание треугольника площадью 207 квадратных дюймов и высотой 18 дюймов?

Какова высота треугольника с площадью 893 квадратных дюйма и основанием 38 дюймов?

Один угол прямоугольного треугольника равен 33 градусам. Чему равен другой малый угол?

Один угол прямоугольного треугольника равен 51 градусу.Чему равен другой малый угол?

Один угол прямоугольного треугольника равен 22,5 градуса. Чему равен другой малый угол?

Один угол прямоугольного треугольника равен 36,5 градусов. Чему равен другой малый угол?

Периметр треугольника равен 39 футам. Одна сторона треугольника на один фут длиннее второй стороны. Третья сторона на два фута длиннее второй. Найдите длину каждой стороны.

Периметр треугольника равен 35 футам.Одна сторона треугольника на пять футов длиннее второй. Третья сторона на три фута длиннее второй. Найдите длину каждой стороны.

Одна сторона треугольника вдвое короче. Третья сторона на пять футов больше, чем самая короткая сторона. Периметр 17 футов. Найдите длины всех трех сторон.

Одна сторона треугольника в три раза больше наименьшей стороны. Третья сторона на три фута больше, чем самая короткая сторона. Периметр 13 футов.Найдите длины всех трех сторон.

Два меньших угла прямоугольного треугольника равны. Найдите меры всех трех углов.

Мера наименьшего угла прямоугольного треугольника на 20° меньше, чем мера следующего большего угла. Найдите меры всех трех углов.

Углы в треугольнике таковы, что один угол в два раза больше наименьшего угла, а третий угол в три раза больше наименьшего угла.Найдите меры всех трех углов.

Углы в треугольнике таковы, что один угол на 20° больше наименьшего угла, а третий угол в три раза больше наименьшего угла. Найдите меры всех трех углов.

Использование теоремы Пифагора

В следующих упражнениях используйте теорему Пифагора, чтобы найти длину гипотенузы.

В следующих упражнениях используйте теорему Пифагора, чтобы найти длину катета.Округлите до десятых, если необходимо.

В следующих упражнениях решите, используя теорему Пифагора. Приблизительно с точностью до десятых, если необходимо.

13-футовая гирлянда будет прикреплена к вершине 12-футового столба для праздничного представления, как показано ниже. На каком расстоянии от основания столба должен быть закреплен конец цепочки огней?

Пэм хочет повесить транспарант на двери гаража, как показано ниже, чтобы поздравить сына с окончанием колледжа.Гаражные ворота имеют высоту 12 футов и ширину 16 футов. Какой длины должен быть баннер, чтобы он подходил к воротам гаража?

Чи планирует выложить дорожку из брусчатки через свой цветник, как показано ниже. Цветник представляет собой квадрат со стороной 10 футов. Какова будет длина пути?

Брайан одолжил 20-футовую удлинительную лестницу, чтобы использовать ее, когда он красит свой дом. Если он установит основание лестницы в 6 футах от дома, как показано ниже, как далеко будет подниматься верх лестницы?

Решение приложений с использованием свойств прямоугольника

В следующих упражнениях решите задачу, используя свойства прямоугольника.

Длина прямоугольника 85 футов, а ширина 45 футов. Что такое периметр?

Длина прямоугольника 26 дюймов, а ширина 58 дюймов. Что такое периметр?

Прямоугольная комната имеет ширину 15 футов и длину 14 футов. Каков его периметр?

Подъездная дорога имеет форму прямоугольника шириной 20 футов и длиной 35 футов. Каков его периметр?

Площадь прямоугольника 414 квадратных метров. Длина 18 метров.Какова ширина?

Площадь прямоугольника 782 квадратных сантиметра. Ширина 17 сантиметров. Какова длина?

Ширина прямоугольного окна 24 дюйма. Площадь 624 кв. Какова длина?

Длина прямоугольного плаката 28 дюймов. Площадь 1316 кв. Какова ширина?

Найдите длину прямоугольника с периметром 124 и шириной 38.

Найдите ширину прямоугольника с периметром 92 и длиной 19.

Найдите ширину прямоугольника с периметром 16,2 и длиной 3,2.

Найдите длину прямоугольника с периметром 20,2 и шириной 7,8.

Длина прямоугольника на девять дюймов больше его ширины. Периметр 46 дюймов. Найдите длину и ширину.

Ширина прямоугольника на восемь дюймов больше его длины. Периметр 52 дюйма. Найдите длину и ширину.

Периметр прямоугольника равен 58 метрам.Ширина прямоугольника на пять метров меньше длины. Найдите длину и ширину прямоугольника.

Периметр прямоугольника равен 62 футам. Ширина на семь футов меньше длины. Найдите длину и ширину.

Ширина прямоугольника на 0,7 метра меньше длины. Периметр прямоугольника равен 52,6 метра. Найдите размеры прямоугольника.

Длина 13,5 м, ширина 12,8 м

Длина прямоугольника равна 1.на 1 метр меньше ширины. Периметр прямоугольника равен 49,4 метра. Найдите размеры прямоугольника.

Периметр прямоугольника равен 150 футам. Длина прямоугольника в два раза больше ширины. Найдите длину и ширину прямоугольника.

Длина прямоугольника в три раза больше ширины. Периметр прямоугольника равен 72 футам. Найдите длину и ширину прямоугольника.

Длина прямоугольника на три метра меньше, чем удвоенная ширина.Периметр прямоугольника 36 метров. Найдите размеры прямоугольника.

Длина прямоугольника на пять дюймов больше его ширины более чем в два раза. Периметр 34 дюйма. Найдите длину и ширину.

Периметр прямоугольного поля равен 560 ярдам. Длина на 40 метров больше ширины. Найдите длину и ширину поля.

Периметр прямоугольного атриума составляет 160 футов. Длина на 16 футов больше ширины. Найдите длину и ширину атриума.

Прямоугольная парковка имеет периметр 250 футов. Длина на пять футов больше, чем ширина в два раза. Найдите длину и ширину парковки.

Прямоугольный ковер имеет периметр 240 дюймов. Длина на 12 дюймов больше ширины в два раза. Найдите длину и ширину ковра.

Математика на каждый день

Криста хочет поставить забор вокруг своей треугольной клумбы. Стороны клумбы составляют шесть футов, восемь футов и 10 футов. Сколько футов забора понадобится ей, чтобы огородить свою клумбу?

Хосе только что убрал детский игровой набор со своего заднего двора, чтобы освободить место для прямоугольного сада.Он хочет поставить забор вокруг сада, чтобы отпугнуть собаку. У него в гараже 50-футовый рулон забора, который он планирует использовать. Чтобы поместиться на заднем дворе, ширина сада должна быть 10 футов. Как долго он может сделать другую длину?

Письменные упражнения

Если вам нужно положить плитку на кухонный пол, вам нужно знать периметр или площадь кухни? Объясните свои рассуждения.

Если вам нужно поставить забор вокруг вашего двора, вам нужно знать периметр или площадь заднего двора? Объясните свои рассуждения.

Посмотрите на два рисунка ниже.

ⓐ Какая фигура имеет большую площадь?
ⓑ Какой из них имеет больший периметр?
ⓒ Теперь вычислите площадь и периметр каждой фигуры.
ⓓ У кого больше площадь?
ⓔ У кого больше периметр?

ⓐ Ответы будут разными.
ⓑ Ответы будут разными.
ⓒ Ответы будут разными.
ⓓ Площади совпадают.
ⓔ Периметр прямоугольника 2×8 больше, чем у квадрата 4×4.

Напишите задачку по геометрии, связанную с вашим жизненным опытом, затем решите ее и объясните все свои действия.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.

ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?

Искусство решения проблем

Искусство решения проблем размещает эту AoPSWiki, а также многие другие онлайн-ресурсы для учащихся, интересующихся математическими соревнованиями. Посмотрите на AoPSWiki. Отдельные статьи часто содержат примеры проблем и решений для многих уровней решения проблем. Многие также имеют ссылки на книги, веб-сайты и другие ресурсы, имеющие отношение к теме.

• Книги по математике
• Математические форумы
• Веб-сайты по математике

Содержание

• 1 Учебные веб-сайты
• 2 Бесплатная электронная книга математических формул и стратегий
• 3 бесплатных курса математики
• 4 Список ресурсов
• 5 математических конкурсов
• 6 задач по математике
  • 6.1 задачник
  • 6.2 Проблемы в сети
    • 6.2.1 Вводные средства решения проблем
    • 6.2.2 Решатели проблем среднего уровня
    • 6.2.3 Решатели олимпиадных задач
• 7 Артикул
• 8 Огромный список ссылок
  • 8.1 Рекомендации по курсу AoPS
  • 8.2 AMC 8 Подготовка
    • 8.2.1 Проблемы
  • 8. 3 AMC 10/12 Подготовка
    • 8.3.1 Проблемы
  • 8.4 Подготовка к AIME
    • 8.4.1 Проблемы
  • 8.5 Начало подготовки к Олимпиаде
    • 8.5.1 Связка общих ссылок
    • 8.5.2 Проблемы
  • 8.6 Средняя/продвинутая подготовка к Олимпиаде
    • 8.6.1 Проблемы
  • 8.7 Ссылки на книги:
    • 8.7.1 Олимпиадный уровень
      • 8.7.1.1 Бесплатно
      • 8.7.1.2 Не бесплатно
  • 8.8 Наборы задач
• 9 См. также

Обучающие веб-сайты

• Тренажер задач AMC: https://amctrainer.ком/играть
• Генератор задач и программа для чтения вики AoPS: https://vqbc.github.io/tribun/
• конкурсы mathRanks: https://mathranks.net/

Бесплатная электронная книга математических формул и стратегий

Более 130 страниц бесплатной электронной книги по математическим формулам и стратегиям: https://www. omegalearn.org/thebookofformulas

Бесплатные курсы по математике

Введение в теорию чисел: https://thepuzzlr.com/math-courses

Бесплатный учебный курс AMC 8, охватывающий все основные понятия: https://thepuzzlr.com/курсы/AMC-8-буткемп/

Бесплатный курс AMC 10: https://thepuzzlr.com/courses/amc-10-crash-course/

Список ресурсов

Начальный уровень: https://www.omegalearn.org/elementary-competition-math

Середина: https://www.omegalearn.org/middle-competition-math

Высокий: https://www.omegalearn.org/high-competition-math

Все необходимое для AMC 8: https://thepuzzlr.com/courses/amc-8-bootcamp/

Все необходимое для AMC 10: https://thepuzzlr.com/курсы/AMC-10-краш-курс/

Класс основ AMC 8: https://www.omegalearn.org/amc8-fundamentals

Плейлист AMC 8 Video Solutions: https://www.youtube.com/watch?v=TRGPF3BxujE&list=PLbhMrFqoXXwmwbk2CWeYOYPRbGtmdPUhL

Класс AMC/MATHCOUNTS: https://www. omegalearn.org/amc8-advanced

Занятия по математике

• «Искусство решения проблем» проводит занятия, пользующиеся популярностью среди многих наиболее успевающих учащихся в Соединенных Штатах.Серия задач AoPS.

Математические конкурсные задачи

Сборники задач

На многих соревнованиях по математике продаются книги о прошлых соревнованиях и решениях. Эти книги могут стать отличным дополнительным материалом для энергичных студентов, изучающих математику.

• В ARML есть четыре сборника задач, охватывающих большинство соревнований ARML, а также некоторые соревнования NYSML. Однако, как правило, их трудно найти. Кое-что можно заказать здесь.
• книг MOEMS доступны здесь, в AoPS.
• книг по MATHCOUNTS доступны здесь, в AoPS.
• книг AMC доступны здесь, в AoPS.
• Книги конкурса Мандельброта доступны здесь, в AoPS.

Проблемы онлайн

Art of Problem Solving поддерживает очень большую базу данных задач по математике. Многие веб-сайты математических конкурсов содержат архивы прошлых задач. Список соревнований по математике ведет к ссылкам на многие из этих домашних страниц соревнований. Вот несколько примеров:

Вводные средства решения проблем

• Мю Альфа Тета.org размещает прошлые конкурсные задачи.
• Математика для ноэтического обучения: решение задач для одаренных учащихся начальной школы.
• Страница MathCounts Drills Элиаса Сааба.
• Домашняя страница олимпиады по математике в средней школе штата Алабама.
• Южноафриканская олимпиада по математике включает многолетние прошлые задачи с решениями.
• Beestar.org — Еженедельные задачи по решению проблем и рейтинг списка почета, классы 1–8

Решатели проблем среднего уровня

• Проблемы и решения математических конкурсов AoPS
• Прошлые проблемы USAMTS можно найти на домашней странице USAMTS.
• Еженедельные математические задачи Иваны Александровой для старшеклассников содержат хорошие задачи, которые заставят вас задуматься и научат вас новым навыкам и материалам
• Сайт Kalva — один из лучших ресурсов по математическим задачам на планете. (В настоящее время не в сети. Зеркало можно найти на этой странице)
• Задачи прошлой математической олимпиады в Колорадо (CMO) можно найти на домашней странице CMO.
• Прошлые задачи Международного поиска математических талантов (IMTS) можно найти здесь
• Brilliant — это веб-сайт, на котором можно решать задачи, чтобы набирать очки и переходить на более высокие уровни.
• Clevermath Аналогичен вышеуказанному

Решатели олимпиадных задач

• Проблемы и решения математических конкурсов AoPS
• Math and CS Research — это издание по математике и информатике, содержащее статьи и наборы задач по широкому кругу тем.
• Прошлые проблемы USAMTS можно найти на домашней странице USAMTS.
• Сайт Kalva — один из лучших ресурсов по математическим задачам на планете. (В настоящее время не в сети, но доступно несколько зеркал, например.г здесь.)
• Математические головоломки Ника. Сложные задачи с подсказками и решениями.
• Канадская математическая олимпиада проводится здесь Канадским математическим обществом.
• Задачи Всесоюзных математических олимпиад 1961-1986 гг. — Задач много, решений нет. [Сайт больше не существует. Сайт заменен веб-захватом]
• Прошлые задачи Международного поиска математических талантов (IMTS) можно найти здесь
• Математическое безумие олимпиады — Стопки сложных задач, без решений.[Сайт больше не существует. Сайт заменен веб-захватом]

Статьи

• Тайм-менеджмент
• Плюсы и минусы математических соревнований Ричарда Рущика.
• Создание позитивной культуры ожиданий в математическом образовании от лауреата премии Sister Scholastica Дэррила Хилла.
• Перестаньте совершать глупые ошибки, Ричард Рущик.
• Какие вопросы действительно глупые вопросы? Ричард Рущик.
• Обучение через обучение
• «Как написать математическое решение» Ричарда Ручика и Мэтью Кроуфорда.
• Неравенство доктора Киран Кедлая
• Олимпиадное неравенство Томаса Дж. Милдорфа
• Теория чисел Олимпиады: абстрактная перспектива Томаса Дж. Милдорфа
• Теория чисел Наоки Сато
• Теория чисел Олимпиады через сложные задачи Джастина Стивенса
• Барицентрические координаты в олимпийской геометрии Макса Шиндлера и Эвана Чена
• Подъем экспоненты (LTE) Амира Хоссейна Парварди
• Метод uvw Матиаса Бэка Тейса Кнудсена
• Китайская теорема об остатках Эвана Чена
• Contest Reflections by Wanlin Li

Огромный список ссылок

Рекомендации по курсу AoPS

• Рекомендации по курсу «Искусство решения проблем»
• Вы все еще не можете выбрать курс? Перейдите по ссылке выше и нажмите , свяжитесь с нами в нижней части раздела «Карта курса», чтобы запросить личные рекомендации!

AMC 8 Подготовка

Бесплатные классы AMC 8: https://thepuzzlr.com/курсы/AMC-8-буткемп/

Проблемы

Бесплатные курсы AMC 8: omegalearn. org/amc8-fundamentals
omegalearn.org/amc8-advanced

Эти курсы охватывают все важные концепции, необходимые для успешной работы с AMC 8.

Видеорешения AMC 8: https://www.youtube.com/watch?v=TRGPF3BxujE&list=PLbhMrFqoXXwmwbk2CWeYOYPRbGtmdPUhL

AMC 8 Проблемы в разделе ресурсов

Проблема и решения: Проблемы AMC 8 в вики AoPS

AMC 10/12 Подготовка

AMC 10/12 130+ страниц Книга математических формул и стратегий: https://www.omegalearn.org/thebookofformulas

Бесплатные занятия AMC 10/12: omegalearn.org/amc10-12

Как подготовка к AIME поможет AMC Оценка 10/12

Какой класс выбрать?

AMC 10 для практики AMC 12

Подготовка АМС

AMC 10/12 Подготовка

AIME/AMC 10 Перекрытие и подготовка

Как подготовиться к amc10 и aime?

Подготовка к AMC 10?

Проблемы

Проблемы AMC 10 в разделе ресурсов

Проблемы AMC 10 в AoPS Wiki

AMC 12 Проблемы в разделе ресурсов

AHSME (старый AMC 12) Проблемы в AoPS Wiki

Проблемы AMC 12 в AoPS Wiki

Препарат AIME

Учеба, чтобы получить право на участие в USAMO

Как подготовиться к AIME

Подготовка к AIME

Использование вопросов, не относящихся к AIME, для подготовки к AIME

Лучшие книги для подготовки к AIME?

Как улучшить оценку AIME, чтобы сделать JMO?

Подготовка к AIME и USAMO

Проблемы

Проблемы AIME в разделе ресурсов

Проблемы AIME в AoPS Wiki

Задачи AIME, отсортированные по сложности

Начало подготовки к Олимпиаде

• Общий
• Общий
• Как подготовиться к USAJMO?
• USAMO проблемы с подготовкой/выполнением
• Упрощенные олимпиады для практики USAJMO?
• Для USAMO: ACoPS или Engel?
• Олимпиадные задачи- как подготовиться
• Подготовка к USAMO/Олимпиадам: с чего начать?
• Подготовка USAJMO

Набор общих ссылок

• Подготовка USAMO
• Подготовка USAMO
• USAMO
• Приготовление Усамо
• Подготовка USAMO
• Обратный отсчет до USAMO
• Подготовка USAMO
• Подготовка USAJMO
• Подготовка USAMO
• Подготовка USAJMO
• Как подготовиться к USAMO/Making Red MOP
• Жесткая подготовка
• Подготовка USAMO и JMO
• ПОДГОТОВКА USAMO
• Новичок в USAMO
• Что мне делать?
• Улучшить до уровня USAMO и IMO
• Подготовка к США(J)MO
• соревнование по математике/советы, как стать лучше
• Подготовка к Олимпиаде
• Подготовка к Олимпиаде
• Подготовка USAJMO
• Правильное обучение
• Что ведет к успеху

Проблемы

• USAJMO Проблемы в разделе ресурсов
• Проблемы USAJMO в AoPS Wiki
• Проблемы USAMO в разделе ресурсов
• Задачи USAMO в AoPS Wiki

Средняя/продвинутая подготовка к Олимпиаде

Проблемы

• Практическая Олимпиада 1
• Тренировочная Олимпиада 2
• Тренировочная Олимпиада 3
• Практические решения олимпиады
• Проблемы USAMO в разделе ресурсов
• Проблемы USAMO в AoPS Wiki
• Проблемы ИМО в разделе ресурсов
• Проблемы IMO в AoPS Wiki

Ссылки на книги:

Олимпиада Уровень

Бесплатно

• Леммы по олимпиадной геометрии, статья
• Плоская геометрия
• Эван Чен OTIS-Выдержки
• Основы олимпиадной теории чисел
• Теория чисел Олимпиады через сложные задачи
• Современная олимпиадная теория чисел

Не бесплатно

• Плоская евклидова геометрия: теория и проблемы
• Евклидова геометрия в математических олимпиадах
• Комплексные числа и геометрия
• Геометрия комплексных чисел
• Комплексные числа от А до … Я
• 103 Задачи по тригонометрии: из тренинга группы ИМО США
• Введение в диофантовы уравнения: проблемный подход
• Введение в теорию чисел и неравенства
• 104 Задачи по теории чисел: из тренинга группы ИМО США
• 102 Комбинаторные задачи
• Путь к комбинаторике для студентов: стратегии подсчета
• -fkmr1 Математические олимпиады США 1972-1986 гг. Задачи и решения
• Искусство и мастерство решения проблем
• Стратегии решения проблем

Наборы задач

• Сборник прошлых статей в формате PDF
• Практические задачи со всего мира
• Общие задачи по олимпиадной математике
• Набор задач условной вероятности
• 31 Олимпиадные задачи по вероятностному методу
• 567 Красивых и жестких неравенств
• Неравенства
• 100 полиномиальных задач
• Тригонометрические задачи
• Общие все уровни
• Теория чисел
• Олимпиадные задачи
• 33 Функциональные уравнения
• Проблемы индукции
• Индукционные решения
• 260 задач по геометрии
• 150 задач по геометрии
• 50 задач с диофантовыми уравнениями
• 60 задач по геометрии
• 116 Проблемы
• Алгебраические неравенства
• 100 задач по комбинаторике
• 100 проблем
• Теория чисел
• Геометрия
• Общий
• 100 задач по теории чисел
• 100 задач на функциональные уравнения
• Начальный/промежуточный счет и вероятность
• 40 функциональных уравнений
• 100 геометрических неравенств
• 10 забавных нестандартных задач 🙂
• 169 функциональных уравнений
• Геометрия треугольника
• Вероятность
• Алгебра
• Теория чисел
• Круговая геометрия
• Другая геометрия

Рейтинг всех олимпиад (уровень сложности)

См.

также

• Список математических олимпиад
• Стипендии по математике
• Научные соревнования
• Соревнования по информатике
• Как подготовить

Wolfram|Alpha Примеры: Геометрия

Другие примеры

Плоская геометрия

Вычислить свойства двумерных геометрических фигур.

Вычислить свойства плоской фигуры:

Вычислите свойства треугольника с заданными длинами сторон:

Еще примеры

Другие примеры

Твердая геометрия

Вычислить свойства трехмерных геометрических фигур.

Вычислить свойства геометрического тела:

Вычислить свойства многогранника:

Еще примеры

Другие примеры

Координатная геометрия

Задайте геометрические фигуры с помощью координат или алгебраических уравнений.

Укажите линию через две точки:

Постройте коническое сечение и определите его тип:

Еще примеры

Другие примеры

Геометрические преобразования

Визуализация и вычисление свойств для различных видов геометрических преобразований.

Визуализируйте вращение и вычислите его матрицу:

Визуализируйте отражение в 3D:

Еще примеры

Другие примеры

Кривые и поверхности

Визуализация и вычисление свойств кривых и поверхностей.

Вычислить свойства именованной кривой:

Вычислить свойства именованной поверхности:

Еще примеры

Многомерная геометрия

Вычислить свойства геометрических фигур размерностью больше трех.

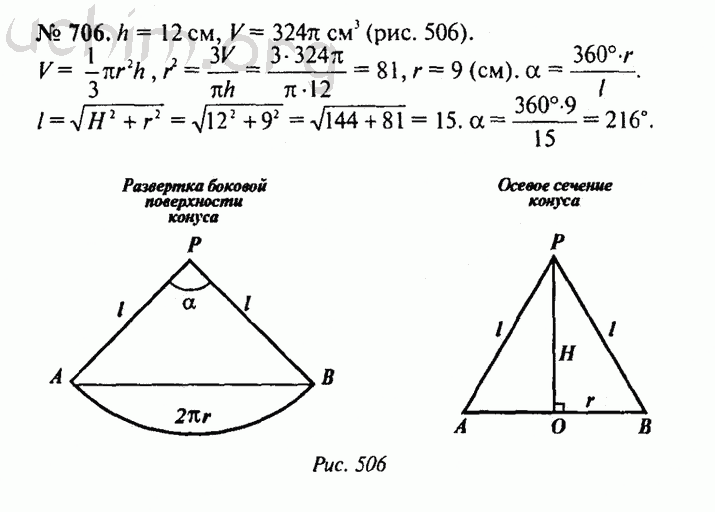
Вычислите свойства многомерного геометрического объекта:

Укажите параметры для многомерного объекта:

Еще примеры

Другие примеры

Проблемы с упаковкой и покрытием

Определите оптимальную упаковку геометрических фигур или создайте оценки, используя реальные объекты.

Вычислить свойства геометрической упаковки:

Укажите размеры контейнера:

Оцените количество предметов, необходимых для заполнения контейнера:

Еще примеры

Другие примеры

Плитки

Визуализируйте как периодические, так и непериодические мозаики.

Получите информацию о периодическом замощении плоскости:

Получить информацию о непериодическом тайлинге:

Еще примеры

Другие примеры

Муаровые узоры

Визуализируйте муаровый узор.

Исследуйте интерференционные картины со смещениями или углами:

Еще примеры

Другие примеры

Полиформы

Вычислить свойства класса полиформ.

Получить информацию о классе полиформ:

Укажите порядок полиформ:

Еще примеры

Другие примеры

Топология

Вычисление топологических свойств различных геометрических объектов.

Вычислить свойства узла:

Вычислить гомотопические группы сферы:

Еще примеры

Ученые решили геометрическую задачу 90-летней давности

Джон Макки (слева) и Марин Хеул десятилетиями пытались решить математическую головоломку, известную как гипотеза Келлера. Они нашли решение, переведя его в проблему выполнимости. Кредит: Стивен Хендерсон

Компьютерщики и математики из Университета Карнеги-Меллона решили последнюю, упрямую часть гипотезы Келлера, геометрическую задачу, над которой ученые ломали голову 90 лет.

Структурируя головоломку как то, что ученые-компьютерщики называют проблемой выполнимости, исследователи решили эту проблему за четыре месяца лихорадочного компьютерного программирования и всего за 30 минут вычислений на кластере компьютеров.

«Я был очень счастлив, когда мы решили ее, но потом мне было немного грустно, что проблема исчезла», — сказал Джон Макки, преподаватель факультета компьютерных наук (CSD) и факультета математических наук, который исследовал гипотезу Келлера. так как он был аспирантом 30 лет назад. «Но потом я снова почувствовал себя счастливым. Просто это чувство удовлетворения».

Решение стало еще одним успехом подхода, предложенного Марин Хеуле, адъюнкт-профессором компьютерных наук, который присоединился к CSD в августе прошлого года. Хьюле использовала SAT-решатель — компьютерную программу, которая использует логику высказываний для решения задач выполнимости (SAT) — для решения нескольких застарелых математических задач, включая задачу о пифагорейских тройках и число Шура 5.

«Эта проблема интересовала многих людей на протяжении десятилетий, почти столетия», — сказал Хеуле о гипотезе Келлера. «Это действительно демонстрация того, что можно сделать сейчас, что было невозможно раньше».

Гипотеза, выдвинутая немецким математиком Эдуардом Оттом-Генрихом Келлером, связана с укладкой мозаики, в частности, с тем, как покрыть площадь плитками одинакового размера без каких-либо промежутков или перекрытий.Гипотеза состоит в том, что по крайней мере две плитки должны иметь общее ребро, и это верно для пространств любого измерения.

Легко доказать, что это верно для двумерных плиток и трехмерных кубов. К 1940 году гипотеза подтвердилась для всех измерений до шести. Однако в 1990 году математики доказали, что это не работает в размерности 10 и выше.

Именно тогда гипотеза Келлера захватила воображение Макки, в то время студента Гавайского университета.Имея офис рядом с вычислительным кластером университета, он был заинтригован тем, что проблема может быть переведена с использованием теории дискретных графов в форму, которую могут исследовать компьютеры. В этой форме, называемой графом Келлера, исследователи могли искать «клики» — подмножества элементов, которые соединяются, не имея общей грани, тем самым опровергая гипотезу.

В 2002 году Макки сделал именно это, обнаружив клику в восьмом измерении.Тем самым он доказал, что гипотеза неверна в этом измерении и, соответственно, в девятом измерении.

Это оставило гипотезу о седьмом измерении нерешенной.

Когда в прошлом году Хеул прибыл в CMU из Техасского университета, он уже имел репутацию специалиста, использующего SAT-решатель для решения давних открытых математических задач.

«Я подумал про себя, может быть, мы сможем использовать его технику», — вспоминал Макки. Вскоре он начал обсуждать, как использовать решатель SAT для гипотезы Келлера, с Хеуле и Джошуа Бракензиком, двумя специалистами по математическим наукам и компьютерным наукам, которые сейчас работают над докторской диссертацией.D. в области компьютерных наук в Стэнфордском университете.

Решатель SAT требует структурирования проблемы с использованием пропозициональной формулы — (A или не B) и (B или C) и т. д. — чтобы решатель мог исследовать все возможные комбинации переменных, которые будут удовлетворять всем условиям.

«Существует много способов сделать эти переводы, и качество перевода обычно влияет на вашу способность решить проблему или лишает вас возможности», — сказал Хеул.

Благодаря 15-летнему опыту Heule отлично справляется с выполнением таких переводов.Одной из целей его исследований является разработка автоматизированных рассуждений, чтобы этот перевод мог выполняться автоматически, позволяя большему количеству людей использовать эти инструменты для решения своих проблем.

Даже с качественным переводом количество комбинаций, которые нужно проверить в седьмом измерении, было ошеломляющим — число из 324 цифр — и решения нигде не было видно даже с помощью суперкомпьютера. Но Хеуле и другие применили ряд уловок, чтобы уменьшить размер проблемы. Например, если одна конфигурация данных оказалась неработоспособной, они могли автоматически отклонить другие комбинации, которые на нее полагались.А поскольку большая часть данных была симметричной, программа могла исключить зеркальные отражения конфигурации, если она заходила в тупик в одном расположении.

Используя эти методы, они сократили свой поиск примерно до миллиарда конфигураций. В этих усилиях к ним присоединился Дэвид Нарваез, доктор философии. студент Рочестерского технологического института, который был приглашенным исследователем осенью 2019 года.

После того, как они запустили свой код на кластере из 40 компьютеров, они, наконец, получили ответ: гипотеза верна в седьмом измерении.

«Причина нашего успеха в том, что Джон обладает многолетним опытом и пониманием этой проблемы, и мы смогли преобразовать его в компьютерный поиск», — сказал Хеул.

Доказательство результата полностью вычисляется компьютером, сказал Хеул, в отличие от многих публикаций, которые комбинируют проверенные компьютером части доказательства с ручными описаниями других частей. Он отметил, что это затрудняет понимание читателями. Компьютерное доказательство решения Келлера включает в себя все аспекты решения, в том числе часть, нарушающую симметрию, предоставленную Нарваэсом, подчеркнул Хеуле, так что ни один аспект доказательства не должен полагаться на ручное усилие.

«Мы можем быть уверены в правильности этого результата», сказал он. Статья, описывающая резолюцию Хеуле, Макки, Бракензика и Нарваеса, получила награду за лучшую статью на Международной объединенной конференции по автоматизированному мышлению в июне.

Решение гипотезы Келлера имеет практическое применение, сказал Макки. Те клики, которые ученые ищут, чтобы опровергнуть гипотезу, полезны для создания нелинейных кодов, которые могут ускорить передачу данных. Таким образом, решатель SAT можно использовать для поиска нелинейных кодов более высокой размерности, чем это было возможно ранее.

Heule недавно предложил использовать решатель SAT для решения еще более известной математической задачи: гипотезы Коллатца. В этой задаче идея состоит в том, чтобы выбрать любое положительное целое число и разделить его на 2, если оно четное, или умножить на 3 и прибавить 1, если оно нечетное. Затем примените те же правила к полученному числу и каждому последующему результату. Предполагается, что конечным результатом всегда будет 1,

.

Решение Коллатца с помощью SAT-решателя «достаточно далеко», признал Хеул.Но это амбициозная цель, добавил он, пояснив, что решатель SAT можно использовать для решения ряда менее пугающих математических задач, даже если Коллатц окажется недостижимым.

Математик представит доказательство гипотезы о чувствительности

Предоставлено
Университет Карнеги Меллон

Цитата :
Ученые решают геометрическую задачу 90-летней давности (2020, 6 октября)
получено 20 февраля 2022 г.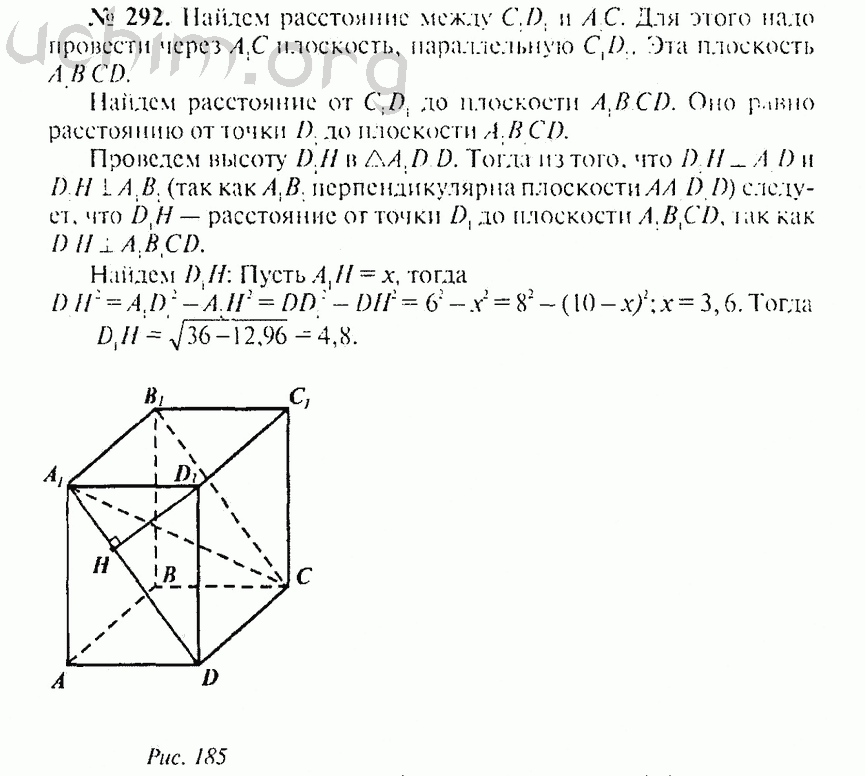
с https://физ.org/news/2020-10-scientists-year-old-geometry-problem.html

Этот документ защищен авторским правом. Помимо любой добросовестной сделки с целью частного изучения или исследования, никакие
часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в ознакомительных целях.

Среднее пропорциональное и правила высоты и длины

… и Высота и Нога Правила

Среднее пропорциональное

Среднее пропорциональное a и b равно значению x здесь:

a x   =   x b

«а относится к х, как х относится к b»

Кажется, это сложно решить, не так ли?

Но когда мы перекрестим умножение (умножим обе части на b , а также на x ), мы получим:

И теперь мы можем найти x:

х = √(ab)

Пример: Чему равно среднее пропорциональное между 2 и 18?

Нас спрашивают «Каково здесь значение x?»

2 x   =   x 18

«2 равно x, как x равно 18»

Мы знаем, как это решить:

х = √(2×18) = √(36) = 6

И вот что у нас получается:

2 6   =   6 18

Это в основном говорит, что 6 — это «умножение в середине » ( 2 умножить на 3 это 6 , 6 умножить на 3 это 18 )

(Это также среднее геометрическое двух чисел. )

Еще один пример, чтобы вы поняли идею:

Пример: каково среднее пропорциональное между 5 и 500?

х = √(5×500)

х = √(2500) = 50

Итак, вот так:

Прямоугольные треугольники

Мы можем использовать среднее пропорциональное с прямоугольными треугольниками.

Во-первых, интересная вещь:

• Возьмем прямоугольный треугольник , лежащий на гипотенузе (длинная сторона)
• Поставить линию высоты
• Он делит треугольник на два других треугольника, да?

Эти два новых треугольника похожи друг на друга и на исходный треугольник!

Это потому, что все они имеют одинаковые три угла.

Попробуйте сами: вырежьте из листа бумаги прямоугольный треугольник, затем разрежьте его по высоте и посмотрите, действительно ли кусочки похожи.

Мы можем использовать эти знания для решения некоторых проблем.

Фактически получаем два правила:

Правило высоты

Высота — это среднее пропорциональное между левой и правой частями гиптонуса, например:

Пример: Найти высоту

ч высоты (AD)

Используйте правило высоты над уровнем моря:

слева высота   =   высота справа

Что для нас:

4. 9 ч   =   ч 10

И найти h:

ч ² = 4,9 × 10 = 49

ч = √49 = 7

Правило для ног

Каждый катет треугольника является средним пропорциональным между гипотенузой и частью гипотенузы непосредственно под катетом :

Пример: Чему равно

x (длина стороны AB)?

Сначала найдите гипотенузу: BC = BD + DC = 9 + 7 = 16

Теперь используйте правило ноги:

гипотенуза катет   =   катет часть

Что для нас:

16 x   =   x 9

И найти х:

х ² = 16 х 9 = 144

х = √144 = 12

Вот реальный пример:

Пример: Сэм любит воздушных змеев!

Сэм хочет сделать очень большого воздушного змея:

• Имеет две стойки PR и QS, которые пересекаются под прямым углом в точке О.
• PO = 80 см и OR = 180 см.
• Ткань воздушного змея имеет прямые углы в точках Q и S.

Сэм хочет знать длину распорки QS, а также длину каждой стороны.

Нам нужно посмотреть только на половину воздушного змея, чтобы произвести расчеты. Вот левая половина повернута на 90°

Используйте правило высоты, чтобы найти ч :

ч ² = 180 × 80 = 14400

ч = √14400 = 120 см

Таким образом, полная длина стойки QS = 2 × 120 см = 240 см

Длина RP = RO + OP = 180 см + 80 см = 260 см

Теперь используйте правило ветвей, чтобы найти r (нога QP):

г ² = 260 × 80 = 20800

r = √20800 = 144 см до ближайшего

см

Снова используйте правило отрезка, чтобы найти p (QR отрезка):

р ² = 260 × 180 = 46800

p = √46800 = 216 см до ближайшего

см

Скажите Сэму, что распорка QS будет 240 см , а стороны будут 144 см и 216 см .

Не могу дождаться ветреного дня!

Внешний угол треугольника

Определение внешнего угла

В каждой вершине треугольника внешний угол треугольника может быть образован продолжением ОДНОЙ СТОРОНЫ треугольника. См. рисунок ниже.

Вычисление углов

Мы можем использовать уравнения для представления мер углов, описанных выше. Одно уравнение может сказать нам сумму углов треугольника.Например,

Мы знаем, что это правда, потому что сумма углов внутри треугольника всегда равна 180 градусам. Что такое ш? Мы еще не знаем. Но мы можем заметить, что мера угла w плюс мера угла z = 180 градусов, потому что они являются парой дополнительных углов. Обратите внимание, как Z и W вместе образуют прямую линию? Это 180 градусов. Итак, мы можем составить новое уравнение:

Затем, если мы объединим два приведенных выше уравнения, мы сможем определить, что мера угла w = x + y. Вот как это сделать:

x + y + z = 180 (это первое уравнение)
w + z = 180 (это второе уравнение)

Теперь, , перепишите второе уравнение как z = 180 — w и подставьте его вместо z в первое уравнение:

х + у + (180 — ш) = 180
х + у — ш = 0
х + у = ш

Интересно. Это говорит нам о том, что мера внешнего угла равна сумме двух других внутренних углов.На самом деле существует теорема, называемая Теоремой о внешнем угле, которая дополнительно исследует эту связь:

Теорема о внешнем угле

Мера внешнего угла (нашего w) треугольника равна сумме мер двух удаленных друг от друга внутренних углов (наших x и y) треугольника.

Давайте попробуем решить две задачи.

Пример А:

Если мера внешнего угла равна (3x — 10) градусов, а мера двух удаленных друг от друга внутренних углов равна 25 градусам и (x + 15) градусам, найдите x.

Чтобы решить, мы используем тот факт, что W = X + Y. Обратите внимание, что здесь я имею в виду углы W, X и Y, как показано на первом изображении этого урока. Их имена не важны. Важно то, что внешний угол равен сумме удаленных внутренних углов.

Приравниваем и находим x.

внешний угол = внутренний угол + другой внутренний угол

$$ (3x — 10) = (25) + (x + 15) $$
$$ 3x — 10 = x + 40 $$
$$ 3x = x + 50 $$
$$ 2x = 50 $$
$$ х = 25 $$

Помните, что «x» здесь не является ответом.Нам нужны сами углы, которые вычисляются как (3x-10), 25 и (x+15). Тогда углы равны 65, 25 и 40 градусов.

Пример В

Внешний угол равен 110 градусам. Два отдаленных внутренних угла имеют размеры 50 и (2x + 30). Найдите х.

Помните: внешний = сумма удаленных внутренних углов

Нам дан внешний угол (110). Приравниваем 110 к (2x + 30) + 50 и находим x.

110 долларов США = 2x + 30 + 50 долларов США
110 долларов США = 2x + 80 долларов США
30$ = 2x $$
$$ 15 = х $$

Урок, проведенный Mr.