Геометрія 8 клас нова програма: ГДЗ 8 клас Геометрія 2021

Содержание

Геометрія 8 клас. Мій конспект. Нова програма

Loading…

Посібник розрахований на вчителів загальноосвітніх закладів, які працюють у 8 класі за навчальною програмою з математики для учнів 5–9 класів загальноосвітніх закладів (травень 2015 року).

Автор: О. О. Старова
Видавництво: Основа
Рік видання: 2016
Кількість сторінок: 144
Формат файлу: .pdf
Розмір файлу: 8 mb

Видання «Мій конспект» — це серія посібників, які ставлять за мету надати допомогу вчителеві в підготовці до уроку. Автори пропонують базову основу, використовуючи яку, кожен учитель може створити власний конспект уроку.

Зміст
ВСТУП 2
Урок № 1. Чотирикутник та його елементи . 5
Урок № 2. Сума кутів чотирикутника 7
Урок № 3. Паралелограм та його властивості 9
Урок № 4. Паралелограм та його властивості 11
Урок № 5. Ознаки паралелограма . 13
Урок № 6. Ознаки паралелограма . 15
Урок № 7. Прямокутник та його властивості . 17
Урок № 8. Ромб та його властивості 19
Урок № 9. Квадрат та його властивості 21
Урок № 10. Трапеція та її властивості 23
Урок № 11. Трапеція та її властивості 25
Урок № 12. Розв’язування типових задач 27
Урок № 13. Контрольна робота № 1 29
Урок № 14. Центральні та вписані кути . 31
Урок № 15. Центральні та вписані кути . 33
Урок № 16. Вписані та описані чотирикутники . . . . . . . 35
Урок № 17. Вписані та описані чотирикутники . . . . . . . 37
Урок № 18. Теорема Фалеса. Середня лінія трикутника та її властивості . 39
Урок № 19. Середня лінія трапеції та її властивості . 41
Урок № 20. Середня лінія трапеції та її властивості . 43
Урок № 21. Розв’язування типових задач 45
Урок № 22. Контрольна робота № 2 47
Урок № 23. Узагальнена теорема Фалеса. Теорема про медіани трикутника . 49
Урок № 24. Властивість бісектриси трикутника . 51
Урок № 25. Означення подібних трикутників . 53
Урок № 26. Ознака подібності трикутників за двома кутами 55
Урок № 27. Ознака подібності трикутників за двома сторонами та кутом між ними . 57
Урок № 28. Ознака подібності трикутників за трьома сторонами 59
Урок № 29. Середні пропорційні відрізки в прямокутному трикутнику . 61
Урок № 30. Розв’язування типових задач 63
Урок № 31. Контрольна робота № 3 65
Урок № 32. Узагальнення матеріалу, вивченого в І семестрі . 67
Урок № 33. Теорема Піфагора . 69
Урок № 34. Теорема Піфагора . 71
Урок № 35. Перпендикуляр і похила, їх властивості 73
Урок № 36. Перпендикуляр і похила, їх властивості 75
Урок № 37. Синус, косинус і тангенс гострого кута прямокутного трикутника . 77
Урок № 38. Значення синуса, косинуса, тангенса для кутів 30°, 45°, 60° . 79
Урок № 39. Співвідношення між сторонами і кутами прямокутного трикутника . 81
Урок № 40. Співвідношення між сторонами і кутами прямокутного трикутника . 83
Урок № 41. Розв’язування прямокутних трикутників 85
Урок № 42. Розв’язування прямокутних трикутників 87
Урок № 43. Розв’язування прямокутних трикутників 89
Урок № 44. Розв’язування типових задач 91
Урок № 45. Розв’язування типових задач 93
Урок № 46. Контрольна робота № 4 95
Урок № 47. Многокутник і його елементи . 97
Урок № 48. Сума кутів опуклого многокутника 99
Урок № 49. Сума кутів опуклого многокутника 101
Урок № 50. Многокутник, вписаний у коло. Многокутник, описаний навколо кола 103
Урок № 51. Поняття площі. Основні властивості площ 105
Урок № 52. Площа прямокутника 107
Урок № 53. Площа паралелограма . 109
Урок № 54. Площа паралелограма . 111
Урок № 55. Площа трикутника . 113
Урок № 56. Площа трикутника . 115
Урок № 57. Площа трикутника . 117
Урок № 58. Площа трапеції . 119
Урок № 59. Площа трапеції . 121
Урок № 60. Розв’язування задач на обчислення площ многокутників 123
Урок № 61. Розв’язування типових задач 125
Урок № 62. Контрольна робота № 5 127
Урок № 63. Повторення. Чотирикутники та їх властивості. Вписані та описані чотирикутники . 129
Урок № 64. Повторення. Площі многокутників 131
Урок № 65. Повторення. Подібність трикутників та її застосування 133
Урок № 66. Повторення. Теорема Піфагора . 135
Урок № 67. Повторення. Розв’язування прямокутних трикутників 137
Урок № 68. Повторення. Вписані та центральні кути. Вписані та описані многокутники . 139
Урок № 69. Підсумкова контрольна робота . 141
Урок № 70. Узагальнення матеріалу, вивченого за рік 143
Література

Календарно-тематичне планування з геометрії для 8 класу за новою програмою

№ уроку	Дата проведення	Тема уроку	Примітки
І семестр
Тема 1. ЧОТИРИКУТНИКИ (21 год)
1		Повторення і узагальнення матеріалу з курсу геометрії 7-го класу
2		Чотирикутник, його елементи. Сума кутів чотирикутника
3		Чотирикутник, його елементи. Паралелограм і його властивості
4		Паралелограм, його властивості й ознаки
5		Паралелограм, його властивості й ознаки. Самостійна робота № 1
6		Прямокутник і його властивості
7		Ромб і його властивості
8		Ромб і його властивості
9		Квадрат і його властивості
10		Самостійна робота № 2. Узагальнення і систематизація знань. Підготовка до контрольної роботи
11		*Тематична контрольна робота № 1*
12		Трапеція
13		Трапеція
14		Центральні і вписані кути
15		Вписані та описані чотирикутники
16		Розв’язування задач і вправ. Самостійна робота № 3
17		Теорема Фалеса. Середня лінія трикутника
18		Середня лінія трикутника. Середня лінія трапеції
19		Середня лінія трапеції
20		Самостійна робота № 4. Узагальнення і систематизація знань. Підготовка до контрольної роботи
21		*Тематична контрольна робота № 2*
Тема 2. ПОДІБНІСТЬ ТРИКУТНИКІВ (11 год)
22		Узагальнена теорема Фалеса
23		Подібні трикутники.
24		Ознаки подібності трикутників
25		Ознаки подібності трикутників. Самостійна робота № 5
26		Середні пропорційні відрізки у прямокутному трикутнику
27		Властивість бісектриси трикутника
28		Застосування подібності трикутників до розв’язування задач
29		Застосування подібності трикутників до розв’язування задач. Самостійна робота № 6
30		Узагальнення і систематизація знань. Підготовка до контрольної роботи
31		*Тематична контрольна робота № 3*
32		Підсумковий урок
ІІ семестр
Тема 3. РОЗВ’ЯЗУВАННЯ ПРЯМОКУТНИХ ТРИКУТНИКІВ (14 год)
33		Теорема Піфагора
34		Теорема Піфагора
35		Теорема Піфагора
36		Перпендикуляр і похила, їх властивості
37		Перпендикуляр і похила, їх властивості
38		Розв’язування задач. Самостійна робота № 7
39		Співвідношення між сторонами і кутами прямокутного трикутника
40		Співвідношення між сторонами і кутами прямокутного трикутника
41		Співвідношення між сторонами і кутами прямокутного трикутника
42		Розв’язування прямокутних трикутників
43		Розв’язування прямокутних трикутників
44		Розв’язування задач. Самостійна робота № 8
45		Узагальнення і систематизація знань. Підготовка до контрольної роботи
46		*Тематична контрольна робота № 4*
Тема 4. МНОГОКУТНИКИ. ПЛОЩІ МНОГОКУТНИКІВ (16 год)
47		Многокутник і його елементи. Сума кутів опуклого многокутника. Многокутник, вписаний у коло, і многокутник, описаний навколо кола
48		Многокутник і його елементи. Сума кутів опуклого многокутника. Многокутник, вписаний у коло, і многокутник, описаний навколо кола
49		Поняття площі многокутника. Площа прямокутника
50		Поняття площі многокутника. Площа прямокутника
51		Розв’язування задач і вправ. Самостійна робота № 9
52		Площа паралелограма
53		Площа паралелограма
54		Площа трикутника
55		Площа трикутника
56		Площа трикутника
57		Площа трапеції
58		Площа трапеції
59		Площа трапеції
60		Розв’язування задач і вправ. Самостійна робота № 10
61		Узагальнення і систематизація знань. Підготовка до контрольної роботи
62		*Тематична контрольна робота № 5*
Тема 5. ПОВТОРЕННЯ І СИСТЕМАТИЗАЦІЯ НАВЧАЛЬНОГО МАТЕРІАЛУ (8 год)
63		Чотирикутники
64		Чотирикутники
65		Подібність трикутників
66		Розв’язування прямокутних трикутників
67		Розв’язування прямокутних трикутників
68		Многокутники. Площі многокутників
69		Підсумкова контрольна робота за 7 клас
70		Підсумковий урок

Образователните медиатори — все по-ценни, но малко ценени — България

В началото на учебната година министърът на образованието Николай Денков се включи в екип за издирване на деца извън образователната система в Берковица.

Година и половина, след като Министерството на науката и образованието (МОН) се зае сериозно със задачата да върне отпадащите от образователната система деца в клас с по-ранни обиколки по домовете им и след като в екипите на образователните медиатори бяха включени и психолози, социални и здравни работници, полицаи и служители на други институции, усилията явно се оказват ненапразни.

От началото на учебната година върнатите по Механизма за обхват ученици са 8700. От тях 2700 са отпаднали през миналата учебна година, а почти 6000 са записани за първи път, се вижда от предоставената на «Дневник» справка на МОН.

Министерството прави уговорката, че медиаторите от съответните детски градини или училища са част от екипите, които посещават семействата и поради това няма как да се направи справка колко деца са записани благодарение само на работата на медиаторите.

В края на миналата година образователните медиатори получиха голямата награда «Човек на годината» на Българския хелзинкски комитет (БХК), а МОН отличи няколко от тях. «Те са хората, на които в немалка степен се крепи образователната система», каза министърът на образованието Николай Денков на церемонията. Всъщност, и Денков, и предишният образователен министър Красимир Вълчев посочват образователните медиатори като ключови за задържането на децата от уязвими групи и реално — като пълноправни участници в образователния процес. Въпреки това обаче позицията им изглежда несигурна, доколкото те се назначават по проект на МОН или от бюджета на училищата.

Несигурно работно място

В системата на предучилищното и училищното образование към началото на ноември 2021 г. са записани над 695 хиляди деца. Това са 94.47% от всички, подлежащи на задължително обучение, се посочва в справката.

Броят на необхванатите деца и ученици в задължителна предучилищна и училищна възраст е близо 48 хиляди, делът им е 5.53% от всички.

В 903 училища наетите медиатори са наети по проект «Подкрепа за успех», а 185 училища поддържат тези длъжности със собствени средства, съобщиха пред «Дневник» от МОН. Проектът е на стойност близо 128 млн. лв. и е по Оперативна програма «Наука и образование за интелигентен растеж» 2014-2020 г., съфинансирана от Европейския съюз чрез Европейските структурни и инвестиционни фондове. «Подкрепа за успех», чийто бенефициент е МОН, е с продължителност 30 месеца, считано от 28 февруари 2019 г. Очаква се от средата на 2022 г. да заработи нова национална програма за наемане на образователни медиатори и социални работници в детските градини и училищата на стойност 10 млн. лв.

Общият брой на медиаторите в българските училища през тази учебна година е 1088. Те получават минималната работна заплата за страната. Предвижда се това да се запази и в новата национална програма. В Закона за бюджета за 2022 г. се предвижда увеличение на минималната заплата от 650 лв. на 710 лв.

Проблемът на медиаторите обаче не е толкова заплащането, колкото несигурността на позицията, споделиха пред «Дневник» образователни медиатори. Някои от тях вземат и допълнителни пари, ако училищният директор реши да ги включи и в някакви други дейности, като тестването на децата с бързи антигенни тестове за COVID-19, например.

МОН изготвя списък на училищата, които имат нужда от образователен медиатор и те се финансират целево по проекта «Подкрепа за успех». Техният статут в момента е малко неопределен, каза пред «Дневник» Теодора Крумова от неправителствената организация «Амалипе», която се занимава с обучението на медиаторите. Те не са назначени на щат нито като част от педагогическия, нито като част от непедагогическия персонал в училищата. «Така всяко едно нещо трябва да се отстоява и предоговаря», посочи и даде за пример 400-те лева, които МОН е отпуснало допълнително през 2020 г. По времето на извънредното положение за хора на първа линия.

«Министерството на образованието и науката работи много за утвърждаването на длъжността образователен медиатор. Тя е създадена именно за нуждите на образователната система и в частност — на приобщаващото образование», отговори министерството на запитване на «Дневник».

Крумова потвърди, че министерството има добра воля и обмисля как да бъде систематизирана работата на медиаторите, за да имат по-голяма устойчивост. По думите й не е устойчив модел назначаването и финансирането им да бъде година за година и да е свързано с условията на различни проекти, както и за всяка година да се явяват отново на конкурс, за да бъдат назначени, без значение дали училищните директори са доволни или не от работата им.

Не само подбират децата от домовете им

Работата на образователните медиатори, за да има траен резултат от нея, е не само всекидневно да събират неявилите се в училище деца от домовете им. За да се върнат трайно в клас, родителите им трябва да проумеят, че образованието е смислено и важно.

«Те трябва да работят и със самите семейства за промяна на нагласата им, да работят за превенция и промяна в общността», посочи Крумова. За това обаче те трябва да бъдат обучени. Обучението предимно е от неправителствените организации и най-вече «Амалипе».

«Назначените по проект «Подкрепа за успех» медиатори бяха обучение от колективи от университетски преподаватели и представители на граждански организации с опит в приобщаващото образование», посочи МОН. Това обучение е било в рамките на 6 часа и явно недостатъчно. Те са организирани в неформална мрежа и получават постоянна подкрепа основно от «Амалипе», както и отговори на всички въпроси, които ги притесняват. Всеки месец организацията провежда и онлайн обучения по различни теми, а когато условията позволяват — и присъствени срещи.

«Децата заслужават днешния ден»

Признанията, които получават образователните медиатори, много ги мотивират — чувстват, че работата им е оценена и са още по-амбицирани да я вършат — това е общата нагласа на медиаторите, с които «Дневник» разговаря. Друго общо за отбелязване е, че не толкова са недоволни от заплащането, колкото от несигурността на позицията им. И да, работата им не е свързана само с размяна на разпечатани уроци и търсене на неявилите се на училище деца.

«Често родителите тръгват за чужбина и оставят децата при възрастните си родители, от които не всички ги е грижа за образованието на децата», каза Фатме Арслан медиатор в професионалната гимназия по транспорт «Гоце Делчев» в Пловдив. Тихомир Георгиев, който от 4 години е образователен медиатор в Криводол разказа, че няма въпроси, с които да не се занимава той лично в работата си — дали е битов конфликт в семействата, които обхожда, дали, ако се налага, да разубеждава деца да изчакат с ранен брак, или да се върнат в училище. Самият той е бил неграмотен до 13-та си година, нарича образованието «по-скъпо от златото» и вярва, че «ако има кой да те подкрепи, можеш във всичко да успееш», затова не щади сили да убеждава родителите и децата да се върнат в училище.

Без средно образование няма как да искате да стане човек от него

Николай Огнянов,

образователен медиатор

Николай Огнянов, медиатов в СУ «Христо Смирненски» в Гулянци, в което учат над 500 деца, има друг подход. «Аз винаги давам пример с моите деца — в 9 и в 12 клас. Без средно образование няма как да искате да стане човек от него», казва на родителите. Огнянов, който получи голямата награда на МОН медиатор на годината, казва, че работата за него е призвание и по принцип — «работа за хора с огромни сърца». «Децата са нашето бъдеще и те ще останат след нас. Заслужават днешният ден да им бъде прекрасен, заслужават да имат сигурност и утре, и вдругиден», казва.

Руководство по математике UnboundEd

Что содержится в Руководстве по содержанию и как его использовать?

Получите ответы на все свои вопросы о Руководстве по содержанию, в том числе о том, что содержится в каждой части и как их можно использовать в вашей роли в вашей школе.

Просмотр часто задаваемых вопросов

8.Г.А | Понимание конгруэнтности и сходства с использованием физических моделей, прозрачных пленок,

или программное обеспечение для геометрии.

8.GB | Поймите и примените теорему Пифагора.

Добро пожаловать в серию руководств по математике UnboundEd! Эти руководства предназначены для того, чтобы объяснить, что говорят новые высокие стандарты математики о том, что учащиеся должны изучать в каждом классе, и что они означают для учебной программы и обучения. Это руководство, первое для 8 класса, состоит из трех частей. В первой части дается «экскурсия» по стандартам в первых двух кластерах области геометрии (касающихся конгруэнтности, сходства и теоремы Пифагора) с использованием свободно доступных онлайн-ресурсов, которые вы можете использовать или адаптировать для своего класса.Во второй части показано, как эти стандарты соотносятся с другими понятиями в 8 классе. А в третьей части объясняется, какое место занимают конгруэнтность, сходство и теорема Пифагора в процессе обучения от начальных классов до старших классов.

Конгруэнтность и сходство

Стандарты для 8-го класса полны важных идей, так зачем же начинать эту серию с конгруэнтности и подобия? Во-первых, эти стандарты являются частью «основной работы» 8-го класса, а это означает, что они заслуживают большей части учебного времени в течение учебного года.¹ Приоритизация основной работы в течение года гарантирует, что этим стандартам будет уделено должное внимание. Соответствие и сходство также необходимы учащимся для понимания других важных понятий в 8 классе, в частности наклона линии. (8.EE.B.6) Следовательно, работа с конгруэнтностью и подобием должна предшествовать линейным уравнениям, что является еще одной важной частью работы.

Конгруэнтность и сходство также являются отличным способом начать год, потому что они предполагают «практический» подход через преобразования, что делает их доступными для любого учащегося с базовым пониманием линий и углов.Более того, стандарты соответствия и сходства напрямую связаны со стандартами геометрии средней школы (в частности, с предметами «Конгруэнтность», «Сходство и правильные треугольники»), поэтому они важны для будущих успехов учащихся. Так что, если вам интересно, с чего начать год, конгруэнтность и сходство — это надежная ставка.

В 8 классе стандарты, касающиеся конгруэнтности и подобия, сгруппированы в один кластер (называемый 8.G.A, так как это первый кластер стандартов по геометрии в классе). Несмотря на то, что он содержит только пять стандартов, этот кластер объединяет ряд математических идей, в том числе три, которые не часто рассматриваются как связанные: конгруэнтность и подобие, преобразования и отношения углов. Давайте посмотрим, что говорят эти стандарты, а затем рассмотрим каждый из них более подробно.

8.Г.А | Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для создания геометрии.

Порядок стандартов не указывает порядок, в котором они должны преподаваться.Стандарты — это всего лишь набор требований к тому, что учащиеся должны знать и уметь делать к концу каждого года; они не предписывают точную последовательность или учебный план. В этом случае имеет смысл сначала познакомить учащихся со свойствами отражений, переносов и поворотов (8.G.A.1), а затем использовать эти преобразования для установления понятия конгруэнтности (8.G.A.2). После этого учащиеся должны быть готовы к расширению и понятию сходства (8. G.A.4). Решение задач с преобразованиями на координатной плоскости (8.G.A.3) можно интегрировать вместе с работой с этими первыми тремя стандартами, а применения трансформаций (8.G.A.5) также можно преподавать в сочетании с другой работой или их можно оставить напоследок.

Прежде чем мы начнем работать с этими стандартами, давайте на мгновение остановимся и подумаем, почему они так важны. В прошлом геометрия в классах K-8, как правило, фокусировалась на широком круге тем, ни одна из которых не преподавала слишком глубоко. Студенты могли выучить термины «конгруэнтный» и «похожий» в очень общем виде (возможно, как «одинаковая форма, тот же размер» и «такая же форма, разный размер»), но это была степень их знакомства с этими двумя важными понятиями. .Преобразования рассматривались как совершенно отдельная идея — если они вообще были освещены — с упором только на выполнение преобразований (без описания их свойств). С другой стороны, геометрия в старших классах посвящала много времени обучению треугольной конгруэнтности и критериям подобия, что не имело ничего общего с тем, что ученики делали раньше. Однако теперь стандарты для 8-го класса и старшей школы используют преобразования, чтобы помочь учащимся понять конгруэнтность и сходство, а также согласовать их ожидания в отношении обучения учащихся.Их внимание сосредоточено не столько на выполнении преобразований, сколько на том, как они улучшают понимание учащимися взаимосвязей между фигурами. Мы хотим, чтобы учащиеся не просто могли выполнить, скажем, отражение прямоугольника над линией, но и объяснить, чем изображение этого прямоугольника похоже или отличается от оригинала. Что мы знаем об изображении этого прямоугольника на основании того, что мы знаем об исходной фигуре и свойствах преобразований?

Отражения, перемещения и вращения: основы

Прежде чем двигаться дальше, давайте сделаем паузу и определим, что мы подразумеваем под отражением, перемещением и вращением.Это сложные идеи для описания словами, поэтому мы начнем с некоторых приблизительных определений, а затем посмотрим на некоторые иллюстрации. ²

Грубо говоря, отражение переносит фигуру (такую как точка, линия, отрезок, многоугольник или окружность) с одной стороны линии (называемой линией отражения) на другую сторону. Например, на приведенной ниже диаграмме △ABC переходит в △A’B’C’ путем отражения через линию DE.

Грубо говоря, перевод перемещает фигуру по определенному вектору.Например, на приведенной ниже диаграмме △ABC теперь преобразуется в △A’B’C’ путем переноса вдоль вектора DE.

Грубо говоря, при повороте фигура вращается вокруг точки (называемой центром вращения) на фиксированный угол. В качестве последнего примера на приведенной ниже диаграмме △ABC превращается в △A’B’C’ путем поворота на 90° по часовой стрелке.

В совокупности эти три преобразования иногда называют основными жесткими движениями из-за того, что они «жестко» перемещают фигуру по плоскости, сохраняя длины сегментов и .(Позже в этом руководстве мы обсудим нежесткое преобразование: расширение.)

Запоминание точного определения каждого преобразования не имеет значения. Будет лучше, если учащиеся попробуют каждое из преобразований, а затем разработают свои собственные определения как способ обработки свойств каждого из них. Сначала следует ожидать таких слов, как «flip», «slide» и «turn». Однако они не охватывают все идеи, указанные в стандарте, и вскоре учащимся потребуется пересмотреть их более подробно.Все учащиеся должны уметь сказать, например, что отражение сохраняет расстояния вдоль линий и отрезков и меры углов. Они также должны заметить, что расстояние между каждой точкой фигуры и линией отражения остается неизменным при отражении фигуры. На проработку всех трех жестких движений может уйти несколько дней — хорошей идеей может быть сосредоточение внимания на одном из них в день, — но это время будет потрачено с пользой, если учащиеся смогут определить и четко сформулировать свойства каждого преобразования.

Понимание свойств отражений, переводов и вращений

Учащиеся должны начать изучение конгруэнтности с практического опыта: самостоятельно пробовать отражения, переводы и повороты и описывать свойства фигур при этих преобразованиях. (8.G.A.1) Лучшие инструменты для этого — прозрачные пластиковые пленки (для кодоскопов) или калька — могут показаться старомодными, но они хорошо справляются со своей задачей. Существуют программные пакеты, которые также позволяют учащимся легко экспериментировать с трансформациями (GeoGebra — один из популярных продуктов, доступный бесплатно в Интернете), но многие учителя на собственном опыте считают, что для учащихся лучше сначала получить тактильное представление обо всех неподвижных движениях. .

Давайте взглянем на пример плана урока, чтобы увидеть, как может выглядеть введение одного типа трансформации. Этот план урока имеет дело с размышлениями, но базовая структура будет работать так же хорошо для переводов или поворотов.

8 класс, модуль 2, урок 4: пример 1

Отражение через линию определяется с помощью следующего примера.

Пусть 𝐿 — вертикальная линия, а 𝑃 и 𝐴 — две точки, не лежащие на 𝐿, как показано ниже. Кроме того, пусть 𝑄 будет точкой на 𝐿.(Черный прямоугольник обозначает границу бумаги.)

Ниже приводится описание того, как отражение перемещает точки 𝑃, 𝑄 и 𝐴 за счет использования прозрачности.

Проведите линию 𝐿 и ровно три точки на прозрачной пленке, используя красный цвет. (Обязательно используйте прозрачную пленку того же размера, что и бумага.)
Удерживая бумагу неподвижной, отразите прозрачность по вертикальной линии (поменяв местами левую и правую), сохраняя при этом вертикальную линию и точку 𝑄 поверх их черных изображений.
Положение красных фигур на прозрачной пленке теперь представляет собой отражение исходной фигуры. Отражение (𝑃) — это точка, представленная красной точкой слева от 𝐿, Отражение (𝐴) — красная точка справа от 𝐿, а точка Отражение (𝑄) — это сама точка 𝑄.
Обратите внимание, что точка не меняется при отражении.

СкрытьПоказать

При чтении помните, что этот урок является частью модуля, использующего формальный язык и нотацию (включая нотацию функций) для преобразований. Стандарты не требуют обозначения функций в 8 классе, и вы можете не захотеть знакомить учащихся с формальными терминами в первый день — это нормально. Что мы действительно хотим подчеркнуть, так это то, как этот урок знакомит учащихся с концепцией отражения:

Урок начинается с практического упражнения с диапозитивами.Студенты могут видеть, как отражение определяет точки изображения, и, вероятно, сразу же начнут замечать взаимосвязь между каждой точкой и ее изображением. Вероятно, лучше, чтобы их первая попытка была не на координатной плоскости; условности построения графиков могут отвлекать учащихся от понимания основных свойств отражений.

Учащиеся пробуют выполнить несколько других упражнений. Прозрачность все еще ожидается на этом этапе. В одном упражнении используется горизонтальная линия отражения, а в другом — фигура с вершиной на линии отражения — оба варианта хороши для учащихся.

Упражнения 3–5 задают несколько важнейших вопросов, которые побуждают учащихся сформулировать ключевые идеи стандарта. Их просят сравнить величины углов и длины отрезков и заметить, что они конгруэнтны. Это поможет им формализовать эти свойства на следующем этапе урока. (Эти идеи могут быть записаны на «привязке», которая висит в классе до конца урока.)

Дальнейшие примеры побуждают учащихся использовать новые понятия.

Ожидайте, что учащиеся будут регулярно использовать свои диапозитивы в течение первых нескольких дней. В конце концов, они начнут интуитивно понимать, как будет выглядеть каждое преобразование, и будут все меньше и меньше полагаться на прозрачность. Это «шестое чувство» того, как будет выглядеть изображение фигуры, и есть то, для чего вы снимаете, и оно позволит учащимся позже представить решения всевозможных проблем.

Конгруэнтность

После того, как учащиеся изучат свойства каждого жесткого движения отдельно, они могут перейти к размышлению о конгруэнтности и случаях, когда одна фигура переходит в другую посредством последовательности жестких движений. (8.G.A.2) Оглядываясь назад на стандарт, мы видим, что он состоит из двух частей:

Учащиеся должны понимать, что одна фигура конгруэнтна другой, если одну можно перевести в другую серией жестких движений.
Студенты должны быть в состоянии описать последовательность жестких движений, которые переводят одну фигуру в другую.

Первая часть означает, что учащиеся должны разработать определение конгруэнтности, основанное на преобразованиях, и должны быть в состоянии объяснить, почему две фигуры конгруэнтны, на основе свойств неподвижных движений.(Обратите внимание, что это отличается от традиционного определения конгруэнтности «такая же форма, тот же размер».) Вторая часть означает в значительной степени то, что она говорит: учащиеся должны быть в состоянии описать в некоторых деталях преобразования, которые переводят одну фигуру в другую. . Эта задача является примером:

Конгруэнтные треугольники

Два треугольника на рисунке ниже равны:

Укажите последовательность вращений, перемещений и/или отражений, которая переводит △𝑃𝑅𝑄 в △𝐴𝐵𝐶.
Можно ли показать конгруэнтность в части (а), используя только переносы и повороты? Объяснять.

«Конгруэнтные треугольники» компании Illustrative Mathematics распространяется по лицензии CC BY 4.0.

СкрытьПоказать

Это задание носит обучающий характер и служит началом урока и приводит к новым идеям по мере его прохождения учащимися. Дайте его учащимся после того, как они познакомятся с твердыми движениями, и они быстро заметят, что ни одно преобразование не поможет — им придется использовать более одного.Поощряйте учащихся быть точными в своих объяснениях. Если вы видите отражение, где должна быть линия отражения? Если видите перевод, то по какому вектору? Может возникнуть большая дискуссия, когда учащиеся делятся несколькими решениями проблемы.

После того, как учащиеся решат задачу, вы можете рассказать о том, что PQR точно отображается на ABC посредством перевода и отражения (или других, более сложных последовательностей) без пробелов или перекрытий. Поскольку они использовали только жесткие преобразования (которые не изменяют меры углов или длины отрезков) для получения одной фигуры из другой, мы можем сказать, что они конгруэнтны.С этого момента вы хотите, чтобы учащиеся использовали это определение конгруэнтности, и если их попросят продемонстрировать конгруэнтность двух фигур, они должны делать это посредством преобразований.

Расширители

Для закрепления жестких преобразований и их связи с конгруэнтностью потребуется некоторое время. Затем пришло время ввести понятие подобия, которое включает в себя еще одно преобразование — расширение. (8.G.A.4) Как и выше, мы начнем с приблизительного определения, а затем уточним его с помощью некоторых иллюстраций.Грубо говоря, расширение — это преобразование фигуры (например, точки, линии, отрезка, многоугольника или круга) в другую фигуру с определенным коэффициентом масштабирования. При расширении расстояние между фиксированной точкой (называемой центром расширения) и расширяемым объектом становится больше или меньше пропорционально масштабному коэффициенту. Примеры ниже показывают два расширения △ABC с центром в точке P, одно с масштабным коэффициентом больше 1, а другое с масштабным коэффициентом меньше 1.

Как мы видим, цифры при расширении могут быть увеличены или уменьшены, в зависимости от коэффициента масштабирования.Это поднимает важный момент: «Расширение» имеет особое математическое значение, отличное от его значения в повседневном английском языке (где оно означает просто увеличение, а не сокращение). Учащимся может потребоваться некоторое время, чтобы приспособиться к этому новому использованию знакомого слова, но просмотр примеров с масштабными коэффициентами разной величины поможет этому процессу.

Как и в случае с жесткими движениями, учащиеся должны иметь некоторый практический опыт дилатации и использовать этот опыт для выработки все более точных определений дилатации.Вы можете использовать прозрачные пленки для такого занятия, но лучшими инструментами могут быть линейка или циркуль: учащиеся могут измерить расстояние от каждой точки на фигуре до центральной точки. Затем они могут попытаться, например, умножить эти длины на масштабный коэффициент 2, чтобы получить расширение. (Аналогичным образом они могут попробовать использовать масштабный коэффициент 1/2.) Этот план урока знакомит учащихся с упражнением, которое выполняется с помощью компаса.

8 класс, модуль 3, урок 2: пример 1

Вернитесь к своей догадке или просмотрите наш список классов.Какие предположения оказались верными? Откуда вы знаете?

Ответы могут различаться в зависимости от предположений, сделанных классом. Учащиеся должны определить, что гипотеза о том, что линия отображается в линию под расширением, верна.

Как вы думаете, что произойдет, если мы выберем другое расположение центра или точек 𝑃 и 𝑄?

Точки 𝑂, 𝑃 и 𝑄 являются произвольными точками. Это означает, что они могли быть где угодно в самолете. По этой причине результаты будут одинаковыми; то есть расширение по-прежнему будет давать линию, и линия будет параллельна оригиналу.

Посмотрите еще раз на рисунок и представьте, что с помощью нашей прозрачности можно перевести отрезок 𝑂𝑃 по вектору 𝑂𝑃 в отрезок 𝑃𝑃 ’ и отрезок 𝑂𝑄 по вектору 𝑂𝑄 в отрезок 𝑄𝑄’. Располагая этой информацией, можете ли вы сказать что-нибудь еще о линиях 𝐿 и 𝐿’?

Поскольку 𝑃 и 𝑄 являются произвольными точками на прямой 𝐿, а переводы отображают прямые в параллельные прямые, когда вектор не параллелен исходной прямой или не является ее частью, мы можем сказать, что 𝐿 параллелен 𝐿’.

СкрытьПоказать

Опять же, вы можете использовать любые имеющиеся у вас инструменты для подобной деятельности. Учащиеся могут использовать линейки для измерения расстояний от центра расширения или они могут использовать прозрачные пленки для отслеживания расстояний. В результате у них развивается интуиция о том, как работает дилатация, и они могут отвечать на различные дополнительные вопросы.Например, как изменение масштабного коэффициента влияет на изображение фигуры? Как перемещение центра расширения влияет на изображение фигуры? Что произойдет, если центр расширения окажется внутри, на или за пределами фигуры? Что даст расширение с коэффициентом масштабирования 1? Любой из них может вызвать интересную дискуссию и помочь учащимся лучше понять, как дилатации ведут себя в различных условиях.

Подобие

Как только у учащихся появится интуитивное представление о том, как работает расширение, они смогут определить сходство и описать серию преобразований подобия.(8.G.A.4) Как и в случае с конгруэнтностью, здесь преследуется двоякая цель; студенты должны:

Поймите сходство с точки зрения жестких движений и расширений.
Опишите последовательность преобразований подобия.

Задача, подобная этой, может быть хорошим способом начать работу:

Вы можете использовать это задание в том виде, в каком оно есть, или использовать его как учебное задание, чтобы представить идею сходства посредством неподвижных движений и растяжений. В этом случае мы могли бы немного упростить вопрос: «Не могли бы вы сопоставить маленькую стрелку с большой, используя жесткие движения и расширения? Поясните свой ответ.” Есть несколько способов сделать это, как показано в разделе решения задачи, и это возможность для содержательного обсуждения. Как только несколько методов будут установлены, вы можете объяснить учащимся, что они только что показали, что эти фигуры похожи, потому что мы смогли перевести одну фигуру в другую посредством отражений, перемещений, поворотов и расширений. Это становится определением сходства. (Обратите внимание, что это отличается от определения подобия «одинаковая форма, разный размер», с которым учащиеся могут быть знакомы.Дело не в том, что эти две фигуры связаны серией трансформаций и оказываются похожими; скорее, они похожи, потому что связаны серией преобразований. Другими словами, как только мы установили трансформационную последовательность, мы установили сходство.)

Конгруэнтны, похожи или и то, и другое?

Учащимся важно понять, что конгруэнтность и сходство не исключают друг друга; это не тот случай, когда две фигуры являются одним, но никогда не являются другим. На самом деле, если две фигуры конгруэнтны, они также подобны.Чтобы понять почему, вспомните определение сходства: одна фигура похожа на другую, если она может быть получена последовательностью отражений, перемещений, вращений и расширений. Любое из преобразований конгруэнтности, которые мы рассмотрели выше, также подходит под это определение — две задействованные фигуры будут конгруэнтны, но также будут соответствовать критериям сходства.

Перемещение на координатную плоскость

Начальные встречи студентов с каждым преобразованием (включая расширение) не обязательно должны происходить на координатной плоскости.На самом деле введение каждого преобразования в «синтетический» контекст (без использования координат, как в приведенных выше примерах) часто позволяет учащимся сосредоточиться на свойствах самих преобразований, не беспокоясь об условностях координатной плоскости. Это также хорошее напоминание о том, что вселенная преобразований — это гораздо больше, чем просто подмножество, которое мы можем описать с помощью целочисленных координат. (Студенты также склонны разрабатывать «правила» для выполнения преобразований на координатной плоскости — например, «поменять местами значения x и y» для поворота на 180 градусов — на самом деле это не должно быть акцентом в раннем обучении.Вспомните, как наш вводный план урока по вращению не включал никаких координатных сеток.)

Однако в какой-то момент учащиеся должны уметь работать с преобразованиями на координатной плоскости и четко описывать эффекты определенных преобразований, используя координаты. (8.G.A.3) По сути, этот стандарт предназначен для того, чтобы взять все, что учащиеся узнали о преобразованиях в целом, и применить это к задачам на координатной плоскости. Разнообразие проблем, подразумеваемых здесь, огромно, и представить исчерпывающую выборку просто невозможно.Но давайте рассмотрим одну задачу как пример того, как ученики совершают прыжок на координатную плоскость:

Опять же, это только один пример, но давайте рассмотрим его внимательно. В дополнение к твердому пониманию свойств преобразований и базового понимания координатной плоскости учащиеся также должны быть знакомы с уравнениями горизонтальных линий. (Если вы еще не достигли этого на своем курсе, ничего страшного; учащиеся все еще могут выполнить аналогичное задание, включающее отражение по оси X.) Если у них все это есть, они могут начать решать. Не нужно много времени, чтобы понять, что эта проблема устойчива к грубой силе; даже если бы лист миллиметровой бумаги размером 2000 х 2000 квадратов существовал, потребовалась бы целая вечность, чтобы нарисовать соответствующую точку и отразить ее. Вместо этого им придется применить некоторые идеи об отражениях: в частности, что расстояние между точкой и линией отражения равно расстоянию между ее изображением и линией отражения. Две стратегии, которые вы могли бы предложить ученикам попробовать:

Попросите их создать грубый набросок координатной плоскости или части плоскости, чтобы помочь им визуализировать ситуацию.Тогда они смогут увидеть, что (1000, 2012) на 12 единиц выше y = 2000, поэтому отраженная точка будет на 12 единиц ниже y = 2000. Более того, отражение вообще не сдвинет изображение влево или вправо. , поэтому координата x обеих точек будет одинаковой. Эти две подсказки должны позволить им собрать решение вместе.

Попросите их подумать о более простом случае, например, отразив точку (1, 10) на линии y = 8. Затем попросите их связать решение более простой задачи с исходным вопросом.Цифры будут немного другими, но процесс будет таким же.

В обоих случаях учащиеся получают гибкое представление о том, как работают преобразования, и применяют их к определенным точкам и расстояниям на координатной плоскости.

Частные случаи конгруэнтности: трансверсали и треугольники

На первый взгляд последний стандарт в кластере 8.G.A может показаться неуместным. Как мы перешли от преобразований к трансверсалям? И какое отношение все это имеет к углам треугольника? Эти идеи — преобразования, трансверсали и треугольники — долгое время рассматривались и преподавались как отдельные идеи.Но теперь все они понимаются как связанные. (8.G.A.5) Чтобы увидеть, как преобразования связаны с трансверсалями, давайте взглянем на этот урок:

8 класс, модуль 2, урок 12: исследовательское задание 2

На рисунке ниже ‖ и 𝑚 — это трансверсаль. С помощью транспортира измерьте углы 1–8. Назовите углы, равные по величине.

∠1 = ∠3 = ∠5 = ∠7 = и ∠2 = ∠4 = ∠6 = ∠8

а. Что вы заметили в измерениях ∠1 и ∠5? Как вы думаете, почему это так? (При необходимости используйте прозрачность.)

∠𝟏 и ∠𝟓 равны по мере. Мы можем перенести ∠𝟏 вдоль вектора на линии 𝒎 так, чтобы вершина ∠𝟏 отображалась на вершину ∠𝟓. Переводы сохраняют угол, поэтому два угла совпадут.

б. Что вы заметили в измерениях ∠3 и ∠7? Как вы думаете, почему это так? (При необходимости используйте прозрачность.) Существуют ли другие пары углов с такими же отношениями? Если да, перечислите их.

∠𝟑 и ∠𝟕 равны по мере. Мы можем перенести ∠𝟑 вдоль вектора на линии 𝒎 так, чтобы вершина ∠𝟑 отображалась на вершину ∠𝟕.Переводы сохраняют угол, поэтому два угла совпадут. Другими парами углов с таким же отношением являются ∠𝟒 и ∠𝟖 и ∠𝟐 и ∠𝟔.

в. Что вы заметили в измерениях ∠4 и ∠6? Как вы думаете, почему это так? (При необходимости используйте прозрачность. ) Есть ли другая пара углов с таким же соотношением?

Меры ∠𝟒 и ∠𝟔 равны. Вращение на 𝟏𝟖𝟎° вокруг центра отобразит ∠𝟒 в ∠𝟔. Повороты сохраняют угол, поэтому мы знаем, что ∠𝟒 и ∠𝟔 равны.∠𝟑 и ∠𝟓 имеют одинаковые отношения.

СкрытьПоказать

Как мы видим, учащиеся используют транспортир для измерения и определения взаимосвязей между углами. Затем они возвращаются к знакомому инструменту (прозрачности) из работы с трансформациями, чтобы понять, почему существуют эти отношения.Последующее обсуждение особенно интересно: учащиеся должны обратить внимание на то, как соотносятся соответствующие углы при переводе одного угла в другой. Точно так же чередующиеся внутренние углы связаны поворотом одного угла на 180 градусов к другому. На самом деле это математическая основа для идей, которые когда-то часто давались учащимся средней школы только как постулаты («чередующиеся внутренние углы конгруэнтны» и т. д.). Потратив время на изучение причин этих угловых взаимосвязей, учащиеся с большей вероятностью запомнят их и будут опираться на свои знания в будущем.

В прошлом другой идеей, которую часто преподавали изолированно и давали студентам в качестве постулата, была сумма внутренних углов треугольника. Но после того, как учащиеся поймут углы, образованные секущими в свете преобразований, они смогут объяснить, откуда взялась эта идея. Чтобы понять, как это сделать, давайте рассмотрим эту задачу.

Как поясняет решение задачи, учащиеся могут разработать неформальный аргумент в пользу того, что a + b + c = 180, используя альтернативные отношения внутренних углов, чтобы установить, что три смежных угла на диаграмме имеют размеры a, b и c, и что вместе они три угла образуют прямой угол.Это не простой аргумент, но он доступен учащимся 8-го класса. Если ваши учащиеся имеют ограниченный опыт выполнения заданий, требующих рассуждений и объяснений такого типа, несколько подмостков могут быть полезны, чтобы помочь им полностью усвоить идеи. вовлеченный. Например, если у ваших учеников возникают проблемы с мерами углов, заданными в виде переменных, вы можете начать с треугольника с целочисленными мерами углов. Вы также можете попросить их повторить ту же технику (удлинить одну сторону, а затем построить параллельную линию через противоположную вершину) на другом треугольнике с целыми числами углов, а затем перейти к «обычному» треугольнику, показанному выше.А во второй части задания учащиеся, не привыкшие объяснять свои мысли, могут извлечь пользу из одного или двух вводных предложений, чтобы начать свои ответы.

Последняя идея, которую учащиеся готовы объяснить посредством преобразований, — это критерий угла-угла для сходства треугольников. Это задание знакомит учащихся с серией вопросов, предназначенных для того, чтобы привести их от конкретного случая к более общему утверждению.

Подобные треугольники II

Треугольники 𝐴𝐵𝐶 и 𝑃𝑄𝑅 имеют две пары конгруэнтных углов, как указано:

Объясните, используя расширения, переводы, отражения и/или повороты, почему △𝑃𝑄𝑅 похоже на △𝐴𝐵𝐶.

Углы 𝐶 и 𝑅 равны?

Можете ли вы показать сходство в части a, не используя отражение? Как насчет того, чтобы не использовать дилатацию? Объяснять.

Предположим, 𝐷𝐸𝐹 и 𝐾𝐿𝑀 — два треугольника с 𝑚(∠𝐷)=𝑚(∠𝐾) и 𝑚(∠𝐸)=𝑚(∠𝐿). Подобны ли треугольники 𝐷𝐸𝐹 и 𝐾𝐿𝑀?

«Similar Triangles II» компании Illustrative Mathematics находится под лицензией CC BY 4.0.

СкрытьПоказать

Части (a), (b) и (c) этой задачи основаны на понимании учащимися преобразований подобия.Затем часть (d) просит их, так же как и в двух предыдущих заданиях, обобщить. Имея «общую» пару треугольников с двумя парами конгруэнтных углов, могут ли они показать сходство? Опять же, учащиеся, не привыкшие объяснять свои мысли, могут нуждаться в поддержке. Им могут быть полезны некоторые возможные диаграммы DEF и KLM, чтобы увидеть, что точные задействованные преобразования не так важны, как тот факт, что некоторая последовательность жестких движений и расширений приведет один треугольник к другому. Одно или два начала предложения также могут быть полезными. Как и в случае с любым из этих заданий, цель состоит не в том, чтобы избавиться от необходимых рассуждений, а в том, чтобы дать учащимся другой способ увидеть, о чем их просят подумать и объяснить.

Теорема Пифагора

Еще одна важная идея, дебютировавшая в геометрии для 8-го класса, — теорема Пифагора. Стандарты, связанные с теоремой Пифагора, также являются частью основной работы класса. Учитывая уравнения, с которыми учащиеся столкнутся при решении задач с теоремой Пифагора, например, c2 = 25 и a2 = 17, может иметь смысл преподавать эти стандарты после того, как учащиеся освоятся с квадратными и кубическими корнями (8.EE.A.2) и работать с иррациональными числами. (8.NS.A.1) (Подробнее о взаимосвязи между стандартами см. в Части 2 данного руководства.) Независимо от того, какую последовательность вы выберете для обучения, важно понимать, что ряд стандартов средней школы зависит от знания теоремы Пифагора, поэтому учащиеся обязательно должны получить это содержание в 8 классе.

Стандарты, связанные с теоремой Пифагора, сгруппированы в другую группу (называемую 8.GB, так как это вторая группа стандартов по геометрии в 8 классе).Давайте посмотрим, что они говорят.

8.GB | Поймите и примените теорему Пифагора.

Опять же, порядок стандартов не указывает порядок, в котором они должны преподаваться. Но в этом случае имеет смысл начать с доказательства теоремы Пифагора (8.G.B.6), а затем перейти к решению разного рода задач (8.G.B.7 и 8.G.B.8).

Прежде чем мы начнем говорить о стандартах в этом кластере, давайте выдвинем на первый план две важные идеи.

Теорема Пифагора гласит: если треугольник прямоугольный, длины катетов равны a и b, а длина гипотенузы равна c, то a2 + b2 = c2.
Обратное утверждение теоремы Пифагора также верно: если треугольник имеет длины сторон a, b и c и a2 + b2 = c2, то этот треугольник прямоугольный.

В прошлом эта тема часто вводилась студентам, давая им формулу (упомянутую выше: a2 + b2 = c2) и объясняя, что обозначают переменные. Затем обучение вращалось вокруг относительно простых задач, в которых учащимся давались длины двух сторон прямоугольного треугольника, и они должны были найти третью. Такое решение задач все еще имеет место, но Стандарты начинаются с того, что студентов просят объяснить доказательство теоремы Пифагора и ее обращение. (8.G.B.6) При этом они узнают две важные вещи:

Теорема Пифагора описывает отношения между сторонами прямоугольного треугольника (а не просто формулу). Когда учащиеся понимают природу взаимосвязи и могут выразить ее устно (а также в алгебраических терминах), они настроены на применение ее в более широком диапазоне ситуаций и расширение своего обучения в дальнейшем.
Обратная теорема Пифагора так же полезна, как и сама теорема. Студенты узнают, что они могут использовать теорему не только тогда, когда знают, что треугольник прямоугольный, но и тогда, когда им нужно установить, что треугольник является прямоугольным.

Итак, откуда взялась теорема Пифагора? На самом деле существует много разных доказательств, некоторые из них сложнее, чем другие. Эти разные доказательства основаны на разных методах и приводят разные причины истинности теоремы Пифагора.В этом уроке используется доказательство «квадрат в квадрате» с использованием площади, начинающееся так:

8 класс, модуль 2, урок 15: обсуждение

Первое доказательство теоремы Пифагора требует знания некоторых основных фактов о геометрии.

Конгруэнтные треугольники имеют равные площади.
Все соответствующие части конгруэнтных треугольников конгруэнтны.
Теорема суммы треугольника. (∠ сумма △)

В прямоугольных треугольниках сумма двух углов, не являющихся прямыми, равна 90°.(∠ сумма рт. △)

Далее мы рассмотрим то, что называется квадратом внутри квадрата. Внешний квадрат имеет длины сторон (a+b), а внутренний квадрат имеет длины сторон c. Наша цель — показать, что +=

Для достижения этой цели мы сравним общую площадь внешнего квадрата с частями, из которых он состоит, то есть с четырьмя треугольниками и меньшим внутренним квадратом.

СкрытьПоказать

Остальная часть доказательства, которую вы видите в плане урока, помогает учащимся понять, что внутренняя фигура на самом деле является квадратом, а затем использует вычисление площади для вывода формулы. Если вы собираетесь использовать этот план урока, подумайте о степени поддержки, которую вы хотите оказать — возможно, учащиеся смогут сами пройти часть проверки и закончить под вашим руководством, или, может быть, им нужно больше структурированности.(Одно предупреждение: алгебра, используемая в этом последнем вычислении, включает в себя умножение двух биномов, что не требуется до старшей школы. Возможно, вам придется помочь учащимся применить распределительное свойство новым способом.) В любом случае, они понимают. что теорема Пифагора включает в себя аспект площади, который полезен для интерпретации определенных типов прикладных задач.

Применение теоремы Пифагора для решения задач

Как только учащиеся понимают происхождение теоремы Пифагора, они приступают к решению задач.(8.G.B.7) Сначала учащиеся могут решать задачи только с целыми числами, чтобы сосредоточиться на интерпретации ситуации с точки зрения прямоугольного треугольника и проведении точных расчетов. (Вышеприведенный план урока включает несколько примеров таких задач начального уровня.) Это задание требует более подробной интерпретации.

Бег на футбольном поле

Во время игры плей-офф дивизиона 2005 года между «Денвер Бронкос» и «Нью-Инглэнд Пэтриотс» игрок «Бронко» Чемп Бэйли перехватил Тома Брэди у линии ворот (см. обведенную букву B).Он довел мяч почти до чужой линии ворот. Бен Уотсон из «Патриотов Новой Англии» (см. обведенную W) погнался за Чемпом и выследил его прямо перед другой линией ворот.

На изображении ниже каждая решетка равна одному ярду: также обратите внимание, что ширина поля составляет 53 ярда.

Как вы можете использовать диаграмму и теорему Пифагора, чтобы примерно определить, сколько ярдов пробежал Бен Уотсон, чтобы выследить Чэмпа Бейли?

Используйте теорему Пифагора, чтобы приблизительно определить, сколько ярдов пробежал Ватсон в этой пьесе.

Кто из игроков пробежал дальше во время этой игры? Примерно на сколько еще ярдов?

«Бег по футбольному полю» от Illustrative Mathematics под лицензией CC BY 4.0.

СкрытьПоказать

Учащимся может потребоваться прочитать задачу несколько раз, чтобы понять, что представляет собой каждая часть диаграммы. И, как вы можете видеть, некоторые оценки в порядке. Учитывая, что все поле имеет длину 100 ярдов и ширину 53 1/2 ярда, какова длина сторон этого почти треугольника? Как только учащиеся смогут увидеть прямоугольный треугольник и его размеры, эта проблема станет очень решаемой.

Нахождение расстояний на координатной плоскости

Студенты также должны использовать теорему Пифагора, чтобы найти расстояния в координатной плоскости. (8.G.B.8) На самом деле это специфический вариант проблем, которые мы только что обсуждали; студенты учатся интерпретировать две точки на координатной плоскости как определяющие гипотенузу прямоугольного треугольника. Эта проблема исходит из вводного урока по этой идее.

8 класс, модуль 7, урок 17: пример 1

Какое расстояние между двумя точками на координатной плоскости? Округлите ответ до десятых.

Прежде чем перейти к этой задаче, учащиеся сталкиваются с последовательностью вопросов, в которых они находят длины некоторых горизонтальных и вертикальных отрезков, понимая, что длина отрезка на координатной плоскости — это просто количество квадратов, которые он покрывает.Более того, они видят, что невозможно найти расстояние диагонального отрезка, считая квадраты. Затем эта конкретная проблема ставится как задача, и у учащихся есть время поработать над ней.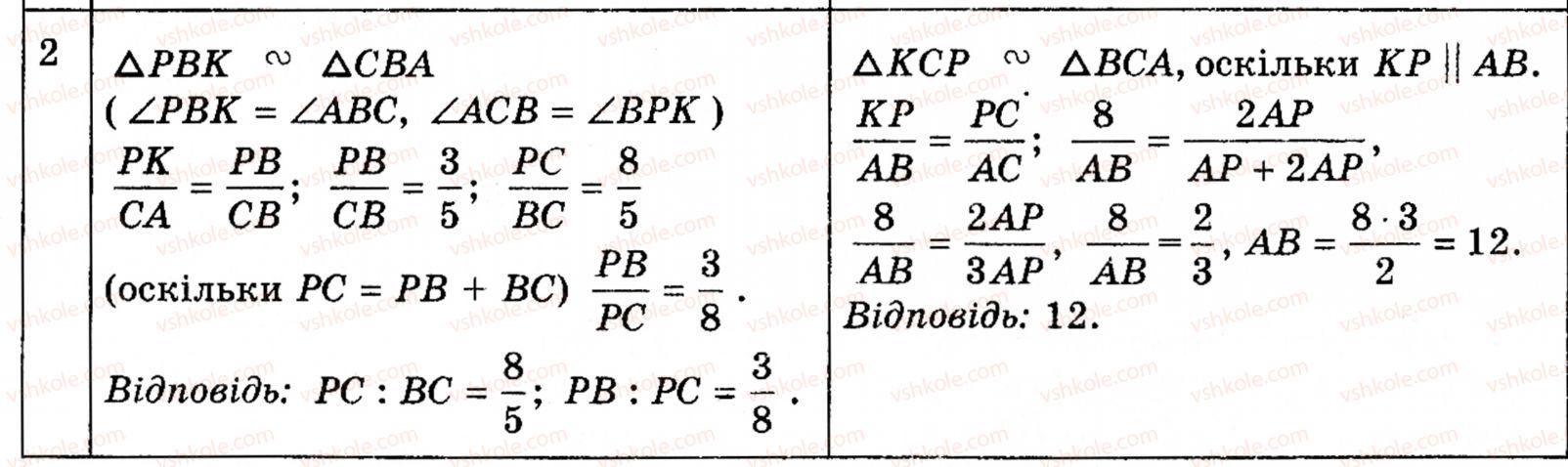 (Возможно, что в контексте раздела по теореме Пифагора некоторые учащиеся решат применить здесь свои новые знания. В идеале учащиеся должны быть в состоянии объяснить своим сверстникам, как построить прямоугольный треугольник из этих точек. и решить для рассматриваемой длины.)

После решения такой задачи учащиеся должны потренироваться в нахождении расстояния между точками в разных квадрантах координатной плоскости, а также расстояния между двумя точками, заданными упорядоченными парами и не нанесенными на плоскость.(Если вас интересует задание, которое может помочь им в этом, ознакомьтесь с разделом «Нахождение расстояния между точками» из «Иллюстративной математики». Комментарии и решения дают некоторые идеи о том, как учащиеся могут перейти от нахождения расстояния между двумя точками. конкретные, пронумерованные точки указывают на общий случай любых двух пар координат.)

Роль математических практик

Стандарты включают не только знания и навыки; они также признают необходимость того, чтобы учащиеся занимались некоторыми важными практиками математического мышления и общения. Эти «Математические практики» имеют свой собственный набор стандартов, которые содержат те же основные цели для классов K-12. ³ (Идея состоит в том, что учащиеся должны с годами развивать одни и те же привычки мышления все более изощренными способами.) на глубоком концептуальном понимании, необходимом в каждом классе. Другими словами, Практики помогают учащимся усвоить содержание.В таблице ниже приведены несколько примеров того, как математические практики могут помочь учащимся понять и применить геометрические понятия в 8 классе.

Подкаст-клип: Важность математических практик с Эндрю Ченом и Питером Коу (начало 30:33, конец 43:39)

Преобразования: связь с выражениями и уравнениями

Преобразования имеют решающее значение для понимания еще одной основной работы для 8 класса: наклона.⁴ Студенты впервые сталкиваются с наклоном на графиках пропорциональных отношений, понимая его как единичную скорость отношения. (Это понятие впервые было разработано в 7 классе.) Почему же наклон линии постоянен? Этот вопрос часто заметают под ковер. Один из способов понимания — применение подобия: каждая линия на координатной плоскости подразумевает любое количество подобных «треугольников наклона» с пропорциональными сторонами. (8.EE.B.6) Это задание показывает пример того, как учащиеся могут подойти к этой концепции.

Уклоны между точками на линии

Наклон между двумя точками вычисляется путем нахождения изменения значений y и деления на изменение значений x. Например, наклон между точками (7, -15) и (-8, 22) можно вычислить следующим образом:

Разница в значениях y составляет −15 − 22 = −37.
Разница в значениях x составляет 7 − (−8) = 15.
Разделив эти две разности, мы находим, что наклон равен −.

Ева, Карл и Мария вычисляют наклон между парами точек на линии, показанной ниже.

Ева находит наклон между точками (0,0) и (3,2). Карл находит наклон между точками (3,2) и (6,4). Мария находит наклон между точками (3,2) и (9,6). Каждый из них нарисовал треугольник, чтобы облегчить свои расчеты (показано ниже).

Какой треугольник нарисовал учащийся? Завершите расчет уклона для каждого ученика. Как можно геометрически интерпретировать различия в значениях x и y в нарисованных ими картинках?

Рассмотрим любые две точки (, ) и (, ) на линии, показанной выше.Нарисуйте треугольник, подобный треугольникам, нарисованным Евой, Карлом и Марией. Каков наклон между этими двумя точками? Почему этот наклон должен быть таким же, как наклоны, рассчитанные тремя студентами?

«Наклоны между точками на линии» от Illustrative Mathematics под лицензией CC BY 4.0.

СкрытьПоказать

Как указано в решении, треугольники в этом задании сконструированы таким образом, чтобы учащиеся могли легко определить их как похожие, используя серию жестких движений и расширений. Поскольку любой треугольник на прямой можно перевести в другой больший или меньший треугольник путем переноса и расширения, они должны быть подобны. Таким образом, учащиеся могут продемонстрировать, что наклон между любыми двумя точками на любой заданной линии будет одинаковым. (Это более дедуктивный и математически обоснованный способ понимания наклона линии, чем простое наблюдение за тем, что наклон между несколькими парами точек на одной конкретной линии одинаков.)

Теорема Пифагора: связь с выражениями и уравнениями и системой счисления

Теорема Пифагора тесно связана с работой в области системы счисления (NS) и выражений и уравнений (EE).Стандарты ЭЭ являются частью основной работы 8-го класса, в то время как стандарты NS обозначены как «вспомогательные» работы, поскольку они могут усилить и расширить основные темы.

В 8-м классе стандарты NS знакомят учащихся с иррациональными числами (числа типа √2, которые не могут быть выражены в виде дробей), (8. NS.A.1), а стандарты EE знакомят учащихся с простыми уравнениями, такими как x2 = 8 и y3 = 27, которые включают решение с квадратными и кубическими корнями. (8.EE.A.2) Поскольку применение теоремы Пифагора естественным образом приводит к уравнениям этого типа, решение задач в контексте прямоугольных треугольников представляет собой сходимость двух стандартов.Возьмем, к примеру, нашу задачу из стандарта 8.G.B.8 выше:

Когда учащиеся решают, они получают уравнение 22 + 62 = c2, и их решение выглядит примерно так:

22 + 62 = с2

4 + 36 = с2

40 = с2

√40 = с

На основе работы со стандартом 8.NS.A.1 учащийся 8-го класса должен уметь сказать, что √40 — это число от 6 до 7, потому что 40 — это число от 36 (62) до 49 (72). Отсюда они могут сделать вывод, что это меньше 6.5, потому что 40 ближе к 36, чем к 49, и используйте последовательные приближения, чтобы найти, что это примерно 6,3. Оглядываясь назад на задачу, которая включает расстояния в 2 единицы и 6 единиц для катетов, можно сказать, что это разумная длина для гипотенузы.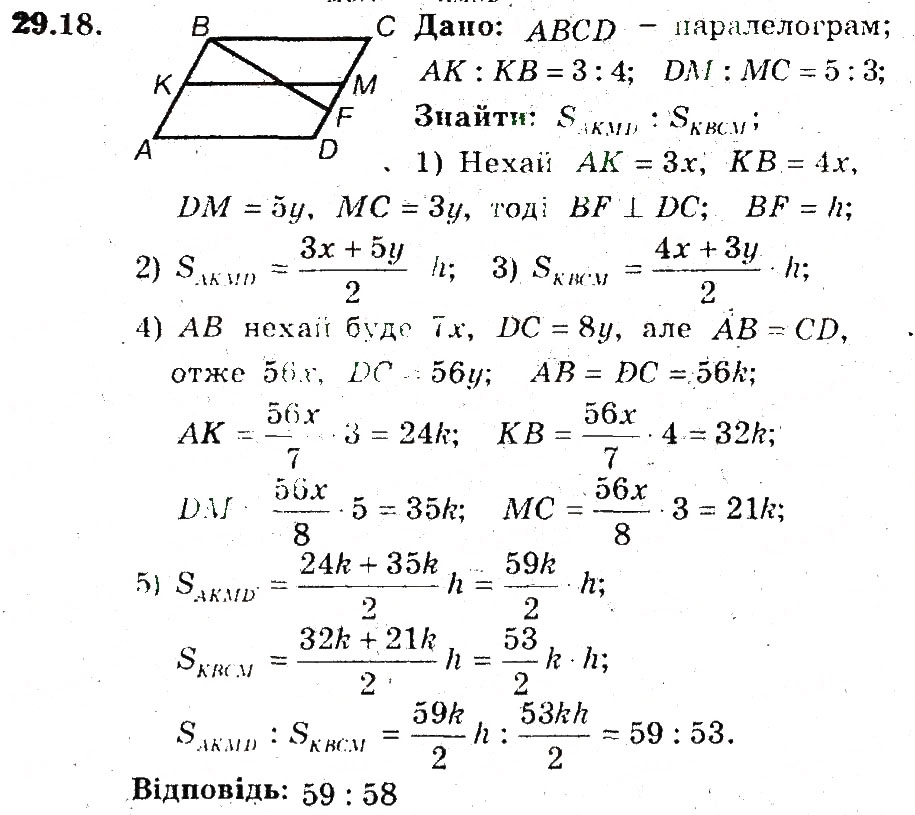

Откуда берутся сходство и сходство?

В то время как конгруэнтность и сходство начинаются в 8 классе, более фундаментальные понятия в геометрии должны развиваться в начальных и средних классах. Уже в детском саду они начинают думать о длине и классифицировать формы.(К.Г.А.2) 4 класс оказывается решающим для работы с конгруэнтностью и подобием: Определяется понятие меры угла, (4.МД.С.5) а также точки, прямые, отрезки и лучи. (4.G.A.1) В 5 классе учащиеся узнают о координатной плоскости и точках графика в первом квадранте. (5.G.A.1) Затем, в 6 классе, учащиеся расширяют свои знания о системе счисления, включая отрицательные числа, тем самым открывая всю координатную плоскость. (6.NS.C.8) Работа над координатной плоскостью продолжается в 7 классе, (7.RP.A.2), а учащиеся решают задачи на чертежи в масштабе. (7.G.A.1) Хотя эти задачи не требуют формального понимания подобия с точки зрения преобразований, они дают учащимся возможность работать с парами похожих фигур и масштабных коэффициентов.

Подкаст-клип: Важность согласованности с Эндрю Ченом и Питером Коу (начало 9:34, конец 26:19)

Откуда взялась теорема Пифагора?

Теорема Пифагора также является новой в 8 классе.Хотя это не требует длительного обучения, некоторые основные предпосылки все же применяются:

Учащиеся должны быть знакомы с экспоненциальной записью с 6 класса, чтобы понимать алгебраическую формулу. (6.EE.A.1)
Как отмечалось выше, учащимся необходим опыт решения уравнений 6, 7 и 8 классов, чтобы решать задачи с теоремой Пифагора. (6.EE.B.7, 7.EE.B.4, 8.EE.A.2)
Точно так же, как и преобразования, четкое понимание теоремы Пифагора опирается на такие элементарные понятия геометрии, как мера длины и угла.(4.G.A.1)

Предложения для учащихся, отстающих от

Если, приступая к разделу о конгруэнтности и сходстве, вы знаете, что ваши ученики не имеют четкого представления о названных выше идеях (или вообще не сталкивались с ними), что вы можете сделать? Нецелесообразно (и даже нежелательно) преподавать заново все, что ученики должны были выучить в 4–7 классах; в 8 классе есть много нового материала для изучения, поэтому основное внимание должно быть уделено стандартам для данного класса. В то же время существуют стратегические способы подведения итогов «незавершенного обучения» предыдущих оценок в рамках модуля конгруэнтности.Вот несколько идей для адаптации вашей инструкции, чтобы восполнить пробелы.

Если значительное число учащихся не полностью понимает углы или другие элементарные понятия, вы можете запланировать один или два урока, посвященных этим идеям, прежде чем приступить к преподаванию материалов для своего класса. (Здесь могут оказаться полезными два урока 4 класса, один по измерению углов, а другой по различению длины и меры угла.) Если вы считаете, что весь урок — это слишком много, вы можете запланировать краткий «мини-урок» или использовать некоторые задачи, связанные с этими идеями, в качестве разминки перед вашими первыми уроками конгруэнтности.
Если у значительного числа учащихся нет опыта работы с координатной плоскостью или они еще не умеют точно наносить точки, вы можете запланировать урок или серию разминок по этой идее перед началом работы с преобразованиями на координатной плоскости. (Этот урок для 6 класса по рисованию многоугольников на координатной плоскости может быть хорошим источником проблем для этого типа урока.)
Если значительное количество учащихся не умеет свободно идентифицировать и описывать геометрические фигуры (точки, прямые, отрезки и т.), вы можете запланировать мини-урок или серию разминок, чтобы повторить их в течение первых нескольких дней модуля, связанного с трансформациями. (Этот урок для 4 класса, который знакомит с только что упомянутыми терминами, содержит простое введение в эти идеи, и задачи, которые следуют за уроком, также могут быть полезны.)

Куда идут эти понятия?

Конгруэнтность и сходство долгое время были важными идеями в старшей школе, и, как объяснялось выше, преобразования теперь играют центральную роль в понимании этих идей.Один из первых опытов, которые учащиеся получат в средней школе по геометрии, — разработка точных определений твердотельных движений. (G-CO.A.4) Использование преобразований позволяет учащимся устанавливать критерии конгруэнтности треугольников (G-CO. B.8) и дает им инструмент для использования при доказательстве теорем. (G-CO.C) Как только учащиеся поймут конгруэнтность, они будут готовы решать задачи, связанные с конгруэнтными фигурами, (G.SRT.B.5) исследовать отношения внутри треугольников, (G-C.A.2) и доказывать утверждения, используя координаты. (Г-ГПЭ.Б.4) В дальнейшем они столкнутся с более специализированными приложениями конгруэнтности; Принцип Кавальери, например, зависит от знания того, что означает конгруэнтность поперечных сечений двух разных фигур. (G-GMD.A.1) Сходство включает в себя аналогичный процесс и ведет к изучению тригонометрии. G-SRT.C.9 Последняя последовательность показывает, как работа в 8-м классе ведет в старшую школу.

Если вы только что закончили это руководство, поздравляем! Надеюсь, это было информативно, и вы можете вернуться к нему в качестве справочного материала при планировании уроков, создании модулей или оценке учебных материалов.Для получения дополнительных руководств из этой серии посетите нашу страницу Enhance Instruction. Чтобы узнать больше о том, как вы можете использовать эти руководства в своей повседневной практике, посетите нашу страницу часто задаваемых вопросов. И если вы хотите узнать больше о конгруэнтности, сходстве и теореме Пифагора в 8 классе, не забудьте эти ресурсы:

Партнеры по успеваемости учащихся: фокус в 8 классе

Хунг-Хси Ву: Преподавание геометрии в соответствии с общими базовыми стандартами

EngageNY: 8 класс, материалы модуля 2 (конгруэнтность)

EngageNY: класс 8, модуль 3, материалы (сходство)

EngageNY: 8 класс, материалы модуля 7 (теорема Пифагора)

Иллюстративные задачи по математике 8 класс

1.Что такое руководство по содержанию?

В нашей работе с высокими академическими стандартами мы часто слышим, как преподаватели спрашивают: «Как выглядит обучение в соответствии со стандартами?» Наши руководства по содержанию призваны ответить на этот вопрос, подробно рассматривая одну или несколько групп математических стандартов одновременно. Справочники по содержанию предназначены для каждого класса и предметной области, и есть руководства для каждого класса или курса, от детского сада до алгебры II. Если вы хотите узнать больше о преподавании пропорций и пропорциональных отношений в 6 классе, например, наше связанное Руководство по содержанию даст вам исчерпывающее, но доступное объяснение этих стандартов, несколько примеров открытых образовательных ресурсов (ООР), которые соответствуют стандартам, и конкретные предложения по поддержке преподавания пропорций и пропорциональных рассуждений в 6 классе.

Наша цель при создании Руководства по содержанию заключалась в том, чтобы предоставить занятым учителям практичный и удобный для чтения ресурс о том, что говорят стандарты математики на уровне класса, а также примеры учебных материалов, которые поддерживают концептуальное понимание, решение задач, и процедурные навыки и беглость для студентов.

Важно отметить, что руководства по содержанию не предназначены для использования в качестве учебной программы (или любого другого документа для учащихся), руководства или исходного материала для подготовки к экзаменам или какого-либо инструмента оценки учителей.

2. Что содержится в руководстве по содержанию?

Каждое руководство по содержанию ориентировано на определенную группу стандартов. Большинство руководств по содержанию имеют одну и ту же структуру, состоящую из трех частей:

Часть 1 разъясняет навыки и понимание учащихся, описываемые этой группой стандартов. Этот раздел иллюстрирует стандарты с использованием нескольких студенческих заданий из свободно доступных онлайн-источников. Учителя могут использовать или адаптировать эти задания для своих учеников.
Часть 2 объясняет, как эта группа стандартов связана с другими стандартами того же класса.Мы подчеркиваем, как эти связи влияют на планирование и преподавание, и как эта согласованность внутри класса может расширить доступ для учащихся. Часть 2 также включает несколько студенческих заданий из свободно доступных онлайн-источников.
Часть 3 отслеживает отдельные этапы обучения, ведущие к содержимому на уровне класса, описанному в конкретном Руководстве по содержанию. 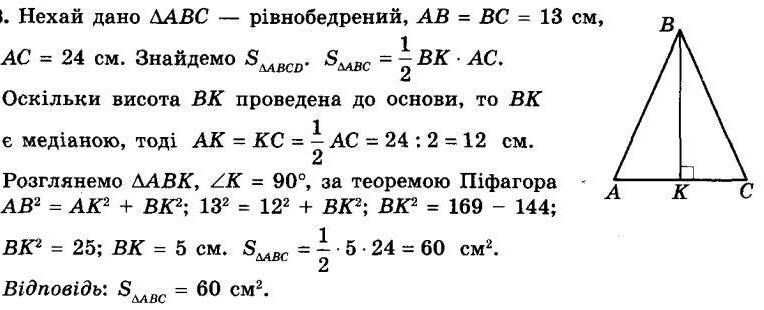Это обсуждение переходит в серию конкретных и практических предложений о том, как учителя могут использовать прогрессии для обучения учащихся, которые могут быть не готовы к математике на уровне класса.Наконец, в части 3 прослеживается переход к содержанию в более высоких классах.

3. Как я могу использовать Руководства по содержанию?

Учителя, прочитавшие наши Руководства по содержанию, говорят, что видят преимущества для всех преподавателей. Вот несколько советов о том, как их могут использовать разные педагоги.

Учителя могут использовать справочники по математике по адресу:

Повысить или освежить свои знания о стандартах и требованиях к тому, что учащиеся должны знать к концу года.
Адаптируйте уроки и модули, используя соответствующие предварительные условия, чтобы помочь учащимся, отстающим в классе.
Получите доступ к лучшим доступным ООР по математике, чтобы использовать их для введения и/или закрепления понятий
Убедитесь, что их учебный план и/или разделы:
- Сосредоточьтесь на основной работе класса и соответствующей глубине каждого стандарта.
- Нацельтесь на соответствующие аспекты строгости — процедурные навыки и беглость, моделирование и применение, а также концептуальное понимание, описанное в стандартах.
- Помогите учащимся установить согласованные связи внутри и между классами.
Создайте или пересмотрите свои уроки и вопросы, чтобы сосредоточиться на важных понятиях в стандартах.

Преподаватели и руководители школ могут использовать руководства по математике по адресу:

Обновить или расширить свои знания о стандартах и требованиях к тому, что учащиеся должны знать к концу года.
Разрабатывайте и сообщайте о последовательных ожиданиях в отношении планирования уроков и обучения в соответствии со стандартами.
Дайте ссылку при планировании и/или обсуждении инструкций с учителями.
Получите представление о том, как должны выглядеть инструкции и работа учащихся, чтобы соответствовать требованиям стандартов.
Разработка и разработка контента и сессий/семинаров по повышению квалификации на основе стандартов.
Поощряйте содержательные, основанные на стандартах обсуждения среди сотрудников и расширяйте их знания.
Разработать и/или пересмотреть планы улучшения школы, чтобы поддержать и включить содержание и основанное на практике преподавание и обучение.

4. Зачем нужны руководства по содержанию?

Переход на более высокие стандарты привел к тому, что учителя по всей стране внесли значительные изменения в свое планирование и обучение, но только одна треть учителей считает, что они готовы помочь своим ученикам пройти более строгие оценки, соответствующие стандартам (Kane et. др., 2016). Этого следовало ожидать, поскольку новые высокие стандарты представляют собой значительный отход от ранее существовавших стандартов. Стандарты требуют более глубокого понимания математического содержания, которое они преподают; различная последовательность того, что учащиеся должны усвоить, к какому классу; а также другая педагогика, которая делает упор на концептуальное понимание учащихся, решение проблем и беглость процедур с одинаковой интенсивностью.

Однако поддержка учителей в обеспечении высоких стандартов в их классах отстает. Исследования показывают, что подготовка учителей в США в настоящее время недостаточна для подготовки учителей к преподаванию требовательных новых стандартов (Центр исследований в области математики и научного образования, 2010 г.). И хотя существуют некоторые ресурсы, которые «распаковывают» стандарты, мало, если таковые вообще имеются, объясняют , а иллюстрируют стандарты. «Распаковка» стандартов один за другим также может привести к бессвязному представлению, пренебрегающему структурой и последовательностью стандартов.Создавая Руководства по содержанию, мы стремились предоставить занятым учителям практичный, легкий для чтения ресурс о стандартах для их классов и о том, как помочь всем учащимся изучить их. Существует множество эмпирических данных о том, что, когда учителя обладают как хорошими знаниями математического содержания, которое они преподают, так и педагогическими знаниями, помогающими учащимся освоить эти содержательные знания, их ученики узнают больше (Baumert et. al., 2010; Hill, Rowan and Ball). , 2005; Rockoff и др., 2008). Мы надеемся, что, имея в руках Руководства по содержанию, учителя добьются большего успеха, помогая своим ученикам продвигаться к подготовке к колледжу и карьере.

5. Какая связь между руководствами по содержанию и последовательностями?

Документы Progressions описывают развитие понимания математики от класса к классу. Они были основаны на исследованиях когнитивного развития детей, а также на логической структуре математики. Прогрессии объясняют, почему стандарты расположены именно так. Руководства по содержанию часто выделяют ключевые идеи из прогрессий, но не добавляют новых стандартов и не меняют ожиданий в отношении того, что учащиеся должны знать и уметь; они стремятся объяснить и проиллюстрировать группу стандартов одновременно, используя свободно доступные онлайн-источники.Хотя задания и уроки ООР в Руководствах по содержанию являются одним из способов соответствовать стандартам для каждого класса, они не являются единственными средствами для этого.

6. Как отбирались ресурсы?

Для иллюстрации Стандартов мы выбрали примеры заданий и уроков из свободно доступных онлайн-источников, таких как EngageNY, Illustrative Mathematics и Student Achievement Partners. Эти источники выбраны потому, что они полностью соответствуют новым высоким стандартам на основе национального обзора учебных программ K-12 или созданы организациями, возглавляемыми авторами новых высоких стандартов.Кроме того, поскольку они являются открытыми образовательными ресурсами (ООР), они свободно доступны для всех видов использования. Все материалы UnboundEd также являются ООР, что является частью нашего стремления сделать высококачественный и согласованный контент доступным для всех преподавателей.

7. Почему Руководства по содержанию касаются лишь нескольких стандартов? Где остальные стандарты?

Каждое руководство по содержанию относится к подмножеству стандартов для оценки. Стандарты, рассматриваемые в первом наборе руководств по содержанию для каждого класса, обычно относятся к высокоприоритетному содержимому; эти стандарты также часто являются хорошим выбором для обучения в начале года. Дополнительную информацию о выборе стандартов можно найти во введении к каждому Руководству по содержанию. Со временем мы разработаем дополнительные Руководства по содержанию для каждого класса и обновим существующие. Мы планируем иметь четыре руководства по содержанию для каждого класса или курса, от детского сада до алгебры II. Руководства будут публиковаться волнами, каждая волна будет состоять из одного руководства для каждого класса. Мы планируем выпустить второй набор руководств по содержанию для каждого класса к концу 2016-17 учебного года.

8.Как я могу быть в курсе новых руководств по содержанию?

Если вы хотите получать обновления контента и событий от UnboundEd, включая новые руководства по контенту, подпишитесь на объявления UnboundEd здесь.

Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для создания геометрии.

Поймите и примените теорему Пифагора.

Экспериментально проверьте свойства поворотов, отражений и переводов:

Линии превращаются в прямые, а отрезки прямых в отрезки прямой одинаковой длины.Углы принимаются равными углам.

Параллельные прямые переводятся в параллельные прямые.

Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников.

Экспериментально проверьте свойства поворотов, отражений и переводов:

Поймите, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность. Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.

Опишите эффект расширения, перевода, поворота и отражения на двухмерных фигурах, используя координаты.Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников.

Экспериментально проверьте свойства поворотов, отражений и переводов:

Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.Опишите эффект расширения, перевода, поворота и отражения на двухмерных фигурах, используя координаты.

Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников. Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что √2 иррационально.

Знайте, что числа, которые не являются рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.Поймите и примените теорему Пифагора.

Поймите и примените теорему Пифагора.

Объясните доказательство теоремы Пифагора и ее обращения.

Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальном мире и математических задач в двух и трех измерениях. Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.

Объясните доказательство теоремы Пифагора и ее обращения.

Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальном мире и математических задач в двух и трех измерениях.

Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.Объясните доказательство теоремы Пифагора и ее обращения.

Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.

Придумывайте жизнеспособные аргументы и критикуйте рассуждения других. Ищите и используйте структуру.

Рассуждайте абстрактно и количественно.

Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для прямой, проходящей через начало координат, и уравнение y = mx + b для прямой, пересекающей вертикальную ось в точке b.Знайте, что числа, которые не являются рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.

Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что √2 иррационально.

Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.

Знайте, что числа, которые не являются рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.Правильно называйте фигуры независимо от их ориентации или общего размера.

Распознавать углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимать принципы измерения углов:

Рисовать точки, прямые, отрезки, лучи, углы (прямые, острые, тупые), перпендикулярные и параллельные прямые.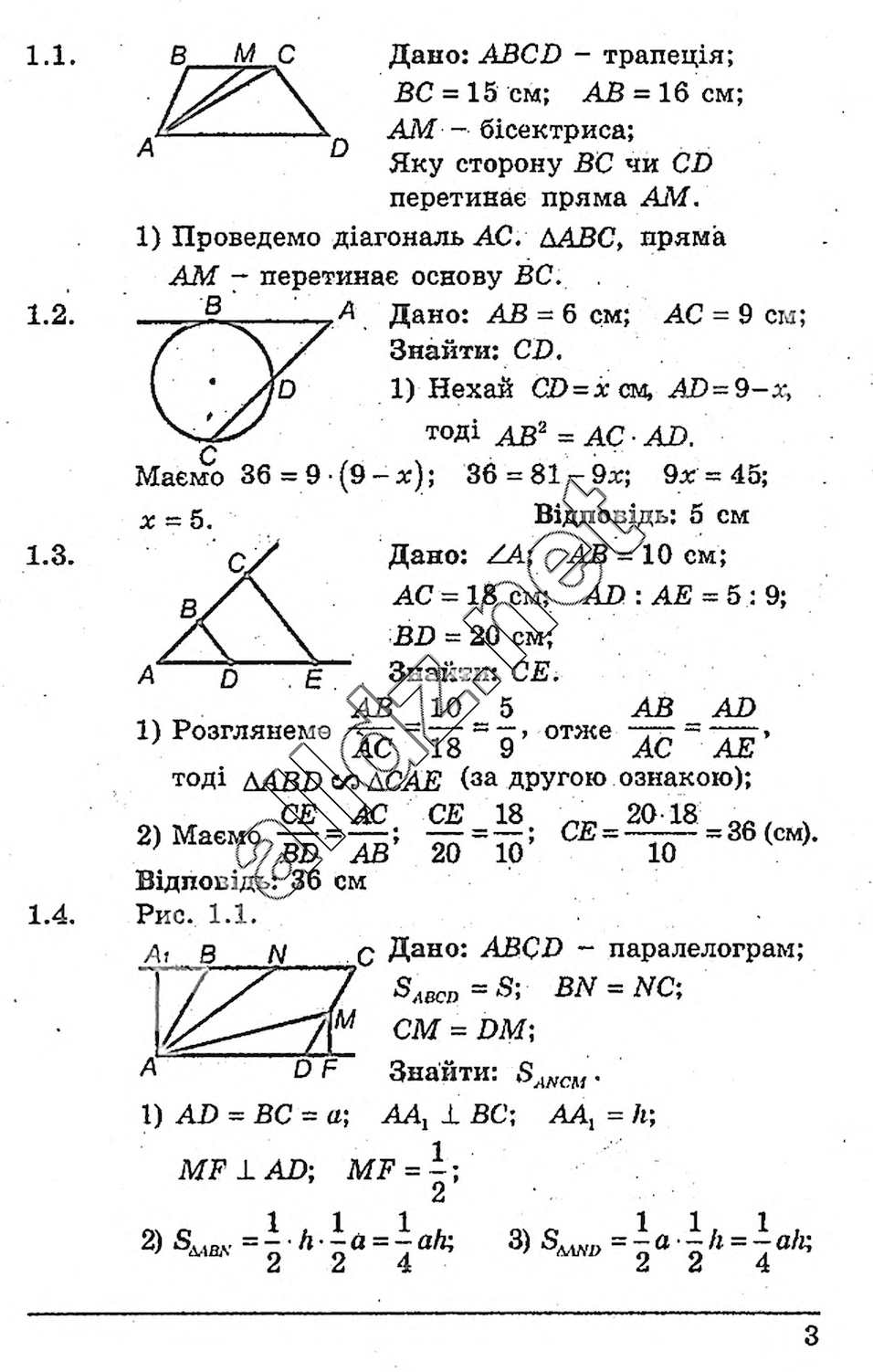 Определите их на двумерных фигурах.Используйте пару перпендикулярных числовых линий, называемых осями, для определения системы координат, где пересечение линий (начало координат) расположено так, чтобы совпадать с 0 на каждой линии, и заданной точкой на плоскости, расположенной с помощью упорядоченной пары координат. числа, называемые его координатами. Поймите, что первое число указывает, как далеко нужно пройти от начала координат в направлении одной оси, а второе число указывает, как далеко нужно пройти в направлении второй оси, при условии, что имена двух осей и координаты соответствовать (т.г., ось x и координата x, ось y и координата y).

Решайте реальные и математические задачи, отображая точки во всех четырех квадрантах координатной плоскости. Включите использование координат и абсолютного значения для нахождения расстояний между точками с одной и той же первой координатой или одной и той же второй координатой.

Распознавать и представлять пропорциональные отношения между величинами.

Решайте задачи, связанные с чертежами геометрических фигур в масштабе, включая вычисление фактических длин и площадей на основе чертежа в масштабе и воспроизведение чертежа в масштабе в другом масштабе.Напишите и оцените числовые выражения, включающие целые числа.

Решайте реальные и математические задачи, записывая и решая уравнения вида x + p = q и px = q для случаев, когда p, q и x являются неотрицательными рациональными числами.

Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах.Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что √2 иррационально.

Рисовать точки, прямые, отрезки, лучи, углы (прямые, острые, тупые), перпендикулярные и параллельные прямые. Определите их на двумерных фигурах.Разработайте определения поворотов, отражений и перемещений с точки зрения углов, окружностей, перпендикулярных линий, параллельных линий и отрезков.

Объясните, как критерии конгруэнтности треугольников (ASA, SAS и SSS) следуют из определения конгруэнтности в терминах жестких движений.

Докажите геометрические теоремы

Используйте критерии конгруэнтности и подобия для треугольников, чтобы решать задачи и доказывать отношения в геометрических фигурах.Определите и опишите отношения между вписанными углами, радиусами и хордами.

Используйте координаты для алгебраического доказательства простых геометрических теорем.

Приведите неформальные аргументы в пользу формул длины окружности, площади круга, объема цилиндра, пирамиды и конуса.

Math Beasts Camp 8-9 (Подготовка к геометрии)

Летняя математика

Летняя программа Math Beasts Camp 8-9 предназначена для учащихся, которые только что закончили курс по алгебре 1.
или эквивалентный урок математики, включая нашу алгебру 1 академический
Годовые курсы.(Студенты не обязаны проходить курсы академического года Академии AoPS перед зачислением.
в летних программах Академии AoPS.) Мы ожидаем, что большинство учащихся Math Beasts Camp 8-9 будут поступать на 8-е или
9-й класс, вместе с некоторыми продвинутыми в математике младшими учениками.

Каждый день Math Beasts Camp 8-9 состоит из компонента решения задач и математического исследования.
компонент. Решение проблем держит студентов в курсе конкретных тем, готовя их к предстоящему
учебный год.Каждое занятие мы начинаем с краткого обзора ключевой темы, с которой учащиеся должны были столкнуться.
в предыдущем учебном году. За этим обзором следует ряд интригующих задач, которые побуждают студентов
понимание темы далеко за пределами стандартного уровня класса. Мы заканчиваем решение каждой проблемы
обсуждение со сложной деятельностью, в которой учащиеся сотрудничают в командах.

Наши математические исследования предназначены для ознакомления с темами, с которыми большинство учащихся не сталкиваются до тех пор, пока не
намного позже в их школьном обучении, и вооружить студентов общими математическими стратегиями, которые будут
полезны на протяжении всего обучения.

Этот двухнедельный курс проводится с понедельника по пятницу по три часа каждый день.

Места для наших летних программ очень ограничены. Пожалуйста, не ждите до последней минуты, чтобы зарегистрироваться.
Если до начала курса осталось более двух недель, при регистрации необходимо внести депозит в размере 200 долларов США, а остаток
за две недели до начала курса.

Сроки летней регистрации:
Запись на летние языковые дисциплины для каждого класса закрывается за неделю до даты начала занятий, чтобы было время подобрать материалы для чтения курса. Запись на Летнюю математику для каждого класса закрывается за день до начала занятий.

Расписание
в 2022 году

На данный момент занятия не запланированы.

Нажмите здесь, чтобы присоединиться к нашему списку рассылки, чтобы получать уведомления о появлении расписания курсов.

Research Sampler 8: Проблемы учащихся с доказательством

Кит Вебер

Что такое доказательство и какова его роль в математике?
Какие трудности возникают у учащихся с доказательствами?
Как можно эффективно преподавать концепцию доказательства?
Каталожные номера

Доказательство — общеизвестно сложная математическая концепция для студентов.Эмпирические исследования показали, что многие студенты выходят из курсов, ориентированных на доказательство, таких как геометрия в средней школе [Senk, 1985], введение в доказательство [Moore, 1994], реальный анализ [Bills and Tall, 1998] и абстрактная алгебра [Weber, 2001]. ] не в состоянии построить ничего, кроме очень тривиальных доказательств.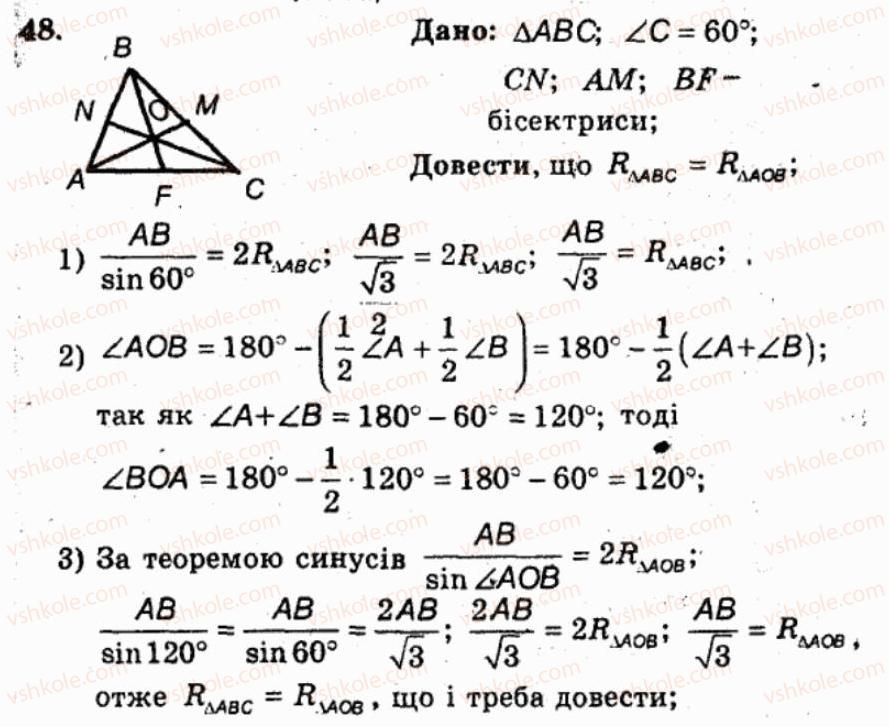 Кроме того, большинство студентов университетов не знают, что представляет собой доказательство [Recio and Godino, 2001], и не могут определить, действительно ли предполагаемое доказательство [Selden and Selden, 2003].

Что такое доказательство и какова его роль в математике?

Многие математики и учителя математики сочли бы ответы на этот вопрос простыми.Традиционная точка зрения состоит в том, что «математическое доказательство — это формальная и логическая линия рассуждений, которая начинается с набора аксиом и проходит через логические этапы к заключению» [Griffiths, 2000, p. 2]. И цель доказательства теоремы состоит в том, чтобы установить ее математическую достоверность. «Доказательство подтверждает истину для математика так же, как эксперимент или наблюдение для естествоиспытателя»? [Гриффитс, 2000, с. 2]. Таких взглядов обычно придерживаются учителя математики, и они передаются нашим ученикам.Однако многие преподаватели математики и некоторые математики считают, что доказательства — это нечто большее.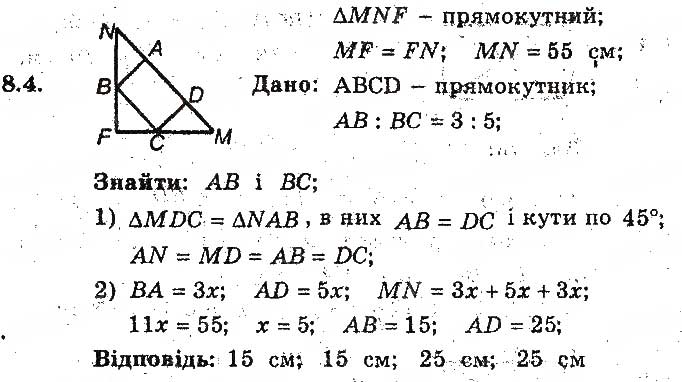

Медалист Филдса Уильям Терстон [1994] утверждает, что важно различать формальные доказательства и доказательства, которые математики фактически строят. В последнем случае подавляются многие рутинные вычисления и логические манипуляции. Такие упущения не из-за небрежности; скорее это делается потому, что доказательства были бы невероятно длинными, если бы в них были включены все логические детали.Ренц [1981] подсчитал, что если продолжить доказательство теоремы Пифагора, используя только аксиомы и правила вывода, разрешенные в Элементах Евклида, то доказательство займет более 80 страниц!

Дэвис и Херш [1981] утверждают, что, вероятно, невозможно точно определить, какой тип аргумента будет принят математическим сообществом в качестве действительного доказательства. Конечно, есть некоторые аспекты доказательства, которые отличают его от других типов аргументов. Например, доказательства концепции должны использовать определение концепции и должны проводиться дедуктивно, в отличие от изучения прототипических случаев или предоставления интуитивного аргумента. И если результат включен в доказательство, этот результат должен быть принят математическим сообществом [Tall, 1989]. Помимо этого, некоторые преподаватели математики утверждают, что принятие аргумента в качестве доказательства зависит не только от его логической структуры, но и от того, насколько убедителен аргумент [Hanna, 1991].

В различных местах литературы по математическому образованию доказательство определяется как аргумент, который убеждает противника [Mason, Burton, and Stacey, 1982], аргумент, который убеждает математика, знающего предмет [Davis and Hersh, 1981]. , или аргумент, достаточный, чтобы убедить разумного скептика [Вольминк, 1990].Другие, которые сосредотачиваются на социальной и контекстуальной природе доказательства, предлагают следующие релятивистские описания: «Мы называем доказательством объяснение, принятое данным сообществом в данное время»? [Балачев, 1987, перевод с французского]. «Аргумент становится доказательством после социального акта принятия его в качестве доказательства» [Манин, 1977]. Многие преподаватели математики считают, что сосредоточение внимания исключительно на логической природе доказательства может нанести вред развитию учащихся. Такой узкий взгляд заставляет студентов сосредотачиваться на логических манипуляциях, а не на формировании и понимании убедительных объяснений того, почему утверждение верно [Alibert and Thomas, 1991].

Преподаватели математики и математики считают, что установление достоверности утверждения является лишь одной из многих причин построения или представления доказательства. Помимо убеждения, преподаватели математики предложили ряд альтернативных целей доказательства. Например,

Объяснение. Изучив доказательство, читатель может понять, почему определенное утверждение верно. Многие преподаватели математики утверждают, что объяснение должно быть основной целью доказательства на уроке математики [например.г., Ханна, 1990; Херш, 1993].
Систематизация. Можно использовать доказательства, чтобы объединить ранее разрозненные результаты в единое целое. Организовав систему дедуктивно, можно также обнаружить аргументы, которые могут быть ошибочными, круговыми или неполными [de Villiers, 1990].
Связь. Язык доказательства можно использовать для общения и обсуждения идей с другими студентами и математиками [например, de Villiers, 1990; Кнут, 2002].
Открытие новых результатов. Исследуя логические следствия определений и аксиоматической системы, можно разработать новые модели или теории [de Villiers, 1990].
Обоснование определения. Можно показать, что определение адекватно схватывает интуитивную сущность понятия, доказав, что все существенные свойства понятия могут быть получены из предложенного определения [Weber, 2002a].
Развитие интуиции. Изучая логические следствия определения понятия, иногда можно развить концептуальное и интуитивное понимание изучаемого понятия [Pinto and Tall, 1999].
Обеспечение автономности. Обучение студентов тому, как доказывать, может позволить им самостоятельно создавать и проверять новые математические знания [Yackel and Cobb, 1996].

Студенты, считающие, что доказательства используются исключительно для установления достоверности математических утверждений, находят доказательства кажущихся очевидными результатов (например, 1+1 = 2 с использованием постулатов Пеано) педантичными [Harel, 1998; Вебер, 2002а]. С другой стороны, осознание различных способов использования доказательства может улучшить понимание учащимися роли доказательства в математике.

Какие трудности возникают у студентов с доказательствами?

Представления студентов о доказательствах

Рассмотрим следующее «доказательство», которое студент недавно представил на вводном курсе по доказательству, который я сейчас преподаю:
Покажите, что для каждого нечетного целого числа n , n ² — 1 делится на 8

1 ² — 1 = 0, которое делится на 8. 3 ² — 1 = 8, которое делится на 8.5 ² — 1 = 24, которое делится на 8.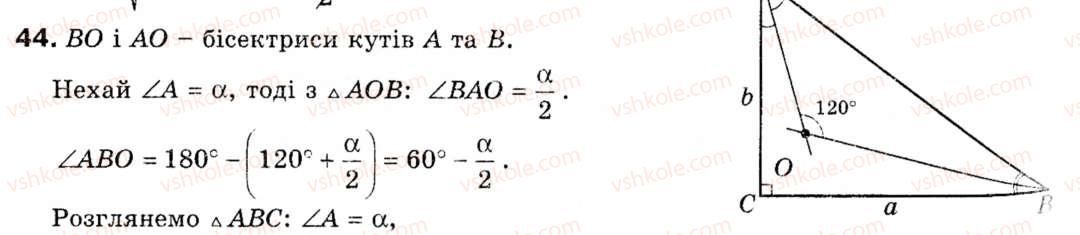 И так далее. Следовательно, если n нечетно, то n ² — 1 делится на 8.

Вариации этого «доказательства» на удивление распространены. Они иллюстрируют одну из самых распространенных трудностей студентов с концепцией доказательства: студенты часто считают, что недедуктивные аргументы составляют доказательство. Ниже приведены некоторые распространенные студенческие представления о том, что представляет собой математическое доказательство. Всеобъемлющая таксономия таких верований дана в Harel and Sowder [1998].

Ритуал. Аргумент является доказательством тогда и только тогда, когда он соответствует определенному математическому соглашению. Например, многие начинающие учителя считают, что аргумент по геометрии должен быть представлен в формате двух столбцов, чтобы быть доказательством [Martin and Harel, 1989].
Авторитетный. Аргумент является доказательством, если он представлен или одобрен признанным авторитетом, например учителем или известным математиком.
Индуктивный. Проверка того, что общее утверждение выполняется для одного или, возможно, нескольких примеров, достаточна для демонстрации его достоверности.Приведенное выше ошибочное доказательство является примером.
Восприятие. С помощью соответствующей диаграммы можно наглядно продемонстрировать выполнение определенного свойства [Harel and Sowder, 1998]. Например, чтобы доказать, что последовательность 1/ n сходится, некоторые учащиеся нарисуют диаграмму, показывающую, что по мере увеличения n члены 1/ n становятся сколь угодно близкими к нулю.

В последнее время исследования были сосредоточены на том, почему у студентов могут быть неверные представления о доказательствах.Recio и Godino [2001] отмечают, что многие из таких недействительных методов доказательства были бы уместны в нематематических областях. Например, в социальных науках вполне уместно делать общий вывод, исследуя множество конкретных случаев. Олкок и Симпсон [2002] отмечают, что рассуждения о понятии с использованием прототипического примера распространены в нашем повседневном опыте, но в сфере формальной математики необходимо рассуждать, используя определение понятия.

Недостаточное когнитивное развитие

Два голландских исследователя, Дина и Пьер ван Хиле, предложили учебный цикл (теперь известный как уровни ван Хиле), через который учащиеся могут продвигаться по мере изучения евклидовой геометрии:

Уровень 0: Визуализация. Учащиеся могут распознавать геометрическую фигуру как сущность (например, квадрат), но не могут распознавать свойства этой фигуры (например, прямой угол).

Уровень 1: Анализ. Учащиеся могут распознавать компоненты и свойства фигуры. Однако учащиеся не могут видеть отношения между свойствами и фигурами, а также не могут определить фигуру с точки зрения ее свойств. Например, учащиеся на этом этапе могут заметить, что все прямоугольники имеют четыре прямых угла, но они не поймут, что это означает, что квадрат является прямоугольником.

Уровень 2: Неформальная дедукция. Учащиеся могут распознавать взаимосвязь между фигурами и свойствами и могут неформально обосновывать эти взаимосвязи. Такие учащиеся могут признать, что квадрат является прямоугольником, поскольку он обладает всеми свойствами прямоугольника, но не смогут привести аргументы, начиная с незнакомых предпосылок. Например, такие студенты не могли построить тривиальные доказательства о незнакомых им объектах, даже если бы они знали, как определяется этот объект.

Уровень 3: Дедукция. Учащиеся могут рассуждать о геометрических объектах, используя их определенные свойства в дедуктивной схеме. Они могут использовать систему аксиом для построения доказательств. Учащиеся на этом этапе могут построить типы доказательств, которые можно найти в типичном курсе геометрии средней школы (например, у равнобедренных треугольников два конгруэнтных угла).

Уровень 4: Строгость. Учащиеся могут сравнивать различные системы аксиом. Геометрия рассматривается как абстрактное строгое поле.[См. Теппо, 1991].

Ван Хилес постулировал, что (а) учащиеся должны пройти через каждую из этих стадий, т. е. они не могут «пропустить» уровень, и (б) инструкции, предназначенные для учащихся более высокого уровня, не будут понятны учащимся более низкого уровня. . Senk [1989] нашел сильное эмпирическое подтверждение утверждения ван Хилеса. В крупномасштабном исследовании Сенк продемонстрировал, что, определив уровень Ван Хиле ученика в начале курса геометрии в средней школе, можно очень точно предсказать его способность к корректуре в конце курса.Сенк также обнаружил, что многие ученики поступают в старшие классы по геометрии с низким уровнем понимания Ван Хиле, и предположил, что это может быть причиной того, что геометрия вызывает у старшеклассников такие трудности [Senk 1985, 1989].

Отсутствие когнитивного развития также может помешать учащимся колледжа понять концепцию доказательства. Пиаже утверждает, что учащиеся не смогут различать или строить дедуктивные аргументы, пока не достигнут того, что он называет формальной операционной стадией когнитивного развития.Ausubel и его коллеги [1968] исследовали стадии когнитивного развития студентов колледжей и обнаружили, что только 22% студентов колледжей достигли стадии формального операционального развития. Эти открытия привели Талла [1991] и других к выводу, что многие студенты университетов могут (по крайней мере, вначале) не понимать дедуктивные доказательства.

Трудности с обозначениями

Многие доказательства, особенно в продвинутых курсах бакалавриата, требуют использования формальных обозначений.Студенты считают, что многие аспекты этой нотации, особенно использование нескольких квантификаторов, вызывают затруднения. Selden и Selden [1995] попросили 61 студента вводного курса по доказательству перевести неформальные математические утверждения на язык исчисления предикатов. Они обнаружили, что учащиеся успешно справились с этой задачей менее чем в 10% случаев. Например, ни один из 20 опрошенных студентов не смог выразить утверждение «Функция f возрастает на интервале I, что означает, что для любых чисел x ₁ и x ₂ в I , если x ₁ x _{9 , потом F ( x x в качестве логического предложения. Другое исследование показало, что извлечение смысла из квантифицированного логического утверждения является очень трудным и сложным процессом [например, Dubinsky, Eltermann, and Gong, 1988]. Рассуждения некоторых студентов о многократных количественных утверждениях включают только предикатную часть утверждения, игнорируя при этом то, как переменные определяются количественно [например, Пинто и Талл, 1999].}

Социально-математические нормы

Рассмотрим студента, который пишет доказательство и хочет использовать следующий факт: «Если f ( x ) = x (1 + x ), то f ² ( x ) ) = 2 х + 1.• Какого типа оправдания можно было бы ожидать от такого студента? Ответ: это зависит. Если бы студент был на традиционном вводном курсе исчисления, от него или нее можно было бы ожидать выполнения математических вычислений. В ориентированном на реформы курсе исчисления может быть достаточно численных приближений или проверки графика f . В курсе реального анализа бакалавриата, вероятно, потребуется аргумент, использующий определение производной. В аспирантуре этот факт будет считаться настолько очевидным, что объяснение будет излишним.

Якель и Кобб [1996] ввели термин социоматематических норм для обсуждения того, как влияния окружающей среды, такие как учебники учащихся, комментарии учителей и их отзывы о заданиях, определяют математические убеждения учащихся и последующее поведение. Дрейфус [1999] утверждает, что «Что считается приемлемым математическим обоснованием?» является одним из примеров социоматематической нормы. Как показано выше, в разное время академической карьеры студента требуются разные типы обоснования.Однако студенту редко объясняют, какой тип обоснования требуется. Часто случается так, что ученик получает смешанные сообщения. Например, многие учебники по математике предлагают интуитивное объяснение одного утверждения, пример для обоснования другого утверждения и строгое (формальное) доказательство другого утверждения, однако переход между интуитивным, эмпирическим и строгим мышлением четко не обозначен [Dreyfus, 1999]. Исследователи предполагают, что это может привести к тому, что у студентов возникнут нежелательные математические представления о строгости, объяснении и доказательстве, и может частично объяснить, почему студенты представляют неформальные аргументы в качестве доказательств на продвинутых курсах [например, .г., Дрейфус, 1999; Раман, 2002].

Плохое концептуальное понимание и неэффективные стратегии доказательства

Даже если учащиеся «логически способны» — то есть они знают, что представляет собой доказательство, и они могут рассуждать дедуктивно, цитировать и манипулировать определениями, а также делать обоснованные выводы — это не гарантирует, что они могут построить что-либо сверх тривиального. доказательства. Знание логических правил и определения понятия не гарантирует, что учащиеся смогут рассуждать об этом понятии.Студентам часто требуется интуитивное (концептуальное) понимание концепции, с которой они работают, прежде чем они смогут построить доказательства. Мур [Moore, 1994] внимательно наблюдал за пятью студентами, проходившими вводный курс доказательства. Он обнаружил, что иногда учащиеся могут давать определение понятия, плохо понимая его. Эти студенты не могли, например, описать понятие своими словами или привести ни одного примера этого понятия. Когда этих студентов попросили написать доказательства этой концепции, они не знали, с чего начать.

При написании доказательства можно сделать много правильных выводов. Ясно, что маловероятно построить доказательство, делая выводы случайным образом. Чтобы проиллюстрировать это, Ньюэлл и Саймон [1972] продемонстрировали, как автоматический доказатель теорем в ширину должен проверить более 10 ¹⁰⁰⁰ доказательств, чтобы доказать некоторые теоремы из классического текста Уайтхеда и Рассела по логике, Principia Mathematica [1935]. ]. Чтобы построить нетривиальные доказательства, студентам нужны стратегии и эвристики, которые помогут им решить, как они должны решать проблемы. В двух исследованиях Вебер [2001, 2002b] наблюдал за тем, как восемь студентов, прошедших курс абстрактной алгебры, строят нетривиальные доказательства гомоморфизмов и изоморфизмов групп. В исследованиях учитывались только те случаи, в которых студенты были осведомлены о фактах и теоремах, необходимых для доказательства утверждения, и могли построить доказательство, когда конкретно было указано, какие факты использовать. Даже в этих случаях студенты не смогли построить доказательство без подсказки в 68% случаев. Изучение поведения этих студентов показало, что их стратегии построения доказательств были неэффективными и грубыми.Например, чтобы доказать утверждение B, эти студенты часто пытались найти 90 648 любую 90 649 теорему вида «A подразумевает B» и пытались доказать A, даже если антецедент был неправдоподобен.

Как можно эффективно преподавать концепцию доказательства?

Модифицированный метод Мура

Модифицированный метод Мура (также называемый обучением в техасском стиле) представляет собой парадигму обучения, основанную на педагогических методах математика Р.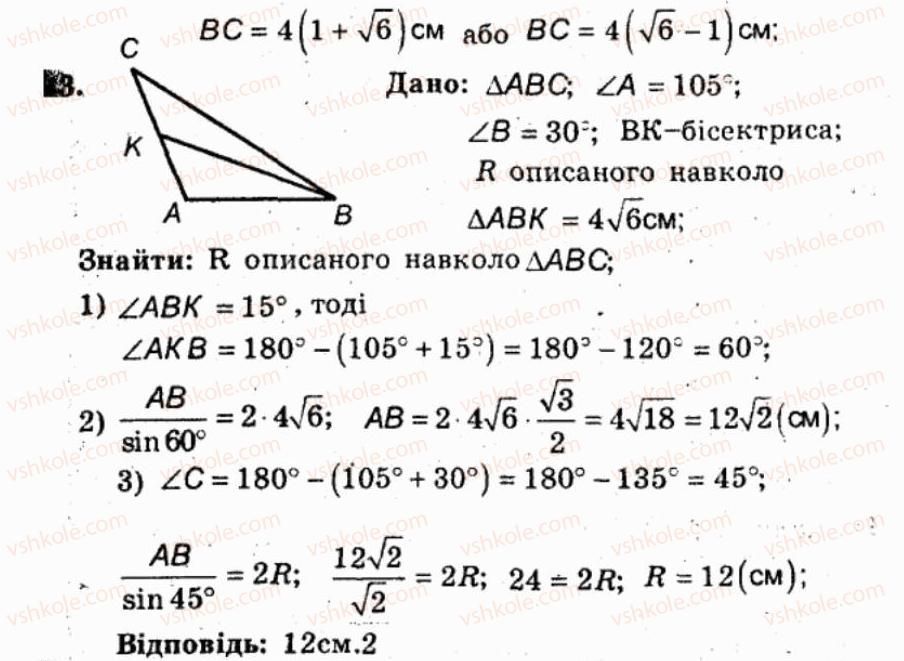 Л. Мура.Мур и сторонники этого метода считают, что студенты мало узнают о высшей математике, пассивно записывая доказательства, которые профессор представляет на доске, и узнают гораздо больше о математических концепциях и доказательствах, если попытаются построить доказательства самостоятельно. Ниже приводится краткое описание этого влиятельного метода обучения.

В типичном классе, использующем метод Мура, преподаватель представляет учащимся определения математических понятий и, возможно, несколько мотивирующих примеров этих понятий.После этого студентов просят доказать или опровергнуть ряд утверждений об этих понятиях. Когда учащийся считает, что он или она доказал утверждение, ему предлагается представить свои аргументы на доске. Преподаватель и сокурсники могут критиковать работу учащегося или просить учащегося разъяснить его или ее аргумент. Если все (включая учителя) убеждены доказательством, класс переходит к другому утверждению.

Если ни один из студентов не может успешно доказать теорему, преподаватель может попросить студентов доказать более простое предложение, отложить предложение на другой день или просто оставить предложение недоказанным. Преподаватель также может оказать помощь, но эта помощь должна быть минимальной, необходимой учащимся для построения доказательства. Что важно, так это то, что преподаватель никогда не предоставляет студентам фактическое доказательство предложения. Все доказательства генерируются самими студентами.

Для краткости некоторые важные вопросы (например, выставление оценок) здесь не обсуждаются. Более полное описание метода Мура дано в [Jones, 1977]. Недавняя статья, в которой обсуждается, как метод Мура можно использовать конкретно в математике бакалавриата, приводится Mahavier [1999].

Научные дебаты

Алиберт и его коллеги из Гренобльского университета во Франции отмечают, что многие специалисты по математике и будущие учителя математики в старших классах считают доказательство педантичным и оторванным от остальной математики [Alibert, 1988; Алиберт и Томас, 1991]. Они подозревают, что это связано с контекстом, в котором эти студенты сталкиваются с доказательствами. Они считают, что:

«Создавая среду, в которой учащиеся могут увидеть и испытать на собственном опыте то, что им необходимо, чтобы убедить других в истинности или ложности суждений, доказательство становится инструментом личной ценности, которым они будут с большим удовольствием пользоваться (или обучать) в будущем?» [Алиберт и Томас, 1991, с.230].

Они создают такую среду в новом курсе реального анализа с помощью «научных дебатов». Чтобы использовать этот метод, преподаватель сначала представляет студентам математическую ситуацию. Такая ситуация может быть:

Предположим, что f ( x ) является функцией с действительным знаком, которая интегрируема по действительным числам. Предположим, что

Затем учащимся предлагается высказать предположения, которые могут быть верными или неверными. Такое утверждение для описанной выше ситуации может быть таким: «Если f ( x ) увеличивается, то F ( x ) тоже увеличивается». (Конечно, это утверждение неверно). Студентов на этом этапе просят выдвинуть аргументы, чтобы убедить своих одноклассников в истинности или ложности гипотезы. Алиберт утверждает, что по ходу семестра студенты осознают необходимость точных определений, четких аргументов и строгих доказательств как средства принятия решения о том, верны ли предположения или нет. Таким образом, студенты начинают рассматривать доказательство как инструмент, используемый для разрешения научных споров. Алиберт обнаружил, что 75 % студентов, ответивших на анкету, предпочли метод научной дискуссии традиционному обучению, и только 10 % отвергли этот метод как недоступный или недостаточно организованный [Alibert, 1988].

Вводный пробный курс Марти

Марти [1986] считает, что недостатком вводных курсов по доказательству является то, что они сосредоточены на содержании (т. е. на значении доказываемых утверждений или самом доказательстве), а не на методах. Чтобы решить эту проблему, Марти создал вводный курс доказательства, в котором основное внимание уделялось методам доказательства, а важность математического содержания была сведена к минимуму.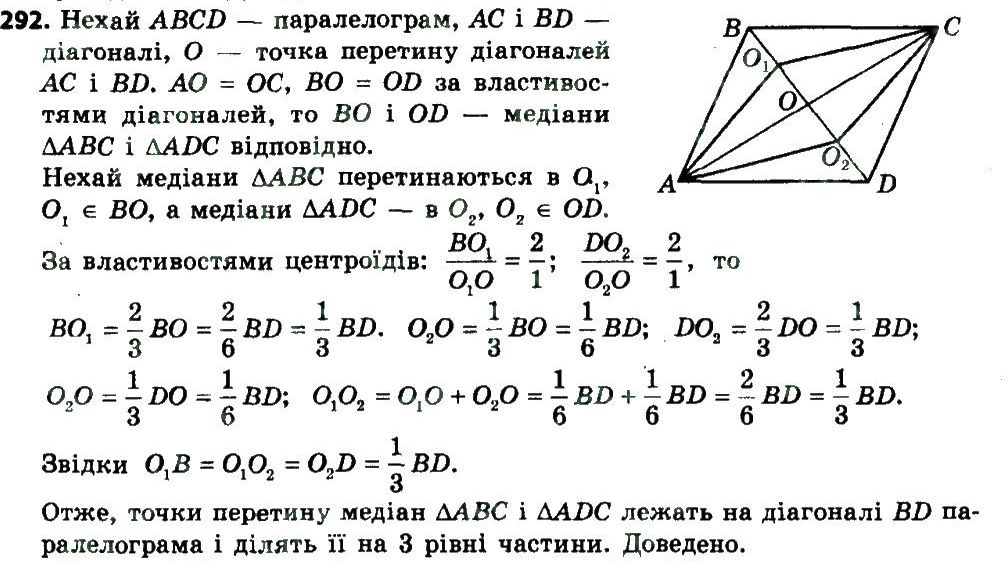 Ниже приведены принципы, которые Марти использовал в своем курсе:

Цель курса состояла в том, чтобы охватить набор методов доказательства (т.г., прямое доказательство, доказательство от противного). Каждый метод доказательства был сосредоточен на одном за раз и в мельчайших деталях.
Студенты столкнулись с каждым методом доказательства в различных математических условиях.
Мало внимания уделялось математическому содержанию. Содержание было раскрыто настолько глубоко, чтобы можно было представить и доказать значимые теоремы.
Студентов попросили применить методы доказательства в различных условиях и представить свои доказательства на доске.Задачи, которые студентов просили решить, были простыми и не требовали сообразительности или трюков.
Поощрялись альтернативные доказательства уже доказанного утверждения.

Чтобы эмпирически проиллюстрировать успешность своих методов, Марти изучил будущие математические успехи каждого студента, прошедшего в его университете вводный курс доказательства за десятилетний период. Марти сравнил студентов, прошедших его обучение, со студентами, которых обучали в традиционном лекционном формате.Он обнаружил, что студенты его класса в два-три раза чаще сдавали следующий курс реального анализа и в четыре раза чаще продолжали изучение высшей математики [Marty, 1990].

Доказательство в классе средней школы

Одна из причин, по которой студенты университетов считают доказательство столь трудным, заключается в том, что их опыт построения доказательств обычно ограничивается школьной геометрией [Moore, 1994]. Чтобы исправить это, в стандарте NCTM [2000] рекомендуется вводить доказательство в начале учебного плана по математике, утверждая, что «рассуждение и доказательство должны быть неотъемлемой частью математического опыта учащихся от дошкольного возраста до 12 класса» [стр. .56]. Кроме того, в стандартах NCTM и других [например, Schoenfeld, 1994] утверждается, что доказательство следует рассматривать не как отдельную математическую тему, а скорее как способ мышления, который можно применить к любой математической теме. Наконец, в стандартах NCTM утверждается, что к тому времени, когда учащиеся завершат 12 ^й класс, они должны признать доказательство фундаментальным элементом математики, уметь конструировать доказательства и уметь определять, является ли данный аргумент доказательством.

Учитывая трудности, с которыми сталкиваются математики с доказательствами, эти цели, безусловно, амбициозны. Чтобы оценить правдоподобие этих целей, Knuth [2002] взял интервью у 16 квалифицированных учителей старших классов средней школы, некоторые из которых имеют степень магистра, чтобы изучить их концепции математического доказательства. Его выводы заключались в том, что убеждения многих этих учителей о доказательствах были довольно наивными. Например, когда его спросили, может ли действительное доказательство когда-либо стать недействительным, шесть учителей ответили, что противоречащее доказательству утверждение сделает доказательство этого утверждения недействительным.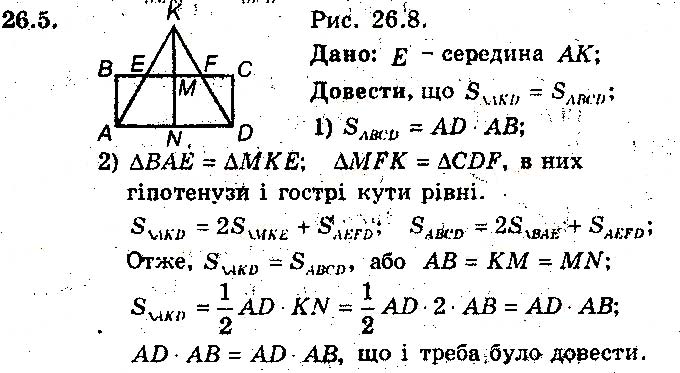 На вопрос о роли доказательства только трое учителей указали, что доказательства могут быть использованы для объяснения истинности утверждений, и ни один из них не ответил, что доказательства могут способствовать пониманию. Кнут пришел к выводу, что многие из этих учителей не смогут эффективно соответствовать стандартам NCTM .

Кнут и другие [например, Alibert and Thomas, 1991] предположили, что представления студентов и преподавателей о доказательствах, вероятно, формируются во время их курсов по математике в бакалавриате.Если кто-то хочет улучшить способности старшеклассников к доказательству, возможно, преподавателям математики и математикам лучше всего обратить внимание на курсы колледжей, ориентированные на доказательство, для будущих учителей математики.

Ссылки

Олкок, Л. и Симпсон, А. (2002). Определения: работа с категориями математически. Для изучения математики , 22(2), 28-34.
Алиберт, Д. (1988). К новым обычаям в классах. 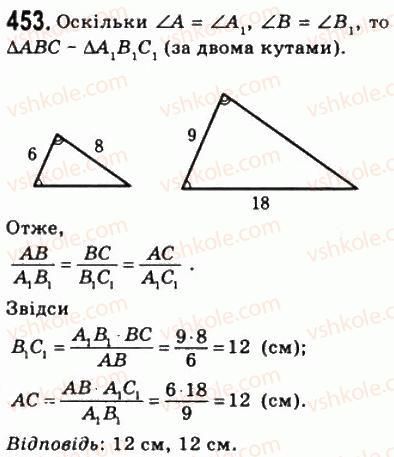Для изучения математики , 8(2), 31-43.
Алиберт Д. и Томас М. (1991). Исследование математических доказательств. В Д. Талле (ред.) Advanced Mathematical Thinking (стр. 215-230). Клювер: Нидерланды.
Осубель, Д.П., Новак, Дж.Д., и Ханесян, Х. (1968). Педагогическая психология, когнитивный взгляд . Холт, Райнхарт и Уинстон: Нью-Йорк.
Балачев, Н. (1987). Processus de preuves и ситуации проверки. Образовательные исследования по математике , 18(2), 147-176.
Биллс, Э. и Талл, Д. (1998). Рабочие определения в высшей математике: случай наименьшей верхней границы. В Proceedings of PME 22 , 2 (стр. 104-111), Stellenbosch, Южная Африка.
Дэвис, П.Дж. и Херш, Р. (1981). Математический опыт . Viking Penguin Inc.: Нью-Йорк.
де Вильерс, доктор медицины (1990). Роль и функции доказательства в математике. Пифагор , 24, 17-24.
Дубинский Э., Элтерман Ф. и Гонг К. (1988). Студенческая конструкция квантификации. Для изучения математики , 8(2), 44-51.
Дрейфус, Т. (1999). Почему Джонни не может доказать. Образовательные исследования по математике , 38 (1), 85-109.
Гриффитс, Пенсильвания (2000). Математика на рубеже тысячелетий. American Mathematical Monthly , 107 (1), 1-14.
Ханна, Г.(1990). Некоторые педагогические аспекты доказывания. Развязка , 21(1), 6-13.
Ханна, Г. (1991). Математическое доказательство. В D. Tall (Ed.) Advanced Mathematical Thinking (стр. 54-61). Клювер: Нидерланды.
Харел, Г. (1998). Два двойных утверждения: первое об обучении, второе об обучении (или наоборот). American Mathematical Monthly , 105(6), 497-507.
Харел, Г. и Саудер, Л. (1998). Схемы проверки учащимися.В A. Schoenfeld, J. Kaput, E. Dubinsky (Eds.), Исследования в области университетского математического образования III (стр. 234-282). Вашингтон, округ Колумбия: Американское математическое общество

Херш, Р. (1993). Доказательство убеждает и объясняет. Образовательные исследования по математике , 24 (4), 389-399.
Джонс, FB (1977). Метод Мура. American Mathematical Monthly , 84(4), 273-278.
Кнут, Э. (2002), Концепция доказательства учителей математики средней школы. Журнал исследований в области математического образования , 33 (5), 2002 г.
Махавьер, В. С., Что такое метод Мура? ПРИМУС , 9, 339-354.
Манин, Ю. (1977). Курс математической логики . Спрингер Верлаг, Нью-Йорк.
Мартин, В.Г. и Харел, Г. (1989). Доказательства кадры до службы учителей начальных классов. Журнал исследований в области математического образования , 20 (1), 41-51.
Марти, Р. Х. (1986).Обучение приемам доказательства. Математика в колледже . Городской университет Нью-Йорка. (весна-лето), 46-53.
Марти, Р. Х. (1991). Как добраться до Эврики! Рассуждения высшего порядка в математике. Преподавание в колледже , 39(1), 3-6.
Мейсон Дж., Бертон Л. и Стейси К. (1982). Математическое мышление . Эддисон Уэсли, Лондон.
Мур, RC (1994). Переходим к формальному доказательству. Образовательные исследования по математике , 27, 249-266.
НКТМ (2000). Принципы и стандарты школьной математики . Рестон, Вирджиния: NCTM.
Ньюэлл, А. и Саймон, Х.А. (1972). Решение человеческих проблем . Энглвудс-Клиффс, Нью-Джерси: Прентис-холл.
Пинто, М.М.Ф. и Талл, Д. (1999). Студенческие конструкции формальных теорий: придание и извлечение смысла. В Proceedings of PME 23, 1, (стр. 281-288), Хайфа, Израиль.
Раман, М. (2002). Координация неформальных и формальных аспектов математики: поведение учащихся и сообщения учебника. Журнал математического поведения , 21 (2), 135-150.
Речио, А.М. и Годино, Дж.Д. (2001). Институциональные и личностные смыслы доказывания. Образовательные исследования по математике , 48(1), 83-99.
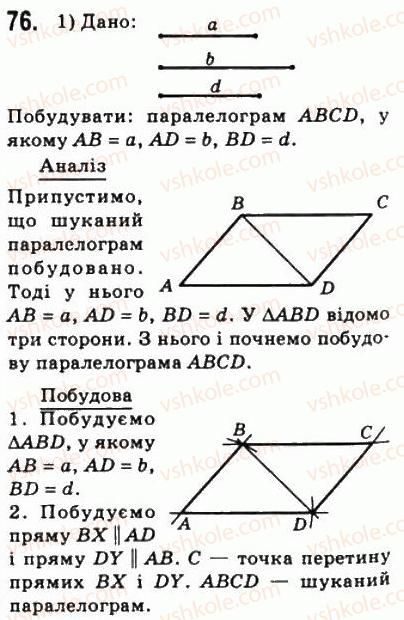
Ренц, П. (1981). Математическое доказательство: что это такое и каким оно должно быть. Математический журнал двухгодичного колледжа , 12 (2), 83–103.
Шенфельд, AH (1994). Что мы знаем об учебных программах по математике? Журнал математического поведения , 13 (1), 55-80.
Селден, А. и Селден, Дж. (2002). Проверка доказательств, записанных в виде текстов: могут ли студенты определить, доказывает ли аргумент теорему? Журнал исследований в области математического образования , 34 (1), 4–36.
Селден, Дж. и Селден, А. (1995). Распаковка логики математических утверждений. Образовательные исследования по математике , 29 (2), 123-151.
Сенк, С.Л. (1985). Насколько хорошо учащиеся пишут геометрические доказательства? Учитель математики , 78, 448-456.
Сенк С. (1989). Уровни Ван Хиле и достижения в написании геометрических доказательств. Журнал исследований в области математического образования , 20 (3), 309-321.
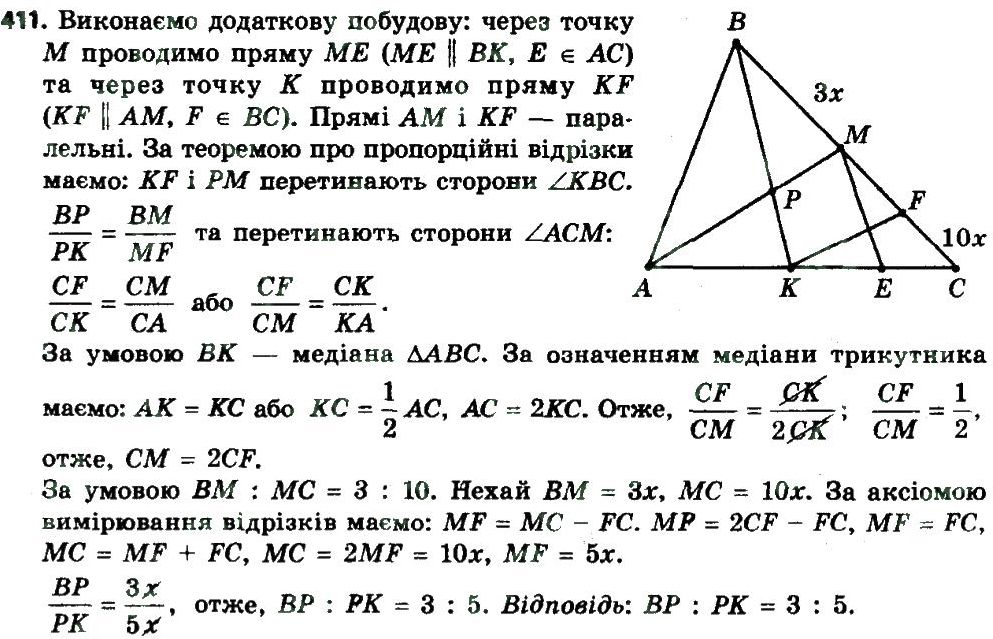
Высокий, Д. (1989). Природа математического доказательства. Преподавание математики , 128, 28-32.
Высокий, Д. (1991). Психология развитого математического мышления. В Д. Талле (ред.) Advanced Mathematical Thinking (стр. 3-23). Клювер: Нидерланды.
Теппо, А.(1991). Пересмотр уровней геометрического мышления Ван Хиле. Учитель математики , 84, 210-221.
Терстон, WP (1994). О доказательстве и прогрессе в математике. Бюллетень АМС , 30, 161-177.
Волминк, JD (1990). Природа и роль доказательства в математическом образовании. Пифагор , 23, 7-10.
Вебер, К. (2001). Студенческие трудности в построении доказательств: потребность в стратегических знаниях. Образовательные исследования по математике , 48 (1), 101-119.
Вебер, К. (2002a). Помимо доказательства и объяснения: доказательства, которые оправдывают использование определений и аксиоматических структур, а также доказательства, иллюстрирующие технику. 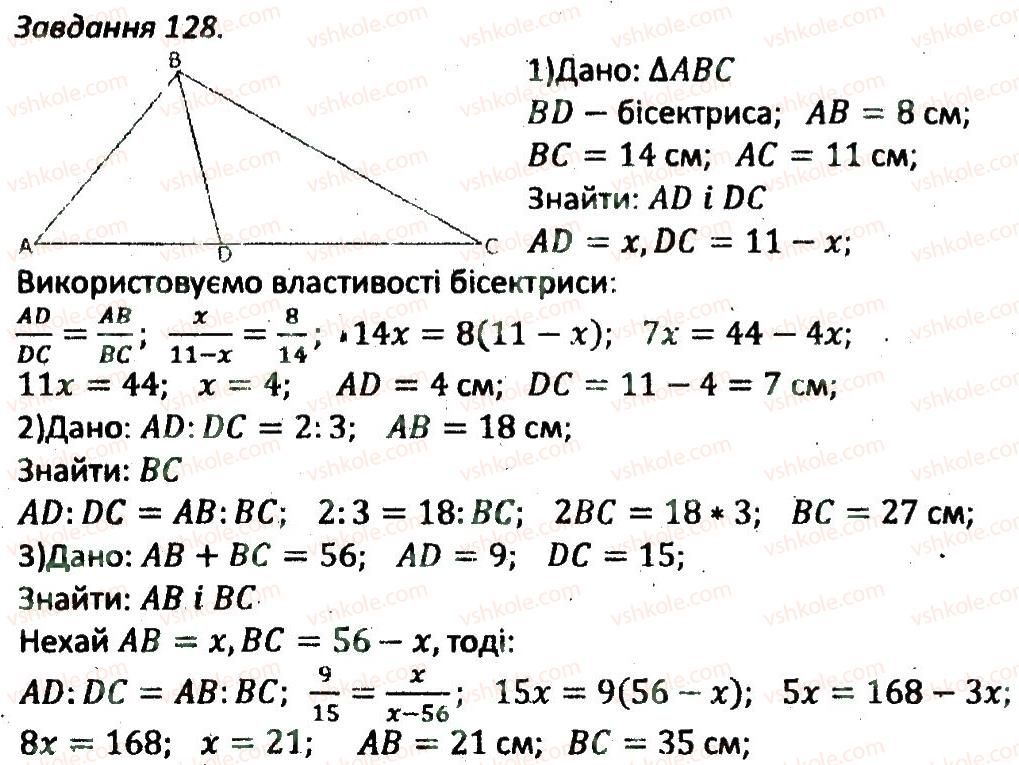Для изучения математики , 22(3), 14-17.
Вебер, К. (2002b) Инструментальное и реляционное понимание передовых математических концепций и их роли в построении доказательств групповых изоморфизмов. Материалы 2-й Международной конференции по преподаванию математики (на уровне бакалавриата) .
Уайтхед, А.Н. и Рассел, Б. (1935). Принципы математики . Кембридж: The University Press [2-е издание]
Якель, Э. и Кобб, П. (1996). Социоматематические нормы, аргументация и автономия в математике. Журнал исследований в области математического образования , 27 (4), 458-477.

Keith Weber
Rutgers University
Высшая педагогическая школа
10 Seminary Place
New Brunswick, NJ 08901
Электронная почта: [email protected]
(732) 932-7496

Введение в план урока геометрии

Длина

1 час

Материалы

Карточки
линейки
Ручки/карандаши
Ножницы
Лента

Стандарты учебной программы

CCSS. МАТЕМАТИЧЕСКОЕ СОДЕРЖАНИЕ.K.G.A.2

Правильно называйте фигуры независимо от их ориентации или общего размера.

CCSS.MATH.CONTENT.K.G.B.5

Моделирование фигур в мире путем создания фигур из компонентов (например, палочек и глиняных шариков) и рисования фигур.

Инструкции

Воспроизведение видеоурока Study.com «Что такое геометрия?» с паузой в 00:32.
Теперь пусть учащиеся осмотрят класс и перечислят все различные фигуры, которые они видят.Попросите их поделиться с классом тем, что они видят, записывая различные фигуры на доске по мере того, как учащиеся их предлагают.
Воспроизведите видеоурок еще раз, сделав паузу на 1:13.
Предложите учащимся поискать в Интернете фотографии древних египетских пирамид и поделиться тем, что они найдут, с классом.
Затем воспроизведите оставшуюся часть видеоурока.
Когда видеоурок будет завершен, предложите учащимся воспользоваться Интернетом и поработать в малых группах, чтобы исследовать внешние размеры древних египетских пирамид. Обсудите их выводы в классе, записав общие размеры на доске.
Теперь предложите учащимся использовать эту информацию, чтобы создать собственную небольшую трехмерную пирамиду, используя картон, линейки, ручки/карандаши, ножницы и ленту.
Когда все учащиеся соберут пирамиду, попросите их поменяться ими с одноклассниками.
Затем учащиеся измерят размеры пирамиды своего одноклассника. Запишите размеры на доске. Обсудите в классе.

Вопросы для обсуждения

Какие сходства мы видим в размерах студенческих пирамид?
Какие трудности возникли при создании трехмерных пирамид?
Как этот проект может помочь нам понять важность геометрии в таких вещах, как архитектура и строительство?

Extensions

Совершите виртуальную экскурсию по некоторым известным сооружениям мира. Как геометрия влияет на их дизайн?
Попросите студентов ознакомиться с требованиями курса для получения степени бакалавра в области архитектуры. Сколько классов геометрии требуется? Какие другие специальности посвящены геометрии? Почему?

Решения NCERT для математики класса 8, глава 4

Страница № 60:

Вопрос 1:

Постройте следующие четырехугольники.

(i) Четырехугольник ABCD

АВ = 4,5 см

ВС = 5,5 см

CD = 4 см

н.э. = 6 см

АС = 7 см

(ii) Четырехугольник JUMP

Ю = 3.5 см

УМ = 4 см

МП = 5 см

ПДж = 4,5 см

УЕ = 6,5 см

(iii) Параллелограмм БОЛЕЕ

ИЛИ = 6 см

RE = 4,5 см

ЭО = 7,5 см

(iv) Ромб БЕСТ

ВЕ = 4,5 см

ЭТ = 6 см

Ответ:

(i) Во-первых, грубый набросок этого четырехугольника можно нарисовать следующим образом.

(1) ΔABC можно построить, используя данные измерения следующим образом.

(2) Вершина D находится на расстоянии 6 см от вершины А. Поэтому, взяв А за центр, начертите дугу радиусом 6 см.

(3) Взяв С за центр, нарисуйте дугу радиусом 4 см, пересекая предыдущую дугу в точке D. Соедините D с А и С.

ABCD — искомый четырехугольник.

(ii) Во-первых, грубый набросок этого четырехугольника можно нарисовать следующим образом.

(1) Δ JUP можно построить, используя данные измерения следующим образом.

(2) Вершина M находится на расстоянии 5 см от вершины P и 4 см от вершины U. Взяв P и U за центры, начертите дуги радиусами 5 см и 4 см соответственно. Пусть точкой пересечения будет М.

(3) Соединить M с P и U.

JUMP — искомый четырехугольник.

(iii) Мы знаем, что противоположные стороны параллелограмма равны по длине, а также параллельны друг другу.

Следовательно, ME = OR, MO = ER

Грубый набросок этого параллелограмма можно нарисовать следующим образом.

(1) Δ EOR можно построить, используя данные измерения следующим образом.

(2) Вершина M находится на расстоянии 4,5 см от вершины O и 6 см от вершины E. Поэтому, взяв за центры O и E, начертите дуги радиусом 4,5 см и радиусом 6 см соответственно. Они пересекутся друг с другом в точке М.

(3) Соединить M с O и E.

БОЛЬШЕ — искомый параллелограмм.

(iv) Мы знаем, что все стороны ромба имеют одинаковую меру.

Отсюда BE = ES = ST = TB

Грубый набросок этого ромба можно нарисовать следующим образом.

(1) Δ BET можно построить, используя данные измерения следующим образом.

(2) Вершина S находится на расстоянии 4,5 см от вершины E, а также от вершины T. Поэтому, взяв E и T за центры, начертите дуги радиусом 4,5 см, которые будут пересекаться в точке S.

(3) Соединить S с E и T.

BEST – искомый ромб.

Видео Решение для практической геометрии (Страница: 60 , Q.No.: 1)

NCERT Решение по математике 8 класса — Практическая геометрия 60 , Вопрос 1

Страница № 62:

Вопрос 1:

Постройте следующие четырехугольники.

(i) Четырехсторонний ПОДЪЕМ

ЛИ = 4 см

ЕСЛИ = 3 см

TL = 2,5 см

LF = 4,5 см

IT = 4 см

(ii) Четырехугольник GOLD

ПР = 7,5 см

Гл = 6 см

ГД = 6 см

LD = 5 см

Внешний диаметр = 10 см

(iii) Ромбовидный изгиб

БН = 5,6 см

ДЭ = 6,5 см

Ответ:

(i) Грубый набросок этого четырехугольника можно нарисовать следующим образом.

(1) Δ ITL можно построить, используя данные измерения следующим образом.

(2) Вершина F находится на расстоянии 4,5 см от вершины L и 3 см от вершины I. Поэтому, взяв за центры L и I, начертите дуги радиусом 4,5 см и радиусом 3 см соответственно, которые будут пересекаться друг с другом в точка Ф.

(3) Соедините F с T и F с I.

ПОДЪЕМ — искомый четырехугольник.

(ii) Грубый набросок этого четырехугольника можно нарисовать следующим образом.

(1) Δ GDL можно построить, используя данные измерения следующим образом.

(2) Вершина O находится на расстоянии 10 см от вершины D и 7,5 см от вершины L. Поэтому, взяв D и L за центры, начертите дуги радиусом 10 см и радиусом 7,5 см соответственно. Они пересекутся друг с другом в точке O.

(3) Соедините O с G и L.

ЗОЛОТО — искомый четырехугольник.

(iii) Мы знаем, что диагонали ромба всегда делят друг друга пополам под углом 90º. Предположим, что они пересекаются друг с другом в точке О этого ромба.

Следовательно, EO = OD = 3,25 см

Грубый набросок этого ромба можно нарисовать следующим образом.

(1) Нарисуйте отрезок BN из 5.6 см и также провести его биссектрису. Пусть он пересекает отрезок BN в точке O.

(2) Взяв О за центр, начертите дуги радиусом 3,25 см, которые пересекают серединный перпендикуляр в точках D и E.

(3) Соедините точки D и E с точками B и N.

ИЗГИБ — искомый четырехугольник.

Видео Решение для практической геометрии (Страница: 62 , Q.№: 1)

NCERT Решение по математике 8 класса — Практическая геометрия 62 , Вопрос 1

Страница № 64:

Вопрос 1:

Постройте следующие четырехугольники.

(i) Четырехугольник БОЛЬШЕ

МО = 6 см

ИЛИ = 4,5 см

∠М = 60°

∠О = 105°

∠R = 105°

(ii) Четырехсторонний ПЛАН

пл = 4 см

ЛА = 6.5 см

∠P = 90°

∠А = 110°

∠N = 85°

(iii) Параллелограмм HEAR

ОН = 5 см

шт. = 6 см

∠R = 85°

(iv) Прямоугольник OKAY

ОК = 7 см

КА = 5 см

Ответ:

(и)

(1)Грубый набросок этого четырехугольника можно нарисовать следующим образом.

(2) Нарисуйте отрезок MO длиной 6 см и углом 105º в точке O.Так как вершина R находится на расстоянии 4,5 см от вершины О, отрежьте от этого луча отрезок OR длиной 4,5 см.

(3) Снова начертите угол 105º в точке R.

(4) Нарисуйте угол 60º в точке M. Пусть этот луч пересекает ранее проведенный луч из R в точке E.

БОЛЬШЕ — искомый четырехугольник.

(ii)

(1)Сумма углов четырехугольника равна 360°.

В четырехугольнике в плане ∠P + ∠L + ∠A + ∠N = 360°

90° + ∠L + 110° + 85° = 360°

285° + ∠L = 360°

∠Д = 360° — 285° = 75°

(2)Грубый набросок этого четырехугольника выглядит следующим образом.

(3) Нарисуйте отрезок PL длиной 4 см и в точке L начертите угол 75º. Так как вершина A находится на расстоянии 6,5 см от вершины L, отрежьте от этого луча отрезок LA длиной 6,5 см.

(4) Снова начертите угол 110º в точке А.

(5) Нарисуйте угол 90º в точке P. Этот луч встретится с ранее проведенным лучом из A в точке N.

ПЛАН – искомый четырехугольник.

(iii)

(1) Во-первых, грубый набросок этого четырехугольника выглядит следующим образом.

(2) Нарисуйте отрезок HE длиной 5 см и углом 85º в точке E. Поскольку вершина A находится на расстоянии 6 см от вершины E, отрежьте от этого луча отрезок EA длиной 6 см.

(3) Вершина R находится на расстоянии 6 см и 5 см от вершин H и A соответственно.Приняв радиус за 6 см и 5 см, проведите дуги из точек Н и А соответственно. Они будут пересекаться друг с другом в точке R.

Соединить R с H и A.

HEAR – искомый четырехугольник.

(iv)

(1)Грубый набросок этого четырехугольника рисуется следующим образом.

(2) Проведите отрезок OK длиной 7 см и углом 90º в точке K. Так как вершина A находится на расстоянии 5 см от вершины K, отрежьте от этого луча отрезок KA длиной 5 см.

(3) Вершина Y находится на расстоянии 5 см и 7 см от вершины О и А соответственно. Приняв радиус за 5 см и 7 см, проведите дуги из точек О и А соответственно. Они будут пересекаться друг с другом в точке Y.

(4) Соедините Y с A и O.

OKAY — искомый четырехугольник.

Видео Решение для практической геометрии (Страница: 64 , Q.No.: 1)

Решение NCERT для математики 8 класса — Практическая геометрия 64 , Вопрос 1

Страница № 67:

Вопрос 1:

Постройте следующие четырехугольники,

(i) Четырехугольник DEAR

ДЭ = 4 см

шт. = 5 см

АР = 4.5 см

∠Е = 60°

∠А = 90°

(ii) Четырехугольник ИСТИНА

ТР = 3,5 см

РУ = 3 см

УП = 4 см

∠R = 75°

∠U = 120°

Ответ:

(и)

(1)Грубый набросок этого четырехугольника можно нарисовать следующим образом.

(2) Нарисуйте отрезок DE длиной 4 см и углом 60º в точке E. Поскольку вершина A находится на расстоянии 5 см от вершины E, отрежьте от этого луча отрезок EA длиной 5 см.

(3) Снова начертите угол 90° в точке А. Так как вершина R находится на расстоянии 4,5 см от вершины А,
, отрежьте от этого луча отрезок RA длиной 4,5 см.

(4) Присоединить D к R.

ДОРОГОЙ — искомый четырехугольник.

(ii)

(1)Грубый набросок этого четырехугольника можно нарисовать следующим образом.

(2) Нарисуйте отрезок RU длиной 3 см и углом 120º в точке U. Поскольку вершина E находится на расстоянии 4 см от вершины U, отрежьте от этого луча отрезок UE длиной 4 см
.

(3) Затем в точке R начертите угол 75º. Так как вершина T находится на расстоянии 3,5 см от вершины R, отрежьте от этого луча отрезок RT длиной 3,5 см.

(4) Соедините T с E.

TRUE — искомый четырехугольник.

Видео Решение для практической геометрии (Страница: 67 , Q.No.: 1)

Решение NCERT для математики 8 класса — Практическая геометрия 67 , Вопрос 1

Страница № 68:

Вопрос 1:

Нарисуй
далее:

Площадь
ПРОЧИТАЙТЕ с RE = 5.1 см

Ответ:

Все
стороны квадрата имеют одинаковую меру, а также все внутренние
углы квадрата равны 90º. Таким образом, данный
квадрат READ можно нарисовать следующим образом.

(1)А
Набросок этого квадрата READ можно нарисовать следующим образом.

(2) Начертите отрезок RE длиной 5,1 см и углом 90º при
точка R и E.

(3) Поскольку вершины A и D равны 5.1 см от вершин E и R
соответственно, отрежьте отрезки EA и RD, каждый по 5,1 см от этих
лучи.

(4) Соедините D с A.

READ — это необходимый квадрат.

Страница № 68:

Вопрос 2:

Нарисуй
далее:

Ромб
диагонали которого равны 5,2 см и 6,4 см.

Ответ:

В
ромба, диагонали которого пересекаются под углом 90°.Следовательно
заданный ромб ABCD можно нарисовать следующим образом.

(1)А
Набросок этого ромба ABCD выглядит следующим образом.

(2) Нарисуйте отрезок AC длиной 5,2 см и проведите к нему перпендикуляр.
биссектриса. Пусть он пересекает отрезок AC в точке O.

(3) Нарисуйте дуги
на
обе стороны от этого серединного перпендикуляра. Пусть дуги пересекают
Биссектриса в точках B и D.

(4) Соедините точки B и D с точками A и C.

ABCD — искомый ромб.

Страница № 68:

Вопрос 3:

Нарисуй
далее:

А
прямоугольник со смежными сторонами 5 см и 4 см.

Ответ:

напротив
стороны прямоугольника имеют одинаковые длины, а также все
внутренние углы прямоугольника равны 90 градусов.данный
прямоугольник ABCD можно нарисовать следующим образом.

(1)А
Набросок этого прямоугольника ABCD можно нарисовать следующим образом.

(2) Нарисуйте отрезок AB длиной 5 см и углом 90º в точке
А и Б.

(3) Поскольку вершины C и D находятся на расстоянии 4 см от вершин B и A соответственно,
Отрежьте от этих лучей отрезки AD и BC по 4 см каждый.

(4) Соедините D с C.

ABCD — искомый прямоугольник.

Страница № 68:

Вопрос 4:

Нарисуйте следующее:

Параллелограмм OKAY, где OK = 5,5 см, а KA = 4,2 см.

Ответ:

Противоположные стороны параллелограмма равны и параллельны друг другу. Данный параллелограмм OKAY можно нарисовать следующим образом.

(1)Грубый набросок этого параллелограмма OKAY нарисован следующим образом.

(2) Нарисуйте отрезок ОК длиной 5,5 см и луч в точке К под удобным углом.

(3) Проведите в точке O луч, параллельный лучу в K. Поскольку вершины A и Y находятся на расстоянии 4,2 см от вершин K и O соответственно, отрежьте отрезки KA и OY по 4,2 см каждый от эти лучи.

(4) Соедините Y с A.

OKAY — искомый параллелограмм.

Геометрія 8 клас. Мій конспект. Нова програма

Post navigation

Календарно-тематичне планування з геометрії для 8 класу за новою програмою

Образователните медиатори — все по-ценни, но малко ценени — България

Несигурно работно място

Не само подбират децата от домовете им

«Децата заслужават днешния ден»

Руководство по математике UnboundEd

Конгруэнтность и сходство

Отражения, перемещения и вращения: основы

Понимание свойств отражений, переводов и вращений

8 класс, модуль 2, урок 4: пример 1

Конгруэнтность

Конгруэнтные треугольники

Расширители

8 класс, модуль 3, урок 2: пример 1

Подобие

Перемещение на координатную плоскость

Частные случаи конгруэнтности: трансверсали и треугольники

8 класс, модуль 2, урок 12: исследовательское задание 2

Подобные треугольники II

Теорема Пифагора

8 класс, модуль 2, урок 15: обсуждение

Применение теоремы Пифагора для решения задач

Бег на футбольном поле

Нахождение расстояний на координатной плоскости

8 класс, модуль 7, урок 17: пример 1

Роль математических практик

Преобразования: связь с выражениями и уравнениями

Уклоны между точками на линии

Теорема Пифагора: связь с выражениями и уравнениями и системой счисления

Откуда берутся сходство и сходство?

Откуда взялась теорема Пифагора?

Предложения для учащихся, отстающих от

Куда идут эти понятия?

1.Что такое руководство по содержанию?

2. Что содержится в руководстве по содержанию?

3. Как я могу использовать Руководства по содержанию?

4. Зачем нужны руководства по содержанию?

5. Какая связь между руководствами по содержанию и последовательностями?

6. Как отбирались ресурсы?

7. Почему Руководства по содержанию касаются лишь нескольких стандартов? Где остальные стандарты?

8.Как я могу быть в курсе новых руководств по содержанию?

Math Beasts Camp 8-9 (Подготовка к геометрии)

Расписание в 2022 году

Research Sampler 8: Проблемы учащихся с доказательством

Кит Вебер

Что такое доказательство и какова его роль в математике?

Какие трудности возникают у студентов с доказательствами?

Как можно эффективно преподавать концепцию доказательства?

Ссылки

Введение в план урока геометрии

Длина

Материалы

Стандарты учебной программы

Инструкции

Вопросы для обсуждения

Extensions

Решения NCERT для математики класса 8, глава 4

Страница № 60:

Вопрос 1:

Ответ:

Видео Решение для практической геометрии (Страница: 60 ​​, Q.No.: 1)

Страница № 62:

Вопрос 1:

Ответ:

Видео Решение для практической геометрии (Страница: 62 , Q.№: 1)

Страница № 64:

Вопрос 1:

Ответ:

Видео Решение для практической геометрии (Страница: 64 , Q.No.: 1)

Страница № 67:

Вопрос 1:

Ответ:

Видео Решение для практической геометрии (Страница: 67 , Q.No.: 1)

Страница № 68:

Вопрос 1:

Ответ:

Страница № 68:

Вопрос 2:

Расписание
в 2022 году

Видео Решение для практической геометрии (Страница: 60 , Q.No.: 1)