Гдз дидактический материал по математике 6 – ГДЗ дидактические материалы по Математике 6 класс Чесноков Нешков

Страница 8 №12-20 ГДЗ к учебнику «Математика» 6 класс Никольский, Потапов, Решетников, Шевкин

Задание 12. Упростите отношение величин по образцу: …

Задание 13. Найдите пройденный путь s, если известны скорость u и время равномерного движения t:
а) u = 2 м/с, t = 3с;
б) u = 2 м/с, t = 1/20мин.

Решение задач

а)
Дано:
u = 2 м/с, t = 3 с;
Найти:
S
Решение:
s = u * t = 2 м/с * 3c = 6м
Ответ: 6 м.

б)
Дано:
u = 2 м/с, t = 1/20 мин.
Найти:
S
Решение:
s = u * t = 2 м/с * 1/20 мин = 2 м/с * 60/20 с = 2 м/с * 3c = 6м.
Ответ: 6 м.

Задание 14. Найдите скорость равномерного движения u, если известны пройденный путь s и время движения t:
а) s = 6м, t = 3 с;
б) s = 6м, t = 1/20 ч.

Решение задач

а)
Дано:
s = 6 м, t = 3 с
Найти:
U
Решение:
u = s / t = 6м / 3c = 2 м/с
Ответ: 2 м/с

б)
Дано:
s = 6 м, t = 1/20ч
Найти:
U
Решение:
u = s / t = 6м / 1/20ч = 6 м / 3мин = 2 м/мин
Ответ: 2 м/мин.

Задание 15. Скорость пешехода 5 1/5 км/ч. Найдите путь пройденный пешеходом за:
а) 2ч;
б) 1 1/2 ч;
в) 45 мин;
г) 125 мин.

Решение

Задание 16. Расстояние в 1 1/2км пешеход прошел за 20 мин. Найдите скорость пешехода. Ответ запишите в следующих единицах:
а) км/ч;
б) км/мин;
в) м/ч;
г) м/мин;
д) м/с.

Решение

Задание 17. Скорость легковой автомашины 72 км/ч. Какой путь она пройдет за:
а) 2/3 ч;
б) 45 мин;
в) 50 мин;
г) 165 мин.

Решение

Задание 18. 

Скорость легковой машины 1200 м/мин. За сколько часов она проедет:
а) 144 км;
б) 36 км;
в) 8 км;
г) 54 км.

Решение

Задание 19. Найдите скорость автомашины, если 80 км она проезжает за:
а) 1 ч;
б) 4/5 ч;
в) 4/3 ч;
г) 8/7 ч;
д) 50 мин;
е) 65 мин;
ж) 90 мин;
з) 100 мин.

Решение

Задание 20. Два конькобежца одновременно стартовали на дистанцию 10000 м по замкнутой дорожке, длина которой равна 400м. Скорость первого конькобежца 20 км/ч, а скорость второго 21 км/ч. Обгонит ли второй конькобежец первого на круг до конца дистанции? А на два круга?

Решение

Дано:
Sдистанции = 10000 м;
Sкруга = 400м;
V1 = 20 км/ч;
V2 = 21 км/ч;
Найти;
t2 – время прохождения дистанции вторым конькобежцем;
t1 – время прохождения круга первым конькобежцем;
К2 – количество кругов, пройденных вторым конькобежцем за всю дистанцию;
К1 − количество кругов, пройденных первым конькобежцем в момент финиша второго конькобежца;
Р − разницу количества кругов, пройденных вторым конькобежцем и первым конькобежцем.

Решение:
Найдем время прохождения дистанции вторым конькобежцем:
Переведем длину дистанции в км:
10000 : 1000 = 10 км.

7gy.ru

Страница 33 №206-210 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков

Задание № 206. Решите уравнение:
а) (х + 36,1) * 5,1 = 245,82;
б) (m − 0,67) * 0,02 = 0,0152;
в) (х + 24,3) : 18,3 = 3,1;
г) (у − 15,7) : 19,2 = 4,7.

Решение

а) (x + 36,1) * 5,1 = 245,82
x + 36,1 = 245,82 : 5,1
x + 36,1 = 48,2
x = 48,2 − 36,1 = 12,1

б) (m − 0,67) * 0,02 = 0,0152
m − 0,67 = 0,0152 : 0,02
m − 0,67 = 0,76
m = 0,76 + 0,67 = 1,43

в) (x + 24,3) : 18,3 = 3,1
x + 24,3 = 3,1 * 18,3
x + 24,3 = 56,73
x = 56,73 − 24,3 = 32,43

г) (у − 15,7) : 19,2 = 4,7
у − 15,7 = 4,7 * 19,2
у − 15,7 = 105,94
y = 105,94 + 15,7 = 121,64

Задание № 207. Запишите в виде дроби частные:
27 : 8;
72 : 8;
483 : 18;
1225 : 12 и выделите из них целые части.

Решение

Задание № 208. Найдите среднее арифметическое чисел: 5,24; 6,97; 8,56; 7,32 и 6,23.

Решение

(5,24 + 6,97 + 8,56 + 7,32 + 6,23) : 5 = 34,32 : 5 = 6,864.

Задача № 209. Поезд шёл 3 ч со скоростью 65,2 км/ч и 2 ч со скоростью 83,3 км/ч. Найдите среднюю скорость поезда за эти 5 ч.

Дано:
t1 = 3ч
v1 = 65,2 км/ч
t2 = 2 ч
v2 = 83,3 км/ч
vср = ? км/ч

Решение
vср = Sвсе : tвсе
vср = (v1 * t1 + v2 * t2) : (t1 + t2)
vср = (65,2 * 3 + 83,3 * 2) : (3 + 2)
vср = (195,6 + 166,6) : 5
vср = 362,2 : 5
vср = 72,44 км/ч.
Ответ: vср = 72,44 км/ч.

Задание № 210. Найдите значение выражения:
а) 51 − (3,75 : 3 + 86,45 : 24,7) * 2,4;
б) (650 000 : 3125 − 196,5) * 3,14.

Решение

а) 51 − (3,75 : 3 + 86,45 : 24,7) * 2,4 = 51 − (1,25 = 3,5) * 2,4 = 51 − (1,25 = 3,5) * 2,4 = 51 − 11,4 = 39,64

б) (650 000 : 3125 − 196,5) • 3,14 = (208 − 196,5) • 3,14 = 36,11

7gy.ru

Страница 46 №280-285 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков

Задание № 280. Можно ли представить в виде десятичной дроби: 2/5; 4/25; 2/3; 4/7; 12/15; 9/18?
В каком случае обыкновенную дробь можно представить в виде десятичной?

Решение

Обыкновенную дробь можно представить в виде десятичной, если ее можно привести к обыкновенной дроби, знаменатель которой будет степенью числа 10.

Задание № 281. Запишите в виде десятичной дроби, приведя:
а) 1/2,1/5,4/5 к знаменателю 10;
б) 1/4,11/25,12/20,39/50 к знаменателю 100;
в) 7/8,6/125,111/125,137/500 к знаменателю 1000.

Решение

Задание № 282. Запишите в виде десятичной дроби: 3/5,2/25,3/4,5/8,13/125,7/200.

Решение

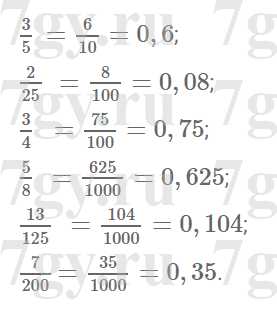
Задание № 283. Приведите к наименьшему общему знаменателю дроби:
а) 1/6 и 3/8;
б) 4/9 и 7/15;
в) 5/12 и 1/8;
г) 8/15 и 11/12;
д) 9/10 и 2/12;
е) 13/12 и 13/18;
ж) 11/30 и 8/45;
з) 11/20 и 9/16;
и) 8/33 и 9/77;
к) 9/98 и 5/56;
л) 13/750 и 7/450;
м) 10/297 и 14/363.

Решение

Задание № 284. Вычислите устно:
а) 16 * 4
+ 11
: 15
* 17
+ 18
?;
б) 95 : 5
+ 56
: 25
* 27
+ 29
?;
в) 38 * 0,01
: 1,9
* 50
* 0,3
— 0,2
?;
г) 0,6 : 3
* 1,5
+ 2,9
: 0,8
— 1,3
?;
д) 2 — 1,2
* 0,5
: 0,1
+ 0,9
: 0,7
?

Ответы 7 гуру

а) 64, 75, 5, 85, 103.
б) 19, 75, 3, 81, 110.
в) 0,38, 0,2, 10, 3, 2,8.
г) 0,2, 0,3, 3,2, 4, 2,7.
д) 0,8, 0,4, 4, 4,9, 7.

Задание № 285. Найдите пропущенные числа, если х = 0,8; 0,16; 0,06; 1:

Решение

0,8 : 0,1 = 8,8 − 0,6 = 7,4, 7,4 + 2,8 = 10,2, 10,2 : 0,2 = 51, 51 * 0,5 = 25,5;

0,16 : 0,1 = 1,6, 1,6 − 0,6 = 1, 1 : 2 = 0,5, 0,5 + 1,9, 2,4, 2,4 * 10 = 24;

0,06 : 0,1 = 0,6, 0,6 − 0,6 = 0,0 + 2,8 = 2,8, 2,8 : 0,2 = 14, 14 * 0,5 = 7;

1 : 0,1 = 10, 10 − 0,6 = 9,4, 9,4 + 2,8 = 12,2, 12,2 : 0,2 = 61, 61 * 0,5 = 30,5.

7gy.ru

Страница 36 №213-222 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков

Задание № 213. Поясните с помощью часов, почему:
а) 2/3=8/12=40/60;
б) 1/6=2/12=10/60;
в) 5/6=10/12=50/60.

Решение

а) 2/3ч=8/12ч=40/60ч=40мин
б) 1/6ч=2/12ч=10/60ч=10мин
в) 5/6ч=10/12ч=50/60ч=50мин

Задание № 214. Начертите два отрезка АВ и CD длиной по 8 см. Отметьте цветным карандашом 3/4 отрезка АВ и 6/8 отрезка CD.
Сравните с помощью циркуля цветные части отрезков АВ и CD.

Решение

Выделенные части отрезков АВ и CD равны.

Задание № 215. Начертите координатный луч, приняв за единичный отрезок 18 клеток тетради. Отметьте на координатном луче точки с координатами 1/9,2/9,3/9,4/9,5/9,6/9,7/9,8/9,1/6,2/6,3/6,4/6,5/6,1/3,2/3. Какие из этих чисел изображаются на координатном луче одной и той же точкой? Запишите соответствующие равенства.

Решение

3 = 2 = 1
9    6    3

6 = 4 = 2
9    6    3

Задание № 216. Умножьте числитель и знаменатель каждой дроби 1/5,3/7,25/8,39/10 на 5. Напишите соответствующие равенства.

Задание № 217. Разделите числитель и знаменатель каждой дроби 6/3,9/6,15/9,21/33 на 3. Запишите соответствующие равенства.

Задание № 218. Сколько двенадцатых долей содержится в 1/4;1/6;3/4;5/6;2/3?

Задание № 219. Объясните, почему верно равенство:
а) 4/5=8/10;
б) 44/100=11/25.

Решение

Равенства верны по основному свойству дроби.

Задание № 220. Запишите в виде обыкновенных дробей частные:
3 : 8;
12 : 32;
20 : 48;
5 : 12.
Какие из полученных дробей равны?

Решение

Задание № 221. Какое натуральное число надо записать вместо буквы, чтобы было верным равенство:
а) 14/21=х/3;
б) m/18=5/9;
в) 17/51=1/n;
г) 15/y=5/6?

Ответы

а) x = 2
б) m = 10
в) n = 3
г) у = 18

Задание № 222. Вычислите устно:
а) 50 * 10
: 125
* 75
— 160
?;
б) 300 : 60
* 40
: 50
* 19
?;
в) 12 + 0,6
: 3
— 0,2
* 2,5
?;
г) 1 — 0,4
* 5
-0,5
: 5
?;
д) 0,7 — 0,06
: 8
* 10
: 0,4
?.

Ответы

а) 500, 4, 300, 140.
б) 5, 200, 4, 76.
в) 12,6, 4,2, 4, 10.
г) 0,6, 3, 2,5, 0,5.
д) 0,64, 0.08, 0,8, 2.

7gy.ru

Страница 4 №1-3 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков

Категория: ГДЗ Математика учебник 6 класс Виленкин, Жохов, Чесноков

Ответы к главе 1. Обыкновенные дроби. Параграф 1. Делимость чисел. Тема 1. Делители и кратные

Задание № 1. На сколько равных кучек можно разложить 36 орехов?

Ответ 7 гуру

Общее количество орехов должно делиться на количество орехов в одной кучке без остатка.
По 1 ореху − 36:1 = 36 кучек;
по 2 ореха − 36:2 = 18 кучек;
по 3 ореха − 36:3 = 12 кучек;
по 4 ореха − 36:4 = 9 кучек;
по 6 орехов − 36:6 = 6 кучек;
по 9 орехов − 36:9 = 4 кучки;
по 12 орехов − 36:12 = 3 кучки;
по 18 орехов − 36:18 = 2 кучки;
по 36 орехов − 36:36 = 1 кучка.

Задание № 2. В каждой коробке лежат 6 чайных ложек. Можно ли, не вскрывая коробок, взять:
а) 42 ложки;
б) 49 ложек?

Ответ к заданию

а) Да, можно так как 42 : 6 = 7. Для этого нужно взять 7 коробок.
б) Нет, нельзя. 49 не делится на 6 без остатка 49 : 6 = 8 * 6 + 1.
Для этого надо взять 8 коробок и ещё одну ложку из вскрытой коробки.

Задание № 3. Верно ли, что:
а) 5 − делитель 45;
б) 16 − делитель 8;
в) 17 − делитель 152;
г) 27 − кратное 3;
д) 6 − кратное 12;
е) 156 − кратное 13?

Ответ

а) 45 : 5 = 9 − верно.
б) неверно.
в) неверно.
г) 27 : 3 = 9 − верно.
д) неверно
е) 156 : 13 = 12 − верно.

© Копирование допустимо только с прямой активной ссылкой на страницу с оригиналом статьи.
При любых заболеваниях не занимайтесь диагностикой и лечением самостоятельно, необходимо обязательно обратиться к врачу — специалисту.
Изображения обложек учебной литературы приведены на страницах сайта исключительно в качестве иллюстративного материала (ст. 1274 п. 1 части четвертой Гражданского кодекса РФ)

7gy.ru

Страницы 6-7 №1-11 ГДЗ к учебнику «Математика» 6 класс Никольский, Потапов, Решетников, Шевкин

Глава 1. Отношения, пропорции, проценты.

Ответы к разделу учебника 1.1. Отношения чисел и величин

Задание 1. Что называют:
а) отношением числа a к числу b;
б) членами отношения.
Приведите примеры.

Решение

а) Ответ: отношением числа a к числу b называют частное двух не равных нулю чисел.
Пример:
7/49 является отношением числа 7 к числу 49.
5/6:3/8 является отношением числа 5/6 к 3/8.

б) Ответ: в отношении чисел а и b членами отношения называют числа а и b.
Примеры:
7/49 является отношением числа 7 к числу 49. Числа 7 и 49 являются членами отношения.
5/6:3/8 является отношением числа 5/6 к 3/8.
5/6 и 3/8 являются членами отношения.

Задание 2. Чем является отношение величин:
а) одного наименования;
б) разных наименований.
Приведите примеры.

Ответы 7 гуру

а) Отношение величин одного наименования есть число.
Пример: 1000 см : 2 м = 5 − отношение длины (1000 см) к длине (2 м) есть число 5.

б) Отношение величин разных наименований есть новая величина.
Пример: 10 км : 2 ч = 5 км/ч − отношение расстояния (10 км) ко времени (2 ч) есть новая величина скорость (5 км/ч).

Задание 3. Используя слово отношение прочитайте запись:
а) 7 : 2;
б) 3/5;
в) 1 : 5;
г) 1/6.

Решение

а) отношение семи к двум,
б)отношение трёх к пяти,
в) отношение одного к пяти,
г) отношение одного к шести.

Задание 4. Запишите отношение, назовите его члены:
а) 7 к 3;
б) 5 к 9;
в) 12 к 4;
г) 10 к 1000.

Решение

а) 7
    3, члены отношения 7 и 3
б) 5
    9, члены отношения 5 и 9
в) 12
     4, члены отношения 12 и 4
г) 10  
  1000, члены отношения 10 и 1000.

Задание 5. Найдите отношение:
а) 3 к 1/2;
б) 5 к 10/13;
в) 7/8 к 21/32;
г) 12/17 к 48/51.

Решение

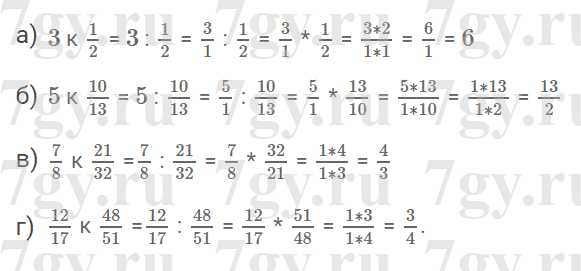
Задание 6. Прочитайте отношение, назовите его члены, упростите отношение с помощью свойства отношения:
а) 40 : 50 = 4 : 5;
б) 99 : 18;
в) 450 : 250;
г) 720 : 81.
В чём заключается свойство отношения.

Решение

а) 40 : 50 − это отношение сорока к пятидесяти, члены отношения 40 и 50.
Свойство отношения: Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю:
a : b = (ac) : (bc), или
a = a∗c , где c ≠0.
b    b∗c
40 : 50 = (40 : 10) : (50 : 10) = 4 : 5

б) 99 : 18 = (99 : 9) : (18 : 9) = 11 : 2
   Ответ: 11 : 2

в) 450 : 250 = (450 : 50) : (250 : 50) = 9 : 5
   Ответ: 9 : 5

г) 720 : 81 = (720 : 9) : (81 : 9) = 80 : 9
   Ответ: 80 : 9

Задание 7. Запишите отношение в виде дроби (там, где можно, упростите отношение):
а) 3:5;
б) 49:28;
в) 35:700;
г) 5:7;
д) 520:460;
е) 27:81.

Решение

Задание 8. Можно ли выразить натуральным числом отношение:
а) 40 : 20;
б) 30 : 60;
в) 1000 : 100;
г) 600 : 30;
д) 20 : 40;
е) 100 : 1000.

Ответы 7 гуру

а) 40 : 20 = (40 : 10) : (20 : 10) = 4 : 2 = 2 (можно)
Ответ: можно

б) 30 : 60 = 30 = 30:10 = 3 = 3:3 = 1
60 60:10 6 6:3 2
Ответ: нельзя

в) 1000 : 100 = (1000 : 100) : (100 : 100) = 10 : 1 = 10
Ответ: можно

г) 600 : 30 = (600 : 10) : (30 : 10) = 60 : 3 = 20
Ответ: можно

д) 20 : 40 = 20 = 20:10 = 2 = 2:2 = 1
40 40:10 4 4:2 2
Ответ: нельзя

е) 100 : 1000 = 100 = 100:100 = 1
1000 1000:100 10
Ответ: нельзя.

Задание 9. Замените отношение дробных чисел равным ему отношением натуральных чисел по образцу:

Решение

Задание 10. Упростите отношение величин:
а) 35м/28м;
б) 45кг/36кг;
в) 420км/720км;
г) 450т/540т;
д) 320ч/48ч;
е) 480 мин/840 мин.

Решение

Задание 11. Упростите отношение величин:
а) 12м/15дм;
б) 18кг/540г;
в) 490см/35дм;
г) 450кг/2т;
д) 3500см³/21дм³;
е) 9900дм³/18м³.

Решение

 

7gy.ru

Страница 6 №8-16 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков

Задание № 8. В спортивном празднике участвовали 90 школьников. Могут ли они на заключительном параде построиться:
− в две одинаковые шеренги?
− в пять одинаковых шеренг?
− в одиннадцать одинаковых шеренг?
− в колонну по шесть человек в ряд?

Решение

Школьники могут построиться:
по 90 : 2 = 45 школьников в две шеренги;
по 90 : 5 = 18 школьников в 5 шеренг;
90 не делится на 11 без остатка;
по 90 : 6 = 15 школьников в 6 рядах.

Задание № 9. Докажите, что число 70525 кратно числу 217, а число 729 является делителем числа 225261.

Решение

Задание № 10. На координатном луче отмечено число а (рис. 1). Отметьте на этом луче четыре числа, кратных числу а.

Решение

Числа а, 2а, 3а, 4а, 5а, 6а кратны числу а.

Задание № 11. Проверьте, что каждое из чисел 6, 28, 496 равно сумме всех его делителей, не считая самого числа.

Решение

Делители числа 6: 1, 2, 3, 6, их сумма делителей не считая самого числа: 1 + 2 + 3 = 6;
число 28: 1, 2, 4, 7, 14, 28; 1 + 2 + 4 + 7 + 14 = 28;
число 496: 1, 2, 4, 8, 16, 31, 62, 124, 248, 496; 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496.

Задание № 12. Проверьте, что каждое из чисел 220 и 284 равно сумме делителей другого числа, не считая его самого.

Решение

Делители числа 220: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220;
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284.
Делители числа 284: 1, 2, 4, 71, 142, 284;
1 + 2 + 4 + 71 + 142 = 220.

Задание № 13. Докажите, что произведение двух натуральных чисел кратно каждому из множителей.

Решение

Пусть a и b натуральные числа, тогда их произведение a * b, и,
a * b = b,
     a

a * b = a,
b
 
то есть a * b кратно a и b.

Задание № 14. На рисунке 2 изображён в натуральную величину один кадр фотоплёнки. Каких размеров получится фотография при пятикратном увеличении? Уместится ли изображение этого кадра при десятикратном увеличении на листе бумаги, размер которого 24 х 30 см?

Решение

Ширина кадра на рисунке а = 2,8 см, а высота b = 4,3 см; после увеличения в 5 раз они будут равны:
a * 5 = 2,8 * 5 = 14 см, b * 5 = 4,3 * 5 = 21,5 см, соответственно;
после увеличения в 10 раз они будут равны:
a * 10 = 2,8 * 10 = 28 см, 6 * 10 = 4,3 * 10 = 43 см, соответственно.
Следовательно при десятикратном увеличении изображение кадра не уместятся на листе бумаги, так как лист имеет размеры − 24 х 30 см.
Ответ: не уместится.

Задание № 15. Вычислите устно:
а) 5 + 0,8; 0,23 + 7; 0,48 + 0,2; 0,6 + 0,34; 2,7 + 1,12;
б) 0,76 − 0,3; 2,54 − 2; 0,82 − 0,02; 0,63 − 0,6; 0,8 − 0,25;
в) 0,2 * 4; 2,1 * 3; 0,7 * 10; 0,5 * 2; 0,25 * 4;
г) 6 : 10; 0,8 : 2; 2,1 : 7; 0,5 : 10; 4,1 : 2.

Решение

а) 5,8; 7,23; 0,68; 0,94; 3,82.
б) 0,46; 0,54; 0,8; 0,03; 0,55.
в) 0,8; 6,3; 7; 1; 1.
г) ,6; 0,4; 0,3; 0,05; 2,05.

Задание № 16. Найдите пропущенные числа:

Решение

а)128 : 2 = 64,
128 : 4 = 32,
128 : 8 = 16,
128 : 16 = 8,
128 : 32 = 4,
128 : 64 = 2.

б) 6 + 6 = 12;
12 + 6 = 18;
18 + 6 = 24;
24 + 6 = 30;
6 * 5 = 30;
6 * 3 = 18.

7gy.ru