Самостоятельная работа по алгебре 9 класс по теме функции и их свойства – Самостоятельная работа по теме: «Функция» (9 класс)

Самостоятельная работа по теме: «Функция» (9 класс)

Вариант 1

1. На одном из рисунков изображен график функции . Укажите номер этого рисунка.

Варианты ответа

1. 2.

3. 4.

2. График какой из приведенных ниже функций изображен на рисунке?

Варианты ответов

1. 2. 3. 4.

3. Найдите значение по графику функции , изображенному на рисунке.

Варианты ответа

1. -1 2. 1 3. 2 4. 3

4. Найдите значение по графику функции , изображенному на рисунке.

5. Найдите значение по графику функции , изображенному на рисунке.

Варианты ответа

1. -3 2. 1 3. 2 4. 3

6. Найдите значение по графику функции , изображенному на рисунке.

7. На одном из рисунков изображен график функции . Укажите номер этого рисунка.

Варианты ответа

1. 2.

3. 4.

8. Уста­но­ви­те со­от­вет­ствие между функ­ци­я­ми и их гра­фи­ка­ми.

Функции

А) y = −2x + 4

Б) y = 2x − 4

В) y= 2x + 4

Графики

Запишите в ответ цифры, рас­по­ло­жив их в порядке, со­от­вет­ству­ю­щем буквам: 

А

Б

В

9. Установите со­от­вет­ствие между гра­фи­ка­ми функ­ций и формулами, ко­то­рые их задают.

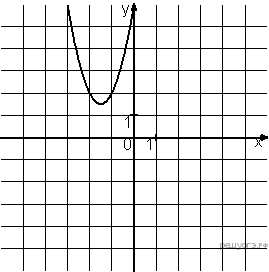
 А) Б) В)

1) у = -2х² + 6х — 6

2) у = -2х² — 6х — 6

3) у = 2х² + 6х + 6

4) у = 2х² — 6х + 6

Запишите в ответ цифры, рас­по­ло­жив их в порядке, со­от­вет­ству­ю­щем буквам: 

А

Б

В

Вариант 2

1. На одном из рисунков изображен график функции . Укажите номер этого рисунка.

Варианты ответа

1. 2.

3. 4.

2. График какой из приведенных ниже функций изображен на рисунке?

Варианты ответа

1. 2. 3. 4.

3. Найдите значение по графику функции , изображенному на рисунке.

4. Найдите значение по графику функции , изображенному на рисунке.

Варианты ответа

1. -2 2. 1 3. 2 4. 3

5. Найдите значение по графику функции , изображенному на рисунке.

6. Найдите значение по графику функции , изображенному на рисунке.

Варианты ответа

1. 2 2. 3. 4. -2

7. На одном из рисунков изображен график функции . Укажите номер этого рисунка.

Варианты ответа

1. 2.

3. 4.

8. На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций вида y = kx + b. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми функ­ций и зна­ка­ми ко­эф­фи­ци­ен­тов k и b.

Графики

Коэффициенты

1) k < 0, b > 0

2) k > 0, b > 0

3) k < 0, b < 0

4) k > 0, b < 0

Запишите в ответ цифры, рас­по­ло­жив их в порядке, со­от­вет­ству­ю­щем буквам: 

А

Б

В

9. Установите со­от­вет­ствие между функ­ци­я­ми и их графиками.

ФУНКЦИИ

А) у = х² — 2х

Б) у = х² + 2х

В) у = — х² — 2х

ГРАФИКИ

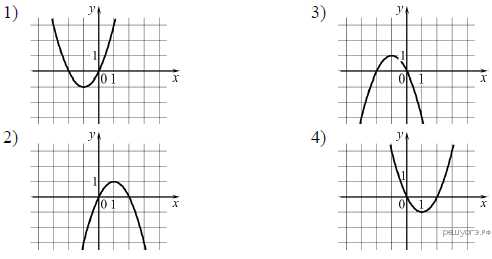
Запишите в ответ цифры, рас­по­ло­жив их в порядке, со­от­вет­ству­ю­щем буквам: 

А

Б

В

infourok.ru

Серия самостоятельных работ по теме «Функции и их свойства»

Самостоятельные работы по алгебре по теме «Функции и их свойства» содержат в себе как теоретические вопросы по теме  (представленные в виде тестов открытого типа, т. е.  тесты с добавлением), так и практические вопросы по теме (они представлены в виде тестов закрытого типа с альтернативным выбором ответа, а также в виде тестов открытого типа со свободным изложением).  Самостоятельные работы как контроль знаний по теме «Функции и их свойства» ориентированы на учебник алгебры авторов Ю.Н. Макарычев, Н.Г. Миндюк и др. Также их могут использовать учителя, работающие по другим учебникам при подготовке обучающихся к ОГЭ.

Просмотр содержимого документа

«Функции и их свойства_самост. раб.»

Вариант 1

1.Вычислить: 3b – a, если b =  4, а = 7

1) 5 2) 19 3) – 5 4) – 19.

2.Указать все значения, при которых выражение имеет смысл

1) х ≥ 5 2) х ≤ 5 3) х ≥ – 5 4) х ≤ – 5.

3. Найти нули функции у = х² – 6х – 7. В ответ указать наименьшее значение.

4. На рисунке изображён график функции

у = х² + 3х. Используя график функции, найдите промежутки знакопостоянства.

5. На рисунке изображён график изменения температуры в течение 12 часов. По горизонтали  время в часах, по вертикали  температура в градусах Цельсия. В течение скольких часов температура была выше 14 ^оС.

Вариант 2

1.Вычислить: 2b – a, если b =  5, а = 3,2

1) 6,8 2) 10,2 3) – 13,2 4) 13,2.

2.Указать все значения, при которых выражения имеет смысл

1) х ≥ 3 2) х ≤ 3 3) х ≥ – 3 4) х ≤ – 3.

3. Найти нули функции у = х² – 3х – 4. В ответ указать наибольшее значение.

4. На рисунке изображён график функции у =  х²  2х. Используя график функции, найдите промежутки знакопостоянства.

5. На рисунке жирными точками показана среднесуточная температура воздуха в Пскове каждый день с 15 по 28 марта 1959 года. По горизонтали указываются числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какой была наибольшая среднесуточная температура в период с 17 марта по 24 марта. Ответ дайте в градусах Цельсия.

Просмотр содержимого документа

«Функции и их свойства_теория и практика»

kopilkaurokov.ru

Материал по алгебре (9 класс) на тему: Самостоятельная работа по теме «Графики и функции»

По теме: методические разработки, презентации и конспекты

Самостоятельная работа по теме : «Линейная функция и ее график» (7 класс)

Вариант I 1. Преобразуйте линейное уравнение с двумя переменными к виду линейной функции и выпишите коэффициенты k  и  m:    2. Найдите значение линейной функции при данн…

Самостоятельные работы по теме: Квадратичная функция.

Варианты заданий….

Самостоятельные работы по алгебре и началам математического анализа для 10 профильного класса по теме «Тригонометрические функции»

Самостоятельные работы по алгебре и началам анализа для 10 профильного класса по теме «Тригонометрические функции»1. Числовая окружность — самостоятельная работа в форме блиц-опроса в двух вариантах2….

Контрольная и самостоятельные работы по теме Показательная функция

Материал содержит две самостоятельные работы в двух вариантах и контрольная работа ( 2 варианта) по решению показательных уравнений и неравенств….

Самостоятельная работа по теме: «Линейная функция» ( 7 класс)

Самостоятельная работа по теме»Линейная функция» ( 7 класс)…

Самостоятельная работа по теме «Числовые функции» (9 класс)

Самостоятельная работа для 9 класса по алгебре к учебнику Мордковича А.Г. «Алгебра 9» в двух вариантах по теме «Числовые функции» (область определения, четность функции, построение графика кусочной фу…

Самостоятельная работа по теме «Линейная функция» (7 класс)

Самостоятельная работа по теме «Линейная функция» (алгебра 7 класс)…

nsportal.ru

Самостоятельные работы по алгебре (9 класс)

Степенная функция. Вариант 1

1) Изобразите схематично график функции . (2 б) 2)Сравните: а) (1б), б) (1б), в) (1б). 3) Принадлежат ли графику функции точки А(-2; 512) и В(-1; -1)? (2б) 4) Сколько корней имеет уравнение а) (1б) б) (1б) в) (1б) г) (1б). 5)Постройте график функции а) (2б), б) (2б).

Всего – 15б. «3» — 6б., «4» — 9 б., «5» -12 б.

Степенная функция. Вариант 2

1) Изобразите схематично график функции . (2 б) 2)Сравните: а) (1б), б) (1б), в) (1б). 3) Принадлежат ли графику функции точки А(-2; -256) и В(-1; 1)? (2б)

4) Сколько корней имеет уравнение а) (1б) б) (1б) в) (1б) г) (1б).

5)Постройте график функции а) (2б), б) (2б).

Всего – 15б. «3» — 6б., «4» — 9 б., «5» -12 б.

Степенная функция. Вариант 1

1) Изобразите схематично график функции . (2 б)

2)Сравните: а) (1б), б) (1б), в) (1б).

3) Принадлежат ли графику функции точки А(-2; 512) и В(-1; -1)? (2б)

4) Сколько корней имеет уравнение а) (1б) б) (1б) в) (1б) г) (1б).

5)Постройте график функции а) (2б), б) (2б).

Всего – 15б. «3» — 6б., «4» — 9 б., «5» -12 б.

Степенная функция. Вариант 1

1) Изобразите схематично график функции . (2 б) 2)Сравните: а) (1б), б) (1б), в) (1б). 3) Принадлежат ли графику функции точки А(-2; 512) и В(-1; -1)? (2б) 4) Сколько корней имеет уравнение а) (1б) б) (1б) в) (1б) г) (1б). 5)Постройте график функции а) (2б), б) (2б).

Всего – 15б. «3» — 6б., «4» — 9 б., «5» -12 б.

Степенная функция. Вариант 2

1) Изобразите схематично график функции . (2 б) 2)Сравните: а) (1б), б) (1б), в) (1б). 3) Принадлежат ли графику функции точки А(-2; -256) и В(-1; 1)? (2б)

4) Сколько корней имеет уравнение а) (1б) б) (1б) в) (1б) г) (1б).

5)Постройте график функции а) (2б), б) (2б).

Всего – 15б. «3» — 6б., «4» — 9 б., «5» -12 б.

Степенная функция. Вариант 2

1) Изобразите схематично график функции . (2 б) 2)Сравните: а) (1б), б) (1б), в) (1б). 3) Принадлежат ли графику функции точки А(-2; -256) и В(-1; 1)? (2б)

4) Сколько корней имеет уравнение а) (1б) б) (1б) в) (1б) г) (1б).

5)Постройте график функции а) (2б), б) (2б).

Всего – 15б. «3» — 6б., «4» — 9 б., «5» -12 б.

infourok.ru

Урок алгебры в 9 классе по теме «Свойства функций».

Урок алгебры в 9 классе

Тема урока «Свойства функций».

Тип урока: урок – практикум.

Цель урока: Расширить представление о свойствах функции.

Задачи: 1. Развивать умение описывать свойства функции по заданному графику.

2. Формировать познавательную активность учащихся.

3. Воспитывать аккуратность при построении графиков функций.

Оборудование: проектор, компьютер, мультимедийный продукт, распечатанные листы с графиками функций, бланки для ответов на тест, учебник «Алгебра, 9 класс» Ю.Н.Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов ( М.: Просвещение, 2012 год).

Структура урока:

1. Ознакомление с темой урока, постановка его целей. (2 мин)

2. Актуализация знаний учащихся :

а) повторение теоретического материала.(4 мин)

б) повторение графиков функций. (5 мин)

3. Отработка свойств функции (10 мин).

4. Психофизиологическая пауза (2 мин).

5. Закрепление материала. Самостоятельная работа (13 мин).

6. Объяснение домашнего задания (2 мин).

7. Подведение итогов урока (2 мин).

Ход урока:

1. Ознакомление с темой урока, постановка его целей.

2. Актуализация знаний учащихся. Повторение теоретического материала:

   • Дать определение функции

   • Что такое область определения функции?

   • Что такое область значений функции?

   • Дать определение нулей функции.

   • Дать определение промежутков знакопостоянства функции.

   • Дать определение возрастающей функции.

   • Дать определение убывающей функции.

Презентация. Слайды 2-6

а) 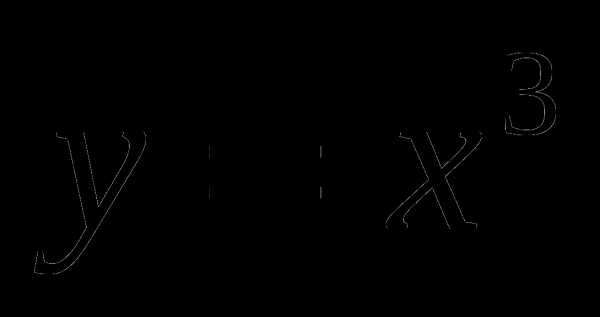б) в) < 0 г) х²

д) е)>0 ж) < 0 з).

• Учащимся раздаются бланки для заполнения. На работу отводится 1 мин.

• Проверяем ответы. Вызываю к доске одного из учащихся для заполнения таблицы.

• Остальным учащимся предлагаю поменяться бланками с соседом и выполнить взаимопроверку

3. а) Устная работа. На рисунке изображен график функции . Найдите значения переменной , при которой:

а) > 0, < 0 , = 0;

б) функция возрастает, убывает;

в) функция на отрезке принимает наибольшее значение, наименьшее значение.

Презентация. Слайд 7

б) разбираем задание из учебника: № 36.

1. D(g) = [ – 5; 5]

2. E(g) = [– 4; 6]

3. g (x) = 0 x = – 3;

4. g (x) > 0 x (– 3; 5]

g (x) < 0 x[– 5;- 3)

5. g(x) возрастает при x[– 5; 0] u [2; 5]

g (x) убывает при x[0; 2].

в) выполняем задание из учебника: № 38:

Начертите график какой-либо функции с областью определения [ – 3; 4] так, чтобы эта функция:

а) возрастала в промежутке [ – 3; 0] и убывала в промежутке [ 0; 4];

б) убывала в промежутке [ – 3; 1] и возрастала в промежутке [ 1; 4].

4. Психофизиологическая пауза. Ученики выполняют зарядку для глаз.

5. Закрепление материала. Самостоятельная работа.

Провести исследование функции по готовым чертежам

Презентация. Слайд 8

1 вариант

Перечислите свойства функции у = f(х), график которой изображен на рисунке:

1) Область определения функции: D(f) = ________________

2) Область значений функции: E (f) = ________________

3) Нули функции:_____________________________________

4) Промежутки знакопостоянства функции:

f(x) > 0 при _________________________________

f(х) < 0 при ________________________________

5) Функция убывает на промежутке _________________________

Функция убывает на промежутке ____________________________

Презентация. Слайд 9

2 вариант

Перечислите свойства функции у = f(х), график которой изображен на рисунке:

1) Область определения функции: D(f) = _______________________________

2) Область значений функции: E (f) = __________________________________

3) Нули функции:____________________________________________________

4) Промежутки знакопостоянства функции:

f(x) > 0 при ________________________________________________

f(х) < 0 при ________________________________________________

5) Функция убывает на промежутке ____________________________________

Функция убывает на промежутке _____________________________________

Ответы к самостоятельной работе:

1 вариант.

2 вариант.

1) D(f) = [- 6; 7]

2) E (f) = [- 3; 5]

3) f(x) = 0, х = — 6; х = — 2

4) f(x) > 0 при х(- 2; 7]

f(х) < 0 при х[- 6; — 2)

5) f(x) возр при х[- 4; 2]

f(x) убыв при х[- 6; — 4] и [2; 7]

1) D(f) = [- 4; 8]

2) E (f) = [-2; 4]

3) f(x) = 0, х = — 2; х = 3; х = 8

4) f(x) > 0при х[- 4;- 2) и (3; 8]

f(х) < 0 при х(- 2; 3)

5) f(x) возр при х [0; 6]

f(x) убыв при х[- 4; 0] и [6; 8]

Презентация. Слайд 10

• Учащиеся самостоятельно выполняют работу в тетрадях, после этого проводят взаимопроверку по готовым ответам и оценивают работу соседа.

6. Объяснение домашнего задания (2 мин).

По учебнику: повторить § 2,

№ 35( записать свойства функции), № 39(а,б) (построить графики), № 52 (в,г) ( повторение — квадратные уравнения)

7. Подведение итогов урока (2 мин).

Вопросы на повторение:

• Дать определение функции.

• Что такое область определения функции?

• Что такое область значений функции?

• Дать определение нулей функции.

• Дать определение возрастающей (убывающей) функции.

Сообщаются оценки за урок.

infourok.ru

Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс) на тему: Самостоятельная работа по теме» Функции» для 9 класса

По теме: методические разработки, презентации и конспекты

Самостоятельная работа по алгебре 9 класс»График квадратичной функции»

Работа состоит из двух вариантов. Содержит разнообразные задания и вопросы по теме «Постороение графика квадратичной функции», для ответов на которые требуется глубокое понимание материала. Количество…

самостоятельная работа по алгебре 9 класс по теме «Квадратичные неравенства»

Данная самостоятельная работа охватывает сразу несколько вопросов по теме «Квадратичные неравенства» и «Квадратный трехчлен», поэтому может быть использована на уроках итогового контроля. Задания пред…

Самостоятельные работы по геометрии. 9 класс, 1 полугодие.

Комплект рейтинговых самостоятельных работ по геометрии. 9 класс….

Самостоятельная работа по алгебре 9 класс по теме «Рациональные неравенства»

Самостоятельная работа состоит  из двух вариантах….

Самостоятельная работа по геометрии 9 класс по теме «Векторы»

Самостоятельная работа состоит из двух вариантов.. Одно задание на  среднюю линии трапеции, второе задание на построение векторов….

Самостоятельная работа по геометрии 9 класс Векторы (по материалам ОГЭ) с ответами

Работа по текстам Закрытого банка заданий ОГЭ 2016…

Самостоятельна работа по алгебре 9 класс по теме: « Область определения функции»

Самостоятельная работа в двух вариантах для учащихся в 9 классе….

nsportal.ru

Самостоятельная работа по алгебре 9 класс по теме

А – 9 Самостоятельная работа по теме: «График квадратичной функции».

1 вариант Ф.И. ______________________________________________________

Постройте графики функций:

у = (х – 3)²;

у = х²— 4;

у = 0,5(х + 7) ²;

у = 2 х²+ 1.

у = 3х²— 2;

у = 0,25 (х – 3)²;

у = 2 (х – 5)² + 4;

у = 0,5 (х+1)²— 5;

А – 9 Самостоятельная работа по теме: «График квадратичной функции».

2 вариант Ф.И. ______________________________________________________

Постройте графики функций:

у = х²— 8;

у = 3 х²+ 2;

у = 2(х + 6)²;

у = 0,5(х — 5)².

у = 0,25(х – 3)²;

у = 3х²— 2;

у = 0,5(х + 4) ²+ 3

у = 3 (х — 2)²— 5;

Самостоятельная работа по алгебре 9 класс по теме «График квадратичной функции» поможет в проверки знаний учащихся по данной теме, умение построить график на координатной плоскости.

Работа выполнена на листе А4 с координатными плоскостями к каждой функции на 2 варианта, что ускоряет процесс построения графиков квадратичной функции.

данная самостоятельная работа является одной из блока проверки знаний учащихся по теме «График квадратичной функции».                                                 

infourok.ru