|
1. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные |
|
|
2. Найдите угол |
|
|
3. В трапеции средняя линия равна 12, меньшее основание 5. Найдите длину большего основания. |
|
|
4. Найдите площадь трапеции, изображённой на рисунке. |
|
|
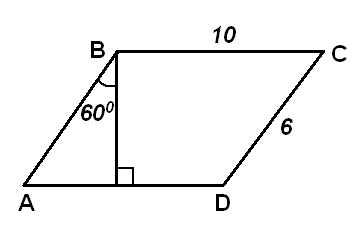
5. Найдите площадь параллелограмма, изображённого на рисунке. |
|
|
6. Величина центрального угла AOD равна 110°. Найдите величину вписанного угла ACB. |
|
|
7. Сторона ромба равна 26, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? |
|
|
8. В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине С равен |
|
|
9. Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см. |
|
|
10. В параллелограмме АВСD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм — прямоугольник. |
|
|
11. В прямоугольном треугольнике ОАВ катет ОА равен 4, катет АВ равен 5. Найдите тангенс угла АОВ. |
|
|
12. Медианы ВК и ЕМ треугольника ВСЕ пересекаются в точке О. Докажите, что треугольники КОМ и ВОЕ подобны. |
|
|
13. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. |
|
|
14. Длина тени громоотвода равна 9,5 м, в это же время вертикально воткнутый в землю кол высотой 1,6 м дает тень длиной 1,9 м. Найдите высоту громоотвода. Запишите ответ в виде целого числа или десятичной дроби. |
|
|
15. Хорды АВ и СD пересекаются в точке М, АМ = 4, ВМ = 6, МD = 2. Найдите CМ. |
|
|
16. В прямоугольном треугольнике АВС с прямым углом С известны катеты: АС=6, ВС=8. Найдите медиану СК этого треугольника. |
|
|
17. В равнобедренном треугольнике КDС угол СКD равен 30°. Найти внешний угол CDF. |
|
|
18. Основание АС равнобедренного треугольника АВС равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания АС. Найдите радиус окружности, вписанной в треугольник АВС. |
|
|
19. В равнобедренной трапеции АВСD сторона АВ равна 4, высота ВН равна 2, угол ВАН равен 30°, основание ВС равно 6. Найдите площадь трапеции. |
|
|
20. Медианы ВК и ЕМ треугольника ВСЕ пересекаются в точке О. Докажите, что треугольники КОМ и ВОЕ подобны. |
|
|
21. В треугольнике КОМ угол К равен 40°, угол О равен 30°. Найдите внешний угол при вершине М. |
|
|
22. Наклонная балка поддерживается тремя столбами, стоящими вертикально на равном расстоянии друг от друга. Длина двух меньших столбов 60см и 90см. Найдите длину большего столба. |
|
|
23. Прямоугольный газон обнесен изгородью длиной 30м. Площадь газона . Найдите длины сторон газона. |
|
|
24. Вершина В ромба ABCD соединена с серединой стороны AD в точке К. Найдите площадь четырехугольника KBCD, если площадь ромба ABCD равна 28 см2. |
|
|
25. Найдите площадь параллелограмма АВСD, если угол А равен 60°, основание АD равно 12 см, а длина стороны DC равна см. |
|
|
26. Найдите тангенс угла АОВ, изображенного на рисунке. |
|
|
27. Из точки M, лежащей вне окружности, проведены две секущие МD и МВ. Длина ВА равна 16см, АМ — 2см, длина СМ равна 4см. Найдите длину секущей МD. |
|
|
28. Треугольник АВС равнобедренный. ВF параллельна основанию треугольника АС. Докажите, что BF — биссектриса угла СВD. |
|
|
29. В трапеции АВСD сторона АВ равна 5см, длина равна 3см, длина основания ВС равна 6см, длина равна 4см. Найдите площадь трапеции АВСD. |
|
|
30. Найдите длину хорды окружности радиусом 13см, если расстояние от центра окружности до хорды равно 5см. |
|
|
31. Из точки А, лежащей вне окружности, проведены касательная АВ и секущая АD. Длина DC равна 9см, длина внешней части секущей СА равна 4см. Найдите длину касательной АВ. |
|
|
32. В выпуклом четырехугольнике KLMN точки А, В, С, D — середины сторон KL, LM, MN, NK соответственно. Известно, что KL = 3. Отрезки АС и BD пересекаются в точке О. Площади четырехугольников KAOD, LAOB и NDOC равны соответственно 6, 6 и 9. Найдите площадь четырехугольника МСОВ. |
|
multiurok.ru
Решение треугольников | Геометрия 9 класс | Примеры решения задач
Содержание страницы:
- – задачи 76 — 77 представлены с примерами решений и ответами по теме «Решение треугольников»;
- – онлайн задания, как найти решение треугольника через синус и косинус угла, рассматриваются в тестах 78 — 81;
- – решения, как найти угол, сторону треугольника, объясняются в контрольных работах 82 — 85.
Задача 76.

Дано: 
Треугольник ΔABC,
стороны треугольника a=10, b=7
Угол A = 60°
Решить треугольник: Угол по сторонам треугольника B, C, сторону c
Решение:
Известно, что формула синуса
, получаем выражение
Sin B = = = = ≈ 0,6062
Используя Sin B ≈ 0,6062, находим из тригонометрической таблицы («Четырехзначные математические таблицы» Владимира Модестовича Брадиса)
B = 37°19’
Тогда C = 180° — (60° + 37°19’) = 82°41’
Используя теорему синусов
, получаем равенство
с=≈ 11
Ответ: B = 37°19’; C = 82°41’; c ≈ 11
***
Задача 77.
Дано:
Треугольник ΔABC, стороны треугольника
a=6,3
b=6,3

C = 54°
Найти: Угол по сторонам треугольника A, B, сторону c
Решение:
Т.к. a=b=6,3, то треугольник ΔABC — равнобедренный.
Тогда A =B = (180° — 54°): 2 = 63°
Используя теорему синусов
, получаем равенство
с = = ≈ 5,7
Ответ: A =B = 63°; с ≈ 5,7
***
Наверх
Решение треугольников через синус и косинус угла
Задача 78.
Дано:
Треугольник ΔABC
A = 60°

B = 40°
c=14
Найти: угол треугольника C, стороны a,b
Решение:
C = 180° — (40° + 60°) = 80°
Используя теорему синусов
, получаем выражение

 a = ≈ 12
a = ≈ 12
b = ≈ 9
Ответ: C = 80°; a ≈ 12; b ≈ 9
***
Задача 79.

Дано:
Треугольник ΔABC
BC=a=6
AC=b=7,3
AB=c=4,8
Найти: углы треугольника A, B, C по сторонам
Решение:
Известно, что формула косинуса
, находим косинус угла B
Cos B = = = = ≈ 0,0998263
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла B
B = 84°16’
Используя формулу теоремы косинусов, находим косинус угла C
Cos C = = =
= ≈ 0,7562785
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла C
C = 40°52’
Тогда угол A равен A =180° — (40°52’ + 84°16’) = 54°52’
Ответ: A = 54°52’ ; C = 40°52’ ; B = 84°16’
***
Задача 80.
Дано:
Треугольник ΔABC
A = 30°
C = 75°
b = 4,5
Найти: угол B, стороны треугольника a,c
Решение:
B = 180° — (30° + 75°) = 75°
Т.к. два угла в треугольнике равны B =C = 75°, тогда треугольник ΔABC — равнобедренный.
Значит, две стороны равны AC=AB=b=c=4,5
Используя теорему синусов
,
находим сторону BC=a
a = ≈ 2,3
Ответ: B = 75°; a ≈ 2,3 ; c = 4,5
***
Задача 81.
Дано:
Треугольник ΔABC, длины трех его сторон
| 1) a=5 , b=c=4 | 2) a=5 , b=9 , c=6 | 3) a=17 , b=15 , c=8 |
Найти: является ли треугольник тупоугольным, прямоугольным, остроугольным
Решение:
1) Т.к. b=c=4, то треугольник ΔABC — равнобедренный, и, значит, остроугольный.

2) Используя формулу теоремы косинусов
, находим косинус угла A
Cos A = 
= =0
Тогда угол A равен A = 90°. Следовательно, треугольник ΔABC — прямоугольный.
3) Используя формулу теоремы косинусов
, находим косинус угла B
Cos B = == -< 0.
Т.к. значение косинуса угла B меньше нуля, следовательно, угол B — тупой, а треугольник ΔABC — тупоугольный.
***
Наверх
Решение треугольника через угол по сторонам
Задача 82.

Дано:
Треугольник ΔABC, два угла и сторона
A = 45°
C = 30°
AD = 3 м
Найти: длину всех сторон треугольника ΔABC = ?
Решение:
Зная размер двух углов в треугольнике ΔABC, находим третий уголB = 180° — (30° + 45°) = 105°
Найдем угол DAB и рассмотрим ΔADC

DAB = 180° — (90° + 45 + 30°) = 15°

DAC = 15° + 45° = 60°
Используя теорему синусов
, находим сторону AC

AC = (3 • 1) • 2 = 6 (м)
Используя теорему синусов
, находим сторону AB


AB = ≈ 3 (м)
Используя теорему синусов
, находим сторону BC
BC =≈ 4 (м)
Ответ: AB ≈ 3 м, AC = 6 м, BC ≈ 4 м.
***

Задача 83.
Дано:
Треугольник ΔABC
Три стороны a = 14, b = 18,
c = 20
Найти:
все углы треугольника ΔABC = ?
Решение:
Т.к. против большего угла лежит большая сторона, то используя формулу теоремы косинусов
Cos C =, находим косинус угла C
Cos C = = ≈ 0,24
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C
C ≈ 76°07’
Используя формулу теоремы косинусов
Cos B =, находим косинус угла B
Cos B = ==≈ 0,4857
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла B
B ≈ 60,941 ≈ 60°57’
Следовательно, A = 180° — (76°13’ + 60°57’) ≈ 42°56’
Ответ: A ≈ 42°56’ ; B ≈ 60°57’ ; C ≈ 76°07’
***

Задача 84.
Дано:
Треугольник ΔEKP, сторона и два угла
EP = 0,75
P = 40°
K = 25°
Найти: сторону треугольника PK = ?
Решение:
Используя теорему синусов
, находим сторону PK

E = 180° — (40° + 25°) =115°
Sin 115° = Sin (180° — 65°) = Sin 65°
Тогда 



PK = ≈ 1,61
Ответ: PK ≈ 1,61.
***
Задача 85.
Дано:
Треугольник ΔABC, две стороны и угол
b = 18, c = 12
A = 50°
Найти: решить треугольник — определить значение стороны и двух углов
(a, B, C ) = ?
Решение:
Используя формулу теоремы косинусов
, получаем
a = = ≈ 13,8
Используя формулу теоремы косинусов
Cos C =, находим косинус угла C
Cos C == ≈ 0,7457
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C
C ≈ 41°47’
Следовательно, B = 180° — (50° + 41°47’) ≈ 88°13’
Ответ: a ≈ 13,8 ; B ≈ 88°13’ ; C ≈ 41°47’
***
www.petrovskov.ru
Решебники (ГДЗ) по предмету Геометрия 9 класс онлайн
Геометрия полна приключений
О том, что математика приводит ум в порядок, известно с древних времен. Не только великие математики, но философы, другие ученые и даже поэты восхищались стройностью гипотез, точностью доказательств и неоспоримостью выводов ее величества геометрии. А. С. Пушкин считал, что вдохновение необходимо в этом предмете ничуть не меньше, чем в поэзии.
Интересные факты об интересном предмете
- Геометрия Евклида, основы которой изучаются в курсе 9 класса, далеко не единственная. Существует сферическая геометрия Римана и Лобачевского.
- Треугольник имеет сумму углов большую 180° в предмете Римана, у Лобачевского – меньшую.
- Правильные многогранники называются: икосаэдр, октаэдр, додекаэдр, тетраэдр, куб. Их всего пять.
- Геометрическая фигура, образующаяся при пересечении трех окружностей радиусом r, центры которых лежат в вершинах треугольника со стороной r ,являющегося равносторонним — это треугольник Рело. С помощью сверла, изготовленного на основе данного треугольника, можно высверлить квадратное отверстие.
- День числа π празднуется математиками дважды: 14 марта (3.14) и 22 июня (22/7=3.14).
Особенности изучения геометрии
Формирование пространственного воображения, развитие логики, невозможно без представлений о свойствах геометрических фигур. Решение конструктивных и вычислительных задач способствует совершенствованию интуиции. Раздел ГДЗ 9 класс геометрия поможет сравнить придуманный ход решения любой задачи, вызывающей затруднения, с наиболее оптимальным. Не так просто разобраться в хитросплетениях разложения векторов, составлении уравнений окружности, теоремах синусов и косинусов. Непростым является и понятие вписанных и описанных окружностей, осевой и центральной симметрии. Все разделы предмета станут доступными и ясными, если проработать решебники 9 класс геометрия, в котором приведены ответы всех домашних заданий. Разобраться в представленном решении и получить хорошую оценку станет гораздо проще.
Доступность информации
Даже если нет возможности воспользоваться компьютером для выхода в интернет, не стоит отчаиваться. Попасть на наш сайт можно в любое время с мобильного телефона. Современные технологии позволяют получать необходимую информацию в режиме онлайн, не требуя при этом оплаты и регистрации. Наш портал – лучший помощник в учебе, экономящий время и силы.
Ждем Вас на нашем сайте!
vklasse.vip
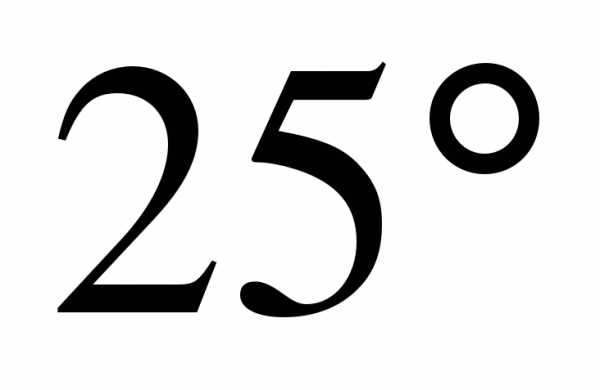 и
и  соответственно.
соответственно.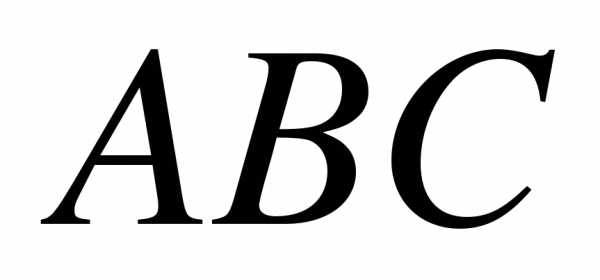 равнобедренной трапеции
равнобедренной трапеции 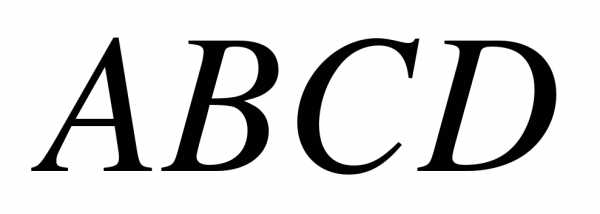 , если диагональ
, если диагональ 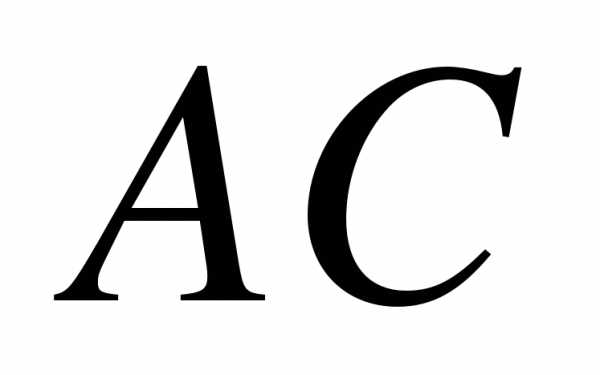 образует с основанием
образует с основанием  и боковой стороной
и боковой стороной  углы, равные
углы, равные  и
и  соответственно.
соответственно.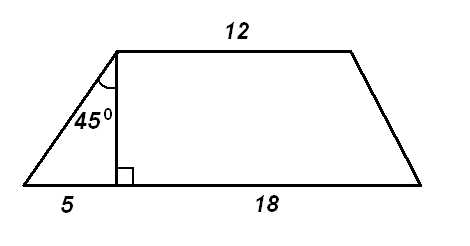
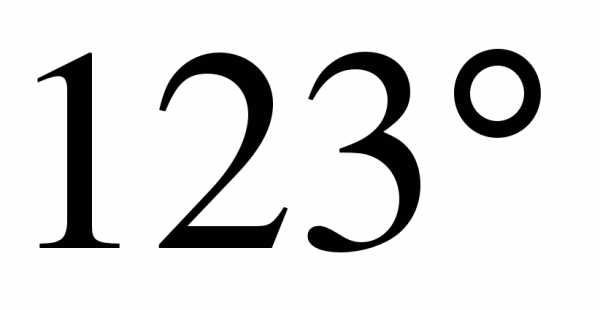 . Найдите величину угла ВАС.
. Найдите величину угла ВАС.