| Этапы урока | Деятельность учителя | Деятельность учащихся |
| 1.Оргмомент
(1 мин) |
|
слайд№1 |
| 2.Постановка
цели урока
(3 мин) |
|
Учащиеся разгадывают шараду и отвечают,
что знают о векторе из физики: слайд№2 бывают
Учащиеся записывают тему урока в тетрадь
|
| 3.Самостоятельная работа в парах по
изучению нового материала( работа с учебником) (5
4. Проверка парной работы
(5 мин) |
Учащимся предлагается прочитать пункт
76 учебника и составить вопросы по материалу пункта учебника:
Учитель слушает и корректирует составленные
|
Учащиеся читают новый материал и вместе
с соседом по парте формулируют вопросы по его содержанию Учащиеся задают составленные
|
| 5. Просмотр презентации нового
материала (10 мин) |
Учитель демонстрирует слайды
презентации , задает вопросы: — назвать все
— найти длины векторов;
— выполнить задания на слайде 10
— указать сонаправленные и противоположно
— отложить вектор с, равный вектору а от точек К,
|
— Учащиеся просматривают презентацию,
записывают определения в тетрадь Слайды №5, 7,8, 10,12 Учащиеся отвечают на вопрос учителя Слайды
Два ученика у доски , все остальные на местах
После выполнения заданий по щелчку мыши
Учащиеся выполняют задание в тетрадях, а один
|
| 6. Музыкальная пауза 1 мин | Учитель просит учащихся встать,
потанцевать вместе с героями слайда |
Слайд №14-музыкальная физминутка,
запускается
|
| 6. Закрепление изученного материала
(10
|
Обучающий тест.
Самопроверка теста
Индивидуальное задание №745 ( на доске)
Проверка работы у доски |
Учащиеся отвечают на вопросы теста
письменно в тетради. Слайд№15 Учащиеся
Один ученик работает у доски
Учащиеся проверяют работу товарища |
| 7. Дифференцированная самостоятельная
работа (5 мин) |
Учитель предлагает учащимся два
задания на выбор для самостоятельной работы |
Учащиеся по выбору выполняют задание№1
или №2 Слайд№17 |
| 7.Подведение итога урока
(2 мин) |
Задаёт классу следующие вопросы:
|
отвечая на вопросы учителя, подводят
итог урока выражают мнение об уроке,
|
| 8. Домашнее задание
(1 мин) |
— задаёт домашнее задание:
выучить
|
записывают домашнее задание в дневники
Слайд №18 |
| 9. Рефлексия
(2 мин) |
Учитель просит учащихся продолжить
фразу «Сегодня на уроке я:
— благодарит учащихся за работу
— объявляет об окончании урока |
Слайд№19 |
xn--i1abbnckbmcl9fb.xn--p1ai
ГЕОМЕТРИЯ
|
|
na-uroke.in.ua
Урок по геометрии по теме «Движение». 9-й класс
Разделы:
Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (3,9 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- ввести понятие движения;
- развивать умения выполнять построения
симметрии относительно точки, симметрии
относительно прямой, построения параллельного
переноса, поворот по и против часовой стрелки;
Задачи урока:
- научить строить виды движений: осевую
симметрию, центральную симметрию, параллельный
перенос, поворот.
Оборудование:
- оформлена доска с названием темы и целью урока;
- документ-камера, экран, ПК;
- презентация “Движение и виды движения.ppt”;
- раздаточный материал (геометрические фигуры,
разного цвета, карточки с заданиями для
выполнения самостоятельной работы).
Ход урока
1. Организационный момент.
Сообщение учителя о цели урока и порядке его
проведения.
2. Вступительное слово учителя.
Теме “Движения” посвящена последняя 13 глава
учебника по геометрии (автор Л.С. Атанасян.
Геометрия. 7-9 кл.)
В это время на экране демонстрируется схема
видов движения (Рисунок1). Учитель предлагает
учащимся нарисовать эту схему в тетрадях.
Рисунок 1
Сделаем краткий исторический экскурс в теорию
движений. Первым, кто начал доказывать некоторые
геометрические предложения, считается
древнегреческий математик Фалес Милетский (625-547
г. до н.э.).: ресурс доступа: https://ru.wikipedia.org/. Именно
благодаря Фалесу геометрия начала превращаться
из свода практических правил в подлинную науку.
До Фалеса доказательств просто не существовало.
Каким же образом проводил Фалес свои
доказательства? Для этой цели он использовал
движения. Движение – это преобразования фигур,
при котором сохраняются расстояния между
точками. Если две фигуры точно совместить друг с
другом посредством движения, то эти фигуры
одинаковы, равны. Именно таким путём Фалес
доказал ряд первых теорем геометрии. Считается,
что он первым сформулировал и доказал несколько
геометрических теорем, а именно:
- вертикальные углы равны;
- имеет место равенство треугольников по одной
стороне и двум прилегающим к ней углам; - углы при основании равнобедренного
треугольника равны; - диаметр делит круг на две равные части;
- вписанный угол, опирающийся на диаметр,
является прямым.
Фалес научился определять расстояние от берега
до корабля, для чего использовал подобие
треугольников. В основе этого способа лежит
теорема, названная впоследствии теоремой Фалеса:
если параллельные прямые, пересекающие стороны
угла, отсекают равные отрезки на одной его
стороне, то они отсекают равные отрезки и на
другой его стороне.
Легенда рассказывает о том, что Фалес, будучи в
Египте, поразил фараона Амасиса тем, что сумел
точно установить высоту пирамиды, дождавшись
момента, когда длина тени палки становится
равной её высоте, и тогда измерил длину тени
пирамиды.
3. Представление нового теоретического
материала.
Любое отображение, при котором сохраняется
расстояние между точками, называется движением.
Кроме того, отображение ещё называют
перемещением.
При движении отрезки переходят в отрезки,
прямые — в прямые, лучи — в лучи, треугольник
переходит в треугольник, сохраняется градусная
мера углов, сохраняется площадь многоугольников.
При изучении геометрии вы уже встречались с
движением при доказательстве теорем о равенстве
треугольников и фигур. Равенство фигур
определяется с помощью наложений.
Учитель: фигура F равна фигуре F1
, если фигуру F можно совместить
наложением с фигурой F1 . Наложение — это
отображение плоскости на себя. При движении
любая фигура отображается на равную ей фигуру.
Параллельный перенос является движением.
Поворот является движением.
Выполним параллельный перенос (Рисунок 2).
Рисунок 2
Для того чтобы построить параллельный перенос
на заданный вектор, необходимо из концов отрезка
провести лучи сонаправленные заданному вектору.
Измерить длину вектора и отложить на
сонаправленных лучах данную длину.
Учитель: Мы познакомились с видом
симметрии — параллельным переносом на заданный
вектор.
Учитель: Построим отрезок А1В1
симметричный отрезку АВ относительно
прямой l. (Рисунок 3).
Рисунок 3
Для того чтобы построить отрезок А1В1
симметричный отрезку АВ относительно
прямой l необходимо:
1) опустить перпендикуляр из точки А на
прямую l ;
2) измерить отрезок АО с помощью циркуля;
3) отложить от точки О отрезок ОА1 = АО
;
4) опустить перпендикуляр из точки В на
прямую l;
5) измерить отрезок ВК с помощью циркуля;
6) отложить от точки К отрезок КВ1 = ВК
;
7) соединить точку А1 с точкой В1.
Учитель: Этот вид симметрии (движения)
называется — осевая симметрия относительно
прямой.
Учитель: Рассмотрим построение
центральной симметрии А1В1С1
симметричного АВС
относительно центра О с помощью рисунка,
изображённого на доске (Рисунок 4).
Рисунок 4
Итак, мы познакомились ещё с одним видом
симметрии — центральная симметрия относительно
точки.
Учитель: Сравним полученные
отображения. Что общего вы заметили в них?
Ученики: (Ответы учащихся).
Учитель: Правильно. Фигуры при
преобразовании перешли в равные фигуры.
Центральная, осевая симметрии и параллельный
перенос являются движением. Это и есть тема
нашего урока.
4. Итог урока: учитель подводит итог урока,
опираясь на цели.
5. Домашнее задание.
п.п. 113,114 №№ 1159, 1162.
6. Задания к уроку.
Сейчас, для закрепления пройденного материала,
посмотрим презентацию к уроку на тему “Движение
и виды движения”, а затем каждый из вас выполнит
самостоятельную работу (работа выполняется на
отдельных листах).
Фамилия, Имя учащегося ______________________
| № 1
осевая |
Построить C1E1K1 симметричный СЕК относительно прямой l.
Рисунок 5 |
| № 2
центральная |
Построить отрезок В1С1 симметричный отрезку ВС относительно центра О.
Рисунок 6 |
| № 3
параллельный |
Построить параллельный перенос МNК на вектор
Рисунок 7 |
Спасибо за урок!
13.02.2016
xn--i1abbnckbmcl9fb.xn--p1ai
|
№ слайда |
Текст |
Советы |
| 1 | Заголовок | |
| 2 | Полезные факты и теоремы. О равенстве углов со взаимно перпендикулярными сторонами. |
Приводится чертеж и даны ссылки на
задачи №1, №2 и №5, которые используют этот факт. Нажав на зеленую кнопку “Задача 1”, Вы попадаете на слайд №13 с текстом задачи №1. Задача занимает слайды №13-15, вернуться – кнопка “Нужный факт”. Нажав на зеленую кнопку “Задача 2”, Вы попадаете на слайд №16 с текстом задачи №2. Задача занимает слайды №16-17, вернуться – кнопка “Нужный факт”. Нажав на зеленую кнопку “Задача 5”, Вы попадаете на слайд №23 с текстом задачи №5. Задача занимает слайды №23-24, вернуться – кнопка “Нужный факт”. |
| 3 | Полезные факты и теоремы. О точках пересечения медиан, биссектрис, высот треугольника. Три биссектрисы треугольника пересекаются в одной точке. Три высоты треугольника пересекаются в одной точке (ортоцентр треугольника). Три медианы треугольника пересекаются в одной точке (центроид треугольника) и делятся ею в отношении 2:1, считая от вершины. |
Нажав на кнопку “Задача 4”, Вы
попадаете на слайд №19 с текстом задачи №4, задача занимает слайды №19-22, вернуться – кнопка “Нужный факт” (расположена только на слайдах 19-20). |
| 4 | Полезные факты и теоремы. Свойства средней линии трапеции. Средняя линия параллельна основаниям трапеции. Средняя линия равна полусумме оснований трапеции. Средняя линия (и только она) делит пополам любой отрезок, заключенный между основаниями трапеции. Эти теоремы справедливы и для средней линии треугольника |
Нажав на зеленую кнопку “Задача 6”, Вы
попадаете на слайд №25 с текстом задачи №6. Задача занимает слайды №25-27, вернуться – кнопка “Нужный факт” (расположена только на слайде 25). |
| 5 | Полезные факты и теоремы. Свойство медианы в прямоугольном треугольнике. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине. Обратная теорема. Если в треугольнике одна из медиан равна половине стороны, к которой она проведена, то этот треугольник прямоугольный. |
Нажав на зеленую кнопку “Задача 5”, Вы
попадаете на слайд №23 с текстом задачи №5. Задача занимает слайды №23-24, вернуться – кнопка “Нужный факт”. |
| 6 | Полезные факты и теоремы. Свойство биссектрисы внутреннего угла треугольника. Биссектриса внутреннего угла треугольника делит сторону, к которой она проведена, на части, пропорциональные прилежащим сторонам. |
Приводится чертеж и дана ссылка на
задачу, которая использует этот факт. |
| 7 | Полезные факты и теоремы. Метрические соотношения в прямоугольном треугольнике. – теорема Пифагора |
Приводится чертеж и дана ссылка на
задачу, которая использует этот факт. |
| 8 | Полезные факты и теоремы. Определение вида треугольника по его сторонам. Пусть а, b и с – стороны треугольника, причем с – наибольшая сторона, тогда: если с2 < а2 + b2, то треугольник остроугольный; если с2 = а2 + b2, то треугольник прямоугольный; если с2 > а2 + b2, то треугольник тупоугольный. |
Приводится чертеж и дана ссылка на
задачу №9, которая использует этот факт. Нажав на кнопку “Задача 9”, Вы попадаете на слайд №34 с текстом задачи №9, вернуться – кнопка “Нужный факт”. |
| 9 | Полезные факты и теоремы. Метрические соотношения в параллелограмме. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: d12 + d22 = 2a2 + 2b2. |
Приводится чертеж и дана ссылка на
задачу №3, которая использует этот факт. Нажав на кнопку “Задача 3”, Вы попадаете на слайд №18 с текстом задачи №3, вернуться – кнопка “Нужный факт”. |
| 10 | Полезные факты и теоремы. Обобщенная теорема подобия. Если два треугольника подобны, то любой линейный элемент (или сумма линейных элементов) одного треугольника относится к соответствующему линейному элементу (или сумме соответствующих линейных элементов) другого треугольника как соответственные стороны (линейными элементами являются соответственные медианы, высоты, биссектрисы, периметры, радиусы описанной и вписанной окружностей) |
Дана ссылка на слайд №36 с задачей №9,
которая использует этот факт, вернуться – кнопка “Нужный факт”. |
| 11 | Три пути доказательства равенства
отрезков. Рассмотреть эти отрезки как стороны двух треугольников и доказать, что треугольники равны. Рассмотреть эти отрезки как стороны одного треугольника и доказать, что треугольник равнобедренный. Заменить отрезок а равным отрезком а1, отрезок b равным отрезком b1 и доказать равенство отрезков а1 и b1. |
|
| 12 | Дополнительные построения. Проведение прямой, параллельной или перпендикулярной одной из имеющихся. Удвоение медианы треугольника с целью достроить треугольник до параллелограмма. Проведение вспомогательной биссектрисы. Дополнительные построения, связанные с окружностью. |
|
| 13 | Задача № 1. Две взаимно перпендикулярные прямые пересекают стороны АВ, ВС, CD, AD квадрата ABCD в точках E, F, K, L соответственно. Докажите, что ЕК = FL. |
Слайд содержит только условие задачи и
чертеж. Кнопка “Нужный факт” переключает на слайд №2. Можно обсудить условие, выслушать предложения учащихся. |
| 14 | Задача № 1. Проведем прямые, параллельные сторонам квадрата, … |
По щелчку появляется чертеж с
дополнительным построением. |
| 15 | Задача № 1. … тогда интересующие нас стороны ЕК и FL станут гипотенузами двух прямоугольных треугольников. Доказав равенство треугольников, докажем равенство гипотенуз. |
Предложите учащимся доказать равенство
прямоугольных треугольников. |
| 16 | Задача № 2. На сторонах АВ и ВС треугольника ABC вне его построены квадраты ABDE и BCKM. Докажите, что отрезок DM в два раза больше медианы BP треугольника ABC. |
Слайд содержит условие задачи и чертеж. Кнопка “Нужный факт” переключает на слайд №2. Можно обсудить условие, выслушать предложения учащихся |
| 17 | Задача № 2. Решение. Применим прием удвоения медианы, докажем, что ABCF – параллелограмм. Затем докажем равенство треугольников DBM и BCF, сделаем вывод о равенстве DM и BF. Учтем свойство диагоналей параллелограмма, откуда следует, что DM = 2BP. |
Предложите учащимся доказать, что ABCF
– параллелограмм, затем равенство треугольниковDBM и BCF. |
| 18 | Задача № 3. Стороны треугольника а, b, c. Вычислить медиануmc, проведенную к стороне с. Решение. Применим прием удвоения медианы докажем, что ABCР – параллелограмм. Затем применим к этому параллелограмму свойство: сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: CP2 + AB2 = 2AC2 + 2BC2, т.е. (2mc)2 + c2= 2b2 + 2a2. Выразим |
Слайд содержит условие задачи и чертеж. Кнопка “Нужный факт” переключает на слайд №9. |
| 19 | Задача № 4. Доказать, что в любом треугольнике сумма медиан меньше периметра, но больше 3/4 периметра. Предлагается краткий план решения. |
Слайд содержит условие задачи и чертеж. Кнопка “Нужный факт” переключает на слайд №3. |
| 20 | Задача № 4. Сначала докажем, что сумма медиан больше 3/4 периметра. |
Используем свойство точки пересечения
медиан и неравенство треугольника. На слайде приведено достаточно полное доказательство. |
| 21 | Задача № 4.
|
Предложите учащимся провести
аналогичные рассуждения для BМС и ABМ. |
| 22 | Задача № 4. Теперь докажем, что сумма медиан меньше периметра. Удвоим медиану ABС и рассмотрим BСК |
|
| 23-24 | Задача № 5. Доказать, что в неравнобедренном прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой, проведенной из той же вершины. |
Слайд содержит условие задачи и чертеж. Кнопка “Нужный факт 1” переключает на слайд №2. Кнопка “Нужный факт 2” переключает на слайд №5. На слайдах полное решение задачи. |
| 25-27 | Задача № 6. В параллелограмме со сторонами а и b проведены биссектрисы внутренних углов. Найдите длины диагоналей четырехугольника, образованного в пересечении биссектрис. |
Слайд содержит условие задачи и чертеж. Кнопка “Нужный факт” переключает на слайд №4. Все появляется по щелчку мыши. На слайдах полное решение задачи. |
| 28 | Важный результат задачи 6. Биссектрисы углов, прилегающих к боковой линии трапеции, пересекаются под прямым углом в точке, лежащей на средней линии трапеции. |
|
| 29 | Замечание, которое пригодится для
решения следующей задачи. Основным методом составления уравнений в геометрических задачах является метод опорного элемента. Он заключается в том, что один и тот же элемент (сторона, угол, площадь, радиус и т.д.) выражается через известные и неизвестные величины двумя различными способами и полученные выражения приравниваются. В качестве опорного элемента часто выбирается площадь фигуры. Тогда говорят, что используется метод площадей. |
|
| 30 | Задача № 7. Стороны треугольника а, b и с. Вычислить высоту hc, проведенную к стороне с. Решение. Высота hc является общим катетом двух прямоугольных треугольников АСН и СНD. Пусть АН = х, тогда ВН = с – х. (Если треугольник АСВ тупоугольный, то ВН = с + х) Воспользовавшись теоремой Пифагора найдем СН2 из АСН и СНD. Тогда из уравнения b2 – x2 = a2 – (c – x)2 получим . Из АСН найдем СН: , . |
Слайд содержит условие задачи и чертеж. Сначала рассматривается случай остроугольного треугольника. Случай тупоугольного треугольника после обсуждения можно предложить для домашней работы. Полезно решить эту же задачу, используя метод площадей. С одной стороны , с другой стороны . |
| 31 | Замечание, которое пригодится для
решения следующей задачи. Если в задаче требуется найти отношение каких-либо величин, то она решается методом введения вспомогательного параметра. В начале решения задачи какая-либо линейная величина принимается как известная. Обозначив ее буквой а, выражаем через нее те величины, отношение которых требуется найти. Тогда при составлении искомого отношения вспомогательный параметр а сократится. |
|
| 32-33 | Задача № 8. В треугольнике АВС стороны АВ и ВС равны, ВН высота. На стороне ВС взята точка D так, что BD : DC = 1 : 4. Найдите в каком отношении отрезок AD делит высоту ВН. |
Слайды содержат условие задачи, чертежи
и полное решение. |
| 34-36 | Задача № 9. В треугольник со сторонами 10, 17 и 21 см, вписан прямоугольник так, что две его вершины находятся на одной стороне треугольника, а две вершины – на двух других сторонах треугольника. Найти стороны прямоугольника, если известно, что его периметр равен 22,5 см. |
Слайды содержат условие задачи и
чертеж. Кнопка “Нужный факт” переключает слайд №34 на слайд №8, а слайд №36 на слайд №10. На слайдах полное решение задачи. |
| 37-38 | Задача № 10. В треугольнике АВС известно, что угол А в два раза больше угла С, сторона ВС на 2 см больше стороны АВ, а АС=5 см. Найти АВ и АС. |
Слайды содержат условие задачи и
чертеж. На слайдах полное решение задачи. |
| 39 | Спасибо за внимание! |
xn--i1abbnckbmcl9fb.xn--p1ai
ПОУРОЧНЫЕ РАЗРАБОТКИ ПО ГЕОМЕТРИИ 9 класс — разработки уроков — авторские уроки — план-конспект урока
Урок 1–2. Повторение. Решение задач
ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ
Урок 1. Понятие вектора. Равенство векторов
Урок 2. Сумма двух векторов. Законы сложения векторов. Правило параллелограмма
Урок 3. Сумма нескольких векторов
Урок 4. Вычитание векторов
Урок 5. Произведение вектора на число
Урок 6. Решение задач. Произведение вектора на число
Урок 7. Применение векторов к решению задач
Урок 8. Средняя линия трапеции
МЕТОД КООРДИНАТ
Урок 1. Разложение вектора по двум данным неколлинеарным векторам
Урок 2. Координаты вектора
Урок 3. Связь между координатами вектора и координатами его начала и конца. Простейшие задачи в координатах
Урок 4. Простейшие задачи в координатах. Решение задач
Урок 5. Уравнение линии на плоскости. Уравнение окружности
Урок 6. Уравнение окружности. Решение задач
Урок 7. Уравнение прямой
Урок 8-9. Решение задач
Урок 10. Контрольная работа № 1
СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
Урок 1. Синус, косинус, тангенс. Основное тригонометрическое тождество
Урок 2. Формулы приведения. Формулы для вычисления координат точки
Урок 3. Решение задач
Урок 4. Теорема о площади треугольника. Теорема синусов
Урок 5. Теорема косинусов
Урок 6. Решение треугольников
Урок 7. Измерительные работы
Урок 8. Решение задач
Урок 9. Угол между векторами. Скалярное произведение векторов
Урок 10. Скалярное произведение в координатах. Свойства скалярного произведения векторов
Урок 11. Решение задач
Урок 12. Контрольная работа № 2
ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА
Урок 1. Правильный многоугольник. Окружность, описанная около правильного многоугольника
Урок 2. Окружность, вписанная в правильный многоугольник
Урок 3. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Урок 4. Построение правильных многоугольников
Урок 5. Длина окружности
Урок 6. Площадь круга
Урок 7. Площадь кругового сектора
Урок 8. Решение задач
Урок 9-10. Решение задач по материалу главы XII
Урок 11. Контрольная работа № 3
ДВИЖЕНИЯ
Урок 1-3. Отображение плоскости на себя. Понятие движения
Урок 4. Параллельный перенос
Урок 5-6. Поворот
Урок 7. Решение задач
Урок 8. Контрольная работа № 4
НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ
Урок 1. Предмет стереометрии. Многогранники
Урок 2. Призма. Параллелепипед
Урок 3. Многогранники. Объем тела
Урок 4. Пирамида
Урок 5. Тела и поверхности вращения
Урок 6. Тела и поверхности вращения
Урок 7. Сфера и шар
Урок 8-9. Об аксиомах и планиметрии
РЕШЕНИЕ ЗАДАЧ
Треугольник
Окружность
Четырехугольники. Многоугольники
Векторы. Метод координат. Движения
Литература
compendium.su
| Рабочие программы | ||
| 8 класс | Рабочая программа по геометрии для 8 класса к УМК Л.С. Атанасяна | |
 |
Презентации к урокам | |
| 7 класс | Признаки равенства треугольников | |
| 8 класс | Вводное повторение курса геометрии 7 класса | |
| 8 класс | Четырёхугольники | |
| 8 класс | Осевая и центральная симметрии | |
| 8 класс | Площадь | |
| 8 класс | Теорема Пифагора | |
| 8 класс | Подобие треугольников | |
| 8 класс | Применение подобия к доказательству теорем и решению задач | |
| 8 класс | Соотношения между сторонами и углами прямоугольного треугольника | |
| 8 класс | Касательная к окружности | |
| 9 класс | Вводное повторение курса геометрии 8 класса | |
| 9 класс | Движение на плоскости | |
| 9 класс | Соотношения между сторонами и углами треугольника | |
| 9 класс | Правильные многоугольники | |
| 9 класс | Решение треугольников | |
| 9 класс | Векторы на плоскости | |
| 9 класс | Метод координат на плоскости | |
| 9 класс | Скалярное произведение векторов | |
| Математические этюды (материалы сайта http://www.etudes.ru/) | ||
| 8 класс | Пифагоров треугольник | |
| 8 класс | Головоломка Пифагора | |
| 8 класс | Площади фигур | |
| 8 класс | Площадь трапеции | |
| Наглядный материал | ||
| 8 класс | Окружность. Касательная к окружности. Центральный и вписанный углы. Задачи на готовых чертежах | |
| 8 класс | Прямоугольный треугольник. Соотношение между сторонами и углами в прямоугольном треугольнике. Задачи на готовых чертежах | |
| 8 класс | Трапеция. Площадь трапеции. Задачи на готовых чертежах | |
| 8 класс | Подобие треугольников | |
| 8 класс | Четыре замечательные точки треугольника | |
| 9 класс | Сложение векторов | |
| 9 класс | Равносторонний треугольник | |
| 9 класс | Правильный шестиугольник | |
| 9 класс | Правильный четырехугольник | |
| 8-9 классы | Прямоугольный треугольник | |
semenova-klass.moy.su
К урокам геометрии в 9 классе по теме ДВИЖЕНИЯ

ДВИЖЕНИЯ
Геометрия, 9 класс
К учебнику Л.С.Атанасяна
Автор: Софронова Наталия Андреевна,
учитель математики высшей категории
МОУ «Упшинская основная общеобразовательная школа»
Оршанского района Республики Марий Эл
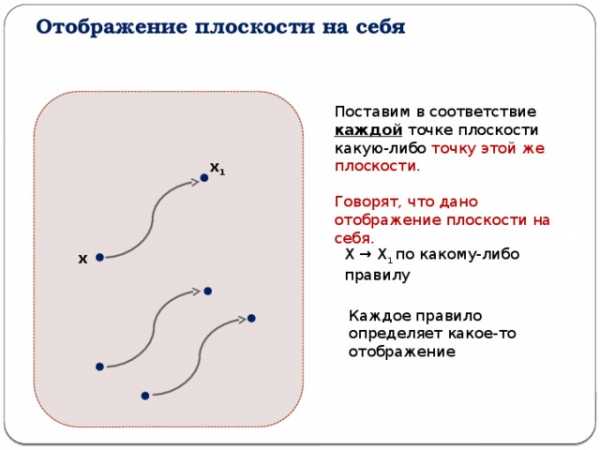
Отображение плоскости на себя
Поставим в соответствие каждой точке плоскости какую-либо точку этой же плоскости.
Говорят, что дано отображение плоскости на себя.
х 1
Х → Х 1 по какому-либо правилу
х
Каждое правило определяет какое-то отображение

Осевая симметрия
Пусть дана какая-то прямая m , которую назовем осью симметрии. Осевой симметрией называется отображение плоскости на себя, при котором каждой точке Х ставится в соответствие точка Х 1 по следующему правилу:
m
М 1
X 1
Как для точки М построить точку М 1 ?
Из точки М опустим перпендикуляр МР на прямую m.
Отложим на прямой МР отрезок РМ 1 , равный отрезку МР.
Точка, лежащая на прямой m, симметрична сама себе
X
Р
К
М
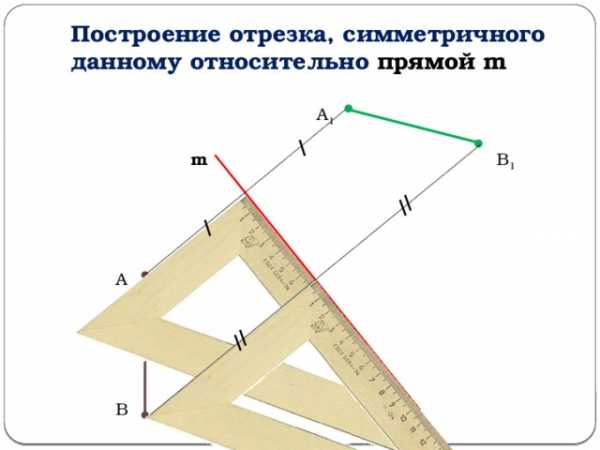
Построение отрезка, симметричного данному относительно прямой m
A 1
m
B 1
A
B
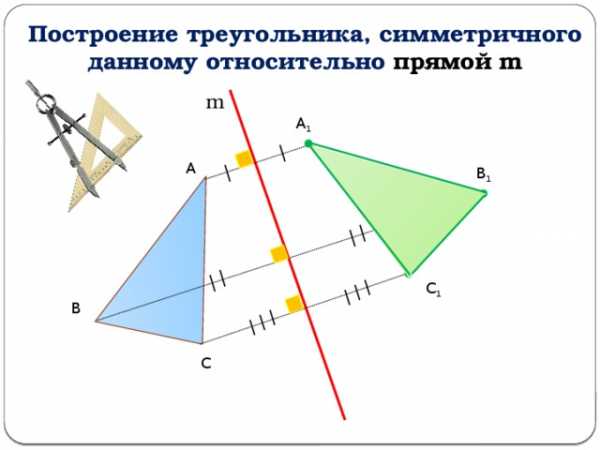
Построение треугольника, симметричного данному относительно прямой m
m
А 1
А
В 1
С 1
В
С
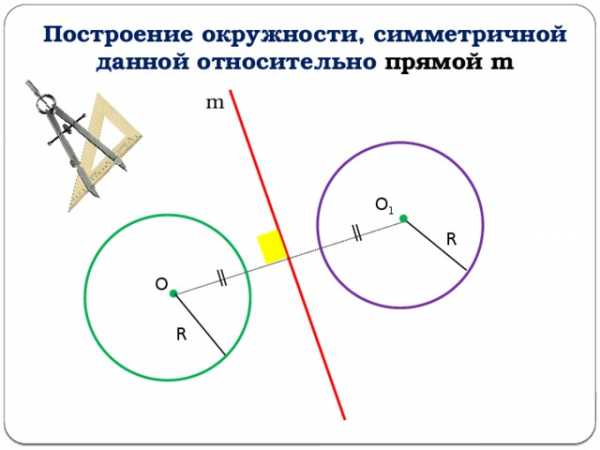
Построение окружности, симметричной данной относительно прямой m
m
О 1
R
O
R
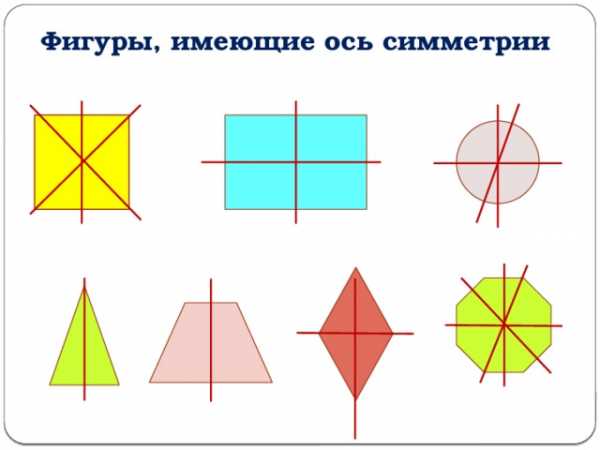
Фигуры, имеющие ось симметрии
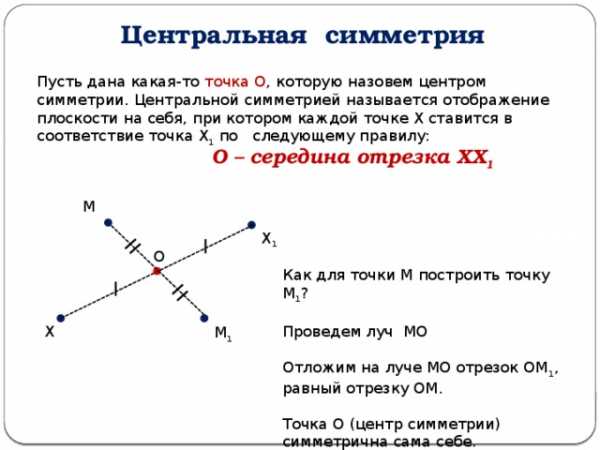
Центральная симметрия
Пусть дана какая-то точка О , которую назовем центром симметрии. Центральной симметрией называется отображение плоскости на себя, при котором каждой точке Х ставится в соответствие точка Х 1 по следующему правилу:
О – середина отрезка ХХ 1
М
Х 1
О
Как для точки М построить точку М 1 ?
Проведем луч МО
Отложим на луче МО отрезок ОМ 1 , равный отрезку ОМ.
Точка О (центр симметрии) симметрична сама себе.
Х
М 1
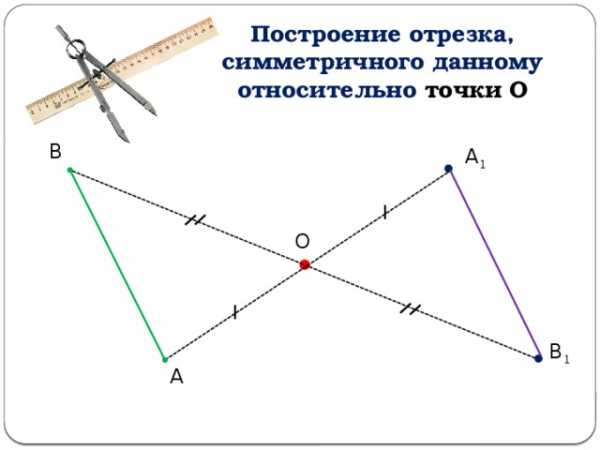
Построение отрезка, симметричного данному относительно точки О
B
A 1
О
B 1
A
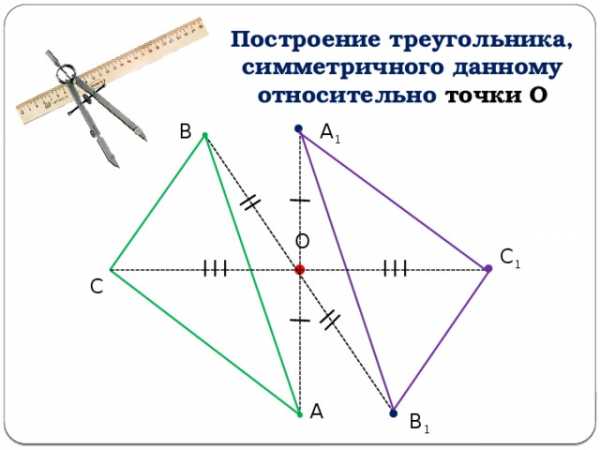
Построение треугольника, симметричного данному относительно точки О
B
A 1
О
С 1
С
A
B 1
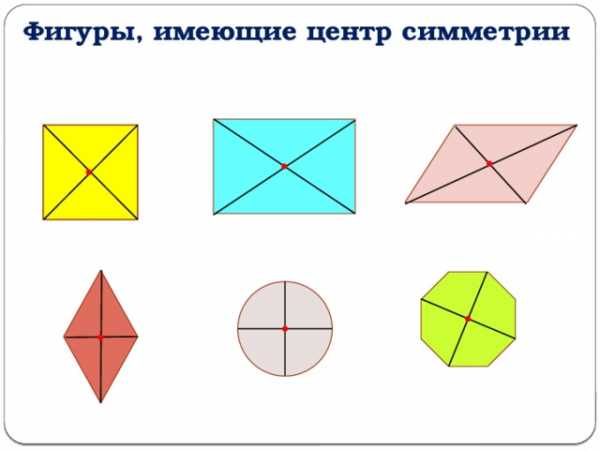
Фигуры, имеющие центр симметрии
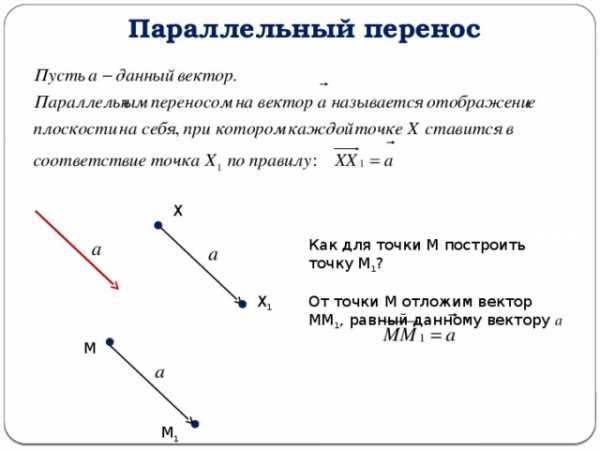
Параллельный перенос
Х
Как для точки М построить точку М 1 ?
От точки М отложим вектор ММ 1 , равный данному вектору а
Х 1
М
М 1
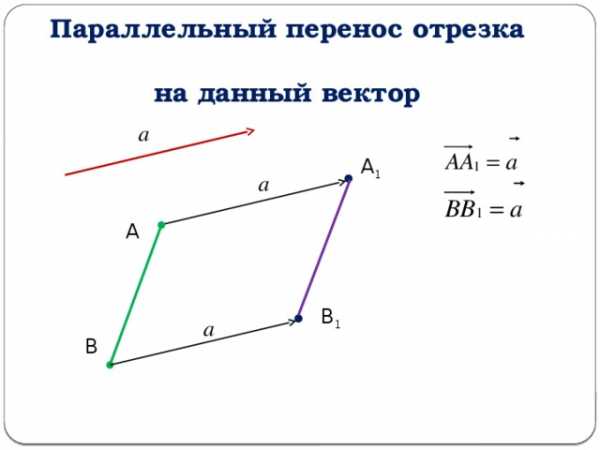
Параллельный перенос отрезка на данный вектор
А 1
А
В 1
В
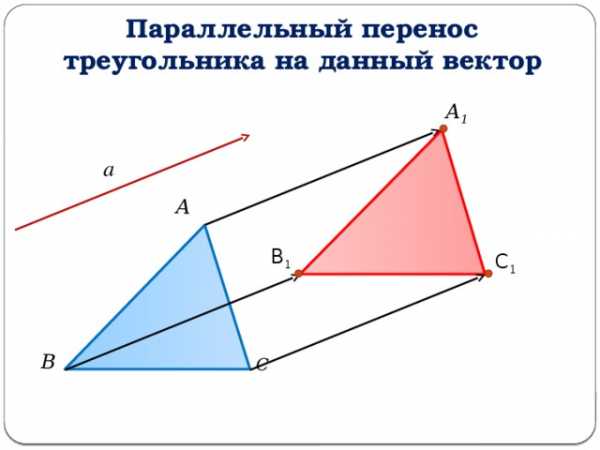
С
А
В
Параллельный перенос треугольника на данный вектор
А 1
В 1
С 1
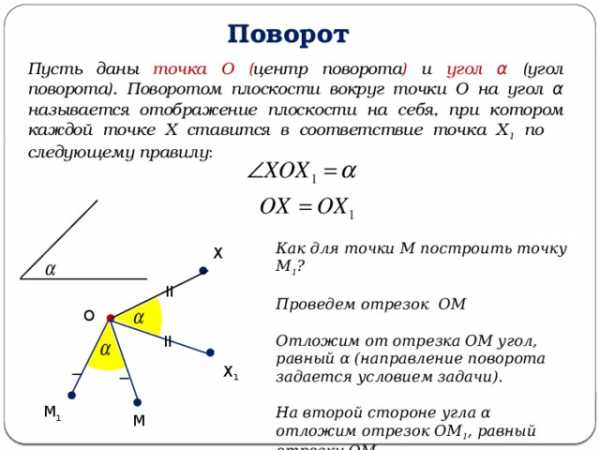
Поворот
Пусть даны точка О ( центр поворота ) и угол α (угол поворота). Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждой точке Х ставится в соответствие точка Х 1 по следующему правилу :
Как для точки М построить точку М 1 ?
Проведем отрезок ОМ
Отложим от отрезка ОМ угол, равный α (направление поворота задается условием задачи).
На второй стороне угла α отложим отрезок ОМ 1 , равный отрезку ОМ.
Х
II
О
II
Х 1
̶
̶
М 1
М
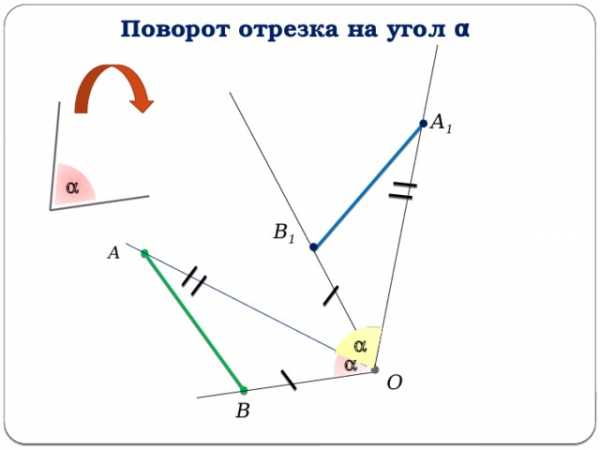
Поворот отрезка на угол α
А 1
В 1
А
О
В
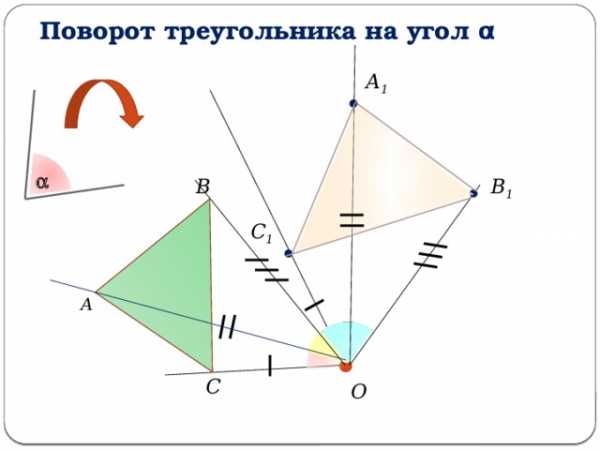
Поворот треугольника на угол α
А 1
В
В 1
С 1
А
С
О
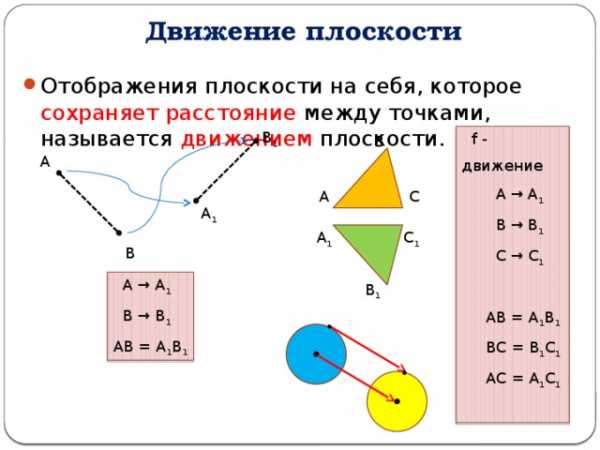
Движение плоскости
- Отображения плоскости на себя, которое сохраняет расстояние между точками, называется движением плоскости.
В 1
f — движение
А → А 1
В → В 1
С → С 1
АВ = А 1 В 1
ВС = В 1 С 1
АС = А 1 С 1
В
А
С
А
А 1
С 1
А 1
В
А → А 1
В → В 1
АВ = А 1 В 1
В 1
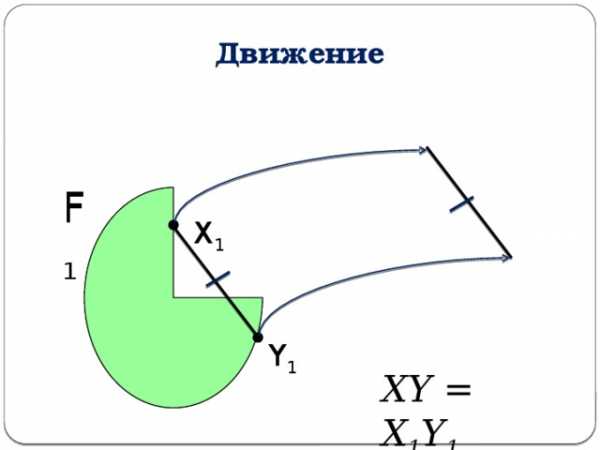
Движение
F 1
F
X 1
X
Y
Y 1
XY = X 1 Y 1

Теорема. Осевая симметрия — движение
Дано: f – осевая симметрия,
прямая m — ось симметрии
Х → Х 1
У → У 1
Доказать: ХУ = Х 1 У 1
m
X 1
У 1
К
Z 1
Р
X
Z
У
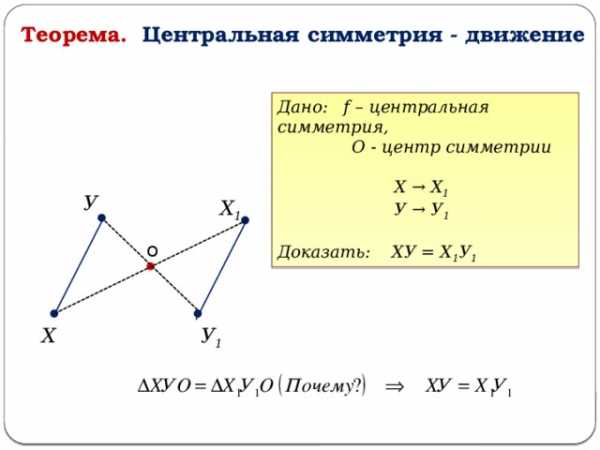
Теорема. Центральная симметрия — движение
Дано: f – центральная симметрия,
О — центр симметрии
Х → Х 1
У → У 1
Доказать: ХУ = Х 1 У 1
У
Х 1
О
У 1
Х
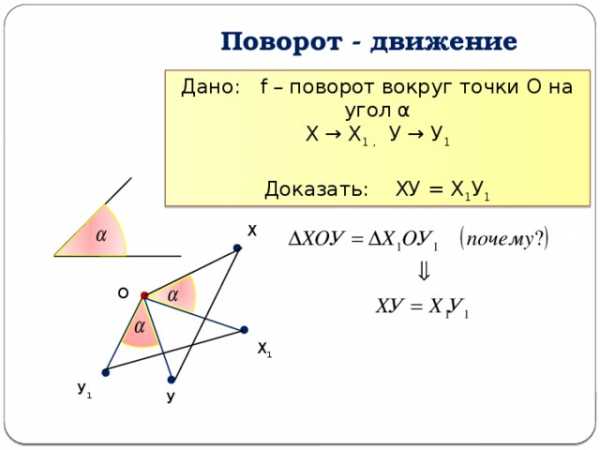
Поворот — движение
Дано: f – поворот вокруг точки О на угол α
Х → Х 1 , У → У 1
Доказать: ХУ = Х 1 У 1
Х
О
Х 1
У 1
У

Свойства движения
1 . При движении отрезок отображается на отрезок
Р
В
А
Р 1
А 1
В 1
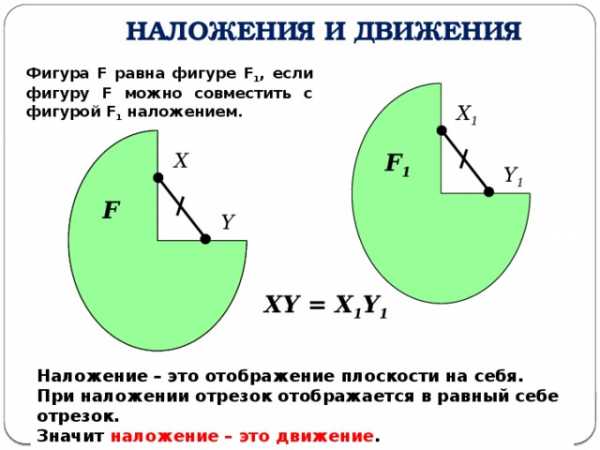
Наложения и движения
Фигура F равна фигуре F 1 , если фигуру F можно совместить с фигурой F 1 наложением.
X 1
X
F 1
Y 1
F
F
Y
XY = X 1 Y 1
Наложение – это отображение плоскости на себя.
При наложении отрезок отображается в равный себе отрезок.
Значит наложение – это движение .
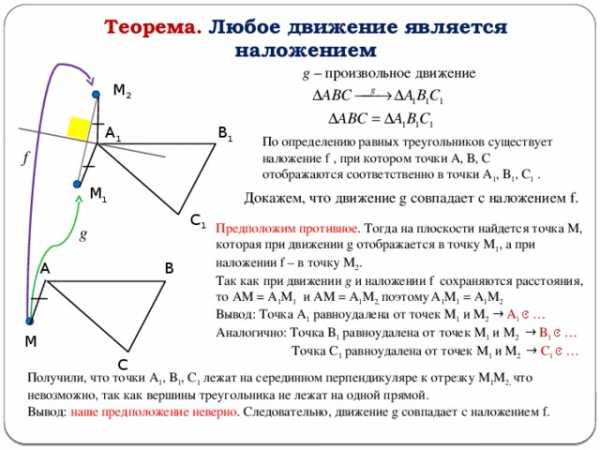
Теорема. Любое движение является наложением
g – произвольное движение
М 2
В 1
А 1
По определению равных треугольников существует наложение f , при котором точки А, В, С отображаются соответственно в точки А 1 , В 1 , С 1 .
f
М 1
Докажем, что движение g совпадает с наложением f.
С 1
Предположим противное . Тогда на плоскости найдется точка М, которая при движении g отображается в точку М 1 , а при наложении f – в точку М 2 .
Так как при движении g и наложении f сохраняются расстояния, то АМ = А 1 М 1 и АМ = А 1 М 2, поэтому А 1 М 1 = А 1 М 2
Вывод: Точка А 1 равноудалена от точек М 1 и М 2 → А 1 ͼ …
Аналогично: Точка В 1 равноудалена от точек М 1 и М 2 → В 1 ͼ …
Точка С 1 равноудалена от точек М 1 и М 2 → С 1 ͼ …
g
В
А
М
С
Получили, что точки А 1 , В 1 , С 1 лежат на серединном перпендикуляре к отрезку М 1 М 2, что невозможно, так как вершины треугольника не лежат на одной прямой.
Вывод: наше предположение неверно . Следовательно, движение g совпадает с наложением f.
multiurok.ru