148 алгебра 8 класс – ГДЗ 148 номер алгебра 8 класс Ю.Н. Макарычев, Н.Г. Миндюк

ГДЗ 148 номер алгебра 8 класс Ю.Н. Макарычев, Н.Г. Миндюк

GDZ.RU

• 1 класс
  

  • Математика
  • Английский язык
  • Русский язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Человек и мир

• 2 класс
  

  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Белорусский язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Человек и мир

• 3 класс
  

  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Белорусский язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Человек и мир
  • Испанский язык

• 4 класс
  

  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Человек и мир
  • Испанский язык

• 5 класс
  

  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык

gdz.ru

Алгебра 8 класс Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова Номер 148

Алгебра 8 класс Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова

авторы: Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова.

издательство: «Просвещение» 2013 г

Раздел:

• ГЛАВА I. РАЦИОНАЛЬНЫЕ ДРОБИ
• §3. ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ
• 7. Преобразование рациональных выражений

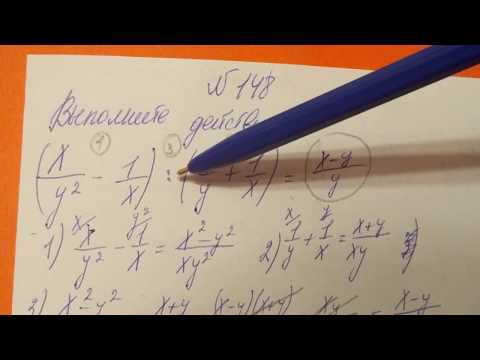
Выполните действия:
а)

$(\frac{x}{y^2} — \frac{1}{x}) : (\frac{1}{y} + \frac{1}{x})$

;
б)

$(\frac{a}{m^2} + \frac{a^2}{m^3}) : (\frac{m^2}{a^2} + \frac{m}{a})$

;
в)

$\frac{ab + b^2}{3} : \frac{b^3}{3a} + \frac{a + b}{b}$

;
г)

$\frac{x — y}{x} — \frac{5y}{x^2} * \frac{x^2 — xy}{5y}$

.

Решение а

$(\frac{x}{y^2} — \frac{1}{x}) : (\frac{1}{y} + \frac{1}{x}) = \frac{x^2 — y^2}{xy^2} : \frac{x + y}{xy} = \frac{(x — y)(x + y)}{xy^2} * \frac{xy}{x + y} = \frac{x — y}{y} * \frac{1}{1} = \frac{x — y}{y}$

Решение б

$(\frac{a}{m^2} + \frac{a^2}{m^3}) : (\frac{m^2}{a^2} + \frac{m}{a}) = \frac{a^2 + am}{m^3} : \frac{m^2 + am}{a^2} = \frac{a(a + m)}{m^3} * \frac{a^2}{m(m + a)} = \frac{a}{m^3} * \frac{a^2}{m} = \frac{a^3}{m^4}$

Решение в

$\frac{ab + b^2}{3} : \frac{b^3}{3a} + \frac{a + b}{b} = \frac{b(a + b)}{3} * \frac{3a}{b^3} + \frac{a + b}{b} = \frac{a + b}{1} * \frac{a}{b^2} + \frac{a + b}{b} = \frac{a(a + b)}{b^2} + \frac{a + b}{b} = \frac{a(a + b) + b(a + b)}{b^2} = \frac{(a + b)(a + b)}{b^2} = \frac{(a + b)^2}{b^2}$

Решение г

$\frac{x — y}{x} — \frac{5y}{x^2} * \frac{x^2 — xy}{5y} = \frac{x — y}{x} — \frac{5y}{x^2} * \frac{x(x — y)}{5y} = \frac{x — y}{x} — \frac{1}{x} * \frac{x — y}{1} = \frac{x — y}{x} — \frac{x — y}{x} = 0$

×

Нашли ошибку?

Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом

Отправить

reshalka.com

148 Алгебра 8 класс

funer.ru