Примеры 7 класса по алгебре примеры с ответами – 7 класс. Алгебра

7 класс. Алгебра

Рубрика «7 класс. Алгебра»

I. Чтобы умножить одночлен на многочлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить.

Пример 1.  Умножить одночлен на многочлен: 2a·(4a²-0,5ab+5a³).

Решение. Одночлен 2а будем умножать на каждый одночлен многочлена:

2a·(4a²-0,5ab+5a³)=2a∙4a²+2a∙(-0,5ab)+2a∙5a³=8a³-a²b+10a⁴. Запишем полученный многочлен в стандартном виде:

10a⁴+8a³-a²b.

Пример 2. Умножить многочлен на одночлен: (3xyz⁵-4,5x²y+6xy³+2,5y²z)∙(-0,4x³).

Решение. Каждое слагаемое, стоящее в скобках, умножаем на одночлен (-0,4x³).

(3xyz⁵-4,5x²y+6xy³+2,5y²z)∙(-0,4x³)=

=3xyz⁵∙(-0,4x³) -4,5x²y∙(-0,4x³)+6xy³∙(-0,4x³)+2,5y²z∙(-0,4x³)=

=-1,2x⁴yz⁵+1,8x⁵y-2,4x⁴y³-x³y²z.

II. Представление многочлена в виде произведения двух или нескольких многочленов называется разложением многочлена на множители.

 III. Вынесение общего множителя за скобки – простейший способ разложения многочлена на множители.

Пример 3. Разложить на множители многочлен:  5a³+25ab-30a².

Решение. Вынесем общий множитель всех членов многочлена за скобки. Это одночлен 5а, потому что на 5а делится каждый из членов данного многочлена. Итак, 5а мы запишем перед скобками, а в скобках запишем частные от деления каждого одночлена на 5а.

5a³+25ab-30a²=5a·(a²+5b-6a). Проверяем себя: если мы умножим 5а на многочлен в скобках a²+5b-6a, то получим данный многочлен 5a³+25ab-30a².

Пример 4.Вынесите общий множитель за скобки: (x+2y)²-4·(x+2y).

Решение. (x+2y)²-4·(x+2y)=(x+2y)(x+2y-4).

Общим множителем здесь являлся двучлен (х+2у). Мы вынесли его за скобки, а в скобках записали частные от деления данных членов (x+2y)² и -4·(x+2y) на их общий делитель

(х+2у). В результате мы представили данный многочлен в виде произведения двух многочленов (x+2y) и (x+2y-4), другими словами, мы разложили многочлен (x+2y)²-4·(x+2y) на множители. Ответ:  (x+2y)(x+2y-4).

IV. Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и записать полученные произведения в виде суммы одночленов. При необходимости привести подобные слагаемые.

Пример 5. Выполнить умножение многочленов: (4x²-6xy+9y²)(2x+3y).

Решение. По правилу мы должны каждый член первого многочлена (4x²-6xy+9y²) умножить на каждый член второго многочлена (2x+3y). Чтобы не запутаться, делайте всегда так: сначала умножьте каждый член первого многочлена на 2х, потом опять каждый член первого многочлена умножайте на 3у.

(4x²-6xy+9y²)(2x+3y)=4x²∙2x-6xy∙2x+9y²∙2x+4x²∙3y-6xy∙3y+9y²∙3y=

=8x³-12x²y+18xy²+12x²y-18xy²+27y³=8x³+27y³.

Подобные слагаемые -12x²y и 12x²y, а также 18xy² и -18xy² оказались противоположными, их суммы равны нулю.

Ответ: 8x³+27y³.

I.  Сумма одночленов называется многочленом. Одночлены, из которых составлен многочлен, называются членами многочлена.

Например, многочлен 2a+3a²b-6b⁴+3,5a³b состоит из суммы четырех одночленов.

II.  Двучлен – это многочлен, состоящий из двух членов (одночленов).

Примеры двучленов: 2a-3b; 6x²+5; 2x-1.

III. Трехчлен – это многочлен, состоящий из трех членов (одночленов).

Например,  2а+3с-х или x²+4x-5 — трехчлены, так как состоят из трех одночленов.

IV. Степенью многочлена называют наибольшую из степеней входящих в него одночленов.

Например, многочлен 2a²-3b+abc-d² имеет третью степень, так как наибольшей степенью входящих в него одночленов является третья степень одночлена abc (складываем показатели: 1+1+1=3).

Многочлен 4x⁴yz+2x²y³-xz⁴+3x²y² имеет шестую степень, так как наибольшей (шестой) степенью является степень его члена 4x⁴yz (складываем показатели: 4+1+1=6).

V. Многочлен стандартного вида не содержит подобных членов и записан в порядке убывания степеней его членов.

Например, приведенный выше многочлен 4x⁴yz+2x²y³-xz⁴+3x²y² является многочленом стандартного вида, так как записан в порядке убывания степеней его членов.

Пример 1. Упростить многочлен, записав каждый его член в стандартном виде: 4aabb∙(-0,5c²)+5a²bb³-6abcab²c.

Решение.

4aabb∙(-0,5c²)+5a²bb³-6abcab²c=-2a²b²c²+5a²b⁴-6a²b³c², а теперь запишем этот многочлен в стандартном виде (в порядке убывания степеней его членов):

-6a²b³c²-2a²b²c²+5a²b⁴.

Пример 2. Вычислить значение многочлена 5y²-3xy+x²при x=-1, y=2.

Решение.

5y²-3xy+x²=5∙2²-3∙(-1)∙2+(-1)²=5∙4+6+1=27.

Пример 3. Упростить многочлен 2aba-a³bb+7bbbb и найти его числовое значение при a=3, b=2.

Решение.

Упрощаем многочлен: 2aba-a³bb+7bbbb=2a²b-a³b²+7b⁴.

Подставляем значения a и b.

2a²b-a³b²+7b⁴=2∙3²∙2-3³∙2²+7∙2⁴=2∙9∙2-27∙4+7∙16=36-108+112=40.

Пример 4. Привести подобные члены многочлена:

Пример 5. Привести к стандартному виду многочлен:

Напоминание: подобными считают одночлены, имеющие одинаковую буквенную часть.

 I. Выражения, которые составлены из чисел, переменных и их степеней, при помощи действия умножения называются одночленами.

Примеры одночленов: 

а) a; б) ab; в) 12; г) -3c; д) 2a²∙(-3,5b)³; е) -123,45xy⁵z; ж) 8ac∙2,5a²∙(-3c³).

II. Такой вид одночлена, когда на первом месте стоит числовой множитель (коэффициент), а за ним переменные с их степенями, называют стандартным видом одночлена.

Так, одночлены, приведенные выше, под буквами а), б), в), г)  и е) записаны в стандартном виде, а одночлены под буквами д) и ж) требуется привести к стандартному виду, т. е. к такому виду, когда на первом месте стоит числовой множитель, а за ним записывают буквенные множители с их показателями, причем, буквенные множители стоят в алфавитном порядке. Приведем одночлены д) и ж) к стандартному виду.

д) 2a²∙(-3,5b)³=2a²∙(-3,5)³∙b³=-2a²∙3,5∙3,5∙3,5∙b³=-85,75a²b³;

ж) 8ac∙2,5a²∙(-3c³)=-8∙2,5∙3a³c³=-60a³c³.

III. Сумму показателей степеней всех переменных, входящих в состав одночлена, называют степенью одночлена.

Примеры. Какую степень имеют одночлены а) — ж)?

а) a.  Первую;

б) ab. Вторую: а в первой степени и b в первой степени-сумма показателей 1+1=2;

в) 12. Нулевую, так как буквенных множителей нет;

г) -3c. Первую;

д) -85,75a²b³. Пятую. Мы привели этот одночлен к стандартному виду, имеем а во второй степени и b в третьей. Складываем показатели: 2+3=5;

е)  -123,45xy⁵z. Седьмую. Сложили показатели степеней буквенных множителей: 1+5+1=7;

ж) -60a³c³. Шестую, так как сумма показателей буквенных множителей 3+3=6.

IV.  Одночлены, имеющие одинаковую буквенную часть, называются подобными одночленами.

Пример. Указать подобные одночлены среди данных одночленов 1) -7).

1) 3aabbc; 2) -4,1a³bc; 3) 56a²b²c; 4) 98,7a²bac; 5) 10aaa²x; 6) -2,3a⁴x; 7) 34x²y.

Приведем одночлены 1), 4) и 5) к стандартному виду. Тогда строчка данных одночленов будет выглядеть так:

1) 3a²b²c; 2) -4,1a³bc; 3) 56a²b²c; 4) 98,7a³bc; 5) 10a⁴x;  6) -2,3a⁴x; 7) 34x²y.

Подобными будут те, которые имеют одинаковую буквенную часть, т.е. 1) и 3); 2) и 4); 5) и 6).

1) 3a²b²c и 3) 56a²b²c;

2) -4,1a³bc и 4) 98,7a³bc;

5) 10a⁴x и  6) -2,3a⁴x.

Очень большие и очень малые числа принято записывать в стандартном виде: a∙10ⁿ, где 1≤а<10 и n  (натуральное или целое) – есть порядок числа, записанного в стандартном виде.

Например, 345,7=3,457∙10²; 123456=1,23456∙10⁵; 0,000345=3,45∙10^-4.

Примеры. 

Записать в стандартном виде число: 1) 40503; 2) 0,0023; 3) 876,1; 4) 0,0000067.

Решение.

1) 40503=4,0503·10⁴;

2) 0,0023=2,3∙10^-3;

3) 876,1=8,761∙10²;

4) 0,0000067=6,7∙10^-6.

Еще примеры на стандартный вид числа.

5) Число молекул газа в 1 см³ при 0°С и давлении 760 мм.рс.ст равно

27 000 000 000 000 000 000. Записать это число в стандартном виде.

Решение.

27 000 000 000 000 000 000=2,7∙10¹⁹.

6) 1 парсек (единица длины в астрономии) равен 30 800 000 000 000 км. Записать это число в стандартном виде.

Решение.

1 парсек=30 800 000 000 000=3,08∙10¹³ км.

В тему:

Киловатт-час — это внесистемная единица энергии или работы, применяется в электротехнике, обозначается кВт·ч.

1 кВт·ч=3,6∙10⁶ Дж (Джоулей).

 I. Определение.  (- n)-й степенью (n – натуральное) числа а, не равного нулю, считается число, обратное n-й степени числа а:

Примеры. Вычислить:

Решение.

II. Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:

Примеры. Вычислить:

Решение.

 Свойства степени с натуральным показателем справедливы и для  степеней с любым показателем.

Свойства степени с натуральным показателем с примерами смотрите в предыдущем уроке здесь.

Примеры на все свойства степени.

Упростить:

Решение.

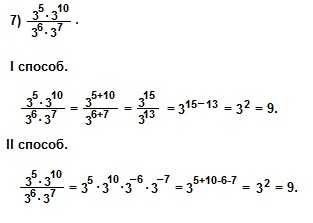       При решении 7) примера  I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями:  a^m∙aⁿ=a^m+n  и a^m:aⁿ=a^m-n. При решении II способом мы использовали понятие степени с отрицательным показателем:  и свойство произведения степеней с одинаковыми основаниями:  a^m∙aⁿ=a^m+n .

Пример 8 ) решаем так же, как решали пример 7) вторым способом.

В примере 9) представим 7³как 7²∙7, а степень 4⁵как 4³∙4², а затем сократим дробь на (7²∙4³).

В 10) примере применим формулу степени произведения: (ab)ⁿ=aⁿ∙bⁿ, а затем сократим дробь на (2⁶∙3⁵).

I. Произведение n сомножителей, каждый из которых равен а называется n-й степенью числа а и обозначается аⁿ.

Примеры. Записать произведение в виде степени.

1) mmmm;          2) aaabb;         3) 5·5·5·5·ccc;        4) ppkk+pppk-ppkkk.

Решение.

1) mmmm=m⁴, так как, по определению степени, произведение четырех сомножителей, каждый из которых равен m, будет четвертой степенью числа m.

  2) aaabb=a³b²;    3) 5·5·5·5·ccc=5⁴c³;     4) ppkk+pppk-ppkkk=p²k²+p³k-p²k³.

II. Действие, посредством которого находится произведение нескольких равных сомножителей, называется возведением в степень. Число, которое возводится в степень, называется основанием степени. Число, которое показывает, в какую степень возводится основание, называется показателем степени. Так, аⁿ – степень, а – основание степени, n – показатель степени. Например:

 2³ — это степень. Число 2 — основание степени, показатель степени равен 3. Значение степени 2³равно 8, так как 2³=2·2·2=8.

Примеры. Написать следующие выражения без показателя степени.

5) 4³;       6) a³b²c³;       7) a³-b³;       8 ) 2a⁴+3b².

Решение.

5) 4³=4·4·4;       6) a³b²c³=aaabbccc;       7) a³-b³=aaa-bbb;       8) 2a⁴+3b²=2aaaa+3bb.

 III. а⁰=1  Любое число (кроме нуля) в нулевой степени равно единице. Например, 25⁰=1. 
 IV. а¹=а  Любое число в первой степени равно самому себе. 

 V. a^m∙aⁿ=a^m+n   При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

Примеры. Упростить:

9) a·a³·a⁷;             10) b⁰+b²·b³;             11) c²·c⁰·c·c⁴.

Решение.

9) a·a³·a⁷=a¹⁺³⁺⁷=a¹¹;           10) b⁰+b²·b³=1+b²⁺³=1+b⁵;             

11) c²·c⁰·c·c⁴=1·c²·c·c⁴=c²⁺¹⁺⁴=c⁷.

VI.  a^m:aⁿ=a^m— n  При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Примеры. Упростить:

12) a⁸:a³;       13) m¹¹:m⁴;         14) 5⁶:5⁴.

12) a⁸:a³=a^8-3=a⁵;       13) m¹¹:m⁴=m^11-4=m⁷;         14) 5⁶:5⁴=5²=5·5=25.

VII. (a^m)ⁿ=a^mn   При возведении степени в степень основание оставляют прежним, а показатели перемножают.

Примеры. Упростить:

15) (a³)⁴;         16) (c⁵)².

15) (a³)⁴=a^3·4=a¹²;         16) (c⁵)²=c^5·2=c¹⁰.

Обратите внимание, что, так как от перестановки множителей произведение не меняется, то:

15) (a³)⁴=(a⁴)³;         16) (c⁵)²=(c²)⁵.

 VIII. (a∙b)ⁿ=aⁿ∙bⁿ   При возведении произведения в степень возводят в эту степень каждый из множителей.

Примеры. Упростить:

17) (2a²)⁵;      18) 0,2⁶·5⁶;        19) 0,25²·40².

Решение.

17) (2a²)⁵=2⁵·a^2·5=32a¹⁰;      18) 0,2⁶·5⁶=(0,2·5)⁶=1⁶=1;

19) 0,25²·40²=(0,25·40)²=10²=100.

       IX. При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.

Примеры. Упростить:

Решение.

Функцию вида y=x³ называют кубической функцией. Графиком кубической функции является кубическая парабола, проходящая через начало координат. Ветви кубической параболы y=x³ находятся в I и III четвертях.

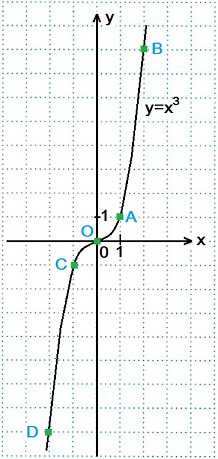Построение графика кубической функции y=x³

Составим таблицу значений функции y=x³ для х=0, х=±1, х=±2.

   x     |    y=x³

   0    |    0³=0            Точка О(0; 0)

   1    |    1³=1            Точка А(1; 1)

  -1    | (-1)³=-1          Точка С(-1; -1)

    2   |   2³=8             Точка В(2; 8 )

  -2   | (-2)³=-8           Точка D(-2; -8)

Функцию вида y=x² называют квадратной функцией. Графиком квадратной функции является парабола с вершиной в начале координат. Ветви параболы y=x² направлены вверх.

Построение графика функции y=x². Составим таблицу значений функции для х=0, х=±1, х=±2, х=±3.

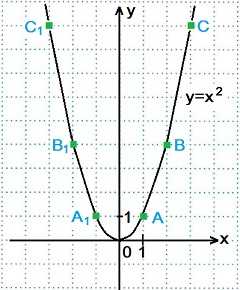х    |   y=x² 

0    |  0²=0  

1    |  1²=1              Точка А(1; 1)

-1   | (-1)²=1           Точка А₁(-1; 1)

2    |   2²=4             Точка В(2; 4)

-2   | (-2)²=4           Точка В₁(-2; 4)

3    |  3²=9              Точка С(3; 9)

-3   | (-3)²=9           Точка С₁(-3; 9)

data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»2890988705″>

1)    Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

       (a+b)² = a²+2ab+b² 

  a) (x + 2y)² = x² + 2 ·x·2y + (2y)² = x² + 4xy + 4y²

б) (2k + 3n)² = (2k)² + 2·2k·3n + (3n)² = 4k² + 12kn + 9n²

2)    Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

        (a-b)² = a²-2ab+b²

 а)   (2a – c)² = (2a)²-2·2a·c + c² = 4a² – 4ac + c²

б)   (3a – 5b)² = (3a)²-2·3a·5b + (5b)² = 9a² – 30ab + 25b²

3)    Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.

         a²–b² = (a–b)(a+b)

a)      9x² – 16y² = (3x)² – (4y)² = (3x – 4y)(3x + 4y)

б)  (6k – 5n)( 6k + 5n) = (6k)² – (5n)² = 36k² – 25n²

4)  Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

        (a+b)³ = a³+3a²b+3ab²+b³

a)  (m + 2n)³ = m³ + 3·m²·2n + 3·m·(2n)² + (2n)³ = m³ + 6m²n + 12mn² + 8n³

б)  (3x + 2y)³ = (3x)³ + 3·(3x)²·2y + 3·3x·(2y)² + (2y)³ = 27x³ + 54x²y + 36xy² + 8y³

5)  Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a-b)³ = a³-3a²b+3ab²-b³

а)  (2x – y)³ = (2x)³-3·(2x)²·y + 3·2x·y² – y³ = 8x³ – 12x²y + 6xy² – y³

б)  (x – 3n)³ = x³-3·x²·3n + 3·x·(3n)² – (3n)³ = x³ – 9x²n + 27xn² – 27n³

6)  Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.

a³+b³ = (a+b)(a²–ab+b²)

a)      125 + 8x³ = 5³ + (2x)³ = (5 + 2x)(5² — 5·2x + (2x)²) = (5 + 2x)(25 – 10x + 4x²)

б)  (1 + 3m)(1 – 3m + 9m²) = 1³ + (3m)³ = 1 + 27m³

7)  Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.

 a³-b³ = (a-b)(a²+ab+b²)

а) 64с³ – 8 = (4с)³ – 2³ = (4с – 2)((4с)² + 4с·2 + 2²) = (4с – 2)(16с² + 8с + 4)

б) (3a – 5b)(9a² + 15ab + 25b²) = (3a)³ – (5b)³ = 27a³ – 125b³

Дорогие друзья! Карта сайта поможет вам выбрать нужную тему.

Страница 1 из 11

www.mathematics-repetition.com

Алгебра, 7 класс: уроки, тесты, задания

www.yaklass.ru

Алгебра 7 класс. Задачи.

Когда-то на уроках алгебры 6-7 класса мы решали эти задачки за несколько секунд. Нас можно было разбудить ночью, и мы бы сказали, чему равен корень из 64 и как найти перенести X из правой части уравнения в левую. И именно благодаря этим замечательным урокам в нас развиты логика и умение быстро считать, не используя калькулятор.

Мы сделали тест, чтобы Вы смогли проверить, сохранились ли в вашей памяти математические знания. Не забудьте после прохождения теста отправить ссылку друзьям, чтобы проверить и их память и знания. И всё же мы надеемся, что сможем поймать Вас хотя бы на одном вопросе

Чему равен квадратный корень из 169?

Далее >>

Решите задачу: Маме и бабушке вместе 120 лет. Сколько лет каждой, если мама в три раза моложе бабушки?

маме — 45, бабушке — 55

маме -30, бабушке — 90

маме-25, бабушке-65

маме -40, бабушке — 70

Далее >>

Чему равен Х в уравнении 3х-5=7+х ?

х = 6

х = 3

х = 12

х = 0

Далее >>

Чему равно число 12, возведенное во вторую степень?

Далее >>

С помощью какой формулы можно расcчитать tg a (тангенс A)?

sin a \ cos a

cos a \ sin a

cos a x sin a

Далее >>

Квадратный корень из 225 равен…

Далее >>

Чему равно число семь, возведенное в третью степень?

Далее >>

Решите пример: (х+4у) — (4у — х), где х=1, а у=2

ответ: 3

ответ: 1

ответ: 5

ответ: 2

Далее >>

Чему равен ctg угла 45 градусов?

Далее >>

Чему равен sin угла 90 градусов?

Далее >>

Тест по алгебре 6-7 класс

С родителями в школу!

Не расстраивайтесь! Почаще возвращайтесь к нам, чтобы пройти тест-другой, и тогда школьная программа будет для Вас не такой сложной! Не забудьте отправить ссылку друзьям — проверим их знания!

Поделитесь результатом с друзьями:

Facebook
Twitter
VK

Тест по алгебре 6-7 класс

На троечку

А когда-то мы эти примеры щёлкали один за одним, верно? Не забудьте отправить ссылку друзьям — проверим их знания!

Поделитесь результатом с друзьями:

Facebook
Twitter
VK

Тест по алгебре 6-7 класс

Четверка!

Почти отлично! Почаще заходите к нам, и тогда точно будете помнить всё из школьной программы! Не забудьте отправить ссылку друзьям — проверим их знания!

Поделитесь результатом с друзьями:

Facebook
Twitter
VK

Тест по алгебре 6-7 класс

Пять с плюсом!

Да Вы отличник! Школьные уроки не прошли даром. Не забудьте отправить ссылку друзьям — проверим их знания!

Поделитесь результатом с друзьями:

Facebook
Twitter
VK

 PLAY AGAIN !

Еще интересные тесты:

Понравилась статья? Поделиться с друзьями:

smtimes.ru

Числовые и алгебраические выражения — урок. Алгебра, 7 класс.

Числовым выражением называют всякую запись из чисел, знаков арифметических действий и скобок, составленную со смыслом.

Например:

3+5⋅7−4 — числовое выражение;

3+:−5 — не числовое выражение, а бессмысленный набор символов.

Очень часто вместо конкретных чисел употребляются буквы, тогда получается алгебраическое выражение.

Алгебраическим выражением называется запись из букв, знаков арифметических действий, чисел и скобок, составленная со смыслом.

Например:

a2−3b — алгебраическое выражение.

Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т. е. можно менять значения букв), эти буквы называют переменными.

Алгебраические выражения могут быть очень громоздкими, и алгебра учит их упрощать, используя правила, законы, свойства, формулы.

При упрощении вычислений часто используются законы сложения и умножения.

Законы сложения

1)  От перемены мест слагаемых сумма не изменяется, т. е.

a+b=b+a — переместительный закон сложения.

2) Чтобы к сумме двух слагаемых прибавить третье слагаемое, можно к первому слагаемому прибавить сумму второго и третьего слагаемых, т. е.

a+b+c=a+b+c — сочетательный закон сложения.

Законы умножения

1) От перемены мест множителей произведение не меняется, т. е.

a⋅b=b⋅a — переместительный закон умножения.

2) Произведение не зависит от группировки его сомножителей, т. е.

a⋅b⋅c=a⋅b⋅c — сочетательный закон умножения.

3) Произведение суммы нескольких чисел на какое-нибудь число равно сумме произведений каждого слагаемого на это число, т. е.

a+b⋅c=ac+bc — распределительный закон умножения относительно сложения.

В результате упрощений числового выражения получается число, которое называют значением числового выражения.

Выполнив указанные действия в первом примере, получим

3&plus;5⋅7−4=18.

Число \(18\) в ответе есть значение данного числового выражения.

О значении алгебраического выражения можно говорить только при конкретных значениях входящих в него букв.

Например, алгебраическое выражение a2−3b при \(a=-16\) и \(b=-14\) имеет значение \(298\), т. к.

a2−3b=−162−3⋅−14=256+42=298,

а вот алгебраическое выражение a2−3a+2 при \(a=-4\) имеет значение \(-6,5\),

т. к. −42−3−4+2=16−3−2=13−2=−6,5.

И это же алгебраическое выражение a2−3a+2 при \(a=-2\) не имеет смысла, т. к. a+2=−2+2=0, т. е. будет деление на нуль.

Обрати внимание!

А на ноль делить нельзя!

Вывод:

если при конкретных значениях букв алгебраическое выражение имеет числовое значение, то указанные значения переменных называют допустимыми;

если же при конкретных значениях букв алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми.

Так, в примере a2−3a+2 значение \(a=-4\) — допустимое, а

значение \(a=-2\) — недопустимое, т. к. при нём будет деление на ноль, а делить на ноль нельзя!

www.yaklass.ru

Линейные уравнения 7 класс | Алгебра

Линейные уравнения, решение которых начинается в курсе алгебры (7 класс) — это уравнения вида

где a и b — числа, x — переменная.

Уравнения, сводящиеся к виду ax=b при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей на число, отличное от нуля (то есть при помощи равносильных преобразований), также часто называют линейными (правильнее называть их уравнениями, сводящимися к линейным).

Рассмотрим примеры уравнений, сводящихся к линейным, которые встречаются в начале курса алгебры 7 класса.

Раскрываем скобки. Если перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках. Если перед скобками стоит знак «+», знаки  не меняем. Если перед скобками стоит знак «-«, знаки меняем на противоположные:

Неизвестные слагаемые переносим в одну сторону, известные — в другую. При переносе знаки слагаемых меняем на противоположные:

Обе части уравнения делим на число, стоящее перед иксом:

Ответ: -9.

Раскрываем скобки:

Неизвестные слагаемые перенесём в левую часть, известные — в правую. Знак каждого слагаемого при переносе из одной части уравнения в другую меняем на противоположный:

(Обратите внимание: хотя сумма слагаемых  с переменной равна нулю, результат записываем не как 0, а как 0x).

Какое бы число мы не подставили в это уравнение вместо x, получим верное равенство.

Ответ: x — любое число.

Раскрываем скобки:

Можно сначала привести подобные слагаемые, чтобы упростить уравнение:

а уже потом перенести: неизвестные — в одну сторону, известные — в другую:

Это уравнение не имеет корней.

Ответ: нет корней.

Раскрываем скобки:

Приводим подобные слагаемые:

Переносим неизвестные слагаемые в одну сторону, известные — в другую, изменив при этом их знаки:

Обе части уравнения делим на число, стоящее перед иксом:

Ответ:

В следующий раз рассмотрим сводящиеся к линейным уравнениям уравнения с дробями.

www.algebraclass.ru

Тесты по алгебре (7 класс), контрольные работы по вариантам с ответами онлайн

1. Выражения, тождества, уравнения

2. Функции

3. Степень с натуральным показателем

4. Многочлены

5. Формулы сокращённого умножения

6. Системы линейных уравнений

7. Другие

Контрольная работа по алгебре (7 класс) больше не застанет врасплох, ведь к ней можно качественно подготовиться при помощи подборок тестов. Они составлены в соответствии с министерской программой, поэтому являются прекрасными помощникам в процессе домашней подготовки к самостоятельным и контрольным работам. Большинство номеров теста посвящено дробям, функциям и уравнениям. Задания проверяют умение решать примеры и задачи в рамках указанных тем, а также работать с графиками. Некоторые подборки касаются выражений с переменными, формул сокращенного умножения, уравнений и неравенств. Предлагаемые вопросы проверяют как знание теории, так и умение применять ее на практике.

Тематические тесты включают вопросы разного уровня сложности, что позволяет объективно оценить свои знания. Прохождение его подразумевает только выбор одного варианта из нескольких, поэтому для выполнения всех заданий понадобится около 10-15 минут. Их можно просматривать в онлайн режиме с любого доступного устройства.

Тесты по алгебре (7 класс) с ответами помогут самостоятельно повторить и систематизировать материал для успешного написания текущих и итоговых проверочных работ.

obrazovaka.ru

Примеры математических задач

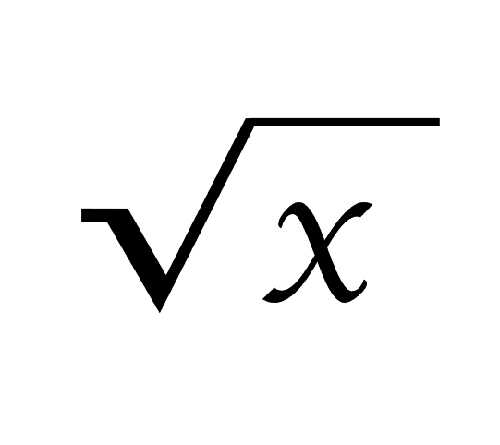
Добрый день, дорогие друзья! Сегодня мы приготовили для вас тест, в котором собраны простые математические примеры, которые можно щелкать как орешки, если в школе вы хотя бы бывали

Добрый день, дорогие друзья! Сегодня мы приготовили для вас тест, в котором собраны простые математические примеры, которые можно щелкать как орешки, если в школе вы хотя бы бывали Решение математических примеров вам понравится

В школе нам казалось, что решение математических примеров иногда очень даже сложное занятие, но сейчас, когда мы прошли огонь, воду и медные трубы, Вам уже ничего не страшно Обычные процедуры: вычитание, сложение, умножение, деление, ну и немного квадратных корней — вот всё, что сегодня Вы увидите в тесте По нашему мнению, тест получился достаточно простым, но в то же время интересным, потому что поможет расшевелить залежалый мозг, который не считает ничего более, чем скидку в магазине продуктов

Кстати, ученые выяснили, что решая простые примеры с утра, мы помогаем головному мозгу проснуться и работать более активно, чем обычно. Поэтому, если вы проснулись недавно, мы поможем вам проснуться не хуже, чем чашка кофе. Математические примеры с ответами ждут Вас, вперед!

Какой ответ верный?

Далее >>

Какой ответ верный?

Далее >>

Какой ответ верный?

Далее >>

Какой ответ верный?

Далее >>

Какой ответ верный?

Далее >>

Какой ответ верный?

Далее >>

Какой ответ верный?

Далее >>

Какой ответ верный?

Далее >>

Какой ответ верный?

Далее >>

Какой ответ верный?

Далее >>

Тест с математическими примерами

Отлично, 5!

Вы математический гений, поздравляем! Не забудьте поделиться результатом с друзьями, пусть завидуют

Поделитесь результатом с друзьями:

Facebook
Twitter
VK

Тест с математическими примерами

Хорошо, 4!

Вы справились на 4+, поздравляем! Не забудьте поделиться результатом с друзьями, пусть завидуют

Поделитесь результатом с друзьями:

Facebook
Twitter
VK

Тест с математическими примерами

Хорошо, 4!

Вы неплохо справились с поставленными задачами Не забудьте поделиться результатом с друзьями, пусть завидуют

Поделитесь результатом с друзьями:

Facebook
Twitter
VK

Тест с математическими примерами

Школа была давно?..)

Не расстраивайтесь, не везет в математике — повезет в любви Не забудьте поделиться тестом с друзьями, пусть они тоже попробуют свои силы

Поделитесь результатом с друзьями:

Facebook
Twitter
VK

 PLAY AGAIN !

Еще интересные тесты:

smtimes.ru