Определения и формулы метематика 6 класс Виленкин
Просмотр содержимого документа
«Определения и формулы метематика 6 класс Виленкин»
Делимость чисел
-
Делителем натурального числа «а» называют натуральное число , на которое «а» делится без остатка.
-
Кратным натурального числа «а» называют натуральное число , которое делится без остатка на «а» .
-
Любое натуральное число имеет бесконечно много кратных.
Признаки делимости на 10 , на 5 и на 2.
-
Если запись натурального числа оканчивается цифрой 0 , то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой , то оно не делится без остатка на 10.
-
Если запись натурального числа оканчивается цифрой 0 или 5 , то это число делится без остатка на 5. Если запись натурального числа оканчивается другой цифрой , то оно не делится без остатка на 5.
-
Если запись натурального числа оканчивается четной цифрой , то это число делится без остатка на 2. Если запись натурального числа оканчивается нечетной цифрой , то это число нечетно.
Признаки делимости на 3 на 9.
-
Если сумма цифр числа делится на 9 , то и число делится на 9 ; если сумма цифр числа не делится на 9 , то и число не делится на 9 ;
-
Если сумма цифр числа делится на 3 , то и число делится на 3 ; если сумма цифр числа не делится на 3 , то и число не делится на 3 ;
Простые и составные числа
-
Натуральное число называют простым , если оно имеет только два делителя : единицу и само это число.
-
Натуральное число называют составным , если оно имеет более двух делителей.
-
Число 1 имеет только один делитель : само это число .Поэтому его не относят ни к составным , ни кпростым.
-
Всякое составное число можно разложить на множители. При любом способе получается одно и то же разложение , если не учитывать порядка записи множителей.
Наибольший общий делитель . Взаимно простые числа.
-
Наибольшее натуральное число , на которое делятся без остатка числа а и б , называют наибольшим общим делителем этих чисел.
-
Натуральные числа называют взаимно простыми , если их наибольший общий делитель равен 1.
-
Чтобы найти НОД нескольких натуральных чисел, надо: 1) состав разложения одного из этих чисел, вычеркнуть те , которые не входят в разложение других чисел; 3) найти произведение оставшихся множителей.
Наименьшее общее кратное (НОК)
-
Наименьшим общим кратным натуральных чисел а и б называют наименьшее натуральное число, которое кратно и а и б.
-
Чтобы найти НОК нескольких натуральных чисел , надо: 1) разложить их на простые множители; 2) выписать множители , входящие в разложение одного из чисел; 3) добавить к ним недостающие множители из разложений остальных чисел; 4) найти произведение получившихся множителей.
Сложение и вычитание дробей с разными знаменателями.
-
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число , то получится равная ей дробь.
-
Деление числителя и знаменателя на их обший делитель , отличный от единицы , называют сокращение дроби.
-
Наибольшее число , на которое можно сократить дробь , — это НОД ее числителя и знаменателя.
-
Дробь называется несократимой – если числитель и знаменатель являются взаимно простыми числами.
-
Чтобы привести дроби к наименьшему общему знаменателю , надо: 1) найти НОК знаменателей этих дробей, оно и будет их наименьшим общим знаменателем; 2) разделить НОЗ на знаменатели данных дробей , т.е. найти для каждой дроби дополнительный множитель; 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
-
Чтобы сравнить ( сложить , вычесть) дроби с разными знаменателями , надо: 1) привести данные дроби к НОЗ; 2) сравнить ( сложить , вычесть ) полученные дроби.
-
Чтобы сложить смешанные числа , надо: 1) привести дробные части этих чисел к НОЗ; 2) отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.
-
Чтобы выполнить вычитание смешанных чисел , надо: 1) привести дробные части этих чисел к НОЗ; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь , уменьшив на единицу целую часть;2) отдельно выполнить вычитание целых частей и отдельно дробных частей.
Умножение и деление обыкновенных дробей.
-
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число , а знаменатель оставить без изменения.
-
Чтобы умножить смешанное число на натуральное число , можно: 1) умножить целую часть на натуральное число; 2) умножить дробную часть на это натуральное число; 3) сложить полученные результаты.
-
Чтобы умножить дробь на дробь ,надо: 1) найти произведение числителей и произведение знаменателей этих дробей; 2) первое произведение записать числителем , а второе – знаменателем.
-
Для того чтобы выполнить умножение смешанных чисел , надо их записать в виде неправильных дробей , а затем воспользоваться правилом умножения дробей.
Нахождение дроби от числа.
-
Чтобы найти дробь от числа , нужно умножить число на эту дробь.
Нахождение числа по его дроби.
-
Чтобы найти число по данному значению его дроби , надо это значение разделить на дробь.
Взаимно обратные числа.
-
Два числа , произведение которых равно единице , называют взаимно обратными.
Деление.
1) Чтобы разделить одну дробь на другую , надо делимое умножить на число , обратное делителю.
Дробные выражения.
-
Частное двух чисел или выражений , в котором знак деления обозначен чертой , называют дробным выражением. Выражение , стоящее над чертой , называют числителем , а выражение стоящее под чертой – знаменателем дробного выражения.
Отношения и пропорции.
-
Частное двух чисел называют отношением этих чисел. Отношение показывает , во сколько раз первое число больше второго , или какую часть первое число составляет от второго.
-
Равенство двух отношений называют пропорцией.
-
В пропорции а/в=с/д числа а и д называют крайними членами пропорции , числа в и с –средними членами пропорции.
-
В верной пропорции произведение крайних членов равно произведению средних .
-
Если произведение крайних членов пропорции равно произведению средних членов пропорции , то пропорция верна. Это свойство называют основным свойством пропорции.
-
Две величины называют прямо пропорциональными , если при увеличении ( уменьшении ) одной из них в несколько раз другая увеличивается ( уменьшается ) во столько же раз.
-
Две величины называют обратно пропорциональными , если при увеличении ( уменьшении ) одной из них в несколько раз другая уменьшается ( увеличивается ) во столько же раз.
-
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
Длина окружности и площадь круга.
-
Замкнутая линия все точки которой лежат на одинаковом расстоянии от одной точки «О»,называется окружностью.
-
Ту часть плоскости , которая лежит внутри окружности ( вместе с самой окружностью), называют кругом.
-
Точку «О» называют центром окружности и круга.
-
Отрезок соединяющий точку окружности с центром называют радиусом. Все радиусы одной окружности равны.
-
Отрезок соединяющий две точки окружности и проходящий через центр окружности называется диаметром. Диаметр состоит из двух радиусов , поэтому диаметр окружности в 2 раза длиннее ее радиуса.
-
Диаметр делит круг на 2 полукруга , а окружность – на 2 полуокружности.
-
Часть окружности между двумя точками называют дугой окружности.
-
Длина окружности прямо пропорциональна длине её диаметра. Поэтому для всех окружностей отношение длины окружности к длине её диаметра является одним и тем же числом. Его обозначают греческой буквой П— пи . Формула длины окружности: С=п d или C=2пr. П= 3,1416…..
-
Все точки поверхности шара одинаково удалены от центра шара.
-
Отрезок, соединяющий точку поверхности шара с центром ,называют радиусом шара.
-
Отрезок , соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара.
-
Диаметр шара равен двум радиусам.
-
Поверхность шара называют сферой.
Рациональные числа.
Положительные и отрицательные числа.
-
Числа со знаком + называют положительными.
-
Числа со знаком – называют отрицательными.
-
Прямую с выбранными на ней началом отсчета , единичным отрезком и направлением называют координатной прямой.
-
Число, показывающее положение точки на прямой , называют координатой этой точки.
-
Два числа , отличающиеся друг от друга только знаками, называют противоположными числами.
-
Натуральные числа , противоположные числа и нуль называют целыми числами.
-
Модулем числа а называют расстояние ( в единичных отрезках) от начала координат до точки А(а).
-
Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу.
-
Противоположные числа имеют равные модули.
Сравнение чисел.
-
Любое отрицательное число меньше любого положительного числа.
-
Из двух отрицательных чисел меньше то, модуль которого больше.
-
Нуль больше любого отрицательного числа , но меньше любого положительного числа.
-
На горизонтальной координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.
Сложение и вычитание положительных и отрицательных чисел.
-
Любое число от прибавления положительного числа увеличивается , а от прибавления отрицательного числа уменьшается.
-
Сумма двух противоположных чисел равна нулю.
-
Чтобы сложить два отрицательных числа , надо: а)сложить их модули; б) поставить перед полученным числом знак — .
-
Чтобы сложить два числа с разными знаками, надо: а) из большего модуля слагаемых вычесть меньший; б) поставить перед полученным числом знак того слагаемого , модуль которого больше.
-
Чтобы из данного вычесть другое ,надо к уменьшаемому прибавить число , противоположное вычитаемому: а-б=а+(-б)
-
Любое выражение содержащее лишь знаки сложения и вычитания , можно рассматривать как сумму.
-
Чтобы найти длину отрезка на координатной прямой ,надо из координаты его правого конца вычесть координату его левого конца.
Умножение и деление положительных и отрицательных чисел.
-
Чтобы перемножить два числа с разными знаками , надо перемножить модули этих чисел и поставить перед полученным числом знак — .
-
Чтобы перемножить два отрицательных числа , надо перемножить их модули.
-
Чтобы разделить отрицательное число на отрицательное , надо разделить модуль делимого на модуль делителя.
-
При делении чисел с разными знаками , надо: а) разделить модуль делимого на модуль делителя; б) поставить перед полученным числом знак — .
Рациональные числа.
-
Число , которое можно записать в виде отношения а/н , где а-целое число , а н-натуральное число , называют рациональным числом.
-
Любое целое число является рациональным.
-
Сумма , разность и произведение рациональных чисел тоже рациональные числа.
-
Если делитель отличен от нуля , то частное двух рациональных чисел тоже рациональное число.
-
Любое рациональное число можно записать либо в сиде десятичной дроби ( в частности целого числа ) , либо в виде периодической дроби.
-
Сложение рациональных чисел обладает переместительным и сочетательным свойствами.
-
Умножение рациональных чисел тоже обладает переместительным и сочетательным свойствами.
-
Произведение может быть равно нулю лишь в том случае , когда хотя бы один из множителей равен нулю.
-
Умножение рациональных чисел обладает распределительным свойством относительно сложения.
Решение уравнений.
-
Если перед скобками стоит знак + , то можно опустить скобки и этот знак + , сохранив знаки слагаемых , стоящих в скобках.Если первое слагаемое записано без знака , то его надо записать со знаком + .
-
Чтобы раскрыть скобки перед которыми стоит знак — , надо заменить этот знак на + , поменяв знаки всех слагаемых в скобках на противоположные , а потом раскрыть скобки.
Подобные слагаемые.
-
Если выражение является произведением числа и одной или нескольких букв , то это число называют числовым коэффициентом ( или просто коэффициентом ).
-
Слагаемые , имеющие одинаковую буквенную часть, называют подобными слагаемыми.
-
Чтобы сложить ( или говорят : привести ) подобные слагаемые , надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Решение уравнений.
-
Корни уравнения не изменяются , если обе части уравнения умножить или разделить на одно и то же число , не равное нулю.
-
Корни уравнения не изменяются , если какое –нибудь слагаемое перенести из одной части уравнения в другую , изменив при этом его знак.
-
Уравнение , которое можно привести к виду ах=в с помощью переноса слагаемых и приведения подобных , называют линейным уравнением с одним неизвестным.
Координаты на плоскости.
-
Две прямые , образующие при пересечении прямые углы , называют перпендикулярными.
-
Отрезки ( или лучи) , лежащие на перпендикулярных прямых , называют перпендикулярными отрезками ( или лучами).
-
Две непересекающиеся прямые на плоскости называют параллельными.
-
Если две прямые в плоскости перпендикулярны третьей , то они параллельны.
-
Через каждую точку плоскости , не лежащую на данной прямой , можно провести только одну прямую , параллельную данной прямой.
-
Отрезки ( или лучи) , лежащие на параллельных прямых , называют параллельными отрезками ( или лучами).
-
Системой координат на плоскости называют две перпендикулярные координатные прямые- х и у , которые пересекаются в начале отсчета – точке О. Тока О называется началом координат.
-
Плоскость на которой выбрана система координат , называют координатной плоскостью.
-
Координатную прямую х называют осью абсцисс , а у – осью ординат.
multiurok.ru
Правила по математике 6 класс
Признаки делимости
Простое число – число, у которого имеются два делителя (единица и оно само)
Составное число – число, у которого больше двух делителей.
Сократить дробь, значит разделить числитель и знаменатель на одно и тоже число.
Чтобы умножить дроби, нужно 1. Посмотреть, можем ли мы что-то сократить, 2. Умножить числитель на числитель, знаменатель на знаменатель.
Чтобы найти дробь (часть) от числа, необходимо умножить дробь(часть) на число.
Взаимно обратные числа – числа, произведение которых равно единице.
Чтобы поделить две дроби, необходимо 1. Нужно первую дробь оставить, 2. Деление заменить умножением, 3. Вторую дробь перевернуть, 4. Посмотреть можем ли мы что-то сократить, 5. Умножить числитель на числитель, знаменатель на знаменатель.
Отношение – это частное(деление) двух чисел.
Пропорция – это равенство (=) двух отношений.
Две переменные прямо пропорциональны – когда при увеличении(уменьшении) одной из них в несколько раз другая увеличивается(уменьшается) во столько же раз.
Две переменные обратно пропорциональны – когда при увеличении(уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
Окружность – геометрическая фигура, состоящая из множества точек, находящихся на одинаковом расстоянии от центра.
Радиус – отрезок, соединяющий центр окружности с любой точкой на окружности.
Диаметр – отрезок, соединяющий две точки на окружности, проходящий через центр.
Связь радиуса и диаметра – диаметр равен двум радиусам.
Хорда – отрезок, соединяющий две точки на окружности, не проходящий через центр.
Длина окружности –
Круг – это плоскость, ограниченная окружностью.
Площадь круга –
Целые числа (обозначается буквой Z) – натуральные числа, противоположные им числа и нуль.
Натуральные числа (обозначается буквой N) – числа, которые мы используем при счёте.
Любое отрицательное число меньше любого положительного числа.
Из двух отрицательных чисел меньше то, модуль которого больше.
Нуль больше любого отрицательного числа, но меньше любого положительного.
Чтобы сложить два отрицательных числа, нужно 1) сложить их модули, 2) поставить перед полученным числом знак «—»
Чтобы сложить два числа с разными знаками, нужно 1) из большего модуля слагаемых вычесть меньший, 2) поставить перед полученным числом знак того слагаемого, модуль которого больше.
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + (– b)
Например, –18 –14 = –18 + (–14)
+
+
+
+
̶
̶
̶
+
̶
̶
̶
+
-
Противоположные числа — два числа, отличающиеся друг от друга только знаками.
-
Координатная прямая – прямая с выбранными на ней началом отсчёта, единичным отрезком и направлением.
-
Число, показывающее положение точки на прямой, называют координатой этой точки.
-
Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.
-
Рациональные числа (обозначается буквой Q) – числа, которые можно записать в виде отношения , где a – целое число, а n – натуральное число.
-
Свойства действий с рациональными числами:
Переместительный: a + b = b + a
Сочетательный: a + (b + c) = (a + b) + c
Распределительный: (a + b) · c = a · c + b · c
Прибавление нуля: a + 0 = a
Умножение на нуль: a · 0 = 0
Умножение на 1: a · 1 = a
-
Модуль числа а – расстояние от начала координат до точки А (а).
-
Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.
-
Две непересекающиеся прямые на плоскости называют параллельными.
-
Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны.
-
Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.
-
Система координат на плоскости – это две перпендикулярные координатные прямые x и y, которые пересекаются в начале отсчёта – точке О.
-
Координатная плоскость – плоскость, на которой выбрана система координат.
-
Начало координат – точка О.
-
Прямая х – ось абсцисс. Прямая у – ось ординат.
-
Пусть М – некоторая точка координатной плоскости. Проведем через неё прямую МА, перпендикулярную координатной прямой х, и прямую МВ, перпендикулярную координатной прямой у. Точка А имеет координату 6, а В – координату -5, тогда точка М определяется парой чисел (6, -5). Эта пара чисел называется координаты точки М.
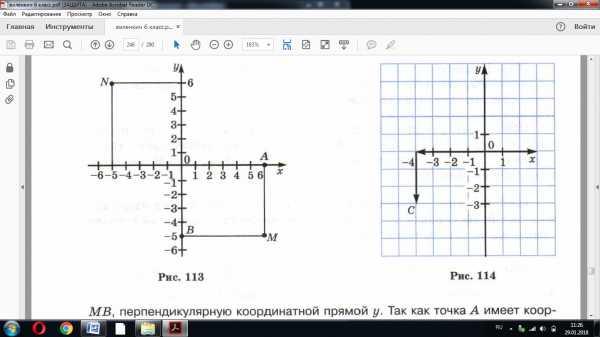
-
Произведение может быть равно нулю тогда, когда один из множителей равен нуль.
a · b = 0, a = 0 или b=0
-
Чтобы раскрыть скобки, перед которыми стоит знак « ̶ », нужно оставить знак перед скобками, а в скобках заменить знаки на противоположные.
-
Если выражение является произведение числа и одной/несколько букв, то это число называют коэффициентом.
-
Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
-
Чтобы сложить подобные слагаемые, нужно сложить их коэффициенты и результат умножить на общую буквенную часть.
-
Корни уравнения не изменяются, если 1) обе части уравнения умножить или разделить на одно и то же число, не равное нулю, 2) какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.
infourok.ru
Напишите пожалуйста правила за 6 класс по математике
Делимость чисел
Делителем натурального числа «а» называют натуральное число , на которое «а» делится без остатка.
Кратным натурального числа «а» называют натуральное число , которое делится без остатка на «а» .
Любое натуральное число имеет бесконечно много кратных.
Признаки делимости на 10 , на 5 и на 2.
Если запись натурального числа оканчивается цифрой 0 , то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой , то оно не делится без остатка на 10.
Если запись натурального числа оканчивается цифрой 0 или 5 , то это число делится без остатка на 5. Если запись натурального числа оканчивается другой цифрой , то оно не делится без остатка на 5.
Если запись натурального числа оканчивается четной цифрой , то это число делится без остатка на 2. Если запись натурального числа оканчивается нечетной цифрой , то это число нечетно.
Признаки делимости на 3 на 9.
Если сумма цифр числа делится на 9 , то и число делится на 9 ; если сумма цифр числа не делится на 9 , то и число не делится на 9 ;
Если сумма цифр числа делится на 3 , то и число делится на 3 ; если сумма цифр числа не делится на 3 , то и число не делится на 3 ;
Простые и составные числа
Натуральное число называют простым , если оно имеет только два делителя : единицу и само это число.
Натуральное число называют составным , если оно имеет более двух делителей.
Число 1 имеет только один делитель : само это число .Поэтому его не относят ни к составным , ни кпростым.
Всякое составное число можно разложить на множители. При любом способе получается одно и то же разложение , если не учитывать порядка записи множителей.
Наибольший общий делитель . Взаимно простые числа.
Наибольшее натуральное число , на которое делятся без остатка числа а и б , называют наибольшим общим делителем этих чисел.
Натуральные числа называют взаимно простыми , если их наибольший общий делитель равен 1.
Чтобы найти НОД нескольких натуральных чисел, надо: 1) состав разложения одного из этих чисел, вычеркнуть те , которые не входят в разложение других чисел; 3) найти произведение оставшихся множителей.
Наименьшее общее кратное (НОК)
Наименьшим общим кратным натуральных чисел а и б называют наименьшее натуральное число, которое кратно и а и б.
Чтобы найти НОК нескольких натуральных чисел , надо: 1) разложить их на простые множители; 2) выписать множители , входящие в разложение одного из чисел; 3) добавить к ним недостающие множители из разложений остальных чисел; 4) найти произведение получившихся множителей.
Сложение и вычитание дробей с разными знаменателями.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число , то получится равная ей дробь.
Деление числителя и знаменателя на их обший делитель , отличный от единицы , называют сокращение дроби.
Наибольшее число , на которое можно сократить дробь , — это НОД ее числителя и знаменателя.
Дробь называется несократимой – если числитель и знаменатель являются взаимно простыми числами.
Чтобы привести дроби к наименьшему общему знаменателю , надо: 1) найти НОК знаменателей этих дробей, оно и будет их наименьшим общим знаменателем; 2) разделить НОЗ на знаменатели данных дробей , т.е. найти для каждой дроби дополнительный множитель; 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Чтобы сравнить ( сложить , вычесть) дроби с разными знаменателями , надо: 1) привести данные дроби к НОЗ; 2) сравнить ( сложить , вычесть ) полученные дроби.
Чтобы сложить смешанные числа , надо: 1) привести дробные части этих чисел к НОЗ; 2) отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.
Чтобы выполнить вычитание смешанных чисел , надо: 1) привести дробные части этих чисел к НОЗ; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь , уменьшив на единицу целую часть;2) отдельно выполнить вычитание целых частей и отдельно дробных частей.
Умножение и деление обыкновенных дробей.
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число , а знаменатель оставить без изменения.
Чтобы умножить смешанное число на натуральное число , можно: 1) умножить целую часть на натуральное число; 2) умножить дробную часть на это натуральное число; 3) сложить полученные результаты.
Чтобы умножить дробь на дробь ,надо: 1) найти произведение числителей и произведение знаменателей этих дробей; 2) первое произведение записать числителем , а второе – знаменателем.
Для того чтобы выполнить умножение смешанных чисел , надо их записать в виде неправильных дробей , а затем воспользоваться правилом умножения дробей.
Нахождение дроби от числа.
Чтобы найти дробь от числа , нужно умножить число на эту дробь.
Нахождение числа по его дроби.
Чтобы найти число по данному значению его дроби , надо это значение разделить на дробь.
Взаимно обратные числа.
Два числа , произведение которых равно единице , называют взаимно обратными.
Деление.
1) Чтобы разделить одну дробь на другую , надо делимое умножить на число , обратное делителю.
Дробные выражения.
Частное двух чисел или выражений , в котором знак деления обозначен чертой , называют дробным выражением. Выражение , стоящее над чертой , называют числителем , а выражение стоящее под чертой – знаменателем дробного выражения.
Отношения и пропорции.
Частное двух чисел называют отношением этих чисел. Отношение показывает , во сколько раз первое число больше второго , или какую часть первое число составляет от второго.
Равенство двух отношений называют пропорцией.
В пропорции а/в=с/д числа а и д называют крайними членами пропорции , числа в и с –средними членами пропорции.
В верной пропорции произведение крайних членов равно произведению средних .
Если произведение крайних членов пропорции равно произведению средних членов пропорции , то пропорция верна. Это свойство называют основным свойством пропорции.
Две величины называют прямо пропорциональными , если при увеличении ( уменьшении ) одной из них в несколько раз другая увеличивается ( уменьшается ) во столько же раз.
Две величины называют обратно пропорциональными , если при увеличении ( уменьшении ) одной из них в несколько раз другая уменьшается ( увеличивается ) во столько же раз.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
Длина окружности и площадь круга.
Замкнутая линия все точки которой лежат на одинаковом расстоянии от одной точки «О»,называется окружностью.
Ту часть плоскости , которая лежит внутри окружности ( вместе с самой окружностью), называют кругом.
Точку «О» называют центром окружности и круга.
Отрезок соединяющий точку окружности с центром называют радиусом. Все радиусы одной окружности равны.
Отрезок соединяющий две точки окружности и проходящий через центр окружности называется диаметром. Диаметр состоит из двух радиусов , поэтому диаметр окружности в 2 раза длиннее ее радиуса.
Диаметр делит круг на 2 полукруга , а окружность – на 2 полуокружности.
Часть окружности между двумя точками называют дугой окружности.
Длина окружности прямо пропорциональна длине её диаметра. Поэтому для всех окружностей отношение длины окружности к длине её диаметра является одним и тем же числом. Его обозначают греческой буквой П- пи . Формула длины окружности: С=п d или C=2пr. П= 3,1416…..
Все точки поверхности шара одинаково удалены от центра шара.
Отрезок, соединяющий точку поверхности шара с центром ,называют радиусом шара.
Отрезок , соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара.
Диаметр шара равен двум радиусам.
Поверхность шара называют сферой.
Рациональные числа.
Положительные и отрицательные числа.
Числа со знаком + называют положительными.
Числа со знаком – называют отрицательными.
Прямую с выбранными на ней началом отсчета , единичным отрезком и направлением называют координатной прямой.
Число, показывающее положение точки на прямой , называют координатой этой точки.
Два числа , отличающиеся друг от друга только знаками, называют противоположными числами.
Натуральные числа , противоположные числа и нуль называют целыми числами.
Модулем числа а называют расстояние ( в единичных отрезках) от начала координат до точки А(а).
Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу.
Противоположные числа имеют равные модули.
Сравнение чисел.
Любое отрицательное число меньше любого положительного числа.
Из двух отрицательных чисел меньше то, модуль которого больше.
Нуль больше любого отрицательного числа , но меньше любого положительного числа.
На горизонтальной координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.
Сложение и вычитание положительных и отрицательных чисел.
Любое число от прибавления положительного числа увеличивается , а от прибавления отрицательного числа уменьшается.
Сумма двух противоположных чисел равна нулю.
Чтобы сложить два отрицательных числа , надо: а)сложить их модули; б) поставить перед полученным числом знак — .
Чтобы сложить два числа с разными знаками, надо: а) из большего модуля слагаемых вычесть меньший; б) поставить перед полученным числом знак того слагаемого , модуль которого больше.
Чтобы из данного вычесть другое ,надо к уменьшаемому прибавить число , противоположное вычитаемому: а-б=а+(-б)
Любое выражение содержащее лишь знаки сложения и вычитания , можно рассматривать как сумму.
Чтобы найти длину отрезка на координатной прямой ,надо из координаты его правого конца вычесть координату его левого конца.
Умножение и деление положительных и отрицательных чисел.
Чтобы перемножить два числа с разными знаками , надо перемножить модули этих чисел и поставить перед полученным числом знак — .
Чтобы перемножить два отрицательных числа , надо перемножить их модули.
Чтобы разделить отрицательное число на отрицательное , надо разделить модуль делимого на модуль делителя.
При делении чисел с разными знаками , надо: а) разделить модуль делимого на модуль делителя; б) поставить перед полученным числом знак — .
Рациональные числа.
Число , которое можно записать в виде отношения а/н , где а-целое число , а н-натуральное число , называют рациональным числом.
Любое целое число является рациональным.
Сумма , разность и произведение рациональных чисел тоже рациональные числа.
Если делитель отличен от нуля , то частное двух рациональных чисел тоже рациональное число.
Любое рациональное число можно записать либо в сиде десятичной дроби ( в частности целого числа ) , либо в виде периодической дроби.
Сложение рациональных чисел обладает переместительным и сочетательным свойствами.
Умножение рациональных чисел тоже обладает переместительным и сочетательным свойствами.
Произведение может быть равно нулю лишь в том случае , когда хотя бы один из множителей равен нулю.
Умножение рациональных чисел обладает распределительным свойством относительно сложения.
Решение уравнений.
Если перед скобками стоит знак + , то можно опустить скобки и этот знак + , сохранив знаки слагаемых , стоящих в скобках.Если первое слагаемое записано без знака , то его надо записать со знаком + .
Чтобы раскрыть скобки перед которыми стоит знак — , надо заменить этот знак на + , поменяв знаки всех слагаемых в скобках на противоположные , а потом раскрыть скобки.
Подобные слагаемые.
Если выражение является произведением числа и одной или нескольких букв , то это число называют числовым коэффициентом ( или просто коэффициентом ).
Слагаемые , имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Чтобы сложить ( или говорят : привести ) подобные слагаемые , надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Решение уравнений.
Корни уравнения не изменяются , если обе части уравнения умножить или разделить на одно и то же число , не равное нулю.
Корни уравнения не изменяются , если какое –нибудь слагаемое перенести из одной части уравнения в другую , изменив при этом его знак.
Уравнение , которое можно привести к виду ах=в с помощью переноса слагаемых и приведения подобных , называют линейным уравнением с одним неизвестным.
Координаты на плоскости.
Две прямые , образующие при пересечении прямые углы , называют перпендикулярными.
Отрезки ( или лучи) , лежащие на перпендикулярных прямых , называют перпендикулярными отрезками ( или лучами).
Две непересекающиеся прямые на плоскости называют параллельными.
Если две прямые в плоскости перпендикулярны третьей , то они параллельны.
Через каждую точку плоскости , не лежащую на данной прямой , можно провести только одну прямую , параллельную данной прямой.
Отрезки ( или лучи) , лежащие на параллельных прямых , называют параллельными отрезками ( или лучами).
Системой координат на плоскости называют две перпендикулярные координатные прямые- х и у , которые пересекаются в начале отсчета – точке О. Тока О называется началом координат.
Плоскость на которой выбрана система координат , называют координатной плоскостью.
Координатную прямую х называют осью абсцисс , а у – осью ординат.
gitun.com
|
Делителемнатурального числаaназывают натуральное число, на котороеaделится без остатка. Число 12 имеет шесть |
|
|
Кратнымнатурального числаaназывают натуральное число, делится Первые пять чисел, |
|
|
Признаки делимости На Если На Если На Если На Если На Если запись натурального |
|
|
Число, Число, имеющее более |
|
|
Наибольшее Чтобы 1.)Разложить 2.)Из 3.)Найти Натуральные числа |
|
|
Наименьшим Чтобы 1.)Разложить 2.)Выписать 3.)Добавить 4.)Найти произведение |
|
|
|
Основное Если числитель и |
|
|
Деление числителя |
|
60 = 2 168 = 2 Наименьший 2 · 2 |
Чтобы 1.)Найти 2.)Разделить 3.)Умножить числитель |
|
Чтобы 1.)Привести 2.)Сравнить (сложить, |
|
|
5 |
Чтобы 1.)Привести 2.)Отдельно выполнить |
|
3 |
Чтобы 1.)Привести 2.)Отдельно выполнить |
|
|
Чтобы Чтобы 1.)Найти 2.)Первое Чтобы выполнить |
|
Чтобы найти дробь |
|
|
|
Два числа, произведение |
|
|
Чтобы разделить |
|
Чтобы найти число |
|
|
|
Частное двух чисел |
|
или a:b=c:d a·d=b·c |
Равенство Числа В Если произведение |
|
4 : 2 = 7 : 21 5 : 25 = 7 : 35 |
Две Если две величины |
|
Две Если две величины |
|
|
Отношение 1 : 100000 = |
|
|
C = 2·π·r |
Длина r – π = 3,14 |
|
S = π·r2 |
Площадь r – π = 3,14 |
|
Прямую, Число, показывающее |
|
|
2,6 и
|
Два Натуральные числа, |
|
Модулемчислаa(|a|) называют расстояние |
|
|
– 8,7 + (– 3,5) = – (8,7 + |
Чтобы 1.)Сложить 2.)Поставить перед |
|
6,1 + или 6,1 + (– 4,2) = 6,1 – 4,2 = |
Чтобы 1.)Из 2.)Поставить перед |
|
Если A(9) |
Чтобы найти длину |
|
(–1,2)·0,3 = |
Чтобы перемножить |
|
(–3,2)·( –9) = |
Чтобы перемножить |
|
(–12) : ( –4) = 12 : 4 = 3 |
Чтобы разделить |
|
3,6 : (–3) = –(3,6:3) = –1,2 |
При 1.)Разделить 2.)Поставить перед |
|
x = |
Число x, которое можно |
|
16–(10–18+12) = |
Чтобы раскрыть |
|
0,3a·(–0,7b) |
Если выражение |
|
2m – 7m + 3m |
Слагаемые, Чтобы сложить (или |
|
Свойства 1.)Корни 2.)Корни уравнения |
|
|
Две прямые, образующие |
|
|
Две Если Через каждую точку |
|
|
|
О – (3;5) – |
studfiles.net
Рабочая программа по математике 6 класс автор Виленкин
№ урока
Тема урока
Количество часов
Номер урока в теме
Тип урока
Элементы содержания
Требования к уровню подготовки учащихся
Вид контроля
Дата проведения урока
План
Факт
1
2
3
4
5
6
7
8
9
Повторение (3 часа)
1
Дроби арифметические действия с дробями
1
1
Урок систематизации и обобщения знаний
Обыкновенная дробь, числитель и знаменатель. Правильная и неправильная дробь. Смешанное число. Десятичная дробь
Знать: определения обыкновенной дроби, правильной и неправильной дроби, смешанного числа, десятичной дроби, порядок выполнения арифметических действий с указанными числами.
Уметь:выполнять арифметические действия с дробями
Фронтальный опрос
2
Решение уравнений
1
2
Урок систематизации и обобщения знаний
Уравнение. Компоненты действий, свойства действий с числами. Упрощение выражений.
Знать: Определения уравнения, корня уравнения.
Уметь: решать уравнения, упрощать выражения, пользоваться свойствами
Устный опрос, выборочный контроль, математический диктант
3
Проценты. Решение задач
1
3
Урок систематизации и обобщения знаний
Процент. Формулы.
Знать: определения процента, правило округления чисел, знать формулы.
Уметь:Решать задачи с процентами, применять формулы при решении задач.
Фронтальный опрос. Индивидуальная работа
Делимость чисел (20 ч)
4
Делители и кратные
1
1
Урок изучения нового материала
Делитель. Кратное. Наименьшее кратное натурального числа
Знать: понятия делитель, кратное натурального числа.
Уметь: находить делители и кратные числа
Фронтальный опрос, работа у доски
5
Делители и кратные
1
2
Комбинированный урок
Фронтальный опрос, работа у доски
6
Делители и кратные
1
3
Урок-практикум
Устный опрос, индивидуальная работа по учебнику
7
Признаки делимости на 10, на 5 и на 2
1
4
Урок изучения нового материала
Признаки делимости чисел на 10, на 5 и на 2. Четные и нечетные числа
Знать: признаки делимости чисел на 10, на 5 и на 2.
Уметь: определять четные и нечетные числа, делимость чисел на 10, на 5 и на 2
Фронтальный опрос, работа у доски
8
Признаки делимости на 10, на 5 и на 2
1
5
Комбинированный урок
Устный опрос, работа у доски
9
Признаки делимости на 10, на 5 и на 2
6
Урок-практикум
Индивидуальная работа (карточки- задания), работа у доски
10
Признаки делимости на 9 и на 3
1
7
Комбинированный урок
Признаки делимости чисел на 9 и на 3
Знать: признаки делимости чисел на 9 и на 3.
Уметь: определять делимость чисел на 9 и на 3
Фронтальный опрос, работа у доски
11
Признаки делимости на 9 и на 3
1
8
Урок-практикум
Индивидуальная работа (карточки- задания), работа у доски
12
Контрольная работа № 1 «Входная контрольная работа»
1
9
Контроль знаний и умений
Арифметические действия с десятичными дробями
Уметь: производить арифметические действия с десятичными дробями
Самостоятельная работа
13
Простые и составные числа
1
10
Комбинированный урок
Простые натуральные числа. Составные натуральные числа. Разложение натуральных чисел на множители
Знать: понятия простое число, составное число.
Уметь: различать простые и составные числа; раскладывать числа на два множителя
Устный опрос, работа у доски
14
Разложение на простые множители
1
11
Урок изучения нового материала
Простые и составные числа. Признаки делимости. Разложение составных чисел на простые множители
Знать: алгоритм разложения числа на простые множители.
Уметь: раскладывать составные числа на простые множители
Фронтальный опрос, работа у доски
15
Разложение на простые множители
1
12
Урок-практикум
Индивидуальная работа (карточки-задания), работа у доски
16
Наибольший общий делитель. Взаимно простые числа
1
13
Урок изучения нового материала
Наибольший общий делитель (НОД) натуральных чисел. Взаимно простые числа. Алгоритм нахождения НОД
Знать: понятия наибольший общий делитель, взаимно простые числа; алгоритм нахождения НОД.
Уметь: находить НОД натуральных чисел
Устный опрос, работа у доски
17
Наибольший общий делитель. Взаимно простые числа
1
14
Урок-практикум
Индивидуальная работа (карточки-задания), работа у доски
18
Наибольший общий делитель. Взаимно простые числа
1
15
Урок проверки и коррекции знаний
Самостоятельная работа, работа у доски
19
Наименьшее общее кратное
1
16
Урок изучения нового материала
Наименьшее общее кратное (НОК) двух натуральных чисел. Алгоритм нахождения НОК. Историческая справка.
Знать: понятие наименьшее общее кратное; алгоритм нахождения НОК.
Уметь: находить НОК двух натуральных чисел
Фронтальный опрос, работа у доски
20
Наименьшее общее кратное
1
17
Урок-практикум
Индивидуальная работа (карточки-задания), работа у доски
21
Наименьшее общее кратное
1
18
Урок-практикум
Индивидуальная работа (карточки-задания), работа у доски
22
Наименьшее общее кратное
1
19
Урок проверки и коррекции знаний
Самостоятельная работа, работа у доски
23
Контрольная работа № 2 по теме «Делимость чисел»
1
20
Урок контроля знаний и умений
Проверка знаний учащихся по теме «Делимость чисел»
Уметь: применять полученные знания и умения при решении примеров и задач
Контрольная работа
§ 2. Сложение и вычитание дробей с разными знаменателями (22 ч)
24
Основное свойство дроби
1
1
Урок изучения нового материала
Основное свойство дроби. Преобразование дробей
Знать: основное свойство дроби. Уметь: применять основное свойство дроби при преобразовании дробей
Фронтальный опрос, работа у доски
25
Основное свойство дроби
1
2
Урок-практикум
Основное свойство дроби. Преобразование дробей
Индивидуальная работа (карточки-задания), работа у доски
26
Сокращение дробей
1
3
Урок изучения нового материала
Сокращение дробей. Сократимые и несократимые дроби. Историческая справка
Знать: понятия сократимая и несократимая дробь.
Уметь: выполнять сокращение дробей при решении примеров и задач
Устный опрос, работа у доски
27
Сокращение дробей
1
4
Урок-практикум
Сокращение дробей. Сократимые и несократимые дроби. Историческая справка
Индивидуальная работа (карточки-задания), работа у доски
28
Сокращение дробей
1
5
Урок-практикум
Сокращение дробей. Сократимые и несократимые дроби. Историческая справка
Индивидуальная работа (карточки-задания), работа у доски
29
Приведение дробей к общему знаменателю
1
6
Комбинированный урок
Основное свойство дроби. Новый знаменатель. Дополнительный множитель. Общий знаменатель. Наименьший общий знаменатель
Знать: понятие дополнительный множитель; правило приведения дробей к наименьшему общему знаменателю.
Уметь: приводить дроби к наименьшему общему знаменателю
Фронтальный опрос, работа у доски
30
Приведение дробей к общему знаменателю
1
7
Урок-практикум
Индивидуальная работа (карточки-задания), работа у доски
31
Приведение дробей к общему знаменателю
1
8
Урок проверки и коррекции знаний
Самостоятельная работа, работа у доски
32
Сравнение дробей
1
9
Урок изучения нового материала
Приведение дробей к наименьшему общему знаменателю. Сравнение дробей с одинаковыми и разными знаменателями. Сравнение дробей с одинаковыми числителями
Знать: правила сравнения, сложения и вычитания дробей с разными знаменателями.
Уметь: выполнять сравнение, сложение и вычитание дробей с разными знаменателями; пользоваться изученными правилами при решении задач
Устный опрос, работа у доски
33
Сложение и вычитание дробей с разными знаменателями
1
10
Комбинированный урок
Сложение и вычитание дробей с разными знаменателями. Историческая справка
Индивидуальная работа (карточки-задания), работа у доски
34
Сложение и вычитание дробей с разными знаменателями
1
11
Урок-практикум
Самостоятельная работа, работа у доски
35
Сложение и вычитание дробей с разными знаменателями
1
12
Урок закрепления изученного материала
Фронтальный опрос, работа у доски
36
Сложение и вычитание дробей с разными знаменателями
1
13
Урок закрепления изученного материала
Сложение и вычитание дробей с разными знаменателями. Историческая справка
Самостоятельная работа, работа у доски
37
Сложение и вычитание дробей с разными знаменателями
1
14
Урок закрепления изученного материала
Сложение и вычитание дробей с разными знаменателями. Историческая справка
Самостоятельная работа, работа у доски
38
Контрольная работа № 3 по теме «Сложение и вычитание дробей с разными знаменателями»
1
15
Урок контроля знаний и умений
Проверка знаний учащихся по теме «Сложение и вычитание дробей с разными знаменателями»
Уметь: применять полученные знания и умения при решении примеров и задач
Контрольная работа
39
Сложение и вычитание смешанных чисел
1
16
Урок изучения нового материала
Смешанные числа. Правила сложения и вычитания смешанных чисел. Свойства сложения и вычитания. Историческая справка
Знать: правила сложения и вычитания смешанных чисел.
Уметь: выполнять сложение и вычитание смешанных чисел
Устный опрос, работа у доски
40
Сложение и вычитание смешанных чисел
1
17
Комбинированный урок
Индивидуальная работа (карточки-задания), работа у доски
41
Сложение и вычитание смешанных чисел
1
18
Урок-практикум
Самостоятельная работа, работа у доски
42
Сложение и вычитание смешанных чисел
1
19
Урок закрепления изученного материала
Фронтальный опрос, работа у доски
43
Сложение и вычитание смешанных чисел
1
20
Урок закрепления изученного материала
Смешанные числа. Правила сложения и вычитания смешанных чисел. Свойства сложения и вычитания. Историческая справка
Самостоятельная работа, работа у доски
44
Контрольная работа № 4 по теме «Сложение и вычитание смешанных чисел»
1
21
Урок контроля знаний и умений
Проверка знаний 1учащихся по теме «Сложение и вычитание смешанных чисел»
Уметь: применять полученные знания и умения при решении примеров и задач
Контрольная работа
45
Сложение и вычитание смешанных чисел
1
22
Урок закрепления изученного материала
Самостоятельная работа, работа у доски
§ 3. Умножение и деление обыкновенных дробей (32 ч)
46
Умножение дробей
1
1
Урок изучения нового материала
Умножение дроби на натуральное число. Умножение обыкновенных дробей. Умножение смешанных чисел. Свойства умножения
Знать: правила умножения дроби на натуральное число и дроби на дробь; правило умножения смешанных чисел; переместительное и сочетательное свойства умножения.
Уметь: выполнять умножение дроби на натуральное число, дроби на дробь, смешанных чисел; применять переместительное и сочетательное свойства умножения при умножении дробей
Устный опрос, работа у доски
47
Умножение дробей
1
2
Комбинированный урок
Индивидуальная работа (карточки-задания), работа у доски
48
Умножение дробей
1
3
Урок проверки и коррекции знаний
Самостоятельная работа, работа у доски
49
Умножение дробей
1
4
Урок-практикум
Математический диктант, самостоятельная работа у доски
50
Нахождение дроби от числа
1
5
Комбинированный урок
Правило нахождения дроби от числа
Знать: правила нахождения дроби от числа, процента от числа.
Уметь: находить дробь и проценты от числа
Устный опрос, работа у доски
51
Нахождение дроби от числа
1
6
Урок закрепления изученного материала
Работа у доски
52
Нахождение дроби от числа
1
7
Урок-практикум
Математический диктант, самостоятельная работа у доски
53
Нахождение дроби от числа
1
8
Урок проверки и коррекции знаний
Самостоятельная работа, работа у доски
54
Применение распределительного свойства умножения
1
9
Урок изучения нового материала
Распределительное свойство умножения относительно сложения и вычитания. Умножение смешанного числа на натуральное число
Знать: правило умножения смешанного числа на натуральное число.
Уметь: выполнять умножение смешанных чисел на натуральные числа
Устный опрос, работа у доски
55
Применение распределительного свойства умножения
1
10
Комбинированный урок
Индивидуальная работа (карточки-задания), работа у доски
56
Применение распределительного свойства умножения
1
11
Урок проверки и коррекции знаний
Самостоятельная работа, работа у доски
57
Применение распределительного свойства умножения
1
12
Урок-практикум
Математический диктант, самостоятельная работа у доски
58
Контрольная работа № 5 по теме «Умножение дробей»
1
13
Урок контроля знаний и умений
Проверка знаний учащихся по теме «Умножение дробей»
Уметь: применять полученные знания и умения при решении примеров и задач
Контрольная работа
59
Анализ контрольной работы
1
14
Урок коррекции знаний
Анализ ошибок, допущенных в контрольной работе, устранение пробелов в знаниях
Уметь: выполнять работу над ошибками, допущенными в контрольной работе
Работа над ошибками, работа у доски
60
Взаимно обратные числа
1
15
Комбинированный урок
Взаимно обратные числа
Знать: понятие взаимно обратные числа.
Уметь: записывать число, обратное натуральному числу, и число, обратное смешанному числу
Индивидуальная работа (карточки-задания), работа у доски
61
Взаимно обратные числа
1
16
Урок-практикум
Самостоятельная работа, работа у доски
62
Деление
1
17
Урок изучения нового материала
Правильные и неправильные дроби, смешанные числа. Умножение дробей. Число, обратное данному. Правила деления дробей и смешанных чисел
Знать: правила деления дробей и смешанных чисел.
Уметь: выполнять деление дробей и смешанных чисел; применять изученные правила при решении задач
Устный опрос, работа у доски
63
Деление
1
18
Комбинированный урок
Фронтальный опрос, работа у доски
64
Деление
1
19
Урок-практикум
Индивидуальная работа (карточки-задания), работа у доски
65
Деление
1
20
Урок проверки и коррекции знаний
Самостоятельная работа, работа у доски
66
Деление
1
21
Урок проверки и коррекции знаний
Самостоятельная работа, работа у доски
67
Контрольная работа № 6 «Деление»
1
22
Урок контроля знаний и умений
Проверка знаний учащихся по теме «Деление»
Уметь: применять полученные знания и умения при решении примеров и задач
Контрольная работа
68
Нахождение числа по его дроби
1
23
Комбинированный урок
Деление на дробь. Правило нахождения числа по его дроби
Знать: правило нахождения числа по его дроби.
Уметь: находить число по его дроби и по данному значению его процента
Фронтальный опрос, работа у доски
69
Нахождение числа по его дроби
1
24
Урок-практикум
Индивидуальная работа (карточки-задания), работа у доски
70
Нахождение числа по его дроби
1
25
Урок проверки и коррекции знаний
Самостоятельная работа, работа у доски
71
Нахождение числа по его дроби
1
26
Урок закрепления изученного материала
Математический диктант, работа у доски
72
Нахождение числа по его дроби
1
27
Урок закрепления изученного материала
Математический диктант, работа у доски
73
Дробные выражения
1
28
Комбинированный урок
Частное выражений. Дробные выражения. Числитель дробного выражения. Знаменатель дробного выражения. Историческая справка
Знать: понятия дробное выражение, числитель дробного выражения, знаменатель дробного выражения. Уметь: выполнять действия с дробными выражениями
Устный опрос, работа у доски
74
Дробные выражения
1
29
Урок-практикум
Самостоятельная работа, работа у доски
75
Дробные выражения
1
30
Урок-практикум
Самостоятельная работа, работа у доски
76
Подготовка к контрольной работе
1
32
Урок коррекции знаний
Устранение пробелов в знаниях
Уметь: устранять ошибки
Работа над ошибками, работа у доски
77
Контрольная работа № 7 по теме «Деление дробей»
1
31
Урок контроля знаний и умений
Проверка знаний учащихся по теме «Деление дробей»
Уметь: применять полученные знания и умения при решении примеров и задач
Контрольная работа
§ 4. Отношения и пропорции (19 ч)
78
Отношения
1
1
Урок изучения нового материала
Отношение двух чисел — показатель того, во сколько раз одно число больше другого. Отношение двух величин
Знать: понятие отношение двух чисел; что показывает отношение двух чисел.
Уметь: определять, какую часть и сколько процентов составляет одно число от другого числа
Устный опрос, работа у доски
79
Отношения
1
2
Урок-практикум
Самостоятельная работа, работа у доски
80
Отношения
1
3
Урок-практикум
Индивидуальная работа (карточки-задания), работа у доски
81
Отношения
1
4
Урок-практикум
Индивидуальная работа (карточки-задания), работа у доски
82
Отношения
1
5
Урок-практикум
Индивидуальная работа (карточки-задания), работа у доски
83
Пропорции
1
6
Урок изучения нового материала
Пропорция. Верная пропорция. Крайние члены пропорции. Средние члены пропорции. Основное свойство пропорции
Знать: понятия пропорция, крайние члены пропорции, средние члены пропорции: основное свойство пропорции.
Уметь: читать и записывать пропорции; приводить примеры верных пропорций; применять основное свойство пропорции
Устный опрос, работа у доски
84
Пропорции
1
7
Урок-практикум
Индивидуальная работа (карточки-задания), работа у доски
85
Прямая и обратная пропорциональные зависимости
1
8
Урок изучения нового материала
Прямо пропорциональные величины. Обратно пропорциональные величины
Знать: понятия прямо пропорциональные величины, обратно пропорциональные величины.
Уметь: приводить примеры прямо и обратно пропорциональных величин; определять вид зависимости и, исходя из этого, выбирать путь решения задачи
Устный опрос, работа у доски
86
Прямая и обратная пропорциональные зависимости
1
9
Урок-практикум
Индивидуальные задания, работа у доски
87
Прямая и обратная пропорциональные зависимости
1
10
Урок-практикум
Индивидуальные задания, работа у доски
88
Контрольная работа № 8 по теме «Отношения и пропорции»
1
11
Урок контроля знаний и умений
Проверка знаний учащихся по теме «Отношения и пропорции»
Уметь: применять полученные знания и умения при решении примеров и задач
Контрольная работа
89
Анализ контрольной работы
1
12
Урок коррекции знаний
Анализ ошибок, допущенных в контрольной работе, устранение пробелов в знаниях
Уметь: выполнять работу над ошибками, допущенными в контрольной работе
Работа над ошибками, работа у доски
90
Масштаб
1
13
Урок изучения нового материала
Масштаб карты. Прямо пропорциональные величины
Знать: понятие масштаб.
Уметь: определять масштаб карты и находить расстояние на местности
Устный опрос, работа у доски
91
Длина окружности и площадь круга
1
14
Урок изучения нового материала
Окружность. Радиус окружности. Диаметр окружности. Длина окружности. Число я. Круг. Радиус круга. Диаметр круга. Площадь круга
Знать: формулы длины окружности и площади круга.
Уметь: по формулам находить длину окружности и площадь круга
Работа у доски
92
Длина окружности и площадь круга
1
15
Урок-практикум
Самостоятельная работа, работа у доски
93
Шар
1
16
Комбинированный урок
Шар. Радиус шара. Диаметр шара. Сфера. Историческая справка
infourok.ru
Справочные таблицы по математике 6 класс — К уроку — Математика, алгебра, геометрия
Делители и кратные 6кл.М.01
Делителем натурального числа а называется натуральное число, на которое а делится без остатка.
Кратным натурального числа а называют натуральное число , которое делится без остатка на а.
Любое натуральное число имеет бесконечно много кратных.
Признаки делимости
Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.
Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.
Если запись натурального числа оканчивается чётной цифрой, то это число делится без остатка на 2.
Если сумма цифр числа делится на 9, то и число делится на 9.
Если сумма цифр числа делится на 3, то и число делится на 3
НОД и НОК 6кл.М.02
Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число.
Натуральное число называют составным, если оно имеет более двух делителей.
Наибольшее натуральное число, на которое делятся без остатка числа a и b , называют наибольшим общим делителем этих чисел. НОД(24;36)=12
Натуральные числа называют взаимно простыми, если наибольший общий делитель равен 1.
Чтобы найти НОД нескольких натуральных чисел , надо:
Разложить их на простые множители;
Из множителей , входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
Найти произведение оставшихся множителей
Наименьшим общим кратным натуральных чисел a и b называют наименьшее натуральное число, которое кратно и a, и b.
Чтобы найти наименьшее общее кратное нескольких натуральных чисел , надо:
Разложить их на простые множители;
Выписать множители, входящие в разложение остальных чисел
Добавить к ним недостающие множители из разложений остальных чисел
Найти произведение получившихся множителей
НОД(24;36)= 2•2•3=12 НОК(24;36)=2•2•2•3•3=72
24 2 36 2 24 2 36 2
12 2 18 2 12 2 18 2
6 2 9 3 6 2 9 3
3 3 3 3 3 3 3 3
1 1 1 1
Сложение и вычитание дробей 6кл.М.03
с разными знаменателями
Чтобы сравнить(сложить, вычесть) дроби с разными знаменателями, надо:
Привести данные дроби к наименьшему общему знаменателю;
Сравнить (сложить, вычесть) полученные дроби
+ —
Чтобы сложить смешанные числа , надо:
Привести дробные части этих чисел к наименьшему общему знаменателю;
Отдельно выполнить сложение целых частей и отдельно – дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части
Чтобы выполнить вычитание смешанных чисел, надо:
Привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть;
Отдельно выполнить вычитание целых частей и отдельно дробных частей
Умножение и деление 6 кл.М.04
обыкновенных дробей
Чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменения.
=
Чтобы умножить дробь на дробь, надо:
Найти произведение числителей и знаменателей этих дробей;
Первое произведение записать числителем, а второе – знаменателем.
Для того чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Чтобы найти дробь от числа , нужно умножить число на эту дробь.
Чтобы умножить смешанное число на натуральное число, можно:
Умножить целую часть на натуральное число
Умножить дробную часть на это натуральное число
Сложить полученные результаты
Два числа, произведение которых равно 1, называют взаимно обратными.
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
Чтобы найти число по данному значению его дроби, надо это значение разделить на эту дробь.
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
Отношения и пропорции 6 кл.М.05
Частное двух чисел называют отношением этих чисел.
Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.
Равенство двух отношений называют пропорцией.
a÷b=c÷d
а и d — крайние члены пропорции, c и b- средние члены пропорции
В верной пропорции произведение крайних членов равно произведению средних.
a•d=b•c
Если произведение крайних членов пропорции равно произведению среднтх членов, то пропорция верна.
Чтобы найти неизвестный крайний член пропорции, надо произведение средних членов разделить на известный крайний член пропорции.
a=
Чтобы найти неизвестный средний член пропорции, надо произведение крайних членов пропорции разделить на известный средний член пропорции
d=
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
Масштаб 6 кл.М.06
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
М=
Длина окружности. Площадь круга.
C=2πr S =
C – длина окружности, r – радиус окружности
S – площадь круга
Шар
r- радиус шара
d – диаметр шара
Положительные и отрицательные числа 6 кл.М.07
Числа со знаком + называют положительными.
Числа со знаком — называют отрицательными.
Два числа, отличающиеся друг от друга только знаками, называют противоположными числами.
Натуральные числа, противоположные им числа и нуль называют целыми числами.
Модуль числа
Модулем числа а называют расстояние ( в единичных отрезках) от начала координат до точки А (а).
5 4
-5 0 4 х
а, если а ≥ 0
│а│=
-а, если а < 0
│0│=0
│4│=4
│-5│=5
Сложение и вычитание 6 кл.М.08
положительных и отрицательных чисел
Чтобы сложить два отрицательных числа, надо:
Сложить их модули;
Поставить перед полученным числом знак — .
-8,7+ (-3,5)= — ( 8,7 + 3,5 ) = — 12,2
-2
Чтобы сложить два числа с разными знаками, надо:
Из большего модуля слагаемых вычесть меньший;
Поставить перед полученным числом знак того слагаемого, модуль которого больше.
6,1 + ( -4,2 ) = + (6,1 – 4,2 ) = 1,9
— 8
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: a-b=a+(-b)
18 – 14 =- 18 + ( — 14) = — ( 18 + 14 )= — 32
Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.
Умножение и деление 6 кл.М.09
положительных и отрицательных чисел
Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак — .
( — 1,2 ) • 0,3 = — ( 1,2 • 0,3 ) = — 0,36
1,2 • ( — 0,3 ) = — ( 1,2 • 0,3 ) = — 0,36
Чтобы перемножить два отрицательных числа, надо перемножить их модули.
( — 3,2 ) • ( — 9 ) = │ — 3,2 │• │ — 9 │= 3,2 • 9 = 28,8
Или ( — 3,2 ) • ( — 9 ) = 3,2 • 9 = 28,8
Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
( — 12 ) ÷ ( — 4 ) =│-12│ ÷ │ -4│ = 3
Или ( — 12 ) ÷ ( — 4 ) =12 ÷ 4 = 3
При делении чисел с разными знаками, надо:
Разделить модуль делимого на модуль делителя;
Поставить перед полученным числом знак — .
3,6 ÷ ( — 3 ) = — ( 3,6 ÷ 3 ) = — 1,2
( —
Делить на нуль нельзя!
Рациональные числа 6кл.М.10
Число, которое можно записать в виде отношения , где a- целое число, а n – натуральное число, называют рациональным числом.
Любое целое число а является рациональным числом, т.к. его можно записать в виде .
-3 = 0=
Сумма, разность и произведение рациональных чисел тоже рациональное число.
Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.
Свойства действий с рациональными числами
• Переместительное свойство сложения
a + b = b + a
• Сочетательное свойство сложения
a + ( b + c ) = ( a + b ) + c
• Прибавление нуля не изменяет числа
а + 0 = а
• Сумма противоположных чисел равна нулю
а + ( — а ) = 0
• Переместительное свойство умножения
ab = ba
• Сочетательное свойство умножения
a ( b c ) = ( a b ) c
• Распределительное свойство умножения относительно сложения
( a + b ) c = ac + bc
• a • 1=a, a • 1, если а≠0, а • 0 = 0
Раскрытие скобок 6 кл.М.11
Если перед скобками стоит знак + , то можно опустить скобки и этот знак +, сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком + .
a + ( b + c ) = a + b + c a + ( — b + c ) = a – b + c
Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.
— ( a + b ) = — a – b
Чтобы раскрыть скобки, перед которыми стоит знак — , надо заменить этот знак на + , поменяв знаки всех слагаемых в скобках на противоположные. А потом раскрыть скобки.
Коэффициент
Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом ( или просто коэффициентом)
0,3а • ( — 0,7 b) = — 0,21 ab
Подобные слагаемые
Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
— 9х + 7х — 5х + 2х = ( -9 +7 -5 +2)х= — 5х
Решение уравнения
Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак.
Перпендикулярные прямые 6 кл.М.12
Две прямые, образующие при пересечении прямые углы, называются перпендикулярными.
А С
АВ СД
О
В
Д
Отрезки или лучи , лежащие на перпендикулярных прямых, называют перпендикулярными отрезками или лучами.
Параллельные прямые
Две не пересекающиеся прямые на плоскости называют параллельными.
В
А АВ │ СД
С Д
Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны.
c a c, b c a││b
а
b
через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.
Математика
6 класс
1. Делители и кратные . Признаки делимости
2. НОД и НОК
3. Сложение и вычитание дробей с разными знаменателями
4. Умножение и деление обыкновенных дробей
5. Отношения и пропорции
6. Длина окружности. Площадь круга.
7. Положительные и отрицательные числа. Модуль числа
8. Сложение и вычитание положительных и отрицательных чисел
9. Умножение и деление положительных и отрицательных чисел
10. Рациональные числа
11. Раскрытие скобок. Подобные слагаемые
12. Перпендикулярные прямые. Параллельные прямые
Полный текст материала Справочные таблицы по математике 6 класс смотрите в скачиваемом файле.
На странице приведен фрагмент.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Есть мнение?
Оставьте комментарий
Оставить комментарий
pedsovet.su
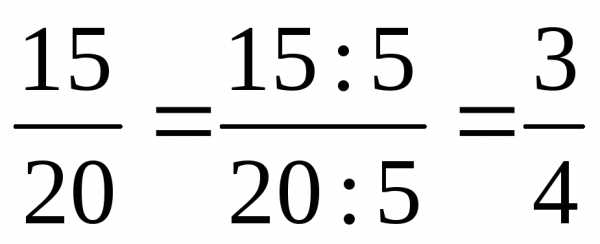
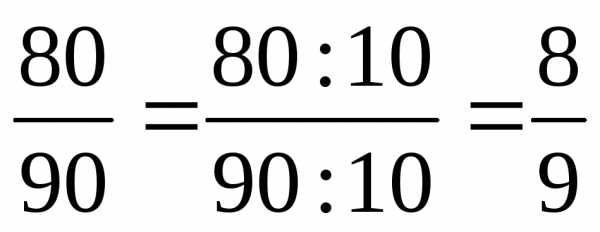
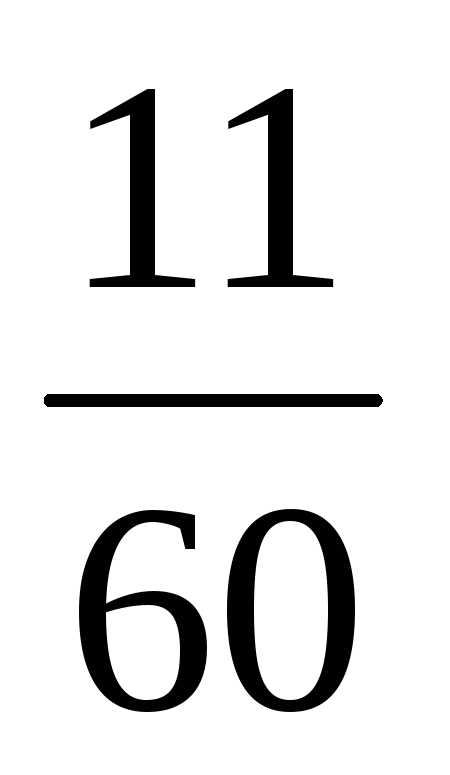 и
и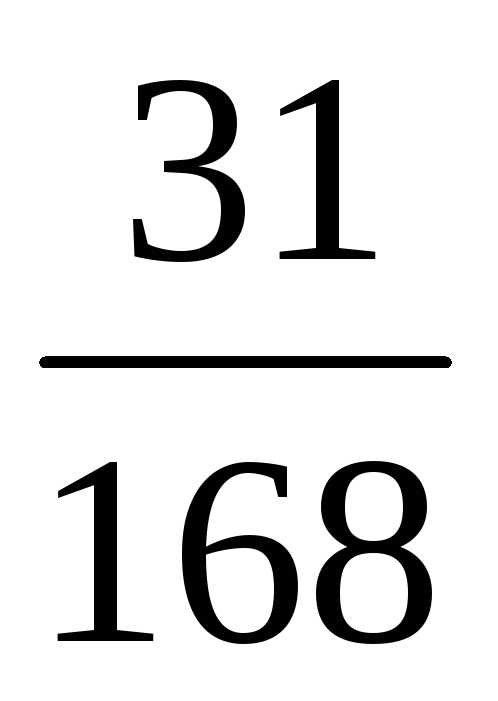
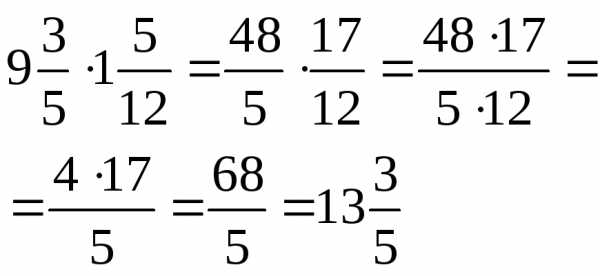
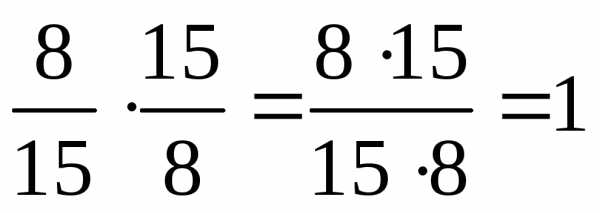
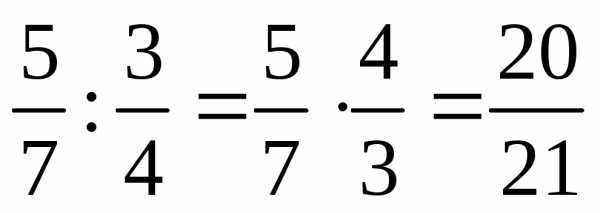
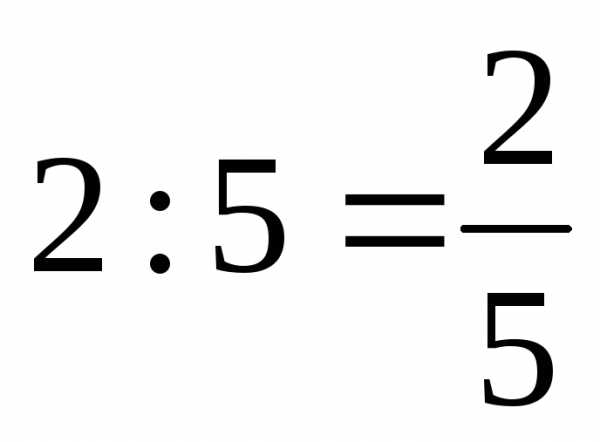
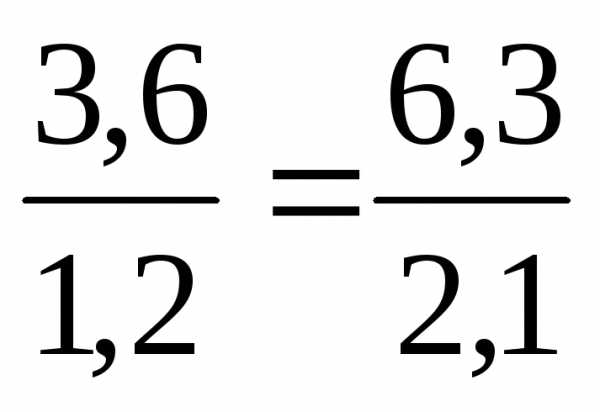
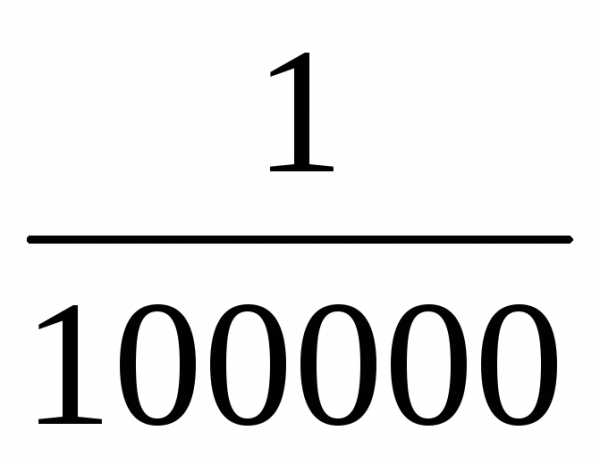 – карта выполнена в масштабе одна
– карта выполнена в масштабе одна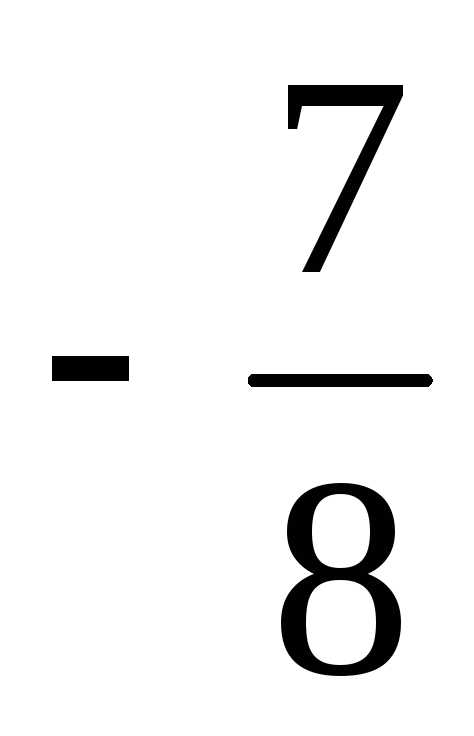 и
и
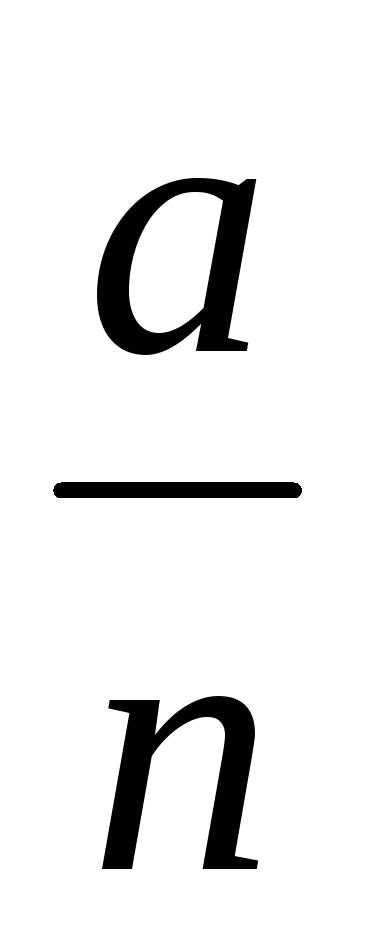
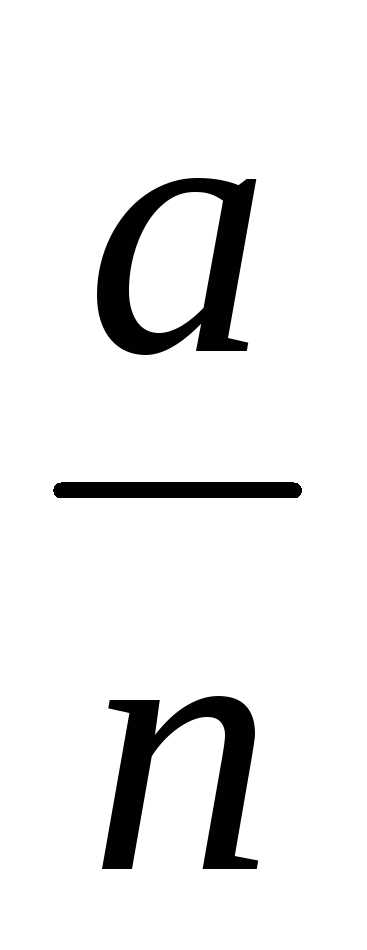 ,
,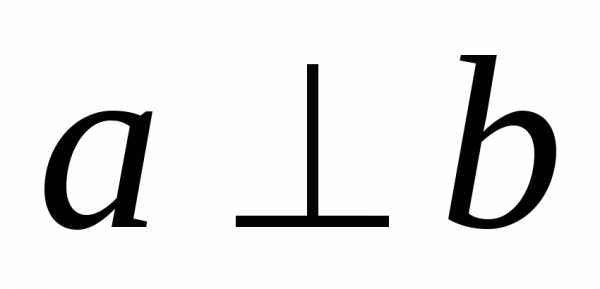 ).
).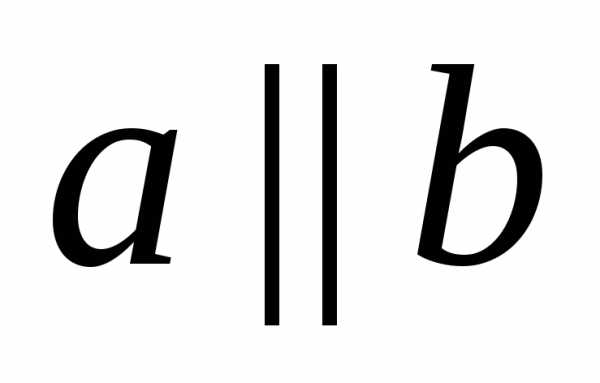 ).
).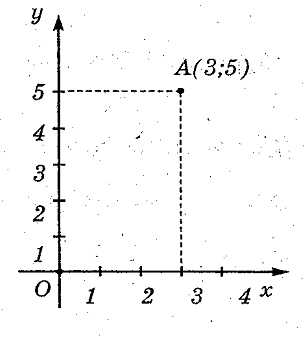
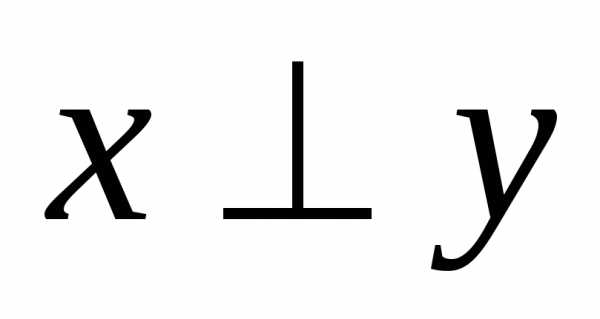 –система координат на плоскости
–система координат на плоскости