ГДЗ по математике 5 класс Бунимович решебник
Авторы: Бунимович Е.А., Дорофеев Г.В., Суворова С.Б.
Просвещение
ГДЗ по математике за 5 класс автора Бунимович Е.А. Пособие по своему объему достаточно большое и охватывает более 300 заданий. Их разнообразие настолько огромно, что школьники смогут самостоятельно подобрать себе те упражнения, которые им под силу.
Однако здесь также имеются и задания, которые обязательны для выполнения, независимо от уровня подготовки учащихся. Все зависит от желания и усвоения материала. Как правило, для каждого ребенка этот процесс происходит по-разному.
При изучении курса математики необходимо помнить и всегда знать прошлые темы. Все предлагаемые ответы к упражнениям в этом издании расписаны четко и лаконично. При необходимости к ним прилагаются дополнительные таблицы и схемы.
Выполненные работы рассчитаны для текущего и итогового контроля знаний школьников. Это довольно удобно, ведь не придется долго искать подходящие виды заданий, а соответственно уйдет минимум времени. Абсолютно все упражнения делятся на 4 варианта и направлены на активизацию учебного процесса.
Абсолютно все упражнения делятся на 4 варианта и направлены на активизацию учебного процесса.
Быстрый поиск
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
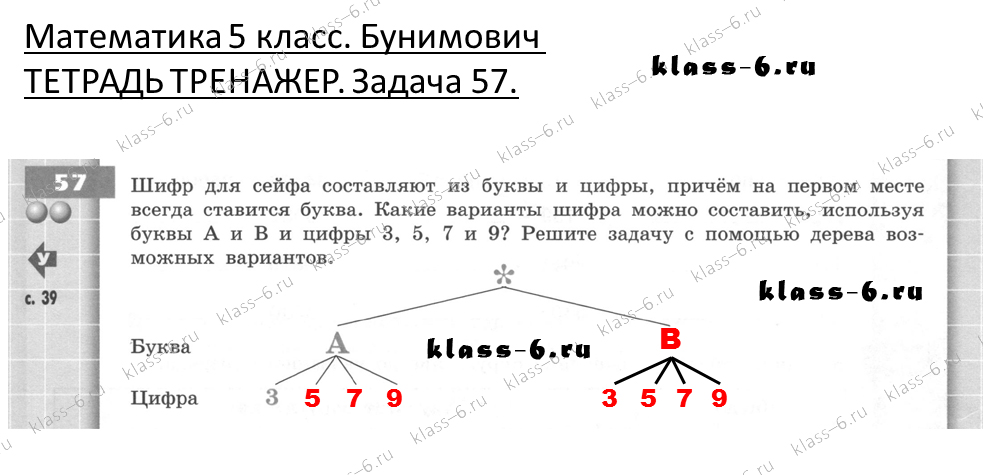
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
|
№ урока |
Дата |
Тема урока |
Виды, формы контроля |
Примечания |
|
|
план |
факт |
||||
|
Глава 1. |
|||||
|
1 2 |
2.09 5.09 |
Разнообразный мир линий. |
Интерактивная доска |
||
|
3 4 |
6.09 7.09 |
Прямая. Части прямой. Ломаная |
Устный опрос |
Интерактивная доска |
|
|
5 6 |
8.09 |
Длина линии. |
Устный опрос |
Интерактивная доска |
|
|
7 8 |
9. |
Окружность |
|||
|
9 |
12.09 |
Обобщающий урок |
Проверочная работа |
||
|
10 |
13.09 |
Контрольная работа № 1. |
|||
|
Глава 2. Натуральные числа (12ч) |
|||||
|
11 12 |
14.09 15.09 |
Как записывают и читают числа |
Интерактивная доска |
||
|
13 14 15 |
16. 19.09 20.09 |
Натуральный ряд. Сравнение натуральных чисел |
Проверочная работа |
||
|
16 17 |
21.09 22.09 |
Округление натуральных чисел |
Интерактивная доска |
||
|
18 19 20 |
23.09 26.09 27.09 |
Комбинаторные задачи. |
Интерактивная доска |
||
|
21 |
28.09 |
Обобщающий урок |
|||
|
22 |
29. |
Контрольная работа № 2. |
|||
|
Глава 3. Действия с натуральными числами (21ч) |
|||||
|
23 24 25 |
30.09 3.10 4.10 |
Сложение и вычитание |
Интерактивная доска |
||
|
26 27 28 29 |
5.10 6.10 7.10 10.10 |
Умножение и деление |
Интерактивная доска |
||
|
30 31 32 33 |
11. 12.10 13.10 14.10 |
Порядок действий в вычислениях |
|||
|
34 35 36 |
17.10 18.10 19.10 |
Степень числа |
Интерактивная доска |
||
|
37 38 39 40 |
20.10 21.10 24.10 25.10 |
Задачи на движение. Подведение итогов |
Флэш-демонстрации |
||
|
41 42 |
26. 27.10 |
Обзорные уроки по теме |
|||
|
43 |
28.10 |
Контрольная работа № 3. |
|||
|
Глава 4. Использование свойств действий при вычислениях (10 ч) |
|||||
|
44 45 |
31.10 |
Свойства сложения и умножения |
|||
|
46 47 48 |
Распределительное свойство |
||||
|
49 50 51 |
Решение задач |
||||
|
52 |
Обзорный урок |
||||
|
53 |
Контрольная работа № 4. |
||||
|
Глава 5. Углы и многоугольники (9ч) |
|||||
|
54 55 |
Как обозначают и сравнивают углы |
Флэш-демонстрации |
|||
|
56 57 58 |
Измерение углов |
Флэш-демонстрации |
|||
|
59 60 |
Многоугольники |
Проверочный тест |
Флэш-демонстрации |
||
|
61 |
Обобщающий урок |
||||
|
62 |
Контрольная работа №5 |
||||
|
Глава 6. |
|||||
|
63 64 65 |
Делители и кратные |
Флэш-демонстрации |
|||
|
66 67 68 |
Простые числа |
Проверочный тест |
|||
|
69 70 |
Делимость суммы и произведения |
Интерактивная доска |
|||
|
71 72 73 |
Признаки делимости |
Проверочный тест |
|||
|
74 75 76 |
Деление с остатком |
Интерактивная доска |
|||
|
77 |
Обобщающий урок |
Проверочная работа |
|||
|
78 |
Контрольная работа № 6. |
||||
|
Глава 7.Треульники и четырехугольники (10ч) |
|||||
|
79 80 |
Треугольники и их виды |
Тренажеры |
|||
|
81 82 |
Прямоугольники |
Устный опрос |
|||
|
83 84 |
Равенство фигур |
Флэш-демонстрация |
|||
|
85 86 |
Площадь прямоугольника |
Проверочная работа |
|||
|
87 |
Обобщающий урок |
||||
|
88 |
Контрольная работа № 7. |
||||
|
Глава 8. Дроби (19ч) |
|||||
|
89 90 91 92 93 94 |
Доли и дроби |
Тренажеры, проверочная работа |
Интерактивная доска |
||
|
95 96 97 98 99 |
Основное свойство дроби |
||||
|
100 101102103 |
Сравнение дробей |
Проверочная работа |
|||
|
104 105 |
Натуральные числа и дроби |
||||
|
106 |
Обобщающий урок |
||||
|
107 |
Контрольная работа №8. |
||||
|
Глава 9. Действия с дробями (35 ч) |
|||||
|
108 109 110 111 112 113 |
Сложение и вычитание дробей |
Тренажеры, проверочная работа |
Интерактивная доска |
||
|
114 115 116 117 118 119 |
Сложение и вычитание смешанных дробей |
Работа в парах, проверочная работа |
Тренажеры |
||
|
120 121 122 123 124 |
Умножение дробей |
Проверочная работа |
|||
|
125 126 127 128 129 130 |
Деление дробей |
Проверочная работа |
|||
|
131 132 133 134 135 |
Нахождение части целого и целого по его части |
Проверочная работа |
|||
|
136 137 138 139 |
Задачи на совместную работу |
Работа в парах, группах |
|||
|
140 141 |
Обобщающий урок |
||||
|
142 |
Контрольная работа № 9. |
||||
|
Многогранники (11ч) |
|||||
|
143 144 |
Геометрические тела и их изображение |
Интерактивная доска |
|||
|
145 146 147 |
Параллелепипед и пирамида |
||||
|
148 148 |
Объем параллелепипеда |
||||
|
150 151 |
Развёртки |
Практическое занятие |
|||
|
152 |
Обобщающий урок |
||||
|
153 |
Контрольная работа № 10. |
||||
|
Глава 11. Таблицы и диаграммы (9ч) |
|||||
|
154 155 156 |
Чтение и составление таблиц |
Флэш-демонстрации |
|||
|
157 158 |
Диаграммы |
||||
|
159 160 |
Опрос общественного мнения |
Практическое занятие |
|||
|
161 |
Обобщающий урок |
||||
|
162 |
Контрольная работа № 11. |
||||
|
163- 173 |
Итоговое повторение |
||||
|
174 175 |
Итоговый контроль |
||||
ЕДМЛ | Рак как многогранное заболевание
А. Фридман
Математическое моделирование природных явлений
(2012)
- Том: 7, Выпуск: 1, стр. 3-28
- ISSN: 0973-5348
Доступ к полной статье
top
Доступ к полному тексту
Полный (PDF)
Аннотация
Топ
Рак недавно обогнал болезни сердца и стал самым большим убийцей в мире. Рак
Рак
инициируется генными мутациями, которые приводят к локальной пролиферации аномальных клеток и их
миграция в другие части человеческого тела, процесс, называемый метастазированием. метастазы
Затем раковые клетки мешают нормальным функциям организма, что в конечном итоге приводит к
смерть. Существует двести видов рака, классифицированных по месту их возникновения. Большинство
у них есть некоторые общие черты, но они также имеют свою специфику. В этом
статье мы рассматриваем математические модели таких общих черт, а затем переходим к описанию
Модели конкретных онкологических заболеваний.
Как цитировать
топ
- MLA
- БибТекс
- РИС
Фридман, А. «Рак как многогранное заболевание». Математическое моделирование природных явлений 7.1 (2012): 3-28.
@article{Friedman2012,
abstract = {Рак недавно обогнал сердечно-сосудистые заболевания и стал самой большой причиной смерти в мире. Рак
Рак
инициируется генными мутациями, которые приводят к локальной пролиферации аномальных клеток и их
миграция в другие части человеческого тела, процесс, называемый метастазированием. метастазы
Затем раковые клетки мешают нормальным функциям организма, что в конечном итоге приводит к
смерть. Существует двести видов рака, классифицированных по месту их возникновения. Большинство
у них есть некоторые общие черты, но они также имеют свою специфику. В этом
статье мы рассматриваем математические модели таких общих черт, а затем переходим к описанию
модели конкретных раковых заболеваний.},
автор = {Фридман А.},
журнал = {Математическое моделирование природных явлений},
ключевые слова = {модели опухолей; задачи со свободной границей; гиперболические уравнения; параболические уравнения; Уравнение Стокса},
язык = {eng},
месяц = {1},
номер = {1},
страницы = {3-28},
издатель = {EDP Sciences},
заголовок = {рак как многогранное заболевание },
URL = {http://eudml. org/doc/222277},
org/doc/222277},
Volume = {7},
year = {2012},
}
TY — JOUR
AU — Friedman, A.
ТИ — Рак как многогранное заболевание
ЖО — Математическое моделирование природных явлений
ДА — 2012/1//
ПБ — ЭДП Науки
ВЛ — 7
ИС — 1
СП — 3
ЭП — 28
АБ — Рак недавно обогнал болезнь сердца как самого большого убийцу в мире. Рак
инициируется генными мутациями, которые приводят к локальной пролиферации аномальных клеток и их
миграция в другие части человеческого тела, процесс, называемый метастазированием. метастазы
Затем раковые клетки мешают нормальным функциям организма, что в конечном итоге приводит к
смерть. Существует двести видов рака, классифицированных по месту их возникновения. Большинство
у них есть некоторые общие черты, но они также имеют свою специфику. В этом
статье мы рассматриваем математические модели таких общих черт, а затем переходим к описанию
Модели конкретных онкологических заболеваний.
LA — eng
KW — модели опухолей; задачи со свободной границей; гиперболические уравнения; параболические уравнения; Уравнение Стокса
UR — http://eudml.org/doc/222277
ER —
Ссылки
топ
- А. Анхель. Доказано, что рак поджелудочной железы
удивительно медленный убийца. Живая наука, 27 октября 2010 г. - Н. Армстронг, К. Пейнтер, Дж. Шерратт. Непрерывный подход
для моделирования межклеточной адгезии. Дж. Теор.
биол., 243 (1),
98–113. - лет назад Аяти, Г.Ф. Уэбб, А.Р.А. Андерсон. Вычислительные методы
и результаты для структурированных мультимасштабных методов исследования опухолей
вторжение. Многомасштабная модель. Симул.,
5 (2006), 1–20. - С. Азнаворян, М. Штраке, Х. Крутч, Э. Шиффманн, Л. Лиотта. Преобразование сигнала для
хемотаксис и гаптотаксис молекулами матрикса в опухолевых клетках.
J. Cell Biol., 110(4),
(1990), 1427–1438. - Б. Базалий, А. Фридман. Глобальное существование и
устойчивость для эллиптико-параболической задачи со свободной границей : Приложение к модели
с ростом опухоли. Университет Индианы. Мат. Дж.,
52 (2003), 1265–1304. - Б.В. Базалий, А. Фридман. Свободная граница
задача для эллиптико-параболической системы: приложение к модели опухоли
рост. Комм. в ПДЭ, 28
(2003), 627. - С. Бунимовича-Мендразицкого,
Э. Шочат, Л. Стоун. Математическая модель БКГ
иммунотерапия при поверхностном раке мочевого пузыря. Бык.
Мат. биол., 69 (2007),
1847–1870 гг. - С. Бунимовича-Мендразицкого,
Дж. К. Глюкман, Дж. Часкалович. математический
модель комбинированной иммунотерапии бациллами Кальметта-Герена (БЦЖ) и интерлейкеном (ИЛ)-2
поверхностного рака мочевого пузыря. Дж. Теор.
Дж. Теор.
биол, 277 (2011),
27–40. - Х.М. Бирн, M.A.J. капеллан. Рост некротических
опухоли в присутствии и в отсутствие ингибиторов.
Мат. Биологические науки, 135 (1996),
187–216. - А. Кэмпбелл, Т. Сивакумаран, М. Дэвидсон, М. Лок, Э. Вонг. Математическое моделирование
метастазы в печень, рост опухоли и контроль с помощью лучевой терапии.
физ. Мед. биол., 53 (2008),
7225–7239. - X. Чен, А. Фридман. Свободная граница
задача для эллиптико-гиперболической системы: приложение к опухоли
рост. СИАМ Дж. Матем. Анальный.,
35 (2003), 974–986. - X. Чен, С. Цуй, А. Фридман. Гиперболический свободный
краевая задача моделирования роста опухоли: асимптотическое поведение.
Транс. амер. Мат. Соц., 357 (2005),
амер. Мат. Соц., 357 (2005),
4771–4804. - С. Кюи, А. Фридман. Анализ
математическая модель роста некротических опухолей.
Дж. Матем. Анальный. и приложение, 255
(2001), 636–677. - С. Кюи, А. Фридман. Свободная граница
Задача для сингулярной системы дифференциальных уравнений: приложение к модели
рост опухоли. Транс. амер. Мат. соц.,
355 (2003), 3537–3590. - С. Кюи, А. Фридман. Гиперболический свободный
краевая задача моделирования роста опухоли. Интерфейсы
и свободные границы, 5 (2003 г.),
159–182. - С.Э. Эйкенберри,
Дж. Д. Надь, Ю. Куанг. Эволюционное влияние
уровней андрогенов на рак предстательной железы в многомасштабном математическом
модель. биол. Прямой, 5
(2010), 24–52.
- ЮВ Эйкенберри, Т. Санкар, М.К. Преул, Э.Дж. Костелич, С. Дж. Тальхаузер, Ю. Куанг. Виртуальная глиобластома:
рост, миграция и обработка в трехмерном математическом
модель. Клеточный пролиф., 42
(2009 г.), 511–528. - С. Эйкенберри, К. Тальхаузер, Ю. Куанг.
Математическое моделирование меланомы. PLoS Comput Biol., 5: e1000362
(2009). - С. Эйкенберри, К. Тальхаузер, Ю. Куанг.
Опухолеиммунное взаимодействие, хирургическое лечение и рецидив рака у
математическая модель меланомы. PLoS Comput Biol., 5: e1000362 (2009), Epub
2009, 24 апреля. - М.А. Фонтелос, А. Фридман. нарушение симметрии
бифуркации задач со свободной границей в трех измерениях.
Асимптотический анализ., 35 (2003),
187–206. - С.
 Дж.Х. Фрэнкс, Х.М. Бирн, Дж. П. Кинг, Дж. С. Э. Андервуд, CE Льюис. Моделирование раннего роста
Дж.Х. Фрэнкс, Х.М. Бирн, Дж. П. Кинг, Дж. С. Э. Андервуд, CE Льюис. Моделирование раннего роста
протоковой карциномы in situ молочной железы. Дж. Матем.
биол., 47 (2003),
424–452. - С.Дж.Х. Фрэнкс, Х.М. Бирн, Дж. П. Кинг, Дж. С. Э. Андервуд, CE Льюис. Моделирование роста
комедо-протоковая карцинома in situ. Мат. Мед. &
биол., 20 (2003),
277–308. - С.Дж.Х. Фрэнкс, Х.М. Бирн, J.C.E. Андервуд, CE Льюис. Биологические выводы
на основе математической модели комедоновой протоковой карциномы in situ
грудь. Дж. Теор. биол.,
232 (2005), 523–543. - С.Дж.Х. Фрэнкс, Дж. П. Кинг. Взаимодействие между
равномерно пролиферирующая опухоль и ее окружение: Однородный материал
характеристики. Мат. Мед. и биол.,
20 (2003), 47–89. - А.
 Фридман. Свободная граница
Фридман. Свободная граница
задача моделирования связанной системы эллиптических, гиперболических уравнений и уравнений Стокса
рост опухоли. Интерфейсы и бесплатные
Границы, 8 (2006),
247–261. - А. Фридман. Многомасштабная опухоль
модель. Интерфейсы и свободные границы,
10 (2008), 245–262. -
А. Фридман. Свободное граничное значение
проблемы, связанные с мультимасштабными моделями опухолей.
Математическое моделирование природных явлений, 4
(2009 г.), 134–155. - А. Фридман, Б. Ху. Бифуркация от стабильности
к неустойчивости для задачи со свободной границей, возникающей в опухолевых
модель. Арка Крыса. мех. Анальный.,
180 (2006), 293–330. - А. Фридман, Б.
 Ху. Асимптотическая устойчивость для
Ху. Асимптотическая устойчивость для
задача со свободной границей, возникающая в модели опухоли. Дж.
Дифф. уравнения, 227 (2006),
598–639. - А. Фридман, Б. Ху. Бифуркация от стабильности
к неустойчивости для задачи со свободной границей, моделирующей рост опухоли по Стоксу
уравнение. Мат. Анальный и прикладной,
327 (2007), 643–664. - А. Фридман, Б. Ху. Раздвоение на халяву
краевая задача моделирования роста опухоли по уравнению Стокса.
СИАМ Дж. Матем. Анал., 39 (2007),
174–194. - А. Фридман, Б. Ху. Стабильность и нестабильность
Бифуркации Ляпунова-Шмидта и Хопфа для задачи со свободной границей, возникающей в опухоли
модель. Транс. амер. Мат. соц.,
360 (2008), 5291–5342. - А.
 Фридман, Б. Ху. Роль кислорода в тканях.
Фридман, Б. Ху. Роль кислорода в тканях.
техническое обслуживание: Математическое моделирование и качественный анализ.
Мат. Мод. Мет. заявл. наук, 18 (2008),
1–33. - А. Фридман, Б. Ху, С-Я. Као. Контроль клеточного цикла в
Первая точка рестрикции и ее влияние на рост тканей.
Дж. Матем. биол., 60 (2010),
881–907. - А. Фридман, Ю. Ким. Опухолевые клетки-пролиферация
и миграции под влиянием своего микроокружения.
Математические бионауки. и инженер., 8 (2011),
373–385. - А. Фридман, Ф. Райтич. Анализ
математическая модель роста опухолей. Дж. Матем.
биол., 38 (1999),
262–284. - А. Фридман, Ф. Райтич. нарушение симметрии
бифуркация аналитических решений задач со свободной границей: приложение к
модель роста опухоли. Транс. амер. Мат.
Транс. амер. Мат.
Соц., 353 (2001),
1587–1634 гг. - А. Фридман, Ю. Тао. Анализ модели
вирус, избирательно реплицирующийся в опухолевых клетках. Дж.
Мат. биол., 47 (2003),
391–423. - А. Фридман, Дж.Дж. Тиан, Г. Фульчи, Э.А. Чиокка, Дж. Ван. Виротерапия глиомы:
эффекты подавления врожденного иммунитета и повышенной репликации вируса
вместимость. Исследования рака,
66 (2006), 2314–2319. - Г. Фульчи, Л. Брейманн, Д. Джанни, К. Курозоми, С. Ри, Дж. Ю, Б. Каур, Д. Луис, Р. Вайследер, М. Калиджури, Э.А. Чиокка. Циклофосфамид
усиливает виротерапию глиомы за счет ингибирования врожденного иммунитета
ответы. ПНАС, 103
(2006), 12873–12878. - V. DeGiorgi, D. Massai, G. Gerlini, F. Mannone, E. Quercioli и др.
 Немедленный местный и регионарный рецидив после иссечения
Немедленный местный и регионарный рецидив после иссечения
полипоидная меланома: покой опухоли или активация опухоли.
Дерматол. Хирург, 29(2003),
664–667. - ДЖ.Э.Ф. Грин, С.Л. Уотерс, К.М. шекешев,
Х.М. Бирн. Математическая модель
Агрегация клеток печени in vitro. Бык. Мат.
биол., 71 (2009),
906–930. - ДЖ.Э.Ф. Грин, С.Л. Уотерс, Дж. П. Уайтли, Л. Эдельштейн-Кешет,
К.М. шекешев,
Х.М. Бирн. Нелокальные модели для
образование гепатоцитарно-звездчатых клеточных агрегатов. Дж.
Теор. биол., 267 (2010),
106–120. - PR Харпер, С.К. Джонс. Математические модели для
раннее выявление и лечение колоректального рака.
Наука управления здравоохранением, 8 (2005),
101–109. - Х.
 Харпольд, Дж. Эк, К. Суонсон. Эволюция
Харпольд, Дж. Эк, К. Суонсон. Эволюция
математическое моделирование пролиферации и инвазии глиом.
Дж. Нейропатол. Эксп. Неврол., 66 (1)
(2007), 1–9. - А. Идета, Г. Танака, Т. Такеучи, К. Айхара. Математическая модель
прерывистая супрессия андрогенов при раке предстательной железы.
Журнал нелинейных наук, 18 (2008),
593–614. - Т.Л. Джексон. Математическая модель
рост опухоли предстательной железы и андрогеннезависимый рецидив.
Дискретный прод. Дин-Б, 4 (2004),
187–201. - Т.Л. Джексон. математический
исследование множественных путей к рецидивирующему раку предстательной железы: сравнение с
экспериментальные данные. неоплазия,
6 (2004), 697–704. - Х.В. Джайн, С. Клинтон, А. Биндер, А.
 Фридман.
Фридман.
Появится математическая модель гормональной терапии рака предстательной железы. - Ю. Цзян, Ю. Пьесивак-Грбович,
К. Кантрелл, Дж. П. Фрейер. Многомасштабная модель для
аваскулярный рост опухоли. Биоф. Дж.,
89 (2005), 3884–3894. - Дж. Б. Джонс, Дж. Дж. Песня, П.М. Хемпен, Г. Пармиджани,
Р.Х.Хрубан, С.Э. Керн. Обнаружение митохондриальных
Мутации ДНК при раке поджелудочной железы дают «массовое» преимущество перед обнаружением
мутации ядерной ДНК. Исследования рака,
61 (2001), 1299–1304. - Ю. Ким, А. Фридман. Взаимодействие опухоли
с его микросредой: математическая модель.
Бык. Мат. биол., 72 (2010),
1029–1068. - Ю. Ким, С. Лоулер, М.О. Новицкий, Э.А. Чиокка, А. Фридман.
 Математическая модель
Математическая модель
опухоли головного мозга: формирование паттерна клеток глиомы вне сфероида опухоли
основной. Дж. Теор. биол., 260
(2009 г.), 359–371. - Ю. Ким, М. Столарска, Х. Отмер. Гибридная модель опухоли
сфероидный рост in vitro I: теоретическая разработка и ранние
полученные результаты. Мат. Мод. Мет. заявл. наук,
17 (2007), 1773–1798. - Ю. Ким, Дж. Уоллес, Ф. Ли, М. Островски, А. Фридман. Трансформированный эпителий
Взаимодействие клеток и фибробластов/миофибробластов в опухоли молочной железы: математический анализ
Модель и эксперименты. Дж. Матем. биол.,
61 (2010), 401–421. - Н.Л. Комарова, К. Ленгауэр, Б. Фогельштейн, М. Новак. Динамика генетических
нестабильность при спорадическом и семейном колоректальном раке.
Биология и терапия рака, 1
(2002), 685–692.
- Х.А. Левин, М. Нильсен-Гамильтон. Ангиогенез-А
биохимическая/математическая перспектива. Конспект лекций
Матем., 1872 (2006),
23–76, Спрингер-Ферлаг,
Берлин-Гейдельберг. - Х.А. Левин, С.Л. Памук, Б.Д. Слиман, М. Нильсен-Гамильтон. математический
моделирование образования и развития капилляров при ангиогенезе опухоли: пенетрация
в строму. Бык. Мат. биол.,
63 (2001), 801–863. - Э. Мандонне, Дж. Делатр, М. Танги, К. Суонсон, А. Карпентье, Х. Дюффо, П. Корню, Р. Эффентер, Дж. Эк, Л. Дж. Капелле. Непрерывный рост
средний диаметр опухоли в подгруппе глиом II степени.
Анна. Неврол., 53 (4)
(2003), 524–528. - Н. Манцарис, С. Уэбб, Х. Г. Отмер. Математическое моделирование
опухолевый ангиогенез. Дж. Матем. биол.,
Матем. биол.,
49 (2004), 111–187. - А. Перумпанани, Х. Бирн. Внеклеточный матрикс
концентрация оказывает селективное давление на инвазивные клетки.
Евро. Дж. Рак, 35(8)
(1999), 1274–1280. - Г.Дж. Петет, К.П. Пожалуйста, М.Дж. Тиндалл, Д.Л.С. Макэлвейн. Миграция клеток
в многоклеточных опухолевых сфероидах. Бык. Мат.
биол., 63 (2001),
231–257. - Л.К. Поттер, М.Г. Загар, Х.А. Бартон. Математическая модель для
Андрогенная регуляция простаты у интактных и кастрированных взрослых мужчин
крысы. Являюсь. Дж. Физиол. Эндокринол. метаб.,
291 (2006), E952–E964. - Р. Рибба, Т. Колин, С. Шнелл. Многомасштабная модель
рак и его использование при анализе лучевой терапии.
Теор. биол. и мед. Мод., 3
Мод., 3
(2006), 7, 1–19.. - Б. Рибба, О. Сант, Т. Колин, Д. Бреш, Э. Греньен, Дж. П. Буассель. Многомасштабная модель
аваскулярный рост опухоли для исследования агентов. Дж.
Теор. биол., 243 (2006),
532–541. - Дж. Шерратт, С. Горли, Н. Армстронг, К. Пейнтер. Ограниченность
решения модели нелокальной реакции диффузии для адгезии при агрегации клеток и
инвазия рака. Евро. J. Appl. мат.,
20 (2009 г.), 123–144. - К. Суонсон, Дж. Эк, Дж. Мюррей. Количественная модель для
дифференциальная подвижность глиом в сером и белом веществе.
Клеточный Пролиф., 33 (5)
(2000), 317–329. - И.М.М. ван Левен,
Х.М. Бирн, О.Э. Дженсен, Дж. Р. Кинг. Динамика склепа и
колоректальный рак: достижения в математическом моделировании.
 Линии (9ч)
Линии (9ч)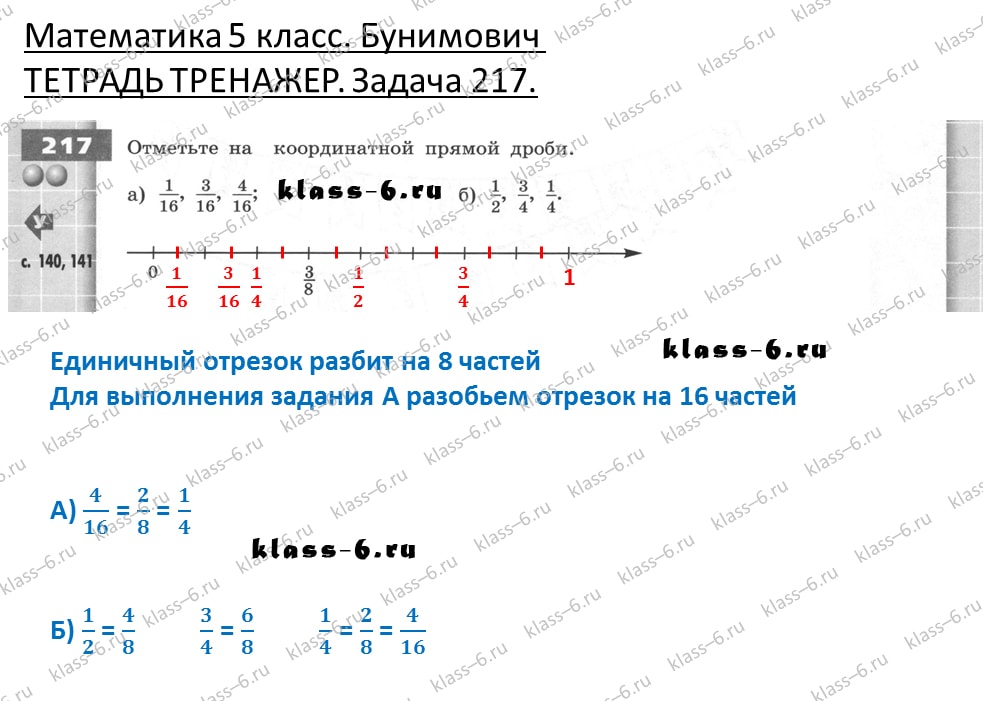 09
09 09
09 09
09 10
10 10
10
 Делимость чисел (16ч)
Делимость чисел (16ч)




