ГДЗ по математике 3 класс Башмаков, Нефедова ответы к учебнику 1, 2 часть
Страница 6, Считаем до тысячи:1;
2;
3;
Страница 7:4;
5;
6;
7;
8;
Страница 8, Разрядные слагаемые:1;
2;
3;
4;
Страница 9:5;
6;
7;
8;
9;
Страница 10, Складываем и вычитаем по разрядам:1;
2;
3;
4;
Страница 11:5;
6;
7;
8;
Страница 12, Меняем одну цифру:1;
2;
3;
4;
Страница 13:5;
6;
7;
8;
Страница 14, Переходим через десяток:1;
2;
3;
Страница 15:4;
5;
6;
7;
Страница 16, Складываем и вычитаем десятки:1;
2;
3;
Страница 17:4;
5;
6;
Страница 18, Вычисляем по разрядам:1;
2;
3;
4;
5;
6;
7;
8;
Страница 20, Решаем задачи:1;
2;
3;
4;
Страница 21:5;
6;
7;
8;
9;
Страница 22, Проверяем, чему мы научились:1;
2;
3;
4;
5;
Страница 22, Математический тренажер:1;
2;
Страница 23:3;
4;
5;
6;
7;
Страница 24, Умножаем и делим на 2:1;
2;
3;
4;
Страница 25:5;
6;
7;
8;
9;
Страница 26, Умножаем и делим на 4:1;
2;
3;
4;
Страница 27:5;
6;
7;
8;
Страница 28, Умножаем и делим на 3:1;
2;
3;
4;
Страница 29:5;
6;
7;
8;
Страница 30, Умножаем на 6:1;
2;
3;
4;
Страница 31:5;
6;
7;
8;
9;
Страница 32, Умножаем на 5:1;
2;
3;
4;
Страница 33:5;
6;
7;
8;
9;
Страница 34, Умножаем на 7:1;
2;
3;
4;
Страница 35:5;
6;
7;
8;
Страница 36, Умножаем на 8 и на 9:1;
2;
3;
4;
Страница 37:5;
6;
7;
8;
Страница 38, Делим и умножаем числа:1;
2;
3;
4;
5;
Страница 39:6;
7;
8;
Страница 40, Решаем задачи, вычисляем, сравниваем:1;
2;
3;
4;
5;
6;
Страница 41:7;
8;
9;
Страница 42, Проверяем, чему мы научились:1;
2;
3;
4;
Страница 42, Математический тренажер:1;
2;
Страница 43:3;
4;
5;
6;
7;
8;
9;
10;
Страница 44, Периметр многоугольника:1;
2;
Страница 45:3;
4;
5;
6;
Страница 46, Единицы длины:1;
2;
3;
Страница 47:4;
5;
6;
7;
8;
9;
Страница 48, Дециметр:1;
2;
3;
4;
Страница 49:5;
6;
7;
8;
9;
Страница 50, Вычисляем площадь:1;
2;
3;
Страница 51:4;
5;
6;
7;
8;
Страница 52, Увеличиваем и уменьшаем фигуры:1;
2;
3;
Страница 53:4;
5;
6;
7;
8;
9;
Страница 54, Строим фигуры из кубиков:1;
2;
3;
4;
Страница 55:5;
6;
7;
8;
Страница 56, Проектируем сад:1;
2;
Страница 57:Практическая работа;
3;
4;
5;
Страница 59, О симметрии:1;
2;
Страница 60, Проверяем, чему мы научились:1;
2;
3;
Страница 60, Математический тренажер:1;
2;
3;
Страница 61:4;
5;
6;
7;
8;
9;
10;
11;
12;
13;
14;
Страница 63:15;
16;
17;
18;
19;
20;
21;
22;
23;
Страница 64, Играем с кенгуру:1;
2;
3;
4;
Страница 65:5;
6;
7;
8;
9;
10;
Страница 68, Переставляем слагаемые:1;
2;
3;
Страница 69:4;
5;
6;
7;
8;
Страница 70, Переставляем множители:1;
2;
3;
Страница 71:4;
5;
6;
7;
Страница 72, Складываем и вычитаем:1;
2;
3;
4;
Страница 73:5;
6;
7;
8;
9;
10;
Страница 74, Умножаем и делим:1;
2;
3;
4;
5;
6;
Страница 75:7;
8;
9;
10;
Страница 76, Группируем слагаемые:1;
2;
3;
4;
Страница 77:5;
6;
7;
Страница 78, Умножаем и делим на 10, 100, 1000:1;
2;
3;
Страница 79:4;
5;
6;
7;
8;
Страница 80, Группируем множители:1;
2;
3;
4;
Страница 81:5;
6;
7;
8;
9;
10;
Страница 82, Проверяем, чему мы научились:1;
2;
3;
4;
Страница 82, Математический тренажер:1;
2;
Страница 83:3;
4;
5;
6;
7;
8;
9;
10;
Страница 84, Умножаем сумму:1;
2;
3;
4;
Страница 85:5;
6;
7;
8;
Страница 86, Умножаем и складываем:1;
2;
3;
Страница 87:4;
5;
6;
Страница 88, Делим сумму:1;
2;
3;
4;
5;
Страница 89:6;
7;
8;
9;
Страница 90, Повторяем все правила:1;
2;
3;
4;
5;
Страница 91:6;
7;
8;
9;
10;
Страница 92, Используем правила вычислений:1;
2;
3;
4;
5;
Страница 93:6;
7;
8;
9;
10;
11;
Страница 94, Размышления о нуле:1;
2;
3;
Страница 95:4;
5;
6;
7;
Страница 96, Идем за покупками:1;
2;
3;
Страница 97:4;
5;
6;
Страница 98, Проверяем, чему мы научились:1;
2;
3;
4;
Страница 98, Математический тренажер:1;
2;
3;
Страница 99:4;
5;
6;
7;
8;
9;
Страница 100, Числа и величины:1;
2;
3;
4;
Страница 101:5;
6;
7;
8;
Страница 102, Минуты в часы и обратно:1;
2;
3;
Страница 103:4;
5;
6;
7;
Страница 104, Сутки, месяц, год:1;
2;
3;
4;
Страница 105:5;
6;
7;
8;
Страница 106, Вычисляем длину пути:1;
2;
3;
4;
Страница 107:5;
6;
Страница 108, Рисуем схемы движения:1;
2;
3;
Страница 109:4;
5;
6;
Страница 110, Скорость:1;
2;
3;
4;
Страница 111:5;
6;
7;
Страница 112, Исследуем зависимость:1;
2;
3;
Страница 113:4;
5;
6;
7;
8;
Страница 116, Проверяем, чему мы научились:1;
2;
3;
Страница 116, Математический тренажер:1;
2;
Страница 117:3;
4;
Страница 118:5;
6;
7;
8;
9;
10;
11;
12;
Страница 119:13;
14;
15;
16;
17;
18;
19;
Страница 120, Играем с кенгуру:1;
2;
3;
4;
5;
Страница 121:6;
7;
8;
9;
10;
11;
 (Страницы с 6 по 139)
(Страницы с 6 по 139)Страница 6, Как составляют выражения:1;
2;
3;
4;
Страница 7:5;
6;
7;
8;
Страница 8, Вычисляем значение выражения:1;
2;
3;
4;
Страница 9:5;
6;
7;
Страница 10, Неизвестное число в равенстве:1;
2;
3;
4;
Страница 11:5;
6;
7;
8;
Страница 12, Преобразуем выражения:1;
2;
3;
Страница 13:4;
5;
6;
7;
Страница 14, Решаем задачи:1;
2;
3;
Страница 15:4;
5;
6;
Страница 16, Проверяем, чему мы научились:1;
2;
3;
4;
Страница 16, Математический тренажер:1;
2;
3;
4;
Страница 17:5;
6;
7;
8;
9;
Страница 18, Что такое масса:1;
2;
3;
Страница 19:4;
5;
6;
7;
8;
9;
Страница 20, Записываем сложение в столбик:1;
2;
3;
4;
Страница 21:5;
6;
7;
8;
Страница 22, Встречаем сложение чисел на практике:1;
2;
3;
4;
Страница 23:5;
6;
7;
Страница 24, Перепись населения:1;
2;
3;
Страница 25:4;
5;
6;
7;
Страница 26, По дорогам России:1;
2;
3;
Страница 27:4;
5;
6;
Страница 28, Проверяем, чему мы научились:1;
2;
3;
Страница 28, Математический тренажер:1;
2;
3;
4;
Страница 29:5;
6;
7;
8;
9;
10;
Страница 30, Играем в шахматы:1;
2;
3;
Страница 31:4;
5;
6;
7;
8;
Страница 32, Путешествуем по городам Европы:1;
2;
3;
Страница 33:4;
5;
6;
Страница 34, Работаем с таблицами и схемами:1;
2;
3;
4;
Страница 35:5;
6;
Страница 36, Решаем задачи на клетчатой бумаге:1;
2;
3;
4;
Страница 37:5;
6;
7;
Страница 38, Площадь квадрата:1;
2;
3;
Страница 39:4;
5;
6;
7;
Страница 41, Разворот истории:1;
2;
Страница 42, Математический тренажер:1;
2;
3;
4;
Страница 43:5;
6;
7;
8;
9;
Страница 44, Вспоминаем, что мы умеем:1;
2;
3;
4;
5;
6;
Страница 45:7;
8;
9;
10;
Страница 46, Записываем вычитание в столбик:1;
2;
3;
Страница 47:4;
5;
6;
7;
Страница 48, Считаем сдачу:1;
2;
3;
4;
Страница 49:5;
6;
7;
8;
9;
Страница 50, По железной дороге:1;
Страница 51:2;
3;
4;
5;
Страница 52, Как вычесть сумму из числа:1;
2;
3;
Страница 53:4;
5;
6;
7;
Страница 54, Знаменательные даты:1;
2;
3;
4;
5;
Страница 55:6;
7;
8;
9;
Страница 56, Подводим итоги:1;
2;
3;
4;
5;
6;
Страница 57:7;
8;
9;
10;
Страница 58, Проверяем, чему мы научились:1;
2;
3;
Страница 58, Математический тренажер:1;
2;
3;
Страница 59:4;
5;
6;
7;
Страница 60:8;
9;
10;
11;
Страница 61:12;
13;
14;
15;
16;
17;
18;
Страница 62, Играем с кенгуру:1;
2;
3;
4;
5;
Страница 63:6;
7;
8;
9;
10;
11;
Страница 68, Записываем умножение в столбик:1;
2;
3;
4;
Страница 69:5;
6;
7;
8;
9;
Страница 70, Откуда берутся нули:1;
2;
3;
4;
5;
Страница 71:6;
7;
8;
9;
10;
Страница 72, Считаем устно и письменно:1;
2;
3;
4;
Страница 73:5;
6;
7;
8;
Страница 74, Пять пишем, три в уме:1;
2;
3;
4;
5;
Страница 75:6;
7;
8;
9;
Страница 76, Вычисляем массу:1;
2;
3;
Страница 77:4;
5;
6;
7;
Страница 78, Измеряем емкости:1;
2;
3;
4;
Страница 79:5;
6;
7;
8;
9;
Страница 80, Шестидесятеричная система счисления:1;
2;
Страница 81:3;
4;
Страница 82, Проверяем, чему мы научились:1;
2;
3;
Страница 82, Математический тренажер:1;
2;
Страница 83:3;
4;
5;
6;
7;
8;
9;
10;
11;
Страница 84, Вспоминаем, что мы знаем и умеем:1;
2;
3;
4;
5;
Страница 85:6;
7;
8;
9;
Страница 86, Делится — не делится:1;
2;
3;
Страница 87:4;
5;
6;
7;
8;
9;
Страница 88, Подбираем наибольшее произведение:1;
2;
3;
Страница 89:4;
5;
6;
7;
8;
Страница 90, Что в остатке?:1;
2;
3;
Страница 91:4;
5;
6;
7;
8;
Страница 92, Записываем деление уголком:1;
2;
3;
Страница 93:4;
5;
6;
7;
Страница 94, Продолжаем осваивать деление:1;
2;
3;
4;
5;
Страница 95:6;
7;
8;
9;
Страница 96, Проверяем, чему мы научились:1;
2;
3;
Страница 96, Математический тренажер:1;
2;
Страница 97:3;
4;
5;
6;
7;
8;
9;
10;
11;
Страница 98, Находим неизвестное:1;
2;
3;
4;
5;
Страница 99:6;
7;
8;
9;
10;
Страница 100, Делим на круглое число:1;
2;
3;
4;
5;
Страница 101:6;
7;
8;
9;
Страница 102, Собираемся в путешествие:1;
2;
3;
4;
Страница 103:5;
6;
7;
8;
Страница 104, Учимся находить ошибки:1;
2;
3;
4;
Страница 105:5;
6;
7;
8;
Страница 106, Проверяем результаты деления:1;
2;
3;
Страница 107:4;
5;
6;
7;
8;
Страница 108, Проверяем, чему мы научились:1;
2;
3;
Страница 108, Математический тренажер:1;
2;
3;
4;
Страница 109:5;
6;
7;
8;
9;
10;
Страница 110, Окружность и круг:1;
2;
3;
Страница 111:4;
5;
6;
7;
Страница 112, Делим на равные части:1;
2;
3;
4;
Страница 113:5;
6;
7;
8;
9;
10;
Страница 114, Рисуем схемы и делим числа:1;
2;
Страница 115:3;
4;
5;
6;
7;
Страница 116, Вычисляем доли:1;
2;
3;
4;
5;
Страница 117:6;
7;
8;
9;
10;
Страница 118, Рисуем схемы и решаем задачи:1;
2;
3;
4;
Страница 119:5;
6;
7;
8;
9;
Страница 120, Проверяем, чему мы научились:1;
2;
3;
Страница 120, Математический тренажер:1;
2;
3;
4;
5;
Страница 121:6;
7;
8;
9;
10;
11;
12;
Страница 122, Полет на луну:1;
2;
3;
Страница 123:4;
5;
6;
7;
Страница 124, Ворота Мории:1;
2;
Страница 125:3;
4;
5;
6;
Страница 126, Золотое руно:1;
2;
Страница 127:3;
4;
5;
6;
Страница 128, Возвращение аргонавтов:1;
2;
3;
Страница 129:4;
5;
6;
Страница 130, Математический тренажер:1;
2;
3;
4;
5;
Страница 131:6;
7;
8;
9;
10;
Страница 132:11;
12;
13;
14;
15;
16;
17;
18;
19;
Страница 133:20;
21;
22;
23;
24;
25;
26;
27;
28;
29;
30;
Страница 134:31;
32;
33;
34;
35;
36;
37;
38;
39;
40;
Страница 135:41;
42;
43;
44;
45;
46;
47;
48;
49;
50;
Страница 136, Умеешь ли ты.
 ..:1;
..:1;2;
3;
4;
5;
6;
7;
Страница 137:8;
9;
10;
11;
Страница 138, Играем с кенгуру:1;
2;
3;
4;
5;
Страница 139:6;
7;
8;
9;
10;
11;
Поделиться:
Предыдущее
Следующее
Онлайн решебник и гдз по математике за 3 класс к учебнику Башмакова, Нефедовой с ответами к номерам.
Чтобы новые знания не казались детям тяжелыми, родители помогают им, пользуясь гдз по математике 3 класс к учебнику Башмакова. Такая помощь намного действенней, чем самостоятельно считать задачки со своим сыном или дочерью. В решебнике присутствуют интересные примеры, помогающие третьекласснику учить уроки в увлекательной форме. В учебнике можно смотреть упражнения, которые проходили в школе или задали на дом. Кроме решенных примеров ГДЗ предоставляет:
- возможность проверить свои знания при помощи интересных тестов;
- поиграть в увлекательные арифметические игры;
- списать правильные ответы на любые номера;
- легко освоить таблицу умножения / деления.

Правильные ответы по математике за 3 класс Башмаков можно смотреть в любое время на нашем ресурсе. Логическое мышление, хорошие отметки, желание осваивать новую науку – то, что приобретают дети, пользуясь эффективным помощником.
Предыдущее
Следующее
Открытый урок по математике 3 класс | Методическая разработка по математике (3 класс) по теме:
Открытый урок по математике в 3 классе по теме: Письменная нумерация в пределах 1000
Тип урока: урок-закрепление
Цели: — закрепить умение читать, записывать числа в пределах 1000, знание десятичного состава чисел, умение представлять числа в виде суммы разрядных слагаемых, умение сравнивать трехзначные числа, умение решать примеры и задачи;
— совершенствовать вычислительные навыки;
— развивать умение рассуждать, мыслить, анализировать;
— воспитывать
Оборудование: мультимедийная презентация, раздаточный материал различного характера.
Ход урока
1.Организационный момент.
Звенит, звенит, звенит звонок,
Мы начинаем наш урок.
Ребята, давайте улыбнёмся друг другу. Я очень рада видеть ваши улыбки. Надеюсь, работать на уроке будет интересно. Каждый узнает что-то новое, познавательное.
– Чему учимся на уроках математики?
– Где это пригодиться нам в жизни? (дети читают стихи)
Математика повсюду. А иначе рамы будут с перекосом,
Глазом только поведёшь, Потолок провалится.
И примеров сразу уйму, А кому, друзья, скажите,
Ты вокруг себя найдёшь. Это может нравится?
Каждый день, вставая бодро, Ох, скажу я вам, ребята,
Начинаешь уж решать: Все примеры не назвать.
Идти тихо или быстро, Но должно быть всем понятно,
Чтобы в класс не опаздать. Что математику вам надо знать на пять.
Что математику вам надо знать на пять.
Вот строительство большое.
Прежде чем его начать
Нужно всё ещё подробно
Начертить и рассчитать.
А ещё “математика ум в порядок приводит”. Чтобы привести ум в порядок, отгадать мою загадку и сформулировать тему нашего урока, мы должны провести разминку или гимнастику для ума. Готовы?
— назовите 4 арифметических действия в математике;
— найдите сумму чисел 42 и 35;
— уменьшите 63 на 8;
— на сколько 52 больше 9;
— первый множитель 5, второй множитель 8, произведение…;
— делимое 63, делитель 9, частное …;
— во сколько раз 24 больше 3?
— я задумала число, увеличила его на 5, а потом в 5 раз и получила 40. Какое это число?
Молодцы! Ум в порядок привели, а теперь загадка.
Звучит цирковая музыка.
Загадка: Все глядят на середину.
В середине – волшебство:
Там чудак зайчишку вынул
Из кармана своего.
Там под купол танцовщица
Улетела, как синица.
Там собачки танцевали…
Вы, конечно, там бывали. (цирк)
Да, ребята, это цирк – вид театрального искусства, смешное зрелище. Мы сегодня не только будем закреплять письменную нумерацию в пределах 1000, но и поговорим об истории цирка и самой увлекательной профессии. А вот о какой вы узнаете позже, если будете правильно давать математические ответы, будете без ошибок считать и цифры правильно писать, потому что без точного счёта не сдвинется с места любая работа. Откройте тетради и запишите число и классная работа (ученик диктует).
А я предлагаю провести устный счёт.
2.Устный счёт
Я хлопаю в ладоши. Отгадайте, какое число я задумала, посчитав хлопки: пять – запишите одну цифру (я пишу на доске). А теперь я топаю. Сколько раз? Семь – запишите рядом эту цифру один раз. А теперь посмотрите, как я красиво и правильно сижу и поднимаю руку. Сколько раз? Восемь раз – запишите красиво один раз. Молодцы! Через одну клеточку в сторону повторите написание до конца строчки.
А теперь посмотрите на первое число 578. Я закрываю всё до цифры 8. Что обозначает это число, охарактеризуйте его? (однозначное, пишется в одной клетке, единица первого разряда). Закрываю рукой цифру 5, назовите число. Что обозначает число?(двузначное, две клетки для написания, восемь единиц 1 разряда, семь единиц 2 разряда, 7д. и 8ед. Открываю всё число, назовите. Дети дают характеристику: трехзначное, пишется в трёх клетках, 8ед. 1 разряда, 7ед. 2 разряда, 5ед. 3 разряда, 57 десятков, 8 единиц или 5 сотен 7 десятков 8 единиц. К какому классу относится это число?(к первому классу, классу тысяч)
А теперь используя эти цифры 5, 7, 8 составьте и запишите все возможные трёхзначные числа, не повторяя одну и ту же цифру в записи числа. Записываем в столбик и начинаем записывать в порядке возрастания. Что значит в порядке возрастания? (начинаем с маленького числа, заканчиваем большим) На доске карточки с числами (дети называют число и бегут к доске вешают карточку).
578 587 758 785 857 875
ш а п и т о
У детей в тетради: 578
587
758
785
857
875
А теперь давайте перевернём карточки и прочитаем слово, которое у нас получилось. (шапито) Что обозначает это слово? Может этот предмет вы видели или слышали об этом предмете. Это вид циркового передвижного помещения, а почему так? Сейчас вы узнаете, если дадите правильный ответ.
(шапито) Что обозначает это слово? Может этот предмет вы видели или слышали об этом предмете. Это вид циркового передвижного помещения, а почему так? Сейчас вы узнаете, если дадите правильный ответ.
Слайд. 1. Найдите число, в котором 7 единиц второго разряда.
709 607 372
2. Какое число при счёте следует за числом 459?
669 460 579
3. Какое число при счёте предшествует числу 500?
400 555 499
4. Назовите число, в котором 1ед. 1разряда, 8ед. 3разряда.
810 81 801
5. Какое число состоит из 3 сотен?
30 333 300
6. Найдите число, которое можно записать в виде суммы разр.сл. так: 400+80+6
684 486 864
Что значит представить число в виде суммы разрядных слагаемых? (сказать сколько в числе сотен, десятков и единиц) Молодцы!
Давайте вернёмся к нашему столбику чисел и представим эти числа в виде суммы разрядных слагаемых (проговаривают и записывают по цепочке) Правильно. Молодцы! А вот теперь послушайте.
Молодцы! А вот теперь послушайте.
Цирк — в переводе с латинского означает «круг». Первые цирки появились в Древнем Риме и представляли собой арену или манеж огромного размера с трибунами. Диаметр арены составлял 13м. Ещё цирком называли длинную дорожку для состязаний в скорости. Представление с наездниками, дрессиро ванными зверями, акробатами и клоунами, которое мы называем цирком, появилось много позже. Оно возникло в 1768 году, когда отставной английский кавалерист Филипп Астлей оградил канатом круглую площадку под открытым небом и стал брать плату у желающих посмотреть на его мастерство в верховой езде. А вот передвижные цирки-шапито появились около 1830 года и постепенно превратились в грандиозные зрелища.
А вот какие мы узнаем позже, а пока, кто был очень внимательным и услышал в моём рассказе о единицах измерения.
Какие единицы вы услышали? (единицы измерения длины, метр)
Какой длины была арена? (13м) Молодцы!
А давайте попробуем начертить вот такую арену или манеж.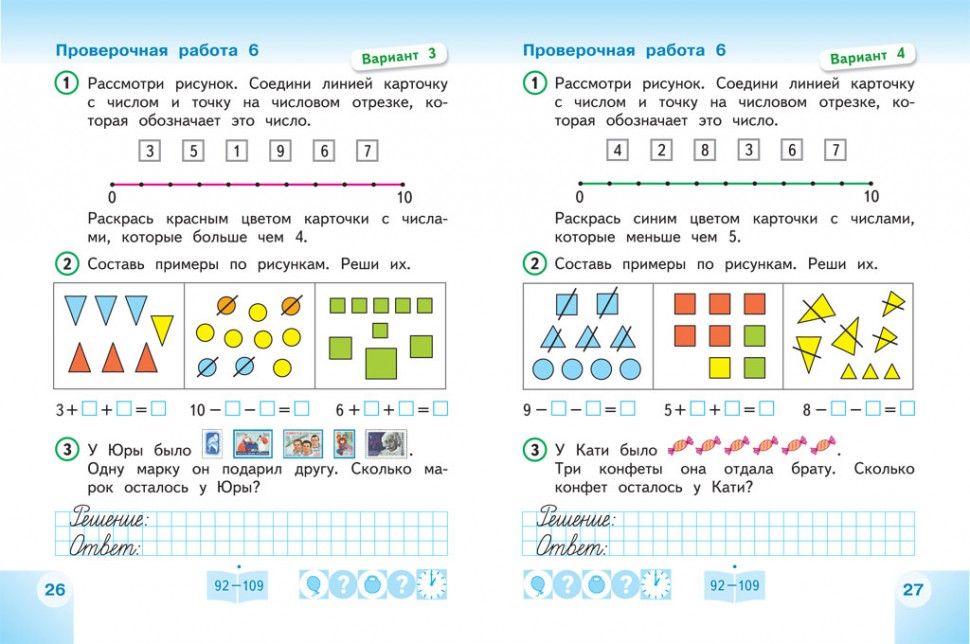
Какая фигура лежит в основе арены? (круг)
Как по другому называется круг? (окружность)
Как правильно начертить окружность, при помощи какого инструмента? (циркуля)
С чего начинаем чертить? ( с центра), а радиус окружности будет равен 2 см.
А что такое радиус? (это линия, соединяющая ценр окружности с любой точкой на окружности ) Радиус это ½ диаметра.
А что такое диаметр? ( это отрезок, который соединяет две точки и проходит через центр, диаметр делит круг на две части) Если радиус равен 2 см, то чему равен диаметр.
Как узнать? (2 умн. 2=4см)
Начертите. Обозначьте центр, проведите радиус красным карандашом, а теперь синим – диаметр.
А теперь сравним: диаметр нашей окружности и диаметр арены самого первого цирка ( дети говорят Д=4см и Д=13м, диаметр нашей окружности меньше диаметра арены цирка, или больше) Конечно, а давайте вспомним начиная с самой маленькой, какие ещё единицы измерения длины вы знаете? (мм, см, дм, м, км) Давайте запишем в тетрадь.
1мм — 1см — 1дм — 1м — 1км
10 10 10 1000
Доказали, молодцы! А теперь, кто справится с этим заданием, тот приглашается на отдых, пока подумайте, как называется перерыв в цирке.
Слайд. 1м это …дм 4м 16см = …см
1дм это …см 420см = …м …дм
1м это …см 300см = …дм
Молодцы! И с этим заданием справились. Так как называется перерыв в цирке (антракт).
Физминутка.
Вот у нас физкультминутка
Вот у нас физкультминутка,
Наклонились, ну-ка, ну-ка!
Распрямились, потянулись,
А теперь назад прогнулись.
Разминаем руки, плечи,
Чтоб сидеть нам было легче,
Чтоб писать, читать, считать
И совсем не уставать.
Голова устала тоже.
Так давайте ей поможем!
Вправо-влево, раз и два.
Думай, думай, голова.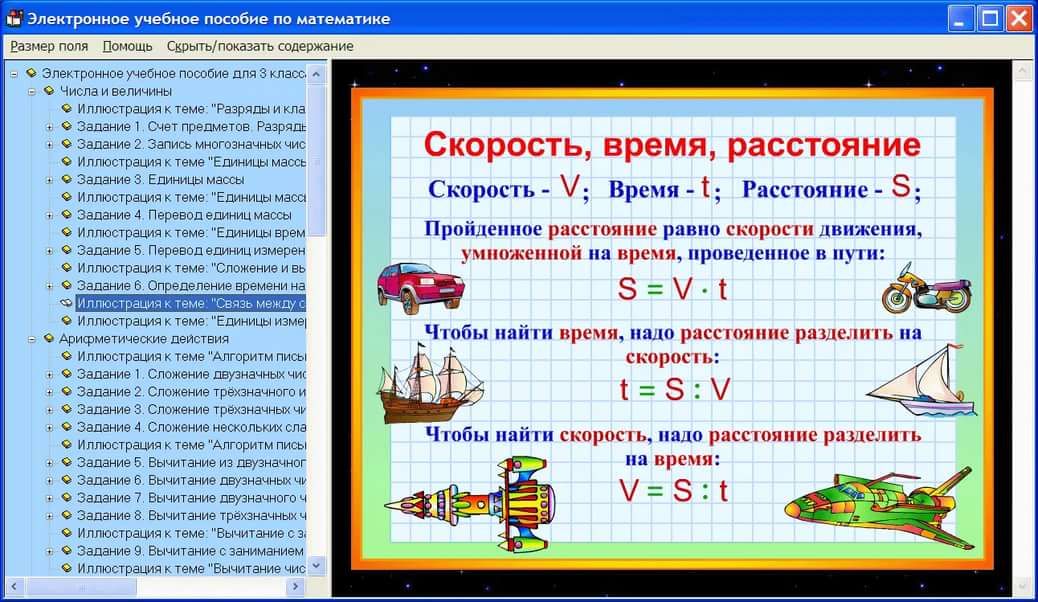
Хоть зарядка коротка,
Отдохнули мы слегка.
3.Работа по теме.
А теперь я продолжаю свой рассказ. На Руси в 18 веке при Петре 1 появились ярмарочные балаганы на народных гуляниях, где выступали акробаты, жонглёры, гимнасты. Это было в Москве и в Санкт-Петербурге, а у нас же есть ещё и другие города, где люди хотели бы встретиться с выступлениями цирковых артистов, поэтому и появился передвижной цирк Шапито. И у нас в наше время тоже приезжает цирк-шапито, куда вы с удовольствием ходите. Шапито представляет собой колпак, систему высоких стоек и центральных мачт, на которых натягивается брезентовый шатёр. На манеже мы можем видеть выступления различных цирковых трупп, каждый артист в труппе имеет свой жанр выступления.
А вот какие есть жанры циркового искусства вы сейчас узнаете, если правильно решите из учебника на стр.45 №5 (дети решают у доски по одному примеру) На каждый пример слайд со словом-жанром и картинкой ( дрессура, акробатика, жонглирование, гимнастика, иллюзия, клоунада).
Эти жанры в своих выступлениях представляют артисты. Артисты цирка демонстрируют силу, ловкость, смелость, гибкость, контактируют с животными, глотают огонь, дрессируют змей, умеют рассмешить зрителей.
А вот ещё одни артисты, давайте решим задачу, возьмите в руки листочки и прочитайте задачу. ( у детях на листочках, которые лежат на столе, записана задача)
Задача. На арене цирка выступало 15 собачек и 3 медведя. На сколько собачек на арене было больше, чем медведей? Во сколько раз медведей было меньше, чем собачек?
(ученик у доски, дети записывают задачу в тетрадь)
Ну что же, чтобы эти артисты в цирке хорошо выступали им нужно давать лакомства. Как вы думаете, что вкусненькое мы можем дать артистам, этим дрессированным животным? (дети перечисляют)Молодцы! Тогда ещё одна задача.
Задача. Из 10кг свёклы получают 2кг сахара. Сколько сахара можно получить из 40кг свёклы? из 80кг? из 100кг? (на первый вопрос ученик отвечает, а на два других дети отвечают самостоятельно, за это получают призы – шарики)
Физминутка.
Мы решали, мы решали.
Что-то очень мы устали.
Мы сейчас потопаем,
Ручками похлопаем.
Раз присядем,
Быстро встанем,
Улыбнемся,
Тихо сядем.
А вот теперь самое главное. Кто же вызвать смех, восторг, удивление, развлечь публику и подшутить над зрителями? Конечно, это клоуны. Клоун — это современное слово, а раньше их называли предворные шуты, странствующие комедианты, скоморохи, а потом только клоуны. Самый основной и сложный жанр циркового искусства – это клоунада. Клоун должен рассмешить, уметь петь и танцевать, жонглировать, выступать с животными, ходить по канату, выполнять различные трюки, при этом не бояться львов. А как узнать клоуна? (ответы) А узнаешь его по ярким парикам, накладным носам, по гриму. (слайд)
А теперь давайте вернёмся к окружности, которую вы нарисовали, и вы дома нарисуете, прямо в тетрадочке своего клоуна. А клоуны бывают разные! Переверните листочки и давайте прочитаем, какие же бывают клоуны? (дети переворачивают листочки и по цепочке читаем).
На листочках. Специализацию клоунов можно подразделить на:
– клоунов-буфф, исполняющих разговорные или мимические сценки;
– коверных клоунов, заполняющих шуточными сценками паузы в представлении, когда униформисты готовят манеж к следующему номеру;
– музыкальных клоунов, играющих на различных, как правило, эксцентрических музыкальных инструментах и исполняющих куплеты под собственный аккомпанемент;
– клоунов-дрессировщиков;
– клоунов-акробатов.
Дети, а каких клоунов известных знаете вы? Правильно, молодцы! ( Карандаш, Олег Попов, Юрий Никулин, Леонид Енгибаров)
А теперь посмотрите, какого клоуна нарисовала я. Как думаете, какой это клоун? Для вас
клоун приготовил фокус Вы любите фокусы? Откройте учебник на стр.51 и посмотрите на поля, на занимательные рамочки, давайте превратим их в уравнения. Первое подскажу я. Есть целое число 100 и два слагаемых, а третье неизвестно, обозначим его латинской буквой «Х», получим уравнение: 34 + Х + 56 = 100. Записываем и решаем. Составьте свои уравнения и проговорите мне их. Молодцы!
Записываем и решаем. Составьте свои уравнения и проговорите мне их. Молодцы!
4. Итог.
Итак! Мы с вами побывали в цирке, узнали историю цирка, познакомились с артистами, решали задачи, выполняли математические вычислительные приёмы. Вы сегодня все хорошо работали, были активными, а настроение каково? (дети отвечают «во») Покажите, какое у вас настроение, прикрепите к моему клоуну свои шарики.
Но, конец, домой пора,
выходим, дождь, как из ведра,
насквозь промокнем,
но зато мы побывали в цирке — шапито.
Физминутка: 1. Гимнастика для глаз.
Заполняем кроссворд.
- — этот предмет может быть зимним, осенним, резиновым (сапоги)
- — этот человек выступает в цирке, снимается в кино (артист)
- — по её проезжей части ездят машины, вы любите гулять на …. (улица)
- — с этим предметом ходят в лес (корзина)
- — ребёнок, который учится в школе (ученик)
- — она может быть трудной или легкой, классной или домашней (работа)
- — он может быть стеклянным, одноразовым, пластиковым (стакан)
- — этот фрукт содержит очень много витамина С, мы с ним пьем чай, но он очень кислый (лимон)
Конспект урока «Сложение и вычитание многозначных чисел»
— Как вы, думаете, над какой темой будем работать сегодня?
СЛАЙД 2
СЛАЙД 3
Научиться письменному сложению и вычитанию многозначных чисел.
ОТКЛЮЧИТЬ ДОСКУ
— Чтобы правильно решать такие примеры, нужно составить алгоритм решения.
— Что такое алгоритм?
— Сейчас вы самостоятельно попробуете его составить.
У вас на партах карточки, на которых напечатаны разные действия алгоритма. Работая и обсуждая в парах, составьте алгоритм для сложения и вычитания многозначных чисел.
Алгоритм:
Алгоритм письменного сложения многозначных чисел
Для того чтобы выполнить сложение многозначных чисел, надо:
-
Пишу единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч.
-
Складываю единицы …….
-
Складываю десятки …….
-
Складываю сотни ……
-
Складываю единицы тысяч
-
Складываю десятки тысяч
-
Складываю сотни тысяч
-
Читаю ответ …….

Алгоритм письменного вычитания многозначных чисел
Для того чтобы выполнить вычитание многозначных чисел,
надо:
-
Пишу единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч.
-
Вычитаю единицы …….
-
Вычитаю десятки …….
-
Вычитаю сотни ……
-
Вычитаю единицы тысяч
-
Вычитаю десятки тысяч
-
Вычитаю сотни тысяч
-
Читаю ответ …….
ПРОВЕРКА (дети зачитывают алгоритм сложения и вычитания) ОЦЕНКА!
-Что изменилось в алгоритме сложения многозначных чисел, по сравнению с трёхзначными числами?
-Что изменилось в алгоритме вычитания многозначных чисел, по сравнению с трёхзначными числами?
(добавились классы тысяч, миллионов, миллиардов)
—Что самое главное при решении?
(правильно записывать числа, чтобы единицы разрядов совпадали, вычислять начинать с единиц)
ВКЛЮЧИТЬ ДОСКУ
Физминутка. (колонки включить)
(колонки включить)
РАБОТА НА ИНТЕРАКТИВНОЙ ДОСКЕ
— Составьте из чисел, которые вы выписали, все возможные варианты примеров (дети называют устно)
Решим у доски, применяя алгоритм сложения и вычитания многозначных чисел, те примеры, где используем нечётное число. (12658, 32496, 85467)
Решение примеров на доске.
12658+32496 = 45154 32496-12658= 19838
*12658+85467 = 98125 * 85467-12658= 72809
*32496+85467= 117963 *85467-32496= 52971
ОТКЛЮЧИТЬ ДОСКУ
У вас на партах лежат листы с заданием. Каждый из вас сам выбирает тот вариант заданий, с которым он справится.
Вариант 1
98765+12232 89456-23124
Вариант 2
3006578+2344612 7689438-4328128
Вариант 3
3274560198+5064789321 6472318059-5708913724
1)Решают типовые задания на новый способ действия;
2) Выполняют проверку по эталону
ВКЛЮЧИТЬ ДОСКУ СЛАЙД 4 (ВРЕМЯ)
ПРОВЕРЯЕМ
-Кто решил 1 вариант? Проверьте. Кто справился с заданием?
Кто справился с заданием?
Вариант 1:
110997 66332
-Кто решил 2 вариант? Проверьте. Кто справился с заданием?
Вариант 2:
5351190 3361310
-Кто решил 3 вариант? Проверьте. Кто справился с заданием?
Вариант 3:
83393494 7634043
ВЫКЛЮЧИТЬ ДОСКУ
ЗАДАЧА Стр. 36 №6.
Рассмотрите картинки внизу страницы.
Какой музей изображён на первой? Кто знает, где находится этот музей?
Какой музей изображён на второй? Кто знает, где находится этот музей?
Какой музей изображён на третьей? Кто знает, где находится этот музей?
Прочитай задачу. О чем говорится в задаче?
Что нам известно?
Какой главный вопрос задачи? Можем сразу ответить на главный вопрос? Почему?
Можем узнать.
Запишите сами решение задачи.
1)396670-290500=106170(э.) в Третьяковской галереи.
2)3000000+396670+106170=3502840(э) всего.
ВКЛЮЧИТЬ ДОСКУ СЛАЙД 5
-Поменяйтесь тетрадями, проверьте, как ваш сосед справился с решением задачи. ОЦЕНКА!
Итог урока:
— Назовите тему урока
— Какую учебную задачу вы решали?
Учились письменному сложению и вычитанию многозначных чисел
— Удалось ли её решить?
— В чём возникли затруднения, и удалось ли их преодолеть?
ВКЛЮЧИТЬ ДОСКУ СЛАЙД 6
Домашнее задание: стр. 36-37 №5, по выбору №7 или №8.
Самооценка. Слайд 7.
-Оцените свою работу сегодня на уроке:
Почему нельзя делить на ноль?
-
dims
10.04.2006 00:31Ответить
По-моему, надо честно признаться, что математики просто ещё не придумали, что будет, если делить на ноль.
 С тем же успехом можно было когда-то сказать, что нельзя вычислять квадратные корни из отрицательных чисел: ну как же ВЕДЬ НЕТ такого числа, которое при умножении самого на себя даёт отрицательное число!
С тем же успехом можно было когда-то сказать, что нельзя вычислять квадратные корни из отрицательных чисел: ну как же ВЕДЬ НЕТ такого числа, которое при умножении самого на себя даёт отрицательное число!Ответить
-
Alf
dims 10.04.2006 15:15Ответить
Почему не придумали, придумали — если устремить к нулю делитель, то будет бесконечность. И почему нельзя квадратный корень из отрицательного числа вычислять — возьмите комплексную плоскость и будет вам корень. Над R же не существует числа, которое при умножении на самоее себя давало бы отрицательное значение.
Ответить
-
-
Jabberwok
dims 17.04.2006 17:10Ответить
На ноль формально делить нельзя, но можно неограниченно стремить знаменатель к нулю, а дробь будет стремится к бесконечности.
 2 = -1
2 = -1Ответить
-
taras
Jabberwok 11.10.2017 16:18Ответить
НЕЛЬЗЯ поливать бесконечность.
Ответить
-
!ё!
Jabberwok 12.10.2017 21:44Комментарий скрыт
Антон Ч
dims 22.07.2006 18:16
Ответить
эээээ. никто ведь не говорит о вычислении корня из минус единицы. Просто ввели новое понятие. Расширили множество чисел. Разрешили проблему введением новых понятий. Это кстати относится к теореме Геделя. Здесь проблема в другом.
Ответить
Mutagen
dims 15.09.2006 13:04
Ответить
корень из минус-единицы ввели потому, что тут есть единственность и экономия — введением всего лишь ОДНОГО понянтия можно описать получение корней из всех отрицательных чисел. Выход — надо ввести число ‘зю’.
Выход — надо ввести число ‘зю’.
i — число, умножение которого на само себя дает -1.
зю — число умножение которого на ноль дает единицу
5/0 = х
х*0 = 5
x*0*зю = 5*зю
x = 5*зю
Теперь результат математической операции, например, ‘деления пяти на ноль’ вполне определен — это ‘пять зю’ ;-)) Наверное за этим должен последовать крутой прорыв в науке, включая перемещение во времени, сверхсветовые скорости, доказательства существования жизни после смерти, контакт с инопланетянами итп…
Ответить
taras
dims 11.10.2017 16:16
Ответить
Как раз давно придумали.
Ответить
APXIMHD
19.05.2006 13:54
Ответить
Можно привести еще более простой пример. Допустим, на ноль делить можно. Оказывается, что такое допущение позволяет доказать любое утверждение. Начнем с тождества:
Оказывается, что такое допущение позволяет доказать любое утверждение. Начнем с тождества:
0*2=0*3
Сократим на ноль. Получим:
2=3
То есть, допущение возможности деления на ноль приводит к выводу, что любые два числа равны между собой. Поскольку любому утверждению можно сопоставить некий числовой код (ну, хотя бы последовательность кодов символов, которыми записано это утверждение), то из возможности деления на ноль, оказывается следует тождественность любых двух утверждений.
Подводя итог: если можно делить на ноль, то Луна сделана из швейцарского сыра.
Ответить
-
Injener
APXIMHD 20.05.2006 14:11Ответить
НЕПРАВИЛЬНО! Сократим на ноль — это значит поделим на ноль левую и правую часть уравнения. Получим неопредленность типа ноль/ноль.
На самом деле есть неопределенности в математике. Такие например как отношение двух бесконечностей.
А делением на ноль уже никого не испугаешь и там все справедливо.Ответить
-
taras
Injener 11.10.2017 16:25Ответить
Неопределённость получится только в случае, если на ноль делить нельзя. А если можно, то ни какой неопределённости не возникнет, так как всякое допустимое деление однозначно.
Ответить
belka
22.05.2006 16:06
Ответить
А по-моему,все правильно объяснено для школьников и добавлено,что в институте на ноль делить все же придется:))
Ответить
-
Injener
belka 28.05.2006 14:06Ответить
Ничего правильного тут нет. А самая главная неправильность в том, что в школе нам рассказывают всякую чушь, которая на самом деле не верна.
 Как то: невозможность деления на ноль, рассказы про строение атома(Боровская модель), то что человек произошел от обезьяны и т.д. (по поводу обезьяны я точно сказать не могу, так как я физик, а не биолог). Неснясным остается следующее — зачем заведомо неверную информацию вводить в школьную программу, может быть проще сразу рассказывать как оно есть на самом деле?
Как то: невозможность деления на ноль, рассказы про строение атома(Боровская модель), то что человек произошел от обезьяны и т.д. (по поводу обезьяны я точно сказать не могу, так как я физик, а не биолог). Неснясным остается следующее — зачем заведомо неверную информацию вводить в школьную программу, может быть проще сразу рассказывать как оно есть на самом деле?Ответить
-
angor6
Injener 30.05.2006 12:49Ответить
Думается, что это как раз тот случай, когда истина где-то посередине. Данная статья объясняет всё на уровне, достаточном для понимания среднего подростка 12-14 лет. А что касается более научного объяснения, то надо иметь в виду, что операции над математическим объектами вводятся с целью обеспечить адекватность математических моделей действительности. С этой точки зрения деление на нуль — операция корректная, но для её описания необходимо оперировать терминами теории функций пространственного комплексного переменного.
 .. По-моему, даже на матфаках университетов немногие представляют себе, что это такое. Явно не детский вопрос!
.. По-моему, даже на матфаках университетов немногие представляют себе, что это такое. Явно не детский вопрос!Ответить
-
teplyi
angor6 25.09.2006 21:39Ответить
Кажется, по поводу упомянутой ТФПКП (Если имеется в виду теория Елисеева) все не утихают споры — считать ли ее корректной.
Ответить
-
jyu
angor6 06.08.2009 11:52Ответить
Я думаю,что если возникают такие вопросы такие,как почему нельзя делить на нуль или откуда произошел человек надо отвечать детям с точки зрения науки ,даже если это очень сложно в понимании.
Ответить
-
taras
angor6 11.10.2017 16:30Ответить
Нет. Операция как раз некорректная.

Ответить
-
-
-
Orange03
Injener 13.07.2013 01:49Ответить
Я могу ответить на вопрос, почему детям сразу не рассказывают все как есть, но это уже немного другая тема.
Просто говоря, дебилами проще управлять. Политикам выгодно, что бы народ их слушался, что бы народ был глуп. Вот ни кто и не заморачивается над тем, что бы создать реально хорошую и продвинутую программу. Проще же сделать так, оставить все как есть.Ответить
-
taras
Orange03 11.10.2017 16:34Ответить
В «США» да. Но дебил на АЭС, или дебил, пытающийся сварить сталь, продуть её на АКОС и разлить на МНЛЗ, как раз не управляем вообще. Более того, такой дебил ОПАСЕН.
Ответить
-
taras
Injener 11. 10.2017 16:29
10.2017 16:29
Ответить
Чушь несёшь как раз ты.
Ответить
taras
belka 11.10.2017 16:28
Ответить
Нет. В институте на ноль тоже не делят. Вычисление пределов — это всё таки не деление.
Ответить
lior-kauf
07.07.2006 19:54
Ответить
А вот учительница в первом классе ашдодской школы учила моего сына:
3 : 0 = 0. И никто из родителей этого не эаметил. Когда я пыталась обратить внимание других родителей на этот факт, мне говорили: «Ну и зануда ты, просто придираешься к учительнице». Интересно, как эта учительница преподает в нашей школе уже 12 лет?
Ответить
-
aleks
lior-kauf 17. 07.2006 18:16
07.2006 18:16Ответить
А что такое «ноль» и что такое число. Это наличие и отсутствие. Как наличие делить на отсуствие. Наличие проявляется на фоне отсутствия. Или вернее даже отсуствие проявляется на фоне наличия. Тут уже нейрофизиология и просхождение разума, Как человек осознал. Так что вопрос только кажется детским, а наукой не проясненный до конца. Возбуждение нейрона -1 , отсуствие возбуждения 0. Отсуствие не количественное понятие, это отсуствие колличества. А наличие колличественное понятие. В одном наличии может быть несколько наличий.
Ноль и число совершенно разные понятия. Ноль не число-проще говоря. Число делить на не число нельзя .Ответить
-
dvaman
aleks 29.07.2006 17:19Ответить
Само выражение «не имеет смысла» уже абсурдно! Смысл имеет все! Фраза «уравнение не имеет решения» еще более нелепа.
 Любое уравнение имеет решение, его просто надо найти и доказать, даже если оно пустое!
Любое уравнение имеет решение, его просто надо найти и доказать, даже если оно пустое!«Математики признают полноценными только два из них — сложение и умножение.»
НЕВЕРНО! Только сложение. Это прекрасно демонстрирует компьютер, который умеет только складывать, причем столько, сколько ему скажут (для умножения), либо со сдвигом разрядов (для вычитания).«0 * x = 5» и далее «То есть наша задача не имеет решения.»
Решение есть! И оно пустое. То, что нам может не нравиться подобные результаты никого не е…(волнует), оно все равно существует!«Да, такое бывает, не у всякой задачи есть решение»
Вообще атас! Думаю комментарии излишне. Вот они — плоды того, чему учат в школе. Любая задача имеет решение!По поводу «0 * x = 0» вообще смех, да и только. Решение не то, что существует, а вообще предоставляет полную свободу выбора. Бери любое число, оно и будет тебе решением. Ну, нет же! У нас ответ: «Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них.
 » Бред сивой кобылы!
» Бред сивой кобылы!
И дальше:
«А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла.» Как же не имеет никакого смысла, когда имеет, и еще какой! Например, если Мы будем постоянно бегать с пустым ведром от колодца к бочке, то бегай хоть 100, хоть 1000 раз — воды Мы не принесем. Уравнение это четко показывает, и имеет очень даже хороший смысл…Теперь давайте разбираться по поводу деления на ноль («нуль» не люблю — устарело).
Проблема в том, как уже ранее было замечено, что существует некая путаница в понятиях и их значениях. Стоит также отметить, что Мы частично признаем (не признаем) полярные стороны. Другими словами «бесконечность» числом считать не принято, а вот ноль (как было замечено «ничто») числом мы считаем. А если так, то чего же мы тогда хотим? Связать два понятия находящихся «в двух разных весовых категориях»? Ноль и бесконечность должны стоять по одну сторону баррикады, сейчас же они по разные.К примеру, в программировании эта проблема решена.
 Просто определено самое большое число max_value (min_value) аналогичное нашему «бесконечность». Все эти числа принадлежат одному множеству и, следовательно, сопоставимы. Поэтому если там Мы будем делить пять на ноль, мы получим самое большое число max_value. Все законно и справедливо.
Просто определено самое большое число max_value (min_value) аналогичное нашему «бесконечность». Все эти числа принадлежат одному множеству и, следовательно, сопоставимы. Поэтому если там Мы будем делить пять на ноль, мы получим самое большое число max_value. Все законно и справедливо.Ответить
-
aleks
dvaman 31.07.2006 16:59Ответить
Я имел в виду не «делить» а «разделить». Если наличие -это конечное множество. А «ноль» это отсутствие. «Ноль» — отсутствие наличия. Допустим есть множество. Если его необходимо разделить на кучки. Не может быть 0,4 кучки. Минимум может быть две кучки и остаток. Я опустился на один уровень ниже. С психического уровня на биологический. Я предположил какая математика в биологии может быть. В биологии с сенсорных нейронов приходит сигнал, или отсутствие сигнала. С ними живое и производит математические операции. Есть конечное множество сигналов от рецепторов, допустим глаз.
 И живое, его нервная система классифицирует сигналы, сравнивает и раскладывает на кучки по какому то признаку. Что не поддалось классификации-то в остаток. В живом действует особая математика ,еще не описанная нигде. Между математикой количества и математикой событий межит огромный пласт неиследованой математики систем или математики живого. Обычной математикой невозможно обработать поступающие сигналы от рецепторов.
И живое, его нервная система классифицирует сигналы, сравнивает и раскладывает на кучки по какому то признаку. Что не поддалось классификации-то в остаток. В живом действует особая математика ,еще не описанная нигде. Между математикой количества и математикой событий межит огромный пласт неиследованой математики систем или математики живого. Обычной математикой невозможно обработать поступающие сигналы от рецепторов.Ответить
-
noindex
aleks 17.08.2006 18:50Ответить
Прочитал статью — огромное спасибо!
Сегодня обязательно детям расскажу почему нельзя делить на 0студент МГУ
Ответить
-
maxx
aleks 25.11.2007 12:24Ответить
Браво!
Ответить
-
taras
aleks 11. 10.2017 17:12
10.2017 17:12Ответить
Есть у тебя лента, а я у тебя прошу кусочек ленты. Ты можешь мне отрезать и 0,4 своей ленты, и даже 0,0055.
Ответить
-
-
-
nickhunter
dvaman 22.02.2007 12:04Ответить
Критика, в целом, довольно спорная (в отличии от статьи, которая спорна с точки зрения чистой математики, но, на мой взгляд, хороша для образовательных целей).
Но больше всего смущает Ваш аргумент по поводу программирования.
Цитата:
«К примеру, в программировании эта проблема решена. Просто определено самое большое число max_value (min_value) аналогичное нашему «бесконечность». Все эти числа принадлежат одному множеству и, следовательно, сопоставимы. Поэтому если там Мы будем делить пять на ноль, мы получим самое большое число max_value. Все законно и справедливо. «
«В реальности:
В программировании не определено, не принадлежат, не получим. Более того, в программировании, вообще говоря, существует понятие типа (и расположено оно на пару уровней абстракции выше, чем понятия об архитектуре ЭВМ), только осознав которое можно говорить о каких-либо операциях с данными вообще!Ответить
-
tih
dvaman 13.07.2007 13:00Ответить
«…Математики признают полноценными только два из них — сложение и умножение.» НЕВЕРНО! Только сложение. Это прекрасно демонстрирует компьютер, который умеет только складывать,…»
— неправда Ваша. Грош-цена такому компутеру.
Компутер — он ить не только «складывает» — он еще и СДВИГАЕТ(коия операция как раз и эквивалентна операции умножения или деления — смотря куда двигать ;), а помимо того — ЛЮБОЙ компутер еще ОБЯЗАТЕЛЬНО выполняет побитовые операции — ИНВЕРСИИ, И, ИЛИ, искл. ИЛИ. И вообще — смотря про какой компутер говорить. Есть и таке — которые не только умножают — но и делят аппаратно… и даже не одно число — а матрицы…
ИЛИ. И вообще — смотря про какой компутер говорить. Есть и таке — которые не только умножают — но и делят аппаратно… и даже не одно число — а матрицы…
;))«…Ноль и бесконечность должны стоять по одну сторону баррикады, сейчас же они по разные. К примеру, в программировании эта проблема решена. Просто определено самое большое число max_value (min_value) аналогичное нашему «бесконечность». … Поэтому если там Мы будем делить пять на ноль, мы получим самое большое число max_value. …»
— ?!!!
марку, марку ЭТОГО чуднОго компутера — в студию!!
На моей памяти — а работал я с добрым десятком самых разных компутеров и процессоров — от БЭСМ-4 до PowerPC880. И — ВЕЗДЕ(!) — при обнаружении деления на «0» — процесоры выдают специальное ПРЕРЫВАНИЕ —
по которому отрабатывается либо утилита обработки исключительной ситуации(если такая предусмотрена программистом) — либо вооще процесс вычисления ОСТАНАВЛИВАЕТСЯ(поскольку по-умолчанию вектор этого прерывания — нулевой). И только в специализированных(!) процессорах обработки сигналов(типа TMS320Cxxx) есть нечто подобное — и то не для деления на нуль — а для переполнения. То есть если к Вашему «max_value-1» прибавить 3, то получится не «-2», а просто «max_value» — и то там этот режим ОПЦИОНАЛЕН — то есть при желании его можно ВКЛЮЧИТЬ.
То есть если к Вашему «max_value-1» прибавить 3, то получится не «-2», а просто «max_value» — и то там этот режим ОПЦИОНАЛЕН — то есть при желании его можно ВКЛЮЧИТЬ.— а деление на нуль — дело сурьезное — с ним шутки плохи.
интеррупт — и весь сказ!Ответить
-
Sterh
tih 21.08.2007 12:04Ответить
Респект, до этого сообщения думал что комменты пишут несгибаемые и..ы
Ответить
-
rod1gin
tih 13.01.2009 18:36Ответить
Ну, ещё надо добавить, что обычный интеловский процессор может обрабатывать числа с плавающей точкой в двух режимах: в одном, действительно, при делении на ноль возникает прерывание, а в другом — прерывания нет, но получается результат «не определено». Соотвественно, формат для чисел с плавающей точкой придуман такой, что в нём можно задать не только обычные числа, но и специальные константы «не определено», «плюс бесконечность», «минус бесконечность» и ещё несколько вариантов, все не помню.
 Очень удобная, кстати, штука, но доступна только на ассемблере.
Очень удобная, кстати, штука, но доступна только на ассемблере.Ответить
-
-
taras
tih 11.10.2017 17:26Ответить
«То есть если к Вашему «max_value-1» прибавить 3, то получится не «-2», а просто «max_value» — и то там этот режим ОПЦИОНАЛЕН — то есть при желании его можно ВКЛЮЧИТЬ.» MAX_INT — обычное значение типа INTEGER НА ЛЮБОМ компьютере и при инкементе, например, 32 767 двухбайтной версии INTEGER MAX_INT получится гарантированно. А переполнение происходит при СЛЕДУЮЩЕМ инкременте. А если прибавить к MAX_INT сразу 3, то получите -32 766 (в двухбайтной версии). И опционально только то, будет ли ИДЕНТИФИКАТОР MAX_INT известен компилятору. И то на уровне языка, а не компьютера. Соответственно на БЭСМ его ещё не было, потому что тогда профессиональные программисты то уж точно знали, чему эта константа равна, так как переносимостью по-настоящему озаботились позже, а остальным это было не нужно.
 Но если сейчас портировать современный диалект паскаля на БЭСМ, то MAX_INT будет и там. А вот на сигнальных камнях MAX_INT водится только ради того, чтоб сообщение об ошибке unknown identificator не выскочило неожиданно, если как какой нибудь предназначенный для таких камней код сначала опробован на компьютере и только потом «скормить» кроскомпилятору.
Но если сейчас портировать современный диалект паскаля на БЭСМ, то MAX_INT будет и там. А вот на сигнальных камнях MAX_INT водится только ради того, чтоб сообщение об ошибке unknown identificator не выскочило неожиданно, если как какой нибудь предназначенный для таких камней код сначала опробован на компьютере и только потом «скормить» кроскомпилятору.
#include
int main()
{
double x=5.0;
double y=0.0;
double z=x/y;
std::cout<<z;
int main()
{
int x=5.0;
int y=0.0;
int z=x/y;
std::cout<<z;
return 0;
}
результат — аварийное завершение программы. Комп один и тот же. Процессор Intel(R) Pentium(R) CPU J2900 @ 2.41GHz.Ответить
-
AMapyaK
dvaman 27.01.2009 17:08
Ответить
Я понимаю, что я злостный некропостер, но не могу удержаться.
1) © Само выражение «не имеет смысла» уже абсурдно! Смысл имеет все! ©
Сытый конному не пеший.
2) © Любое уравнение имеет решение, его просто надо найти и доказать, даже если оно пустое! ©
Вы путаете понятия. «Решение» и «Множество решений» — это разные вещи. Если множество решений пусто, это значит, что решений нет. Курите теорию множеств.
3) © НЕВЕРНО! Только сложение. Это прекрасно демонстрирует компьютер, который умеет только складывать, причем столько, сколько ему скажут (для умножения), либо со сдвигом разрядов (для вычитания). ©
Если вы определите умножение иррациональных чисел (например, число е умножить на число пи) с помощью одного лишь сложения, я буду аплодировать стоя. Компьютер оперирует преимущественно с целыми числами — в этом все дело. К тому же не стоит привязываться к стандартной алгебре на множестве вещественных чисел. Операции можно ввести по-разному.
Пионеры, комсомольцы,
Изучайте группы, кольца,
И поля, и модуля,
И делители нуля.
4)© Решение есть! И оно пустое. То, что нам может не нравиться подобные результаты никого не е…(волнует), оно все равно существует! ©
Да? Предъявите его. Впрочем, написано выше. Не путайте множество и его элементы.
© «Да, такое бывает, не у всякой задачи есть решение» Вообще атас! Думаю комментарии излишне. Вот они — плоды того, чему учат в школе. Любая задача имеет решение! По поводу «0 * x = 0» вообще смех, да и только. Решение не то, что существует, а вообще предоставляет полную свободу выбора. Бери любое число, оно и будет тебе решением. Ну, нет же! У нас ответ: «Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них.» Бред сивой кобылы! ©
Опять путаете. Только теперь вы путаете уравнение и операцию. Если бы изначально задача стояла в нахождении х, такого, что 0*х=0, я бы с вами согласился. Мы же говорим об операции деления на ноль.
Можно говорить, что уравнение a*x=b только если решение существует и единственно при любых a и b. Если это условие не выполняется (а оно не выполняется при a=0), то никакой операции нет и быть не может.
Если это условие не выполняется (а оно не выполняется при a=0), то никакой операции нет и быть не может.
© Как же не имеет никакого смысла, когда имеет, и еще какой! Например, если Мы будем постоянно бегать с пустым ведром от колодца к бочке, то бегай хоть 100, хоть 1000 раз — воды Мы не принесем. Уравнение это четко показывает, и имеет очень даже хороший смысл… ©
Уравнение — умеет смысл, а запись 0/0 не имеет смысла.
© ы частично признаем (не признаем) полярные стороны. Другими словами «бесконечность» числом считать не принято, а вот ноль (как было замечено «ничто») числом мы считаем. А если так, то чего же мы тогда хотим? ©
Дайте определение бесконечности, если хотите считать ее числом.
Ответить
-
taras
AMapyaK 11.10.2017 16:48Ответить
«По поводу «0 * x = 0» вообще смех, да и только. Решение не то, что существует, а вообще предоставляет полную свободу выбора.
 » Свобода выбора не есть решение.
» Свобода выбора не есть решение.Ответить
-
taras
AMapyaK 11.10.2017 16:52Ответить
«Опять путаете. Только теперь вы путаете уравнение и операцию. Если бы изначально задача стояла в нахождении х, такого, что 0*х=0, я бы с вами согласился. Мы же говорим об операции деления на ноль.» Путаешь ты. Операция деления определена именно так: делением называется операция, обратное умножению. Что эквивалентно определению: деление есть не элементарная операция решения уравнения вида x*a=b, где a — делитель, а b — частное.
Ответить
-
taras
AMapyaK 11.10.2017 16:57Ответить
«Как же не имеет никакого смысла, когда имеет, и еще какой! Например, если Мы будем постоянно бегать с пустым ведром от колодца к бочке, то бегай хоть 100, хоть 1000 раз — воды Мы не принесем.
 Уравнение это четко показывает, и имеет очень даже хороший смысл… ©
Уравнение это четко показывает, и имеет очень даже хороший смысл… ©
Уравнение — умеет смысл, а запись 0/0 не имеет смысла.» Наоборот. На дроби 0/0 построена четверть теории пределов. Три другие четверти теории пределов построены на произведении 0*0, разности бесконечность-бесконечность и дроби бесконечность/бесконечность. А уравнение 0*x=0 смысла не имеет.Ответить
-
taras
AMapyaK 11.10.2017 17:45Ответить
На любом компьютере обязательно реализованы операции с действительными числами. Иначе это не компьютер. Вот целые могут и не поддерживаться, например, ZX SPECTRUM целых не знает вовсе. При этом он на процессоре Z80, который, наоборот, не знает чисел с плавающей точкой.
Ответить
0x000000
dvaman 07.07.2010 09:21
Ответить
Простите, не мог пройти мимо вашего комментария.
>> прекрасно демонстрирует компьютер, который умеет только складывать, причем столько, сколько ему скажут (для умножения), либо со сдвигом разрядов (для вычитания).
Во-первых, все зависит от архитектуры компьютера. Допустим, мы говорим про IA-86 или x86 для простоты. Процессоры этой архитектуры умеют делать все четыре арифметические действия. Да, их можно свести к двум, вы правильно заметили, и есть архитектуры, где это действительно так. Вот только сложение и вычитание производится операцией сложения с помощью прямых и обратных кодов. А умножение и деление более сложной последовательностью из сложений и побитовых сдвигов. Побитовый сдвиг ничего не вычетает, грубо говоря, он делит либо умножает исходное число на основание системы счисления. Для двоичной сс после одного сдвига число либо будет увеличено на 2 либо уменьшено на 2.
>> К примеру, в программировании эта проблема решена. Мы будем делить пять на ноль, мы получим самое большое число max_value.
Да, проблема решена очень давно, но не так. В большинстве случаев, при делении на ноль будет либо вызвано прерывание процессором (для x86 это будет нулевое прерывание), если деление происходило с помощью него, либо аналог ошибки от среды исполнения. Min и Max_value в большинстве императивных языков — это ограничение на тип переменной (какие значение она может принимать в памяти), деление на ноль тут вообще не причем. Для «операций» с бесконечностью, в некоторых языках есть типы Inf и -Inf. Однако опять же повторюсь, что обычное деление на ноль в программировании подразумевает генерацию некого уведомления программисту или пользователю и штатной ситуацией не является ни на железном ни на программном уровне.
В большинстве случаев, при делении на ноль будет либо вызвано прерывание процессором (для x86 это будет нулевое прерывание), если деление происходило с помощью него, либо аналог ошибки от среды исполнения. Min и Max_value в большинстве императивных языков — это ограничение на тип переменной (какие значение она может принимать в памяти), деление на ноль тут вообще не причем. Для «операций» с бесконечностью, в некоторых языках есть типы Inf и -Inf. Однако опять же повторюсь, что обычное деление на ноль в программировании подразумевает генерацию некого уведомления программисту или пользователю и штатной ситуацией не является ни на железном ни на программном уровне.
Ответить
san
dvaman 08.06.2011 04:55
Ответить
Замечу, что в современных компьютерах все немного сложнее.
Деление на ноль целочисленного значения приведет к так называемому исключению, т. е. программа рухнет.
е. программа рухнет.
В случае с числами с плавающей точкой, деление на ноль даст как раз +inf, т.е. то самое «очень большое число».
А если поделить ноль на ноль, то результат будет еще интересней: получится NaN. Расшифровывается это как «Not a Number». И результат вычислений, в которых принимает участие NaN, не определен.
Ответить
-
taras
san 11.10.2017 17:51Ответить
int числом не является. Это бесконечность.
Ответить
-
taras
san 11.10.2017 17:53Ответить
«А если поделить ноль на ноль, то результат будет еще интересней: получится NaN. Расшифровывается это как «Not a Number». И результат вычислений, в которых принимает участие NaN, не определен.» Не важно, что оно так «расшифровывается», а int — нет. Не числа обе всё равно.
 И на самом деле nan значит «не определённость». В математике она не тождественна бесконечности.
И на самом деле nan значит «не определённость». В математике она не тождественна бесконечности.Ответить
taras
dvaman 11.10.2017 16:38
Ответить
Нет. Уравнение может не иметь решений. И бред не имеет смысла.
Ответить
taras
dvaman 11.10.2017 16:39
Ответить
Пустыми бывают только множества, а не решения.
Ответить
taras
dvaman 11.10.2017 16:43
Ответить
«НЕВЕРНО! Только сложение. Это прекрасно демонстрирует компьютер, который умеет только складывать, причем столько, сколько ему скажут (для умножения), либо со сдвигом разрядов (для вычитания).» НЕ БЫВАЕТ компьютеров, умеющих только складывать.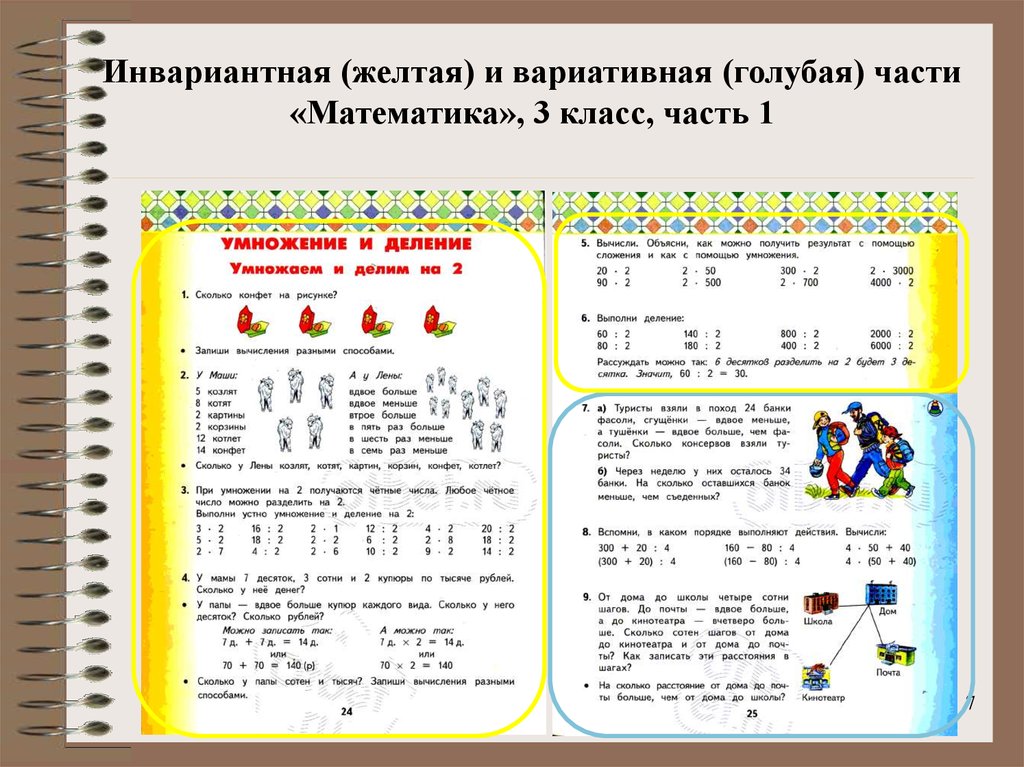 И умножение на дробь не эквивалентно какой либо серии сложений. Кстати, сдвиг разрядов — это как раз умножение в чистом виде. Но только на степень основания системы счисления.
И умножение на дробь не эквивалентно какой либо серии сложений. Кстати, сдвиг разрядов — это как раз умножение в чистом виде. Но только на степень основания системы счисления.
Ответить
taras
dvaman 11.10.2017 16:47
Ответить
«Да, такое бывает, не у всякой задачи есть решение»
Вообще атас! Думаю комментарии излишне. Вот они — плоды того, чему учат в школе. Любая задача имеет решение!» Ну реши задачу: найти действительное значение угла, при котором синус равен четырём. Комплексный результат не не нравится, а не допустим согласно типу искомой величины. Задача вычисления арксинуса ведь может быть подзадачей в задаче построения треугольника с заданным отношением катетов, а треугольник с комплексным углом при вершине построить нельзя.
Ответить
taras
dvaman 11.10.2017 17:04
Ответить
Ноль и бесконечность не могут стоять по одну сторону. Вот есть у тебя карман, в нём могут быть деньги. Я у тебя спрашиваю: СКОЛЬКО у тебя денег? А ты мне: у меня их совсем нет. Это ответ на вопрос сколько, то есть количество. А количество выражается только числом. А с бесконечностью этот фокус не пройдёт. И отрицательное число — это тоже количество. Есть Довгань, у него могут быть деньги. Его спрашивают: СКОЛЬКО у Вас сейчас? А он: я ещё и должен столько то миллионов. Это ответ на вопрос сколько, то есть количество. Количество может быть и дробным, но не в случае денег. Сложно объяснить, как с количеством соотносятся мнимые и гиперкомплексные числа, но они хотя бы однозначны, а это свойство числа. Но если сложить две бесконечности, то бесконечность получится только одна, а если одну бесконечность из другой вычесть, то можно получить сколько угодно, включая бесконечность. Бесконечность не однозначна. А ноль однозначен.
Вот есть у тебя карман, в нём могут быть деньги. Я у тебя спрашиваю: СКОЛЬКО у тебя денег? А ты мне: у меня их совсем нет. Это ответ на вопрос сколько, то есть количество. А количество выражается только числом. А с бесконечностью этот фокус не пройдёт. И отрицательное число — это тоже количество. Есть Довгань, у него могут быть деньги. Его спрашивают: СКОЛЬКО у Вас сейчас? А он: я ещё и должен столько то миллионов. Это ответ на вопрос сколько, то есть количество. Количество может быть и дробным, но не в случае денег. Сложно объяснить, как с количеством соотносятся мнимые и гиперкомплексные числа, но они хотя бы однозначны, а это свойство числа. Но если сложить две бесконечности, то бесконечность получится только одна, а если одну бесконечность из другой вычесть, то можно получить сколько угодно, включая бесконечность. Бесконечность не однозначна. А ноль однозначен.
Ответить
taras
dvaman 11.10.2017 17:07
Ответить
«К примеру, в программировании эта проблема решена. Просто определено самое большое число max_value (min_value) аналогичное нашему «бесконечность».» Нет. Во-первых MAX_INT. А во-вторых оно определено одновременно с inf. MAX_INT инт конечна, а int — нет.
Просто определено самое большое число max_value (min_value) аналогичное нашему «бесконечность».» Нет. Во-первых MAX_INT. А во-вторых оно определено одновременно с inf. MAX_INT инт конечна, а int — нет.
Ответить
taras
dvaman 11.10.2017 17:09
Ответить
«Поэтому если там Мы будем делить пять на ноль, мы получим самое большое число max_value. Все законно и справедливо.» Нет. Можно получить исключение, его низкоуровневый аналог, или inf. Но ни какой MAX не получится. Кстати, MAX_INT-MAX_INT==0, а inf-inf==nan.
Ответить
taras
aleks 11.10.2017 16:35
Ответить
Нет. Ноль — тоже число. И число ни какого отношения к наличию не имеет. Наличие и отсутствие — это флаг. А число — это только количество.
Ответить
kemist
22. 08.2006 21:06
08.2006 21:06
Ответить
А вот что получается, когда это «нельзя» не признается http://piramyd.express.ru/disput/lebedev/h-func.htm
Ответить
inf
29.09.2006 19:10
Ответить
Вообще-то есть тогда только сложение 🙂 Потому как умножение это n раз повтореное сложение.
3*3=9
3 раза по 3 сложить вот и 9 будет О_о
Ответить
-
nobody
inf 13.11.2006 11:00Ответить
Это верно только для чисел. В математике операции «сложения» и «умножения» могут быть определены над самыми разными объектами, например, матрицами или функциями. Для них «умножение» совсем неравно «сложению» X раз.. Да и трудно понять сколько раз нужно «прибавить», скажем, одну матрицу к другой.. 🙂
Ответить
taras
inf 11. 10.2017 17:57
10.2017 17:57
Ответить
Попробуйте pi*exp(1) выразить через сложение. exp — экспонента, то есть степень основания натурального логарифма. Или выразите через сложение, причём, не аргументов, а самих логарифмов ln(2)*ln(10).
Ответить
AnT
21.11.2006 10:30
Ответить
давайте уравнение 0*х=0 сведем от умножения к сложению???
у древних народов ваще никаких нолей не было, хотя были предпосылки к отрицательным числам, и трактовались они по бытовому — «кто кому должен», а если никому не должен — так и нет никаких отношений — ноль искусственно придумали, и он в операциях арифметики ваще присутствовать не должен — только башку засоряет))))
Ответить
-
Andrec
AnT 02.03.2007 14:13Ответить
Полностью согласенн.

Кто то вставил ноль в уравнение и все. Интересно, а если бы в математике не было ноля, как бы тогда она развивалась? Может и не было бы всяких этих неопределенностей и всяких там математических загадок? И тогда все проще было бы описать?Ответить
-
AMapyaK
AnT 27.01.2009 17:42Ответить
© давайте уравнение 0*х=0 сведем от умножения к сложению??? ©
В смысле?© у древних народов ваще никаких нолей не было… bla-bla-bla ©
А также у «древних народов» не было электричества, лазеров, ракетных двигателей, ядерного оружия и канализации — и что? Это значит, что все вышеперечисленное — бесполезно?© и трактовались они по бытовому — «кто кому должен» ©
Бытовое, называемое также наивным, понимание чего угодно — главная проблема людей, далеких от науки, при этом любящих о ней порассуждать.
Скажем, математическая теория хаоса, теория интегрирования дифференциальных форм, дифференциальная геометрия, теория функций комплексного переменного, аксиоматическая теория вероятностей — все это не имеет с бытовыми неурядицами ничего общего, однако тем не менее с успехом используется на практике. Это раз. Во-вторых, если определить отрицательные числа и не определять нуля, то вместо деления на ноль возникнет другая проблема: 12-12 равно чему? Т.е. нельзя вычитать одинаковые числа и складывать противоположные. Где выигрыш?
Это раз. Во-вторых, если определить отрицательные числа и не определять нуля, то вместо деления на ноль возникнет другая проблема: 12-12 равно чему? Т.е. нельзя вычитать одинаковые числа и складывать противоположные. Где выигрыш?Ответить
-
taras
AnT 11.10.2017 18:00Ответить
Ноль был как пустой карман. А отрицательных чисел как раз не было. Был долг, но даже умножать долг на долг ни кто не умел. Даже целый долг на целый долг. В том виде, как долг понимался тогда, если каменотёс должен охотнику 2 шкурки, а охотник должен две шкурки собирателю, а собиратель должен 2 шкурки каменотёсу, то они все трое должны друг другу. По-современному же они ничего друг другу не должны, так как могут взаимозачесть свои долги в ноль, всего лишь выяснив, что каменотёс, которому должен собиратель, — это тот самый каменотёс, который должен охотнику, охотник, который должен каменотёсу, — это тот самый охотник, которых должен собирателю, а собиратель, которому должен охотник, — это тот самый собиратель, который должен каменотёсу.
 2 с особым произведением векторов, которое и делает его полем комплексных чисел.
2 с особым произведением векторов, которое и делает его полем комплексных чисел.Ответить
-
taras
valkoivo 11.10.2017 18:11Ответить
«И, кстати, корень из -1 — это бессмыслица. Под корнем не может стоять отрицательного числа. » Бред.
Ответить
Fingolfin
20.02.2007 14:57
Ответить
Есть два замечания по поводу статьи:
1. В мат анализе никто не научит делить на ноль.
Выражение «неопределенность вида 0:0» является жаргонным названием предела дроби, чисслитель и знаменатель которой стремятся к нулю.
И еще решение уравнения 0*х=0 это х — любое число и оно вполне имеет смысл в алгебре например (когда реч идет о всяких там ядрах операторов, пространствах «натянутых» на решения и т.д.).
2. Вопрос почему на ноль нельзя делить, а вычитать ноль можно — не логичен. У дотошного читателя скорее должен возникнуть вопрос, а почему можно вычитать 1, а на ноль делить нельзя (1 — нейтральный элемент относительно умножения, 0 — нейтральный элемент относительно сложения).
У дотошного читателя скорее должен возникнуть вопрос, а почему можно вычитать 1, а на ноль делить нельзя (1 — нейтральный элемент относительно умножения, 0 — нейтральный элемент относительно сложения).
Ответить
Natawa
22.03.2007 17:53
Ответить
Спасибо, Александр. Вот, если бы всегда на вопросы отвечали человеческим языком, а то пишут всякие непонятные слова (определения) на своем заумном жаргоне, а ты как идиот над сносками паришься.
Ответить
eqlipt
01.10.2007 13:32
Ответить
Очень жаль, что комментарии на «Элементах» не модерируются. Господа, сайт хоть и научный, но все такие еще и популярный. Прежде чем писать свой довод, задумывайтесь, пожалуйста, насколько адекватно Ваше объяснение и понятно для людей не ученых, а просто интересующихся.
Для удовлетворения личных амбиций, уверен, существуют тематические форумы.
Ответить
DaVinci
01.02.2008 15:39
Ответить
Читая все комментарии, задаюсь я вопросом: «Тема-то интересная, но до каких пор можно отвечать на этот вопрос?» Ответов так много, что мне их хватило на долго. А вопрос про деление на ноль в школе остается простым, ответ всегда будет один — нельзя. Спасибо тем, кто загрузил меня. Оканчивая 11 класс, было приятно узнать что-то новое, кроме «нельзя» 🙂
Ответить
-
[email protected]
DaVinci 21.03.2008 12:55Ответить
Деление на ноль это математическая метафизика. В алгебраическом пространстве на ноль делить нельзя. В пространстве в котором операция деления на ноль, допустим закреплена как x/0=1.
 75 это вполне возможно. Я создаю свой мир и в моем мире деление происходит таким образом. Могу в нем задать и появление объектов посредством произнесения слова. Параллельные пространства. Во сне человек может оказаться в подобном пространстве и при определённых условиях оно будет казаться ему объективной реальностью. Сон другое пространство.
75 это вполне возможно. Я создаю свой мир и в моем мире деление происходит таким образом. Могу в нем задать и появление объектов посредством произнесения слова. Параллельные пространства. Во сне человек может оказаться в подобном пространстве и при определённых условиях оно будет казаться ему объективной реальностью. Сон другое пространство.Если взять пространство в котором на ноль можно делить с определённой вероятностью, т.е допустим в 75% операций деления на ноль мы будем получать случайное число, в 25% будет ответ «делить на ноль нельзя».
Получим множество ответов(на ноль делить можно, на ноль делить нельзя). В статье обсуждалась арифметика, относительно неё на ноль делить нельзя, автор в действительности сказал, что это не имеет смысла в арифметике. Математика очень интересная наука, можно встретить числа бесконечно стремящиеся к нолю, бесконечность и ноль в одном флаконе).
Ответить
-
taras
DaVinci 11. 10.2017 18:15
10.2017 18:15Ответить
А в институте ещё объяснят, как много раз сложить ноль с нолём и в итоге получить не ноль.
Ответить
bogdan.r
22.04.2008 19:41
Ответить
Попробую представить свое видение данной проблемы. Математика, как и любая другая наука была изначально создана, можно сказать, как формализованный язык описания мира в котором мы живем, с целью его понимания. А потому, она может допускать некоторые условности, упрощающие это описание. Одной из таких условностей является ноль. А поскольку человек создал этот язык, эту модель мира, то не он ли обладает свободой (ограниченной) устанавливать в ней свои правила? Так есть ли смысл ставить под сомнение запрет на деление на ноль, если это, возможно, просто правило введенное создателем языка?
Ответить
boo
12. 09.2008 18:48
09.2008 18:48
Ответить
Приношу свои извинения, если подобный комментарий уже встреался, но слишком их много (и одно, да по тому же), возможно, что и пропустил.
Но…
Я разделяю такую точку зрения (к которой пришел сначала экспериментально, а только потом убедился, что так оно, в ппринципе, и есть).
Операция деления — есть суть операция последовательных вычитаний делителя от делимого, а частное — есть суть — количество итераций, проведенных до остатка не превшающего делителя.
Т.е.
10:3 =
шаг 1. 10-3=7
шаг 2. 7-3=4
шаг 3. 4-3=1
т.о. имеем частное = 3 (количество шагов) и остаток =1
а что с нулем?
1:0=
шаг 1. 1-0=1
шаг 2. 1-0=1
…
шаг N 1-0=1
— отнимаем последовательно до бесконечности, вот и выходит, что решили школьникам просто голову не морочить «перевернутой восьмеркой».
Ну, и попутно про вычитание: я своему чаду объяснил так 10-4 = 10 + (-4)
и на этом экскурс «в дебри» закончил.
Ответить
-
webanut
boo 16.09.2008 00:59Ответить
самое удивительное, что вчера засыпая, думал примерно о том же :)))
———-
моя теория такова:
существует множество бесконечностей, бесконечное множество
нельзя приравнивать бесконечность к бесконечности, можно лишь сказать, что вот эта восьмёрка, повёрнутая на пи-пополам — ТОЖЕ бесконечность (принадлежит множеству бесконечностей), а не РАВНА любой другой бесконечности
это необходимо принять за аксиому, потому как:
оо + 1 (бесконечность плюс один) — это тоже бесконечность, равно как и просто оо
оо + 2 — это бесконечность
…
оо + оо — это бесконечность (а не «равно бесконечности»)
исходя из такого рассуждения (интересно, а как его вообще можно оспорить?), делаю следующий вывод (повторяя предыдущего «оратора» 🙂 ):
1/0 = ?
шаг 1. 1-0 = 1
шаг 2. 1-0 = 1
. .. (операции одинаковы, ничего не меняется от первой операции ко второй, а следовательно — не изменится и до бесконечности)
.. (операции одинаковы, ничего не меняется от первой операции ко второй, а следовательно — не изменится и до бесконечности)
шаг оо. 1-0 = 1
отсюда вывод, что 1/0 = оо + 1, что тоже является бесконечностью, равно как и 5/0 = оо + 5
последнее — для тех, кто утверждает, что получается алогизм, когда при сокращении единица становится равна пятёрке…
———-
«решили школьникам просто голову не морочить «перевернутой восьмеркой»»
а кто решил-то? почитать тему, так можно найти ярых противников деления на ноль — вот такие же и «решили», потому что сами так считают… тут дело вовсе не в слабости детского восприятия или фантазии — это скорее дело во взрослых 🙁
———-
и вообще, на делении на ноль можно и не останавливаться (хоть лично я и люблю эту тему) — ведь есть ещё интересные вещи типа 0/0, оо/0 и т.п. :)))Ответить
-
Nihil
webanut 02.06.2017 14:31Ответить
Если 10/3 означает, что нужно сделать 3 шага вычитания тройки из десятки, разве 1/0 означает, что нужно сделать оо шагов вычитания нуля из единицы?
Скорее это означает, что нужно сделать 0 шагов вычитания нуля из единицы. В результате, по идее, 1 должна стать нетронутой единицей. В смысле, все остальные числа в результате деления на все остальные числа остаются тронутыми, а в результате деления на 0 все остальные числа становятся нетронутыми
В результате, по идее, 1 должна стать нетронутой единицей. В смысле, все остальные числа в результате деления на все остальные числа остаются тронутыми, а в результате деления на 0 все остальные числа становятся нетронутымиОтветить
-
Kostja
29.11.2008 18:13
Ответить
В статье чтобы осветить один вопрос приведено несколько доводов в свою очередь вызывающих разные вопросы. Дети, не ленитесь, учите матчасть! 😉
Ответить
Bon
03.12.2008 13:57
Ответить
К единственному ответу на этот вопрос Вы не приблизитесь, пока не начнете рассматривать понятие «ноль» в рамках какой-то определенной теории! В зависимости от системы аксиом, на которой строится Ваша теория, Вы можете делить на ноль, вычислять 0^0 и т. д. Вопрос в том, можно ли с пользой применить такую теорию на практике?
д. Вопрос в том, можно ли с пользой применить такую теорию на практике?
В школах изучаются теории, в которых на ноль делить нельзя. Ваши предложения по введению в эти теории понятий бесконечности и неопределенности просто строят теорию, в которой уже делить на ноль можно, но это другая теория, которую в школе не изучают, да это и не нужно!
Добавьте в систему аксиом геометрии Лабочевского аксиому параллельности прямых, и получится геометрия Евклида.
Как ответить на вопрос «Чему равна сумма углов в треугольнике»?!
Одни ответят — 180 градусов! — и будут правы.
Другие возразят — нет! Треугольник, который строится из 2 меридиан, пересекающихся под прямым углом, и экватора, имеет сумму углов 90*3=270 градусов! — и тожке будут правы!
Так что правы и те и другие, к чему спор?
Теперь, что касается вопроса — «Почему» на ноль делить нельзя?
Сам вопрос уже с подвохом.
Ноль просто не входит в область определения знаменателей операции деления. Почему нельзя делить на фиолетовый? По той же причине! Просто фиолетового нет на числовой прямой, а ноль есть, и это сбивает с толку.
Для тех, кто хочет делить на ноль — введите в множество, в которое вы хотите ввести бесконечность и неопределенность еще и фиолетовость — возможно эта новая теория будет революционным скачком в науке, но к теориям, изучаемым на данный момент в школе и ВУЗах отношения иметь не будет.
Ответить
den4
18.02.2009 14:31
Ответить
А кто сказал, что на ноль делить нельзя? этому учат на уроках арифметики в начальных классах… А людям с высшим образованием, хотябы отдаленно слышавших о теории пределов, товарище Лопитале и всем таком, должно быть понятно, что деление на 0 в полне нормальная математическая операция, которая в ответе дает бесконечности различных порядков. А по поводу статьи могу сказать следующее: никакого отношение она к математике не имеет, скорее к эпистолярному жанру литературы, я, к примеру, могу путем подобных софистических рассуждений доказать, что единственная арифметическая операция — возведение в степень, а все остальные производные от нее. .. ))
.. ))
Думаю, перед тем как писать подобную чушь, автору нужно было хоть немного почитать историю развития математики и историю теории множеств…
Ответить
kesha
06.04.2009 20:57
Ответить
Из научного фольклора: «Необходимость делить на ноль выглядит катастрофой в глазах математика и может даже вызвать лёгкое смущение у физика-теоретика.»
Ответить
djanubis
28.09.2009 15:56
Ответить
По моему, кол-во комментариев само по себе говорит о том, что…но давайте без оскорблений.
Лично я нашёл для себя удобный выход. Числа — это числа, а ноль и бесконечность — это ПРОЦЕСС. Нет ноля и бесконечности — это пределы. То есть какое бы вы не выбрали ЧИСЛО, можно НАЙТИ число большее\\меньшее данному. Именно поэтому ноль и бесконечность -процесс. Им вообще нечего делать в математике. Это исскуственные формации. Как темная материя, возможно. Так что, вопрос, почему делить на ноль нельзя, сродни вопросу «что общего между цифрой 8 и зелёным цветом». Это просто несовместимые понятия. Всё равно что прибавить к одному метру одну секунду. Что получится? ДА НИЧЕГО! А вы тут развели дурацкие дебаты. Чуть ли не докторскую защищаете.
Им вообще нечего делать в математике. Это исскуственные формации. Как темная материя, возможно. Так что, вопрос, почему делить на ноль нельзя, сродни вопросу «что общего между цифрой 8 и зелёным цветом». Это просто несовместимые понятия. Всё равно что прибавить к одному метру одну секунду. Что получится? ДА НИЧЕГО! А вы тут развели дурацкие дебаты. Чуть ли не докторскую защищаете.
Типичные математики :)))))
Ответить
taras
djanubis 11.10.2017 18:27
Ответить
И уж или нечего делать в математике, или искусственные формации. Стремиться, кстати, величины могут к чему угодно. Так что, числа вообще не существуют?
Ответить
Nesch
29.11.2009 11:54
Ответить
Мне когда-то объяснили примерно так (от меня надо было срочно отвязвться): дали несколько спичек и сказали «а теперь раздай их пустому месту так, чтоб было поровну», я сказала «но тогда все спички у меня будут», на что мне ответили «но ты ведь не пустое место». . и я ушла умножать на бесконечность))))
. и я ушла умножать на бесконечность))))
Ответить
mikheyev.sergey
01.09.2010 17:21
Ответить
Внимательно всё прочитал, и решил: делить на ноль нельзя, но если очень хочется, то можно. В таком случае, придётся расширить число математических сущностей — существует бесконечное число нулей и бесконечное число бесконечностей различных порядков, которые не равны друг другу, и которые можно перемножать и делить друг на друга. Придётся смириться с парадоксом бесконечности – часть равна целому. Например, число всех чётных чисел равно числу всех целых чисел. Будьте осторожны, применяя эту теорию на практике. Мавроди не учёл, что число вкладчиков финансовой пирамиды отлично от бесконечности, и за конечное время был привлечён к уголовной ответственности, за свою математическую ошибку.
А дискретная топология и математика конечных множеств, скучна и банальна, также как наша реальная дискретная и конечная вселенная. Прошло примерно 30 лет как учёные рассчитали максимальный и минимальный размер в нашей вселенной, долю тёмной энергии (75%), структуру «суперструн» (вихри в сверхтекучей жидкости), начальную и конечную энтропию и температуру нашей вселенной (реликтовое излучение). Нас всех посчитали!!! Давно известно, как и когда разрушится пространство нашей вселенной и во что, оно превратится. Просто, скучно, грустно, и никому не нужно.
Прошло примерно 30 лет как учёные рассчитали максимальный и минимальный размер в нашей вселенной, долю тёмной энергии (75%), структуру «суперструн» (вихри в сверхтекучей жидкости), начальную и конечную энтропию и температуру нашей вселенной (реликтовое излучение). Нас всех посчитали!!! Давно известно, как и когда разрушится пространство нашей вселенной и во что, оно превратится. Просто, скучно, грустно, и никому не нужно.
Ответить
VladNSK
05.11.2010 00:22
Ответить
В математике есть такое понятие, как бинарная операция. В каждом конкретном случае строго определяется множество элементов, над которыми выполняется операция, и указывается правило, как по двум элементам можно вычислить результат операции.
Математики допускают, что для некоторых элементов результат операции может быть не определен. Но если результат есть, то он должен быть один, и обязательно должен принадлежать исходному множеству элементов. На таком определении операции построена вся арифметика, теория групп и много еще чего.
На таком определении операции построена вся арифметика, теория групп и много еще чего.
Конечно, можно определить или привести свой пример операции, у которой более одного результата. Но это будет не операция, а что-то другое.
Что касается фразы «на ноль делить нельзя», то она математически не корректна, потому что в этой фразе непонятно что означает слово «нельзя». Почему нельзя ?! Потому что учитель не разрешает ? Или потому, что если начать делить, то что-то нехорошее произойдет, например, компьютер сломается, если делить на компьютере ?
Математический корректная формулировка такая: на множестве целых чисел для любого целого числа N результат операции N : 0 не определен.
Кстати, в невозможности делении на ноль нет ничего уникального. В математике можно найти очень много других операций, которые не всюду определены. Например, если мы возьмем множество ПОЛОЖИТЕЛЬНЫХ целых чисел и рассмотрим на этом множестве операцию вычитания, то можно привести сколько угодно примеров, когда результат вычитания не определен: 1-2, 10-20, 100-105 — во всех этих случаях результат вычитания не определен, потому что получается отрицательное число.
Ответить
VladNSK
05.11.2010 15:25
Ответить
Если посмотреть на процесс решения уравнений, то там используются эквивалентные преобразования, то есть исходное уравнение заменяется другим, более простым, и так по цепочке, пока не получим все решения.
Одно из эквивалентных преобразований — это умножение или деление обеих частей уравнения на одно и то же выражение. И вот тут есть правило, что умножать или делить можно на что угодно, но только не на ноль. На ноль делить обе части уравнений нельзя! И умножать на ноль нельзя! Здесь под «нельзя» понимается то, что если это сделать, то уравнение будет решено неверно: например, могут появиться лишние корни.
Есть также чисто житейское соображение почему на ноль делить нельзя 🙂
Например, если на экзамене в ВУЗ вы будете решать уравнение (x*x -1)/(x-1) = 2 и не сделаете отметку, что x не равно 1, то есть забудете правило, что на ноль делить нельзя, затем поделите числитель и знаменатель на (x-1), получите x+1=2, то есть напишете x=1, то вы дадите неверное решение.
Таким образом, на ноль делить нельзя еще и потому, что можно получить плохую оценку и не поступить 🙂
Ответить
-
taras
VladNSK 11.10.2017 18:38Ответить
Как Вы лихо многочлен на многочлен делите. Там вообще то левая и правая части умножаются на (x-1).
(x*x-1)/(x-1)=2
(x*x-1)=2*(x-1)
x*x-1=2*x-2
x*x-2*x+1=0
D=0
x=1.
И только ПОСЛЕ ЭТОГО результат сравнивается с областью определения левой части исходного уравнения. Точнее он вообще подставляется в исходное уравнение для проверки решения и обнаруживается нулевой делитель, из чего делается вывод об отсутствии решений.Ответить
-
VladNSK
taras 13.10.2017 15:34Ответить
Taras написал:
<
Как Вы лихо многочлен на многочлен делите. Там вообще то левая и правая части умножаются на (x-1).
Там вообще то левая и правая части умножаются на (x-1).
>
Вы забыли, что x*x-1 равно (x-1)(x+1). Так что ничего лихого в делении на (x-1) нет.Ответить
-
taras
VladNSK 15.10.2017 19:34Ответить
Нет. Это Вы забыли, что любому школьнику проще запомнить алгоритм, чем таблицу. Тем более чем найти в ней по памяти столбец по значению ячейки на его пересечении со строкой, а не наоборот. А у Вас сразу результат деления многочлена на многочлен без каких либо операций для его получения. Вот в этом и лихость. Результат же я не оспариваю.
Ответить
-
-
-
VladNSK
taras 14.10.2017 10:09Ответить
Кроме того, Вы, taras, основательно подзабыли курс школьной алгебры.
Если вы умножили уравнение, зная (из области определения) что множитель ненулевой, то, получив окончательное решение (решения), ничего проверять НЕ надо.

Лишние решения могут появиться при возведении обеих частей уравнения в квадрат. Вот тогда надо проверять.
Если вы извлекли квадратный корень из обеих частей уравнения, то чтобы не потерять корни, надо будет решать отдельно ДВА уравнения.
Ответить
-
taras
VladNSK 15.10.2017 19:31Ответить
«Кроме того, Вы, taras, основательно подзабыли курс школьной алгебры.» В отличие от Вас нет. Откуда я заранее знаю, что множитель не нулевой, если он содержит искомую переменную? Решения положено проверять подстановкой ВСЕГДА. То, что многие ленятся, решая уравнения, допускающие абсолютно все значения искомой величины, к правилам ни как не относится. Реальные же задачи всегда ещё и ограничения имеют. Соответственно решения ещё и на них должны проверяться. Единственное, когда проверка не требуется, — это если в методе бисекций f(c)=0.
Ответить
-
VladNSK
taras 16. 10.2017 17:47
10.2017 17:47Ответить
Taras написал: «Откуда я заранее знаю, что множитель не нулевой, если он содержит искомую переменную? Решения положено проверять подстановкой ВСЕГДА. «
Да уж …
При решении уравнения сначала выписывается область определения неизвестного (чтобы не было деления на ноль, чтобы у логарифма был строго положительный аргумент и т. д.).Далее вы делаете постепенные преобразования уравнения.
На каждом шаге вы УЖЕ должны четко знать, что либо число корней не изменится, либо их может стать больше, либо их может стать меньше. Если вы этого не знаете, значит вы не понимаете самой сути решения уравнений.
В частности, если вы умножаете обе части уравнения (или делите) на какой-либо множитель, то прямо на этом шаге вы УЖЕ должны быть уверены, что он не нулевой. Для такой проверки у вас есть область допустимых значений.
Если в процессе решения у вас все преобразования были эквивалентными, то есть вы знаете, что не может быть потерянных корней и не может быть лишних корней, то и проверять найденные корни НЕ надо.

Я тут имею ввиду, что не надо делать проверку в тетрадке, которую вы преподу сдаете. Ну, либо можно написать, что проверять решения не надо, так как все преобразования были эквивалентными.Совсем другое дело, что для себя лично, где-нибудь на промакашке нужно обязательно проверить корни, чтобы убедится, что вы не допустили ошибку.
Ответить
-
taras
VladNSK 17.10.2017 10:46Ответить
Да хоть за выписывайтесь. ЗАРАНЕЕ НЕ ИЗВЕСТНО, ЧТО ПОЛУЧИТСЯ В ХОДЕ ВЫЧИСЛЕНИЙ, соответственно проверка на попадание в область выполняется только для почти готового ответа. Ну как почти. Когда только проверить и осталось. И обратите внимание: деление на ноль не выполняется даже в случае сокращения числителя на знаменатель, а критикую я такой ход решения только за выброшенный черновик. Потому что раскрыть то скобки и привести подобные может любой старший школьник, причём, быстр и часто в уме, а над обратной операцией может задуматься даже дипломник, тем более когда делитель задан.
 Об ошибке при делении многочлена на многочлен речи не было. Нулевым же знаменатель оказывается ПОСЛЕ деления. Все ограничения выписываются максимально рано, на сколько это возможно, но их соблюдение проверяется ПОСЛЕ ТОГО, КАК ПОЛУЧЕНЫ СООТВЕТСТВУЮЩИЕ ЗНАЧЕНИЯ. В случае корня квадратного одно из ограничений проверяется после того, как получено значение подкоренного выражения. Вообще в случае функции с ограниченной областью определения проверка выполняется после того, как получено значение аргумента.
Об ошибке при делении многочлена на многочлен речи не было. Нулевым же знаменатель оказывается ПОСЛЕ деления. Все ограничения выписываются максимально рано, на сколько это возможно, но их соблюдение проверяется ПОСЛЕ ТОГО, КАК ПОЛУЧЕНЫ СООТВЕТСТВУЮЩИЕ ЗНАЧЕНИЯ. В случае корня квадратного одно из ограничений проверяется после того, как получено значение подкоренного выражения. Вообще в случае функции с ограниченной областью определения проверка выполняется после того, как получено значение аргумента.Ответить
-
VladNSK
taras 17.10.2017 11:53Ответить
Taras написал :
<
ЗАРАНЕЕ НЕ ИЗВЕСТНО, ЧТО ПОЛУЧИТСЯ В ХОДЕ ВЫЧИСЛЕНИЙ, соответственно проверка на попадание в область выполняется только для почти готового ответа.
>Конечно заранее не всё известно, что получится, потому что тогда и решать бы не надо было.
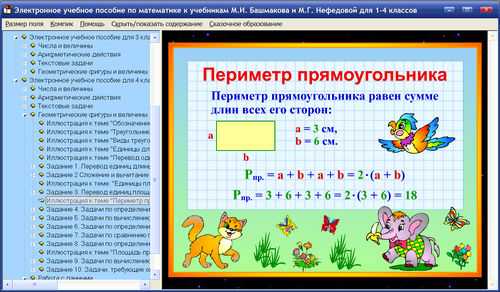
Но на каждом шаге, применяя очередное преобразование уравнения, должно быть совершено точно известно по поводу корней уравнения (значения которых будут получены только в самом конце) : останется ли число корней прежним, либо могут появиться лишние корни (например, при возведении в квадрат) и тогда надо в решении сделать отметку об обязательности проверки корней, либо далее придется отдельно решать два разных уравнения (например, чтобы не потерять корни при извлечении квадратного корня из обеих частей уравнения).
Когда вы закончите решение и найдете один или несколько корней, вам нужно будет просмотреть ход вашего решения, и если в нем нет ни одной отметки о возможности появления лишних корней, то проверять найденные корни не надо.
<
И обратите внимание: деление на ноль не выполняется даже в случае сокращения числителя на знаменатель,
>
Нет, тот, кто так считает, делает грубейшую ошибку.
Сокращение числителя и знаменателя это и есть деление, и прежде, чем его провести, надо проверить по ОДЗ, что такое деление возможно<
Потому что раскрыть то скобки и привести подобные может любой старший школьник, причём, быстр и часто в уме, а над обратной операцией может задуматься даже дипломник, тем более когда делитель задан. 2-1) на (X-1) в числителе будет (X+1), а знаменатель будет единичным, и поэтому от него в дальнейшем можно отказаться.
2-1) на (X-1) в числителе будет (X+1), а знаменатель будет единичным, и поэтому от него в дальнейшем можно отказаться.<
В случае корня квадратного одно из ограничений проверяется после того, как получено значение подкоренного выражения.
>
Если вы имеете ввиду извлечение квадратного корня из обеих частей уравнения, то в таком случае ничего проверять не нужно. А нужно далее решать отдельно два разных уравнения, а в конце их корни нужно будет объединить в общее решение.Ответить
-
-
-
-
-
taras
VladNSK 15.10.2017 19:36Ответить
«Лишние решения могут появиться при возведении обеих частей уравнения в квадрат. Вот тогда надо проверять.» Проверять положено даже в том случае, если уравнение вообще не преобразовывалось. И дело, как показывает данный пример, не только в лишних решениях, но и в допустимых значениях.
 2+a*c.
2+a*c.Ответить
Штейн
02.12.2010 04:22
Ответить
я считаю что любое действие в математике должно иметь обратное действие, так что если нельзя делить на ноль то и умножать тоже например х*0=0 следовательно обратное действие х =0:0 где х в принципе может быть абсолютно любым числом. в этой связи предлагаю относиться к нулю как к отсутствию действия будь то сложение или умножение. Либо предлагаю определить 0 как минус бесконечность плюс бесконечность и полное отсутствие у нуля стремления к действию.
Ответить
-
VladNSK
Штейн 13.12.2010 07:39Ответить
Штейн написал: «я считаю что любое действие в математике должно иметь обратное действие»
Согласен, что отсутствие обратного действия может вызвать у школьника недоумение.

Тут всё дело в том, что школьникам дается только малая часть математики. Математика очень трудная наука, и поэтому математики постоянно стремятся как можно больше упростить свои определения и доказательства.
Уверяю вас, что если бы от вашего предложения была хоть малейшая польза, то математики давно бы уже им воспользовались.
На самом деле, если последовать вашему предложению, то количество «непоняток» с нулем возрастет многократно.
Ответить
-
VladNSK
Штейн 13.12.2010 07:51Ответить
Вы совершенно напрасно припутываете бесконечность к числам. Ноль, 10, -3.5 — это всё числа. А бесконечность числом не является.
Понятие беконечность возникает не в теории чисел, а в математическом анализе. Причем и тут строго говоря, беконечность как математический объект не существует. Нет такого объекта как бесконечность в математике!
Когда математики говорят, что, например, сумма ряда стремится к бесконечности, то они просто имеют ввиду, что рано или поздно сумма ряда превысит любое наперед заданное число.
 Говорить при этом, что сумма ряда равна бесконечности — это неточность, так иногда физики выражаются. Правильно говорить, что сумма ряда стремится к бесконечности, или что ряд расходится. Иными словами, здесь нигде нет бесконечности как какого-то вполне определенного числа или математического объекта.
Говорить при этом, что сумма ряда равна бесконечности — это неточность, так иногда физики выражаются. Правильно говорить, что сумма ряда стремится к бесконечности, или что ряд расходится. Иными словами, здесь нигде нет бесконечности как какого-то вполне определенного числа или математического объекта.Ответить
-
taras
VladNSK 11.10.2017 18:54Ответить
Вот только есть ещё бесконечность минус бесконечность и бесконечность, делённая на бесконечность. А ещё интеграл определён как бесконечная сумма бесконечно малых слагаемых. Но при этом многие интегралы имеют вполне строго определённые значения. Так что, интеграл тоже теперь не математичен? И физики так не выражаются, физики как раз обожают такие преобразования, при которых бесконечность изгоняется.
Ответить
-
VladNSK
taras 13. 10.2017 15:28
10.2017 15:28Ответить
Taras написал :
<
Вот только есть ещё бесконечность минус бесконечность и бесконечность, делённая на бесконечность.
>
А это и вовсе математически некорректные выражения. Так говорят некоторые преподы на первом курсе ПТУ, причем они имеют ввиду вовсе не какие-то математические объекты, а просто разделы из задачника.Например, мы ищем предел от деления двух функций в некоторой заданной точке, причем каждая из этих функций стремится в этой точке к бесконечности. Вроде бы имеем бесконечность делить на бесконечность?
Но тут все зависит от самих функций. Предел от деления может быть каким угодно: конечным числом, уходить в плюс бесконечность, уходить в минус бесконечность, и даже уходить просто в бесконечность, и, наконец, предел может вообще не существовать.
Пример : f1(x) = 1/2x, f2(x) = 1/3x. Обе функции стремятся к бесконечности в точке ноль, но их частное всегда равно 1.
 2 — это х в квадрате), f2(x) = 1/x. Обе функции стремятся к бесконечности в точке ноль, и их тоже стремится к бесконечности.
2 — это х в квадрате), f2(x) = 1/x. Обе функции стремятся к бесконечности в точке ноль, и их тоже стремится к бесконечности.Так что выражение «бесконечность деленная на бесконечность» — это математически некорректное выражение. Если уж хочется что-то подобное сказать, то надо уточнять, например, так : O(2) деленное на O(10).
Ответить
-
taras
VladNSK 15.10.2017 19:41Ответить
«А это и вовсе математически некорректные выражения. Так говорят некоторые преподы на первом курсе ПТУ, причем они имеют ввиду вовсе не какие-то математические объекты, а просто разделы из задачника.» А ничего, что это вполне стандартные неопределённости? В ПТУ я, кстати, не был ни разу. И ПТУшные задачники ни разу не видел.
Ответить
-
taras
VladNSK 15.10.2017 19:46Ответить
«Так что выражение «бесконечность деленная на бесконечность» — это математически некорректное выражение.
 4) при x, стремящемся к бесконечности. Водится в сходимости рядов. А обозначение O() лично я видел только в контексте вычислительной сложности и расхода памяти. Бесконечности там как раз не водятся, как и неопределённости.
4) при x, стремящемся к бесконечности. Водится в сходимости рядов. А обозначение O() лично я видел только в контексте вычислительной сложности и расхода памяти. Бесконечности там как раз не водятся, как и неопределённости.Ответить
-
VladNSK
taras 16.10.2017 17:55Ответить
Тарас, эта ветка началась с выяснения, есть или нет такой математический объект как бесконечность.
Так вот, такого объекта в математике НЕТ.
Число 78 есть, число пи есть, есть функции, значения которых в некоторой точке стремятся к бесконечности, а просто бесконечности нет. И бесконечность/бесконечность тоже нет.
Ответить
-
-
-
taras
Штейн 11.10.2017 18:48
Ответить
Бред.
Ответить
sawa
22.12.2010 20:07
Ответить
кто нибудь может объяснить почему при умножении на 0 всегда получается 0 ?
Ответить
-
VladNSK
sawa 23.12.2010 13:37Ответить
Для любого n верны следующие выражения:
(n * 2) — (n * 2) = 0, потому что когда из числа отнимаешь его же, то получается ноль. Теперь приведем подобные:
n * (2-2) = 0
n * 0 = 0Конечно, это не строгое математическое доказательство, а объяснение. Но вы ведь и просили дать объяснение.
Ответить
-
Human
VladNSK 17.12.2011 22:41Ответить
А по-моему очень даже строго )
Здесь требуется только показать, что (-1)*n=-n, то есть что противоположное к действительному число есть то же самое число, умноженное на «-1», то есть на число, противоположное «1». Я думаю этот факт не вызывает вопросов (как например с делением на нуль). Тогда:
Я думаю этот факт не вызывает вопросов (как например с делением на нуль). Тогда:
n+(-n)=0 (определение противоположного числа)
n*1+n*(-1)=0 (определение единицы и названный выше факт)
n*(1+(-1))=0 (дистрибутивность)
n*0=0 (ещё раз определение противоположного числа)Ответить
-
D.-.i.-.m.-.a
10.02.2011 08:03
Ответить
Статья познавательная.
Не удержался:
По поводу компьютеров: там используется теория циклических полей, где числа это скорей «порядковые номера» элементов – после максимального значения следует минимальное (а после минимального максимальное), при этом устанавливается признак переполнения. И если в каких-то приложениях этот признак интерпретируется как запрет деления на ноль, то это проблема/преимущество этих приложений. В компьютерах проблему «решили» …по своему…
По поводу ноля: еще индейцы для обозначения единиц использовали не яблоки а «раковины с едой», а «раковина без еды» и есть ноль еды.
Ответить
rostaman
14.05.2011 01:16
Ответить
Попытка объединить философию и математику http://www.zengarden.in/filosofiya-deleniya-na-nol/ См. также комментарии
Ответить
TutorState.com
01.07.2011 02:29
Ответить
На школьном этапе обучения все надо как-то объяснить детям, исходя из их естественного опыта. Нельзя (!!!) вводить, например, сложение из аксиом, а надо показывать, что если было два яблока, а затем добавили еще три, то теперь, если пересчитать яблоки, их окажется пять. Так как же школьникам обьяснить деление на ноль? Может так?: Если вы делите на маленкое (положительное) число, которое много меньше единицы, то в результате получается большое число. (1:0.01=100) Если делитель ещё уменьшить, результат ещё станет больше. (1:0.00001=100000) А при делении на самое маленькое число результат получается больше всех чисел, но такого числа, которое больше всех чисел, нет, поэтому мы и говорим, что делить на ноль нельзя. — Как вы думаете, понятно и полезно ли будет детям такое объяснение?
(1:0.00001=100000) А при делении на самое маленькое число результат получается больше всех чисел, но такого числа, которое больше всех чисел, нет, поэтому мы и говорим, что делить на ноль нельзя. — Как вы думаете, понятно и полезно ли будет детям такое объяснение?
Ответить
-
Human
TutorState.com 17.12.2011 22:44Ответить
Вполне себе. Даже мне понятно стало )
Ответить
-
taras
TutorState.com 11.10.2017 19:01Ответить
Именно из-за такого объяснения я и был уверен, что на ноль делить можно. Даже диссертацию защитил, будучи уверенным, что можно. Ведь бесконечность — не число и больше любого числа, а раз она может получиться при делении на ноль, то всё в порядке. И только потом мне попалось обоснование через уравнение.

Ответить
Простой но гениальный ЧЕЛОВЕК
26.09.2011 03:03
Ответить
На самом деле всё проще! я солидарен с теми кто говорит что деление на ноль приведёт к бесконечности. во первых, если делить на число меньше целой единицы(например x/0.01) и приближать число всё ближе к нолю(x/0.00001) то в итоге будет получаться всё большее число, а теоретически поделив на ноль выйдет=бесконечность. Это я как бы для детей объяснил, а сейчас будет пример чуть по сложнее. Во вторых, если ноль умножить на бесконечность то с одной стороны можно сказать что останется ноль, а с другой стороны останется всё та же бесконечность!(тоже что сказать про стакан который на половину пустой или же он на половину полный(я согласен что в этом случае проще было бы сказать что останется ноль, а не бесконечность, потому что это означало бы прекращение каких либо вычислений и умственных процессов, но по сути бесконечность не чуть не уступает нолю)), а если быть более точным то ноль умноженный на бесконечность это=»любое число». (допустим X это «любое число») то есть 0*∞=X или 0/0=X(как было в статье) и ∞/∞=X,в этих случаях ответом будет «любое число». а если ∞*X=∞, X/∞=0 и X*0=0 так же и X/0=∞
(допустим X это «любое число») то есть 0*∞=X или 0/0=X(как было в статье) и ∞/∞=X,в этих случаях ответом будет «любое число». а если ∞*X=∞, X/∞=0 и X*0=0 так же и X/0=∞
Ответить
gssgssgss
27.10.2011 04:05
Ответить
Делить на ноль нельзя потому, что это лишено смысла… например арифметического и не только … +0 значит ничего не добавить (дать)… -0 ничего не забрать (отнять)… *0 значит обнулить — превратиь результат в 0… /0 значит поделить число на 0 частей — действие лишено смысла — вот поэтому его делать нельзя — так детям понятно — нельзя делать то, что лишено смысла…
Ответить
-
1
gssgssgss 27.11.2011 09:20Ответить
соглашусь
Ответить
-
daria_dsm
gssgssgss 13. 06.2013 15:53
06.2013 15:53Ответить
да,верно))) просто как все)
Ответить
-
?ё!
gssgssgss 16.09.2015 16:00Ответить
Смысл есть всегда и во всём, например, чтобы увести от истины или обозначить новое правило игры с истиной. А смысл математики в том, что она должна отражать реальную действительность. Каждое число обозначает количество чего-то вещественного (материального) или количество каких-то действий. Смысл 0 состоит в том, что он не имеет ни вещественного наполнения, ни наполнения действиями. Но обозначить-то (записать, запротоколировать) это как-то нужно, значит нужен и 0. Про сложение и вычитание gssgssgss правильно сказал: ни дать, ни взять, а потом съехал с пути истинного. Ведь про деление и умножение можно так же сказать: ни делить, ни умножать, т.к. нуль это отсутствие действия.
Разделить на 0 это значит не делить ни на что (ни на какие части), т. е. оставить всё как есть. Ведь не делить ни на что и разделить ни на что это одно и то же. Отсюда следует, что с 5-ю ничего не нужно делать ни сколько раз. Тогда 5/0 = 5. А если не нужно умножать, то и 5*0 = 5, т.е. противоположные «не действия» подтверждают друг друга строго математически. Правда получается кажущееся противоречие с единицей: 5/1 = 5 и 5*1 = 5. Но если подумать, то и здесь нет никаких противоречий. 5/1 это значит из 5 счётных палочек сделать (сформировать) одну кучку, в которой было бы 5 палочек. Скажем палочки лежали на столе разрозненно, а мы их положили одной кучкой (в одном месте). Но на столе-то при этом осталось прежнее количество палочек, т.е. 5/1 = 5. Умножение, 5*1 это значит, что 5 палочек нужно посчитать (учесть) только один раз. Тогда 5*1 = 1+1+1+1+1 = 5.
е. оставить всё как есть. Ведь не делить ни на что и разделить ни на что это одно и то же. Отсюда следует, что с 5-ю ничего не нужно делать ни сколько раз. Тогда 5/0 = 5. А если не нужно умножать, то и 5*0 = 5, т.е. противоположные «не действия» подтверждают друг друга строго математически. Правда получается кажущееся противоречие с единицей: 5/1 = 5 и 5*1 = 5. Но если подумать, то и здесь нет никаких противоречий. 5/1 это значит из 5 счётных палочек сделать (сформировать) одну кучку, в которой было бы 5 палочек. Скажем палочки лежали на столе разрозненно, а мы их положили одной кучкой (в одном месте). Но на столе-то при этом осталось прежнее количество палочек, т.е. 5/1 = 5. Умножение, 5*1 это значит, что 5 палочек нужно посчитать (учесть) только один раз. Тогда 5*1 = 1+1+1+1+1 = 5.
В результате 5/0 = 5*0 = 5*1 = 5/1 = 5. И в этом так же нет никаких противоречий, т.к. единичное действие с одним и тем же наполнением означает, что с этим наполнением нужно провести такое действие, при котором наполнение не изменится. Так оно и есть. При делении на 1 мы соединили палочки в одну кучку, а при умножении на 1 мы их просто заново пересчитали, т.е. действие-то есть, но результат не изменился.
Так оно и есть. При делении на 1 мы соединили палочки в одну кучку, а при умножении на 1 мы их просто заново пересчитали, т.е. действие-то есть, но результат не изменился.
При сложении и вычитании всё несколько иначе, т.к. эти действия связаны с другим наполнением, чем то, над которым необходимо произвести действие.
А детям можно сказать просто: нуль это значит ничего не делать, т.е. при всех математических действиях числа с нулём число не изменяется. Куда ещё проще?Ответить
-
taras
?ё! 11.10.2017 19:06Ответить
Бред. А бред ни когда не имеет смыла.
Ответить
-
withoutthetime
?ё! 07.04.2019 20:04Ответить
Еще в школе было вот какое объяснение деления: предположим 100÷20 — это вычислить сколько в одной сотне раз по двадцать, сколько двадцаток в сотне.
 Ну вроде все понятно — кончно пять!
Ну вроде все понятно — кончно пять!
А теперь как бы расчитать сколькл в той же сотне нолей ( 100÷0)??? И мне кажется что их не то, что бы нет ( нолей в сотне) похоже что нет и самого ответа на этот вопрос!
В то же время мне не даёт покоя X×0=0 и нахождение из этого уравнения «X»!!!Ответить
-
taras
gssgssgss 11.10.2017 19:03
Ответить
Ну так лишено смысла, что на дроби 0/0 построена четверть теории пределов. Дробного количества частей тоже не бывает, но делить на дробь можно. Проблема же именно в самом определении операции деления. Она не самостоятельна, а введена как обратная операция, то есть её результат есть решение уравнения. А уравнение x*0=a лишено смысла.
Ответить
-
!ё!
taras 11.10.2017 21:25Комментарий скрыт
-
taras
!ё! 15. 10.2017 21:25
10.2017 21:25Ответить
Нет. Вот есть у тебя лента. Ты её порезал на три части, мне отдал две. Их не может быть ни две с половиной, ни полторы. Дробной бывает доля от целого. Один кусок — четверть, другой — треть, третий — то, что осталось, то есть пять двенадцатых. Доля от целой ленты, приходящаяся на два отданных куска — семь двенадцатых. Но кусков два. Одно количество — дробное, другое — целое. «А вот осмысление физики, т.е. действительности на основе решения математических уравнений действительно не имеет смысла, т.к. смысл математики в физике, но никак не наоборот. Не так ли?» Ну разумеется смысл математики — физика. Ведь именно математика описывает физику, а не наоборот. Для того и создана. И именно поэтому в любой реальной задаче есть ограничения и на типы величин, и на их значения. Например, если уравнение описывает высоту полёта дирижабля, то решение не только может быть только действительным, но и не может ни быть отрицательным, ни превышать толщину атмосферы.
 Если тангенс описывает отношение расстояния к базе дальномера, то угол может быть только действительным в диапазоне от ноля до ставосьмидесяти градусов, а аргумент — половина угла. Соответственно тангенс не может превратиться в отношение двух экспонент. И именно поэтому имеет смысл именно осмысление и физическая интерпретация решений математических уравнений.
Если тангенс описывает отношение расстояния к базе дальномера, то угол может быть только действительным в диапазоне от ноля до ставосьмидесяти градусов, а аргумент — половина угла. Соответственно тангенс не может превратиться в отношение двух экспонент. И именно поэтому имеет смысл именно осмысление и физическая интерпретация решений математических уравнений.Ответить
-
-
taras
!ё! 17.10.2017 14:52Ответить
Вот и приведите к целому числителю. Это ведь не сложно.
Ответить
Jill2zso5i
29.11.2011 23:19
Ответить
Господа, отправьте малограмотную к тому посту, где определяется 0 — как число, как его отсутсвие или как ЧТО (так ноль-это число или нет вообще?!!!)? Вопрос блондинки: с точки зрения двоичной системы я понимаю про «наличие отсутствия» и «отсутствие наличия» (здесь сарказм), ну то есть, почему 1 и 0 -это метафизические противоположности, но как тогда быть с -1 и всемы вытекающими отовсюду последствиями????Повторяю:»я гуманитарий»!!!!
Ответить
-
taras
Jill2zso5i 11. 10.2017 19:10
10.2017 19:10Ответить
Определение: нолём называется такое число, что сумма его с любым числом равна второму слагаемому. Ноль это число, означающее отсутствие, что роднит его со сброшенным флагом, но сброшенному флагу противопоставляется установленный флаг, означающий просто факт наличия, а не ноль имеет бесконечное количество вариантов, каждый из которых — конкретное количество.
Ответить
-
!ё!
taras 11.10.2017 23:37Комментарий скрыт
-
taras
!ё! 12.10.2017 10:57Ответить
Нет. Отсутствие количества — это совсем другое. А ноль — это количество. Вот есть у тебя карман и карман этот пустой. Если он пустой, то денег в нём ровно ноль. А теперь я у тебя спрашиваю: СКОЛЬКО денег у тебя в кармане. Ты же отвечаешь, что их там нет вовсе.
 Это ответ. Теперь другая ситуация. Вернулись я в прошлое и спрашиваю свою краснокожую прапрапрапрапрапрапрапрапрапрапрапрапрапрапрапрабабку: а сколько у тебя автомобилей в гараже? Она НЕ МОЖЕТ ответить, потому что само понятие «автомобиль» ещё не придумано, соответственно нет и количества автомобилей. В этом случае их не ноль, а брошен флаг их существования. Противоположность нолю — не ноль, противоположность сброшенному флагу — установленный флаг. Но не ноль — это и 1, и 2, и 120, и 390, и 8. И каждое значение отмечается своим числом. А установленный флаг — это просто есть. Вот есть и всё без указания количества. То есть если автомобиль изобретён, то в патенте количества автомобилей нет всё равно, но есть информация, что автомобили теперь есть. Просто есть. Как понятие. Без указания количества. Не значимость — это вообще третье. Вот есть у тебя термометр. А у него какие то показания. От чего они зависят? От температуры воздуха. А ещё? Как ни странно, от атмосферного давления: под действием атмосферного давления и резервуар с подкрашенным спиртом, и капилляр, по которому он течёт мимо шкалы, сжимаются, а объём спирта остаётся прежним, высота столба увеличивается.
Это ответ. Теперь другая ситуация. Вернулись я в прошлое и спрашиваю свою краснокожую прапрапрапрапрапрапрапрапрапрапрапрапрапрапрапрабабку: а сколько у тебя автомобилей в гараже? Она НЕ МОЖЕТ ответить, потому что само понятие «автомобиль» ещё не придумано, соответственно нет и количества автомобилей. В этом случае их не ноль, а брошен флаг их существования. Противоположность нолю — не ноль, противоположность сброшенному флагу — установленный флаг. Но не ноль — это и 1, и 2, и 120, и 390, и 8. И каждое значение отмечается своим числом. А установленный флаг — это просто есть. Вот есть и всё без указания количества. То есть если автомобиль изобретён, то в патенте количества автомобилей нет всё равно, но есть информация, что автомобили теперь есть. Просто есть. Как понятие. Без указания количества. Не значимость — это вообще третье. Вот есть у тебя термометр. А у него какие то показания. От чего они зависят? От температуры воздуха. А ещё? Как ни странно, от атмосферного давления: под действием атмосферного давления и резервуар с подкрашенным спиртом, и капилляр, по которому он течёт мимо шкалы, сжимаются, а объём спирта остаётся прежним, высота столба увеличивается. На сколько? На незаметную величину. И изменения показаний термометра под действием меняющегося атмосферного давления полностью маскируются изменениями показаний того же термометра под действием меняющейся температуре воздуха. Вот атмосферное давление и не значимо для показаний термометра. Оно не ноль, а как раз огромно. На одну и ту же поверхность атмосферное давление действует с силой, эквивалентной весу полуторатонной гири, а температура воздуха — с силой, меньшей веса граммовой гири. Но температура значима, а давление — нет.
На сколько? На незаметную величину. И изменения показаний термометра под действием меняющегося атмосферного давления полностью маскируются изменениями показаний того же термометра под действием меняющейся температуре воздуха. Вот атмосферное давление и не значимо для показаний термометра. Оно не ноль, а как раз огромно. На одну и ту же поверхность атмосферное давление действует с силой, эквивалентной весу полуторатонной гири, а температура воздуха — с силой, меньшей веса граммовой гири. Но температура значима, а давление — нет.Ответить
-
!ё!
taras 12.10.2017 12:51Комментарий скрыт
-
taras
!ё! 15.10.2017 20:56Ответить
Нет. Именно это я и оспариваю. Сброшенный флаг обозначает отсутствие чего либо как категории. Ноль означает только фактическое отсутствие объектов, к этой самой категории относящихся, и требует для своего существования существования и категории.
 Пока автомобиль не изобретён, сброшен именно флаг существования автомобилей, при наличии патента на автомобиль он существует как понятие, но в конкретном гараже может не стоять ни одного автомобиля. Это разные классы отсутствия: пока автомобиль не изобретён, за вопрос об их количестве можно вообще в психушку угодить, а то и на костёр, если церковь зверствует, а когда категория существует, можно уже спрашивать вполне безопасно даже о фактически пустом гараже. Значимость — это вообще другое. Значимость — это когда количество важно, а не значимость — это на количество плевать. Атмосфера, у самого её бак с жидким гелием, у дна пластина, в ней в виде резервуара и канала жидкостного термометра, в ней жидкий гелий и некоторое количество паров гелия, площадь пластины два квадратных метра. С какой силой на неё давят гидростатиченское и атмосферное давления? Весом нескольких десятков тонн. А с какой силой по той же пластине бьют молекулы за счёт только теплового движения при температуре 3 Кельвина? Много меньше.
Пока автомобиль не изобретён, сброшен именно флаг существования автомобилей, при наличии патента на автомобиль он существует как понятие, но в конкретном гараже может не стоять ни одного автомобиля. Это разные классы отсутствия: пока автомобиль не изобретён, за вопрос об их количестве можно вообще в психушку угодить, а то и на костёр, если церковь зверствует, а когда категория существует, можно уже спрашивать вполне безопасно даже о фактически пустом гараже. Значимость — это вообще другое. Значимость — это когда количество важно, а не значимость — это на количество плевать. Атмосфера, у самого её бак с жидким гелием, у дна пластина, в ней в виде резервуара и канала жидкостного термометра, в ней жидкий гелий и некоторое количество паров гелия, площадь пластины два квадратных метра. С какой силой на неё давят гидростатиченское и атмосферное давления? Весом нескольких десятков тонн. А с какой силой по той же пластине бьют молекулы за счёт только теплового движения при температуре 3 Кельвина? Много меньше. Но эти удары значимы, а давление нет. Почитай сначала теорию регрессионного анализа, а потом пиши, что такое значимость и как она соотносится с существованием. Самого количества может не быть, только если чего то нет как категории. Но тогда вопрос о значимости вообще не стоит.
Но эти удары значимы, а давление нет. Почитай сначала теорию регрессионного анализа, а потом пиши, что такое значимость и как она соотносится с существованием. Самого количества может не быть, только если чего то нет как категории. Но тогда вопрос о значимости вообще не стоит.Ответить
-
!ё!
taras 16.10.2017 16:56Комментарий скрыт
-
taras
!ё! 17.10.2017 11:53Ответить
«Категория — это всего лишь обобщающая систематизация (перечень, каталог), того, что есть.» Оно конечно так. Но вот придумал некто фотонный звездолёт, а звездолёта не построил. Это тоже обобщающая категория, в которую войдут корабли разных классов с разным отношением массы топлива к массе корабля и, соответственно, разной скоростью. Одни корабли достигнут десятой части скорости света, другие — половины, третьи на десятую отстанут.
 Одни корабли одноместны, другие возят сотни тысяч колонистов, третьи — вообще беспилотные зонды. У них и само топливо разное. На одних это протоны и антипротоны, на других — свинец и антисвинец. Категория есть, она обобщает, а самих объектов в ней нет. И даже в фантастических книгах всё это разнообразие появилось позже, а сначала был сам принцип аннигиляции чего то с чем то для получения излучения, масса которого будет достаточна для разгона корабля. То есть признак, по которому весь этот «зоопарк» снесён в одну категорию, придуман заранее, до того, как в ней появились даже конкретные образы кораблей. А спросите того фантаста, сколько таких кораблей на реальной Земле. Он скажет, что их нет и быть не может. Вот это и есть ноль. Но вопрос то понят и на него получен ответ. А теперь такой вопрос: «Сколько на Земле дерабузоторов?». Теперь не понят даже вопрос. Потому что нет даже такой категории. Ноль не состоит из элементов и добавлять их в него нельзя. Вот есть пустая полка. Раз она пустая, значит предметов на ней ноль.
Одни корабли одноместны, другие возят сотни тысяч колонистов, третьи — вообще беспилотные зонды. У них и само топливо разное. На одних это протоны и антипротоны, на других — свинец и антисвинец. Категория есть, она обобщает, а самих объектов в ней нет. И даже в фантастических книгах всё это разнообразие появилось позже, а сначала был сам принцип аннигиляции чего то с чем то для получения излучения, масса которого будет достаточна для разгона корабля. То есть признак, по которому весь этот «зоопарк» снесён в одну категорию, придуман заранее, до того, как в ней появились даже конкретные образы кораблей. А спросите того фантаста, сколько таких кораблей на реальной Земле. Он скажет, что их нет и быть не может. Вот это и есть ноль. Но вопрос то понят и на него получен ответ. А теперь такой вопрос: «Сколько на Земле дерабузоторов?». Теперь не понят даже вопрос. Потому что нет даже такой категории. Ноль не состоит из элементов и добавлять их в него нельзя. Вот есть пустая полка. Раз она пустая, значит предметов на ней ноль. Поставим на неё глобус. Теперь предметов на полке уже не ноль. Число изменилось. Теперь введём множество объектов на полке. Полка пуста? Ну тогда и множество пустое. Поставим на полку глобус. Множество больше не пустое. Но это ТОЖЕ САМОЕ МНОЖЕСТВО. Просто в него добавлен элемент. Полка то у нас осталась той же, а изменилось количество предметов на ней. В чём же разница? Если нас интересует только количество, то полка описывается числом, а пустая полка — нолём. А если нас интересует, стоит ли на полке именно глобус, лежит ли там именно калькулятор и так далее, то полка описывается множеством, а пустая полка — пустым множеством. Именно это отличает множество от числа: каждый элемент множества уникален и может быть задан вопрос о наличии именно его в множестве, число же от конкретных элементов абстрагируется полностью, с точки зрения счётчика змея не отличима не только от черепахи в том же зоопарке, но даже от бомбарды в музее, хотя бомбарда входит в множество экспонатов музея старинного оружия, а змея — в множество животных зоопарка.
Поставим на неё глобус. Теперь предметов на полке уже не ноль. Число изменилось. Теперь введём множество объектов на полке. Полка пуста? Ну тогда и множество пустое. Поставим на полку глобус. Множество больше не пустое. Но это ТОЖЕ САМОЕ МНОЖЕСТВО. Просто в него добавлен элемент. Полка то у нас осталась той же, а изменилось количество предметов на ней. В чём же разница? Если нас интересует только количество, то полка описывается числом, а пустая полка — нолём. А если нас интересует, стоит ли на полке именно глобус, лежит ли там именно калькулятор и так далее, то полка описывается множеством, а пустая полка — пустым множеством. Именно это отличает множество от числа: каждый элемент множества уникален и может быть задан вопрос о наличии именно его в множестве, число же от конкретных элементов абстрагируется полностью, с точки зрения счётчика змея не отличима не только от черепахи в том же зоопарке, но даже от бомбарды в музее, хотя бомбарда входит в множество экспонатов музея старинного оружия, а змея — в множество животных зоопарка. Эти объекты — элементы разных множеств, но при определении мощности этих множеств учитываются одинаково. И у множества только мощность выражается числом. Пустое множество отвечает на вопрос ЧТО СТОИТ на пустой полке, ноль — на вопрос СКОЛЬКО предметов стоят на пустой кнопке, а сброшенный флаг — на вопрос МОЖЕТ ЛИ БЫТЬ ПОНЯТ САМ ВОПРОС. Это разные вопросы. И ответы на них разнотипны.
Эти объекты — элементы разных множеств, но при определении мощности этих множеств учитываются одинаково. И у множества только мощность выражается числом. Пустое множество отвечает на вопрос ЧТО СТОИТ на пустой полке, ноль — на вопрос СКОЛЬКО предметов стоят на пустой кнопке, а сброшенный флаг — на вопрос МОЖЕТ ЛИ БЫТЬ ПОНЯТ САМ ВОПРОС. Это разные вопросы. И ответы на них разнотипны.Ответить
-
taras
!ё! 17.10.2017 12:14Ответить
«А сжигать на кострах — это вы умеете. Только правду не сожжёшь!Ё!» Учёные как раз на кострах горели, а не жгли.
Ответить
-
taras
!ё! 17.10.2017 12:22Ответить
«А раз чего-то нет то нет и его значимости.». Бред. Вот есть у нас вакуум и есть барометр. Что покажет барометр? Ноль. Это значит, что давление не значимо? Нет.
 Накачайте в шлюз воздух и тот же барометр покажет треть атомосферы. Так как же может быть не значимо для положения стрелки то, что давление только что не было? Ведь барометр показывал ноль ТОЛЬКО ПОТОМУ, что давления не было. Другой пример. Есть барометр и есть прожектор, яркость которого можно регулировать. Прожектор светит на барометр максимально ярко, барометр показывает 16 атмосфер. Значит ли это, что яркость света значима для положения стрелки? Нет. Уменьшите яркость. Да не в жалкие два раза, а пусть теперь прожектор притворится ручным фонариком. Стрелка с места не сдвинется. Потому что яркость в данном случае не значима.
Накачайте в шлюз воздух и тот же барометр покажет треть атомосферы. Так как же может быть не значимо для положения стрелки то, что давление только что не было? Ведь барометр показывал ноль ТОЛЬКО ПОТОМУ, что давления не было. Другой пример. Есть барометр и есть прожектор, яркость которого можно регулировать. Прожектор светит на барометр максимально ярко, барометр показывает 16 атмосфер. Значит ли это, что яркость света значима для положения стрелки? Нет. Уменьшите яркость. Да не в жалкие два раза, а пусть теперь прожектор притворится ручным фонариком. Стрелка с места не сдвинется. Потому что яркость в данном случае не значима.Ответить
-
taras
!ё! 17.10.2017 12:27Ответить
«Нуль и в пустых разрядах сам по себе не имеет значения. » Бред. Ноль имеет значение, так как отмечает, в каких же на самом деле разрядах стоят остальные цифры. А в другом случае не значащ.
 Значимость означает, что что то чему то равно ИМЕННО ПОТОМУ, что вот это значимое именно такое. И значимость цифры означает, что число чему то равно ИМЕННО ПОТОМУ, что цифра именно такая. То есть если величина значима, то её изменение означает изменение другой величины и если цифра значаща, то её изменение означает изменение самого числа. Вне контекста изменения нет ни понятия значимости, ни понятия значимости цифры. Кстати, обратите внимание на различие в прилагательных: значимая величина, но значащая цифра и ни когда наоборот.
Значимость означает, что что то чему то равно ИМЕННО ПОТОМУ, что вот это значимое именно такое. И значимость цифры означает, что число чему то равно ИМЕННО ПОТОМУ, что цифра именно такая. То есть если величина значима, то её изменение означает изменение другой величины и если цифра значаща, то её изменение означает изменение самого числа. Вне контекста изменения нет ни понятия значимости, ни понятия значимости цифры. Кстати, обратите внимание на различие в прилагательных: значимая величина, но значащая цифра и ни когда наоборот.Ответить
-
-
-
-
-
-
!ё!
Jill2zso5i 11.10.2017 23:38
Комментарий скрыт
-
taras
!ё! 12.10.2017 10:59Ответить
Ноль не обозначает отсутствие цифр, он сам — цифра. Но не только.
 Ноль — это ещё и число.
Ноль — это ещё и число.Ответить
-
!ё!
taras 12.10.2017 13:35Комментарий скрыт
-
taras
!ё! 15.10.2017 20:28Ответить
Нет. Просто «значимость» и «значимость цифры» — совершенно разные термины. Вы же, когда в такси садитесь, не говорите вместо «Улица Кирова 73»: «ли рова се ри»? Вот и здесь не глотайте слова. Кроме того, не путайте значение числа и знаки, которыми оно записано. Ноль бывает не значим только в ипостаси цифры, ещё бывает не значима сама величина при любом значении. Но вне ЗАПИСИ числа не может быть не значим только ноль.
Ответить
-
-
taras
!ё! 15.10.2017 20:36Ответить
Да и цифра 0 бывает значима.
 232 и 00232 — одно и то де число, но 232, 20032, 23002, 23200, 20302, 20320 и 23020 — разные числа. А различаются только нолями. И даже ноль слева бывает значим: 0,2 и 0,002 — разные числа. А справа бывает не значим: 0,200 и 0,2 — одно и то же число.
232 и 00232 — одно и то де число, но 232, 20032, 23002, 23200, 20302, 20320 и 23020 — разные числа. А различаются только нолями. И даже ноль слева бывает значим: 0,2 и 0,002 — разные числа. А справа бывает не значим: 0,200 и 0,2 — одно и то же число.Ответить
-
yu_nick
02.01.2012 00:04
Ответить
я думаю что этот вопрос мы сами себе придумали)) теперь и мучаемся . 0 это что ? это пустота! и мы пытаемся узнать о пустоте.. ноль это ничто.. я считаю что есть только сложение .. а умножение это просто что бы не писать 5+5+5+5 а мы просто пишем 5*4 … мне кажеться это самое большое заблуждение что умножать вообщще можно , можно только прибавлять . а вот за это упрощение и и получили такой парадокс х/0= ? а может его и нет)) если с моей точки зрение он ничего не играет роли..если убрать нах умножение то и пропадет деление. . и останеться отнимание и прибавление
. и останеться отнимание и прибавление
Ксати это и не так уж и детский вопрос..
З,Ы я подхоил с точки образного мышления)
Ответить
-
taras
yu_nick 11.10.2017 19:12Ответить
Попробуйте через сложение выразить pi*exp(1). Функция exp — это экспонента, то есть степень основания натурального логарифма. Или попробуйте через сложение не аргументов, а самих логарифмов выразить ln(2)*ln(10).
Ответить
-
!ё!
taras 11.10.2017 22:14Комментарий скрыт
-
taras
!ё! 15.10.2017 21:09Ответить
» А для того, чтобы вернуться к физике, т.е. к действительности рекомендую вам ознакомиться двумя материалами: http://alaa.ucoz.ru/publ/fizika_i_matematika/moi_stati/fizic
heskie_oshibki_arifmeticheskikh_operacij_operacii_s_nuljom/2 -1-0-51 и http://alaa.  ucoz.ru/publ/fizika_i_matematika/moi_stati/fizic
ucoz.ru/publ/fizika_i_matematika/moi_stati/fizicheskie_oshibki_differencirovanija_chast_i/2-1-0-45.» Не случайно на укозе. Жёлтая «пресса» называется жёлтой по цвету бумаги, так как этим «газетам» не хватает денег на покупку более дорогой белой бумаги из-за того, что они не интересны ни одному серьёзному человеку, а шпаны нет денег на покупку дорогих изданий. Укоз же даже до неё не «дорос». Математика одна и та же, хоть ты стержни в активной зоне реактора считай, хоть овец. Ни каких таких физических основ она не имеет. Физическим бывает смысл отдельных математических понятий. Например, производная — это скорость. А в других случаях это расход жидкости. Или электрический ток. Или вообще артангенс уклона горы. А вторая производная — это ускорение. Или кривизна горного склона. Или скорость изменения электрического тока. Или скорость изменения расхода жидкости. И ошибки в операциях с числами, соответственно бывают только математическими. Физические ошибки бывают в выборе модели, а значит и самих операций. 
Ответить
-
!ё!
taras 12.10.2017 20:50
Комментарий скрыт
-
taras
!ё! 15.10.2017 20:20Ответить
За операцией и»тоже сложение стоит? А за или? За исключающим или? За сдвигом? За сравнением? За переходом по адресу? Сложение вообще не обязательно реализовывать аппаратно, его отлично можно заменить логическими операциями. А наоборот не получится. А умножение обязательно, но только на основание внутреннего представления. Потому что сдвиг нельзя представить через какие бы то ни было другие операции.
Ответить
ferst
06.01.2012 14:32
Ответить
А инженеры уже давно сделали прибор, при помощи которого можно делить и умножать на ноль. Каждый из нас таким прибором регулярно пользуется по нескольку раз на день :)))http://www.webstaratel.ru/2012/01/delenie-na-nol-v-fizik
Каждый из нас таким прибором регулярно пользуется по нескольку раз на день :)))http://www.webstaratel.ru/2012/01/delenie-na-nol-v-fizik
Ответить
Gringbanderdam
07.01.2012 22:54
Ответить
Основы логики: 0→0=1 (Из нуля следует ноль. Значит это может быть равно чему угодно, т.е 1)
Ответить
JunX
27.12.2012 09:40
Ответить
«Компутер — он ить не только «складывает» — он еще и СДВИГАЕТ»
Быть может зная больше о программирование на низших языках, вы бы знали что действительно все основные математические операции представлены через сложение, есть даже формулы выражения всех операций через сложение. Достаточно почитать учебник высшей математики 1 курса, там это всё есть.
«То есть 5 – 3 — это просто сокращенная запись уравнения: x + 3 = 5»
Нет. Также читайте учебники — вычитание это сложение с отрицательным числом, т.е. 5 — 3, это 5 + (-3), опять же в школе рассказывают в начальных классах, только мы не обращаем внимания. Да и ещё вы переносили цифры, составляли уравнение, вводили какую-то переменную «x» (которой кстати нет в первоначальной записи 5 — 3) — это лишние действия.
«То есть это задание найти такое число, которое при умножении на 0 даст 5»
«Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует»
Быть может, вы имели ввиду целое число, так как я знаю — это дробь (5/0), ведь и правда (5/0) * 0 = 5.
«Зато на лекциях по математике в университете вас в первую очередь будут учить именно этому.»
В первую очередь вам скажут забудьте всё что учили в школе. И затем расскажут как и с 0 обходится и что корень из 2 это рациональное число и прочие изыски. Автору полезно было бы ознакомится хотя бы с началами мат. анализа, прежде чем такие статьи писать.
анализа, прежде чем такие статьи писать.
Ответить
-
taras
JunX 11.10.2017 19:18Ответить
Бред. Во-первых НЕ БЫВАЕТ низших и высших языков. Есть языки разных уровней и парадигм, но уровни не превосходны. Например, язык ассемблера — язык низкого уровня. Низкого, а не низшего. Тем более не низший. А во-вторых все операции реализуются через and, or, xor и сдвиг. Сдвиг — это умножение в чистом виде, а сложение как раз реализовано через or, xor и and.
Ответить
Артем12345
26.06.2013 14:53
Ответить
Люди, у меня такое мнение на этот вопрос. Математика описывает жизненные ситуации, помогает людям решать реальные задачи. Все операции, определения и т д нужны для реальных задач. Даже мнимые числа имеют применение. А вот деление на нуль не пригодится ни в одной(!) жизненной ситуации. По-этому деление на ноль не имеет смысла.
А вот деление на нуль не пригодится ни в одной(!) жизненной ситуации. По-этому деление на ноль не имеет смысла.
Ответить
-
NekoNeko
Артем12345 06.08.2013 15:30Ответить
>Математика описывает жизненные ситуации, помогает людям решать реальные задачи. Все операции, определения и т д нужны для реальных задач.
Нет.
>Даже мнимые числа имеют применение.
Да.
>А вот деление на нуль не пригодится ни в одной(!) жизненной ситуации.
Нет.
>По-этому деление на ноль не имеет смысла.
Нет.Ответить
-
taras
Артем12345 11.10.2017 19:19Ответить
Ну так не имеет, что на дроби 0/0 построена четверть теории пределов и всё дифференциальное исчисление.
Ответить
-
!ё!
taras 12. 10.2017 20:57
10.2017 20:57Комментарий скрыт
-
taras
!ё! 15.10.2017 20:14Ответить
Дифференцирование — это поиск производной. А производная есть предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нолю. Но ведь в этом случае приращение гладкой непрерывной функции тоже стремится к нолю. И получается, что всё дифференциальное исчисление — это поиск значения именно дроби 0/0. Пределы бывают чего угодно. В том числе, отношения двух величин. В том числе, стремящихся к нолю. И опять получается дробь 0/0. Просто пределы этой дробью не исчерпываются.
Ответить
-
-
taras
!ё! 15.10.2017 20:15Ответить
Не зная даже что такое ноль, берёшься оценивать мою диссертацию и даже науку в целом.
 Капец.
Капец.Ответить
landlawyer
10.12.2013 16:55
Ответить
Кто может объяснить, почему когда я 5 делю на 0,000000000000001 калькулятор с ошибкой выдает число 1,004504505255465 ? то, что ошибка — понятно — все число не влезло, но если потом его умножить на 0,00…01 то получится только это самое 0,00…01, даже близко к 5 нет. НО такого правила нет, что на 0,00…01 нельзя делить, значит все-равно должно после деления более-менее разумно число получаться, которое если умножить на делитель, должно результировать примерно то же самое делимое, что было в начале (5). ПРостите за такой язык, я не математик, просто интересно стало.
Ответить
-
Ди Ради
landlawyer 06.08.2014 03:47Ответить
Не влезает в разряд.

Будет 5 и куча нулей.
Но калькулятор вычисляет по-другому. Из-за архитектуры микрухи.Делить 5 на 0,000…001 это тоже самое, что умножить 5 на 10000…0000, т.е. будет в итоге 50000…000000000
По основному вопросу статьи:
Ноль не число. Поэтому делить на ноль нельзя, точно так же, как делить на стулья. Ноль это пустое множество, оно не является числом. Числом может являться элемент внутри множества, но не множество.Т.е. пытаться разделить 37 на 0, это тоже самое, что пытаться разделить 37 на акведук или римского императора Нерона, ну или на зубную щетку.
Т.е. вся проблема вопроса в определениях, которыми оперируют те, кто не изучал deep матан.
Если вы поймете, что ноль не является числом, то вы поймете почему нельзя проводить составные операции с нулем в поле чисел.Ну т.е. мы тогда, грубо говоря, пытаемся разделить пчел на киев, огород и бузину.
Ответить
-
taras
landlawyer 11. 10.2017 19:20
10.2017 19:20Ответить
Он бракованный. Должен сообщить о переполнении явно и отказаться выполнять над результатом дальнейшие операции.
Ответить
SeLin
16.09.2014 18:48
Ответить
Ну во первых, при сложении (умножении, вычитании, делении) на ноль второе число должно быть — не ноль, потому что в таких примерах теряется всякое представление о несущей, в этом примере информации, т.е. информация должна составляться минимум из двух разных единиц (например двоичный код), из которой впоследствии можно составить более сложную информацию. Так что такие примеры как 0+0=0, 0-0=0, 0*0=0, 0/0=0 существовать не могут в принципе. Что же касается ДУРИ, которая описана в этой статье, могу сказать, что если ученые не нашли способ при котором деление на ноль не приводит к какому-то определенному результату, то они могли бы обратить внимание, хотя-бы, на массу логических (системных) противоречий содержащихся в этой статье.
Ответить
-
Ди Ради
SeLin 09.01.2015 23:07Ответить
Не слушайте детишки. Эти альтернативщики вам заморочат голову.
Официальный матан позволяет операции 0+0, 0-0, 0*0, 0/0.
Пустое множество плюс пустое множество = пустое множество.
То же самое с минусом и умножением.А вот с делением выйдет неопределенность, которую дальше можно раскрыть по законам теорвера.
А вот числа нельзя делить на ноль, не потому что нельзя, а потому что ноль не является числом.
То же самое как 32 нельзя разделить на банановую кожуру. Потому что банановая кожура не является числом.Ответить
-
afffr
Ди Ради 12.07.2015 17:33Ответить
Тогда почему умножать на ноль можно??? По Вашему такое уравнение: «32 * банановую кожуру» более осмыслена чем «32 / банановую кожуру?»
Ответить
-
Ди Ради
afffr 04. 01.2016 19:29
01.2016 19:29Ответить
Потому что 0 это пустое множество.
Если умножить что-то на пустое множество, то мы получим это что-то в пустом множестве, т.е. нету места там для числа. Оно пустое, содержит нисколько элементов. Поэтому если умножить на пустое множество банановую кожуру то и получим пустое множество.Вся непонятка из-за того что в школах не объясняют что такое «арабские» (индоарабские) цифры вообще. Т.е. наши современные (Еще в средние века европейцы пользовались римскими цифрами).
Так вот, наши цифры — комплексны. Т.е. имеют сложность от позиции.
Например в числе 38448 — первая восьмерка означает 8000, а последняя просто 8. А выглядят они одинаково. Просто меняется положение и порядок цифр.Так вот 0, когда он находится за другими числами или перед — например 100, 550, 20, 0,005, 0,1 — является Цифрой.
А когда он без чисел ни слева ни справа то он не является числом вообще. А обозначает пустое множество.
А обозначает пустое множество.Если пустое множество разделить на пустое множество — будет неопределенность. Т.е. 0/0 = неопределенность.
А умножая на ноль мы помещаем число которое умножаем в пустое множество (множество без элементов) и места числу не остается. В итоге на выходе мы получаем пустое множество. Вот почему 5*0 = 0.А что будет если мы разделим 5/0? А ничего не будет, т.к. в данном случае мы делим число на пустое множество без элементов. Данная операция означает «сколько в 5 содержится пустых множеств?» — бесконечное количество. Вот такой ответ.
Сам ноль был изобретен Индусами (и как цифра и как пустое множество) и конкретно благодаря ему стали возможны уравнения.
Ответить
-
afffr
Ди Ради 24.01.2016 23:22Ответить
Хорошо. 5+5+5+5+5+0=25 ; 5+5+5+5+5*0=20 все сходится! Просто при умножении на пустое множество число растворяется в пучине бездны, уходит в некуда, наплевав на закон сохранения энергии.
 А вот если прибавить пустое множество, то закон сохранения энергии сохраняется, и числа в таком пустом множестве чувствуют себя вполне нормально. 5*5*0=0 наперстники нервно курят в сторонке.
А вот если прибавить пустое множество, то закон сохранения энергии сохраняется, и числа в таком пустом множестве чувствуют себя вполне нормально. 5*5*0=0 наперстники нервно курят в сторонке.Ответить
-
-
VladNSK
Ди Ради 31.10.2016 04:10Ответить
Ди Ради написал: «Потому что 0 это пустое множество.
Ноль — такое же число, как, например, 1 или -5.23. Чтобы это понять — достаточно поглядеть на термометр за окном: там на шкале есть положительные числа, ноль и отрицательные.
Утверждать, что «ноль — не число, а пустое множество» — столь же глупо, как и утверждать, что не бывает нулевой температуры.
Ответить
-
taras
Ди Ради 11.10.2017 19:29Ответить
Бред. Ноль — это вообще не множество.
 Это число. А пустое множество — не ноль. Также как и нуль-вектор или нуль-матрица. А 0i, 0+0i, нулевой кватернион и нулевой октанион — это всё тот же ноль. То есть ноль — это особое число не одного, а шести разных типов.
Это число. А пустое множество — не ноль. Также как и нуль-вектор или нуль-матрица. А 0i, 0+0i, нулевой кватернион и нулевой октанион — это всё тот же ноль. То есть ноль — это особое число не одного, а шести разных типов.Ответить
-
-
taras
Ди Ради 11.10.2017 19:30Ответить
И НЕ ВОЗМОЖНО получить «это что то в пустом множестве», так как множество, в котором есть «это что то» уже не пусто.
Ответить
-
taras
Ди Ради 11.10.2017 19:25
Ответить
Не переживай. Скоро в школу, там объяснят.
Ответить
taras
Ди Ради 11.10.2017 19:26
Ответить
0 — тоже число. И матан не разрешает ОПЕРАЦИЮ 0/0, вычисление же предела — это нифига не деление.
Ответить
!ё!
Ди Ради 11.10.2017 22:49
Комментарий скрыт
-
taras
!ё! 15.10.2017 20:01Ответить
Задумывался. Но пустое множество — не ноль, а множество. Также, как нуль-вектор — это вектор, а нуль-матрица — это матрица. Нуль-вектор даже не единственен, он бывает разных размерностей. А нуль-матрица может иметь разное количество и столбцов, и строк. Ноль же — это разве что МОЩНОСТЬ пустого множества. Но не само множество. В программировании, кстати, в множество, даже в пустое, можно добавлять элементы (после этого оно точно не будет пустым). А в ноль элементы добавлять нельзя. Это ли не пример того, что ноль и множество — величины РАЗНЫХ ТИПОВ? «аз уж вы такой сторонник слова «нельзя» в точной науке математике, то вам не кажется, что пустоту нельзя называть множеством, » Пустоту как раз можно.
 В ОТЛИЧИЕ ОТ НОЛЯ. Ноль — это количество. Например, количество элементов пустоты. С точки зрения моей прапрапрапрапрапрапрапрапрапрапрапрапрапрапрапрабабки пустой мешок и ноль (если ей объяснить, что такое ноль) — одно и то же. Но для меня пустой мешок — это только контейнер, описываемый нолём. И только в случае, когда каждый отдельный предмет в мешке не имеет индивидуального значения. А если имеет, то мешок описывается множеством и ноль к нему уже относится косвенно, даже если он пустой.
В ОТЛИЧИЕ ОТ НОЛЯ. Ноль — это количество. Например, количество элементов пустоты. С точки зрения моей прапрапрапрапрапрапрапрапрапрапрапрапрапрапрапрабабки пустой мешок и ноль (если ей объяснить, что такое ноль) — одно и то же. Но для меня пустой мешок — это только контейнер, описываемый нолём. И только в случае, когда каждый отдельный предмет в мешке не имеет индивидуального значения. А если имеет, то мешок описывается множеством и ноль к нему уже относится косвенно, даже если он пустой.Ответить
taras
SeLin 11.10.2017 19:22
Ответить
НЕ БЫВАЕТ несущей информации. Несущими бывают стены, балки, частоты. Но не информация.
Ответить
taras
SeLin 11.10.2017 19:24
Ответить
«теряется всякое представление о несущей, в этом примере информации, т. е. информация должна составляться минимум из двух разных единиц (например двоичный код), из которой впоследствии можно составить более сложную информацию. Так что такие примеры как 0+0=0, 0-0=0, 0*0=0, 0/0=0 существовать не могут в принципе.» Не путай систему кодирования и отдельно взятое утверждение.
е. информация должна составляться минимум из двух разных единиц (например двоичный код), из которой впоследствии можно составить более сложную информацию. Так что такие примеры как 0+0=0, 0-0=0, 0*0=0, 0/0=0 существовать не могут в принципе.» Не путай систему кодирования и отдельно взятое утверждение.
Ответить
basil_vi
03.02.2015 19:27
Ответить
Мне кажется, что в природе частица (атом или ещё что-то) либо есть, либо частицы нет – абсолютный ноль как отсутствие. Другого ноля в природе нет.
Математика – произведение рук человеческих, модель природы для облегчения жизни человека. Ноль в математике не значит «отсутствие», как в природе. Это недоработка математиков, неточность модели. На этом дефекте модель (математику) заклинивает.
Я уже много лет веду всевозможные расчёты для практических целей (сметы, режимная наладка, тепловые и прочностные расчёты и прочее) и сделал себе пользовательскую функцию, типа: «если делитель=0, то принять результат за 0».
Много лет считаю, ставлю при отсутствии данных ноль, и все расчёты проскакивают на «ура».
Для практических расчётов этот метод очень даже годится.
Ответить
-
afffr
basil_vi 12.07.2015 18:07Ответить
Полностью согласен, нынешняя модель математики далека от совершенство. Уже на данном этапе развития человечества, с помощью действующей десятеричной модели исчисления не возможно вычислить правильный ответ на вполне физическое явление. К примеру, давайте вычислим за какое время спортсмен обгонит черепаху, если нам известно что спортсмен бежит со скоростью 10 км/час, черепаха со скоростью 1 км/час, и спортсмен дает фору черепахе в 10 км. Ответ будет следующий: через 1,1111….до бесконечности часов., то есть никогда, но физический это произойдет. Как можно записать правильный ответ?
х*0=0; у*0=0
следовательно х=у, но по факту х=5 а у=7. По моему противоречий нет, иначе умножение на ноль тоже бы запретили.
По моему противоречий нет, иначе умножение на ноль тоже бы запретили.Ответить
-
Kaitena
afffr 24.08.2015 14:03Ответить
Судя по вашим комментариям, Вы сами весьма далеки от математики
ответ 1.11111… говорит лишь о том, что момент этот произойдет спустя 1 час 6 минут и 6 секунд с небольшим (далее идет лишь определение погрешности с точностью до какого разряда будет выполнен расчет)
но это не говорит нам о том, что этого не произойдет никогда вовсе
А поскольку изначально вопрос ставился о том, через сколько мы сможем зафиксировать непосредственно факт обгона, то ответ с точностью до секунды будет выглядеть как 1 час 6 минут и 7 секунд.
И не надо тут выдумывать ничего лишнего.Ответить
-
-
taras
afffr 11.10.2017 19:37Ответить
Не переживай, скоро научишься.

Ответить
taras
basil_vi 11.10.2017 19:36
Ответить
Не путай число с флагом. Есть/нет — это флаг. А ноль — это число. И он относится не к частице, а к энергии, времени, пространству. К непрерывным сущностям, которых может быть разное количество.
Ответить
PirDuha
14.10.2015 14:58
Ответить
1. Полностью согласен с «?ё!». как можно умножая на ничто получить ничто, если умножение — это многократное сложение? 5+0+0 = 5
2. Ошибка в том, что ученые «признаю полноценными только [+] и [*]
Отрицая существование [-] и [:] отрицается закон сохранения энергии.
5-3 = 2 Тройка в данном случае не исчезает, а трансформируется в то, что уже не учитывается в рамках данного выражения. В противном случае [х+2=5]иногда не ровнялось бы [3]
В противном случае [х+2=5]иногда не ровнялось бы [3]
PS: аксиомы — способ обмана человечества
Ответить
melaikin
30.10.2016 08:22
Ответить
У меня такое впечатление, что для математиков не проблема поделить на 0, а физики давно и успешно делят). Правда, для этого приходится придумывать разные обходные пути. А это как я поделил:
https://youtu.be/_U1WP1s2EUI
Ответить
-
afffr
melaikin 04.11.2016 13:17Ответить
Вся проблема в том, что когда в качестве доказательства какой либо теории используется ошибочный аргумент (заведомо неправильный эксперимент), то и результат будет соответственный (неверный).
В Вашем примере в частности, и во всех в целом, в качестве главного аргумента в пользу запрета деления на ноль является тот факт что: «Любое число умноженное на ноль дает ноль».
 Но это-же неверно!
Но это-же неверно!Эту проблему можно решить другим путем. Можно разрешить деление на ноль, а умножение запретить, тогда получим что 5/0=0 ; 4/0=0, следовательно 0*0=(любое число) и 5*0=(умножение на ноль запрещено), следовательно умножение на ноль запрещаем, так как это ведет к противоречиям.
То-есть у нас получается, что мы запрещаем одну операцию потому что она противоречит другой операции, хотя они обе являются неправильными.
Умножение на ноль, так-же как и деление, говорит только об одном, что никакой операции не происходит. То-есть, либо в результате обеих операциях нужно выдавать ошибку, либо результат должен быть аналогичен с результатом деления или умножением на единицу.
И потом, более логично представить что при деление целого можно прийти к нулю, нежели при умножении…
Ответить
Nihil
02.06.2017 15:29
Ответить
Короче, ноль это дверь в хаос. Эту дверь открывать нельзя. Поэтому и на ноль делить нельзя
Эту дверь открывать нельзя. Поэтому и на ноль делить нельзя
Ответить
taras
11.10.2017 16:13
Ответить
«Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них. То есть мы не можем сказать, какому числу соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. » Ну так не имеет, что на этой дроби даже определение производной построено. Более того, дробь 0/0 — важная часть ВСЕЙ теории пределов.
Ответить
!ё!
12.10.2017 22:38
Комментарий скрыт
taras
17.10.2017 06:07
Ответить
Сложение и вычитание не только не стоят за остальными операциями, но даже больше того. Это ЕДИНСТВЕННЫЕ операции, которые ВСЕГДА приходится реализовывать через другие. А именно как комбинации or, xor и умножения на основание. И умножение только в младшей школе реализуется через многократное сложение одного из множителей, да ещё на некоторых арифмометрах. В остальных случаях умножение не на основание реализуется через сложение промежуточных произведений, умножение на основание и умножения одного множителя на цифру другого. В двоичной системе через сложение промежуточных произведений, умножение на основание и and. Обязательными же операциями являются: копирование данных из памяти в регистр, копирование данных из регистра в память, умножение на степень основания, сравнение, or, and, xor и переход. Только эти операции во-первых необходимы, а во-вторых действительно элементарны. Ну для перехода к следующей операции ещё приходится реализовывать инкремент. Но это та же комбинация or, xor и умножения на основание, что и сложение. Точнее это сложение с единицей. Так что переход к следующей операции как ни странно элементарным только числится на уровне логической структуры системы команд, а не на уровне физики процессов в АЛУ.
Это ЕДИНСТВЕННЫЕ операции, которые ВСЕГДА приходится реализовывать через другие. А именно как комбинации or, xor и умножения на основание. И умножение только в младшей школе реализуется через многократное сложение одного из множителей, да ещё на некоторых арифмометрах. В остальных случаях умножение не на основание реализуется через сложение промежуточных произведений, умножение на основание и умножения одного множителя на цифру другого. В двоичной системе через сложение промежуточных произведений, умножение на основание и and. Обязательными же операциями являются: копирование данных из памяти в регистр, копирование данных из регистра в память, умножение на степень основания, сравнение, or, and, xor и переход. Только эти операции во-первых необходимы, а во-вторых действительно элементарны. Ну для перехода к следующей операции ещё приходится реализовывать инкремент. Но это та же комбинация or, xor и умножения на основание, что и сложение. Точнее это сложение с единицей. Так что переход к следующей операции как ни странно элементарным только числится на уровне логической структуры системы команд, а не на уровне физики процессов в АЛУ.
Ответить
maksut-ko
22.11.2018 20:19
Ответить
Что тут за гении математики сидят? Почему вы тут обсуждаете почему нельзя делить на ноль, а не создаете с физиками машину времени и разрушаете физические законы?
Ответить
aksayskiy
19.03.2020 05:06
Ответить
А почему бы не говорить школьникам, что делить на ноль нельзя, потому что никто не знает, как это сделать? И добавлять — …тому, кто сумеет – подарят ноутбук с играми. Не исключено, это может подтолкнуть некоторых из них к математическому творчеству.
Ответить
joandavis
11.12.2020 12:58
Ответить
There are reliable criminal justice research writing services that are very popular for students in search of criminal justice paper writing services and criminal justice assignment writing services.
https://researchpapers247.com/criminal-justice-research-writ
Ответить
ferst
02.01.2021 14:02
Ответить
Делить на ноль можно, главное понимать, что всё это означает. Доказательство — тангенс прямого угла, который равен синусу прямого угла, деленному на косинус прямого угла. Получается единица, деленная на ноль.
Уже очень давно занимаюсь этим вопросом, наконец-то до меня начало доходить. Чтобы ввести в математику результат деления на ноль, многие стереотипы нужно пересмотреть. И начинать нужно с того, что ноль не является числом. Уже одно это утверждение может вызвать бурю в тихом болоте математики.
Ответить
KAAB
24.04.2021 02:46
Ответить
На самом деле, всё просто: n/0=n*∞,
где n — любое число.
Ответить
kunitza
10.06.2021 00:24
Ответить
Давайте внесем немного лирики в строгий строй арифметики.
Когда-то в детстве, глядя на звезды в ночное небо, этот черный, бесконечной глубины космос, украшенный мириадами звезд, я задавал себе вопрос, который, как сейчас догадываюсь, не может иметь единственного и точного решения: Каким образом из ничего может образоваться нечто материальное и весь наш Мир?
Чтобы не зациклиться и не расплавиться, мой детский разум, выдал тогда такое решение: пустота каким-то образом взаимодействует с другой пустотой, образуя нечто первичное материальное. И тогда понимал всю натянутость совы на глобус этого решения, но пришлось удовлетвориться тем что есть.
А вообще, если не запрещать деление на ноль, то n*0=0 <=> n=0/0
Ответить
Написать комментарий
Конспект урока по математике на тему «Деление нацело» (5 класс).
 Конспект урока по математике на тему «Деление нацело» (5 класс) Умножение на 5 конспект урока
Конспект урока по математике на тему «Деление нацело» (5 класс) Умножение на 5 конспект урока
Цели урока: решать текстовые задачи арифметическим способом, используя зависимость между скоростью, временем, расстоянием; анализировать и осмысливать текст задачи; моделировать условие с помощью схем и рисунков; переформулировать условие; строить логическую цепочку рассуждений; критически оценивать полученный ответ, осуществлять самоконтроль, проверяя ответ на соответствие условию.
Скачать:
Предварительный просмотр:
Тема урока. Решение задач на движение.
Класс: 5 «б».
Цели урока:
Обучающая: умение решать текстовые задачи арифметическим способом, используя связь между временем, скоростью и расстоянием;
Развивающие: развитие умение анализировать и осмысливать текст задачи; моделировать условие с помощью схем и рисунков; переформулировать условие; строить логическую цепочку рассуждений; критически оценивать полученный ответ, осуществлять самоконтроль, проверяя ответ на соответствие условию;
Воспитательные: воспитывать сознательное отношение к учебному труду, прививать аккуратность и трудолюбие.
Планируемые результаты:
Личностные:
способствовать формированию мотивации обучения, заинтересованности в расширении получаемых математических знаний, развитие находчивости и активности при решении задач, точно и грамотно выражать свои мысли в устной и письменной речи.
Метапредметные:
способствовать развитию умения ставить вопросы, сравнивать, делать выводы, создавать модели изучаемых объектов, видеть математическую задачу в окружающей жизни, оценивать итоговую деятельность.
Предметные:
способствовать развитию умения работать с математическим текстом, вычислять расстояние, скорость, время, готовности использовать математические знания в учебной деятельности и при решении прикладных задач.
Тип урока:
урок обобщения и систематизации знаний.
Оборудование:
УМК:
Бунимович Е.А., Дорофеев Г.В., Суворова С.Б. и др. Математика. Арифметика. Геометрия. 5 класс. Серия «Сферы» (издательство «Просвещение») – учебник, тетрадь – тренажер;
компьютер, мультимедийный проектор, экран;
карточки для самостоятельной работы, карточки с домашним заданием, наборы задач.
Формы работы:
фронтальная, парная и индивидуальная работа в сочетании с разными видами самостоятельной деятельности.
Структура урока.
1.Организационный момент.
2. Мотивация учебной деятельности учащихся.
«Считай несчастным тот день или тот час, в который ты не решил новую задачу и ничего не прибавил к своему образованию». (Я.А.Каменский)
Эти слова будут девизом нашего урока. Кто-то из вас сегодня пришел в школу пешком, кто-то добирался на автобусе или на машине. Нужно ежедневно рассчитывать время, скорость, расстояние. Вокруг нас движутся воздушные массы, сегодня скорость ветра на территории нашего региона от 4м/с до 6м/с. Каждый из вас должен уметь устанавливать связь между скоростью, временем и расстоянием.
3. Сообщение темы урока, постановка цели и задач урока.
4. Устные упражнения.
Вступительное слово Полянской Полины.
Ни костяшек, ни ручек, ни мела – устный счет
мы творим это дело только силой ума и души!
На каждом столе текст устного счета.
- Тройка лошадей пробежала в упряжке 15 км. Сколько км пробежала каждая лошадь?
- Тройка лошадей проехала за 1час 15 км. С какой скоростью ехала каждая лошадь?
- На прямолинейном участке пути каждое колесо двухколесного велосипеда проехало 5 км. Сколько км проехал велосипед?
- Из Курска до Солнцево электропоезд идет 70 минут, а обратно 1ч10мин. На какой путь он тратит больше времени?
- Скорость ветра 3м/с. Чайка летит по ветру 7м/с. С какой скоростью она будет лететь против ветра?
а) скорость-это расстояние между двумя точками,
б) скорость-это быстрая езда,
в) скорость-это расстояние, пройденное телом за единицу времени.
- Выберите правильное утверждение:
а) чтобы найти расстояние, надо скорость разделить на время,
б) чтобы найти расстояние, надо время разделить на скорость,
в) чтобы найти расстояние, надо скорость умножить на время.
В жизни очень важно уметь рассуждать, анализировать различные ситуации.
5. Решение задач.
Анализируем и рассуждаем все вместе.
Во время экскурсии в лес учеников настигла гроза. Когда сверкнула молния, учительница по своим часам стала отсчитывать вслух секунды, от момента вспышки молнии до момента, когда был услышан гром. Она насчитала 15 с. Скорость звука (грома) 330м/с. На каком расстоянии от них находилась грозовая туча?
Потом дети насчитали между последующими вспышками молнии и громом сначала 13с, потом 10с и 8с. Дайте совет детям, как поступить в этой ситуации.
Известный математик Жак Адамар говорил:
«Прежде чем решать задачу, внимательно прочитайте условие».
На каждом столе лежит текст задания. Каждый ряд выполняет одно из следующих заданий.
330*15=4950м.
330*13=4290м.
330*10=3300м.
330*8=2640м.
Какой вывод можно сделать относительно расстояния?
Как бы вы поступили в этой ситуации?
Посоветоваться всем вместе и возвращаться домой, так как грозовая туча приближается к детям.
Где бы вы не находились, всегда помните, что купить здоровья нельзя. Главная задача каждого — беречь свое здоровье.
6. Работаем с моделями.
В жизни мы должны помнить, что ум хорошо, а два лучше. Сейчас вы работаете в парах.
Тетрадь-тренажёр стр.30 №69.
Проверка выполнения заданий.
С какой скоростью должен двигаться автомобиль по улице Первомайской, где расположена наша школа?
Автомобиль должен двигаться со скоростью 40 км//ч.
Какую народную пословицу должны помнить те, кто находится за рулем?
7.
Решение олимпийской задачи.
Из одной и той же точки одновременно в противоположных направлениях выехали два фигуриста. Через 3с расстояние между ними стало 21м. Найдите скорость второго фигуриста, если скорость первого 4м/с.
В Сочи проходили 22 Олимпийские игры. Эта задача будет посвящена нашим фигуристам, которые стали призерами Олимпийских игр.
Схема к задаче. Слайд №1.
Как движутся фигуристы?
Чему равна скорость первого фигуриста?
Чему равно расстояние между фигуристами?
Что еще известно в условии задачи?
Что нужно знать, чтобы ответить на вопрос задачи?
После анализа и обсуждения плана решения ученики оформляют решение задачи в тетрадях, выбирая рациональный способ решения.
8. Физкультминутка
.
Для разминки
из-за парт поднимаемся на старт.
Физкультминутку провела Соклакова Даша.
Включить музыку.
Раз — подняться, потянуться.
Два — согнуться, разогнуться.
Три в ладошки три хлопка.
Головою три кивка.
На четыре – руки шире.
Пять – руками помахать,
Шесть – за парту тихо сесть.
9.Самостоятельная работа по двум вариантам.
Вариант №1
Два поезда отправились одновременно из одного пункта в противоположных направлениях. Скорость первого поезда 70 км/ч, скорость второго поезда 50км/ч. Какое расстояние будет между поездами через 5 часов?
Вставьте пропущенные слова, числа и знаки арифметических действий в решение задачи.
Решение
1
.
Чему равна скорость поездов?
2. Какое расстояние будет между поездами через 5 часов?
1
.
Чему равна скорость
автомобилей?
2. Через сколько часов автомобили встретятся?
Ответ:
Возьмите в руки простые карандаши: у вас взаимопроверка.
10. Работа в группах.
Решение задач различного уровня сложности. На столах находятся карточки.
Разведчик доложил командиру, что поезд, за которым он вел наблюдение, прошел мимо него за 15секунд, а мост прошел полностью за 45 секунд. Командир знал, что длина моста 450м и быстро вычислил длину и скорость поезда. Как он это сделал?
Слайд №2 подготовила Асеева Даша.
Я с собакой пошел встречать папу. Когда собака увидела папу,
она побежала к нему со скоростью 300 м/мин. Добежав до него, она сразу же побежала ко мне. Так она продолжала свой бег до нашей встречи. Какое расстояние пробежала собака, если я шел со скоростью 50 м/мин, папа 60 м/мин, а первоначальное расстояние между нами 440 м?
Слайд №3 подготовил Холодов Дима.
По плану игры «Зарница» 5 «А» занимает оборону около озера, а 5 «Б» наступает из пункта, расположенного от озера на 2км300м. Чтобы узнать намерения противника, командир 5 «А» выслал разведчиков, которые двигались со скоростью 65 м/мин. Через сколько минут разведка достигнет противника, если 5 «Б» наступает со скоростью 50м/мин?
Через сколько минут разведка достигнет противника, если 5 «Б» наступает со скоростью 50м/мин?
Слайд №4 подготовила Хлопова Настя.
Проверка решения задач 1-3 группы.
Показ слайдов.
Я хочу вам пожелать, чтобы вы каждый день решали новые задачи и приносили их в класс. Ведь « Математика – это гимнастика ума» — так сказал о нашей науки великий русский полководец А.В.Суворов.
11. Задание на дом.
Тетрадь-тренажер. № 69 (в, г) стр.31
№ 200 учебник.
Дополнительно.
Задача №1.
Поезд длиной 225 метров идет со скоростью 54 км/ч. За сколько секунд поезд пройдет мост длиной в 450 метров?
54000:3600=15м/с-скорость поезда.
450+225=675м- общее расстояние, которое будет пройдено началом локомотива.
675:15=45с.
Ответ: 45с.
Задача №2.
Петя обнаружил, что папа, уходя на работу, забыл документы, которые подготовил вечером. Петя взял документы и побежал догонять папу. Через сколько минут Петя догонит папу, если он идет со скоростью65м/мин, Петя бежит со скоростью 80м/мин и папа успел уйти от дома 90м?
Слайд подготовила Полянская Полина.
12. Рефлексия.
На уроке я работал активно/пассивно.
Своей работой на уроке я доволен/ не доволен.
Материал урока мне был понятен/ не понятен,
Полезен/бесполезен,
интересен/скучен.
13. Подведение итогов и выставление оценок.
На уроке вы были активны, хорошо решали задачи, правильно отвечали на поставленные вопросы. То, что вы узнали хорошее, не забывайте, а чего не умеете еще, тому учитесь. Так писал первый русский князь Владимир Мономах в «Поучениях детям».
Спасибо за работу на уроке.
Литература
- Математика. Арифметика. Геометрия. 5 класс: учебник для общеобразовательных учреждений. Е.А.Бунимович, Л.В.Кузнецова, С.С.Минаева и др., «Просвещение» 2013 г.
- Математика. Арифметика. Геометрия. Задачник. 5 класс: пособие для учащихся Математика. Арифметика. Геометрия. Е.А.Бунимович, Г.В.Дорофеев, С.Б.Суворова и др., «Просвещение» 2013 г.
- Тетрадь-тренажёр. 5 класс: пособие для учащихся общеобразовательных учреждений/ Е.
 А.Бунимович, Л.В.Кузнецова, С.С.Минаева и др., «Просвещение» 2013 г.
А.Бунимович, Л.В.Кузнецова, С.С.Минаева и др., «Просвещение» 2013 г.
- Математика. Арифметика. Геометрия. Тетрадь-экзаменатор. 5 класс: пособие для учащихся общеобразовательных учреждений/ Е.А.Бунимович, Л.В.Кузнецова, С.С.Минаева и др., «Просвещение» 2013 г.
- Математика. Арифметика. Геометрия. Поурочное тематическое планирование. 5 класс: пособие для учителей общеобразовательных учреждений/ Л.В.Кузнецова, С.С.Минаева, Л.О. Рослова, С.Б.Суворова и др., «Просвещение» 2013 г.
- Электронное приложение к учебнику. – М.:Просвещение,2013
- Постоева О.А./ Под ред. Чаплыгиной М.Е. Сотрудничество, сотворчество учителя и ученика — путь к учебной мотивации школьников при изучении математики. Курск. 2014.
Долгожданный дан звонок, начинается урок.
Прибавляю, отнимаю, умножаю и делю.
Математику я знаю и поэтому люблю.
Здравствуйте, ребята! Садитесь.
Посмотрите друг другу в глаза, улыбнитесь, пожелайте товарищу хорошего рабочего настроения на весь учебный день.
Я тоже желаю вам хорошего настроения
-– У нас с вами есть повод порадоваться и улыбнуться, к нам в гости пришел Дед Мороз со своими помощницами-снежинками.
На снежинках записаны числа: 3, 12, 5, 20.
– Прочитайте числа.
– Прочитайте в порядке возрастания, убывания.
– Разделите числа на два множества.
– По какому принципу разделим числа? (Делятся на 3 и не делятся на 3; делятся на 5 и не делятся на 5.)
– Назовите самое большое однозначное число.
– Это число связано с темой нашего урока. Сформулируйте тему урока.те тему урока.
Сегодня мы будем выполнять упражнения для закрепления. Какие целевые установки можно перед собой поставить, работая над закреплением пройденного материала?
Как вы думаете, какие качества характера помогут вам справиться с заданиями?
Работа над материалом урока
1)– Назовите фигуры.
– Какие это фигуры?
– Какие фигуры вы еще знаете?
– А сейчас вспомните, какую объемную фигуру вы часто встречаете зимой? Особенно во время детских зимних забав. (Шар)
(Шар)
– На что он похож? (Снежок)
– Дети играли в снежки. И вот что произошло (ответы закрыты снежками).
5 . 3 5 . 6
2 . 5 8 . 5
5 . 4 5 . 9
7 . 5 5 . 5
2)Работа по карточкам. (работа в парах).
– Представьте, что вы на катке. Взявшись за руки, вы дружно катаетесь по льду. Нужно не поскользнуться, используя знания таблицы умножения на 5, выполнить деление. Поддержите друг друга.
– Какой вывод можно сделать? (Умножение связано с делением).
Проверка работы.
– По дорожкам между сугробами выходим во двор
3) Решение задач
Сугробами засыпаны
Бугры, дворы, дорожки
Не могут пташки отыскать
Ни зёрнышка, не крошки.
И вот летают все слабее
Ворона, галка, воробей…
– Каких птиц еще мы можем встретить зимой?
– Как называют таких птиц?
– Что вы знаете о зимующих птицах?
– Как вы можете помочь птицам?
– Представьте себе, что на вашу кормушку прилетели птицы. Давайте сосчитаем, сколько их.
– Нужно составить несколько разных решений.
На кормушку прилетели
Воробьев драчливых пара.
И синичек тоже пара,
Пара сизых голубей
И две пары снегирей.
(2 + 2 + 2 + 2 + 2 = 10; 2 . 5 = 10).
– Сколько птиц прилетело на кормушку?
– Какой способ самый рациональный? Почему?
4)Физкультурная минутка для профилактики простудных заболеваний.
5)Работа в тетради №1
– Что значит найти пятую часть числа?
– Что для этого нужно сделать?
На доске числа: 12, 18, 15.
– Назовите число, в котором мы можем найти половину, треть и четверть числа; треть числа и пятую часть числа.
Физкультурная минутка
Я мороза не боюсь.
С ним я крепко подружусь
Подойдет ко мне мороз,
Тронет руки, тронет нос.
Значит надо не зевать,
Прыгать, бегать и скакать.
– Под сугробами видим задание. Выражения записаны парами:
5 . 4 6 . 2 3 . 6 4 . 3
4 . 5 2 . 6 6 . 3 3 . 5
– Можно ли утверждать, что значение выражений в каждой паре одинаковы?
– Что можно сказать о первой паре?
– А если я не смогла бы найти значения выражений. Могла бы ответить на поставленный вопрос? (Да, в выражениях одни и те же числа).
Могла бы ответить на поставленный вопрос? (Да, в выражениях одни и те же числа).
– О каком свойстве умножения идет речь? (Умножать числа можно в любом порядке).
– О каких парах можно сказать, что значения выражений одинаковы?
– Что можно сказать о четвертой паре? (Значения разные, числа разные).
6). Групповая работа.
В прямоугольнике помещена таблица
– Постарайтесь понять закономерность, на основании которой составлена таблица. Продолжите ее.
– Что нужно знать, чтобы продолжить? (Таблицу умножения).
– Дед Мороз приготовил нам сюрприз. Он принес к нам елочку, ведь скоро Новый год. Мы должны сделать ее еще более нарядной. На партах у вас кружки разного цвета. Сейчас проанализируйте свою деятельность на уроке и те, кто считает, что выполнял задания:
быстро, правильно и самостоятельно повесьте на елку красный игрушку;
кто правильно, но медленно – синюю;
кто правильно, но с помощью других – желтую.
кто быстро, но правильно – белую игрушку.
– Какая замечательная елка у нас получилась. Огромное спасибо вам за работу.
Тема урока: «Умножение и деление на 5, пятая часть числа»
Цель урока
:
создать условия для формирования навыка табличного умножения и деления
Задачи урока:
Познавательная
:
способствовать запоминанию таблицы умножения пяти, на 5, соответствующих случаев деления.
Развивающая:
способствовать развитию психических процессов (внимания, памяти,), математической речи, познавательных умений (умения рассуждать, делать выводы, анализировать, сравнивать), универсальных учебных действий (целеполагания, самоконтроля, взаимоконтроля, поиска информации)
Воспитательная:
способствовать воспитанию любви к своему краю, чувства гордости за земляков, прославивших родной край, патриотизма, пробуждению интереса к предмету..
Оборудование урока:
Слайд №1 и № 2
Магнитная и интерактивная доска
Наглядный материал и раздаточный материал.
Музыкальное сопровождение
I
.Организация класса
. (создание эмоционального настроя)
Громко прозвенел звонок, начинается урок.
Мы пришли сюда (учиться), не лениться, а (трудиться).
Работаем (старательно), слушаем (внимательно).
У нас гости. Давайте поздороваемся. Создадим хорошее, дружелюбное настроение. Улыбнитесь друг другу. У нас всё хорошо, а будет ещё лучше!
Математика пришла,
Занимай свои места. (Посадить детей)
Найди для головы полезное занятье!
Чтоб от безделья не зевать,
Полезно голову ломать!
– Как вы понимаете выражение “ломать голову”? (Стараться думать, понять что – нибудь сложное, трудное)
Чем мы сегодня будем заниматься на уроке, вы скажите сами, когда послушайте стихотворение.
Гриб помножим на сосну.
Лист помножим на весну
Тёплый ветер на зерно
Землянику на звено
Множим солнце на лучи
Всех мальчишек на мячи
Всех девчонек на хи-хи.
Всех поэтов на стихи.
2.Введение в тему:
Задание: отгадать загадки (решить) и определить тему урока, предположить задачи урока.
*У нашей кошки 5 котят и все мышей ловить хотят.
Каждый котенок поймал по 3 мышки.
Сколько поймали мышат 5 маленьких котят? (Слайд)
*Паслись на лугу 5 телят,
5овец, 5 коров, 5 ягнят.
«Я мал» — говорит пастушок, —
Сколько животных всего на лугу»?(Слайд)
Какая тема нашего урока?
Отгадайте-ка, ребятки,
Месяц в этой вот загадке.
Дни его всех дней короче,
Всех ночей длиннее ночи.
На поля и на луга
До весны легли снега.
О каком месяце говорится в этой загадке? (Декабрь)
Открыли тетради
2.Минута красивого письма
Продолжи ряд 0,4,812,..,..,..,… 40
.
50,45,40,35, 0.
(Слайд)
Взаимопроверка
3.Блиц-турнир
*
Сколько вершин у треугольников.
*Как называются числа при сложении.
*Что нужно сделать, чтобы узнать, на сколько одно число больше другого.
*Как называется результат, полученный при сложении.
*Как называется фигура, имеющая начало, но не имеющая конца.
*Какое самое большое однозначное число, двузначное.
*Как называется четырехугольник, у которого все стороны равны.
*Что такое периметр.
* Увеличь 8 на 7.
4. Беседа о зиме. Игра в снежки
Не деревья, не кусты
С неба падают цветы.
Белые, пушистые,
Только не душистые.
(Снежинки)
А сейчас давайте поиграем в снежки. Я буду одна против вас всех. Только я буду кидать один снежок, а вы мне два. Я назову число, а вы назовите два числа при умножении которых получается мое число.
27..3..7=23
46..3..5=48
(58..8)..6=56(Слайд)
6.Табличное умножение и деление.
Вычисли. Покажи ответ.
7.Чему равна 3 часть.
(Слайд)
8.Сколько яичек снесли куры?
(Слайд)
9. Распредели выражения на две группы.
Распредели выражения на две группы.
(Слайд)
Почему 3,5,7 выражения объединили в одну группу.
Найдите значения последнего выражения работая в парах.
Как мы должны работать в парах.(Работать тихо разговаривать вполголоса, при завершении работы поднять руку.)
Кому было очень трудно.
В чём затруднения.
Какая цель.
Как можно записать последнее выражение.
10.
Составление таблицы умножения числа 5.
Сегодня мы продолжаем работу с таблицей умножения. Как вы думаете, какова тема сегодняшнего урока? Какие цели поставим перед собой?
Пред тобой – пятерка братьев.
Дома все они без платьев,
А на улице зато
Нужно каждому пальто.
Эти братья и помогут нам сегодня в счете.
1) Работа с абаком, запись примеров на доске. Как с помощью этих братьев можно проиллюстрировать каждый случай умножения?
○○○○○ 5∙1=5 (поднять 1 руку)
○○○○○ 5∙2=10 (поднять 2 руки, сцепить над головой – «десяток»)
○○○○○ 5∙3=15 (поднять 3 руки – как?) уч-ся объединяются в пары
○○○○○ 5∙4=20 …
○○○○○ 5∙5=25 …
○○○○○ 5∙6=30 …
○○○○○ 5∙7=35 …
○○○○○ 5∙8=40 …
○○○○○ 5∙9=45 …
○○○○○ 5∙10=50 …
Понаблюдайте за ответами. Что вы заметили?
Что вы заметили?
7.Физминутка.
Я мороза не боюсь,
С ним я крепко подружусь.
Подойдет ко мне мороз,
Тронет руки, тронет нос.
Значит, надо не зевать…
Сколько раз ногами топнем?
Сколько раз руками хлопнем?
Мы присядем сколько раз?
Мы наклонимся сейчас.
Мы подпрыгнем ровно столько.
Ай да счет, игра и только!
8. Работа по учебнику.
№3,стр.5
№9,стр.6 (работа в парах)
№10,стр.6
9.Закрась числа, которые делятся на5
VII
.Домашняя работа.№11, стр.6,№12,стр.7
VIII
. Итог урока.
1.
— Наши знания – это наше богатство, которое мы складываем в сундучок, а когда нужно, достаем и используем. Какие знания приобрели сегодня вы? Что положили в свои сундучки?
3. – Каждый оценил свою работу. А я оценю вашу работу. Вы все сегодня молодцы! (Слайд)
Приложение № 2
Закрась числа, которые делятся на 5.
Предмет: Математика Класс: 2 Б УМК: «Планета знаний» Тип урока: Урок изучения нового материала
Цели деятельности учителя:
достижение образовательных результатов посредством технологии проблемного обучения, способствовать составлению таблицы умножения на 5; содействовать развитию умений умножать и делить на 5.
Планируемые результаты образования.
Предметные:
имеют представления
о том, как самостоятельно составить таблицу умножения на 5, соотносить взаимно обратные случаи умножения и деления чисел; умеют
умножать и делить числа на 5, выполнять вычисления в 2–3 действия, различать речевые обороты «увеличение / уменьшение на… (несколько единиц)» и «увеличить / уменьшить в… (несколько раз)» и соотносить их с математическими действиями, наблюдать за числовыми закономерностями; знают,
как решать задачи в 2 действия (увеличение / уменьшение в несколько раз, нахождение суммы, разностное сравнение).
Личностные УУД:
понимают значение знаний для человека и принимают его; сохраняют мотивацию к учебной деятельности; -формирование интереса к познанию, проявляют интерес к новому учебному материалу.
Метапредметные
регулятивные
:
целеполагание как постановка учебной задачи, учитывают ориентиры, данные учителем, при освоении учебного материала; определяют цель, адекватно воспринимают указания на ошибки и исправляют найденные ошибки;
познавательные:
постановка и формулирование проблемы,
извлекают, перерабатывают и
; формулируют ответы на вопросы учителя;анализ,синтез.
коммуникативные:
участвуют в коллективном обсуждении проблем; обмениваются мнениями, слушают друг друга, понимают позицию партнера; планируют цели и способы взаимодействия.
Мыслительные операции, необходимые на этапе проектирования:
анализ, сравнение, обобщение.
Педагогические технологии:
проблемного обучения
Оборудование
: Мультимедийный проектор, компьютер, карточки
Помогите своему ребенку развить ранние математические навыки
До того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания в ходе повседневного общения. Узнайте, какие неформальные занятия дают детям преимущество в раннем развитии математических навыков, когда они идут в школу.
Дети используют ранние математические навыки в повседневной жизни и деятельности. Это хорошая новость, так как эти навыки важны для подготовки к школе. Но ранняя математика не означает вынимание калькулятора во время игры. Еще до того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания посредством повседневного взаимодействия. Например, у Томаса две машины; Джозеф хочет одного. После того, как Томас поделится одной, он видит, что у него осталась одна машина (Bowman, Donovan, & Burns, 2001, стр. 201). Другие математические навыки вводятся через ежедневные занятия, которыми вы делитесь со своим ребенком — например, подсчет шагов, когда вы поднимаетесь или спускаетесь. Неформальные занятия, подобные этому, дают детям толчок к формальному обучению математике, которое начинается в школе.
Это хорошая новость, так как эти навыки важны для подготовки к школе. Но ранняя математика не означает вынимание калькулятора во время игры. Еще до того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания посредством повседневного взаимодействия. Например, у Томаса две машины; Джозеф хочет одного. После того, как Томас поделится одной, он видит, что у него осталась одна машина (Bowman, Donovan, & Burns, 2001, стр. 201). Другие математические навыки вводятся через ежедневные занятия, которыми вы делитесь со своим ребенком — например, подсчет шагов, когда вы поднимаетесь или спускаетесь. Неформальные занятия, подобные этому, дают детям толчок к формальному обучению математике, которое начинается в школе.
Какие знания по математике потребуются вашему ребенку позже в начальной школе? К ранним математическим концепциям и навыкам, на которых строится учебная программа по математике в первом классе, относятся: (Bowman et al., 2001, стр. 76).
- Понимание размера, формы и узоров
- Умение считать устно (сначала вперед, потом назад)
- Распознавание цифр
- Идентификация большего и меньшего количества
- Понимание однозначного соответствия (т.
 е. сопоставление наборов или знание того, в какой группе четыре, а в какой пять)
е. сопоставление наборов или знание того, в какой группе четыре, а в какой пять)
Ключевые математические навыки для школы
Более продвинутые математические навыки основаны на раннем математическом «фундаменте» — точно так же, как дом строится на прочном фундаменте. В дошкольном возрасте вы можете помочь своему ребенку начать развивать ранние математические навыки, познакомив его с такими идеями, как: (Из Diezmann & Yelland, 2000, и Fromboluti & Rinck, 1999.)
Чувство числа
Это способность точно считать — первый вперед. Затем, в школе, дети научатся считать в обратном порядке. Более сложный навык, связанный с чувством чисел, — это способность видеть отношения между числами, такие как сложение и вычитание. Бен (2 года) увидел кексы на тарелке. Он считал с папой: «Раз, два, три, четыре, пять, шесть…»
Представление
Превращение математических идей в реальность с помощью слов, изображений, символов и объектов (например, блоков). Кейси (3 года) устраивала воображаемый пикник. Он аккуратно разложил четыре пластиковых тарелки и четыре пластиковых стаканчика: «Чтобы вся наша семья могла приехать на пикник!» В его семье было четыре члена; он смог применить эту информацию к количеству выбранных им тарелок и чашек.
Кейси (3 года) устраивала воображаемый пикник. Он аккуратно разложил четыре пластиковых тарелки и четыре пластиковых стаканчика: «Чтобы вся наша семья могла приехать на пикник!» В его семье было четыре члена; он смог применить эту информацию к количеству выбранных им тарелок и чашек.
Пространственное чувство
Позже в школе дети будут называть это «геометрией». Но для малышей он знакомит с идеями формы, размера, пространства, положения, направления и движения. Азиз (28 месяцев) хихикал внизу слайда. — Что смешного? — удивилась его тетя. «Я поднялся, — сказал Азиз, — потом я спустился!»
Измерение
Технически это определение длины, высоты и веса объекта с использованием таких единиц измерения, как дюймы, футы или фунты. Измерение времени (например, в минутах) также относится к этой области навыков. Габриэлла (36 месяцев) снова и снова спрашивала свою бабушку: «Сделать печенье? Я сделаю это!» Ее бабуля показала ей, как наполнить мерный стаканчик сахаром. «Нам нужно две чашки, Габи. Наполните его один раз и положите в чашу, а затем снова наполните».
«Нам нужно две чашки, Габи. Наполните его один раз и положите в чашу, а затем снова наполните».
Оценка
Это способность сделать хорошее предположение о количестве или размере чего-либо. Маленьким детям это очень трудно сделать. Вы можете помочь им, показав им значение таких слов, как больше, меньше, больше, меньше, больше чем, меньше чем. Нолан (30 месяцев) посмотрел на два рогалика: один был обычным бубликом, другой был мини-бубликом. Его папа спросил: «Какой бы ты хотел?» Нолан указал на обычный рогалик. Его отец сказал: «Ты, должно быть, голоден! Этот бублик больше. Этот бублик меньше. Хорошо, я дам тебе большую. Скоро завтрак!»
Узоры
Узоры — это вещи — числа, формы, изображения — которые повторяются логическим образом. Шаблоны помогают детям научиться делать прогнозы, понимать, что будет дальше, устанавливать логические связи и использовать навыки рассуждения. Ава (27 месяцев) указала на луну: «Луна. Солнце идет ночь-ночь. Ее дедушка подобрал ее: «Да, маленькая Ава. Утром выходит солнце и уходит луна. Ночью солнце засыпает, а луна выходит играть. А вот Аве пора спать, прямо как солнцу.
Ее дедушка подобрал ее: «Да, маленькая Ава. Утром выходит солнце и уходит луна. Ночью солнце засыпает, а луна выходит играть. А вот Аве пора спать, прямо как солнцу.
Решение проблем
Способность обдумывать проблему, осознавать, что есть более одного пути к ответу. Это означает использование прошлых знаний и навыков логического мышления, чтобы найти ответ. Карл (15 месяцев) посмотрел на сортировщик формы — пластиковый барабан с 3 отверстиями в верхней части. Отверстия имели форму треугольника, круга и квадрата. Карл посмотрел на коренастые фигуры на полу. Он взял треугольник. Он положил его в свой месяц, а затем стукнул им об пол. Он коснулся края пальцами. Затем он попытался засунуть его в каждое из отверстий новой игрушки. Сюрприз! Он упал в треугольную дыру! Карл потянулся за другим блоком, на этот раз круглым…
Математика: часть целого
Математические навыки — это лишь часть большой сети навыков, которые дети развивают в раннем возрасте, включая языковые, физические и социальные навыки. Каждая из этих областей навыков зависит от других и влияет на них.
Каждая из этих областей навыков зависит от других и влияет на них.
Трина (18 месяцев) укладывала кубики. Она положила два квадратных блока один на другой, а затем еще один треугольный. Она обнаружила, что на вершине треугольного блока больше не будет балансировать ни один блок. Она посмотрела на своего отца и показала ему блок, который она не могла поднять, чтобы остаться на вершине, фактически говоря ему своим жестом: «Папа, мне нужна помощь, чтобы понять это». Ее отец показал ей, что, если она уберет треугольный блок и вместо него возьмет квадратный, она сможет сложить больше сверху. Затем она добавила еще два блока к своей башне, прежде чем с гордостью показать свое творение отцу: «Папа, ок! Хорошо!»
В этом обычном взаимодействии вы можете увидеть, как все области развития Трины работают вместе. Ее физические способности позволяют ей манипулировать блоками и использовать свои мыслительные способности, чтобы выполнить свой план по строительству башни. Она использует свой язык и социальные навыки, когда просит отца о помощи. Ее эффективное общение позволяет папе реагировать и оказывать ей необходимую помощь (еще больше улучшая ее социальные навыки, поскольку она считает себя важным и хорошим коммуникатором). Затем это еще больше развивает ее мыслительные способности, поскольку она узнает, как решить проблему увеличения высоты башни.
Ее эффективное общение позволяет папе реагировать и оказывать ей необходимую помощь (еще больше улучшая ее социальные навыки, поскольку она считает себя важным и хорошим коммуникатором). Затем это еще больше развивает ее мыслительные способности, поскольку она узнает, как решить проблему увеличения высоты башни.
What You Can Do
В приведенных ниже советах рассказывается о том, как вы можете помочь своему ребенку освоить ранние математические навыки, опираясь на его природное любопытство и весело проводя время вместе. (Примечание. Большинство этих советов предназначены для детей старшего возраста — в возрасте 2–3 лет. Детей младшего возраста можно знакомить с рассказами и песнями, используя повторения, рифмы и числа.)
Приготовьтесь.
Поиграйте с формовщиками. Поговорите с ребенком о каждой фигуре — посчитайте стороны, опишите цвета. Сделайте свои собственные фигуры, вырезая большие фигуры из цветной плотной бумаги. Попросите ребенка «запрыгнуть на круг» или «прыгнуть на красную фигуру».
Подсчитайте и отсортируйте.
Соберите корзину с маленькими игрушками, ракушками, камешками или пуговицами. Считайте их вместе с ребенком. Сортируйте их по размеру, цвету или тому, что они делают (т. е. все машины в одну кучу, все животные в другую).
Позвоните.
Вместе с 3-летним ребенком начните учить его адресу и номеру телефона вашего дома. Поговорите с ребенком о том, что у каждого дома есть номер, и что их дом или квартира является одним из ряда, каждый со своим номером.
Какой размер?
Обратите внимание на размеры предметов в окружающем вас мире: этот розовый бумажник самый большой. Синий бумажник самый маленький. Попросите ребенка подумать о своем размере относительно других предметов («Ты помещаешься под столом? Под стулом?»).
Готовь!
Даже маленькие дети могут помочь наполнить, перемешать и налить. Благодаря этим занятиям дети совершенно естественно учатся считать, измерять, складывать и оценивать.
Проваливай.

Прогулка дает детям много возможностей сравнить (какой камень больше?), оценить (сколько желудей мы нашли?), отметить сходства и различия (есть ли у утки мех, как у кролика?) и классифицировать (см. если вы можете найти несколько красных листьев). Вы также можете говорить о размере (делая большие и маленькие шаги), оценивать расстояние (парк находится близко к нашему дому или далеко?) и практиковаться в счете (давайте посчитаем, сколько шагов, пока мы не дойдем до угла).
Время изображения.
Используйте песочные часы, секундомер или таймер для выполнения коротких (1–3 минут) занятий. Это помогает детям развить чувство времени и понять, что некоторые вещи занимают больше времени, чем другие.
Придайте форму.
Укажите на различные формы и цвета, которые вы видите в течение дня. Во время прогулки вы можете увидеть желтый знак в форме треугольника. Внутри магазина вы можете увидеть прямоугольную вывеску красного цвета.
Прочитайте и спойте свои номера.

Пойте песни, которые рифмуются, повторяются или содержат числа. Песни укрепляют шаблоны (что также является математическим навыком). Они также являются интересным способом практиковать язык и развивать социальные навыки, такие как сотрудничество.
Начните сегодня.
Используйте календарь, чтобы говорить о дате, дне недели и погоде. Календари укрепляют счет, последовательности и закономерности. Развивайте навыки логического мышления, рассказывая о холодной погоде и спрашивая ребенка: что мы носим, когда холодно? Это побуждает вашего ребенка установить связь между холодной погодой и теплой одеждой.
Передайте это всем.
Попросите вашего ребенка помочь в раздаче таких предметов, как закуски, или в раскладывании салфеток на обеденном столе. Помогите ему дать по одному крекеру каждому ребенку. Это помогает детям понять переписку один на один. Когда вы раздаете предметы, подчеркивайте концепцию числа: «Один для тебя, один для меня, один для папы». Или: «Обуваемся: раз, два».
Или: «Обуваемся: раз, два».
Большие кубики.
Дайте ребенку возможность поиграть с деревянными кубиками, пластмассовыми блоками, пустыми коробками, пакетами из-под молока и т. д. Складывание этих игрушек и манипулирование ими помогает детям узнать о формах и взаимосвязях между ними (например, два треугольника составляют квадрат). Скворечники и чашки для детей младшего возраста помогают им понять взаимосвязь между объектами разного размера.
Туннельное время.
Откройте большую картонную коробку с каждой стороны, чтобы превратить ее в туннель. Это помогает детям понять, где находится их тело в пространстве и по отношению к другим объектам.
Длинная и короткая.
Отрежьте несколько (3–5) кусочков ленты, пряжи или бумаги разной длины. Говорите о таких идеях, как длинные и короткие. Вместе с ребенком расположите их в порядке от самого длинного к самому короткому.
Учитесь на ощупь.
Вырежьте фигуры — круг, квадрат, треугольник — из прочного картона. Пусть ваш ребенок коснется фигуры с открытыми глазами, а затем с закрытыми.
Пусть ваш ребенок коснется фигуры с открытыми глазами, а затем с закрытыми.
Игра по шаблону.
Развлекайтесь с узорами, предлагая детям раскладывать сухие макароны, крупные бусины, разные виды сухих хлопьев или кусочки бумаги с разными узорами или рисунками. Внимательно следите за своим ребенком во время этого занятия, чтобы предотвратить удушье, и уберите все предметы, когда закончите.
Обучение стирке.
Превратите работу по дому в удовольствие. Пока вы сортируете белье, попросите ребенка сделать стопку из рубашек и стопку из носков. Спросите его, какая стопка больше (оценка). Вместе посчитайте, сколько рубашек. Посмотрим, сможет ли он сделать пары носков. Можете ли вы взять два носка и положить их в отдельную стопку? (Не волнуйтесь, если они не совпадают! Это упражнение больше связано со счетом, чем с сопоставлением.)
Математика на игровой площадке.
Пока ваш ребенок играет, сравнивайте его по росту (высокий/низкий), положению (больше/меньше) или размеру (большой/маленький).
Платье для успехов в математике.
Попросите ребенка выбрать рубашку на день. Спросите: Какого цвета ваша рубашка? Да, желтый. Можете ли вы найти что-нибудь в своей комнате, что тоже желтое? Когда вашему ребенку исполнится три года и больше, обратите внимание на узоры в его одежде — полоски, цвета, формы или рисунки: Я вижу узор на вашей рубашке. Есть полосы, которые идут красный, синий, красный, синий. Или: Твоя рубашка покрыта пони — большой пони рядом с маленьким пони, по всей твоей рубашке!
Графические игры.
Когда вашему ребенку исполнится три года и больше, сделайте диаграмму, на которую ваш ребенок может приклеивать стикер каждый раз, когда идет дождь или каждый раз, когда солнечно. В конце недели вы можете вместе оценить, в какой колонке больше или меньше наклеек, и сосчитать, сколько их, чтобы быть уверенным.
Ссылки
Боуман, Б.Т., Донован, М.С., и Бернс, М.С., (ред.). (2001). Стремление учиться: обучение наших дошкольников. Вашингтон, округ Колумбия: Национальная академия наук.
Вашингтон, округ Колумбия: Национальная академия наук.
Diezmann, C., & Yelland, NJ (2000). Развитие математической грамотности в раннем детстве. В Йелланде, штат Нью-Джерси (ред.), Содействие осмысленному обучению: инновации в обучении специалистов дошкольного возраста. (стр. 47–58). Вашингтон, округ Колумбия: Национальная ассоциация образования детей младшего возраста.
Фромболути, К.С., и Ринк, Н. (июнь 1999 г.). Раннее детство: с чего начинается обучение. Министерство образования США, Управление образовательных исследований и усовершенствований, Национальный институт развития и образования детей младшего возраста. Получено 11 мая 2018 г. с https://www2.ed.gov/pubs/EarlyMath/title.html 9.0003
Как литература может улучшить математику и естествознание в начальной школе
Образовательный фонд Джорджа Лукаса
Edutopia
Edutopia
Поиск
Интегрированные истории и стихи для повышения понимания математики учащимися
9000 давая им дополнительную практику чтения.
Тиффани Перри
10 января 2022 г.
SDI Productions / iStock
Многие из моих учеников удивляются тому, как сильно я люблю читать. Я слышу: «Но вы учитель математики и естественных наук!» и «Почему бы вам просто не научить читать?» Я всегда объясняю, что того, как мы делим предметы в школе, в реальном мире не существует. В повседневной жизни мы не делим свое время на короткие блоки, чтобы сосредоточиться на одном наборе навыков, так почему же мы делаем это в школе? Вот три способа включить чтение в уроки математики и естествознания.
Чтение по учебной программе
1. Читательский театр: Когда мой класс приближается к концу нашего раздела человеческого тела в науке, мы показываем читательский театр под названием «Я самый важный: сценарий о системах человеческого организма». , Эми Боуден. Я надеваю импровизированную судейскую мантию, раздаю сценарии, а мои ученики разыгрывают части систем человеческого организма, каждый доказывая, что они самые важные.
Учащиеся не только повторяют то, что они узнали о функциях систем человеческого организма, но и тренируют беглость речи и понимание. Это вдохновляет многих студентов выбирать читательский театр для представления проектов. Они пишут целые сценарии для своих одноклассников, чтобы они могли их исполнить, и с энтузиазмом включают других в то, что они узнали. Этот энтузиазм помогает им естественным образом углубляться в темы, которые мы изучаем.
2. Поэзия: Каждый год я начинаю свой модуль Солнечной системы со стихотворения «Одинокая планета размышляет» Джона П. Кертина. Проанализировав его, мы начинаем обсуждать планеты и галактики. Я обнаружил, что когда мои ученики начинают с поэтического анализа, это помогает им войти в свободное пространство, способствующее обсуждению абстрактных понятий. Они более охотно задают большие вопросы по теме, которая, естественно, им интересна.
На протяжении этого раздела учащиеся пишут стихи, чтобы описать характеристики планет и продемонстрировать свои знания, используя описательные образы. Помимо абстрактных понятий, моим ученикам нравится использовать поэзию для понимания циклов, которые мы изучаем в науке. Учащиеся пишут стихи, творчески описывая этапы процесса. Поэзия особенно хорошо работает в старших классах начальной школы.
Помимо абстрактных понятий, моим ученикам нравится использовать поэзию для понимания циклов, которые мы изучаем в науке. Учащиеся пишут стихи, творчески описывая этапы процесса. Поэзия особенно хорошо работает в старших классах начальной школы.
3. Чтение вслух и рассказывание историй: Многие ученики приходят в наши математические классы, нервничая из-за того, что занимаются математикой. Используя чтение вслух и рассказывание историй, мы можем не только стимулировать у учащихся установку на рост, но и помочь им разобраться в проблемах. Одна книга, которую я люблю читать вслух, — это « Девушка, которая никогда не делала ошибок » Марка Петта и Гэри Рубинштейна. Напоминание ученикам (особенно моим одаренным ученикам) о том, что ошибки являются важной частью процесса обучения, может помочь им чувствовать себя более комфортно, рискуя в математике.
Когда учащиеся борются с определенной концепцией, мне нравится превращать ее в рассказ. Мои ученики добиваются успеха, когда могут обосновать абстрактные понятия в реальности. Будь то создание историй о моих учениках и обмен ими или просьба придумать сценарии, в которых мы могли бы использовать определенный навык, мы можем расти как ученики и одновременно проявлять творческий потенциал.
Будь то создание историй о моих учениках и обмен ими или просьба придумать сценарии, в которых мы могли бы использовать определенный навык, мы можем расти как ученики и одновременно проявлять творческий потенциал.
Например, учащимся может быть трудно понять деление и дроби. Мы можем придумать историю о том, как наш класс заказывает пиццу на обед. Если в классе 20 учеников, и у нас есть три пиццы, каждая из которых разрезана на восемь кусочков, и нам не нужны остатки, как нам разделить пиццу? Какую часть целой пиццы получает каждый? Когда это возможно, мы создаем истории о нашем классе или конкретных учениках и используем свои математические способности для решения задач в общих ситуациях.
Мне также нравится читать студентам длинные романы, когда я могу связать их с темой или проектом. Когда мои ученики изучают дроби, мне всегда нравится включать романы, в которых дети пекут или готовят еду (серия «Все четыре звезды» Тары Дайрман и « со стола Зои Вашингтон » Джейны Маркс — две из моих любимых книг). . Помимо прослушивания истории, учащиеся могут создать кулинарную книгу для класса или выполнить проект.
. Помимо прослушивания истории, учащиеся могут создать кулинарную книгу для класса или выполнить проект.
Например, в Со стола Зои Вашингтон , Зои пробует несколько рецептов кексов и корректирует количество каждого ингредиента, который она использует. Она пробует каждую партию, чтобы определить, какая из них лучше. Воспроизводя это в классе, учащиеся не только узнают больше об использовании дробей в реальной жизни, но и изучают химические изменения.
Литература отлично подходит и для занятий по естественным наукам. В науке я использую ресурс «Повседневные тайны науки» Ричарда Коника-Морана. Каждый урок в этой серии начинается с рассказа и включает в себя исследовательское задание, которое можно использовать на уроках естественных наук. Книга также включает способы адаптации уроков для разных учащихся.
Студенты постоянно спрашивают: «Зачем нам это знать?» и на этот вопрос можно легко ответить, если мы сможем показать, как то, что мы делаем в классе, связано с реальным миром. Некоторые учителя математики и естественных наук (по вполне понятным причинам) опасаются обучать чтению. Тем не менее, некоторые школы переходят на учебную программу по чтению, которая больше фокусируется на формировании базовых знаний, чем на явном изолированном обучении стратегиям чтения. Когда мы используем разные тексты по математике и естественным наукам, понимание прочитанного нашими учащимися улучшится просто благодаря практике.
Некоторые учителя математики и естественных наук (по вполне понятным причинам) опасаются обучать чтению. Тем не менее, некоторые школы переходят на учебную программу по чтению, которая больше фокусируется на формировании базовых знаний, чем на явном изолированном обучении стратегиям чтения. Когда мы используем разные тексты по математике и естественным наукам, понимание прочитанного нашими учащимися улучшится просто благодаря практике.
Filed Under
- Integrated Studies
- Literacy
- Math
- Science
- 3-5 Upper Elementary
Jigsaw | Классные стратегии | Reading Rockets
Jigsaw — это стратегия совместного обучения, которая позволяет каждому учащемуся «домашней» группы специализироваться в одном аспекте темы (например, одна группа изучает места обитания тропических лесных животных, другая группа изучает хищников тропических лесных животных). Студенты встречаются с членами других групп, которым назначен тот же аспект, и после освоения материала возвращаются в «домашнюю» группу и преподают материал членам своей группы. При этой стратегии каждый учащийся в «домашней» группе служит частью головоломки по теме, и когда они работают вместе как единое целое, они создают полную головоломку.
Студенты встречаются с членами других групп, которым назначен тот же аспект, и после освоения материала возвращаются в «домашнюю» группу и преподают материал членам своей группы. При этой стратегии каждый учащийся в «домашней» группе служит частью головоломки по теме, и когда они работают вместе как единое целое, они создают полную головоломку.
| Когда использовать: | Прежде чем читать | Во время чтения | После прочтения |
| Как использовать: | Индивидуально | С небольшими группами | Установка для всего класса |
Другие стратегии понимания
Зачем использовать головоломку?
- Это помогает улучшить понимание.
- Поощряет совместное обучение учащихся.
- Это помогает улучшить навыки слушания, общения и решения проблем.
Как пользоваться головоломкой
- Представьте стратегию и тему для изучения.

- Назначьте каждого учащегося в «домашнюю группу» из 3–5 учащихся, обладающих различными способностями к чтению.
- Определите набор вариантов чтения и назначьте один вариант каждому учащемуся.
- Создайте «экспертные группы», состоящие из учащихся «домашних групп», которые будут читать один и тот же выбор.
- Дайте всем учащимся основу для управления своим временем на различные части задачи-головоломки.
- Задайте ключевые вопросы, чтобы помочь «экспертным группам» собрать информацию в своей конкретной области.
- Предоставление материалов и ресурсов, необходимых всем учащимся, чтобы они могли изучить свои темы и стать «экспертами».
Примечание: Важно, чтобы назначенный материал для чтения был на соответствующем уровне обучения (точность чтения 90–95%).
- Обсудите правила повторного собрания в «домашних группах» и дайте рекомендации, когда каждый «эксперт» сообщает полученную информацию.
- Подготовьте сводную диаграмму или графический органайзер для каждой «домашней группы» в качестве руководства для составления информационного отчета экспертов.

- Напомните учащимся, что члены «домашней группы» несут ответственность за изучение всего контента друг у друга.
Смотреть: Jigsaw
Зайдите в класс второго класса Кэти Дойл в Эванстоне, штат Иллинойс, чтобы увидеть, как ее ученики используют стратегию головоломки, чтобы глубже понять тему садоводства и поделиться тем, что они узнали. Джоанна Мейер, наш директор по исследованиям, представляет стратегию и рассказывает о важности тщательного планирования и организации, чтобы сделать эту стратегию действительно эффективной.
Собирайте ресурсы
Узнайте, как использовать стратегию головоломки в различных областях контента, включая исследования авторов, письмо и математику. См. пример >
Узнайте, как одна учительница использовала мозаику, чтобы помочь своим ученикам разработать собственное определение сказки, и как ее ученики отреагировали на самостоятельную деятельность. См. пример >
См. пример >
Посетите Jigsaw Classroom, сайт, посвященный обучению учителей тому, как использовать мозаику, чтобы «уменьшить расовые конфликты среди школьников, способствовать лучшему обучению, повысить мотивацию учащихся и повысить удовольствие от обучения». В нем также рассказывается, как учителя могут способствовать реализации стратегии с несколькими различными типами учащихся. См. пример >
Дифференцированное обучение
Для изучающих второй язык, учащихся с разными навыками чтения, учащихся с ограниченными возможностями обучения и учащихся младшего возраста
- Дайте учащимся возможность научиться навыкам обучения в малых группах, прежде чем участвовать в стратегии «головоломка».
- Предложите учащимся заполнить графический органайзер в «домашней группе», чтобы собрать всю информацию, представленную каждым «экспертом».
- «Домашние группы» могут представлять результаты всему классу или участвовать в некоторых оценочных мероприятиях.

- Распространение, чтобы убедиться, что группы выполняют задание и хорошо справляются со своей работой; попросите группы остановиться и подумать о том, как они проверяют понимание каждого и гарантируют, что голос каждого будет услышан; и
- Следите за пониманием членов группы, задавая вопросы и перефразируя информацию, пока не станет ясно, что все члены группы понимают суть.
См. исследование, подтверждающее эту стратегию
Аронсон, Э. (2000-2008). Jigsaw Classroom: Обзор техники.
Аронсон Э. и Гуд Э. (1980). Обучение учителей методам обучения мозаике: Пособие для учителей . В S. Sharan, P. Hare, C. Webb и R. Hertz-Lazarowitz (Eds.), Сотрудничество в образовании (стр. 47-81). Прово, Юта: Издательство Университета Бригама Янга.
Аронсон, Э., и Патно, С. (1997). Класс головоломки: построение сотрудничества в классе (2-е изд.). Нью-Йорк: Аддисон Уэсли Лонгман.
Кларк, Дж. (1994). Кусочки головоломки: метод головоломки. В С. Шаран (ред.), Справочник по методам совместного обучения . Вестпорт, Коннектикут: Greenwood Press.
В С. Шаран (ред.), Справочник по методам совместного обучения . Вестпорт, Коннектикут: Greenwood Press.
Колорин Колорадо. (2007). Совместные стратегии обучения.
Кроун, Т.С., и Портильо, М.К. (2013). Вариации мозаики и отношение к обучению и себе в когнитивной психологии. Преподавание психологии , 40 (3), 246–251. https://doi.org/10.1177/0098628313487451
Хэтти, Дж. (2017). 256 влияний, связанных с достижениями. Видимое обучение.
Право Ю.-К. (2011). Влияние совместного обучения на улучшение целей достижения пятиклассников из Гонконга, автономной мотивации и навыков чтения. Журнал исследований чтения , 34 (4), 402–425. https://doi.org/10.1111/j.1467-9817.2010.01445.x
Морено, Р. (2009). Построение знаний с помощью учебной программы на основе агентов: сравнение совместного и индивидуального создания смысла. Обучение и инструкции , 19(5), 433–444. https://doi.org/10.1016/j.learninstruc.2009.02.018
Московиц, Дж. М., Малвин, Дж. Х., Шеффер, Г. А., и Шапс, Э. (1985). Оценка головоломки, метод совместного обучения. Современная педагогическая психология, 10 (2), 104–112. https://doi.org/10.1016/0361-476X(85)
М., Малвин, Дж. Х., Шеффер, Г. А., и Шапс, Э. (1985). Оценка головоломки, метод совместного обучения. Современная педагогическая психология, 10 (2), 104–112. https://doi.org/10.1016/0361-476X(85)
Славин Р.Е. (1980). Совместное обучение в группах: современное состояние . Педагог-психолог, 15, 93-111.
Славин Р.Е. (1995). Совместное обучение: теория, исследования и практика (2-е изд.). Бостон: Аллин и Бэкон. Тирни, Р. (1995) Стратегии и практики чтения. Бостон: Аллин и Бэкон.
А. Станчак, К. Дарнон, А. Роберт, М. Демолльен, К. Санрей, П. Брессу, П. Хьюге, К. Букс, Ф. Бутера и Консорциум PROFAN . (2022). Улучшают ли классы-головоломки результаты обучения? Пять экспериментов и внутренний метаанализ. Журнал педагогической психологии , 114(6), 1461-1476.
15 приложений и веб-сайтов для онлайн-обучения математике [обновлено]
107,9 тыс.
просмотров
FacebookTwitterSubscribe
предоставлено Jennifer Smith
С ростом популярности обучения, ориентированного на STEM, все больше и больше студентов изучают все более и более сложные математические курсы.
Тем не менее, для некоторых студентов этот предмет может стать настоящим испытанием; но знание того, к кому обратиться за помощью, может значительно облегчить борьбу и улучшить их понимание.
Многие школы предлагают учащимся творчески использовать свои математические ресурсы, обращаясь к приложениям, веб-сайтам и онлайн-программам, которые помогают им буквально решать стоящие перед ними задачи. Выбор наиболее полезных, подходящих и приятных математических онлайн-инструментов может быть проблемой сам по себе, но, к счастью, с помощью нескольких учителей CalPac, чартерной онлайн-школы, обслуживающей Южную Калифорнию, эта проблема легко решается. решено.
Вот их 15 любимых онлайн-ресурсов для онлайн-обучения математике, которые помогут сделать математику более доступной и увлекательной для учащихся всех классов.
1. Академия Хана
Академия Хана — это полностью бесплатный персонализированный учебный ресурс с онлайн-курсами, видео и упражнениями. Учащиеся могут выполнять ежедневные обзоры и отслеживать свои успехи на учебной панели платформы. Учебники по математике разбиты на категории по предметам и уровням обучения для удобства навигации и используют специализированный контент — с помощью таких организаций, как НАСА, Калифорнийская академия наук и Музей современного искусства — для воплощения уроков в жизнь.
Учащиеся могут выполнять ежедневные обзоры и отслеживать свои успехи на учебной панели платформы. Учебники по математике разбиты на категории по предметам и уровням обучения для удобства навигации и используют специализированный контент — с помощью таких организаций, как НАСА, Калифорнийская академия наук и Музей современного искусства — для воплощения уроков в жизнь.
Что нравится учителям: Практические задачи содержат подсказки пошагово, поэтому учащиеся могут получить помощь, когда они застряли на определенном этапе, но им не обязательно нужна помощь в решении всей задачи. Это позволяет им работать над собой и учиться в своем собственном темпе.
Уровни обучения: K-12; среднее
См. также 25 лучших математических ресурсов
2 . IXL
Хотя IXL является учебным сайтом на основе подписки, он предлагает бесплатные ежедневные математические задачи. Студенты могут отвечать на десять бесплатных вопросов (по каждому предмету) в день и улучшать свои математические навыки. Членство в подписке включает неограниченное количество практических вопросов, аналитику, сертификаты и персональные рекомендации по навыкам.
Членство в подписке включает неограниченное количество практических вопросов, аналитику, сертификаты и персональные рекомендации по навыкам.
Что нравится учителям: Если учащийся неправильно решает задачу, программа показывает все шаги, необходимые для решения задачи, чтобы он мог увидеть, где он ошибся, и учиться на своих ошибках.
3. Desmos
Desmos — это бесплатный графический онлайн-калькулятор, который учащиеся могут использовать для построения графиков функций, построения данных и расчета уравнений. На сайте также есть математические примеры и даже рисунки, чтобы учащиеся могли максимально эффективно использовать калькулятор.
Что нравится учителям: Веб-сайт и программа чрезвычайно удобны для пользователя, с обширным справочным центром; а с Desmos семьям не нужно беспокоиться о покупке дорогого графического калькулятора.
Уровни обучения: 6–12; среднее
4.
Quizlet
Quizlet — это веб-сайт и приложение, которое обучает самым разным вещам с помощью цифровых карточек. В этом приложении учащиеся могут учиться с помощью карточек, совпадающих карточек, карточек для краткосрочного запоминания, карточек для долгосрочного запоминания и т. д. Учащиеся или преподаватели могут использовать готовые колоды карточек или создавать свои собственные колоды. Это приложение бесплатное и доступно на любой платформе.
В этом приложении учащиеся могут учиться с помощью карточек, совпадающих карточек, карточек для краткосрочного запоминания, карточек для долгосрочного запоминания и т. д. Учащиеся или преподаватели могут использовать готовые колоды карточек или создавать свои собственные колоды. Это приложение бесплатное и доступно на любой платформе.
Уровни обучения: K-12
5. Wolfram MathWorld
MathWorld — это бесплатный онлайн-ресурс для всего, что связано с математикой. Сайт включает в себя интерактивные GIF-файлы и демонстрации, загружаемые записные книжки и «краткие сводки» для различных математических терминов. Учащиеся могут изучить более 13 000 статей, чтобы укрепить свои математические знания и улучшить свое понимание.
Что нравится учителям: Сайт позволяет старшим и более продвинутым учащимся по-настоящему погрузиться в математику, предлагая темы и статьи по нескольким различным предметам, связанным с математикой, для разных уровней подготовки и способностей.
6. Искусство решения задач
С помощью программы «Искусство решения задач» учащиеся могут получить помощь и ресурсы, связанные с математикой, тремя разными способами. Онлайн-школа позволяет учащимся записаться на дополнительные занятия по математике, а книжный магазин AoPS предлагает сложные, углубленные учебники, чтобы учащиеся могли глубже изучить предмет.
Что нравится учителям: Учащиеся могут бросить себе вызов и глубже изучить математические предметы, которые им интересны, с помощью модерируемых досок объявлений, игр и статей.
Уровни: 2-12
7. Math is Fun
Как следует из названия, Math is Fun призвана сделать математику увлекательной и занимательной. На сайте используются головоломки, игры, викторины, рабочие листы и форум, чтобы помочь учащимся пройти обучение.
Что нравится учителям: Все проблемы и решения объясняются простым языком, что облегчает учащимся самостоятельное обучение без необходимости «перевода» со стороны взрослого или учителя.
8. Математическая игра Prodigy
Целью этой игры является обучение математике с помощью игры, а не только базового обучения математике, и при этом дать вашему ученику/ребенку необходимое математическое образование. Эта игра позволяет отлично отслеживать прогресс, поскольку учителя или родители проверяют вопросы, с которыми у их ученика или ребенка возникают проблемы, отслеживают, как они учатся вместе со своими сверстниками, корректируют уровень успеваемости, устанавливают цели, получают доступ к видеоурокам и т. д. Эта игра имеет базовые бесплатные функции, или вы можете купить обновленную версию за 6,25–8,33 доллара в месяц.
9.
Математическая игровая площадка
Это приложение призвано сделать процесс обучения интересным для учащихся, обучая в основном с помощью игр, таких как головоломки, животные, рисование и многое другое. Math Playground предназначена для учащихся от детского сада до 6-го класса. Math Playground бесплатна и доступна на любой платформе с поисковой системой.
Math Playground бесплатна и доступна на любой платформе с поисковой системой.
10. edX
На edX учащиеся могут получить доступ к более чем 3500 бесплатных курсов — эти курсы проводятся в престижных колледжах, таких как Гарвард, Беркли, Массачусетский технологический институт, Корнелл, Дартмут и других небольших колледжах. edX может стать отличным местом для изучения математики для учащихся 6–12 классов.
11. ABC Mouse
ABC Mouse — одно из самых популярных и образцовых обучающих приложений. Благодаря более чем 10 000 заданий и мобильному обучению это приложение отлично подходит для онлайн-обучения. ABC Mouse учит чтению, математике, счету, естественным наукам и многому другому. Это приложение предназначено для детей от 2 до 8 лет и является отличным местом для начала обучения математике для школьников и детей.
12. Академия приключений
Академия приключений — это учебный ресурс, который может научить студентов самым разным вещам. Благодаря более чем 4000 заданий, мобильному обучению и отслеживанию прогресса, это приложение может заставить учащихся забыть, что они даже учатся. Академия приключений преподает множество предметов: чтение, математику, естественные науки, социальные науки и многое другое. Это приложение, ориентированное на учащихся 8–13 лет, привносит в процесс обучения инновационную игровую атмосферу.
Благодаря более чем 4000 заданий, мобильному обучению и отслеживанию прогресса, это приложение может заставить учащихся забыть, что они даже учатся. Академия приключений преподает множество предметов: чтение, математику, естественные науки, социальные науки и многое другое. Это приложение, ориентированное на учащихся 8–13 лет, привносит в процесс обучения инновационную игровую атмосферу.
13. Mathplanet
Math Planet – это онлайн-ресурс, на котором можно бесплатно изучать математику. Учащиеся могут проходить школьные математические курсы по подготовительной алгебре, алгебре 1, алгебре 2 и геометрии. Они также подготовили практические тесты для SAT и ACT.
Учебный материал посвящен математике для средней школы США. Однако, поскольку математика одинакова во всем мире, Mathplanet приглашает всех изучать математику вместе с ними бесплатно.
14. Иллюстративная математика
Иллюстративная математика Математика — это основная учебная программа, основанная на задачах, разработанная с учетом содержания и практических стандартов для содействия обучению для всех. Учащиеся учатся, занимаясь математикой, решая задачи в математическом и реальном контексте, а также строя аргументы, используя точный язык. Преподаватели могут смещать свои инструкции и облегчать обучение учащихся с помощью высокоэффективных процедур, помогающих учащимся понять и установить связи между концепциями и процедурами.
Учащиеся учатся, занимаясь математикой, решая задачи в математическом и реальном контексте, а также строя аргументы, используя точный язык. Преподаватели могут смещать свои инструкции и облегчать обучение учащихся с помощью высокоэффективных процедур, помогающих учащимся понять и установить связи между концепциями и процедурами.
Уровни обучения: 6-8
15. Адаптированный разум
Оценки: K -5
15 приложений и веб -сайтов для обучения математике онлайн
3 класс — Piercecurriculum
|
Язык. Математика | Наука | Социальные исследования | Изображения
|
Примеры логического математического интеллекта — MentalUP
🎒 Распродажа «Снова в школу»: СКИДКА 30% на + Получите бесплатный семейный план !
Что такое логико-математический интеллект, также известный как секрет гениев? По какому пути могут пойти дети, если они хотят повысить уровень своего логического интеллекта?
Что такое логический математический интеллект?
Логико-математический интеллект — это способность логически анализировать ситуации или проблемы, находить решения, проводить научные исследования и легко решать логические/математические операции. Это один из восьми типов множественного интеллекта, предложенных Говардом Гарднером.
Это один из восьми типов множественного интеллекта, предложенных Говардом Гарднером.
- Языковой интеллект
- Математический интеллект
- Экзистенциальный разум
- Кинестетический интеллект
- Музыкальный интеллект
- Внутриличностный интеллект
- Пространственный интеллект
- Социальный интеллект
Люди с высоким уровнем числового интеллекта анализируют свои данные, используя логику и исследуя причинно-следственные связи, как указано в определении логического математического интеллекта.
Они часто не работают с субъективной информацией — вместо этого они ценят четкие факты и достоверные данные. Способность делать выводы и наблюдения также является важной характеристикой лиц с математическим интеллектом. Хотя иногда создается впечатление, что они сбиты с толку, их разум работает как компьютер в фоновом режиме.
Уверены ли вы в своих навыках? 🚀
Тест на множественный интеллект поможет вам раскрыть свои навыки и убедиться, что вы на правильном пути. Это самый простой способ определить ваши особые интересы и типы интеллекта .
Будьте готовы к мгновенным и точным результатам ! 📊
Пройдите тест на множественный интеллект
Характеристики логико-математического интеллекта
Как и другие типы интеллекта, характеристики логико-математического интеллекта можно легко наблюдать у людей. В основном, эти люди хороши в математических операциях. Им легко распознавать, рассуждать и анализировать проблемы. Таким образом, они лучше сдают такие экзамены, как тест кенгуру по математике.
Вот наиболее распространенные логико-математические характеристики интеллекта людей с этим типом интеллекта:
- Отлично разбираются в числах, закономерностях и их отношениях,
- Отлично справляется со сложными задачами и вычислениями,
- Склонен к научным экспериментам,
- Люблю думать об абстрактных идеях,
- Исключительное умение анализировать,
- Максимальные организаторские и классификационные способности.

Это характеристики логико-математического интеллекта, и эти исключительные способности могут помочь определить, какие люди обладают логико-математическим интеллектом.
Примеры логико-математического интеллекта
Некоторые люди могут знать типы интеллекта теоретически, но примеры логико-математического интеллекта могут облегчить понимание и определение.
Приведенные ниже примеры логико-математического интеллекта могут показать, что если вы, взрослый или ребенок, можете иметь логико-математический интеллект более четко.
Итак, какие наиболее распространенные примеры логико-математического интеллекта могут быть вам знакомы?
- Ребенок любит играть в шахматы, стратегические игры, подходящие карточные игры для детей и математические игры и преуспевает в них.
- Человек увлекается чтением детективов и с удовольствием смотрит криминальные фильмы.
- Студент любит проводить научные эксперименты и решать математические задачи.
 Студент может с удовольствием заниматься такими предметами, как электроника, счета, логика и т. д.
Студент может с удовольствием заниматься такими предметами, как электроника, счета, логика и т. д. - Человеку нравится планировать мероприятие и организовывать его бюджет с помощью графиков и т. д.
- Взрослый готов рискнуть на фондовом рынке. Этот человек может успешно управлять своими инвестициями.
Подобные примеры логико-математического интеллекта полезны для оценки наличия у кого-либо логико-математического интеллекта.
Примеров математического логического интеллекта может быть еще много, но основная идея в том, что характеристики математического логического интеллекта настолько очевидны в жизни этих людей.
10 Занятия по развитию логического математического интеллекта
Хотя широко распространено мнение, что те, кто хочет улучшить свой логический интеллект, должны очень хорошо разбираться в математике, это не обязательно так . Все, что вам нужно, это самоотверженность, чтобы улучшить свой логический математический интеллект.
Развить логический интеллект не так сложно, как вы думаете. Людей с высоким уровнем логического интеллекта часто называют «логичными», что означает, что они могут легко идентифицировать формы и устанавливать связи между абстрактными понятиями.
У нас есть хорошие новости для тех, кто не знает, как улучшить свой потенциал логического математического интеллекта! Вот развернутый ответ на вопрос « Как развить логический математический интеллект? » с предельно простыми заданиями на логико-математический интеллект!
1. MentalUP
Быстро и эффективно проверьте умственные способности вашего ребенка, чтобы увидеть его текущий уровень логического математического интеллекта с помощью MentalUP! Затем ваш ребенок может начать совершенствовать свои навыки с помощью ряда логических математических вопросов, логических головоломок и интеллектуальных игр.
Отмеченное наградами приложение MentalUP является одним из лучших логических и математических упражнений среди других математических приложений для детей, которые им нравятся, развивая их умственные способности.
MentalUP, одна из самых популярных игр для детей, была разработана академиками , педагогами и геймдизайнерами. Он содержит множество увлекательных логических математических заданий , таких как упражнения для ума, математические игры и головоломки!
Вы также хотите улучшить другие типы множественного интеллекта вашего ребенка? Нет необходимости искать другие приложения, потому что MentalUP предлагает 150+ обучающих игр и упражнений для мозга для поддержки любого типа интеллекта!
НАЧНИТЕ СЕЙЧАС
2. Решайте головоломки
Почти всем нравятся вопросы на интеллект, загадки и головоломки. По сути, эти упражнения — просто занятия для математического логического интеллекта в разных формах.
Решение логических головоломок, развивающих логическое мышление вашего ребенка, не займет много времени и может быть очень увлекательным.
Вот несколько математических заданий для вас, полных головоломок: Математические головоломки! Наслаждайся ими!
3.
 Играйте в настольные игры
Играйте в настольные игры
Настольные игры — отличный способ развить навыки стратегического мышления и логического математического интеллекта.
Они полезны как одно из занятий логико-математического интеллекта взрослых, так же как и для детей. Неудивительно, что существует так много популярных настольных игр!
«Все, чему стоит учить, можно представить по-разному. Эти многочисленные способы могут использовать наш множественный интеллект». — Говард Гарднер
4. Разгадывайте загадки и каверзные вопросы
Вы можете улучшить свой логический интеллект с помощью каверзных загадок с ответами или каверзных вопросов с ответами, развлекаясь. Они очень полезны для улучшения нашей умственной работоспособности и отличной логической/математической интеллектуальной деятельности.
5. Пишите рассказы
Составление плана — одно из лучших логико-математических упражнений на множественный интеллект. С помощью этих видов письменных упражнений для развития логико-математического интеллекта ваши дети могут работать над своими навыками письма, а также над своим интеллектом.
Просто попросите их составить план истории, включая время, прошедшее между каждой записью, и убедитесь, что в каждой записи есть как минимум два предложения.
6. Проведение научных экспериментов
Проведение научных экспериментов — один из лучших видов деятельности для развития логико-математического интеллекта. Дети с логико-математическим интеллектом уже склонны проводить научные эксперименты, чтобы понять, как все устроено, потому что любознательность — одна из их самых сильных характеристик.
7. Изучите программирование
Программирование — один из лучших примеров логико-математической интеллектуальной деятельности.
Это требует одновременного использования множества навыков, таких как решение задач, математика, язык и т. д., чтобы дети могли раскрыть свои способности в мире программирования даже в таком юном возрасте!
Вы можете прочитать нашу статью о 20 лучших обучающих приложениях для детей, чтобы узнать список лучших игр для программирования. Смело выбирайте любой из них!
Смело выбирайте любой из них!
8. Проведение опроса
Может показаться, что это не игра, но проведение опроса может стать одним из самых интересных логико-математических заданий для детей!
Требуется более одного навыка одновременно, например, математика, категоризация и общение.
Побуждайте своих детей находить правильные вопросы по выбранной ими теме. Затем они могут упорядочивать ответы и превращать их в логические результаты с помощью графиков данных.
9. Классифицировать различные объекты
Вот одно из очень полезных логико-математических заданий для дошкольников.
Вы можете понять, что ваши дети обладают логическим математическим интеллектом еще до школьного возраста. Если это так, вы можете извлечь пользу из этого упражнения, которое фокусируется на логическом математическом интеллекте.
Попросите ребенка классифицировать различные предметы. Вы можете захотеть, чтобы они упорядочили предметы по размеру, цвету, форме и т. д. Вы можете одновременно указать на две разные функции, чтобы усложнить игру, например, расположить красные и квадратные объекты справа, а синие и овальные — справа. оставил.
д. Вы можете одновременно указать на две разные функции, чтобы усложнить игру, например, расположить красные и квадратные объекты справа, а синие и овальные — справа. оставил.
Выполняйте исследовательские проекты
Это упражнение может быть одним из лучших логико-математических упражнений для чтения и организации того, что они изучают!
Всем детям с логическим математическим интеллектом обычно нравится заниматься исследовательскими проектами. Вы можете превратить этот интерес в веселый проект!
Выберите с детьми тему, которая может быть им интересна. Это может быть связано с планетами, животными или чем угодно, что они предпочитают. Скажите им, чтобы они собрали достаточно информации, а затем создайте и систематизируйте рабочие листы! Вы можете направлять младших детей, если они нуждаются в вашей помощи.
Учебные советы по логическому математическому стилю обучения
Логический математический стиль обучения идеально подходит для учащихся, которые методичны и мыслят линейно. Логико-математический стиль обучения относится к способности анализировать причинно-следственные связи, рассуждать, решать проблемы и учиться, используя числа и абстрактную визуальную информацию. Вы можете воспользоваться приведенными ниже советами, чтобы подготовиться к математическому кенгуру, сдаче экзамена 8 plus или другим тестам.
Логико-математический стиль обучения относится к способности анализировать причинно-следственные связи, рассуждать, решать проблемы и учиться, используя числа и абстрактную визуальную информацию. Вы можете воспользоваться приведенными ниже советами, чтобы подготовиться к математическому кенгуру, сдаче экзамена 8 plus или другим тестам.
Вот несколько советов по обучению для логические учащиеся :
- Учащиеся с логико-математическими способностями к обучению лучше всего учатся, используя наглядные материалы, ноутбуки и практические проекты.
- Им нужна структура с правилами, целями и процедурами, поскольку они иногда борются с двусмысленностью.
- Некоторые из целей могут быть краткосрочными, но вы также должны поощрять их мыслить целостно и ставить долгосрочные цели. Вы можете получить планировщик, чтобы планировать дни, недели и месяцы и отслеживать их прогресс.
- Поработайте с ними, чтобы выяснить, в каком порядке они хотели бы работать над своими предметами, и создайте календарь, которому они смогут легко следовать.

- Маркеры могут очень помочь им в определении наиболее важных частей чтения. Кроме того, временные шкалы, в которых факты перечислены в подробном чтении, — отличный способ заинтересовать вашего логического ученика. Четкая структура и организация позволяют им легко изучать предмет.
- Постарайтесь поощрять их процесс обучения с помощью решения проблем и классификации, чтобы помочь им достичь своих целей.
- Учащиеся, обучающиеся логике и математике, любят создавать и рассматривать карты, диаграммы, схемы и графики. Вы можете помочь им в этом процессе, разбивая большие объемы информации на диаграммы и графики.
- Для логических учащихся, которым трудно писать, попросите их составить план для себя. Это поможет им превратить мелкие детали в общие идеи.
Веселые логические вопросы и игры на математический интеллект
Существует множество вариантов, которые помогут вашему ребенку повысить уровень логического интеллекта. Игры на логический и эмоциональный интеллект, а также математические игры для детского сада являются самыми веселыми и эффективными.
Игры на логический и эмоциональный интеллект, а также математические игры для детского сада являются самыми веселыми и эффективными.
С помощью приведенных ниже игровых упражнений ваш ребенок может начать повышать свой потенциал логического математического интеллекта и других областей множественного интеллекта. 👇️🎉️
Чтобы пройти эту игру, вам понадобится высокий математический потенциал интеллекта!
НАЧАЛО
Давайте проверим и улучшим ваш логический математический потенциал в веселой игре.
НАЧАЛО
Этот волшебный шар пытается спрятаться от зорких глаз! Сможете ли вы найти его, используя свой логический интеллект?
НАЧАЛО
С математическими интеллектуальными играми дети могут развивать свое логическое мышление, математические способности.
НАЧАЛО
10 Известные личности с логическим математическим интеллектом
Когда вы смотрите на мир науки, искусства и технологий, довольно легко встретить известных людей с логико-математическим интеллектом. Уникальное сочетание их интеллекта, сильных и слабых сторон сделало их невероятно успешными людьми.
Уникальное сочетание их интеллекта, сильных и слабых сторон сделало их невероятно успешными людьми.
Вот некоторые люди с известным логико-математическим интеллектом:
Логический математический интеллект Карьера
Профессии в области логико-математического интеллекта предлагают так много возможностей для детей в цифровом мире, в котором мы живем. логический математический интеллект.
Не забывайте, что некоторые профессии с логико-математическим интеллектом требуют и других типов интеллекта.
Вот наиболее подходящие логико-математические профессии для детей:
- Компьютерный инженер/программист/техник
- Инженер-программист
- Системный аналитик
- Сетевой аналитик
- Специалист по базам данных/дизайнер
- Инженер (электрик, строительство, механика, химия, промышленность)
- Специалист по бухгалтерскому учету
- Специалист по финансам
- Консультант по финансам и инвестициям
- Специалист по математике
- Статистик
- Архитектор/архитектор интерьеров
- Физик
- Специалист по астрономии/астроном
- Врач/медсестра/фельдшер/фармацевт
Поскольку данные и аналитика играют все более важную роль в нашей жизни, разнообразие профессий для логико-математического интеллекта может увеличиваться день ото дня.
 к. именно они позволяют подсчитать принципиальновозможное
к. именно они позволяют подсчитать принципиальновозможное Таких пар тоже будет n 2 .
Таких пар тоже будет n 2 .
 к. нечетных цифр
к. нечетных цифр


 Так как в процессе рукопожатия порядок не важен, выбираем формулу для числа сочетаний:
Так как в процессе рукопожатия порядок не важен, выбираем формулу для числа сочетаний: а) Для студентов порядок не важен, поэтому выбираем формулу числа сочетаний:
а) Для студентов порядок не важен, поэтому выбираем формулу числа сочетаний:
 Общее число шестизначных телефонных номеров, у которых могут быть любые, в том числе и повторяющиеся, цифры, равно разности:
Общее число шестизначных телефонных номеров, у которых могут быть любые, в том числе и повторяющиеся, цифры, равно разности:
 Каждая из 29 букв может быть инициалом и
Каждая из 29 букв может быть инициалом и Умение решать задачи – критерий успешности в учебе. Очень важно показать, как обычную жизненную ситуацию можно описать математической моделью.
Умение решать задачи – критерий успешности в учебе. Очень важно показать, как обычную жизненную ситуацию можно описать математической моделью.
 Ян Амос Коменский (),
Ян Амос Коменский (), 1, 2, 3, 4, 5
1, 2, 3, 4, 5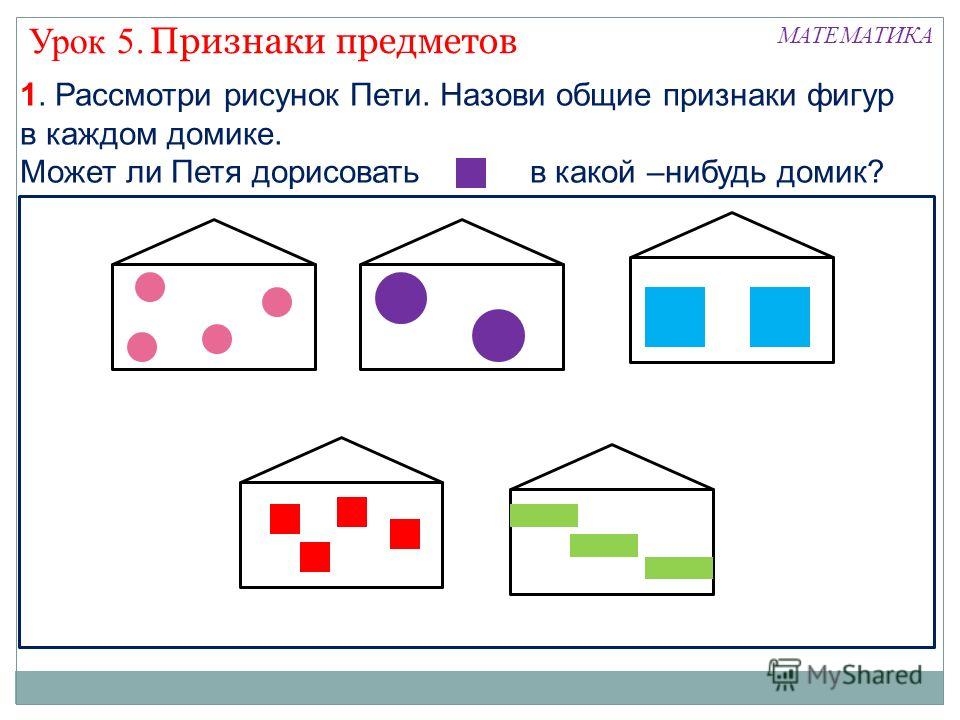
 Сколькими способами можно взять один любой шар? зеленый и желтый шар? красный или желтый?
Сколькими способами можно взять один любой шар? зеленый и желтый шар? красный или желтый? Решая подобные задачи, приходится перебирать различные варианты, переставлять заданные элементы, комбинировать их. Такие задачи называются комбинаторными, а раздел математики, занимающийся решением этих задач, называется комбинаторикой.
Решая подобные задачи, приходится перебирать различные варианты, переставлять заданные элементы, комбинировать их. Такие задачи называются комбинаторными, а раздел математики, занимающийся решением этих задач, называется комбинаторикой.


 Сколько различных вариантов обеда из двух блюд можно заказать? (28 вариантов)
Сколько различных вариантов обеда из двух блюд можно заказать? (28 вариантов) )
) Значит, пару цифр мы составляем 3 · 3 = 9 способами, т. е. получится 9 чисел.
Значит, пару цифр мы составляем 3 · 3 = 9 способами, т. е. получится 9 чисел. Поэтому получается
Поэтому получается )
)

 Обычный вопрос в
Обычный вопрос в
 Сколько вариантов выбора одного плода?
Сколько вариантов выбора одного плода?


 Сколько различных вариантов
Сколько различных вариантов 000.000
000.000



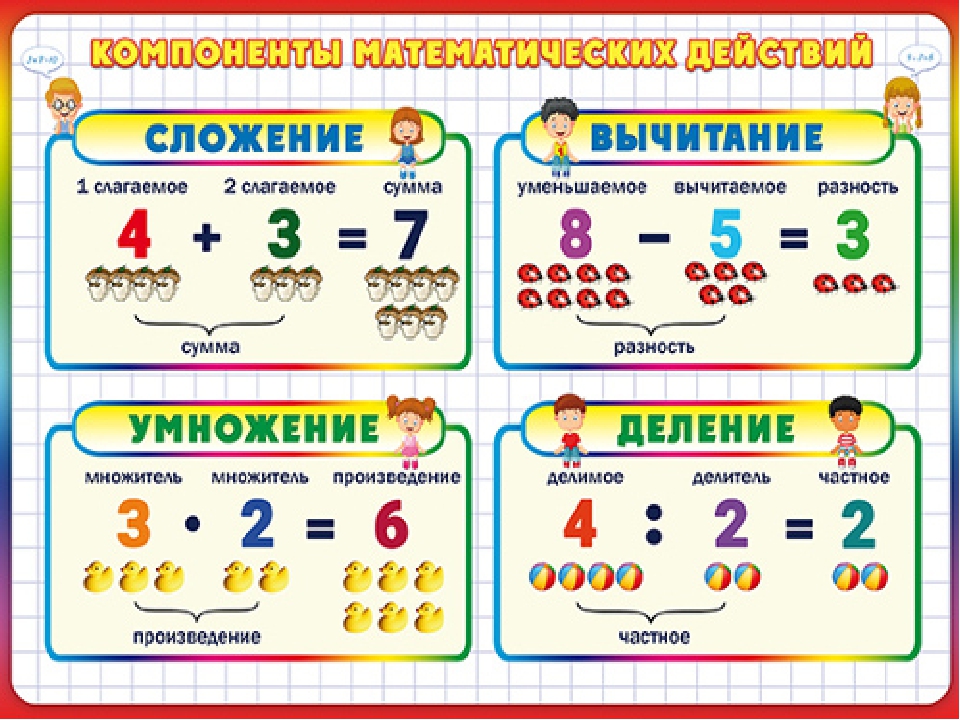 Воспользуемся формулой для числа размещений: A 7 3 = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел.
Воспользуемся формулой для числа размещений: A 7 3 = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел. Так как в соединении существенным есть порядок, и все элементы используются, значит это перестановки из 8 элементов (7 книг + условная 1 книга). Их количество Р 8 . Далее будем переставлять между собой только сборники стихотворений. Это можно сделать Р 5 способами. Поскольку нам нужно расставить и сборники, и другие книги, то воспользуемся правилом произведения. Следовательно, Р 8 · Р 5 = 8! · 5!. Число способов будет большим, поэтому ответ можно оставить в виде произведения факториалов.
Так как в соединении существенным есть порядок, и все элементы используются, значит это перестановки из 8 элементов (7 книг + условная 1 книга). Их количество Р 8 . Далее будем переставлять между собой только сборники стихотворений. Это можно сделать Р 5 способами. Поскольку нам нужно расставить и сборники, и другие книги, то воспользуемся правилом произведения. Следовательно, Р 8 · Р 5 = 8! · 5!. Число способов будет большим, поэтому ответ можно оставить в виде произведения факториалов. В результате число способов будет вычисляться таким образом:
В результате число способов будет вычисляться таким образом: