Методические рекомендации для учителей, начинающих работать по курсу математики Л.Г. Петерсон «Учусь учиться»
1 класс, часть 3
Консультация 6. Уроки 11 – 17
«Можно научить учеников решать достаточно много типов задач, но подлинное удовлетворение придет лишь тогда, когда мы сумеем передать нашим воспитанникам не просто знания, а гибкость ума» У. У. Сойер
- Линия уравнений и неравенств является стержнем алгебраического материала школьного курса математики. А умение устанавливать связь между целым и частями является базовым для решения уравнений. Данное умение формируется у учащихся на первых уроках математики. В основе лежит умение классифицировать предметы по разным свойствам (например, размер). Это отношение между частью и целым моделируется сначала на совокупности, записывается в знаковом виде с помощью букв: Б – большие фигуры, М – маленькие, Ф – все фигуры.
 Части в полученной записи подчеркиваются чертой, целое обводится замкнутой линией. Затем данное отношение моделируется на числах, затем на отрезках. В подготовительный этап входит изучение сравнения совокупностей. Совокупности сначала сравниваются по наполнению группы (по факту), а затем по количеству предметов. Для решения уравнений важно то, что изображено слева, так как дети будут решать уравнения с мешками и находить в целом ту часть, которая известна. Для этого ученики устанавливают взаимно однозначное соответствие, ищут те же самые элементы. Важное направление подготовительной работы – заполнение пропусков в равенствах, так называемые примеры с «окошками». Следует обратить внимание на предлагаемые способы заполнения окошек: подбор; с помощью числового отрезка; на основе связи между целым и частью. На подготовительном этапе у учащихся формируется представление о равенстве, так как уравнение – это равенство.
Части в полученной записи подчеркиваются чертой, целое обводится замкнутой линией. Затем данное отношение моделируется на числах, затем на отрезках. В подготовительный этап входит изучение сравнения совокупностей. Совокупности сначала сравниваются по наполнению группы (по факту), а затем по количеству предметов. Для решения уравнений важно то, что изображено слева, так как дети будут решать уравнения с мешками и находить в целом ту часть, которая известна. Для этого ученики устанавливают взаимно однозначное соответствие, ищут те же самые элементы. Важное направление подготовительной работы – заполнение пропусков в равенствах, так называемые примеры с «окошками». Следует обратить внимание на предлагаемые способы заполнения окошек: подбор; с помощью числового отрезка; на основе связи между целым и частью. На подготовительном этапе у учащихся формируется представление о равенстве, так как уравнение – это равенство.
- В первом классе уравнение рассматривается как равенство, содержащее неизвестный компонент арифметического действия.
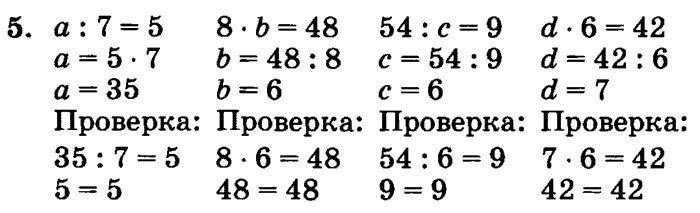 Этот неизвестный компонент обозначается буквой латинского алфавита. Сначала учащиеся выполняют задание с мешками. Умение устанавливать взаимно-однозначное соответствие, «волшебной ниткой» проводить от одного элемента до такого же является базовым. Его важно отработать в ходе выполнения заданий на части и целое.
Этот неизвестный компонент обозначается буквой латинского алфавита. Сначала учащиеся выполняют задание с мешками. Умение устанавливать взаимно-однозначное соответствие, «волшебной ниткой» проводить от одного элемента до такого же является базовым. Его важно отработать в ходе выполнения заданий на части и целое.
- В первом классе ученики встречаются с разными видами уравнений: не только с числами, но и на отрезках, с символами. Последние относятся к заданиям повышенного уровня сложности, поэтому решать такие уравнения целесообразно предлагать по желанию, или в ходе фронтальной работы.
- На уроке 11 вводится понятие уравнения как равенства, в котором неизвестен один из компонентов действий, который надо найти. Дети учатся решать уравнения с неизвестным слагаемым. Затруднение связано с ошибками в решении и обосновании примеров с «окошками».
В результате учащиеся получают следующий способ (алгоритм) решения уравнения с неизвестной частью:
1) Внимательно прочитать уравнение.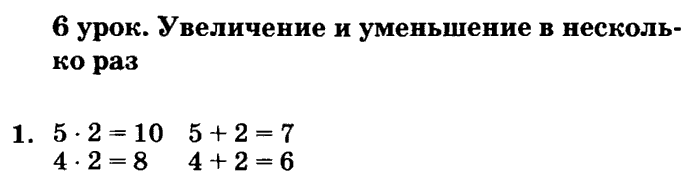
2) Найти в уравнении части и целое (если нужно составить схему).
3) Определить, что неизвестное х является частью.
4) Применить правило: чтобы найти неизвестную часть, можно из целого вычесть известную часть.
5) Выполнить действие и найти х .
6) При необходимости сделать проверку
7) Назвать ответ
На данном уроке полезно ввести способ (алгоритм) комментирования решения уравнения с неизвестной частью, который непосредственно следует из способа его решения: [1]
1) Читаю уравнение: …
2) В этом уравнении части – … и …, целое – …
3) Неизвестна часть. Чтобы найти неизвестную часть, можно из целого вычесть известную часть.
4) х равен разности … и …
5) При необходимости делаю проверку.
6) Ответ: х равен . ..
..
На этом же этапе можно уже обсудить с учащимися, как проверить правильность решения уравнения: подставить в него полученное значение х и установить, верно ли полученное равенство.
- На уроке 12 решение уравнений с неизвестным слагаемым закрепляется. Его можно провести в форме урока рефлексии либо развернуть проблемную ситуацию вокруг обобщенной записи решения уравнений данного типа.
Проверка к уравнениям, как правило, выполняется устно. Решение одного или нескольких уравнений с числами можно записать в тетради в клетку вместе с письменной проверкой решения.
- Аналогичным образом на уроках 13–14 вводятся уравнения с неизвестным вычитаемым, а на уроках 15–16 – уравнения с неизвестным уменьшаемым. Учитывая приобретенный детьми опыт, проблемную ситуацию можно развернуть вокруг поиска правила для решения уравнений нового типа. На этапе постановки учебной задачи учащиеся должны выявить существенный признак отличия новых уравнений от уравнений, встречавшихся раньше (неизвестно уменьшаемое, вычитаемое), и поставить перед собой цель − построить правило и научиться с его помощью решать уравнения нового типа.

- На уроке 17 подводится итог изучению темы: все типы уравнений «собираются» вместе и сопоставляются. Дети на данном уроке должны продемонстрировать умение решать уравнения всех типов в ситуации, когда надо не просто применить заданный способ решения, а выбрать его из трех возможных.
- В результате общий способ (алгоритм) решения уравнений всех трех данных типов приобретает вид. [2]
1) Внимательно прочитать уравнение.
2) Найти в уравнении части и целое (если нужно составить схему).
3) Определить, чем является неизвестное х – частью или целым.
4) Применить нужное правило (нахождения части или целого).
5) Выполнить действия и найти х.
6) При необходимости сделать проверку.
Обобщается и способ (алгоритм) комментирования решения уравнений:
1) Внимательно читаю уравнение: …
2) В этом уравнении … и … – части, а … – целое.
3) Определяю, что неизвестно – целое или часть, и применяю нужное правило.
4) Неизвестное х равно сумме (разности) … и …
5) Делаю проверку: … (при необходимости).
6) Ответ: х равен …
- В задачах на повторение уроков 11–17 тренируется автоматизированный навык счета в пределах 9, закрепляются представления о величинах, решение составных задач на нахождение целого (не известна одна из частей).
При решении составных текстовых задач следует постепенно переходить от обсуждения задач в вопросно-ответной форме к их самостоятельному монологическому анализу учащимися.
До сих пор все этапы работы над задачей учащиеся проходили вместе с учителем, отвечая на его вопросы: «Что известно в задаче?», «Что нужно найти?», «Можно ли сразу ответить на вопрос задачи?», «Что нужно узнать вначале?», «Почему?» и т. д. Теперь детей надо поэтапно подвести к умению самостоятельно проговаривать условие и вопрос задачи, находить и обосновывать решение, то есть к умению самостоятельно анализировать задачу.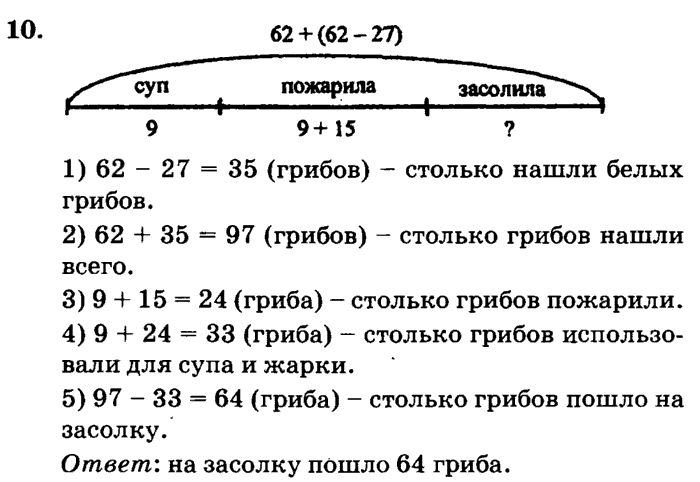 Для выработки этого умения требуется достаточно продолжительное время. Например, самостоятельно анализировать задачи в 2–3 действия все учащиеся должны научиться примерно к концу 3 класса. Однако поставить перед ними такую цель, чтобы они осознали ее как личностно значимую, следует уже сейчас. Подробнее с организацией работы по формированию умения самостоятельно анализировать задачи вы можете познакомиться в методических рекомендациях для учителя [3].
Для выработки этого умения требуется достаточно продолжительное время. Например, самостоятельно анализировать задачи в 2–3 действия все учащиеся должны научиться примерно к концу 3 класса. Однако поставить перед ними такую цель, чтобы они осознали ее как личностно значимую, следует уже сейчас. Подробнее с организацией работы по формированию умения самостоятельно анализировать задачи вы можете познакомиться в методических рекомендациях для учителя [3].
Таким образом, к концу первого класса учащиеся умеют решать простые уравнения на сложение и вычитание с предметами, фигурами, числами на основе взаимосвязи между частью и целым; умеют прокомментировать решение простых уравнений на сложение и вычитание на основе взаимосвязи между частью и целым; знакомы с комментированием по компонентам действий.
«Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе». М.И. Калинин. (1875 – 1946)
М.И. Калинин. (1875 – 1946)
Желаем Вам удачи и творческих успехов!
Мы вместе, значит, у нас все получится!
[1] Л.Г. Петерсон. Построй свою математику. Блок-тетрадь эталонов, 1 класс. – М, Ювента, 2010. Стр.61
[2] Там же. – Стр. 64
[3] Петерсон Л.Г. Методические рекомендации к учебнику математики 1 класса. Пособие для учителя – М, Ювента, 2010. Стр.218-220
х = b; х : а = b» (автор учебника: Л.Г.Петерсон)
Конспект урока математики во 2 классе по теме:
«Уравнения вида а · х = b; а : х = b;
х : а = b»(автор учебника: Л.Г.Петерсон)
Тип урока: Открытие новых знаний
Автор: учитель начальных классов МОУ «СОШ №8»
г. Железногорска Курской области Щегликова Оксана Юрьевна
Основные цели:
1) формировать
умение строить алгоритм и использовать его при решении уравнения на умножение;
сформировать умение решать уравнения вида а · х = b;
2) закрепить
таблицу умножения и деления на 2 и на 3.
Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение,
обобщение.
Демонстрационный материал:
1) стихотворение
для этапа 1:
По дороге знаний смело путь держи,
Даже, если трудно, ты вперёд иди!
2) задание 1 для
этапа 2:
3) формулы
нахождения площади и неизвестной стороны прямоугольника:
4) задание 2 для
этапа 2:
5) формулы нахождения
части и целого:
Ц = ч+ч ч = ц – ч
6) задание для
пробного действия:
7) алгоритм решения
уравнения на умножение:
Алгоритм
1. Обозначь
Обозначь
компоненты, соответствующие сторонам и площади прямоугольника.
2.Нанеси числа из
уравнения на модель.
3.Определи, что неизвестно.
4.Примени правило.
Раздаточный материал:
1) Карточки с заданием для пробного действия
2)План работы в
группах на этапе построения проекта выхода из затруднения.
Реши уравнение по плану:
х·3=24 План работы:
1.Обозначь компоненты, соответствующие сторонам
и площади
прямоугольника.
2.Нанеси числа из уравнения на модель.
х =
3.Определи, что неизвестно.
4.Примени правило.
х= 5.Сформулируй
алгоритм решения.
3)Вариант комментирования:
1.Обозначаю компоненты,
соответствующие
сторонам и
площади прямоугольника.
2.Определяю, что
неизвестно.
3.Вспоминаю правило.
4.Применяю правило.
4)
Лесенка успеха для самооценки на этапе 9.
Ход
урока:
1.Мотивация к
учебной деятельности.(1-2 мин.)
Цель: включение учащихся в учебную деятельность на личностно значимом
уровне.
Организация
учебного процесса на этапе 1:
— Здравствуйте,
ребята! Сегодня на уроке математики мы будем работать под таким девизом: (2
слайд) По дороге знаний
Смело
путь держи!
Даже
если трудно,
Ты
вперёд иди!
— Каким образом мы идём по дороге знаний?( I шаг-если чего-то не знаем,II шаг-сами найдём
способ) (3 слайд)
— Как вы сами находите способ?(Сначала повторяем то, что
необходимо, потом открываем новые знания)
— Я желаю вам преодолеть все трудности на уроке.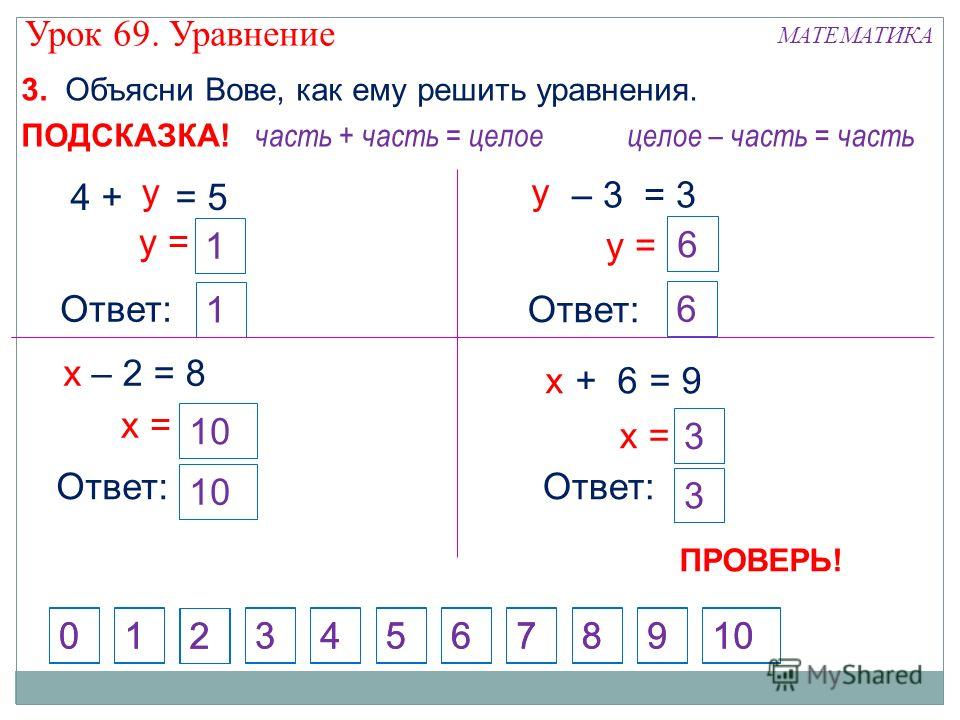
2.Актуализация знаний и
фиксация индивидуального затруднения в пробном действии.(4-5 мин.)
Цель: организовать пробного
действия и фиксацию затруднения.
Организация учебного процесса на этапе 2:
1)(4 слайд) На слайде то же, что и на доске. Начало слайда:
-Предлагаю вспомнить формулы нахождения площади и стороны
прямоугольника.
-Что означают буквы
на данной модели?
-Проверьте.(На
слайде: a и b — стороны прямоугольника
S— площадь прямоугольника)
— Составьте все
возможные равенства по рисунку(открываю опору на доске) и обозначьте
компоненты, соответствующие сторонам и площади.
a·b=S (Если перемножить стороны
прямоугольника, то получим площадь; стороны-подчёркиваем, а площадь обводим
прямоугольником)
b·a=S (переместительное свойство…
S:a=b(если S
разделить…
S:b=a(если S
разделить…
— Предлагаю сгруппировать равенства. В какие группы и по какому
В какие группы и по какому
признаку их можно объединить?(1-е,2-е равенства-для нахождения площади-I группа; 3-е,4-е-для нахождения стороны- II
группа)
-Проверим.(Слайд)
-А теперь сформулируйте правила и допишите формулу №1) S=a·b и формулу №2) a=S:b
-Проверим.(Слайд)
2)- Дальше предлагаю вспомнить формулы нахождения целого и
части и решить уравнение.(Чтобы найти целое-надо…,чтобы найти часть-…)
-Проверим.(5 слайд)
На доске: x+3=15
х=
х= (Ребёнок решает у доски с
комментированием-обозначим компоненты уравнения, х и 3-это части-подчёркиваем,
а 15-целое-обводим кружочком, неизвестна часть, чтобы…)
Выключаю оборудование.
-Что мы повторили?
(Формулы нахождения площади и стороны прямоугольника и решение уравнения на
сложение)
— Как вы думаете,
почему вы повторяли именно это? (Эти знания нам пригодятся на уроке)
— Какое следующее
задание я вам предложу?(Где есть что-то новое, пробное действие)
Пробное
действие. Фиксация затруднения.
Фиксация затруднения.
3)-Попробуйте на
карточках решить уравнение. (Делают пробное действие)
Пишу на доске
под уравнением на сложение:
x+3=15
x·3=15
-Итак, у кого нет
ответа?
-Что вы не смогли
сделать?(Не смогли решить уравнение)
-У кого есть ответ?
Ты сможешь рассказать алгоритм?
-Что вы не можете
сделать?(Не можем решить уравнение, не можем рассказать алгоритм)
-Какой следующий
шаг на уроке?(Разобраться, в чём у нас затруднение)
3.Выявление места и причины затруднения.(3-4 мин.)
Цель: выявить место и причину
затруднения.
Организация учебного процесса на этапе 3:
-Какое задание вы
должны были выполнить? (Решить уравнение на умножение)
-С каким
затруднением вы столкнулись?(Не можем решить уравнение, не знаем алгоритма)
-Сравним новое
уравнение с тем, которое уже решали.
-Чем они
отличаются?(В новом уравнении вместо знака +,· )
-Покажите место
затруднения. (Выходит к доске и обводит)
(Выходит к доске и обводит)
-Почему же возникло
затруднение?(Не знаем как решить новое уравнение, не знаем алгоритм)
4. Построение проекта выхода из затруднения(4-6 мин.)
Цель: построить план и
определить средства достижения цели.
Организация учебного процесса на этапе 4:
-Какова цель вашей дальнейшей работы?(Узнать алгоритм
решения для новых уравнений)
-Дальше предлагаю
продолжить работу в группах.
-Вспомним правила
работы в группах.(Перечисляют)
-Проверим. (Слайд
6)
-План работы на
парте. Действуйте по плану. Ответственный в группе представляет свой алгоритм.
5.Реализация построенного проекта(5-8 мин.)
Цель: организовать фиксацию
преодоления затруднения.
Организация учебного процесса на этапе 5:
Дети работают в
группах по предложенному учителем плану.
Реши уравнение по
плану:
х·4=12
х=
х=
План
работы (Слайд7)
1. Обозначь компоненты, соответствующие сторонам и площади прямоугольника.
Обозначь компоненты, соответствующие сторонам и площади прямоугольника.
2.Нанеси числа из уравнения на модель.
3.Определи,
что неизвестно.
4.Примени правило.
5.Сформулируй алгоритм решения.
-Проверяем.(Ответственный
из каждой группы выходит, вывешивает свой план и объясняет)
-Какое
задание было дано?(Решить уравнение по плану)
-Расскажите, как вы действовали? (Мы действовали по плану.
Сначала…,потом…)
-Сформулируй
алгоритм.(Обозначь компоненты, нанеси на модель числа, определи-что
неизвестно, вспомни правило и примени)
-Сравним с верным
алгоритмом.(Открываю опору- алгоритм)
Алгоритм
1.Обозначь
компоненты, соответствующие сторонам и площади прямоугольника.
2.Нанеси
числа из уравнения на модель.
3.Определи,
что неизвестно.
4.Примени
правило.
-Молодцы, алгоритм
составили правильно.
-Вернёмся к
пробному действию. Решим уравнение, которое вы не смогли решить, по
алгоритму.(х·3=15 Решает у доски с проговариванием по алгоритму, остальные в
тетрадях)
-Какой формулой при
обозначении компонентов в уравнении на умножение вы пользовались? ( Формулой
№1)
— Как вы думаете,
при решении каких уравнений можно воспользоваться равенствами на деление и
формулой №2(При решении уравнений на деление)
-С ними мы
познакомимся на следующем уроке.
-А сегодня вы сами
открыли новые знания. Составили алгоритм для решения уравнений на умножение.
-Как проверить своё
«открытие»?(Посмотреть в учебник)
-Откройте учебник
на с.1.Сравните ваш алгоритм с алгоритмом в учебнике.
-Смогли вы
преодолеть затруднение?(Да, молодцы)
-Какой следующий
шаг на уроке?(Потренироваться применять алгоритм при решении уравнений на
умножение)
Ф/м Зарядка для
глаз(7 слайд)
6.Первичное
закрепление с проговариванием во внешней речи. (4-5 мин.)
(4-5 мин.)
Цель: зафиксировать во внешней речи умение решать уравнение на умножение по
алгоритму.
Организация
учебного процесса на этапе 6:
1) Фронтальная
работа.
-Выполним задание
№1 в учебнике.
—Первое уравнение решить у доски с комментированием.
-Вариант
комментирования на парте.(Ребёнок решает у доски, проговаривает, опираясь на
алгоритм)
Примерный вариант
комментирования:
1.Обозначаю компоненты, соответствующие сторонам и площади прямоугольника.
2.Наношу числа из уравнения на модель.
3.Определяю,
что неизвестно.
4.Применяю правило, пользуясь формулой №2
2) Работа в парах.
-Для работы в парах
предлагаю задание №1 (2 уравнение).(Учащиеся выполняют задание в парах,
проговаривая вслух с опорой на алгоритм 9·х=27;на партах лежит вариант
для комментирования)
-Проверим.(Один ребёнок
с места комментирует, опираясь на алгоритм)
-Какой следующий шаг на уроке?(Самостоятельная работа)
7. Самостоятельная работа с самопроверкой по эталону.(3-5
Самостоятельная работа с самопроверкой по эталону.(3-5
мин.)
Цель: тренировать способность к
самоконтролю и самооценке.
Организация учебного процесса на этапе 7:
-Для самостоятельной работы предлагаю третье уравнение из
№1: х·8=24
Учащиеся выполняют самостоятельную работу. Далее
проверяют себя по эталону для самопроверки.
-Проверьте себя по
эталону для самопроверки.(8 слайд)(На слайде подробное решение, правило)
-Кто ошибся?
-В чём ошибка?
-Исправьте ошибку.
-Сделайте вывод.
(Нужно ещё потренироваться)
-Кто не ошибся?
-Сделайте вывод.(Мы
всё хорошо усвоили)
8.Включение в систему знаний.(5-8 мин.)
Цель: включить новое знание в
систему знаний.
Организация учебного процесса на этапе 8:
-Теперь предлагаю решить уравнение с проверкой. Какие
знания нам потребуются? №3,(1)
Учащийся у доски выполняет задание с комментированием.
Дети работают в тетради.
9.Рефлексия учебной деятельности на уроке.(2-3 мин.)
Цель: зафиксировать новое
содержание и оценит свою работу на уроке.
Организация учебного процесса на этапе 9:
-(9 слайд)С каким
затруднением мы столкнулись на сегодняшнем уроке?(Мы не знали алгоритма решения
новых уравнений)
-Какую цель вы
перед собой ставили?(Узнать алгоритм решения для новых уравнений)
-Удалось ли достичь
цели? Докажите.(Проговаривают алгоритм)
-(10 слайд)Теперь я
предлагаю вам оценить свою работу на уроке с помощью «лестницы успеха».
-Если допускали
ошибки и вам было сложно-поставьте себя на 1-ю ступеньку.
-Если решали без
ошибок, но у вас остались вопросы-поставьте себя на следующую ступеньку .
-Если вам всё
понятно и легко-поставьте на верхнюю ступеньку.
-Кому было трудно?
Какую задачу перед собой поставите? (Дома потренироваться ещё)
Домашнее задание:
-Дома предлагаю
выполнить задания по выбору в соответствии с индивидуальными затруднениями:
1) Детям, которые
поставили себя на 1-ю и 2-ю ступеньки предлагаю выполнить №2(3) уравнение.
2) Детям, которые
поставили себя на верхнюю ступеньку, предлагаю №3(3) уравнение.(11 слайд)
-Спасибо за работу!
МАТЕМАТИКА: Математика — Академии Фрэнка Х. Петерсона
Все курсы (3)
-
МАТЕМАТИКА 123
- 3 Документы
- 4 Вопросы и ответы
-
МАТЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ
- 5 Документы
-
МАТЕМАТИКА ТРИГОНОМЕТ
- 3 Документы
{[ filteredCoursesMessage ]}
Mathematics Documents
Показаны с 1 по 11 из 11
Просмотреть все
Математика Вопросы и ответы
Показаны с 1 по 4 из 4
Просмотреть все
-
- Подробнее см.
 в приложении
в приложении
- Подробнее см.
-
- Подробнее см. в приложении
-
- мне нужен наборщик и интервал
-
- Подробнее см. в приложении
Снова в школу
Peterson, Allan C.
 [WorldCat Identities]
[WorldCat Identities]
Обзор
| Работы: | 26 работает в 117 публикации в 2 языки и 2123 библиотечные фонды |
|---|---|
| Жанры: | Учебники Академические диссертации |
| Роли: | Коллекционер, htt, автор, участник |
| Классы: | КА431, 515.625 |
Хронология публикации
.
Самые популярные произведения
Allan C Peterson
Теория дифференциальных уравнений: классическая и качественная
Уолтер Дж. Келли (англ.
)
32
выпуски опубликованы
между
2003 г.
а также
2010
в
Английский
и проводится
580 членов WorldCat
библиотеки
Мировой
«Более 300 лет дифференциальные уравнения служили важным инструментом для описания и анализа задач во многих
научные дисциплины. Этот тщательно написанный учебник представляет собой введение во многие важные темы, связанные с
с обыкновенными дифференциальными уравнениями. В отличие от большинства учебников по этому предмету, этот текст включает нестандартные темы, такие как
В отличие от большинства учебников по этому предмету, этот текст включает нестандартные темы, такие как
глава о методах возмущений и раздел в главе 3, в котором показано, как решать дифференциальные уравнения с помощью Mathematica.
коды. В дополнение к нестандартным темам этот текст также содержит современный материал в этой области, а также его классические
темы. Это второе издание обновлено для совместимости с Mathematica версии 7.0, и все коды Mathematica находятся в
сама книга. Это новое издание также содержит 81 дополнительное упражнение, новый раздел в Главе 1, посвященный обобщенной логистике.
уравнение, дополнительную теорему в главе 2, касающуюся фундаментальных матриц, и многие дальнейшие усовершенствования первого издания.
Эту книгу можно использовать как для второго курса обыкновенных дифференциальных уравнений, так и в качестве вводного курса для хорошо подготовленных
ученики. Предпосылками для этой книги являются три семестра исчисления и курс линейной алгебры, хотя необходимые
Предпосылками для этой книги являются три семестра исчисления и курс линейной алгебры, хотя необходимые
концепции из линейной алгебры вводятся вместе с примерами в книге. Нужен курс бакалавриата по анализу
для более теоретических тем, затронутых в последних двух главах ». — Веб-сайт издателя
Разностные уравнения: введение с приложениями
Уолтер Дж. Келли (англ.
Книга
)
32
выпуски опубликованы
между
1991 г.
а также
2006 г.
в
Английский
и проводится
574 члена WorldCat
библиотеки
Мировой
«Встречно-разностные уравнения, второе издание» представляет собой практическое введение в эту важную область решений для
инженерные и физические науки. Тема охвата включает численный анализ, численные методы, дифференциальные уравнения,
Тема охвата включает численный анализ, численные методы, дифференциальные уравнения,
комбинаторика и дискретное моделирование. Отличительной чертой этого пересмотра является разнообразное применение ко многим разделам математики».
— Описания издателя
Динамические уравнения в масштабах времени: введение с приложениями
Мартин Бонер (англ.
Книга
)
12
выпуски опубликованы
в
2001 г.
в
Английский
и проводится
313 член WorldCat
библиотеки
Мировой
Изучение динамических уравнений на цепочке мер (временной шкале) восходит к ее основателю С. Хильгеру (1988) и является новой областью
Хильгеру (1988) и является новой областью
все еще довольно теоретических исследований в области математики. Мотивацией субъекта является представление о том, что динамические уравнения по мере
цепочки могут строить мосты между непрерывной и дискретной математикой. Кроме того, изучение теории цепей мер привело к
несколько важных приложений, например, при изучении моделей популяций насекомых, нейронных сетей, теплопередачи и эпидемий.
модели. Ключевые особенности книги: * Введение в теорию цепей мер; обсуждение его полезности в разрешении
одновременная разработка дифференциальных и разностных уравнений без повторения аналогичных доказательств * Многие
классические формулы или процедуры для дифференциальных и разностных уравнений предстают в новом свете * Новые аналоги многих
изучаемые «специальные функции» * Исследование свойств «экспоненциальной функции» на шкалах времени, которые могут быть
определяется и исследуется с помощью особенно простого линейного уравнения * Дополнительные темы: самосопряженные уравнения,
линейные системы, уравнения высших порядков, динамические неравенства и симплектические динамические системы * Ясное, мотивированное изложение,
начиная с вводных и переходя к более сложному тексту * Большое количество примеров и упражнений в книге
* Решения отдельных задач, требующих только первого семестра исчисления и линейной алгебры, динамических уравнений во времени
Шкалы можно рассматривать как интересный подход к дифференциальным уравнениям посредством непрерывного и дискретного анализа.
Этот подход обеспечивает раннее знакомство со многими приложениями в таких областях, как биология, физика и инженерия. Части
книги может быть использована на семинаре по специальным темам на старших курсах бакалавриата или на начальном уровне магистратуры. Наконец,
работа 9 мая0029
Дискретное дробное исчисление по
Кристофер С. Гудрич (англ.
)
17
выпуски опубликованы
между
2015
а также
2018
в
английский и немецкий
и проводится
307 член WorldCat
библиотеки
Мировой
Этот текст представляет собой первое всестороннее рассмотрение дискретного дробного исчисления. Опытные исследователи найдут
Опытные исследователи найдут
текст полезен в качестве справочника по дискретному дробному исчислению и актуальным темам. Студенты, которым интересно
при изучении дискретного дробного исчисления этот текст станет полезной отправной точкой. Несколько упражнений
предлагаются в конце каждой главы, а избранные ответы приведены в конце книги. Презентация содержания
разработан, чтобы обеспечить достаточную гибкость для потенциального использования во множестве курсов и для самостоятельного изучения. Новый подход
предпринятые авторами, включают одновременное рассмотрение разностного исчисления дробного и целого порядка (на множестве
масштабов времени, включая как обычные прямые, так и обратные разностные операторы). Читатель получит прочную основу
в классических темах дискретного исчисления, знакомясь с захватывающими недавними разработками, доводя их до
границы предмета. Большинство глав могут быть охвачены или опущены, в зависимости от опыта учащегося. Например,
Большинство глав могут быть охвачены или опущены, в зависимости от опыта учащегося. Например,
текст может быть использован в качестве основного справочного материала во вводном курсе по разностным уравнениям, который также включает в себя дискретные
дробное исчисление. Главы 1-2 представляют собой базовое введение в дельта-исчисление, включая дробное исчисление на
набор целых чисел. Для курсов, где студенты уже имеют опыт элементарного реального анализа, могут быть рассмотрены главы 1-2.
быстро, а затем читатели могут перейти к главам 6-7, в которых представлены некоторые основные результаты в задачах с дробными краевыми значениями.
(ФБВП). Главы 6-7 в сочетании с некоторыми современными литературными данными, перечисленными в библиографии, могут служить основой для
семинар по современной теории FBVP. В рамках двухсеместрового курса главы 1–5 могут быть рассмотрены более подробно, что дает очень
подробное введение как в дискретное дробное исчисление, так и в исчисление целочисленного порядка
Улучшения в динамических уравнениях во временных масштабах на
Мартин Бонер (англ.
Книга
)
1
издание опубликовано
в
2003 г.
в
Английский
и проводится
120 членов WorldCat
библиотеки
Мировой
Тема динамических уравнений во временных масштабах продолжает оставаться быстро растущей областью исследований. За основной мотивацией
ключевой концепцией предмета является то, что динамические уравнения во временных масштабах являются способом объединения и расширения непрерывных и
дискретный анализ. Эта работа выходит за рамки более раннего вводного текста Dynamic Equations on Time Scales: An Introduction with
Applications (ISBN 0-8176-4225-0) и предназначен для второго курса динамических уравнений на уровне выпускников. Ключевая особенность
Ключевая особенность
книги: отличный вводный материал по исчислению масштабов времени и динамических уравнений * многочисленные примеры и
упражнения * охватывают следующие темы: экспоненциальная функция на шкале времени, краевые задачи, положительные решения,
верхние и нижние решения динамических уравнений, теория интегрирования во временных масштабах, неосцилляция и динамические уравнения более высокого порядка,
динамические уравнения дельта, набла и альфа во временных масштабах * единое и систематическое изложение вышеуказанных тем с хорошим
переходы от главы к главе * полезны для второго курса динамических уравнений на уровне выпускника, с направлениями
предлагается для будущих исследований * исчерпывающая библиография и указатель * полезен в качестве всеобъемлющего ресурса для чистой и прикладной
математики Соавторы: Р. Агарвал, Э. Акин-Бохнер, Д. Андерсон, Ф. Мердивенчи Атичи, Р. Эйвери, М. Бонер, Дж. Буллок,
Агарвал, Э. Акин-Бохнер, Д. Андерсон, Ф. Мердивенчи Атичи, Р. Эйвери, М. Бонер, Дж. Буллок,
Дж. Дэвис, О. Досли, П. Элоэ, Л. Эрбе, Г. Гусейнов, Дж. Хендерсон, С. Хилгер, Р. Хилшер, Б. Каймакалан, К. Мессер, Д. О’Реган,
А. Петерсон, Х. Тран, В. Инь
Дискретные гамильтоновы системы: разностные уравнения, непрерывные дроби и уравнения Риккати
Кэлвин Д Альбрандт (англ.
Книга
)
2
выпуски опубликованы
в
1996 г.
в
Английский
и проводится
112 член WorldCat
библиотеки
Мировой
Предоставляет базовую работу для студентов инженерных специальностей, изучающих оптимальное управление и оценку, а также вариационные задачи.
возникает в физике, химии и экономике
Достижения в области динамических уравнений во временных масштабах (
)
в
Английский
и проводится
19 член WorldCat
библиотеки
Мировой
Дискретные гамильтоновы системы: разностные уравнения, непрерывные дроби и уравнения Риккати
Кэлвин Д Альбрандт (англ.
)
в
Английский
и проводится
18 член WorldCat
библиотеки
Мировой
Динамические уравнения на временных шкалах: Введение в приложения
Мартин Бонер (англ.
)
в
Английский
и проводится
18 член WorldCat
библиотеки
Мировой
Теория дифференциальных уравнений: классическая и качественная
Уолтер Дж. Келли (англ.
)
1
издание опубликовано
в
2010
в
Английский
и проводится
15 член WorldCat
библиотеки
Мировой
Теория дифференциальных уравнений: классическая и качественная
Уолтер Дж. Келли (англ.
Келли (англ.
)
1
издание опубликовано
в
2010
в
Английский
и проводится
13 член WorldCat
библиотеки
Мировой
Дискретные гамильтоновы системы: разностные уравнения, непрерывные дроби и уравнения Риккати
Кэлвин Д Альбрандт (англ.
)
1
издание опубликовано
в
1996 г.
в
Английский
и проводится
12 член WorldCat
библиотеки
Мировой
Эта книга должна быть доступна для студентов, прошедших первый курс теории матриц. Теорема существования и единственности
Теорема существования и единственности
из главы 4 требует теоремы о неявной функции, но мы даем автономное конструктивное доказательство этой теоремы. Читатель
желающие принять теорему о неявной функции могут читать книгу без углубленного изучения исчисления. Глава 8 использует
псевдоинверсия Мура-Пенроуза, но доступна для студентов, умеющих работать с матрицами. Упражнения размещаются в тех.
те места в тексте, где они уместны. Для университетов США мы предполагаем, что книга будет использоваться на старших курсах бакалавриата.
уровень или начальный уровень выпускника. Глава 2, посвященная непрерывным дробям, не имеет существенного значения для материала остальных
главы, но тесно связана с остальным материалом. Непрерывные дроби обеспечивают представление замкнутой формы
экстремальные решения некоторых дискретных матричных уравнений Риккати. Методы решения непрерывных дробей для разности Риккати
Методы решения непрерывных дробей для разности Риккати
уравнения обеспечивают подход, аналогичный методам решения рядов для линейных дифференциальных уравнений. Книга развивает несколько
тем, которые не были доступны на этом уровне. В частности, материал глав о цепных дробях (гл.
2), симплектические системы (глава 3) и теория дискретных вариаций (глава 4) обобщают недавнюю литературу. Точно так же
материал по преобразованию уравнений Риккати, представленный в главе 3, дает самостоятельную унификацию различных форм уравнений Риккати.
уравнения. Мотивация для нашего подхода к разностным уравнениям исходила из работ Харриса, Вогана, Хартмана, Рида, Патулы,
Хукер, Эрбе и Ван и Бонер
Разностные уравнения по
Уолтер Дж. Келли (англ.
Книга
)
2
выпуски опубликованы
в
1991 г.
в
Английский
и проводится
3 член WorldCat
библиотеки
Мировой
Распределение нулей решений линейных дифференциальных уравнений четвертого порядка по
Аллан С. Петерсон (англ.
Книга
)
1
издание опубликовано
в
1968 г.
в
Английский
и проводится
2 член WorldCat
библиотеки
Мировой
Об асимптотике решений уравнений Эмдена-Фаулера на временных шкалах
Линн Эрбе (англ.
)
1
издание опубликовано
в
2010
в
Английский
и проводится
2 член WorldCat
библиотеки
Мировой
Краевые задачи для дискретных дробных уравнений Пушпа Авасти(
)
1
издание опубликовано
в
2013
в
Английский
и проводится
2 член WorldCat
библиотеки
Мировой
В этой диссертации мы развиваем некоторые аспекты теории дискретного дробного исчисления. Автор начинает с
Автор начинает с
введение в дискретное дельта-исчисление вместе с дробным дельта-исчислением, которое используется в этой диссертации.
Функция Коши, функция Грина и некоторые их важные свойства для дробной краевой задачи
разрабатываются. Данная диссертация состоит из четырех глав. В первой главе мы вводим дробное дельта-исчисление.
Во второй главе мы даем некоторые предварительные определения, свойства и теоремы для дробного дельта-исчисления и
вывести соответствующую функцию Грина и указать некоторые ее важные свойства. Это позволяет доказать некоторые важные
теоремы, используя известные теоремы о неподвижной точке. В третьей главе мы изучаем и доказываем различные результаты, касающиеся так называемого
самосопряженное уравнение с краевыми условиями типа Штурма-Лиувилля. В четвертой главе мы доказываем некоторые теоремы, касающиеся
В четвертой главе мы доказываем некоторые теоремы, касающиеся
существование и единственность положительного решения вынужденного дробного уравнения с конечным пределом
Асимптотическое поведение линейных динамических уравнений во временных масштабах Дженнифер Л. Лэнгдон(
)
1
издание опубликовано
в
2005 г.
в
Английский
и проводится
2 член WorldCat
библиотеки
Мировой
Уравнения динамики с запаздыванием с устойчивостью Дугласа Р. Андерсона (
)
1
издание опубликовано
в
2006 г.
в
Английский
и проводится
2 член WorldCat
библиотеки
Мировой
Краевая задача Капуто в дробном исчислении Набла
Юлия Сент-Гоар(
)
1
издание опубликовано
в
2016
в
Английский
и проводится
2 член WorldCat
библиотеки
Мировой
Краевые задачи уже давно вызывают интерес в контексте непрерывных дифференциальных уравнений. Однако с появлением
Однако с появлением
таких новых областей, как исчисление дробей Наблы, мы можем рассматривать такие проблемы в новых контекстах. В данной работе мы рассмотрим
несколько правых фокусных краевых задач с оператором дробной разности Капуто в дробном исчислении Наблы
контекст. Будут исследованы свойства функций Грина для каждой из этих краевых задач и, в случае
конкретной краевой задачи, используемой для установления существования положительных решений нелинейной версии
краевая задача
Экспоненциальная устойчивость динамических уравнений во временных масштабах по
Аллан С. Петерсон (англ.
)
1
издание опубликовано
в
2005 г.
в
Английский
и проводится
2 член WorldCat
библиотеки
Мировой
больше
меньше
Уровень аудитории
| 0 | 1 | |||
| Общий | Специальный | |||
Уровень аудитории:
0,00
(из
0,00
за
Теория
. .. к
.. к
0,00
за
Теория
…)
Связанные личности
- Келли, Уолтер Г. Автор
- Bohner, Martin 1966- Автор Коллекционер
- Гудрич, Кристофер С. Автор
- Альбрандт, Кэлвин Д. Автор
- Петерсон, Аллан К. 1942-
- Springer International Publishing Publishing
- SpringerLink (онлайн-сервис) Другое
- Университет Небраски – Линкольн
- Эрбе, LH 1941-
- Raffoul, Youssef N.

 Части в полученной записи подчеркиваются чертой, целое обводится замкнутой линией. Затем данное отношение моделируется на числах, затем на отрезках. В подготовительный этап входит изучение сравнения совокупностей. Совокупности сначала сравниваются по наполнению группы (по факту), а затем по количеству предметов. Для решения уравнений важно то, что изображено слева, так как дети будут решать уравнения с мешками и находить в целом ту часть, которая известна. Для этого ученики устанавливают взаимно однозначное соответствие, ищут те же самые элементы. Важное направление подготовительной работы – заполнение пропусков в равенствах, так называемые примеры с «окошками». Следует обратить внимание на предлагаемые способы заполнения окошек: подбор; с помощью числового отрезка; на основе связи между целым и частью. На подготовительном этапе у учащихся формируется представление о равенстве, так как уравнение – это равенство.
Части в полученной записи подчеркиваются чертой, целое обводится замкнутой линией. Затем данное отношение моделируется на числах, затем на отрезках. В подготовительный этап входит изучение сравнения совокупностей. Совокупности сначала сравниваются по наполнению группы (по факту), а затем по количеству предметов. Для решения уравнений важно то, что изображено слева, так как дети будут решать уравнения с мешками и находить в целом ту часть, которая известна. Для этого ученики устанавливают взаимно однозначное соответствие, ищут те же самые элементы. Важное направление подготовительной работы – заполнение пропусков в равенствах, так называемые примеры с «окошками». Следует обратить внимание на предлагаемые способы заполнения окошек: подбор; с помощью числового отрезка; на основе связи между целым и частью. На подготовительном этапе у учащихся формируется представление о равенстве, так как уравнение – это равенство.