Математика 2 класс дидактический материал: Книга: «Математика. 2 класс. Дидактические материалы. В 2-х частях. Часть 2. ФГОС» — Виктория Рудницкая. Купить книгу, читать рецензии | ISBN 978-5-360-11524-3

Математика. 2 кл. Дидактические материалы. В 2-х ч. (Комплект). Начальная школа XXI века (ФГОС), Рудницкая В.Н. | ISBN: 978-5-360-05185-5

Рудницкая В.Н.

Аннотация

Пособие включает разнообразные задачи и упражнения по
всем основным содержательным линиям программы по
математике для 2 класса. Предлагаемые материалы
помогут учителю организовать работу по
совершенствованию и развитию арифметических,
логических и геометрических представлений
первоклассников. Предназначено для использования как
на уроках, так и во внеклассной и индивидуальной
работе с учащимися в школах любого типа.

Дополнительная информация

Регион (Город/Страна где издана):	Москва
Год публикации:	2014
Страниц:	160
Ширина издания:	205
Высота издания:	260
Вес в гр. :	302
Язык публикации:	Русский
Тип обложки:	Мягкий / Полужесткий переплет
Цвета обложки:	Белый, Бронзовый/желто-коричневый
Полный список лиц указанных в издании:	Рудницкая В.Н.

ГДЗ по Математике для 2 класса дидактические материалы Козлова С.А., Гераськин В.Н., Волкова Л.А. ФГОС

Авторы: Козлова С.А., Гераськин В.Н., Волкова Л.А..

Издательство:

Баласс 2014

«ГДЗ по Математике 2 класс дидактические материалы Козлова, Гераськин, Волкова (Баласс)» – сборник верных ответов, предназначенный для учащихся российских общеобразовательных учреждений. К помощи данного пособия могут прибегать не только школьники, но и их родители, а также педагоги. В представленном решебнике вы найдете:

1. Разборы заданий по каждому из 104 уроков.
2. Верные ответы к разделу, посвященному отработке вычислительных навыков.
3. Подробное описание текстовых задач.

Представленный сборник поможет упростить жизнь маленькому ученику, при этом не нанося ущерб качеству знаний. Открыв ГДЗ, ребенок сможет проверить уже выполненные задания, обнаружить новые методы решения и сделать работу над ошибками.

Рабочая программой с решебником дидактических материалов по математике для 2 класса от Козловой

Новая ступень школьного образования всегда предвещает много интересных открытий. Программа для малышей действительно насыщена разнообразными темами, например:

1. Порядок действий и выражений со скобками.
2. Действие и знак умножения.
3. Деление на равные части.
4. Задание на увеличение и уменьшение числа в несколько раз.
5. Определение цены, количества и стоимости.

Выполняя практические упражнения, направленные на развитие логического мышления, вычислительных навыков и расширения кругозора, учащийся заложит прочную базу фундаментальных знаний для дальнейшего обучения и успешного освоения таких предметов, как алгебра, химия, физика, геометрия в старших классах.

Когда нужно использовать ГДЗ

«ГДЗ к дидактическим материалам по Математике за 2 класс Козлова С. А., Гераськин В. Н., Волкова Л. А. (Баласс)» – многофункциональный помощник, научившись работать с которым в юном возрасте, ребенок закладывает полезную привычку. Если вы замечаете, что второклассник потерял мотивацию, учебная деятельность вызывает негативные ассоциации, он стал приносить плохие оценки и не может справиться с заданиями без посторонней помощи, решебник – это то, что нужно.

Даже в том случае, если школьник абсолютно самостоятелен, с легкостью справляется со всеми упражнениями, что иногда также приводит к потере интереса, вы можете дополнить его подготовку готовыми домашними заданиями. Вы обязательно найдете там что-то новое, увидите более эффективные и рациональные способы выполнения задач, и второклассник снова начнет посещать уроки с любопытством. Главное, сразу объяснить своему чаду, что ГДЗ не для механического переписывания ответов, они служат дополнительным ресурсом для успешной учебы.

Книга «Математика: 2 класс. Дидактический материал. Разрезные карточки» из жанра Дидактические материалы, практикумы

Математика: 2 класс. Дидактический материал. Разрезные карточки

	Автор: Стромчинская Е.М. Жанр: Дидактические материалы, практикумы Издательство: Учитель Год: 2009 Количество страниц: 175 Формат:  PDF (8. 75 МБ) Дата загрузки: 11 августа 20112012-09-24 Скачать с нашего сайта Скачать в два клика Поделись с друзьями!
Аннотация В настоящем пособии предложен дидактический материал по математике для 2 класса. Задания-карточки предназначены для организации самостоятельной дифференцированной работы обучающихся и содержат разнообразный материал, который может быть использован на различных этапах изучения темы. Данное пособие окажет помощь учителю в подборе дополнительных заданий как для усвоения, так и закрепления программного материала. Пособие адресовано учителям начальной школы, может быть полезно студентам педагогических заведений, а также родителям.
Комментарии Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикаци.

Картотека дидактических игр по математике, 2 младшая группа

Рекомендуемые материалы по математике: Математика для 2 класса

Приборная доска

Математика 2 класс

Предлагаемые математические материалы

Перейти к содержанию

Приборная доска

• Авторизоваться

• Приборная панель

• Календарь

• Входящие

• История

• Помощь

Закрывать

• 
  Мой Dashboard
  
• Математика 2 класс
• Страницы
• Рекомендуемые материалы по математике

северо-восток

• Главная
• Мартики
• Закрытие
• Банк ресурсов
• Курс 1 класса
• Курс класса
• Учебная программа
• Учебный план 9001
• Семья класса и сообщество
• СОЕДИНЕНИЯ
• Google Drive
• HCPS. я

Математические стандарты, которые чаще всего неправильно понимают во 2 классе

Когда меня попросили расширить серию статей о самых непонятых стандартах до классов K, 1 и 2, я ухватился за эту возможность. У меня дома четверо сыновей, которые часто говорят, что я никогда не упускаю возможности поговорить о математике и преподавании! Я также заядлый читатель и пользователь предыдущих постов этой серии для 3-8 классов, поэтому я был рад внести свой вклад в это!

В своей роли тренера по математике и путешествуя по стране, работая с преподавателями по согласованному обучению математике, я заметил некоторые общие моменты в обучении в классе K-2, возникающие из-за непонимания математических стандартов.Преподавание математики в начальных классах совсем не начальное! Это сложная работа, требующая обучения и пристального внимания к обучению, особенно когда учителя углубляются в развитие у учащихся концептуального понимания фундаментальной математики в младших классах. Я надеюсь, что этот пост поможет вам задуматься и научиться поддерживать своих юных математиков!

Инструкция

Стандарт	Общая смещенная инструкция
2.OA.A.1 Используйте сложение и вычитание в пределах 100 для решения одно- и двухшаговых задач со словами, включающих ситуации сложения, взятия, сложения, разъединения и сравнения с неизвестными во всех позициях, например, с помощью использования рисунки и уравнения с символом неизвестного для представления проблемы.	Инструкция ориентирована на определение ключевых слов для решения задачи. Инструкция акцентирует внимание на методах получения ответов, а не на математическом мышлении и осмыслении. При обучении не учитываются все 15 типов задач на сложение и вычитание или игнорируются типы задач, которые учащиеся должны освоить к концу второго класса. Мы хотим, чтобы студенты: Придайте смысл, продумывая контекст ситуации, чтобы определить, какую операцию использовать. Иметь преднамеренные возможности участвовать в решении проблем всех типов.* *Распространенные ситуации сложения и вычитания можно найти здесь .
2.OA.C.4 Используйте сложение, чтобы найти общее количество объектов, расположенных в прямоугольных массивах до 5 строк и до 5 столбцов; напишите уравнение, выражающее сумму в виде суммы равных слагаемых.	выходит за рамки стандартов уровня обучения и вводит умножение до уровня 3 rd .
2.NBT.A.4 Сравните два трехзначных числа на основе значений цифр сотен, десятков и единиц, используя символы >, = и < для записи результатов сравнения.	Инструкция сосредоточена на процедуре без понимания разрядного значения. Инструкция делает упор на упорядочивание чисел с использованием процедурных стратегий, а не на сравнение, основанное на более глубоком понимании трехзначных чисел. Инструкция рассматривает это обучение как новый навык, а не намеренно опирается на обучение в первом классе, делая связи со сравнением двузначных чисел. Мы хотим, чтобы студенты: Развивайте глубокое понимание ценности места и демонстрируйте это понимание, выполняя различные задания.Вот несколько примеров. Развитие концептуального понимания, начатого в 1 классе (1.NBT.B.3)
2.NBT.B.7 Сложение и вычитание в пределах 1000 с использованием конкретных моделей или рисунков и стратегий, основанных на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием; связать стратегию с письменным методом. Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.	Инструкция фокусируется только на процедурных методах для стандартного алгоритма* без построения концептуального понимания. Обучение сосредоточено на следующих шагах в процедуре и не способствует пониманию учащимися сложения или вычитания одинаковых единиц или составления и разложения единиц десятков и сотен. Мы хотим, чтобы студенты: Установите связь между конкретными и графическими представлениями, системой разрядных значений и отношениями между операциями сложения и вычитания. *Язык «по стандартному алгоритму» не вводится в стандарты до 4 класса.
2.MD.B.6 Представлять целые числа в виде длин от 0 на числовой линейной диаграмме с равноотстоящими точками, соответствующими числам 0, 1, 2, …, и представлять суммы и разности целых чисел в пределах 100 на числовой линейной диаграмме.	Инструкция сосредоточена на процедуре или этапах процесса, а не на понимании того, как сложение и вычитание длины могут быть представлены на числовой прямой. Инструкция сосредоточена на использовании числовой линии в качестве стратегии сложения и вычитания. Мы хотим, чтобы студенты: Поймите, что числовая линия имеет определенные атрибуты, подобные линейке. Они должны понимать, что каждая отметка представляет собой число, что числа идут подряд, а расстояние между одинаковыми отметками неизменно одинаково.

Я хотел бы более подробно рассмотреть два моих любимых стандарта, оба из которых требуют согласованного обучения для формирования у учащихся концептуального понимания фундаментальных математических идей: 2.НБТ.Б.7 и 2.МД.Б.6. Давайте копать!

2.НБТ.Б.7

Сложение и вычитание в пределах 1000 с использованием конкретных моделей или рисунков и стратегий, основанных на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием; связать стратегию с письменным методом. Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.

Сколько я себя помню учителем начальных классов и тренером по математике, стандартный алгоритм сложения и вычитания был проблематичным. Учащиеся могут научиться этому как процедуре, без понимания, от благонамеренных учителей или родителей. Меня даже в детстве так учили! Теперь мы знаем, насколько важно для студентов понять «почему» за процедурой. Это лучше готовит их к будущей математике и углубляет их понимание порядкового значения и операций сложения и вычитания, которые позже будут применяться для более успешного понимания дробей, десятичных знаков и работы по алгебре.

Когда я вижу задачу вроде 600 – 432, я знаю, что есть много разных способов помочь учащимся решить это выражение. Студенты, скорее всего, разложат одну из 6 сотен на 10 десятков, а затем разложат десятку на 10 единиц. После того, как 600 написано, нарисовано или представлено конкретными объектами, такими как блоки с основанием 10 или дисками с разрядным числом, как 5 сотен, 9 десятков и 10 единиц, учащиеся могут вычитать. Можно показать эту работу, используя письменный метод, напоминающий стандартный алгоритм, если установлены явные связи между различными представлениями (моделями или чертежами) и письменным методом.См. пример ниже.

Другим способом решения 600–432 для учащихся может быть использование сложения, сложения из 432, тем самым подчеркивая связь между сложением и вычитанием.

Важным следствием обучения при работе с 2.NBT.B.7 является то, что нельзя переходить к процедурному обучению до того, как учащиеся поймут смысл системы разрядов при сложении и вычитании в пределах 1000. Дайте учащимся возможность разработать свои собственные методы решения, помогите им установить связи между представлениями и методами и перейти к эффективности процедуры после того, как будет развито концептуальное понимание.

2.MD.B.6

Представлять целые числа как длины от 0 на линейной диаграмме с равноотстоящими точками, соответствующими числам 0, 1, 2, …, и представлять суммы и разности целых чисел в пределах 100 на линейной диаграмме.

Помню, в начале моей преподавательской карьеры, 20 лет назад (здесь я встречаюсь с самим собой!), и много лет спустя я преподавал числовую прямую как стратегию или метод сложения и вычитания для своих первоклассников.Была вовлечена милая лягушка и много говорили о «прыжках» на числовой прямой. Студенты «использовали» эту стратегию и в большинстве случаев приходили к правильному ответу, но понятия не имели, что они делают. Они определенно не связывали числовую прямую с единицами длины и не считали эти единицы. Я мог бы все еще делать это сегодня, если бы не учился у некоторых замечательных Основных Защитников и учителей-лидеров!

В стандартах есть три места, где прямо упоминается числовой ряд: здесь во 2-м классе, в 3-м классе, посвященном дробям как числам, и снова в 6-м классе, когда учащиеся изучают рациональные числа.Числовая линия намеренно не используется до 2-го класса. Также намеренно она вводится с подсчетом «длины». Важно отметить, что заголовок кластера для 2. MD.B.6 относится к «Связать сложение и вычитание с длиной».

Диаграммы с числовыми линиями могут быть сложными для учащихся, поскольку они используют единицы длины, которые труднее увидеть и сосчитать, чем конкретные объекты или изображения. Диаграммы с числовыми линиями вводятся во 2 классе, когда учащиеся имеют опыт подсчета единиц длины на измерительных инструментах, которые по сути представляют собой специальные диаграммы с числовыми линиями.Важно помочь учащимся «видеть» единицы длины, которые считаются между конечными точками, а также числа, обозначающие конечные точки длин от 0,

.

Давайте посмотрим на это задание из учебного плана Engage NY:

Вы увидите, что учащиеся используют числовую прямую для представления длины в сантиметрах. Они добавляют «больше» к заданному числу, а затем составляют соответствующее уравнение. Эта задача иллюстрирует сложность и цель 2.MD.B.6 без процедур или акцентирования ответа.

Я надеюсь, что это помогло вам изучить и поразмышлять над мощными, согласованными инструкциями по математике. Я также надеюсь, что это может дать вам новые идеи для преподавания математики в 2 ^и классах. Я с нетерпением жду вашего ответа и продолжения этой беседы! Пожалуйста, оставьте свои комментарии ниже или вы можете найти меня в Твиттере @mrsmillergrade1. Следите за новостями о моих оценках K и 1!

Обучение математике. 2 класс. | Академия цветущих умов |

1. Первый и самый важный аспект преподавания математики во 2 классе – это понимание общих основных требований к учащимся этого возраста.Пожалуйста, перейдите по ссылке ниже, чтобы изучить.

2. Далее необходимо понимать российские требования. Пожалуйста, читайте и изучайте. Требования по математике для Российской Федерации.

3. БМА STEAM обучает детей по программам математики в следующих странах: Россия, Беларусь, США, Сингапур. Пожалуйста, ознакомьтесь с подходами.

4. Изучите психологию ребенка 7 лет: https://vseprorebenka.ru/vospitanie/psihologija/krizis-7-let-u-rebenka. html, https://www.verywellfamily.com/7-year-old-developmental-milestones-620704

5.  Основной подход: первоочередной задачей учителя является мотивировать ребенка к развитию сильного интереса к математике путем обучения этому предмету путем сочетания обучения, групповой работы и игр. Учителю крайне важно понимать особенности физического, познавательного и психологического развития детей 7-9 лет. 

6. Ниже представлена ​​структура плана урока, которую мы хотели бы видеть на каждом уроке:

Соберите домашнее задание до начала урока.

Урок Plan
Manital Mathth	Подсчитайте и назад и обратно, охватывают номера на номер.	Числовая строка над полем	3 мин.
	Пропустить счет на 2 с, 3 с, 5 с, 10 с; Умновидение / практика подразделения (когда придет время)	Postboard	2 мин	2 мин
соседей номер, числа между заданными числами, числами больше, менее чем	линия Boardnumber	3 мин
	Основы числового состава, сложения, вычитания	Счетчики, другие предметы.	2 мин.
Введение новой темы	Введение темы по программе	Разноплановые игровые материалы, распечатки, игры.	5 мин	5 мин
Практика новой темы	Упражнения для независимой практики	Распечатать выходы, книги, ноутбуки	10 мин
логика	ввести упражнения для логического развития студентов	Или упражнения для логического развития	10 мин	10 мин
Упражнения на предыдущий урок	Упражнения для пересмотра	Упражнения для пересмотра Материал в последнем уроке	Распечатать, работа на белой доске	5 мин
Домашнее задание	Дайте домашнее задание.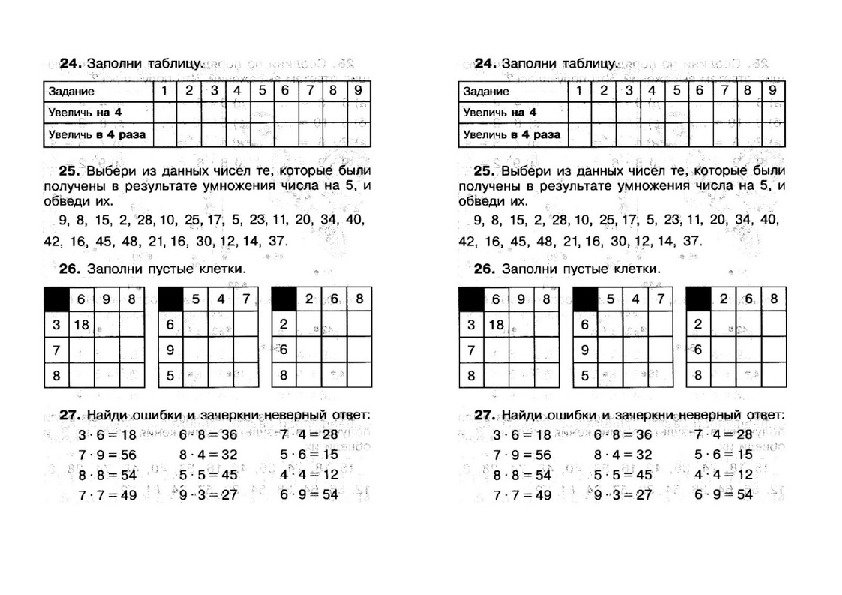 Проверка домашнего задания к следующему уроку. Спросите, если ученики что-то не поняли.	Поместите домашнее задание в папку каждого учащегося.	5 мин.

Перед каждым занятием спрашивайте учащихся, не поняли ли они неправильно некоторые упражнения из домашней работы. Если вы видите, что у 50 % класса возникли трудности с выполнением некоторых заданий, включите работу над этим заданием в начале занятия. Сократите время на умственную арифметику и проработайте недоразумения.

7. Так как классы небольшие, предусмотрите самостоятельную работу на уроке.Можно 5 минут. В это время проверяйте домашнее задание учащихся. Убедитесь, что у вас есть готовые ответы, так как это облегчит вашу работу. Если ответ неверный, ищите процесс. Возможно, у студента была правильная логика, просто он допустил простую ошибку в расчетах. Ищите ошибки во всем классе. Проанализируйте ошибки; посмотрите, как вы можете повторно представить тему, чтобы все учащиеся ее поняли.

8. Политика BMA STEAM заключается в том, чтобы продвигать класс вперед в соответствии с самым сильным учеником в классе.Если в классе есть большое расхождение в уровне учеников, поговорите с директором, чтобы найти наилучший подход к персонализации работы класса, чтобы обеспечить прогресс каждого ученика. Обычно добавляют дополнительную работу для более продвинутых учеников, чтобы поддерживать их мотивацию.

9. Учитель обязан подготовить к каждому уроку следующее:

            1) План урока

            2) Распечатки классных работ (если в классе еще нет учебника и рабочей тетради)

            3) Домашнее задание

            4) Дополнительный материал для продвинутых учащихся или отстающих.

            5) Определите игры/материалы, используемые в классе, и подготовьте их до начала занятия.

10. Методика обучения математике в этом возрасте:

1. Состав числа:

5 = 0 + 5; 1 + 4; 2 + 3; 3 + 2; 4 + 1; 5 + 0

1. Перед переходом к сложению или вычитанию в столбик делаем это мысленно и подряд.
2. Сложение над десяткой: 7 + 8 = 7 + 3 + 5 = 10 + 5 = 15 (дети должны записать на миллиметровке)
3. Научить учащихся писать аккуратно на миллиметровке: должно быть 1 число на квадрат, а если потом они будут работать в столбце, то числа должны быть записаны точно одно под другим.Учителя должны исправлять учеников и поощрять их писать аккуратно.
4. Работа над пониманием разницы между десятками и единицами.
5. Решение проблем должно осуществляться в соответствии со следующими шагами:
   1. Определите, что мы знаем. Подчеркните ключевые факты.
   2. Четко понять, что требуется/вопрос.
   3. Подумайте о стратегиях решения проблемы. Рисуйте, когда это возможно.
   4. Решить.
   5. Проверьте ответ.

11.  Основной подход: нам нравится пробуждать интерес учащихся к математике.В этом возрасте дети еще верят в волшебство, они открыты и целеустремленны. Работа учителя состоит в том, чтобы быть партнером учеников в процессе обучения, а не тем, кто насильно их учит. Учитель обязан найти способы сделать урок интересным. Мы видим детей как цветок, и чтобы цветок расцвел, мы не можем дернуть его за листья; мы можем только питать почву.

12.  Дисциплина . Иногда у всех учителей есть ученики, которые не принимают активного участия или не мешают классу.В редких случаях, когда это АБСОЛЮТНО необходимо, учителя могут наказать учеников, посадив их на стул для «непослушных» учеников. Максимальное время, в течение которого учащиеся могут оставаться там, составляет минуту в зависимости от их возраста. Пожалуйста, поймите, что такая суровая дисциплина — это крайняя мера. Мы считаем, что обязанностью учителя является поддержание интереса и интереса в классе, что обычно предотвращает плохое поведение в классе. Если вы постоянно сталкиваетесь с плохим поведением, обратитесь к директору. Общением с родителями будет заниматься директор.Пожалуйста, воздержитесь от ругани ребенка перед его родителями. Мы считаем это непрофессионализмом и отсутствием опыта.

13.  Общение с родителями : пожалуйста, поговорите со своим директором до любого общения с родителями. Родители – это люди, которые очень заботятся о своих детях и иногда очень щепетильно относятся к любым вопросам, которые могут возникнуть в классе. Мы с уважением относимся к их чувствительности и стараемся общаться в абсолютно позитивной, уважительной и полезной манере. Пожалуйста, не переходите эти границы.

14.  Материалы . Как только вы начнете работать в BMA STEAM, вам будет показано местонахождение материалов, которые у нас есть на данный момент. Если вы чувствуете, что дополнительные материалы помогут, пожалуйста, поговорите с директором. Если у нас есть бюджет для этого, мы сделаем все возможное, чтобы получить его.

Спасибо, что стали частью нашей семьи BMA STEAM. Мы рады видеть вас в качестве нашего учителя, и мы искренне верим, что вам также понравится это академическое путешествие, поскольку у нас есть замечательные ученики, которые в большинстве случаев хотят учиться.

Материалы для дистанционного обучения | Karen Fuson Math

Моя математическая программа Math Expressions тщательно спроектировала классную среду для изучения определенных понятий. В детском саду и в первом классе они включают в себя манипуляции, которые дети используют для создания чисел или отношений. Для каждого класса есть свои манипуляторы. Дети описывают то, что они видят, сравнивают и противопоставляют то, что делают они и другие, и изучают словарный запас и понятия, взаимодействуя с этой манипулятивной обучающей средой.Дети также рисуют математические рисунки во всех классах, часто используя специальные большие доски MathBoards, которые содержат специальные средства обучения для каждого класса. Поскольку в 2020/21 учебном году многим школам придется частично или полностью проводить обучение дистанционно, нам необходимо иметь цифровые версии этих учебных сред, в которых дети могли бы перемещать предметы, мастерить предметы и рисовать. Как и в классе, учителю необходимо видеть, что делают все дети, чтобы была возможна обратная связь, и учитель может выбирать примеры для обсуждения со всеми детьми. Поддержка учителей в максимально возможной степени для организации в классе сообщества «Разговоры о воспитании математики» имеет жизненно важное значение для эмоционального и концептуального функционирования учащихся и учителей.

 

Поэтому я работал с двумя опытными учителями математических выражений, Робин Декер и Шэннон Киблер, которые работали со многими школьными округами, поддерживая учителей в разработке и использовании в классе Сообщества развивающих математических разговоров. Ежедневные занятия в детском саду, 1-м и 2-м классах, а также быстрые практические занятия во всех классах, начиная с детского сада и заканчивая 6-м классом, имеют решающее значение для построения сложных и центральных математических понятий и для создания чувства общности, когда дети вместе занимаются этими упражнениями.Это трудно сделать без плакатов и манипуляторов, используемых в классе. Поэтому мы создали цифровые наборы слайдов в Google Slides, чтобы учителя могли использовать их для удаленного выполнения этих ежедневных рутин и быстрых практических занятий. Студенческие лидеры также могут вести их, как в классе, с физическими материалами. Преподаватель может дать ссылку на Quick Practices конкретным учащимся, которые будут руководителем учащегося, и сказать им, какие слайды использовать. Студенческий лидер показывает свой экран и включает микрофон, чтобы все учащиеся могли видеть и слышать, как студенческий лидер ведет быструю практику или ежедневную рутину.

 

Учащимся также необходимы специальные большие доски Math Expressions MathBoards, которые содержат специальные средства обучения на уровне класса и манипуляции на уровне класса, включая карточки стратегии/беглости. Эти манипуляторы и карточки можно раздать учащимся для использования дома для дистанционного обучения. Но учителю немного сложно увидеть, что делает ученик, а для младших школьников это требует организованности и помощи с манипуляторами. Поэтому мы также сделали важные манипулятивные упражнения на уровне класса на презентациях Google Slide и сделали Math Expressions MathBoards на Jamboards, бесплатном приложении от Google, которое имеет хорошую функцию письма.

 

Это исследовательский веб-сайт, который я разработал для всех, а не только для пользователей Math Expressions. Любой желающий может использовать эти материалы для дистанционного обучения. И, пожалуйста, посетите другие части моего веб-сайта, включая «Прогресс обучения», который представляет собой 22 часа визуальных и устных объяснений путей обучения в Стандартах Common Core State, организованных по математической области и использующих визуальную поддержку, основанную на исследованиях, в Math Expressions.

 

Время от времени проверяйте наличие новой информации.Например, теперь у нас есть наборы слайдов Google Pre-Kindergarten Teaching, Home Activity и Daily Routine, к которым вы можете получить доступ, перейдя по ссылке ниже. Новые материалы будут выкладываться по мере их готовности, так что также время от времени проверяйте диаграмму МАСТЕР, доступную по ссылке ниже.

 

Позаботьтесь о себе и своих учениках в этот непростой год. Карен Фьюсон

 

Вы можете просмотреть файл с описанием всех этих материалов для дистанционного обучения и ссылками для доступа к этим материалам до

НАЖМИТЕ ЗДЕСЬ

​

Затем переместите курсор в нижнюю часть файла, чтобы получить изображение стрелки и компьютера справа; затем нажмите на эту стрелку и компьютер, чтобы загрузить файл.

Управляемая математика К, 1 и 2!

 

Здравствуйте! Я так взволнован этим постом! Наконец-то я могу поделиться тем, что делаю уроки по математике с пошаговыми инструкциями для всех трех начальных классов K, 1 и 2! Полностью готовы первый и второй классы, а в детском саду построено 3 единицы! Год уроков математики с гидом в соответствии с общим ядром и Texas Teks! (все)

Я прикрою тебя с первого дня…..

до самого последнего дня!!!

Прежде чем я разобью это по классам, вертикальная ориентация K, 1 и 2 проходит через эти единицы! Если у вас есть старшие или младшие дети, которые не соответствуют урокам или различиям в вашем собственном классе, попробуйте следующий уровень выше или ниже! Единицы не должны быть изучены в определенном порядке! Так что смешивайте и сочетайте все, что вам нравится!

Я начал приключение в детском саду с цифрами от 0 до 10 для единицы 1. Давайте взглянем на некоторые из этих уроков!

Внутри блока:

Каждый урок содержит

• Существенный вопрос
• Цель урока
• Время обучения всей группы
• Вопросы для обсуждения
• Список материалов
• Практика с гидом/малая группа
• Игры/Занятия

Уроки 1–10 посвящены числам до 5

Уроки 10–19 посвящены числам 6–10

Урок 20 представляет собой модульную оценку

Как бы вы ни структурировали свой математический блок, вы найдете именно те материалы, которые вам нужны!

Я храню планы уроков в черно-белом виде (с несколькими вариантами цвета здесь и там). Их легко распечатать и учить! Мне нравится добавлять цвет, чтобы вызвать интерес к ламинированным практическим упражнениям.

 

Чтобы ознакомиться с блоком по математике для детского сада 1, нажмите ЗДЕСЬ.

Чтобы получить скидку 40%, вы можете ознакомиться с растущим пакетом ЗДЕСЬ!

Мой милый первоклассник, дорогой моему сердцу! Единицы для управляемой математики готовы!

Чтобы найти записи в блоге по математике для первоклассников, нажмите на ссылки ниже! Это посты прошлого года. Я не писал пост о каждом разделе, предлагаемом в серии управляемых математических упражнений, но многие из них помогут вам составить отличное представление об управляемой математике!

 

Чтобы найти сообщения в блоге по математике с подсказками для второго класса, нажмите на ссылки ниже! У меня нет поста для каждого из 9 модулей, но планы уроков на этот год завершены!

Я составил бесплатное руководство по запуску управляемых математических ротаций, чтобы сопровождать все эти уроки! Просто нажмите на картинку ниже, чтобы загрузить это руководство! Вы найдете пошаговые инструкции на каждый день, пока у вас не появятся ученики в управляемой математической ротации!

 Надеюсь, этот пост вдохновит вас в летние месяцы!

Если вы ищете математические центры, чтобы заполнить свои математические ротации с гидом, ознакомьтесь с ЭТОЙ СТАТЬЕЙ

Использование Манипуляторов — TeacherVision

Страница 1 из 4

Использование Манипулятивов

Что это такое?

Манипуляторы — это физические объекты, которые используются в качестве учебных инструментов для вовлечения учащихся в практическое изучение математики. Их можно использовать для введения, практики или исправления концепции. Манипулятор может быть простым, как рисовое зернышко, или сложным, как модель нашей солнечной системы. Они могут быть куплены в магазине, принесены из дома или сделаны учителем или учеником. Их можно использовать во всех областях математики — обучении числам и операциям, алгебре, геометрии, измерениям и т. д. — и на всех уровнях обучения.

Ниже приведены несколько манипуляций, которые можно использовать на начальном уровне.

Числа и операции

• Счетчики можно использовать для обучения прямому соответствию, порядковым числам и основам сложения и вычитания.

• Двусторонние счетчики можно использовать для моделирования однозначного соответствия, сложения и вычитания или пропуска счета.

• Коврики разрядности можно использовать для отображения разрядности каждой цифры при использовании блоков с основанием 10.

• Блоки Base-10 можно использовать для моделирования различных способов представления числа, а также для моделирования перегруппировки при сложении, вычитании, умножении и делении.

• Деньги в монетах или купюрах можно использовать для подсчета, пропуска счета или перегруппировки моделей при сложении или вычитании.

• Полосы дробей можно использовать для отображения эквивалентных дробей, сложения дробей, вычитания дробей или для нахождения общих знаменателей.

Алгебра

• Блоки шаблонов можно использовать для создания, поиска или расширения шаблонов.

• Блоки атрибутов можно использовать для сортировки и классификации по форме, цвету, размеру или другим атрибутам.

• Чашечные весы или весы можно использовать с предметами или гирями для отображения эквивалентных значений.

Геометрия

• Геоборды можно использовать для идентификации простых геометрических фигур и описания их свойств, а также для развития пространственного чувства.

• Геометрические твердотельные модели можно использовать для обучения сетям или пространственному мышлению.

Измеритель

• Стандартные и нестандартные линейки и мерные чашки могут использоваться для представления длины или объема.

• Тайлы можно использовать для определения площади или периметра объекта.

Анализ данных и вероятность

• Спиннеры можно использовать для определения экспериментальной вероятности приземления в заданной области.

• Числовые кубики или игральные кости можно использовать для определения экспериментальной вероятности выпадения определенного числа или комбинации чисел.

Почему это важно?

Согласно теории обучения, основанной на исследованиях психолога Жана Пиаже, дети являются активными учениками, которые осваивают понятия, продвигаясь по трем уровням знаний: конкретному, изобразительному и абстрактному.Использование манипулятивных средств позволяет учащимся исследовать концепции на первом, или конкретном, уровне понимания. Когда учащиеся манипулируют объектами, они делают необходимые первые шаги к пониманию и усвоению математических процессов и процедур. Например, при обучении сложению дробей учащиеся могут использовать полоски дробей для представления каждого слагаемого. Затем они складывают дробные части, чтобы найти сумму. Попрактиковавшись с ними, они могут перейти к нахождению сумм для задач на бумаге, представленных картинками с соответствующими цифрами дробей (уровень иллюстраций).Со временем они будут разрабатывать стратегии и применять алгоритмы, чтобы находить суммы, имея только выражение сложения (абстрактный уровень).

Чтобы учащийся мог успешно понимать и обращаться с понятием на абстрактном или символическом уровне, он или она должны сначала понять понятие на двух других уровнях в указанном порядке: конкретное, затем изобразительное. Использование конкретных манипулятивных средств — это первый шаг к использованию мысленных образов и моделей. Когда учащиеся демонстрируют понимание концепции на этом физическом или конкретном уровне, они готовы перейти на следующий уровень, где они могут применить свои знания, используя 90 595 представлений 90 043 объектов вместо самих объектов.

Маленькие дети часто решают задачи на сложение и вычитание, считая конкретные предметы, начиная с пальцев. Они продолжают использовать конкретные объекты, такие как десятичные кубики и счетчики, для разработки более сложных стратегий решения проблем, основанных на том, что они знают о счете (Siegler, 1996).

Бетонные модели могут помочь учащимся представлять числа и развивать чувство числа; они также могут помочь придать смысл письменным символам и могут быть полезны при построении концепций позиционного значения.Вы должны попытаться «проникнуть в головы студентов», когда они работают с конкретными материалами, задавая вопросы, которые вызывают их мысли и рассуждения. Таким образом, вы сможете лучше понять, что учащиеся знают и чего не знают, а также выявить неправильные представления, тем самым разработав основу для стратегий вмешательства. Вам также следует выбирать интересные задания с использованием манипуляторов (таких как счеты), которые вовлекают учащихся в математическое мышление и рассуждения, что формирует их понимание чисел, а также взаимосвязей между числами (NCTM 2000).

На самом деле исследования показывают, что использование манипулятивных приемов может способствовать развитию обоснованного, взаимосвязанного понимания математических идей. Студенты могут легче вспомнить, что они делали, и объяснить, о чем они думали, когда использовали манипулятивные методы для решения проблемы (Stein, 2001).

3 Суперсовета по обучению разрядному значению

Вот преуменьшение года: ценность места преподавателя — это большое дело! Начиная с детского сада и заканчивая пятым классом, «Числа и действия в десятичной системе счисления» проявляются в основных математических стандартах, как часовой механизм.

Задача «понимания места» усложняется с каждым годом и действительно увеличивается, начиная с 3-го класса. Ожидается, что учащиеся узнают, как «свободно складывать и вычитать в пределах 1000», используя стратегии восприятия чисел, основанные на разрядном значении. Эта трехзначная математическая стратегия может показаться неудобной, как высшая лига для детей, борющихся со значением разряда. Итак, я собираюсь поделиться:

Прежде чем я поделюсь тремя советами, давайте создадим предысторию. Учащиеся уже в детском саду и в 1-м классе приходят в школу, зная некоторые вещи о двузначных числах, например, как устно считать от 10 до 100 и считать предметы в пределах 15 или 20.

Однако их понимание чисел сильно отличается от нашего тем, что оно основано на методе счета единицами. Поэтому они обычно считают по одному и не сразу понимают связь между числом и группами десятков и единиц.

Например, если мы спросим учащегося, сколько десятков в числе 67, он может сказать 6 в разряде десятков, потому что просто называет позицию, мало что в ней понимая. Но они могут не понимать, что 6 представляет собой 6 групп по десять вещей, а 7 представляет 7 отдельных вещей.Понимание того, что группа из десяти человек может представлять собой единое целое, — это огромный сдвиг!

Учащиеся, как правило, испытывают затруднения, потому что понять значение разряда совсем не просто. Это все большая головоломка, в которой нужно собрать три больших кусочка или соединения.

3 Ключевые связи с созданием ценности места

Первым ключом является понимание концепций десятичной системы счисления для визуального представления чисел. Хотя многие учителя могут предоставить учащимся возможность представлять числа, используя стандартные группы, для учащихся не менее важно представлять числа, используя эквивалентные группы.Я считаю это краеугольным камнем ценности места.

Учащиеся также должны уметь произносить числа в устной форме, будь то стандартные («семьдесят два») или десятичные («7 десятков и 2 единицы»).

Наконец, учащиеся должны научиться читать и писать числительные. Установление этих трех связей зависит от использования на практике различных стратегий счета: счет единицами, счет группами и одиночками, счет десятками и единицами.

Видите, как все это работает вместе? Если учащиеся пропустят одну часть, им будет сложно получить полное представление о позиционной ценности. Вот почему так важно дать детям правильные инструменты для понимания системы ценностей места.

Вот несколько советов, которые развивают разрядность:

Совет № 1. Используйте коврики для обозначения разрядов, чтобы упростить чтение и запись чисел

Да, манипуляции отлично подходят для перехода учащихся от конкретного понимания к абстрактному. Коврики с расстановочными значениями хорошо работают с манипуляторами, помогая донести абстрактные концепции до сознания.

Помогите отстающим учащимся, сделав обучение практическим и наглядным.Это означает использование манипулятивных приемов, таких как десятичные блоки. Блоки с основанием десять — лучший инструмент в блоке. Отличительной особенностью блоков с основанием десять является универсальность построения целых чисел или десятичных дробей.

С блоком единиц, представляющим единицу, дайте учащимся время изучить взаимосвязь между единицами (маленький блок) и стержнями, а также стержнями и плоскостью на коврике с разрядными значениями. Изучение этих взаимосвязей подтверждает соотношение разрядности 10:1, в том числе: 10 единиц равняются 1 десятку, 10 десятков равняются 1 сотне и так далее.

Предупреждение : Блоки с основанием 10 связаны с отношениями. Каждый блок может представлять разные суммы в зависимости от того, как они используются. Не заставляйте своих детей думать, что каждый блок может представлять ТОЛЬКО одну вещь. Например, при использовании десятичных блоков для представления десятичных дробей плоскость может представлять 1, а наименьший блок может представлять 1 сотую. В разговоре с детьми мне легко использовать фразу: В этой ситуации _______ представляет _______.

Теперь давайте поговорим о таблицах значений мест.Создавайте простые диаграммы стоимостных значений, которые можно использовать повторно, добавляя разряды для сотен, десятков и единиц. Этот макет имитирует способ написания числа слева направо. В разделе единиц убедитесь, что есть два кадра из десяти, чтобы продвигать концепцию группы из десяти и устранить необходимость подсчета один за другим. Десять кадров также помогают учащимся визуализировать, сколько еще единиц необходимо, чтобы составить полный набор из десяти.

Также дайте учащимся время представить число, используя стандартные группы и эквивалентные группы.Например, числительное 49 можно представить в стандартной форме как 4 десятка и 9 единиц.

Также используйте эквивалентные группы из 49, чтобы показать 3 десятка и 19 единиц. Без такого опыта детям действительно трудно понять, что обе ценности эквивалентны.

Совет № 2. Обеспечьте возможность подсчета по группам из 10 и 100

У вас могут быть дети во 2-м и 3-м классах, которые продолжают считать по единицам, а не группировать по 10.Группировка по 10 важна, потому что так легче считать, плюс наша система счисления основана на десятках! Поскольку мы хотим привить учащимся способность считать до 10 (а не навязывать им это), ознакомьтесь с этими двумя полезными упражнениями.

Испытание на счет карандашей

Соберите учеников в круг. Найдите набор цветных мелков (или любые предметы, которые можно считать от 25 до 100) и разложите их в центре круга. Спросите учащихся: «Как мы можем считать эти мелки так, чтобы это было проще, чем считать единицами?» Проверьте любое из предложенных учащимися предложений по счету (т.если они говорят, считайте по 3, тогда группируйте и считайте мелки по три, пока вы не сможете больше составлять группы по 3).

После тестирования различных стратегий обсудите, что сработало хорошо, а что не очень. Если никто не предлагает идею счета до 10, предложите ее группе и обсудите, как она работает по сравнению с другими предложениями по счету. Учащиеся обычно обнаруживают, что счет 5 или 10 — это самый простой способ группировать и считать предметы.

Оценка деятельности в классе

Создайте банку оценки в своем классе.Наполните прочную прозрачную пластиковую банку от 200 до 1000 предметов. Такие предметы, как крошечные ластики, бобы или скрепки для бумаг, хорошо работают и довольно недороги.

Сначала дайте всем учащимся возможность записать свои оценки количества предметов в банке. Например, ниже каждый ученик записывает количество ластиков, которое, по его мнению, находится в банке. После того, как учащиеся придут к своим оценкам, обсудите в классе стратегии, которые они использовали для получения записанной суммы.

Далее высыпать все предметы (т.ластики) в несколько чашечек.

Объедините учащихся в пары и дайте им чашку для подсчета и группировки предметов по 10 за раз.

После того, как учащиеся сгруппировали все предметы по 10, разместите все группы перед классом и задайте следующие вопросы:

• Как мы можем использовать чашки по 10, чтобы узнать, сколько всего у нас есть?
• Можем ли мы создать новые группы, используя группы по десять человек? Какие новые группы мы можем сформировать?
• Сколько человек в каждой новой группе?

После обсуждения в классе раздайте большие контейнеры для новых групп. Например, учащиеся могут сформировать новые группы по 50 или 100 человек, объединив 5 стаканчиков по 10 ластиков в один контейнер по 50 штук. Убедитесь, что у вас достаточно больших контейнеров для новых групп (т. е. 50 ластиков в каждой новой группе), и пометьте каждый. новая группа.

Когда все новые группы сформированы, считайте сотни, десятки и единицы отдельно. Запишите общее количество предметов (ластиков) на листе бумаги и обсудите, насколько их оценки были похожи или отличались от фактического подсчитанного количества.

Совет № 3. Используйте ежедневную разминку для повышения уверенности в себе

Еще одна отличная стратегия повышения ценности места — это ежедневная разминка, особенно если она включает в себя математические рассуждения. Поскольку разрядное значение и понимание десятичной системы счисления являются основой нашей системы счисления, важно, чтобы учащиеся много практиковались.

Вы, наверное, слышали, что людям нужно что-то делать в течение 30 дней, чтобы это вошло в привычку. То же самое справедливо и для детей. Чтобы помочь вашим ученикам освоить ценность места, я разработал 30-дневную программу разминки.Эта процедура вовлекает ваш класс в содержательные математические обсуждения, помогая лучше понять разрядное значение в пределах 1000.

Каждый день проецируйте один урок математики на интерактивную доску. Учащиеся будут отвечать на 4 ежедневных вопроса. С 3 уровнями и 10 занятиями по математике, включенными в каждый уровень, у вас будет 30 дней обучения по месту.

Уровень A: начинающий

Включает 10 бесед по математике с:

• 4 основных вопроса
• На 10 больше и на 10 меньше
• Понимание десятичных моделей
• Сравнение значения одной цифры с другой

Уровень B: Средний

Включает 10 бесед по математике с:

• 4 Промежуточные вопросы
• Поместить значение Обсуждения
• Понимание базы-десять моделей
• Добавление или вычитание Маркивым из десяти
• Сравнение значений
• PLUS 1 Дополнительный бонусный вопрос

Уровень C: Advanced

Включает 10 бесед по математике с:

• 4 сложных вопроса
• Понимание значения заданной цифры
• Понимание десятичной модели
• Применение понимания разряда
• Нанесение чисел на числовую прямую
• Плюс 1 дополнительный БОНУСНЫЙ вопрос

4

• vale на следующий уровень с помощью этой процедуры.