Вводная контрольная работа по алгебре в 10 классе
Предмет: алгебра и начала анализа Класс 10 «Б» Дата __________
Урок № 6
Тема урока: Вводная контрольная работа
Цели урока: 1) проверить знания учащихся на начало учебного года
2) развитие, памяти, внимания, самостоятельности
3) воспитание трудолюбия и аккуратности.
Тип урока: Комплексное применение ЗУН
Оборудование: тетрадь для контрольных работ
Домашнее задание:
Содержание
Учитель
Ученики
Время
I Организационный момент
Психологический настрой
Слушают
1
II Постановка цели урока
Сообщает
Слушают, запоминают
1
III Контрольная работа
Поясняет задания
Слушают, запоминают
2
Контролирует
Решают самостоятельно на местах
40
IV Подведение итогов урока
Собирает тетради
Сдают тетради
1
Контрольная работа
Вариант 2.
№1. Упростить выражение:
(2х+1 + ) : (2х — )
№2. Решить неравенство, используя метод интервалов.
> 0
№3. Докажите тождество:
= 2
№4. В арифметической прогрессии d= -0,4, n= 12, = 2,4.
Найти , .
№5. У треугольника со сторонами 16 см и 8 см проведены высоты к этим сторонам. Высота, проведенная к стороне 16 см, равна 6 см. Чему равна высота, проведенная к стороне 8 см?
Вариант 1.
№1. Упростить выражение:
( — ) : (p – q + )
№2. Решить неравенство, используя метод интервалов.
0
№3. Докажите тождество:
=
№4. В арифметической прогрессии d= 5, = -35, = 250.
Найти , n.
№5. Стороны параллелограмма 6 см и 8 см, а его площадь 96 см2 . Чему равна большая сторона параллелограмма?
infourok.ru
Входная контрольная работа по алгебре 10 класс
1. Закатилова Ирина Павловна
2.МОУ»Средняя школа №13» г.Кимры Тверской области
3.Учитель математики
Входная контрольная работа в 10 классе.
Вариант 1.
1.Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
2.На диаграмме показано распределение выплавки цинка (в тысячах тонн) в 11 странах мира за 2009 год. Среди представленных стран первое место по выплавке цинка занимало Марокко, одиннадцатое место — Болгария. Какое место занимала Греция?
3.Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
4. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
5.Найдите значение выражения
6.Решите на выбор одно из неравенств системы:
7.Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.Решение.
Пустькм/ч — скорость моторной лодки, тогда скорость лодки по течению равна км/ч, а скорость лодки против течения равна км/ч. На путь по течению лодка затратила на 2 часа меньше, отсюда имеем:
Ответ: 16.
Ответ: 16
Вариант 2
1.Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
2.На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по математике в 2007 году (по 1000-балльной шкале). По данным диаграммы найдите число стран, в которых средний балл ниже, чем в Нидерландах.
3.Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
4. Решите уравнение
5.Найдите значение выражения
6. Решите на выбор одно из неравенств системы:
7.Решение.
Область определения уравнения задается соотношением. На области определения имеем:
Оба найденный решения удовлетворяют условию , меньший из них равен −0,5.
Ответ: −0,5.
Ответ: -0,5
|
www.prodlenka.org
Учебно-методический материал по алгебре (10 класс) на тему: вводная контрольная работа по математике 10 класс
Вводная контрольная работа по математике 10 класс
Вариант 1.
В заданиях 1-10 напишите краткое решение и ответ.
- Сократите дробь
- Найдите наибольшее значение функции у = -х2 + 6х – 4.
- Решите неравенство методом интервалов
- Найдите сумму сорока первых членов последовательности (bn), заданной формулой bn = 4п – 2
- Найдите шестой член геометрической прогрессии (bn), если b1 = 0,81 и q = —
- В окружности с центром О проведена хорда MK. Найдите , если ∠OMK = 51°
- Длина окружности равна 13. Найдите радиус этой окружности.
- Сторона ромба АВСD равна 5 см, ∠C = 120°. Найдите скалярное произведение векторов
- Из прямоугольного листа бумаги, длина которого 36 см, а ширина – 29 см, хотят сделать развертку куба. Чему равна площадь поверхности этого куба?
- В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых
В заданиях 11-12 напишите полное решение и ответ.
- Две сенокосилки, работая вместе, могут убрать поле за 7,5 ч, а работая порознь, первая сенокосилка убирает поле на 8 ч быстрее второй. За сколько часов могут убрать поле первая и вторая сенокосилки, работая по отдельности?
- Каждое основание АD и BС трапеции ABCD продолжено в обе стороны. Биссектрисы внешних углов А и В этой трапеции пересекаются в точке К, биссектрисы внешних углов C и D пересекаются в точке Е. Найдите периметр трапеции ABCD, если длина отрезка КЕ равна 28.
Вариант 2.
В заданиях 1-10 напишите краткое решение и ответ.
- Сократите дробь
- Найдите наименьшее значение функции у = х2 — 8х + 7.
- Решите неравенство методом интервалов
- Найдите сумму шестидесяти первых членов последовательности (bn), заданной формулой bn = 3п — 1.
- Найдите седьмой член геометрической прогрессии (bn), если b1 = -32 и q = .
- Точки B,D и N лежат на окружности с центром О. Найдите , если ∠BND =48°
- Длина окружности равна 26. Найдите радиус этой окружности.
- Сторона ромба MNPK равна 3 см, ∠Р = 60°. Найдите скалярное произведение векторов
- Из прямоугольного листа бумаги, длина которого 36 см, а ширина – 27 см, хотят
сделать развертку куба. Чему равна площадь поверхности этого куба?
- В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых.
В заданиях 11-12 напишите полное решение и ответ.
- Две бригады трактористов, работая вместе, могут вспахать поле за 3 ч. Работая порознь, первая бригада вспахивает поле на 4 ч быстрее второй. За сколько часов могут вспахать поле первая и вторая бригады, работая по отдельности?
- Каждое основание АD и BС трапеции ABCD продолжено в обе стороны. Биссектрисы внешних углов А и В этой трапеции пересекаются в точке F, биссектрисы внешних углов C и D пересекаются в точке M. Найдите периметр трапеции ABCD, если длина отрезка FM равна 26.
Задания 1- 10 оцениваются 1 баллом, задания 11 и 12 от 0 до 3 баллов.
Максимальное количество баллов – 16
«5» — 13-16 баллов
«4» — 9-12 баллов (включая 2 балла по геометрии)
«3» — 6-8 баллов (включая 1 балл по геометрии)
«2» менее 6 баллов
nsportal.ru
|
Контрольная работа № 1 |
|
|
1 вариант 1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а).у = – х + 5 б).у = х2 – 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
2 вариант 1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а).у = х – 7 б).у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
|
Контрольная работа № 2 |
|
|
1 вариант 1). Вычислите: 2). Упростите: 3).Известно, что: Вычислить . 4). Решите уравнение: 5). Докажите тождество: |
2 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество:
|
|
Контрольная работа № 3 |
|
|
1 вариант 1). Найти наименьшее и наибольшее значения функций:
2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
2 вариант 1). Найти наименьшее и наибольшее значения функций:
2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
|
Контрольная работа № 4 |
|
|
1 вариант 1). Решить уравнение: 2). Найти корни уравнения 3). Решить уравнение: 4). Найти корни уравнения |
2 вариант 1). Решить уравнение: 2). Найти корни уравнения 3). Решить уравнение: 4). Найти корни уравнения |
|
Контрольная работа № 5 |
|
|
1 вариант 1). Вычислить: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что |
2 вариант 1). Вычислите: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что |
|
Контрольная работа № 6 |
|
|
1 вариант 1). Найдите производную функции: а). ; б). в). д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции 3). Прямолинейное движение точки описывается законом 4). Дана функция Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке |
2 вариант 1). Найдите производную функции: а). ; б). в). д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом 4). Дана функция Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . |
|
Контрольная работа № 7( итоговая ) |
|
|
1 вариант 1). Дана функция 2). Решите уравнение: 3). Упростите выражение: а). б). 4). Постройте график функции с полным исследованием функции |
2 вариант 1). Дана функция 2). Решите уравнение: 3). Упростите выражение: а). б). . 4). Постройте график функции с полным исследованием функции . |
nsportal.ru
Контрольная работа по алгебре и начала ананлиза 10 класс. Автор учебника Мордкович А.Г.
Скипина С.Н. учитель математики МАОУ «Аромашевская СОШ»
Административная контрольная работа
по алгебре и началам анализа
1 полугодие
10 класс
-
Пояснительная записка
1). Цель проведения работы – проверить практические навыки и умения обучающихся по темам «Тригонометрические функции», «Тригонометрические уравнения».
2). Документы, на которые опирались при составлении работы – Федеральные государственные образовательные стандарты.
3). Класс, на который рассчитана данная работа — 10
4). Рекомендуемое время для проведения работы (количество часов на выполнение работы) — 1 урок (40 минут)
5). Описание структуры контрольно-измерительного материала: работа состоит из трёх частей.
Часть А содержит семь заданий базового уровня с выбором ответов, которые проверяют овладение конкретным материалом по данным темам. Ученик решает задание и выбирает букву, под которой, по его мнению, записан верный ответ и заносит данную букву в бланк ответов. Предлагаемые варианты ответов, кроме правильного, подобраны так, что содержат наиболее характерные для данных тем ошибки.
Часть В содержит три задания повышенного уровня, которые обеспечивают овладение учащимися общими и специфическими приемами учебной и умственной деятельности. Ученик решает задание и записывает полученный ответ в бланк ответов.
Часть С содержит одно задание высокого уровня, которое предусматривает свободное овладение практическим материалом, приемами учебной работы умственных действий и поднимает учащихся на уровень осознанного творческого применения знаний. Ученик решает задание и полностью записывает решение на бланке ответов.
Согласно методике составления теста, разработанной в лаборатории образования ИОСО РАО, основная часть должна состоять из заданий первого и второго уровней. Именно задания этих уровней соответствуют обязательным требованиям к знаниям и умениям учащихся.
6). Суть ключа.
Работа состоит из трёх частей.
Каждое задание части А (А1-А7) оценивается в 1 балл.
Каждое задание части В (В1-В3) оценивается в 1 балл.
Задание части С (С1) оценивается от 0 до 2 баллов.
Критерии оценки выполнения задания части С.
2
Верно выполнена замена, решено квадратное уравнение, выполнена обратная замена и найдены корни тригонометрического уравнения, верно найдены значения п и корни уравнения, принадлежащие данному отрезку.
1
Верно выполнена замена, решено квадратное уравнение, выполнена обратная замена и найдены корни тригонометрического уравнения.
0
Все случаи решения, которые не соответствуют вышеуказанным критериям.
Соотношение тестового балла и аттестационной отметки:
Аттестационная отметка
11-12
5
8-10
4
5-7
3
0-4
2
Административная контрольная работа
по алгебре и началам анализа
10 класс
Вариант № 1.
Инструкция по выполнению работы.
На выполнение работы отводится 40 минут.
Работа состоит из трёх частей. Часть А содержит семь заданий (А1-А7) обязательного уровня, часть В содержит три задания (В1-В3) повышенного уровня и часть С содержит одно задание (С1) высокого уровня по материалу курса «Алгебры и началам анализа» 10 класса. К каждому заданию части А даны 4 варианта ответов, из которых только один верный. В бланк ответов на задания части А вписывается буква, соответствующая верному, на Ваш взгляд, ответу. При решении заданий части В в бланк ответов вписывается ответ, получившийся в результате решения задания. Если Вы записали неверный ответ, аккуратно зачеркните его и рядом запишите другой ответ.
Задание С1 с развёрнутым ответом требует записи полного решения с необходимым обоснованием выполненных действий.
За каждое верно выполненное задание части А и В Вы получаете 1 балл, за задание части С – от 0 до 2 баллов.
Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у Вас останется время.
Желаем успехов!
Часть А.
А1. Найдите значение sin1200
а)  б)
б) 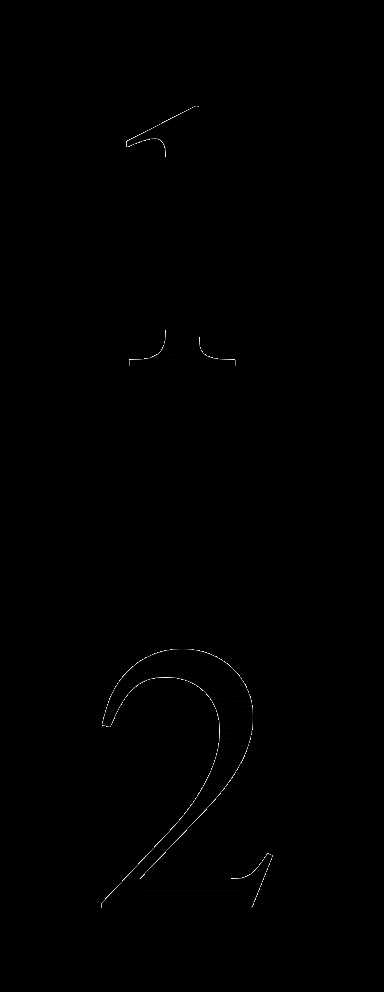 в) —
в) —  г) —
г) —
А2. Упростите выражение: 12+7sin2х+7cos2х
А) 12 б) 7 в) 26 г) 19
А3. Решите уравнение cos х=
а) ±  +2πп, пϵZ б) ±
+2πп, пϵZ б) ±  +2πп, пϵZ в) ±
+2πп, пϵZ в) ±  +πп, пϵZ г) ±
+πп, пϵZ г) ±  +2πп, пϵZ
+2πп, пϵZ
А4. Укажите, на каком рисунке изображен график функции у= sinх.
а) б)
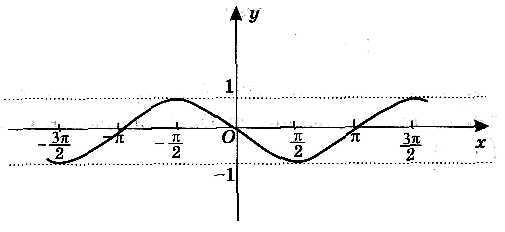
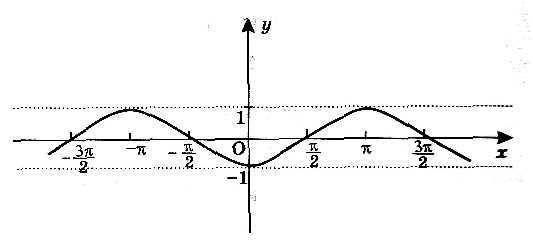
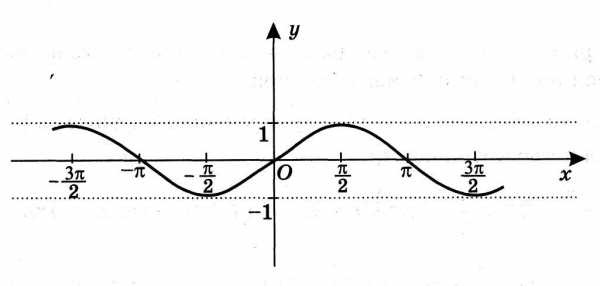
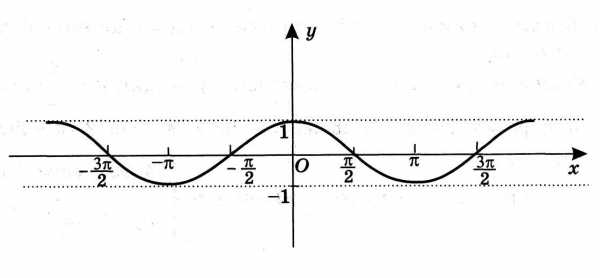 в) г)
в) г)
А5. Вычислите: sin + tg
+ tg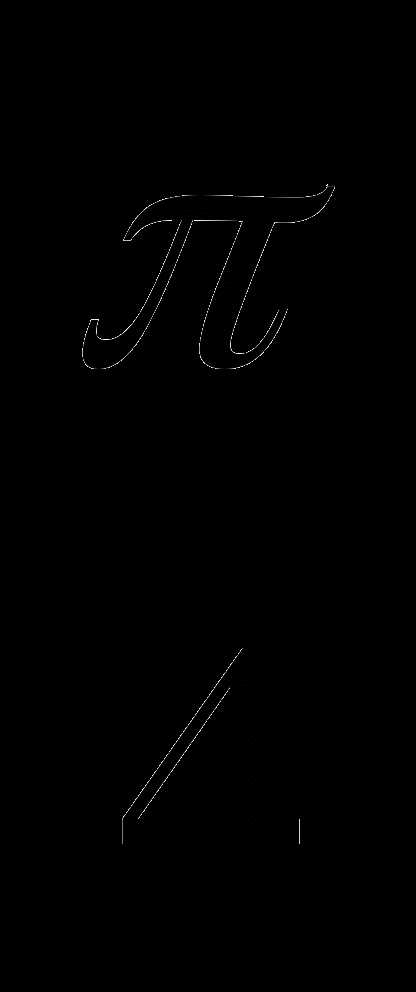 — cos
— cos
а) 1,5 б) — 0,5 в) 0,5 г) 1
А6. Вычислите: arccos( —  ) – arctg1 + arcsin0
) – arctg1 + arcsin0
а) 0 б) -1 в) π г) 
А7. Найдите множество значений функции у= cosх – 3
а) [-1;1] б) [- ∞; + ∞] в) [- 4;- 2] г) [2;4]
Часть В.
В1. Упростите выражение:
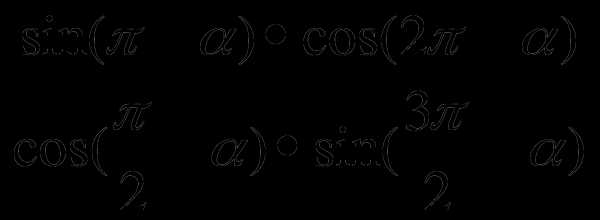 .
.
В2. Найдите сtgα, если sinα = — 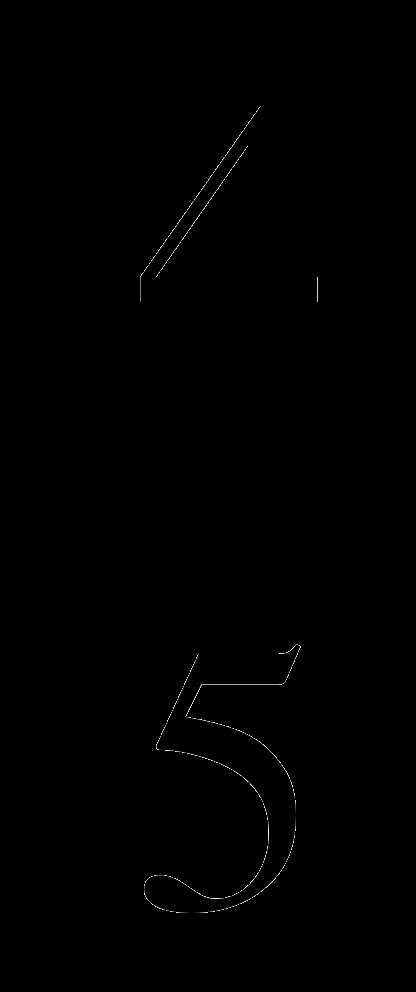 , π˂ α ˂
, π˂ α ˂ .
.
В3. Решите уравнение tg( ) = —
) = —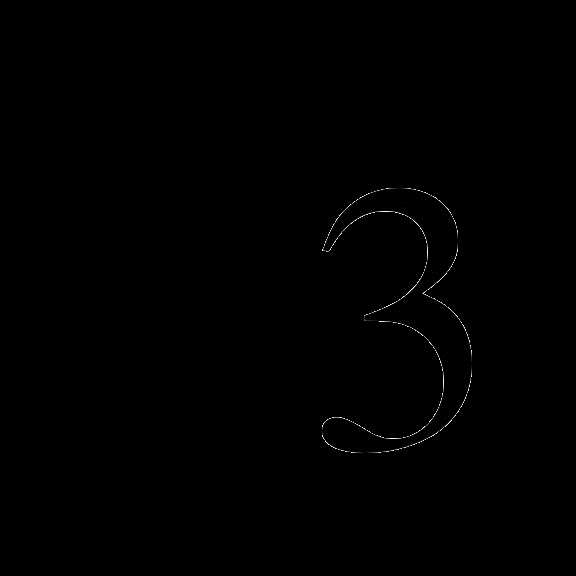
Часть С.
С1. Найдите корни уравнения 2cos2х – cosх – 3 = 0, принадлежащие отрезку
[ — 3π; 3π] .
Административная контрольная работа
по алгебре и началам анализа
10 класс
Вариант № 2.
Инструкция по выполнению работы.
На выполнение работы отводится 40 минут.
Работа состоит из трёх частей. Часть А содержит семь заданий (А1-А7) обязательного уровня, часть В содержит три задания (В1-В3) повышенного уровня и часть С содержит одно задание (С1) высокого уровня по материалу курса «Алгебры и началам анализа» 10 класса. К каждому заданию части А даны 4 варианта ответов, из которых только один верный. В бланк ответов на задания части А вписывается буква, соответствующая верному, на Ваш взгляд, ответу. При решении заданий части В в бланк ответов вписывается ответ, получившийся в результате решения задания. Если Вы записали неверный ответ, аккуратно зачеркните его и рядом запишите другой ответ.
Задание С1 с развёрнутым ответом требует записи полного решения с необходимым обоснованием выполненных действий.
За каждое верно выполненное задание части А и В Вы получаете 1 балл, за задание части С – от 0 до 2 баллов.
Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у Вас останется время.
Желаем успехов!
Часть А.
А1. Найдите значение cos1500
а)  б)
б) в) —
в) —  г) —
г) —
А2. Упростите выражение: 15+3sin2х+3cos2х
А) 18 б) 15 в) 19 г) 21
А3. Решите уравнение sinх=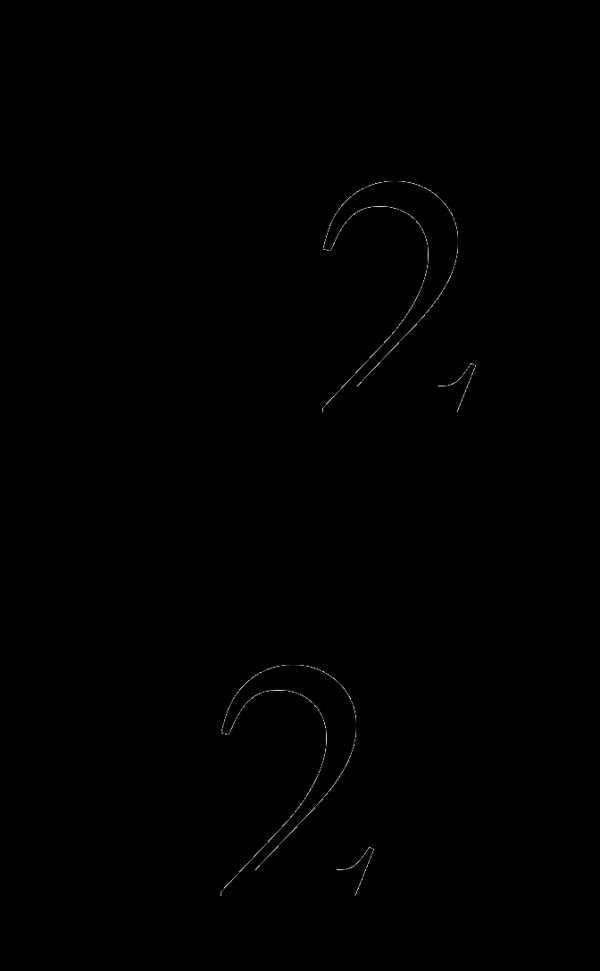
а) (-1)п  +πп, пϵZ б) (-1)п
+πп, пϵZ б) (-1)п 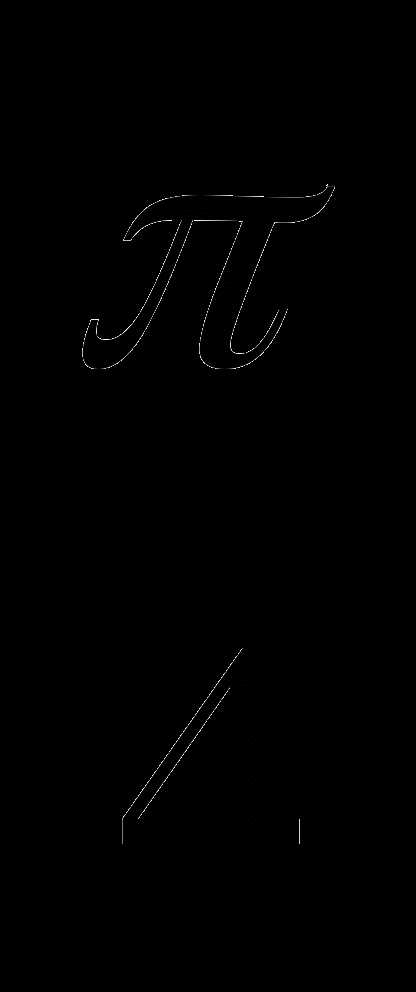 +πп, пϵZ в) ±
+πп, пϵZ в) ± 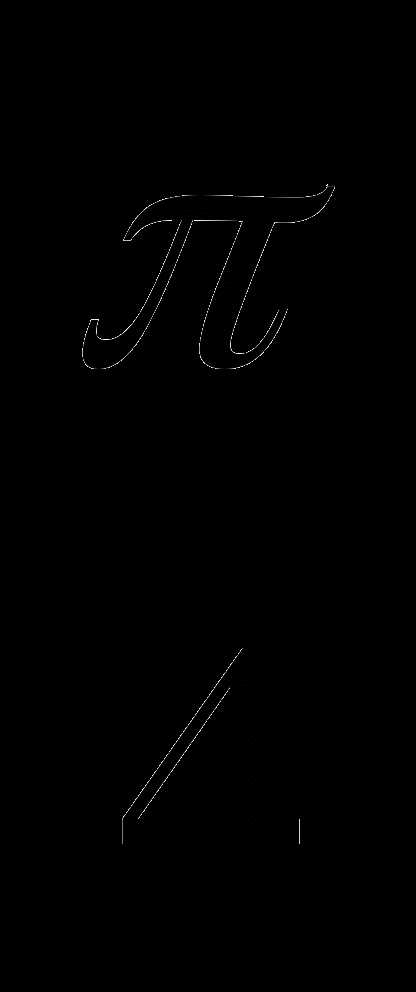 +2πп, пϵZ г) (-1)п
+2πп, пϵZ г) (-1)п 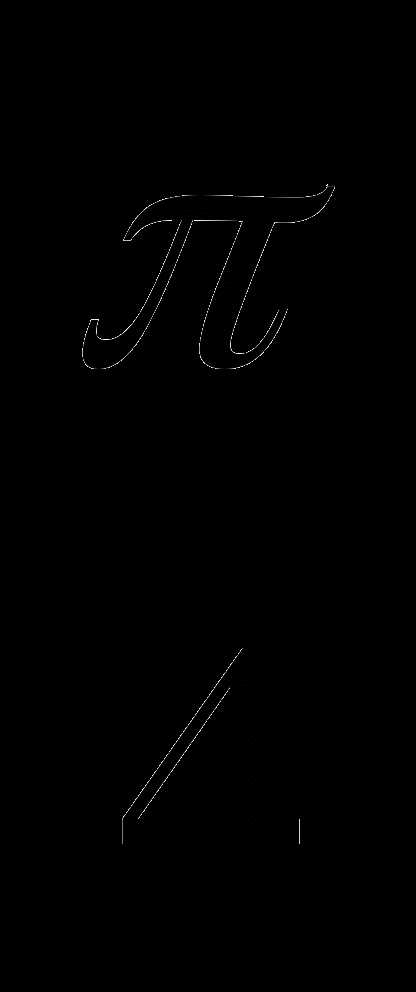 +2πп, пϵZ
+2πп, пϵZ
А4. Укажите, на каком рисунке изображен график функции у=cosх.

 а) б)
а) б)


в) г)
А5. Вычислите: cos — сtg
— сtg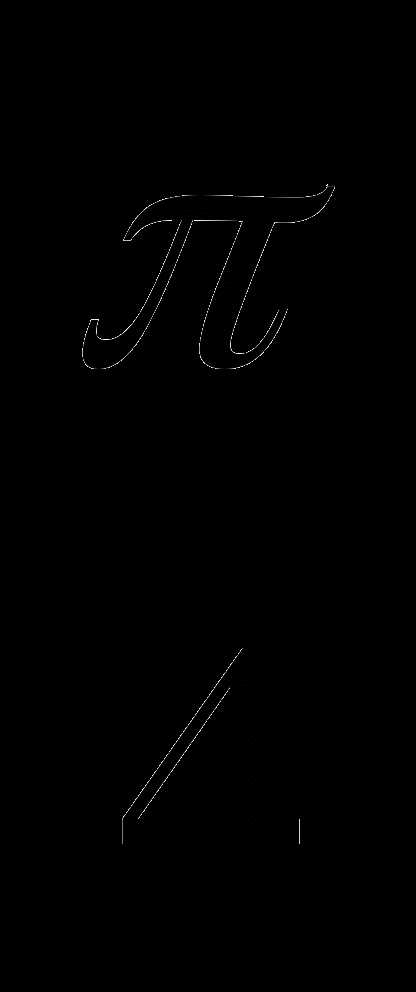 + sin
+ sin
а) — 0,5 б) 1,5 в) 1 г) 0,5
А6. Вычислите: arcsin + arccos( —
+ arccos( — 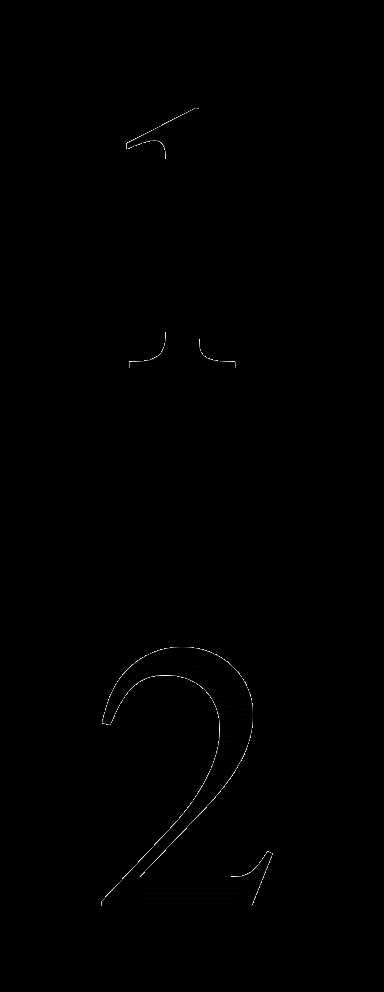 ) – arctg0
) – arctg0
а) 1 б) 0 в) π г) — 
А7. Найдите множество значений функции у=sinх+2
а) [- ∞; + ∞] б) [-1;1] в) [- 3;- 1] г) [1;3]
Часть В.
В1. Упростите выражение:
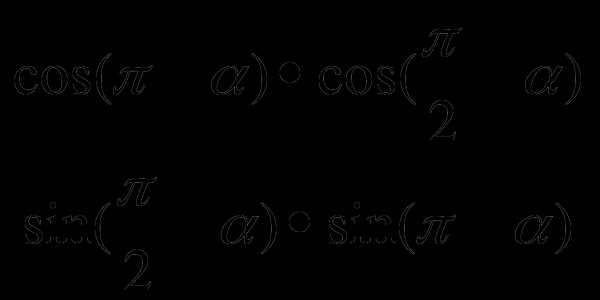 .
.
В2. Найдите tgα, если cosα = —  ,
,  ˂ α ˂ π.
˂ α ˂ π.
В3. Решите уравнение сtg(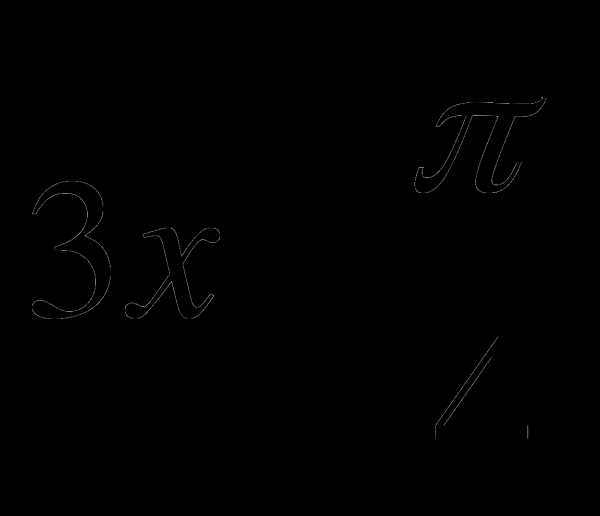 ) = 1
) = 1
Часть С.
С1. Найдите корни уравнения sin2х – 6sinх +5 = 0, принадлежащие отрезку
[ —  ;
;  ] .
] .
Ключ к работе
1 вариант.
Номер
задания
Правильный ответ
А1
а
А2
г
А3
а
А4
в
А5
б
А6
г
А7
в
В1
— 1
В2
¾=0,75
В3
2πк, к ϵ Z
С1
— 3π; — π; π; 3π
2 вариант.
Номер
задания
Правильный ответ
А1
в
А2
а
А3
б
А4
г
А5
а
А6
в
А7
г
В1
1
В2
— = — 1
= — 1
В3
 , к ϵ Z
, к ϵ Z
С1
—  ;
;  ;
; 
infourok.ru
|
1 вариант 1)Для функции f (х) = 2х2 –x +1. Найти f (0), f (1), f (х-3). 2) Найти D(у), если: 3). Построить график функции: а). у = – х + 5 б). у = х2 – 2 По графику определить :монотонность функции. 4)Дана прямая и не принадлежащая ей точка. Докажите, что все прямые, проходящие через эту точку и пересекающие данную прямую, лежат в одной плоскости. 5)Определите число вершин, ребер и граней: а) куба; б) 7-угольной призмы; в) n-угольной пирамиды. 6)Определите вид призмы, если она имеет: а) 10 вершин; б) 21 ребро; в) 5 граней. |
2 вариант 1)Для функции f (х) = 3х2 – х + 2. Найти f (0),f (1+х), 2). Найти D(у), если: 3). Построить график функции: а). у = х – 7 б). у = – х2 + 2 По графику определить :монотонность функции. 4). Даны две пересекающиеся прямые. Докажите, что все прямые, пересекающие эти прямые и не проходящие через точку их пересечения, лежат в одной плоскости. 5)Определите число вершин, ребер и граней: а) прямоугольного параллелепипеда; б) 6-угольнойной пирамиды; в) n-угольной призмы. 6) Определите вид пирамиды, если она имеет: а) 5 вершин; б) 14 ребер; в) 9 граней. |
3 вариант 1)Для функции f (х) = х2 + 2х – 1. Найти f (0), f (1), f (х-3). 2) Найти D(у), если: 3). Построить график функции: а). у = х — 5 б). у = -х2 -2 По графику определить :монотонность функции. 4) В плоскости проведены две параллельные прямые a и b. Докажите, что все прямые, пересекающие данные прямые, лежат в одной плоскости 5)Определите число вершин, ребер и граней: а) куба; б) 7-угольной призмы; в) m-угольной пирамиды. 6)Определите вид призмы, если она имеет: а) 12 вершин; б) 24 ребро; в) 15 граней. |
4 вариант 1)Для функции f (х) = х2 – 3х + 2. Найти f (0),f (1+х), 2). Найти D(у), если: 3). Построить график функции: а). у = -х – 7 б). у = х2 + 2 По графику определить :монотонность функции. 4). Даны три точки, не принадлежащие одной прямой. Докажите, что все прямые, пересекающие два из трех отрезков, соединяющих данные точки, лежат в одной плоскости 5)Определите число вершин, ребер и граней: а) прямоугольного параллелепипеда; б) 8-угольнойной пирамиды; в) k-угольной призмы. 6) Определите вид пирамиды, если она имеет: а) 6 вершин; б) 16 ребер; в) 19 граней. |
infourok.ru
Контрольная работа по алгебре. 10 класс
4. Решить уравнение:
2 — 9х + 14 = 0
5. Периметр равностороннего треугольника равен 12 см.
Найти радиус описанной окружности.
6. Моторная лодка прошла против течения реки 84 км и вернулась в пункт
отправления, затратив на обратный путь на 8 часов меньше.
Найдите скорость
течения реки,
если скорость лодки в неподвижной воде равна 10 км/ч.
Ответ дайте в км/ч.
3 вариант
1. Чему равно значение выражения при а=1/4
2. Решить неравенство: х(х-3)(2х+7 ) 0
3. Решите систему уравнений
х + у =3
4. Найдите нули функции:
5. Периметр квадрата равен 12 см.
Найти радиус описанной окружности.
6. Моторная лодка прошла против течения реки 143 км и вернулась в пункт
отправления, затратив на обратный путь на 2 часа меньше.
Найдите скорость
лодки в неподвижной воде,
если скорость течения равна 1 км/ч.
Ответ дайте в км/ч.
infourok.ru