Видеоуроки по геометрии 10 класс: Геометрия 10 класс

Урок геометрии 10 класс

МБОУ «Школа № 13 г. Феодосии Республики Крым»

Урок по геометрии в 10 –А классе

(С применением информационных технологий и презентации)

Тема: «Аксиомы стереометрии».

Учитель математики Вышковская М.С.

г. Феодосия

2014

Тема урока: «Аксиомы стереометрии».

Цель урока: познакомить учащихся с аксиомами стереометрии, с основными фигурами в пространстве, вспомнить аксиомы планиметрии. Применить полученные знания при выполнении упражнений.

Методы : словесный, объяснительно-иллюстративный, индивидуальная работа.

Применение информационных технологий с целью повышения интереса к изучаемому предмету.

Ход урока.

1. Организационный момент.

2. Постановка темы и учебной цели урока.

Учитель: Мы начинаем изучать новый раздел геометрии, который называется «Стереометрия». Тема нашего сегодняшнего урока – «Аксиомы стереометрии» (слайд1). Мы познакомимся с новыми аксиомами и вспомним уже ранее изученные. В конце урока, чтобы проверить, как вы усвоили новый материал, проведем самостоятельную работу.

3. Изложение нового материала.

( Весь теоретический материал показывается в виде презентации и сопровождается комментариями учителя. Учащиеся записывают конспект в тетрадь.).

Учитель: В названии темы урока два новых слова. Узнаем, что они обозначают.

«Стереометрия»- это раздел геометрии, в котором изучаются фигуры в пространстве. (слайд 2)

«Аксиомы»- это утверждения, содержащиеся в формулировках основных свойств простейших фигур, которые не требуют доказательства . (слайд 3)

Учитель: В стереометрии, так же как и в планиметрии свойства геометрических фигур устанавливаются путём доказательства соответствующих теорем. При этом отправными являются свойства основных геометрических фигур, выражаемые аксиомами. Основными фигурами в пространстве являются точка, прямая и плоскость.

Основные фигуры в пространстве. (слайд 4)

Точка

Прямая

Плоскость

Учитель: В стереометрии появляется новая фигура – плоскость

Представление о плоскости дает гладкая поверхность стола, поверхность оконного стекла, поверхность мраморной плиты и т.д. На рисунках плоскости изображают в виде параллелограмма или в виде произвольной области. Обозначаются плоскости греческими буквами

Введение нового геометрического образа (плоскости ) заставляет расширить систему аксиом. Поэтому мы введем группу трёх аксиом, которая выражает основные свойства плоскостей в пространстве.

А1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.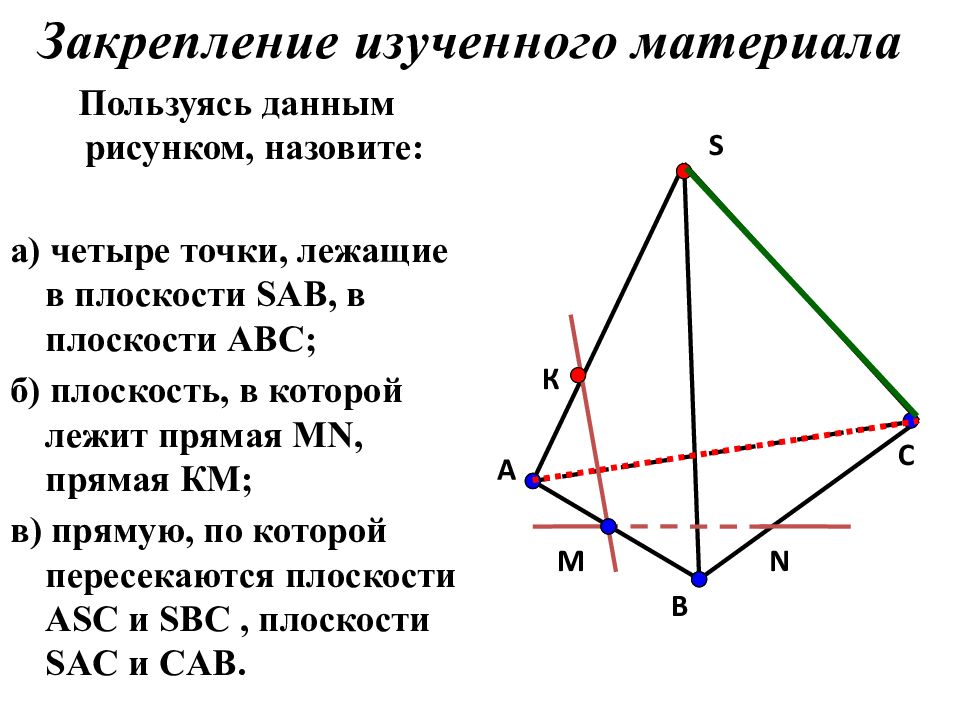 (слайд 5)

А2.Если две различные плоскости имеют общую точку, то они пересекаются по прямой проходящей через эту точку. (слайд 6)

Учитель: Чтобы построить этот чертёж, сначала строим плоскость , затем проводим прямую а, от её концов две параллельные линии, так строим плоскость β.

Обратите внимание, что невидимые линии проводим пунктиром.

А3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну. (слайд 7)

Учитель: Таким образом, система аксиом стереометрии состоит из аксиом планиметрии и группы аксиом стереометрии. Вспомним 2 аксиомы планиметрии, на которые будем опираться при изучении тем «Перпендикулярность» и «Параллельность прямых и плоскостей». Вспомним аксиомы планиметрии первой группы.

(слайд 8)

1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки не принадлежащие ей.

2. Через любые две точки можно провести прямую, и притом только одну.

Учитель: Обратите внимание на сходство аксиомы А1 и 1 аксиомы планиметрии.

(слайд 9)

Учитель: Прежде чем перейти к закреплению материала, предлагаю отдохнуть и провести физкультминутку.

А теперь, ребята, встали.

Быстро руки вверх подняли,

В стороны, вперед, назад.

Повернулись вправо, влево,

Тихо сели, вновь за дело.

4. Закрепление знаний.

Учитель: И так, мы с вами познакомились с аксиомами стереометрии. Применить эти знания мы сможем при решении задач. Вы знаете, что в геометрии есть вычислительные задачи, и задачи на доказательство. Задачи на доказательство чаще всего решаются методом от противного. Вспомним основные этапы этого метода

(слайд11)

1. Делаем предположение, противоположное тому, что надо доказать.

2. Путем рассуждений, опираясь на аксиомы и теоремы, приходим к выводу, противоречащему условию.

3. Заключаем, что наше предположение не верно.

4. В ответ записываем верное утверждение, которое доказывали.

(К доске вызывается ученик).

Задача. Точки A, B, C и D не лежат в одной плоскости. Докажите, что прямые AB и CD не пересекаются.

Учитель: С чего начинаем решать задачу по геометрии?

Ученик: С построения чертежа.

Учитель: Что потом делаем?

Ученик: Делаем краткую запись условия. Дано. Доказать. Доказательство.

Дано:

Доказать: _{АВ и СД не пересекаются}

Учитель: Каким методом будем решать задачу?

Ученик: Методом от противного.

Доказательство:

Предположим, что АВ и СD пересекаются, тогда по аксиоме А3 через них можно провести плоскость, в которой лежат все четыре данные точки, что противоречит условию задачи. Следовательно, наше предположение неверно и прямые АВ и СД не пересекаются.

Устные упражнения:

1. Даны две прямые а и в, через которые нельзя провести плоскость. Докажите, что эти прямые не пересекаются.

2. Могут ли две плоскости иметь только одну общую точку?

3. Могут ли три плоскости иметь только одну общую точку?

Вопросы для закрепления:

— что изучает стереометрия?

— каковы основные (простейшие) фигуры в пространстве?

— сформулируйте стереометрические аксиомы?

5. Домашнее задание.

П. 1,2; № 2,4

6. Подведение итогов урока.

Учитель благодарит учащихся за работу на уроке, отмечает наиболее активных и проводит оценивание ответов учащихся.

Математика- это жизнь!: Видеоуроки 10-11 класс

Видеоуроки по алгебре

Общие методы решения уравнений

Общие методы решения неравенств

Системы уравнений

Уравнения и неравенства с параметрами

Производная

1. Числовые последовательности

2. Предел числовой последовательности

3. Сумма бесконечной геометрической прогрессии

4. Предел функции на бесконечности

5. Предел функции в точке

6. Приращение аргумента и приращение функции

7. Определение производной

8. Вычисление производных

9. Правила дифференцирования

10. Сложная функция

11. Число е

12. Натуральный логарифм

13. Производная показательной и логарифмической функции

14. Наибольшее и наименьшее значение функции

15. Задачи на отыскание наибольших и наименьших значений величин

Построение графиков функций с помощью производной

 Первообразная

19. Первообразная

20. Определенный интеграл

21. Площади плоских фигур

22. Обобщающий урок «Первообразная»

Тригонометрия

Синус и косинус

Степенная функция

Корни и степени

Показательная функция, её свойства и график

Свойства числовых функций
https://drive. google.com/open?id=14e9wEXb4BWGclSFmSK2TGRwpsBh2n4Yj
Числовые функции. Графики числовых функций
https://drive.google.com/open?id=1rUhv8mk8xqDXla_C5KXglNxop06cb6Gs

Видеоуроки по геометрии

02. Аксиомы стереометрии

03. Некоторые сведенияиз аксиом стереометрии

04. Параллельные прямые в пространстве

05. Параллельность трех прямых

06. Параллельность прямой и плоскости

07. Скрещивающиеся прямые

08.Углы с сонаправленными сторонами

09. Углы между прямыми

10. Параллельные плоскости

11. Свойства параллельных плоскостей

Перпендикулярность прямых и плоскостей

Задачи на построение сечений

Векторы в пространстве. 10-й класс

В школьный курс геометрии векторы входят в 9
классе. Продолжение эта линия находит лишь в
конце 10 класса, и на нее отводится 6 часов в
соответствии с программой к учебному пособию
“Геометрия 10-11” авторов Л. С. Атанасян,
В.Ф.Бутузов и др. Создавая данную презентацию, я
ставила задачу с минимальными временными
потерями повторить материал, изученный в 9 классе
и изучить новый, опираясь на анимационные
чертежи и слайды. Большое внимание уделяется в
презентации задачам. Многие из них – задачи
вышеуказанного учебника. Чаще всего они решаются
устно, акцентируя внимание школьников на суть
процесса решения, а не на записи символов и
выполнение чертежей. К задачам имеются ответы с
отсроченным появлением. В таких случаях ученики
могут предлагать свои решения, делая необходимые
записи на готовых чертежах и сравнивать их с
предложенными в презентации. В данной работе
сделаны интерактивные чертежи к теоремам,
сформулированным и доказанным в учебнике. А
также присутствуют доказательства этих теорем,
которые в соответствии с текстом учебника и с
помощью коллективной работы ведет учитель на
уроке. Презентация подготовлена для работы на
всех шести уроках темы. Можно на конкретном уроке
использовать только несколько слайдов,
соответствующих теме данного урока. Так,
например параграф 1 “Понятие вектора” содержит
14 слайдов, которые могут быть использованы
учителем и для актуализации знаний, и для решения
задач по курсу 10 класса. Параграф 2 “Сложение и
вычитание векторов” представлен восемью
слайдами, которые демонстрируют определения и
правила сложения и вычитания и их свойства.
Параграф 3 “Компланарные векторы” содержит 10
слайдов. Это демонстративные модели определений,
теорем и свойств, которые сформулированы в
учебнике. Презентация не отяжелена выводами
фактов, она рассчитана на слово учителя, которое
будет подтверждено активными чертежами слайдов.

Урок № 1 . Понятие вектора, Равенство
векторов.

Как уже отмечалось выше с понятием вектора
ученики знакомы, поэтому данный материал
переносится из плоскости в пространство и
фактически проводятся параллели с ранее
изученными фактами, дополняя изображения
векторов на многогранниках, плоскостях. Важно
отметить использование векторов в физике,
продемонстрировав векторы магнитной индукции и
электрического тока.

На этом же уроке рассматриваются определения
сонаправленных и противоположно направленных
векторов, равных векторов, коллинеарных, теорема
об откладывании вектора, равного данному от
заданной точки. Материал насыщен, поэтому первые
14 слайдов рассчитаны на помощь ученику в
актуализации знаний. Задачи на слайдах 12,13,14
решаются устно.

Урок №.2. Сложение и вычитание векторов.

К известным правилам “треугольника и
параллелограмма” для сложения векторов
добавляется правило многоугольника, выходящее
за пределы плоскости, правило параллелепипеда.
Все правила снабжены анимационными моделями для
лучшего запоминания и понимания.
Рассматривается вычитание векторов через два
различных способа. Через замену разности
векторов суммой уменьшаемого с вектором,
противоположным вычитаемому и через нахождение
неизвестного слагаемого. Для практической
отработки действия на слайд № 20 вынесена задача
№332 учебника и другие устные задачи.

Урок № 3. Умножение вектора на число.

Определение произведения вектора на число
является традиционно трудным для большинства
учащихся. Поэтому ему уделено достаточно
внимания в презентации. Задача 344 способствует
закреплению данного определения. Которую можно
выполнить в рамках первичного закрепления.

Урок № 4. Компланарные векторы.

Определение компланарых векторов и признак
компланарности сопровождаются динамичными
моделями, а также приведено доказательство
теорем из учебника, выполненное с использованием
анимационных действий, что поможет учителю
уделять большее внимание работе с классом,
избавив от вычерчивания на доске. На этом же
уроке вводится и правило параллелепипеда для
сложения некомпланарных векторов.

Урок № 5. Разложение вектора по трем
некомпланарным векторам.

На данном уроке рассматривается теорема о
разложении векторов по трем некомпланарным
векторам и ее доказательство. Решается ряд задач
по теме.

На уроке № 6 обобщаются и
систематизируются знания по теме.

Хочу еще раз отметить, что я не ставила целью
составить планы уроков по данному разделу
геометрии, а собрала только тот материал, который
помогает оптимизировать временные затраты на
изучение нового материала. Каждый учитель может
по своему усмотрению использовать отдельные
слайды в контексте урока. К тому же за счет
экономии времени можно расширить круг задач,
решаемых в соответствии с конкретным планом
урока.

Видеоуроки декабрь 2013 года

Дата проведения	Предмет, класс	Тема	Направлен- ность дистанцион- ных курсов	Преподаватели
2.12.2013 г. 14.00	Математика, 9 класс	Текстовые задачи на смеси и сплавы (занятие №1)	Подготовка к ГИА	Парфенова Лариса Петровна, учитель математики МБОУ «Гимназия №25» г. Курска
2.12.2013 г. 15.00	Спецкурс для углубленного изучения географии 10-11 класс	Решение картографических заданий (Часть1 )	Работа с одаренными детьми	Горин Владимир Борисович, кандидат технических наук, доцент кафедры экономической и социальной географии КГУ
3.12.2013 г. 15.00	9-11 класс	Электротехниче- ские специальности	Профориен тационная работа	Чернышев Александр Савельевич, кандидат технических наук, доцент кафедры электроснабжения ЮЗГУ
4.12.2013 г. 14.00	География, 11 класс	Численность, естественное движение населения России. Решение заданий С6 1 часть.	Подготовка к ЕГЭ	Желунина Оксана Владимировна, учитель географии МБОУ «СОШ №49» г. Курска
4. 12.2013 г. 15.00	Спецкурс для углубленного изучения правоведения (10-11 класс)	Правовые системы современности	Работа с одаренными детьми	Мурашова Виктория Анатольевна, учитель истории МБОУ «СОШ №16» г. Курска
5.12.2013 г. 14.00	История, 11 класс	Россия на рубеже 16-17 веков	Подготовка к ЕГЭ	Фисенко Ирина Владимировна, учитель истории МБОУ «СОШ с углубленным изучением отдельных предметов №28» г. Курска
5.12.2013 г. 15.00	Спецкурс для углубленного изучения географии 10-11 класс	Решение заданий повышенного уровня сложности по теме: «Население»	Работа с одаренными детьми	Стоянова Ольга Федоровна, учитель географии МКОУ «Свердликовская СОШ» Суджанского района Курской области
6. 12.2013 г. 14.00	Информатика, 11 класс	Информационное моделирование	Подготовка к ЕГЭ	Захарова Ольга Михайловна, учитель информатики МБОУ «СОШ с углубленным изучением отдельных предметов №28» г. Курска
6.12.2013 г. 15.00	Спецкурс для углубленного изучения математики (8- 9класс)	Логические задачи	Работа с одаренными детьми	Белкина Елена Николаевна, учитель математики ОБОШИ «Лицей-интернат №1» г. Курска
9.12.2013 г. 15.00	9-11 класс	Профессиональное обучение и техносферная безопасность	Профориен тационная работа	Костин Николай Анатольевич, кандидат технических наук, декан ИПФ КГУ
11.12.2013 г. 14.00	География, 11 класс	Миграционный прирост (убыль) населения России. Решение заданий С6 2 часть.	Подготовка к ЕГЭ	Желунина Оксана Владимировна, учитель географии МБОУ «СОШ №49» г. Курска
11.12.2013 г 15.00	Спецкурс для углубленного изучения русского языка (10 класс)	Сложные явления русской морфологии (разбор олимпиадных заданий)	Работа с одаренными детьми	Татаренкова Светлана Константиновна, учитель русского языка МБОУ «Косиновская СОШ» Курского района
12.12.2013 г. 14.00	История, 11 класс	Россия в 17 веке на пороге Нового времени.	Подготовка к ЕГЭ	Клименко Валентина Сергеевна, учитель истории МБОУ «СОШ №1» г. Курска
13.12.2013 г. 14.00	Информатика, 11 класс	Основы алгоритмизации	Подготовка к ЕГЭ	Захарова Ольга Михайловна, учитель информатики МБОУ «СОШ с углубленным изучением отдельных предметов №28» г. Курска
13.12.2013 г. 15.00	Спецкурс для углубленного изучения географии 10-11 класс	Решение картографических заданий (Часть1 )	Работа с одаренными детьми	Горин Владимир Борисович,кандидат технических наук, доцент кафедры экономической и социальной географии КГУ
16.12.2013 г. 14.00	Спецкурс для углубленного изучения математики (10 класс)	Принцип Дирихле (занятие №2)	Работа с одаренными детьми	Фрундин Владимир Николаевич, кандидат педагогических наук, доцент кафедры алгебры, геометрии и теории обучения математике КГУ
17.12.2013 г. 14.00	Математика, 11 класс	Отбор корней в тригонометриче- ских уравнениях (занятие №1)	Подготовка к ЕГЭ	Белкина Елена Николаевна, учитель математики ОБОШИ «Лицей-интернат №1» г. Курска
17.12.2013 г. 15.00	Спецкурс для углубленного изучения химии (9-11 класс)	Марганец и его соединения	Работа с одаренными детьми	Билибенко Наталья Михайловна, учитель химии МБОУ «СОШ №31» г. Курска
18.12.2013 г. 14.00	Русский язык, 9 класс	Осложненное простое предложение (В4)	Подготовка к ГИА	Мишустина Вера Викторовна, учитель русского языка МБОУ «СОШ с углубленным изучением отдельных предметов №56» г. Курска
18.12.2013 г. 15.00	Спецкурс для углубленного изучения математики (8-9 класс)	Инварианты	Работа с одаренными детьми	Белкина Елена Николаевна, учитель математики ОБОШИ «Лицей-интернат №1» г. Курска
19.12.2013 г. 14.00	Обществознание, 11 класс	Проблемы познания мира в философии. Познание как особый вид деятельности.	Подготовка к ЕГЭ	Падогова Марина Валерьевна, учитель обществознания МБОУ «СОШ №59» г. Курска
23.12.2013 г. 14.00	Математика, 9 класс	Текстовые задачи на смеси и сплавы (занятие №2)	Подготовка к ГИА	Парфенова Лариса Петровна, учитель математики МБОУ «Гимназия №25» г. Курска
23.12.2013 г. 15.00	Спецкурс для углубленного изучения русского языка (10 класс)	Синтаксические функции инфинитива	Работа с одаренными детьми	Татаренкова Светлана Константиновна, учитель русского языка МБОУ «Косиновская СОШ» Курского района
24.12.2013 г. 14.00	Математика, 11 класс	Отбор корней в тригонометриче- ских уравнениях (занятие №2)	Подготовка к ЕГЭ	Белкина Елена Николаевна, учитель математики ОБОШИ «Лицей-интернат №1» г. Курска
24.12.2013 г. 15.00	Психологическое консультирование (9-11 класс)	Способности и профессионально важные качества	Профориен тационная работа	Сухих Наталья Александровна, кандидат психологических наук, зав. кафедрой методики, педагогики и психологии профессионального образования КГУ

Математические курсы — онлайн-курсы с видео

Study.com предлагает увлекательные математические онлайн-курсы по предварительной алгебре, алгебре, геометрии, статистике, исчислению и многому другому! Наши самостоятельные видеоуроки могут помочь вам подготовиться к экзаменам, заработать кредит в колледже или повысить свою оценку по математике. Выберите курс ниже и начните!

Как это работает

• Выберите курс математики: Мы предлагаем широкий выбор онлайн-курсов по математике, включая обзор базовых математических навыков, а также курсы по алгебре, геометрии, тригонометрии, исчислению и статистике.
• Смотрите занимательные видеоуроки: Десятиминутные видеоуроки помогут вам разобраться даже в самых сложных математических понятиях.
• Попробуйте свои силы в решении практических задач: Существует множество практических задач, которые можно найти в викторинах по каждому курсу, викторинах по главам и практических выпускных экзаменах.
• Обратитесь за помощью к нашим знающим инструкторам по математике: Наши инструкторы готовы ответить на ваши вопросы по математике и помочь вам решить практические задачи, если вы застряли.

Для кого предназначены наши курсы?

• Взрослые учащиеся, изучающие математическую часть GED
• Учащиеся старших классов, готовящиеся к выпускным экзаменам или вступительным экзаменам в колледжи
• Студенты колледжей, желающие получить зачет на экзамене
• Родители учащихся, обучающихся на дому, которые хотят дополнить обучение
• Преподаватели, которые ищут ресурсы для преподавания математических стандартов Common Core

Почему наши курсы работают

• Исследование на ходу: Используйте исследование. com Android-приложение для загрузки математических видеороликов, которые можно смотреть в автономном режиме в любое время и в любом месте! У нас также есть мобильное приложение Study.com для iOS для загрузки математических видеороликов.
• Самостоятельное обучение: Переходите к следующему уроку, когда будете готовы. Вам не нужно беспокоиться о том, что вы останетесь позади или вам станет скучно, благодаря индивидуальному темпу наших уроков, разработанных с учетом ваших математических способностей.
• Практическое обучение: На наших онлайн-уроках математики преподаватели используют реальные примеры для демонстрации важных математических понятий, которые могут помочь их понять.
• Практические задачи и викторины: Просматривайте практические задачи, включенные в уроки, викторины и выпускные экзамены, до тех пор, пока вы не почувствуете уверенность в том, что овладели ключевыми навыками решения задач.
• Сотни математических ресурсов: Просмотрите все наши онлайн-уроки по математике всего за одну подписку. Вы можете вернуться назад и просмотреть основные математические концепции, чтобы улучшить свое положение в текущем курсе обучения, или продолжить работу над более сложным предметом.

DIVE Stream & Download: Видеолекции по саксонской геометрии

Др.Шорманн не рекомендует этот курс. Этот курс, опубликованный компанией Houghton Mifflin, которая приобрела Saxon после смерти Джона Саксона, не использует оригинальные методы обучения Joh n по интеграции геометрии и алгебры.

Вместо этого он рекомендует нашу новую математику Шормана, которая использует методы Джона Саксона, но обновлена ​​с учетом концепций 21-го века, таких как компьютерная математика, технологические приложения, и обучает всем концепциям переработанных PSAT и SAT, а также ACT.

Shormann Math размещается в ультрасовременном кампусе электронного обучения с видеоинструкциями, интерактивными домашними заданиями, автоматическим оцениванием, записью оценок и поддержкой вопросов и ответов с доктором Шорманном. Узнать больше: Shormann Math

ЧТО ВКЛЮЧЕНО

• 120 УРОКОВ ВИДЕОЛЕКЦИИ

• 12 ВИДЕОЛЕКЦИИ ПО РАССЛЕДОВАНИЮ

• ТАБЛИЦА НА НЕДЕЛЮ

• СЛУЖБА ВОПРОСОВ И ОТВЕТОВ ПО ЭЛЕКТРОННОЙ ПОЧТЕ

• РУКОВОДСТВО ДЛЯ УЧИТЕЛЯ И ТАБЛИЦА ЗАДАНИЙ

ЧТО ВАМ НУЖНО

• КОМПЬЮТЕР: ВСЕ MAC И WINDOWS XP, VISTA, 7 и 8 ИЛИ CHROMEBOOK

ВИДЕОЛЕКЦИИ ОБУЧЕНИЕ ШАГ ЗА ШАГОМ

Др.Шорманн ведет каждый урок шаг за шагом на цифровой доске, которая выглядит и звучит как настоящая классная комната. Единственная разница в том, что вы можете легко приостанавливать, перематывать и перематывать лекцию вперед; обучение в своем собственном темпе. Имея ученые степени в области аэрокосмической техники и науки, доктор Шорманн имеет более чем 15-летний опыт преподавания саксонской математики на всех уровнях. Его уникальный опыт позволяет ему понять, как все уроки в книге сочетаются друг с другом, а также как учебная программа строится на всем протяжении математических вычислений и физики. СМ. РЕКОМЕНДУЕМОЕ РАСПИСАНИЕ КУРСА НА СТРАНИЦЕ РЕСУРСОВ.

КРАТКИЕ УРОКИ ПОВЫШАЮТ ПОНИМАНИЕ

На каждом уроке д-р Шорманн обучает от трех до пяти практических задач, повторяя ранее изученные понятия и связывая каждое «маленькое» понятие с последующим. Это облегчает понимание сложных концепций, показывая учащимся общую картину. Во время лекции студенты работают в интерактивном режиме, делая заметки и решая с ним практические задачи.Им рекомендуется делать паузу, перематывать назад и вперед, пока они полностью не поймут новую концепцию. ПОСМОТРЕТЬ ОБРАЗЦЫ ВИДЕОУРОКОВ ПО ЭТОЙ ССЫЛКЕ.

НАУЧЕН БИБЛЕЙСКИМ ОСНОВАНИЕМ

Соединяя Писание с математикой и естественными науками, он преподает математику как данный Богом язык науки, инструмент для понимания Божьего творения, а также цели и модели, очевидных в Творении. Также обсуждается история математики, которая показывает огромное христианское наследие математики и естественных наук и то, как вся математика возникла в результате изучения Его творения.Обсуждение не займет много времени, но важно напомнить всем учащимся, что Бог является Автором и Творцом всех знаний, включая математику. Подумайте вот о чем: в нашем мире существует огромное количество фактов, и все они подлежат интерпретации. Кого вы хотите интерпретировать эти факты для вашего ребенка, христианина или нехристианина? ПОСМОТРЕТЬ ДР. ПОКАЗАНИЯ ШОРМАНА НА ОБ СТРАНИЦЕ.

ПОСТОЯННЫЙ ПЕРЕСМОТР ПОВЫШАЕТ ДОЛГОСРОЧНОЕ СОХРАНЕНИЕ

После лекции студенты выполняют домашнее задание по учебнику саксонского языка. Каждый набор домашних заданий обеспечивает постоянный повтор ранее изученных понятий. Исследования показали, что этот метод лучше всего подходит для увеличения продолжительности удержания и времени припоминания, но это может быть проблемой для учащихся, которым необходимо заново выучить забытые понятия. В DIVE студент просто пересматривает соответствующую лекцию DIVE, которая печатается в скобках рядом с каждым вопросом. Вместо того, чтобы давать им ответ, учащийся заново усваивает забытое понятие и сразу же применяет его к задаче; значительно увеличивает удержание. ПРОСМОТРИТЕ ОБРАЗЕЦ ДОМАШНЕГО ЗАДАНИЯ, НАЖИМАЯ НА ИЗОБРАЖЕНИЯ ПРОДУКТА, И НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПРОСМОТРЕТЬ СОДЕРЖАНИЕ.

.

ДОПОЛНИТЕЛЬНАЯ ПОМОЩЬ ДЛЯ ПОНИМАНИЯ

В набор Saxon Homestudy Kit входит руководство по решению, в котором шаг за шагом показано, как решать каждую задачу. Мы рекомендуем сначала просмотреть соответствующий урок DIVE, а затем обратиться к Руководству по решениям, если потребуется дополнительная помощь. Если вам нужна дополнительная помощь, вы можете написать Dr.Шорманн для более подробных объяснений. Однако наша программа настолько обширна, что в этом редко возникает необходимость. (Обратите внимание, что руководство по решениям для геометрии не включает решения для тестов.)  ПОСМОТРИТЕ, ЧТО ГОВОРЯТ НАШИ КЛИЕНТЫ, НАЖИМАЯ НА ВКЛАДКУ ОТЗЫВЫ.

ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ

  Почему вы не рекомендуете этот курс геометрии?

Вся геометрия, необходимая для успешной сдачи экзаменов PSAT, SAT, ACT и математических курсов высшего уровня, содержится в курсах DIVE Algebra 2 и Advanced Math.Прохождение этого курса является излишним и тратит драгоценное время, не позволяя учащемуся пройти математический анализ в старшей школе. Поскольку исчисление отвечает за большинство технических достижений за последние 300 лет, доктор Шорманн считает, что это гораздо важнее. Не дайте себя обмануть преподавателям государственных школ, которые отупляют математическое образование в Америке, уделяя слишком много внимания геометрии. СМОТРИТЕ РЕКОМЕНДУЕМОЕ РАСПИСАНИЕ КУРСА ЗДЕСЬ.

Зачем использовать Saxon Math?

Saxon Math — это проверенная исследованиями учебная программа по математике, разработанная в 1980-х годах Джоном Саксоном.Саксонский подход уникален тем, что вместо массового обучения, практики и оценок, Саксон распределяет их по урокам и учебному году. В большинстве математических программ используется массовый подход, при котором обучение, практика и оценка навыка или концепции происходят в течение короткого периода времени и обычно группируются в рамках одной главы или раздела. Исследования показали, что постепенное развитие, распределенная практика и кумулятивная оценка превосходят все другие методы обучения, увеличивая долгосрочное запоминание и скорость припоминания, что, естественно, приводит к более высоким результатам стандартизированных тестов.Однако в большинстве учебных программ этот метод не используется, потому что его сложнее преподавать и он требует постоянного повторного преподавания ранее изученных понятий. Как опытный саксонский преподаватель, д-р Шорманн предлагает подробные лекции в формате, позволяющем легко повторно преподавать забытые или пропущенные концепции. Узнайте больше о Джоне Саксоне и его невероятно успешной программе по математике в блоге доктора Шорманна здесь.

Куда мне поместить моего ребенка?

Если ваш ребенок хорошо учился на предыдущем курсе, и это довольно строгая учебная программа, такая как A Beka, Horizons или Bob Jones, ваш ребенок сможет сразу перейти на саксонский язык в соответствующем классе.Если у вашего ребенка в прошлом были проблемы с математикой, он учился в государственной школе или у вас есть другие проблемы, мы рекомендуем пройти вступительный тест. Мы также предлагаем бесплатные консультационные услуги, которые помогут вам наметить курс успеха для вашего ребенка. РЕКОМЕНДУЕМОЕ РАСПИСАНИЕ КУРСА ЗДЕСЬ.

Репетитор по геометрии, помощь и практика онлайн

Не видите, что вам нужно?

Не беспокойтесь, попробуйте выполнить поиск по всем нашим темам

Искать по всем StudyPug

Что такое геометрия?

Понимание геометрии может быть трудным. С таким количеством подтем под эгидой геометрии может быть трудно понять, что такое геометрия, почему и когда она может быть полезна? Вообще говоря, геометрия — это изучение форм — как их можно преобразовывать, масштабировать, измерять/вычислять найденные в них углы, а также другие характеристики, такие как площадь, объем и так далее. Изучение геометрии также включает в себя изучение линий, строительных блоков форм и их свойств. Здесь, в StudyPug, геометрия также познакомит вас со сферой статистики, где мы рассматриваем вероятность и как это относится к формам (т.е. диаграммы Венна).

Кто известен как отец геометрии?

Честь и престиж этого титула были дарованы единственному и неповторимому Евклиду Александрийскому. Он был невероятным математиком, учился в Академии Платона в Греции и первым начал изучать геометрию. Он продолжал публиковать множество учебников, используемых математиками по сей день. Он наиболее известен своей работой над публикацией под названием «Элементы», в которой представлены новаторские материалы по алгебре, теории чисел и, конечно же, геометрии. Говорят, что этот шедевр принес ему титул «отца геометрии» (https://en.wikipedia.org/wiki/Euclid).

Геометрия сложная?

Изучение геометрии может быть связано с трудностями и трудностями обучения, но именно поэтому мы здесь! Здесь, в StudyPug, мы предлагаем помощь всем — тем, кто подпадает под категорию «Геометрия для чайников», или тем, кто ищет больше практики и/или сложных вопросов. В StudyPug мы стремимся сделать изучение геометрии простым, доступным и увлекательным.Имея более 1000 уроков, пошаговые примеры и круглосуточную помощь, мы готовы предоставить учащимся бесконечные возможности для легкой практики, будь то подготовка к экзамену по геометрии или просто закрепление знаний. Здесь, в StudyPug, мы рассматриваем широкий спектр вопросов, с которыми вы можете столкнуться, и мы также используем различные учебники по геометрии (например, геометрия Прентиса Холла, геометрия Гленко, геометрия Макдугала Литтела, математическая геометрия больших идей), чтобы всесторонне удовлетворить содержание, которое вы можете изучать. . Будьте уверены, у нас есть все необходимое, чтобы помочь с фундаментальными понятиями и базовыми проблемами, которые позволят вам уверенно переходить к более сложным и сложным вопросам в своем собственном темпе.

Что такое евклидова геометрия?

Евклидова геометрия — это раздел геометрии, который сосредоточен на изучении двухмерной твердотельной геометрии и плоскостей. Некоторые примеры включают основные факты, такие как внутренние углы треугольников должны быть равны 180 градусам и что кратчайшее расстояние между точками A и B является прямой линией. Евклидова геометрия была построена на основе математических теорий и постулатов Евклида, в первую очередь составленных и синтезированных в его публикации «Элементы».В более широком смысле евклидова геометрия также указывает на важность использования когнитивных способностей в математике. Это предполагает, что учащийся откладывает приемы запоминания и формул и опирается на сильное целостное понимание предмета, которое позволяет применять навыки и методы для решения математических задач. Хотя вы, возможно, начали изучать евклидову геометрию еще в школе, вскоре вы начнете изучать концепции неевклидовой геометрии (например, свойства трехмерных фигур, таких как сфера).

Как сдать геометрию?

Независимо от того, готовитесь ли вы к тесту по геометрии, экзамену или просто нуждаетесь в помощи по геометрии, StudyPug здесь, чтобы помочь вам добиться успеха и сдать экзамены с помощью наших уроков геометрии и репетиторства по геометрии. Наши преподаватели по геометрии расскажут о содержании, изучают советы, стратегии и практические вопросы, которые предоставят вам столько помощи по геометрии, сколько вам нужно. Мы рекомендуем начинать со сложных подтем/глав, с которыми вы боретесь, следуйте нашим руководствам по геометрии, поскольку мы шаг за шагом проведем вас через процесс понимания концепции или проблемы, которая может у вас возникнуть.Некоторые концепции или проблемы сложнее, чем другие, поэтому вам может потребоваться вернуться к этим областям более одного раза, что не должно быть проблемой, учитывая ваш неограниченный доступ 24/7. Как только вы почувствуете себя уверенно, мы призываем вас практиковаться, практиковаться, практиковаться! Это позволяет вам быть готовым к разным стилям вопросов, а также разным уровням сложности. Эти вопросы дополнят ваше обучение и действительно проверят ваше понимание.

Какой класс геометрии?

Учащиеся начинают изучать геометрию в 10-м классе.Учащиеся должны хорошо понимать алгебру 1 (завершенную в 9-м классе), прежде чем приступить к изучению тем, изучаемых в геометрии. Чтобы освежить в памяти, пожалуйста, посетите нашу страницу Алгебра 1. После завершения геометрии учащиеся могут приступить к изучению алгебры 2. Впереди игра? Интересно, что будет после геометрии? Посетите нашу страницу Алгебра 2 для получения дополнительной информации.

Геометрия — 1206310 | CPALMS.org

Угол ВВЕРХ: Игрок 1:

Изучите процессы построения для построения биссектрисы угла, копирования угла и построения линии, параллельной заданной линии, через точку, не находящуюся на линии, с использованием различных инструментов в этом интерактивном учебном пособии в стиле ретро-видеоигры.

ПРИМЕЧАНИЕ. В этом учебном пособии используется как построение биссектрисы угла, так и построение для копирования угла в качестве возможности расширения, чтобы также построить линию, параллельную заданной линии, через точку, не находящуюся на линии. Учащиеся также учатся определять соответствующие углы, образующиеся при пересечении секущей параллельных прямых, и обнаруживают с помощью Geogebra, что эти углы равны.

Тип: оригинальное учебное пособие для учащихся

Круглогодичные школьные дебаты: выявление ошибочных рассуждений — часть вторая:

Научитесь выявлять ошибочные рассуждения в этом интерактивном учебном пособии по английскому языку, состоящем из двух частей.Вы узнаете, что некоторые эксперты говорят о круглогодичных школах, какие исследования были проведены по поводу их эффективности и какие аргументы можно привести за и против круглогодичного образования. Затем вы прочитаете речь в пользу круглогодичных школ и определите ошибочные рассуждения в аргументе, в частности использование поспешных обобщений.

Обязательно завершите первую часть перед второй! Нажмите ЗДЕСЬ , чтобы запустить первую часть.

Тип: оригинальное учебное пособие для учащихся

Вымпел компании Challenge: вписанные круги треугольников:

Узнайте, как легко Кэти создать круговой логотип с надписью на шаблоне треугольного вымпела своей компании.Если она выполнит задание первой, она выиграет бонус в размере 1000 долларов США! Следуйте этому интерактивному руководству.

Тип: оригинальное учебное пособие для учащихся

Круглогодичные школьные дебаты: выявление ошибочных рассуждений — часть первая:

Научитесь выявлять ошибочные рассуждения в этом интерактивном учебном пособии по английскому языку, состоящем из двух частей. Вы узнаете, что некоторые эксперты говорят о круглогодичных школах, какие исследования были проведены по поводу их эффективности и какие аргументы можно привести за и против круглогодичного образования. Затем вы прочитаете речь в пользу круглогодичных школ и определите ошибочные рассуждения в аргументе, в частности использование поспешных обобщений.

Обязательно выполните обе части этой серии! Нажмите ЗДЕСЬ , чтобы открыть вторую часть.

Тип: оригинальное учебное пособие для учащихся

Встретить меня на полпути:

Спланируйте экспедицию на байдарке, научившись выполнять основные геометрические построения, включая копирование сегмента, построение биссектрисы сегмента, построение перпендикулярной биссектрисы сегмента и построение перпендикулярных сегментов с помощью различных инструментов в этом интерактивном учебном пособии.

Тип: оригинальное учебное пособие для учащихся

Оценка аргумента – Часть четвертая: Инаугурационная речь Джона Кеннеди:

Изучите инаугурационную речь президента Джона Ф. Кеннеди в этом интерактивном руководстве. Вы изучите аргумент Кеннеди, основное утверждение, более мелкие утверждения, причины и доказательства.

В четвертой части вы будете использовать то, что вы узнали из этой серии, чтобы оценить общую аргументацию Кеннеди.

Перед тем, как приступить к части 4, обязательно выполните предыдущие части этой серии.

• Нажмите ЗДЕСЬ , чтобы запустить первую часть.
• Нажмите  ЗДЕСЬ  , чтобы запустить вторую часть.
• Нажмите  ЗДЕСЬ  , чтобы запустить третью часть.

Тип: оригинальное учебное пособие для учащихся

Человек не на своем месте:

Узнайте, как построить вписанный квадрат в круг и почему в этом интерактивном руководстве используются определенные конструкции.

Тип: оригинальное учебное пособие для учащихся

Оценка аргумента – Часть третья: Инаугурационная речь Джона Кеннеди:

Изучите инаугурационную речь президента Джона Ф. Кеннеди в этом интерактивном руководстве. Вы изучите аргумент Кеннеди, основное утверждение, более мелкие утверждения, причины и доказательства. К концу этой серии из четырех частей вы сможете оценить его общую аргументацию.

В третьей части вы прочтете больше о речи Кеннеди и определите меньшее утверждение в этом разделе его речи. Вы также оцените соответствие этого меньшего утверждения основному утверждению и оцените причины и доказательства Кеннеди.

Обязательно выполните все четыре части этой серии!

• Нажмите ЗДЕСЬ , чтобы запустить первую часть.
• Нажмите  ЗДЕСЬ  , чтобы запустить вторую часть.
• Нажмите ЗДЕСЬ , чтобы запустить четвертую часть.

Тип: оригинальное учебное пособие для учащихся

Где эта вышка сотовой связи?:

Найдите расположение и зону покрытия вышек сотовой связи, чтобы определить центр и радиус круга по его уравнению, используя стратегию заполнения квадрата в этом интерактивном руководстве.

Тип: оригинальное учебное пособие для учащихся

Проектирование с помощью шестиугольников:

Узнайте, как построить вписанный правильный шестиугольник и равносторонний треугольник в окружность в этом интерактивном учебном пособии.

Тип: оригинальное учебное пособие для учащихся

Как новый:

Узнайте, как описать окружность вокруг треугольника в этом интерактивном руководстве по построению.Возьмите циркуль, линейку, карандаш и бумагу, чтобы следовать!

Тип: оригинальное учебное пособие для учащихся

Высокотехнологичные качели:

Из этого интерактивного руководства вы узнаете, как найти точку на направленном отрезке, которая делит его в заданном отношении.

Тип: оригинальное учебное пособие для учащихся

Круг вверх!:

Узнайте, как написать уравнение окружности, используя теорему Пифагора , зная ее центр и радиус, используя пошаговые инструкции в этом интерактивном руководстве.

Тип: оригинальное учебное пособие для учащихся

Готов к взлету! — Часть вторая:

Это вторая часть серии руководств, состоящей из двух частей.В этом интерактивном учебном пособии вы потренируетесь определять цель говорящего, используя речь пионера авиации Амелии Эрхарт. Вы изучите использование ею риторических призывов, включая этос, логос, пафос и кайрос. Наконец, вы оцените эффективность использования Эрхартом риторических призывов.

Обязательно сначала выполните первую часть. Щелкните здесь, чтобы запустить ЧАСТЬ ПЕРВУЮ.

Тип: оригинальное учебное пособие для учащихся

Готов к взлету! — Первая часть:

Это первая часть серии руководств, состоящей из двух частей.В этом интерактивном учебном пособии вы потренируетесь определять цель говорящего, используя речь пионера авиации Амелии Эрхарт. Вы изучите использование ею риторических призывов, включая этос, логос, пафос и кайрос. Наконец, вы оцените эффективность использования Эрхартом риторических призывов.

Щелкните здесь, чтобы запустить ЧАСТЬ ВТОРАЯ .

Тип: оригинальное учебное пособие для учащихся

Описательное письмо: Глаза в небе (часть 4 из 4):

Попрактикуйтесь в написании различных аспектов описательного эссе об ученых, использующих дроны для исследования ледников в Перу.Этот интерактивный учебник является четвертой частью серии из четырех частей. В этом заключительном уроке вы узнаете об элементах основного абзаца. Вы также создадите основной абзац с подтверждающими доказательствами. Наконец, вы узнаете об элементах заключения и потренируетесь в создании «подарка».

Это руководство является четвертой частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.

Тип: оригинальное учебное пособие для учащихся

Описательное письмо: Глаза в небе (часть 3 из 4):

Узнайте, как написать введение для описательного эссе в этом интерактивном руководстве. Этот учебник является третьей частью серии из четырех частей. В предыдущих уроках этой серии учащиеся проанализировали информационный текст и видео об ученых, использующих дроны для исследования ледников в Перу. Студенты также определили центральную идею и важные детали текста и написали эффективное резюме. В третьей части вы узнаете, как написать введение для описательного эссе об исследованиях ученых.

Это руководство является третьей частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.

Тип: оригинальное учебное пособие для учащихся

Чертежи строительства:

С помощью этого интерактивного учебного пособия вы научитесь строить биссектрису отрезка прямой с помощью линейки и циркуля.

Тип: оригинальное учебное пособие для учащихся

Сравнение митоза и мейоза:

Сравните и сопоставьте митоз и мейоз в этом интерактивном руководстве. Вы также свяжете их с процессами полового и бесполого размножения и их последствиями для генетической изменчивости.

Тип: оригинальное учебное пособие для учащихся

Кусочки ниндзя Нэнси:

Узнайте, как определить форму поперечного сечения, созданного пересечением секущей плоскости с пирамидой или призмой, в этом интерактивном учебном пособии на тему ниндзя.

Тип: оригинальное учебное пособие для учащихся

Вокруг света с прямоугольными треугольниками:

Из этого интерактивного руководства вы узнаете, как использовать тригонометрические соотношения для определения высоты известных памятников и решить задачу из реальной жизни.

Тип: оригинальное учебное пособие для учащихся

Доказательство теорем о треугольниках:

Используйте свойства, постулаты и теоремы, чтобы доказать теорему о треугольнике.В этом интерактивном уроке вы также узнаете, как доказать, что линия, параллельная одной стороне треугольника, пропорционально делит две другие.

Тип: оригинальное учебное пособие для учащихся

Рак: мутировавшие клетки вышли из-под контроля!:

Изучите взаимосвязь между мутациями, клеточным циклом и неконтролируемым ростом клеток, который может привести к раку, с помощью этого интерактивного руководства.

Тип: оригинальное учебное пособие для учащихся

Банковский выстрел:

В этом задании учащимся предлагается использовать сходство для решения задачи в контексте, который будет знаком многим, хотя большинство учащихся привыкли использовать интуицию, а не геометрические рассуждения, для построения кадра.

Тип: Задача решения проблем

Они похожи?:

В этой задаче учащимся дается изображение двух треугольников, которые кажутся подобными, но сходство которых нельзя доказать без дополнительной информации.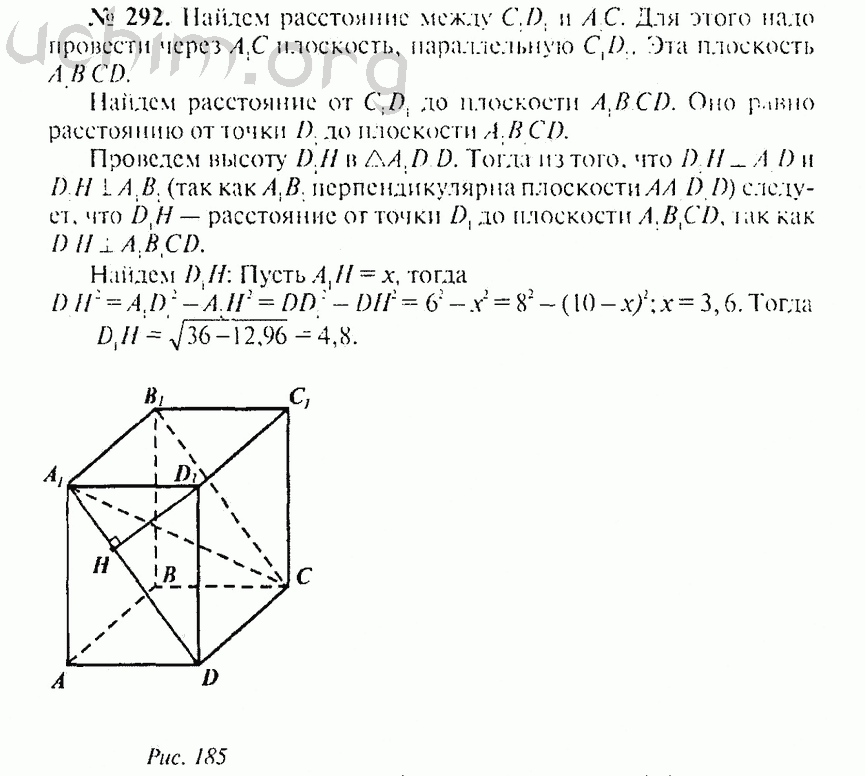 Попросите учащихся предоставить последовательность преобразований подобия, которая отображает один треугольник в другой, используя определение подобия в терминах преобразований подобия.

Тип: Задача решения проблем

Рулон туалетной бумаги:

Целью этого задания является привлечение учащихся к геометрическому моделированию и, в частности, к выводу алгебраических взаимосвязей между переменными, вытекающими из геометрических ограничений.

Тип: Задача решения проблем

Монеты по кругу:

Используя таблицу диаметров монет разного достоинства, учащихся просят определить, сколько монет помещается вокруг центральной монеты.

Тип: Задача решения проблем

Проблема с маяком:

В этой задаче учащимся предлагается смоделировать явления на поверхности земли, исследуя видимость лампы на маяке с лодки.

Тип: Задача решения проблем

Солнечное затмение:

Это задание на решение задач побуждает учащихся исследовать, почему солнечные затмения случаются редко, путем изучения радиуса Солнца и самого дальнего расстояния между Луной и Землей.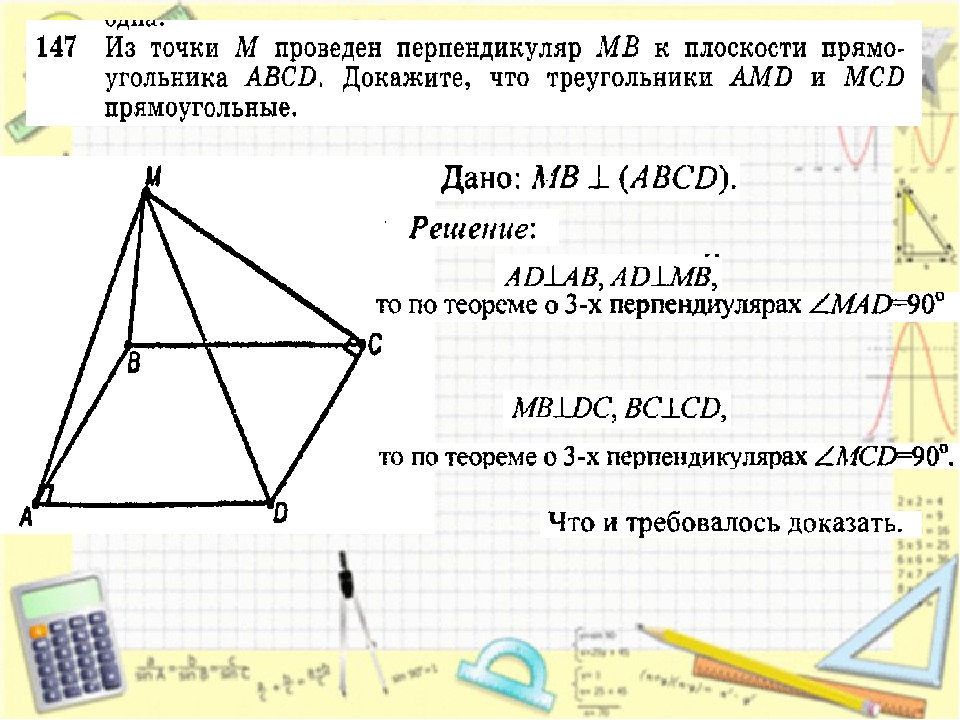

Тип: Задача решения проблем

Чудо средней точки:

Это задание на решение задач дает учащимся возможность доказать факт о четырехугольниках: если мы соединим середины произвольного четырехугольника, чтобы образовать новый четырехугольник, то новый четырехугольник будет параллелограммом, даже если первоначальный четырехугольник таковым не был.

Тип: Задача решения проблем

От горы Уитни до Долины Смерти:

Это задание вовлекает учащихся в открытое задание по моделированию, в котором используется подобие прямоугольных треугольников.

Тип: Задача решения проблем

Кратчайший отрезок линии от точки P до линии L:

Это базовое задание по геометрии, предназначенное для того, чтобы помочь учащимся развить некоторые фундаментальные геометрические свойства, которые на первый взгляд могут показаться довольно очевидными.В этом случае основное свойство, о котором идет речь, состоит в том, что кратчайший путь от точки к линии встречается с линией под прямым углом, что имеет решающее значение для многих дальнейших разработок предмета.

Тип: Задача решения проблем

Семь кругов III:

Это дает возможность смоделировать конкретную ситуацию с помощью математики. После того, как репрезентативная картина ситуации, описанной в задаче, будет нарисована (преподаватель может дать здесь указания по мере необходимости), решение задачи требует понимания определения функции синуса.

Тип: Задача решения проблем

Расширение линии:

В этом задании учащимся предлагается сделать выводы о линии после того, как она была увеличена в 2 раза.

Тип: Задача решения проблем

Бег по дорожке II:

Цель этого задания — смоделировать знакомый объект, олимпийскую трассу, используя геометрические фигуры. Расчеты периметров этих фигур объясняют ступенчатый старт бегунов в беге на 400 метров.

Тип: Задача решения проблем

Бег по дорожке I:

В этой задаче геометрия применяется к 400-метровой дорожке, чтобы найти ее периметр.

Тип: Задача решения проблем

Скрепка:

В этом задании типографская сетка служит фоном для стандартной скрепки.Метрическая шкала измерений нарисована поперек нижней части сетки, а скрепка проходит в обоих направлениях немного за пределы сетки. Ученикам дают примерную длину скрепки и определяют количество одинаковых скрепок, сделанных из проволоки заданной длины.

Тип: Задача решения проблем

Рожок мороженого:

В этом задании учащиеся сделают эскиз бумажной обертки от рожка для мороженого, с помощью этого эскиза выведут формулу площади поверхности обертки и оценят максимальное количество оберток, которые можно вырезать из прямоугольного листа бумаги. .

Тип: Задача решения проблем

Насколько толстая банка газировки? (Вариант I):

В этом задании на решение задач учащиеся должны найти площадь поверхности банки из-под газировки, вычислить, сколько кубических сантиметров алюминия она содержит, и оценить ее толщину.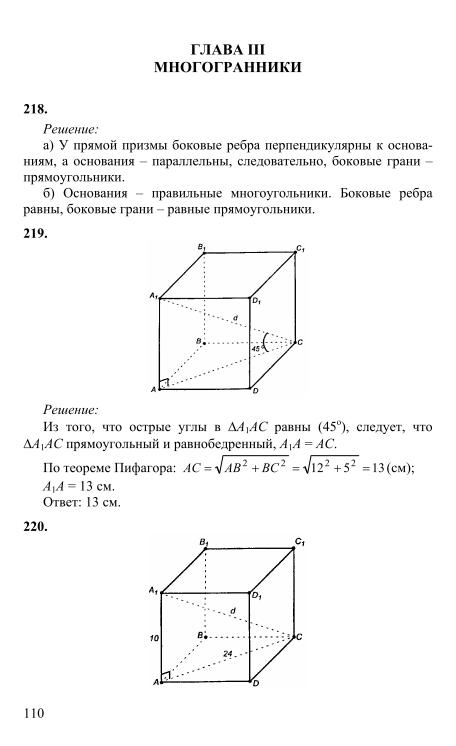

Тип: Задача решения проблем

Сколько листьев на дереве? (Версия 2):

Это задача математического моделирования, направленная на разумную оценку чего-то, что слишком велико для точного подсчета, а именно количества листьев на дереве.

Тип: Задача решения проблем

Сколько листьев на дереве?:

Это задача математического моделирования, направленная на разумную оценку чего-то, что слишком велико для точного подсчета, а именно количества листьев на дереве.

Тип: Задача решения проблем

Сколько клеток в теле человека?:

В этом задании по решению проблем учащимся предлагается применить понятия массы, объема и плотности в контексте реального мира, чтобы определить, сколько клеток содержится в организме человека.

Тип: Задача решения проблем

Глобальная система позиционирования II:

Отражая современность задействованных технологий, это сложное задание по геометрическому моделированию, в котором учащиеся с нуля открывают для себя геометрические принципы, лежащие в основе программного обеспечения, используемого системами GPS.

Тип: Задача решения проблем

Архимед и королевская корона:

В этом задании на решение задач используется сказка об Архимеде и короне царя Сиракуз, чтобы определить объем и массу золота и серебра.

Тип: Задача решения проблем

Склоны и круги:

Цель этого задания — познакомить учащихся с алгебраическим подходом к хорошо известному результату классической геометрии, а именно к тому, что точка X лежит на окружности диаметра AB, если угол ?AXB прямой

Тип: Задача решения проблем

Единичные квадраты и треугольники:

В этом задании на решение задач учащимся предлагается найти площадь треугольника, используя единичные квадраты и отрезки.

Тип: Задача решения проблем

Треугольники, вписанные в окружность:

Это задание на решение проблем побуждает учащихся использовать идеи о линейных функциях, чтобы определить, когда определенные углы являются прямыми углами.

Тип: Задача решения проблем

Прием у доктора:

Целью задания является анализ правдоподобного сценария реальной жизни с использованием геометрической модели. Задача требует знания формул объема для цилиндров и конусов, некоторых геометрических рассуждений, связанных с подобными треугольниками, а также уделяет внимание разумным приближениям и поддержанию разумного уровня точности во всем.

Тип: Задача решения проблем

Почему АСА работает?:

В этом задании на решение задач учащимся предлагается показать отражение одного треугольника в другом треугольнике.

Тип: Задача решения проблем

Когда SSA работает для определения конгруэнтности треугольников?:

В этой задаче мы рассматривали SSA.Критерии соответствия треугольника, SSS, SAS, ASA, требуют трех частей информации. Интересно, однако, что не всех трех частей информации о сторонах и углах достаточно, чтобы определить треугольник с точностью до конгруэнтности.

Тип: Задача решения проблем

Семь кругов II:

Эта задача обеспечивает конкретную геометрическую постановку для изучения жестких преобразований плоскости.

Тип: Задача решения проблем

Середины сторон параллелограмма:

Это достаточно прямое задание, направленное на то, чтобы учащиеся использовали ранее полученные результаты для изучения новых фактов о параллелограммах, а не для получения их из первых принципов.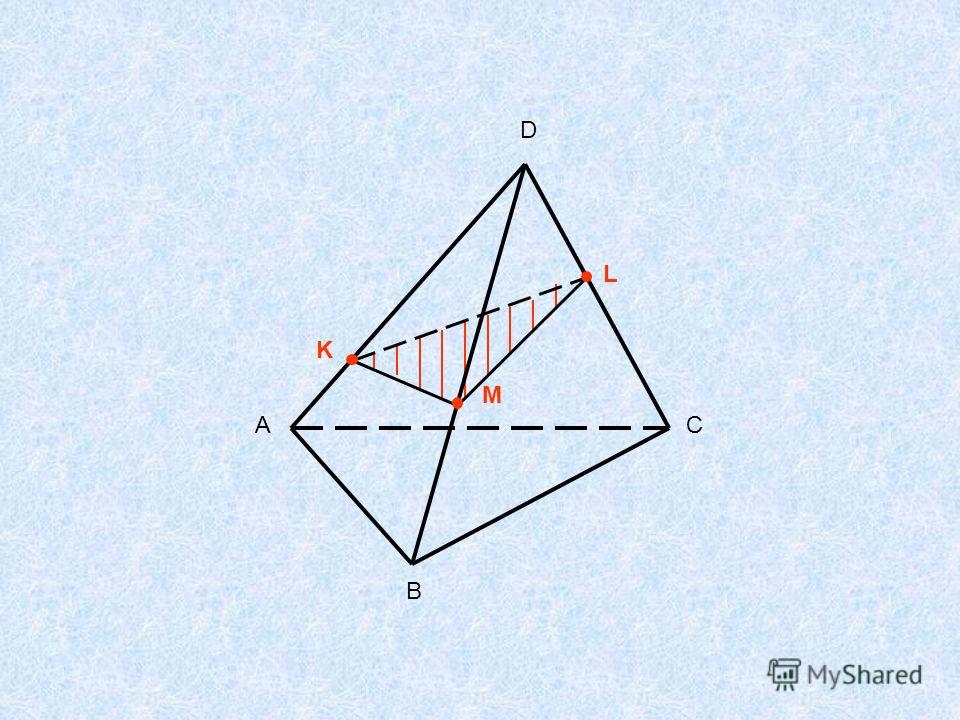

Тип: Задача решения проблем

Вписывание квадрата в круг:

Это задание дает учащимся возможность применить теоремы о конгруэнтности треугольников в явном, интересном контексте.

Тип: Задача решения проблем

Вписывание шестиугольника в окружность:

В этом задании на решение задач учащимся предлагается вписать равносторонние треугольники и правильные шестиугольники в круг с помощью циркуля и линейки.

Тип: Задача решения проблем

Почему SAS работает?:

В этом задании на решение задач учащимся предлагается объяснить причину, по которой данные треугольники равны, и построить отражения точек.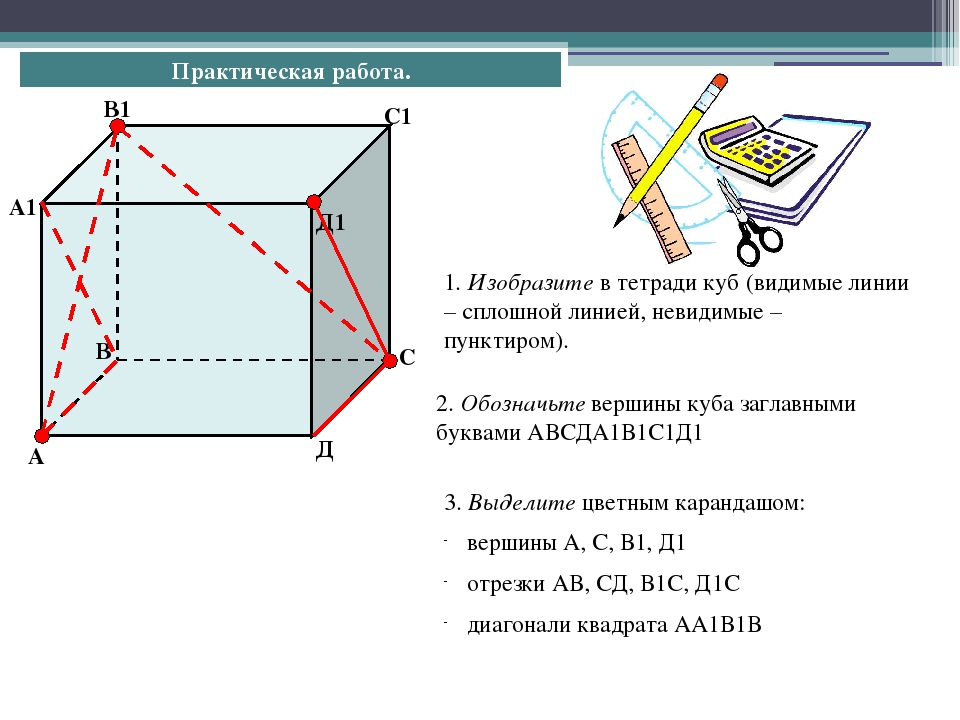

Тип: Задача решения проблем

Отражения и равносторонние треугольники II:

Это задание дает учащимся возможность увидеть влияние отражений на явный объект и увидеть, что отражения не всегда коммутируют.

Тип: Задача решения проблем

Отражения и равносторонние треугольники:

Это задание является одним из серии заданий, использующих жесткие преобразования плоскости для изучения симметрии классов треугольников, причем это задание, в частности, сосредоточено на классе равносторонних треугольников

Тип: Задача решения проблем

Отраженные треугольники:

В этом задании учащимся предлагается с помощью линейки и циркуля построить линию, через которую отражается треугольник.

Тип: Задача решения проблем

Центральная часть:

Целью этого задания является использование геометрических и алгебраических рассуждений для моделирования реального сценария. В частности, учащиеся в нескольких местах (явно или неявно) должны рассуждать о том, когда делать приближения разумно и когда округлять, когда использовать равенство, а когда нет.неравенства и выбор единиц измерения для работы (например, мм против см).

Тип: Задача решения проблем

Теннисные мячи в банке:

Эта задача основана на выводе формулы объема сферы. Если сфера радиуса 1 заключена в цилиндр радиуса 1 и высоты 2, то объем, не занимаемый сферой, равен объему «двухвершинного конуса» с вершиной в центре сферы и основаниями, равными к основаниям цилиндра

Тип: Задача решения проблем

Два колеса и ремень:

В этом задании сочетаются два навыка: использование отношения между касательным сегментом к окружности и радиусом, касающимся этого касательного сегмента, и вычисление длин дуг окружности с учетом радиусов и центральных углов.

Тип: Задача решения проблем

Прямоугольные треугольники, вписанные в окружности I:

Это задание дает хорошую возможность использовать равнобедренные треугольники и их свойства, чтобы показать интересный и важный результат о треугольниках, вписанных в окружность: тот факт, что эти треугольники всегда прямоугольные, часто называют теоремой Фалеса.

Тип: Задача решения проблем

Размещение пожарного гидранта:

В этом задании на решение задач учащимся предлагается разместить пожарный гидрант на равном расстоянии от трех заданных точек.

Тип: Задача решения проблем

Почему SSS работает?:

Эта конкретная задача по решению проблем демонстрирует соответствие между двумя треугольниками, демонстрируя перемещение, отражение и вращение.

Тип: Задача решения проблем

Построение рисунка плитки путем отражения восьмиугольников:

В этом задании отражения применяются к правильному восьмиугольнику для построения шаблона из четырех восьмиугольников, охватывающих четырехугольник: основное внимание в задании уделяется использованию свойств отражений для вывода о том, что четырехугольник на самом деле является квадратом.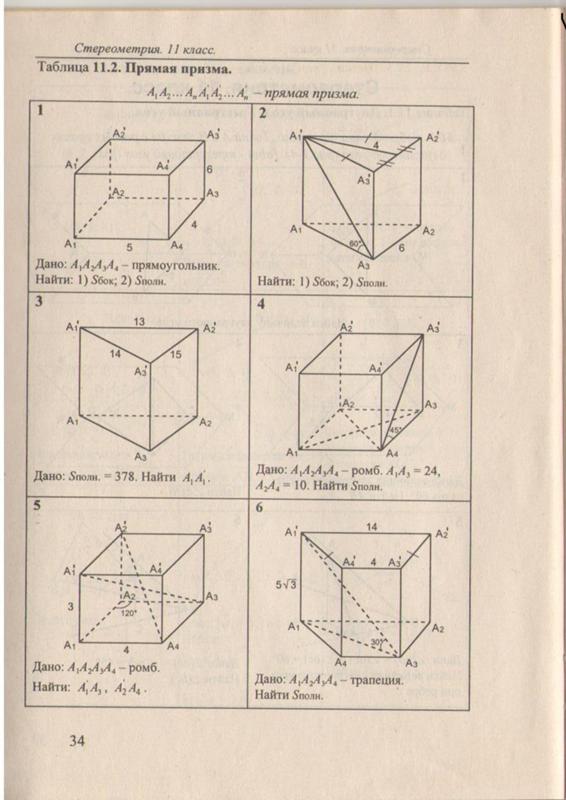

Тип: Задача решения проблем

Построение рисунка плитки путем отражения шестиугольников:

В этом задании отражения применяются к правильному шестиугольнику, чтобы построить шаблон из шести шестиугольников, заключающих в себе седьмой: основное внимание в задании уделяется использованию свойств отражений для получения этого шаблона из семи шестиугольников.

Тип: Задача решения проблем

Разделение угла пополам:

В этом задании на решение учащимся предлагается разделить заданный угол пополам.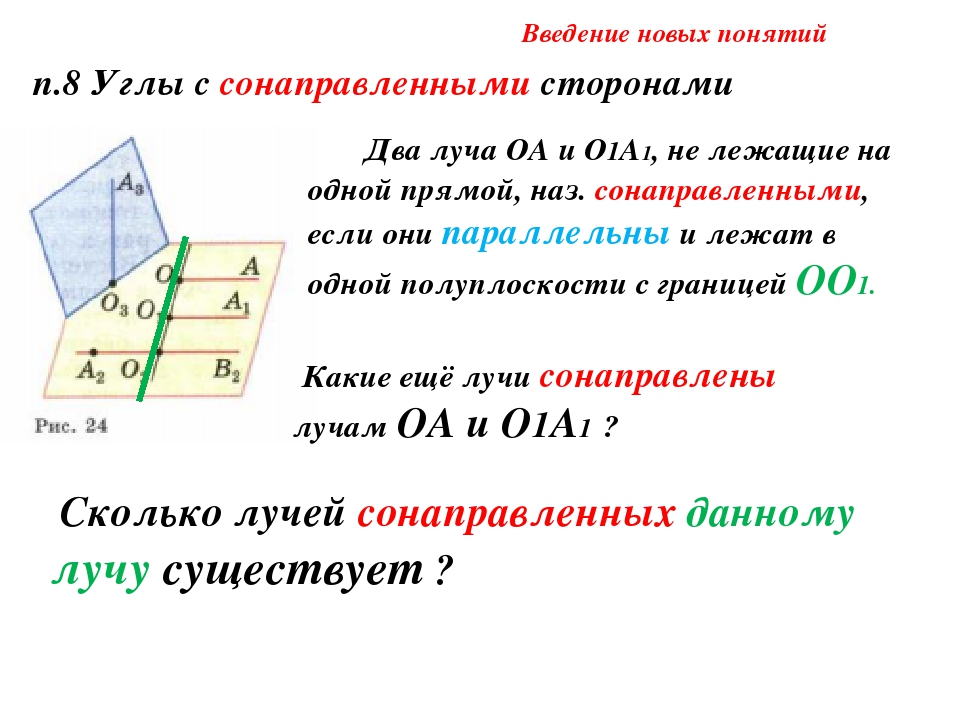

Тип: Задача решения проблем

Конгруэнтны ли треугольники?:

Цель этого задания в первую очередь ориентирована на оценивание: учащимся предлагается продемонстрировать знания о том, как определять конгруэнтность треугольников.

Тип: Задача решения проблем

Расположение склада:

В этом задании на решение задач учащимся предлагается разместить склад (точку) на равном расстоянии от трех дорог (линий).

Тип: Задача решения проблем

Вписывание треугольника в окружность:

Эта задача знакомит с центром описанной окружности треугольника и показывает, как его можно использовать для вписания треугольника в окружность.

Тип: Задача решения проблем

Центр окружности треугольника:

Эта задача показывает, что все три серединных перпендикуляра сторон треугольника пересекаются в одной точке, используя характеристику биссектрисы отрезка как множества точек, равноудаленных от двух концов отрезка.

Тип: Задача решения проблем

Касательные линии и радиус окружности:

В этом задании на решение задач учащимся предлагается найти точку пересечения перпендикуляра отрезка из центра окружности и касательной.

Тип: Задача решения проблем

Семь кругов I:

Эта задача предназначена для моделирования конкретной ситуации с геометрией. Размещение семи монет в виде круга — это конкретный и забавный эксперимент, который приводит к подлинному математическому вопросу: дает ли физическая модель с монетами понимание того, что происходит с семью кругами на плоскости?

Тип: Задача решения проблем

Установка разбрызгивателей:

Эта задача моделирования включает в себя несколько различных типов геометрических знаний и решения задач: нахождение площадей секторов окружностей, использование тригонометрических соотношений для решения прямоугольных треугольников и разложение сложной фигуры, включающей несколько дуг окружности, на части, площади которых можно найти.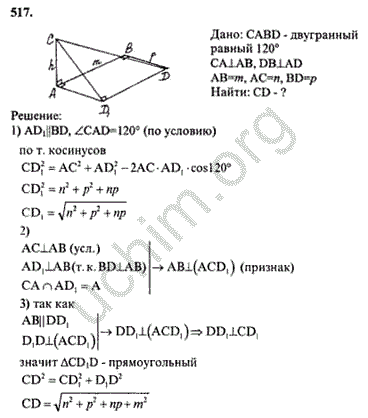

Тип: Задача решения проблем

Пренебрегая кривизной Земли:

В этом задании геометрические понятия, а именно свойства касательных окружностей и прямоугольных треугольников, применяются в ситуации моделирования. Ключевым геометрическим моментом в этой задаче является признание того, что линия обзора от вершины горы к горизонту касается земли.Затем мы можем использовать прямоугольный треугольник, в котором одна сторона касается окружности, а другая сторона является радиусом окружности, чтобы исследовать эту ситуацию.

Тип: Задача решения проблем

Разделение пополам угла и середины отрезков:

Эта задача обеспечивает построение биссектрисы угла путем сведения ее к биссектрисе угла с нахождением середины отрезка.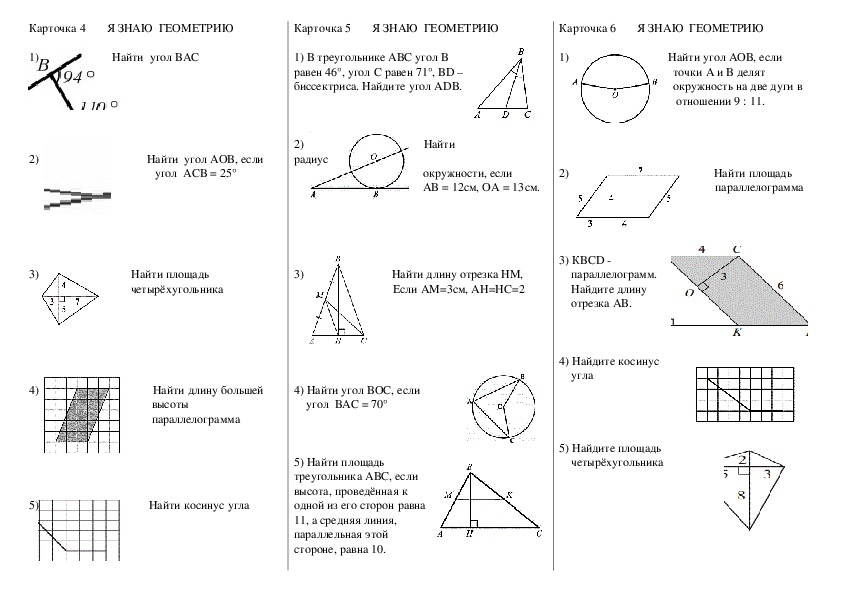 Стоит соблюдать симметрию — как для нахождения середины, так и для биссектрисы цель состоит в том, чтобы разрезать объект на две равные части.

Тип: Задача решения проблем

Вписывая окружность в треугольник II:

Это задание на решение проблемы фокусируется на замечательном факте, который вытекает из построения вписанной окружности в треугольник: все биссектрисы трех углов треугольника ABC пересекаются в одной точке.

Тип: Задача решения проблем

Регулярные замощения плоскости:

В этом задании исследуются способы покрытия плоскости правильными многоугольниками в очень строгом порядке, называемом правильной мозаикой.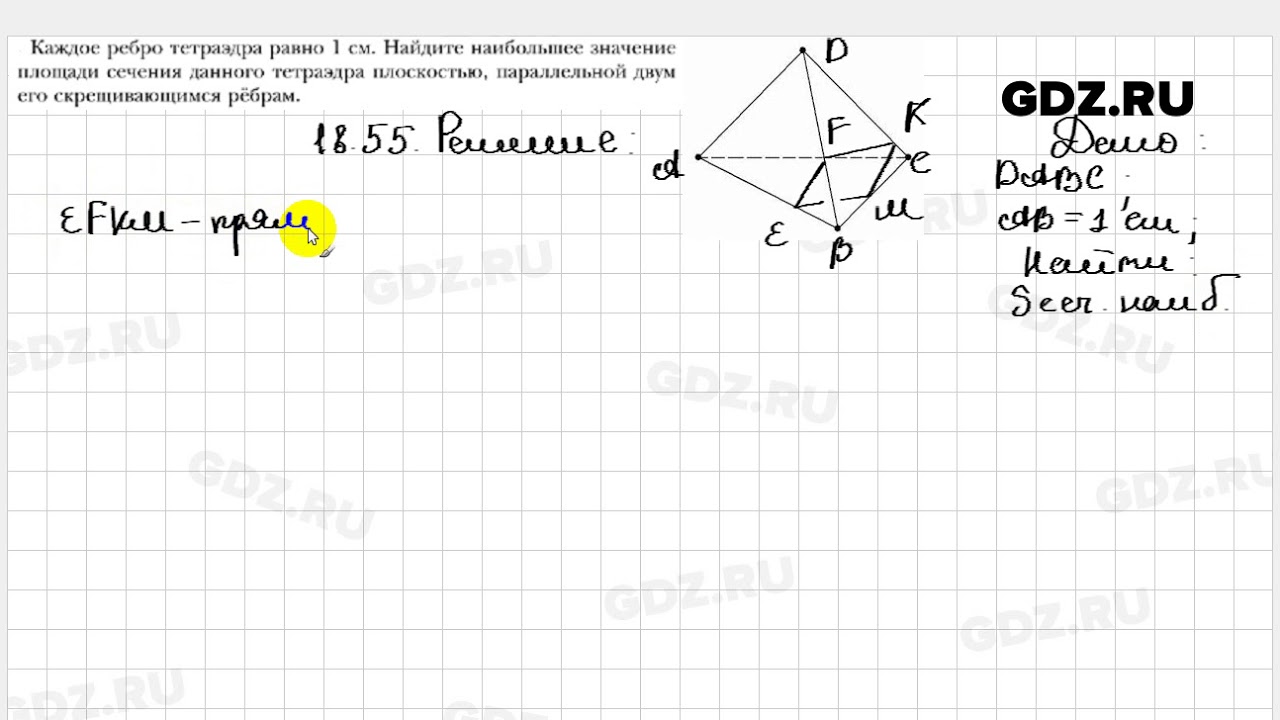 Эти мозаики изучаются здесь с помощью алгебры, которая входит в картину через формулу для измерения внутренних углов правильного многоугольника (которую, следовательно, следует ввести или повторить перед началом задачи). Цель задания — с помощью алгебры понять, какие замощения плоскости правильными многоугольниками возможны.

Тип: Задача решения проблем

Нахождение равных треугольников:

В этом учебном пособии учащиеся будут использовать постулаты SSS, ASA, SAS и AAS для нахождения конгруэнтных треугольников

Тип: Учебник

Использование SSS в доказательстве:

В этом руководстве обсуждается разница между теоремой и аксиомой. Он также показывает, как использовать SSS в доказательстве.

Тип: Учебник

Постулаты конгруэнтности треугольников:

В этом руководстве обсуждаются постулаты SSS, SAS, ASA и AAS для конгруэнтных треугольников. Это также показывает, что AAA подходит только для сходства, а SSA не годится ни для того, ни для другого.

Тип: Учебник

Конгруэнтные треугольники и SSS:

В этом видео учащиеся узнают о конгруэнтных треугольниках и постулате «Сторона-Сторона-Сторона».

Тип: Учебник

Линия отражения:

С помощью интерактивного инструмента учащимся показано, как отразить отрезок прямой.Перед просмотром этого видео учащиеся должны иметь представление об уклоне и средней точке.

Тип: Учебник

Линия отражения:

В этом уроке используется средняя точка двух линий, чтобы найти линию отражения.

Тип: Учебник

Очки после ротации:

Студенты увидят, что происходит, когда фигуру поворачивают вокруг начала координат на -270 градусов. Перед просмотром этого видео рекомендуется иметь представление о прямоугольных треугольниках.

Тип: Учебник

Параллельные прямые, секущие и треугольники:

В этом учебном пособии учащимся показаны восемь углов, образованных при пересечении двух параллельных прямых поперечной линией.Также в этом видео есть обзор треугольников.

Тип: Учебник

Язык геометрии:

Прежде чем изучать какое-либо новое понятие, важно, чтобы учащиеся выучили и использовали общий язык и последовательно обозначали понятия. Этот учебник знакомит учащихся с точкой, линией и плоскостью.

Тип: Учебник

Доказательство равенства вертикальных углов:

В этом уроке учащиеся доказывают, что вертикальные углы равны. Перед просмотром этого видео учащиеся должны иметь представление о дополнительных ракурсах.

Тип: Учебник

Нахождение меры вертикальных углов:

С помощью алгебры учащиеся найдут величину вертикальных углов или углов, противоположных друг другу при пересечении двух прямых. Перед просмотром этого видео учащиеся должны иметь представление о дополнительных и дополнительных ракурсах.

Тип: Учебник

Введение в вертикальные углы:

В этом учебном пособии учащиеся будут использовать свои знания о дополнительных, смежных и вертикальных углах для решения задач, связанных с пересечением двух прямых.

Тип: Учебник

Использование тригонометрии для поиска недостающей информации:

Этот учебник покажет учащимся, как использовать тригонометрию для поиска недостающей информации в прямоугольных треугольниках. В этом видео показаны рабочие примеры использования тригонометрических соотношений для поиска недостающей информации и оценки других тригонометрических соотношений.

Тип: Учебник

Базовая тригонометрия:

Этот учебник дает введение в тригонометрию.В этом ресурсе обсуждаются три основные функции тригонометрии: синус, косинус и тангенс.

Тип: Учебник

Параллельные линии:

Параллельные прямые имеют одинаковый наклон и не имеют общих точек. Однако не всегда очевидно, описывают ли два уравнения параллельные прямые или одну и ту же прямую.

Тип: Учебник

Перпендикулярные линии:

Перпендикулярные линии имеют наклоны, которые являются отрицательными обратными величинами друг к другу, но почему?

Тип: Учебник

Снаряд под углом:

В этом видео обсуждается, как вычислить горизонтальное смещение снаряда, запущенного под углом.

Тип: Учебник

8 отличных каналов YouTube по математике

Это сообщение было обновлено в декабре 2021 г.

В приведенном ниже списке представлены некоторые из лучших математических каналов YouTube, которые помогут вашим ученикам и детям изучать математику с помощью видео. Я составил список, чтобы включить только те математические каналы, которые представляют реальную образовательную ценность для студентов.

Используя эти каналы, учащиеся смогут изучать сложные и абстрактные математические понятия в увлекательной игровой форме. Объяснения и учебные пособия наглядно иллюстрированы, что облегчает развитие более тонкого понимания математики.

Если вас беспокоят отвлекающие факторы , которые часто окружают видео на YouTube (например, оскорбительные выражения в комментариях, неприемлемый контент в связанных видео и т. д.), я настоятельно рекомендую использовать такие инструменты, как Safeshare TV и Viewpure; два лучших инструмента, которые обеспечивают удобную и не отвлекающую среду для просмотра видео на YouTube.

1- Numberphile

Numberphile, безусловно, является одним из самых популярных математических каналов на YouTube, созданным видеожурналистом Брэди Хароном. Он включает в себя сотни видеороликов, посвященных всевозможным математическим концепциям, и часто с участием математиков и других гостей со всего мира. Он предоставляет отличные обучающие видео по математике, геометрии, физике и многим другим.

3- MooMooMath

«MooMooMath предлагает забавные полезные видео по математике и естественным наукам, чтобы помочь людям изучать математику и естественные науки. Мы добавляем новое видео каждый день и очень гордимся этим.»

4- Socratica

Socratica предоставляет образовательные видеоролики по различным предметам, включая математику, естественные науки, компьютерное программирование и многое другое. Некоторые из математических плейлистов, которые он включает, включают: основы Mathematica, абстрактную алгебру, теорию чисел, исчисление, уроки геометрии, геометрические построения, евклидову геометрию, глоссарий геометрии и многое другое.

5- 3Blue1Brown

«3Blue1Brown Гранта Сандерсона представляет собой комбинацию математики и развлечения, в зависимости от вашего настроения. Цель состоит в том, чтобы объяснения приводились в движение анимацией, а сложные задачи упрощались с изменением точки зрения.»

6- Матолог

Матолог, профессор математики Университета Монаша в Мельбурне, предлагает доступные объяснения сложных математических задач. Некоторые из его популярных видео включают в себя: «Математика в Симпсонах», «Числофил против математики», «Секреты бесполезного гриндера», «Бесконечные дроби и самое иррациональное число», «Как не умереть упорно с математикой» и многое другое.

7- Репетитор по органической химии
«Репетитор по органической химии занимается предоставлением обучающих видео по органической химии, общей химии, физике, алгебре, тригонометрии, предварительному исчислению и исчислению».

8- Бесплатные математические видеоролики PatrickJMT

Бесплатные математические видеоролики PatrickJMT  предоставляет видеоконтент на различные темы, такие как исчисление, производные, дифференциальные уравнения, пределы, интегралы и многое другое.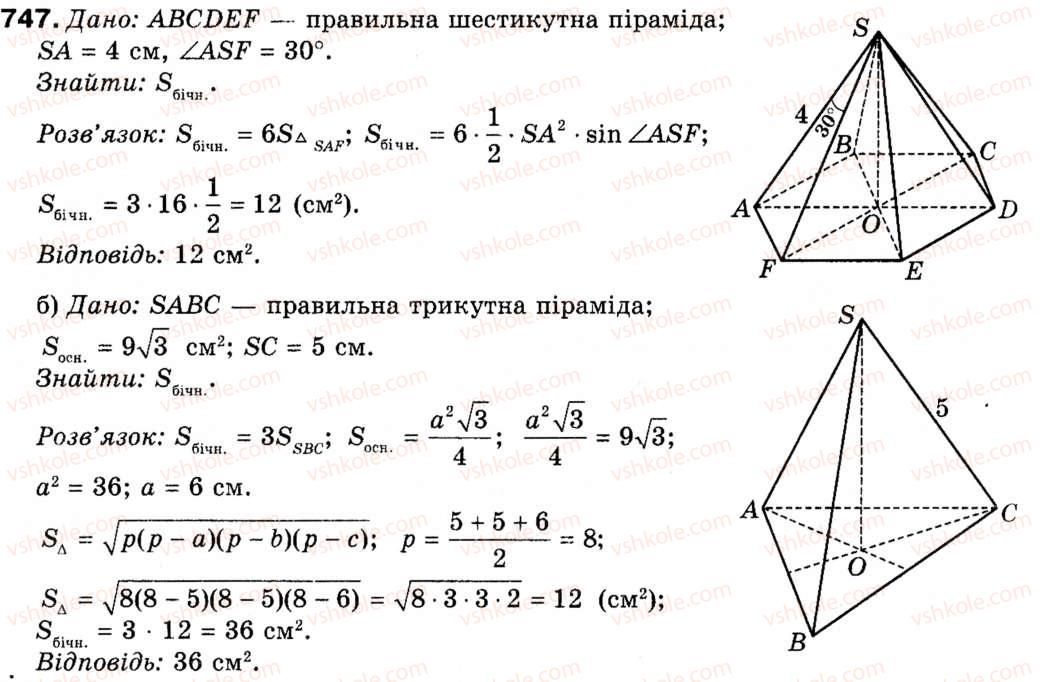

Другие известные каналы по математике включают:

1- The Video Math Tutor

Это отличный канал, который предоставляет несколько учебных видеороликов по математике на разные темы, включая уроки базовой математики, советы по калькулятору, головоломки и многое другое

2- Математика

Это еще один классный канал, предлагающий уроки математики по таким темам, как дроби и десятичные числа, алгебра и функции, чувство чисел, арифметика, геометрия…и больше.

3- Десять баллов

Это веб-программа для учащихся, позволяющая практиковать и осваивать математические понятия. Они могут изучать математику с помощью подсказок, видеоуроков и персонализированных рабочих листов.

4- Math Mammoth

Этот канал предоставляет советы по обучению математике, которые помогут учителям, родителям и репетиторам в обучении математике.

5- Math TV

Это канал учителя математики со стажем, который преподает математику и пишет учебники более 30 лет. Вы обязательно найдете что-то для своих учеников.

NextGen — прототип LMS

Обеспечивает онлайн-поддержку для Face2Face, дистанционного обучения, коротких курсов, онлайн-курсов.

НА БАЗОВОМ УРОВНЕ используется для обмена учебными материалами. Обеспечить онлайн-диалог для совместного обучения между учителем и учащимися и между учащимися.

На более ПРОГРЕССИВНОМ УРОВНЕ он предлагает викторины, автоматизированные задания, проекты рецензирования, интерактивные видеоуроки и полноценные уроки электронного обучения.Все это поддерживается своевременной аналитикой учащихся, чтобы облегчить массовую настройку обучения и внимание к каждому учащемуся.

На этих уровнях это учебный ресурс, улучшающий результаты учащихся.

На более ПРОДВИНУТОМ УРОВНЕ это одновременно учебный и бизнес-инструмент, обеспечивающий конкурентное преимущество для вашего колледжа/университета/школы.

  Загрузить брошюру и цифровую демонстрацию

Какая LMS есть у ваших конкурентов?

Moodle LMS — самая популярная LMS; у него 158 МИЛЛИОНОВ ПОЛЬЗОВАТЕЛЕЙ по всему миру. Это, FirstGEN Moodle является примитивным по внешнему виду и функциональности, чтобы произвести впечатление на сегодняшний рынок. Просто наличие LMS уже не новость; он не дает никаких конкурентных преимуществ.

  Загрузить брошюру и цифровую демонстрацию

LMS NextGEN ставит вас впереди конкурентов

;Привлекательный современный внешний вид NextGEN Moodle сразу выделяет ваш колледж/школу/университет. Это демонстрирует вашу приверженность лучшим методам обучения и поддержке учащихся. Загрузить брошюру и цифровую демонстрацию

NextGEN защищает новый бизнес 

Привлекает новых учащихся для увеличения доходов Расширяет ваш рынок, поскольку особенно ценен для учащихся, обучающихся неполный рабочий день, дистанционных учащихся и краткосрочных курсов.Но также обращается к учащимся очного обучения.

Кроме того, надстройки электронной коммерции открывают новые возможности для получения дохода.

 NextGEN сохраняет существующий бизнес 

Удержание нынешних учащихся в 10–15 раз выгоднее, чем привлечение новых. Поддержка учащихся LMS повышает показатели успеваемости учащихся и повышает их пропускную способность, повышая прибыльность.

NextGEN улучшает результаты учащихся

Во всем мире колледжи/университеты/школы приходят к выводу, что факт наличия у вас LMS не является гарантией того, что люди действительно будут ее использовать.Даже если бы они добились лучших результатов.
NextGEN LMS имеет внешний вид, который привлекает учащихся. Кроме того, он предлагает стимулирующие форматы обучения, которые постоянно поощряют участие.

Как эти более 20 математических инструментов могут сделать ваши уроки более увлекательными

К сожалению, не все любят математику. Кому-то будет скучно, кому-то сложно! Используя забавные математические приложения на уроках математики, вы поможете каждому узнать, насколько интересна математика на самом деле.

В этой записи блога я покажу вам некоторые из самых интересных математических приложений, которые вы можете использовать в своем цифровом классе.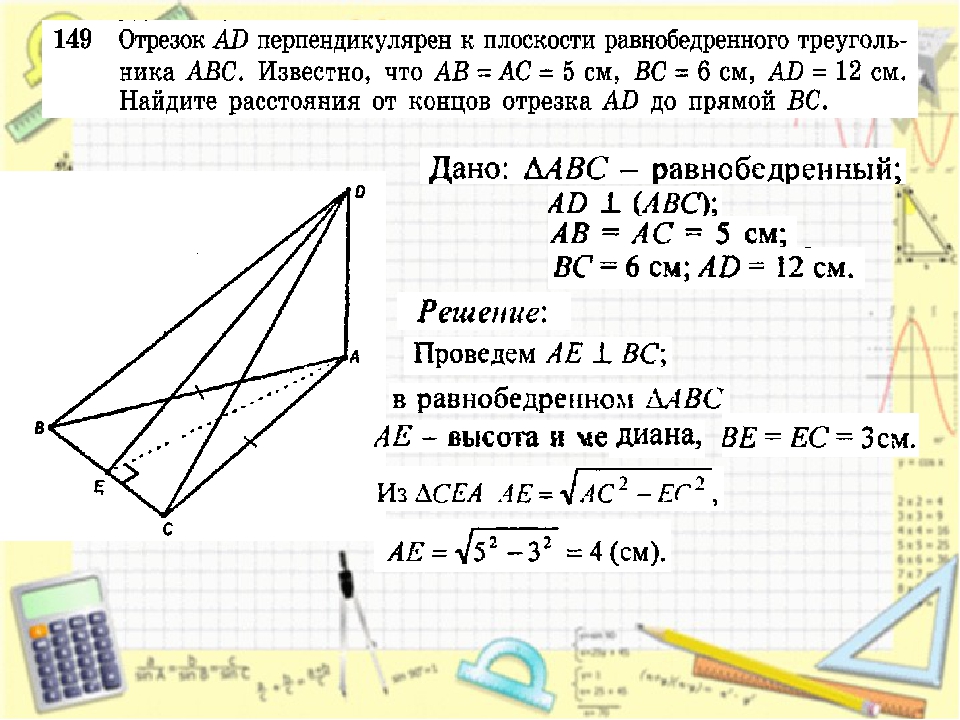

Эти математические приложения помогают учителям сделать уроки более интерактивными и интересными. В настоящее время существуют приложения для учащихся всех возрастов. Надеемся, что эти математические инструменты для учителей заставят учащихся больше полюбить математику, научив их делать это в забавной форме или помогая решать задачи.

Большинство этих приложений бесплатны. Единственное, что вам, как учителю, нужно сделать, это убедиться, что ваши ученики загрузили и установили эти приложения на свои смартфоны или устройства 1-to-1.

Более 20 математических приложений для учителей математики

1.GeoGebra

GeoGebra — это динамическая математическая программа. Это сделано для каждого уровня образования, от новичка до эксперта. Это приложение сочетает в себе геометрию, алгебру, электронные таблицы, графики, статистику и анализ, исчисление в одном удобном для пользователя пакете. Сообщество GeoGebra очень быстро расширяется и насчитывает миллионы пользователей по всему миру.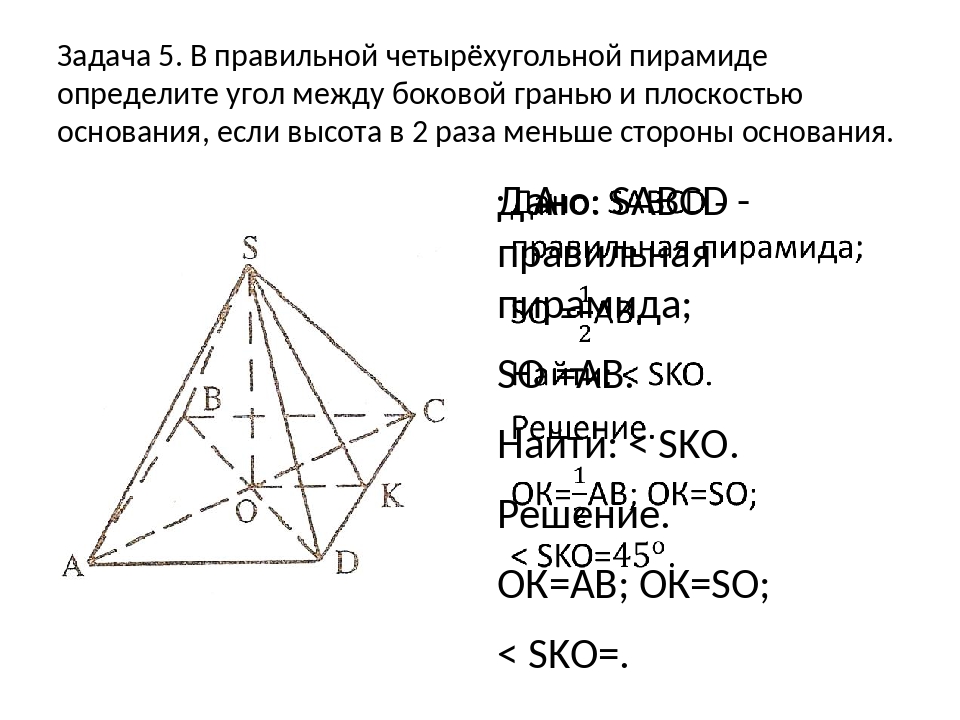 Они являются поставщиком программного обеспечения для динамических математических вычислений номер один во всем мире.

2. Геометрическая подушка

Geometry Pad предлагает увлекательный способ изучения геометрии и отработки важных построений.Это ваш личный помощник в изучении геометрии. Студенты могут легко представлять свои геометрические построения, проводить измерения, пользоваться компасом и экспериментировать с множеством различных геометрических фигур.

Это приложение можно сравнить с математическим инструментом GeoGebra, описанным выше, и оно предназначено специально для использования на iPad и планшетах. Сегодняшние студенты очень хорошо знают, как пользоваться iPad или планшетом; возможно, учителя тоже могут чему-то научиться у них?

3. Фотоматематика

Чтобы выучить математику, избавиться от разочарования в математике и сделать жизнь ученика (и учителя) более спокойной, используйте приложение Photomath.Это приложение поможет вам понять математические задачи с содержанием, чтобы улучшить свои математические навыки. Каждый месяц они решают и объясняют более 1 миллиона математических задач.
Сканируя вашу математическую задачу, это приложение мгновенно поможет вам решить ее. Вы можете сделать это с помощью камеры на вашем мобильном устройстве.
Узнав, в чем заключается ваша математическая задача, приложение дает вам пошаговое объяснение. Photomath объясняет вам шаги расчета с анимацией, как это сделал бы учитель в реальной жизни!

4.Академия Хана

В приложении Khan Academy используются учебные видеоролики по математике, практические упражнения и персонализированная панель обучения, чтобы вы могли учиться в своем собственном темпе в классе и вне его.
Помимо математики, они также предлагают естественные науки, компьютерное программирование, историю (искусства), экономику и многое другое.
Весь контент, который они предлагают, является бесплатным, потому что они хотят предоставить бесплатное образование мирового уровня для всех и в любом месте. Khan Academy — некоммерческая организация, работающая с сообществом волонтеров и спонсоров.

5.Фигуры 3D

Shapes 3D — это приложение дополненной реальности для обучения геометрии. Вы можете создавать призмы, пирамиды, тела вращения и Платоновы тела. Для начала выберите простую фигуру и постепенно увеличивайте ее, пока не дойдете до самых сложных фигур. Этот инструмент призван улучшить возможности учителя и дать возможность показать то, что вы не можете показать с помощью физических инструментов или в классе.

6. Обучение математике для детей

Это математическое приложение предназначено для детей в возрасте от 3 лет и старше.Это помогает учащимся легко усвоить четыре основных понятия математики: вычитание, сложение, деление и умножение. Чтобы дать детям хорошую практику, вы можете найти различные упражнения и игры в этом приложении.

7. СК 12

Это бесплатное математическое приложение доступно практически на любом устройстве. Он предлагает адаптивную практику, рабочие тетради, викторины, тесты и несколько симуляций.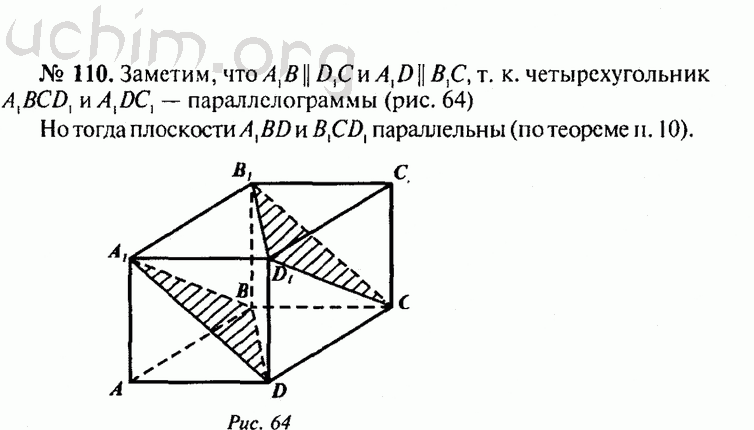 Приложение разделено на разные разделы, поэтому в зависимости от вашего уровня вы можете справиться с определенным разделом или нет. Поскольку он доступен практически на каждом устройстве, к нему легко подключиться в любое время и в любом месте.

8. Баззмат

Это математическое приложение для учащихся начальной и средней школы. Поскольку оно ориентировано на студентов, студенты более заинтересованы в использовании этого приложения. Он предлагает более 3000 математических задач, которые учащиеся могут решать снова и снова, пока не найдут правильное решение. Раньше это было только веб-приложение, но теперь вы можете использовать его на любом устройстве.

9. Мысли

Cuethink — инновационное приложение для учащихся 2–12 классов. С одной стороны, он пытается привлечь учащихся, которые уже хорошо успевают, а с другой, поддерживает учащихся, у которых есть трудности с математикой.Они хотят, чтобы учащиеся рассматривали проблемы как возможности с растущим мышлением.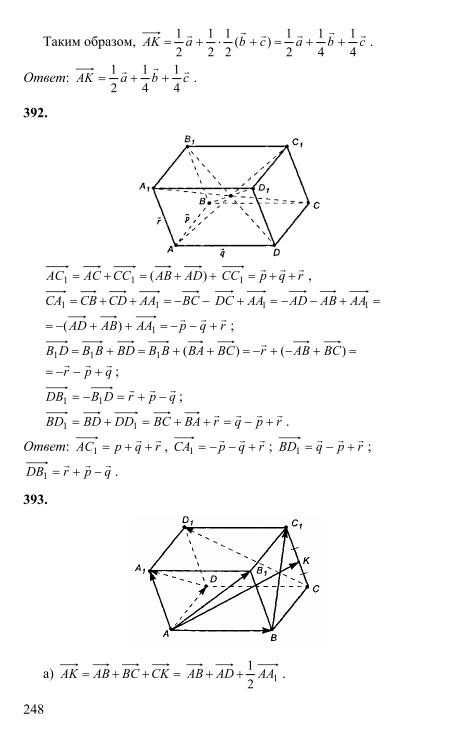

Учителя могут давать учащимся математические задачи из так называемого «банка задач». Задания привязаны к определенному уровню, поэтому у каждого ученика есть задания на своем уровне. Студенты используют процесс для создания и представления своих решений. Cuethink — это сообщество, в котором студенты могут работать вместе в виртуальных группах. Благодаря этим группам они могут учиться друг у друга, как на своих успехах, так и на ошибках.

10.Жидкостная математика

Fluidmath является одним из первых, кто создал такой инструмент обучения и обучения. Инструмент создан для использования на платформах Pen-Centric, таких как планшеты и доски. Учащиеся и учителя могут создавать, решать, графически и анимировать математические и физические задачи от руки очень простым способом. Учителя могут создавать динамические учебные материалы для классов, в то время как ученики могут понимать математические концепции. Вы можете рассматривать Fluidmath как умный лист математической бумаги.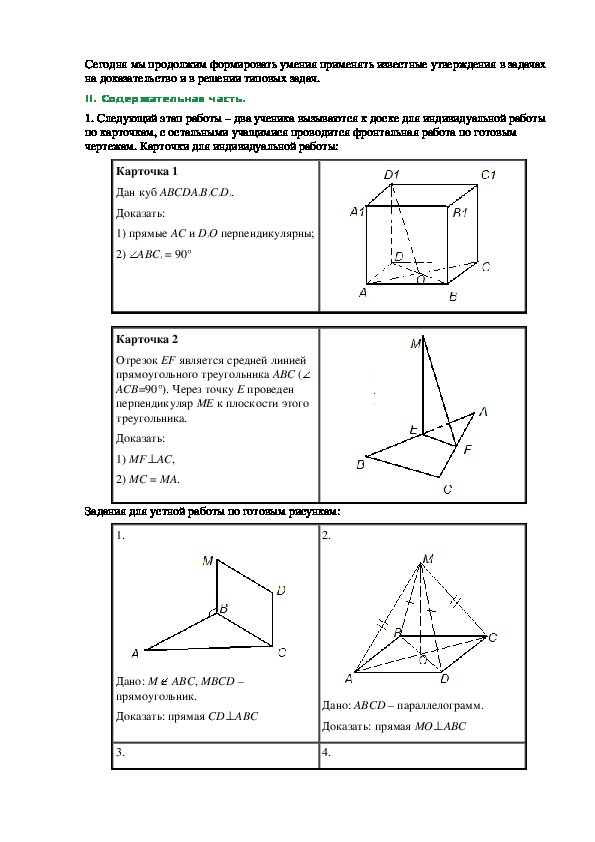

11.Ракетная математика

Основатель Rocket Math говорит, что учащиеся мотивируются, когда видят собственное обучение и успехи. Вот почему он изобрел ракетную математику. Это математическое приложение предлагает способ обучать учащихся математике, весело проводя время, стараясь изо всех сил и делая это в быстром темпе. Rocket math предлагает «программу с рабочими листами» и онлайн-игру.
Рабочий лист программы можно распечатать. Распечатки представляют собой «одноминутные тесты», в которых учащиеся должны работать в парах и пытаться решить лист как можно быстрее, увеличивая ошибки друг друга.

В онлайн-игре учащиеся должны отвечать на вопросы, используя имеющиеся у них знания о числах, чтобы проходить миссии. Чем дальше они погружаются в инструмент, тем сложнее становятся миссии. Онлайн-игра дает немедленную обратную связь, поэтому вмешательство учителя больше не требуется.

12. Десмос

Инструмент Desmos отлично подходит для обучения работе с графиками. Они предлагают бесплатный графический калькулятор, которым могут бесплатно пользоваться студенты во всем мире.Он доступен даже для слабовидящих школьников. В дополнение к калькулятору они также предлагают более сотни цифровых занятий, таких как небольшие математические игры.

Учащиеся могут выполнять эти действия или даже создавать свои собственные математические идеи. Этими идеями можно поделиться друг с другом. Не только ученики могут создавать свои собственные действия и идеи, учителя также могут делать это благодаря конструктору действий. Таким образом, учителя могут предложить правильный материал, соответствующий потребностям учащихся.

13.Буквиджеты

BookWidgets предлагает широкий выбор различных виджетов или упражнений, которые вы можете создать сами для своих учеников. Таким образом, в зависимости от уровня ваших учеников, вы можете создавать очень простые или очень сложные виджеты. Вы выбираете контент, который вставляете.

• В BookWidgets есть различные виджеты, разработанные для самых маленьких учеников для обучения основам математики. Например, есть виджет «Арифметика», где ученики учатся складывать, вычитать, умножать, делить и т. д.

• Вы также можете использовать виджет «Активный график».В этом виджете учащиеся узнают, как разные функции выглядят на графике. Они также видят, что происходит с графиком при изменении параметров.

• Затем есть виджет «Случайность», если вы хотите научить своего ученика вероятности. Здесь вы можете сделать что угодно случайным образом от чисел до символов.

• Чтобы сделать урок более увлекательным, вы можете использовать виджет «Бинго». Есть много разных способов играть в бинго на уроке математики.

• В виджете «Кроссворд» вопросы представляют собой математические расчеты, которые ученики должны решить.

• Еще один интересный способ изучения математики — это игра в пары, в которой учащиеся должны найти правильные пары, вы можете вставить математические формулы или дроби и соответствующие им изображения.
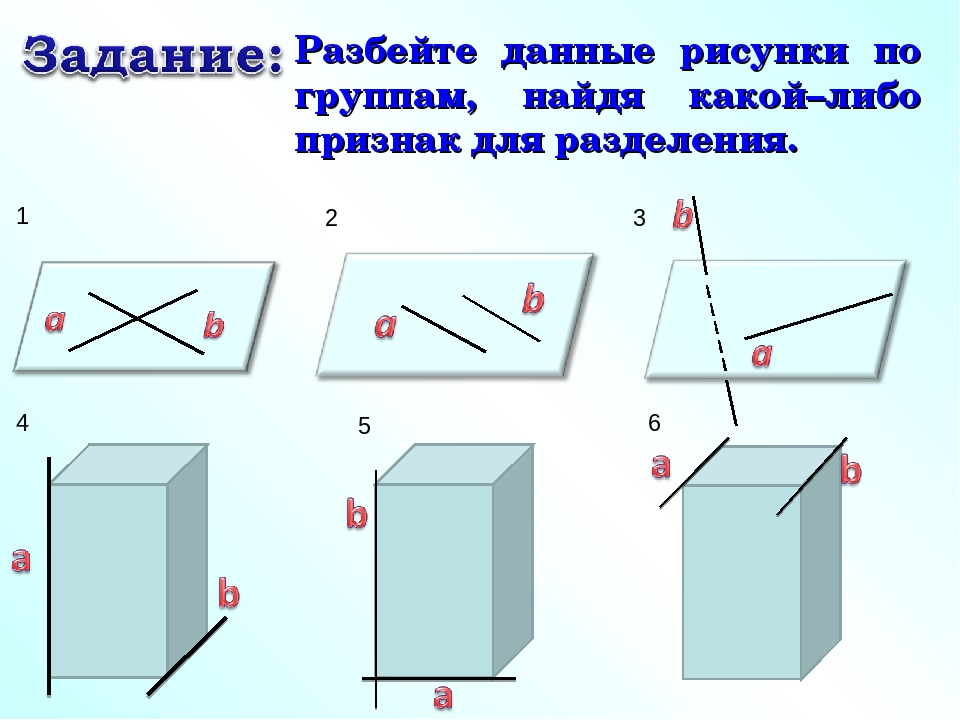
• Если учащимся трудно запоминать математические формулы, вы можете использовать виджет «Флэш-карта». Здесь они могут сначала потренироваться, а затем использовать тренировочный режим, чтобы как можно быстрее иметь как можно больше правильных флеш-карт.
• Наконец, вы также можете использовать виджет «Викторина», чтобы проверить знания учащихся по математике.

Возможности здесь безграничны, так как вы сами добавляете контент.

14. Маталисиус

Matalicious смотрит на математику с другой точки зрения. Чтобы обучать студентов математике, они не используют старомодную, скучную математику. Вместо этого они изучают математику, используя предметы из реальной жизни, такие как спорт, еда, экономика, игры и т. д.

Например, темой урока может быть «Пробуксовка колес: почему в некоторых рекламных роликах кажется, что шины крутятся назад?» Студенты научатся преобразовывать скорости, вычислять длину окружности шины, преобразовывать скорость автомобиля в скорость вращения его колес, …

Благодаря этим различным урокам ученики не сразу увидят в этом математику, хотя на самом деле это чистая математика.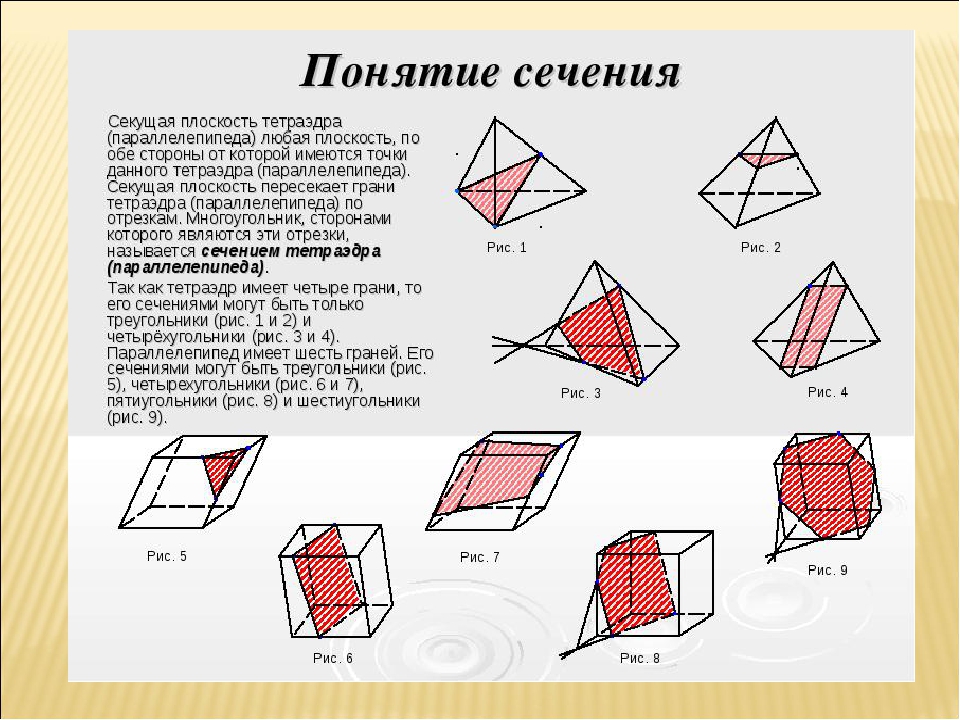 Таким образом, они свяжут математику с повседневными делами, что сделает математику для них гораздо более увлекательной и ценной.

15. Математическая игра Prodigy

Эта математическая онлайн-игра, основанная на покемонах, создана для учащихся 1–8 классов. Учащиеся должны создать свой собственный аватар и изменять его по мере прохождения игры. Поскольку это забавная игра, учащиеся также будут играть в нее дома, чтобы удвоить время, затрачиваемое на занятия по математике.

Благодаря отчетам учителя могут видеть, над какими навыками работали учащиеся, сколько времени они потратили на игру и что им показалось трудным.Самым большим преимуществом этого математического приложения является то, что учащиеся могут играть в него везде, где есть подключение к Интернету.

16. Математическое пространство

Эта онлайн-программа по математике предназначена для учащихся от 7 до 18 лет. Ученики должны решить вопросы. Когда они преуспевают, вопросы становятся сложнее.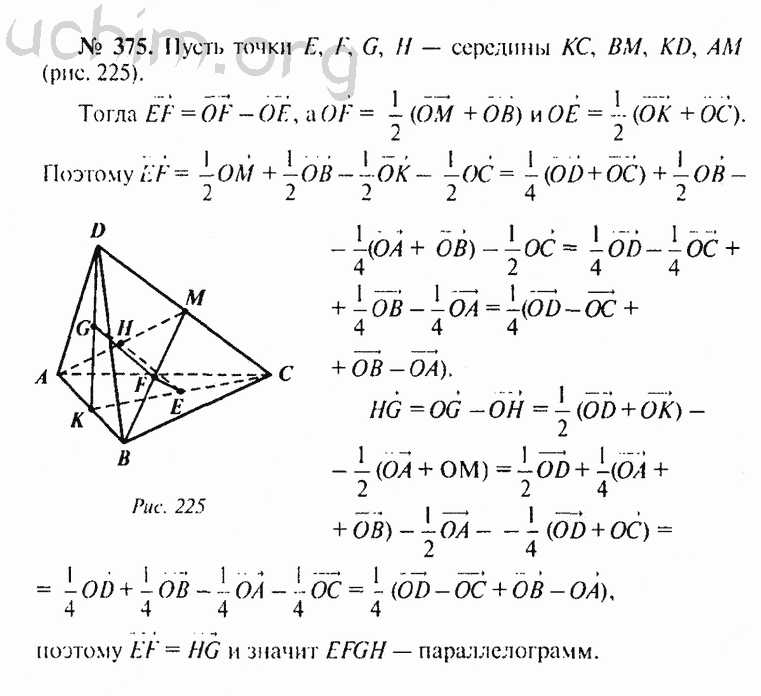 Приложение Mathspace запоминает прошлые результаты учащихся и благодаря этому может определять уровень сложности вопросов.

Студенты также могут оставлять отзывы о своих успехах.Приложение берет на себя роль учителя, помогая ученику, когда он сталкивается с трудностями. Поддержка предлагается с помощью видеоуроков и советов, которые помогают учащимся решить проблему.

17. Математическая доска

Приложение MathBoard создано для всех учащихся школьного возраста. Чем моложе ученики, тем проще упражнения. В начале студенты получают упражнения, где они должны складывать и вычитать. По мере взросления вы переходите к следующему шагу: делите и умножайте.

Студенты могут сами установить свой уровень в приложении.
Чтобы предотвратить угадывание, ответ показан в виде нескольких вариантов и на доске для заметок, где учащиеся могут решить задачу вручную. Когда это становится слишком сложно, они могут обратиться к Решателю задач MathBoard, который даст им подсказки и советы по решению проблемы.

18. Виртуальный ботаник

Virtual Nerd можно использовать на каждом уроке математики. Единственное, что вам нужно, это устройство с подключением к Интернету. Virtual Nerd создан для учащихся всех возрастов.На их веб-сайте вы можете найти всевозможные видеоролики, объясняющие всевозможные математические задачи. В этих видео они шаг за шагом объясняют, как решить эти проблемы. По сути, это виртуальный учитель. Это может быть простым инструментом для учителей, позволяющим учащимся решать математические задачи. Если учащиеся не понимают объяснение своего учителя, они могут понять это через объяснение видео Virtual Nerd.

19. Мангахай

Mangahigh — это игровой инструмент для обучения.Они хотят, чтобы школы и учителя использовали больше игр в своих классах, особенно на уроках математики. Это платформа, которую дети понимают и любят использовать вместо скучных книг, по которым им обычно приходится учиться. Играя в игру, учащиеся не чувствуют давления, которое они испытывают, отвечая перед всем классом. Вместо этого они обретают больше уверенности, что очень хорошо для них.

Если детям действительно нравится что-то, чему они только что научились в классе, они с большей вероятностью будут продолжать это дома.Так барьеры между школой и семейной жизнью исчезнут.

20. Умный

С помощью Brainly учащиеся могут задавать свои математические (и другие) вопросы сообществу людей. Это приложение на базе сообщества представляет собой своего рода форум, где все собираются вместе и помогают друг другу по школьным вопросам. Каким бы ни был ваш вопрос, люди из этого сообщества помогут вам.

Это приложение создано для вопросов от самых младших школьников до студентов колледжей. Иногда вам нужно немного подождать, пока вы не получите ответ, но это потому, что это бесплатное приложение, основанное на помощи сообщества.

21. Геометрия CanFigureIt

CanFigureIt Geometry — это математическая платформа, на которой учащиеся могут работать над геометрическими доказательствами с помощью руководства или самостоятельно. Они могут выбрать работу вперед или назад. Двигайтесь вперед с предоставленной информацией (так называемые «подарки») или работайте в обратном направлении от цели, используя пошаговый подход. Если студент застрял в решении геометрических доказательств, он получает подсказки. Когда студент доходит до окончательного доказательства, появляется отличное всплывающее окно с поздравлением.

Эта платформа охватывает множество различных типов геометрических доказательств. Вы можете попытаться доказать простые факты о прямых сложным доказательствам об окружностях, треугольниках и так далее. Этот инструмент позволяет учащимся учиться самостоятельно и тому, как что-то доказывать, а не просто копировать это у учителя.

22. Формы узоров

С помощью Pattern Shapes учащиеся могут изучать все виды геометрических фигур. Учащиеся могут сами создавать вещи, комбинируя разные формы друг с другом.Таким образом, учащиеся открывают для себя все геометрические формы и геометрические отношения, такие как углы, симметрия и многое другое. Это идеальный инструмент для студентов, которые плохо знакомы с геометрическими фигурами. С помощью этого инструмента они изучают существующие геометрические фигуры в игровой форме в своем собственном темпе.

23. Мэтуэй

Приложение Mathway — это гораздо больше, чем просто приложение-калькулятор. С помощью этого приложения учащиеся учатся шаг за шагом решать математические задачи, потому что математика — это гораздо больше, чем просто возможность дать правильный ответ.Учащиеся могут легко решить свою математическую задачу или сделать снимок с помощью камеры, а приложение шаг за шагом объяснит, как найти правильное решение.
Приложение имеет широкий спектр тем от базовой математики до статистики, алгебры и так далее.

Это очень полезное учебное пособие, за исключением двух опасностей: ленивые ученики будут только искать решение и не научатся решать его шаг за шагом, и это приложение, к сожалению, не бесплатное.

24. Математика Чейз

Maths Chase — это бесплатный сайт, где вы можете быстро проверить свои таблицы умножения, сложения, вычитания и многое другое.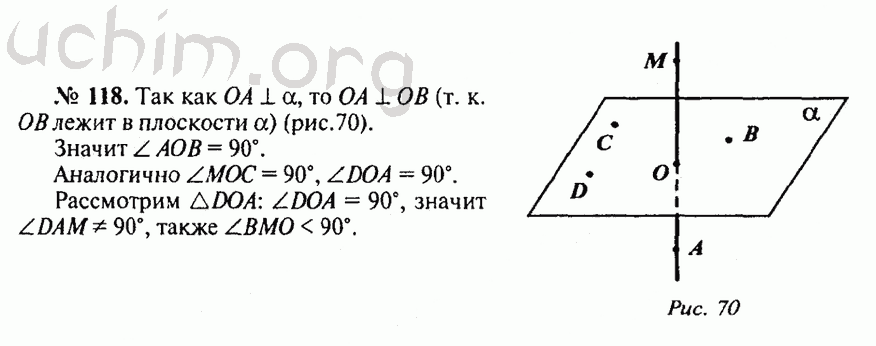 Сайт представляет собой очень простую игру, но дети найдут в ней действительно увлекательный способ изучения арифметики.

Заключение

Вот оно! Это было более 20 математических приложений для учителей математики, которые вы, безусловно, можете использовать, если хотите научить своих учеников чему-то новому или если вы хотите, чтобы они изучали что-то в своем собственном темпе. Если бы мой учитель математики использовал некоторые из этих инструментов, мне (и большинству моих друзей) математика наверняка понравилась бы гораздо больше!

Не забудьте поделиться этим постом со своими коллегами-учителями математики, так как он
поможет им преподавать математику более интерактивным способом.

.