Самостоятельные работы по алгебре и начала анализа 10 класс. Учебник Ю.М. Колягин, М.В.Ткачева, Н.Е. Федорова и др.
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Ср 1.1 Повторение курса основной школы.doc
Выбранный для просмотра документ Ср 2.1 Арифметический корень. Степень с рациональным показателем.doc
Выбранный для просмотра документ Ср 2.2 Действительные числа.doc
Выбранный для просмотра документ Ср 3.1 Степенная функция, ее свойства и график.doc
Выбранный для просмотра документ Ср 3.2 Иррациональные уравнения и неравенства.doc
Выбранный для просмотра документ Ср 4.1 Показательная функция, ее свойства и график.doc
Выбранный для просмотра документ Ср 4.2 Показательные уравнения и неравенства. doc
doc
Выбранный для просмотра документ Ср 4.3 Показательная функция.doc
Выбранный для просмотра документ Ср 5.1 Логарифмы. Свойства логарифмов.doc
Выбранный для просмотра документ Ср 5.2 Логарифмические уравнения и неравенства.doc
Самостоятельная работа 5.2
Логарифмические уравнения и неравенства
Вариант 1
А1. Вычислите: log7343.
А2. Решите уравнения:
а) ; б)
А3. Решите неравенство: log0,5(3 -2x) ≥ 1.
В1 Найдите наименьший корень уравнения .
______________________________________________________________________
Самостоятельная работа 5.2
Логарифмические уравнения и неравенства
Вариант 2
А1. Вычислите: log262 + log2613
Вычислите: log262 + log2613
А2. Решите уравнения:
а) ; б)
А3. Решите неравенство: log2(x -5) ≥ 1.
В1 Найдите наименьший корень уравнения .
______________________________________________________________________
Самостоятельная работа 5.2
Логарифмические уравнения и неравенства
Вариант 3
А1. Найдите значение выражения: log513 + log254.
А2. Решите уравнения:
а) ; б)
А3. Решите неравенство: log (1 – 0,5x) ≤ -1.
В1 Укажите целый корень уравнения: .
______________________________________________________________________
Самостоятельная работа 5.2
Логарифмические уравнения и неравенства
Вариант 4
А1. Вычислите:
А2. Решите уравнения:
а) ; б)
А3. Решите неравенство: log0,5(1-0,5x) >-3.
Решите неравенство: log0,5(1-0,5x) >-3.
В1 Решите уравнение
Выбранный для просмотра документ Ср 6.1 Тригонометрические выражения.doc
Выбранный для просмотра документ Ср 6.2 Тригонометрические преобразования.doc
Выбранный для просмотра документ Ср 6.3 Тригонометрические преобразования.doc
Выбранный для просмотра документ Ср 7.1 Простейшие тригонометрические уравнения.doc
Выбранный для просмотра документ Ср 7.2 Тригонометрические уравнения.doc
Выбранный для просмотра документ Ср 7.3 Тригонометрические уравнения.doc
Выбранный для просмотра документ Ср 7.4 Тригонометрические уравнения.doc
Выбранный для просмотра документ Ср 8.1 Повторение. Числа и вычисления. doc
doc
Выбранный для просмотра документ Ср 8.2 Повторение. Выражения и преобразования.doc
Выбранный для просмотра документ Ср 8.3 Повторение. Уравнения и неравенства.doc
-
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта,
Вы можете оставить жалобу на материал.Пожаловаться на материал
- Сейчас обучается 943 человека из 80 регионов
- Сейчас обучается 701 человек из 75 регионов
- Сейчас обучается 331 человек из 72 регионов
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс:
Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник:
Все учебники
Выберите тему:
Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала:
ДБ-1292733
Похожие материалы
Вам будут интересны эти курсы:
Самостоятельные и контрольные работы по алгебре 10 клас.
 Ершова А.П
Ершова А.П
Предлагаемое пособие в первую очередь предназначено для учителей и учащихся, работающих по двухуровневому учебнику «Нелин Е.П., Лазарев В.А. Алгебра и начала математического анализа. 10 класс: базовый и профильный уровни» (издательство «Илекса»), но может использоваться и при работе по другим учебникам алгебры и начал математического анализа, особенно при подготовке учащихся к решению заданий ЕГЭ и ГИА.
Основные особенности предлагаемого сборника самостоятельных и контрольных работ:
1. Сборник содержит полный набор самостоятельных и контрольных работ по всему курсу алгебры и начал математического анализа 10 класса, как базового, так и профильного уровней. Контрольные работы рассчитаны на один урок, самостоятельные работы — на 25—40 минут, в зависимости от темы и уровня подготовки учащихся.
2. Сборник позволяет осуществить дифференцированный контроль знаний, так как задания распределены по трем уровням сложности А, Б и В. Задания уровня А предназначены для учащихся, которые обучаются по программе базового уровня, а задания уровней Б и В — для учащихся, которые обучаются по программе профильного уровня. Задания уровня В предназначены для учащихся, проявляющих повышенный интерес к математике, а также для использования в классах, школах, гимназиях и лицеях с углубленным изучением математики. Для каждого уровня приведено два расположенных рядом равноценных варианта (как они обычно записываются на доске), поэтому на уроке достаточно одной книги на парте.
Задания уровня В предназначены для учащихся, проявляющих повышенный интерес к математике, а также для использования в классах, школах, гимназиях и лицеях с углубленным изучением математики. Для каждого уровня приведено два расположенных рядом равноценных варианта (как они обычно записываются на доске), поэтому на уроке достаточно одной книги на парте.
3. В книгу включены также домашние самостоятельные и практические работы, содержащие творческие, нестандартные задачи по каждой изучаемой теме, а также задачи повышенной сложности. Эти задания могут в полном объеме или частично предлагаться учащимся в качестве зачетных, а также использоваться как дополнительные задания для проведения контрольных работ. По усмотрению учителя выполнение нескольких или даже одного такого задания может оцениваться отличной оценкой.
Ответы к контрольным и домашним самостоятельным работам приводятся в конце книги.
СОДЕРЖАНИЕ
ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА 5
С-1. Числовые функции, их свойства и графики 5
С-2. Уравнения 7
Уравнения 7
С-3. Применение свойств функций к решению уравнений 10
С-4. Неравенства. Метод интервалов 12
С-5. Уравнения и неравенства, содержащие знак модуля 14
С-6. Построение графиков функций, уравнений и неравенств 17
С-7. Уравнения и неравенства с параметрами 19
К-1 (КП-1). Функции, уравнения, неравенства 20
С-8. Метод математической индукции. Делимость целых чисел 24
С-9. Многочлены. Теорема Безу. Схема Горнера. Формулы Виета 25
(КП-2). Многочлены и их корни. Метод математической индукции 27
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 30
С-10. Радианная мера углов. Тригонометрические функции угла и числового аргумента 30
С-11. Свойства и графики тригонометрических функций 32
С-12*. Исследование тригонометрических функций и построение их графиков (домашняя практическая работа) 36
С-13. Соотношения между тригонометрическими функциями одного аргумента 37
С-14. Формулы сложения. Формулы двойного аргумента. Формулы приведения 39
С-15. Формулы преобразования суммы тригонометрических функций в произведение и произведения в сумму 42
С-16. Формулы половинного аргумента. Формулы преобразования выражения a sin* + Ь cos* 44
Формулы половинного аргумента. Формулы преобразования выражения a sin* + Ь cos* 44
К-2 (КП-3). Тригонометрические функции 46
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 50
С-17. Обратная функция. Обратные тригонометрические функции 50
С-18*. Применение свойств обратных тригонометрических функций (домашняя самостоятельная работа) 53
С-19. Простейшие тригонометрические уравнения 55
С-20. Тригонометрические уравнения 57
С-21. Отбор корней тригонометрических уравнений. Системы уравнений 58
К-3 (КП-4). Тригонометрические уравнения и неравенства 60
С-22. Более сложные тригонометрические уравнения 62
С-23. Системы тригонометрических уравнений 64
С-24. Тригонометрические уравнения с параметрами 65
С-25. Простейшие тригонометрические неравенства 67
С-26. Более сложные тригонометрические неравенства 68
(КП-5). Тригонометрические уравнения, неравенства и их системы 69
СТЕПЕННАЯ ФУНКЦИЯ 72
С-27. Корень n-ой степени и его свойства 72
С-28. Иррациональные уравнения 75
Иррациональные уравнения 75
С-29. Степень с рациональным показателем и ее свойства 77
С 30. Методы решения иррациональных уравнений 81
С-31. Системы иррациональных уравнений. Иррациональные неравенства 82
С-32. Иррациональные уравнения и неравенства с параметрами 84
С-33*. Методы решения иррациональных уравнений, неравенств, систем (домашняя самостоятельная работа) 86
К-4 (КП-6). Степени и корни 88
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ 92
С-34. Показательные уравнения и их системы 92
С-35. Показательные неравенства 93
С-36*. Методы решения показательных уравнений и неравенств (домашняя самостоятельная работа) 95
К-5 (КП-7). Показательная функция 97
С-37. Логарифм. Свойства логарифмов 100
С-38. Логарифмические уравнения и их системы 103
С-39. Логарифмические неравенства 104
С-40*. Методы решения логарифмических уравнений, неравенств и систем (домашняя самостоятельная работа) 106
К-6 (КП-8). Логарифмическая функция 108
С-41. Показательно-степенные уравнения и неравенства 111
Показательно-степенные уравнения и неравенства 111
С-42*. Применение логарифмов к решению трансцендентных уравнений и систем (домашняя самостоятельная работа) 112
С-43. Показательные и логарифмические уравнения. Задачи с параметрами 113
(КП-9) Показательно-степенные уравнения и неравенства. Показательные и логарифмические уравнения и неравенства .115
ОТВЕТЫ 117
Ответы к контрольным работам 117
Ответы к домашним самостоятельным работам 128
ЛИТЕРАТУРА 133
ПРИЛОЖЕНИЕ.
ОРИЕНТИРОВОЧНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ 134
СОДЕРЖАНИЕ 142
Пособие содержит самостоятельные и контрольные работы к двухуровневому учебнику «Алгебра и начала математического анализа. 10 класс: базовый и профильный уровни» Е.П.Нелина, В.А.Лазарева. Пособие также можно использовать при работе по любому учебнику и для самообразования, например, при подготовке к решению заданий ЕГЭ. Предлагаемые работы состоят из 6 вариантов трех уровней сложности и предназначены для организации дифференцированной самостоятельной работы учащихся.
▶▷▶▷ гдз по алгебре 10 класс самостоятельные работы
▶▷▶▷ гдз по алгебре 10 класс самостоятельные работы
| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 15-09-2019 |
гдз по алгебре 10 класс самостоятельные работы — Самостоятельные работы по алгебре 10 класс Александрова ответы gdz-na-5comalgebra 10 -klasssamostoyatelnye Cached Самостоятельные работы по алгебре 10 класс Александрова ответы На этой странице Вы найдете онлайн ответы к учебнику Алгебра и начала математического анализа 10 класс Решебник самостоятельные работы по Алгебре за 10 класс gitemmereshebnik 10 classalgebra Cached Данное пособие содержит решебник ( ГДЗ ) самостоятельные работы по Алгебре за 10 класс Гдз По Алгебре 10 Класс Самостоятельные Работы — Image Results More Гдз По Алгебре 10 Класс Самостоятельные Работы images Решебник (ГДЗ) самостоятельные работы по Алгебре за 10 класс gitemmereshebnik 10 classalgebra Cached Данное пособие содержит решебник ( ГДЗ ) самостоятельные работы по Алгебре за 10 класс Автора: Александрова ЛА Издательство: Мнемозина Полные и подробные ответы к упражнениям на Гитем ГДЗ по алгебре за 10 класс самостоятельные работы onlinegdzapp 10 -klassalgebrasamostoyatelnie Cached Лучшие гдз по алгебре за 10 класс самостоятельные работы , Александрова ЛА ФГОС С подробными решениями и удобным интерфейсом от Онлайн ГДЗ ГДЗ решебник по алгебре 11 класс самостоятельные работы gdzputinaco11-klass-onlajnalgebra-11gdz Cached ГДЗ решебник по алгебре 11 класс самостоятельные работы Александрова Здесь представлены ответы к самостоятельным работам по алгебре 11 класс Александрова ГДЗ по алгебре самостоятельные работы 10 класс Александрова Л reshebamegdzalgebra 10 -klasssamostoyatelnie Cached Качественные решения и подробные гдз по алгебре для учеников 10 класса самостоятельные работы Базовый уровень, авторы учебника:Александрова ЛА ГДЗ решебник самостоятельные работы по алгебре 7 класс gdzputinaco7-klass-onlajnalgebra-7gdz Cached ГДЗ решебник самостоятельные работы по алгебре 7 класс Александрова Здесь представлены ответы к самостоятельным работам по алгебре 7 класс Александрова ГДЗ по алгебре самостоятельные и контрольные работы 1011 reshebamegdzalgebra 10 -klasssamostoyatelnie Cached Качественные решения и подробные гдз по алгебре для учеников 10 11 класса самостоятельные и контрольные работы , авторы учебника:Ершова АП, Голобородько ВВ ГДЗ Алгебра 10 класс Александрова — Самостоятельные работы gdzltd 10 -classalgebraAleksandrova Cached ГДЗ по алгебре 10 класс Александрова поможет лучшим образом усвоить всю необходимую информацию, чтобы в дальнейшем показывать отличные результаты во время проверочных испытаний ГДЗ по Алгебре для 7 класса самостоятельные и контрольные na5fungdzclass-7algebrareshebnik Cached Решебник ( ГДЗ ) для 7 класса по алгебре самостоятельные и контрольные работы Авторы учебника: АП Ершова, ВВ Голобородько Содержит в себе полные и подробные ответы на все упражнения онлайн на пять фан Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 66,600
- Мордкович 11 класс контрольные работы.
 Подробное решение задач из сборника ершова 10 класс. Math hel
Подробное решение задач из сборника ершова 10 класс. Math hel - per 10 класс самостоятельные работы по алгебре.
ГДЗ по алгебре 11 класс Алимов 2003-2007 г (10-11 класс) пособие для самостоятельной работы старшеклассников с подробным разбором типовых заданий и го - ласс) пособие для самостоятельной работы старшеклассников с подробным разбором типовых заданий и готовыми ответами на все задания, предложенные в учебнике. Не стоит злоупотреблять списыванием, поскольку контрольные и проверочные работы…
Мордкович 10 класс самостаятельные работы. Самостоятельные работы для учащихся общеобразовательных учреждений. Проверочные работы по химии 8 класс ким. Алгебра и начала анализа 10 класс александрова решебник.
Контрольные работы по алгебре 10 класс (Колмогоров): Дудницын Ю.П., Кронгауз В.Л. — 2007 год. Образовательный сайт — Рускопибук (Роскопибук) — Электронные учебники и ГДЗ.
Скачать бесплатно Алгебра и начала математического анализа. 10 класс. Самостоятельные работы. Александрова Л.А. Данное пособие предназначено. Пособие содержит материал для проведения самостоятельных работ по каждой теме и может быть использовано учителем для осуществления текущего контроля …
Александрова Л.А. Данное пособие предназначено. Пособие содержит материал для проведения самостоятельных работ по каждой теме и может быть использовано учителем для осуществления текущего контроля …
Самостоятельные работы по алгебре 10 класс Александрова ответы. Не всегда нужно переплачивать за услуги репетитора, частично справиться с выполнением упражнений и проверочных работ позволит ГДЗ к сборнику.
Скачать решебники 10 класс. Данный решебник содержит 38 самостоятельных работ, в двух вариантах. Контрольные и самостоятельные работы по алгебре за 7 класс скачать бесплатно.
Структура пособия и содержание разноуровневых заданий позволяют использовать тетрадь при работе по любым действующим учебникам по математике для 10 класса (уровень стандарта). Предназначено для учащихся 10 класса общеобразовательных учебных заведений, учителей математики. Итоговые контрольные …
7 класс (авторы учебника Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др.; Издательство Просвещение. Контрольные работы. quot; Александрова Л.А. 2014 год.
quot; Александрова Л.А. 2014 год.
Самостоятельные работы по алгебре 10 класс никольский решебник. Никольский С.М. 2013 г. Решебник ГДЗ математика 5 класс Никольский Потапов Решетников.
Миндюк Н.Г.
предложенные в учебнике. Не стоит злоупотреблять списыванием
- Голобородько ВВ ГДЗ Алгебра 10 класс Александрова — Самостоятельные работы gdzltd 10 -classalgebraAleksandrova Cached ГДЗ по алгебре 10 класс Александрова поможет лучшим образом усвоить всю необходимую информацию
- авторы учебника:Александрова ЛА ГДЗ решебник самостоятельные работы по алгебре 7 класс gdzputinaco7-klass-onlajnalgebra-7gdz Cached ГДЗ решебник самостоятельные работы по алгебре 7 класс Александрова Здесь представлены ответы к самостоятельным работам по алгебре 7 класс Александрова ГДЗ по алгебре самостоятельные и контрольные работы 1011 reshebamegdzalgebra 10 -klasssamostoyatelnie Cached Качественные решения и подробные гдз по алгебре для учеников 10 11 класса самостоятельные и контрольные работы
- smarter
гдз по алгебре класс самостоятельные работы Все результаты Решебник самостоятельные работы по Алгебре за samostoyatelnierabotibazovijurovenaleksandrova Данное пособие содержит решебник ГДЗ самостоятельные работы по Алгебре за класс Автора Александрова ЛА Издательство Мнемозина ГДЗ по алгебре за класс самостоятельные GDZRU Алгебра самостоятельные работы Александрова ГДЗ Спиши готовые домашние задания самостоятельные работы по алгебре за класс , решебник Александрова ЛА, Базовый и углубленный ГДЗ по Алгебре за класс Самостоятельные работы gdzalgebra class samostoyatelnieraboti Убедись в правильности решения задачи вместе с ГДЗ по Алгебре за класс Александрова ЛА самостоятельные работы Базовый уровень Ответы ГДЗ по Алгебре за класс самостоятельные работы самостоятельные работы Александрова Подробный решебник ГДЗ по Алгебре для класса самостоятельные работы , Авторы учебника Александрова ЛА Базовый и углубленный Решебник к сборнику самостоятельных работ по алгебре и izbrannoe reshebnikksbornikusamostoyatelnyih Информация об этой странице недоступна Подробнее Самостоятельные работы по алгебре класс Алгебра класс Самостоятельные работы по алгебре класс Александрова ответы, На сайтах с ГДЗ , посмотреть ответы обычно можно в любое время суток, ГДЗ по алгебре для класса самостоятельные работы poalgebre klass samostoyatelnierabotibazo Тут отличные гдз по алгебре самостоятельные работы для класса , Александрова ЛА от Путина Очень удобный интерфейс с решениями ГДЗ по Алгебре класс Самостоятельные работы gdzfreeru gdz Похожие Готовое Домашнее Задание ГДЗ по Алгебре и началам анализа класс Самостоятельные работы Александрова ЛА Ваша самостоятельная Алгебра и начала анализа класс самостоятельные pin класс самостоятельные работы гдз ответы Решебник алгебра класс контрольными Picture Dictionary, Pos, Algebra, Literature, Literatura Александрова Л А Алгебра и начала математического izbrannoe aleksandrovalaalgebrainachalamatema Александрова Л А Алгебра и начала математического анализа класс ГДЗ к сборнику находится здесь класс Самостоятельные работы Базовый урове Данное пособие предназначено для общеобразовательных ГДЗ класс по Алгебре самостоятельные работы klass algebra samostoyatelnierabotibazovijiuglu ГДЗ содержит верные и подробные ответы с несколькими вариантами решения по Алгебре за класс , автор издания Александрова ЛА Александрова ЛА Алгебра и начала математического file Александрова ЛА Алгебра и начала математического анализа класс Самостоятельные работы Файл формата djvu; размером , КБ Математика, алгебра и начала математического анализа Экзамены Экзамены по Математике апр г класс Самостоятельные работы для учащихся общеобразовательных для общеобразовательных классов, обучающихся курсу алгебры и начал Учебники, ГДЗ , решебники, ЕГЭ, ГИА, экзамены, книги Алгебра и начала анализа Самостоятельные работы shop product Купить книгу Алгебра и начала анализа Самостоятельные работы класс Александрова ЛА в Интернетмагазине Myshopru Низкая цена PDF Гдз алгебра класс александрова самостоятельные gdzalgebraklassal ГДЗ по Алгебре класс Контрольные работы Глизбург ВИ ГДЗ по Алгебре и начала анализа класс Самостоятельные работы Александрова ЛА александрова класс самостоятельные гдз lazartschoolru pic aleksandrovaklasssamostoiatelnyegdz авг г александрова класс самостоятельные гдз Самостоятельные работы по алгебре класс Александрова ответы Алгебра Решебник по алгебре класс ГДЗ класс Алгебра Самые подробные решения и гдз по алгебре для класса на Алгебра классы самостоятельные и контрольные работы Ершова АП ГДЗ решебник Алгебра класс класс ГДЗ решебники подробные готовые домашние задания Алгебра класс Самостоятельные работы Базовый и углубл уровень Алгебра класс Алгебра и начала математического анализа класс books algebra klassy algebrainachalama Скачать бесплатно Алгебра и начала математического анализа класс Самостоятельные работы Александрова ЛА Данное пособие Год издания ГДЗ С вариант алгебра класс самостоятельные самостоятельные работы Александрова подробное решение с вариант по алгебре самостоятельные работы для учащихся класса базовый и углубленный уровень, авторов Гдз самостоятельные работы по Алгебре за класс samostoyatelnierabotibazovijurovenaleksandrova Мегаботан подробные гдз самостоятельные работы по Алгебре для класса , авторов Александрова ЛА ГДЗ по алгебре класс самостоятельные работы Алгебра класс Решебник по алгебре за класс авторы Александрова издательство Мнемозина ГДЗ Алгебра класс Самостоятельные работы load _klass algebra gdz_algebra__klass_s сент г Домашняя работа по алгебре класс ГДЗ Алгебра класс Самостоятельные работы Александрова с подробным решением и Ершова голобородько класс решебник ГДЗ Решебник klass ershovagoloborodkoklassreshebni Перейти к разделу Решебник самостоятельные и контрольные работы по Решебник по алгебре за класс самостоятельные и ГДЗ от Путина по алгебре класс самостоятельные класс Алгебра ГДЗ от Путина по алгебре класс самостоятельные работы Александрова ГДЗ по Показательные уравнения и неравенства ГДЗ Алгебра к учебникам и рабочим тетрадям за класс gdz algebra class Решебник по алгебре класс АН Колмогоров Алегбра Самостоятельные И Контрольные Работы по алгебре класс Ершова АП Алгебра александрова ла алгебра класс контрольные работы wwwinfotechsystemsonlinecom ital www img aleksandroval_aal нояб г александрова ла алгебра класс контрольные работы Yahoo ГДЗ по Алгебре и начала анализа класс Самостоятельные ГДЗ решебник по алгебре класс Муравин от Путина класс Алгебра Рейтинг голос Представляем вам решебник по алгебре за класс , автор учебника зачеты, контрольные и самостоятельные работы , математические диктанты , Алгебра класс учебники, ГДЗ, учебные пособия XUNI xunicom books Похожие ГДЗ по алгебре для классов к Алгебра и начала анализа классы Контрольные работы для общеобразовательных учреждений, ГДЗ по алгебре класс самостоятельные работы КЛАСС ГДЗ по алгебре для класса ГДЗ решебник по алгебре за класс самостоятельные работы автор Александрова Ответы к задачам и примерам на отлично Готовые решения ГДЗ по Алгебре класс Готовые Домашние Задания, ГДЗ gdzbestru gdz_class algebra Похожие Здесь, вы можете просмотреть онлайн или скачать Готовые Домашние Задания ГДЗ по Алгебре для класса Скачать бесплатно или посмотреть онлайн ГДЗ, домашнюю работу, решебник, Самостоятельные работы ГДЗ решебники по алгебре wwwmegashporaru gdz algebra Похожие Алгебра и начала анализа класс Контрольные работы для контрольных и самостоятельных работ по алгебре и началам анализа за класс алгебра класс самостоятельные работы мордкович гдз adlerhudozhkaru pic algebraklasssamostoiatelnyerabotymordk авг г алгебра класс самостоятельные работы мордкович гдз Самостоятельные работы по алгебре класс Александрова ответы Самостоятельные работы по алгебре класс ГДЗ тв algebra klass samostoyatelnyerabotypoalgebre дек г Самостоятельные работы по алгебре класс Александрова ответы, решебники и ГДЗ с ответами на для рабочих тетрадей Решебник По Контрольным Работам По Алгебре Класс georgiabazaweeblycom blog reshebnikpokontroljnimrabotampoa Решебник Контрольных Работ По Алгебре Класс Мерзляк контрольных и самостоятельных работ по алгебре и началам анализа за класс к Самостоятельная работа вариант В сборник watch мар г Добавлено пользователем algebra channel Самостоятельная работа Вариант В из сборника и контрольные работы по алгебре и геометрии для класса Ершовой АП и алгебра класс алимов гдз ezszxrytu Eklablog fourthtermigereklablogcom ГДЗ по алгебре класс Алимов, Колягин, Сидоров Cправка Школьникам всегда Дидактические материалы по алгебре и началам анализа класс и практических работ Габриелян ГДЗ к контрольным и самостоятельным решебник по алгебре класса макарычев года treatsaramrieklablogcom Алгбpа и нач aнализа Д ля класcов АНКолмогоров е изд НГ Миндюк Алгебра класс самостоятельные и контрольные работы решебник по алгебре класса макарычев года tm manXML mln answers Картинки по запросу гдз по алгебре класс самостоятельные работы Показать все Другие картинки по запросу гдз по алгебре класс самостоятельные работы Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты ГДЗ по алгебре классы самостоятельные и ️ класс ️ Решебник ГДЗ по алгебре классы самостоятельные и контрольные работы авторы Ершова АП, Голобородько ВВ В и классах изучать ГДЗ Никольский класс Reshakru reshebniki algebra nikol Где найти нужный решебник ГДЗ по алгебре Никольский класс ? Правильный ответ здесь Данный гдз содержит как ответы из книги для учителя, ГДЗ, решебники для класса по всем предметам онлайн klass reshebniki Перевести эту страницу Полные и качественные решебники ГДЗ для класса по всем предметам онлайн Доступно на ваших смартфонах алгебре для класса Решение задач по booklist math класс Самостоятельные работы Ткачева МВ гАлгебра и начала Домашняя работа ГДЗ решебник по алгебре за класс к задачнику ГДЗ по алгебре класс Мордкович онлайн решебник gdz gdzklassalgebramordkovich ГДЗ по алгебре и началам математического анализа за класс к задачнику АГ Мордковича и др Алгебра и начала математического анализа Самостоятельные работы по алгебре класс александрова cafebezpovodaru main samostoyatelnierabotipoalgebreklassal Похожие Выручили эти гдз , наконец нашел их, весь рунет облазил У нас вы можете скачать Самостоятельные работы по алгебре класс александрова гдз класс география ответы на вопросы Prakard Property Investment дня назад гдз класс география ответы на вопросы tm sasXML mln answers found found thsd номер гдз по алгебре класс мордкович поможет в выполнении и проверке задания авторы м pdf Математика класс тесты самостоятельные работы для ฉันกำลังมองหา ซื้อ ขาย เช่า อสังหาฯ น้อยกว่า ทรัพย์สิน Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше Показать скрытые результаты В ответ на официальный запрос мы удалили некоторые результаты с этой страницы Вы можете ознакомиться с запросом на сайте LumenDatabaseorg Вместе с гдз по алгебре класс самостоятельные работы часто ищут самостоятельные работы по алгебре класс александрова скачать самостоятельные работы по алгебре класс александрова профильный уровень гдз самостоятельные работы по алгебре класс профильный уровень самостоятельные работы по алгебре класс александрова базовый уровень гдз самостоятельные работы по алгебре класс александрова базовый уровень гдз по алгебре класс александрова контрольные работы самостоятельные работы по алгебре класс александрова читать гдз по алгебре класс самостоятельные работы александрова ла базовый и углубленный уровень Ссылки в нижнем колонтитуле Россия Подробнее Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Переводчик Фото Покупки Ещё Документы Blogger Duo Hangouts Keep Jamboard Подборки Другие сервисы Приложения
Мордкович 11 класс контрольные работы. Подробное решение задач из сборника ершова 10 класс. Math helper 10 класс самостоятельные работы по алгебре.
Подробное решение задач из сборника ершова 10 класс. Math helper 10 класс самостоятельные работы по алгебре.
ГДЗ по алгебре 11 класс Алимов 2003-2007 г (10-11 класс) пособие для самостоятельной работы старшеклассников с подробным разбором типовых заданий и готовыми ответами на все задания, предложенные в учебнике. Не стоит злоупотреблять списыванием, поскольку контрольные и проверочные работы…
Мордкович 10 класс самостаятельные работы. Самостоятельные работы для учащихся общеобразовательных учреждений. Проверочные работы по химии 8 класс ким. Алгебра и начала анализа 10 класс александрова решебник.
Контрольные работы по алгебре 10 класс (Колмогоров): Дудницын Ю.П., Кронгауз В.Л. — 2007 год. Образовательный сайт — Рускопибук (Роскопибук) — Электронные учебники и ГДЗ.
Скачать бесплатно Алгебра и начала математического анализа. 10 класс. Самостоятельные работы. Александрова Л.А. Данное пособие предназначено. Пособие содержит материал для проведения самостоятельных работ по каждой теме и может быть использовано учителем для осуществления текущего контроля . ..
..
Самостоятельные работы по алгебре 10 класс Александрова ответы. Не всегда нужно переплачивать за услуги репетитора, частично справиться с выполнением упражнений и проверочных работ позволит ГДЗ к сборнику.
Скачать решебники 10 класс. Данный решебник содержит 38 самостоятельных работ, в двух вариантах. Контрольные и самостоятельные работы по алгебре за 7 класс скачать бесплатно.
Структура пособия и содержание разноуровневых заданий позволяют использовать тетрадь при работе по любым действующим учебникам по математике для 10 класса (уровень стандарта). Предназначено для учащихся 10 класса общеобразовательных учебных заведений, учителей математики. Итоговые контрольные …
7 класс (авторы учебника Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др.; Издательство Просвещение. Контрольные работы.quot; Александрова Л.А. 2014 год.
Самостоятельные работы по алгебре 10 класс никольский решебник. Никольский С.М. 2013 г. Решебник ГДЗ математика 5 класс Никольский Потапов Решетников.
ГДЗ Алгебра 10 класс Александрова Л.А.
- Алгебра 10 класс
- Тип пособия: Самостоятельные работы
- Авторы: Александрова Л.А.
- Издательство: «Мнемозина 2008»
Похожие ГДЗ Алгебра 10 класс
C-1: Вариант 1
Предыдущее
Следующее
Предыдущее
Следующее
Главные достоинства решебника
«ГДЗ Алгебра 10 класс Самостоятельные работы Александрова (Мнемозина)» поможет школьникам справиться со всеми задачами от учителя и как следует подготовиться к предстоящему учебному дню. Решебник сможет грамотно проконсультировать юного пользователя по необходимому способу решения сложного уравнения из учебника. Рассмотрим важнейшие преимущества учебно-методического пособия ГДЗ:
- содержит в себе только верные ответы на все номера из дидактического материала;
- поможет досконально разобрать проблемную тему;
- способствует развитию таких важных навыков у подростка, как самопроверка и работа над ошибками.

К тому же, следует помнить и о том, что сам решебник был размещён в онлайн-формате на популярном сайте в интернете. Благодаря такой удобной функции, старшеклассники могут получить доступ к верным ответам и остальным материалам пособия ГДЗ в любое удобное для себя время дня и ночи. Необходимо лишь наличие мобильного телефона или персонального компьютера с работающим браузером и подключением к интернету.
Характеристика процесса изучения алгебры в старшей школе
На занятиях по данной точной науке ученики смогут подробно разобрать теоретические аспекты по каждому разделу учебника и с головой погрузиться в изучение популярных математических формул. Они позволят быстро и качественно вычислять уравнения и неравенства. А учителя с удовольствием расскажут своим воспитанникам о способах построения различных графиков функций. Мы выделили следующие важные темы, в рамках данного предмета:
- решение простейших тригонометрических уравнений;
- синус и косинус разности аргументов;
- решение степенных выражений.

Но, чтобы успешно освоить представленные выше параграфы и без труда завоевать расположение преподавателя улучшенными результатами и непреодолимой тягой к знаниям, школьникам понадобится такой полезный вспомогательный ресурс, как учебно-методическое пособие «ГДЗ Алгебра 10 класс Самостоятельные работы Александрова Л.А. (Мнемозина)».
Польза решебника для преподавателя
Пособие ГДЗ станет отличным решением и для самих учителей. С помощью сборника верных ответов, они смогут составить интересные и сложные карточки заданий для контрольных работ. Помимо этого, решебник позволит преподавателю существенно повысить скорость проверки написанных самостоятельных работ и заняться личными делами.
ГДЗ к учебникам и тетрадям по Алгебре за 10 класс. Готовые ответы бесплатно
Считается, что математике — сложнейшая дисциплина в школьной программе. Многие недолюбливают её, а некоторые души в ней не чают. Но одно известно точно — её изучение практически всегда вызывает сложности у школьников. Многие попросту не понимают предметный материал, и допускают многочисленные ошибки, которые крайне негативно сказываются на успеваемости. Даже если старшеклассник предпочитает изучать гуманитарные науки, то это вовсе не освобождает его от выполнения домашних заданий по алгебре. Порой на решение одной сложной задачи может уйти больше часа. А ведь есть остальные уроки, к которым нужно хорошенько подготовиться. Чтобы сэкономить драгоценные часы, специалисты в подобной ситуации советуют воспользоваться помощью вспомогательной литературы в виде ГДЗ.
Многие попросту не понимают предметный материал, и допускают многочисленные ошибки, которые крайне негативно сказываются на успеваемости. Даже если старшеклассник предпочитает изучать гуманитарные науки, то это вовсе не освобождает его от выполнения домашних заданий по алгебре. Порой на решение одной сложной задачи может уйти больше часа. А ведь есть остальные уроки, к которым нужно хорошенько подготовиться. Чтобы сэкономить драгоценные часы, специалисты в подобной ситуации советуют воспользоваться помощью вспомогательной литературы в виде ГДЗ.
Чем полезна алгебра
Начиная с седьмого класса, математика разделяется на две самостоятельные дисциплины, одной из которых является алгебра. Она даёт знания о свойствах действий над разнообразными величинами и учит решать системы уравнений различными способами. Ее изучение не только благотворно влияет на развитие интеллекта и абстрактного мышления, но и на дедуктивные, критические и аналитические способности. Поэтому так важно качество учебника. В нашей стране их разрабатывают только профессиональные методисты: А.Г. Мордкович, П. В. Семенов, Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева, А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и т.д. Дисциплина учит грамотно рассуждать, четко формулировать свои мысли и просчитывать свои действия на несколько шагов вперёд. На десятой ступени обучения в школе ребятам предстоит познакомиться со следующими разделами учебника:
В нашей стране их разрабатывают только профессиональные методисты: А.Г. Мордкович, П. В. Семенов, Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева, А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и т.д. Дисциплина учит грамотно рассуждать, четко формулировать свои мысли и просчитывать свои действия на несколько шагов вперёд. На десятой ступени обучения в школе ребятам предстоит познакомиться со следующими разделами учебника:
- Длина дуги окружности.
- Синус и косинус.
- Тангенс и котангенс.
- Формулы приведения.
- Простейшие тригонометрические уравнения.
- Степенные, показательные и логарифмические выражения.
Чем поможет решебник по алгебре за 10 класс
Пособие содержит образцы готовых решений ко всем упражнениям, от простых до самых сложных. К тому к каждому решению имеется подробный комментарий, с помощью которого будет гораздо проще понять сам принцип. С помощью всего этого ученик сможет:
- подготовиться к предстоящей проверке знаний на уроке;
- качественно выполнить и оформить домашнее задание;
- дополнительно поработать над уже пройденным материалом, чтобы закрепить его;
- значительно сэкономить время и силы на поиск нужной информации.

Пользоваться сборником легко и удобно. Найти необходимый ответ не составит никакого труда. Огромным преимуществом решебника является то, что он представлен в электронном формате, то есть онлайн. Это обеспечивает круглосуточный доступ к готовым ответам с любого устройства, будь то компьютер или телефон. Систематическое применение готовых домашних заданий только положительно отразится на результатах обучения, к тому же ученик всегда будет во всеоружии перед любой самостоятельной работой в классе.
Если не применять решебник, то школьнику будет очень тяжело разобраться во всех тонкостях и нюансах изучаемых тем. Готовые домашние задания вовсе не предназначены для того, чтобы ученик просто переписывал верные ответы в чистовик, как многие ошибочно полагают. Пособием могут воспользоваться и родители учащихся, желающие принять полноценное участие в образовательном процессе подростков. Им вовсе не обязательно знакомиться с материалами основного учебника, и тратить на это время. За считанные минуты они смогут проверить правильность выполнения домашнего задания и то, как ученик подготовился к уроку. И все это благодаря ГДЗ.
За считанные минуты они смогут проверить правильность выполнения домашнего задания и то, как ученик подготовился к уроку. И все это благодаря ГДЗ.
Независимая система уравнений Примеры
Дополнительная практика — Независимые системы уравнений
В следующих примерах учащиеся определят, является ли система независимой или зависимой, изучая графики или уравнения, и найдут решения для независимых систем.
Практические задачи
1. Определить, является ли система уравнений независимой. Если она независима и прямые не параллельны, решите систему.
2.Определить, является ли система уравнений независимой. Если она независима и прямые не параллельны, решите систему.
3. Определить, является ли система уравнений независимой. Если она независима и прямые не параллельны, решите систему.
4. Определить, является ли система уравнений независимой. Если она независима и прямые не параллельны, решите систему.
Определить, является ли система уравнений независимой. Если она независима и прямые не параллельны, решите систему.
Решения
1.Мы преобразуем второе уравнение в форму пересечения наклона. Решив y во втором уравнении, мы получим
Наклон первой линии равен 3, а наклон второй линии равен -1, поэтому уравнения относятся к разным линиям. Эта система независима, и линии не параллельны. Используя замену, мы можем заменить y во втором уравнении на 3 x + 1, чтобы получить
Тогда, подставив x = -1 в первое уравнение, мы получим
Решение (-1, -2).
2. Преобразование первого уравнения в форму пересечения наклона,
Преобразование второго уравнения в форму пересечения наклона,
Уравнения имеют другую точку пересечения и , поэтому они представляют разные линии. Таким образом, система независима. Однако прямые параллельны, так как обе имеют наклон 2/3, поэтому система не имеет решения.
Таким образом, система независима. Однако прямые параллельны, так как обе имеют наклон 2/3, поэтому система не имеет решения.
3. Система независима, поскольку на графике видно, что две линии различны.Решение системы находится там, где пересекаются линии, поэтому решение (4, 0).
4. Преобразуя второе уравнение в форму пересечения наклона, мы имеем
Оба уравнения представляют одну и ту же прямую, поэтому это зависимая система уравнений.
4.4 Решение одновременных уравнений | Уравнения и неравенства
\(- 10 х = -1\) и
\(- 4 х + 10 у = -9\).
Найдите \(x\):
\начать{выравнивать*}
— 10х = -1\\
\следовательно, x = \frac{1}{10}
\конец{выравнивание*}
Подставьте значение \(x\) во второе уравнение и найдите \(y\):
\начать{выравнивать*}
-4х+10у&=-9\
-4\влево(\frac{1}{10}\вправо) + 10y & = -9 \\
\frac{-4}{10} + 10y & = -9 \\
100у&=-90+4\
y & = \frac{-86}{100} \\
& = \фракция{-43}{50}
\конец{выравнивание*}
Следовательно, \(x = \frac{1}{10} \text{ и } y = — \frac{43}{50}\).
\(3x — 14y = 0\) и \(x — 4y + 1 = 0\)
Запишите \(x\) через \(y\):
\начать{выравнивать*}
3х — 14у&=0\
3х&=14у\
х & = \фракция{14}{3}у
\конец{выравнивание*}
Подставьте значение \(x\) во второе уравнение:
\начать{выравнивать*}
х — 4у + 1 & = 0 \
\frac{14}{3}y — 4y + 1 & = 0 \\
14у — 12у + 3 & = 0\
2у&=-3\
у & = -\фракция{3}{2}
\конец{выравнивание*}
Подставить значение \(y\) обратно в первое уравнение:
\начать{выравнивать*}
х & = \ гидроразрыва {14 \ влево (- \ гидроразрыва {3} {2} \ вправо)} {3} \\
& = -7
\конец{выравнивание*}
Следовательно, \(x = -7 \text{ и } y = -\frac{3}{2}\).
\(х + у = 8\) и \(3х + 2у = 21\)
Запишите \(x\) через \(y\):
\начать{выравнивать*}
х + у & = 8 \\
х & = 8 — у
\конец{выравнивание*}
Подставьте значение \(x\) во второе уравнение:
\начать{выравнивать*}
3х+2у&=21\
3(8 — у) + 2у & = 21 \\
24 — 3у + 2у & = 21\
у & = 3
\конец{выравнивание*}
Подставить значение \(y\) обратно в первое уравнение:
\[х = 5\]
Следовательно, \(x = 5 \text{ и } y = 3\).
\(у = 2х + 1\) и \(х + 2у + 3 = 0\)
Запишите \(y\) через \(x\):
\[у = 2х + 1\]
Подставьте значение \(y\) во второе уравнение:
\начать{выравнивать*}
х + 2у + 3 & = 0 \\
х + 2 (2х + 1) + 3 & = 0 \\
х + 4х + 2 + 3 & = 0 \\
5х&=-5\
х & = -1
\конец{выравнивание*}
Подставить значение \(x\) обратно в первое уравнение:
\начать{выравнивать*}
у & = 2 (-1) + 1 \\
& = -1
\конец{выравнивание*}
Следовательно, \(x = -1 \text{ и } y = -1\).
\(5x-4y = 69\) и \(2x+3y = 23\)
Сделать \(x\) предметом первого уравнения:
\начать{выравнивать*}
5х-4у &= 69\
5x &= 69+4y \\
х &= \фракция{69+4y}{5}
\конец{выравнивание*}
Подставьте значение \(x\) во второе уравнение:
\начать{выравнивать*}
2х+3у &= 23\\
2 \left(\frac{69+4y}{5} \right) +3y &= 23 \\
2(69+4г) +3(5)г &= 23(5) \\
138+8л+15л &= 115\\
23г&=-23\\
\поэтому у &= -1
\конец{выравнивание*}
Подставить значение \(y\) обратно в первое уравнение:
\начать{выравнивать*}
х &= \frac{69+4y}{5} \\
&= \frac{69+4(-1)}{5} \\
&= 13
\конец{выравнивание*}
Следовательно, \(x = 13 \text{ и } y = -1\).
\(х + 3у = 26\) и \(5х + 4у = 75\)
Сделать \(x\) предметом первого уравнения:
\начать{выравнивать*}
х + 3у &= 26 \\
х &= 26 — 3г
\конец{выравнивание*}
Подставьте значение \(x\) во второе уравнение:
\начать{выравнивать*}
5х+4у &= 75\\
5(26 — 3г) + 4г &= 75\
130 — 15у + 4у &= 75\
-11у &= -55\
\поэтому у &= 5
\конец{выравнивание*}
Подставить значение \(y\) обратно в первое уравнение:
\начать{выравнивать*}
х &= 26 — 3у \\
&= 26 — 3(5) \\
&= 11
\конец{выравнивание*}
Следовательно, \(x = 11 \text{ и } y = 5\).
\(3x — 4y = 19\) и \(2x — 8y = 2\)
Если умножить первое уравнение на 2, то коэффициент при \(у\) будет таким же
в обоих уравнениях:
\начать{выравнивать*}
3х — 4у &= 19\
3(2)х — 4(2)у & = 19(2) \\
6x — 8y & = 38
\конец{выравнивание*}
Теперь мы можем вычесть второе уравнение из первого:
\[\begin{массив}{cccc}
&6х — 8у &=&38\
— & (2x — 8y & = & 2) \\\hline
& 4x + 0 & = & 36
\конец{массив}\]
Найдите \(x\):
\начать{выравнивать*}
\поэтому x &= \frac{36}{4} \\
& = 9
\конец{выравнивание*}
Подставьте значение \(x\) в первое уравнение и найдите \(y\):
\начать{выравнивать*}
3х-4у &=19\
3(9)-4у &= 19\\
\поэтому y &= \frac{19-3(9)}{-4} \\
&= 2
\конец{выравнивание*}
Следовательно, \(x = 9 \text{ и } y = 2\).
\(\dfrac{a}{2} + b = 4\) и \(\dfrac{a}{4} — \dfrac{b}{4} = 1\)
Сделать \(a\) предметом первого уравнения:
\начать{выравнивать*}
\frac{a}{2} + b & = 4 \\
а+2б&=8\
а & = 8 — 2b
\конец{выравнивание*}
Подставьте значение \(a\) во второе уравнение:
\начать{выравнивать*}
\frac{a}{4} — \frac{b}{4} & = 1 \\
а — б & = 4 \\
8 — 2б — б и = 4\
3б&=4\
б & = \ гидроразрыва {4} {3}
\конец{выравнивание*}
Подставить значение \(b\) обратно в первое уравнение:
\начать{выравнивать*}
а & = 8 — 2 \ влево (\ гидроразрыва {4} {3} \ вправо) \\
& = \фракция{16}{3}
\конец{выравнивание*}
Следовательно, \(a = \frac{16}{3} \text{ и } b = \frac{4}{3}\).
\(-10x + y = -1\) и
\(-10х — 2у = 5\)
Если мы вычтем второе уравнение из первого, то мы можем найти \(y\):
\[\begin{массив}{cccc}
&-10х+у&=&-1\
— & (-10x — 2y & = & 5) \\\hline
& 0 + 3г & = & -6
\конец{массив}\]
Найдите \(y\):
\начать{выравнивать*}
3у&=-6\
\поэтому у &= -2
\конец{выравнивание*}
Подставьте значение \(y\) в первое уравнение и найдите \(x\):
\начать{выравнивать*}
-10x + у &= -1 \\
-10x — 2 &= -1\\
-10x &= 1 \\
х &= \фракция{1}{-10}
\конец{выравнивание*}
Следовательно, \(x = \frac{-1}{10} \text{ и } y = -2\).
\(- 10 х — 10 у = -2\) и \(2 х + 3 у = 2\)
Сделать \(x\) предметом первого уравнения:
\начать{выравнивать*}
— 10 х — 10 у = -2\\
5х+5у&=1\
5х & = 1 — 5у\
\следовательно, x = -y + \frac{1}{5}
\конец{выравнивание*}
Подставьте значение \(x\) во второе уравнение и найдите \(y\):
\начать{выравнивать*}
2х+3у&=2\
2\влево(-y + \frac{1}{5}\right) + 3y & = 2 \\
-2y + \frac{2}{5} + 3y & = 2 \\
у & = \ гидроразрыва {8} {5}
\конец{выравнивание*}
Подставьте значение \(y\) в первое уравнение:
\начать{выравнивать*}
5х+5у&=1\
5x + 5\влево(\frac{8}{5}\вправо) & = 1 \\
5х+8&=1\
5х&=-7\
х &= \фракция{-7}{5}
\конец{выравнивание*}
Следовательно, \(x = — \frac{7}{5} \text{ и } y = \frac{8}{5}\).
\(\dfrac{1}{x} + \dfrac{1}{y} = 3\) и \(\dfrac{1}{x} — \dfrac{1}{y} = 11\)
Переставьте оба уравнения, умножив на \(xy\):
\начать{выравнивать*}
\frac{1}{x} + \frac{1}{y} & = 3 \\
у + х & = 3ху \\\\
\frac{1}{x} — \frac{1}{y} & = 11 \\
у — х & = 11xy
\конец{выравнивание*}
Сложите два уравнения вместе:
\[\begin{массив}{cccc}
& у + х & = & 3xy \\
+ & (y — x & = & 11xy) \\ \hline
& 2y + 0 & = & 14xy
\конец{массив}\]
Найдите \(x\):
\начать{выравнивать*}
2у&=14ху\
у & = 7ху \\
1&=7х\
х & = \ гидроразрыва {1} {7}
\конец{выравнивание*}
Подставить значение \(x\) обратно в первое уравнение:
\начать{выравнивать*}
y + \frac{1}{7} & = 3\left(\frac{1}{7}\right)y \\
7у + 1 & = 3у \\
4у&=-1\
у & = -\фракция{1}{4}
\конец{выравнивание*}
Следовательно, \(x = \frac{1}{7} \text{ и } y = -\frac{1}{4}\). {2}+2}\) становится очень маленькой
{2}+2}\) становится очень маленькой
(подумайте о том, что происходит, когда вы делите небольшое число на очень большое число).2 &= 3 — аб
\конец{выравнивание*}
Обратите внимание, что это то же самое, что и второе уравнение
\(a\) и \(b\) могут быть любыми действительными числами, кроме \(\text{0}\).
|
Колледж алгебры
Цели обучения
Введение
Учебник
Практические задачи
|
Перевернутый опыт для изучения линейной алгебры (FELLA)
Меню сайта:
Перевернутый опыт для изучения линейной алгебры
В этом перевернутом классе учащиеся несут ответственность за обучение и создание знаний при содействии инструктора.Этот веб-сайт представляет собой дорожную карту, которая поможет учащимся стать независимыми учениками и опытными специалистами в решении проблем.
Этот проект поддерживается Программой награждения «Повышение эффективности образования с помощью технологий» 2013 года: Flipping the Classroom в Калифорнийском государственном университете, Лонг-Бич. Любой вопрос или комментарий следует направлять профессору Джен-Мей Чанг ([email protected]).
Материалы курса:
Класс №
Предварительные задания
Классные задачи
Послеклассовые задачи
1.26.08.13
Цель обучения
Знакомство с перевернутым классом и программой курса
2. 28.08.13
Цель обучения
Знакомство с ожиданиями учителей и результатами обучения по курсу
- HW.2 :
Запись на 5-минутную встречу
со мной по электронной почте до 29.08.13
(определить мою доступность с помощью этого календаря)
3.04.09.13
Цель обучения
Базовое понимание систем линейных уравнений
- Решение систем линейных уравнений в классах алгебры ( Panopto video ->)
- Системы линейных уравнений: геометрическая интерпретация и типы ( Панорамное видео ->)
- Решение системы с помощью операций со строками ( Panopto video ->)
- Чтение (Lay pg.2-9)
- Индивидуальная викторина ( BB.Quiz.3 ->)
- HW.3: Проложить стр.10: 7,11,15,17,23-25
- Общие сведения о групповых ролях [PDF, 496 КБ]
4. 9/9/13
Цель обучения
Линейная комбинация, наборы и диапазон
- Векторы: Set Notations (видео Академии Хана)
- Векторы: геометрические и алгебраические интерпретации (видео Академии Хана)
- Математические множества и операторы (видеолекция (1 мин 57 с ~ 7 мин 41 с) Билла Шиллито)
- Linear Combination & Span (видео Академии Хана)
- Чтение (Lay pg.24-31)
- Индивидуальная викторина ( BB.Quiz.4 ->)
- HW.4 : Уложить стр.32: 3,7,9,11,17,19,23,25
5. 11.09.13
Цель обучения
Уменьшенная ступенчатая форма строк и исключение Гаусса
- Сокращение ряда, эшелонированные формы и уменьшенные эшелонированные формы
( Панорамное видео ->) - Решение систем линейных уравнений с исключением Гаусса (GE) или сокращенной эшелонированной формой строк
( Панорамное видео ->) - Пример GE для большей практики
(видео Академии Хана) - Чтение (Lay pg.12-21)
- Индивидуальная викторина ( BB.Quiz.5 ->)
- HW.5 : Уложить стр.21:
1,3,9,11,13,21,23,29
6. 16.09.13
Цель обучения
Техника доказательства или опровержения утверждений «если-то» для задач «истина/ложь»
- Как доказать или опровергнуть утверждение
(видеолекция ГВСУмат) - A x = b ( Панорамное видео ->)
- Наборы решений линейных систем: алгебраические и геометрические интерпретации ( Panopto video ->)
- Чтение (Lay pg.34-37; стр. 43-46)
- Индивидуальная викторина ( BB.Quiz.6 ->)
- HW.6 :
Лей стр.40: 9,11,13,15,17,19,23,31;
стр.47: 1,11,13,19,23,29,31
7. 18.09.13
Цель обучения
Линейная зависимость/независимость
- Линейная независимость/зависимость: геометрическая интерпретация (видео Академии Хана)
- Линейная независимость/зависимость: формальное определение (видео Академии Хана)
- Логика тогда и только тогда, когда (видео Кевина де Лапланте на YouTube)
- Чтение (Lay pg.55-60)
- Индивидуальная викторина ( BB.Quiz.7 ->)
- HW.7 : Уложить стр.60:
1,5,7,9,11,15,17,19,21,
23,25,27,29,33,35,37
8. 23.09.13
Цель обучения
Суммарное оценивание
9.25.09.13
Цель обучения
Линейное преобразование
- Умножение матриц как линейное преобразование ( Панорамное видео ->)
- Примеры линейных преобразований ( Панорамное видео ->)
- Чтение (Lay стр.62-67)
- Индивидуальная викторина ( BB.Quiz.8 ->)
- HW.8 : Уложить стр.68: 1,3,7,11,13,17,21,31
10. 30.09.13
Цель обучения
1-1 и далее
- Стандартная матрица линейного преобразования ( Панорамное видео ->)
- Определение и примеры карт One-to-One и Onto ( Панорамное видео ->)
- Чтение (Lay стр.70-76)
- Индивидуальная викторина ( BB.Викторина.9 ->)
- HW.9 : Уложить стр.78: 3,5,7,19,21,23,25,27
11. 02.10.13
Цель обучения
Два вида умножения матриц
- Матричные умножения и свойства ( Панорамное видео ->)
- Чтение (Lay pg.92-100)
- Индивидуальная викторина ( BB.Quiz.10 ->)
- ТП.10 : Проложить стр.100: 5,9,13,15,17,21,27
12. 07.10.13
Цель обучения
Обратная матрица и ее приложения
- Обратная матрица ( Панорамное видео ->)
- Криптография: применение обратной матрицы (Примечания Мены [PDF, 5,72 МБ] на стр. 46)
- Чтение (Lay стр.102-108)
- Индивидуальная викторина ( BB.Викторина.11 ->)
- HW.11 : Уложить стр.109: 5,7,9,11,23,31
13. 09.10.13
Цель обучения
Свойства обратимых матриц и определителей
- Теорема об обратимой матрице (Lay стр. 112 — 114)
- Определитель матрицы ( Панорамное видео ->)
- Свойства определителей ( Панорамное видео ->)
- Чтение (Lay pg.164-167; стр.169-174)
- Индивидуальная викторина ( BB.Quiz.12 ->)
- HW.12 : Lay стр.115: 7,11,13,21,23,33; стр.167: 9,17,39; стр.175: 9,11,15,17,19,23,27,31
14. 14.10.13
Цель обучения
Векторные пространства и подпространства
- Определение и примеры векторных пространств ( Панорамное видео ->)
- Определение и примеры векторных подпространств ( Панорамное видео ->)
- Чтение (Lay pg.190-195)
- Индивидуальная викторина ( BB.Quiz.13 ->)
- HW.13 : Lay стр.195: 1,3,5,7,9,11,13,15,17,23
15. 16.10.13
Цель обучения
Суммативное оценивание
- Экзамен 2: укладка 1,8–1,9; 2.1-2.3;3.1-3.2
16. 21.10.13
Цель обучения
Пустые пробелы и столбцы
- Нулевые пространства матрицы и ядра линейного преобразования ( Паноптическое видео ->)
- Пространства столбцов матрицы и диапазон линейного преобразования ( Паноптическое видео ->)
- Чтение (Lay pg.198-205)
- Индивидуальная викторина ( BB.Quiz.14 ->)
- HW.14 : Уложить стр.205: 5,11,15,17,21,23,25
17. 23.10.13
Цель обучения
База
- Базис как линейно независимый и остовный набор ( Паноптическое видео ->)
- Пример базиса и небазиса для матриц и многочленов ( Panopto video ->)
- Теорема о остовном множестве ( Panopto video ->)
- Чтение (Lay pg.208-213)
- Индивидуальная викторина ( BB.Quiz.15 ->)
- HW.15: Проложить стр.213: 9,11,13,15,21,25
18. 28.10.13
Цель обучения
Системы координат
- Знакомство с системой координат ( Панорамное видео ->)
- Координаты относительно основы ( Панорамное видео ->)
- Чтение (Lay pg.216-222)
- Индивидуальная викторина ( BB.Quiz.16 ->)
- HW.16 : Lay стр.222: 3,7,13,15,16,29,31(a)
19. 30.10.13
Цель обучения
Размерность векторного пространства в зависимости от ранга матрицы
- Размерность векторных пространств ( Панорамное видео ->)
- Ранг и теорема о рангах ( Panopto video ->)
- Чтение (Lay pg.225-228;стр.230-236)
- Индивидуальная викторина ( BB.Quiz.17 ->)
- HW.17 : Lay стр.229: 5,7,9,11,13,19,20; стр.236: 3,5,7,9,11,13,15,17,18,19 ,25
20. 04.11.13
Цель обучения
Изменение базы
- Изменение базы ( Панорамное видео ->)
- Чтение (Lay pg.239-242)
- Индивидуальная викторина ( BB.Quiz.18 ->)
- HW.18 : Уложить стр.242: 1,5,7,11,13
21. 06.11.13
Цель обучения
Собственные векторы и собственные значения
- Собственные значения и собственные векторы ( Паноптическое видео ->)
- Геометрическая и алгебраическая кратность собственных значений ( Паноптическое видео ->)
- Чтение (Lay pg.266-271;стр.274-279)
- Индивидуальная викторина ( BB.Quiz.19 ->)
- HW.19 : Lay стр.272: 7,13,17,21,25; стр.279: 7,11,15,21;
См. предварительное задание от 12 ноября, будьте готовы
22. 12.11.13
Цель обучения
Развитие навыков самостоятельного обучения
- Работайте с членами вашей команды, чтобы придумать пробный экзамен из 5 вопросов 3 с ответами (для обмена с другими группами во время занятий)
- Индивидуальная и групповая работа на пробных экзаменах
23.13.11.13
Цель обучения
Суммативное оценивание
24. 18.11.13
Цель обучения
Диагонализация матрицы
- Почему мы диагонализируем матрицу?
( Паноптическое видео ->) - Диагонализация как преобразование подобия
( Панорамное видео ->) - Как провести диагонализацию матрицы? ( Панорамное видео ->)
- Чтение (Lay pg.281-286)
- Индивидуальная викторина ( BB.Quiz.20 ->)
- HW.20: Проложить стр.286: 1,7,11,15,21,22,23,31,32
25. 20.11.13
Цель обучения
Аппроксимация Ax = b; количественный Ax-b
- Приближение к Ax = b
( Паноптическое видео ->) - Внутренний продукт, нормализация, длины и расстояния
( Паноптическое видео ->) - Понятие ортогональности, теорема Пифагора и ортогональное дополнение ( Panopto video ->)
- Чтение (Lay pg.330-336)
- Индивидуальная викторина ( BB.Quiz.21 ->)
- HW.21 : Lay стр.336: 1-19 нечетные,22,25,27,31
26. 25.11.13
Цель обучения
Ортогональные проекции
- HW.22 : Lay стр.344: 9,13,17,23,24; стр.352: 9,11,15,17,21,22
27.02.12.13
Цель обучения
Кульминация навыков
Группы 1-4:
- сочинять, практиковать, редактировать, печатать плакат
Группы 5-8:
- ознакомиться с рубриками выставления оценок [PDF, 268 КБ]
- Процесс Грама-Шмидта для получения ортонормированного базиса ( Panopto video ->)
- QR-факторизация ( Панорамное видео ->)
- Чтение (Lay pg.354-358)
- Индивидуальная викторина ( BB.Quiz.23 ->)
- Группы 1-4: присутствует
- Группы 5-8: критический анализ
Группы 1:4:
Группы 5-8:
- HW.23 : Уложить стр.358: 3,7,11,15
28. 04.12.13
Цель обучения
Кульминация навыков
Группы 1-4:
- ознакомиться с рубриками выставления оценок [PDF, 268 КБ]
- Процесс Грама-Шмидта для получения ортонормированного базиса ( Panopto video ->)
- QR-факторизация ( Панорамное видео ->)
- Чтение (Lay pg.354-358)
- Индивидуальная викторина ( BB.Quiz.23 ->)
Группы 5-8:
- сочинять, практиковать, редактировать, печатать плакат
- Группы 1-4: критический анализ
- Группы 5-8: присутствует
Группы 1-4:
- HW.23 : Уложить стр.358: 3,7,11,15
Группы 5-8:
29. 09.12.13
Цель обучения
Процесс Грама-Шмидта; Задачи наименьших квадратов
- Нормальное уравнение и задачи наименьших квадратов
( Паноптическое видео ->) - Чтение (Lay pg.360-365; стр.368-372)
- Индивидуальная викторина ( BB.Quiz.24 ->)
- HW.24 : Lay стр.366: 5,11,15,17,18; стр.374: 3
30. 13.12.13
Цель обучения
Суммативное оценивание
- Общий выпускной экзамен: 8:00–10:00
Бесконечные решения — определение, условия и примеры
Все мы хорошо знакомы с уравнениями и выражениями.Мы решаем ее почти ежедневно по математике. Давайте еще раз быстро освежим значения терминов, прежде чем углубляться в них. Уравнение – это выражение, между которым стоит знак равенства (=). Например, 4+3 = 7. А выражение состоит из таких переменных, как x или y, и постоянных членов, которые соединяются вместе с помощью алгебраических операторов. Например, 2x + 4y — 9, где x и y — переменные, а 9 — константа. Насколько мы смотрим, обычно есть одно решение уравнения. Но не исключено, что уравнение не может иметь более одного решения, бесконечное число решений или вообще не может иметь решений.Отсутствие решения означает, что уравнение не имеет ответа, тогда как бесконечные решения уравнения означают, что любое значение переменной сделает уравнение верным.
Что такое бесконечные решения?
Общее количество переменных в уравнении определяет количество возможных решений. И на основании этого решения можно разделить на три типа, это:
-
Уникальное решение (у которого только 1 решение).
-
No Solutions (нет решений)
-
Infinite Solutions (имеет множество решений)
Но как узнать, является ли решение решаемого вами уравнения бесконечным решением? Ну, есть простой способ узнать, является ли ваше решение бесконечным решением.У бесконечного решения обе стороны равны. Например, 6x + 2y — 8 = 12x + 4y — 16. Если вы упростите уравнение, используя формулу или метод бесконечных решений, вы получите равные обе части, следовательно, это бесконечное решение. Бесконечность представляет безграничность или безграничность. Обычно обозначается символом «∞».
Условия для бесконечного решения
Уравнение будет иметь бесконечное решение, если оно удовлетворяет некоторым условиям для бесконечного решения. Бесконечное решение может быть получено, если линии совпадают и они должны иметь одинаковую точку пересечения по оси Y.Две линии, имеющие одинаковую точку пересечения по оси Y и наклон, на самом деле являются одной и той же линией. Проще говоря, мы можем сказать, что если две линии пересекают одну и ту же линию, то система приведет к бесконечному решению. Следовательно, система будет состоятельной, если система уравнений имеет бесконечное число решений.
Например, рассмотрим следующие уравнения.
y = x + 3
5y = 5x + 15
Если мы умножим 5 на уравнение 1, мы получим уравнение 2, а разделив уравнение 2 на 5, мы получим точное первое уравнение.
Пример бесконечного решения
Что является примером бесконечного решения? Это вопрос, которого мы так долго ждали. Но для того, чтобы решать системы уравнений с двумя или тремя переменными, важно понимать, является ли уравнение зависимым или независимым, является ли оно состоятельным уравнением или несовместным уравнением. Непротиворечивая пара линейных уравнений всегда будет иметь уникальные или бесконечные решения.
Пример 1) Вот два уравнения с двумя переменными.
a1x + b1y = c1 ——- (1)
a2x + b2y = c2 ——- (2)
Если (a1/a2) = (b1/b2) = (c1/c2)
Тогда Уравнение является непротиворечивым и зависимым уравнением, которое имеет бесконечно много решений.
Пример 2) Вот несколько уравнений с бесконечными решениями -6x + 4y = 2
3x — 2y = -1
Теперь, если мы умножим второе уравнение на -2, мы получим первое уравнение.
-2(3x-2y) = -2(-1)
-6x + 4y = 2
Следовательно, уравнения эквивалентны и имеют один и тот же график.Таким образом, решение, которое будет работать для одного уравнения, будет работать и для других уравнений. Следовательно, они являются бесконечными решениями системы.
Пример 3) x-10 + x = 8 + 2x-18
Теперь, вот как мы действуем
x-10 + x = 8 + 2x-18
2x-10 = 2x-10
-2x=-2x
__________________
-10 = -10
Поскольку -10 = -10 = -10 = -10
Пример 4) Давайте возьмем еще один пример: x + 2x + 3 + 3 = 3 (x + 2)
x + 2x + 3 + 3 = 3 (x + 2)
3x + 6 = 3x + 6
-3x = -3x
6 = 6
Коэффициенты и константы соответствуют после объединения подобных терминов.Это дает нам истинное утверждение. Поэтому их можно назвать бесконечными решениями.
Пример 5) Рассмотрим уравнение 4(x+1)=4x+4.
4(x+1)=4x+4
Следовательно, это бесконечное решение.
Решение нестандартных задач по математике
Что такое решение нестандартных задач?
Решение нестандартных задач, также называемое творческим решением проблем, требует определенной степени творчества или оригинальности.Нестандартные проблемы обычно не имеют сразу очевидной стратегии их решения. Часто эти проблемы можно решить несколькими способами и с помощью различных стратегий. Так же, как и вычислительные упражнения (например, деление в большую сторону), решение нестандартных задач должно преподаваться учащимся в явном виде.
Почему решение нестандартных задач всегда будет не входить в мои инструкции:
- Готовит учащихся к решению реальных задач. В реальных проблемах нет предписанных шагов по их решению.Люди должны мыслить творчески и логически, чтобы решить их.
- Это дает учащимся подарок на выбор. Я использую слово «подарок», однако для многих студентов этот аспект очень важен. Они привыкли, что им говорят, что и как делать. Это буквально калечит учащихся, когда приходит время решать задачу, которая не следует заученному алгоритму. Что касается нестандартных задач, учащиеся должны выбрать, как они будут их решать. Со временем они учатся доверять себе, чтобы определить подходящие стратегии для использования и решения этих проблем с уверенностью.
- Как упоминалось выше, это укрепляет уверенность учащихся. Учащиеся вскоре понимают, что могут самостоятельно выбирать подходящую стратегию (или стратегии) и успешно ее применять.
- Он дает ученикам здоровую дозу «борьбы». Я полностью за преподавание на уровне обучения студентов. Тем не менее, я твердо верю, что студенты также должны иногда чувствовать себя немного некомфортно, даже разочарованно. Нестандартное решение проблем расстроит некоторых ваших учеников, особенно поначалу.Не сдавайся! Поговорите со своими учениками о том, что они чувствуют. Обеспечьте соответствующую поддержку, необходимую, чтобы помочь им справиться с этой проблемой. Со временем ваши ученики поразят вас своими способностями.
- Это весело!!! Я говорю это не только потому, что я помешан на математике. Это действительно весело, и вашим ученикам понравится это разнообразие, которое оно предлагает. Даже мои ученики, которые не дают правильного ответа, получают удовольствие от процесса.
- Развивает коммуникативные навыки учащихся. Студенты должны задокументировать и объяснить стратегии, которые они используют.
- Это для ВСЕХ. Я никогда не резервировал эти занятия для своих «более успевающих» учеников. На самом деле, многие учащиеся, которые боролись с вычислительными концепциями , РАЗВИВАЛИСЬ, решая нестандартные задачи.
Шаги для нестандартного решения проблем:
Есть четыре широко используемых шага, которые должны быть смоделированы для ваших студентов, чтобы дать им основу при работе с этими проблемами.
- Понять
- План
- Выполнить
- Обзор
Обучающие приложения:
У вас есть несколько вариантов того, как вы можете представить эти
проблемы своим ученикам.
- Вся группа: Вы можете спроектировать проблему для всего класса
для просмотра с помощью ЖК-дисплея или диапроектора.
Учащиеся могут работать на доске или просто использовать бумагу и карандаш для
решать проблему. Работа может быть выполнена
самостоятельно, или вы можете предложить учащимся работать вместе в парах или небольшими группами.
группы. В последнем варианте я бы
требовать, чтобы все учащиеся записывали работу на своей доске или
бумага. Этот вариант всей группы может следовать
с несколькими студентами, представляющими свой план решения проблемы; это
хорошая возможность для класса увидеть несколько стратегий, которые можно использовать для
решить ту же проблему. - Самостоятельная работа: учащиеся могут подготовить свою задачу
в любое время, когда им нужно работать независимо (т. е. быстрые финишеры, центровые,
утренняя работа и др.) - Совместное обучение:
Объедините учащихся в пары для совместной работы над проблемой. Это ценный вариант, поскольку он добавляет
учебные преимущества общения и сотрудничества в процессе.
Презентация:
И последнее, что следует учитывать: в дополнение к вышеупомянутым приложениям,
подумайте о том, как бы вы хотели, чтобы ваши ученики делились или представляли свои
Работа.Это важный компонент для
ряд причин:
- Выдерживает
учащиеся несут ответственность за свою работу. - Обеспечивает
студенты с важной возможностью объяснить решение своих проблем
процессы. - Позволяет
другим учащимся, чтобы увидеть различные способы решения проблемы. - Обеспечивает
студенты, у которых есть «время проявить себя», когда они представляют свою работу другим.
Учащиеся могут выступать несколькими способами:
- Они могут
представляют свою работу всему классу, в основном проводя собственные «мысли
вслух», аналогично тому, что делал учитель, когда он/она непосредственно моделировал
процесс в классе. - Они могут
представить свою работу другому студенту или небольшой группе студентов. - Они могут подарить
свою работу родителям или старшему брату или сестре. - Они могут
представить свою работу на онлайн-форуме (например, Edmodo и т. д.), организованном
учитель.
Несколько примеров (и решений), которые вы можете попробовать сегодня со своими учащимися:
Приведенные выше задачи взяты из моих Brain Power Math Books .Если ваши дети «голодны» по больше, проверьте их!
Стратегии вмешательства в математику для учащихся, испытывающих затруднения
Математика может заставить некоторых учеников чувствовать себя беспомощными.
И когда мы видим, как они уткнулись головой в руки или тупо смотрят на очередное занятие, которое просто не имеет смысла, учителя могут начать чувствовать себя беспомощными, тоже.
Как нам с ними связаться?
Стратегии вмешательства по математике дадут вам возможность помочь этим учащимся, испытывающим затруднения.
Мы собрали здесь шесть из них, чтобы вы могли с уверенностью поддержать следующего ученика, который скажет: «Я просто не понимаю».
Прямая инструкция
Отстающие учащиеся часто нуждаются в систематическом обучении, а не в деятельности, ориентированной на ученика.
Прямое обучение (также известное как « явное обучение ») обеспечивает именно это, когда учитель ведет учащихся по содержанию на каждом этапе пути. Вот как это работает:
- Учитель вводит понятие, связывая его с предыдущим содержанием.
- Учитель моделирует навык, который необходимо изучить.
- Учащиеся следуют четким инструкциям, чтобы самостоятельно использовать навык поэтапно.
- Учитель проверяет понимание на каждом этапе.
- Описанные выше шаги повторяются до тех пор, пока учащиеся не смогут практиковаться самостоятельно.
Прямое обучение отлично подходит для математических вмешательств, поскольку оно позволяет направлять учащихся к выполнению отдельных процедур шаг за шагом И немедленно устранять пробелы в обучении.
Наконечник учителя
Эффективность прямых инструкций зависит от вашей ясности и точности при разбивке на части — так что не жалейте деталей!
Используйте стратегию думать вслух , проговаривая все, что вы думаете, даже когда не пишете («Теперь я думаю, что мне было бы легче, если бы я округлил 48 до 50. Я сделаю это и запомню в конец, что у меня 2 лишних надо снять»).
Чтобы убедиться, что вы ничего не пропустили, лучше всего заранее написать свое объяснение наполовину и использовать PowerPoint (или написать на доске), чтобы поддержать объяснение.
Найдите бесплатные ресурсы поддержки для вашего класса
Наглядные пособия
Визуальное представление поможет учащемуся усвоить математическую концепцию, которая в противном случае превратилась бы в абстрактный беспорядок. Вот несколько примеров распространенных наглядных пособий и представлений:
Числовые линии: Это прямые линии с последовательностью чисел от конца до конца. Они полезны для развития у учащихся чувства числа и навыков счета.
Диаграммы и графики: Их можно использовать для обозначения взаимосвязи между различными наборами чисел или для визуализации абстрактных понятий (например, круговая диаграмма для дробей).
Иллюстрации: Иллюстрации конкретных, узнаваемых предметов могут сделать числовые предложения или текстовые задачи менее абстрактными.
Графические органайзеры: Они особенно полезны для демонстрации взаимосвязи между числовыми предложениями и более буквальными представлениями. В приведенном ниже примере учащийся достигает суммы 2 + 2 = 4, считая круги между двумя шагами.
Наконечник учителя
Учащиеся могут обнаружить, что визуализации помогают им в классе, но они не знают, как использовать их самостоятельно.Продвигайте ее как стратегию разработки, которую они могут использовать самостоятельно (например, дайте бумагу для разработки и поощряйте их рисовать при самостоятельном решении проблем).
Инструкция схемы
Если учащийся понятия не имеет, что от него требуется в словесной задаче, ему поможет инструкция по схеме. Это позволяет им расшифровать основную математическую операцию (схему), на которую намекают слова.
Проведите учащегося через ряд текстовых задач, которые работают по одной и той же схеме, а затем помогите им разработать математическую основу предложения, которую они могут заполнить для задач того же типа.В качестве примера возьмем следующие две задачи:
У Джека три лимона, а у Соломона два. Сколько их всего?
Николь собирает деньги на подарок другу на день рождения. У нее пока есть 10 долларов, и теперь она добавляет еще пять своих. Сколько денег у нее есть на данный момент?
В обоих случаях основной операцией является сложение. Таким образом, схема может выглядеть так:
Номер A + Номер B = Итого
Затем вы можете сделать это для другой схемы (например, вычитание, деление и т.д.).Это дает учащимся формулу, поэтому им не нужно подходить к каждой задаче со словами, как если бы она спрашивала что-то совершенно незнакомое.
Обучение метакогнитивным стратегиям
Часто, когда вы спрашиваете отстающего ученика, в чем у него трудности, он отвечает вам одним из следующих ответов:
Все это.
Я просто не понимаю.
Не знаю .
На самом деле это означает, что у них нет метакогнитивных способностей – способности думать о собственном математическом мышлении.Без этого они не смогут определить, где у них возникла проблема или , и что-нибудь с этим сделать.
Есть два метакогнитивных навыка, которые необходимо развивать учащимся математики:
Самоконтроль
Самоконтроль — это способность внутренне решать проблему шаг за шагом. Например, учащийся может решить проблему, задавая себе следующие вопросы:
- Я понял вопрос? Если нет, перечитайте.
- Напоминает ли это мне о задаче, которую я уже решал раньше? Давайте попробуем стратегию, которую я использовал для этого.
- Это не сработало. Что еще я мог бы попробовать?
Самоконтроль
Отстающие учащиеся часто ждут, пока не придут к окончательному ответу, чтобы проверить свою работу, если вообще проверяют. С другой стороны, более сильные ученики будут постоянно проверять свое мышление, чтобы убедиться, что они на правильном пути. Научите студентов задавать такие вопросы, как:
- Это выглядит правильно?
- Если я поставлю свой ответ «обратно» в задачу, будет ли это иметь смысл?
- Совершил ли я какие-нибудь ошибки на этом пути?
Наконечник для учителя
Лучший способ научить метакогнитивным навыкам – думать вслух .Всякий раз, когда вы моделируете математический навык, говорите вслух, чтобы учащиеся слышали каждое ваше движение мысли, которое вы делаете, чтобы прийти к окончательному ответу.
Лучше сделать это самому, прежде чем делать это перед классом. Вы можете быть удивлены тем, сколько быстрых шагов вы делаете, чтобы решить простую задачу со словами или двузначную сумму!
Стратегии взаимного обучения (PALS)
Иногда сверстники учащегося лучше справляются с переводом сложной концепции на знакомый язык.Студенты также будут чувствовать меньше давления и беспокойства при работе с надежным партнером.
PALS позволяет вам извлечь из этого максимум пользы, объединяя учащихся с высокими способностями с теми, кто нуждается в дополнительной поддержке.
Затем эти студенты работают вместе по 20–30 минут пару раз в неделю, по очереди выступая в роли «тренера» и «игрока». Таким образом, они получают поддержку один на один и возможность закрепить знания посредством обучения.
Сначала дайте учащимся стратегии, которые им нужны, чтобы поддерживать друг друга.Рекомендуется установить структуру или последовательность действий, чтобы направлять их, например:
- Тренер показывает игроку, как он будет решать задачу со словами, все время думая вслух.
- Затем игрок решает другую задачу, думая вслух под руководством тренера.
- Игрок самостоятельно решает задачу, которую проверяет тренер.
Наконечник для учителя
Еженедельное чередование учеников с разными партнерами познакомит их с разными способами мышления и подходами к математическим понятиям.Если повезет, один из них зажжет лампочку в тот момент, когда борющийся ученик ждет.
Индивидуальная поддержка студентов
Если у вас есть учащийся, который сильно отстает, ему может понадобиться индивидуальная поддержка в дополнение к вышеупомянутым инициативам. Посмотрите, сможете ли вы найти время для регулярных встреч, когда вы сможете работать с ними индивидуально и шаг за шагом проводить с ними математические задания.



 В этой ситуации они
В этой ситуации они
 для x и 1 шт. для y
для x и 1 шт. для y 






 2
2 

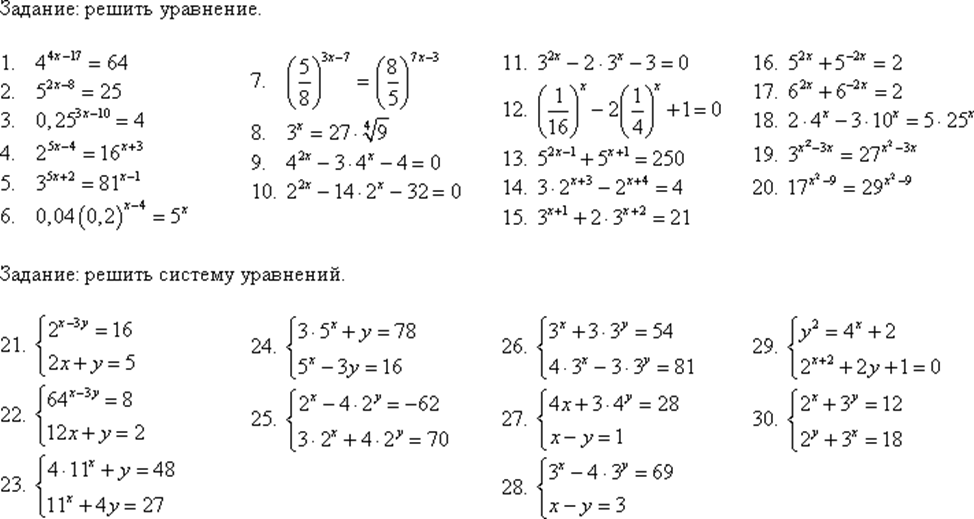
 3
3 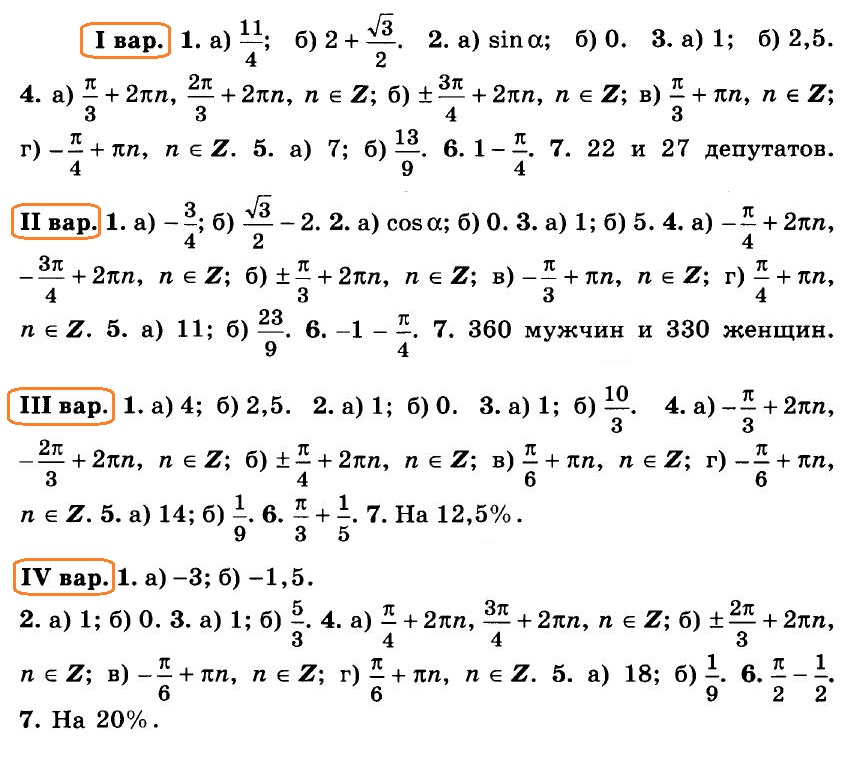
 Мы
Мы


 Подставьте найденное значение в
Подставьте найденное значение в
 г + 1 дюйм
г + 1 дюйм
 по ЖК 2
по ЖК 2  -3 х + 4
-3 х + 4

 Они в конечном итоге
Они в конечном итоге Упростите и
Упростите и
 Ты
Ты


 по ЖК 6
по ЖК 6