Математика функции 10 класс – Тема “Функция. Свойства функции” в 10 классе

Тема “Функция. Свойства функции” в 10 классе

Краткое описание работы.

Тема “Функция. Свойства функции” рассматривается в 10-м классе в курсе “Алгебра и начала анализа”. Данной темой заканчивается рассмотрение главы “Тригонометрические функции”. Цель данных уроков состоит не только в том, чтобы научиться строить график тригонометрических функций, а так же рассмотреть свойства этих функций. Поэтому рассмотрение данной темы целесообразно проводить, основываясь на свойствах других функций изученных учащимися в 9 классе.

Пояснительная записка.

Место урока в образовательной области и предмете:

— урок по алгебре и началам анализа в 10-м классе, глава 1 “Функция. Свойства функции”, §14 тема “График гармонического колебания”;

— уроки по физике входит в раздел “Динамика” в 10 классе по теме “Гармонические колебания”, 2 урок.

Тема: Функция. Свойство функции. Преобразование графиков функции.

Цели: Обучающая: совершенствование умений и навыков построения графиков функций, свойств функций, процессов мыслительной деятельности: сравнение, сопоставление, анализ, синтез.

Развивающая: развитие нестандартного, критического и творческого мышления, математической речи, самостоятельности и творческой активности

Воспитательная: содействие раскрытию творческого потенциала, повышению интереса к предмету.

Вид урока: Изучение нового материала.

Тип: Закрепления и усовершенствования знаний и умений (вторичное осмысление материала, воспроизведение и применение полученных знаний для достижения их прочности)

Конструирование урока: на основе модульной технологии

Технология: элементы продуктивного обучения (креативного мышления), уровневой дифференциации, критического мышления, модульного обучения, личностно-ориентированного обучения.

Методы: частично — поисковый, исследовательский, практический, самостоятельная работа.

ФОПД: Интерактивные формы взаимодействия (фронтальная, индивидуальная, работа в парах и творческих группах).

Форма контроля: самоконтроль, взаимоконтроль, контроль со стороны учителя.

Оборудование: карточки устного счета, карточки оперативного контроля.

ТСО: интерактивное оборудование, компьютер.

Мотивация: занимательная форма подачи материала.

Применение знаний: социализация личности школьников

Профиль школы, класса. Урок разработан для учащихся общеобразовательной школы, гуманитарного класса.

Объем урока. 3 часа.

Принцип отбора содержания учебного материала: содержание отобрано в соответствии с возрастными и психологическими особенностями учащихся.

Цели урока:

1. Научиться строить график тригонометрических функции.

2. Продолжить формирование умений преобразования графиков элементарных функций.

3. Изучить динамику преобразования тригонометрических функций.

4. Показать межпредметную связь областей математики, информатики.

Задачи:

• Развитие исследовательской и познавательной деятельности учащихся.

• Показать практическое применение свойств функций.

• Развитее коммуникативных способностей учащихся.

• Показать взаимосвязь между основными понятиями алгебры. Тригонометрические изучаются в курсе алгебры 10-го класса. Таким образом, мы создаем своеобразный мостик: изучая понятия в одном курсе 6-9 класс, создаем базу для другого курса 10 классов. А повторяя затем это понятие функций, мы закрепим его на практическом уровне.

Материально-техническое обеспечение урока.

• компьютер;

• интерактивная доска;

• программа Visual Basic 6.0.

• CD: Алгебра и начала анализа. Версия 2.5. Часть 1.

Актуальность использования ИКТ на уроке:

• наглядность;

• небольшие затраты времени на объяснение;

• новизна представления информации;

• оптимизация работы учителя при подготовке к уроку;

• установление межпредметных связей;

• привлечение учащихся к представлению практической стороны рассматриваемого урока;

• возможность показа опытов в записи, проведенных учащимися при подготовке к уроку.

Знания, умения и навыки, формируемые на уроке:

• Умение строить графики элементарных функций.

• Знать понятия функции, область определения, область значения, четные и нечетные функции, периодические функции.

• Уметь по графику описывать свойства функции, выполнять лабораторную работу с применением интерактивного оборудования.

• Умение анализировать условие задачи.

• Умение обобщать и делать выводы.

• Умение применять полученные знания в измененной ситуации.

• Умение выполнять самоанализ, самооценку, самоконтроль и взаимопроверку.

Информационные ресурсы учителя и ученика.

Учебник. Алгебра и начала анализа 10-11-е кл., автор А.Г. Мордкович. Учебник. Физика 10. Г.Я. Мякишев, Б.Б. Буховцев. Сборник задач по физике для 10–11-х классов. Г.И. Степанова. Дидактические материалы. Физика. А.Е. Марон, Е.А. Марон.

1. Модель урока (1 час)

1.1. Мотивационный этап.

• Организационный момент: Приветствие и подготовка к уроку.

• Мотивация.(Страница флипчарта 1) Нет ни одной области математики, которая когда-нибудь не окажется применимой к явлениям действительного мира.

1.2. Активизация знаний учащихся.

В начале урока используется электронный учебник, чтобы систематизировать и обобщить сведения о функциях полученных учащимися в курсах математики 6-9 классах (работа сопровождается электронным учебником).

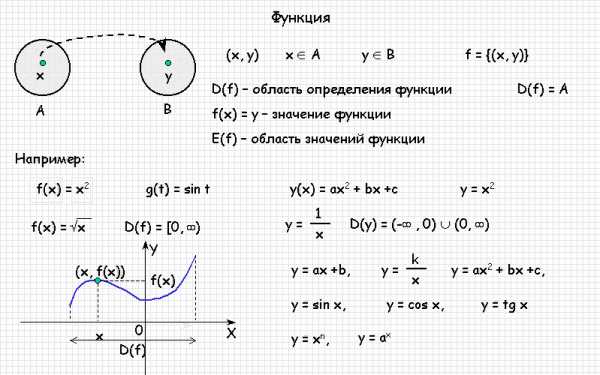
2. Практическая часть (работа на интерактивной доске).

А) Выбрать из заданных формул функции (аналитический способ задания функции).

Ученик с помощью ручки заполняет таблицу, если шаг его неверен, то формула принимает исходное положение на доске. Учитель просит пояснить учеников почему данная зависимость, записанная формулой не является функцией.

Б) Выбрать на рисунках графики функций (графический способ задания функции).

Аналогично, первому заданию ученик работает с ручкой над выбором правильного ответа. Учитель обращает внимание учеников, что не каждый график является функциональной зависимостью

В) Установить соответствие (возрастание и убывание функции на промежутках).

Учитель ведет диалог с учащимися, выясняет, когда функция возрастает на промежутке и убывает.

Г) Сортировка функций (аналитический способ задания функции). Ученик дает определение: четные, нечетные, ни четные и ни нечетные). Ученик используя инструмент ручка, производит сортировку данных функций.

Д) Сортировка функций (графический способ задания функции).

Е) Область определения функции, определить по графику.

Ж) Область определения функции, установить соответствие между формулой и заданными промежутками.

3. Решение проблемной ситуации.

Затем класс делится на группы, каждой дается индивидуальное задание, целью которых является повторить правила преобразования графиков функций у=х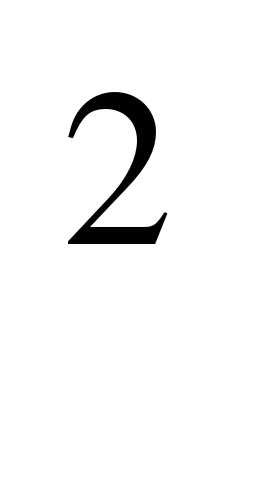 с помощью сжатия (растяжения) и параллельного переноса (используется программа построения графика функции Visual Basic 6.0.) Обратить внимание учащихся, что полученные знания в работе с данной программой помогут им на следующем уроке при построении преобразований синусоиды.

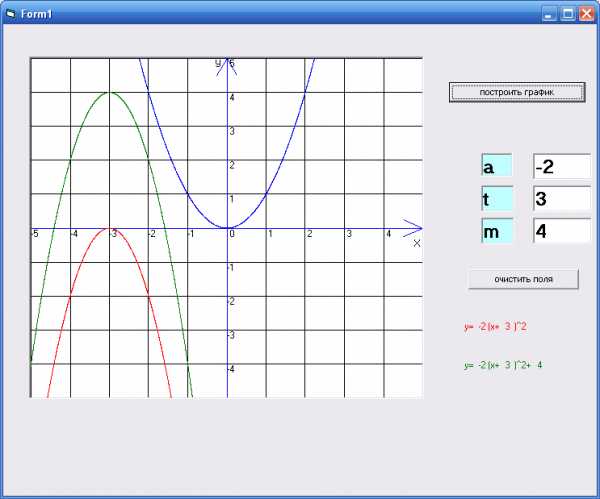
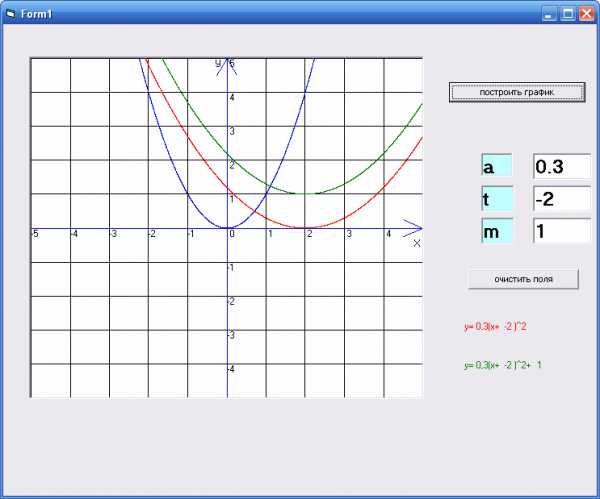
4. Интерактивная лабораторная работа.

1. Затем учащимся предстоит работа на интерактивной доске для различных элементарных функции показать их преобразование и построение на координатной плоскости.

2. По заданному графику функции записать формулу.

5. Творческая работа.

Учитель. На сегодняшнем уроке мы повторили свойства и преобразований графиков элементарных функции. Предлагаю вам самостоятельно составить формулу функции и написать алгоритм построения данного графика функции.

1. Сообщение учащихся сопровождается флипчартом. Группа учащихся в своем выступлении рассказывает как выполнили данное задание (защита).

2. Учитель математики. Завершает урок рефлексией.

Вывод: Оцените степень вашего усвоения материала:

1. усвоил полностью, могу применять

2. усвоил полностью, но затрудняюсь с применением

3. усвоил частично

4. не усвоил

1. Подводит итоги работы учащихся (отметки), дает пояснение по выполнению домашнего задания

2. Модель урока (2 час)

1. Мотивационный этап.

1.Организационный момент. Психологический настрой.

2.Сообщение темы и цели урока.

3. Побуждение. Проблемный вопрос.

2. Активизация знаний учащихся.

В начале урока проводиться тестирование, с целью выявить качество и уровень овладения знаниями и способами действий, обеспечить их оперативную коррекцию.

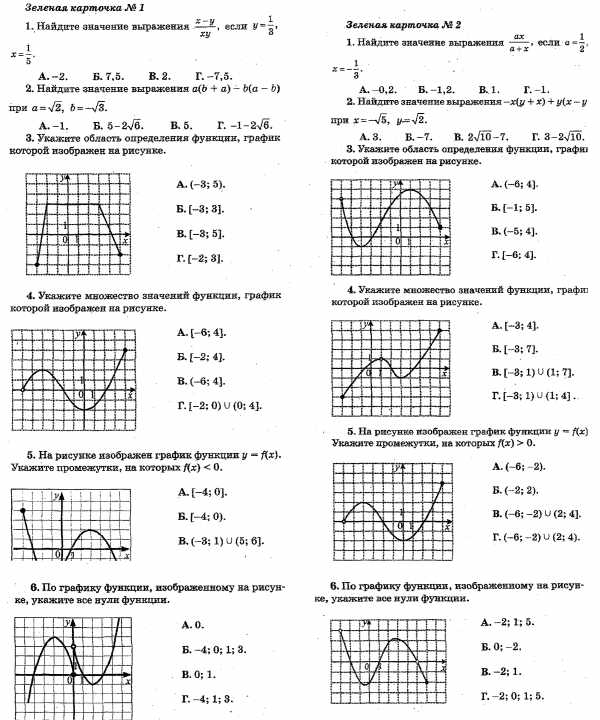
3. Изучение нового материала.

Диалогическое общение.

1. Блиц – опрос.

Свойства функции:

• Область определения функции

• Область значения функции

• Периодичность

• Четность, нечетность

• Нули функции

• Промежутки знакопостоянства

• Промежутки монотонности

• Наибольшее (наименьшее) значение функции

1. Углубление знаний.

Учитель показывает преобразование графиков функций у=sinх с помощью сжатия (растяжения) и параллельного переноса (используется программа построения графика функции Visual Basic 6.0.). Учащиеся делают выводы.

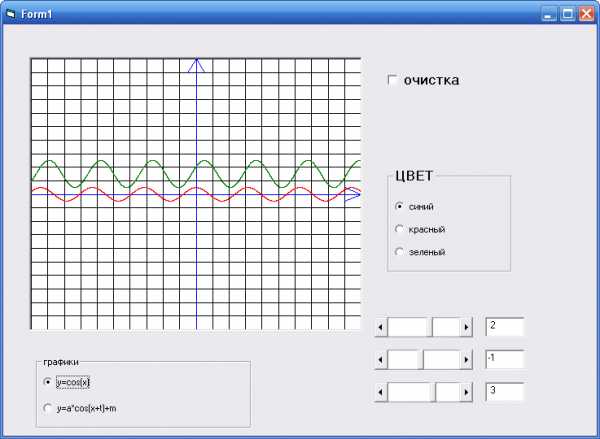
6. Практикум.

Затем учащимся предстоит работа на интерактивной доске для различных тригонометрических функции показать их преобразование и построение на координатной плоскости.

7. Работа в парах (взаимопроверка).

Учащиеся оценивают знания своего товарища.

6. Инструктаж по домашнему заданию.

• Выделение основного в домашнем задании.

• Изучение материала по новой теме

• Выполнение упражнений по новой теме

7. Подведение итогов урока.

1. Оценивание деятельности учащихся на уроке.

2. Выставление отметок в журнал

3. Слово учителю

3. Модель урока (3 час).

1. Мотивационный этап.

• Организационный момент: Приветствие и подготовка к уроку.

• Мотивация (Страница флипчарта 1)

2. Творческая работа (защита проекта).

1. Организация усвоения способов деятельности путем воспроизведения информации и упражнений в ее применении.

2. Творческое применение знаний и умений при построению графиков тригонометрических функций.

3. Использование разноуровневого дидактического материала.

3. Итоговая часть. Контроль.

1. На уроке можно ошибаться, сомневаться, консультироваться.

2. Дать самому себе установку: «понять и быть тем первым, который видит ход решения».

4.Рефлексия

1. Систематизация и обобщение знаний

2. Анализ усвоение учащихся программного материала

3. Выставление и корректирование отметок

4. Анализ проделанной на уроке работы

kopilkaurokov.ru

Свойства функции — Математика — 10 класс

Что такое функция.

Определение. Соответствия, при которых каждому элементу одного множества сопоставляется единственный элемент другого множества называются функциями.

Пишут: у = f(x), x Є X.

Переменную х называют независимой переменной или аргументом.

Множество всех допустимых значений независимой переменной является областью определения функции и обозначается D(y).

Переменную у – зависимой переменной .

Множество всех значений зависимой переменной является областью значений функции и обозначается Е(у ).

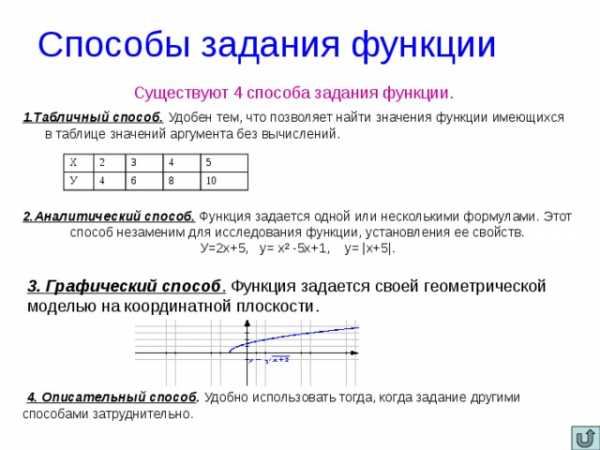
Способы задания функции

Существуют 4 способа задания функции.

1.Табличный способ. Удобен тем, что позволяет найти значения функции имеющихся в таблице значений аргумента без вычислений.

Х

2

У

4

3

4

6

5

8

10

2.Аналитический способ. Функция задается одной или несколькими формулами. Этот способ незаменим для исследования функции, установления ее свойств.

У=2х+5, у= х² -5х+1, у= |х+5|.

3. Графический способ . Функция задается своей геометрической моделью на координатной плоскости.

4. Описательный способ . Удобно использовать тогда, когда задание другими способами затруднительно.

§3

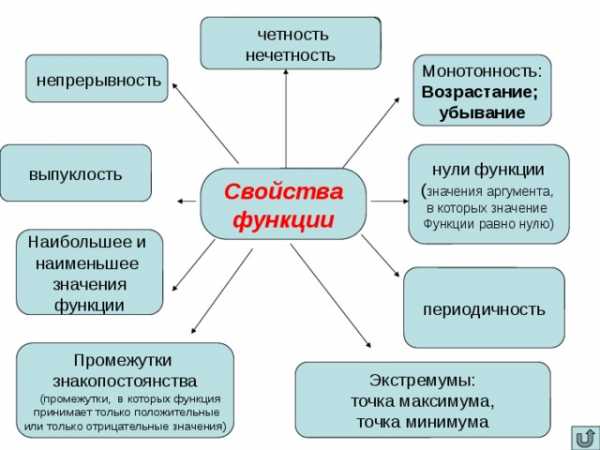
Свойства

функции

четность

нечетность

Монотонность:

непрерывность

Возрастание;

убывание

выпуклость

нули функции

( значения аргумента,

в которых значение

Функции равно нулю)

Наибольшее и

наименьшее

значения

функции

периодичность

Промежутки

знакопостоянства

(промежутки, в которых функция

принимает только положительные

или только отрицательные значения)

Экстремумы:

точка максимума,

точка минимума

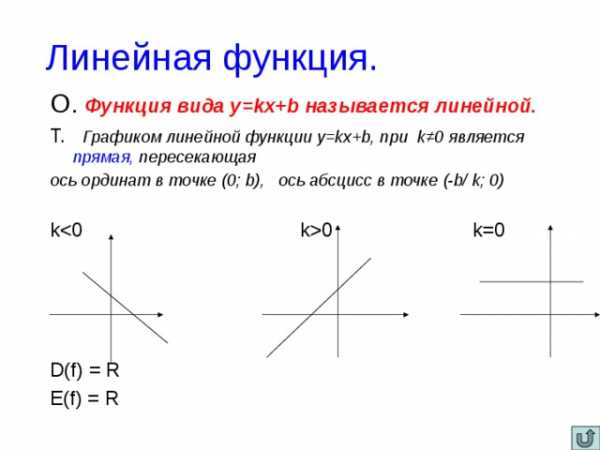
Линейная функция.

О. Функция вида y=kx+b называется линейной.

Т. Графиком линейной функции y=kx+b, при k ≠0 является прямая, пересекающая

ось ординат в точке (0; b), ось абсцисс в точке (-b/ k; 0)

k0 k=0

D(f) = R

E(f) = R

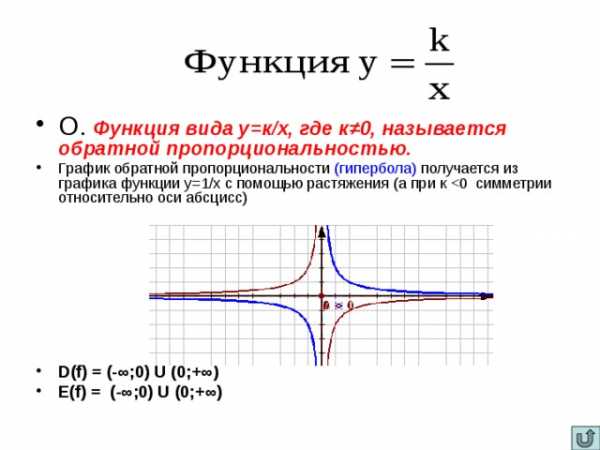
• О. Функция вида у=к/х, где к ≠0, называется обратной пропорциональностью.
• График обратной пропорциональности (гипербола) получается из графика функции у=1/х с помощью растяжения (а при к

• D(f) = (-∞;0) U (0;+∞)
• E(f) = (-∞;0) U (0;+∞)

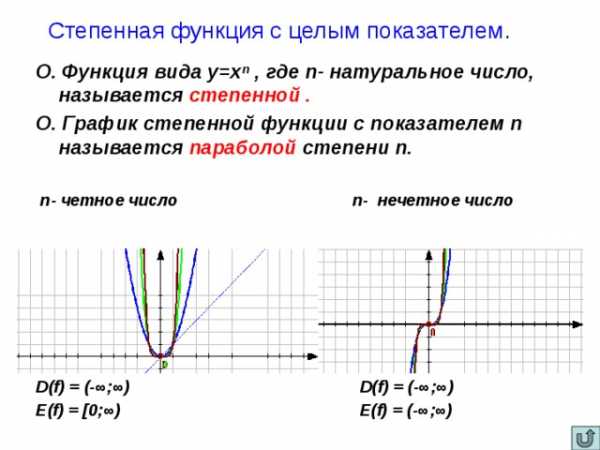
Степенная функция с целым показателем .

О. Функция вида у=х ⁿ , где n- натуральное число, называется степенной .

О. График степенной функции с показателем n называется параболой степени n.

n- четное число n- нечетное число

D(f) = (-∞;∞) D(f) = (-∞;∞)

E(f) = [0;∞) E(f) = (-∞;∞)

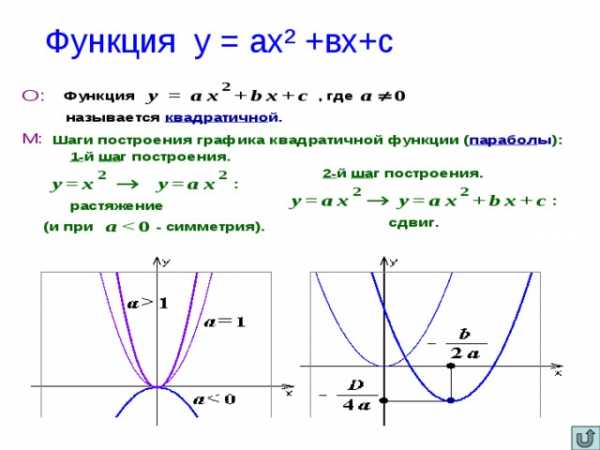
Функция у = ах² +вх+с

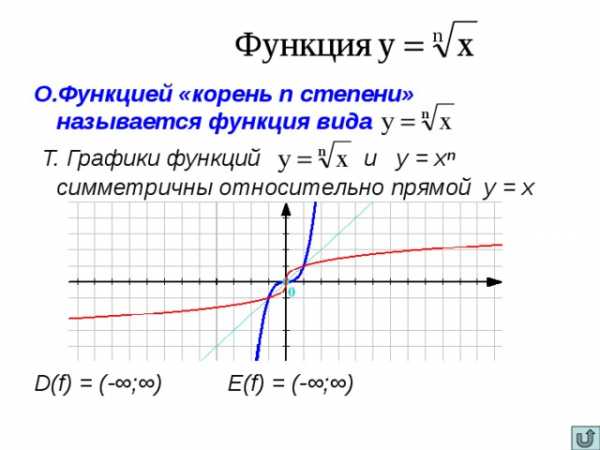
О.Функцией «корень n степени» называется функция вида

Т. Графики функций и у = хⁿ симметричны относительно прямой у = х

D(f) = (-∞;∞) E(f) = (-∞;∞)

Функция у = |х|

у= |х |= х, если х≥0

-х, если х Функция задается кусочно.

х

Т. Область определения функции

D( y)= (-∞; + ∞)

Множество значений функции

Е(у)= [0; + ∞)

Т. Функция у = |х | убывает

при х Є(-∞; 0]

возрастает при х Є [0; + ∞)

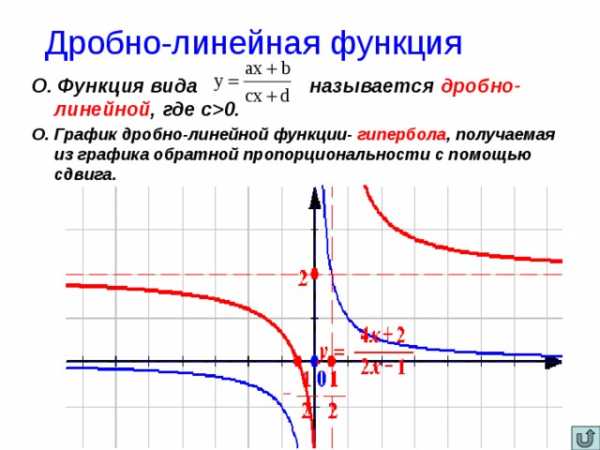0. О. График дробно-линейной функции- гипербола , получаемая из графика обратной пропорциональности с помощью сдвига. «

Дробно-линейная функция

О. Функция вида называется дробно-линейной , где с 0.

О. График дробно-линейной функции- гипербола , получаемая из графика обратной пропорциональности с помощью сдвига.

Нахождение области определения функции

1.

2.

3.

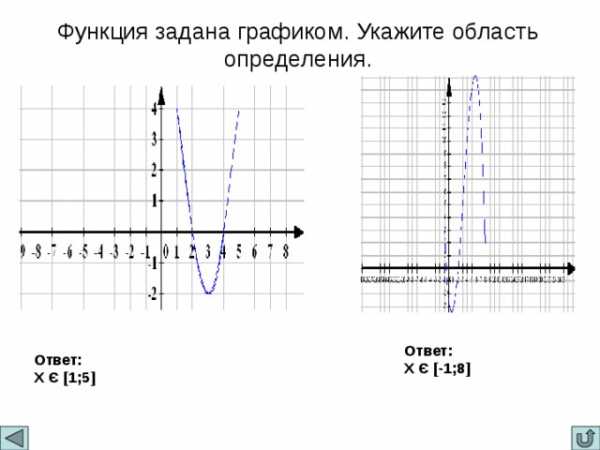
Функция задана графиком. Укажите область определения.

Ответ:

X Є [-1;8]

Ответ:

X Є [1;5]

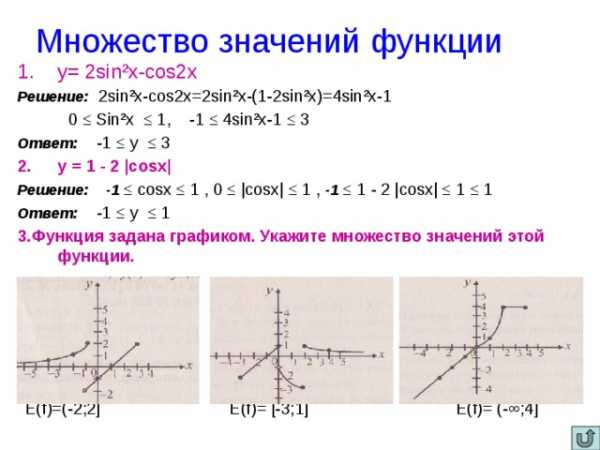
Множество значений функции

Решение: 2sin²x-cos2x=2sin²x-(1-2sin²x)=4sin²x-1

0 ≤ Sin²x ≤ 1, -1 ≤ 4sin²x-1 ≤ 3

Ответ: -1 ≤ у ≤ 3

Решение: -1 ≤ cosx ≤ 1 , 0 ≤ |cosx| ≤ 1 , -1 ≤ 1 — 2 |cosx| ≤ 1 ≤ 1

Ответ: -1 ≤ у ≤ 1

3.Функция задана графиком. Укажите множество значений этой функции.

E(f)=(-2;2] E(f)= [-3;1] E(f)= (-∞;4]

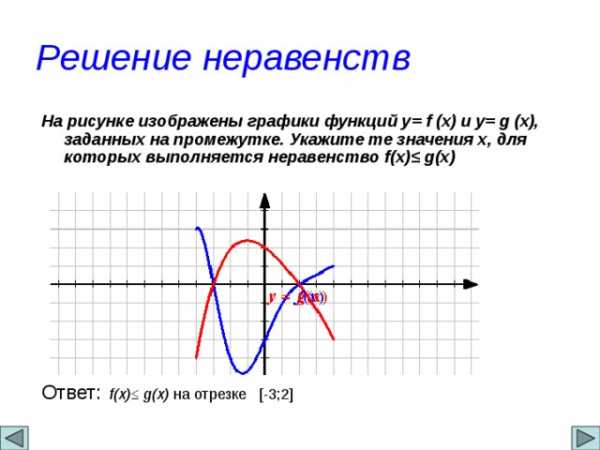
Решение неравенств

На рисунке изображены графики функций y= f (x) и y= g (x), заданных на промежутке. Укажите те значения х, для которых выполняется неравенство f(x) ≤ g(x)

Ответ: f(x)≤ g(x) на отрезке [-3;2]

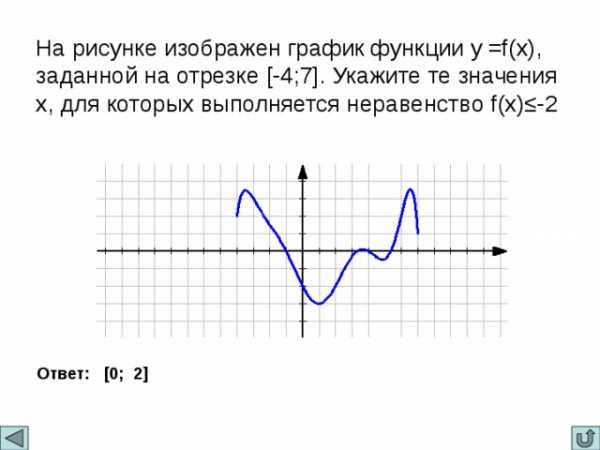
На рисунке изображен график функции у =f(x), заданной на отрезке [-4;7]. Укажите те значения х, для которых выполняется неравенство f(x)≤-2

Ответ: [0; 2]

Какие из данных линий являются функцией?

multiurok.ru

Урок по математике на тему «Числовые функции» (10 класс)

Тема урока «Функции. Свойства функций»

Цели урока:

Образовательные: систематизировать и обобщить знания о свойствах функций, развивать навыки построения и прочтения графиков функций;

Развивающие: развивать логическое мышление, умение делать обобщения и выводы;

Воспитательные: формирование умений работать в микро группах, способствовать воспитанию чувства успеха от интеллектуального труда.

Тип урока:урок обобщения и систематизации знаний.

Используемое оборудование :мультимедийный проектор, компьютер.

Используемые технологии: системно – деятельностный подход, развивающее обучение.

Форма организации деятельности учащихся: групповая, индивидуальная, фронтальная.

Структура урока:

Организационный момент.

Актуализация знаний.

Обобщение и систематизация знаний.

Применение знаний и умений в новой ситуации.

Контроль усвоения знаний, коррекция.

Рефлексия.

Организационный момент.

Современная математика их знает множество, и у каждой свой неповторимый облик, как неповторим облик каждого из людей, живущих на земле.

Её облик можно представить сложенным из набора характерных свойств.

О каком математическом понятии идет речь? (о функции)

Итак, центральное место занимает функция, (на магнитной доске учитель переворачивает кружок со словом – функция, это центр ромашки, на лепестках которой напечатаны известные учащимся функции).

А что же такое функция? (ученики дают определение).

Сформулируйте цель урока.

Учащиеся в тетрадях записывают тему урока «Свойства функций».

II. Актуализация знаний.

В течение 1 минуты посовещайтесь в парах и вспомните свойства функций. Затем каждая пара называет по 1 свойству.

Учащиеся называют:

-Область определения

-Множество значений

-Монотонность

-Ограниченность

-Наибольшее и наименьшее значения функции

-Непрерывность

-Нули функции

-Промежутки знакопостоянства

-Четность

Вопросы учащимся:

Какому свойству отведем центральное место? (область определения)

Дайте определения следующим понятиям:

1)область определения функции;

2)множество значений функции;

3)возрастание и убывание функции.

Остальные свойства функций мы вспомним с вами в ходе выполнения заданий в течение урока.

Обобщение и систематизация знаний.

Устная работа :

Задает ли указанное правило функцию ?

_{Какую информацию можно получить о функции?}

2. Устное задание «Найди ошибку»

Для построения графика любой функции необходимо уметь находить ее область определения. Вашему вниманию предлагается два способа нахождения области определения функции. Со всем ли вы согласны или есть ошибка в решении?

D (y):

Рассмотрим функцию

Найдем нули функции: x= — 3

┼ ─ ┼

● ○ x

— 3 2

Ответ:

D (y):

х

— 32

Ответ:

Поиск правильного решения данного задания.

3. Применение знаний и умений в новой ситуации.

Задание в группах:

1.Постройте график функции (Один ученик от любой группы работает у доски)

Задания по графику:

а) Найдите наибольшее и наименьшее значения функции на;

б) Укажите промежутки монотонности и знакопостоянства функции;

2.Найдите функцию, обратную функции . Постройте на одном чертеже графики указанных двух взаимно обратных функций.

3.Построить график функции .

Строить графики элементарных функций, которые заданы аналитическим способом, мы умеем. А я вам предлагаю сейчас изобразить «портрет незнакомки» по ее характерным деталям.

Учащимся раздаются листы (в группах одинаковое).

«Портрет незнакомки»

1. D(y) =

2. E(y) =

5. Нули функции х = — 1, х = 1, х = 3

6. у(2) = — 2, у(0) = 2

7. Функция возрастает на

8. Функция убывает на .

Все получившиеся портреты выставляются на доске. Краткий разбор портретов и вывод.

5. Контроль усвоения знаний, коррекция.

1. Математику нельзя изучать, наблюдая, как это делает сосед. Поэтому проверим свои знания с помощью теста, (выполняют тест по вариантам, проверка — презентация) см. приложение 2.( или блиц опрос).

2. Где в жизни находят применение графики? (кардиограмма сердца, график активности избирателей, график изменения температуры…).

6. Рефлексия.

Сегодня на уроке мы систематизировали наши знания о функциях, их свойствах и графиках. Повторили алгоритм исследования и чтения графика функции.

Сегодня на уроке:

• Я узнал …

• Я научился…

• Я повторил…

• Я закрепил…

А теперь попробуйте в группах изобразить график вашего настроения на уроке. Каждая группа поясняет свой график.

V.Домашнее задание.

(домашняя контрольная работа по карточкам)

Приложения

Приложение 1.

1. Найти область определения функции

а) б) в) г)

2. Найти область определения функции Ответ:_————

3. Найти область определения функции Ответ:_————

4. Какой из графиков, изображённых на рисунках, задаёт функцию у=f(х).

1) 2)

3) 4)

5. Среди заданных функций укажите возрастающие

1. 2) 3) 4)

а) 2 и 3 б) 1 и 2 в) 3 и 4 г) 1 и 4

6. Исследуйте на ограниченность функцию

а) ограничена сверху б) ограничена снизу

в) ограничена снизу и сверху г) не ограничена ни снизу, ни сверху

7. Среди заданных функций укажите чётные:

1) 2) 3) 4)

а) 1 и 2 б) 2 и 3 в) 1 и 3 г) 3 и 4

8. Найдите наименьшее значение функции . Ответ:_————

Приложение 2.

ВАРИАНТ 1.

1. Найти область определения функции

1) 2)

3) 4)

2. Функции заданы формулами:

а) б) в) г)

Какие из них являются возрастающими?

1. а и б 2) а и г 3) в и г 4) а, б и г

3. Какая из данных точек принадлежит графику функции ?

1. А( — 6; 3) 2) В(8; 2) 3) С( -3; — 6) 4) D(2; — 8)

3. Найдите наименьшее значение функции

1. 4 2) 0 3) не существует 4) 8.

3. Среди заданных функций укажите нечётные:

а) б) в) г)

1) а и б 2) б и г 3) а и в 4) в и г

ВАРИАНТ 2.

1. Найти область определения функции

1) 2)

3) 4)

2. Функции заданы формулами:

а) б) в) г)

Какие из них являются убывающими?

1. а и б 2) а и в 3) в и г 4) а, б и г

3. Какая из данных точек принадлежит графику функции ?

1. А( — 4; — 6) 2) В(- 6; 4) 3) С( 4; 8) 4) D(8; — 4)

3. Найдите наименьшее значение функции

1. 9 2) 0 3) не существует 4) 18

5. Среди заданных функций укажите чётные:

а) б) в) г)

1) а и в 2) б и г 3) а и б 4) в и г

Домашняя контрольная работа

1.Задает ли указанное правило функцию :

В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках -0,75; 0; 3.

в) постройте график функции;

г) найдите промежутки монотонности функции.

2. Исследуйте функцию на четность.

_3. периодическая функция с периодом Т = 2. Известно, что

а) Постройте график функции;

б) найдите нули функции;

в) найдите ее наибольшее и наименьшее значения.

4. Найдите функцию, обратную функции . Постройте

на одном чертеже графики указанных двух взаимно обратных функций.

infourok.ru

Обратная функция. Видеоурок. Алгебра 10 Класс

На этом уроке вы познакомитесь с понятием обратной функции. Научитесь решать прямые и обратные задачи и выясните, что для каждой монотонной функции существует обратная функция. А также узнаете, как связаны между собой графики прямой и обратной функций и разберетесь с методикой построения обратной функции и ее графика

Пусть задана функция , множество  и множество . Функция из  в :  Каждому элементу из первого множества  соответствует единственный элемент второго множества . С этой функцией связано две основные задачи:

1 задача – прямая. Вычислить значение функции по заданному значению аргумента.

задано, необходимо вычислить .

2 задача – обратная. Найти те значения аргумента, при которых функция принимает заданное значение . Задаем , далее необходимо решить уравнение , которое может иметь одно решение, второе решение и т. д. …

Пример обратной задачи: требуется найти время  для достижения ракетой заданной высоты, самолетом скорости звука, автомобилем заданной скорости 100 км/ч. Нас будет интересовать такая обратная задача, которая имеет единственное решение.

Пусть  – множество слов. Слово – конечная последовательность букв, смысл здесь не важен.  – множество слов из тех же букв, но записанных в обратном порядке.

Например: .

Итак, задана функция, два множества и соответствие между ними. Обратная задача для этой функции имеет единственное решение. Слову «ток» из множества  соответствует единственное слово «кот» из множества .

Пусть задано множество , состоящее из двух элементов  и множество , состоящее также из двух элементов

interneturok.ru

Построение графиков функций — урок. Алгебра, 10 класс.

построить график функции y=x2+1×2−1.

Решение 1. Введём обозначение: f(x)=x2+1×2−1. Найдём область определения функции. Она задаётся условиями x≠1,x≠−1. Итак, D(f)=(−∞;−1)∪(−1;1)∪(1;+∞).

2. Исследуем функцию на чётность:

f(−x)=−x2+1−x2−1=x2+1×2−1=f(x).

Значит, заданная функция чётна, её график симметричен относительно оси ординат, а потому можно для начала ограничиться построением ветвей графика при x≥0.

3. Найдём асимптоты. Вертикальной асимптотой является прямая \(x=1\), поскольку при этом значении \(x\) знаменатель дроби обращается в нуль, а числитель отличен от нуля. Для отыскания горизонтальной асимптоты надо вычислить limx→∞f(x):

limx→∞x2+1×2−1=limx→∞x2x2+1x2x2x2−1×2=limx→∞1+1×21−1×2=1.

 Значит, \(y=1\) — горизонтальная асимптота графика функции.

4. Найдём стационарные и критические точки, точки экстремума и промежутки монотонности функции:

y′=x2+1×2−1′=(x2+1)′⋅(x2−1)−(x2+1)⋅(x2−1)′x2−12=2x⋅(x2−1)−(x2+1)⋅2xx2−12==−4xx2−12.

Производная существует всюду в области определения функции, значит, критических точек у функции нет.

Стационарные точки найдём из соотношения y′=0. Получаем: \(-4x=0\) — откуда находим, что \(x=0\). При \(x<0\) имеем: y′>0; при \(x>0\) имеем: y′<0. Значит, \(x=0\) — точка максимума функции, причём ymax=f(0)=02+102−1=−1.

При \(x>0\) имеем: y′<0; но следует учесть наличие точки разрыва \(x=1\). Значит, вывод о промежутках монотонности будет выглядеть так: на промежутке 0;1) функция убывает, на промежутке (1;+∞) функция также убывает.

5. Составим таблицу значений функции f(x)=x2&plus;1×2−1 при x≥0:

6. Отметим найденные точки на координатной плоскости, учтя при этом, что \((0;-1)\) — точка максимума, что \(y=1\) — горизонтальная асимптота, что \(x=1\) — вертикальная асимптота, построим ветви искомого графика при x≥0. Добавив ветви, симметричные построенным относительно оси ординат, получим весь график.

www.yaklass.ru

Функции и графики — Математика — Теория, тесты, формулы и задачи

Оглавление:

Основные теоретические сведения

Координаты и базовые понятия о функциях

К оглавлению…

Длина отрезка на координатной оси находится по формуле:

Длина отрезка на координатной плоскости ищется по формуле:

Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:

Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.

Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.

Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).

Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.

Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.

Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.

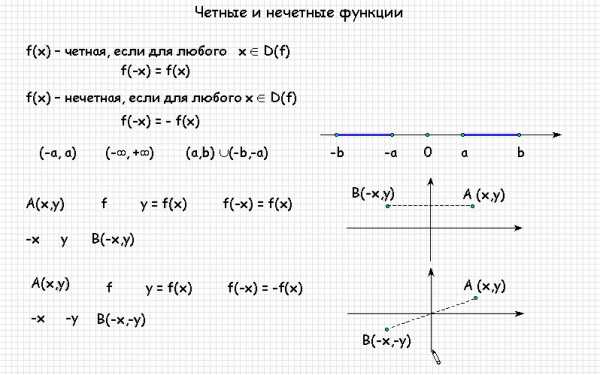
Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.

Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.

Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.

Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.

График линейной функции

К оглавлению…

Линейной функцией называют функцию, которую можно задать формулой:

График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):

График квадратичной функции (Парабола)

К оглавлению…

График параболы задается квадратичной функцией:

Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x₁; 0) и (x₂; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x₀; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):

При этом:

• если коэффициент a > 0, в функции y = ax² + bx + c, то ветви параболы направлены вверх;
• если же a < 0, то ветви параболы направлены вниз.

Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):

Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:

Графики других функций

К оглавлению…

Степенной функцией называют функцию, заданную формулой:

Приведем несколько примеров графиков степенных функций:

Обратно пропорциональной зависимостью называют функцию, заданную формулой:

В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:

Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.

Показательной функцией с основанием а называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):

Логарифмической функцией называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:

График функции y = |x| выглядит следующим образом:

Графики периодических (тригонометрических) функций

К оглавлению…

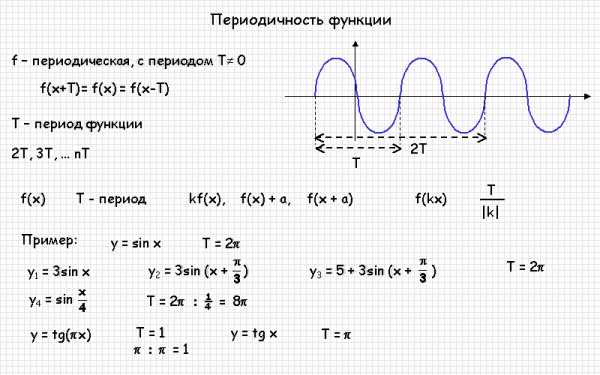
Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x). Если функция f(x) является периодической с периодом T, то функция:

где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T₁, который определяется формулой:

Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:

График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:

График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

educon.by

Презентация к уроку по алгебре (10 класс) на тему: Презентация по теме «Определение числовой функции»

Слайд 1

ОПРЕДЕЛЕНИЕ ЧИСЛОВОЙ ФУНКЦИИ И СПОСОБЫ ЕЕ ЗАДАНИЯ. СВОЙСТВА ФУНКЦИИ.

Слайд 2

Определение Если даны числовое множество Х и правило f , позволяющее поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят, что задана функция у= f(x) с областью определения Х. Пишут: у= f(x) , х ∈ Х. (Область определения обозначают D( у)) Переменную х называют независимой переменной или аргументом , а переменную у – зависимой переменной . Множество значений функции у= f(x) , х ∈ Х называют областью значений функции и обозначают Е(у )

Слайд 3

Задание Найдите область значения функции Задание Найдите область определения функции

Слайд 4

Определение Если дана функция у= f(x) , х ∈ Х и на координатной плоскости хОу отмечены все точки вида ( х;у ), где х ∈ Х, а у= f(x) , то множество этих точек называют графиком функции у= f(x) , х ∈ Х. Если известен график функции у= f(x) , х ∈ Х, то область (множество) значений функции можно найти, спроецировав график на ось ординат.

Слайд 5

Задание Найдите D(y), E(y)

Слайд 6

Определение Функцию у= f(x) называют возрастающей на множестве Х ⊂ D ( f ) , если для любых точек x 1 и x 2 множества Х, таких, что x 1 f ( x 2 ) Термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность

Слайд 8

Определение Функцию у= f(x) называют ограниченной снизу на множестве Х ⊂ D ( f ), если все значения этой функции на множестве Х больше некоторого числа. (Если существует такое число m , что для любого значения x ∈ X выполняется неравенство f(x)>m ) Определение Функцию у= f(x) называют ограниченной сверху на множестве Х ⊂ D ( f ), если все значения этой функции на множестве Х меньше некоторого числа. (Если существует такое число m , что для любого значения x ∈ X выполняется неравенство f(x)

Слайд 11

Определение Число m называют наименьшим значением функции у= f(x) на множестве Х ⊂ D ( f ), если: 1) во множестве Х существует такая точка x 0 , что f( x 0 )=m ; 2) для любого значения х из множества Х выполняется неравенство f ( x ) ⩾ f( x 0 ) Определение Число m называют наибольшим значением функции у= f(x) на множестве Х ⊂ D ( f ), если: 1) во множестве Х существует такая точка x 0 , что f( x 0 )= М; 2) для любого значения х из множества Х выполняется неравенство f ( x ) ⩽ f( x 0 )

Слайд 12

Точку x 0 называют точкой максимума функции у= f ( х ), если у этой точки существует окрестность, для всех точек которой (кроме самой точки x 0 ) выполняется неравенство f ( x ) f( x 0 )

nsportal.ru