Урок по алгебре и наачалам анализа 10 класс
|
Дата: |
|||
|
Тема: Решение тригонометрических уравнений 2 урока |
|||
|
Цели: сформировать навыки в решении простых тригонометрических уравнений Задачи учащиеся должны: — знать – формулы нахождения корней тригонометрических уравнений; — находить корни уравнения Критерии успешности: -знают формулы нахождения корней тригонометрических уравнений; -находят корни уравнения |
|||
|
Деятельность учителя |
Деятельность учащихся |
наглядности |
|
|
3 мин. |
I. Организационный момент. Приветствует учеников, проверяет готовность к уроку, желает успеха. Для создания |
Ученики осмысливают поставленную цель. |
|
|
10 мин. |
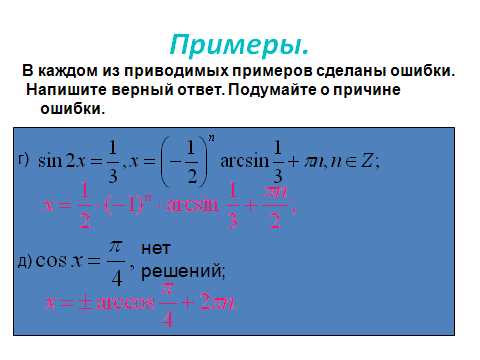
II. Проверка домашней работы. Проверка домашней работы. взаимопроверка тетрадей 1 теоритический материал при помощи постера Критерии для создания постера 1 Какой вид у данной функции. Ее свойства. График 2 Для нахождения нулей функции используется формула. 3 Рассмотреть случаи, когда а ≤, ≥ 0 4 Частные случаи. Оценивание постеров группами 2 устный счет, проверка знаний формул Вы видите 8 формул. Определите, какие из них записаны не верно. 1. sin x =, – 1 1, x= (– 1) n arcsin + n, nÎZ; 2. cos x =, – 1 1, x= ± arccos+ n, nÎZ; 3. tg x=,x= arctg + n, nÎZ; 4. ctg x=,x= arcctg + 2n, nÎZ; 5. arccos () =– arccos ; 6. arcsin (–)= arcsin ; 7. arcctg (–)=–arcctg ; 8. arctg (–)=–arcctg ; 3«Лови ошибку»
4 Составить Пазл Приложение (закрепление пройденного материала) |
Ученики проверяют дом работу. Рисуют постер защищают находят ошибки |
Бумага А3, маркеры |
|
мин. |
Актуализация знаний. С помощью метода «Джиксо» осуществляется изучение решение уравнений со сложным аргументом. 1 гр Решить уравнение 2cos (4x — π/6) = √3 2 гр Решить уравнение sin(2x — π/3) = — 0,5 3 гр Решить уравнение tg() = -3 |
Демонстрируют свои знания. Изучают данный материал, объясняют одноклассникам решениеуравнений Решают на месте и у доски |
карточки |
|
5 мин. |
IV. Закрепление урока Практическая часть Задание для группы: Дополнительно |
. |
Карточки |
|
5 мин. |
V. Итог урока. Проводит рефлексию. Стратегия «Телеграмма» — Что нового я узнал на уроке? Обратная связь «Нарядить новогоднюю елку» |
стикеры елка, вырезанные игрушки |
|
|
2 мин. |
VI. Домашняя работа
|
Записывают домашнюю работу в дневниках. |
|
Приложение








Изучение способов решения уравнений
1 группа
Решить уравнение
2cos (4x — π/6) = √3
Делим обе части уравнения на 2, получаем
cos (4x — π/6) = , неизвестен аргумент 4х —
Используя формулу сosx = ±arccosa +2, получаем
4х — = ±arccos +2,
4х — = , неизвестно 4х – значит переносим в правую часть с противоположным знаком
4х = , так как у неизвестного есть коэффициент (в данном случае 4), делим на него обе части.
Получаем х= Данный ответ в общем виде, если же необходимо записать ответы данного уравнения, то данный ответ разбивается на два
-
х = + , выполняем действия для двух первых слагаемых
х = + впервом слагаемом выполняем сокращение на 2
х=
-
х = — + , выполняем действия для двух первых слагаемых
х = ,
Ответ х= , х =
Решите сами
cos (2x- ) = 1 (ответ х1= x2=)
2 группа
Решить уравнение
sin(2x — π/3) = — 0,5
неизвестен аргумент 2х —
Используя формулу sinx = (-1)k+1 arcsin a +, так как а отрицательно получаем
2х — = (-1)k+1 arcsin 0.5 +,
2х — = (-1)k+1 +, неизвестно 2х – значит переносим в правую часть с противоположным знаком
2х = (-1)k+1 + +, так как у неизвестного есть коэффициент (в данном случае 2), делим на него обе части.
Получаем х= (-1)k+1 + +
Ответ х= (-1)k+1 + +
Решите сами
sin(2x — ) = — Ответ х= (-1)k+1
3 группа
Решить уравнение
tg() = -3
Обратите внимание на аргумент (), это формула приведения, так как половинный аргумент, то функция тангенса меняется на кофункцию то есть на котангенс. Данный угол находится в третьей четверти, а котангенс в этой четверти положителен , то получим
tg = -3 , разделим обе части на , получим
сtg = , избавимся от иррациональности в знаменателе
сtg = ,
сtg = ,
сtg = , сократим на 3
сtg = — , так как а отрицательное, то спользуем формулу
сtg = — а, х = tga )+ Тогда
2х =( tg +
2х = )+ , выполним действие в скобках
2х = + , разделим на коэффициент 2
х = +
Ответ х = +
Решите сами
tg() = 1
Дополнительное задания на урок:
Лист успеха
Наблюдал – 0,
Составлял – 1,
Озвучивал — 1
Составления постера
Предлагал идею – 1
Выполнял постер -1
«Лови ошибку»
Нашел — 0,5
2- 1
3 — 2
Изучение нового материала
Решил уравнение – 2
Помогал членам группы разобраться с решением – 1
Объяснял другой группе — 1
Решение уравнений
Решил уравнение
(каждое уравнение 1 балл)
-
9 баллов и выше – «5», 7-8 баллов –«4», 5-6 баллов – «3»
infourok.ru
Авторские разработки уроков с презентационным материалом, календарным планированием и Фосами. «Алгебра
Алгебра и начала математического анализа – 10 класс Урок № 70
Тема: «Простейшие показательные неравенства».
Цели урока:
Дидактические
-
Развивать вычислительные навыки при решении показательных уравнений и неравенств.
-
Сформировать понятие показательного неравенства.
-
Рассмотреть два способа решения показательных неравенств (уравнивание оснований и вынесение наименьшего множителя за скобки) и научиться их решать, пользуясь алгоритмом.
-
Проконтролировать степень усвоения материала по теме.
-
Подготовка к ЕГЭ.
Развивающие:
-
Способствовать развитию навыка самостоятельного применения знаний.
-
Развивать навыки самоконтроля.
-
Продолжить работу по развитию логического мышления и устной математической речи при поиске решения поставленной проблемы.
Воспитательные:
-
Приучать к умению общаться и выслушивать других.
-
Воспитывать внимательность и наблюдательность.
-
Стимулировать мотивацию и интерес к изучению математики.
Оборудование: презентация, интерактивная доска, учебник.
Ход урока.
-
Организационный момент. (слайд 1)
– Мы не раз убеждались в том, что математика – это универсальный иностранный язык, на котором общаются все страны и все народы. Но для такого международного общения нужно знать математику. И эпиграфом нашего урока будут слова Альберта Эйнштейна: «Мне приходится делить своё время между политикой и решением уравнений и неравенств. Однако решение уравнений и неравенств, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения и неравенства будут существовать вечно». Давайте продолжим изучение этого вечного универсального математического языка.
-
Актуализация опорных знаний. Повторение.
-
Проверка выполнения домашнего задания. Разбор нерешенных заданий.
-
Повторение.
1 ) тест с самопроверкой (слайд 2)
) тест с самопроверкой (слайд 2)
1. Какая из показательных функций возрастает?
А) 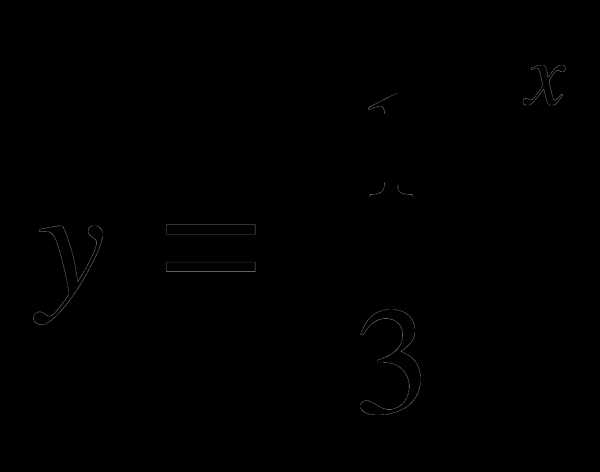 Б)
Б) 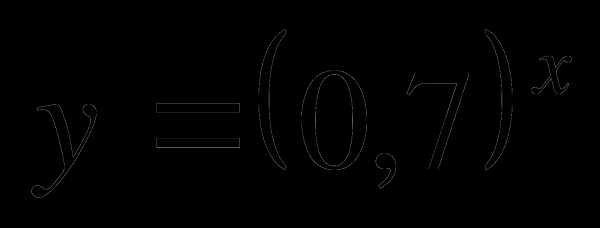
В) 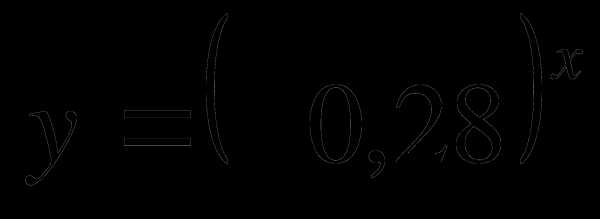 Г)
Г) 
2. График какой функции изображен на рисунке?
А)  Б)
Б) 
В) 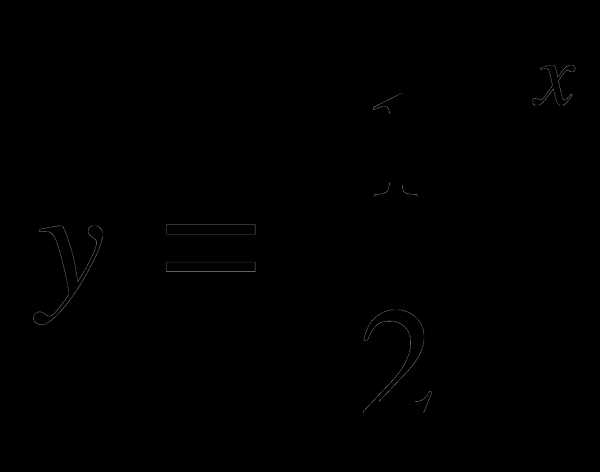 Г)
Г) 
3. Решите уравнение 3х =27
А) 3 Б) 9 В) 4 Г) нет решений
4. Решите уравнение 7х = 0
А) 0 Б) 1 В) — 7 Г) нет решений
5. Решите уравнение 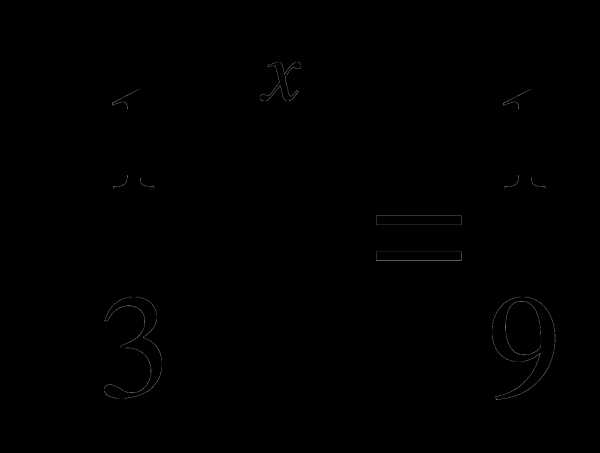
А) — 2 Б) 2 В) 3 Г) — 3
6. Решите уравнение 3х =5х
А) 2 Б) 0,5 В) 0 Г) нет решений
7. Решите уравнение 
А) 3 Б) 1 В) -3 Г) — 1
8. Решите уравнение 
А)  Б)
Б) 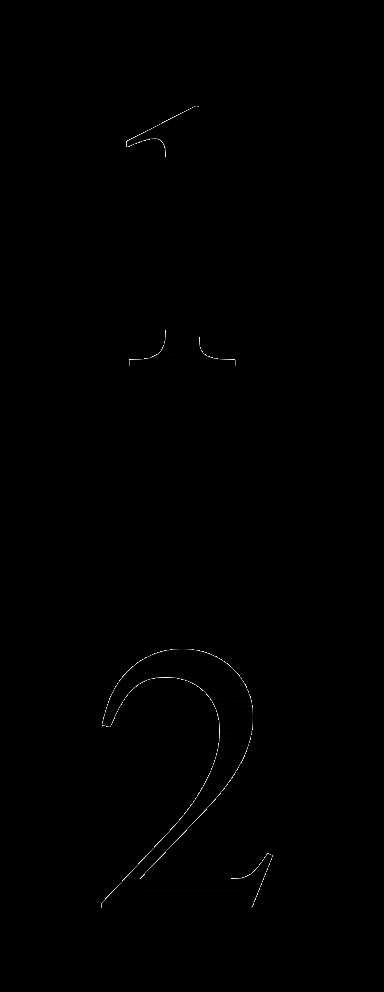 В) 1 Г) — 1
В) 1 Г) — 1
9. Решите уравнение 6(х-1)(х+2) = 1
А) -1; 2 Б) 1; — 2 В) 5; 8 Г) нет решений
Ответы: Г; В; А; Г; Б; В; А; А; Б. – самопроверка.
Критерии оценок: (работы сдаются учителю)
-
«5» — 9
-
«4» — 7 — 8
-
«3» — 5 – 6
-
«2» — 0 – 4
2) Фронтальный опрос
1) Как называются уравнения, которые вы решали в тесте? (Показательные)
2) Какие уравнения называются показательными? (Уравнения, содержащие неизвестную в показателе степени)
3) Дайте определение показательной функции. (Функция вида y = ax, где а>0, a≠1 называется показательной)
4) Как аналитически определить, возрастает или убывает показательная функция? ( Если а>1, то возрастает, если 0<а<1, то убывает)
5) Приведите примеры, где в жизни и на практике мы встречаемся с показательной функцией. (Уравнения органического роста, радиоактивный распад, ЛСД и т.д.)
3) Задача проблемного характера (слайд 3)
— Давайте рассмотрим ещё один пример процесса, где используются знания о показательной функции.
Рост древесины происходит по закону: y = y0∙ at, где t – время, y0 – начальное количество древесины, y – изменяющееся со временем количество древесины, а = const ≈ 1,2.
За какое время t количество древесины y не превышает 1000 м3, если её начальное количество y0 25 м3.
— Как решается эта задача?
Отвлечёмся от биологического процесса органического роста и запишем задачу на языке математики.
1000 ≥ 25∙ (1,2)t
Чтобы вычислить множество значений t надо уметь решать показательные неравенства.
-
Изучение нового материала.
Целеполагание ( слайд 4)
Поэтому тема урока:
Показательные неравенства (запись в тетради темы и даты урока).
— Сегодня на уроке мы рассмотрим 2 способа решения показательных неравенств, научимся их решать, пользуясь алгоритмом, чтобы потом применять их на практике.
Решить задачу мы сможем в конце урока.
1) Определение показательного неравенства. (слайд 5-6)
— Попробуйте сами дать определение показательного неравенства (запись в тетрадь).
Определение: Показательные неравенства – это неравенства, в которых неизвестная находится в показателе степени.
Слово «показательные» объяснили. А переведите на математический язык слово «неравенства»? (Алгебраические выражения, содержащие знаки >, < , ≥ , ≤ )
Определение:
Неравенство вида ах > ab ,где а>0, a≠1 называется простейшим показательным неравенством.
— Что значит решить неравенство? (найти множество его решений или установить, что их нет)
— Как решить простейшее показательное неравенство?
Рассмотрим график функции y=ax при a>1 и произвольное значение этой функции аb, где b – любое действительное число.
— Каким свойством обладает данная функция? (возрастает).
— Тогда при каких значениях переменной х ax < ab (ниже)? (при х < b).
— А при каких ax > ab (выше)? (при х > b).
Таким образом, если показательная функция возрастает, то знак неравенства сохраняется.
(Аналогично рассмотреть при 0<а<1).
2) 1 способ: Уравнивание оснований (слайд 7)
— Именно на свойствах возрастания и убывания показательной функции основан первый способ решения показательных неравенств – уравнивание оснований (в тетрадь).
Неравенство аf(x) > ag(x), где а>0, a≠1 будет равносильно неравенству
при а>1 (y = ax возрастает) при 0<а<1 (y = ax убывает)
f(x)>g(x) f(x)<g(x)
(знак неравенства сохраняется) (знак неравенства изменяется на противоположный)
В тетрадь : при а>1, y = ax возрастает, то при 0<а<1, y = ax убывает, то
знак неравенства сохраняется знак неравенства изменяется
Практические задания:
1) 3х > 9; 2) 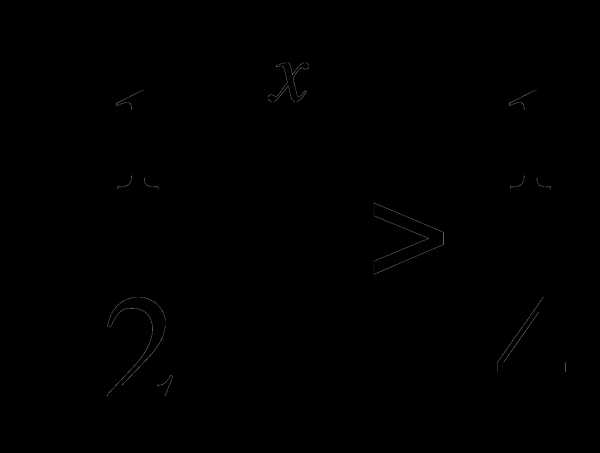 ; 3)
; 3)  ; 4) 4х <
; 4) 4х <  .
.
5) 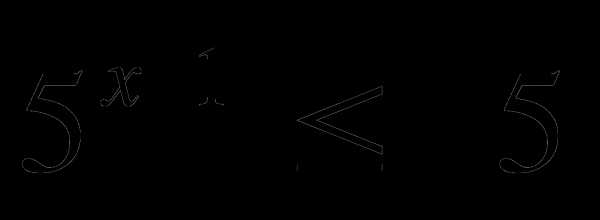 — учитель; 6)
— учитель; 6) 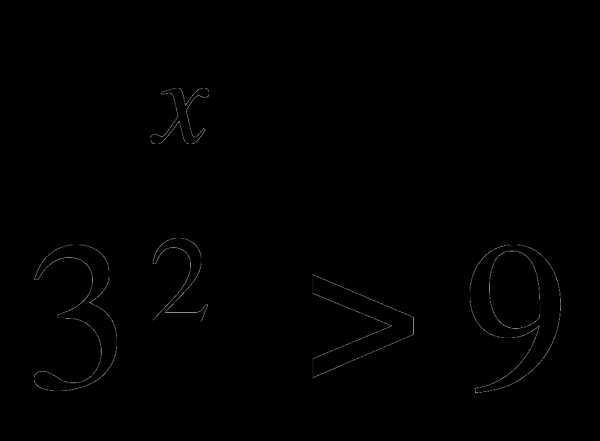 — обучающийся; 7)
— обучающийся; 7) 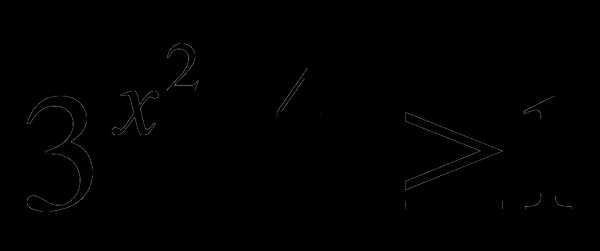 — обучающийся.
— обучающийся.
8) 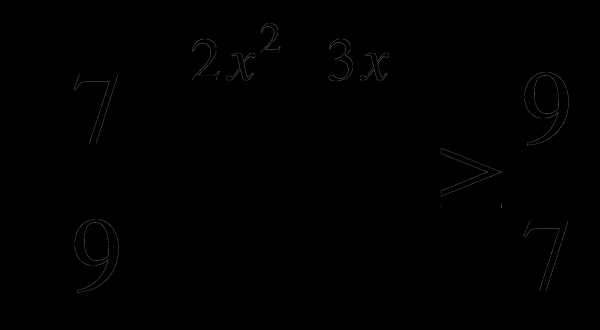 — сильный обучающийся; 9)
— сильный обучающийся; 9)  — дополнительное задание.
— дополнительное задание.
3) 2 способ: Вынесение наименьшего множителя за скобки. (слайд 8)
— Данные показательные неравенства решаются по тому же алгоритму, что и показательные уравнения, но не забываем о знаке неравенства в зависимости от основания показательной функции.
№ 1 письменно на доске
1) 3х+2+ 3х-1 < 28 – учитель; 3) 22х-1 + 22х-2 + 22х-3 ≥ 448 – обучающийся.
4) Решение задачи (слайд 9)
— Теперь мы сможем решить задачу и вычислить время t.
1000 ≤ 25∙ (1,2)t | :25≠0
40 ≤ (1,2)t 40≈(1,2)20
(1,2)20 ≤ (1,2)t.
а = 1,2 > 1, то y = at возрастает
20 ≤ t , т.е. время не превышает 20 лет.
Математический более точный ответ можно записать с помощью логарифмов (t ≥ log1,240), изучением которых мы займёмся на последующих уроках.
-
Анализ достижений и коррекция деятельности. (слайд 10)
1) Разноуровневая самостоятельная работа (тетради собрать на проверку)
Решить неравенства:
1) 3х+1 > 9
2) 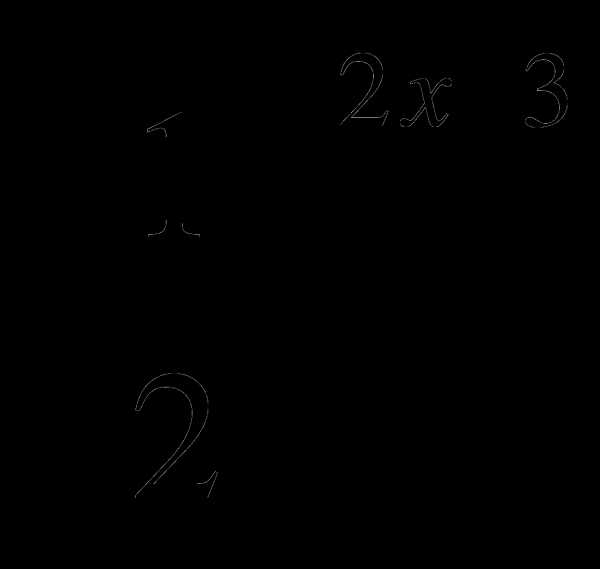 ≤ 4
≤ 4
3) 5х-1 – 5х + 5х+1 ≥ 21
2) Вопрос на «засыпку»: Решите неравенства (устно) 2х-1 ≤ — 3 и 72х ≥ 0.
-
Подведение итогов урока. Рефлексия. (слайд 11)
Подвести итоги урока, сделать основные выводы, выставить отметки обучающимся за урок.
— Довольны ли вы своей работой на уроке?
— Какой этап урока вам наиболее понравился?
— Где вам пришлось труднее всего?
Математику мы на слух воспринимать не можем, нам нужно обязательно увидеть, как решается задача или пример. А понимаем и усваиваем её только тогда, когда решаем задания сами. Поэтому попробуйте закончить предложение китайской мудрости:
«Я слышу — я забываю, я вижу — я запоминаю, я делаю — …(я усваиваю)».
-
Домашнее задание: п. 6.4, разобрать примеры 4; 5 и выполнить № 6.34 (а, д), № 6.35 (а, г).
infourok.ru
Контрольные работы по алгебре 10 класс.
Контрольная работа №2
Показательная и логарифмическая функции
Вариант 1
А1. Вычислите 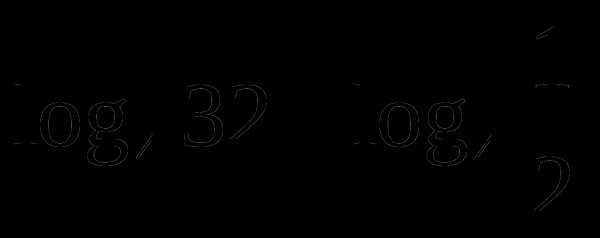 .
.
А2. Решите уравнение: а) ; б) .
А3. Решите неравенство .
А4. Найдите область определения функции .
В1. Решите уравнение .
В2. Решите уравнение .
С1. Решите уравнение .
Нормы оценок: «3» — любые 4А, «4» — 3А + 1В, «5» — 3А + 1В +1С или 5А + 2В.
______________________________________________________________________
Контрольная работа №2
Показательная и логарифмическая функции
Вариант 2
А1. Вычислите 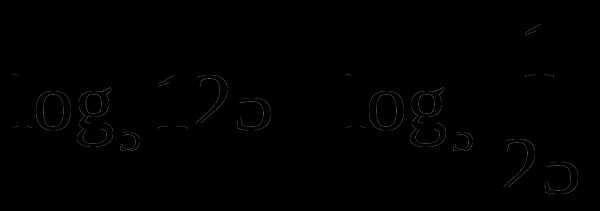 .
.
А2. Решите уравнение: а) 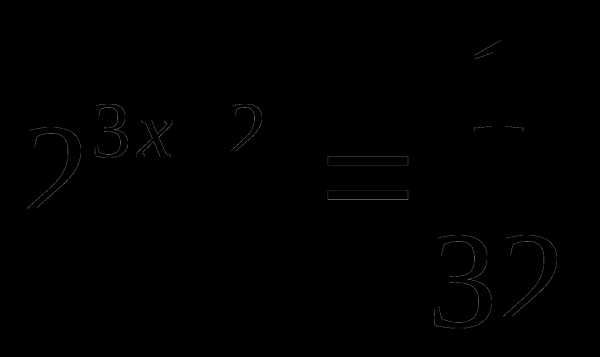 ; б) .
; б) .
А3. Решите неравенство .
А4. Найдите область определения функции .
В1. Решите уравнение .
В2. Решите уравнение .
С1. Решите уравнение .
Нормы оценок: «3» — любые 4А, «4» — 3А + 1В, «5» — 3А + 1В +1С или 5А + 2В.
Контрольная работа №2
Показательная и логарифмическая функции
Вариант 3
А1. Вычислите .
А2. Решите уравнение: а)  ; б) ; в) .
; б) ; в) .
А3. Решите неравенство .
А4. Найдите область определения функции .
В1. Решите уравнение .
В2. Решите уравнение .
С1. Решите уравнение .
Нормы оценок: «3» — любые 4А, «4» — 3А + 1В, «5» — 3А + 1В +1С или 5А + 2В.
__________________________________________________________________________________
Контрольная работа №2
Показательная и логарифмическая функции
Вариант 4.
А1. Вычислите .
А2. Решите уравнение: а)  ; б) ; в) .
; б) ; в) .
А3. Решите неравенство .
А4. Найдите область определения функции .
В1. Решите уравнение .
В2. Решите уравнение .
С1. Решите уравнение .
Нормы оценок: «3» — любые 4А, «4» — 3А + 1В, «5» — 3А + 1В +1С или 5А + 2В.
infourok.ru
Отзыв об уроке по алгебре и началам анализа в 10 классе по теме «Уравнения».
Отзыв об уроке
по алгебре и началам анализа в 10 -А классе учителя математики высшей квалификационной категории МОУ «Школа №2» города Алушта по теме «Уравнения». Дата проведения 22.11.16 года.
Весна Лилия Анатольевна продемонстрировала дидактически и методически грамотный урок с высоким развивающим потенциалом. Тип урока – урок систематизации знаний и закрепления нового материала. В начале урока учитель сообщила тему и цель урока, создала благоприятный психологический микроклимат, настрой на четкую и организованную работу.
Цели и задачи урока достигнуты благодаря мастерству педагога, продуманной смене деятельности учащихся и тщательному отбору материала.
Для активации знаний учащихся (повторение видов уравнений и методов их решения) использовались принципы доступности, наглядности, научности.
Учитель мастерски вёл учащихся к цели через создание проблемных ситуаций и способы их разрешения, постоянно предлагая ученикам право выбора или несколько способов решения уравнений.
Повторение материала выстроено логично, оптимально по содержанию, разнообразно по средствам, приемам, методам обучения, способам организации учебной деятельности.
В ходе урока учитель развивает логическое мышление, интеллектуальные способности учащихся, познавательный интерес, применяя элементы современных образовательных технологий: проблемного, поисково-исследовательского, личностно-ориентированного.
Учитель умело направляет самостоятельную работу учащихся по закреплению умений решать простейшие уравнения, используя групповую форму работы, где сильный ученик помогает слабым.
Доступность материала, хороший темп урока, активность учащихся позволили учителю охватить большой объём материала: от линейных уравнений до уравнений с параметрами.
В конце занятия для отработки полученных знаний учащиеся использовали Интернет-ресурсы для подготовки к ЕГЭ: http://inf.reshuege.ru/manual — образовательный портал для подготовки к экзаменам. Выполнение тестовых заданий позволило ученикам закрепить полученные знания.
Хочется отметить партнёрский стиль общения учителя и учеников, что создаёт комфортную обстановку на уроке, позволяет учащимся свободно участвовать в обсуждении проблем, задавать вопросы, предлагать свои способы решения, проводить рефлексию своей деятельности. Урок получился интересным и методически насыщенным.
Руководитель городского МО учителей математики: Ярошко Л.Н.
infourok.ru
План конспект урока №1- №2. Алгебра 10 класс. Базовый уровень
План конспект урока № 1 – 2 . (1 четверть). Алгебра 10 класс.
Определение числовой функции и способы ее задания.
УМК Мордкович А.Г. Базовый уровень.
Цели урока:
-
Повторить определение функции, область определения, область значений функции
-
Вспомнить определение графика функции
-
Разобрать способы определения функции (аналитический, графический, табличный, словесный)
-
Развитие творческой самостоятельности мышления учащихся.
Ход урока.
-
Решите неравенство а) , б)
В) г)
-
Определение функции, область определения область значений функции.
Г) постройте график этой функции
-
Решить упражнения: № 1.1(а, б), №1.2(а, б), № 1.4 – 1.8(а, б)
-
Самостоятельная работа (найти область определения функции)
I вариант.
№1. Дана функция: .
Найдите значения х, при которых: а) ; б) ; в) ; г) .
№2. Найдите область определения функции: .
№3.Построить график функции (учебник А9кл. № 11.24, стр.78)
II вариант.
№1. Дана функция: .
Найдите значения х, при которых: а) ; б) ; в) ; г) .
№2. Найдите область определения функции: .
№3. Построить график функции. (учебник А9кл. № 11.23, стр.78)
-
Домашнее задание: № 1.1(в), №1.2 (в), №1.4 (в), №1.5 (в, г), №1.6 (в, г) № 1.19, № 2.13
infourok.ru
Алгебра 10 класс «Показательная функция»
ДОНЕЦКАЯ НАРОДНАЯ РЕСПУБЛИКА
УПРАВЛЕНИЕ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ ГОРОДА ДОНЕЦКА
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ШКОЛА № 89 ГОРОДА ДОНЕЦКА»
10 класс
алгебра и начала математического анализа
Обобщение и систематизация знаний по теме: «Показательная функция»
Подготовила:
учитель математики
Тронь Раиса Алексеевна
Донецк-2017
Алгебра и начала математического анализа
Тема: Обобщение и систематизация знаний по теме: «Показательная функция».
Цели: обобщить и систематизировать знания учащихся по теме: «Показательная функция», формировать умения применять знания на практике.
Ход урока
-
Проверка домашнего задания
№ 225 (1; 2) – учащиеся объясняют с места
№ 226 (1) – выполняет один ученик на доске, после чего учащиеся проверяют задание.
Ответ: 1, 2.
№ 220 – выборочная проверка. Из 4 уравнений учащиеся объясняют и комментируют основные тапы решения
-
Ответ: 1.
-
Во время проверки этого задания два ученика у доски работают по карточкам:
-
Решить уравнение
-
Решить неравенство
-
Учащимся предлагается уравнение для самостоятельного решения:
-
Время решения этого задания учитель использует для проверки заданий по карточкам и индивидуальной работы.
-
Проверка самостоятельной работы:
-
Сообщение учащимся задач урока и мотивация познавательной деятельности.
-
Как известно функции – это математические портреты устойчивых закономерностей, познаваемых человеком.
-
Поистине безграничны приложения показательной функции в самых различных областях науки и техники.
-
И сегодня на уроке мы обобщим сведения об этой функции, показательных уравнениях и неравенствах.
-
Обобщение изученного материала:
-
Какая функция называется показательной?
-
Какие свойства этой функции вам известны? (используется таблица: График показательной функции)
-
Какие функции возрастающие, а какие убывающие:
-
Сравнить числа
-
Верно ли, что если
-
Учащиеся указывают ошибки (б, в) и аргументируют свои выводы.
-
Решить уравнения (устно):
-
Какие уравнения и неравенства называются показательными?
-
Устно решить неравенства и уравнение (задание проецируется на доску):
-
Решение уравнений и неравенств (с записью решения на доске)
-
Учащиеся выполняют самостоятельно, комментируя решение с места.
-
№ 264 (3) – с записью решения на доске
-
Решить неравенство
-
Учащимся, которые раньше справятся с заданием, предлагается № 262 (г) – решить систему уравнений.
-
Подведение итогов урока
-
При математическом описании каких процессов применяется показательная функция? (радиоактивный распад, зависимость давления воздуха от высоты подъема, в описании биологических процессов).
-
Предлагаю учащимся составить синквейн к слову «функция»
1.
-
-
Функция
-
Два прилагательных
-
2.
-
Показательная, степенная (можно: важная, возрастающая, убывающая, и т. д.)
-
3 глагола
-
3.
-
Характеризует, описывает, возрастает (можно: связывает, убывает, решает, создает)
-
Короткая фраза
-
4.
-
Решает разнообразные задачи
-
существительное
-
5.
-
Проблема
-
-
Домашнее задание.
-
Повторить п. 11, решить №262 (1), 264 (4), 251, 261 (2).
infourok.ru
Разработка урока по алгебре 10 класс
Министерство образования Республики Мордовия
ГБОУ РМ СПО (ССУЗ) «Краснослободский промышленный техникум»
УТВЕРЖДАЮ
Зам.директора по УПР Спиркина Т.В.______
«___»__________2009
Методическая разработка
по математике
«Применение тригонометрических формул»
Разработка урока математики по теме «Применение тригонометрических формул»
Аннотация
Тема «Тригонометрия » -достаточно сложная тема, требующая знания большого количества однотипных формул. Поэтому удобно иметь сюжетную «картинку», позволяющую запомнить формулы, привязать их к единичной окружности. Применять ИКТ целесообразно в обучающем, тренировочном режимах для отработки элементарных умений и навыков после изучения отдельных тем тригонометрии, например, «Преобразование тригонометрических выражений» с применением основных формул тригонометрии.
Содержание
Введение
Основная часть
Заключение
Список литературы и другие источники
Приложение А.
Введение
В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд». Со временем в нее начали вкрапляться некоторые аналитические моменты. В первой половине 18-го века произошел резкий перелом, после чего тригонометрия приняла новое направление и сместилась в сторону математического анализа. Именно в это время тригонометрические зависимости стали рассматриваться как функции. Это имеет не только математико-исторический, но и методико-педагогический интерес.
В настоящее время изучению тригонометрических функций именно как функций числового аргумента уделяется большое внимание в курсе математики. Существует несколько различных подходов к преподаванию данной темы. Тригонометрия всегда вызывает затруднения у учащихся. Часто можно услышать вопрос — «Для чего нам учить эти формулы?» Целью данного урока является повторение основных тригонометрических формул и закрепление их в ходе выполнения упражнений.
Тема урока: Применение тригонометрических формул к преобразованию выражений.
Цели:
Обучающие:
— уметь использовать основные формулы тригонометрии при упрощении тригонометрических выражений;
— совершенствование навыков использования и применения формул приведения;
— повторить основные тригонометрические формулы и закрепить их знания в ходе выполнения упражнений;
Развивающие:
— интеллектуальное, эмоциональное, личностное развитие учащегося;
— организовывать себя на работу, пользоваться умением самопроверки;
— развивать познавательный интерес;
— вызвать интерес к урокам математики.
Воспитательные:
— воспитывать настойчивость и упорство в достижении цели;
— эстетическое воспитание осуществляется через формирование умения рационально, аккуратно оформлять задание в тетради, через наглядные и дидактические пособия.
Базовые знания:
Тип урока: Урок совершенствования и закрепления знаний.
Формы учебной работы:
Оборудование:
-
тригонометрический круг;
-
компьютер, презентация;
-
мультимедийный проектор;
-
таблица значений тригонометрических функций;
-
дидактические карточки с математическим диктантом
-
тесты
Девиз урока: «Не бойтесь формул!
Учитесь владеть этим инструментом
Человеческого гения!
В формулах заключено величие и могущество
разума…»
Марков А.А.
Основные этапы урока:
-
Сообщение темы, цели урока и мотивация учебной деятельности.
-
Устный счёт
-
Повторение формул тригонометрии с помощью компьютерной презентации
-
Сообщение из истории математики.
-
Математический диктант.
-
Применение тригонометрических формул к преобразованию выражений
-
Выполнение теста.
-
Подведение итогов урока
-
Задание на дом
Ход урока:
I. Организационный момент.
Сообщение темы, цели урока и мотивация учебной деятельности
II. Проверка знаний учащимися тригонометрических формул.
У доски 3 учащихся записывают тригонометрические формулы:
1.Формулы, которые устанавливают соотношения между тригонометрическими функциями одного и того же угла.
2 Формулы сложения.
3 Формулы суммы и разности и разности тригонометрических функций.
В это время с остальными уч-ся провести устную разминку.
1.Устная разминка (задания заранее написаны на доске):
1.Какому выражению соответствует значение 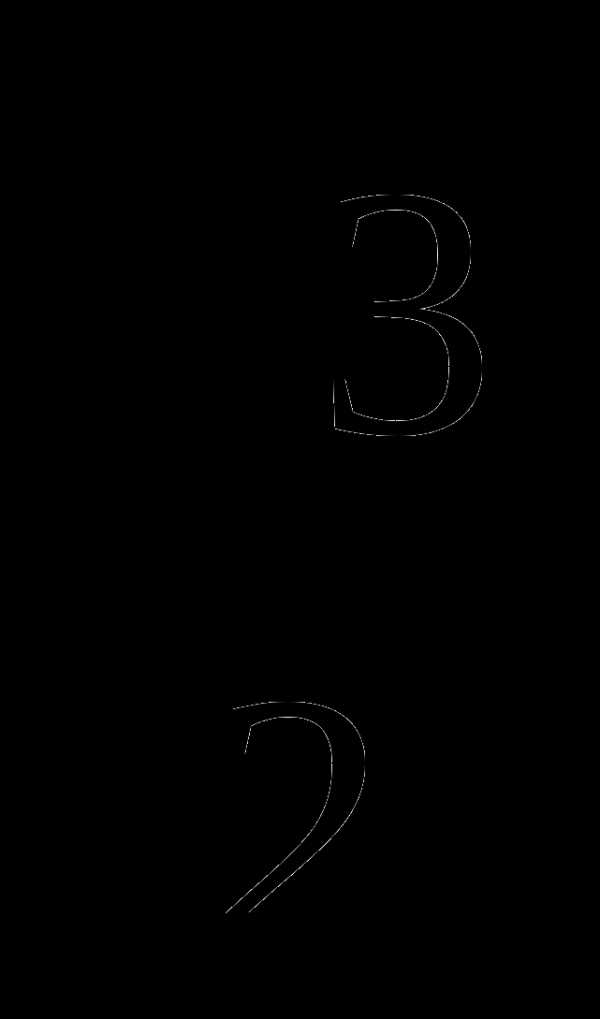 ?
?
а)sin30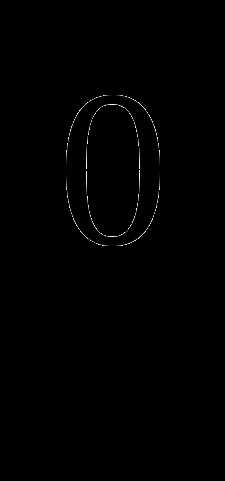 ; б) cos
; б) cos ; в) tg
; в) tg
2.Выбрать возможный вариант.
а) sin = ; б) cos =
; б) cos = 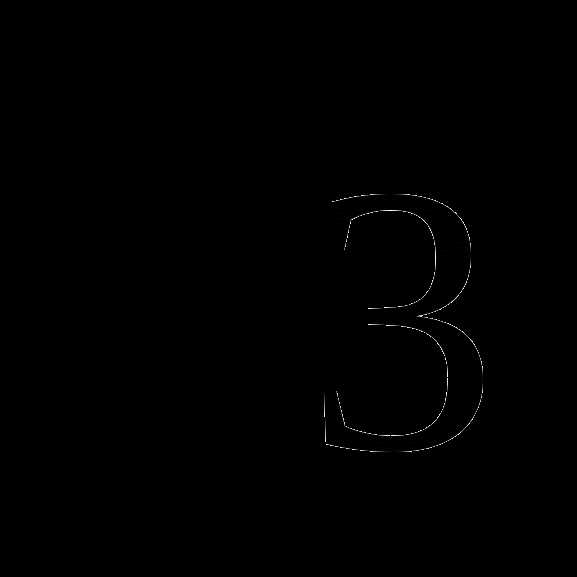 -2; в) sin = -3,7.
-2; в) sin = -3,7.
3. Какой из углов является углом II четверти?
а) 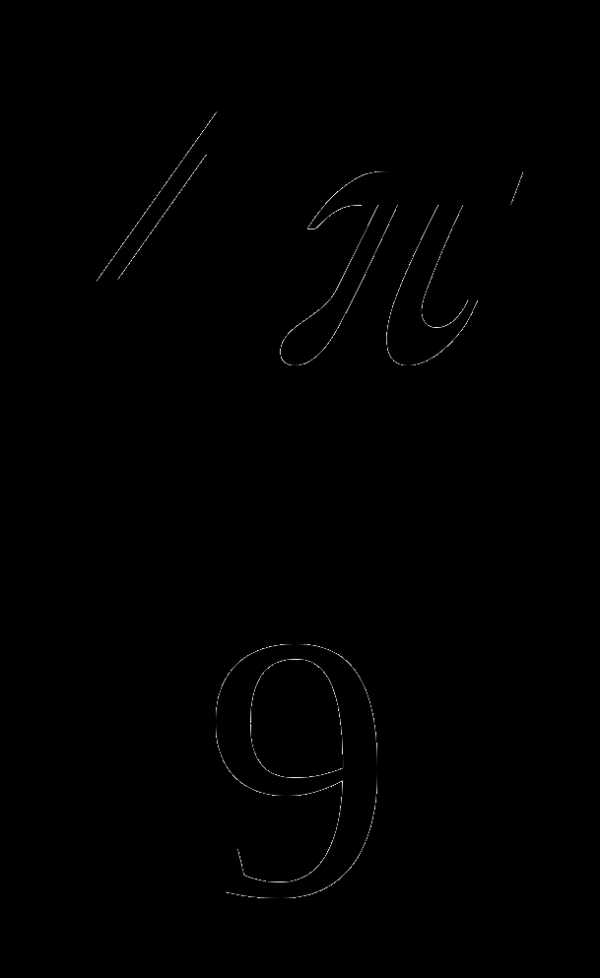 ; б) –145 ; в)
; б) –145 ; в) 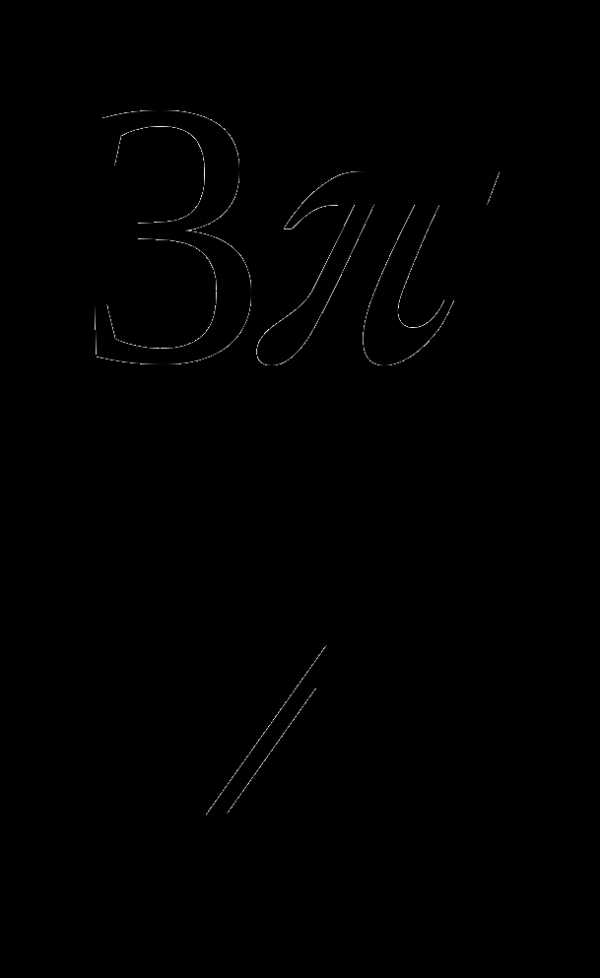
4.В каких четвертях sin и имеют разные знаки?
а) II и IV; б) I и III; в) I и IV.
5. Каким выражением можно заменить 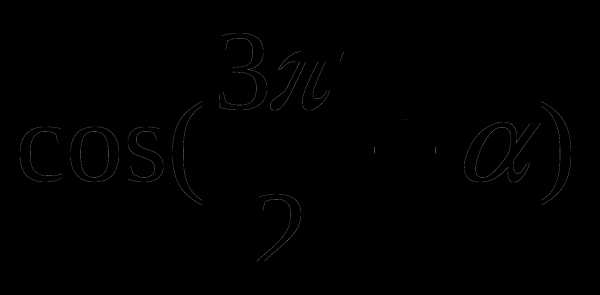 ?
?
а) cos ; б) sin ; в) — sin.
2. Компьютерная презентация тригонометрических формул.
Презентация «Тригонометрические формулы»
3. Математический диктант.
Вариант1
Вариант2
1+tg2 =
cos(/2+)=
tg (3/2+)=
1+ctg2=
1- sin2 =
sin(+)=
sin(-)=
tg.ctg=
sin2 + cos2=
cos(+)=
sin2=
сos2=
cos (-)=
1-cos2=
sin — sin=
сos — cos=
Двое учащихся выполняют работу на закрытых досках.
Критерии оценок:
верные ответы 8 оценка «5»
7 «4»
5-6 «3»
менее 5 «2»
Учащиеся проверяют работы одногруппников, работающих на обратной стороне доски, и одновременно свои работы.
III. Сообщение из истории математики
Тригонометрия возникла и развивалась в древности как один из разделов астрономии, как её вычислительный аппарат, отвечающий практическим нуждам человека.
Некоторые тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции.
Греческий астроном Гиппарх во II в. до н. э. составил таблицу числовых значений хорд в зависимости от величин стягиваемых ими дуг. Более полные сведения из тригонометрии содержатся в известном “Альмагесте” Птолемея. Сделанные расчёты позволили Птолемею составить таблицу, которая содержала хорды от 0 до 180 .
Название линий синуса и косинуса впервые были введены индийскими учёными. Они же составили первые таблицы синусов, хотя и менее точные, чем птолемеевы.
В Индии начинается по существу учение о тригонометрических величинах, названное позже гониометрией (от “гониа” — угол и “метрио” — измеряю).
На пороге XVII в. в развитии тригонометрии начинается новое направление – аналитическое.
Тригонометрия даёт необходимый метод развития многих понятий и методы решения реальных задач, возникающих в физике, механике, астрономии, геодозии, картографии и других науках. Кроме этого, тригонометрия является большим помощником в решении стереометрических задач.
IV. Применение тригонометрических формул к преобразованию выражений.
На доске самостоятельно по карточкам работают 2 учащихся.
Карточка№1. Найти значение выражения 2sin+5сos , если tg=2
3сos- sin
Карточка№2. Вычислить сos2, если sin=-3/4, 3/2.
V.Выполнение теста.
Тест по теме «Тригонометрические формулы»
Вариант I
1.Запишите cos61/10 с помощью наименьшего положительного числа: а) sin  ; б) sin
; б) sin  ; в) cos
; в) cos  ; г) cos
; г) cos  .
.
2. Сравните с нулём выражения sin 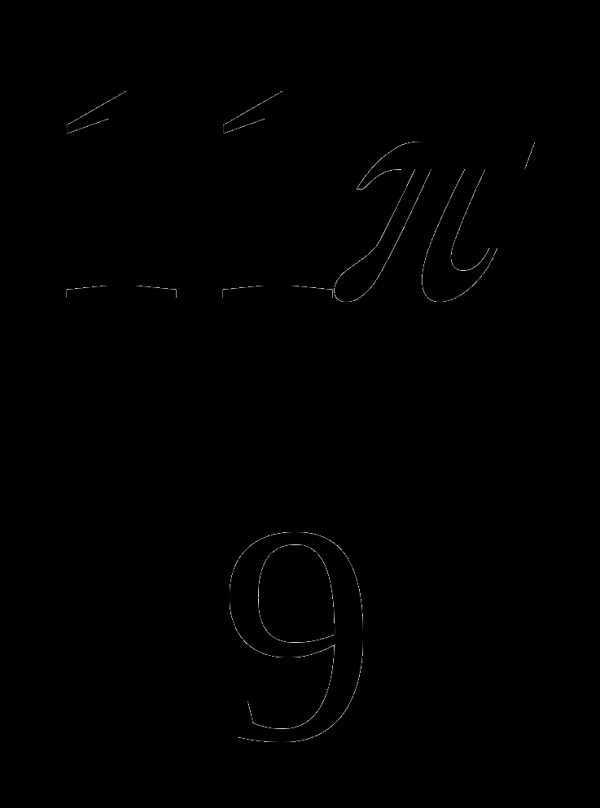 , cos 5 и tg 1,6
, cos 5 и tg 1,6 . Выберите правильную серию ответов:
. Выберите правильную серию ответов:
а) — — + ; б) + + — ; в) — + -; г) — + +.
3.Найдите значение выражения 7 cos — 5.
а) 2; б) -2; в) -1; г) 1.
4.Упростите выражение 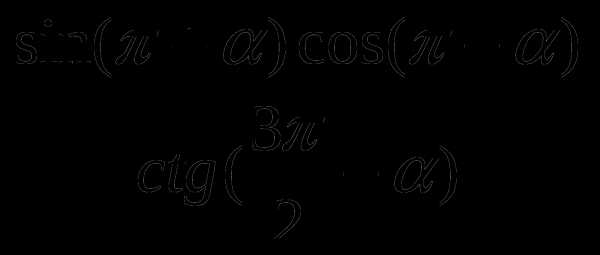 а) cos
а) cos  ; б) -sin
; б) -sin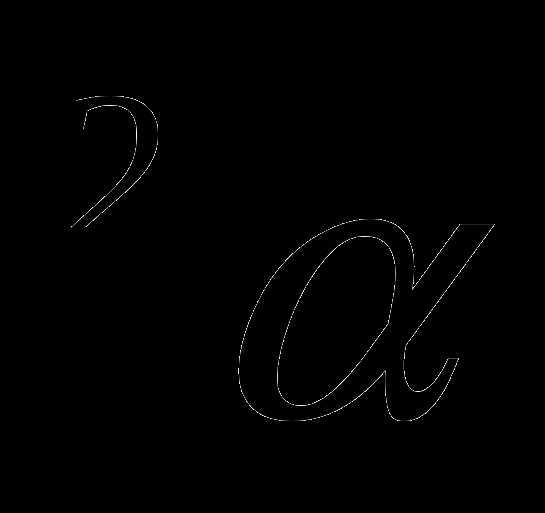 ; в) sin
; в) sin 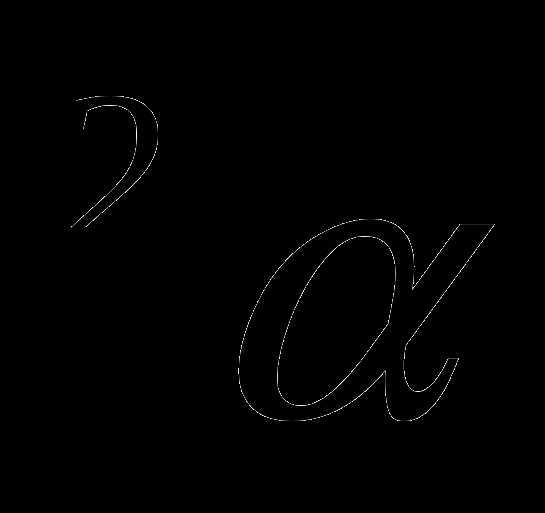 ; г) cos
; г) cos 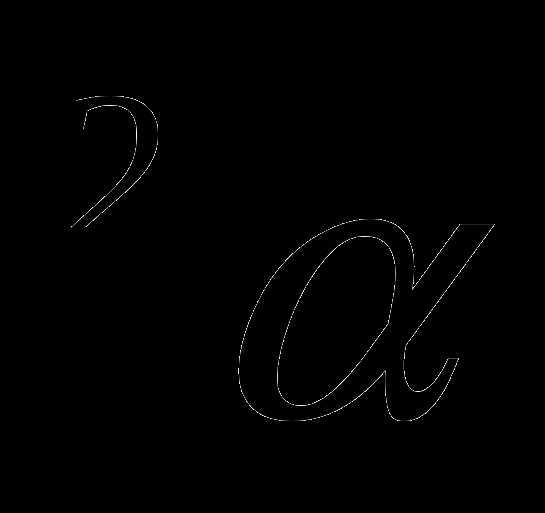 .
.
5.Оцените значение выражения 2 – 3 sin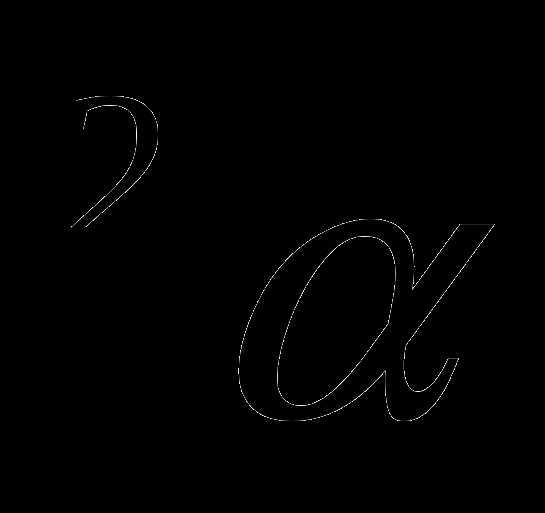 а)
а) 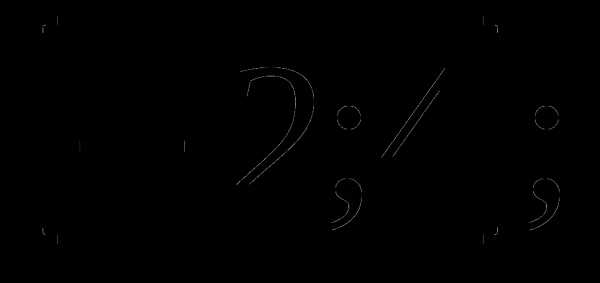 б)
б)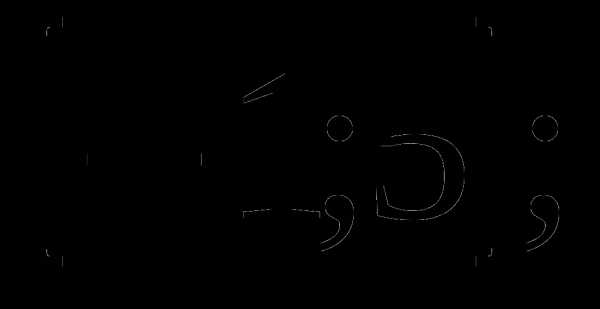 в)
в) 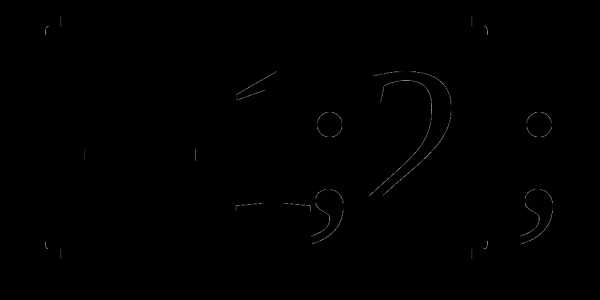 г)
г) 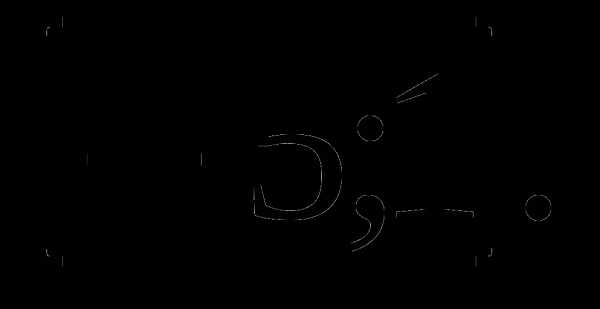
Выполнить задание, выбрать верный ответ из предложенных, результат записать в таблицу.
Вариант№
Фамилия,имя
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Тест по теме «Тригонометрические формулы»
Вариант II
-
Запишите cos 91/15 с помощью наименьшего положительного числа: а) sin
 ; б) sin
; б) sin  ; в) cos
; в) cos  ; г) cos
; г) cos  .
. -
Сравните с нулём выражения cos
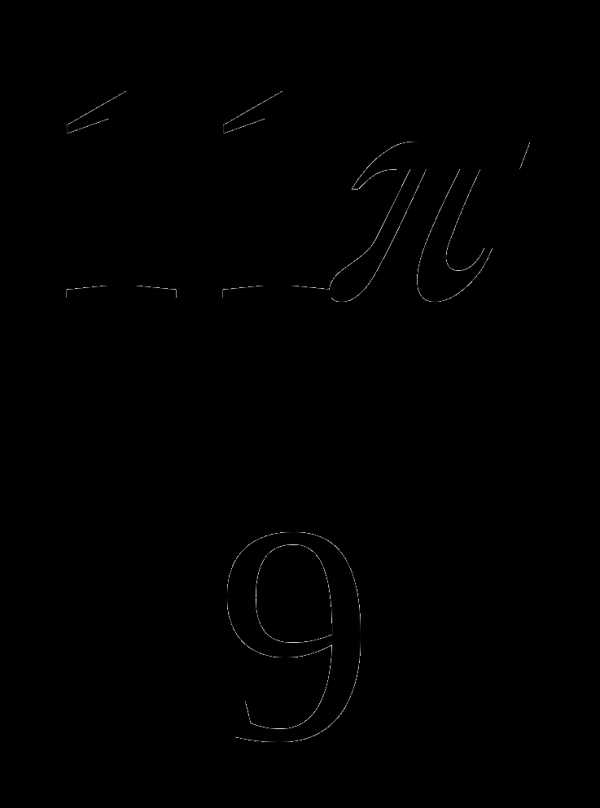 , cos 0,7 и ctg 1,6
, cos 0,7 и ctg 1,6 . Выберите правильную серию ответов:
. Выберите правильную серию ответов:
а) — — + ; б) + + — ; в) — + -; г) — + +.
3 .Найдите значение выражения 5 – 4 sin
а) 2; б) -2; в) -1; г) 1.
4.Упростите выражение 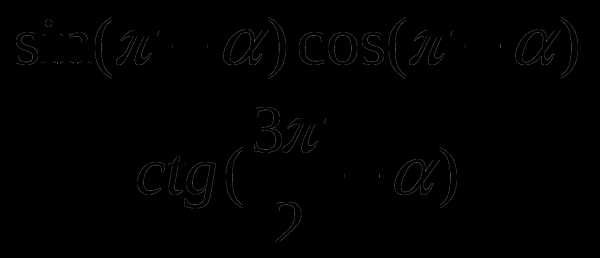
а) cos  ; б) -sin
; б) -sin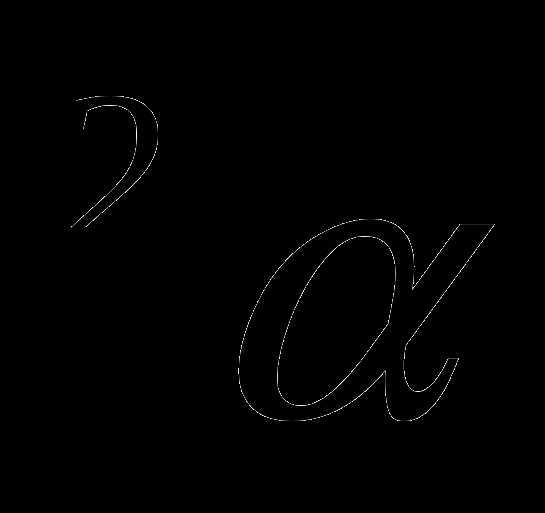 ; в) sin
; в) sin 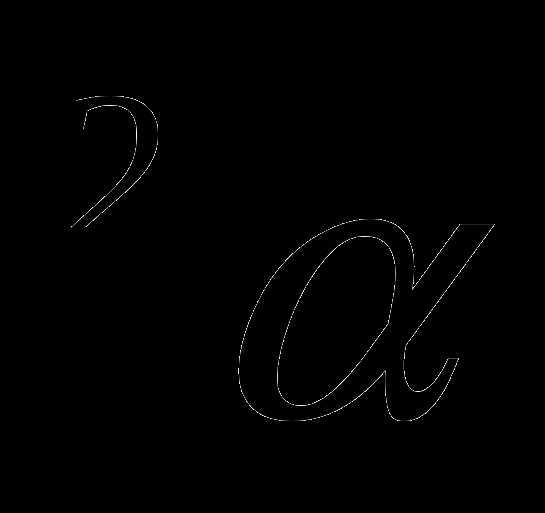 ; г) cos
; г) cos 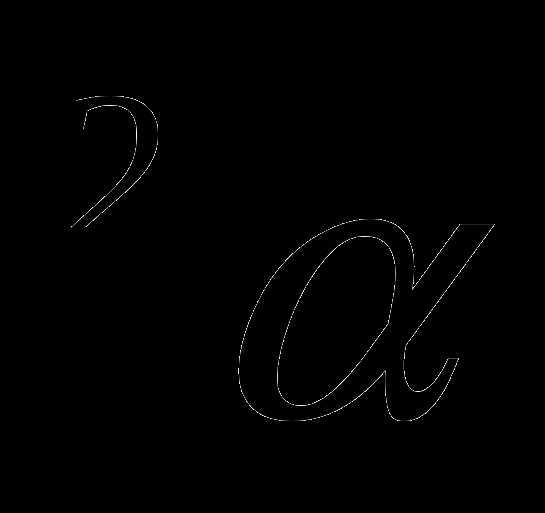 .
.
5.Оцените значение выражения 2 – 3 cos 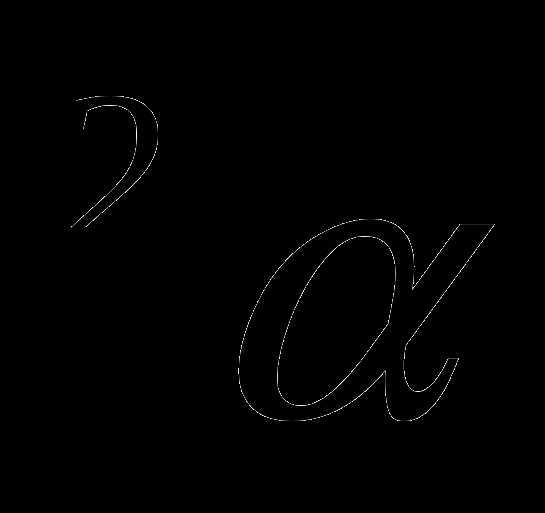
а) 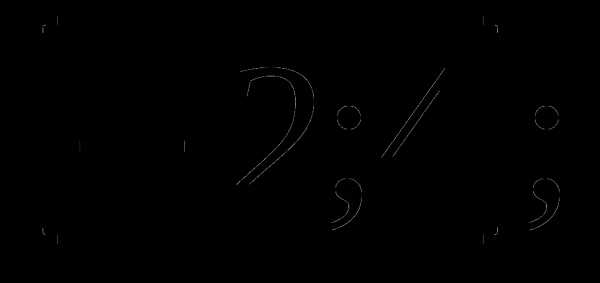 б)
б)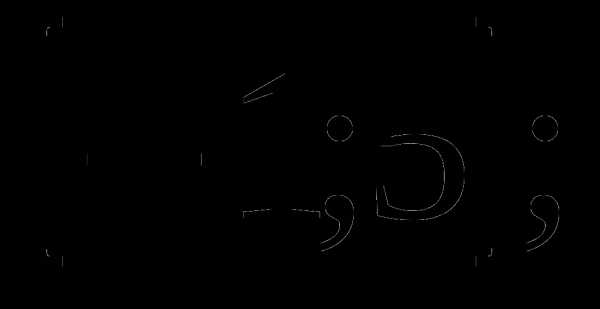 в)
в) 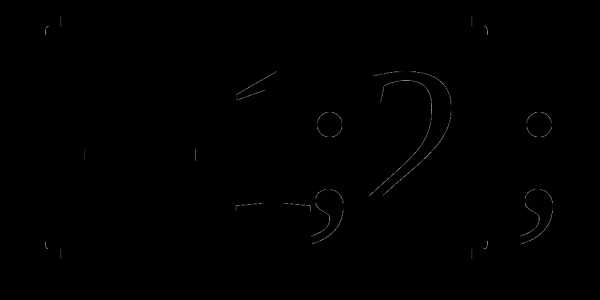 г)
г) 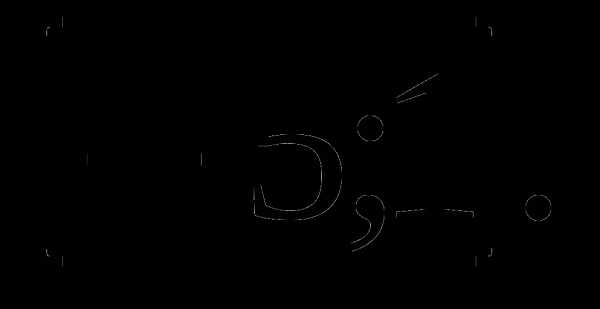
Выполнить задание, выбрать верный ответ из предложенных, результат записать в таблицу.
Вариант№
Фамилия,имя
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Ответы:
Вариант I ввагв Вариант II гвггв
VI.Итоги урока
Продолжи фразу
«Сегодня на уроке я повторил…»
«Сегодня на уроке я закрепил…»
Комментирование и выставление оценок.
VII. Домашнее задание: повторение темы «Тригонометрические формулы»
infourok.ru