|
Контрольная работа № 1 |
1 вариант 1). Основание АD трапеции АВСD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно. а). Каково взаимное расположение прямых ЕF и АВ? б). Чему равен угол между прямыми ЕF и АВ, если АВС = 1500? Ответ обоснуйте. 2). Дан пространственный четырехугольник АВСD, в котором диагонали АС и ВD равны. Середины сторон этого четырехугольника соединены последовательно отрезками. а). Выполните рисунок к задаче; б). Докажите, что полученный четырех – угольник – ромб. |
2 вариант 1). Треугольники АВС и АDС лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны АD, точка К – середина DС. а). Каково взаимное расположение прямых РК и АВ? б). Чему равен угол между прямыми РК и АВ, если АВС = 400 и ВСА = 80? Ответ обоснуйте. 2). Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно, Е СD, К D, DА : ЕС = 1 : 2, DК : КА = 1 : 2. а). Выполните рисунок к задаче; б). докажите, что четырехугольник МNЕК – трапеция. |
Контрольная работа № 2 |
1 вариант 1). Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть: а). Параллельными; б). Скрещивающимися? Сделайте рисунок для каждого возможного случая. 2). Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4. 3). Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1. |
2 вариант 1). Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть: а). Параллельными; б). Скрещивающимися? Сделайте рисунок для каждого возможного случая. 2). Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5. 3). Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3. |
Контрольная работа № 3 |
1 вариант 1). Диагональ куба равна 6 см. Найдите: а). Ребро куба; б). Косинус угла между диагональю куба и плоскостью одной из его граней. 2). Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D. а). Найдите расстояние от точки С до плоскости α; б). Покажите на рисунке линейный угол двугранного угла DABM, М α. в) Найдите синус угла между плоскостью ромба и плоскостью α. |
2 вариант 1). Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна см, а его измерения относятся как 1:1:2. Найдите: а). Измерения параллелепипеда; б). Синус угла между диагональю параллеле – пипеда и плоскостью его основания. 2). Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В. а). Найдите расстояние от точки С до плоскости α. б). Покажите на рисунке линейный угол двугранного угла BADM, М α. в). Найдите синус угла между плоскостью квадрата и плоскостью α. |
Контрольная работа № 4 |
1 вариант 1). Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды. 2). Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите: а) высоту ромба; б) высоту параллелепипеда; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда. |
2 вариант 1). Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды. 2). Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите: а). меньшую высоту параллелограмма; б). угол между плоскостью АВС1 и плоскостью основания; в). площадь боковой поверхности параллелепипеда; г). площадь поверхности параллелепипеда. |
nsportal.ru
|
1 вариант 1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно. а) Каково взаимное положение прямых ЕF и АВ? б) Чему равен угол между прямыми ЕF и АВ, если АВС = 150°? Поясните. 2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками. а) Выполните рисунок к задаче. б) Докажите, что полученный четырехугольник есть ромб. |
2 вариант 1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC. а) Каково взаимное положение прямых РK и АВ? б) Чему равен угол между прямыми РK и АВ, если АВС = 40° и ВСА = 80°? Поясните. 2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2. а) Выполните рисунок к задаче. б) Докажите, что четырехугольник MNEK есть трапеция. |
1 вариант 1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4. 3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1. |
2 вариант 1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5. 3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3. |
1 вариант 1. Диагональ куба равна 6 см. Найдите: а) ребро куба; б) косинус угла между диагональю куба и плоскостью одной из его граней. 2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла DABM, в) найдите синус угла между плоскостью ромба и плоскостью α |
2 вариант 1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите: а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью его основания. 2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла BADM, в) Найдите синус угла между плоскостью квадрата и плоскостью α. |
1 вариант 1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите: а) высоту ромба; б) высоту параллелепипеда; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда |
2 вариант 1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны a и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите: а) меньшую высоту параллелограмма; б) угол между плоскостью АВС1 и плоскостью основания; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда. |
multiurok.ru
Контрольная работа по геометрии (10 класс)
КОНТРОЛЬНЫЕ РАБОТЫ
ПО ГЕОМЕТРИИ
10 КЛАСС
УЧЕБНИК АТАНАСЯН Л.С.
Контрольная работа № 1
Тема: Параллельность прямых и плоскостей
Вариант I
1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
а) Каково взаимное положение прямых ЕF и АВ?
б) Чему равен угол между прямыми ЕF и АВ, если АВС = 150°? Поясните.
2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник есть ромб.
Контрольная работа № 1
Тема: Параллельность прямых и плоскостей
Вариант II
1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC.
а) Каково взаимное положение прямых РK и АВ?
б) Чему равен угол между прямыми РK и АВ, если АВС = 40° и ВСА = 80°? Поясните.
2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2.
а) Выполните рисунок к задаче.
б) Докажите, что четырехугольник MNEK есть трапеция.
Контрольная работа № 2
Тема: Параллельность плоскостей. Тетраэдр и параллелепипед.
Вариант I
1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
а) параллельными;
б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.
3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1.
Контрольная работа № 2
Тема: Параллельность плоскостей. Тетраэдр и параллелепипед.
Вариант II
1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:
а) параллельными;
б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5.
3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3.
Контрольная работа № 3
Тема: Перпендикулярность прямых и плоскостей
Вариант I
1. Диагональ куба равна 6 см. Найдите:
а) ребро куба;
б) косинус угла между диагональю куба и плоскостью одной из его граней.
2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла DABM,
М α.
в) Найдите синус угла между плоскостью ромба и плоскостью α.
Контрольная работа № 3
Тема: Перпендикулярность прямых и плоскостей
Вариант II
1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите:
а) измерения параллелепипеда;
б) синус угла между диагональю параллелепипеда и плоскостью его основания.
2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла BADM,
М α.
в) Найдите синус угла между плоскостью квадрата и плоскостью α.
Контрольная работа № 4
Тема: Многогранники
Вариант I
1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.
2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:
а) высоту ромба;
б) высоту параллелепипеда;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
Контрольная работа № 4
Тема: Многогранники
Вариант II
1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны а и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а) меньшую высоту параллелограмма;
б) угол между плоскостью АВС1 и плоскостью основания;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
infourok.ru
Контрольные работы по геометрии 10 класс к учебнику АТАНАСЯН и ЕРШОВ
Контрольная работа №2 по теме:
«Параллельностьпрямых и плоскостей.»
Вариант 1.
-
Даны параллельные плоскости α и β .Через точки А и В плоскости проведены параллельные прямые ,пересекающие плоскость β в точках А1 и В1. Найдите А1В1 ,если АВ=5 см.
-
Верно ,что плоскости параллельны ,если прямая, лежащая в одной плоскости, параллельна другой плоскости?
-
Две плоскости параллельны между собой .Из точки М ,не лежащей ни в одной из этих плоскостей, ни между плоскостями, проведены две прямые ,пересекающие эти плоскости соответственно в точках А1 и А2, В1 и В2. Известно, что МА1 = 4 см., В1В2 = 9 см., А1А2 = МВ1. Найдите МА2 и МВ2.
Вариант 2.
-
Отрезки АВ и СD параллельных прямых заключены между параллельными плоскостями. Найдите АВ ,еслиCD=3 см.
-
Верно ли утверждение ,что плоскости параллельны ,если две прямые ,лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?
-
Из точки О ,лежащей вне двух параллельных плоскостейα и β, проведены три луча, пересекающие плоскости α и β соответственно в точках АВС и А1В1С1 (ОА < ОА1). Найдите периметр А1В1С1, если ОА= m ,АА1= n ,АВ= b ,ВС=а.
Контрольная работа №3 по теме :
« Перпендикулярность прямых и плоскостей.»
Вариант 1.
-
Длина стороны ромба АВСD равна 5 см , длина диагонали ВD равна 6 см. Через точку О пересечения диагоналей ромба проведена прямая ОК ,перпендикулярная его плоскости. Найдите расстояние от точки К до вершины ромба, если ОК=8 см.
-
Длина катета прямоугольного равнобедренного треугольника равна 4 см. Плоскость α , проходящая через катет, образует с плоскостью треугольника угол, величина которого равна 30⁰. Найдите длину проекции гипотенузы на плоскость α .
Вариант 2.
-
Длины сторон прямоугольника равны 8 и 6 см. Через точку О пересечения его диагоналей проведена прямая ОК , перпендикулярная его плоскости .Найдите расстояние от точки К до вершин прямоугольника ,если ОК=12 см.
-
Длины сторон треугольника АВС соответственно равны : ВС=15 см, АВ=13 см, АС =4 см. Через сторону АС проведена плоскость α ,составляющая с плоскостью данного треугольника угол 30⁰. Найдите расстояние от вершины В до плоскости α.
Контрольная работа №4 по теме :
« Многогранники.»
Вариант 1.
-
Основание прямой призмы –прямоугольный треугольник с катетами 6 и 8 см. Найдите площадь боковой поверхности призмы ,если её наибольшая боковая грань- квадрат.
-
Боковое ребро правильной четырёхугольной пирамиды равно 4 см и образует с плоскостью основания пирамиды угол 45⁰.
а) Найдите высоту пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
-
Ребро правильного тетраэдра DАВС равно а. Постройте сечение тетраэдра ,проходящее через середину ребра DА параллельно плоскости DВС, и найдите площадь этого сечения.
Вариант 2.
-
Основание прямой призмы-прямоугольный треугольник с гипотенузой 13 см и катетом 12 см. Найдите площадь боковой поверхности призмы, если её наименьшая боковая грань- квадрат.
-
Высота правильной четырёхугольной пирамиды равна √6см, а боковое ребро наклонено к плоскости основания под углом 60⁰.
а) Найдите боковое ребро пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
-
Ребро правильного тетраэдр DАВС равно а Постройте сечение тетраэдра , проходящее через середину рёбер DА и АВ параллельно ребру ВС ,и найдите площадь этого сечения.
infourok.ru
Проверочные работы по геометрии для 10 класса
Проверочные работы по геометрии для 10 класса охватывают несколько тем по учебнику Атанасян, Геометрия для 10-11 классов. Работа включает в себя также ключ к вопросам. В каждой проверочной работе по 8 вопросов. Всего 9 проверочных работ по каждому разделу.
Просмотр содержимого документа
«Проверочные работы по геометрии для 10 класса »
|
Самостоятельные работы по геометрии |
|
10 класс |
|
Подготовила: преподаватель математики ГАПОУ МО «Мурманский колледж экономики и информационных технологий» Конурова Алёна Николаевна, г. Мурманск |
Проверочная работа №1.
Аксиомы стереометрии и следствия из них
-
Верно ли, что если концы отрезка лежат в данной плоскости, то и его середина лежит в данной плоскости?
-
Могут ли две плоскости иметь общую точку, но не иметь общей прямой?
-
Точка А не лежит в плоскости KMN. Назовите прямую пересечения плоскостей AMN и AKM.
-
Даны точки А, В, С и D. Плоскость α проходит через прямую АВ, но не проходит через точку С. Прямые AD и ВС пересекаются в точке В. Сколько данных точек лежит в плоскости α?
-
В пространстве даны прямая и точка. Сколько различных плоскостей можно через них провести?
-
*Верно ли, что если три данные точки лежат в одной плоскости, то они не лежат на одной прямой?
-
*Могут ли три прямые иметь общую точку, но не лежать в одной плоскости?
-
*Три прямые пересекаются в точке А. Через данную точку необходимо провести плоскость, содержащую ровно две из трех данных прямых.
Сколько таких плоскостей можно провести? Рассмотрите все возможные случаи.
|
|
|
|
|
|
|
|
|
|
да |
нет |
АМ |
три |
одну или бесконечно много |
нет |
да |
три или не одной |
Проверочная работа №2.
Параллельные прямые в пространстве.
Параллельность прямой и плоскости
-
Верно ли, что две параллельные прямые лежат в одной плоскости?
-
Может ли прямая, параллельная плоскости, пересекать какую-либо прямую этой плоскости?
-
Определите взаимное расположение прямой а и плоскости α, если:
a || b и прямая b пересекает плоскость α.
-
Дана плоскость β и прямые а, b, с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если:
а || с , прямые b и с пересекаются, а прямая с лежит в плоскости β.
-
Может ли прямая в пространстве пересекать одну из двух параллельных прямых, но не пересекать другую?
-
Определите взаимное расположение прямой а и плоскости α, если в плоскости α не существует прямой, пересекающей а.
-
Верно ли, что две прямые, параллельные одной плоскости, параллельны?
-
Могут ли прямые AB и CD быть параллельными, если прямые AD и BC пересекаются?
|
|
|
|
|
|
|
|
|
|
да |
нет |
пересекаются |
а |
да |
параллельны |
нет |
да |
Проверочная работа №3.
Взаимное расположение прямых в пространстве
-
Верно ли, что если две прямые в пространстве не пересекаются, то они параллельны?
-
Может ли угол в пространстве быть тупым?
-
Определите взаимное расположение прямых a и b , если прямая а лежит в плоскости α, а прямая b пересекает плоскость α в точке, не лежащей на прямой а.
-
Прямая l пересекает плоскость треугольника АВС в точке В. Назовите прямую, скрещивающуюся с l и содержащую сторону данного треугольника.
-
Определите, верно ли на плоскости, в пространстве или и на плоскости, и в пространстве данное утверждение:
«Если две различные прямые не пересекаются, то они параллельны.
-
Верно ли, что две прямые, параллельные одной плоскости, могут быть скрещивающимися?
-
Могут ли в пространстве два угла с соответственно параллельными сторонами не быть равными?
-
Определите, какой из случаев взаимного расположения прямых a и b невозможен, если прямая а пересекается с с, а b||с.
|
|
|
|
|
|
|
|
|
|
нет |
нет |
скрещивающиеся |
АС |
на плоскости |
да |
да |
параллельность |
Проверочная работа №4.
Параллельность плоскостей.
Тетраэдр и параллелепипед
-
Верно ли, что прямая, лежащая в одной из двух параллельных плоскостей, параллельна второй плоскости?
-
Могут ли рёбра тетраэдра лежать на параллельных прямых?
-
Параллельные плоскости α и β пересекают плоскость γ по прямым a и b соответственно. Определите взаимное расположение прямых a и b .
-
Определите вид сечения параллелепипеда плоскостью, проходящей через середины четырёх боковых рёбер.
-
Дана плоскость α и точка А вне данной плоскости. Определите, какую фигуру в пространстве образуют все прямые, параллельные данной плоскости и проходящие через данную точку. Как расположена эта фигура по отношению к плоскости α?
-
Верно ли, что если в каждой из двух параллельных плоскостей проходит прямая, то эти прямые скрещивающиеся?
-
Может ли в тетраэдре DABC грань DBC содержать прямую, параллельную ребру DA?
-
Плоскость γ пересекает параллельные плоскости α и β по прямым a и b соответственно. Прямая с скрещивается с прямой b . Укажите, какой из случаев взаимного расположения прямых а и с невозможен.
-
Определите, какую фигуру в пространстве образуют середины всех отрезков с концами на двух данных скрещивающихся прямых. Как расположена эта фигура по отношению к данным прямым?
|
|
|
|
|
|
|
|
|
|
|
да |
нет |
параллельны |
параллелограмм |
плоскости – параллельно – α |
нет |
нет |
параллельны |
плоскость параллельна данным прямым |
,
Проверочная работа №5.
Перпендикулярность прямой и плоскости
-
Верно ли, что две прямые, перпендикулярные к одной плоскости, параллельны?
-
Может ли прямая, перпендикулярная к плоскости, быть параллельной прямой, лежащей в этой плоскости?
-
Даны прямые a и b и плоскость α. Определите угол между данными прямыми, если a α, b || α.
-
ОА – прямая, перпендикулярная к плоскости равностороннего треугольника АВС. Назовите отрезок, равный отрезку ОС.
-
Могут ли две скрещивающиеся прямые быть перпендикулярными к одной плоскости?
-
Даны прямые a, b, c и плоскость α. Укажите среди данных прямых прямую, перпендикулярную к двум другим, если a α, b || α, с лежит в плоскости α.
-
Прямая a лежит в плоскости α, α. Вставьте вместо пропусков обозначения a, b или α так, чтобы данное утверждение было верным:
«Если прямая перпендикулярна к …, то она перпендикулярна к … и параллельна …»
|
|
|
|
|
|
|
|
|
да |
нет |
90° |
ОВ |
нет |
а |
α – a — b |
Проверочная работа №6.
Перпендикуляр и наклонные.
Угол между прямой и плоскостью
-
Верно ли, что длина перпендикуляра меньше длины наклонной, проведённой из этой же точки?
-
Может ли угол между прямой и плоскостью быть тупым?
-
SA – перпендикуляр к плоскости треугольника АВС. Определите вид треугольника АВС, если SB ВС.
-
SA – перпендикуляр к плоскости прямоугольника АВСD. Назовите отрезок, изображающий расстояние от точки S до прямой СD.
-
Через сторону ВС треугольника АВС проведена плоскость α. АО – перпендикуляр к плоскости α. Назовите угол между АС и плоскостью α.
-
*Верно ли, что расстояние между параллельными плоскостями равно расстоянию от любой прямой одной плоскости до другой плоскости?
-
*Могут ли две прямые, образующие с данной плоскостью неравные углы, быть параллельными?
-
* SA – перпендикуляр к плоскости треугольника АВС. Назовите наибольшую сторону треугольника, если SС ВС.
|
|
|
|
|
|
|
|
|
|
да |
нет |
прямоуг. |
SD |
угол АСО |
да |
нет |
АВ |
Проверочная работа №7.
Двугранный угол.
Перпендикулярность плоскостей.
Прямоугольный параллелепипед
-
Верно ли, что любая прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна к другой плоскости?
-
Может ли диагональ прямоугольного параллелепипеда быть меньше одного из рёбер?
-
Плоскости α и β перпендикулярны. Прямая а не лежит в плоскости α. Определите взаимное расположение прямой а и плоскости α, если а β.
-
Равносторонние треугольники АВС и АDС не лежат в одной плоскости. М – середина АС. Назовите линейный угол двугранного угла между плоскостями треугольников.
-
*Верно ли, что если одна из двух плоскостей проходит через прямую, перпендикулярную к линии пересечения плоскостей, то эти плоскости перпендикулярны?
-
*Может ли сечение прямоугольного параллелепипеда плоскостью, перпендикулярной к основаниям, не являться прямоугольником?
-
*DА – перпендикуляр к плоскости прямоугольного треугольника АВС. Назовите линейный угол двугранного угла между плоскостями АВС и DВС, если АВ – гипотенуза треугольника АВС.
|
|
|
|
|
|
|
|
|
нет |
нет |
а ||α |
ВМD |
нет |
нет |
DСА |
Проверочная работа №8.
Призма. Пирамида
-
Верно ли, что основания любой призмы лежат в параллельных плоскостях?
-
Может ли высота пирамиды быть больше её бокового ребра?
-
Определите количество сторон многоугольника, лежащего в основании, если она имеет семь граней.
-
Определите вид четырёхугольника (прямоугольник, ромб, трапеция), который является сечением правильной треугольной призмы, если это сечение проходит через ребро нижнего основания и пересекает две стороны верхнего основания.
-
Могут ли три боковых грани пирамиды быть перпендикулярными к плоскости основания?
-
Верно ли, что параллелепипед является четырёхугольной призмой?
-
Может ли площадь боковой поверхности пирамиды быть равной площади её основания?
|
|
|
|
|
|
|
|
|
да |
нет |
5 |
трапеция |
нет |
да |
нет |
Проверочная работа №9.
Векторы. Действия с векторами в пространстве
-
Верно ли что векторы, имеющие равные длины, равны?
-
Могут ли коллинеарные векторы лежать на скрещивающихся прямых?
-
В тетраэдре DАВС назовите вектор, равный сумме .
-
Диагонали куба АВСD пересекаются в точке О. Найдите число из равенства .
-
Даны точки А, В, С и D, причём никакие три из них не лежат на одной прямой. Определите взаимное расположение прямых АВ и СD, если векторы сонаправлены.
-
SО – высота правильной четырёхугольной пирамиды SАВСD. Найдите число 𝝀 из равенства .
-
Даны точки А, В, С и D, причём никакие три из них не лежат на одной прямой. Определите взаимное расположение прямых АВ и СD, если векторы не коллинеарны, а векторы коллинеарны.
|
|
|
|
|
|
|
|
|
нет |
нет |
0,5 |
параллельны |
-0,5 |
пересекаются |
При подготовки данного материала использовался учебник по геометрии Атанасян, 10-11кл., Геометрия.
kopilkaurokov.ru
Все контрольные работы по алгебре и геометрии 10 класс
Контрольные работы по геометрии (учебник Атанасяна) и алгебре и началам анализа ( учебник Колягин и др.) 10 класс
1) Контрольная работа по геометрии 10 класс по теме «Повторение планиметрии». вариант №1
|
2) |
7) Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен . Найдите боковую сторону |
|
3) Найти площадь треугольника ABC |
8) Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник |
|
4) В треугольнике угол равен 90°, , . Найдите . |
9) Острый угол ромба равен . Радиус вписанной в этот ромб окружности равен 2. Найдите сторону ромба |
|
5) |
10) В треугольнике , , угол равен 90°. Найдите радиус описанной окружности этого треугольника. Решение. вписанный угол, опирающийся на диаметр окружности, является прямым, значит, – диаметр.
Ответ: 2,5. Ответ: 2,5 |
Контрольная работа по геометрии 10 класс по теме «Повторение планиметрии». вариант №2
|
2) |
7) Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен . Найдите меньшее основание. |
|
3) Найти площадь треугольника ABC |
8) Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
|
|
4) В треугольнике ABC угол C равен , , . Найдите AC |
9) Сторона ромба равна 1, острый угол равен . Найдите радиус вписанной окружности этого ромба. Решение.
Ответ: 0,25. Ответ: 0,25 |
|
5) Найти стороны треугольника ABC |
10) В треугольнике , угол равен 90°. Радиус описанной окружности этого треугольника равен 5. Найдите . Решение. Гипотенуза прямоугольного треугольника является диаметром описанной вокруг него окружности, поэтому ее длина 10. Тогда по теореме Пифагора:
Ответ: 8. Ответ: 8 |
2) Контрольная работа по геометрии № 2 Начальные сведения по стереометрии 10 класс
2)Дан параллелепипед . Точки M и N на рёбрах  и
и 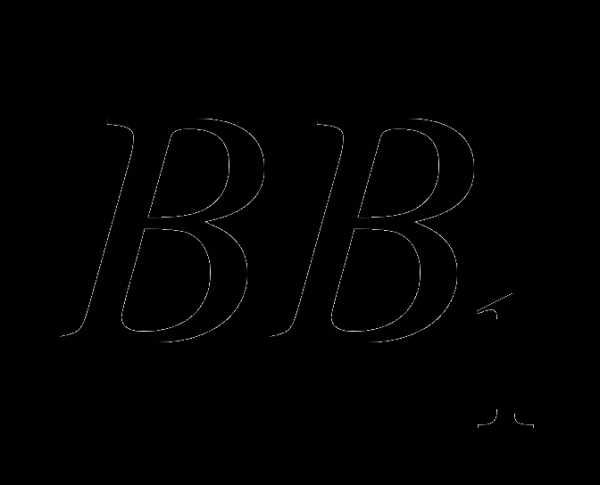
 соответственно . Каково взаимное расположение прямых:
соответственно . Каково взаимное расположение прямых:
а)  и
и  ; в)
; в)  и MN ; с) MN и
и MN ; с) MN и 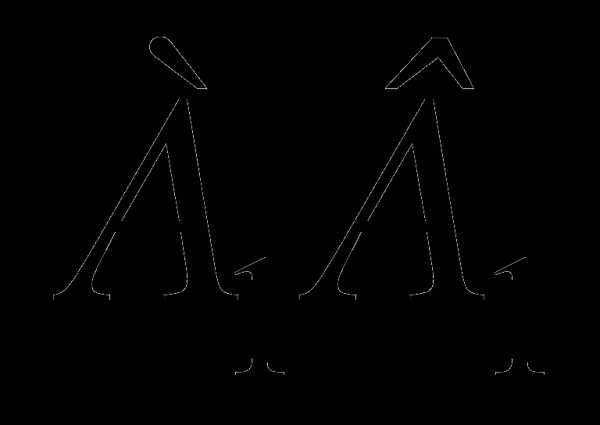
2)Дан параллелепипед . Точки K и P на рёбрах  и
и 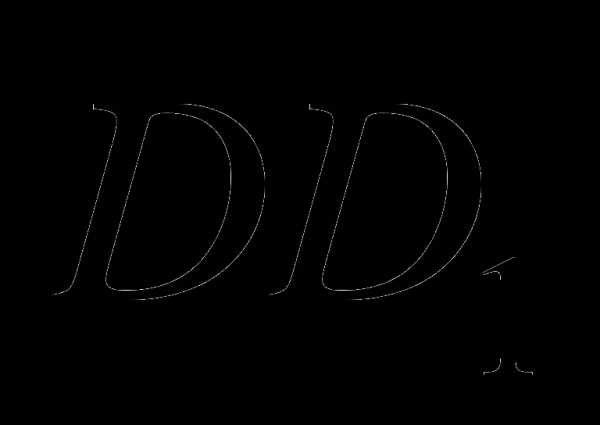
 соответственно . Каково взаимное расположение прямых:
соответственно . Каково взаимное расположение прямых:
а) 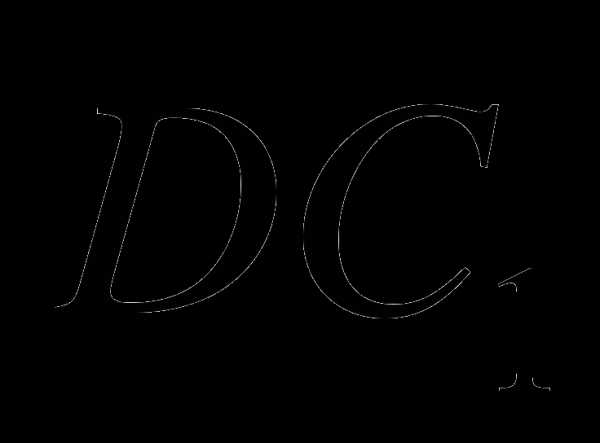 и
и 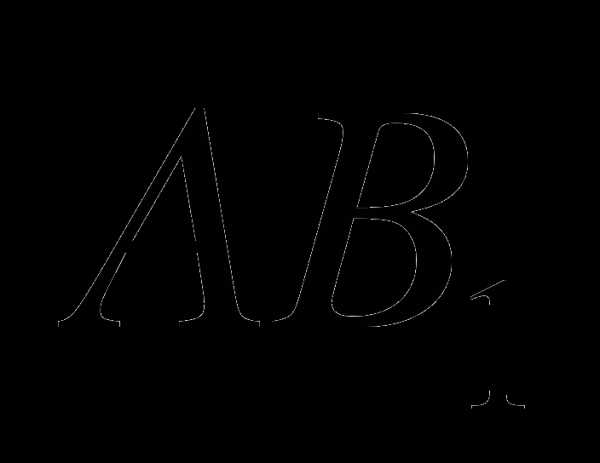 ; в)
; в) 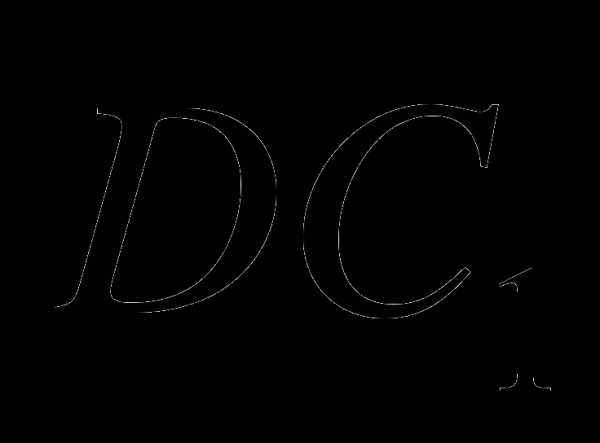 и PK ; с) PK и
и PK ; с) PK и 
3) Доказать параллельность плоскостей
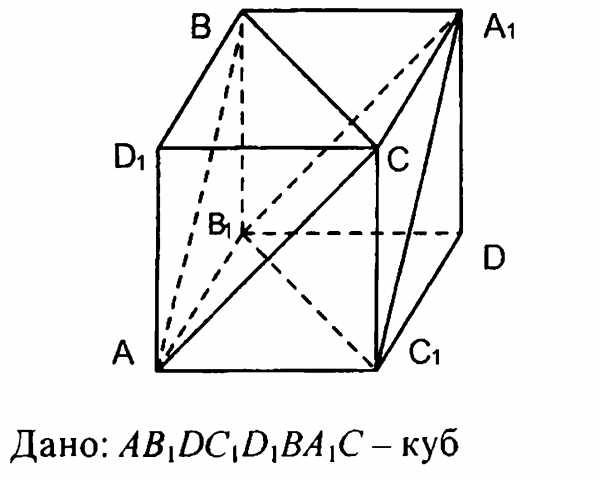
3) доказать параллельность плоскостей :
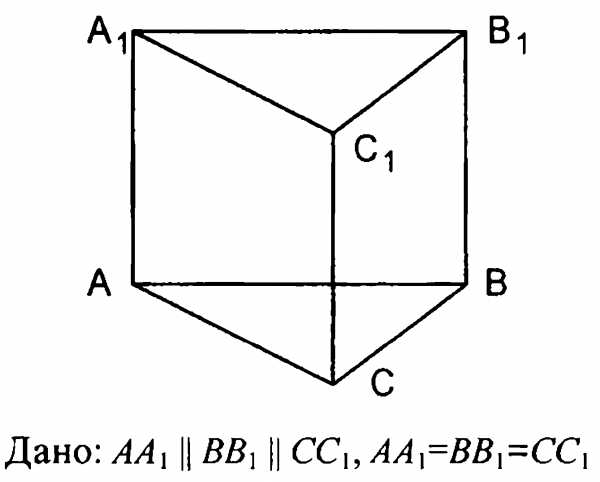
4) Изобразите параллелепипед и постройте его сечение плоскостью, проходящей через точки 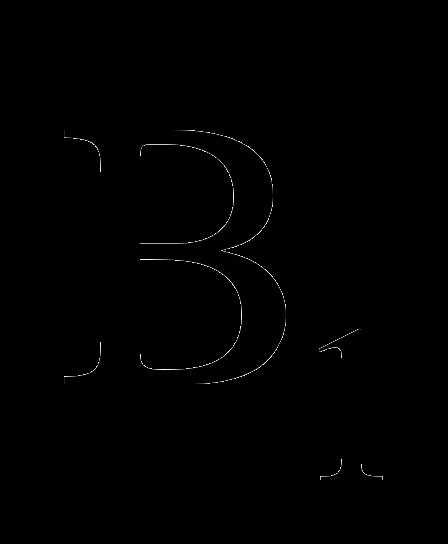 ,
,  и середину ребра CD. Докажите, что построенное сечение – трапеция
и середину ребра CD. Докажите, что построенное сечение – трапеция
4) Изобразите параллелепипед и постройте его сечение плоскостью, проходящей через точки  ,
,  и точку M на ребре CD, такую что MD:MC= 1:3. Докажите, что построенное сечение – трапеция.
и точку M на ребре CD, такую что MD:MC= 1:3. Докажите, что построенное сечение – трапеция.
3) Контрольная работа по геометрии 10 класс по главе « Площади поверхностей многогранников»
1) Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
2) Боковые ребра правильной четырёхугольной призмы равна 5, диагональ основания 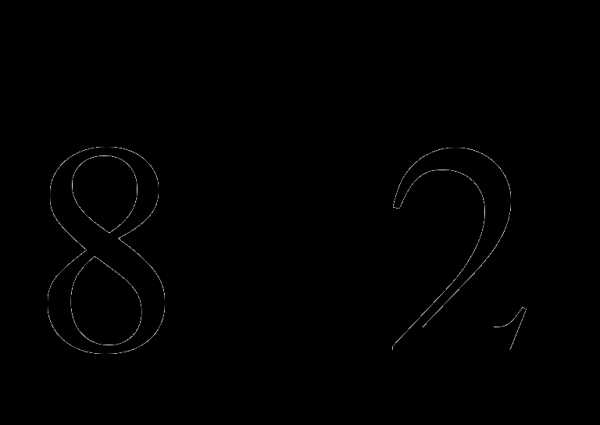 . Найти площадь полной поверхности
. Найти площадь полной поверхности
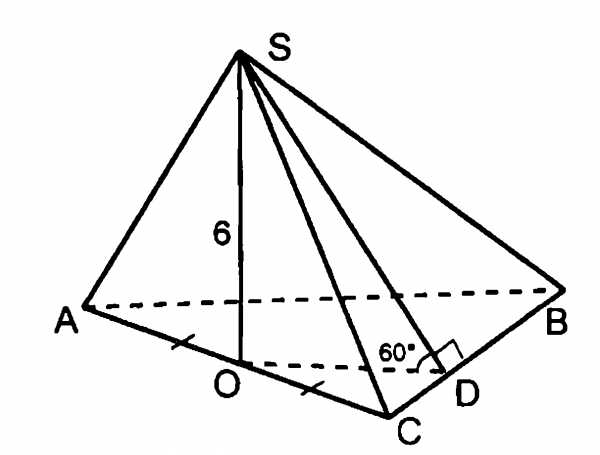
3)Найти площадь полной поверхности пирамиды, если SO- высота пирамиды, а ABCD- квадрат
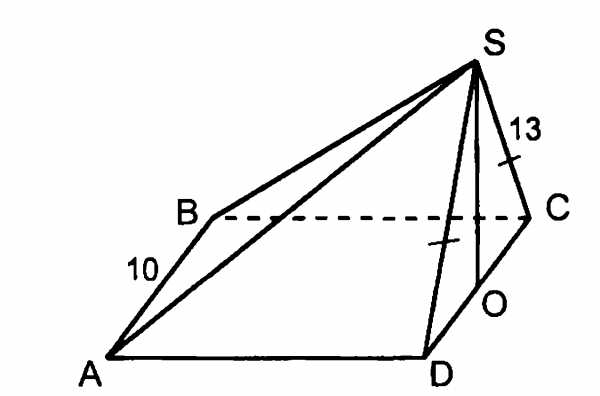
4)Стороны основания правильной шестиугольной пирамиды равны 16, боковые ребра равны 10. Найдите площадь боковой поверхности этой пирамиды
5)В основании прямой призмы лежит ромб с диагоналями, равными 15 и 36. Площадь ее поверхности равна 2100. Найдите боковое ребро этой призмы
6) В пирамиде МАВС боковое ребро МА перпендикулярно к плоскости основания АВС, а грань МВС составляет с ним угол 60о АВ=АС=10, ВС= 16. Найти площадь полной поверхности
1)Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 9 и 12, высота призмы равна 14. Найдите площадь ее поверхности
2) Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 7.
3)Найти площадь полной поверхности пирамиды, если ABC- правильный треугольник, SO –высота пирамиды
4)Стороны основания правильной шестиугольной пирамиды равны 18, боковые ребра равны 15. Найдите площадь боковой поверхности этой пирамиды
5) В основании прямой призмы лежит ромб с диагоналями, равными 16 и 30. Площадь ее поверхности равна 2588. Найдите боковое ребро этой призмы
6) Основанием пирамиды DABC является правильный треугольник ABC, сторона которого равна 10. Ребро DA перпендикулярно к плоскости ABC, а плоскость DBC составляет с плоскостью ABC угол 30о. Найти площадь полной поверхности.
4) Контрольная работа по алгебре(« Тригонометрические формулы»)
в)
1)а)
в)известно, что:
2)
2) Вычислить:
3)Упростить:
3) Упростить:
5) Найдите значение выражения , если .
5) Найдите значение выражения , если .
5) Контрольная работа по теме « Тригонометрические уравнения»
4)
Дано уравнение
а) Решите уравнение; б) Укажите корни уравнения, принадлежащие отрезку
4) Дано уравнение
а) Решите уравнение; б) Укажите корни уравнения, принадлежащие отрезку
5) Решите уравнение . В ответе напишите наименьший положительный корень
5) Решите уравнение . В ответе напишите наибольший отрицательный корень
6)Домашняя самостоятельная работа по теме « Простейшие тригонометрические уравнения»
3) 4)
1) 2)
3) 4)
4) а)
б)
4) а)
б)
5)
5)
7) Самостоятельная работа по теме «Простейшие тригонометрические уравнения»
г)
8) Самостоятельная работа по теме « Теоремы сложения. Синус и косинус двойного угла.»
3) Найдите значение выражения .
3) Найдите значение выражения
4) Найдите если
4) Найдите если
9) Самостоятельная работа по теме « Теоремы сложения. Синус и косинус двойного угла.»
3) Найдите значение выражения .
3) Найдите значение выражения
4) Найдите если
4) Найдите если
10) Самостоятельная работа по теме « Простейшие тригонометрические уравнения»
3) 4)
1) 2)
3) 4)
4) а)
б)
4) а)
б)
5)
5)
11) самостоятельная работа по теме «Поворот точки на единичной окружности»
б) М на угол α =
в) М на угол α =
г) М на угол α =
д) М на угол α =
2) Найдите координаты точки N, полученной поворотом точки Р ( 1; 0) на угол:
а)
на угол α =
ответ : N ( ; )

б)
на угол α =
ответ : N ( ; )
в)
на угол α =
ответ : N ( ; )
3) Записать все углы, на который нужно повернуть точки Р ( 1; 0), чтобы получилась точка М с координатами:
а)
М ( ; )
Ответ:
б)
М ( ; )
Ответ:

5)

б) М на угол α =
в) М на угол α =
г) М на угол α =
д) М на угол α =
2) Найдите координаты точки N, полученной поворотом точки Р ( 1; 0) на угол:
а)
на угол α =
ответ : N ( ; )

б)
на угол α =
ответ : N ( ; )
в)
на угол α =
ответ : N ( ; )
3) Записать все углы, на который нужно повернуть точки Р ( 1; 0), чтобы получилась точка М с координатами:
а)
М ( ; )
Ответ:
б)
М ( ; )
Ответ:

5)
Итоговая контрольная работа математике
Вариант 1
Найдите корень уравнения .
8
9
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Часть II
C1
Решить уравнение
А) Б)
С2
Дано уравнение
а) Решите уравнение; б) Укажите корни уравнения, принадлежащие отрезку
С3
Основанием прямой призмы ABCA1B1C1 является равнобедренный треугольник ABC, AB = AC = 5, BC = 8. Высота призмы равна 3. Найдите угол между прямой A1B и плоскостью BCC1.
infourok.ru
|
Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости» Вариант 1 1. Плоскость α проходит через середины боковых сторон АВ и СD трапеции АВСD — точки М и N. А) Докажите, что АD||α Б) Найдите ВС, если АD =10см, МN=8см 2. Прямая МА проходит через вершину квадрата АВСD и не лежит в плоскости квадрата. А) Докажите, что МА и ВС скрещивающиеся прямые Б) Найдите угол между прямыми МА и ВС, если угол МАD равен 45°. 3.Точка М не лежит в плоскости трапеции АВСD ( АD|| ВС). А) Докажите, что треугольники МАD и МВС имеют параллельные средние линии. Б) Найдите длины этих средних линий, если АD : ВС = 5 : 3, а средняя линия трапеции равна 16 см. 4*. Через вершину А квадрата АВСD проведена прямая КА, не лежащая в плоскости квадрата. А) Докажите, что КА и СD — скрещивающиеся Б) Найдите угол между прямыми КА и СD, если угол АКВ равен 85°, угол АВК равен 45° |
Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости» Вариант 2 1. Плоскость α проходит через основание АD трапеции АВСD. М и N — середины боковых сторон трапеции. А) Докажите, что МN|| α Б) Найдите АD, если ВС=4см, МN =6 см. 2. Прямая СD проходит через вершину треугольника АВС и не лежит в плоскости АВС. Е и F — середины отрезков АВ и ВС. А) Докажите, что прямые СD и ЕF — скрещивающиеся Б) Найдите угол между прямыми СD и ЕF, если угол DСА равен 60°. 3. Плоскость α пересекает стороны АВ и ВС треугольника АВС в точках М и N соответственно, причем АМ: МВ=3:4, СN:ВС=3:7. А)Докажите, что АС| α Б) Найдите АС, если МN= 16см. 4*. Точка М не лежит в плоскости ромба АВСD. А) докажите, что МС и АD — скрещивающиеся; Б) Найдите угол между МС и АD, если угол МВС равен 70°, угол ВМС равен 65° |
Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости» Вариант 1 1. Плоскость α проходит через середины боковых сторон АВ и СD трапеции АВСD — точки М и N. А) Докажите, что АD||α Б) Найдите ВС, если АD =10см, МN=8см 2. Прямая МА проходит через вершину квадрата АВСD и не лежит в плоскости квадрата. А) Докажите, что МА и ВС скрещивающиеся прямые Б) Найдите угол между прямыми МА и ВС, если угол МАD равен 45°. 3.Точка М не лежит в плоскости трапеции АВСD ( АD|| ВС). А) Докажите, что треугольники МАD и МВС имеют параллельные средние линии. Б) Найдите длины этих средних линий, если АD : ВС = 5 : 3, а средняя линия трапеции равна 16 см. 4*. Через вершину А квадрата АВСD проведена прямая КА, не лежащая в плоскости квадрата. А) Докажите, что КА и СD — скрещивающиеся Б) Найдите угол между прямыми КА и СD, если угол АКВ равен 85°, угол АВК равен 45° |
Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости» Вариант 2 1. Плоскость α проходит через основание АD трапеции АВСD. М и N — середины боковых сторон трапеции. А) Докажите, что МN|| α Б) Найдите АD, если ВС=4см, МN =6 см. 2. Прямая СD проходит через вершину треугольника АВС и не лежит в плоскости АВС. Е и F — середины отрезков АВ и ВС. А) Докажите, что прямые СD и ЕF — скрещивающиеся Б) Найдите угол между прямыми СD и ЕF, если угол DСА равен 60°. 3. Плоскость α пересекает стороны АВ и ВС треугольника АВС в точках М и N соответственно, причем АМ: МВ=3:4, СN:ВС=3:7. А)Докажите, что АС| α Б) Найдите АС, если МN= 16см. 4*. Точка М не лежит в плоскости ромба АВСD. А) докажите, что МС и АD — скрещивающиеся; Б) Найдите угол между МС и АD, если угол МВС равен 70°, угол ВМС равен 65° |
Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости» Вариант 1 1. Плоскость α проходит через середины боковых сторон АВ и СD трапеции АВСD — точки М и N. А) Докажите, что АD||α Б) Найдите ВС, если АD =10см, МN=8см 2. Прямая МА проходит через вершину квадрата АВСD и не лежит в плоскости квадрата. А) Докажите, что МА и ВС скрещивающиеся прямые Б) Найдите угол между прямыми МА и ВС, если угол МАD равен 45°. 3.Точка М не лежит в плоскости трапеции АВСD ( АD|| ВС). А) Докажите, что треугольники МАD и МВС имеют параллельные средние линии. Б) Найдите длины этих средних линий, если АD : ВС = 5 : 3, а средняя линия трапеции равна 16 см. 4*. Через вершину А квадрата АВСD проведена прямая КА, не лежащая в плоскости квадрата. А) Докажите, что КА и СD — скрещивающиеся Б) Найдите угол между прямыми КА и СD, если угол АКВ равен 85°, угол АВК равен 45° |
Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости» Вариант 2 1. Плоскость α проходит через основание АD трапеции АВСD. М и N — середины боковых сторон трапеции. А) Докажите, что МN|| α Б) Найдите АD, если ВС=4см, МN =6 см. 2. Прямая СD проходит через вершину треугольника АВС и не лежит в плоскости АВС. Е и F — середины отрезков АВ и ВС. А) Докажите, что прямые СD и ЕF — скрещивающиеся Б) Найдите угол между прямыми СD и ЕF, если угол DСА равен 60°. 3. Треугольник АВС и трапеция КМNР имеют общую среднюю линию ЕF, причем КР|| МN, ЕF|| АС. А) Докажите, что АС|| КР. Б) Найдите КР и МN, если КР : МN= 3:5, АС= 16см. 4*. Точка М не лежит в плоскости ромба АВСD. А) докажите, что МС и АD — скрещивающиеся; Б) Найдите угол между МС и АD, если угол МВС равен 70°, угол ВМС равен 65° |
4*. Через вершину А квадрата АВСD проведена прямая КА, не лежащая в плоскости квадрата. А) Докажите, что КА и СD — скрещивающиеся Б) Найдите угол между прямыми КА и СD, если угол АКВ равен 85°, угол АВК равен 45° |
4*. Точка М не лежит в плоскости ромба АВСD. А) докажите, что МС и АD — скрещивающиеся; Б) Найдите угол между МС и АD, если угол МВС равен 70°, угол ВМС равен 65° |
4*. Через вершину А квадрата АВСD проведена прямая КА, не лежащая в плоскости квадрата. А) Докажите, что КА и СD — скрещивающиеся Б) Найдите угол между прямыми КА и СD, если угол АКВ равен 85°, угол АВК равен 45° |
4*. Точка М не лежит в плоскости ромба АВСD. А) докажите, что МС и АD — скрещивающиеся; Б) Найдите угол между МС и АD, если угол МВС равен 70°, угол ВМС равен 65° |
nsportal.ru
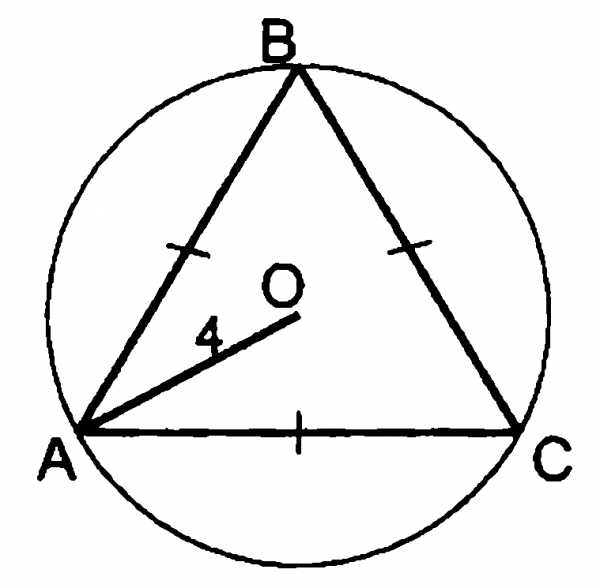
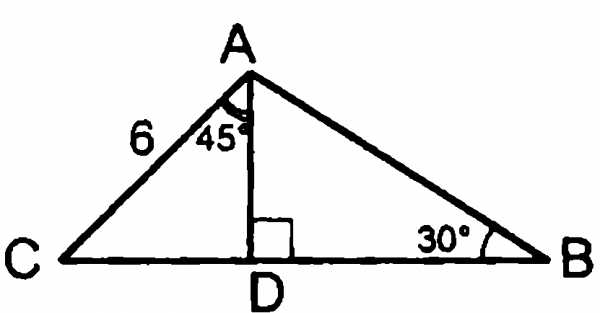
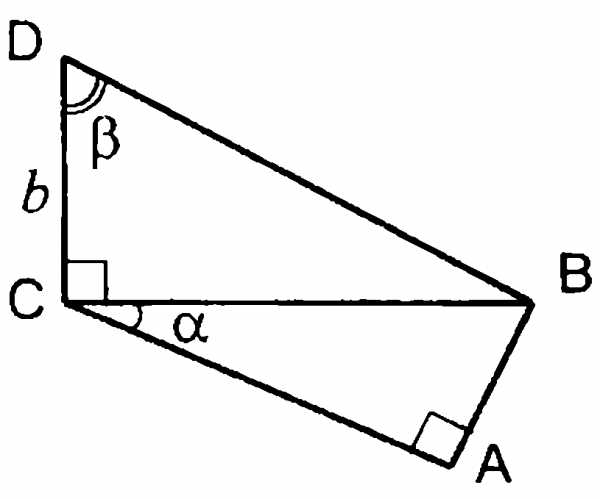 Найти стороны треугольника ABC
Найти стороны треугольника ABC