Самостоятельные и контрольные работы по геометрии 11 класс атанасян ответы – ГДЗ к учебнику геометрии для 11 класса Атанасяна Л.С. ОНЛАЙН

Самостоятельные и контрольные работы по геометрии 11 класс

КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ «Цилиндр. Конус. Сфера»

Вариант 1

1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь боковой поверхности цилиндра.

2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 60. Найдите площадь сечения, проходящего через две образующие, угол между которыми равен 45 и площадь боковой поверхности конуса.

3. Диаметр шара равен 4. Через конец диаметра проведена плоскость под углом 45 к нему. Найдите площадь сечения шара этой плоскостью.

4. В цилиндре проведена плоскость, параллельная оси и отсекающая от окружности основания дугу в 90. Диагональ сечения равна 10 см и удалена от оси на 4 см. Найдите площадь боковой поверхности цилиндра.

КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ «Цилиндр. Конус. Сфера»

Вариант 2

1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16 см². Найдите площадь боковой поверхности цилиндра.

2. Высота конуса равна 6см, угол при вершине осевого сечения равен 90. Найдите площадь сечения, проходящего через две образующие, угол между которыми равен 30 и площадь боковой поверхности конуса.

3. Площадь сечения шара плоскостью, проведенной через конец диаметра под углом 30 к нему, равна 75 см². Найдите диаметр шара.

4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 3 см, и стягивающей дугу 120. Плоскость сечения составляет с плоскостью основания угол 45. Найдите площадь боковой поверхности конуса.

КОНТРОЛЬНАЯ РАБОТА ПО ТЕМЕ «Цилиндр. Конус. Сфера»

Вариант 3

1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 25 см². Найдите площадь боковой поверхности цилиндра.

2. Высота конуса равна 9 см, угол при вершине осевого сечения равен 120. Найдите площадь сечения, проходящего через две образующие, угол между которыми равен 90 и площадь боковой поверхности конуса.

3. Длина линии пересечения сферы и плоскости, проходящей через конец диаметра под углом 60º к нему, равна 5 см. Найдите диаметр сферы.

4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 5 см, и стягивающей дугу 90. Плоскость сечения составляет с плоскостью основания угол 60. Найдите площадь боковой поверхности конуса.

Домашняя работа

1. Осевое сечение цилиндра – квадрат, диагональ которого равна 8 см. Найдите площадь боковой поверхности цилиндра.

2. Радиус основания конуса равен 10 см, а образующая наклонена к плоскости основания под углом 45. Найдите площадь сечения, проходящего через две образующие, угол между которыми 30 и площадь боковой поверхности конуса.

3. Диаметр шара равен 6. Через конец диаметра проведена плоскость под углом 30 к нему. Найдите длину линии пересечения сферы и плоскости.

4. В цилиндре проведена плоскость, параллельная оси и отсекающая от окружности основания дугу в 120. Диагональ сечения равна 20 см и удалена от оси на 3 см. Найдите площадь боковой поверхности цилиндра.

Домашняя работа

1. Осевое сечение цилиндра – квадрат, диагональ которого равна 8 см. Найдите площадь боковой поверхности цилиндра.

2. Радиус основания конуса равен 10 см, а образующая наклонена к плоскости основания под углом 45. Найдите площадь сечения, проходящего через две образующие, угол между которыми 30 и площадь боковой поверхности конуса.

3. Диаметр шара равен 6. Через конец диаметра проведена плоскость под углом 30 к нему. Найдите длину линии пересечения сферы и плоскости.

4. В цилиндре проведена плоскость, параллельная оси и отсекающая от окружности основания дугу в 120. Диагональ сечения равна 20 см и удалена от оси на 3 см. Найдите площадь боковой поверхности цилиндра.

Домашняя работа

1. Осевое сечение цилиндра – квадрат, диагональ которого равна 8 см. Найдите площадь боковой поверхности цилиндра.

2. Радиус основания конуса равен 10 см, а образующая наклонена к плоскости основания под углом 45. Найдите площадь сечения, проходящего через две образующие, угол между которыми 30 и площадь боковой поверхности конуса.

3. Диаметр шара равен 6. Через конец диаметра проведена плоскость под углом 30 к нему. Найдите длину линии пересечения сферы и плоскости.

4. В цилиндре проведена плоскость, параллельная оси и отсекающая от окружности основания дугу в 120. Диагональ сечения равна 20 см и удалена от оси на 3 см. Найдите площадь боковой поверхности цилиндра.

Домашняя работа

1. Осевое сечение цилиндра – квадрат, диагональ которого равна 8 см. Найдите площадь боковой поверхности цилиндра.

2. Радиус основания конуса равен 10 см, а образующая наклонена к плоскости основания под углом 45. Найдите площадь сечения, проходящего через две образующие, угол между которыми 30 и площадь боковой поверхности конуса.

3. Диаметр шара равен 6. Через конец диаметра проведена плоскость под углом 30 к нему. Найдите длину линии пересечения сферы и плоскости.

4. В цилиндре проведена плоскость, параллельная оси и отсекающая от окружности основания дугу в 120. Диагональ сечения равна 20 см и удалена от оси на 3 см. Найдите площадь боковой поверхности цилиндра.

Ответы к контрольной работе по теме «Тела вращения», 11 класс

1 вариант

1. 8 см².

2. 36см², 72 см².

3. см².

4. 48 см².

2 вариант

1. 64 см².

2. 18 см², 36см².

3. 20 см.

4. см².

3 вариант

1. 100 см².

2. 162 см², 162 см².

3. 10 см.

4. см².

4 вариант

1. 32 см².

2. 50 см², 100 см².

3. см.

4. 24 см².

Цилиндр, конус, шар

Готовимся к контрольной работе по теме «Цилиндр, конус и шар»

Задача 1. Осевое сечение цилиндра — квадрат. Площадь основания цилиндра равна 36π см². Найдите площадь полной поверхности цилиндра.

Решение. Из условия площадь основания цилиндра равна 36π = πR², то есть 36 = R², R=6.

Так как осевое сечение цилиндра – квадрат, значит, высота цилиндра равна диаметру его основания h=2R=12.

Подставляем найденные величины в формулу полной поверхности цилиндра S = 2πR(R+h) = 2π*6*(6+12) = 216π.

Ответ 216π.

Задача 2. Высота конуса равна 6 см. Угол при вершине осевого сечения равен 120º.

а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30º.

б) Найти площадь боковой поверхности конуса.

Решение. Из условия угол АРВ равен 120 градусам, значит, угол ОРВ равен 60 градусам, а угол РВО – 30 градусов. По свойству катета, лежащего против угла, равного 30 градусам РО = 0,5 РВ. Образующая РВ = 2*РО = 12см.

а) Найдём площадь сечения конуса плоскостью, проходящей через две образующие РВ и РС, угол между которыми равен 30º. Площадь треугольника РВС равна половине произведения двух сторон РВ и РС на синус угла между ними. Синус же 30 градусов равен 0,5. То есть получаем

S_РВС = 0,5*12*12*0,5 =36 см².

б) Найдём площадь боковой поверхности конуса. Для этого надо знать радиус конуса. Его найдём из треугольника РВО по теореме Пифагора

R²= ОВ²= РВ² – ОР² = 144 – 36 = 108, R=6 квадратных корней из трёх.

S_бок = Rl =*6 квадратных корней из трёх*12 = 72*ПИ* квадратный корень из трёх см².

Ответ а) 36.

б) 72*ПИ* квадратный корень из трёх

Задача 3. Диаметр шара равен 8. Через конец диаметра проведена плоскость под углом 45º к нему. Найдите длину линии пересечения сферы этой плоскостью.

Решение. Из условия следует, что радиус ОВ равен 4. В прямоугольном треугольнике ОО₁В катеты ОО₁ и О₁В равны. Тогда по теореме Пифагора можно найти их длину

О₁В²+ О₁В²=ОВ², 2О₁В²=4², 2О₁В²= 16, О₁В²= 8. О₁В=2*квадратный корень из двух.

Найдём длину окружности — линии пересечения сферы плоскостью. С = 2*ПИ*R = 22* квадратный корень из двух= 4*ПИ*квадратный корень из двух.

Ответ 4квадратный корень из двух.

Задача 4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 6 см, и стягивающей дугу 90°. Плоскость сечения составляет с плоскостью основания угол 60°. Найдите площадь боковой поверхности конуса.

 Решение. Из условия следует, что треугольник ВОС равнобедренный и прямоугольный, значит ОК = ВК = КС = 6:2 =3 см.

По теореме Пифагора найдём радиус основания конуса ОВ, ОК²+ КВ²=ОВ², 3²+ 3²=ОВ²,

ОВ²= 18. ОВ=3.

В треугольнике РОК угол РКО равен 60 градусам, по условию. Значит угол КРО равен 30 градусам РК = 2*ОК =6 см. Из треугольника РВК найдём образующую РВ по теореме Пифагора РВ²=РК²+ВК² = 6²+3² = 45. РВ=3.

Площадь боковой поверхности конуса будет равна S_бок = Rl =*3 *3= 9 см².

Ответ 9.

Задача 1. Осевое сечение цилиндра — квадрат. Площадь основания цилиндра равна 36π см². Найдите площадь полной поверхности цилиндра.

Задача 2. Высота конуса равна 6 см. Угол при вершине осевого сечения равен 120º.

а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30º.

Задача 3. Диаметр шара равен 8. Через конец диаметра проведена плоскость под углом 45º к нему. Найдите длину линии пересечения сферы этой плоскостью.

Задача 4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 6 см, и стягивающей дугу 90°. Плоскость сечения составляет с плоскостью основания угол 60°. Найдите площадь боковой поверхности конуса.

Задача 1. Осевое сечение цилиндра — квадрат. Площадь основания цилиндра равна 36π см². Найдите площадь полной поверхности цилиндра.

Задача 2. Высота конуса равна 6 см. Угол при вершине осевого сечения равен 120º.

а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30º.

Задача 3. Диаметр шара равен 8. Через конец диаметра проведена плоскость под углом 45º к нему. Найдите длину линии пересечения сферы этой плоскостью.

Задача 4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 6 см, и стягивающей дугу 90°. Плоскость сечения составляет с плоскостью основания угол 60°. Найдите площадь боковой поверхности конуса.

Задача 1. Осевое сечение цилиндра — квадрат. Площадь основания цилиндра равна 36π см². Найдите площадь полной поверхности цилиндра.

Задача 2. Высота конуса равна 6 см. Угол при вершине осевого сечения равен 120º.

а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30º.

Задача 3. Диаметр шара равен 8. Через конец диаметра проведена плоскость под углом 45º к нему. Найдите длину линии пересечения сферы этой плоскостью.

Задача 4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 6 см, и стягивающей дугу 90°. Плоскость сечения составляет с плоскостью основания угол 60°. Найдите площадь боковой поверхности конуса.

Задача 1. Осевое сечение цилиндра — квадрат. Площадь основания цилиндра равна 36π см². Найдите площадь полной поверхности цилиндра.

Задача 2. Высота конуса равна 6 см. Угол при вершине осевого сечения равен 120º.

а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30º.

Задача 3. Диаметр шара равен 8. Через конец диаметра проведена плоскость под углом 45º к нему. Найдите длину линии пересечения сферы этой плоскостью.

Задача 4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 6 см, и стягивающей дугу 90°. Плоскость сечения составляет с плоскостью основания угол 60°. Найдите площадь боковой поверхности конуса.

infourok.ru

Контрольно-измерительные материалы по геометрии 11 класс (профильный уровень) по учебнику «Геометрия 10-11» Л.С. Атанасян, В.Ф. Бутузов и др.

Приложение 1

Оценочные материалы

1.Контрольные работы

Контрольная работа №1 «Метод координат»

Вариант 1

1.Даны точки А(-3;1;4), В(1;-5;2), С(-4;6;2), D(2;-4;8).Вычислите расстояние между серединами отрезков АВ и СD.

2.Известны координаты трех точек А(-1;2;-5), В(3;-1;6) и С(4;5;-7). Определите координаты точки пересечения медиан треугольника АВС.

3.В кубе АВСDА₁В₁С₁D₁ точка М — центр грани ВВ₁С₁С. Найдите угол между прямыми АМ и DВ₁.

4.Вершины треугольника АВС имеют координаты А(-8;7;-4), В(-6;5;-5) и С(-5;3;-4). Найдите площадь треугольника АВС.

5*.Точки А(5;-1;2) и В(1;3;-4) симметричны относительно плоскости α. Напишите уравнение этой плоскости.

Вариант 2

1.Даны точки А(5;-1;3), В(3;-5;1), С(2;-6;4), D(-4;2;6). Вычислите расстояние между серединами отрезков АВ и СD.

2.Известны координаты трех точек А(2;-1;7), В(-4;3;-1) и С(-1;4;3). Определите координаты точки пересечения медиан треугольника АВС.

3.В кубе АВСDА₁В₁С₁D₁ точка М — центр грани АА₁В₁В. Найдите угол между прямыми DМ и С₁В.

4.Вершины треугольника АВС имеют координаты А(-5;2;-3), В(-3;1;-5) и С(-8;6;-3). Найдите площадь треугольника АВС.

5*.Точки А(-3;4;7) и В(1;-2;3) симметричны относительно плоскости α. Напишите уравнение этой плоскости.

Ответы

Контрольная работа №1 «Метод координат»

№1

№2

№3

№4

№5

Вариант 1

(2;2;-2)

arccos

2х-2у+3z-1=0

Вариант 2

(-1;2;3)

arccos

2х-3у-2z+15=0

Контрольная работа №2 «Цилиндр, конус, шар»

Вариант 1

1.Диаметр основания цилиндра равен 10 см. На расстоянии 3 см от оси цилиндра проведено сечение, параллельное оси и имеющее форму квадрата. Вычислите площадь этого сечения и площадь осевого сечения цилиндра.

2.Площадь основания конуса равна 15 см², а площадь боковой поверхности 17 см². Найдите площадь осевого сечения конуса.

3.В усеченном конусе радиус меньшего основания равен R, высота h, угол между образующей и большим основанием равен α. Вычислите площадь боковой поверхности конуса.

4.Сфера касается одной из параллельных плоскостей и пересекает другую плоскость по окружности радиуса r. Найдите радиус сферы, если расстояние между плоскостями равно а.

5.Сфера, заданная уравнением х²+у²+z²-2х+6у-4z=11, пересечена плоскостью с уравнением х=4. Вычислите площадь сечения и площадь поверхности сферы.

Вариант 2

1.Радиус основания цилиндра, осевое сечение которого квадрат, равен 10 см. На расстоянии 8 см от оси цилиндра проведено сечение, параллельное оси. Вычислите площадь этого сечения и площадь осевого сечения цилиндра.

2.Площадь основания конуса равна 12 см², а площадь боковой поверхности 13 см². Найдите площадь осевого сечения конуса.

3.В усеченном конусе радиус меньшего основания равен R, образующая l, угол между высотой конуса и его образующей равен α. Вычислите площадь боковой поверхности конуса.

4.Сфера радиуса R касается одной из параллельных плоскостей и пересекает другую плоскость по окружности. Найдите радиус этой окружности, если расстояние между плоскостями равно а.

5.Сфера, заданная уравнением х²+у²+z²-4х+2у+6z=7, пересечена плоскостью с уравнением у=-3. Вычислите площадь сечения и площадь поверхности сферы.

Ответы

Контрольная работа №2 «Цилиндр, конус, шар»

№1

№2

№3

№4

№5

Вариант 1

64см² ; 80см²

8/π см²

16π; 100π

Вариант 2

240см²; 400см²

5/π см²

17π; 84π

Контрольная работа №3

«Объемы прямого параллелепипеда, прямой призмы и цилиндра»

Вариант 1

1.В прямоугольном параллелепипеде диагонали трех граней, выходящих из одной вершины, равны 7см, 8см и 9см. Вычислите объем параллелепипеда.

2.Площадь большего диагонального сечения правильной шестиугольной призмы равна площади ее основания. Найдите объем призмы, если сторона ее основания равна а.

3.В основании прямой призмы лежит трапеция. Площади параллельных боковых граней призмы равны S₁ и S₂, а расстояние между ними равно а. Вычислите объем призмы.

4.Периметры боковых граней прямоугольного параллелепипеда равны 16см и 24см. Найдите объем параллелепипеда, имеющего наибольшую боковую поверхность.

5.Прямоугольник с диагональю, равной 2см, вращается вокруг одной из сторон. Вычислите объем тела вращения, если этот объем имеет наибольшее возможное значение.

Вариант 2

1.В прямоугольном параллелепипеде диагонали трех граней, выходящих из одной вершины, равны 5см, 7см и 8см. Вычислите объем параллелепипеда.

2.Площадь меньшего диагонального сечения правильной шестиугольной призмы равна площади ее основания. Найдите объем призмы, если ее высота равна h.

3.В основании прямой призмы лежит трапеция. Объем призмы равен V.Площади параллельных боковых граней призмы равны S₁ и S₂. Вычислите расстояние между ними.

4.Периметры боковых граней прямоугольного параллелепипеда равны 20см и 28см. Найдите объем параллелепипеда, имеющего наибольшую боковую поверхность.

5.Прямоугольник с диагональю, равной 3см, вращается вокруг одной из сторон. Вычислите объем тела вращения, если этот объем имеет наибольшее возможное значение.

Ответы

Контрольная работа №3

«Объемы прямого параллелепипеда, прямой призмы и цилиндра»

№1

№2

№3

№4

№5

Вариант 1

48см³

105см³

16π см³

Вариант 2

20см³

192см³

54π см³

Контрольная работа №4

«Объемы наклонной призмы, пирамиды, конуса и шара»

Вариант 1

1.В основании призмы лежит треугольник, у которого одна сторона равна 2см, а две другие по 3см.Боковое ребро равно 6см и составляет с плоскостью основания угол 60º. Найдите объем призмы.

2.Сторона основания правильной треугольной пирамиды равна а, боковое ребро равно в. Найдите объем пирамиды.

3.Радиусы оснований усеченного конуса равны 5см и 20см, образующая равна 17см. Найдите объем усеченного конуса.

4.Сечение, перпендикулярное диаметру шара, делит этот диаметр в отношении 1:2. Вычислите объем меньшего шарового сегмента, отсекаемого от шара, если площадь поверхности шара равна 144π см².

5.В основании пирамиды лежит ромб со стороной а и углов 60º. Одна из боковых граней перпендикулярна основанию, а две соседние с ней грани образуют с основанием двугранные углы по 30º.Найдите объем пирамиды.

Вариант 2

1.В основании призмы лежит треугольник, у которого одна сторона равна 6см, а две другие по 5см.Боковое ребро равно 4см и составляет с плоскостью основания угол 45º. Найдите объем призмы.

2.Сторона основания правильной четырехугольной пирамиды равна а, боковое ребро равно в. Найдите объем пирамиды.

3.Радиусы оснований усеченного конуса равны 5см и 13см, образующая равна 17см. Найдите объем усеченного конуса.

4.Сечение, перпендикулярное диаметру шара, делит этот диаметр в отношении 1:3. Площадь поверхности шара равна 144π см². Вычислите объем большего шарового сегмента, отсекаемого от шара.

5.В основании пирамиды лежит ромб со стороной а и углов 30º. Одна из боковых граней перпендикулярна основанию, а две соседние с ней грани образуют с основанием двугранные углы по 45º.Найдите объем пирамиды.

Ответы

Контрольная работа №4

«Объемы наклонной призмы, пирамиды, конуса и шара»

№1

№2

№3

№4

№5

Вариант 1

6см³

1400π см³

см³

Вариант 2

24см³

1295π см³

см³

Итоговая контрольная работа

Вариант 1

В правильной четырехугольной пирамиде МАВСD сторона основания равна 6, а боковое ребро 5. Найдите:

1. площадь боковой поверхности пирамиды;

2. объем пирамиды;

3. угол наклона боковой грани к плоскости основания;

4. скалярное произведение векторов ;

5. площадь описанной около пирамиды сферы;

6. *угол между ВD и плоскостью DMC.

Вариант 2

В правильной четырехугольной пирамиде МАВСD боковое ребро равно 8 и наклонено к плоскости основания под углом 60º. Найдите:

1. площадь боковой поверхности пирамиды;

2. объем пирамиды;

3. угол между противоположными боковыми гранями;

4. скалярное произведение векторов  , где Е – середина DС;

5. объем описанного около пирамиды шара;

6. *угол между боковым ребром АМ и плоскостью DМС.

Ответы

Итоговая контрольная работа

№1

№2

№3

№4

№5

№6

Вариант 1

48

12

arccos

36

arcsin

Вариант 2

6

12

arccos

-12

-2)³

arcsin

2.Зачеты

Зачет по теме «Векторы в пространстве»

Вопросы к зачету:

1. Дайте определение: вектора; коллинеарных векторов; сонаправленных векторов; противоположно направленных векторов; компланарных векторов; произведения вектора на число.

2. Опишите с помощью чертежа: правило треугольника сложения векторов; правило параллелограмма сложения векторов; правило вычитания векторов; правило параллелепипеда для сложения трех некомпланарных векторов

3. Сформулируйте: признак компланарности векторов; теорему о разложении вектора по трем некомпланарным векторам.

Задания для зачета

Вариант 1.

1. Верно ли, что векторы, лежащие на боковых ребрах призмы, коллинеарны?

2. Могут ли три компланарных вектора лежать на трех взаимно перпендикулярных прямых?

3. Верно ли, что векторы, лежащие на двух прямых, перпендикулярных к третьей, коллинеарны?

4. Могут ли три вектора, один из которых является суммой двух других, быть некомпланарными?

5. Точки А и С симметричны относительно плоскости α, а точки В и D симметричны относительно прямой АС. Назовите вектор, равный вектору

6. Даны ненулевые векторы , , некомпланарны. Назовите два данных вектора, которые вместе с вектором образуют тройку некомпланарных векторов, если =2.

7. Назовите вектор, равный + —

8. В параллелепипеде АВСDА₁В₁С₁D₁ назовите вектор, равный — — + .

Вариант 2.

1. Верно ли, что векторы, лежащие на боковых ребрах пирамиды, коллинеарны?

2. Могут ли три некомпланарных вектора лежать на трех параллельных прямых?

3. Верно ли, что векторы, лежащие в двух параллельных плоскостях, коллинеарны?

4. Могут ли три вектора, один из которых является разностью двух других, быть некомпланарными?

5. Точки А и С симметричны относительно плоскости α, а точки В и D симметричны относительно прямой АС. Назовите вектор, равный вектору

6. Даны ненулевые векторы , , некомпланарны. Назовите два данных вектора, которые вместе с вектором образуют тройку некомпланарных векторов, если = — 3.

7. Назовите вектор, равный + —

8. В параллелепипеде АВСDА₁В₁С₁D₁ назовите вектор, равный — — + .

Зачет по теме «Метод координат в пространстве»

Вопросы к зачету:

1. 1. Дайте определение: радиус-вектора точки. Назовите координаты радиус-вектора точки А(а₁;а₂;а₃).

   2. Сформулируйте: правило вычисления координат вектора по координатам его концов.

   3. Запишите формулу: координат середины отрезка; разложения вектора {х;у;z} по координатным векторам; длины вектора; Расстояния между двумя точками.

   4. Дайте определение: скалярного произведения векторов в пространстве.

   5. Запишите формулу: вычисления скалярного произведения двух векторов по их координатам.

   6. Перечислите: виды движений в пространстве и виды симметрии в пространстве.

Задания для зачета

Вариант 1.

1. 1. 1. Может ли вектор с тремя ненулевыми координатами быть параллелен одной из координатных плоскостей?

      2. Дан вектор {-1;2;0}. Назовите координатный вектор, образующий с вектором тупой угол.

      3. Закончите утверждение: «Если две точки симметричны относительно плоскости Охz , то их ординаты…».

      4. Верно ли, что точки симметричны относительно оси Оz , имеют противоположные аппликаты?

      5. Может ли вектор, коллинеарный одному из координатных векторов, иметь ровно одну ненулевую координату?

      6. При зеркальной симметрии куба АВСDА₁В₁С₁D₁ относительно одной из плоскостей его симметрии, ребро АА₁ отображается на ребро ВА. Назовите плоскость симметрии.

      7. Закончите утверждение: «Если вектор лежит на прямой а, то при параллельном переносе на вектор прямая а…».

      8. Закончите утверждение: «Если при осевой симметрии плоскость отображается на себя, то она перпендикулярна к оси симметрии либо …».

Вариант 2.

1. 1. 1. Может ли вектор с тремя ненулевыми координатами быть перпендикулярен к одной из координатных плоскостей?

      2. Дан вектор {-1;2;0}. Назовите координатный вектор, образующий с вектором острый угол.

      3. Закончите утверждение: «Если две точки симметричны относительно оси Оz , то они имеют равные…».

      4. Верно ли, что точки симметричны относительно плоскости Охz , имеют противоположные ординаты?

      5. Может ли вектор, коллинеарный одному из координатных векторов, иметь ровно две ненулевые координаты?

      6. При зеркальной симметрии куба АВСDА₁В₁С₁D₁ относительно одной из плоскостей его симметрии, ребро ВВ₁ отображается на ребро ВА. Назовите плоскость симметрии.

      7. Закончите утверждение: «Если вектор лежит на прямой, параллельной прямой а, то при параллельном переносе на вектор прямая а…».

      8. Закончите утверждение: «Если при зеркальной симметрии прямая отображается на себя, то она лежит в плоскости симметрии либо …».

Зачет по теме «Цилиндр. Конус. Шар»

Вопросы к зачету:

1. Дайте определение: радиус-вектора точки. Назовите координаты радиус-вектора точки А(а₁;а₂;а₃).

2. Сформулируйте: правило вычисления координат вектора по координатам его концов.

3. Запишите формулу: координат середины отрезка; разложения вектора {х;у;z} по координатным векторам; длины вектора; Расстояния между двумя точками.

4. Дайте определение: скалярного произведения векторов в пространстве.

5. Запишите формулу: вычисления скалярного произведения двух векторов по их координатам.

6. Перечислите: виды движений в пространстве и виды симметрии в пространстве.

Задания для зачета

Вариант 1.

1. Может ли вектор с тремя ненулевыми координатами быть параллелен одной из координатных плоскостей?

2. Дан вектор {-1;2;0}. Назовите координатный вектор, образующий с вектором тупой угол.

3. Закончите утверждение: «Если две точки симметричны относительно плоскости Охz , то их ординаты…».

4. Верно ли, что точки симметричны относительно оси Оz , имеют противоположные аппликаты?

5. Может ли вектор, коллинеарный одному из координатных векторов, иметь ровно одну ненулевую координату?

6. При зеркальной симметрии куба АВСDА₁В₁С₁D₁ относительно одной из плоскостей его симметрии, ребро АА₁ отображается на ребро ВА. Назовите плоскость симметрии.

7. Закончите утверждение: «Если вектор лежит на прямой а, то при параллельном переносе на вектор прямая а…».

8. Закончите утверждение: «Если при осевой симметрии плоскость отображается на себя, то она перпендикулярна к оси симметрии либо …».

Вариант 2.

1. Может ли вектор с тремя ненулевыми координатами быть перпендикуляре к одной из координатных плоскостей?

2. Дан вектор {-1;2;0}. Назовите координатный вектор, образующий с вектором острый угол.

3. Закончите утверждение: «Если две точки симметричны относительно оси Оz , то они имеют равные…».

4. Верно ли, что точки симметричны относительно плоскости Охz , имеют противоположные ординаты?

5. Может ли вектор, коллинеарный одному из координатных векторов, иметь ровно две ненулевые координаты?

6. При зеркальной симметрии куба АВСDА₁В₁С₁D₁ относительно одной из плоскостей его симметрии, ребро ВВ₁ отображается на ребро ВА. Назовите плоскость симметрии.

7. Закончите утверждение: «Если вектор лежит на прямой, параллельной прямой а, то при параллельном переносе на вектор прямая а…».

8. Закончите утверждение: «Если при зеркальной симметрии прямая отображается на себя, то она лежит в плоскости симметрии либо …».

Зачет по теме «Объемы тел»

Вопросы к зачету:

Запишите формулу:

— объема прямоугольного параллелепипеда;

— объема куба;

— объема цилиндра;

— объема конуса;

— объема пирамиды;

— объема шара;

— объема усеченной пирамиды;

— объема усеченного конуса;

— площади сферы.

Задания для зачета

Вариант 1.

1. Верно ли, что прямая и наклонная призмы с соответственно равными основаниями могут иметь равные объемы?

2. Могут ли два цилиндра с равными объемами иметь неравные радиусы?

3. Основание пирамиды SАВСD – ромб АВСD. Определите, какую часть объема данной пирамиды составляет объем пирамиды SАВD?

4. Определите, цилиндром, конусом или усеченным конусом является данное тело, если сечение, параллельное основанию и делящее высоту пополам, делит данное тело на два тела с равными объемами.

5. Верно ли, что отношение высот двух пирамид с равными основаниями равно отношению объемов пирамид?

6. Может ли плоскость, делящая объем шара пополам, делить поверхность шара на части неравной площади?

7. Два цилиндра с радиусами r₁ и r₂ и объемами V₁ и V₂ имеют равные площади осевых сечений. Сравните V₁ и V₂ , если r₁ > r₂.

Вариант 2.

1. Верно ли, что правильная и неправильная пирамиды с равными основаниями могут иметь неравные объемы?

2. Могут ли два шара с равными объемами иметь неравные радиусы?

3. Основание пирамиды SАВСD – ромб АВСD. Определите, какую часть объема данной пирамиды составляет объем пирамиды SСОD, где О – точка пересечения диагоналей ромба АВСD.

4. Определите, цилиндром, конусом или усеченным конусом является данное тело, если сечение, параллельное основанию и делящее объем данного тела пополам, проходит через середину его высоты.

5. Верно ли, что отношение сторон оснований двух правильных треугольных пирамид с равными высотами равно отношению объемов пирамид?

6. Может ли плоскость, делящая поверхность шара пополам, делить шар на два тела с неравными объемами ?

7. Два цилиндра с радиусами r₁ и r₂ и объемами V₁ и V₂ имеют равные площади осевых сечений. Сравните r₁ и r₂ , если V₁ < V₂ .

infourok.ru

Контрольные и самостоятельные работы по всем темам геометрии 10-11.

Контрольные и самостоятельные работы

по геометрии

для 10-11 классов

средней (полной) общеобразовательной школы

Подготовила

учитель математики

МБОУ Алексеево-Лозовская СОШ

Шконда И.А.

2014– 2015 учебный год

.

Контрольные и самостоятельные работы по всем темам курса геометрии 10-11 го класса.

Контрольные и самостоятельные работы по всем темам курса геометрии 10-11 го класса средней общеобразовательной школы разработаны в двух вариантах.( по УМК Л.С. Атанасян; мет. пособие С.М.Саакян, В.Ф.Бутузов) Общее число контрольных работ в 10 классе – 4; самостоятельных работ 6. В 11 классе число контрольных работ– 5; самостоятельных работ -5. Время, отводимое на каждую контрольную работу, – 1 час; самостоятельную работу 15-20 минут.

Контрольные работы 10 класс

1. Контрольная работа № 1 «Параллельность прямой и плоскости».

2. Контрольная работа № 2. «Параллельность плоскостей».

3. Контрольная работа № 3 «Перпендикулярность прямых и плоскостей».

4. Контрольная работа № 4 «Многогранники».

Самостоятельные работы 10 класс

1. 1. Самостоятельная работа № 1«Аксиомы стереометрии и их следствия»

   2. Самостоятельная работа № 2«Параллельность прямых; прямой и плоскости

   3. Самостоятельная работа № 3«Перпендикулярность прямой и плоскости»

   4. Самостоятельная работа № 4 « Перпендикуляр и наклонная»

   5. Самостоятельная работа № 5«Понятие многогранника. Призма»

   6. Самостоятельная работа № 6«Пирамида»

11 класс

1. Контрольная работа № «Координаты точки и координаты вектора»

2. Контрольная работа № 2 «Скалярное произведение векторов. Движения»

3. Контрольная работа № 3 «Цилиндр, конус и шар»

4. Контрольная работа № «Объём призмы, цилиндра, пирамиды и конуса»

5. Контрольная работа № 5 «Объём шара и площадь сферы».

Самостоятельные работы 11 класс

1. Самостоятельная работа № 1 «Координаты точки и координаты вектора».

2. Самостоятельная работа № 2 «Скалярное произведение векторов».

3. Самостоятельная работа № 3 «Цилиндр».

4. Самостоятельная работа № 4 «Объём прямоугольного параллелепипеда».

5. Самостоятельная работа № 5 «Объём наклонной призмы, пирамиды и конуса».

Литература:

1. Геометрия 10-11. Авторы: А.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев .

2. Изучение геометрии в 10-11 классах. Авторы: С.М.Саакян, В.Ф. Бутузов

Контрольные и самостоятельные работы по геометрии в 10 классе

Контрольная работа № 1

«Параллельность прямой и плоскости»

ВАРИАНТ 1

ВАРИАНТ 2

1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках E и F соответственно.

а) Каково взаимное расположение прямых EF и АВ?

б) Чему равен угол между прямыми EF и АВ, если угол АВС равен 150⁰? Ответ обоснуйте.

2. Дан пространственный четырёхугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырёхугольника соединены последовательно отрезками.

а) Выполните рисунок к задаче.

б) Докажите, что полученный четырёхугольник – ромб.

1. Треугольники АВС и ADC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, точка К – середина DC.

а) Каково взаимное расположение прямых РК и АВ?

б) Чему равен угол между прямыми РК и АВ, если угол АВС равен 40⁰ и угол ВСА равен 80⁰? Ответ обоснуйте.

2. Дан пространственный четырёхугольник ABCD, М и N – середины сторон АВ и ВС соответственно, точка Е принадлежит стороне CD, точка К принадлежит стороне DA, DE : EC = 1 : 2, DK : KA = 1 : 2.

а) Выполните рисунок к задаче.

б) Докажите, что четырёхугольник MNEK – трапеция.

Контрольная работа № 2

«Параллельность прямых и плоскостей»

ВАРИАНТ 1

ВАРИАНТ 2

1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая.

2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А₁ и А₂ соответственно, прямая m – в точках В₁ и В₂. Найдите длину отрезка А₂В₂, если А₁В₁ = 12 см, В₁О : ОВ₂ = 3 : 4.

3. Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью, проходящей через точки M, N и К, являющиеся серединами рёбер АВ, ВС и DD₁.

1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая.

2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А₁ и А₂ соответственно, прямая m – в точках В₁ и В₂. Найдите длину отрезка А₁В₁,если А₂В₂ = 15 см, ОВ₁ : ОВ₂ = 3 : 5.

3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N , являющиеся серединами рёбер DС и ВС, и точку К, принадлежащую прямой DA, такую, что АК : КD = 1 : 3.

Контрольная работа № 3

«Перпендикулярность прямых и плоскостей»

ВАРИАНТ 1

ВАРИАНТ 2

1. Диагональ куба равна 6 см. Найдите:

а) ребро куба;

б) косинус угла между диагональю куба и плоскостью одной из его граней.

2. Сторона AB ромба ABCD равна а, один из углов ромба равен 60⁰. Через сторону AB проведена плоскость α на расстоянии а/2 от точки D.

а) Найдите расстояние от точки С до плоскости α.

б) Покажите на рисунке линейный угол двугранного угла DАВМ, где М принадлежит плоскости α.

в) Найдите синус угла между плоскостью ромба и плоскостью α.

1. Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна 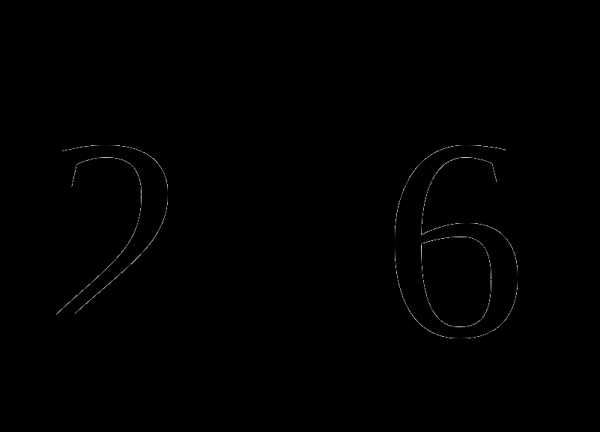см, а его измерения относятся как 1 : 1 : 2. Найдите:

а) измерения параллелепипеда;

б) синус угла между диагональю параллелепипеда и плоскостью его основания.

2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии а/2 от точки В.

а) Найдите расстояние от точки С до плоскости α.

б) Покажите на рисунке линейный угол двугранного угла ВАDМ, где М принадлежит плоскости α.

в) Найдите синус угла между плоскостью квадрата и плоскостью α.

Контрольная работа № 4

«Многогранники»

ВАРИАНТ 1

ВАРИАНТ 2

1. Основанием пирамиды DABC является правильный треугольник ABC, сторона которого равна а. Ребро DА перпендикулярно к плоскости ABC, а плоскость BCD составляет с плоскостью ABC угол 30⁰. Найдите площадь боковой поверхности пирамиды.

2. Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁^{является ромб ABCD, сторона которого равна а и угол равен 600. Плоскость АC₁D₁ составляет с плоскостью основания угол 600. Найдите:}

а) высоту ромба;

б) высоту параллелепипеда;

в) площадь боковой поверхности параллелепипеда;

г) площадь поверхности параллелепипеда.

1. Основанием пирамиды МABCD является квадрат ABCD, ребро МD перпендикулярно к плоскости основания, AD = DМ = а. Найдите площадь поверхности пирамиды.

2. Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁^{является параллелограмм ABCD, стороны которого равны 2а и 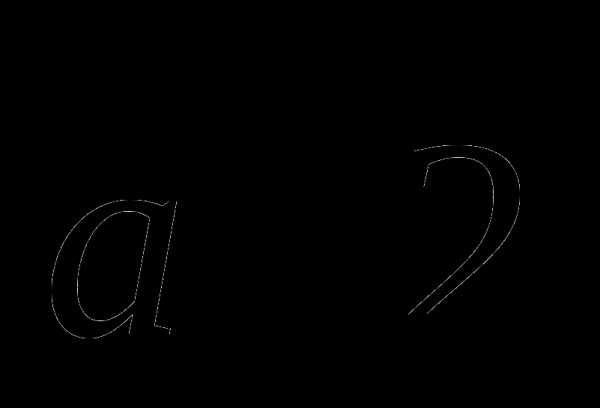, острый угол равен 450. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:}

а) меньшую высоту параллелограмма;

б) угол между плоскостью АВС₁ и плоскостью основания;

в) площадь боковой поверхности параллелепипеда;

г) площадь поверхности параллелепипеда.

Самостоятельная работа № 1

«Аксиомы стереометрии и их следствия»

ВАРИАНТ 1

ВАРИАНТ 2

1. Даны четыре точки, из которых три лежат на одной прямой. Верно ли утверждение, что все четыре точки лежат в одной плоскости? Ответ обоснуйте.

2. а) Докажите, что все вершины четырёхугольника ABCD лежат в одной плоскости, если его диагонали АС и BD пересекаются.

б) Вычислите площадь четырёхугольника, если его диагонали АС и BD взаимно перпендикулярны, АС = 10 см, BD = 12 см.

1. Даны две пересекающиеся прямые. Верно ли утверждение, что все прямые, пересекающие данные, лежат в одной плоскости? Ответ обоснуйте.

2. а) Дан прямоугольник ABCD, О – точка пересечения его диагоналей. Известно, что точки А, В и О лежат в плоскости α. Докажите, что точки С и D также лежат в плоскости α.

б) Вычислите площадь прямоугольника, если АС = 8 см, < АОВ = 60⁰.

Самостоятельная работа № 2

«Параллельность прямых, прямой и плоскости»

ВАРИАНТ 1

ВАРИАНТ 2

Дан треугольник АВС, Е є АВ, К є ВС,

ВЕ : ВА = ВК : ВС = 2 : 5.

Через прямую АС проходит плоскость α,

не совпадающая с плоскостью треугольника АВС.

а) Докажите, что ЕК || α.

б) Найдите длину отрезка АС, если ЕК = 4 см

Дан треугольник АВС, М є АВ, К є ВС,

ВМ : МА = 3 : 4.

Через прямую МК проходит плоскость α,

параллельная прямой АС.

а) Докажите, что ВС : ВК = 7 : 3.

б) Найдите длину отрезка МК, если АС = 14 см.

Самостоятельная работа № 3

«Перпендикулярность прямой и плоскости»

ВАРИАНТ 1

ВАРИАНТ 2

1. Прямая АВ перпендикулярна плоскости α, М и К – произвольные точки плоскости α. Докажите, что АВ перпендикулярна прямой МК.

2. Треугольник АВС правильный, точка О – его центр. Прямая ОМ перпендикулярна к плоскости АВС.

а) Докажите, что МА = МВ = МС.

б) Найдите МА, если АВ = 6 см, МО = 2 см.

1. Прямая МА перпендикулярна к плоскости треугольника АВС. Докажите, что МА перпендикулярна прямой ВС.

2. Четырёхугольник АВСD – квадрат, точка О – его центр. Прямая ОМ перпендикулярна к плоскости квадрата.

а) Докажите, что МА = МВ = МС = MD.

б) Найдите МА, если АВ = 4 см, ОМ = 1 см

Самостоятельная работа № 4

«Перпендикуляр и наклонные. Угол между прямой и плоскостью»

ВАРИАНТ 1

ВАРИАНТ 2

Из точки М проведён перпендикуляр МВ, равный 4 см, к плоскости прямоугольника АВСD. Наклонные МА и МС образуют с плоскостью прямоугольника углы 45⁰ и 30⁰ соответственно.

а) Докажите, что треугольники МАD и МСD прямоугольные.

б) Найдите стороны прямоугольника.

в) Докажите, что треугольник ВDС является проекцией треугольника МDС на плоскость прямоугольника, и найдите его площадь.

Из точки М проведён перпендикуляр МD, равный 6 см, к плоскости квадрата АВСD. Наклонная МВ образует с плоскостью квадрата угол 60⁰.

а) Докажите, что треугольники МАВ и МСВ прямоугольные.

б) Найдите сторону квадрата.

в) Докажите, что треугольник АВD является проекцией треугольника МАВ на плоскость квадрата, и найдите его площадь.

Самостоятельная работа № 5

«Понятие многогранника. Призма»

ВАРИАНТ 1

ВАРИАНТ 2

Сторона основания правильной четырёхугольной призмы равна а, диагональ призмы образует с плоскостью основания угол 45⁰. Найдите:

а) диагональ призмы;

б) угол между диагональю призмы и плоскостью боковой грани;

в) площадь боковой поверхности призмы;

г) площадь сечения призмы плоскостью, проходящей через сторону нижнего основания и противоположную сторону верхнего основания.

Диагональ правильной четырёхугольной призмы равна а и образует с плоскостью боковой грани угол 30⁰. Найдите:

а) сторону основания призмы;

б) угол между диагональю призмы и плоскостью основания;

в) площадь боковой поверхности призмы;

г) площадь сечения призмы плоскостью, проходящей через диагональ основания параллельно диагонали призмы.

Самостоятельная работа № 6

«Пирамида»

ВАРИАНТ 1

ВАРИАНТ 2

Высота правильной треугольной пирамиды равна 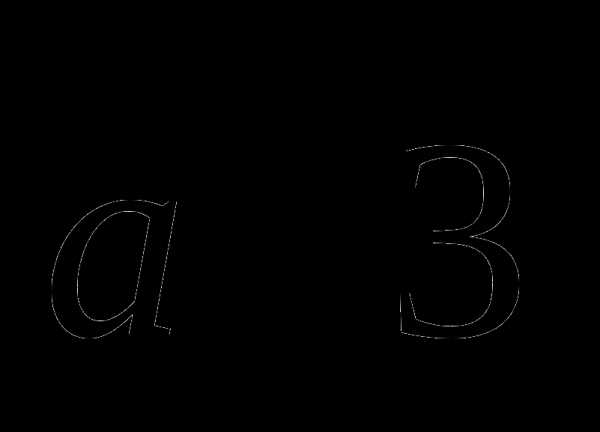, радиус окружности, описанной около её основания, 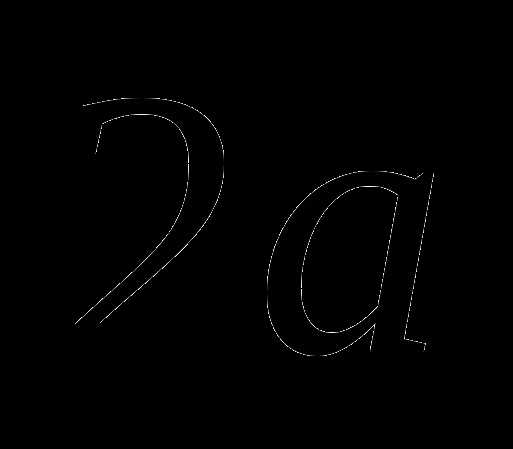. Найдите:

а) апофему пирамиды;

б) угол между боковой гранью и основанием;

в) площадь боковой поверхности;

г) плоский угол при вершине пирамиды.

Апофема правильной четырёхугольной пирамиды равна 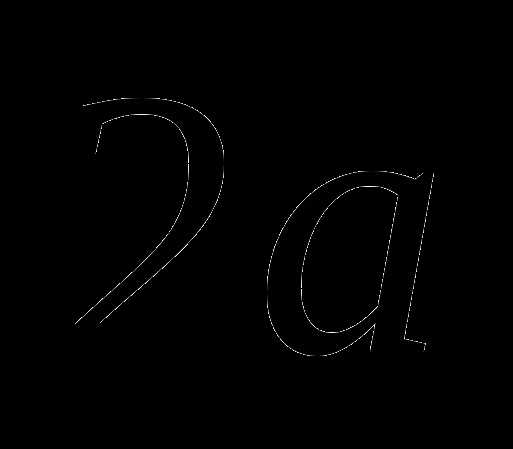, высота пирамиды равна 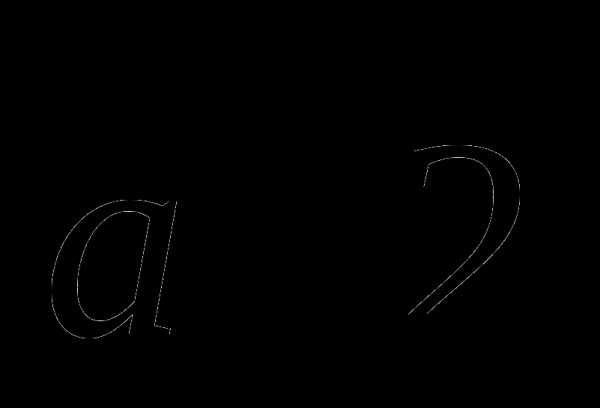. Найдите:

а) сторону основания пирамиды;

б) угол между боковой гранью и основанием;

в) площадь поверхности пирамиды;

г) расстояние от центра основания пирамиды до плоскости боковой грани

Контрольные и самостоятельные работы по геометрии в 11классе

Контрольная работа № 1

«Координаты точки и координаты вектора»

ВАРИАНТ 1

ВАРИАНТ 2

1. ВАРИАНТ 1

1. Найдите координаты вектора 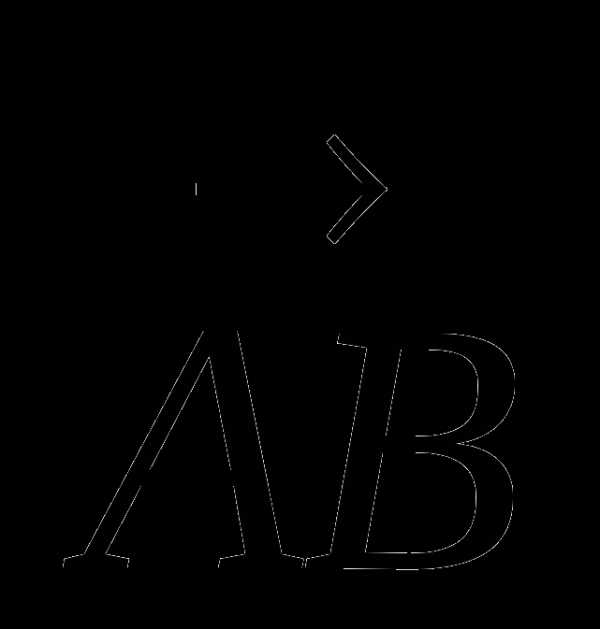, если А(5; −1; 3), В(2; −2; 4).

2. Даны векторы . Найдите .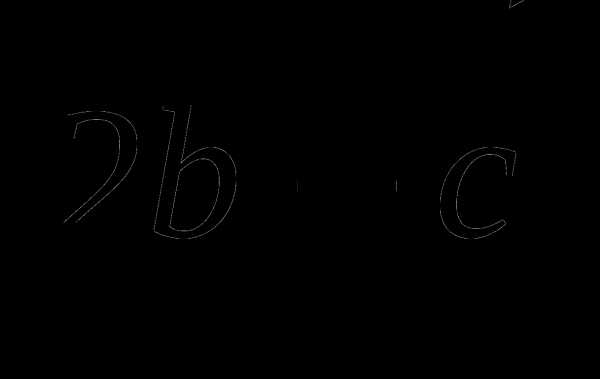

3. Изобразите систему координат Oxyz и постройте точку

А(1; −2; −4). Найдите расстояние от этой точки до координатных плоскостей.

1. Найдите координаты вектора 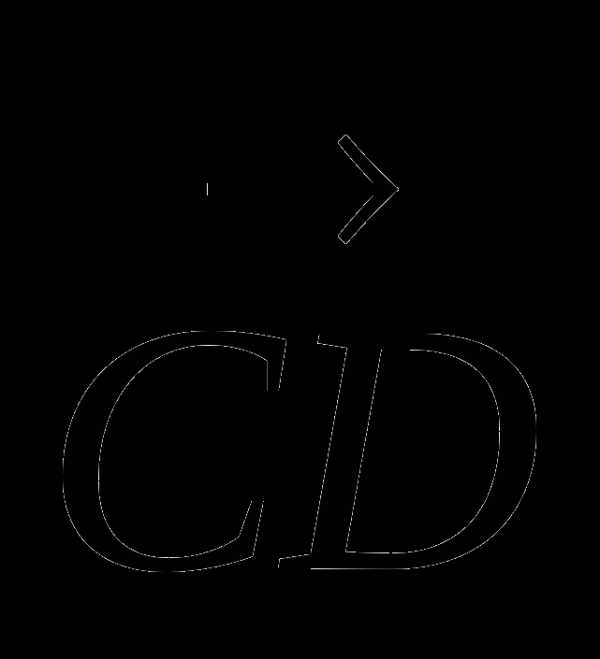, если С(6; 3; −2), D(2; 4; −5).

2. Даны векторы . Найдите .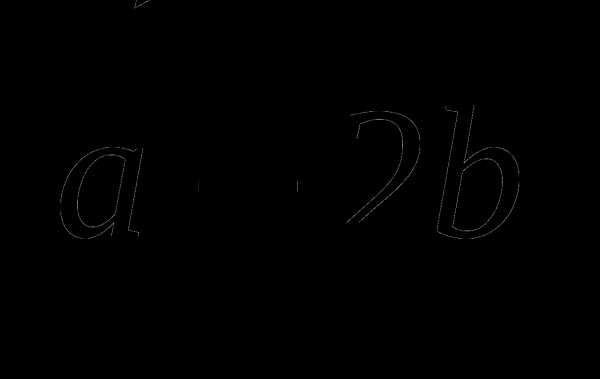

3. Изобразите систему координат Oxyz и постройте точку

В(−2; −3; 4). Найдите расстояние от этой точки до координатных плоскостей.

Контрольная работа № 2

«Скалярное произведение векторов. Движения»

ВАРИАНТ 1

ВАРИАНТ 2

1. Вычислите скалярное произведение векторов 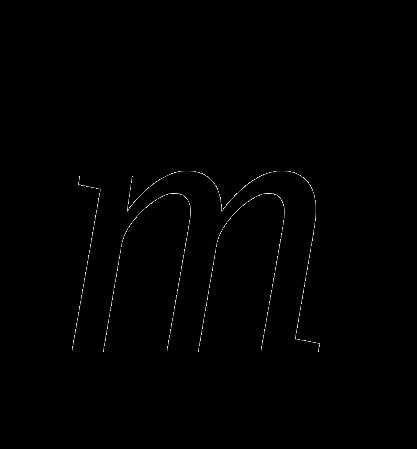и , если , угол между векторами и равен 60⁰, .

2. Дан куб ABCDA₁B₁C₁D₁. Найдите угол между прямыми AD₁ и ВМ, где М – середина ребра DD₁.

3. При движении прямая а отображается на прямую а₁, а плоскость α – на плоскость α₁. Докажите, что, если а||α, то а₁||α₁.

1. Вычислите скалярное произведение векторов 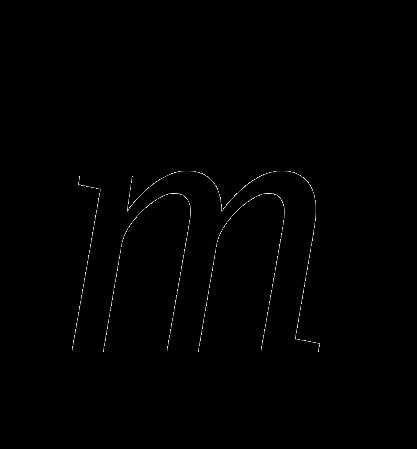и , если , , угол между векторами и равен 60⁰, .

2. Дан куб ABCDA₁B₁C₁D₁. Найдите угол между прямыми АС и DC₁.

3. При движении прямая а отображается на прямую а₁, а плоскость α – на плоскость α₁. Докажите, что, если , то .

Контрольная работа № 3

«Цилиндр, конус и шар»

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 1

1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 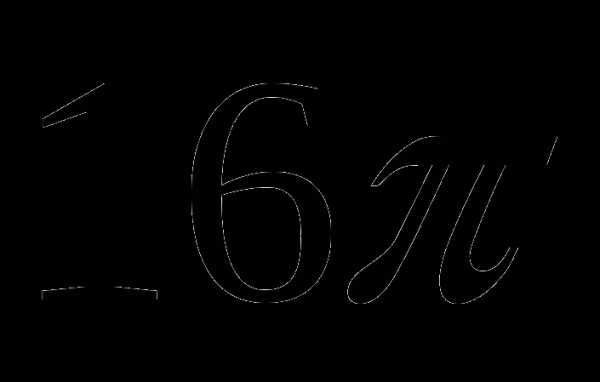см². Найдите площадь полной поверхности цилиндра.

2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120⁰. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30⁰; б) площадь боковой поверхности конуса.

3. Диаметр шара равен 2т. Через конец диаметра проведена плоскость под углом 45⁰ к нему. Найдите длину линии пересечения сферы этой плоскостью

ВАРИАНТ 2

1. Осевое сечение цилиндра – квадрат, диагональ которого равна 4 см. Найдите площадь полной поверхности цилиндра.

2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30⁰. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 60⁰; б) площадь боковой поверхности конуса.

3. Диаметр шара равен 4т. Через конец диаметра проведена плоскость под углом 30⁰ к нему. Найдите площадь сечения шара этой плоскостью.

Контрольная работа № 4

«Объём призмы, цилиндра, пирамиды и конуса»

ВАРИАНТ 1

ВАРИАНТ 2

1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60⁰. Найдите объём пирамиды.

2. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 60⁰. Диагональ большей боковой грани призмы составляет с плоскостью её основания угол 45⁰. Найдите объём цилиндра.

1. Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол 60⁰. Найдите объём пирамиды.

2. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30⁰. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол 45⁰. Найдите объём конуса.

Контрольная работа № 5

«Объём шара и площадь сферы»

ВАРИАНТ 1

ВАРИАНТ 2

1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол 60⁰. Найдите отношение объёмов конуса и шара.

2. Объём цилиндра равен 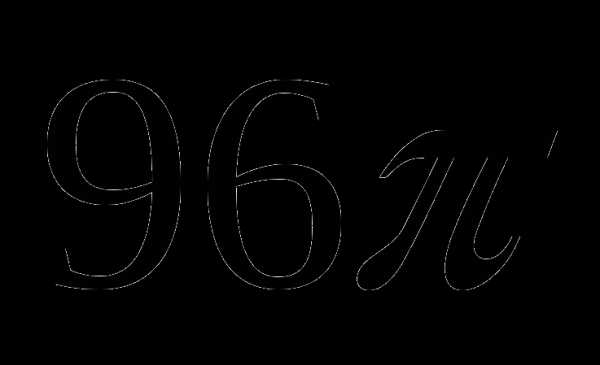см³, площадь его осевого сечения – 48 см². Найдите площадь сферы, описанной около цилиндра.

1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.

2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объёмов шара и цилиндра.

Самостоятельные работы 11класс

Самостоятельная работа № 1

«Координаты точки и координаты вектора»

ВАРИАНТ 1

ВАРИАНТ 2

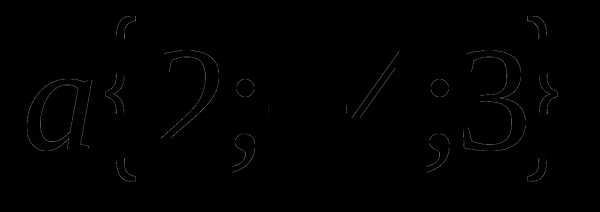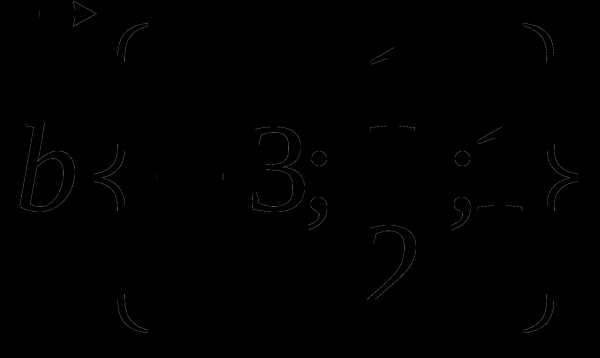1. Даны векторы и . Найдите координаты вектора .

2. Даны векторы . Найдите координаты вектора .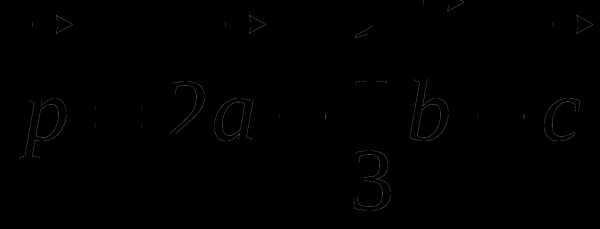

3. Найдите значения 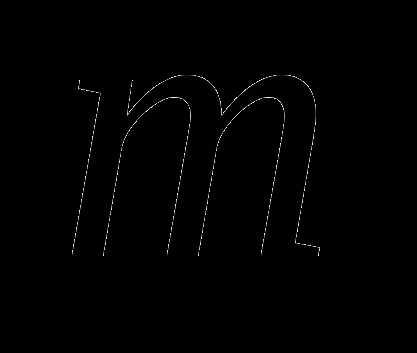и 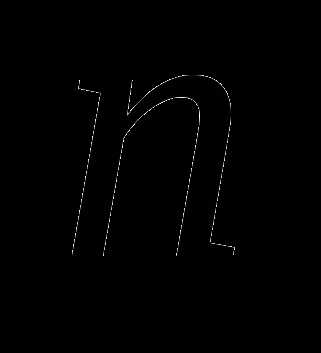, при которых векторы 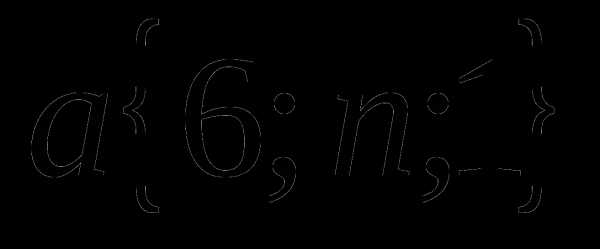и 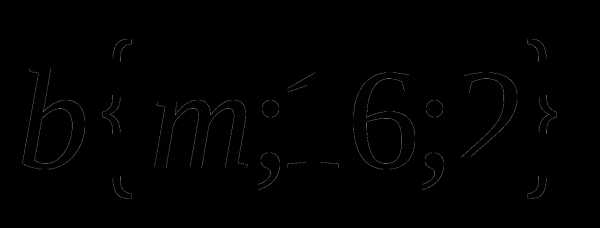коллинеарны.

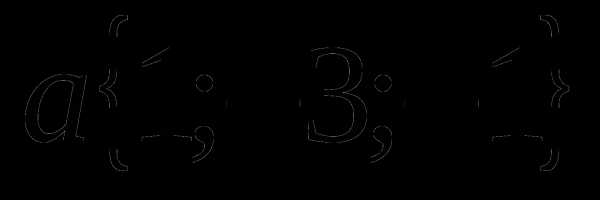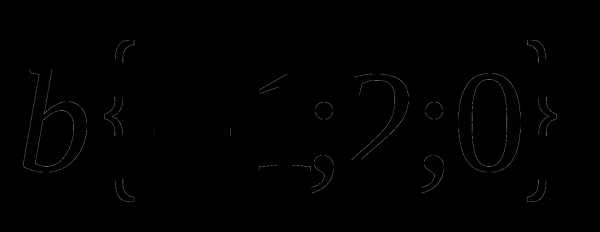1. Даны векторы и . Найдите координаты вектора .

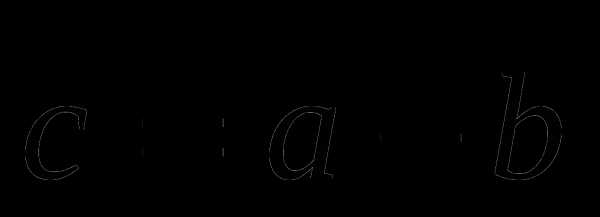2. Даны векторы . Найдите координаты вектора .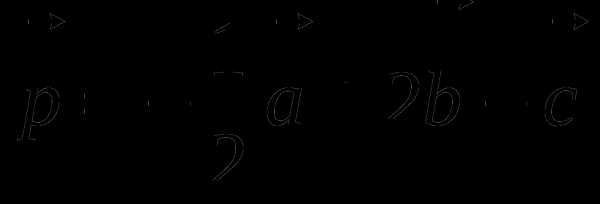

3. Найдите значения 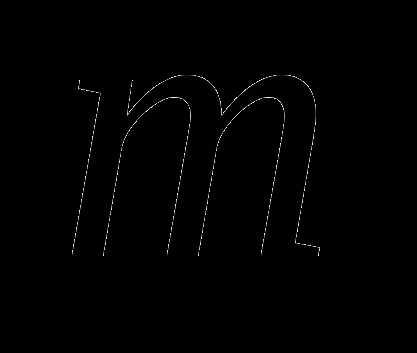и 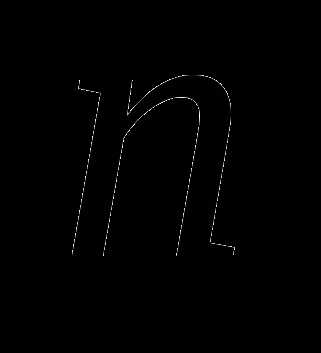, при которых векторы и 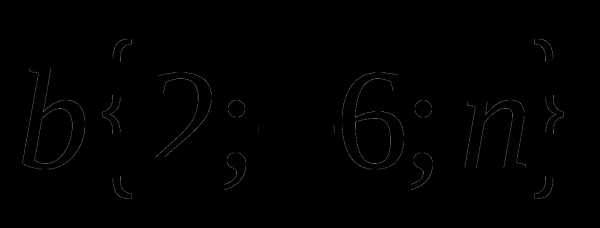коллинеарны.

Самостоятельная работа № 2

«Скалярное произведение векторов»

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 1

1. Даны векторы и . Вычислите .

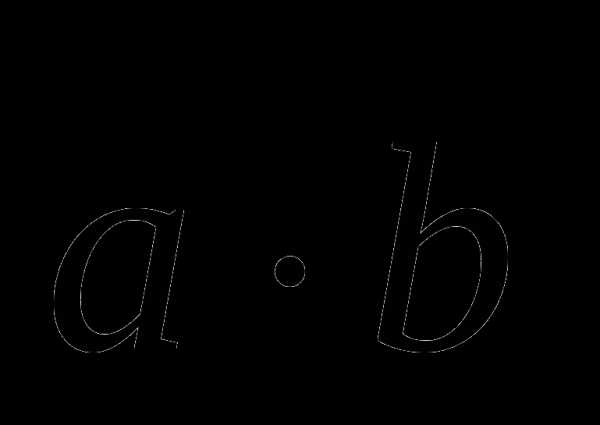2. Вычислите угол между прямыми АВ и CD, если .

ВАРИАНТ 2

1. Даны векторы и . Вычислите .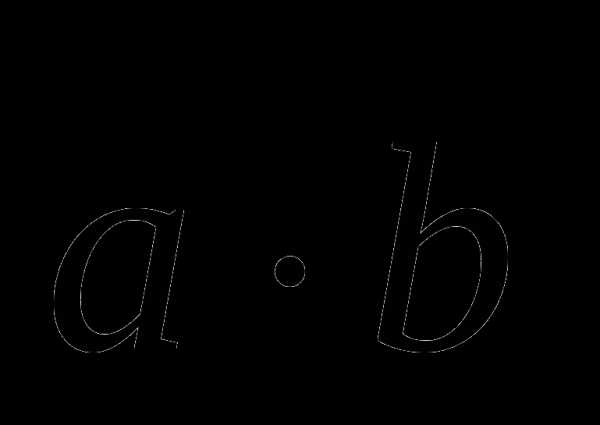

2. Вычислите угол между прямыми АВ и CD, если .

Самостоятельная работа № 3

«Цилиндр»

ВАРИАНТ 1

ВАРИАНТ 2

АРИАНТ 1

1. Развёртка боковой поверхности цилиндра является квадратом, диагональ которого равна 10 см. Найдите площадь боковой поверхности цилиндра.

2. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 120⁰. Высота цилиндра равна 5 см, радиус цилиндра 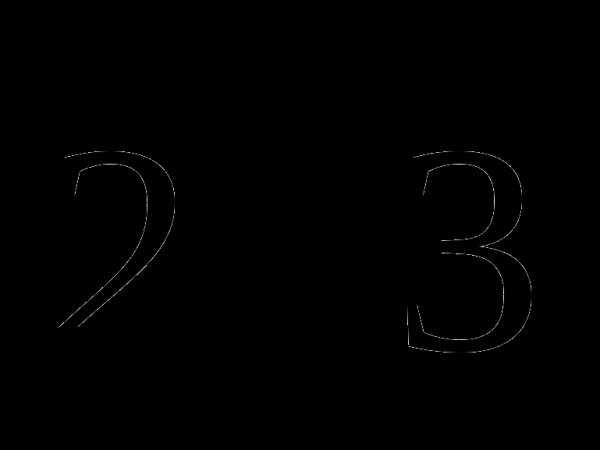см. Найдите площадь сечения.

1. Развёртка боковой поверхности цилиндра является прямоугольником, диагональ которого равна 8 см., а угол между диагоналями 30⁰. Найдите площадь боковой поверхности цилиндра.

2. Сечение цилиндра плоскостью, параллельной его оси, есть квадрат. Эта плоскость отсекает от окружности основания дугу в 90⁰. Радиус цилиндра равен 4 см. Найдите площадь сечения.

Самостоятельная работа № 4

«Объём прямоугольного параллелепипеда»

ВАРИАНТ 1

ВАРИАНТ 2

1. Измерения прямоугольного параллелепипеда равны 2,5 см, 5 см и 5 см. Найдите ребро куба, объём которого в два раза больше объёма данного параллелепипеда.

2. Найдите объём прямой призмы АВСА₁В₁С₁, если угол АСВ равен 90⁰, угол ВАС равен 30⁰, АВ = а, СВ = ВВ₁.

1. Измерения прямоугольного параллелепипеда равны 2 см, 6 см и 6 см. Найдите ребро куба, объём которого в три раза больше объёма данного параллелепипеда.

2. Найдите объём прямой призмы АВСА₁В₁С₁, в которой угол АСВ равен 90⁰, АВ = ВВ₁ = а, АС = СВ.

Самостоятельная работа № 5

«Объём наклонной призмы, пирамиды и конуса»

ВАРИАНТ 1

Найдите объём правильной треугольной пирамиды с боковым ребром l = 10 см, если боковое ребро составляет с плоскостью основания угол, равный 30⁰.

ВАРИАНТ 2

Найдите объём правильной четырёхугольной пирамиды, если её высота Н = 10 см, а двугранный угол при основании равен 60⁰.

infourok.ru