Самостоятельная работа алгебра 11 класс – Самостоятельные работы алгебра 11 класс Александрова 2009

ГДЗ решебник по алгебре 11 класс самостоятельные работы Александрова

Алгебра относиться к предметам, которые учат не только считать и выполнять примеры и задачи. Кроме этого, она помогает развивать логическое мышление. Решебник 11 класс, автора Александровой содержит все необходимые учебные темы, такие как степени и корни, логарифмические функции, неравенства и уравнения, интегралы, элементы, имеющие отношение к математической статистике, повторение пройденного и ответы. В данном ГДЗ, максимально собрано все, что поможет повторить школьную программу по алгебре, научится решать самому задачи, улучшить свои познания этого сложного предмета. Также, потренировать существующие навыки и успешно применить их в будущем на практике.

Понятие корня n-ой степени из действительного числа 12


Функции у = корень n степени из х, их свойства и графики1234


Свойства корня n -ой степени12345


Преобразование выражений, содержащих радикалы 12345


Обобщение понятия о показателе степени 12345


Степенные функции, их свойства и графики.1234


Дифференцирование степенной функции с рациональным показателем 1234567891011


Показательная функция, ее свойства и график123456


Показательные уравнения и неравенства123456789101112


Понятие логарифма123


Функция у = logaX, ее свойства и график123456


Свойства логарифмов123


Логарифмические уравнения123456789


Логарифмические неравенства1234567891011


Переход к новому основанию логарифма12345678


Дифференцирование показательной и логарифмической функций12345678910


Первообразная123456


Определенный интеграл12345678


Статистическая обработка данных12


Простейшие вероятностные задачи1234


Сочетания и размещения123456


Формула бинома Ньютона1234


Случайные события и их вероятности1234


Равносильность уравнений123456


Общие методы решения уравнений12345678910


Решение неравенств с одной переменной12345678


Уравнения и неравенства с двумя переменными12345678


Системы уравнений1234567891011


Уравнения и неравенства с параметрами12345678910111213


Итоговое повторение12345678

Загрузка…

gdzgo.org

Самостоятельные работы по алгебре для 11 класса

ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ ДЛЯ 10 — 11 КЛАССА ПО АЛГЕБРЕ

ДЛЯ ПОДГОТОВКИ К ЕГЭ

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Пределы)

Вычислить пределы:

1) 5)

2) 6)

3) 7)

4) 8)

9) Найти сумму геометрической прогрессии 32, 16, 8, 4, 2, …

10) Найти первый член геометрической прогрессии (), если S = 10, q = 0,1.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Производные)

За правильное выполнение 20 заданий оценка «5»;

За правильное выполнение 18 — 19 заданий оценка «4»;

За правильное выполнение 11 — 17 заданий оценка «3»;

Найти производные следующих функций:

1). 8). 14).

2). 9). 15).

3).

4). 10). 16).

5). 11). 17).

6). 12). 18).

7). 13). 19).

20).

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Производная)

Найти производную функции:

1). 7). 13). 19).

2). 8). 14). 20).

3). 9). 15). 21).

4). 10). 16). 22).

5). 11). 17). 23).

6). 12). 18). 24).

26).

Вычислить тангенс угла между касательной к графику функции в точке с абсциссой :

26). ; =

27). ; = 0

Вычислить угловой коэффициент касательной к графику функции в точке с абсциссой :

28). ; =

29). ; =

30). Вычислить скорость изменения функции в точке с абсциссой = 0.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Производная)

1). Материальная точка движется прямолинейно по закону , где

Х – расстояние от точки отсчёта в метрах, – время в секундах, измеренное с начала движения. Найти её скорость (в метрах в секунду) в момент времени t = 9 сек.

2). Материальная точка движется прямолинейно, её скорость выражается формулой

V=2+5t. Найти закон движения, если известно, что в момент времени t = 2 координата точки равнялась числу 20.

3). Материальная точка движется прямолинейно по закону , где

Х – расстояние от точки отсчёта в метрах, – время в секундах, измеренное с начала движения. Найти её скорость (в метрах в секунду) в момент времени t = 9 сек.

4). Скорость прямолинейного движения материальной точки задаётся формулой

. Найти закон движения ,если S(0) = 9.

5). Материальная точка движется прямолинейно по закону , где

Х – расстояние от точки отсчёта в метрах, – время в секундах, измеренное с начала движения. Найти её скорость (в метрах в секунду) в момент времени t = 6 сек.

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Интеграл. Площадь фигуры)

1). Вычислить определённый интеграл: а) ; б) ; в) ;

г) ;

2). Вычислить площадь фигуры, ограниченной прямыми

3). Вычислить площадь фигуры, ограниченной графиками функций

и

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Преобразования алгебраических выражений и дробей)

1. Найдите значение выражения  .

2. Найдите значение выражения   при  .

3. Найдите  , если  .

4. Найдите значение выражения  , если  .

5. Найдите значение выражения  , если  , а  .

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Преобразование числовых и буквенных иррациональных выражений)

1). Найдите значение выражения  при .

2). Найдите значение выражения  при  .

3). Найдите значение выражения  при .

4). Найдите , если  при .

5). Найдите значение выражения .

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Преобразование буквенных показательных выражений)

1. Найдите значение выражения .

2. Найдите значение выражения .

3. Найдите значение выражения  при .

4. Найдите значение выражения  при .

5. Найдите значение выражения  при .

6. Найдите значение выражения  при .

7. Найдите значение выражения  при .

8. Найдите значение выражения  при .

9. Найдите значение выражения , если .

10. Найдите значение выражения  при .

11. Найдите значение выражения  при .

12. Найдите значение выражения  при .

13. Найдите значение выражения 

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Преобразование числовых и буквенных логарифмических выражений)

1. Найдите значение выражения .

2. Найдите значение выражения .

3. Найдите значение выражения .

4. Найдите значение выражения .

5. Найдите значение выражения .

6. Найдите значение выражения .

7. Найдите значение выражения .

8. Найдите значение выражения .

9. Найдите значение выражения .

10. Найдите значение выражения .

11. Найдите значение выражения .

12. Найдите значение выражения .

13. Найдите значение выражения .

14. Найдите значение выражения .

15. Найдите значение выражения .

16. Найдите значение выражения .

17. Найдите значение выражения .

18. Вычислите значение выражения: .

19. Найдите значение выражения 

20. Найдите значение выражения 

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Преобразование числовых и буквенных тригонометрических выражений)

1. Найдите , если   и  

2. Найдите , если  и .

3. Найдите , если  и .

4. Найдите , если .

5. Найдите , если  и .

6. Найдите , если .

7. Найдите , если .

8. Найдите , если .

9. Найдите значение выражения , если .

10. Найдите значение выражения .

10. Найдите значение выражения .

10. Найдите значение выражения .

10. Найдите значение выражения .

14. Найдите значение выражения .

15. Найдите значение выражения .

16. Найдите значение выражения .

17. Найдите значение выражения .

18. Найдите значение выражения .

19. Найдите значение выражения .

20. Найдите значение выражения .

21. Найдите значение выражения .

22. Найдите значение выражения: .

23. Найдите значение выражения .

24. Найдите значение выражения 

25. Найдите значение выражения 

САМОСТОЯТЕЛЬНАЯ РАБОТА

(Тема: Линейные, квадратные, кубические, рациональные уравнения)

1. Найдите корень уравнения 

2. Решите уравнение .

3. Решите уравнение .

4. Решите уравнение .

5. Найдите корень уравнения .

6. Найдите корень уравнения .

7. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

8. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

9. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

10. Найдите корень уравнения:  Если уравнение имеет более одного корня, укажите меньший из них.

11. Найдите корень уравнения .

12. Найдите корень уравнения .

13. Решите уравнение .

14. Решите уравнение .

infourok.ru

Самостоятельные работы Алгебра 11 класс

Самостоятельные работы разработаны по программе учебника Алгебра 11 класс, Кузнецовой. Данный материал можно использовать для проведения на уроках контроля знаний, как дополнительный материал по закреплению умений и навыков. 

Просмотр содержимого документа

«Д З Показательные уравнения»

Домашнее задание. Показательные уравнения

1 вариант

Решите уравнения:

1.

2.

3.

4.

5.Решите систему:

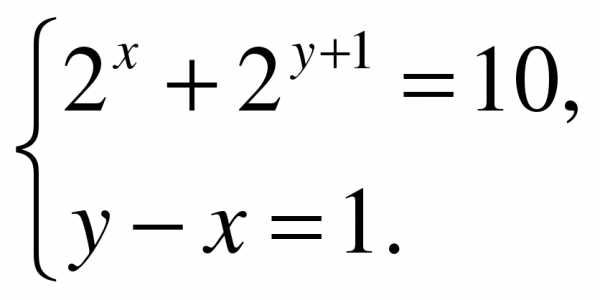
6.Решите уравнение:

2 вариант

Решите уравнения:

1.

2.

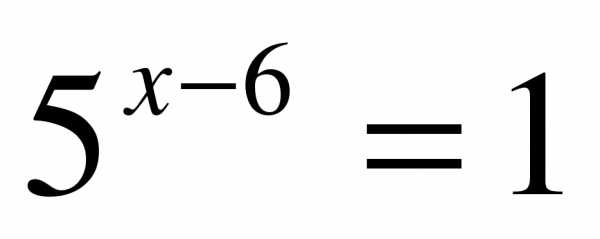
3.

4.

5. Решите систему:

6. Решите уравнение:

3 вариант

Решите уравнения:

1.

2.

3.

4.

5. Решите систему:

6. Решите уравнение:

4 вариант

Решите уравнения:

1.

2.

3.

4.

5. Решите систему:

6. Решите уравнение:

5 вариант

Решите уравнения:

1.

2.

3.

4.

5. Решите систему:

6. Решите уравнение:

6 вариант

Решите уравнения:

1.

2.

3.

4.

5. Решите систему:

6. Решите уравнение:

7 вариант

Решите уравнения:

1. ;

2. .

3.;

4. .

5. Решите систему:

6. Решите уравнение:

8 вариант

Решите уравнения:

1.;

2. .

3.

4. .

5. Решите систему:

6. Решите уравнение:

Просмотр содержимого документа

«С Р Бесконечно убыв прогрессия»

Просмотр содержимого документа

«С Р Показательные неравенства»

Просмотр содержимого документа

«С Р Показательные уравнения»

Просмотр содержимого документа

«С Р Понятие логарифма»

Просмотр содержимого документа

«С Р иррац неравенства»

Просмотр содержимого документа

«C Р №1 11 класс»

Просмотр содержимого документа

«С Р Иррационалные уравнения»

Просмотр содержимого документа

«С Р Логарифмические нераввенства»

Просмотр содержимого документа

«С Р Логарифмические уравения»

multiurok.ru

Материал по алгебре (11 класс) на тему: самостоятельные работы для 11 класса

Самостоятельная работа. Вариант №1.

Задание B1. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B2. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B3. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Задание B4. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Задание B5. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Самостоятельная работа. Вариант №2.

Задание B1. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B2. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Задание B3. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B4. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B5. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Самостоятельная работа. Вариант №3.

Задание B1. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B2. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B3. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B4. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Задание B5. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Самостоятельная работа. Вариант №4.

Задание B1. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B2. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B3. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B4. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Задание B5. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Самостоятельная работа. Вариант №5.

Задание B1. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Задание B2. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B3. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B4. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B5. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Самостоятельная работа. Вариант №6.

Задание B1. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B2. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B3. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B4. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Задание B5. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Самостоятельная работа. Вариант №7.

Задание B1. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B2. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B3. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Задание B4. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Задание B5. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Самостоятельная работа. Вариант №8.

Задание B1. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B2. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B3. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Задание B4. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Задание B5. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Самостоятельная работа. Вариант №9.

Задание B1. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B2. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B3. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B4. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Задание B5. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Самостоятельная работа. Вариант №10.

Задание B1. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B2. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B3. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Задание B4. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B5. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Самостоятельная работа. Вариант №11.

Задание B1. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Задание B2. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B3. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B4. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B5. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Самостоятельная работа. Вариант №12.

Задание B1. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B2. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B3. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Задание B4. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B5. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Самостоятельная работа. Вариант №13.

Задание B1. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Задание B2. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B3. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B4. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Задание B5. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Самостоятельная работа. Вариант №14.

Задание B1. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

Задание B2. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B3. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Задание B4. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B5. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Самостоятельная работа. Вариант №15.

Задание B1. 

    В конусе длина образующей равна 5, а радиус основания равен 4. Найдите объем конуса.

    Правильный ответ: 10n

Задание B2. 

    В усеченном конусе радиусы оснований равны 5 и 2, а высота равна 4. Найдите площадь боковой поверхности конуса.

    Правильный ответ: 57

Задание B3. 

    В конусе радиус основания равен 2, а длина образующей меньше площади основания в 2n раз. Найдите площадь полной поверхности конуса.

    Правильный ответ: 8n

Задание B4. 

    В правильной треугольной призме сторона основания равна , а высота равна 4. Найдите объем призмы.

    Правильный ответ: 

Задание B5. 

    В конусе радиус основания равен 3, а длина образующей 4. Найдите площадь полной поверхности конуса.

    Правильный ответ: 2n

nsportal.ru

Учебно-методический материал по алгебре (11 класс) на тему: самостоятельные работы11 класс

Самостоятельная работа 2.2

Свойства тригонометрических функций

Вариант 1

А1. Найдите область определения функции  у = 2sin 3x. 

А2. Определить, является ли данная функция четной или нечетной:

      у = 3х2 – cos x.                                                                                                      

А3. Доказать, что данная функция является периодической с периодом   Т = π.

       у = 2cos 2x.                                                                                                      

А4. Сравните числа   cos   и  cos.

В1. Найти наименьший положительный период функции  у= sin 5x.            

В2. Найти область определения функции     .                          

C1. Найти все корни уравнения  sin x = -1 , принадлежащие промежутку          .                                                                                                                  

С2. Найти множество значений функции  у = cos x,  если  х  принадлежит промежутку  .  

Самостоятельная работа 2.2

Свойства тригонометрических функций

Вариант 2

А1. Найдите область определения функции  у =3sin 4x.

А2. Определить, является ли данная функция четной или нечетной:

      у = 3х3 –sin x.                                                                                                      

А3. Доказать, что данная функция является периодической с периодом Т = π.

       у = 2sin 2x.                                                                                                    

А4. Сравните числа   cos  и   cos .

В1. Найти наименьший положительный период функции  у= sin 6x.             

В2. Найти область определения функции     .                      

C1. Найти все корни уравнения  6sin x = 3принадлежащие промежутку  .                                                                                                                

С2. Найти множество значений функции  у = sin x, если  х  принадлежит промежутку  .  

Самостоятельная работа 2.2

Свойства тригонометрических функций

Вариант 3

А1. Найдите область определения функции  у = 2 + sin 4x.

А2. Определить, является ли данная функция четной или нечетной:

      у = 2х2 –cos 3x.                                                                                                      

А3. Доказать, что данная функция является периодической с периодом   Т =    

у = 2cos 4x.                                                                                        

А4. Сравните числа   sin  и  sin .

В1. Найти наименьший положительный период функции  у= cos 3x.            

В2. Найти область определения функции  .                            

C1. Найти все корни уравнения  2sin x = -1  принадлежащие промежутку    .     С2. Найти множество значений функции  у = cos x, если х принадлежит промежутку  .  

Самостоятельная работа 2.2

Свойства тригонометрических функций

Вариант 4

А1. Найдите область определения функции  у = 2 — sin 5x. 

А2. Определить, является ли данная функция четной или нечетной:

      у = х2 –sin |x|.                                                                                                    

А3. Доказать, что данная функция является периодической с периодом   Т = 4π.       у = 3cos .                                                                                                      

А4. Сравните числа    cos    и    cos .

В1. Найти наименьший положительный период функции  у= cos 4x.            

В2. Найти область определения функции  .                          

C1. Найти все корни уравнения cos x = -1, принадлежащие промежутку.                                                                                                                  С2. Найти множество значений функции  у = cos x, если  х  принадлежит промежутку  .  

nsportal.ru

Самостоятельная работа, 11 класс, алгебра и начала математического анализа

videouroki.net

ГДЗ решебник по Алгебре Самостоятельные работы 11 класс Александрова 2011

Авторы: Александрова Л.А.
Класс: 11
Предмет: Алгебра

Готовые задания

Понятие корня n-ой степени из действительного числа1 2
Функции у = корень n степени из х, их свойства и графики1 2 3 4
Свойства корня n -ой степени1 2 3 4 5
Преобразование выражений, содержащих радикалы1 2 3 4 5
Обобщение понятия о показателе степени1 2 3 4 5
Степенные функции, их свойства и графики.1 2 3 4
Дифференцирование степенной функции с рациональным показателем1 2 3 4 5 6 7 8 9 10 11
Показательная функция, ее свойства и график1 2 3 4 5 6
Показательные уравнения и неравенства1 2 3 4 5 6 7 8 9 10 11 12
Понятие логарифма1 2 3
Функция у = logaX, ее свойства и график1 2 3 4 5 6
Свойства логарифмов1 2 3
Логарифмические уравнения1 2 3 4 5 6 7 8 9
Логарифмические неравенства1 2 3 4 5 6 7 8 9 10 11
Переход к новому основанию логарифма1 2 3 4 5 6 7 8
Дифференцирование показательной и логарифмической функций1 2 3 4 5 6 7 8 9 10
Первообразная1 2 3 4 5 6
Определенный интеграл1 2 3 4 5 6 7 8
Статистическая обработка данных1 2
Простейшие вероятностные задачи1 2 3 4
Сочетания и размещения1 2 3 4 5 6
Формула бинома Ньютона1 2 3 4
Случайные события и их вероятности1 2 3 4
Равносильность уравнений1 2 3 4 5 6
Общие методы решения уравнений1 2 3 4 5 6 7 8 9 10
Решение неравенств с одной переменной1 2 3 4 5 6 7 8
Уравнения и неравенства с двумя переменными1 2 3 4 5 6 7 8
Системы уравнений1 2 3 4 5 6 7 8 9 10 11
Уравнения и неравенства с параметрами1 2 3 4 5 6 7 8 9 10 11 12 13
Итоговое повторение1 2 3 4 5 6 7 8

Не каждому под силу изучить такую сложную науку, как математику, поэтому к ее изучению важно подходить со всей серьезностью. Без знания основ алгебры жить нельзя — это основа экономики, программирования, бухгалтерии. Иногда полезно считать без использования калькулятора. Математика является тренировкой для ума, поэтому ее иногда нужно сдавать при поступлении на филологический факультет. Любому школьнику уже пора тренировать свой мозг при помощи решебника к рабочей тетради по алгебре за 11 класс Александровой Л.А. Издание рассматривает основные темы и разные задания. Подобные задания могут встретиться на тестировании и экзаменах.

Чтобы проверить правильность своих решений, необходимо иметь при себе гдз к учебнику. Долго гдз искать не придется — для этого нужно зайти на сайт и посмотреть готовые ответы онлайн. Гдз помогает понять, какие темы еще сырые для восприятия, какие формулы и уравнения придется подучить. Важно заниматься регулярно, не отлынивать. Зубрежка правил в математике — не выход.

Кто может пользоваться решебником?

Учебник создан для школьников 11 класс образовательных учреждений, которые изучают предмет алгебра и математический анализ. В издании указаны готовые ответы на 93% упражнений из учебника Александровой для самостоятельного контроля знаний, умений, навыков. Гдз можно использовать для самостоятельного контроля знаний по конкретной теме и самообучения математике. Издание придет на помощь родителям, которые привыкли с начальных классов контролировать знания детей. При помощи решебника по алгебре школьники закрепят знания в таких правилах, как:

• уравнения и неравенства,
• логарифмы,
• интегралы,
• корни и степени,
• элементы математической статистики и теории вероятности.

Решебник по алгебре от автора Александровой дает каждому удивительную возможность решить сложные задачи и примеры за короткий срок. Проверенные ответы помогут не только получить высокие отметки, но и проверить уровень знаний. Благодаря доступному описанию хода действий, можно за короткое время понять тему. Таким образом, школьники продуктивно подготовятся к самостоятельной и контрольной работе. Теперь не придется тратить время на учебники и бессонные ночи, когда под рукой есть ценный помощник. Учителя оценят старания школьников и поставят высокие оценки.

Решебник по алгебре: помощь в подготовке к контрольным и экзаменам

Решебник по алгебре за 11 класс к рабочей тетради поможет не только правильно справиться с написанием любого задания из учебной программы, но и проверит степень имеющихся знаний. Это возможность за короткое время поднять успеваемость, не прибегая к помощи преподавателей и репетиторов. Зайдите на сайте и скачайте бесплатно проверенные решебники с готовыми ответами. Многие школьники не любят тратить время на монотонные предметы, от которых одна скука. Теперь каждый забудет бессонные ночи и походы в библиотеку и начнет пользоваться гдз с проверенными ответами.

Школьники получат высокий аттестат, а родители больше не будут переживать и ругать за низкую успеваемость. Решебник к рабочей тетради по математике является отличным помощником для каждого ученика. 11 класс — серьезный и последний год обучения в школе. Огромное количество предметов никто не отменял, и, кроме алгебры, нужно им уделить внимание, поэтому применяется ценный учебник — решебник Александровой.

Алгебра считается трудным предметом, по которому в 11 классе школьникам придется сдавать экзамен, а в дальнейшем — тестирование, если они соберутся поступать на экономический факультет. Важно использовать гдз к рабочей тетради, чтобы понимать, насколько правильно школьник переварил информацию. Иногда ученикам проще списать готовые ответы. Некоторые так поступают, однако не понимают всей серьезности ситуации. Можно списать готовое решение пару раз, но в будущем будет только сложнее усваивать правила и формулы.

Применяя умеренно решебник, ученики повысят успеваемость, проверят знания и подготовятся к контрольным работам и экзаменам. Было доказано, что школьники, применяя гдз, заметно подняли успеваемость и легко чувствуют себя на самостоятельных работах.

gdzmonster.net