Самостоятельная работа по теме «Теория вероятностей» 11 класс (подготовка к ЕГЭ)
Самостоятельная работа по теме «Теория вероятностей» 11 класс
(подготовка к ЕГЭ)
Вариант 1.
-
В группе туристов 10 человек. С помощью жребия они выбирают четырёх человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?
-
Вероятность того, что новый сканер прослужит больше года, равна 0,9. Вероятность того, что он прослужит больше двух лет, равна 0,88. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
-
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что наступит исход ОРР (в первый раз выпадает орёл, во второй и третий — решка).
-
Биатлонист 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.
-
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,3. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
————————————————————————————————————————
Вариант 2.
-
На борту самолёта 15 мест рядом с запасными выходами и 25 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Б. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Б. достанется удобное место, если всего в самолёте 400 мест.
-
Вероятность того, что новый пылесос в течение года поступит в гарантийный ремонт, равна 0,079. В некотором городе из 1000 проданных пылесосов в течение года в гарантийную мастерскую поступило 86 штук. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
-
В группе туристов 25 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 5 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Н. полетит вторым рейсом вертолёта.
-
По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,86. Вероятность того, что этот товар доставят из магазина Б, равна 0,8. Игорь Игоревич заказал товар сразу в обоих магазинах. найдите вероятность того, что ни один магазин не доставит товар.
-
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 60% этих стекол, вторая – 40%. Первая фабрика выпускает 3% бракованных стекол, а вторая – 5%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Вариант 3.
-
Конкурс исполнителей проводится в 3 дня. Всего заявлено 40 выступлений — по одному от каждой страны. В первый день 12 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
-
Вероятность того, что новый персональный компьютер прослужит больше года, равна 0,95. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
-
Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 спортсменов, среди которых 13 спортсменов из России, в том числе Владимир Егоров. Найдите вероятность того, что в первом туре Владимир Егоров будет играть с каким-либо спортсменом из России.
-
Вероятность того, что батарейка бракованная, равна 0,04. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
-
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,8. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,02. Известно, что 24% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
———————————————————————————————————————-
Вариант 4.
-
Научная конференция проводится в 4 дня. Всего запланировано 60 докладов — первые два дня по 18 докладов, остальные распределены поровну между третьим и четвертым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,80 С, равна 0,75. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 0С или выше.
-
Фабрика выпускает сумки. В среднем 15 сумок из 170 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов. Результат округлите до сотых.
-
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,12 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
-
Ковбой Джон попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежит 10 револьверов, из них только 3 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Вариант 5.
-
На олимпиаде по русскому языку участников рассаживают по трём аудиториям. В первых двух по 160 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
-
Вероятность того, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,093. В некотором городе из 1000 проданных блендеров в течение года в гарантийную мастерскую поступило 94 штуки. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
-
В большой партии насосов в среднем на каждые 992 исправных приходится 8 неисправных насосов. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
-
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
-
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 70% этих стекол, вторая – 30%. Первая фабрика выпускает 3% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
———————————————————————————————————————
Вариант 6.
-
В группе туристов 8 человек. С помощью жребия они выбирают двух человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?
-
При изготовлении подшипников диаметром 66 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,962. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 65,99 мм, или больше, чем 66,01 мм.
-
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что наступит исход ООР (в первый и второй разы выпадает орёл, в третий — решка).
-
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что оба автомата неисправны.
-
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,8. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 35% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Вариант 7.
-
На борту самолёта 24 мест рядом с запасными выходами и 11 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Б. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Б. достанется удобное место, если всего в самолёте 350 мест.
-
Вероятность того, что на тесте по истории учащийся У. верно решит больше 9 задач, равна 0,68. Вероятность того, что У. верно решит больше 8 задач, равна 0,79. Найдите вероятность того, что У. верно решит ровно 9 задач.
-
В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 3 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Ш. полетит третьим рейсом вертолёта.
-
По отзывам покупателей Михаил Михайлович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,82. Вероятность того, что этот товар доставят из магазина Б, равна 0,87. Михаил Михайлович заказал товар сразу в обоих магазинах. Найдите вероятность того, что ни один магазин не доставит товар.
-
Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стратор» по очереди играет с командами «Монтёр», «Стартер» и «Протор». Найдите вероятность того, что «Стратор» будет начинать только первую игру.
——————————————————————————————————————-
Вариант 8.
-
Конкурс исполнителей проводится в 3 дня. Всего заявлено 40 выступлений — по одному от каждой страны. В первый день 14 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
-
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 23 пассажиров, равна 0,95. Вероятость того, что окажется меньше 13 пассажиров, равна 0,52. Найдите вероятность того, что число пассажиров будет от 13 до 22.
-
Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 46 теннисистов, среди которых 19 спортсменов из России, в том числе Ярослав Исаков. Найдите вероятность того, что в первом туре Ярослав Исаков будет играть с каким-либо теннисистом из России.
-
Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,02. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
-
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 6 очков в двух играх. Если команда выигрывает, она получает 5 очков, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
Вариант 9.
-
Научная конференция проводится в 4 дня. Всего запланировано 80 докладов — первые два дня по 30 докладов, остальные распределены поровну между третьим и четвертым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,80 С, равна 0,72. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,80 С или выше.
-
В большой партии насосов в среднем на каждые 496 исправных приходится 4 неисправных насоса. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
-
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,09 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
-
Ковбой Джон попадает в муху на стене с вероятностью 0,7, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,1. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
—————————————————————————————————————
Вариант 10.
-
На олимпиаде по физике участников рассаживают по трём аудиториям. В первых двух по 180 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 450 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
-
При изготовлении подшипников диаметром 65 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,971. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 64,99 мм, или больше, чем 65,01 мм.
-
Фабрика выпускает сумки. В среднем 2 сумки из 120 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов. Результат округлите до сотых.
-
Вероятность того, что батарейка бракованная, равна 0,05. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
-
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 8 очков в двух играх. Если команда выигрывает, она получает 7 очков, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Ответы:
Задание 2
Задание 3
Задание 4
Задание 5
Вариант 1
0,4
0,02
0,125
0,13
0,46
Вариант 2
0,1
0,007
0,2
0,028
0,038
Вариант 3
0,35
0,08
0,48
0,9216
0,2072
Вариант 4
0,2
0,25
0,91
0,9856
0,48
Вариант 5
0,2
0,001
0,008
0,04
0,024
Вариант 6
0,25
0,038
0,125
0,0025
0,2865
Вариант 7
0,1
0,11
0,1
0,0234
0,125
Вариант 8
0,325
0,43
0,4
0,9996
0,33
Вариант 9
0,125
0,28
0,008
0,9919
0,78
Вариант 10
0,2
0,029
0,98
0,9025
0,32
infourok.ru
Материал для подготовки к ЕГЭ (ГИА) по алгебре (11 класс) по теме: Тематические самостоятельные работы из открытого банка задач ЕГЭ (с ответами)
Вариант 1. 1. В треугольнике ABC угол C равен , . Найдите .
2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 13. 1. В треугольнике ABC угол C равен , . Найдите .
2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 2. 1. В треугольнике ABC угол C равен , . Найдите .
2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 14. 1. В треугольнике ABC угол C равен , . Найдите .
2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 3. 1. В треугольнике ABC угол C равен , CH — высота, , . Найдите .
2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 15. 1. В треугольнике ABC угол C равен , CH — высота, , . Найдите .
2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 4. 1. В треугольнике ABC угол C равен , CH — высота, , . Найдите .
2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 16. 1. В треугольнике ABC угол C равен , CH — высота, , . Найдите .
2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 5. 1. В треугольнике ABC угол C равен , CH — высота, , . Найдите .
2. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
Вариант 17. 1. В треугольнике ABC угол C равен , CH — высота, , . Найдите .
2. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Вариант 6. 1. В треугольнике ABC , . Найдите .
2. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .
Вариант 18. 1. В треугольнике ABC , . Найдите .
2. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Вариант 7. 1. В треугольнике ABC , . Найдите .
2. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Вариант 19. 1.В треугольнике ABC , . Найдите .
2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Вариант 8. 1. В треугольнике ABC , . Найдите .
2. Объем куба равен 8. Найдите площадь его поверхности.
Вариант 20. 1. В треугольнике ABC , . Найдите .
2. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
Вариант 9. 1. В треугольнике ABC , , высота AH равна 6. Найдите .
2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 21. 1. В треугольнике ABC , , высота AH равна 6. Найдите .
2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 10. 1. В треугольнике ABC , , высота AH равна . Найдите
2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 22. 1. В треугольнике ABC , , высота AH равна . Найдите .
2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 11. 1.В треугольнике ABC , , AH — высота, . Найдите
2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Вариант 23. 1. В треугольнике ABC , , AH — высота, . Найдите
2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Вариант 12. 1. В тупоугольном треугольнике ABC , , высота CH равна 5. Найдите синус угла ACB.
2. Диагональ куба равна . Найдите его объем.
Вариант 24. 1.В тупоугольном треугольнике ABC , , высота CH равна 2. Найдите синус угла ACB.
2. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
nsportal.ru
|
Вариант 1 1. На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос. 2. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. 3. При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным 4. Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции? 5. На борту самолёта 12 кресел расположены рядом с запасными выходами и 18 — за перегородками, разделяющими салоны. Все эти места удобны для пассажира высокого роста. Остальные места неудобны. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест. 6. За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом. |
Вариант 2 1.В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. 2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. 3.Фабрика выпускает сумки. В среднем 8 сумок из 100 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов. 4.Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса? 5. На олимпиаде по русскому языку 250 участников разместили в трёх аудиториях. В первых двух удалось разместить по 120 человек, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории. 6. За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом. |
Вариант 3 1.На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. 2.Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»? 3.Фабрика выпускает сумки. В среднем 11 сумок из 160 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов. Результат округлите до сотых. 4.В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе? 5.В классе 26 учащихся, среди них два друга — Андрей и Сергей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе. 6. За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом. |
Вариант 4 1.В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. 2.В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что наступит исход ОР (в первый раз выпадает орёл, во второй — решка). 3. Из каждых 100 лампочек, поступающих в магазин, в среднем 3 неисправны. Какова вероятность того, что случайно выбранная в магазине лампочка, окажется исправной? 4.Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 16 спортсменов из России, в том числе Игорь Чаев. Какова вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России. 5.В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта. 6. За круглый стол на 201 стул в случайном порядке рассаживаются 199 мальчиков и 2 девочки. Найдите вероятность того, что между девочками будет сидеть один мальчик. |
kopilkaurokov.ru
Самостоятельные и контрольные работы по алгебре и началам анализа 11 класс
Контрольная работа по теме «Первообразная. Интеграл»
1 вариант 2 вариант
1. Найти общий вид первообразной для функции:
1) у =  — cos х 2) у = 4 sin х cosх 1) у =
— cos х 2) у = 4 sin х cosх 1) у =  + sin х 2) у = 2sin2х – 2cos2х
+ sin х 2) у = 2sin2х – 2cos2х
3) у = е6х+1+ 3х2 – 5 3) у = 4х3 + 3 – е8х-5
2. Для функции найти первообразную, график которой проходит через точку:
у = 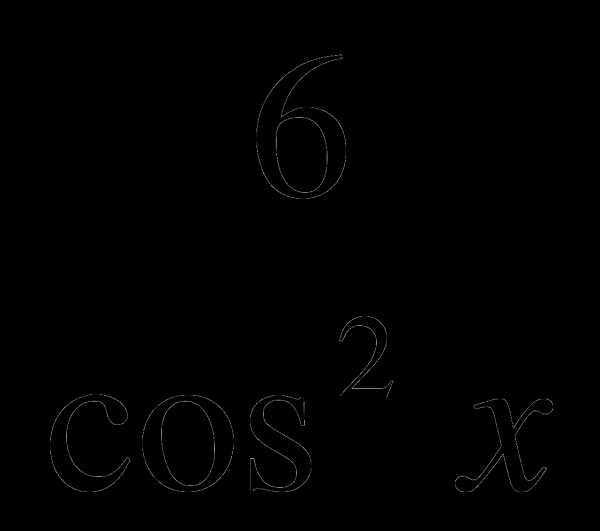 + 1, М (
+ 1, М (  ) у = 3 —
) у = 3 — 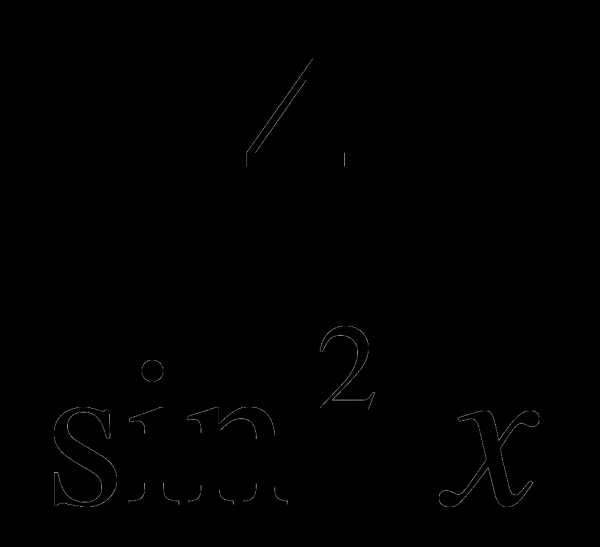 , М ( —
, М ( — )
)
3. Вычислить интегралы:
1) 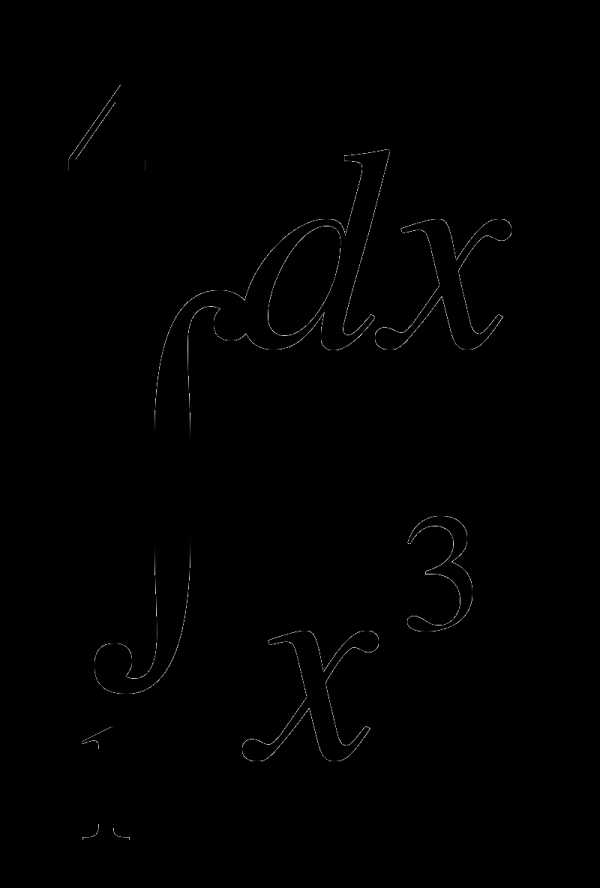 2)
2) 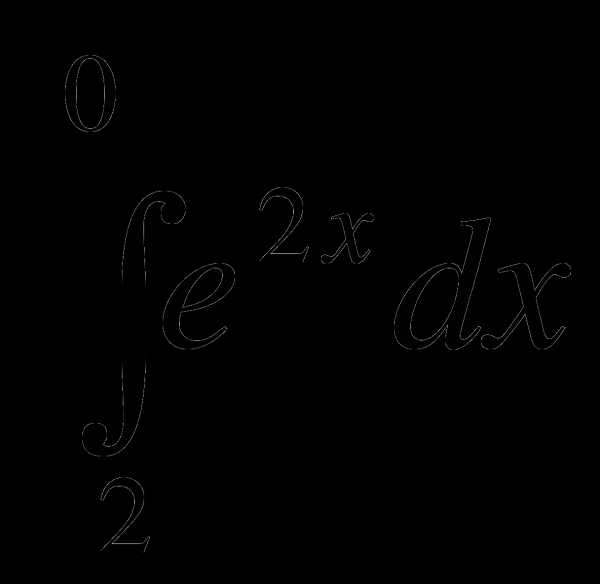 3)
3) 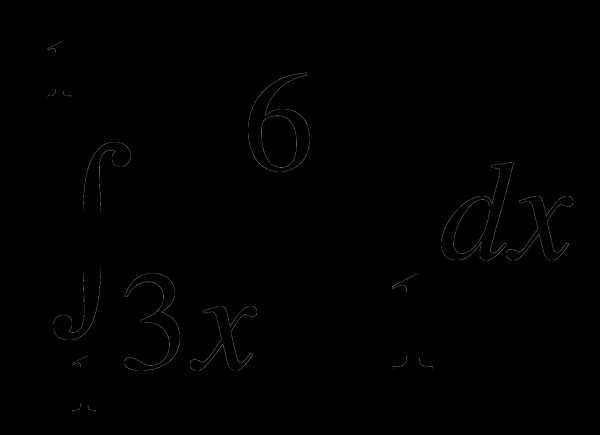 1)
1) 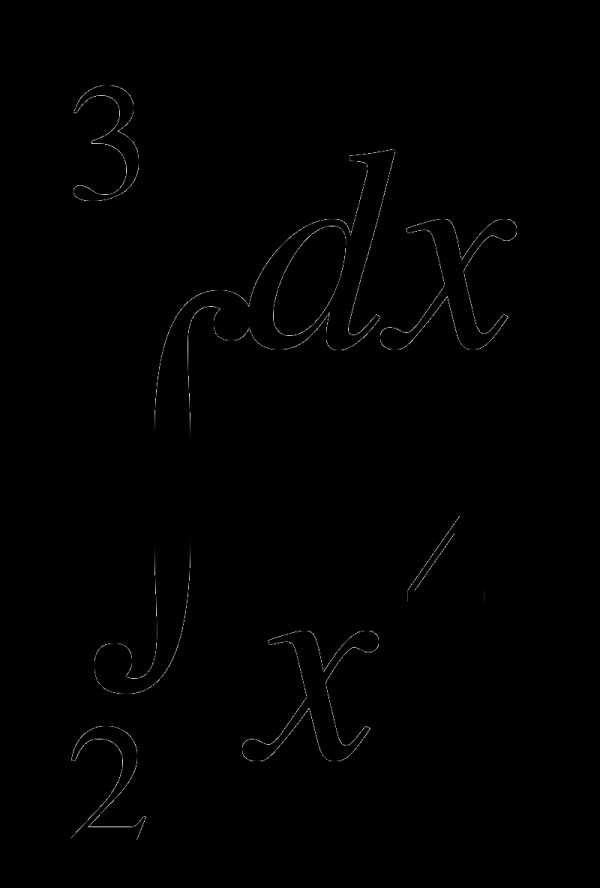 2)
2) 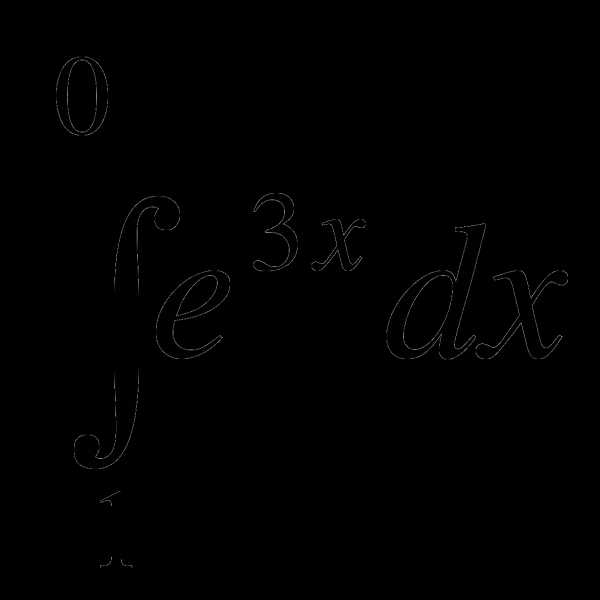 3)
3) 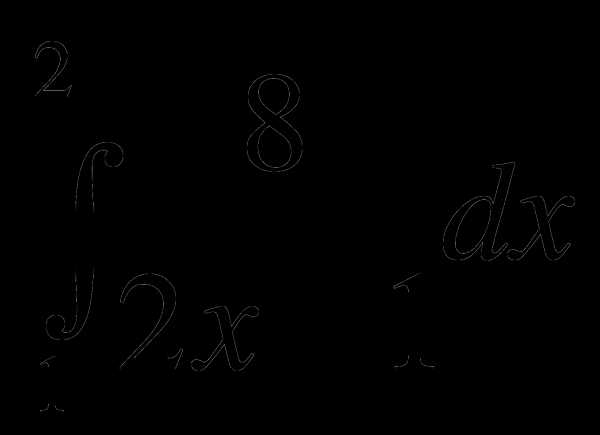
4. Вычислить площадь фигуры, ограниченной линиями
1) у = х2 + 2, у = 0, х = — 1, х = 2 1) у = х2 + 3, у = 0, х = — 2, х = 1
2) у =  , у = — 0,5х + 4 , у = 0 2) у = х3 , у = — 0,5х + 1,5, у = 0
, у = — 0,5х + 4 , у = 0 2) у = х3 , у = — 0,5х + 1,5, у = 0
Контрольная работа по теме «Первообразная. Интеграл»
1 вариант 2 вариант
1. Найти общий вид первообразной для функции:
1) у =  — cos х 2) у = 4 sin х cosх 1) у =
— cos х 2) у = 4 sin х cosх 1) у =  + sin х 2) у = 2sin2х – 2cos2х
+ sin х 2) у = 2sin2х – 2cos2х
3) у = е6х+1+ 3х2 – 5 3) у = 4х3 + 3 – е8х-5
2. Для функции найти первообразную, график которой проходит через точку:
у = 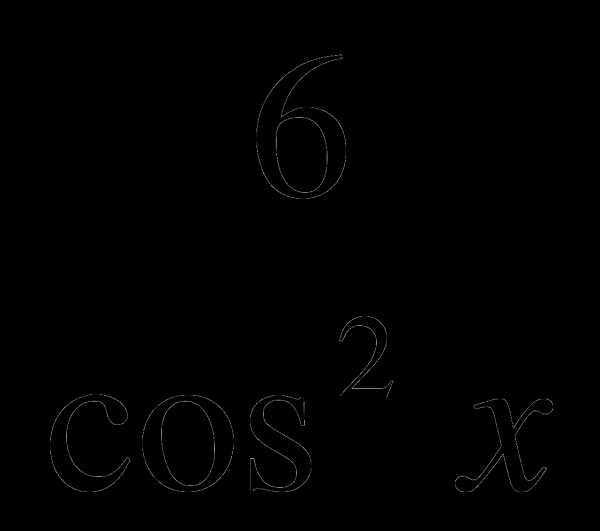 + 1, М (
+ 1, М (  ) у = 3 —
) у = 3 — 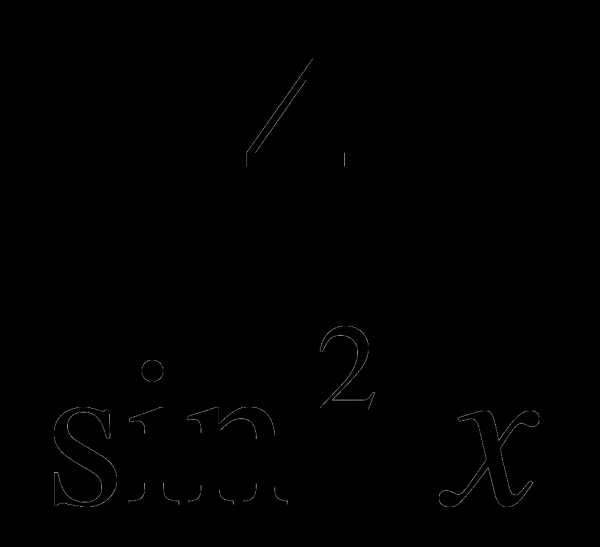 , М ( —
, М ( — )
)
3. Вычислить интегралы:
1) 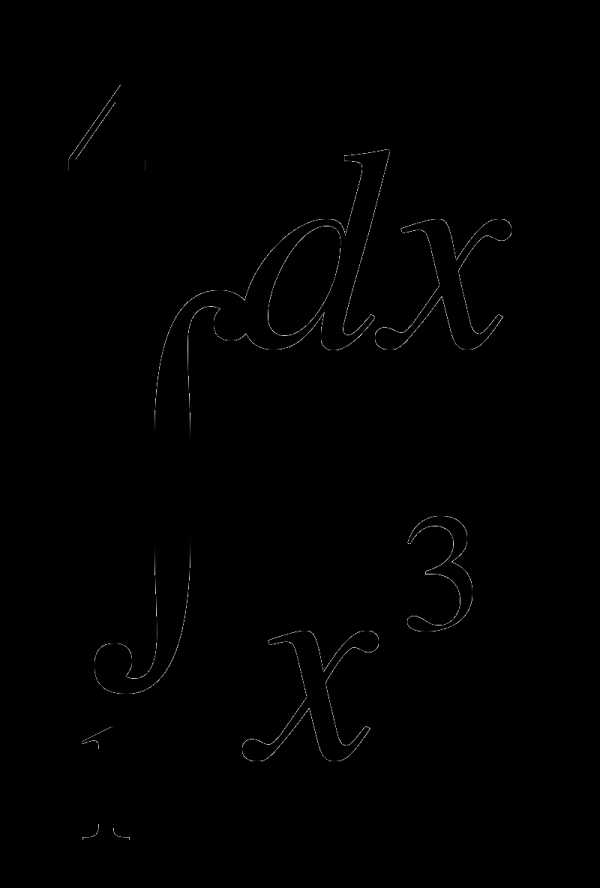 2)
2) 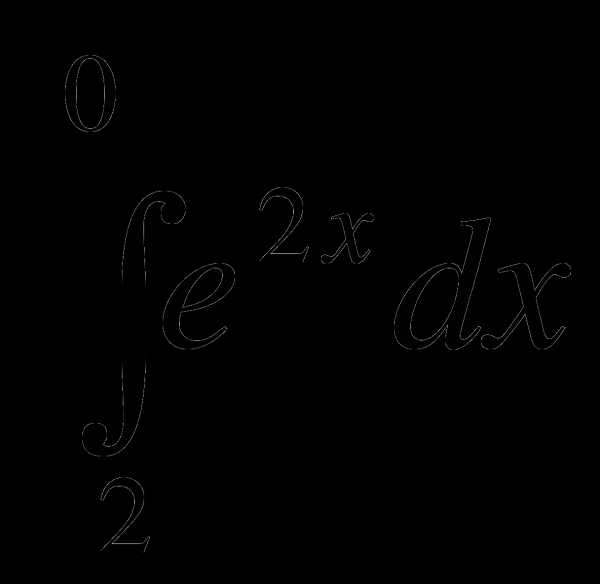 3)
3) 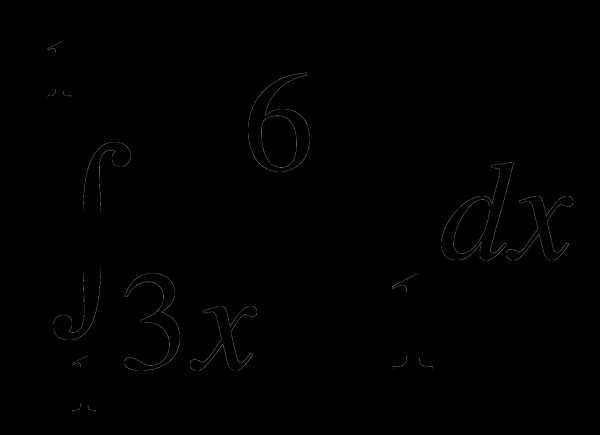 1)
1) 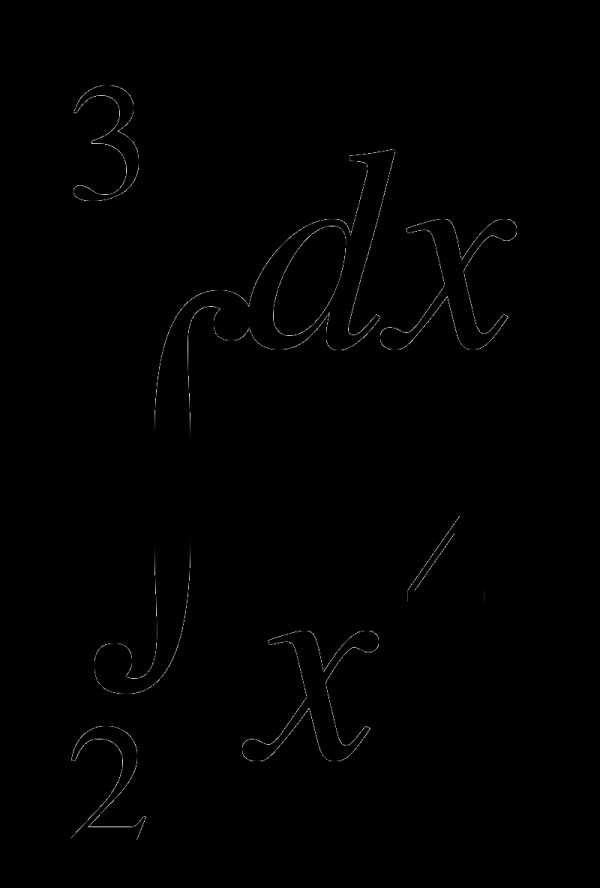 2)
2) 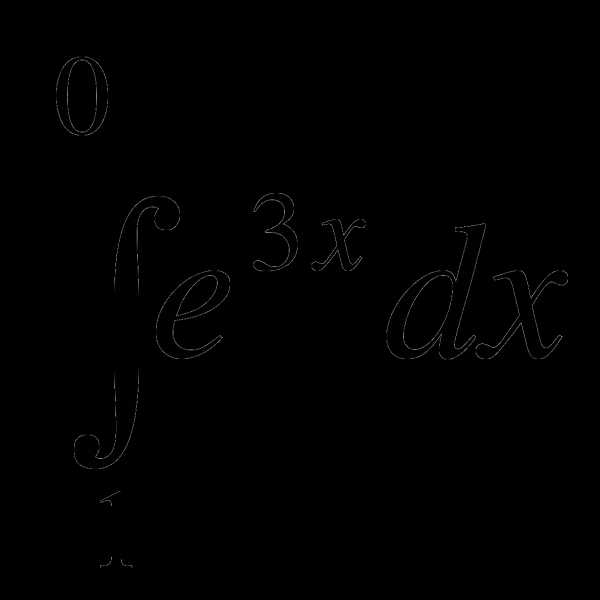 3)
3) 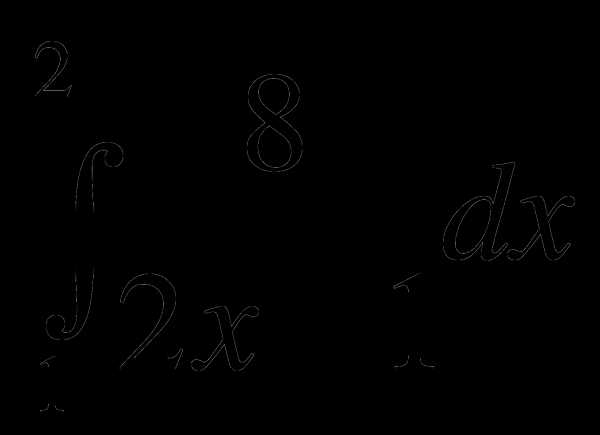
4. Вычислить площадь фигуры, ограниченной линиями
1) у = х2 + 2, у = 0, х = — 1, х = 2 1) у = х2 + 3, у = 0, х = — 2, х = 1
2) у =  , у = — 0,5х + 4 , у = 0 2) у = х3 , у = — 0,5х + 1,5, у = 0
, у = — 0,5х + 4 , у = 0 2) у = х3 , у = — 0,5х + 1,5, у = 0
Контрольная работа по теме «Первообразная. Интеграл»
1 вариант 2 вариант
1. Найти общий вид первообразной для функции:
1) у =  — cos х 2) у = 4 sin х cosх 1) у =
— cos х 2) у = 4 sin х cosх 1) у =  + sin х 2) у = 2sin2х – 2cos2х
+ sin х 2) у = 2sin2х – 2cos2х
3) у = е6х+1+ 3х2 – 5 3) у = 4х3 + 3 – е8х-5
2. Для функции найти первообразную, график которой проходит через точку:
у = 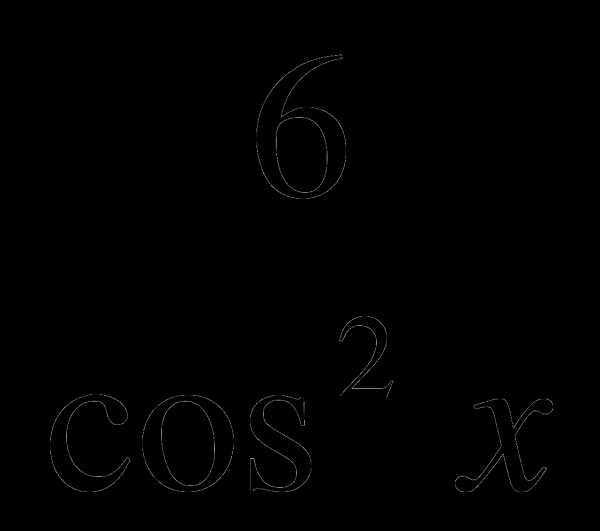 + 1, М (
+ 1, М (  ) у = 3 —
) у = 3 — 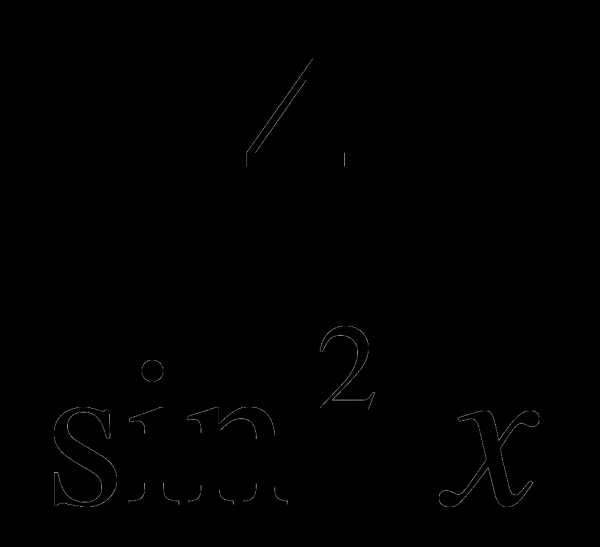 , М ( —
, М ( — )
)
3. Вычислить интегралы:
1) 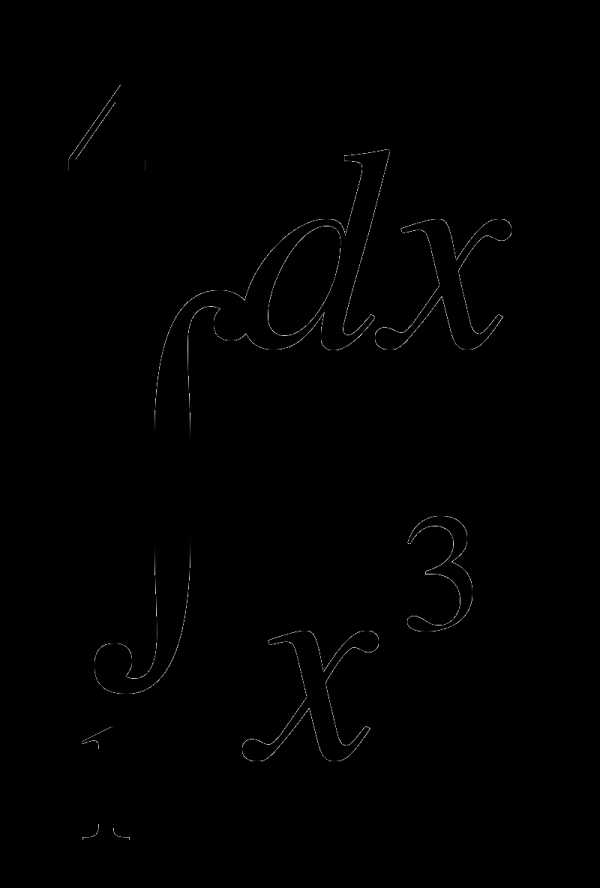 2)
2) 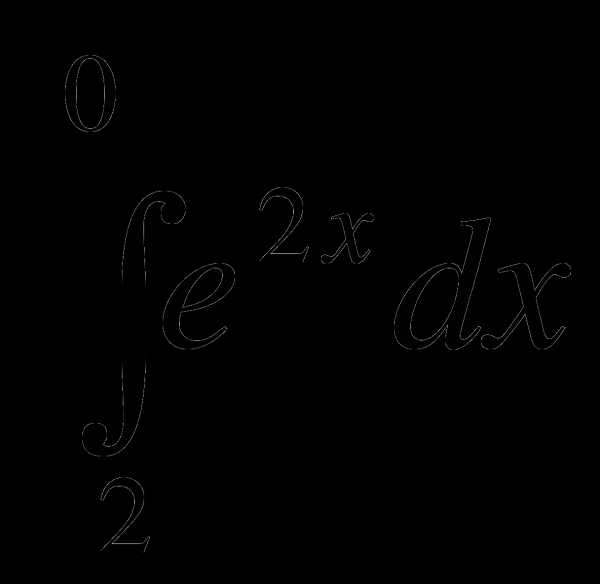 3)
3) 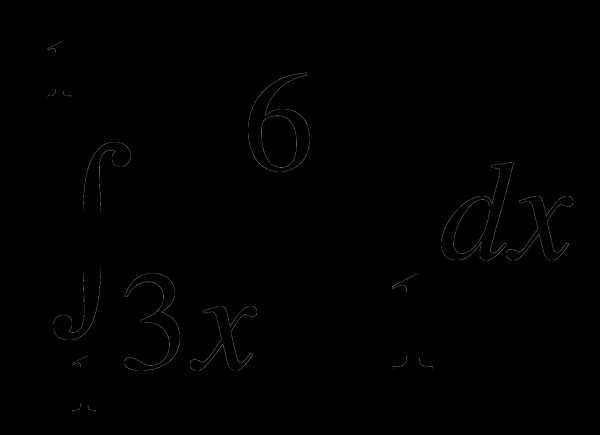 1)
1) 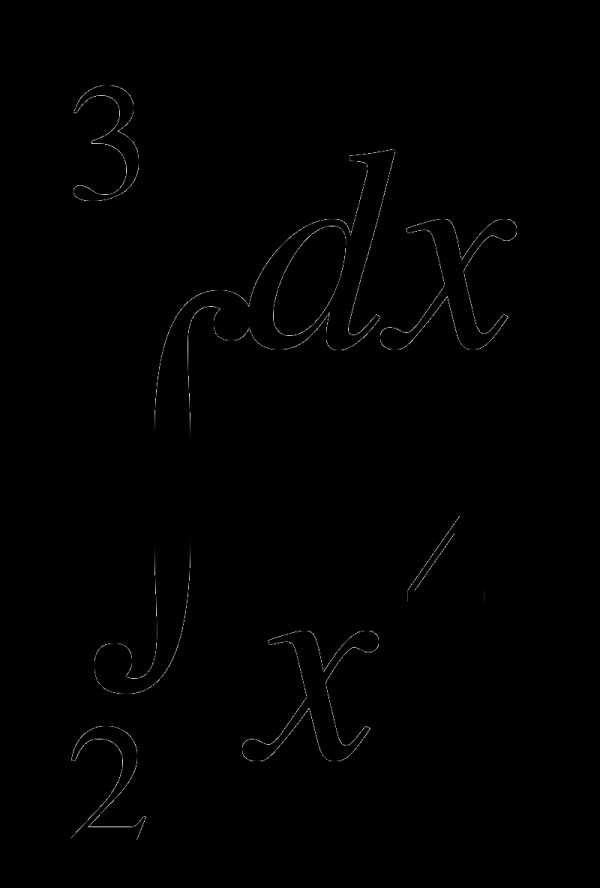 2)
2) 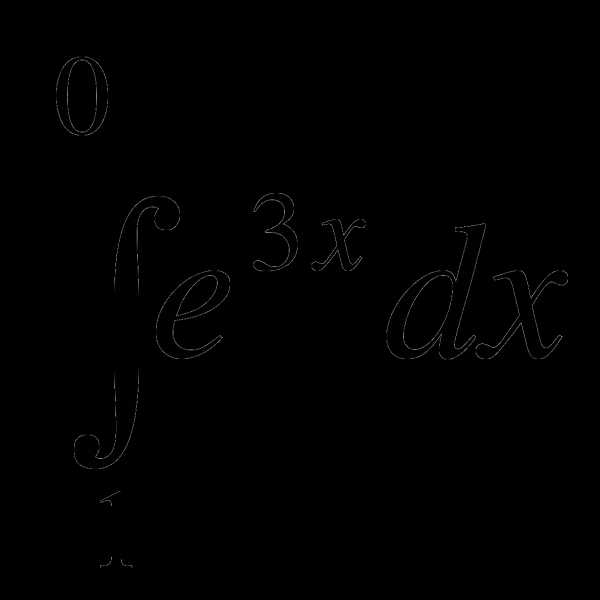 3)
3) 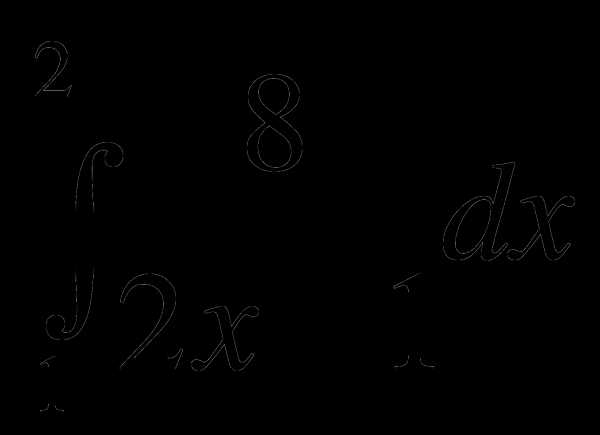
4. Вычислить площадь фигуры, ограниченной линиями
1) у = х2 + 2, у = 0, х = — 1, х = 2 1) у = х2 + 3, у = 0, х = — 2, х = 1
2) у =  , у = — 0,5х + 4 , у = 0 2) у = х3 , у = — 0,5х + 1,5, у = 0
, у = — 0,5х + 4 , у = 0 2) у = х3 , у = — 0,5х + 1,5, у = 0
infourok.ru
ГДЗ к сборнику Ершовой, Голобородько Самостоятельные и контрольные работы по алгебре для 10 класса ОНЛАЙН
Решебник к сборнику задач «Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10 класса». Рукопись. — 2014.
В решебнике представлены подробные решения задач из сборника «Ершова А. П., Голобородько В. В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов.— М.: Илекса, 2005,— 208 с.»
Решены задачи двух уровней сложности: А и Б .
Решебник поможет Вам проверить правильность решения задач и упражнений.
Страницы решебника представлены в виде слайдов. Кликните на нужный слайд, чтобы прочитать содержание страницы.
ВНИМАНИЕ! Варианты В1 и В2 а также домашние самостоятельные работы, содержащие задания повышенной трудности, не решены. Учащиеся, претендующие на высокую оценку по математике должны уметь решать их самостоятельно!
СОДЕРЖАНИЕ
Тригонометрия
С-1. Определение и свойства тригонометрических функций. Градусная и радианная меры угла
С-2. Тригонометрические тождества
С-3. Формулы приведения. Формулы сложения
С-4. Формулы двойного и половинного угла
С-5. Тригонометрические формулы преобразования суммы в произведение и произведения в сумму
К-1. Преобразование тригонометрических выражений
С-7. Общие свойства функций. Преобразования графиков функций
С-8. Четность и периодичность функций
С-9. Монотонность функций. Экстремумы
К-2. Тригонометрические функции
С-11. Обратные тригонометрические функции
С-13. Простейшие тригонометрические уравнения
С-14. Тригонометрические уравнения
С-15. Отбор корней в тригонометрических уравнениях. Системы тригонометрических уравнений
С-18. Простейшие тригонометрические неравенства
К-3. Тригонометрические уравнения, неравенства, системы
Алгебра
С-20. Корень и-ой степени и его свойства
С- 21. Иррациональные уравнения
С-22. Иррациональные неравенства. Системы иррациональных уравнений
С-24. Обобщение понятия степени
К-4. Степени и корни
С-25. Показательные уравнения. Системы показательных уравнений
С-26. Показательные неравенства
К-5. Показательная функция
С-29. Логарифм. Свойства логарифмов
С-30. Логарифмические уравнения и системы
С-32. Логарифмические неравенства
К-6. Логарифмическая функция
gdz.math-helper.ru
Учебно-методический материал по алгебре (11 класс) на тему: Самостоятельная работа по теме «Комбинаторика»
По теме: методические разработки, презентации и конспекты
Самостоятельная работа по теме «Состав и работа ПК»
СОСТАВ И РАБОТА КОМПЬЮТЕРНОЙ СИСТЕМЫТЕСТК тесту имеется ключ-ответы….
Работа учителя по формированию у учащихся навыков самостоятельной работы по выполнению тестов в рамках подготовки к ЕГЭ и самостоятельного анализа ошибок.
В этой презентации говорится о том, что самостоятельная работа учеников при подготовке к ЕГЭ даёт положительные результаты. Для этого рассматривается урок, на котором ребята вспоминают материал, прора…
Влияние самостоятельной работы по биологии на качество знаний и развитие самостоятельности учащихся.
Влияние самостоятельной работы по биологии на качество знаний и развитие самостоятельности учащихся….
ВНЕАУДИТОРНАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА ОБУЧАЮЩИХСЯ ПО ПРОФЕССИИ 19.01.17 ПОВАР, КОНДИТЕР Методические рекомендации по выполнению самостоятельных работ по МДК 01-08
Методические рекомендации предназначены для преподавателей и мастеров п/о , СПО по профессии 19.01.17 «Повар, кондитер» .Состоят из восьми разделов: методические рекомендации по организац…
Методическая разработка самостоятельных работ по черчению. Графическая работа по теме «Соединение половины вида и половины разреза» (9 класс)
Периодический учет ограничивать только текущим учетом успеваемости нельзя, так как в этом случае невозможно проверить, насколько систематизированы знания учащихся, полученные после прохождения определ…
Самостоятельная работа по теме «Конус». 11 класс. Домашняя работа по теме «Конус» задания взяты Открытый банк ЕГЭ
Самостоятельная работа по теме «Конус». 11 класс. Домашняя работа по теме «Конус». Задания взяты Открытый банк ЕГЭ базовый уровень задание 13 и профильный уровень задание 8….
Самостоятельная работа по теме «Цилиндр» и домашняя работа по теме «Цилиндр»
Самостоятельная работа по теме «Цилиндр» и домашняя работа по теме «Цилиндр» составлены по материалам открытого банка ЕГЭ базового уровня. Предназначена для…
nsportal.ru
Статья по алгебре (10, 11 класс) на тему: Организация внеаудиторной самостоятельной работы по математике.
Организация внеаудиторной самостоятельной работы по математике.
В современном обществе значительно повысились требования к качеству подготовки специалистов СПО. Современный профессионал – это не только человек, обладающий знаниями и умеющий применить их на практике, но и человек, который постоянно совершенствуется, повышает свою квалификацию и мастерство. Поэтому, в системе образования стоит задача не только дать студентам знания, но и научить их добывать эти знания самим, научить их учиться. Этому и должна помочь внеаудиторная работа студентов.
Внеаудиторная самостоятельная работа — планируемая учебная, учебно-исследовательская, научно-исследовательская работа студентов, выполняемая во внеаудиторное время по заданию и при методическом руководстве преподавателя, но без его непосредственного участия. Внеаудиторная самостоятельная работа призвана повысить качество учебного процесса. Ведь, знания, которые студент приобретает самостоятельно, усваиваются значительно лучше, чем готовые знания, которые ему сообщает преподаватель.
Самостоятельная работа студентов включает в себя:
- подготовку к аудиторным занятиям и выполнение соответствующих заданий;
- самостоятельную работу над отдельными темами учебных дисциплин в соответствии с учебно-тематическими планами;
- подготовку к практикам и выполнение заданий, предусмотренных практиками;
- выполнение письменных контрольных и самостоятельных работ, электронных презентаций;
- подготовку ко всем видам контрольных испытаний, в том числе курсовым, цикловым и комплексным экзаменам и зачётам;
- подготовку к итоговой государственной аттестации,
- работу в студенческих научных обществах, кружках, семинарах и т.п.;
- участие в работе факультативов, семинаров и т.п.;
- участие в научной и научно-методической работе;
- участие в научных и научно-практических конференциях, семинарах, и т.п.
Задания внеаудиторных самостоятельных работ способствуют формированию следующих общих компетенций:
- понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес;
- организовывать собственную деятельность, исходя из цели и способов её достижения, определенных руководителем;
- анализировать рабочую ситуацию, осуществлять текущий и итоговый контроль, оценку и коррекцию собственной деятельности, нести ответственность за результаты своей работы;
- осуществлять поиск информации, необходимой для эффективного выполнения профессиональных задач;
- использовать информационно-коммуникативные технологии в профессиональной деятельности;
- работать в команде, эффективно общаться с коллегами, руководством, клиентами.
Преподаватели должны правильно организовать самостоятельную работу студентов. Это прежде всего относится к методическому обеспечению работ и разнообразию форм этих работ. Можно выделить следующие виды самостоятельной работы:
- самостоятельное изучение теоретического курса;
- конспектирование литературы;
- написание реферата, доклада, сообщения по теме;
- составление глоссария;
- создание презентаций;
- выполнение творческих работ;
- выполнение тестовых заданий;
- выполнение индивидуальных домашних заданий.
Ниже приведена таблица, в которой показано, как можно организовать внеаудиторную работу студентов 1 и 2 курса по математике в количестве 150 часов.
ВНЕАУДИТОРНАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА УЧАЩИХСЯ ПО МАТЕМАТИКЕ
Тема 1. «Развитие понятия о числе»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Развитие понятия о числе ( 3ч.) |
1. Целые и рациональные числа |
1. Доклад и презентация 2. Работа со справочниками, составление конспекта. |
1 час 1 час |
|
2. Действительные числа. Система чисел |
1.. Работа со справочниками, составление конспекта. |
1 час |
Тема 2. «Корни, степени и логарифмы»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Корни, степени и логарифмы (23 ч.) |
|
Доклад и презентация Работа со справочниками, составление конспекта. Практическая работа Выполнение тестовых заданий |
2 час 2 час 2 час 2 час |
|
Работа с конспектом Практическая работа |
2 час 2 час |
|
|
Практическая работа |
2 час |
|
|
Доклад и презентация |
2 часа |
|
|
Практическая работа |
2 часа |
|
|
Практическая работа |
2час |
Тема 3. «Прямые и плоскости в пространстве»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Прямые и плоскости в пространстве (10 ч.) |
1. Взаимное расположение 2-х прямых в пространстве |
Глоссарий Вопросы Презентация |
2 ч. |
|
2. Параллельность прямой и плоскости. Параллельность плоскостей. |
Глоссарий Вопросы Презентация |
2 ч. |
|
|
3. Перпендикулярность прямой и плоскости. |
Глоссарий Вопросы |
2 ч. |
|
|
4. Угол между прямой и плоскостью. Угол между плоскостями. |
Глоссарий Вопросы |
2 ч. |
|
|
5. Подготовка к контрольной работе №3 |
Практическая работа |
2 ч. |
|
|
ИТОГО |
10 час |
Тема 4. «Элементы комбинаторики»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Элементы комбинаторики (10 ч.) |
|
презентация |
2 ч. |
|
практическая работа |
2 ч. |
|
|
практическая работа |
2 ч. |
|
|
доклад |
2 ч. |
|
|
сообщение |
2 ч. |
|
|
практическая работа |
2 ч. |
Тема 5. «Координаты и векторы»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Координаты и векторы (10 ч.) |
1. Действия с векторами |
тест |
2 ч. |
|
2. Скалярное произведение векторов |
задачи презентация |
2 ч. |
|
|
3. Уравнение сферы, плоскости и прямой |
задачи презентация |
2 ч. |
|
|
4. Решение прикладных задач |
задачи |
2 ч. |
|
|
5. Подготовка к контрольной работе №4 |
практическая работа |
2 ч. |
|
|
итого |
10 ч. |
Тема 6. « Основы тригонометрии»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Основы тригонометрии (14 ч.) |
2. Определение тригонометрических функций |
работа с конспектом доклад и презентация |
1 ч. 1 ч. |
|
3. Основные тригонометрические тождества |
работа с конспектом практическая работа |
2 ч. |
|
|
4. Формулы сложения |
работа с конспектом практическая работа |
2 ч. |
|
|
5. Формулы двойного и половинного аргумента |
доклад и презентация работа с конспектом практическая работа |
2 ч. |
|
|
6. Формулы приведения |
Практическая работа |
3 ч. |
|
|
7. Решение тригонометрических уравнений, неравенств и систем уравнений |
Практическая работа |
3 ч. |
Тема 7. «Функции, их свойства, графики»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Функции, их свойства и графики (12ч.) |
|
1. Доклад и презентация 2. Работа со справочниками, составление конспекта. 3. Практическая работа 4. Выполнение тестовых заданий |
1 час 1 час 1,5 час 0,5 час |
|
1.Работа с конспектом 2. Тренажер 1 3. Практическая работа |
1 час 1 час |
|
|
Тренажер 2 |
1 час |
|
|
1.Доклад и презентация 2. Тренажер 3 |
2 часа |
|
|
Практическая работа |
2 часа |
|
|
Практическая работа |
1 час |
Тема 8. «Начала математического анализа»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Начала математического анализа (12ч.) |
|
доклад и презентация работа со справочниками, составление конспекта. практическая работа тестовые задания |
2 ч. 2 ч. 2 ч. |
|
практическая работа практическая работа |
2 ч. |
|
|
практическая работа |
2 ч. |
|
|
доклад и презентация практическая работа |
2 ч. |
Тема 9. «Многогранники»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Многогранники (12ч.) |
1. Призма. Правильная призма |
презентация практическая работа |
2 ч. |
|
2. Пирамида. Правильная пирамида |
презентация практическая работа |
2 ч. |
|
|
3. Сечение куба и призмы |
презентация практическая работа |
2 ч. |
|
|
4. Усеченная пирамида |
доклад и презентация |
2 ч. |
|
|
5. Правильные многогранники |
сообщение и презентация |
2 ч. |
|
|
6. Решение задач |
Практическая работа |
2 ч. |
Тема 10. «Тела и поверхности вращения»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Тела и поверхности вращения (10ч.) |
1. Цилиндр. Решение задач |
презентация практическая работа |
2 ч. |
|
2. Конус. Решение задач |
презентация практическая работа |
2 ч. |
|
|
3. Шар и сфера. Сечение шара плоскостью |
практическая работа |
2 ч. |
|
|
4. Усеченный конус |
сообщение |
2 ч. |
|
|
5. Решение задач |
практическая работа |
2 ч. |
Тема 11. «Измерения в геометрии»
|
Измерения в геометрии (10 ч.) |
Формулы объема геометрических тел |
работа с конспектом доклад и презентация |
2 ч. |
|
2.Формулы площади поверхностей цилиндра и конуса |
работа с конспектом практическая работа |
2 ч. |
|
|
3. Формулы объема шара и площади сферы |
работа с конспектом практическая работа |
2 ч. |
|
|
4. Формулы площади поверхностей геометрических тел |
доклад и презентация работа с конспектом практическая работа |
2 ч. |
|
|
5. Подобие тел |
Практическая работа |
2 ч. |
|
Тема 12. «Элементы теории вероятностей и математической статистики»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Элементы теории вероятностей и математической статистики (12ч.) |
1. Вероятность события |
презентация практическая работа |
3 ч. |
|
2. Числовые характеристики дискретной случайной величины |
презентация практическая работа |
2 ч. |
|
|
3. Основные понятия математической статистики |
презентация практическая работа |
3 ч. |
|
|
4. Понятие о задачах математической статистики |
сообщение |
2 ч. |
|
|
5. Решение практических задач |
практическая работа |
2 ч. |
Тема 13. «Уравнения и неравенства»
|
Тема программы |
Тема самостоятельной работы |
Виды самостоятельных работ |
Количество часов |
|
Уравнения и неравенства (12 ч.) |
1. Рациональные и иррациональные уравнения и системы |
конспект практическая работа |
2 ч. |
|
2. Показательные и логарифмические уравнения, неравенства и системы уравнений |
работа с конспектом практическая работа |
2 ч. |
|
|
3. Тригонометрические уравнения и системы |
практическая работа |
2 ч. |
|
|
4. Рациональные, иррациональные, показательные и логарифмические уравнения |
практическая работа |
2 ч. |
|
|
5.Метод интервалов |
презентация |
2 ч. |
|
|
6. Применение мат. методов для решения задач |
практическая работа |
2 ч. |
nsportal.ru