Сборник контрольных работ по математике в 11 классе
Сборник
контрольных работ по математике
11 класс
естественно-математического направления
Авторы: Соколова В.А., Лутченко А.Н.
учителя математики
КГУ «Майская средняя школа Отдела образования
акимата Тарановского района»
2014 г
Пояснительная записка
Сборник содержит полный набор контрольных работ по всему курсу алгебры и началам анализа и геометрии для 11 класса естественно-математического направления : в двух вариантах по каждой теме и итоговые контрольные работы.
Тематика и содержание работ охватывают требования действующих программ по математике для 10-11 классов естественно-математического направления утверждённых приказом Министра образования и науки Республики Казахстан №115 от 3 апреля 2013 года.
Материалы сборника будут полезны учителям и учащимся и их можно использовать при организации тематического и обобщающего контроля, итогового повторения.
Сборник можно применять в школах с различными учебно-методическими планами. Учитель сможет выбирать задания из сборника, которые гармонично впишутся в его индивидуальный творческий процесс.
Содержание
11 класс Алгебра и начала анализа
Контрольная работа по теме «Первообразная и интеграл»
Вариант 1
-
Найдите общий вид первообразной
для функции:
-
;
-
;
-
f(x)=3 .
-
Вычислите интеграл
-
dx;
-
.
-
Вычислить площадь фигуры, ограниченной линиями
у=х2-5х+6, у=3-x.
-
При каких значениях а верно неравенство:
Вариант 2
1.Найдите общий вид первообразной для функции:
1) ;
2) ;
3) f(x)= .
-
Вычислите интеграл
1) dx;
2).
-
Вычислить площадь фигуры, ограниченной линиями
у=х2-2x+1, у=3-x.
-
При каких значениях а верно неравенство:
11 класс Алгебра и начала анализа
Контрольная работа по теме «Применение интеграла»
Вариант 1
-
Найдите площадь фигуры, ограниченной линиями:
у = 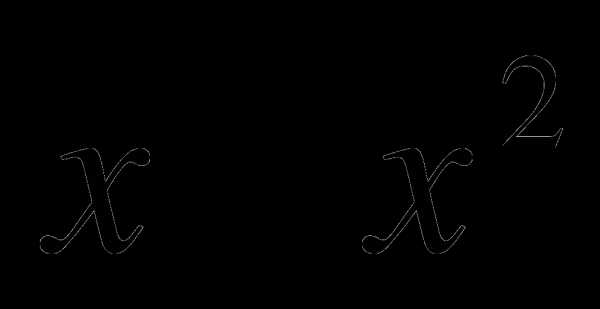 и у =
и у = 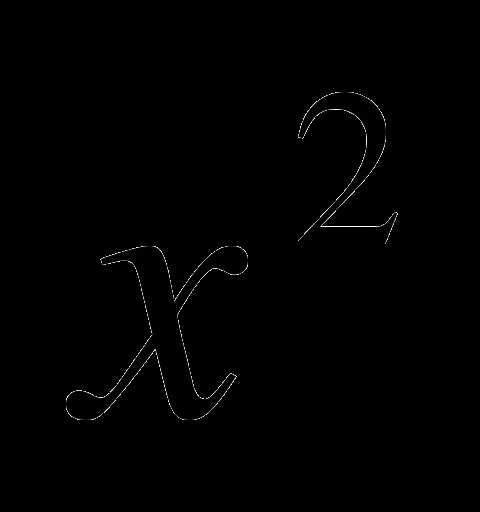 — х
— х
-
Найти объём тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
у = 1 — х и у = 0.
и у = 0.
-
Найти площадь фигуры , ограниченной линиями :
у = х + 1; у = 2 и осью ОУ.
+ 1; у = 2 и осью ОУ.
Вариант 2
-
Найдите площадь фигуры, ограниченной линиями:
у = 2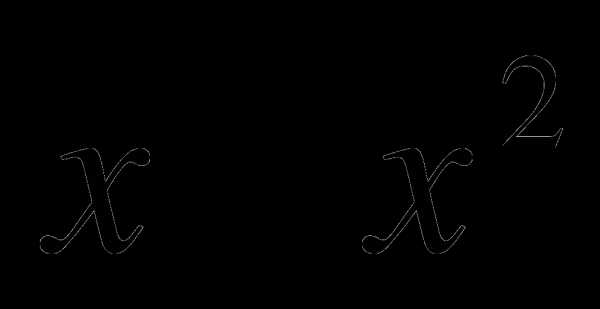 и у =
и у = 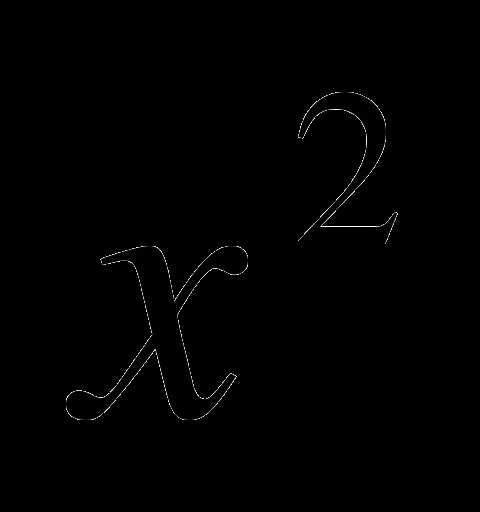
-
Найти объём тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
у = 2 + х , х= -1, х =1, у = 0.
, х= -1, х =1, у = 0.
-
Найти площадь фигуры , ограниченной линиями :
у = 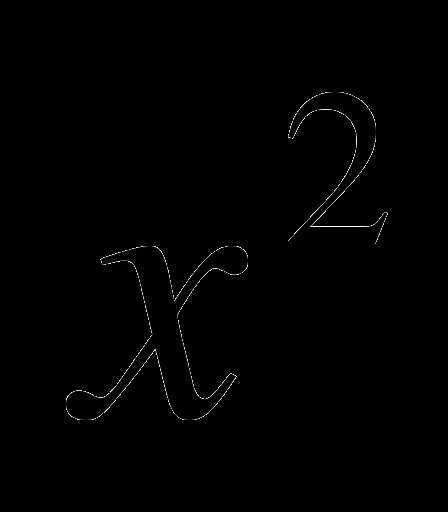 + 4,5 ; у = 4,5
+ 4,5 ; у = 4,5
11 класс Алгебра и начала анализа
Контрольная работа по теме «Преобразование иррациональных выражений»
Вариант 1
-
Упростите выражение: а)
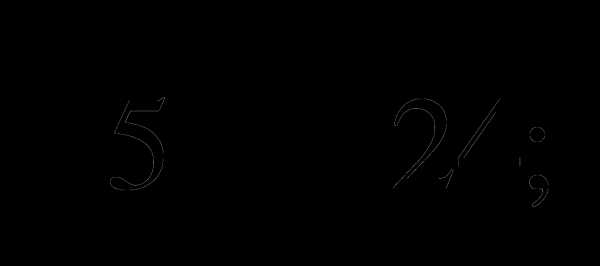 б)
б) 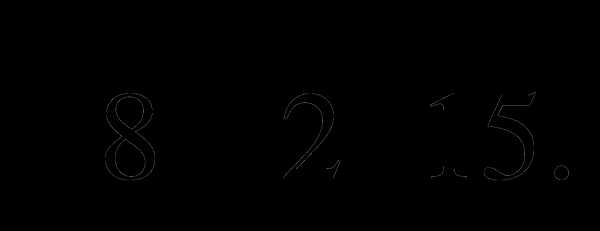
-
Вычислите:
-
Сократите дробь: а)
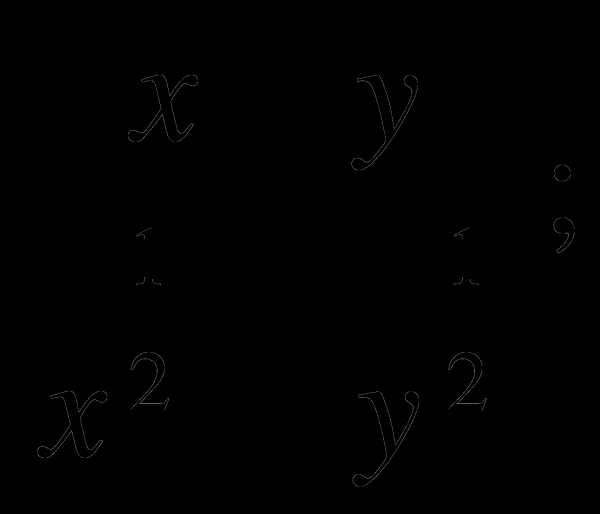 б)
б) 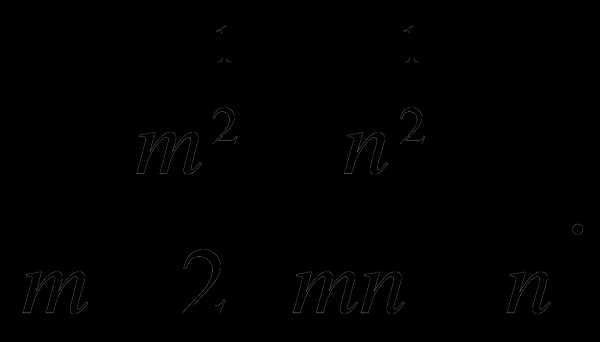
-
Вынести множитель из-под знака корня:
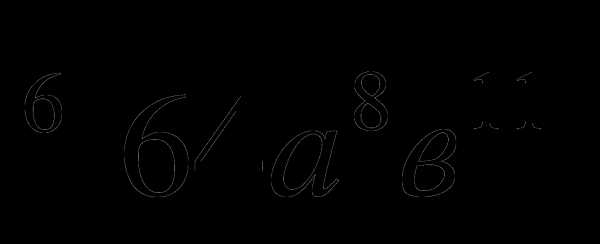
-
Избавиться от иррациональности в знаменателе дроби:
а)  б)
б)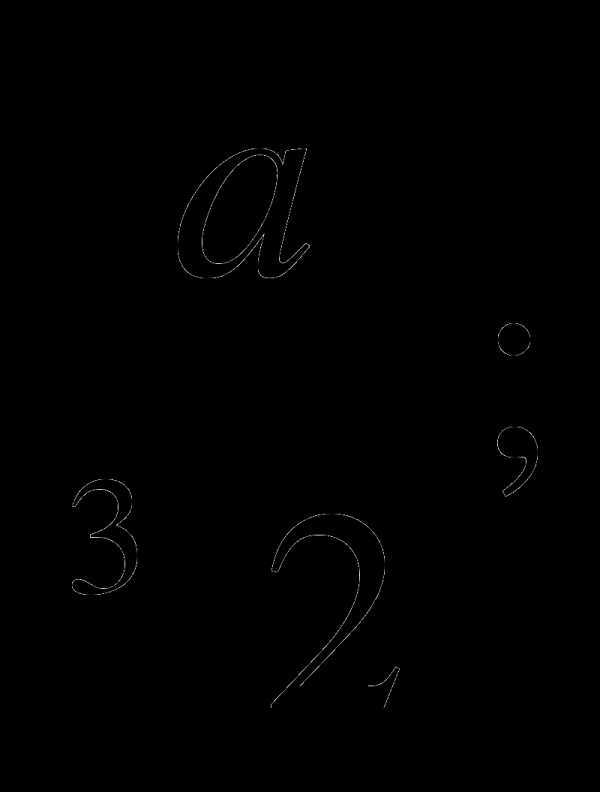 в)
в)  г)
г) 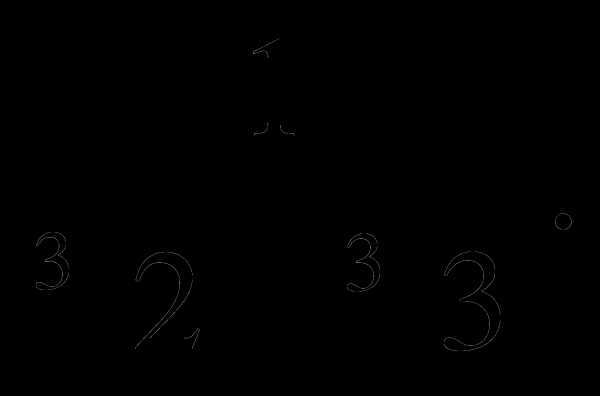
6. Упростите выражение: 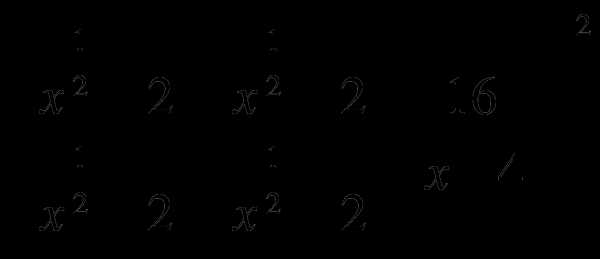
Вариант 2
-
Упростите выражение: а)
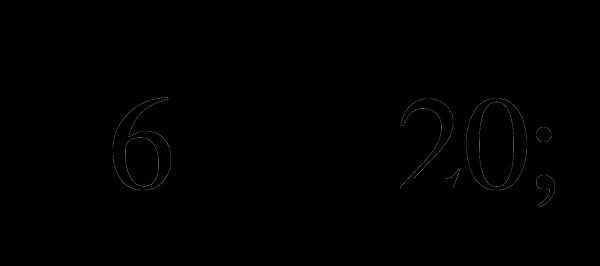 б)
б) 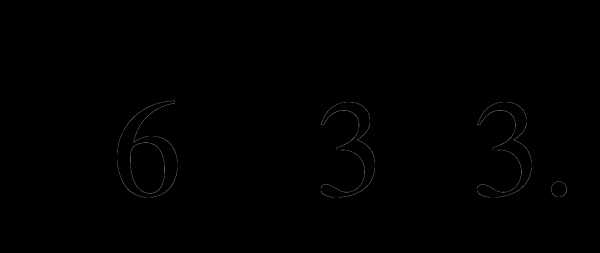
-
Вычислите:
-
Сократите дробь: а)
 б)
б) 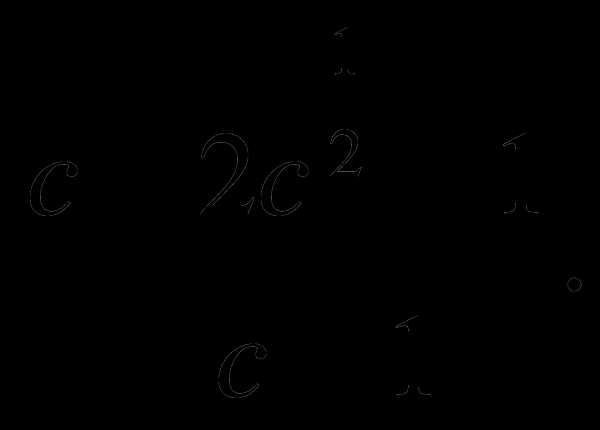
-
Вынести множитель из-под знака корня:
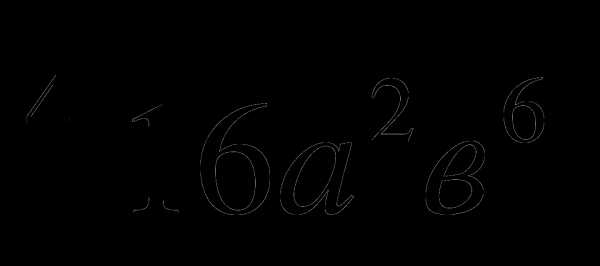
-
Избавиться от иррациональности в знаменателе дроби:
а)  б)
б) в)
в)  г)
г) 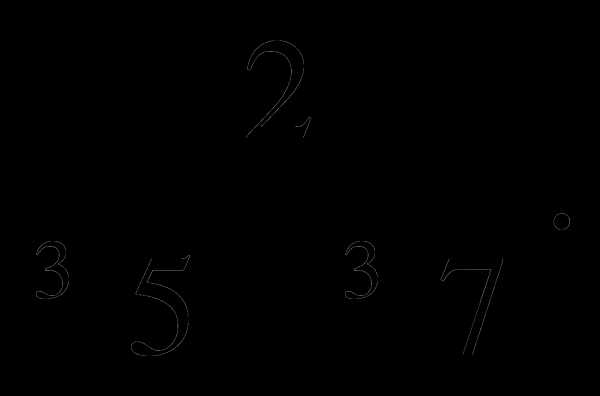
6. Упростите выражение:  .
.
11 класс Алгебра и начала анализа
Контрольная работа по теме
«Решение иррациональных уравнений, неравенств и их систем»
Вариант 1.
-
Решить уравнения:
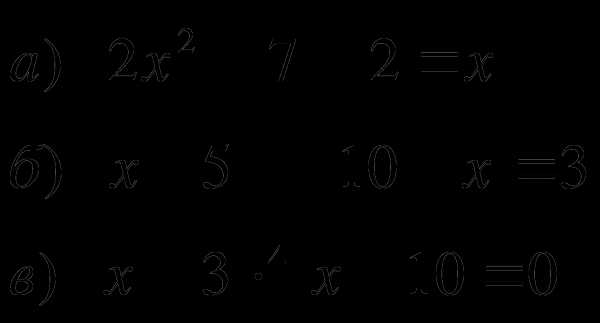
-
Решить неравенства:
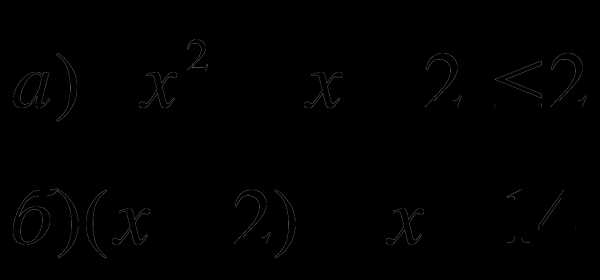
-
Решить систему уравнений:

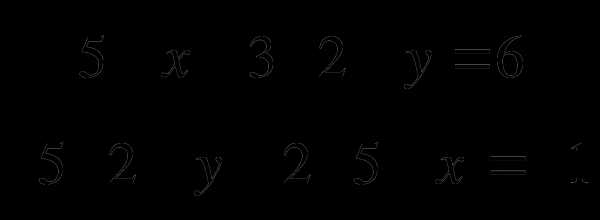
Вариант 2.
1.Решить уравнения:
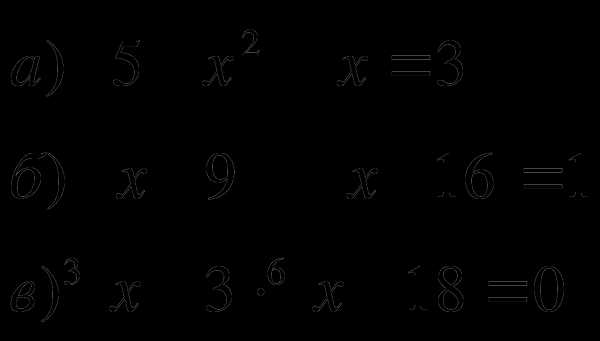
2.Решить неравенства:
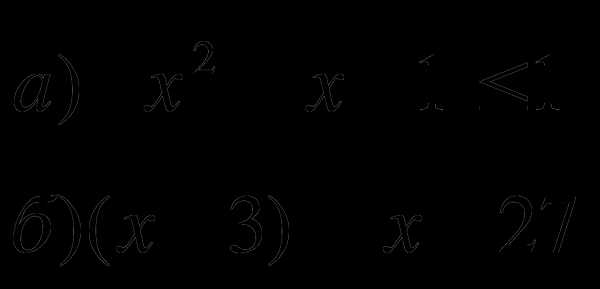
3.Решить систему уравнений:
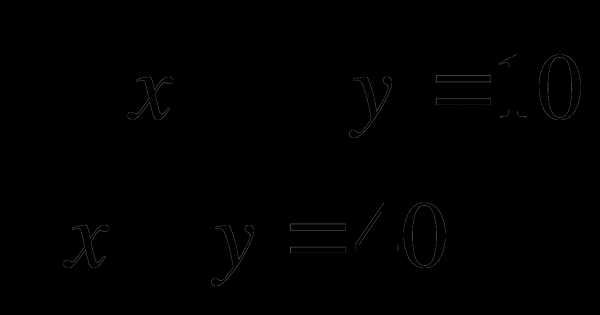
11 класс Алгебра и начала анализа
Контрольная работа по теме
«Дифференцирование и интегрирование степенной функции
с действительным показателем»
Вариант 1
1. Найти производные функции:
a) 
b)
c) 
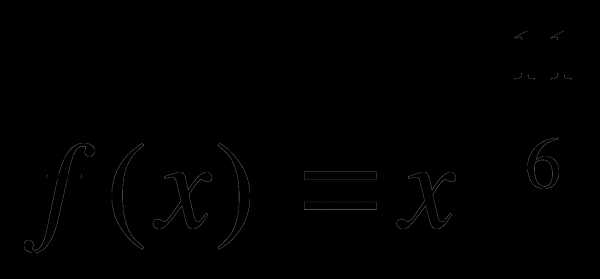
2. Составить уравнение касательной к графику функции 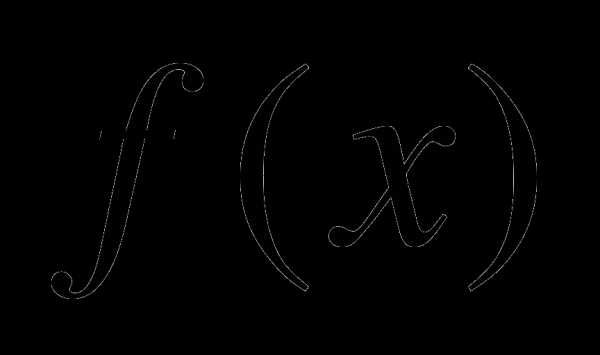 в точке с абсциссой
в точке с абсциссой 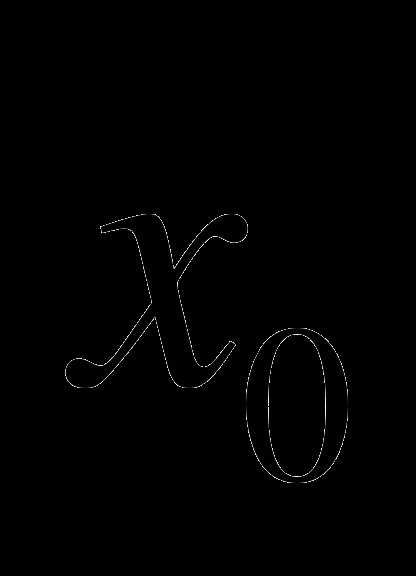 : .
: .
3. Вычислить площадь фигуры, ограниченной линиями:
Вариант 2
1. Найти производные функции:
a) 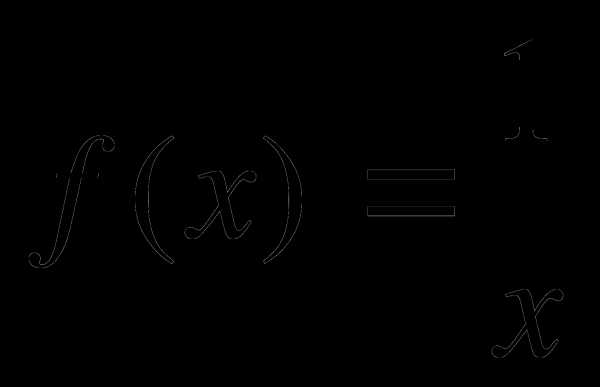
b) 
c) 
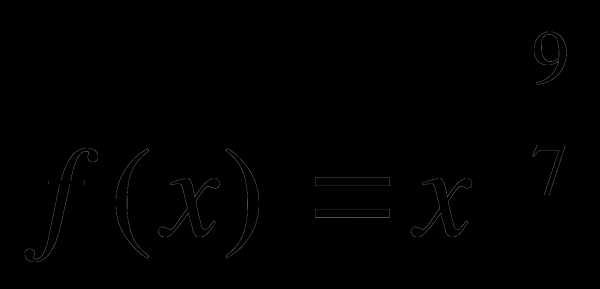
2. Составить уравнение касательной к графику функции 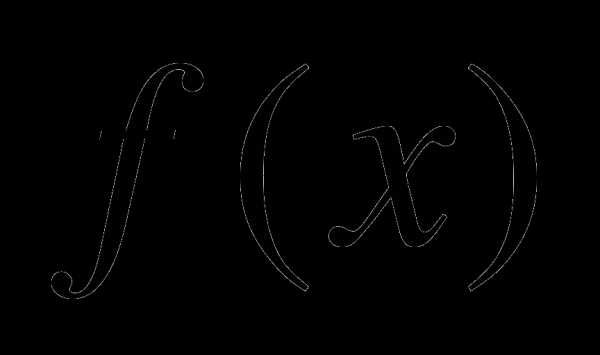 в точке с абсциссой
в точке с абсциссой 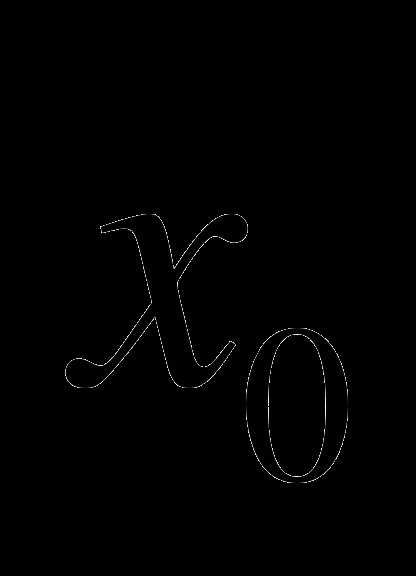 : .
: .
3. Вычислить площадь фигуры, ограниченной линиями:
11 класс Алгебра и начала анализа
Контрольная работа по теме
«Дифференцирование и интегрирование показательной и логарифмической функций»
Вариант 1
-
Найдите
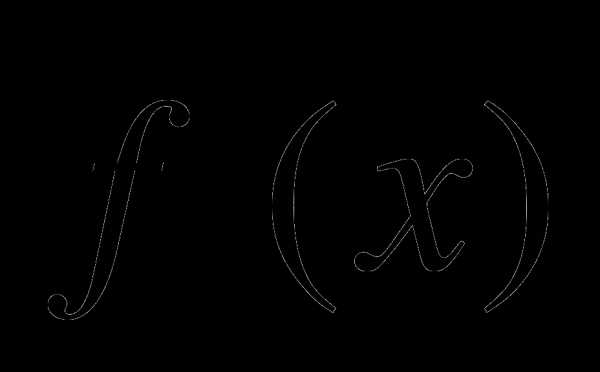 и
и 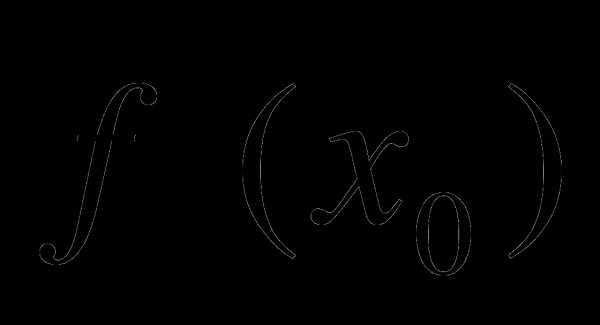 , если
, если
f(x) = 4 lnx, x =2.
=2.
-
Составьте уравнение касательной к графику функции f(x) = 3
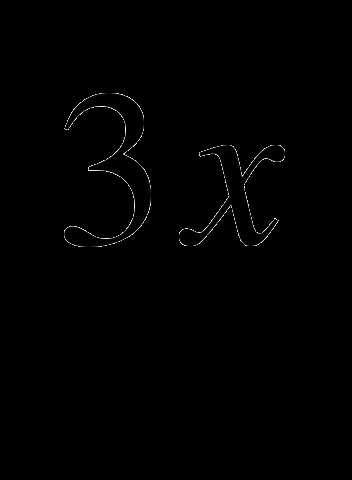 , проведённой через точку пересечения его с осью ординат.
, проведённой через точку пересечения его с осью ординат.
-
Найдите промежутки возрастания и убывания функции f(x) = 2х е
 .
.
-
Вычислите площадь фигуры, ограниченной линиями :
у =  , у = 0, у = 2, х = 0, х = 2.
, у = 0, у = 2, х = 0, х = 2.
Вариант 2
-
Найдите
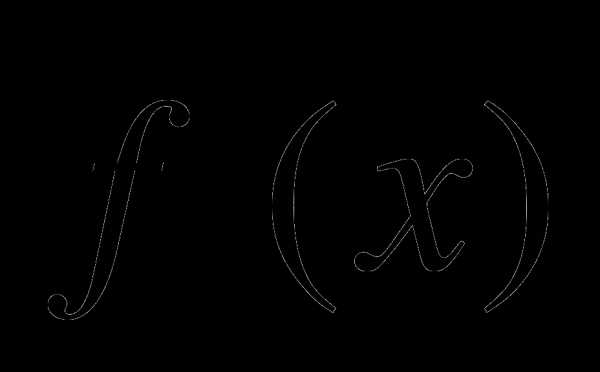 и
и 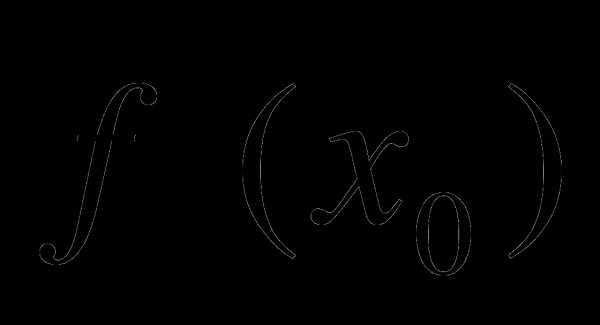 , если
, если
f(x) = 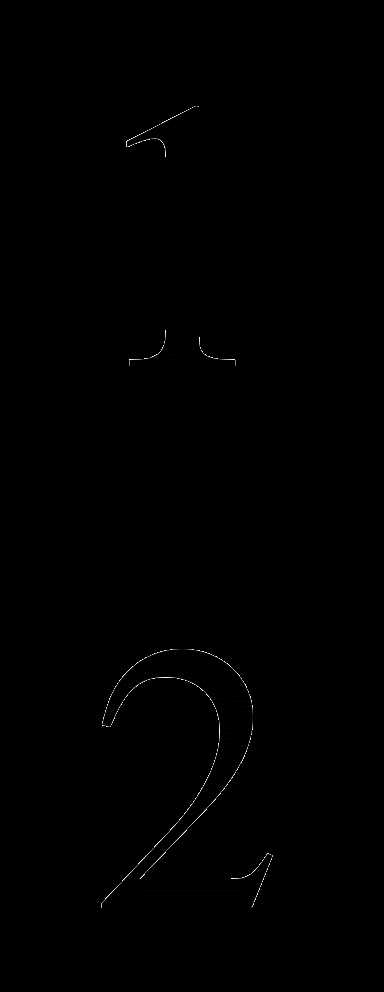 lnx, x
lnx, x =
=  .
.
-
Составьте уравнение касательной к графику функции f(x) = е
 , проведённой через точку пересечения его с осью ординат.
, проведённой через точку пересечения его с осью ординат.
-
Найдите промежутки возрастания и убывания функции f(x) =
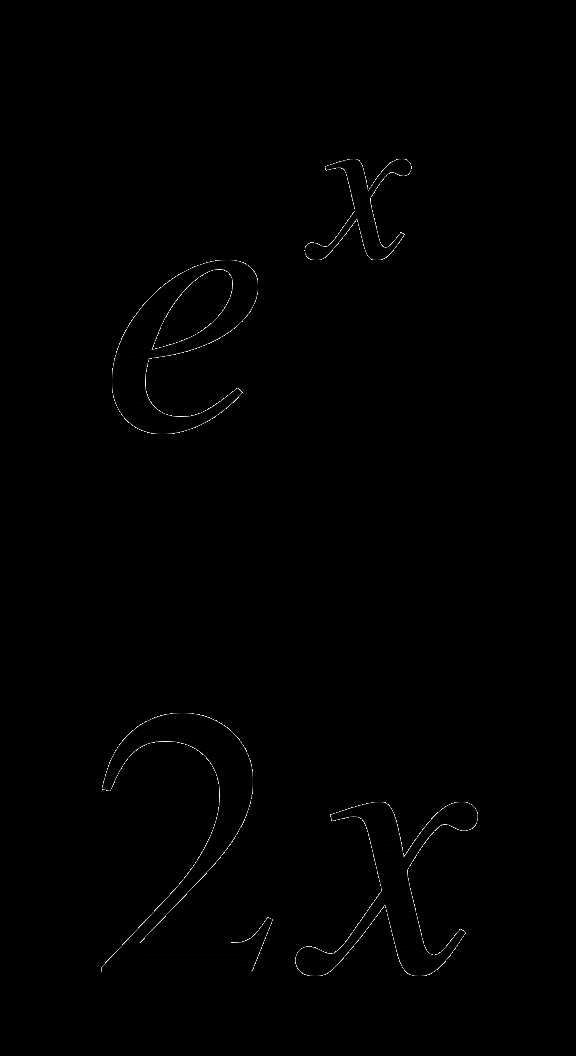 .
.
-
Вычислите площадь фигуры, ограниченной линиями :
у = 2 , у =
, у =  , х = 1.
, х = 1.
11 класс Алгебра и начала анализа
Контрольная работа по теме «Показательные уравнения и их системы»
Вариант 1
-
Решить уравнение:
1)
2)
-
3
-
Найти сумму квадратов корней уравнения:
-
Решить систему уравнений:
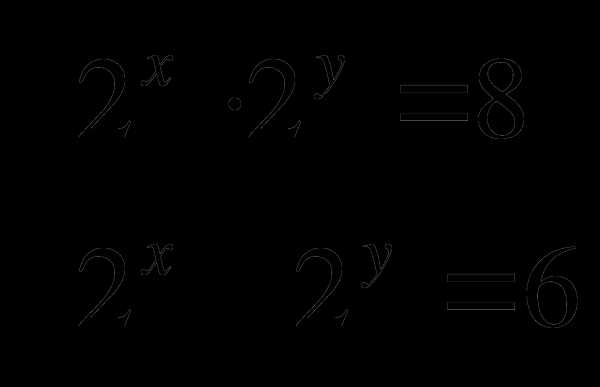
-
Найти х + 2у, где х и у решения системы уравнений:
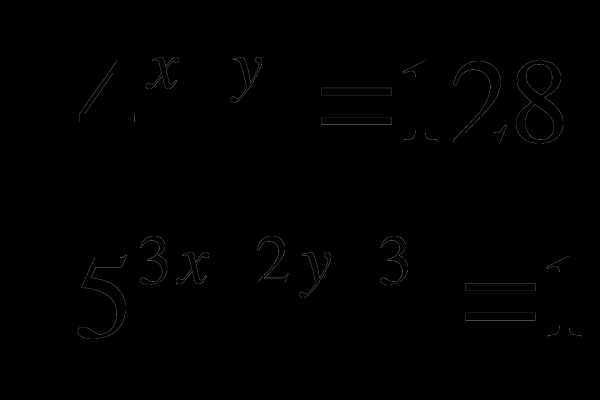
Вариант 2
-
Решить уравнение:
1)
2) 3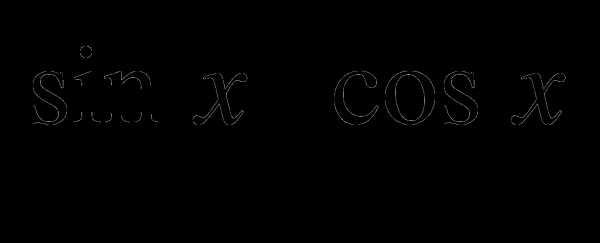 =1
=1
3) 2
2. Найти наибольший корень уравнения:
3. Решить систему уравнений: 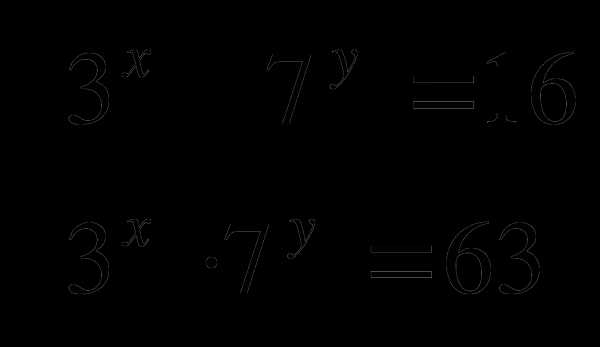
-
Найти
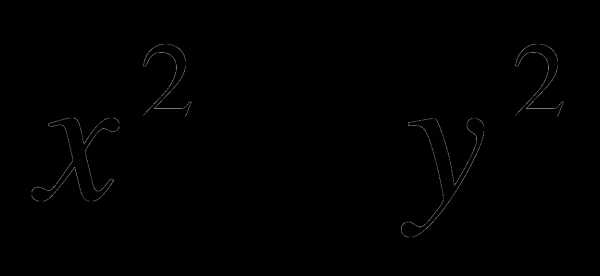 , где х и у решения системы уравнений:
, где х и у решения системы уравнений:
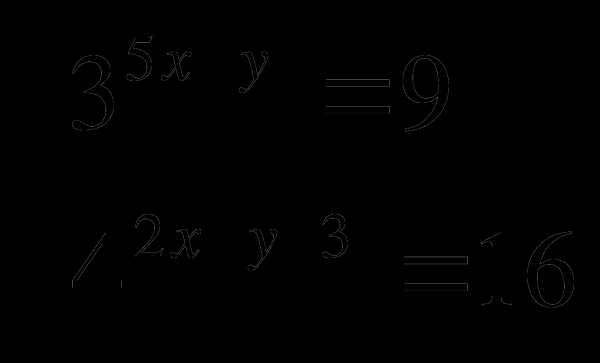
11 класс Алгебра и начала анализа
Контрольная работа по теме «Показательные неравенства и их системы»
Вариант 1
-
Решить неравенства:
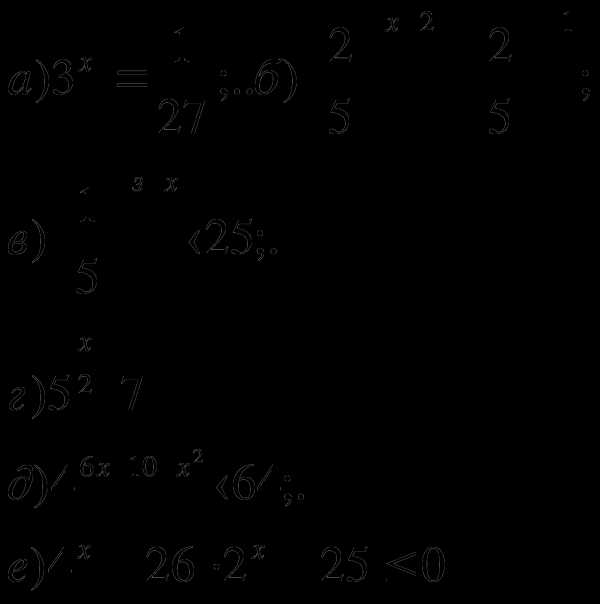
2.Найти длину отрезка, являющегося решением неравенства
3.Найти наименьшее целое решение неравенства:
4. Решить систему неравенств: 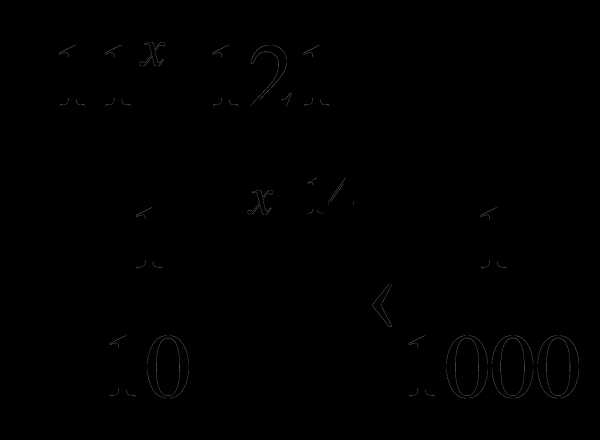
Вариант 2
-
Решить неравенства:
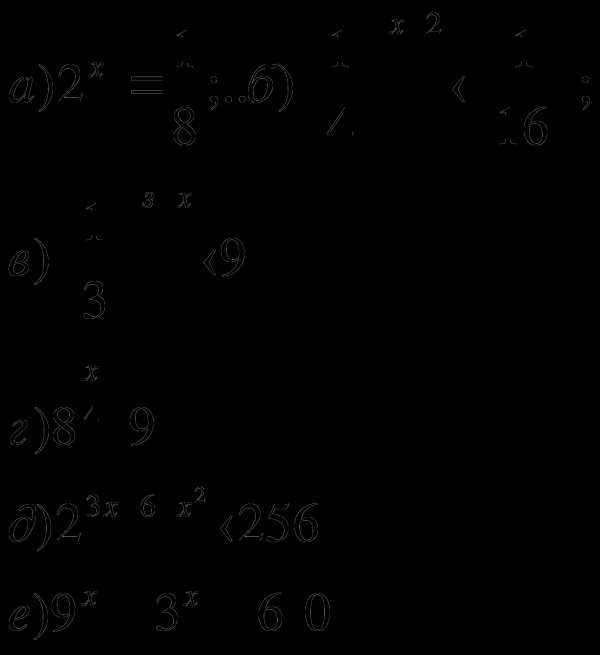
2.Найти длину отрезка, являющегося решением неравенства
3.Найти наименьшее целое решение неравенства:
4. Решить систему неравенств :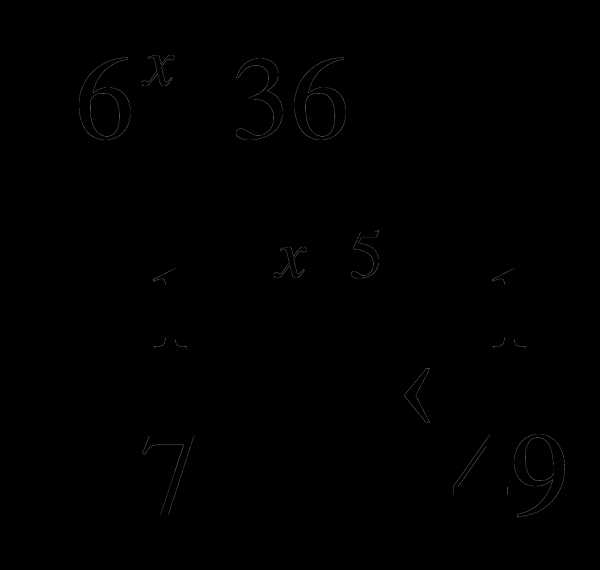
11 класс Алгебра и начала анализа
Контрольная работа по теме
«Логарифмические уравнения, неравенства и их системы»
Вариант 1
1. Решить систему уравнений:
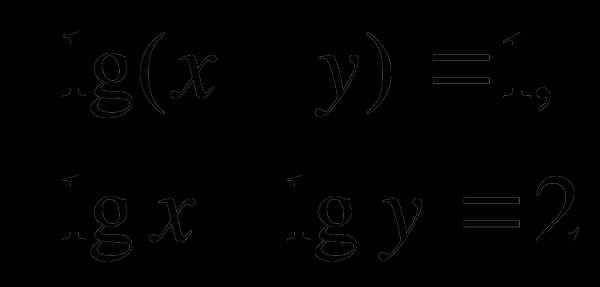
2. Решить уравнение:
3. Решить неравенство:
4.Найти сумму корней уравнения:
*5. Решить систему уравнений:
Вариант 2
1. Решить систему уравнений:
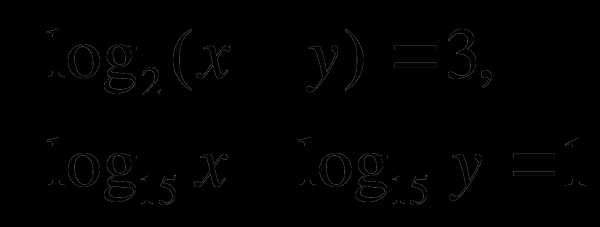
2. Решить уравнение:
3. Решить неравенство:
4.Найти произведение корней уравнения:
*5. Решить систему уравнений:
11 класс Алгебра и начала анализа
Итоговая контрольная работа (2часа)
Вариант 1
-
Найти сумму 75 первых членов последовательности, общий член которой определяется формулой .
-
Вычислить:
 .
. -
Найти область определения функции: .
-
Найдите общий вид первообразной функции: .
-
Решить систему уравнений:
-
Найдите наибольшее и наименьшее значения данных функций на указанных промежутках:
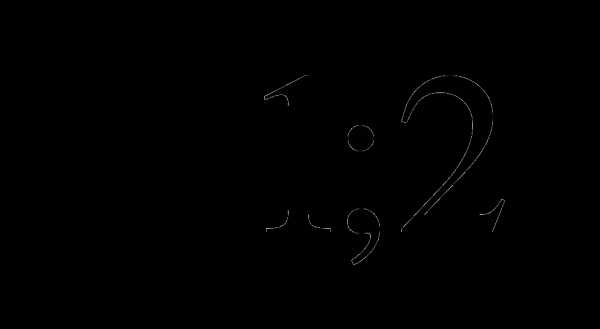
Вариант 2
-
Найти сумму 10 первых членов последовательности, общий член которой определяется формулой
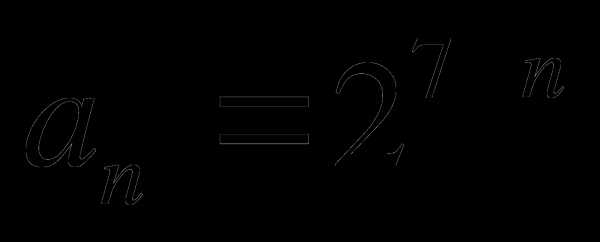 .
. -
Вычислить:
 .
. -
Найти область определения функции: .
-
Найдите общий вид первообразной функции: .
-
Решить систему уравнений:
-
Найдите наибольшее и наименьшее значения данных функций на указанных промежутках:
11 класс Геометрия
Контрольная работа по теме «Призма»
Вариант 1
1.Найти сторону основания и высоту правильной четырёхугольной призмы, если площадь полной поверхности равна 140 кв см, а площадь боковой поверхности равна 12 кв см.
2. В прямой треугольной призме стороны основания 10,17,21, а высота призмы 20. Найти площадь полной поверхности призмы.
3.В прямом параллелепипеде стороны основания 4 см и 10 см. Один из углов между сторонами равен 30 градусов. Площадь боковой поверхности равна 160 кв см. Найти площадь полной поверхности.
Вариант 2
1.Найти сторону основания и высоту правильной четырёхугольной призмы, если площадь полной поверхности равна 40 кв см, а площадь боковой поверхности равна 8 кв см.
2. В прямой треугольной призме основание — прямоугольный треугольник с катетами 16см и 12 см. Боковое ребро призмы равно 7см. Найдите площадь полной поверхности призмы.
3. Найдите площадь поверхности прямоугольного параллелепипеда, у которого стороны основания 5м и 12м, а диагональ наклонена к плоскости основания под углом 450.
11 класс Геометрия
Контрольная работа по теме «Пирамида. Усечённая пирамида»
Вариант 1
-
Основанием пирамиды является прямоугольник со сторонами 18см и 10 см. Основанием высоты пирамиды, равной 12см, является точка пересечения диагоналей прямоугольника. Найти площадь боковой поверхности пирамиды ,площадь полной поверхности пирамиды.
-
Высота правильной четырёхугольной усечённой пирамиды равна 5см. Стороны оснований – 8см и 6см. Найти боковое ребро пирамиды.
Вариант 2
-
В правильной четырёхугольной пирамиде сторона основания равна 10м, а высота-12м. Найдите площадь боковой поверхности пирамиды, площадь полной поверхности пирамиды.
-
Стороны оснований правильной усечённой треугольной пирамиды 12дм и 3дм. Боковое ребро 6дм. Найдите высоту пирамиды.
11 класс Геометрия
Контрольная работа по теме «Конус . Цилиндр. Усечённый конус »
Вариант 1
1.Диагональ осевого сечения цилиндра равна 12 см и наклонена к плоскости его основания под углом 300. Найдите площадь полной поверхности цилиндра
2.Осевым сечением конуса является прямоугольный треугольник. Расстояние от центра до образующей равно 5 см. Найти площадь боковой поверхности конуса.
3.В усечённом конусе высота равна 24см, а радиусы оснований 3см и 10 см. Вычислите площадь боковой поверхности усечённого конуса.
Вариант 2
1.Угол при вершине осевого сечения конуса равен 1200. Образующая его 16см. Найдите площадь полной поверхности конуса.
2.Площщадь осевого сечения цилиндра равна 40см2. Длина окружности его основания 8π см. Найти площадь боковой поверхности цилиндра.
3.Найдите, чему равна площадь осевого сечения и площадь боковой поверхности усечённого конуса, если радиусы его оснований 3 и 6 см, а высота равна 4 см.
11 класс Геометрия
Контрольная работа по теме «Шар и сфера»
Вариант 1
-
В шаре радиуса 84мм на расстоянии 30мм от центра проведена секущая плоскость. Найдите площадь сечения.
-
Шар с центром в точке О касается плоскости в точке В. Точка А лежит в этой плоскости, ОА = 20см, АВ = 16 см. Найдите площадь поверхности шара.
-
Радиусы шаров 25см и 29см, а расстояние между их центрами 36см. Найдите радиус круга, являющегося пересечением шаров и длину линии, по которой пересекаются поверхности шаров.
Вариант 2
-
Радиус шара равен 13дм. Секущая плоскость проходит на расстоянии 5дм от центра шара. Найдите площадь сечения.
-
Точка В лежит на касательной к шару плоскости на расстоянии 17см от центра и 15см от точки касания. Найдите площадь поверхности шара.
-
Два шара с радиусом 10см расположены так, что расстояние между их центрами равно 12см. Найдите радиус круга, являющегося пересечением шаров и длину линии, по которой пересекаются поверхности шаров.
11 класс Геометрия
Контрольная работа по теме «Объёмы»
Вариант 1
-
В правильной треугольной призме сторона основания 12 см, а высота 5см. Найдите объём призмы.
-
Равнобедренный треугольник с основанием 48см и высотой 10 см вращается вокруг основания. Найдите объём тела вращения.
Вариант 2
-
В правильной четырёхугольной пирамиде высота равна 8 дм, а боковое ребро 10дм. Найдите объём пирамиды.
-
Стороны прямоугольника 14см и 16см. Найдите объём тела вращения, полученного вращением данного прямоугольника вокруг меньшей стороны..
11 класс Геометрия
Контрольная работа по теме «Комбинации геометрических тел»
Вариант 1
1. Около правильной треугольной пирамиды со стороной основания 6см и высотой 8см описан шар. Найдите радиус шара.
2. Правильная четырёхугольная призма вписана в шар. Найдите высоту призмы, если радиус шара 5 см, а ребро основания призмы 6 см.
3.В конус вписан шар объёмом  см
см . Найти объём конуса, если его высота 9 см.
. Найти объём конуса, если его высота 9 см.
4.Угол между высотой правильной треугольной пирамиды и боковой гранью равен 300. Найти длину стороны основания, если радиус вписанного в пирамиду шара равен 1 см.
Вариант 2
-
В правильную треугольную пирамиду со стороной основания 6см и высотой 8см вписан шар. Найдите радиус шара.
-
Длина бокового ребра правильной треугольной пирамиды равна см. Боковое ребро составляет с плоскостью основания угол 600 . Найти радиус описанного около пирамиды шара.
-
Правильная треугольная призма вписана в шар. Найдите высоту призмы, если радиус шара
 , а ребро основания 2см.
, а ребро основания 2см.
-
Образующая конуса, вписанного в шар равна 16 см, а радиус шара 10 см. Найдите радиус основания конуса.
11 класс Геометрия
Итоговая контрольная работа
Вариант 1
-
Правильная четырёхугольная призма вписана в шар. Найдите высоту призмы, если радиус шара 5 см, а ребро основания призмы 6 см.
-
В конус вписан шар объёмом см3 . Найти объём конуса, если его высота 3 см.
Вариант 2
-
Длина бокового ребра правильной треугольной пирамиды равна см. Боковое ребро составляет с плоскостью основания угол 600 . Найти радиус описанного около пирамиды шара.
-
В шар объёмом 36π см3 вписан цилиндр с квадратным сечением. Найдите боковую поверхность цилиндра.
infourok.ru
Тест по алгебре (11 класс) по теме: Контрольная работа по алгебре за 2 полугодие 11 класс
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №1»
УТВЕРЖДАЮ:
Директор МБОУ «СОШ №1» ______________А.В.Петряев
«____» ____________ 2012 г.
Согласовано:
Зам. директора МБОУ «СОШ №1»
___________________________
«____» _____________ 2012 г.
Протокол заседания методического
совета школы №____ от _________
КОНТРОЛЬНО – ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ
по предмету «Алгебра и начала анализа»
( наименование предмета)
для 11-х классов
Составители:
Хайржанова Ольга Николаевна
учитель математики
высшей квалификационной категории
Вищунова Елена Викторовна
учитель математики
второй квалификационной категории
Пояснительная записка
Содержание работы определяется на основе Федерального компонента государственного стандарта основного общего образования (Приказ Минобразования России от 05.03.2004 г. №1089) и соответствует календарно-тематическому планированию рабочей программы по математике для обучающихся 11 классов (приказ МОУ «СОШ №1» от 19.09.2011 года №311 – О).
Контрольные измерительные материалы позволяют установить уровень освоения обучающимися федерального компонента государственного образовательного стандарта среднего (полного) общего образования. Обучение может быть эффективным только в том случае, если существует надёжная обратная связь от обучающегося к преподавателю. Тестирование является стандартизированной формой контроля, так как процедура проведения теста и оценка знаний единообразны (стандартны) для всех учеников.
Цели проведения работы:
- Оперативно выявлять знания, умения и навыки обучающихся, а также понимание ими закономерностей, лежащих в основе изучаемых фактов.
- В течение короткого времени получить представление о пробелах в знаниях и организовать работу по предупреждению отставания обучающихся.
- Способствовать рациональному использованию времени на уроке.
- Активизировать мышление обучающихся.
- Дать возможность преподавателю критически оценить свои методы преподавания.
Содержание работы определяется на основе Федерального компонента государственного стандарта основного общего и среднего (полного) общего образования (приказ Минобразования России от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования»). Задания составлены на основе Федерального компонента государственного образовательного стандарта среднего (полного) общего образования. Тексты заданий в целом соответствуют формулировкам, принятым в учебниках и учебных пособиях, включенных в Федеральный перечень.
Контрольно-измерительные материалы по алгебре и началам анализа для обучающихся 11 класса применимы при работе как по УМК А.Г. Мордковича и др., так и по УМК А.Н. Колмогорова и др.
Работа рассчитана на 40 минут. В соответствии с форматом ЕГЭ задания теста разделены на две части, которые различаются по содержанию, сложности и числу заданий.
Определяющим признаком каждой части работы является форма заданий:
– задания части В требуют краткого ответа;
– задания части С требуют развернутого ответа.
Уровень В – уровень понимания предусматривает знание обучающимися понятий и отношений между ними и применение знаний в стандартных условиях.
|
Усвоение знаний на уровне В. |
Проверка знаний, умений и навыков на уровне В. |
|
Выяснение умений решать по данному алгоритму задачи или упражнения по приведённому образцу и распознавать понятие в ситуациях, стандартных или незначительно отличающихся от них. |
Уровень С – уровень переноса, предусматривает применение знаний в нестандартных условиях, умение анализировать сложные ситуации и находить новые доказательства известных математических фактов.
|
Усвоение знаний на уровне С. |
Проверка знаний, умений и навыков на уровне С. |
|
Распознавание понятий в нестандартной ситуации и решение нестандартных задач. |
Структура теста
|
Число заданий |
Часть В |
Часть С |
|
10 |
8 |
2 |
|
Тип заданий и форма ответа |
В1–В8 с кратким ответом в виде целого числа или конечной десятичной дроби |
С1–С2 с развернутым ответом (полная запись решения с обоснованием выполненных действий) |
|
Уровень сложности |
Базовый |
Повышенный и высокий |
|
Проверяемый учебный материал |
Алгебра и начала анализа 10– 11-х классов |
Алгебра и начала анализа 10–11-х классов |
За каждое правильно выполненное задание части В дается 1 балл, задание части С оценивается в 2 балла
|
Тестовый балл |
Правильность (ошибочность) решения заданий части С |
|
2 |
Приведена верная последовательность всех шагов решения, вычисления выполнены верно, получен верный ответ |
|
1 |
Приведена верная последовательность всех шагов решения, допущена описка и/или вычислительная ошибка, не влияющая на дальнейший ход решения, В результате этой описки или ошибки может быть получен неверный ответ |
|
0 |
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1 и 2 балла |
Соотношение тестового балла и аттестационной отметки
|
Тестовый балл |
Аттестационная отметка |
|
9-10 |
5 |
|
7-8 |
4 |
|
4-6 |
3 |
|
0-3 |
2 |
Спецификация работы
|
Номер задания |
Проверяемое содержание |
|
В1 |
Умение использовать свойства арифметического корня |
|
В2 |
Умение решать иррациональные уравнения |
|
В3 |
Умение решать показательные уравнения |
|
В4 |
Умение исследовать функцию с помощью производной |
|
В5 |
Умение решать показательные неравенства |
|
В6 |
Умение решать логарифмические уравнения |
|
В7 |
Умение использовать свойства логарифма |
|
В8 |
Умение исследовать функцию на монотонность, находить наименьшее и наибольшее значения функции |
|
С1 |
Умение решать показательные и логарифмические неравенства |
|
С2 |
Умение решать показательные и логарифмические уравнения и их системы |
Текст работы
I вариант
Инструкция по выполнению работы
На выполнение теста даётся 40 минут. Работа состоит из двух частей и содержит 10 заданий. Часть 1 содержит 8 заданий с кратким ответом (В1–В8) базового уровня по материалу курса алгебры и начала анализа. Ответом является целое число или конечная десятичная дробь. Часть 2 содержит 2 более сложных заданий (С1–С2) по материалу курса алгебры и начала анализа. При их выполнении надо записать полное решение и ответ.
При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценке работы. Советуем выполнять задания в том порядке, в котором они даны.
Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
Часть 1
Ответом на задания В1–В8 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке.
В1. Вычислить при .
В2. Найти корень уравнения: .
В3. Найти корень уравнения: .
В4. На рисунке изображен график производной функции , определенной на интервале . Найти количество точек максимума функции на отрезке .
В5. Сколько целочисленных решений имеет неравенство: ?
В6. Решите уравнение, используя свойство логарифмов .
В7. Найти значение выражения: .
В8. Найти наибольшее значение функции: на отрезке .
Часть 2
Для записи решений и ответов на задания С1–С2 используйте бланк ответов № 2. Запишите сначала номер выполняемого задания (С1, С2), а затем полное обоснованное решение и ответ.
С1. Найти решение неравенства:
С2. Найти решения системы уравнений:
II вариант
Инструкция по выполнению работы
На выполнение теста даётся 40 минут. Работа состоит из двух частей и содержит 10 заданий. Часть 1 содержит 8 заданий с кратким ответом (В1–В8) базового уровня по материалу курса алгебры и начала анализа. Ответом является целое число или конечная десятичная дробь. Часть 2 содержит 2 более сложных заданий (С1–С2) по материалу курса алгебры и начала анализа. При их выполнении надо записать полное решение и ответ.
При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценке работы. Советуем выполнять задания в том порядке, в котором они даны.
Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям. Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
Часть 1
Ответом на задания В1–В8 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке.
В1. Вычислить: при .
В2. Найти корень уравнения:
В3. Найти корень уравнения: .
В4. На рисунке изображен график производной функции , определенной на интервале . Найти количество точек минимума функции на отрезке .
В5. Сколько целочисленных решений имеет неравенство: ?
В6. Решить уравнение, используя свойство логарифмов .
В7. Найти значение выражения: .
В8. Найти наименьшее значение функции на отрезке .
Часть 2
Для записи решений и ответов на задания С1–С2 используйте бланк ответов № 2. Запишите сначала номер выполняемого задания (С1, С2), а затем полное обоснованное решение и ответ.
С1. Найти решение неравенства:
С2. Найти решения системы уравнений:
Ключ к работе
|
Номер задания |
Правильный ответ |
|
|
I вариант |
II вариант |
|
|
В1 |
0,5 |
|
|
В2 |
11,8 |
|
|
В3 |
0,4 |
1,6 |
|
В4 |
2 |
2 |
|
В5 |
4 |
6 |
|
В6 |
0,75 |
1,5 |
|
В7 |
19 |
6 |
|
В8 |
2 |
— 7 |
|
С1 |
|
|
|
С2 |
nsportal.ru
Итоговая контрольная работа по алгебре 11 класс (2 варианта, 3 уровня)
Итоговая контрольная работа по математике для 11 класса
Вариант 1
I уровень. В заданиях 1–5 укажите букву верного ответа.
1. Найдите значение выражения
А. 49 Б. 27 В. 14 Г. 9
2. Найдите производную функции
А. Б. В. Г.
3. Найдите область определения функции
А. Б. В. Г.
4. Решите уравнение
А. Б. В. –4 Г. –3
5. Найдите все первообразные функции f(x)=6х –4х–2.
А. F(x)=6–4xln4+С Б. F(x)=6х2–4xln4–2х В. F(x)=3х2– –2х Г. F(x)=3х2– –2х+С
II уровень
6. Найдите значение выражения если
7. Напишите уравнение касательной к графику функции в точке с абсциссой х0=2. Найдите координаты всех точек графика этой функции, касательные в которых параллельны найденной касательной.
8. Решите уравнение
III уровень
9. Найдите точки максимума функции
10. Найдите все значения параметра a, при которых уравнение 9x–a3x+a=1 имеет единственный корень.
Итоговая контрольная работа по математике для 11 класса
Вариант 2
I уровень. В заданиях 1–5 укажите букву верного ответа.
1. Найдите значение выражения
А. 12 Б. 34 В. 64 Г. 7
2. Найдите производную функции
А. Б. В. Г.
3. Найдите область определения функции
А. Б. В. Г.
4. Решите уравнение
А. – Б. В. –5 Г. –4.
5. Найдите все первообразные функции f(x)=8x3+3–5х.
А. F(x)=24х2–5хln5 Б. F(x)= 8х4+3х+ В. F(x)=2х4+3х– Г. F(x)=2х4+3х–+С
II уровень
6. Найдите значение выражения если
7. Составьте уравнение касательной к графику функции параллельной прямой у=–х.
8. Решите уравнение
III уровень
9. Найдите точки максимума функции
10. Найдите все значения параметра a, при которых уравнение имеет единственный корень.
infourok.ru
тематические тесты,контрольные работы 11 класс алгебра и начала анализа
Самостоятельная работа 5.1
Статистическая обработка данных
Вариант 1
1. В ходе опроса 40 учащихся школы было выяснено, сколько времени (с точностью до 0,5 ч) в неделю они затрачивают на занятия в кружках и спортивных секциях. Получили следующие данные:
2, 2,5, 5, 1,5, 4, 3, 1,5, 3,5, 4, 3, 3,5, 2,5, 3, 1,5, 4,5, 3,5, 4,
3,5, 2,5, 2, 4, 0, 2,5, 0,5, 3,5, 2, 3,5, 3, 2,5, 5, 1,5, 3,5, 2,5,
4,5, 2,5, 3,5, 1, 3,5, 1, 1,5.
а) Составьте сгруппированный ряд этих данных.
б) Чему равна мода этого измерения и какова ее кратность?
в) Выпишите таблицу распределения данных.
г) Найдите среднее значение времени, затрачиваемое учащимися на занятие в кружках.
2. Учащиеся одиннадцатых классов некоторого города сдавали пробный экзамен по алгебре. Итоги этого экзамена представили в таблице:
Оценка
Число учащихся
1
2
3
4
5
0
64
184
55
38
Составьте гистограмму распределения данных.
______________________________________________________________________
Самостоятельная работа 5.1
Статистическая обработка данных
Вариант 2
1. В ходе опроса 30 учащихся школы было выяснено, сколько времени (с точностью до 0,5 ч) в неделю они затрачивают на занятия с компьютером. Получили следующие данные:
3, 2,5, 5,5 , 3,5, 4, 3, 6, 2,5, 2, 5, 4,5, 6,5, 4, 3, 4,5, 3,5, 4,
5, 5,5, 2, 4, 3, 3,5, 2,5, 4,5, 4, 3,5, 2, 2,5, 5.
а) Составьте сгруппированный ряд этих данных.
б) Чему равна мода этого измерения и какова ее кратность?
в) Выпишите таблицу распределения данных.
г) Найдите среднее значение времени, затрачиваемое учащимися на занятие в кружках.
2. Учащиеся одиннадцатых классов некоторого города выполняли контрольную работу по алгебре. Итоги этой работы представили в таблице, в которой указали число учащихся, верно выполнивших одно, два, три и т.д. задания:
Число выполненных заданий
Число учащихся
0
1
2
3
4
5
6
0
23
58
91
216
162
80
Составьте гистограмму распределения данных.
infourok.ru
Контрольные работы по математике 11 класс
Контрольные работы по алгебре и началам анализа в 11 классе
Контрольная работа № 1 «Тригонометрические функции»
1. Найдите область определения и множество значений функции у = sin2x+1.
2. Выясните, является ли функция у = sin x – tg x четной или нечетной.
3. Сравните числа:
А) sin и ) sin ; Б) cos и cos ; В) sin 2 и cos 2,3
4. Найдите все числа из отрезка [-], для которых выполняется равенство sin x= — .
5. Постройте график функции у = -2 cos (х -.
Контрольная работа № 2 «Производная и ее геометрический смысл»
1. Найдите производную функции: а) 4 х 3 + б) sin х; в) ; г)
2.Найдите значения х, при которых значения производной функции f(x) = -3 равны нулю.
3. Запишите уравнение касательной к графику функции f(x) = 1+4х-sin x в точке с абсциссой х0 = 0.
4. На графике функции f(x)=х3 -3х2+2 найдите все такие точки, в которых касательная, проведенная к графику, параллельна прямой у=3х.
Контрольная работа № 3 «Применение производной к исследованию функции»
-
Найдите интервалы возрастания и убывания функции у=1+2х2—.
-
Постройте график функции у=2х2 .
-
Найдите ромб наибольшей площади,если известно, что сумма его диагоналей равна 10.
-
Найдите направления выпуклости графика функции у=х+
Контрольная работа № 4 «Интеграл»
1. Докажите, что функция F(x) = ех+х3-cos х является первообразной функции f (x) = 2е2х+3х2+sin х на всей числовой оси.
2. Найдите первообразную F функции f (x) = 3х2+2х-3 , график которой проходит через точку М(1;-2).
3. Вычислите площадь фигуры, ограниченной параболой у=х2+х-6 и осью Ох.
4. Найдите площадь фигуры, ограниченной линиями у=2+4х-х2 и у=х2-2х+2.
5. Найдите площадь фигуры, ограниченной параболой у=х2-12 и касательными к ней, проведенными из точки А (0;3).
Контрольная работа № 5 «Комплексные числа»
-
На комплексной плоскости постройте точки –i, -2+2i.
-
Выполните действия: а) i4+i5-2i; б) -.
-
Решите уравнение 2z2-6z+5=0/
-
Найдите все аргументы комплексного числа z=-2-2 и запишите его в тригонометрической форме.
-
Пользуясь формулой Муавра, возведите в степень (1+i)6 и результат запишите в алгебраической форме.
-
Решите уравнение z3=-27.
Контрольная работа № 6 «Элементы комбинаторики»
-
Упростите , где n€N, n>4.
-
Найдите значение выражения +.
-
Сколько различных трехзначных чисел можно записать с помощью цифр 0,1,2,3 при условии, что цифры в числе могут повторяться?
-
Сколькими способами можно составить букет из трех цветков, выбирая цветы из девяти имеющихся?
-
Запишите разложение бинома (1+х)6.
Контрольная работа № 6 «Теория вероятности»
-
В ящике находится 3 белых, 5 черных, 6 красных шаров. Наугад вынимают один шар. Какова вероятность того, что вынутый шар: а) белый или черный; б) желтый; в) не белый?
-
Брошены 2 игральные кости. Какова вероятность того, что на одной кости выпало 3 очка, а на другой – четное число очков?
-
В корзине лежат 5 яблок и 3 апельсина. Наугад дважды из корзины вынимают по одному плоду (не возвращая их в корзину). Какова вероятность того, что вторым было взято яблоко, при условии, что первым был апельсин?
-
Имеется 13 карт черной масти и 5 карт красной масти. Какова вероятность того, что среди двух карт, вынутых наугад, хотя бы одна будет красной?
Контрольные работы
по геометрии
в 11 классе
Контрольная работа № 1 «Метод координат в пространстве»
Вариант 1
1. Вычислите скалярное произведение векторов и , если , , = 2, = 3, = 60°, , .
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AD1 и BM, где M – середина ребра DD1.
3. При движении прямая а отображается на прямую а1, а плоскость β – на плоскость β1. Докажите, что если а|| β, то b1 || β1.
Контрольная работа №1 «Метод координат в пространстве»
Вариант 2
1. Вычислите скалярное произведение векторов и , если , , = 3, = 2, = 60°, , .
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AC и DC1.
3. При движении прямая a отображается на прямую a1, плоскость α – на плоскость α1, и . Докажите, что .
Контрольная работа № 2 «Цилиндр, конус, шар»
Вариант 1
1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см2. Найдите площадь полной поверхности цилиндра.
2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120°. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30°; б) площадь боковой поверхности конуса.
3. Диаметр шара равен 2m. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите длину линии пересечения сферы с этой плоскостью.
Контрольная работа № 2 «Цилиндр, конус, шар»
Вариант 2
1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь полной поверхности цилиндра.
2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30°. Найдите: а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60°; б) площадь боковой поверхности конуса.
3. Диаметр шара равен 4m. Через конец диаметра проведена плоскость под углом 30° к нему. Найдите площадь сечения шара этой плоскостью.
Контрольная работа № 3 «Объемы тел»
Вариант 1
1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60°. Найдите отношение объемов конуса и шара.
2. Объем цилиндра равен 96π см3, площадь его осевого сечения 48 см2. Найдите площадь сферы, описанной около цилиндра.
Контрольная работа № 3 «Объемы тел»
Вариант 2
1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.
infourok.ru
Материал по алгебре (11 класс) на тему: Контрольные работы по алгебре 11 класс
Контрольная работа №1
Вариант I
1.Найти область определения и множество значений функции y = 2 cos x
2.Выяснить, является функция y = sin x – tg x четной или нечетной.
3.Изобразить схематически график функции y = sin x + 1 на отрезке
4.Найти наибольшее и наименьшее значения функции y = 3 sin x · cos x + 1
Контрольная работа №1
Вариант II
1.Найти область определения и множество значений функции y = 0,5 sin x
2.Выяснить, является функция y = cos x – x2 четной или нечетной.
3.Изобразить схематически график функции y = cos x – 1 на отрезке
4.Найти наибольшее и наименьшее значения функции
Контрольная работа №2
Вариант I
1.Найти производную функции: а) , б) , в) ех· cos x , г)
2.Найти значение производной функции y = f(x) в точке хо, если
3.Записать уравнение касательной к графику функции f(x) = sin x — 3x + 2 в точке
хо = 0
4.Найти значения х, при которых значения производной функции положительны.
Контрольная работа №2
Вариант II
1.Найти производную функции: а) , б) (4 – 3х)7, в) ех · sin x, г)
2.Найти значение производной функции y = f(x) в точке хо, если
3.Записать уравнение касательной к графику функции f(x) = 4x – sin x + 1 в точке
xo = 0.
4.Найти значения х, при которых значения производной функции отрицательны.
Контрольная работа №3
Вариант I
1.Найти экстремумы функции
2.Найти интервалы возрастания и убывания функции f(x)=x3 – 2×2 + x +3
3.Построить график функции f(x)=x3 – 2×2 + x +3 на отрезке [-1; 2]
4.Найти наибольшее и наименьшее значения функции f(x)=x3 – 2×2 + x +3 на отрезке [0; 1,5]
Контрольная работа №3
Вариант II
1.Найти экстремумы функции
2.Найти интервалы возрастания и убывания функции f(x)=x3 – х2 – х +2
3.Построить график функции f(x)= x3 – х2 – х +2
4.Найти наибольшее и наименьшее значения функции f(x)= x3 – х2 – х +2
Контрольная работа №3
Вариант I
nsportal.ru
Учебно-методический материал по алгебре (11 класс) по теме: Контрольные работы по алгебре 11 класс
Входной срез по алгебре и началам анализа (11 класс)
Вариант I
ЧАСТЬ 1
Ответ каждого задания этой части надо записать в бланк ответов рядом с номером задания (В1 – В8).
- На рисунке изображен график функции . Найдите по графику множество значений функции.
- Найдите наименьшее значение функции .
- Упростите выражение .
- Найдите значение выражения , если
- Решите уравнение .
- Найдите производную функции .
- Найдите наименьшее значение функции .
- Функция определена на промежутке . График ее производной изображен на рисунке. Укажите число промежутков возрастания функции.
Входной срез по алгебре и началам анализа (11 класс)
Вариант II
ЧАСТЬ 1
Ответ каждого задания этой части надо записать в бланк ответов рядом с номером задания (В1 – В8).
- На рисунке изображен график функции . Найдите наибольшее значение функции по ее графику.
- Найдите область значений функции .
- Упростите выражение .
- Найдите значение выражения , если
- Решите уравнение .
- Найдите производную функции .
- Найдите наибольшее значение функции на заданном отрезке .
- Функция определена на промежутке (–3; 7). На рисунке изображен график ее производной. Найдите точку , в которой функция принимает наибольшее значение.
ЧАСТЬ 2
Для решения заданий этой части, используйте специальный бланк. Запишите сначала номер задания (С1 и т.д.), а затем запишите полное решение.
- Найдите , если .
- Упростите выражение .
- Решите уравнение .
ЧАСТЬ 2
Для решения заданий этой части, используйте специальный бланк. Запишите сначала номер задания (С1 и т.д.), а затем запишите полное решение.
- Найдите , если .
- Упростите выражение .
- Решите уравнение .
Входной срез по алгебре и началам анализа (11 класс)
Вариант III
ЧАСТЬ 1
Ответ каждого задания этой части надо записать в бланк ответов рядом с номером задания (В1 – В8).
- На рисунке изображен график функции . Найдите промежутки возрастания этой функции.
- Найдите область значений функции .
- Упростите выражение .
- Найдите значение выражения , если
- Решите уравнение .
- Найдите производную функции .
- Найдите максимум функции .
- На рисунке изображен график производной от функции . К графику функции проведена касательная. Определите по графику угол наклона касательной в точке с абсциссой .
Входной срез по алгебре и началам анализа (11 класс)
Вариант IV
ЧАСТЬ 1
Ответ каждого задания этой части надо записать в бланк ответов рядом с номером задания (В1 – В8).
- На рисунке изображен график функции . Решите графически неравенство .
- Найдите наибольшее значение функции .
- Упростите выражение .
- Найдите значение выражения , если
- Решить уравнение .
- Найдите производную функции .
- Найдите минимум функции .
- Функция определена на промежутке (-5; 7). На рисунке изображен график ее производной. Найдите промежутки убывания функции . В ответе укажите наибольшую из длин этих промежутков.
ЧАСТЬ 2
Для решения заданий этой части, используйте специальный бланк. Запишите сначала номер задания (С1 и т.д.), а затем запишите полное решение.
- Найдите , если .
- Упростите выражение .
- Решите уравнение .
ЧАСТЬ 2
Для решения заданий этой части, используйте специальный бланк. Запишите сначала номер задания (С1 и т.д.), а затем запишите полное решение.
- Найдите , если.
- Упростите выражение .
- Решите уравнение .
nsportal.ru