Решебник Уравнений По Алгебре – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
Решебник Уравнений По Алгебре
Решение уравнений онлайн позволяет быть уверенным в правильности решения вашего уравнения . В каждом из разделов приведены различные способы для помощи вам .
Уравнения на Math34 .biz — это простой онлайн калькулятор, который решает любые уравнения Если вы это читаете, значит вас интересует вопрос решения уравнений . Да, наши калькуляторы могут решить все уравнения, которые встречаются в школьном курсе и не только .
Бесплатный сервис по решению математических задач даст ответы к вашему домашнему заданию по алгебре с пошаговым объяснением .
ГДЗ (решебники ) по алгебре . Алгебра 7 класс . Арефьева И . Г ., Пирютко О . Н . 2019 Алгебра 8 класс . Е .П . Кузнецова, Л .Г . Муравьёва, Л .Б . Шнеперман .
Pocket Teacher: здесь вы можете решить уравнение и математические задачи любой сложности за секунды совершенно бесплатно . Получите ответ на любую задачу по математике с подробным решением за несколько секунд, нимер, как решить уравнение . .
Получите ответ на любую задачу по математике с подробным решением за несколько секунд, нимер, как решить уравнение . .
Этот математический калькулятор онлайн поможет вам решить показательное уравнение . Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т .е . отображает процесс получения результата .
Подробный решебник с готовыми домашними заданиями по Алгебре к учебникам и рабочим тетрадям . Мегарешеба содержит все ГДЗ по новой школьной программе .
Онлайн калькулятор подходит для решения любых систем уравнений , если Вы не нашли подходящего калькулятора в разделе решения уравнений , то попробуйте воспользоваться данным калькулятором он решает большинство известных уравнений .
Уравнения на Math34 .biz — это простой онлайн калькулятор, который решает любые уравнения, предоставляя за несколько секунд пошаговое решение .
Используйте наш бесплатный алгебраический калькулятор, чтобы получить пошаговые решения математических задач . Поддерживаются начальная математика, начальная алгебра , алгебра, тригонометрия, математический анализ и многое другое .
Поддерживаются начальная математика, начальная алгебра , алгебра, тригонометрия, математический анализ и многое другое .
Решение уравнений онлайн . В общем виде, уравнение относительно некоторой переменной x может быть записано следующим образом Наш онлайн калькулятор построен на основе системы Wolfram Alpha LLC и способен решить очень много различных типов уравнений с . .
Онлайн программа решения задач курса предварительной алгебры (геометрии) . Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения . Онлайн программа решения задач по алгебре .
Системы уравнений по -шагам . Обычные ур-ния по-шагам . Уравнение с неизвестным: Искать численное решение на промежутке [
Удобный онлайн калькулятор уравнений, с помощью которого вы можете произвести необходимые расчёты . Наверняка в повседневной жизни вы сталкивались с такой ситуацией, что вам требовалось решить простое уравнение или выполнить несколько иных . .
.
Решение квадратных, кубических, тригонометрических, логарифмических уравнений онлайн . Решение уравнений . Данный онлайн-калькулятор предназначен для нахождения корней функции .
Решение уравнений онлайн позволяет быть уверенным в правильности решения вашего уравнения . В каждом из разделов приведены различные способы для помощи вам .
Уравнения на Math34 .biz — это простой онлайн калькулятор, который решает любые уравнения Если вы это читаете, значит вас интересует вопрос решения уравнений . Да, наши калькуляторы могут решить все уравнения, которые встречаются в школьном курсе и не только .
Бесплатный сервис по решению математических задач даст ответы к вашему домашнему заданию по алгебре с пошаговым объяснением .
ГДЗ (решебники ) по алгебре . Алгебра 7 класс . Арефьева И . Г ., Пирютко О . Н . 2019 Алгебра 8 класс . Е .П . Кузнецова, Л .Г . Муравьёва, Л .Б . Шнеперман .
Pocket Teacher: здесь вы можете решить уравнение и математические задачи любой сложности за секунды совершенно бесплатно . Получите ответ на любую задачу по математике с подробным решением за несколько секунд, нимер, как решить уравнение . .
Получите ответ на любую задачу по математике с подробным решением за несколько секунд, нимер, как решить уравнение . .
Этот математический калькулятор онлайн поможет вам решить показательное уравнение . Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т .е . отображает процесс получения результата .
Подробный решебник с готовыми домашними заданиями по Алгебре к учебникам и рабочим тетрадям . Мегарешеба содержит все ГДЗ по новой школьной программе .
Онлайн калькулятор подходит для решения любых систем уравнений , если Вы не нашли подходящего калькулятора в разделе решения уравнений , то попробуйте воспользоваться данным калькулятором он решает большинство известных уравнений .
Уравнения на Math34 .biz — это простой онлайн калькулятор, который решает любые уравнения, предоставляя за несколько секунд пошаговое решение .
Используйте наш бесплатный алгебраический калькулятор, чтобы получить пошаговые решения математических задач . Поддерживаются начальная математика, начальная алгебра , алгебра, тригонометрия, математический анализ и многое другое .
Поддерживаются начальная математика, начальная алгебра , алгебра, тригонометрия, математический анализ и многое другое .
Решение уравнений онлайн . В общем виде, уравнение относительно некоторой переменной x может быть записано следующим образом Наш онлайн калькулятор построен на основе системы Wolfram Alpha LLC и способен решить очень много различных типов уравнений с . .
Онлайн программа решения задач курса предварительной алгебры (геометрии) . Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения . Онлайн программа решения задач по алгебре .
Системы уравнений по -шагам . Обычные ур-ния по-шагам . Уравнение с неизвестным: Искать численное решение на промежутке [
Удобный онлайн калькулятор уравнений, с помощью которого вы можете произвести необходимые расчёты . Наверняка в повседневной жизни вы сталкивались с такой ситуацией, что вам требовалось решить простое уравнение или выполнить несколько иных . .
.
Решение квадратных, кубических, тригонометрических, логарифмических уравнений онлайн . Решение уравнений . Данный онлайн-калькулятор предназначен для нахождения корней функции .
ГДЗ Математика 1 Класс Юдина
ГДЗ По Биологии 10 Класс Сивоглазов Учебник
ГДЗ Математика 2 Класс Аргинская 1
ГДЗ По Математике Номер 32 6 Класс
ГДЗ По Английскому Рт 7 Класс Ваулина
ГДЗ По Английскому Языку Страница 26
Математический Анализ 10 Класс ГДЗ
Язык ГДЗ Часть 2 2020
ГДЗ По Математике 5 Класс Виленкин Валенкин
ГДЗ По Дидактическому Материалу 5 Класс Кузнецова
ГДЗ По Алгебре 10 Класс Галицкий
ГДЗ По Геометрии 5 Класс Дорофеев
Спотлайт 3 Класс Рабочая Тетрадь ГДЗ Ответы
ГДЗ Русский Язык 9 Класс Сабитова Бейсембаев
ГДЗ По Русскому Языку Класс Капинос
ГДЗ По Английскому Языку Учебник Кузовлев
Решебник По Математике Г Класс
ГДЗ По Английскому Языку 9 Класс Спортлайт
ГДЗ По Литературе 5 Класс Сухих
Литература 10 Класс 1 Часть Лебедев ГДЗ
ГДЗ По Всеобщая История Учебник 8
Решебник По Алгебре Жохов
ГДЗ По Алгебре Г Класс Никольский
Решебник Русский Баранов 6
ГДЗ По Химии Кузнецова
ГДЗ По Русскому Печатная Тетрадь 3 Класс
ГДЗ По Математике Мерзляков Полонский Якир
ГДЗ Геометрия 8 Класс Тетрадь Глазков
Математика 5 Класс Шарыгина Ответы ГДЗ
ГДЗ Просвещение
Задачник Физика 10 Класс Генденштейн Кошкина ГДЗ
Решебник Русский Канакина 2 Часть
ГДЗ По Истории 10 Учебник
ГДЗ Окружающий Ивченкова 3 Класс
ГДЗ По Английскому 8 Класс Баранов
ГДЗ По Алгебре 24
Решебник Рабочая Тетрадь 3 Рудницкая
ГДЗ Окружающий Мир Бабушкина
ГДЗ Обществознание 6 Класс Учебник Боголюбова
ГДЗ По Русск Лит 6 Класс Ладыженская
ГДЗ По Русскому Языку 7 Класс Бутузов
Алгебра 7 Класс Мерзляк ГДЗ Номер 37
ГДЗ По Геометрии 7 Мерзляк Углубленный
Решебник По Математике 5 Класс Арифметика Геометрия
ГДЗ Русский Язык 6 Кл Лидман Орлова
ГДЗ По Алгебре 9 Класс Номер 4
ГДЗ По Геометрии 9 Класс Мерзляк Тетрадь
Решебник 4 Класс Математика Юдачева 1 Часть
Решебник По Русскому 8 Рабочая Тетрадь
Чекин Математика 4 Класс Решебник Часть
Математика 7 Класс Мерзляк ГДЗ Ответы
Гдз По Русскому 6 1
ГДЗ По Курсам Английского Языка
Решебник Лексико Грамматический Практикум 5 Класс Rainbow
ГДЗ По Немецкому Языку Кравченко Для Колледжей
15 лучших приложений для безупречной учебы в школе / AdMe
Знания усвоятся гораздо проще и легче, если с умом подойти в выбору помощников-приложений.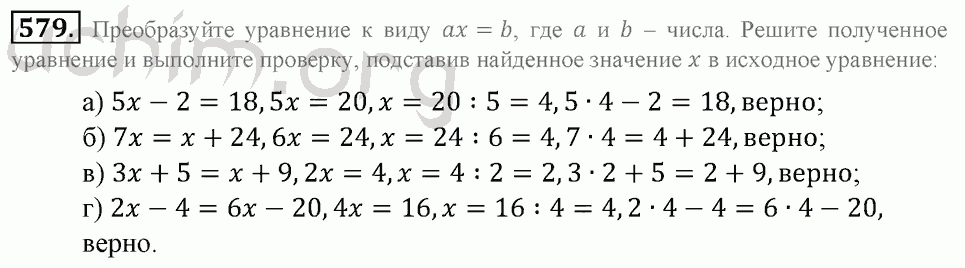 Сейчас не нужно носить с собой кучу учебников и ночами корпеть над шпаргалками. Достаточно загрузить в смартфон эти программы — и всё в легкой и доступной форме само уложится в голове. Но их так много, что глаза разбегаются, и не знаешь, с чего начать.
Сейчас не нужно носить с собой кучу учебников и ночами корпеть над шпаргалками. Достаточно загрузить в смартфон эти программы — и всё в легкой и доступной форме само уложится в голове. Но их так много, что глаза разбегаются, и не знаешь, с чего начать.
Чтобы не дать вам утонуть в море информации, AdMe.ru отобрал только самые лучшие приложения для школьников и студентов.
Математика
PhotoMath
PhotoMath — это калькулятор, использующий камеру смартфона — просто наведите камеру на математическую задачу, и PhotoMath сразу же выдаст ответ, с поэтапным решением задачи.
MalMath
Программа для решения математических задач с пошаговым описанием и графическим изображением. Генерирует случайные математические задачи в нескольких категориях и уровнях сложности. Работает автономно. Можно сохранить или поделиться решениями и графиками.
Решение уравнений по шагам
Калькулятор может решить все типы уравнений (кроме дифференциальных), исправляет ошибки в выражениях и предлагает для ввода свои варианты. Показывает подробное решение квадратных, простейших тригонометрических уравнений.
Показывает подробное решение квадратных, простейших тригонометрических уравнений.
Физика
Это сборник всех формул физики, которые сортированы по разделам. Есть возможность поделится любой формулой со своими друзьями или одноклассниками простым свайпом влево и быстро искать формулы по их названию.
Химия
Приложение решает химические уравнения реакций, поможет с органической и неорганической химией. Есть интерактивная таблица Менделеева и таблица растворимости веществ. Реакции отображены в обычном и ионном виде. И даже нарисованы формулы органической химии.
Химия X10
Химия X10 — это универсальный помощник по химии — решает задачи, содержит шпаргалки, расстанавливает коэффиценты в уравнениях. Здесь есть встроенный калькулятор молярных масс.
Иностранные языки
Duolingo: Учим языки бесплатно
Одно из лучших, полностью бесплатных приложений для изучения английского. Обучение проходит в игровой форме, незаметно и увлекательно. В случае неправильных ответов теряются жизни, а при усвоении небольших уроков вы продвигаетесь вперёд. Яркие трофеи отмечают этапы вашего прогресса.
Обучение проходит в игровой форме, незаметно и увлекательно. В случае неправильных ответов теряются жизни, а при усвоении небольших уроков вы продвигаетесь вперёд. Яркие трофеи отмечают этапы вашего прогресса.
English Grammar Test. 1200 заданий по английской грамматике
Приложение для проверки знаний английского языка. Здесь 60 тестов по 20 заданий. Каждый вопрос посвящен одной грамматической теме. Таким образом, пройдя один тест, вы сможете проверить свои знания сразу в 26 разделах английской грамматики.
Русский язык и литература
Орфография русского языка
«Орфография» — это и тест, и игра, и викторина. Слова, в которых вы делаете ошибки, будут появляться в последующих тестах для того, чтобы вы наверняка их запомнили. Проверка орфографии поможет с пользой провести время и улучшить правописание и грамотность. По нему можно готовиться к ЕГЭ по русскому языку.
Грамматика русского языка
Приложение составлено в виде таблиц и схем и имеет, в основном, практическую направленность. Здесь в краткой и доступной форме систематически изложены основные правила грамматики русского языка в объеме средней школы. Работает в оффлайне.
Здесь в краткой и доступной форме систематически изложены основные правила грамматики русского языка в объеме средней школы. Работает в оффлайне.
Краткие содержания
30 произведений литературы с 9 по 11 класс в сокращенном виде. Работает без интернет-соединения.
Слово дня – толковый словарь
Каждый день приложение будет показывать новые актуальные слова и термины русского языка, значение которых многие не знают. Команда филологов изучает их определения в толковых словарях Даля и Ожегова и других авторитетных источниках. А потом адаптирует эту информацию в краткие определения для простоты понимания.
Универсальные помощники
Фоксфорд Учебник
Это интерактивный справочник по школьной программе за 4–11 классы. В учебнике вы найдете теорию, отличные примеры и просто шпаргалки по разным предметам. Бонус — более 500 подробных видеоуроков с лучшими преподавателями страны.
Универсариум
Математика, химия, экономика, а, может быть, еще история искусства — изучайте столько предметов, сколько хотите и можете. Вы сами создаете свою программу. Основная часть обучения — это видеолекции. В конце каждого модуля следует проверочный тест.
Вы сами создаете свою программу. Основная часть обучения — это видеолекции. В конце каждого модуля следует проверочный тест.
Знания
Если не справляетесь с заданием, или нужна подсказка — задайте вопрос и в течение нескольких минут можете получить решение от пользователей.
Урок 21. решение уравнений — Математика — 4 класс
Математика, 4 класс
Урок 21. Решение уравнений
Перечень вопросов, рассматриваемых в теме:
- Что такое уравнение?
- Как решить уравнение, где в ответе не число, а числовое выражение.
- Что такое корень уравнения?
- Как найти неизвестное вычитаемое?
Глоссарий по теме:
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.
Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Обязательная и дополнительная литература по теме урока:
1. Моро М. И. Учебник для 4 класса четырехлетней начальной школы. М. «Просвещение» — 2017.С. 62,63
2. Волкова Е. В. математика Всероссийская проверочная работа за курс начальной школы. Издательство «Экзамен» 2018.С.27
3. Петерсон Л. Г. математика 3 класс. Часть 2. Ювента, 2015.-96с.: ил. С.77-78
Теоретический материал для самостоятельного изучения:
Рассмотрите записи:
376 + 282; (х — у) : 3
Являются ли эти записи уравнениями?
Это не уравнения, так как в уравнении должен быть знак «=». Это выражения.
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Рассмотрите другие записи:
24 + х = 49; 24 + х = 79 — 30
Это уравнения, так как это равенства, содержащие переменную.
Попробуем их решить.
Что значит решить уравнение?
Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.
Вспомните алгоритм решения уравнений.
Алгоритм:
- Вспомнить компоненты действия данного уравнения.
- Определить неизвестный компонент.
- Вспомнить правило нахождения неизвестного компонента.
- Применить правило и найти неизвестный компонент.
- Записать ответ.
- Сделать проверку
Используя алгоритм, решите первое уравнение
24 + х = 49
х = 49 — 24
х = 25
Значение неизвестного х = 25. Это корень уравнения.
Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении. В данном случае – это х.
Можно ли решить второе уравнение, используя этот же алгоритм?
Нет.
Такие уравнения не рассматривались. Какова же цель нашего урока?
Цель урока: научиться решать уравнения, в которых в ответе не число, а числовое выражение.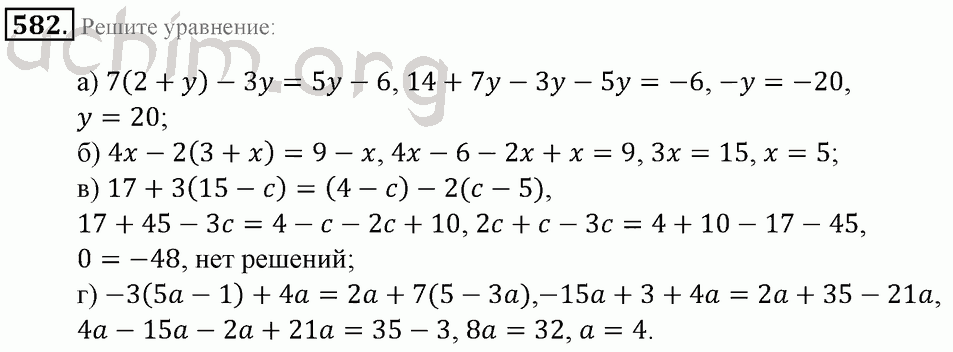
Такие уравнения мы будем называть составные. Поэтому тема урока: «Решение составных уравнений»
Чтобы решить это уравнение, нужно упростить правую часть.
24 + х = 79 — 30, после чего получаем уравнение известного вам вида
24 + х = 49
х = 49 — 24
х = 25
Проверка:
24 + 25 = 79 — 30
49 = 49
Ответ: корень уравнения 25
Составим алгоритм решения составных уравнений.
Алгоритм решения составных уравнений
1. Найти значение числового выражения.
2. Вспомнить компоненты действия данного уравнения.
3. Определить неизвестный компонент.
4. Вспомнить правило нахождения неизвестного компонента.
5. Применить правило и найти неизвестный компонент.
6. Записать ответ.
7. Сделать проверку.
Решим еще одно уравнение:
75 — х = 9 ∙ 7
Применяем алгоритм решения составных уравнений:
- Найти значение числового выражения: 75 — х = 9 ∙ 7
75 — х = 63
- Вспомнить компоненты действия данного уравнения: 75 — х = 63
3. Определить неизвестный компонент.
Определить неизвестный компонент.
Неизвестно – вычитаемое.
4. Вспомнить правило нахождения неизвестного компонента.
5. Применить правило и найти неизвестный компонент.
х = 75 — 63
6. Записать ответ.
х = 12
7. Сделать проверку.
75 — 12 = 9 ∙ 7
63 = 63
Ответ: корень уравнения 12
Вывод: чтобы решить составное уравнение, в которых в ответе не число, а числовое выражение, необходимо упростить правую часть ( т.е решить выражение), после чего получаем уравнение известного вам вида и решаем его, используя алгоритм решения уравнений.
Решим задачу, составив уравнение:
Сумма неизвестного числа и числа 390 равна произведению чисел 70 и 6. Найди это число.
1. Сумма неизвестного числа и числа 390 – обозначим неизвестное число переменной х, тогда получим х + 390
2. Произведение чисел 70 и 6: 70 ∙ 6
3. Получаем уравнение: х + 390 = 70 ∙ 6
Применяя алгоритм решения составных уравнений, решим его:
х + 390 = 70 ∙ 6
х + 390 = 420
х = 420 — 390
х = 30
Проверка:
30 + 390 = 70 ∙ 6
420 = 420
Ответ: неизвестное число — 30
| 3223 | а) Решите уравнение sin^2(x/4+pi/4)sin^2(x/4-pi/4). cos(x)-4=0 б) Укажите все корни уравнения, принадлежащие отрезку [2pi; 5pi]. cos(x)-4=0 б) Укажите все корни уравнения, принадлежащие отрезку [2pi; 5pi].Решение График |
а) Решите уравнение 16/9 cosx + 3 4/3 cosx — 4 = 0 ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 12 Задание 12 # Приведенорешениепрототипаcolor{blue} text{Приведено решение прототипа 2970} Аналог 2970 | |
|
|
|||
Упростите радикальное, рациональное выражение с помощью пошагового решения математических задач
В разделе 3 главы 1 есть несколько очень важных определений, которые мы использовали много раз. Поскольку эти определения приобретают новое значение в этой главе, мы повторим их.
Когда алгебраическое выражение составлено из частей, соединенных знаками + или -, эти части вместе со своими знаками называются членами выражения.
a + b имеет два термина.
2x + 5y — 3 имеет три члена.
| В a + b термины a и b. В 2x + 5y — 3 члены равны 2x, 5y и -3. |
Когда алгебраическое выражение состоит из частей, подлежащих умножению, эти части называются множителями выражения.
ab имеет множители a и b.
Очень важно уметь различать термины и факторы. Правила, применимые к терминам, в общем случае не будут применяться к факторам. При именовании терминов или факторов необходимо учитывать выражение целиком.
| С этого момента во всей алгебре вы будете использовать слова термин и фактор . Убедитесь, что вы понимаете определения. |
Показатель степени — это число, используемое для обозначения того, сколько раз коэффициент должен использоваться в продукте. Показатель степени обычно записывается в виде меньшего (по размеру) числа немного выше и правее множителя, на который влияет показатель степени.
| Показатель степени иногда называют степенью.» Например, 5 3 может называться «пять в третьей степени». |
Обратите внимание на разницу между 2x 3 и (2x) 3 . Из использования круглых скобок в качестве группирующих символов мы видим, что
2x 3 означает 2(x)(x)(x), тогда как (2x) 3 означает (2x)(2x)(2x) или 8x 3 .
| Если не используются круглые скобки, показатель степени влияет только на коэффициент, непосредственно предшествующий ему. |
В таком выражении, как 5x 4
5 , это коэффициент ,
x это основание ,
4 это показатель степени .
5x 4 означает 5(x)(x)(x)(x).
Обратите внимание, что показатель степени влияет только на основание.
| Многие ученики делают ошибку, умножая основание на показатель степени. Например, вместо правильного ответа они скажут 3 4 = 12, 3 4 = (3)(3)(3)( 3) = 81. |
Когда мы пишем буквальное число, такое как x, будет понятно, что коэффициент равен единице и показатель степени равен единице. Это может быть очень важно во многих операциях.
х означает 1 х 1 .
| Также понятно, что письменное числительное, такое как 3, имеет показатель степени 1. Мы просто не утруждаем себя записью показателя степени 1. |
ЗАКОН УМНОЖЕНИЯ ПОКАЗАТЕЛЕЙ
ЗАДАЧИ
После завершения этого раздела вы сможете правильно применять первый закон показателей.
Теперь, когда мы рассмотрели эти определения, мы хотим установить очень важные законы показателей. Эти законы выводятся непосредственно из определений.
Эти законы выводятся непосредственно из определений.
Первый закон экспонент Если a и b — положительные целые числа, а x — действительное число, то
| Чтобы умножить множители с одинаковым основанием, сложите показатели степени. |
Для любого правила, закона или формулы мы всегда должны быть очень осторожны, чтобы выполнить необходимые условия, прежде чем пытаться применить их. Обратите внимание, что в приведенном выше законе основание одинаково для обоих множителей.Этот закон применяется только при соблюдении этого условия.
| Эти факторы не имеют одинаковой базы. |
Показатель степени 1 обычно не пишется. Когда мы пишем x, предполагается показатель степени: x = x1. Этот факт необходим для применения законов экспонент.
Если выражение содержит произведение разных оснований, мы применяем закон к тем основаниям, которые подобны.
УМНОЖЕНИЕ МОНОМОВ
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Распознать моном.
- Найдите произведение нескольких одночленов.
Одночлен — это алгебраическое выражение, в котором буквенные числа связаны только операцией умножения.
| не является мономом, так как задействована операция сложения. |
| предполагает операцию деления. |
Чтобы найти произведение двух мономов , умножьте числовые коэффициенты и примените первый закон показателей к буквальным множителям.
| Вы помните первый закон показателей? |
Умножьте 5 на 3 и сложите показатели x. Помните, что если показатель степени не указан, то понимается показатель степени единицы. |
МОНОМЫ, УМНОЖЕННЫЕ НА ПОЛИНОМЫ
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Распознавание многочленов.
- Определите двучлены и трехчлены.
- Найдите произведение одночлена на двучлен.
Многочлен представляет собой сумму или разность одного или нескольких одночленов.
| Обычно, если имеется более одной переменной, многочлен записывается в алфавитном порядке. |
Для некоторых многочленов используются специальные имена. Если многочлен имеет два члена, он называется биномом .
Если многочлен состоит из трех членов, он называется трехчленом .
В процессе удаления круглых скобок мы уже заметили, что на все термины в круглых скобках влияет знак или число, предшествующее скобкам.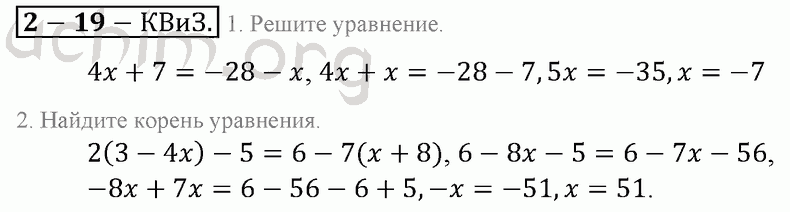 Теперь мы расширим эту идею, чтобы умножить одночлен на многочлен.
Теперь мы расширим эту идею, чтобы умножить одночлен на многочлен.
| Размещение 2x непосредственно перед скобками означает умножение выражения в круглых скобках на 2x. Обратите внимание, что каждый член умножается на 2x. |
| Снова каждое слагаемое в скобках умножается на 3y 2 |
| Снова каждое слагаемое в скобках умножается на 3y 2 . В каждом из этих примеров мы используем свойство распределения . |
ПРОИЗВЕДЕНИЕ ПОЛИНОМОВ
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Найдите произведение двух двучленов.
- Используйте свойство дистрибутивности для умножения любых двух многочленов.
В предыдущем разделе вы узнали, что произведение A(2x + y) расширяется до A(2x) + A(y).
Теперь рассмотрим произведение (3x + z)(2x + y).
Поскольку (3x + z) заключено в скобки, мы можем рассматривать его как один множитель и разложить (3x + z)(2x + y) так же, как A(2x + y). Это дает нам
Если мы теперь расширим каждое из этих условий, мы получим
Обратите внимание, что в окончательном ответе каждый член одной скобки умножается на каждый член других скобок.
| Обратите внимание, что это применение свойства распределения. |
| Обратите внимание, что это применение свойства распределения. |
Так как — 8x и 15x похожи, мы можем объединить их, чтобы получить 7x.
В этом примере мы смогли объединить два термина, чтобы упростить окончательный ответ.
Здесь мы снова объединили некоторые термины, чтобы упростить окончательный ответ. Обратите внимание, что порядок членов в окончательном ответе не влияет на правильность решения.
Обратите внимание, что порядок членов в окончательном ответе не влияет на правильность решения.
| Свойство коммутативности позволяет менять порядок. |
| Попробуйте установить систему умножения каждого члена одной скобки на каждый член другой скобки.В этих примерах мы взяли первый член в первом наборе скобок и умножили его на каждый член во втором наборе скобок. Затем мы взяли второй член первого набора и умножили его на каждый член второго набора, и так далее. |
СТЕПЕНИ СТЕПЕН И КВАДРАТНЫЕ КОРНИ
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Правильно применить второй закон показателей.
- Найдите квадратные корни и главные квадратные корни чисел, являющихся полными квадратами.
Теперь мы хотим установить второй закон показателей. Обратите внимание на следующие примеры, как этот закон выводится с использованием определения показателя степени и первого закона показателей степени.
по смыслу показателя степени 3.
Теперь по первому закону показателей у нас есть
В общем отметим, что
Это означает, что ответ будет
| Помните, чтобы умножить общие основания, добавьте показатели степени. |
Если мы суммируем член a b раз, мы получим произведение a и b. Отсюда мы видим, что
Второй закон экспонент Если a и b — положительные целые числа, а x — действительное число, то
.
Другими словами, «чтобы возвести степень основания x в степень, умножьте показатели».
.
| Обратите внимание, что каждый показатель должен быть умножен на 4. |
Обратите внимание, что когда факторы сгруппированы в скобках, каждый фактор зависит от показателя степени.
.
Опять же, каждый множитель нужно возвести в третью степень.
Используя определение степени, (5) 2 = 25. Мы говорим, что 25 есть квадрат 5. Теперь мы вводим новый термин в наш алгебраический язык. Если 25 — это квадрат 5, то говорят, что 5 — это квадратный корень из 25.
Если x 2 = y, то x является квадратным корнем из y.
| Обратите внимание, мы говорим, что 5 — это , квадратный корень из , а не — квадратный корень из .Вскоре вы увидите, почему. |
.
Из последних двух примеров вы заметите, что 49 имеет два квадратных корня, 7 и — 7. Действительно, каждое положительное число имеет два квадратных корня.
| На самом деле, один квадратный корень положительный, а другой отрицательный. |
.
| Сколько квадратных корней из 36? |
главный квадратный корень из положительного числа является положительным квадратным корнем.
Символ «» называется подкоренным знаком и указывает на главное
| указывает главный квадратный корень или положительный квадратный корень из 9. |
Обратите внимание на разницу в этих двух задачах.
а. Найдите квадратные корни из 25.
b. Находить .
| Очень важно понимать разницу между этими двумя утверждениями. |
Для а. ответ равен +5 и -5, так как (+ 5) 2 = 25 и (- 5) 2 = 25.
Для б. ответ равен +5, так как знак радикала представляет главный или положительный квадратный корень.
Целые числа, такие как 16, 25, 36 и т.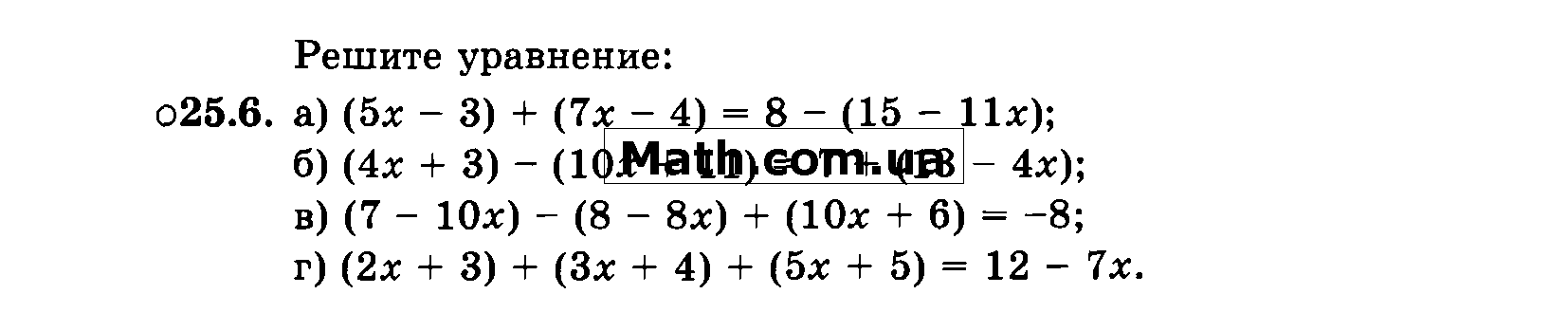 д., квадратные корни которых являются целыми числами, называются совершенными квадратными числами . В настоящее время нас интересуют только квадратные корни из совершенных квадратных чисел. В одной из последующих глав мы займемся оценкой и упрощением указанного квадратного корня из чисел, не являющихся совершенными квадратными числами.
д., квадратные корни которых являются целыми числами, называются совершенными квадратными числами . В настоящее время нас интересуют только квадратные корни из совершенных квадратных чисел. В одной из последующих глав мы займемся оценкой и упрощением указанного квадратного корня из чисел, не являющихся совершенными квадратными числами.
| Иногда вы можете увидеть символ +/- .Это означает, что требуются оба квадратных корня числа. Например,
+/- 5 — это сокращенный способ записи + 5 и -5. |
ЗАКОН ДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ
ЗАДАЧИ
После завершения этого раздела вы сможете правильно применять третий закон показателей.
Перед тем, как приступить к установлению третьего закона показателей, мы сначала рассмотрим некоторые факты об операции деления.
- Разделение двух чисел может быть обозначено знаком деления или записью одного числа над другим с чертой между ними.
 Шесть разделить на два записывается как
Шесть разделить на два записывается как - Деление связано с умножением по правилу, если тогда a = be. Это проверка на все проблемы деления. Например, мы знаем это, потому что 18 = (6)(3).
- Деление на ноль невозможно. Для оценки нам требуется найти число, которое при умножении на ноль даст 5. Такого числа не существует.
- Ненулевое число, разделенное само на себя, равно 1.
.
| . Умножьте обведенные количества, чтобы получить a. Это очень важно! Если a — любое ненулевое число, то оно не имеет смысла. |
Из (3) мы видим, что такое выражение, как не имеет смысла, если мы не знаем, что y ≠ 0. В этом и последующих разделах всякий раз, когда мы пишем дробь, предполагается, что знаменатель не равен нулю. Теперь, чтобы установить закон деления показателей, воспользуемся определением показателей.
| Важно! Прочтите этот абзац еще раз! |
Мы знаем, что = 1. Мы также предполагаем, что x представляет собой ненулевое число. Мы также предполагаем, что x представляет собой ненулевое число. |
В таком примере нам не нужно разделять количества, если мы помним, что количество, деленное само на себя, равно единице. В приведенном выше примере мы могли бы написать
| Три крестика в знаменателе делят три крестика в числителе. |
| Помните, что 1 нужно писать, если это единственный член в числителе. |
Из предыдущих примеров мы можем обобщить и прийти к следующему закону:
Третий закон показателей Если a и b — положительные целые числа, а x — ненулевое действительное число, то
| Если мы попытаемся использовать только ту часть закона, которая утверждает такое выражение, как мы получили бы На данный момент отрицательные показатели не определены.  Мы обсудим их позже. Мы обсудим их позже. |
ДЕЛЕНИЕ МОНОМА НА МОНОМ
ЗАДАЧИ
По завершении этого раздела вы сможете упростить выражение, сократив дробь с коэффициентами, а также используя третий закон показателей.
Мы должны помнить, что коэффициенты и показатели регулируются разными законами, потому что они имеют разные определения. При делении одночленов коэффициенты делятся, а показатели степени вычитаются по закону деления показателей.
Если деление невозможно или возможно только сокращение дроби с коэффициентами, это не влияет на использование закона показателей деления.
| Сократите этот тип дроби в два этапа: 1. Сократите коэффициенты. 2. Используйте третий закон показателей. |
ДЕЛЕНИЕ ПОЛИНОМА НА МОНОМ
ЗАДАЧИ
После завершения этого раздела вы должны уметь делить многочлен на одночлен.
Деление многочлена на одночлен связано с одним очень важным фактом в дополнение к тому, что мы уже использовали. Дело в том, что если в числителе дроби несколько членов, то каждое из них нужно разделить на знаменатель.
| Таким образом, мы фактически используем свойство распределения в этом процессе. |
ДЕЛЕНИЕ ПОЛИНОМА НА ДВУМОЯ
ЗАДАЧИ
По завершении этого раздела вы сможете правильно применять алгоритм деления в длину для деления многочлена на двучлен.
Процесс деления многочлена на другой многочлен будет полезен в следующих темах. Здесь мы разработаем методику и обсудим причины, по которым она будет работать в будущем.
Этот метод называется алгоритмом длинного деления . Алгоритм — это просто метод, которому нужно точно следовать. Поэтому представим его в пошаговом формате и на примере.
| Вспомните три выражения в делении:
Если бы нас попросили расположить выражение в убывающей степени, мы бы написали . |
Решение
Шаг 1: Расположите и делитель, и делимое в убывающей степени переменной (это означает, что первым будет самый высокий показатель, второй самый высокий и т. д.) и задайте нулевой коэффициент для всех отсутствующих членов. (В этом примере расположение не нужно менять, и отсутствуют пропущенные термины.) Затем расположите делитель и делимое следующим образом:
Шаг 2: Чтобы получить первый член частного, разделите первый член делимого на первый член делителя, в данном случае . Записываем это так:
Шаг 3: Умножьте весь делитель на член, полученный в шаге 2. Вычтите результат из делимого следующим образом:
Убедитесь, что вы пишете частное непосредственно над количеством, на которое вы делите. В этом случае х делится на х 2 х раз. В этом случае х делится на х 2 х раз. |
Шаг 4: Разделите первый член остатка на первый член делителя, чтобы получить следующий член частного. Затем умножьте весь делитель на полученный член и снова вычтите следующим образом:
| Первый член остатка (-2x — 14) равен -2x. Умножить (x + 7) на -2. |
Этот процесс повторяется до тех пор, пока либо остаток не станет равным нулю (как в этом примере), либо степень первого члена остатка не станет меньше степени первого члена делителя.
Как и в арифметике, деление проверяется умножением. Мы должны помнить, что (частное) X (делитель) + (остаток) = (делимое).
Чтобы проверить этот пример, мы умножаем (x + 7) и (x — 2), чтобы получить x 2 + 5x — 14.
Поскольку это делимое, ответ правильный.
| Снова (частное) X (делитель) + (остаток) = (делимое) |
Ответ х — 3.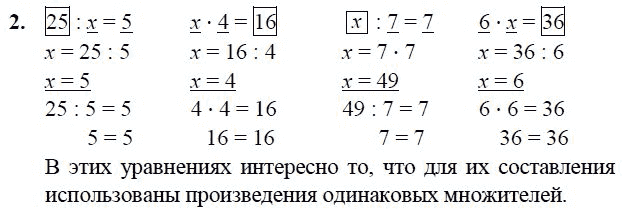 Проверяя, находим (х + 3)(х — 3)
Проверяя, находим (х + 3)(х — 3)
| Распространенная ошибка — забыть записать пропущенный член с нулевым коэффициентом. |
ОБЗОР
Ключевые слова
- Одночлен — это алгебраическое выражение, в котором буквенные числа связаны только операцией умножения.
- Многочлен представляет собой сумму или разность одного или нескольких одночленов.
- Бином — многочлен, имеющий два члена.
- Трехчлен — многочлен, состоящий из трех членов.
- Если x 2 = y, то x является квадратным корнем из y.
- главный квадратный корень из положительного числа является положительным квадратным корнем.
- Символ называется подкоренным знаком и указывает на главный квадратный корень числа.
- идеально квадратное число имеет целые числа в качестве квадратных корней.
Процедуры
- Первый закон показателей: x a x b = x a+b .
- Чтобы найти произведение двух одночленов, умножьте числовые коэффициенты и примените первый закон показателей к буквальным множителям.
- Чтобы умножить многочлен на другой многочлен, умножьте каждый член одного многочлена на каждый член другого и объедините одинаковые члены.
- Второй закон показателей равен (x a ) b = x ab .
- Третий закон показателей равен
- Чтобы разделить одночлен на одночлен, разделите числовые коэффициенты и используйте третий закон показателей для буквенных чисел.
- Чтобы разделить многочлен на одночлен, разделите каждый член многочлена на одночлен.
- Чтобы разделить многочлен на двучлен, используйте алгоритм длинного деления.
Решатель системы уравнений 3×3
О правиле Крамера
Этот калькулятор использует правило Крамера для решения систем из трех уравнений с тремя
неизвестные. Правило Крамера можно сформулировать следующим образом:
Правило Крамера можно сформулировать следующим образом:
Учитывая систему:
$$
\begin{выровнено}
а_1х+б_1у+с_1з=д_1\
а_2х+б_2у+с_2з=д_2\
a_3x + b_3y + c_3z = d_3
\end{выровнено}
$$
с
|
$$ D = \left|\begin{массив}{ccc} а_1 и б_1 и с_1 \\ а_2 и б_2 и с_2 \\ а_3 и б_3 и с_3 \\ \конец{массив}\право| \ne 0 $$ |
$$ D_x = \left|\begin{массив}{ccc} д_1 и б_1 и с_1 \\ д_2 и б_2 и с_2 \\ д_3 & б_3 & с_3 \\ \конец{массив}\право| $$ |
$$ D_y = \left|\begin{массив}{ccc} а_1 и д_1 и с_1 \\ а_2 и д_2 и с_2 \\ а_3&d_3&c_3\\ \конец{массив}\право| $$ |
$$ D_z = \left|\begin{массив}{ccc} а_1 и б_1 и д_1 \\ а_2&б_2&д_2\\ а_3&б_3&д_3\\ \конец{массив}\право| $$ |
, то решение этой системы:
|
$$ х = \ гидроразрыва {D_x} {D} $$ |
$$ у = \ гидроразрыва {D_y} {D} $$ |
$$ г = \ гидроразрыва {D_z} {D} $$ |
Пример: Решить систему уравнений с помощью правила Крамера
$$
\begin{выровнено}
4х+5у-2з=&-14\
7x — ~y +2z= & 42 \\
3x + ~y + 4z= & 28 \\
\end{выровнено}
$$
Решение: Сначала мы вычисляем $D,~D_x,~D_y$ и $D_z$.
$$
\begin{выровнено}
& D~~ = \left|\begin{массив}{ccc}
{\ цвет {синий} {4}} & {\ цвет {красный} {~ 5}} & {\ цвет {зеленый} {-2}} \\
{\ цвет {синий} {7}} & {\ цвет {красный} {-1}} & {\ цвет {зеленый} {~ 2}} \\
{\цвет{синий}{3}} и {\цвет{красный}{~1}} и {\цвет{зеленый}{~4}}
\конец{массив}\право| = -16 + 30 — 14 — 6 — 8 — 140 = -154\\
& D_x = \left|\begin{массив}{ccc}
-14 & {\ color {красный} {~ 5}} & {\ color {зеленый} {-2}} \\
~ 42 & {\ color {красный} {-1}} & {\ color {зеленый} {~ 2}} \\
~ 28 и {\ color {красный} {1}} & {\ color {зеленый} {~ 4}}
\конец{массив}\право| = 56 + 280 — 84 — 56 + 28 — 840 = -616\\
& D_y = \left|\begin{массив}{ccc}
{\ color {синий} {4}} & -14 & {\ color {зеленый} {- 2}} \\
{\ color {синий} {7}} & ~ 42 & {\ color {зеленый} {~ 2}} \\
{\color{синий}{3}} & ~28 & {\color{зеленый}{~4}}
\конец{массив}\право| = 672 — 84 — 392 + 252 — 224 + 392 = 616\\
& D_Z = \left|\begin{массив}{ccc}
{\ цвет {синий} {4}} & {\ цвет {красный} {~ 5}} & -14 \\
{\color{синий}{7}} & {\color{красный}{-1}} & ~42 \\
{\цвет{синий}{3}} и {\цвет{красный}{~1}} и ~28
\конец{массив}\право| = -112 + 630 — 98 — 42 — 168 — 980 = -770\\
\end{выровнено}
$$
Следовательно,
$$
\begin{выровнено}
& x = \frac{D_x}{D} = \frac{-616}{-154} = 4 \\
& y = \frac{D_y}{D} = \frac{616}{-154} = -4 \\
& z = \frac{D_z}{D} = \frac{-770}{-154} = 5
\end{выровнено}
$$
Примечание: Вы можете проверить решение, используя приведенный выше калькулятор
Решатель уравнений и систем — решение MATLAB
Если решить, не может найти решение и
ReturnConditions is false ,
решить функция внутренне вызывает числовой решатель
vpasolve , который пытается найти численное решение. Для полинома
Для полинома
уравнения и системы без символьных параметров, числовой решатель возвращает все
решения. Для неполиномиальных уравнений и систем без символьных параметров
числовой решатель возвращает только одно решение (если решение существует).
Если решить не может найти решение и
ReturnConditions равно true ,
решить возвращает пустое решение с предупреждением. Если нет решений
существует, решить возвращает пустое решение без предупреждения.
Если решение содержит параметры и ReturnConditions равно true , решить возвращает
параметры раствора и условия, при которых
решения верны. Если ReturnConditions равно false ,
функция решает либо выбирает значения
параметры и возвращает соответствующие результаты или возвращает параметризованные
решения без выбора конкретных значений.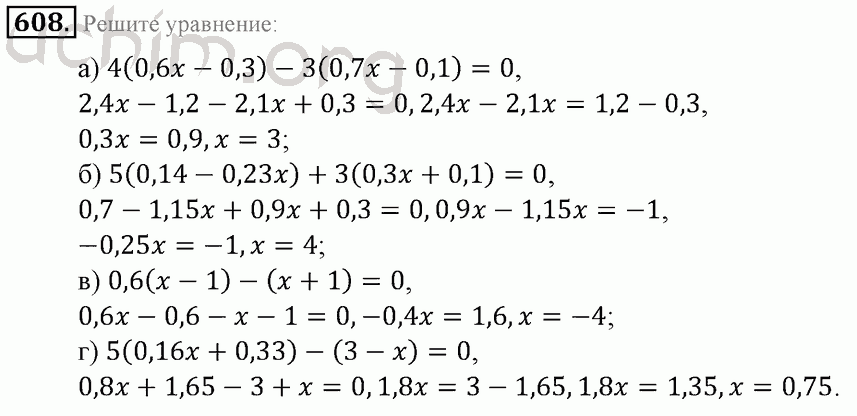 В последнем случае
В последнем случае также решают .
выдает предупреждение, указывающее значения параметров в возвращаемом
решения.
Если параметр не отображается ни в каком состоянии, он
означает, что параметр может принимать любое комплексное значение.
Результат решения может содержать
параметры из входных уравнений в дополнение к введенным параметрам
на решить .
Параметры введены решить сделать
не отображаются в рабочей области MATLAB. Доступ к ним должен осуществляться с помощью
выходной аргумент, который их содержит. В качестве альтернативы, чтобы использовать
параметры в рабочей области MATLAB используют syms для
инициализировать параметр.Например, если параметр равен k ,
используйте syms k .
Имена переменных параметры и условия
не допускается, поскольку входные данные для решают .
Для решения дифференциальных уравнений используйте функцию dsolve .
При решении системы уравнений всегда присваивайте
результат для выходных аргументов. Выходные аргументы позволяют вам получить доступ к
значения решений системы.
MaxDegree принимает только положительные
целые числа меньше 5, потому что, как правило, нет явных
выражения для корней многочленов степеней выше 4.
Выходные переменные y1,...,yN не указывают переменные для
которые решают решают уравнения или системы. Если
y1,...,yN — это переменные, которые появляются в
eqns , то нет гарантии, что
solve(eqns) назначит решения
у1,...,yN в правильном порядке. Таким образом, когда вы запускаете
[b,a] = решить(уравнения) , вы можете получить решения для
a присваивается b и наоборот.
Чтобы обеспечить порядок возвращаемых решений, укажите переменные
вар . Например, вызов [b,a] = присваивает решения для
solve(eqns,b,a) a
a и решения для b до
б .
Решение линейного уравнения с одним неизвестным
Быстрый! Мне нужна помощь с:
Выберите элемент математической справки … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Нахождение всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги, График hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLines Theotation, The Equation from slopeLines Theotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансов, Математика, Практика многочленов, Математика, Практика основ Квадратные многочлены, Деление многочленов, Факторизация разности квадратов Многочлены, Факторизация триномов Полиномы, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение , Правые треугольники, Ветер, Рисунок
Решение одновременного набора двух линейных уравнений
Быстрый! Мне нужна помощь с:
Выберите элемент справки по математике . ..Исчисление, Вычисление производных, Вычисление интеграции, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Расчет с комплексными числами, Умножение комплексных чисел, Полномочия комплексных чисел, Вычитание, преобразование площади, преобразование длины, преобразование массы, преобразование мощности, преобразование скорости, преобразование температуры, анализ объемных данных, поиск Анализ средних данных, Нахождение стандартного отклонения Анализ данных, ГистограммыДесятичные числа, Преобразование в дробьЭлектричество, Стоимость факторинга, Целочисленные коэффициенты, Наибольшие общие коэффициенты, Наименьшие общие дроби, Сложение дробей, Сравнение дробей, Преобразование дробей, Преобразование в десятичные дроби, Деление дробей, Умножение дробей, Сокращение дробей, Вычитание дробей, Что такое геометрия , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Any functionGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x,y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Уравнение из точки и наклонных линий, Уравнение из наклона и y-intLines, Уравнение из двух точек.
..Исчисление, Вычисление производных, Вычисление интеграции, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Расчет с комплексными числами, Умножение комплексных чисел, Полномочия комплексных чисел, Вычитание, преобразование площади, преобразование длины, преобразование массы, преобразование мощности, преобразование скорости, преобразование температуры, анализ объемных данных, поиск Анализ средних данных, Нахождение стандартного отклонения Анализ данных, ГистограммыДесятичные числа, Преобразование в дробьЭлектричество, Стоимость факторинга, Целочисленные коэффициенты, Наибольшие общие коэффициенты, Наименьшие общие дроби, Сложение дробей, Сравнение дробей, Преобразование дробей, Преобразование в десятичные дроби, Деление дробей, Умножение дробей, Сокращение дробей, Вычитание дробей, Что такое геометрия , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Any functionGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x,y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Уравнение из точки и наклонных линий, Уравнение из наклона и y-intLines, Уравнение из двух точек. Практика полиномовМатематика, Практика основ Метрическая система, Преобразование чисел, Добавление чисел, Вычисление с числами, Вычисление с переменными числами, Разделение чисел, Умножение чисел, Сравнение чисел в ряду, Числовые числа в ряду, Размещение значений чисел, Произношение чисел, Округление чисел, Вычитание парабол, Графический полином, Сложение/вычитание многочленов. , Разложение на множители Разность квадратовПолиномы, Разложение на множители трехчленовПолиномы, Разложение на множители с GCFПолиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Что это такоеКвадратные уравнения, Квадратная формулаКвадратное уравнение ns, Решить с помощью факторингаРадикалы, Другие корниРадикалы, Соотношения квадратных корней, Что они представляют собойВыход на пенсию, Сбережение для продажной цены, Расчет научной записи, Преобразование научной записи, Разделение научной записи, Умножение фигур, Прямоугольники, Упрощение, Все, что угодно, Упрощение экспоненты, Как термины, Упрощение, Продукты, Время, Размышление о совете, Вычисление тригонометрии, Выражения Прямоугольные треугольникиWindchill, фигура
Практика полиномовМатематика, Практика основ Метрическая система, Преобразование чисел, Добавление чисел, Вычисление с числами, Вычисление с переменными числами, Разделение чисел, Умножение чисел, Сравнение чисел в ряду, Числовые числа в ряду, Размещение значений чисел, Произношение чисел, Округление чисел, Вычитание парабол, Графический полином, Сложение/вычитание многочленов. , Разложение на множители Разность квадратовПолиномы, Разложение на множители трехчленовПолиномы, Разложение на множители с GCFПолиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Что это такоеКвадратные уравнения, Квадратная формулаКвадратное уравнение ns, Решить с помощью факторингаРадикалы, Другие корниРадикалы, Соотношения квадратных корней, Что они представляют собойВыход на пенсию, Сбережение для продажной цены, Расчет научной записи, Преобразование научной записи, Разделение научной записи, Умножение фигур, Прямоугольники, Упрощение, Все, что угодно, Упрощение экспоненты, Как термины, Упрощение, Продукты, Время, Размышление о совете, Вычисление тригонометрии, Выражения Прямоугольные треугольникиWindchill, фигура
Лучшие приложения для решения математических уравнений для Linux
В этой статье перечислены некоторые полезные приложения для Linux, которые можно использовать для выполнения математических расчетов и решения уравнений. Эти приложения либо полностью решат математические уравнения, либо помогут вам в их решении. Обратите внимание, что эти приложения отличаются от других математических инструментов, обычно используемых для ввода математических и научных символов при подготовке документов и журналов. Эти приложения будут выполнять вычисления и возвращать результат в соответствии с пользовательским вводом.
Эти приложения либо полностью решат математические уравнения, либо помогут вам в их решении. Обратите внимание, что эти приложения отличаются от других математических инструментов, обычно используемых для ввода математических и научных символов при подготовке документов и журналов. Эти приложения будут выполнять вычисления и возвращать результат в соответствии с пользовательским вводом.
GeoGebra Classic
GeoGebra Classic — это бесплатное математическое программное обеспечение с открытым исходным кодом, которое может выполнять различные вычисления и решать уравнения.Вы можете использовать его для рисования векторов, ввода формул, расчета вывода алгебраических уравнений, создания функций, построения квадрантов, создания конических сегментов, ввода координат, выполнения тригонометрических вычислений, выполнения геометрических вычислений и создания для них визуализаций, выполнения математических вычислений, динамического обновления уравнения и формулы, создавать трехмерные диаграммы и графики, использовать встроенный режим экзамена и так далее.
Вы можете установить GeoGebra Classic в Ubuntu с помощью указанной ниже команды:
$ sudo apt установить геогебру
Вы можете установить Geogebra Classic в других дистрибутивах Linux из диспетчера пакетов.Дополнительные инструкции по установке и портативные пакеты доступны здесь. Сборка flatpak доступна здесь. Вы также можете использовать классическую версию GeoGebra непосредственно в веб-браузере отсюда. Подробная документация доступна здесь. Исходный код доступен на GitHub.
Вычислить
Qalculate — это бесплатный калькулятор с открытым исходным кодом, способный решать уравнения и выполнять сложные вычисления. Он имеет минималистичный пользовательский интерфейс без особого беспорядка и ориентирован на простоту использования. Вы можете использовать его в качестве базового калькулятора, вводить свои собственные пользовательские функции, конвертировать валюту и единицы измерения, решать интегралы и другие уравнения, создавать графики, создавать выражения с пользовательскими векторами и переменными, сравнивать неравенства, определять константы, экспортировать вычисления и результаты в несколько файлов. форматы, создавать предположения, изменять систему счисления, выполнять логарифмические вычисления и т. д.
форматы, создавать предположения, изменять систему счисления, выполнять логарифмические вычисления и т. д.
Вы можете установить Qalculate в Ubuntu с помощью команды, указанной ниже:
$ sudo apt установить qalculate-gtk
Qalculate можно установить в других дистрибутивах Linux из диспетчера пакетов. Исходный код, пакеты для других дистрибутивов, а также пакеты flatpak и snap можно загрузить отсюда.
Октава GNU
GNU Octave — это бесплатный язык программирования с открытым исходным кодом и интегрированная среда разработки, специально разработанная для решения математических уравнений и задач.Приложение с графическим интерфейсом имеет встроенную консоль интерпретатора команд, которую можно использовать для решения уравнений. Вы также можете использовать встроенный редактор кода для написания полнофункциональных программ или сценариев для решения определенных математических задач. Другие основные функции GNU octave включают инструменты для создания 2D- и 3D-визуализации и графиков, возможность запуска кода Matlab, интерфейс командной строки для выполнения вычислений в терминале, поддержку линейных и нелинейных уравнений, поддержку пользовательских функций, возможность запуска расчетных выражений. , и так далее.
, и так далее.
Вы можете установить GNU Octave в Ubuntu с помощью команды, указанной ниже:
$ sudo apt установить октаву
GNU Octave можно установить в других дистрибутивах Linux из диспетчера пакетов. Исходный код доступен здесь. Пакеты для других дистрибутивов, а также пакеты flatpak и snap доступны здесь.
Scilab
Scilab — еще одна бесплатная программа с открытым исходным кодом, работающая аналогично GNU Octave. Это графическое приложение, которое поставляется с собственным языком программирования, специально разработанным для выполнения математических вычислений.Вы можете использовать его для создания графических визуализаций и графиков, моделирования математических моделей, выполнения статистического анализа данных, разработки собственных алгоритмов, создания научных приложений, обработки сигналов, анализа систем управления, решения нелинейных уравнений, выполнения расчетов с использованием интерфейса командной строки и т. д. на.
на.
Вы можете установить Scilab в Ubuntu с помощью команды, указанной ниже:
$ sudo apt установить scilab
Scilab можно установить в других дистрибутивах Linux из диспетчера пакетов.Другие пакеты для конкретного дистрибутива доступны здесь. Пакет flatpak также доступен здесь.
Гений
Genius — бесплатная программа-калькулятор с открытым исходным кодом, которая может выполнять сложные математические вычисления и решать уравнения. Его язык выражений почти идентичен реальным математическим уравнениям и выражениям, что упрощает быстрое выполнение вычислений. Основные функции Genius включают возможность экспорта выражений и результатов в несколько форматов файлов, возможность выполнения тригонометрических вычислений, поддержку создания 2D и 3D графиков, включает систему расширений с собственным языком программирования, возможность выполнять математические выражения и так далее.
Вы можете установить Genius в Ubuntu с помощью команды, указанной ниже:
$ sudo apt установить gnome-genius
Genius можно установить в других дистрибутивах Linux из диспетчера пакетов. Другие пакеты для конкретного дистрибутива доступны здесь.
Другие пакеты для конкретного дистрибутива доступны здесь.
Калькулятор GNOME
GNOME Calculator — это бесплатное приложение-калькулятор с открытым исходным кодом, которое поставляется с большинством дистрибутивов Linux на основе GNOME. Он имеет множество режимов расчета, и вы можете использовать его «расширенный» и «программный» режим для выполнения различных математических расчетов и решения уравнений.Вы можете использовать его для выполнения логарифмических вычислений, решения математических задач, ввода тригонометрических функций, преобразования единиц, расчета процентов и выполнения других подобных финансовых расчетов и так далее. Обратите внимание, что он может быть не в состоянии решать сложные выражения и уравнения. Этого достаточно для простых уравнений и математических выражений, но если вам нужна дополнительная функциональность, попробуйте другие приложения, перечисленные в этой статье.
Вы можете установить калькулятор GNOME в Ubuntu с помощью команды, указанной ниже:
$ sudo apt установить гном-калькулятор
Калькулятор GNOME можно установить в других дистрибутивах Linux из диспетчера пакетов. Сборка flatpak также доступна здесь.
Сборка flatpak также доступна здесь.
Заключение
Это одни из лучших графических приложений для решения математических уравнений. Некоторые из этих приложений также поставляются с консолями интерпретатора и интерфейсами командной строки, чтобы помочь вам выполнять быстрые вычисления из терминала. Некоторые приложения также позволяют экспортировать входные уравнения и результаты расчетов во многие форматы файлов и делиться ими с другими.
Математический алгебраический решатель в App Store
Приложение
Algebra Math Solver — ваш лучший помощник в решении математических задач и уравнений.Algebra Math Solver предоставляет вам точные решения, которым вы можете доверять, от более простой алгебры до самых сложных уравнений исчисления функций. Вы даже можете сфотографировать свои сложные математические уравнения и задачи, и приложение решит их за вас! Как только мы решим задачу, приложение научит вас, как она была решена, чтобы вы могли понять уравнение, чтобы вы могли повторить математические шаги самостоятельно для будущих математических решений. Выполняйте идеальные домашние задания по математике и получайте более высокие оценки за тесты и тесты по математике.
Выполняйте идеальные домашние задания по математике и получайте более высокие оценки за тесты и тесты по математике.
Математика важна в повседневной жизни и используется повсеместно, и теперь процесс стал проще, чем когда-либо:
— Сфотографируйте свою рукописную математическую задачу или введите ее вручную с помощью нашей математической клавиатуры. Мгновенно математический движок решит задачу за вас.
— Посмотреть результаты и математические шаги для решения проблемы. Для лучшего понимания мы также предоставляем визуальные представления для некоторых математических задач, таких как уравнения и вычисления.
— Вы даже можете сохранить свои результаты для дальнейшего использования и просмотра!
Математика может быть интересной, и мы делаем ее проще для вас! Получите приложение Algebra Math Solver прямо сейчас!
———————————————————
Приложение Алгебра Math Solver Премиум-подписка
———————————————————
Присоединиться » Algebra Math Solver App Premium Features Club», чтобы получить:
— Неограниченное количество математических решений и пошаговые инструкции по математическим упражнениям, уравнениям и задачам
— Без рекламы
Приложение Algebra Math Solver имеет различные планы подписки.
Подписка продлевается автоматически, если автоматическое продление не будет отключено по крайней мере за 24 часа до окончания текущего периода подписки или пробного периода. Подписки, начинающиеся с пробного периода и автоматически продлеваемые по указанной цене после окончания пробного периода. Любая неиспользованная часть бесплатного пробного периода, если она предлагается, будет аннулирована при покупке премиум-подписки в течение пробного периода.
Вы можете управлять подписками, а автоматическое продление можно отключить, перейдя в настройки своей учетной записи после покупки («Настройки» -> «iTunes & App Store» -> «Apple ID» и выберите «Подписки»)
* Ссылка на условия использования: http://алгебраматрешатель.com/pp.html#terms-of-service
* Ссылка на Политику конфиденциальности: http://alphamathsolver.com/pp.html#privacy-policy
.
 Нулевой коэффициент дает 0x 3 = 0. По этой причине член x 3 отсутствовал или не был записан в исходном выражении.
Нулевой коэффициент дает 0x 3 = 0. По этой причине член x 3 отсутствовал или не был записан в исходном выражении.