ГДЗ по математике 2 класс учебник Моро, Волкова 1 часть
№1.
1) 20, 18, 16, 15, 11, 10, 8, 5, 0.
2) 19, 9.
№2.
8 + 2 = 10 10 — 4 = 6
7 + 3 = 10 14 — 4 = 10
6 + 4 = 10 8 — 4 = 4
9 + 1 = 10 9 — 4 = 5
5 + 5 = 10 4 — 4 = 0
№3.
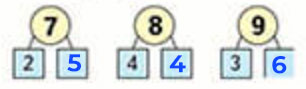

№4.
4 6 4 6
№5.
9 + 6 = 15 17 — 7 = 10 14 — 4 = 10
9 + 7 = 16 18 — 7 = 11 14 — 8 = 6
8 + 4 = 12 16 — 6 = 10
8 + 5 = 13 16 — 8 = 12
№6.


№7.
1 ряд – 8 м
2 ряд — ? на 2 м больше.
1) 8 + 2 = 10 (м) – во втором ряду.
2) 8 + 10 = 18 (м) – в двух рядах.
Ответ: 18 мест.
№8.
1 дм = 10 (см) – длина первого звена.
1) 10 — 3 = 7 (см) – длина второго звена.
2) 10 + 7 = 17 (см) – длина всей ломаной.
Картинка
№9.
Фигуры под №2 и 5 – четырехугольники.
Другие четырехугольники составлены из:
1 и 2;
3 и 4;
4 и 5;
3, 4, 5;
1, 2, 3, 4, 5.
№10.
6 — 4 = 2
Даша старше Оли на 2 года.
Задание внизу страницы
8 + 6 = 14
7 + 4 = 11
12 — 5 = 7
13 — 9 = 4
Учебник Моро 2 класс. 2 часть. Страница 10
Страница 10
1. На поле 6 игроков команды “Луна” и столько же игроков команды “Марс”. Ждут своей очереди ещё 16 игроков. Сколько всего человек в обеих командах?

2. В руках у игроков команды “Марс” 14 клюшек, а запасных клюшек на 6 меньше. Сколько всего клюшек у команды “Марс”?

3. Игра закончилась со счётом 10 : 12. Сколько раз шайба была в воротах? С какой разницей в счёте закончилась игра?

4. 1) Начерти четырёхугольник, в котором 2 угла прямые. Есть ли в нём тупой угол? острый угол? 2) Начерти треугольник с прямым углом.

№ 5
8 + 17 = 25
6 + 28 = 34
4 + 39 = 43
63 – 8 = 55
30 – (6 + 6) = 30 – 12= 18
40 – (7 + 7) = 40 – 14 = 26
50 – (8 + 8) = 50 – 16 = 34
60 – (9 + 9) = 60 – 18 = 42
62 + 30 – 2 = 92 – 2 = 90
20 + 75 + 5 = 95 + 5 = 100
83 – 60 + 7 = 23 + 7 = 30
72 – 40 + 8 = 32 + 8 = 40
6. Вычисли, записывая решение столбиком, и сделай проверку.

7. Из 9 палочек сложили такую фигуру. Переложи 2 палочки так, чтобы получилось 3 треугольника.


9 + 9 = 18
18 – 10 = 8
8 + 6 = 14
14 – 14 = 0
0 + 20 = 20
[block_reclama1]
Учебник Моро 2 класс. 2 часть. Страница 33
Страница 33
1. Объясни, как узнать длину каждой из четырёх сторон прямоугольника, если известно, что длина одной стороны 4 см, а другой — 5 см.
Ответ: противоположные стороны прямоугольника равны. Значит, две другие стороны 4 см и 5 см.
2. Длина комнаты 6 м, а её ширина 3 м. По верхнему краю обоев решили наклеить красивую бумажную полоску с узором. Узнай, какой длины должна быть эта полоска.
6 + 6 + 3 + 3 = 18 (метров)
Ответ: длина полоски для оклейки верхнего края обоев – 18 м.
3. Составь задачу по краткой записи и реши её.

Для пошива костюмов купили ткань. Когда от неё отрезали 6 м, осталось ещё 4 м ткани. Сколько метров ткани купили?
6 + 4 = 10 (м) – купили
Ответ: купили 10 м ткани.

Купили 12 кг картофеля. После того как часть картофеля израсходовали, осталось 6 кг. Сколько картофеля израсходовали?
12 – 6 = 6 (кг) картофеля израсходовали
Ответ: 6 кг.
4. Выполни вычисления удобным способом.
36 + 18 + 2 + 4 = (36 + 4) + (18 + 2) = 60
27 + 6 + 14 + 3 = (27+ 3) + (14 + 6) = 50
17 + 20 + 40 + 3 = (17 + 3) + (20 + 40) = 80
29 + 50 + 1 + 20 = (29 + 1) + (50 + 20)= 100
5. Вычисли сумму одинаковых слагаемых.

2 + 2 + 2 + 2 = 8
4 + 4 + 4 = 12
6. Замени суммой одинаковых слагаемых числа:
4 = 2 + 2
8 = 4 + 4
8 = 2 + 2 + 2 + 2
10 = 5 + 5
10 = 2 + 2 + 2 + 2 + 2
14 = 7 + 7
14 = 2 + 2 + 2 + 2 + 2 + 2 + 2
18 = 9 + 9
18 = 6 + 6 + 6
18 = 3+ 3 + 3 + 3 + 3 + 3
18 = 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2
7. Вычисли и проверь правильность вычислений.

8. 1) Четырёхугольник 1 дополни до прямоугольника. Начерти фигуры 2 и 3. Дополни каждую из них до прямоугольника.

2) Скажи, не вычисляя, периметр какого прямоугольника самый большой. Почему?
Самый большой периметр имеет прямоугольник № 1. Потому, что ширина всех полученных прямоугольников одинаковая, а высота больше всего у первого (зеленого) прямоугольника.
Начерти в тетради прямоугольник, длины сторон которого 2 см и 5 см, и найди его периметр.

[block_reclama1]
Учебник Моро 2 класс. 2 часть. Страница 52
Страница 52
1. Измерь стороны прямоугольника и объясни, как по-разному можно вычислить его периметр:

1) 2 + 5 + 2 + 5 = 14 (см)
Ответ: 14 см.
2) (2 • 2) + (5 • 2) = 14 (см)
Ответ: 14 см.
3) (2 + 5) • 2 = 14 (см)
Ответ: 14 см.
2. Начерти прямоугольник со сторонами 3 см и 4 см и вычисли его периметр.

3. У хозяина было 12 кроликов: 8 черных, а остальные белые. Сколько было белых кроликов? Составь и реши задачи, обратные данной.

4. Маме 32 года, дедушка старше мамы на 30 лет, а бабушка на 3 года моложе дедушки. Сколько лет бабушке?

5. Составь задачу по краткой записи и реши её.

1) На приготовление варенья до обеда использовали 5 кг сахара, а после обеда 6 кг сахара. Сколько всего было сахара, если его осталось 30 кг?
1) 5 + 6 = 11 (кг) − сахара использовали всего;
2) 30 + 11 = 41 (кг) − сахара было всего.
Ответ: было сахара 41 кг

2) В магазине было 12 кг черешни. Когда завезли ещё несколько килограммов черешни, стало – 50 кг. Сколько черешни завезли?
50 − 12 = 38 (кг) − черешни завезли.
Ответ: завезли 38 кг черешни.
6. Найди значения выражений k − 8 и k + 8 при k = 14, k = 36, k = 58, k = 90.

7. Вычисли с проверкой.

№ 7
70 − (12 − 6) = 70 – 6 = 64
13 − 9 + 7 = 4 + 7 = 11
56 − (40 − 34) = 56 – 6 = 50
9. Начерти такие фигуры и проведи в каждой 2 отрезка так, чтобы, разрезав по ним фигуры, можно было получить в каждом случае 1 прямоугольник и 2 треугольника.

80 − (14 − 8) = 80 – 6 = 74
12 − 7 + 9 = 5 + 9 = 14
93 − (50 − 47) = 93 – 3 = 90
[block_reclama1]
Учебник Моро 2 класс. 2 часть. Страница 55
Страница 55
№ 1

2. В каждом столбике найди значение второго выражения, используя значение первого.
9 • 2 = 18
9 • 3 = 18 + 9 = 27
2 • 6 = 12
2 • 7 = 12 + 2 = 14
7 • 4 = 28
7 • 5 = 28 + 7 = 35
3. Составь задачу по её решению.
В одной банке 3 литра молока. Сколько литров молока в 5 таких банках?
3 • 5 = 15 (л.)
Ответ : 15 литров молока в 5 банках.
4. Объясни, как узнавали разными способами, на сколько клеток разбит прямоугольник. Вычисли результаты. Расскажи, чем похожи и чем различаются полученные произведения.

1 способ:
В прямоугольнике 4 ряда по 6 клеток в каждом:
1) 6 + 6 + 6 + 6 = 24 (к.)
2) 6 • 4 = 24 (к.)
Ответ: 24 клетки.
2 способ:
В прямоугольнике 6 столбцов по 4 клетки в каждом:
1) 4 + 4 + 4 + 4 + 4 + 4 = 24 (к.)
2) 4 • 6 = 24 (к.)
Ответ: 24 клетки.
Результаты одинаковые. Различается порядок множителей.
5. Начерти ломанную, у которой длина первого звена равна 20 мм, второго – 40 мм, а длина третьего равна сумме длин первого и второго звеньев.

6. Вычисли с проверкой.

№ 7

8. Переложи 3 палочки так, чтобы домик повернулся в другую сторону.

[block_reclama1]
ГДЗ по математике 2 класс учебник Моро, Волкова 2 часть
№1.
2 : 2 = 1 8 : 2 = 4 14 : 2 = 7
4 : 2 = 2 10 : 2 = 5 16 : 2 = 8
6 : 2 = 3 12 : 2 = 6 18 : 2 = 9
№2.


1) 15 : 3 = 5 (л.) — в одном классе
Ответ: 5 ламп.


2) 16 : 2 = 8 (п.) — заняты
Ответ: 8 парт.
№3.
12 + 16 — длина зала в шагах Ани
12 + (12 + 16) — длина коридора в шагах Ани
№4.
75 — 16 57
75 + 16 > 75 61 — 28 = 33
№5.
1 р. = 100 к.
1) 25 + 32 = 57 (к.) — стоимость покупки
2) 100 — 57 = 43 (к.) — сдачи получит мальчик
Ответ: 43 копейки.
№6.
8 * 3 — 10 = 14 47 + 14 +3 = 64 48 + 9 = 57
5 * 2 + 18 = 28 59 + 12 + 8 = 79 48 + 39 = 87
9 * 3 + 14 = 41 66 + 15 + 4 = 85 48 + 52 = 100
№7.
Получаем два квадрата на каждом рисунке.
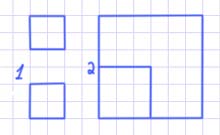

Задание внизу страницы
7 * 21 (л) — воды израсходовали
Ответ: 21 л.
Учебник Моро 2 класс. 2 часть. Страница 9
Страница 9
№ 1

1. 1) Сколько углов в каждом многоугольнике?
розовая фигура — 3 угла
зелёная фигура — 4 угла
голубая фигура — 5 углов
2) Запиши номера углов: прямых, острых, тупых.
Прямые углы: 2, 4, 7, 8, 10, 12.
Острые углы: 1, 3, 5.
Тупые углы: 6, 9, 11.
2. Вычисли и выполни проверку.

№ 3
30+ (24 – 8) = 30 + 16 = 46
40 – (30 – 6) = 40 – 24= 16
60 + (42 – 7) = 60 + 35 = 95
35 – 3 + 8 = 32 + 8 = 40
6 + 24 – 7 = 30 – 7 = 23
2 + 86 – 8 = 88 – 8 = 80
80 – 1 = 79
90 – 61 = 29
70 – 61 = 9
4. Составь задачу по выражению: (12 + 7) – 3.
Коля нашел 12 грибов, а Миша 7 грибов. 3 гриба пришлось выбросить, потому что они были несъедобными. Сколько грибов принесли ребята домой.
(12 + 7) – 3 = 16 (г.)
Ответ: 16 грибов.
5. Дети сделали 10 фонариков и 6 хлопушек. Сколько всего ёлочных игрушек они сделали?

6. В цирковом представлении выступили 9 собачек и 5 медвежат. На сколько больше собачек, чем медвежат, выступали в этом цирковом представлении?

№ 7

Сколько острых углов на чертеже?
Сколько прямых углов? тупых углов?

Ответ: 5 прямых углов, 2 острых угла, 1 тупой угол.

Ответ: Не хватает жёлтого треугольника, зеленого треугольника, фиолетового круга.
[block_reclama1]
Введение в математику 2 — Математика II MATEL02 — MUT
Предупреждение: TT: неопределенная функция: 22
MUT
Maths 2
MATHEMATICS 2 TUTORIAL
MANUAL
Введение и краткое изложение содержания S1
Введение
Поздравляем с успешной сдачей экзамена Maths 1 и добро пожаловать в Maths 2. В этом модуле мы
начиная с того места, где мы остановились в математике 1, и поэтому я посвятил раздел
обсудить связь между двумя модулями, а также подвести некоторые итоги процесса.В отличие от Учебного пособия по математике 1, это руководство состоит из отдельных изданий, а не
один непрерывный документ. Причина в том, что по мере того, как вы начинаете изучать математику,
2, ваш контент отличается из-за вашей разной специализации. Ваши тесты и экзамены
тоже будет немного отличаться. Таким образом, у вас будет возможность скачать только
материал, который вам нужен, без лишних затрат.
Каков учебный подход в Maths 2?
Вы должны проконсультироваться с соответствующими учебными пособиями по поводу содержания курса, поскольку я не буду
повтори здесь.Однако в большинстве случаев вы делаете то же самое, за исключением более поздних тем, таких как
Численные методы и матрицы.
Есть учебные занятия по математике 2, в настоящее время по субботам. Посещение необязательно
но очень рекомендуется. На этом этапе мы ожидаем, что вы начнете брать на себя ответственность за свои
учится без «полицейского контроля». Есть две учебные группы, одна для механики,
Электротехническая и химическая инженерия и еще одна группа по строительству и геодезии.
Места проведения этих уроков объявляются в начале семестра.
В математике 2 есть учебный тест, который можно использовать как классный тест и
третья отметка к вашей семестровой отметке. На данный момент нет задания и поэтому ваш
Третья оценка полностью состоит из учебного (классного) теста. Учебный тест написан во время
нормальный ход ваших лекций, а не по субботам. Вам следует проконсультироваться со своим
соответствующих лекторов о том, когда будет написан учебный тест.
Maths 1 revision
В этом разделе мы кратко перечисляем некоторые важные разделы, которые вам нужно взять с собой.
по математике 2.Знание этих концепций предполагается, и они не будут повторяться в
класс.
Экспоненциальные и логарифмические уравнения
В этом разделе вы узнали, как применять законы логарифмов и показателей для решения
экспоненциальные и логарифмические уравнения.
-
lnx + = lny lnxy
-
lnxyln ln x
y
— =
- lnx rxr = ln
Решение
22
2
1
2
22
22 1
2 21
хх
хх
х х х х
хх
хх
ее
ee e
ee ee e e
ee e e
ее е е
—
—
−−
— =
+
⋅ − ⋅ = +
⋅− = +
⋅− = +
2 ()
2
21 21
21
21
2 лн 21
21
х
х
ee e
е
е
e
x e
e
⋅ — = +
+
=
—
= +
—
121 21
ln ln
221 21
ее
Икс
ее
++
⇒ = =
−−
Упражнения
Решите следующие вопросы
1) 32 1eexx = −−
2) ()
1
3
2
eexx + = —
3) 1 ()
2
eexx — = — −e
4) 2
3
хх
хх
ее
ее
—
—
—
=
+
5)
xx 1
хх
ее
ее е
—
—
—
=
+
Ответы
1) пер 2
3
х =
2) х = +3 22
3) хе е = + — 21
4) x = ln 5
5)
пер 1
1
x e
e
= +
—
Дифференциация
Приступая к изучению Математики 2, вам, в буквальном смысле, потребуются навыки построения цепных правил на кончиках пальцев.Практически 60% того, что вы изучаете в математике 2, включает в себя дифференциацию
и интеграция. Чтобы подготовить вас, мы сделаем быстрый пересмотр правила цепочки.
Мы используем цепочку, чтобы различать функцию функции или составную функцию.
Пример
Найди ди
dx
при условии, что ye = cos () x.
Решение
Дифференциация довольно проста. Помните, вы различаете обе стороны,
дача:
грех () xx xsin () x
дней
ee e e
dx
= — ⋅ = —
Пример
Найдите
дней
dx
дает, что yx = sin cos 3 3 ()
Решение
() () ()
() ()
‘
2
3sin cos 3 cos cos 3 sin 3 3
9 sin 3 sin cos 3 cos cos 3
у х хх
хх х
= ⋅ ⋅− ⋅
= —
Пример
Найдите производную от
21
желто-коричневый
х
y
х
+
=
Решение
Этот вопрос включает внутреннюю функцию, которая является частным и, как таковая, частным
Правило должно применяться к внутренней функции.Вам нужно быть очень терпеливым с
упрощения и вопросы такого рода, как правило, вы увидите в Maths 2.
Следовательно, у нас
3)
()
3
2 греха
1 1
хх
х х
— +
+
+
4) 833 сек 222
22
хх
хх х
−−
—
—
Интеграция
Интеграция — очень важная тема в математике 2. Фактически, большинство концепций, которые вы
будет охватывать математику 2, требовать применения интегрирования.Тем не менее, идеи, необходимые в
Математика 2 об интеграции — это основные методы математики 1. Если вы упустили интеграцию
в математике 1, то я предлагаю вам внимательно изучить этот раздел.
() () ()
’11
, 1
1
нн
fx f xdx fx C n
п
+
= + ≠ —
∫ +
Эта формула является обратной цепному правилу. Это очень важно, и вы можете с этим столкнуться
больше, чем любое другое правило.
Пример
Вычислите следующий интеграл
212
2 24
x dx
хх
+
+ —
∫
Решение
Я буду использовать два подхода, вы можете выбрать тот, который вам больше подходит.Т он
два подхода эквивалентны.
- Метод 1: Прямая интеграция
Сначала перепишем интеграл как
() ()
2 12
2
21 2 12 2 4
2 24
х дх х х х дх
хх
Затем,
пусть fxxx () = + — ⇒ 2 2 ‘2 4 fxx () = + = + 4 2 2 2 (x 1)
Убедитесь, что вы факторизуете fx ‘() так, чтобы оно было кратно (2 1.x +) Таким образом,
() () () ()
()
1122
12
22
2
2
12
1
2 12 2 4 22 12 2 4
2
1 2 24
2 24
2
x x x dx x x x dx
хх
C xx C
−−
+ —
= ⋅ + = + — +
∫∫
- Метод 2: Замена переменных, более известный как метод u
Многие учебники по математическому анализу первого года обучения используют этот метод, чтобы познакомить студентов с интеграцией.Я также считаю этот метод весьма удобным, и вы можете использовать его, пока не почувствуете, что готовы
прогресс к прямой интеграции.
()
()
Пусть 2 2 2 4.
4 2 22 1
22 1
ux x
du xx
dx
ду
dx
х
= + —
⇒ = + = +
⇒ =
+
Следовательно,
2 ()
21 21
2 24 22 1
x dx x du
xx u x
++ = ⋅
∫∫ + — +
12
2
11 1
22
2 24
ед.
du C
ты
xx C
= ⋅ +
= + — +
∫
Естественно, оба подхода дают одинаковый ответ.
Пример
Вычислите следующий интеграл
()
3
1
13
dx
∫ + х
Решение
Как и раньше, перепишем интеграл в виде
()
()
3
3
1
13
13
дх х дх
х
= + —
∫∫ +
Пусть fx () = + ⇒ = 1 3 x f x ‘() 3
Следовательно
() ()
()
()
2
133311313 13 1
3 3 2 61 3
х
х д х х д х C C
х
–
Пусть 1 3 3
3
дю дю
u x dx
dx
= + ⇒ = ⇒ =
1
13
dx
∫ + х
Решение
fx () = + ⇒ = 1 3 x f x ‘() 3
Следовательно,
1 13 1 пер 1 3 ()
13 313 3
dx dx x C
хх
= = ++
∫∫ ++
МЕТОД 2
1 3 3
3
дю дю
u x dx
dx
= + ⇒ = ⇒ =
Следовательно,
()
1 1 11 1 1
ln ln 1 3
13 3 3 3 3
du
dx du u C x C
xu u
= ⋅ = = + = + +
∫ ∫∫ +
Пример
Вычислите следующий интеграл
12102
10 5 3
x dx
хх
—
∫ + —
Решение
fx () = + — ⇒ = −10 5x x 3 2 ‘f x () 5 6x
Следовательно,
12 10 222 5 6 2 пер 10 5 (32)
10 5 3 10 5 3
ххдх дх х х С
хх хх
−− = — = — + — +
∫∫ + — + —
МЕТОД 2
10 5 3 2 5 6
56
u x x du x du dx
dx x
= + — ⇒ = — ⇒ =
—
()
()
2
2
12 10 12 10
10 5 3 5 6
25 6
56
1
2 2 вп 2 вп 10 5 3
х дх х дю
хх и х
x du
ux
du u C x x C
u
−− = ⋅
+ — —
−−
= ⋅
—
= — = — + = — + — +
∫∫
∫
∫
Упражнение
Вычислите следующие интегралы
1)
1
пер
dx
∫xx
2) 2
21
2 24
х
dx
хх
+
∫ + —
3) 2
7 14
4 12 3
9000 2 х
dx
хх
—
∫ + —
4) 2 1
2 47
x dx
хх
+
∫ ++
.
Инженерная математика 2A Учебное пособие Вопросы и ответы
ИНЖЕНЕРНАЯ МАТЕМАТИКА 2A (SCEE08009)
Учебный лист 1
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- Упражнения
Вопросы (1), (2) и (3) взяты из упражнения 10.8.3, а вопрос (4) из 10.9.2 в
Современная инженерная математика. Если у вас возникли трудности с этими вопросами, потренируйтесь
используя оставшиеся вопросы из этого упражнения. Вы получите лучшее из этого урока
работая над этими примерами перед учебником и прося своих преподавателей помочь вам с
вопросы, с которыми у вас возникли проблемы.
(1) Какие из следующих наборов линейно независимы, а какие линейно зависимы?
(а) {1, t, t 2, t 3, t 4, t 5, t 6}
(б) {1 + t, t 2, t 2 — t, 1 — t 2}
(c) {синт, стоимость, синт-стоимость, 2 синт + стоимость, 2 синт-стоимость}
(d) {1–2 t 2, t− 3 t 3, 3 t 2 + 4t 3, t 3}
(e) {et, e 2 t − et, e 3 t − e 2 t, e 2 t}
(f) {1 — 2 t 2, t− 3 t 3, 2 t 2 — 4 t 4, 4 t 3}
(2) Для каждого из следующих дифференциальных уравнений запишите дифференциальный оператор L,
что позволит выразить уравнение в виде L [x (t)] = 0.(а)
dx
dt
-кх = 0
(б)
d 3 x
dt 3
д 2 х
dt 2
(
т 2
dx
dt
)
= т
д
dt
(xt)
(г)
d
dt
(
1
т
д
dt
(т 2 х)
)
= xt.
(3) Определите, какие элементы данных наборов являются решениями дифференциального уравнения.
Поэтому запишите общее решение дифференциального уравнения
(а)
d 2 x
dt 2
-р 2 х = 0
{
ept, e-pt, cospt, sinpt
}
(б)
d 2 x
dt 2
+ 2
dx
dt
= 0
{
cos 2t, sin 2t, e− 2 t, e 2 t, t 2, t, 1
}
(с)
d 3 x
dt 3
—
д 2 х
dt 2
–
dx
dt
+ х = 0
{
et, e − t, e 2 t, e− 2 t, tet, te − t, te 2 t, te− 2 t
}
Дата: 23 сентября 2014 г.1
2 Учебный лист 1 ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
(4) Решите следующие задачи начального значения:
(а)
2
д 2 х
dt 2
— 2
dx
dt
dx
dt
∣
∣
∣
∣
x =
= 0.
(б)
d 3 x
dt 3
— 6
d 2 x
dt 2
+ 11
dx
dt
— 6 х = 0, х (0) = 1,
dx
dt
∣
∣
∣
∣
x =
= 0,
d 2 x
dt 2
∣
∣
∣
∣
x =
= 1.
(в)
d 3 x
dt 3
+ 6
д 2 х
dt 2
+ 12
dx
dt
dx
dt
∣
∣
∣
∣
x =
= 1,
d 2 x
dt 2
∣
∣
∣
∣
x =
= 0.
- Курсовая работа
Следующий вопрос должен быть передан в ЕТО до 16:00 23 сентября - Это курс № 1 из 5.Пройти курсовую составляющую Инжиниринга
Математика 2А, вы должны подать как минимум четыре решения и получить средний балл.
отметьте за пять курсовых работ более 40%. Неспособность представить четыре или другие решения
приведет к принудительному провалу курса.
г.
(1) Температура T (в Кельвинах) реакционного сосуда во время особенно нестабильной
химическая реакция моделируется линейным дифференциальным уравнением,
d 4 т
dt 4
+ 5
д 3 т
dt 3
— 21
д 2 т
dt 2
+ 23
дТ
dt
— 8 Т = 0.
В начале эксперимента температура корпуса реактора 293К. Предполагая, что в начале
реакции первая производная −20 Ks − 1, вторая производная −10 Ks − 2 и
все остальные производные равны нулю, определить температуру реакционного сосуда через 3
секунд.
[20]
SCEE08009 Инженерная математика 2A Урок 2
(г)
(
d 3 x
dt 3
) 12
+ т
д 2 х
dt 2
+ x 2 t = синт, x (1) = 1, x ̇ (1) = 0, x ̈ (1) = — 2.
- Найдите значения x (t) fort≤ 1 ≤2, где x (t) — решение следующего начального
проблема стоимости,
д 3 х
dt 3
+
(
д 2 х
dt 2
) 2
+ 4
(
dx
dt
) 2
−xt = sint, x (1) = 0. 2, x ̇ (1) = 1, x ̈ (1) = 0,
с использованием прямого Эйлера с размером шага ∆t = 0,025 с. Повторите расчет с
∆t = 0,0125 и, следовательно, оцените точность вашего решения att = 2.
Стр. 2
SCEE08009 Инженерная математика 2A Урок 2
- Курсовая работа [20]
Следующий вопрос должен быть передан в ЕТО до 16:00 7 октября- г.
- Это задание № 2 из 5. Сдать курсовой компонент
по инженерной математике 2А вы должны подать как минимум четыре решения
и получить средний балл по пяти курсовым работам более 40%. Неспособность
отправить четыре или больше решений приведет к принудительному провалу курса.
- Это задание № 2 из 5. Сдать курсовой компонент
Смещение поплавка x моделируется с помощью
4
г 2 х
dt 2
— 12
dx
dt
ч 0
2
sinωt.
где h 0 — высота волн, воздействующих на поплавок, а ω — частота
волны.
В конкретном эксперименте поплавок возбуждается волнами 700 мм с периодом 2 с. Поплавок
находится в состоянии покоя в начале эксперимента sox (0) = 0,0 и ̇x (0) = 0,0.
Аналитическое решение этого BVP —
х = е
3 т
2
(
(28π 3 + 35π) синт
320 π 4 + 800π 2 + 3380
—
21 πcost
80 π 4 + 200π 2 + 845
)
—
(28π 2 −91) sinπt− 84 πcosπt
320 π 4 + 800π 2 + 3380
Рассчитайте прогнозируемое положение x 50, которое находится путем выполнения 50 временных шагов с
прямой решатель ОДУ Эйлера с равномерным шагом по времени, ∆t = 0.1с. Сравнивая
x 50 с аналитическим решением x (5), прокомментируйте точность вашего решения.
Подсказка: вы должны использовать либо электронную таблицу, например Excel, либо пакет lineMatlab
для расчета численного решения.
Стр. 3
SCEE08009 Инженерная математика 2A Учебник 3
функции.
F 1 (с) =
1
с 3
, ℜ (s)> 0
F 2 (s) =
α
(s + β) 2 + α 2
, ℜ (s)> — β
F 3 (s) =
2 (с 2 + α 2) + с 4
с 3 (с 2 + α 2)
, ℜ (s)> 0
F 4 (s) =
с 3 − с 2 + 25
с 2 (с 2 −25)
, ℜ (s)> 5
F 5 (s) =
e− 3 с
(с + 3) (с + 7)
ℜ (т)> — 3
Страница 2 из 5 Продолжение
SCEE08009 Инженерная математика 2A Учебник 3
- Курсовая работа
Следующий вопрос должен быть передан в ЕТО до 16:00 21 октября- г.
- Это курс № 3 из 5.Пройти курсовую составляющую
по инженерной математике 2А вы должны подать как минимум четыре решения
и получить средний балл по пяти курсовым работам более 40%. Неспособность
отправить четыре или больше решений приведет к принудительному провалу курса.
- Это курс № 3 из 5.Пройти курсовую составляющую
Примечание: α и β — положительные и действительные константы.
(a) Вычислить преобразование Лапласа — использовать свойства преобразования Лапласа [10]
из Таблицы 1, и функция преобразуется из Таблицы 3 для вычисления Лапласа
преобразование следующей функции во временной области.
f (t) = (αt) 5 e − βtH (t) + (t − β) sinh (t − β) H (t − β)
(b) Рассчитайте обратное преобразование Лапласа — используйте свойство преобразования Лапласа — [10]
значений из таблицы 1, и функция преобразуется из таблицы 3, чтобы инвертировать следующее:
функция понижения частотной области.
Ф (с) =
e − αs 3
(с + 7) 2 (с − 1)
Страница 3 из 5 Продолжение
SCEE08009 Инженерная математика 2A Учебник 3
Таблица 3: Преобразования функций
Название f (t), t≥ 0 F (s) Область сходимости
Единичный импульс δ (t) 1 все
Идеальная задержка δ (t − α) exp (−αs) ℜ (s) ≥α
Единичный шаг H (t) 1 с ℜ (s)> 0
Темп t s 12 ℜ (s)> 0
n-я степень tn, n = 1, 2,… snn + 1! ℜ (s)> 0
Синус sin (αt) s 2 + αα 2 ℜ (s)> 0
Косинус cos (αt) s 2 + sα 2 ℜ (s)> 0
Гиперболический синус sinh (αt) s 2 −αα 2 ℜ (s)> | α |
Гиперболический косинус ch (αt) s 2 — sα 2 ℜ (s)> | α |
Экспоненциальный спад exp (−αt) s + 1 α ℜ (s)> — α
Страница 5 из 5 КОНЕЦ
SCEE08009 Инженерная математика 2A Учебник 4
Вопросы (1) и (2) взяты из Упражнения 5.3.5 или аналогичны им, а вопрос (3) из
5.5.7 по продвинутой современной инженерной математике (вопросы (1) — (2) также входят в 11.3.4,
11.3.6 и 11.4.3 в современной инженерной математике). Если у вас возникли трудности с
Эти вопросы тренируют, используя оставшиеся вопросы из этого упражнения. Ты получишь
лучшее из этого учебника, проработав эти примеры перед учебником и
просить ваших наставников помочь вам с вопросами, с которыми у вас возникают проблемы.
- Решите дифференциальные уравнения — Используя методы преобразования Лапласа, решите fort≥ 0
следующие дифференциальные уравнения при указанных начальных условиях.
(я)
dx
dt
при условии tox = 2 att = 0
(ii)
d 2 x
dt 2
+ 2
dx
dt
при условии tox = 0 и ddxt = 0 att = 0
(iii)
д 3 года
dt 3
+
д 2 года
dt 2
+
dy
dt
+ у = соз (3т)
предметная игрушка = 0, ddyt = 1 и d
2 года
dt 2 = 1 att = 0
- Решите систему дифференциальных уравнений — Используя методы преобразования Лапласа,
Решите для ≥0 следующие совместные дифференциальные уравнения с учетом спецификаций
заданы начальные условия.
(я)
2
dx
dt
— 2
дней
dt
— 9 y = e− 2 т
2
dx
dt
+ 4
dy
dt
при условии, что x = 0 и y = 0,25 att = 0
(ii)
д 2 х
dt 2
= у — 2 х
д 2 года
dt 2
= х — 2 у
при условии x = 4, y = 2, dx / dt = 0 и dy / dt = 0 att = 0
Страница 1 из 3 Продолжение
SCEE08009 Инженерная математика 2A Учебник 4
- Курсовая работа
Следующий вопрос должен быть передан в ЕТО до 10:00 5 ноября- Это курс № 4 из 5.Пройти курсовую составляющую
по инженерной математике 2А вы должны подать как минимум четыре решения
и получить средний балл по пяти курсовым работам более 40%. Неспособность
отправить четыре или больше решений приведет к принудительному провалу курса.
- Это курс № 4 из 5.Пройти курсовую составляющую
Связанная система ODE — Определите токи i 1 (t) и i 2 (t) в связанных элек-
Трехмерная схема представлена следующей схемой.
(a) Покажите, что токи описываются следующим интегро-дифференциальным уравнением [4]
тионы
(я 1 (t) −i 2 (t)) R 1 + L 1
di 1 (т)
dt
= е (т)
L 2
di 2 (т)
dt
- (i 2 (t) −i 1 (t)) R 1 = 0
(b) Найдите преобразование Лапласа системы дифференциальных уравнений в терминах [4]
I 1 (с) и I 2 (с) для форсирования
e (t) =
{
3, 0
и с параметрами R 1 = 2 Ом и L 1 = L 2 = 1 H.Начальные условия:
i 1 (0) = i 2 (0) = 0 и в цепи нет заряда att = 0.
Подсказка: Writee (t) с функцией шага единицы Хевисайда.
(c) Рассчитайте обратное преобразование Лапласа для I 2 (s). [8]
(d) Вычислить i 1 (t), подставив i 2 (t) и его производную в исходное уравнение. [4]
Подсказка: напишите i 2 (t) без ступенчатой функции Хевисайда, т.е. аналогично
форсинг (т).
Страница 3 из 3 КОНЕЦ
SCEE08009 Инженерная математика 2A Учебник 5
Вопросы (1) — (5) взяты из современной инженерной математики.Если у вас есть
трудности с этими вопросами, потренируйтесь использовать упражнения из книги. Вы получите
лучше всего из этого учебника, проработав эти примеры перед учебником и спросив
ваши наставники, чтобы помочь вам с вопросами, с которыми у вас возникли проблемы.
- В каждом из следующих случаев периодическая функция f (t) периода 2π задается на одном
период. В каждом случае нарисуйте график функции для — 4 π≤t≤ 4 π и получите
Представление функции рядами Фурье.(а) f (t) = 1−
т
π
(0≤t≤ 2 π)
(б) f (t) = (π − t) 2 (0≤t≤ 2 π) и используйте ряд Фурье, чтобы показать, что 1 π 2 = n = (-1) п + ф (т) = 0 (- 4 Найдите разложение в ряд Фурье. Найдите разложение в ряд Фурье периодической функции f (t) = t, определенной для (−l≤ Периодическая функция f (t) периода 2 определяется для одного периода Определите его разложение в ряд Фурье. Страница 1 из 8 Продолжение SCEE08009 Инженерная математика 2A Определите разложение косинусного ряда половинного диапазона off (t) = 2t − 1, действительно для 0 Функция f (t) = 1 − t 2 должна быть представлена разложением в ряд Фурье по У туго натянутой гибкой однородной струны концы закреплены в точках x = 0 и 0,0 0,5 1,0 1,5 2,0 2,5 3. 0. 0. 0. 0. 0. 1. Рисунок 5: Смещенная колонна ф (т) = π n = № (-1) п + 1sin шт. Посредством почленного интегрирования показать, что функция g (t) = t 2 с периодом 2T определена г (т) = π 2 n = (-1) п + cos шт. Страница 1 из 3 Продолжение SCEE08009 Инженерная математика 2A 0 1 2 3 4 5 6 0 π т Рисунок 6: Движущая сила f (t) Страница 2 из 3 Продолжение ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ: РЕШЕНИЯ Дата: 23 сентября 2014 г. 2 ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯ: РЕШЕНИЯ Начиная с ∣ Система линейно независима. Очевидно, что эта система линейно независима , хотя, поскольку коэффициентов пять, мы -кх = 0 д −k (б) д 2 х L = д 3 д 2 (в) т 2 dx = т д (xt) В первую очередь раскройте скобки 2 т dx + т 2 д 2 х = т 2 dx + TX. . Это второй учебник в серии учебных пособий Microsoft Mathematics. В этом руководстве мы узнаем, как выполнять базовые математические вычисления с помощью Microsoft Mathematics. В числовых вычислениях используются три части Microsoft Mathematics: панель калькулятора (зеленое поле), где расположены командные кнопки, поле ввода (желтое поле), где вводятся команды, и поля вывода где отображаются входные данные, пошаговые вычисления (если применимо) и выходные данные вычислений.Текстовое поле ввода и поля вывода расположены на вкладке Рабочий лист. Откройте Microsoft Mathematics для выполнения вычислений ниже. Пример 1 : Вычислить 2 (5 + 3) Пример 2 : Получение логарифма 7 (основание 10.) Пример 3: Добавление матриц 2 на 2.
f (t) = cos (t / 2) (−π
за период 0≤t≤ 2 π на
12 ∑∞
п 2
{
t≤l) при f (t + 2l) = f (t).
{
-Kl (l + t) (-l
разложение для - 2
интервал 0
x = 3. Средняя точка струны смещена на расстояние 3/2.Iff (x) обозначает
смещенный профиль струны, выразите f (x) как ряд Фурье, состоящий только из синуса
условия.
для (−T 2 т
∑∞
1
Т
в том же интервале имеет разложение в ряд Фурье 1
3
T 2 -
4 T 2
∑∞
п 2
Т
constantk = 4 Н / М, приводится в действие внешней силой f (t) периода 2, как показано ниже.Найти частное решение дифференциального уравнения mx ′ ′ + kx = f (t), описывающего
система. (Подсказка: получите соответствующее периодическое продление от (t) и замените его на
дифференциальное уравнение. Ищите решение x (t), представленное в том же базисе (синус
или косинус) в качестве движущей силы.)
ИНЖЕНЕРНАЯ МАТЕМАТИКА 2A (SCEE08009) Учебный лист 1
(1) Какие из следующих множеств линейно независимы, а какие линейно зависимы?
(а) {1, t, t 2, t 3, t 4, t 5, t 6}
Приравнивая коэффициенты, имеем
1 т т 2 т 3 т 4 т 5 т 6
ж 1 1 0 0 0 0 0 0
ж 2 0 1 0 0 0 0 0
ж 3 0 0 1 0 0 0 0
ж 4 0 0 0 1 0 0 0
ж 5 0 0 0 0 1 0 0
ж 6 0 0 0 0 0 1 0
ж 7 0 0 0 0 0 0 1
Таким образом, уравнения линейно независимы.Если коэффициент можно записать как
квадратная матрица M, то система линейно независима, если det (M) ̸ = 0.
(б) {1 + t, t 2, t 2 - t, 1 - t 2}
Приравнивая коэффициенты, имеем
1 т т 2
ж 1 1 1 0
ж 2 0 0 1
f 3 0 −1 1
ж 4 1 0 - 1
Ясно, что f 1 = f 4 - f 3 + 2f 2, поэтому система не является линейно независимой.
(c) {синт, стоимость, синт-стоимость, 2 синт + стоимость, 2 синт-стоимость}
Приравнивая коэффициенты, имеем
синт стоимость
ж 1 1 0
ж 2 0 1
ж 3 1 - 1
ж 4 2 1
ж 5 2 - 1
Ясно, что f 3 = f 1 - f 2, f 4 = 2f 1 + f 2 и f 5 = 2f 1 - f 2, поэтому система не является линейной
независимый.(d) {1–2 t 2, t− 3 t 3, 3 t 2 + 4t 3, t 3}
Приравнивая коэффициенты, имеем
1 т т 2 т 3
f 1 1 0 −2 0
ж 2 0 1 0 - 3
ж 3 0 0 3 4
ж 4 0 0 0 1
1
∣ ∣ ∣ ∣ ∣ ∣ ∣
1 0 −2 0
0 1 0 - 3
0 0 3 4
0 0 0 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣
= 3
(e) {et, e 2 t − et, e 3 t − e 2 t, e 2 t}
Приравнивая коэффициенты, имеем
и т е 2 т е 3 т
ж 1 1 0 0
f 2 −1 1 0
f 3 0 −1 1
ж 4 0 1 0
Ясно, что f 2 = f 4 - f 1, поэтому система не является линейно независимой.(f) {1 - 2 t 2, t− 3 t 3, 2 t 2 - 4 t 4, 4 t 3}
Приравнивая коэффициенты, имеем
1 т т 2 т 3 т 4
f 1 1 0 −2 0 0
ж 2 0 1 0 −3 0
ж 3 0 0 2 0 - 4
ж 4 0 0 0 4 0
упрощая, в матричной форме, используя операции со строками и записывая R3 = R 3/2 и
R4 = R 4/4 имеем
1 0 −2 0 0
0 1 0 −3 0
0 0 1 0-2
0 0 0 1 0
может потребоваться дополнительное уравнение в наборе.(2) Для каждого из следующих дифференциальных уравнений запишите дифференциальный оператор L,
что позволит выразить уравнение в виде L [x (t)] = 0.
(а)
dx
dt
По осмотру
L =
dt
d 3 x
dt 3
dt 2
dt 3
dt 2
d
dt (
dt )
dt
dt
dt 2
dt Microsoft Mathematics Tutorial 2 - Выполнение основных вычислений
- Щелкните группу кнопок Linear Algebra на панели калькулятора.
- Щелкните вставить матрицу , а затем введите 2 в столбце и 2 в поле строки диалогового окна Вставить матрицу
- Введите числа в первую матрицу выше (используйте клавиши со стрелками или мышь для перехода к разным текстовым полям)
- После завершения ввода переместите курсор к правой части матрицы (вне скобки) и затем введите символ +
- Повторите шаги 2-3, за исключением того, что на этот раз вводятся числа из второй матрицы выше.
- Нажмите кнопку ENTER или нажмите кнопку ENTER, чтобы выполнить добавление.
Этих трех примеров достаточно, чтобы вы продолжали. Чтобы узнать, как пользоваться калькулятором, изучите группы кнопок. Кроме того, напоминаем следующее:
- Кнопки калькулятора сгруппированы в Calculus , Statistics , Linear Algebra , Trigonometry , Standard и Favorite кнопки. Просто щелкните знак +, чтобы отобразить кнопки, знак -, чтобы скрыть их.
- Когда вы щелкаете команду (например, log ), примеры и примечания о том, как использовать эту команду, всегда появляются под текстовым полем ввода (см. Пример на рисунке для команды lcm ).
- Вы можете щелкнуть правой кнопкой мыши наиболее часто используемую команду и добавить ее в группу Избранные кнопки .
.
Tutorial 02 (LMS) - Introduction to Financial Mathematics II
Introduction to Financial Mathematics II
Комментарии
- Пожалуйста, войдите или зарегистрируйтесь, чтобы оставлять комментарии.
Предварительный текст
FNCE10002 Принципы финансов
1 семестр 2019 г.
FNCE10002 Принципы финансов
1 семестр 2019 г.
Введение в финансовую математику II
Учебные вопросы для второй недели
Это руководство разделено на две части. Ответы на вопросы в Части I необходимо отправить на
начало вашего урока.Все ответы должны быть написаны от руки и в оригинале (ксерокопии / электронные письма будут
не приниматься). Пожалуйста, следуйте инструкциям в руководстве, доступном в LMS через
ссылка на Учебники. Ответы на вопросы в Части II присылать не нужно, они будут обсуждаться.
в вашем учебнике. Убедитесь, что вы ответили на эти вопросы и готовы к
обсудите их, если их попросит учитель.
Обратите внимание, что вопросы с пометкой «EXM» - это вопросы прошлых экзаменов, которые я использовал по этому предмету или предметам.
похожи по объему на этот предмет, а те, которые помечены как «TXT», взяты из учебника.Подробно
ответы на вопросы в части II будут предоставлены только в учебных пособиях. Краткие ответы можно получить через
LMS через некоторое время. Эта политика предназначена для того, чтобы вы регулярно посещали свои учебные курсы и
получать своевременную обратную связь от наставника. Если вы не уверены в каком-либо ответе, обратитесь к своему
репетитор, репетитор пит-стопа, онлайн-репетитор или я.
Часть I. Ответы на вопросы наставника
А.
Проблемы
EXM
A1.
Вы только что выиграли первый ежегодный конкурс двойников премьер-министра, и вам предложили
следующие альтернативные способы получения призовых.Предположим, что каждая альтернатива
безрисковый (то есть денежные потоки обязательно возникнут) и процентная ставка 8% годовых.
а) 140 000 долларов в конце года 3.
б) 28 000 долларов США в конце каждого из следующих 5 лет, при этом первый денежный поток возникает в конце
года 1.
c) 9000 долларов США в конце каждого года на неограниченный срок, при этом первый денежный поток происходит в конце каждого года.
год 1.
г) 12 000 долларов США в конце каждого года на неограниченный срок, при этом первый денежный поток возникает в конце
4 года.
Предполагая денежные потоки на конец года, как лучше всего получить призовые деньги? Шоу
все ваши расчеты.A2.
См. Тематическое исследование «Нет латте для вас!» обсуждали в классе. Мы сделали упрощение
предположение, что стоимость латте со временем не увеличится. Теперь предположим, что вы пьете
Латте 4 доллара в день, в месяц - 80 долларов. Предположим, что стоимость латте ожидаема.
Учебные вопросы для второй недели
1
FNCE10002 Принципы финансов
1 семестр 2019 г.
увеличивать из расчета 6% годовых, или 0,5% в месяц навсегда. Как и раньше, вы выбираете
откажитесь от ежедневного латте и вместо этого инвестируйте эту (теперь растущую) сумму в конце каждого месяца
в инвестиционном фонде с процентной ставкой 12% р.а. В чем ценность вашего выращивания
инвестиции в конце: (а) 10 лет и (б) 50 лет? Каковы нынешние ценности вашего
инвестиции? Округлите окончательные ответы до ближайшего доллара.
A3.
Обратитесь к тематическому исследованию «Заряжать или не заряжать», обсуждаемому в классе, где в конце ее
временной горизонт, ваша подруга задолжала по кредитной карте 58 126 долларов. Посчитайте сумму, которую ваш друг
ей придется выплачивать ежемесячно, чтобы она могла выплатить этот долг по кредитной карте к концу: (а)
24 месяц и (б) месяц 36.Показать все расчеты.
Часть II: Отправка ответов не требуется
Б.
Вопросы с множественным выбором
На каждый вопрос выберите наиболее разумный ответ, основанный только на предоставленной информации.
EXM
B1.
Ваша подруга только что увидела в своем местном банке следующую рекламу: «Внесите сегодня 40 000 долларов и
получать 2000 долларов каждый год, постоянно увеличиваясь с постоянной годовой скоростью ». Предположим, банк платит
процентная ставка 8% годовых и первый денежный поток, который вы получите от банка, будет в конце
год 1. Предполагаемый годовой темп роста этих денежных потоков, ближайший к:
а)
б)
в)
г)
EXM
БИ 2.Предположим, вам 25 лет и вы решили начать откладывать на пенсию. Вы планируете
экономить 5000 долларов в конце каждого года (так что первый депозит будет сделан через год), и
внесет последний депозит, когда вы выйдете на пенсию в возрасте 65 лет. Предположим, вы можете зарабатывать 8% годовых на
ваши пенсионные сбережения. Сумма, которую вы накопите на пенсию, ближе всего к:
а)
б)
в)
г)
текст
B3.
EXM
1 194 706 долларов.
1 295 283 долл. США.
1 398 905 долларов.
1 403 905 долларов.
Consumer Insurance, Inc. продает расширенные гарантии на бытовую технику, которые обеспечивают покрытие после
гарантия производителя истекает.Аналитик компании прогнозирует, что компания
придется платить по гарантии в размере 5 миллионов долларов в год в течение трех лет, с первыми расходами
ожидается, что это произойдет через четыре года после сегодняшнего дня. Компания хочет выделить сегодня единовременную выплату на
Покройте эти расходы, и деньги, вложенные сегодня, будут приносить процентную ставку 10% годовых.
Если исходить из денежных потоков на конец года, сумма, которую компании необходимо инвестировать сегодня, составляет
ближайший к:
а)
б)
в)
г)
B4.
–3%.
3%.
5%.
8%.
3 756 574 долл. США.
9 342 044 долл. США.
11 907 834 долл. США.12 434 260 долларов США.
Инвестор ожидает получить 20 000 долларов в течение следующих четырех лет, при этом денежные потоки должны быть
получаются в начале каждого года. Если процентная ставка 6% годовых ежегодно увеличивать
будущая стоимость этих денежных потоков на конец 4 года наиболее близка к:
Учебные вопросы для второй недели
2
.