Гдз по геометрии самостоятельные работы: ГДЗ по геометрии 7 класс самостоятельные и контрольные работы Иченская, Атанасян Просвещение ответы и решения онлайн Контрольные работы, КР-2. Глава II. Треугольники. Задание: Вариант 1

Страница не найдена

Новости

24 янв

В 16 школах Благовещенска проводится эвакуация по причине поступивших сообщений о минировании зданий. Об этом рассказал мэр города Олег Имамеев.

24 янв

В Морском государственном университете им. Невельского во Владивостоке после сообщения о минировании началась эвакуация, аналогичные сообщения поступили ещё в 56 городских школ города. Об этом заявили в мэрии Владивостока.

22 янв

Более 20 школ Улан-Удэ с 24 января переходят на режим дистанционного обучения из-за роста заболеваемости коронавирусной инфекцией и ОРВИ среди детей.

22 янв

Районный суд Красноярска арестовал двух подростков по подозрению в рассылке ложных сообщений о минировании учебных заведений.

21 янв

Заммэра по вопросам экономической политики и имущественно-земельных отношений Владимир Ефимов сообщил, что после согласования в декабре 2021 года Департаментом городского имущества 11 проектов с застройщиками город безвозмездно получит ещё 17 школ и детских садов, а также благоустроенный участок улично-дорожной сети.

21 янв

Уполномоченный по правам ребёнка в Красноярском крае Ирина Мирошникова рассказала об организации проверки после случая с девочкой-инвалидом, которую оставили в школе во время эвакуации.

21 янв

В Симферополе, Керчи и Советском районе Крыма поступили сообщения о минировании школ, всех детей отпустили домой, заявил глава республики Сергей Аксёнов.

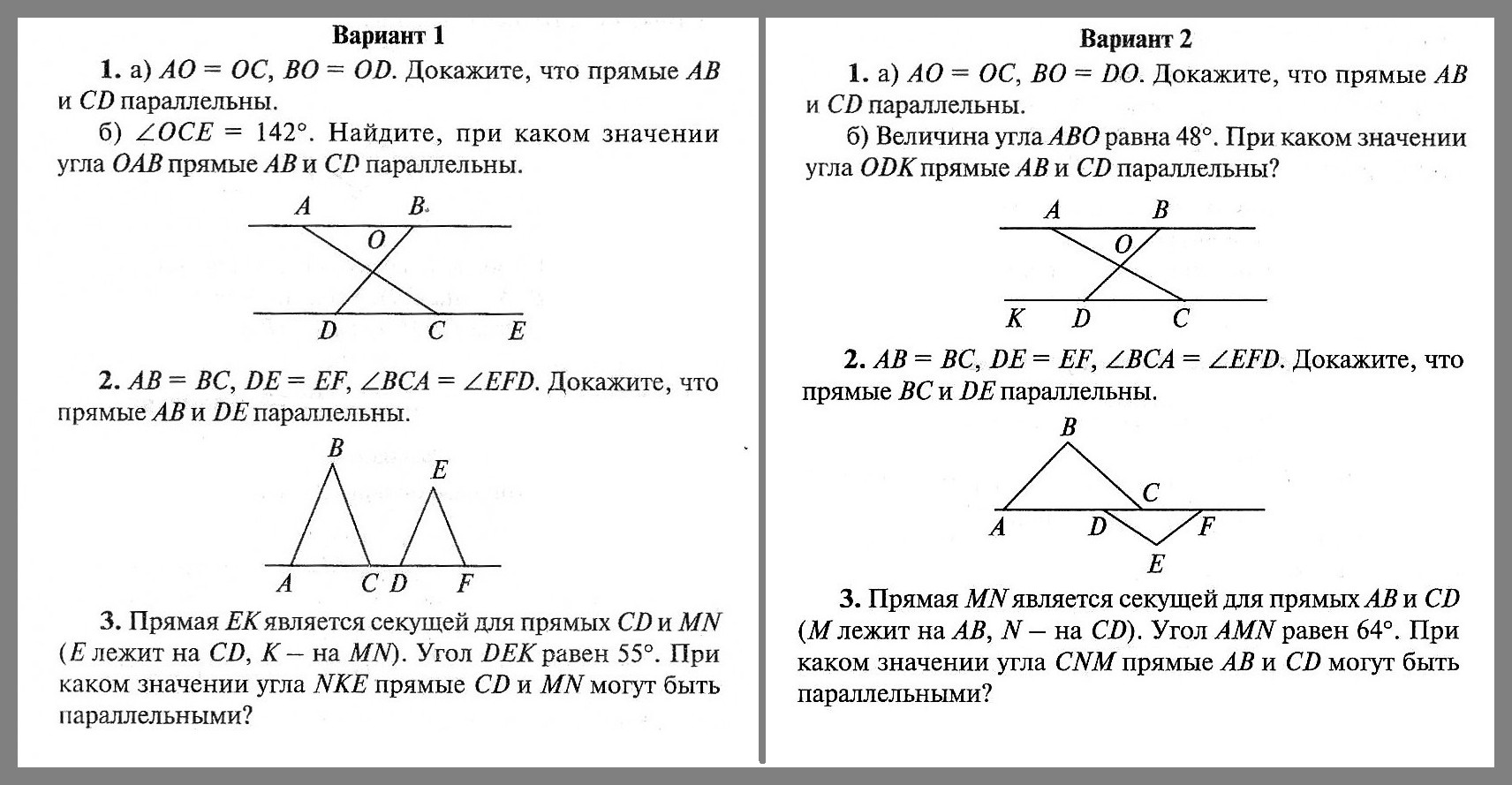
Решебник по Геометрии 10 класс Самостоятельные и контрольные работы Ершова А.П., Голобородько В.В.

Геометрия 10 класс
Ершова А.П.
самостоятельные и контрольные работы

Авторы: Ершова А.П., Голобородько В.В.

«ГДЗ по геометрии за 10 класс Самостоятельные и контрольные работы Ершова (Илекса)» – прекрасный повод подтянуть учебу, и дать жару отличникам. Геометрия считается одной из самых сложных дисциплин в программе обучения школьников. Если на литературе для подготовки достаточно перечитать классическое произведение Пушкина или Некрасова, то здесь по-другому — масса комплексных правил, которые имеют несколько путей рассуждения, и не менее замысловатые задачи. Особенно бывает сложно, когда пропустил пару занятий, и уже не в силах догнать класс по успеваемости. В этом и поможет ГДЗ, в котором содержится вся необходимая информация о ключевых темах геометрии 10 класса, и ответы к заданиям.

ГДЗ по геометрии 10 класс самостоятельные и контрольные работы Ершова не только для детей

Этот решебник подойдет не только для детей, но и для взрослых. Сложно отказать ребенку, когда тот просит выполнить с ним геометрическую задачку, но вы уже давно позабыли школьную программу, или не обладаете математическим складом ума. В решебнике содержится вся необходимая информация для взрослого, чтобы вникнуть в тему, проверить ход мыслей ученика, и подсказать ему в затруднительных моментах. Среди других плюсов сборника:

• ГДЗ помогает анализировать задачу уже со стороны ответа, то есть, почему автор указал именно на такое решение, и как он к этому пришел. Это вырабатывает критическое мышление ученика, а не принуждает к простому списыванию;
• возможность самостоятельно разбирать новые темы;
• закрепление пройденного в классе;
• только правильные ответы.

Можно самостоятельно разобрать принципы разбора задачи, а не идти с пустыми руками в школу или ждать родителей, когда они будут дома. «ГДЗ по Геометрии для 10 класса Самостоятельные и контрольные работы Ершова А. П., Голобородько В. В. (Илекса)» содержит все темы дисциплины за десятый класс:

1. Планиметрия.
2. Стереометрия.
3. Многогранники.

Если вы потратили бессонные вечера на исписанный до дыр черновик, стерли карандаш при рисовании фигур, но все бесполезно – не поленитесь заглянуть в ГДЗ. Свериться с информацией, и найти для себя правильное решение, никто не запрещает. К тому же, что плохого в том, что вы поймете суть решения задачи, и сможете рассказать о ней на уроке. Тем более, формат онлайн-ГДЗ позволяет не тратиться на учебники, а находить любую информацию в веб-версии. Это удобно, практично, и экономит деньги родителям.

ГДЗ по Геометрии за 7‐9 класс Иченская М.А. самостоятельные и контрольные работы

автор: Иченская М.А..

Издательство: Просвещение 2017 год.

Убедись в правильности решения задачи вместе с ГДЗ по Геометрии за 7‐9 класс Иченская М.А. самостоятельные и контрольные работы . Ответы сделаны к книге 2017 года от Просвещение

ГДЗ к учебнику по геометрии за 7-9 классы Атанасян Л.С. можно посмотреть

тут.

ГДЗ Геометрия 7 класс рабочая тетрадь Атанасян можно посмотреть

тут.

ГДЗ Геометрия 7 класс Дидактические материалы Зив можно посмотреть

тут.

ГДЗ к тематическим тестам по геометрии за 7 класс Мищенко Т.М. можно посмотреть

тут.

ГДЗ к рабочей тетради по геометрии за 8 класс Атанасян Л.С. можно посмотреть

тут.

ГДЗ к дидактическим материалам по геометрии за 8 класс Зив Б.Г. можно посмотреть

тут.

ГДЗ к сборнику заданий по геометрии за 8 класс Ершова А.П. можно посмотреть

тут.

ГДЗ Геометрия 9 класс рабочая тетрадь Атанасян можно посмотреть

тут.

ГДЗ Геометрия 9 класс Дидактические материалы Зив можно посмотреть

тут.

ГДЗ к контрольным работам по геометрии за 7 класс Мельникова Н.Б. можно посмотреть

тут.

ГДЗ к контрольным работам по геометрии за 8 класс Мельникова Н.Б. можно посмотреть

тут.

ГДЗ к контрольным работам по геометрии за 9 класс Мельникова Н.Б. можно посмотреть

тут.

ГДЗ к тетради контрольных тестовых работ по геометрии за 7 класс Парфентьева О.Н. можно посмотреть

тут.

ГДЗ к тетради контрольных тестовых работ по геометрии за 8 класс Стокоз В.И. можно посмотреть

тут.

ГДЗ к рабочей тетради по геометрии за 9 класс Глазков Ю.А. Егупова М.В. можно посмотреть

тут.

ресурсов | Ресурсы по теории чисел

| Теория чисел

Математика и статистика

Ресурсы

Интернет

Региональные конференции

• Серия по теории чисел пальметто (PANTS): Серия встреч по теории чисел пальметто (PANTS) представляет собой серию собраний по теории чисел, проводимых в колледжах и университетах Юго-Востока с 2006 года. Цель собраний PANTS — предоставить возможность теоретикам чисел в Южной Каролине и вообще на юго-востоке, чтобы узнать о последних исследованиях во всех областях теории чисел, чистой и прикладной.
• Юго-Восточная региональная встреча по числам (ПРОПОВЕДЬ): ПРОПОВЕДЬ — это небольшое, дружеское и неформальное собрание теоретиков чисел и комбинаторов. Начатая в 1988 году Терезой Воан, она превратилась в ежегодную двухдневную конференцию, в которой участвуют представители различных университетов юго-востока.

Программное обеспечение

• KASH/KANT: KANT — это библиотека для алгебраической теории чисел. Он содержит функции для сложных вычислений в алгебраической теории чисел. KASH — это система компьютерной алгебры, объединяющая библиотеку KANT и оболочку GAP 3.
• Magma: Magma — это большой хорошо поддерживаемый программный пакет, предназначенный для вычислений в алгебре, теории чисел, алгебраической геометрии и алгебраической комбинаторике. Он обеспечивает математически строгую среду для определения и работы с такими структурами, как группы, кольца, поля, модули, алгебры, схемы, кривые, графики, конструкции, коды и многие другие.
• PARI/GP: PARI/GP — это широко используемая система компьютерной алгебры, разработанная для быстрых вычислений в теории чисел (разложение на множители, алгебраическая теория чисел, эллиптические кривые…), но также содержащая большое количество других полезных функций для вычислений с математическими объектами, такими как как матрицы, многочлены, степенные ряды, алгебраические числа и т. д., и много трансцендентных функций.
• Sage: Sage — бесплатная математическая программная система с открытым исходным кодом, распространяемая под лицензией GPL. Он сочетает в себе мощь многих существующих пакетов с открытым исходным кодом в общем интерфейсе на основе Python.

Литература

• MathSciNet: MathSciNet представляет собой электронную публикацию, предлагающую доступ к тщательно поддерживаемой и удобной для поиска базе данных обзоров, рефератов и библиографической информации по большей части литературы по математическим наукам.
• Project Euclid: Миссия проекта Euclid состоит в том, чтобы продвигать научное общение в области теоретической и прикладной математики и статистики. Project Euclid предназначен для удовлетворения уникальных потребностей недорогих независимых и общественных журналов.
• JSTOR: JSTOR — это цифровая библиотека, содержащая более 1500 академических журналов, книг и первоисточников.
• Springer Link: Тексты для выпускников по математике
• Центр ретроспективной оцифровки (ГДЗ): Задачей ГДЗ является регистрация данных, таких как гравюры, рукописи и иллюстрации, и их представление.Ученые, преподаватели и студенты найдут большое количество научных текстов в оцифрованном виде.
• arXiv.org: открытый доступ к электронным изданиям по физике, математике, информатике, количественной биологии, количественным финансам и статистике.

«Гиперболические» полисфериконы — HITS gGmbH

1. Сентябрь 2019

«Гиперболические» полисфериконы отличаются от обычных полисфериконов кривизной своих поверхностей. Поэтому для проведения различия необходимо понятие кривизны.

Как видно из статьи «Полисфериконы» на этом сайте, полисфериконы строятся из тел вращения. Поэтому они локально плоские (кривизна сечения равна нулю). Однако следующие полисфериконы являются локально гиперболическими. Это означает, что секционная кривизна отрицательна. Образно поверхность гиперболических полисфериконов локально выглядит как изображенная ниже знаменитая картофельная стружка.

• Знаменитые картофельные чипсы с отрицательной гауссовой кривизной.
• Нормаль к поверхности, обозначенной красными стрелками.
• Окружности, приближающие кривизну. Они располагаются как над, так и под поверхностью.

Образное Объяснение отрицательной кривизны:

Чтобы объяснить отрицательную кривизну, можно использовать концепцию гауссовой кривизны, которая хорошо подходит для ситуации с картофельными чипсами:

На сетке показаны две главные кривизны. Это линии, наиболее сильно искривленные относительно оси, стоящей вертикально (как маленькая башня в долине) на поверхности. Величина этой кривизны определяется радиусом окружности, аппроксимирующей эту линию. Чем меньше круг, тем сильнее искривление линии и, следовательно, значение кривизны дальше от нуля (при попытке подогнать круг к плоской поверхности нужен бесконечно большой круг, поэтому кривизна равна нулю).

Глядя на две перпендикулярные линии сетки, можно понять, что центры аппроксимирующих окружностей лежат выше и ниже поверхности соответственно.Это показывает, что изгиб линий сетки соответствует отрицательной кривизне. Гауссова кривизна по определению является произведением двух главных кривизн. Это произведение отрицательно для чипа, так как два изгиба идут в разные стороны и, следовательно, являются положительными и отрицательными.

«Гиперболические» полисфериконы

• Слева: локально гиперболический сферикон. Справа: «нормальный», локально плоский сферикон
• Слева: локально гиперболический двойственный (6,1)-полисферикон.Справа: сдвоенный (6,0)-полисферикон (=тело вращения из шестиугольника с загнутыми внутрь ребрами).
• Слева: локально гиперболический четный (6,1)-полисферикон. Справа: тело вращения из загнутого внутрь шестиугольника.
• Слева: неровный (5,1)-полисферикон. Справа: тело вращения из пятиугольника с загнутыми внутрь краями.

Края полисферикона явно проблемные. Поскольку на этих ребрах нет оси нормали, нельзя правильно определить кривизну в этих точках сингулярности.На самом деле не существует тела, которое было бы глобально гиперболическим без этих проблем. Глядя на чип, можно представить, что такое твердое тело без краев должно быть бесконечно большим. Это контрастирует со сферой, которая может быть конечно большой без границ. В конце концов, сфера имеет положительную гауссову кривизну.

Катящийся «гиперболический» сферикон.

Подробнее о гиперболической геометрии

Гиперболическая геометрия очень интересна и активно исследуется.Многие концепции математики могут быть применены к гиперболической геометрии и, следовательно, оправдывают необходимую работу по преодолению незнакомости человеческого мозга с этим типом геометрии.

Если вы хотите узнать больше о гиперболической геометрии, вы можете найти вводную информацию (за пределами веб-сайта HITS) для дальнейшего чтения ниже:

Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung на YouTube.
Mehr erfahren

Видео нагруженные Immer

YouTube entsperren

PGlmcmFtZSB0aXRsZT0iQW5uYSBXaWVuaGFyZDogJnF1b3Q7RGllIEdlb21ldHJpZSBkYXMgUmF1bWVzOiBWb20gTGViZW4gaW4gdmVyc2NoaWVkZW5lbiBXZWx0ZW4mcXVvdDsiIHdpZHRoPSI1MDAiIGhlaWdodD0iMjgxIiBzcmM9Imh0dHBzOi8vd3d3LnlvdXR1YmUtbm9jb29raWUuY29tL2VtYmVkLzZMOVo1dldxN2c0P2ZlYXR1cmU9b2VtYmVkIiBmcmFtZWJvcmRlcj0iMCIgYWxsb3c9ImFjY2VsZXJvbWV0ZXI7IGF1dG9wbGF5OyBlbmNyeXB0ZWQtbWVkaWE7IGd5cm9zY29wZTsgcGljdHVyZS1pbi1waWN0dXJlIiBhbGxvd2Z1bGxzY3JlZW4 + PC9pZnJhbWU +

Обзор различных типов геометрии с введением в гиперболическую геометрию (немецкий).

%PDF-1.4
%
1282 0 объект
>
эндообъект

внешняя ссылка
1282 342
0000000016 00000 н
0000008351 00000 н
0000008544 00000 н
0000008590 00000 н
0000008627 00000 н
0000008765 00000 н
0000008861 00000 н
0000009265 00000 н
0000009430 00000 н
0000029708 00000 н
0000030285 00000 н
0000031020 00000 н
0000031518 00000 н
0000084397 00000 н
0000084471 00000 н
0000084550 00000 н
0000084668 00000 н
0000084785 00000 н
0000084825 00000 н
0000084942 00000 н
0000085073 00000 н
0000085118 00000 н
0000085197 00000 н
0000085237 00000 н
0000085316 00000 н
0000085447 00000 н
0000085484 00000 н
0000085601 00000 н
0000085641 00000 н
0000085758 00000 н
0000085851 00000 н
0000085889 00000 н
0000085933 00000 н
0000085964 00000 н
0000086043 00000 н
0000086086 00000 н
0000086165 00000 н
0000086296 00000 н
0000086340 00000 н
0000086419 00000 н
0000086462 00000 н
0000086541 00000 н
0000086672 00000 н
0000086750 00000 н
0000086829 00000 н
0000086872 00000 н
0000086951 00000 н
0000087082 00000 н
0000087134 00000 н
0000087213 00000 н
0000087256 00000 н
0000087335 00000 н
0000087371 00000 н
0000087416 00000 н
0000087454 00000 н
0000087499 00000 н
0000087539 00000 н
0000087584 00000 н
0000087613 00000 н
0000087658 00000 н
0000087689 00000 н
0000087734 00000 н
0000087827 00000 н
0000087865 00000 н
0000087910 00000 н
0000088003 00000 н
0000088041 00000 н
0000088086 00000 н
0000088124 00000 н
0000088169 00000 н
0000088203 00000 н
0000088248 00000 н
0000088341 00000 н
0000088377 00000 н
0000088422 00000 н
0000088460 00000 н
0000088505 00000 н
0000088544 00000 н
0000088623 00000 н
0000088666 00000 н
0000088745 00000 н
0000088778 00000 н
0000088823 00000 н
0000088916 00000 н
0000088947 00000 н
0000088992 00000 н
0000089021 00000 н
0000089066 00000 н
0000089095 00000 н
0000089138 00000 н
0000089269 00000 н
0000089316 00000 н
0000089395 00000 н
0000089438 00000 н
0000089517 00000 н
0000089578 00000 н
0000089623 00000 н
0000089716 00000 н
0000089763 00000 н
0000089808 00000 н
0000089901 00000 н
0000089952 00000 н
0000089997 00000 н
00000

00000 н
0000090164 00000 н
0000090209 00000 н
0000090280 00000 н
0000090325 00000 н
0000090395 00000 н
0000090438 00000 н
0000090508 00000 н
0000090587 00000 н
0000090631 00000 н
0000090710 00000 н
0000090841 00000 н
0000090888 00000 н
0000091005 00000 н
0000091049 00000 н
0000091166 00000 н
0000091259 00000 н
0000091292 00000 н
0000091336 00000 н
0000091467 00000 н
0000091506 00000 н
0000091585 00000 н
0000091629 00000 н
0000091708 00000 н
0000091801 00000 н
0000091834 00000 н
0000091878 00000 н
0000091971 00000 н
0000092012 00000 н
0000092057 00000 н
0000092150 00000 н
0000092181 00000 н
0000092226 00000 н
0000092319 00000 н
0000092350 00000 н
0000092394 00000 н
0000092487 00000 н
0000092515 00000 н
0000092559 00000 н
0000092652 00000 н
0000092726 00000 н
0000092770 00000 н
0000092863 00000 н
0000092905 00000 н
0000092949 00000 н
0000093080 00000 н
0000093114 00000 н
0000093179 00000 н
0000093223 00000 н
0000093316 00000 н
0000093377 00000 н
0000093421 00000 н
0000093454 00000 н
0000093500 00000 н
0000093555 00000 н
0000093600 00000 н
0000093693 00000 н
0000093719 00000 н
0000093764 00000 н
0000093895 00000 н
0000093923 00000 н
0000094002 00000 н
0000094047 00000 н
0000094126 00000 н
0000094258 00000 н
0000094286 00000 н
0000094365 00000 н
0000094410 00000 н
0000094489 00000 н
0000094582 00000 н
0000094612 00000 н
0000094657 00000 н
0000094689 00000 н
0000094740 00000 н
0000094833 00000 н
0000094860 00000 н
0000094910 00000 н
0000095003 00000 н
0000095032 00000 н
0000095082 00000 н
0000095175 00000 н
0000095237 00000 н
0000095287 00000 н
0000095380 00000 н
0000095407 00000 н
0000095457 00000 н
0000095550 00000 н
0000095585 00000 н
0000095635 00000 н
0000095728 00000 н
0000095770 00000 н
0000095820 00000 н
0000095913 00000 н
0000095942 00000 н
0000095992 00000 н
0000096085 00000 н
0000096115 00000 н
0000096165 00000 н
0000096202 00000 н
0000096252 00000 н
0000096289 00000 н
0000096339 00000 н
0000096432 00000 н
0000096457 00000 н
0000096507 00000 н
0000096600 00000 н
0000096630 00000 н
0000096680 00000 н
0000096773 00000 н
0000096800 00000 н
0000096850 00000 н
0000096943 00000 н
0000096978 00000 н
0000097028 00000 н
0000097121 00000 н
0000097150 00000 н
0000097200 00000 н
0000097226 00000 н
0000097276 00000 н
0000097303 00000 н
0000097348 00000 н
0000097384 00000 н
0000097463 00000 н
0000097508 00000 н
0000097587 00000 н
0000097718 00000 н
0000097811 00000 н
0000097890 00000 н
0000097935 00000 н
0000098014 00000 н
0000098079 00000 н
0000098129 00000 н
0000098222 00000 н
0000098265 00000 н
0000098315 00000 н
0000098408 00000 н
0000098455 00000 н
0000098505 00000 н
0000098539 00000 н
0000098589 00000 н
0000098627 00000 н
0000098677 00000 н
0000098770 00000 н
0000098810 00000 н
0000098860 00000 н
0000098953 00000 н
0000098985 00000 н
0000099035 00000 н
0000099128 00000 н
0000099163 00000 н
0000099213 00000 н
0000099306 00000 н
0000099346 00000 н
0000099396 00000 н
0000099489 00000 н
0000099527 00000 н
0000099577 00000 н
0000099670 00000 н
0000099711 00000 н
0000099761 00000 н
0000099804 00000 н
0000099854 00000 н
0000099895 00000 н
0000099974 00000 н
0000100019 00000 н
0000100098 00000 н
0000100166 00000 н
0000100216 00000 н
0000100309 00000 н
0000100359 00000 н
0000100409 00000 н
0000100502 00000 н
0000100549 00000 н
0000100599 00000 н
0000100692 00000 н
0000100728 00000 н
0000100778 00000 н
0000100871 00000 н
0000100910 00000 н
0000100960 00000 н
0000101053 00000 н
0000101097 00000 н
0000101147 00000 н
0000101240 00000 н
0000101298 00000 н
0000101348 00000 н
0000101384 00000 н
0000101434 00000 н
0000101471 00000 н
0000101516 00000 н
0000101609 00000 н
0000101788 00000 н
0000101833 00000 н
0000101926 00000 н
0000102029 00000 н
0000102074 00000 н
0000102167 00000 н
0000102252 00000 н
0000102297 00000 н
0000102390 00000 н
0000102458 00000 н
0000102503 00000 н
0000102582 00000 н
0000102627 00000 н
0000102686 00000 н
0000102765 00000 н
0000102808 00000 н
0000102887 00000 н
0000102923 00000 н
0000102968 00000 н
0000103099 00000 н
0000103135 00000 н
0000103214 00000 н
0000103259 00000 н
0000103338 00000 н
0000103469 00000 н
0000103505 00000 н
0000103584 00000 н
0000103629 00000 н
0000103708 00000 н
0000103801 00000 н
0000103844 00000 н
0000103889 00000 н
0000103926 00000 н
0000103976 00000 н
0000104069 00000 н
0000104102 00000 н
0000104152 00000 н
0000104185 00000 н
0000104235 00000 н
0000104267 00000 н
0000104317 00000 н
0000104344 00000 н
0000104394 00000 н
0000104422 00000 н
0000104467 00000 н
0000104507 00000 н
0000104551 00000 н
0000007136 00000 н
трейлер
]>>
startxref
0
%%EOF

1623 0 объект
>поток
xWmLSW~O[Zm)RfEBR. l&n Y,YE»c+[Q>I$D%h,+jc:tsf&ddd;wk{/p?=>y?Nr

Произошла ошибка при настройке пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка браузера на прием файлов cookie

Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:

• В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
• Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались.
  Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
• Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
• Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
  браузер автоматически забудет файл cookie.Чтобы это исправить, установите правильное время и дату на своем компьютере.
• Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.
  Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie
потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.

Как правило, в файле cookie может храниться только та информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, если вы не решите ввести его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступ к
остальной части вашего компьютера, и только сайт, создавший файл cookie, может его прочитать.

Редукция Харди для класса интегралов Лиувилля от элементарных функций на JSTOR

Абстрактный

Эта статья посвящена классу интегралов, подынтегральные выражения которых являются произведением рациональной функции на экспоненту непостоянной рациональной функции. Мы называем эти интегралы Лиувилля. Для этих интегралов мы предлагаем удобный для студентов алгоритм, производящий двухчленное разложение с минимальными трансцендентными и максимальными элементарными компонентами.Это разложение удовлетворяет условиям теории редукции Харди, определяет, являются ли эти интегралы элементарными функциями, и в случае положительного ответа находит их. Для достижения нашей цели мы используем разложение на неполные дроби, простые понятия линейной алгебры и частный случай теоремы Лиувилля 1835 года, которую мы называем критерием Лиувилля при интегрировании. В литературе есть полный алгоритм, чтобы решить, является ли интеграл элементарной функции также элементарным. У нас есть мягкая альтернатива классу интегралов Лиувилля.

Информация о журнале

The Monthly публикует статьи, а также заметки и другие материалы о математике и профессии. Его читатели охватывают широкий спектр математических интересов и включают в себя профессиональных математиков, а также студентов всех университетских уровней. Авторам предлагается представить статьи и заметки, которые доносят интересные математические идеи до широкой аудитории читателей Ежемесячника.
Читатели Ежемесячника ожидают высокого уровня экспозиции; они ожидают, что статьи будут информировать, стимулировать, бросать вызов, просвещать и даже развлекать. Ежемесячные статьи предназначены для того, чтобы их читали, наслаждались и обсуждали, а не просто архивировали. Статьи могут представлять собой изложение старых или новых результатов, исторические или биографические очерки, рассуждения или окончательные трактовки, широкие разработки или исследования одного приложения. Новизна и общность гораздо менее важны, чем ясность изложения и широкая привлекательность. Приветствуются соответствующие рисунки, диаграммы и фотографии.
Заметки короткие, четко сфокусированные и, возможно, неформальные. Часто это жемчужины, которые обеспечивают новое доказательство старой теоремы, новое изложение знакомой темы или живое обсуждение одного вопроса.

Информация об издателе

Основываясь на двухвековом опыте, Taylor & Francis быстро выросла за последние два десятилетия и стала ведущим международным академическим издателем. Каждый год Группа издает более 800 журналов и более 1800 новых книг, охватывающих широкий спектр предметных областей и включающих журнал отпечатки Routledge, Carfax, Spon Press, Psychology Press, Martin Dunitz и Taylor & Francis.