Входная контрольная работа по математике (9 класс)
ВАРИАНТ 1
1. Найдите значение выражения
Ответ: __________________
2. На координатной прямой отмечены числа a и b.
Какое из следующих чисел наибольшее?
1) a + b 2) −a 3) 2b 4) a − b
3. Найдите корни уравнения x2 + 7x −18 = 0.
Ответ:__________________
4. Установите соответствие между графиками функций и формулами, которые их задают.
А) Б) В)
5. Вычислите  .
.
1) 7; 2)  ; 3) 5; 4)
; 3) 5; 4) 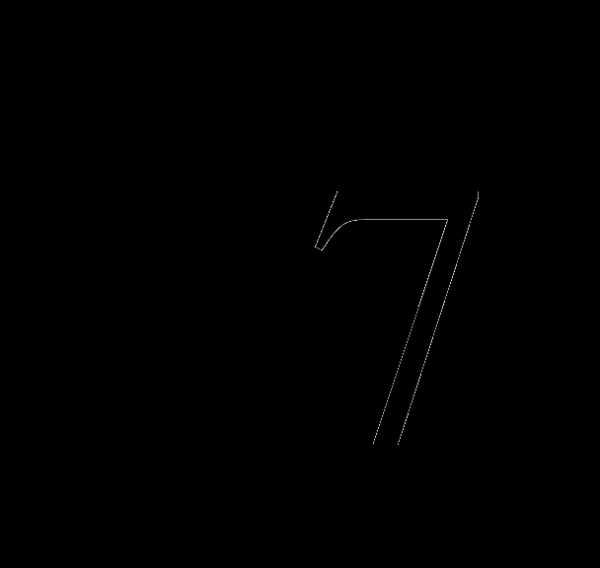 .
.
6. Найдите решения неравенства
1) 0<х<4 2) -4<х<0 3) х>0 4) х<-4;х>0.
7. При каком условии полное квадратное уравнение не имеет корней.
1) D=0 2) D>0 3) D<0
Ответ:_________________
8. Найдите сумму большего и меньшего корней уравнения х2+5х-24=0.
9. Упростите выражение: 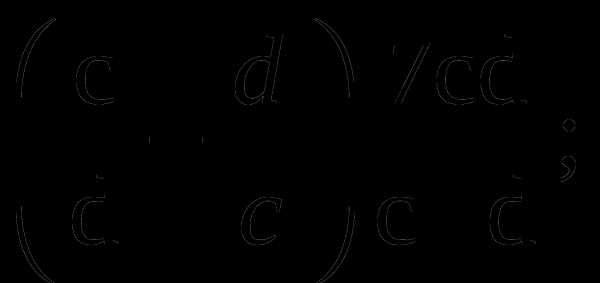
10. . Решите уравнение: 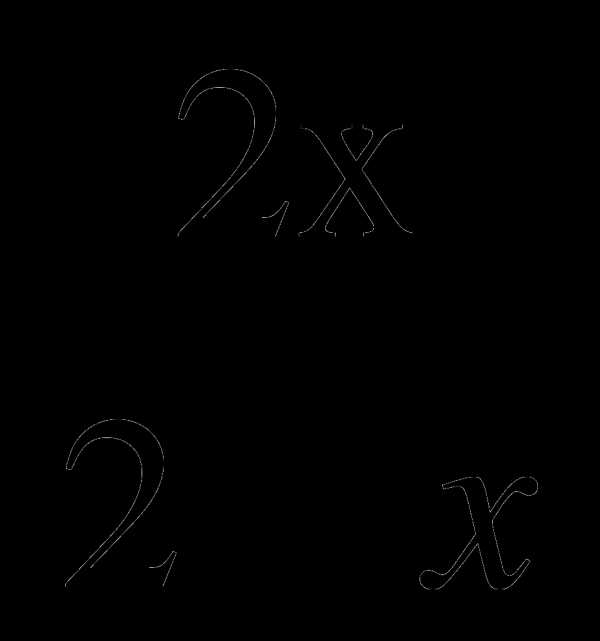 =
= 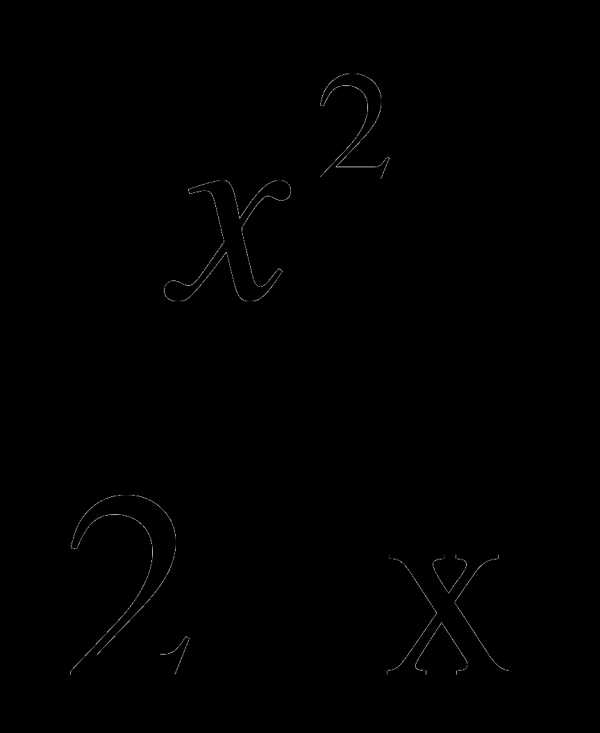 .
.
ВАРИАНТ 2
1. Найдите значение выражения: 
а)  ; б) 6,5; в)
; б) 6,5; в)  ; г) 5,2.
; г) 5,2.
2. Выберите верное утверждение.
1) Если а > 5, в > 7, то а + в > 10; 2) если а < 7, в < 3, то а в < 21;
3) если а > 4, в > 6, то а в > 25; 4) если -12 < а < 10, то -10 < 2 а < 12;
3. Среди чисел 2; 3; -3; -4 найдите корень уравнения х — х-12=0.
— х-12=0.
1) -3; 2) 3; 3) 2; 4) -4.
4. Установите соответствие между графиками функций и формулами, которые их задают.
А)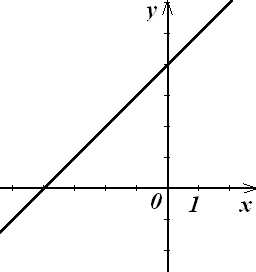
Б)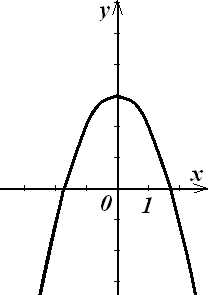
В)
1) y = x 3
2) y = x + 4
3) y = 
4) y = – x2 + 3
А)
Б)
В)
5. Вычислите 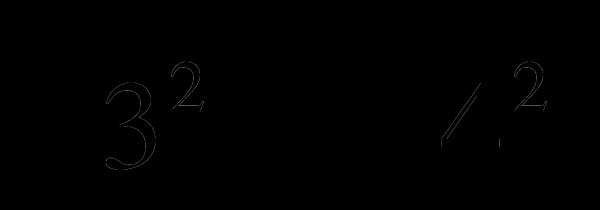 .
.
1) 7; 2)  ; 3)
; 3) 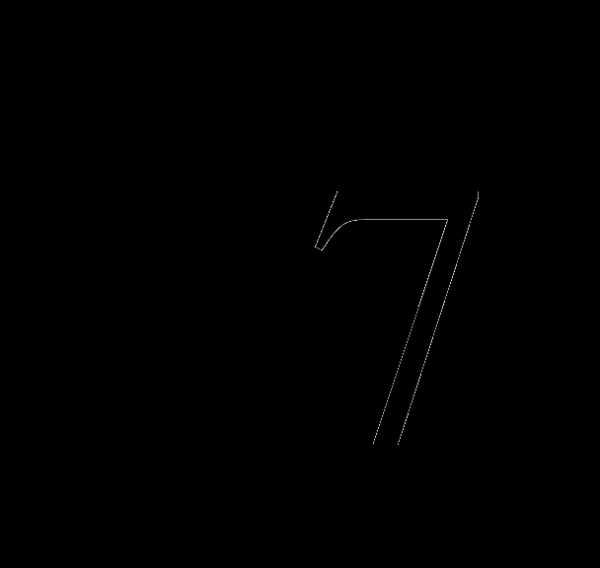 ; 4) 4.
; 4) 4.
6. Найдите решения неравенства 3х –х2 <0
1) х >3 2) х<0; х>3 3) х<0 4) 0<х<3
7. При каком условии полное квадратное уравнение имеет единственный корень.
1) D=0; 2) D>0; 3)D<0.
Ответ:____________________
8 . Найдите разность большего и меньшего корней уравнения х2-9х+14=0.
9. Упростите выражение: 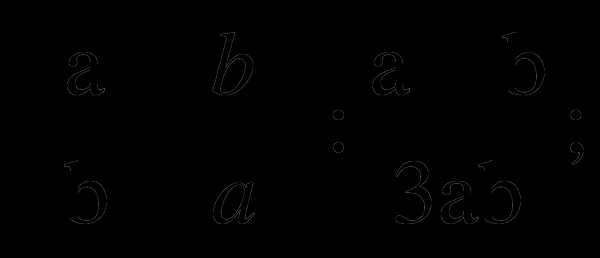
10. Решите уравнение: 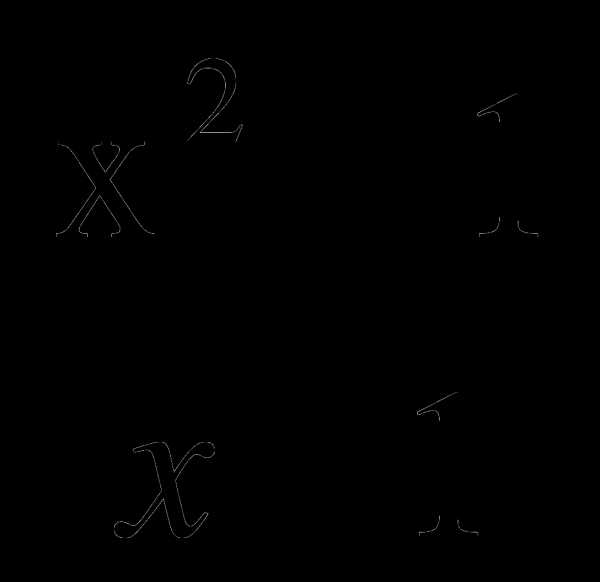 =
= 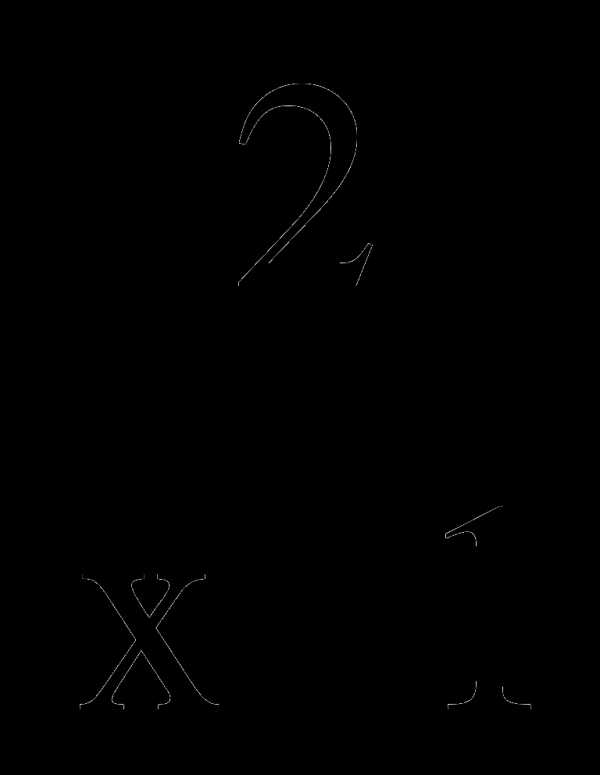 .
.
infourok.ru
Входная контрольная работа по математике 9 класс
Вариант 1
На каком рисунке изображено множество решений неравенства ?
В ответе укажите номер правильного варианта.
1) 1 2) 2 3) 3 4) 4
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера в порядке возрастания.
1) Функция возрастает на промежутке (−∞; −1].
2) Наибольшее значение функции равно 8.
3) f(−4) ≠ f(2).
Найдите значение выражения при
Какое из данных ниже чисел является значением выражения ?
1)
2)
3)
4) 38
Решите уравнение .
Если корней несколько, то в ответ запишите больший.
Найдите корни уравнения .
Если корней несколько, запишите их в ответ через точку с запятой в порядке возрастания.
Решите систему уравнений
х + у = 2
х + у2 = 32
Найдите тангенс угла , изображённого на рисунке.
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.
Укажите номера неверных утверждений.
1) При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.
2) Диагонали ромба перпендикулярны.
3) Центром окружности, описанной около треугольника, является точка пересечения его биссектрис.
Если утверждений несколько, запишите их номера в порядке возрастания.
К окружности с центром в точке проведены касательная и секущая . Найдите радиус окружности, если , .
Решите систему неравенств
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Вариант 2
Решите неравенство
В ответе укажите номер правильного варианта.
1) 2)
3) 4)
Решите уравнение
Если корней несколько, то в ответ запишите меньший.
Значение какого из чисел является наибольшим?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Найдите значение по графику функции изображенному на рисунке.
-
-3 2) 4 3) 2 4) 3
Найдите значение выражения при
Найдите корни уравнения .
Если корней несколько, запишите их в ответ через точку с запятой в порядке возрастания.
Решите систему уравнений
х + 2у = 1
+х + у2 = 4
Найдите тангенс угла , изображённого на рисунке.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
Высота ромба делит его сторону на отрезки и . Найдите площадь ромба.
Какое из следующих утверждений верно?
1) Диагонали параллелограмма равны.
2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Если утверждений несколько, запишите их номера в порядке возрастания.
Найдите ∠KOM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°.
Решите уравнение:
Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 3. Найдите высоту ромба.
Решите систему неравенств
Решите уравнение
Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 1. Найдите высоту ромба.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
Какое из данных ниже чисел является значением выражения
1)
2)
3)
4)
Значение какого из данных выражений является наименьшим?
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
Найдите значение выражения при
Найдите значение по графику функции , изображенному на рисунке.
1)
2)
3)
4)
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(−1) = f(3).
2) Наибольшее значение функции равно 3.
3) f(x)>0 при −1<x<3.
Решите неравенство .
В ответе укажите номер правильного варианта.
1)
2)
3)
4)
На каком из рисунков изображено решение неравенства
В ответе укажите номер правильного варианта.
1) 1
2) 2
3) 3
4) 4
Решение.
Последовательно получаем:
Правильный ответ указан под номером: 1.
Ответ: 1
338745
1
система квур
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 8 и HD = 40. Диагональ параллелограмма BD равна 50. Найдите площадь параллелограмма.
площадь трапеции по клеткам, тангенс по клеткам
Укажите номера верных утверждений.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
4) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
Если утверждений несколько, запишите их номера в порядке возрастания.
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
Если утверждений несколько, запишите их номера в порядке возрастания.
Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера ∠AOC равна 96°.
Задание 17 № 102
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
К окружности с центром в точке проведены касательная и секущая . Найдите радиус окружности, если , .
infourok.ru
Входная контрольная работа по математике для 9 класса
|
Входная контрольная работа по математике 9 класс ВАРИАНТ № 1 Инструкция по выполнению работы Работа состоит из 8 заданий. На выполнение работы отводится 45 минут. При выполнении заданий 1-8 нужно указать ответы в бланке ответов. При этом: если к заданию приводятся варианты ответов (четыре ответа, верный только один), то надо вписать цифру, соответствующую верному ответу; если ответы к заданию не приводятся, то надо вписать ответ. Задание 8 выполняется с записью хода решения. Текст задания можно не переписывать. ЖЕЛАЕМ УСПЕХА! Найдите значение выражения 7 4, 2 — 7 5, 2 + 3. 1) 1 2) 0 3) – 1 4) – 4 Упростите выражение Вычислите 1 2) 7 3) 18 4) 9 |
Решите уравнение Решите неравенство Упростите выражение 3 b 2) 4 b 3) 4) Расстояние от поселка до турбазы составляет 24 км по реке. В 10.00 моторная лодка вышла на турбазу и в 17.00 этого же дня вернулась обратно. Какова собственная скорость моторной лодки, если скорость течения реки 3 км/ч и стоянка на турбазе длилась 1 час? В прямоугольном треугольнике один из внешних углов равен . Найдите меньший из углов прямоугольного треугольника. Ответ дайте в градусах. |
|
Входная контрольная работа по математике 9 класс ВАРИАНТ № 2 Инструкция по выполнению работы Работа состоит из 8 заданий. На выполнение работы отводится 45 минут. При выполнении заданий 1-8 нужно указать ответы в бланке ответов. При этом: если к заданию приводятся варианты ответов (четыре ответа, верный только один), то надо вписать цифру, соответствующую верному ответу; если ответы к заданию не приводятся, то надо вписать ответ. Задание 7, 8 выполняется с записью хода решения. Текст задания можно не переписывать. ЖЕЛАЕМ УСПЕХА! Найдите значение выражения 6 2,2 + 1,8 6 – 14. 1) 3 2) 10 3) – 3 4) – 6 Упростите выражение Вычислите 7 2) 12 3) 23 4) 8 |
Решите уравнение Решите неравенство Упростите выражение 2) 3) 4) 9 Моторная лодка прошла 16 км против течения реки и 12 км по течению реки, затратив на весь путь 3 часа. Скорость течения реки равна 2 км/ч. Какова собственная скорость моторной лодки? В треугольнике АВС угол В в 2 раза больше угла С и в 3 раза меньше угла А. Найдите его градусную меру. |
Дидактическое описание использования работы в образовательном процессе:
|
Предмет |
Математика |
|
Класс |
9 |
|
Тема |
Входная контрольная работа |
|
Тип контроля |
Входной |
|
Форма контроля |
Контрольная работа |
|
Время на выполнение работы |
45 минут |
|
Цель |
Контроль знаний учащихся на начало учебного года |
|
Планируемые образовательные результаты |
Соответствие уровня и качества знаний учащихся образовательной программе |
|
Назначение и способы практического использования |
Входная контрольная работа по математике в общеобразовательном 9 классе, как средство контроля знаний учащихся на начало учебного года |
Ответы:
|
1 вариант |
2 вариант |
|||
|
Задание |
Ответ |
Задание |
Ответ |
|
|
1. |
4
|
1. |
2
|
|
|
2. |
2. |
|||
|
3. |
2 |
3. |
4 |
|
|
4. |
– 2 и 3
|
4. |
– 5 и – 3 |
|
|
5. |
5. |
|
||
|
6. |
3 |
6. |
2 |
|
|
7. |
9 |
7. |
10 |
|
|
8. |
25 |
8. |
40 |
|
Критерии оценивания:
При проверке работы за каждое из шести первых заданий выставляется 1 балл, если ответ правильный и 0 баллов, если ответ неправильный. За выполнение седьмого и восьмого задания, в зависимости от полноты и правильности ответа выставляется от 0 до 2 баллов, согласно критериям, представленным ниже. При оценке выполнения задания 7 и 8 работы необходимо учитывать требования единого орфографического режима.
Итого, максимальное количество баллов за работу 6 х 1 + 2 х 2 = 10
|
Баллы |
Критерии оценки выполнения задания 7 |
|
2 |
Правильно составлена и описана математическая модель задачи, произведены все вычисления, получен верный ответ. |
|
1 |
Правильно составлена математическая модель задачи, но допущена описка и / или негрубая вычислительная ошибка, не влияющая на правильность дальнейшего хода решения. В результате этой описки и /или ошибки может быть получен неверный ответ. |
|
0 |
Все случаи решения, не соответствующие указанным выше критериям выставления оценок в 1 или 2 балла. |
|
Баллы |
Критерии оценки выполнения задания 8 |
|
2 |
Правильно изображен рисунок к задаче, оформлено краткое условие, произведены все вычисления, получен верный ответ. |
|
1 |
Правильно изображен рисунок к задаче, оформлено краткое условие, но допущена описка и / или негрубая вычислительная ошибка, не влияющая на правильность дальнейшего хода решения. В результате этой описки и /или ошибки может быть получен неверный ответ. |
|
0 |
Все случаи решения, не соответствующие указанным выше критериям выставления оценок в 1 или 2 балла. |
Нормы выставления оценок:
|
Баллы |
0 – 4 |
5 – 6 |
7 – 8 |
9 – 10 |
|
Оценка |
«2» |
«3» |
«4» |
«5» |
xn--j1ahfl.xn--p1ai
Учебно-методический материал по алгебре (9 класс) по теме: Входная контрольная работа 9 класс по математике
|
Входная контрольная работа по математике 9 класс ВАРИАНТ № 1 Инструкция по выполнению работы Работа состоит из 8 заданий. На выполнение работы отводится 45 минут.
ЖЕЛАЕМ УСПЕХА!
1) 1 2) 0 3) – 1 4) – 4
|
|
|
Входная контрольная работа по математике 9 класс ВАРИАНТ № 2 Инструкция по выполнению работы Работа состоит из 8 заданий. На выполнение работы отводится 45 минут.
ЖЕЛАЕМ УСПЕХА!
1) 3 2) 10 3) – 3 4) – 6
|
|
Дидактическое описание использования работы в образовательном процессе:
|
Предмет |
Математика |
|
Класс |
9 |
|
Тема |
Входная контрольная работа |
|
Тип контроля |
Входной |
|
Форма контроля |
Контрольная работа |
|
Время на выполнение работы |
45 минут |
|
Цель |
Контроль знаний учащихся на начало учебного года |
|
Планируемые образовательные результаты |
Соответствие уровня и качества знаний учащихся образовательной программе |
|
Назначение и способы практического использования |
Входная контрольная работа по математике в общеобразовательном 9 классе, как средство контроля знаний учащихся на начало учебного года |
Ответы:
|
1 вариант |
2 вариант |
||
|
Задание |
Ответ |
Задание |
Ответ |
|
1. |
4 |
1. |
2 |
|
2. |
2. |
||
|
3. |
2 |
3. |
4 |
|
4. |
– 2 и 3 |
4. |
– 5 и – 3 |
|
5. |
5. |
||
|
6. |
3 |
6. |
2 |
|
7. |
9 |
7. |
10 |
|
8. |
25 |
8. |
40 |
Критерии оценивания:
При проверке работы за каждое из шести первых заданий выставляется 1 балл, если ответ правильный и 0 баллов, если ответ неправильный. За выполнение седьмого и восьмого задания, в зависимости от полноты и правильности ответа выставляется от 0 до 2 баллов, согласно критериям, представленным ниже. При оценке выполнения задания 7 и 8 работы необходимо учитывать требования единого орфографического режима.
Итого, максимальное количество баллов за работу 6 х 1 + 2 х 2 = 10
|
Баллы |
Критерии оценки выполнения задания 7 |
|
2 |
Правильно составлена и описана математическая модель задачи, произведены все вычисления, получен верный ответ. |
|
1 |
Правильно составлена математическая модель задачи, но допущена описка и / или негрубая вычислительная ошибка, не влияющая на правильность дальнейшего хода решения. В результате этой описки и /или ошибки может быть получен неверный ответ. |
|
0 |
Все случаи решения, не соответствующие указанным выше критериям выставления оценок в 1 или 2 балла. |
|
Баллы |
Критерии оценки выполнения задания 8 |
|
2 |
Правильно изображен рисунок к задаче, оформлено краткое условие, произведены все вычисления, получен верный ответ. |
|
1 |
Правильно изображен рисунок к задаче, оформлено краткое условие, но допущена описка и / или негрубая вычислительная ошибка, не влияющая на правильность дальнейшего хода решения. В результате этой описки и /или ошибки может быть получен неверный ответ. |
|
0 |
Все случаи решения, не соответствующие указанным выше критериям выставления оценок в 1 или 2 балла. |
Нормы выставления оценок:
|
Баллы |
0 – 4 |
5 – 6 |
7 – 8 |
9 – 10 |
|
Оценка |
«2» |
«3» |
«4» |
«5» |
nsportal.ru
Входная контрольная работа по математике 9 класс
Входная контрольная работа по математике в 9 классе.
Вариант 1
- Выполните действия:
- Постройте графики функций и у = х + 4. Укажите координаты точек пересечения этих графиков.
3.Решите неравенство .
4.Решите уравнение 4х2+4х+1 = 0
- В равнобедренном треугольнике боковая сторона равна 10 дм и основание равно 12 см. Найдите:
а) высоту треугольника, проведенную к основанию треугольника;
б) площадь треугольника
- Моторная лодка прошла расстояние 45 км против течения реки и такое же расстояние по течению реки, затратив на весь путь 14 ч. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч
Просмотр содержимого документа
«Входная контрольная работа по математике 9 класс»
9 класс. Входная контрольная работа по математике
Вариант 1
-
Выполните действия:
-
Постройте графики функций и у = х + 4. Укажите координаты точек пересечения этих графиков.
-
Решите неравенство .
-
Решите уравнение 4х2+4х+1 = 0
-
В равнобедренном треугольнике боковая сторона равна 10 дм и основание равно 12 см. Найдите:
а) высоту треугольника, проведенную к основанию треугольника;
б) площадь треугольника
-
Моторная лодка прошла расстояние 45 км против течения реки и такое же расстояние по течению реки, затратив на весь путь 14 ч. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч
Вариант 2
-
Выполните действия:
-
Постройте графики функций Укажите координаты точек пересечения этих графиков.
-
Решите неравенство .
-
Решите уравнение 9х2 – 6х + 1 = 0
-
В равнобедренном треугольнике боковая сторона равна 13 дм и основание равно 10 см. Найдите:
а) высоту этого треугольника, проведенную к основанию треугольника;
б) площадь треугольника
6. Моторная лодка прошла расстояние 45 км против течения реки и такое же расстояние по течению реки, затратив на весь путь 14 ч. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч
Вариант 1
-
Выполните действия:
-
Постройте графики функций и у = х + 4. Укажите координаты точек пересечения этих графиков.
-
Решите неравенство .
-
Решите уравнение 4х2+4х+1 = 0
-
В равнобедренном треугольнике боковая сторона равна 10 дм и основание равно 12 см. Найдите:
а) высоту треугольника, проведенную к основанию треугольника;
б) площадь треугольника
-
Моторная лодка прошла расстояние 45 км против течения реки и такое же расстояние по течению реки, затратив на весь путь 14 ч. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч
Вариант 2
-
Выполните действия:
-
Постройте графики функций Укажите координаты точек пересечения этих графиков.
-
Решите неравенство .
-
Решите уравнение 9х2 – 6х + 1 = 0
-
В равнобедренном треугольнике боковая сторона равна 13 дм и основание равно 10 см. Найдите:
а) высоту этого треугольника, проведенную к основанию треугольника;
б) площадь треугольника
6. Моторная лодка прошла расстояние 45 км против течения реки и такое же расстояние по течению реки, затратив на весь путь 14 ч. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч
Вариант 1
-
Выполните действия:
-
Постройте графики функций и у = х + 4. Укажите координаты точек пересечения этих графиков.
-
Решите неравенство .
-
Решите уравнение 4х2+4х+1 = 0
-
В равнобедренном треугольнике боковая сторона равна 10 дм и основание равно 12 см. Найдите:
а) высоту треугольника, проведенную к основанию треугольника;
б) площадь треугольника
-
Моторная лодка прошла расстояние 45 км против течения реки и такое же расстояние по течению реки, затратив на весь путь 14 ч. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч
Вариант 2
-
Выполните действия:
-
Постройте графики функций Укажите координаты точек пересечения этих графиков.
-
Решите неравенство .
-
Решите уравнение 9х2 – 6х + 1 = 0
-
В равнобедренном треугольнике боковая сторона равна 13 дм и основание равно 10 см. Найдите:
а) высоту этого треугольника, проведенную к основанию треугольника;
б) площадь треугольника
6. Моторная лодка прошла расстояние 45 км против течения реки и такое же расстояние по течению реки, затратив на весь путь 14 ч. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч
multiurok.ru
Входная контрольная работа по геометрии, 9 класс
Пояснительная записка
Тестовая контрольная работа по геометрии составлена в форме ГИА. Контрольная работа состоит из двух частей. 1 часть – 7 заданий, 2 часть – 2 задания.
Задания 1 части оцениваются в 1 балл, задания 2 части – 2 балла.
Задания, оцениваемые одним баллом, считаются выполненными верно, если указан верный ответ.
Задания, оцениваемые двумя баллами, считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается 1 балл.
Контрольная работа рассчитана на 45 минут.
11-13 б – оценка «5»
9-10 б – оценка «4»
7-8 б – оценка «3»
При составлении контрольной работы использовались задания открытого банка заданий по математике. ( http://mathgia.ru/or/gia12/Main.html )
Административная контрольная работа по геометрии
Класс: 9
1 вариант
-
Площадь прямоугольника АВСD равна 15. Найдите сторону ВС прямоугольника, если известно, что АВ = 3.
-
Найдите медиану прямоугольного треугольника, проведенную к гипотенузе, равной 14.
-
Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол треугольника. Ответ дайте в градусах.
-
В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно, что
ÐАСD = 25°.
-
В прямоугольном треугольнике АВК гипотенуза АВ равна 13, катет АК равен 12, катет ВК равен 8. Найдите тангенс угла А.
-
На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах
-
Укажите в ответе номера верных утверждений в порядке возрастания:
-
в прямоугольном треугольнике высота может совпадать с одной из его сторон.
-
точка пересечения высот произвольного треугольника – центр окружности, описанной около этого треугольника.
-
высота может лежать и вне треугольника.
-
треугольник со сторонами 6,8,10 — прямоугольный.
-
существует треугольник со сторонами 6, 8, 15.
-
-
Человек ростом 1,7 м стоит на расстоянии 12 шагов от столба, на котором висит фонарь. Тень человека равна двум шагам. На какой высоте (в метрах) расположен фонарь?
-
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
Административная контрольная работа по геометрии
Класс: 9
2 вариант
-
Площадь параллелограмма АВСD равна 35. Найдите сторону ВС параллелограмма, если известно, что высота, проведенная к этой стороне, равна 7 .
-
Найдите гипотенузу прямоугольного треугольника, если медиана, проведенная к этой гипотенузе, равна 4.
-
Один из двух острых угла прямоугольного треугольника на 200 больше другого. Найдите больший острый угол. Ответ дайте в градусах.
-
В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно,
что ÐАСD = 15°.
-
В прямоугольном треугольнике АВК гипотенуза АВ равна 16, катет АК равен 12, катет ВК равен 8. Найдите синус угла А.
-
На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах
-
Укажите в ответе номера верных утверждений в порядке возрастания:
-
в равностороннем треугольнике все высоты равны.
-
точка пересечения медиан произвольного треугольника – это центр окружности, описанной около этого треугольника.
-
медиана, это отрезок соединяющий середины двух сторон треугольника.
-
треугольник со сторонами 6,8,9 — не существует.
-
треугольник со сторонами 3, 4, 5 — прямоугольный.
-
-
Найдите длину солнечной тени от здания высотой 16 м, если солнечная тень от человека ростом 1 м 80 см равна 2 м 70 см.
-
Касательные в точках A и B к окружности с центром O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах.
Административная контрольная работа по геометрии
Класс: 9
3 вариант
-
Площадь прямоугольника АВСD равна 45. Найдите сторону ВС прямоугольника, если известно, что АВ = 9.
-
Найдите гипотенузу прямоугольного треугольника, если радиус описанной окружности равен 11.
-
Один из острых углов прямоугольного треугольника на 240 больше другого. Найдите больший острый угол. Ответ дайте в градусах.
-
В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно, что ÐАСD = 10°.
-
В прямоугольном треугольнике АВК гипотенуза АВ равна 13, катет АК равен 12, катет ВК равен 8. Найдите косинус угла А.
-
На клетчатой бумаге с клетками размером 1 см х1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах
-
Укажите в ответе номера верных утверждений в порядке возрастания:
-
точка пересечения биссектрис является центром вписанной окружности любого треугольника.
-
отношение периметров подобных многоугольников равно квадрату коэффициента подобия.
-
в прямоугольнике диагонали перпендикулярны.
-
в равнобокой трапеции диагонали равны
-
треугольник со сторонами 5, 12, 13 – прямоугольный.
-
-
Человек ростом 1,6 м стоит на расстоянии 10 шагов от столба, на котором висит фонарь. Тень человека равна пяти шагам. На какой высоте (в метрах) расположен фонарь?
-
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Административная контрольная работа по геометрии
Класс: 9
4 вариант
-
Площадь параллелограмма АВСD равна 45. Найдите сторону ВС параллелограмма, если известно, что высота, проведенная к этой стороне, равна 5.
-
Найдите медиану прямоугольного треугольника, проведенную к гипотенузе, если гипотенуза равна 14.
-
Два острых угла прямоугольного треугольника относятся как 1:9. Найдите больший острый угол. Ответ дайте в градусах.
-
В ромбе АВСD проведена диагональ АС. Найдите ÐАВС, если известно, что ÐАСD = 20°.
-
В прямоугольном треугольнике АВК гипотенуза АВ равна 17, катет АК равен 15, катет ВК равен 8. Найдите тангенс угла А.
-
На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах
-
Укажите в ответе номера верных утверждений в порядке возрастания:
-
у прямоугольника диагонали равны.
-
медиана всегда делит пополам один из углов треугольника.
-
радиус описанной около прямоугольного треугольника окружности равен одной из его медиан.
-
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
-
треугольник со сторонами 3, 4, 6 – не существует.
-
-
Длина солнечной тени от дерева равна 24 м. Вертикальный шест высотой 1 м 50 см в тот же момент отбрасывает тень длиной 1 м 60 см. Вычислите высоту дерева.
-
На отрезке AB выбрана точка C так, что AC = 75 и BC = 10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Ключ:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4,5 |
7 |
5 |
130 |
2/3 |
28 |
134 |
11,9 |
7 |
Вариант 1
Задание 8.
Рассм. два подобных треугольника: первый с катетами — 1,7 м и 2 шага, а второй х (высота столба) и 14 шагов (2+12), т.к. эти треугольники подобны, Составим пропорцию: 1,7 м /2 шага=х/14 шаг, х= 1,7 м * 7 = 11,9 метров высота столба.
Задание 9.
Угол, образованный хордой и касательной равен половине дуги, которую он заключает, поэтому величина дуги MK равна 2 · 83° = 166°. Угол MOK — центральный, поэтому он равен величине дуги, на которую опирается. Значит, угол MOK равен 166°. В треугольнике OMK стороны OK и OM равны как радиусы окружности, поэтому треугольник OMK — равнобедренный, следовательно, углы при основании равны. Сумма углов треугольника равна 180°, поэтому ∠OKM = ∠OMK = (180° − ∠KOM)/2 = (180° − 166°)/2 = 7°.
Вариант 2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
5 |
8 |
55 |
150 |
3 |
76 |
48 |
24 |
36 |
Задание 8.
Переведем см в м: 1 м 80 см = 1,8 м; 2 м 70 см = 2,7 м
Составим пропорцию:
1,8 /16= 2,7/x
х = (16*2,7) / 1,8
х = 24
Задание 9.
Введём обозначение (см. рисунок). Касательные, проведённые к окружности из одной точки равны, поэтому следовательно, треугольник — равнобедренный. Откуда Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга равна 108°. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 108°. Рассмотрим треугольник AOB, он равнобедренный, следовательно,
Вариант 3
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
5 |
22 |
57 |
160 |
12/13 |
10 |
145 |
4,8 |
4 |
Задание 8.
Пусть х м — высота фонаря, 10+5=15м — расстояние от столба до конца тени.
Составляем пропорцию:
х/1,6 = 15/5; X=1.6*15/5= 4,8
Задание 9.
Опустим радиусы на каждую касательную. Соединим точки A и O. Получившиеся треугольники — прямоугольные, так как радиус, проведенный в точку касания, перпендикулярен касательной. По гипотенузе и катету эти треугольники равны, таким образом, мы получили, что угол, лежащий напротив катета равен Катет, лежащий напротив угла в равен половине гипотенузы, тогда радиус равен 4.
Вариант 4
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
53 |
2.5 |
2 |
431 |
4 |
65 |
20 |
22,5 |
40 |
Задание 8.
Пусть х м — высота дерева.
Составим пропорцию:
х/1,5 = 24/1,6; X=1,5*24/1,6= 22,5
Задание 9.
Проведём радиус в точку касания. Из прямоугольного треугольника по теореме Пифагора найдём
12.10.2015 г.
Административная контрольная работа
по геометрии
Ученика (цы) 9__ класса
ФИО (в родительном падеже)
Вариант______
Задания 1-7, считаются выполненными верно, если указан верный ответ. Эти задания оцениваются одним баллом.
Задания 8,9 (задания с развернутым ответом), считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается 1 балл.
|
Отметка |
«2» |
«3» |
«4» |
«5» |
|
Кол-во баллов |
0-2 |
3-5 |
6-8 |
9-11 |
12.10.2015 г.
Административная контрольная работа
по геометрии
Ученика (цы) 9__ класса
ФИО (в родительном падеже)
Вариант______
Задания 1-7, считаются выполненными верно, если указан верный ответ. Эти задания оцениваются одним баллом.
Задания 8,9 (задания с развернутым ответом), считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается 1 балл.
|
Отметка |
«2» |
«3» |
«4» |
«5» |
|
Кол-во баллов |
0-2 |
3-5 |
6-8 |
9-11 |
12.10.2015 г.
Административная контрольная работа
по геометрии
Ученика (цы) 9__ класса
ФИО (в родительном падеже)
Вариант______
Задания 1-7, считаются выполненными верно, если указан верный ответ. Эти задания оцениваются одним баллом.
Задания 8,9 (задания с развернутым ответом), считаются выполненными верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется 2 балла. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается 1 балл.
|
Отметка |
«2» |
«3» |
«4» |
«5» |
|
Кол-во баллов |
0-2 |
3-5 |
6-8 |
9-11 |
kopilkaurokov.ru
|
Входная контрольная работа по математике 9 класс ВАРИАНТ № 1 Инструкция по выполнению работы Работа состоит из 8 заданий. На выполнение работы отводится 45 минут. При выполнении заданий 1-8 нужно указать ответы в бланке ответов. При этом: если к заданию приводятся варианты ответов (четыре ответа, верный только один), то надо вписать цифру, соответствующую верному ответу; если ответы к заданию не приводятся, то надо вписать ответ. Задание 8 выполняется с записью хода решения. Текст задания можно не переписывать. ЖЕЛАЕМ УСПЕХА! Найдите значение выражения 7 4, 2 — 7 5, 2 + 3. 1) 1 2) 0 3) – 1 4) – 4 Упростите выражение Вычислите 1 2) 7 3) 18 4) 9 |
Решите уравнение Решите неравенство Упростите выражение 3 b 2) 4 b 3) 4) Расстояние от поселка до турбазы составляет 24 км по реке. В 10.00 моторная лодка вышла на турбазу и в 17.00 этого же дня вернулась обратно. Какова собственная скорость моторной лодки, если скорость течения реки 3 км/ч и стоянка на турбазе длилась 1 час? В прямоугольном треугольнике один из внешних углов равен . Найдите меньший из углов прямоугольного треугольника. Ответ дайте в градусах. |
Входная контрольная работа по математике 9 класс ВАРИАНТ № 2 Инструкция по выполнению работы Работа состоит из 8 заданий. На выполнение работы отводится 45 минут. При выполнении заданий 1-8 нужно указать ответы в бланке ответов. При этом: если к заданию приводятся варианты ответов (четыре ответа, верный только один), то надо вписать цифру, соответствующую верному ответу; если ответы к заданию не приводятся, то надо вписать ответ. Задание 7, 8 выполняется с записью хода решения. Текст задания можно не переписывать. ЖЕЛАЕМ УСПЕХА! Найдите значение выражения 6 2,2 + 1,8 6 – 14. 1) 3 2) 10 3) – 3 4) – 6 Упростите выражение Вычислите 7 2) 12 3) 23 4) 8 |
Решите уравнение Решите неравенство Упростите выражение 2) 3) 4) 9 Моторная лодка прошла 16 км против течения реки и 12 км по течению реки, затратив на весь путь 3 часа. Скорость течения реки равна 2 км/ч. Какова собственная скорость моторной лодки? В треугольнике АВС угол В в 2 раза больше угла С и в 3 раза меньше угла А. Найдите его градусную меру. |
www.prodlenka.org