|
1. |
Деление неравенства на отрицательное число
|
2 |
|
2. |
Число, которое является или не является решением неравенства с модулем
|
1 |
|
3. 
|
Линейное неравенство
|
3 |
|
4. |
Дробное неравенство, сводимое к линейному
|
4 |
|
5. 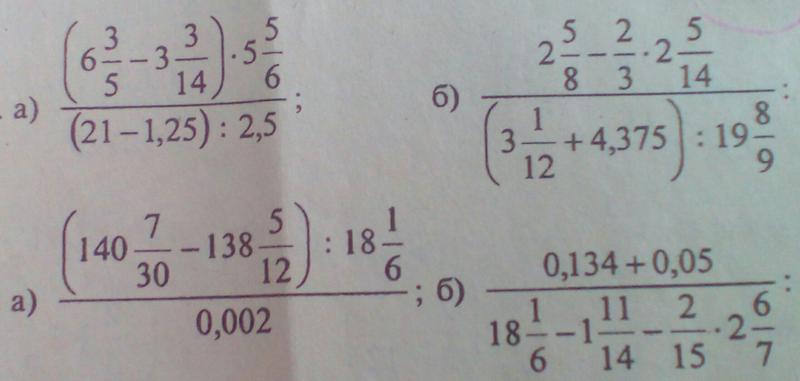
|
Квадратное неравенство, сводимое к линейному (распределительный закон умножения)
|
3 |
|
6. |
Значения переменной, при которых выражение имеет смысл
|
4 |
|
7. 
|
Область определения корня из квадратного трёхчлена
|
5 |
|
8. |
Область определения корня из дроби
|
6 |
|
9. 
|
Значения переменной, при которых дробь имеет смысл (корень в знаменателе)
|
5 |
|
10. |
Целочисленные значения параметра
|
6 |
|
11. 
|
Натуральное значение параметра (целые числа из множества решений)
|
6 |
|
12. |
Натуральное значение параметра (натуральные числа из множества решений)
|
6 |
|
1. |
Метод сложения (линейные уравнения)
|
|
|
2. |
Метод подстановки (линейные уравнения)
|
|
|
3. 
|
Корни квадратного уравнения, теорема Виета
|
|
|
4. |
Метод подстановки (линейное и квадратное)
|
|
|
5. |
Метод алгебраического сложения
|
|
|
6. |
Способ сложения
|
|
|
7. 
|
Пары чисел, которые являются решением системы уравнений
|
|
|
8. |
Графический метод (парабола и прямая)
|
|
|
9. 
|
Графический метод (гипербола и прямая)
|
|
|
10. |
Графический метод (элементарные функции)
|
|
|
11. 
|
Система квадратных уравнений
|
|
|
12. |
Система уравнений (линейное и квадратное) I
|
|
|
13. 
|
Система уравнений (линейное и квадратное) II
|
|
|
14. |
Система уравнений (линейное и квадратное) III
|
|
|
15. 
|
Задача на составление системы уравнений
|
|
|
16. |
Система рациональных уравнений
|
|
|
17. 
|
Система, состоящая из рационального и квадратного уравнений
|
|
|
18. |
Система, состоящая из рационального и линейного уравнений
|
|
|
19. 
|
Система рациональных уравнений, вводится одна новая переменная
|
|
|
20. |
Система, состоящая из рациональных уравнений
|
|
|
21. 
|
Система, состоящая из квадратного и рационального уравнений
|
|
|
22. |
Система линейных уравнений
|
|
|
23. 
|
Система, состоящая из квадратного и рационального уравнений, метод умножения
|
|
|
24. |
Пары чисел, которые являются решением системы уравнений
|
|
|
25. 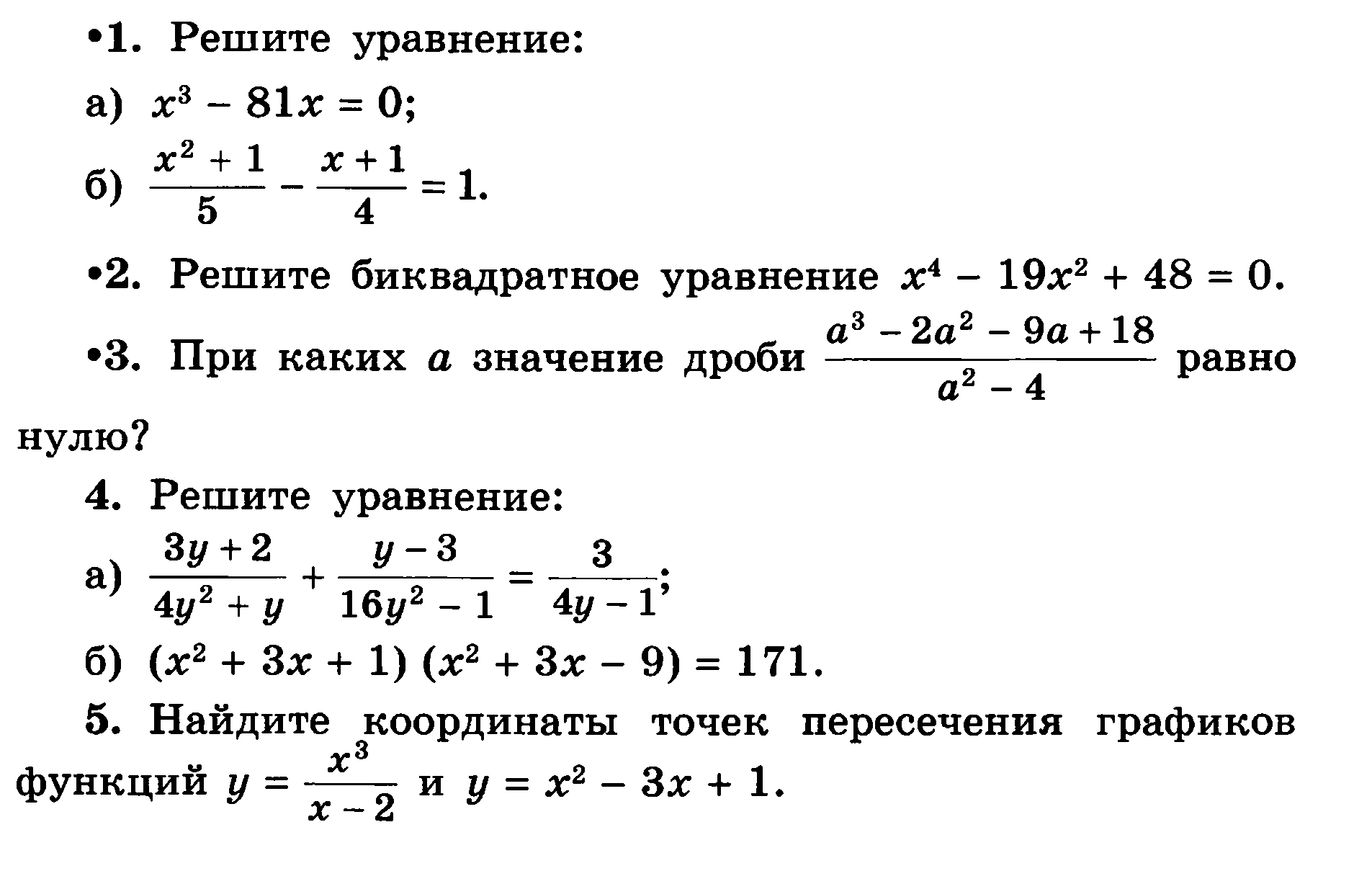
|
Графический метод (окружность и парабола)
|
|
Как решить Факториал числа. Таблица, Свойства, Примеры
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
| Формула факториала n!=1⋅2⋅3⋅.  ..⋅(n−2)⋅(n−1)⋅n ..⋅(n−2)⋅(n−1)⋅n |
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Например:
- 3! = 1*2*3 = 6
- 4! = 1*2*3*4 = 24
- 5! = 1*2*3*4*5 = 120
- 6! = 1*2*3*4*5*6 = 720
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
Запоминаем
0! = 1
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
Чтобы всегда быть готовым решить пример, запомните основные формулы:
- (n — 1)! = 1*2*3*4*5*…*(n — 2)(n — 1)
- n! = 1*2*3*4*5*…*(n — 2)(n — 1)n
- (n + 1)! = 1*2*3*4*5*…*(n — 2)(n — 1)n(n + 1)
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
Пример:
Рекуррентная формула
Примеры:
- 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
- 6! = 6*(6-1)! = 6*5! = 6*120 = 720
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
- Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
- Или раскладывайте факториалы отдельно, если хотите потренироваться:
5! = 1*2*3*4*5 = 4! * 5 =120
7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
120 * 5040 = 604800
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
Как решаем:
При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Как решаем:
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
Как решаем:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Как решаем:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*…..*69 = 69! * 70
49! = 1*2*3*. …49! * 48
…49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Как решаем:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
Тест по математике для учеников 9 класса. Онлайн — тест по математике (9 класс). Онлайн
Предлагаемый тест предназначен для девятиклассников и позволяет проверить базовые знания учащихся по алгебре и геометрии. Для успешного решения теста не требуется знаний, выходящих за рамки школьной программы по математике для 9 класса.
Вам будет предложено 20 вопросов различной сложности. Каждый правильный ответ приносит 1 балл. Максимальная оценка за выполнение теста равна 20.
Постарайтесь затратить на решение предложенного варианта не более 120 минут. Не используйте в процессе работы микрокалькулятор, учебники, справочную литературу.
Ответом к заданию в большинстве случаев является целое число или конечная десятичная дробь. Не пишите в ответе размерности величин, не забывайте переводить обыкновенные дроби в десятичные! В качестве разделителя разрядов используйте запятую, а не точку!
Если ваш результат превысит 16 баллов, можете быть уверены: вы заслуживаете оценки «отлично». Если вы наберете 12-16 баллов, это можно считать хорошим итогом.
А вот в случае, если ваша оценка будет ниже 7 баллов, ситуация плачевная! Вы плохо знакомы со школьным курсом математики, причем речь идет не только о программе 9 класса, но и о существенных пробелах за 5-8 классы. И неважно, что в школе вы имеете оценку «хорошо» по алгебре и геометрии. К сожалению, часто школьные оценки бывают необъективны. Пора начинать работать! Не забывайте, что в конце этого учебного года вам предстоит сдавать ОГЭ по математике!
К сожалению, часто школьные оценки бывают необъективны. Пора начинать работать! Не забывайте, что в конце этого учебного года вам предстоит сдавать ОГЭ по математике!
Успехов!
01. Вычислите без использования микрокалькулятора: (1,87 + 0,13):(5,241 — 5,239).
02. Каждый год количество автомобилей в городе Х увеличивается на 5%. Сейчас в городе Х 4000000 автомобилей. Сколько машин будет в городе через 3 года?
03. Решите уравнение (x+3)2 = (x-2)2. Если уравнение имеет несколько корней, в ответе укажите меньший из них.
04. 1 Сентября Маша решила один пример, 2 Сентября — три примера, 3 Сентября — 5 и т. д. Если данная закономерность сохранится, сколько примеров придется решить Маше 25 Сентября (того же года)?
05. Установите соответствие между формулой, задающей функцию, и описанием графика данной функции.
| А) y = -3x2 + 17x — 38 | 1) парабола, вершина которой находится в точке N(2;5) |
| Б) y = x2 — 10x + 25 | 2) парабола, ветви которой направлены вниз |
| В) y = x2 — 4x + 9 | 3) гипербола |
| Г) y = 8/(x-3) + 160 | 4) парабола, касающаяся оси Ох |
06. {140} }
{140} }
12. Отметьте верные утверждения (ответов может быть несколько).
- Диагональ квадрата со стороной 5 выражается рациональным числом.
- При умножении рационального числа на иррациональное не может получиться целый результат.
- Между двумя неравными числами можно поместить бесконечное количество рациональных чисел.
- Квадратный корень из натурального числа может быть лишь целым или иррациональным числом.
- При умножении рационального числа на иррациональное не может получиться целый результат.
13. Два игральных кубика подброшены одновременно. Какова вероятность того, что суммарное количество очков, выпавшее на двух кубиках, не превысит 3?
14. Найдите те значения р, при которых уравнение | 3x2 -12x +10 | — p = 0 имеет ровно 3 корня. Если таких значений будет несколько, в ответе укажите наибольшее из них.
15. Вычислите площадь ромба, если сумма длин его диагоналей равна 15 и одна из них в 2 раза больше другой.
16. Найдите длину вектора АВ, если известны координаты точек А и В: A(124;761), B(127;765).
17. Стороны параллелограмма равны 6 см и 8 см, а угол между ними составляет 120о. Найдите меньшую диагональ параллелограмма. Ответ округлите до сотых.
18. Длина окружности равна 20 π. Найдите высоту правильного треугольника, вписанного в эту окружность.
19. Отметьте верные утверждения (ответов может быть несколько).
20. Сплав №1 содержит 30% золота по массе, сплав №2 — 70% золота. Сплавы соединили в отношении 2:3 (по массе) и получили 7.6 кг нового сплава №3. Сколько кг чистого золота следует добавить к образцу №3, чтобы получить сплав, содержащий 62% золота?
Возможно, вас заинтересуют следующие онлайн-тесты по математике:
Темы исследовательских проектов по математике в 9 классе
В этом разделе можно выбрать тему исследовательской работы по математике для 9 класса школы. По данным темам предполагается проведение исследовательских работ, связанных с аналитическим и графическим способами решения уравнений и неравенств с одной и с двумя переменными.
По данным темам предполагается проведение исследовательских работ, связанных с аналитическим и графическим способами решения уравнений и неравенств с одной и с двумя переменными.
Представленные темы проектов по математике для 9 класса позволяют ученикам в процессе проведения исследовательской деятельности изучить квадратичную функцию и её свойства, арифметическую и геометрическую прогрессии, элементы комбинаторики и теории вероятности, освоить различные способы решения уравнений второй степени.
Любую из тем проектов по математике для 9 класса учащимся можно расширить или упростить в зависимости от сложности и объемности темы. Необходимо внимательно выбирать тему исследовательской проектной работы по математике, представляя объем предстоящей работы и цель проекта.
Темы исследовательских работ по математике в 9 классе
Примерные темы исследовательских работ по математике для учащихся 9 класса:
Алгоритмический подход к решению геометрических задач.
Вероятность получения положительной отметки при написании тестовой контрольной работы путем угадывания правильного ответа.
Виды уравнений и способы их решения.
Вписанные и описанные окружности. Вневписанные окружности.
График дробно-линейной функции.
Загадки арифметической прогрессии.
Замечательные точки треугольника.
Золотое сечение
Информация, кибернетика и математика.
Иррациональные неравенства.
Иррациональные уравнения.
Использование тригонометрических формул при измерительных работах
История развития учения об уравнениях.
Летопись открытий в мире чисел и фигур.
Математика – царица или слуга для других наук.
Метод подобия в задачах на построение.
Методы решения текстовых задач.
Методы решения уравнений 4 степени.
Можно ли считать мир геометрически правильным.
На правильном пути по ступенькам прогрессии.
Неравенства и системы неравенств с двумя переменными.
Неравенства с параметром.
Нестандартные задачи по алгебре.
Нестандартные задачи по геометрии.
Нестандартные решения уравнений
Нестандартные способы нахождения площадей некоторых многоугольников.
Нестандартные способы решения квадратных уравнений.
О среднем арифметическом, о среднем гармоничном, о среднем геометрическом, о среднем квадратичном.
Парабола и я
Последовательности и прогрессии в жизни.
Построение графиков сложных функций
Презентации избранных вопросов алгебры или геометрии.
Приложения математики в экономике.
Применение векторов к доказательству свойств и признаков параллелограмма.
Применение векторов к доказательству теорем о треугольниках.
Применение подобия к доказательству и решению задач.
Применение свойств квадратичной функции при решении задач.
Прогрессии в нашей жизни
Простые и сложные проценты
Путешествие в историю математики.
Темы проектов по математике для 9 классе
Примерные темы проектов по математике для учащихся 9 класса:
Равносильные преобразования неравенств: теория и практика.
Равносильные преобразования уравнений: теория и практика.
Равносоставленные многоугольники.
Развитие понятия числа. Понятие о действительных числах и действиях над ними.
Различные способы доказательства теоремы Пифагора
Решение задач на смеси и сплавы
Сложные проценты
Способы решения систем уравнений с двумя переменными.
Стандартные и нестандартные методы решения неравенств.
Стандартные и нестандартные методы решения уравнений.
Статистические исследования.
Сценарий математического праздника, викторины, нетрадиционного урока с использованием мультимедийных технологий.
Теория игр. Кубик Рубика.
Теория чисел
Треугольник Паскаля
Треугольник Эйлера-Бернулли
Уравнения высших степеней.
Уравнения с параметром.
Уравнения с переменной под знаком модуля.
Функции в окружающем мире
Характеристические свойства окружности.
Частота и вероятность событий.
Чем геометрия Лобачевского отличается от геометрии Евклида.
Перейти к разделу:
Ученические проекты по математике
Тему исследовательской работы по математике
Если страница Вам понравилась, поделитесь в социальных сетях:
Каким математическим понятиям учат в девятом классе?
Математические понятия в девятом классе могут охватывать несколько тем. Однако девятый
математика в классе обычно фокусируется на общей математике, алгебре или геометрии.
Это связано с тем, на какой курс зачислен ученик девятого класса;
нет стандарта того, какой математический предмет следует преподавать в
девятый класс. Это математические понятия, которые учащиеся должны понимать
к концу девятого класса на основе их курса они зачислены
и Национальные математические стандарты.
Числа и операции концепции фокусируются на рациональном и иррациональном
числа для решения сложных математических задач. Они также используют
квадратные уравнения для решения реальных задач,
решения. Они развивают понимание векторов и действительных систем счисления.
решить проблемы. Они используют векторы и матрицы для объяснения свойств
и представления, которые включают основные математические вычисления через
использование дробей, процентов, десятичных и целых чисел.Они тоже
научиться применять эти понятия, используя ментальную арифметику и бумагу карандашом
решения.
Геометрия концепции для учащихся 9-х классов направленность на развитие
понимание двух- и трехмерных объектов, таких как: призмы,
пирамиды, кубы, конусы, сферы, цилиндры и т. д. Они исследуют отношения
форм, включая конгруэнтность и подобие, чтобы решить геометрическую
проблемы. Они также используют декартовы координаты, чтобы найти отношения
двух- и трехмерных объектов.
Учащиеся девятого класса используют и понимают геометрические переводы, отражения,
повороты, симметрия и расширение объектов с помощью эскизов
и матрицы. Учащиеся строят двух- и трехмерные объекты.
использование различных инструментов для объяснения геометрических ситуаций. Они используют рисунки,
модели и графики для соединения геометрических ситуаций в
другие области предметного содержания и объекты реального мира.
Алгебра понятий, которые изучают учащиеся, представляют собой отношения к функциям
такие как скорость изменения.Кроме того, они учатся использовать несколько
переменные для перехватов, нулей и поведения. Они учатся использовать
более часто используемые алгебраические функции за счет использования технологий,
такие как: графические калькуляторы и компьютерные программы для решения и представления
уравнения.
Учащиеся учатся писать и решать уравнения и неравенства, используя
умственные процессы, наряду с традиционной бумагой и карандашом. Ученики’
исследования включают применение манипуляций с уравнениями, которые
логичны и символичны.Они делают обоснованные выводы на основе
их решения, а также установление связей с другими математическими
концептуальные области.
Измерение концепции сосредоточены на использовании стандартных и нестандартных
(обычные) единицы измерения для определения отношений между
разные объекты. Это также связано с геометрией, поскольку они изучают
как измерить площадь, объем и массу различных геометрических фигур
используя различные инструменты. Они учатся измерять все аспекты сфер,
Они учатся измерять все аспекты сфер,
призмы, пирамиды и т.. Они используют измерения, чтобы сделать чертежи и
модели уравнений для объяснения решения проблемы как в математической
и условия реального мира.
Анализ данных и вероятность , учащиеся используют соответствующий язык
объяснить свои выводы в экспериментах и моделировании. Они учатся
как разработать вопросы, чтобы помочь им найти различия между
несколько выборок в популяции. Они развивают изучение ситуаций
включить роль случайных и экспериментальных опросов.Они учатся
использовать и объяснять одномерные и двумерные измерения и
Категориальные данные. Эта информация используется для построения точечных диаграмм,
коэффициенты регрессии и уравнения регрессии с использованием технологических
инструменты.
Учащиеся также изучают применение выборочной статистики для разработки
объяснения с использованием соответствующего анализа данных. Это используется для разработки
шаблоны случайности для вероятности того, что определенные события могут
быть независимым от других событий. Они учатся использовать симуляции для объяснения
Они учатся использовать симуляции для объяснения
случайность событий.
Решение задач для учащихся девятого класса ориентирован на развитие
стратегий решения проблем, чтобы помочь им развить фундаментальное понимание
математики. Учащиеся используют текстовые задачи и другие симуляторы реального мира.
в ситуациях решения задач.
Представление концепций ориентированы на учащихся, которые учатся собирать
и организовать данные, а затем использовать данные для решения проблем. Ответы
представлены в виде моделей, которые являются числовыми, письменными, физическими и
Социальное.Они могут рисовать графики, диаграммы, таблицы и другие формы.
чтобы объяснить, как они решили проблему.
Концепции
Connection предназначены для учащихся девятых классов.
чтобы продемонстрировать, как устанавливать соединения с реальными приложениями
и другие области предметного содержания. Это включает в себя установление связей
с другими понятиями в математике.
Сообщать свои математические идеи в форме предложений,
рисунки, плакаты и мультимедийные приложения — еще одна концепция
которые студенты должны освоить. Это используется для определения их уровня
Это используется для определения их уровня
понимания, когда они объясняют математические концепции другим учащимся
и учителей.
Рассуждение и доказательство понятия используются для объяснения математических
находки и методы решения проблем. Это необходимо, чтобы
они развивают навыки представления логических аргументов в математических ситуациях.
Все эти математические концепции используются для разработки всестороннего
базовые знания математических идей и языка по мере прогресса учащихся
на более высокие уровни математики.
|
Решения NCERT для математики класса 9 (обновлено для 2021-22)
Если вы ищете Решения NCERT для математики класса 9 , вы попали в нужное место. LearnCBSE.in создал наиболее точные и подробные решения для решений NCERT по математике для класса 9. Решения NCERT по математике для класса 9 включают все вопросы, представленные в соответствии с новой пересмотренной программой в учебнике по математике для класса 9 NCERT.Вы можете скачать PDF-файлы книжных решений NCERT по математике для 9 класса без ВХОДА. Вы также можете попрактиковаться в дополнительных вопросах по математике для 9 класса на сайте LearnCBSE.in
Вы также можете попрактиковаться в дополнительных вопросах по математике для 9 класса на сайте LearnCBSE.in
.
Решения NCERT для математики класса 9
В 9 классе 15 глав по математике. Эти главы закладывают основу для глав, которые будут представлены в 10-м классе. Этот PDF-файл доступен для всех, и они могут использовать его в зависимости от своего удобства. Здесь ниже мы помогаем вам с обзором каждой главы, появляющейся в учебнике.
Решения NCERT для математики класса 9 Глава 1
Решения NCERT для математики класса 9, глава 2
Решения NCERT для математики класса 9, глава 3
Решения NCERT для математики класса 9, глава 4
Решения NCERT для математики класса 9, глава 5
Решения NCERT для математики класса 9 Глава 6
Решения NCERT для математики класса 9 Глава 7
Решения NCERT для математики класса 9 Глава 8
Решения NCERT для математики класса 9 Глава 9
Решения NCERT для математики класса 9 Глава 10
Решения NCERT для математики класса 9 Глава 11
Решения NCERT для математики класса 9 Глава 12
Решения NCERT для математики класса 9 Глава 13
Решения NCERT для математики класса 9 Глава 14
Решения NCERT для математики класса 9 Глава 15
Решения NCERT по математике
В этой статье мы предоставим вам всю необходимую информацию о NCERT Solutions Maths Class 9. Решения NCERT для класса 9 по математике решаются опытными учителями, которые обеспечивают прочную основу для изучения математики. Математика класса 9 NCERT Solutions решается с учетом различных параметров, таких как пошаговые оценки, формулы, распределение оценок и т. Д. Это, в свою очередь, помогает вам не потерять ни одной отметки.
Решения NCERT для класса 9 по математике решаются опытными учителями, которые обеспечивают прочную основу для изучения математики. Математика класса 9 NCERT Solutions решается с учетом различных параметров, таких как пошаговые оценки, формулы, распределение оценок и т. Д. Это, в свою очередь, помогает вам не потерять ни одной отметки.
Важно создать прочную базу по математике. Это один предмет, который будет полезен для каждого студента, независимо от его отрасли. И поэтому мы помогаем вам с решениями NCERT для математики 9 класса.Этот PDF-файл поможет вам найти все решения, данные в учебнике NCERT вместе с упражнением.
Математика играет важную роль в жизни каждого школьника. Работа над решениями NCERT для математических заметок 9-го класса не только поможет вам получить хорошие оценки в 9-м классе, но также поможет вам сдать самые сложные конкурсные экзамены, такие как JEE, NEET, JEE Advanced и т. Д. также будет полезно сдать такие экзамены, как олимпиада, NTSE, с помощью которых вы можете легко получить стипендию и сделать свое образование без проблем. Читайте дальше, чтобы узнать все о NCERT Solutions Maths Class 9, чтобы получить красочные отметки в 9 классе CBSE.
Читайте дальше, чтобы узнать все о NCERT Solutions Maths Class 9, чтобы получить красочные отметки в 9 классе CBSE.
CBSE Class 9 Math Unit Wise Weightage
| Математика CBSE Class 9 Unit-wise Weightage | ||
| БЛОК № | Наименование МОДУЛЯ | Оценочные знаки |
| БЛОК I | Системы счисления | 8 |
| БЛОК II | Алгебра | 17 |
| БЛОК III | Координатная геометрия | 4 |
| БЛОК IV | Геометрия | 28 |
| БЛОК В | Измерение | 13 |
| БЛОК VI | Статистика и вероятность | 10 |
| Итого | 80 баллов | |
Решения NCERT для математики класса 9 Скачать PDF
Просмотрите все решения NCERT для математики класса 9 со своего мобильного или настольного компьютера и получите больше оценок на экзаменах. Вы также можете просмотреть важные вопросы по математике для 9-го класса по главам, которые помогут вам в дополнительной практике и на экзаменах. Он состоит из вопросов на 1 балл, вопросов на 2 балла, числовых вопросов на 3 балла, вопросов на 4 балла, задач со словами и вопросов предыдущего года (VSAQ, SAQ, LAQ и вопросы на основе значений) из всех глав 9 класса по математике, разработанных в соответствии с Учебная программа по математике CBSE Class 9 построена последовательно, что поможет набрать больше баллов на экзаменах.
Вы также можете просмотреть важные вопросы по математике для 9-го класса по главам, которые помогут вам в дополнительной практике и на экзаменах. Он состоит из вопросов на 1 балл, вопросов на 2 балла, числовых вопросов на 3 балла, вопросов на 4 балла, задач со словами и вопросов предыдущего года (VSAQ, SAQ, LAQ и вопросы на основе значений) из всех глав 9 класса по математике, разработанных в соответствии с Учебная программа по математике CBSE Class 9 построена последовательно, что поможет набрать больше баллов на экзаменах.
Класс 9 Математика Глава 1 Системы счисления
Эта глава является продолжением числового ряда, который вы изучали в предыдущих стандартах. В этой главе вы также узнаете, как размещать различные типы чисел на числовой прямой. В общей сложности 6 упражнений в этой главе проведут вас через представление завершающих или не завершающих повторяющихся десятичных знаков на числовой прямой. Наряду с рациональными числами вы также узнаете, куда на числовой прямой помещать квадратные корни из 2 и 3. В этой главе также изучаются законы рациональных показателей и интегральных степеней.
В этой главе также изучаются законы рациональных показателей и интегральных степеней.
Класс 9 Математика Глава 2 Многочлены
Эта глава знакомит вас с алгебраическими выражениями, называемыми полиномиальными, и различными терминами, связанными с ними. В этой главе можно многое узнать об определении и примерах многочленов, коэффициентов, степеней и членов многочлена. В этой главе изучаются различные типы многочленов, такие как квадратичные многочлены, линейная константа, кубические многочлены, теоремы о факторах, теоремы о факторизации.
Класс 9 Математика Глава 3 Координатная геометрия
В общей сложности 3 упражнения в этой главе помогут вам понять геометрию координат в деталях. Наряду с такими понятиями, как понятия декартовой плоскости, термины и различные термины, связанные с координатной плоскостью, изучаются в этой главе. Вы также узнаете о построении точки на плоскости XY и процессе именования этой точки.
Класс 9 Математика Глава 4 Линейные уравнения с двумя переменными
Эта глава познакомит вас с новым уравнением ax + by + c = 0 с двумя переменными. Вопросы в этой главе будут связаны с доказательством того, что линейное число имеет бесконечные решения, с использованием барграфа для построения линейного уравнения и обоснованием любой точки на прямой. В общей сложности 4 упражнения для вашей практики и понимания.
Вопросы в этой главе будут связаны с доказательством того, что линейное число имеет бесконечные решения, с использованием барграфа для построения линейного уравнения и обоснованием любой точки на прямой. В общей сложности 4 упражнения для вашей практики и понимания.
Класс 9 Математика Глава 5 Введение в геометрию Евклида
Глава начинается с введения в индийскую геометрию, поскольку она имеет некоторую основу в геометрии Евклида. Введение в геометрию Евклида в этой главе поможет вам в процессе определения геометрических терминов и форм.Всего есть 2 упражнения, в которых вы подробно рассмотрите взаимосвязь между теоремами, постулатами и аксиомами.
Класс 9 Математика Глава 6 Линии и углы
В этой главе учебника NCERT также есть 2 упражнения. В этой главе есть различные теоремы об углах и прямых, которые можно попросить для доказательства. Первая теорема, которую потребуют для доказательства, звучит так: «Если две прямые пересекают друг друга, то образовавшиеся вертикально противоположные углы будут равны». Кроме того, второе доказательство, которое задают, звучит так: «Сумма всех углов, образованных в треугольнике, равна 180°». Приводятся и другие теоремы, но они основаны только на этих двух теоремах.
Кроме того, второе доказательство, которое задают, звучит так: «Сумма всех углов, образованных в треугольнике, равна 180°». Приводятся и другие теоремы, но они основаны только на этих двух теоремах.
Класс 9 Математика Глава 7 Треугольники
Содержание этой главы поможет понять конгруэнтность треугольников, а также правила конгруэнтности. В этой главе также есть две теоремы и в общей сложности 5 упражнений для студентов. Эти две теоремы приведены в качестве доказательства, а другая используется в задачах или приложениях.Кроме того, в этой главе учащимся предстоит изучить множество свойств неравенств и треугольников.
Класс 9 Математика Глава 8 Четырехугольники
Эта глава очень интересна для изучения студентами, и в ней всего 2 упражнения. Вопросы в этой главе связаны со свойствами, относящимися к четырехугольнику и их сочетаниям с треугольниками.
Класс 9 Математика Глава 9 Площади треугольников и параллелограмм
Эта глава важна для понимания значения площади с этим, площади треугольника, параллелограмма и их комбинации задаются в этой главе вместе с их доказательствами. Есть также примеры an, которые используются в качестве доказательства теорем в этой главе.
Есть также примеры an, которые используются в качестве доказательства теорем в этой главе.
Класс 9 Математика Глава 10 Круги
В этой главе вы познакомитесь с некоторыми интересными темами, такими как равные хорды и их расстояние от центра, хорда точки и стягиваемый ею угол, углы, стягиваемые дугой окружности, и вписанные четырехугольники. В этой главе также есть теоремы, которые помогут доказать вопросы, основанные на четырехугольниках, треугольниках и окружностях.
Класс 9 Математика Глава 11 Конструкции
Эта глава поможет вам изучить две разные категории строительства. Одним из них является построение треугольника вместе с его основанием, разностью или суммой двух оставшихся сторон и одним углом при основании с углом при основании и параметрами. Другой — построение биссектрис для отрезков и измерение углов, включающих 45/60/90 и т. д.
Класс 9 Математика Глава 12 Формула Герона
Эта глава присоединяется к длинному списку глав NCERT, в котором также есть 2 упражнения. В этой главе вы изучите понятия, являющиеся расширением понятий, связанных с площадью треугольника. Кроме того, вы узнаете, как находить площади треугольников, четырехугольников и различных типов многоугольников. Наряду с этим имеется также знание формулы плоских фигур, приведенной в главе.
В этой главе вы изучите понятия, являющиеся расширением понятий, связанных с площадью треугольника. Кроме того, вы узнаете, как находить площади треугольников, четырехугольников и различных типов многоугольников. Наряду с этим имеется также знание формулы плоских фигур, приведенной в главе.
Класс 9 Математика Глава 13 Площади поверхности и объем
Каждый из вас уже изучал измерение в предыдущих стандартах. Таким образом, вы должны знать о поверхностных областях, и эта глава посвящена им.Наряду с этим в этой главе также есть объем кубов, цилиндров, прямоугольных параллелепипедов, конусов, полушарий и сфер. Кроме того, в этой главе вы узнаете о преобразовании одной фигуры в другую и сравнении объемов двух фигур.
Класс 9 Математика Глава 14 Статистика
В этой главе вы получите знания об описательной статистике и сборе данных, основанных на различных аспектах жизни. Это полезно для интерпретации и формулирования выводов из данных.Эта глава дает базовые знания о сборе данных, поскольку данные доступны в необработанном виде. По мере того, как вы продвигаетесь вперед и изучаете 5 упражнений, вы научитесь представлять данные в табличной форме, сохраняя их вместе через равные промежутки времени, рисуя многоугольники, гистограммы или гистограммы. Вы также перейдете к таким темам, как среднее значение, медиана и мода, а также к нахождению центральной тенденции с помощью необработанных данных.
По мере того, как вы продвигаетесь вперед и изучаете 5 упражнений, вы научитесь представлять данные в табличной форме, сохраняя их вместе через равные промежутки времени, рисуя многоугольники, гистограммы или гистограммы. Вы также перейдете к таким темам, как среднее значение, медиана и мода, а также к нахождению центральной тенденции с помощью необработанных данных.
Класс 9 Математика Глава 15 Вероятность
Вероятность в этой книге основана на подходе наблюдения или нахождения частоты.Вопросы в этой главе очень интуитивны, поскольку они основаны на повседневной жизни или повседневных ситуациях. Например, такие инциденты, как бросание игральных костей, подбрасывание монеты, вероятность выпадения колоды карт и простые события. Если вам любопытно, эта глава может быть очень интересна для изучения и понимания.
Может быть несколько раз, когда вы чувствуете, что застряли и не получаете желаемых решений. Здесь мы можем помочь вам с решениями NCERT для математики класса 9. Вы можете использовать эту статью в качестве справочника по всем главам книги NCERT.
Вы можете использовать эту статью в качестве справочника по всем главам книги NCERT.
Часто задаваемые вопросы о решениях NCERT для математики класса 9
1. Как подготовиться к 9 классу CBSE по математике?
Попрактикуйтесь в решениях NCERT по математике для 9 класса и постарайтесь тщательно осветить все темы и вопросы.
2. Как я могу эффективно и быстро выучить математику для 9 класса?
Лучший способ быстро научиться — решить NCERT. NCERT имеет мало вопросов, но имеет большое значение в документах. Если вы можете решить весь NCERT с примерами, вы легко получите хороший результат.Если у вас достаточно времени, попробуйте также обратиться к Р. Д. Шарме, поскольку это лучшая книга.
3. Могу ли я решить математические вопросы для 9 класса CBSE?
Да, вы можете получить решения по математике для экзаменов CBSE класса 9 на нашей странице. Получите доступ к прямым ссылкам, доступным на нашей странице, и загрузите их бесплатно.
4. Какое руководство по математике лучше для 9-го CBSE?
NCERT Solutions for Class 9 Maths поможет вам в подготовке. Получите хорошее представление о предмете, практикуя все больше и больше решений NCERT, преобладающих на нашей странице.
5. Как я могу загрузить книгу решений NCERT для математики класса 9 CBSE?
Претенденты
могут загрузить решения NCERT по математике класса 9 CBSE, нажав на доступные прямые ссылки. Заложите более прочную основу концепций, обратившись к решениям NCERT.
6. Как долго ученик 9 класса должен заниматься математикой?
Дело не в ограничении времени. Старайтесь практиковаться как можно больше и пересмотреть полную программу по математике для 9 класса, чтобы экзамены набрали хорошие баллы.
Теперь, когда вам предоставлена вся необходимая информация о решениях NCERT для класса 9 по математике, мы надеемся, что эта подробная статья о решениях NCERT по математике для класса 9 окажется полезной. Если у вас есть какие-либо сомнения относительно этой статьи или решений NCERT по математике для класса 9, оставьте свои комментарии в разделе комментариев ниже, и мы свяжемся с вами как можно скорее.
Если у вас есть какие-либо сомнения относительно этой статьи или решений NCERT по математике для класса 9, оставьте свои комментарии в разделе комментариев ниже, и мы свяжемся с вами как можно скорее.
Математические формулы для 9 класса
Студенты часто боятся математики, поскольку она связана со сложностью изучения формул.Беглый взгляд на формулы может вызвать тревогу у студентов, и именно по этой причине многие из них не хотят изучать этот предмет. Чтобы помочь учащимся успокоиться и упростить изучение математических формул для 9-го класса, в этой статье приводится краткое изложение всех важных формул и несколько полезных советов по их запоминанию.
Список важных математических формул для класса 9
Вот краткий список важных математических формул для 9 класса.
- (а + б) (а — б) = а 2 — б 2
- (а + b) 2 = а 2 + 2ab + b 2
- (a — b) 3 = a 3 — b 3 — 3ab(a — b)
- Формула Герона для нахождения площади треугольника = √s(s — a)(s — b)(s — c), где s – полупериметр треугольника, который рассчитывается по формуле s = (а + b + с)/2
- Площадь криволинейной поверхности конуса = 1/2 × l × 2πr = πrl, где «r» — радиус основания, а «l» — наклонная высота.
 ‘l’ = квадратный корень из (r 2 + h 2 )
‘l’ = квадратный корень из (r 2 + h 2 )
Система счисления Класс 9 Математические формулы
Математические формулы класса 9 системы счисления охватывают важные факты о рациональных и иррациональных числах, которые помогают укрепить математическую основу. Предположим, что число «а» рационально, а «b» иррационально, тогда «a + b» и «a — b» — иррациональные числа, «ab» и «a/b» — иррациональные числа, а «b ‘ не равно нулю.
Для положительных действительных чисел «a» и «b» следующие объекты будут истинными:
- √ab = √a √b
- √(а/б) = √а / √б
- (√a + √b) (√a — √b) = a — b
- (√а + √б) 2 = а + 2√аб + б
- (а + √b) (а — √b) = а 2 — б
- (а + б) (а — б) = а 2 — б 2
Алгебраические формулы для 9 класса по математике
Фундаментальные свойства и теоремы полиномов образуют строительные блоки для полиномов высшей алгебры. Процесс факторизации многочленов помогает найти корни уравнения, и это важная концепция, которая может улучшить понимание алгебры учащимися.
Процесс факторизации многочленов помогает найти корни уравнения, и это важная концепция, которая может улучшить понимание алгебры учащимися.
- (а + б) 2 = а 2 + 2аб + б 2
- (a — b) 3 = a 3 — b 3 — 3ab(a — b)
Площадь и объем Класс 9 Математические формулы
В повседневной жизни мы сталкиваемся со всевозможными формами, и, следовательно, возникает необходимость найти их размеры, что в дальнейшем приводит к вычислению площади и объема.Эти расчеты необходимы в повседневной жизни, независимо от того, нужно ли выяснить, сколько жидкости необходимо для заполнения контейнера, или нужно рассчитать площадь поверхности любого объекта. Математические формулы класса 9 относительно того же можно найти, как показано ниже:
- Площадь поверхности прямоугольного параллелепипеда = 2 (lb + bh + hl), где l, b и h — длина, ширина и высота соответственно.
- Площадь криволинейной поверхности конуса = 1/2 × l × 2πr = πrl, где «r» — радиус основания, а «l» — наклонная высота
Тогда ‘l’ = квадратный корень из (r 2 + h 2 )
- Площадь поверхности сферы = 4 π r 2
- Объем прямоугольного параллелепипеда = Площадь основания × Высота = Длина × Ширина × Высота
- Объем куба = a 3 , где «a» — ребро куба.

- Объем конуса = (1 / 3)πr 2 ч
- Объем сферы = (4/3) πr 3
- Объем полушария = (2/3) πr 3
Статистика и формулы вероятностей для 9 класса по математике
Статистика играет решающую роль практически во всех аспектах жизни. Концепция вероятности связана с предсказанием событий, и формулы, касающиеся того же самого, используются почти везде, включая предсказание погоды и некоторые области науки.Чтобы делать важные выводы из данных, нужно сначала научиться анализировать данные, и следующие формулы помогают сделать то же самое.
- Знак класса = (Верхний предел + Нижний предел)/ 2
- Среднее значение = Сумма наблюдений / Общее количество наблюдений
- Режим = Наблюдение, происходящее наиболее часто
- Экспериментальная формула вероятности: количество испытаний, в которых произошло событие (E) / сумма испытаний
раз
Применение математических формул 9 класса
Математические формулы класса 9 применяются в различных областях. Давайте посмотрим, как эти формулы играют роль в нашей повседневной жизни.
Давайте посмотрим, как эти формулы играют роль в нашей повседневной жизни.
- Математика прочно вошла в нашу повседневную жизнь, начиная с измерений на кухне и заканчивая любыми операциями в магазине. Числа играют важную роль почти во всех сферах жизни. Правильное понимание чисел также может помочь учащимся в управлении деньгами. Следовательно, понимание системы счисления является одним из важных навыков, которые необходимо изучить не только для изучения тем высшей математики, но и для жизни в целом.
- Формы окружают нас повсюду. Следовательно, изучение геометрических формул помогает нам выявлять и решать реальные проблемы, возникающие при их аналитическом анализе. Будь то решение, сколько краски потребуется для покраски зала или сколько кирпичей потребуется для возведения стены, математические формулы 9-го класса помогут решить эту проблему из реальной жизни.
- Данные повсюду, и при правильном анализе они могут дать потрясающие сведения.
 Статистика и формулы вероятности 9 класса помогают осмыслить данные и сделать из них логические выводы.
Статистика и формулы вероятности 9 класса помогают осмыслить данные и сделать из них логические выводы.
Советы по запоминанию математических формул для 9 класса
- Чтобы хорошо усвоить математические формулы для 9 класса, необходимо использовать их в различных задачах. Чем больше студенты будут практиковаться, тем легче будет запоминать эти формулы на кончиках пальцев.
- Учащиеся могут получить изображения формул из онлайн-ресурсов. Они могут установить их в качестве заставки или обоев на своих цифровых устройствах. Таким образом, всякий раз, когда они будут использовать свое устройство, им будет предложено просмотреть формулы в течение дня, что приведет к быстрому пересмотру.
- Учащиеся могут заниматься со своими друзьями, что не только поможет им развеять сомнения друг с другом, но и облегчит процесс обучения благодаря обмену идеями.
Примеры математических формул для класса 9
Пример 1: Упростите следующее выражение: (3 + √7)(3 — √7)
Решение: Используя формулу, (a + b)(a — b) = a 2 — b 2
Мы можем решить это как (3 + √7)(3 — √7) = 9 — 7 = 2
Пример 2 : Здание школы должно поддерживаться цилиндрическими колоннами. Если высота столбов = 10 м, а радиус столба = 20 см, сколько бетона потребуется для изготовления 7 цилиндрических столбов?
Если высота столбов = 10 м, а радиус столба = 20 см, сколько бетона потребуется для изготовления 7 цилиндрических столбов?
Решение: Чтобы узнать, сколько бетона необходимо, нам нужно найти объем цилиндра, а затем умножить его на количество необходимых цилиндров.
Мы знаем, что объем цилиндра = πr 2 ч
итак, подставляя значения радиуса = 0,2 м и высоты = 10 м, получаем
= 22/7 х 0,2 х 0,2 х 10
= 8.8 / 7 = 1,257 м 3
Поскольку необходимо 7 столбов, необходимая чистая бетонная смесь составляет
.
8,8/7×7 = 8,8 м 3
Учащиеся могут загрузить распечатанный лист математических формул для 9-го класса снизу:
Часто задаваемые вопросы по математическим формулам для 9 класса
Каковы важные формулы по математике для 9 класса?
Математика класса 9 включает такие темы, как система счисления, многочлены в алгебре, объемная геометрия, статистика и вероятность. Некоторые из важных формул из этих тем можно увидеть ниже:
Некоторые из важных формул из этих тем можно увидеть ниже:
Какие основные формулы в математике для 9 класса?
Основные формулы по математике для 9 класса относятся к системам счисления, алгебре, геометрии, статистике и вероятности. Запоминание основных объектов из системы счисления поможет учащимся лучше понять рациональные и иррациональные числа. Формулы разложения многочленов помогают находить корни уравнений. В геометрии важно, чтобы учащиеся запомнили основные формулы нахождения площади и объема различных форм и объектов.
Какие важные формулы изучаются в 9 классе Алгебры?
Важные формулы из курса алгебры 9 класса помогают продемонстрировать разницу между линейными, квадратичными и кубическими полиномами. Помимо основных формул факторизации многочленов, как указано ниже, учащимся рекомендуется пересмотреть важные концепции теоремы об остатках и теоремы о факторах, которые помогают определить факторы многочлена.
- (а + б) (а — б) = а 2 — б 2
- (а + b) 2 = а 2 + 2ab + b 2
- (a — b) 3 = a 3 — b 3 — 3ab(a — b)
Сколько формул в математике для 9 класса?
Существует около 30 важных математических формул для 9-го класса, которые, если их хорошо выучить, могут помочь учащимся в решении многих задач, потому что обычно большинство других формул являются производными от этих основных. Если мы посмотрим, сколько формул в каждой из тем математики в 9 классе, то получится следующее:
Если мы посмотрим, сколько формул в каждой из тем математики в 9 классе, то получится следующее:
- Система счисления состоит из 5 основных единиц, которые помогают учащимся понять взаимосвязь рациональных и иррациональных чисел.
- В алгебре 5 основных значимых формул объясняют концепцию факторизации, которая полезна при изучении алгебры для облегчения нахождения корней уравнений.
- Сегмент площади поверхности и объема имеет около 15 формул, охватывающих размеры параллелепипеда, сферы, цилиндра и конуса.
- Статистика и вероятность имеет 5 простых формул, которые помогают в статистическом анализе и предсказуемости событий в вероятности.
Как запомнить математические формулы для 9 класса?
Лучший способ запомнить математические формулы для 9-го класса — это попрактиковаться в решении задач, основанных на них. Это не только помогает понять использование и соответствующую релевантность всех формул, но также помогает избежать ненужного бремени их нагромождения.
Учащиеся также могут воспользоваться электронными заметками, доступными в Интернете.Они могут сохранить лист формул в качестве заставки для мобильного телефона или обоев рабочего стола. Это гарантирует, что каждый раз, когда они используют свой мобильный телефон или ноутбук, обои с формулой будут напоминать им о необходимости быстрого пересмотра в течение дня.
Ошибка проектирования или демонтажа — Headwaters Academy
Новая учебная программа по математике для 9-го класса: ошибка в разработке или разрушение передового опыта?
Министерство образования Онтарио недавно выпустило новую учебную программу по математике для 9 класса.Самым большим изменением, безусловно, стал отказ от потоковой передачи математики в 9 классе. Математика больше не будет предлагаться в «прикладном» и «академическом» потоках — вместо этого все учащиеся будут иметь одинаковый математический опыт.
Убедившись, что наши «продвинутые» ученики были немедленно зачислены в «академическую» программу по математике, я отправился посмотреть, что изменилось между старой программой и новой.
Положительные изменения
Во-первых, новый учебный план включает программирование как обязательный элемент обучения.Хотя мы не верим, что каждый учащийся будет создавать новые «приложения», мы приветствуем обучение каждого учащегося основам программирования.
Во-вторых, в новую учебную программу включена финансовая грамотность. Это долгое время было основой математического образования в Хедвотере, и никогда не было смысла в том, что школьная система Онтарио выпускала учеников, которые не понимали разницы между дебетом и кредитом.
Новая учебная программа по математике, однако, вызывает беспокойство тем, что часть мышления высшего порядка была удалена. В частности, я отмечаю, что учащимся больше не требуется манипулировать выражениями для решения задач, а также использовать свойства линейных уравнений для решения задач. Скорее, эти ожидания были сведены к «представлению» и «сравнению» линейных выражений (предположительно из заданных уравнений). В то же время новая учебная программа направлена на то, чтобы научить студентов «через решение задач» и тому, что «математика может быть субъективной».
В частности, я отмечаю, что учащимся больше не требуется манипулировать выражениями для решения задач, а также использовать свойства линейных уравнений для решения задач. Скорее, эти ожидания были сведены к «представлению» и «сравнению» линейных выражений (предположительно из заданных уравнений). В то же время новая учебная программа направлена на то, чтобы научить студентов «через решение задач» и тому, что «математика может быть субъективной».
Обеспокоенность новой учебной программой № 1 – ошибка в проекте
Концепция обучения математике «посредством решения задач» и «аутентичного опыта» похвальна.Однако, хотя математика окружает нас каждый день, она также чрезвычайно сложна. Возьмем, к примеру, проблему горнолыжного подъемника в этом выступлении на TED. Чтобы применить это понимание, скажем, на экскурсии в лыжном клубе Бивер-Вэлли, моим ученикам потребуются не только измерения, но и понимание тригонометрии и уклона (кстати, полностью отсутствующие в новом учебном плане). Таким образом, согласно приведенному выше выступлению на TED, у нас остается некачественный математический опыт, претендующий на «подлинность», но лишенный каких-либо проблем.
Таким образом, согласно приведенному выше выступлению на TED, у нас остается некачественный математический опыт, претендующий на «подлинность», но лишенный каких-либо проблем.
Обеспокоенность новой учебной программой № 2 — ликвидация превосходства?
Во-вторых, сказать, что «математика субъективна», значит с самого начала разрушить красоту математики. Мои ученики часто называют математику любимым предметом именно потому, что «правила не меняются». Бросать вызов истинам математики, которые самоочевидны в самой математике, обречено на провал. Это объяснялось необходимостью
« бросают вызов системам власти и привилегий как внутри, так и за пределами класса, чтобы устранить системные барьеры и помочь учащимся, принадлежащим к группам, которые исторически находились в неблагоприятном положении и недостаточно получали математическое образование .”
Я согласен с тем, что не каждому учащемуся средней школы понадобится математика или решение линейных уравнений в повседневной жизни.
 Алгебра, 9 класс: уроки, тесты, задания.
Алгебра, 9 класс: уроки, тесты, задания.
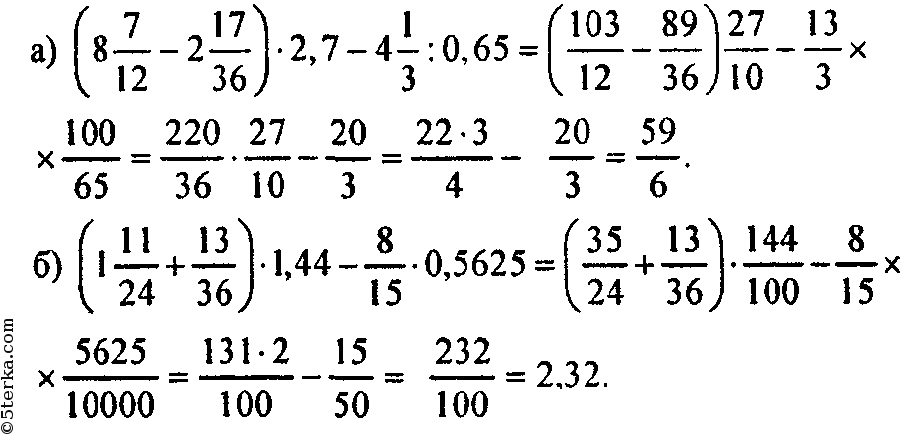 1
1  pdf
pdf  1
1  pdf
pdf  1
1