Контрольные работы по геометрии 9 класс (Атанасян)
|
Контрольная работа №1. Векторы. |
Контрольная работа №1. Векторы. |
|
Вариант 1. |
Вариант 2. |
|
1. ABCD – параллелограмм, Найдите разложение вектора по неколлинеарным векторам . 2. Дана трапеция ABCD с основаниями AD=20 и BC=8, О —точка пересечения диагоналей. Разложите вектор по векторам =и . 3. Диагонали ромба АС = а, BD = b. Точка K BD и BK : KD = 1 : 3. Найдите величину ||. 4. В равнобедренной трапеции острый угол равен 60, боковая сторона равна 12 см, большее основание равно 30 см. Найдите среднюю линию трапеции. 5. В прямоугольнике ABCD известно, что AD=a, DC=b, O точка пересечения диагоналей. Найдите величину |
1. ABCD – параллелограмм, Найдите разложение вектора по неколлинеарным векторам . 2. Дана трапеция ABCD с основаниями AD=15 и BC=10, О —точка пересечения диагоналей. Разложите вектор по векторам =и . 3. Диагонали ромба АС = а, BD = b. Точка K AC и AK : KC = 2: 3. Найдите величину ||. 4. В равнобедренной трапеции острый угол равен 60, боковая сторона равна 10 см, меньшее основание равно 14 см. Найдите среднюю линию трапеции. 5. В прямоугольнике ABCD известно, что AB=a, BC=b, O точка пересечения диагоналей. Найдите величину . |
Контрольная работа №2.
Метод координат.
Контрольная работа №2.
Метод координат.
Вариант 1.
Вариант 2.
1. Установите связь между векторами
2. Векторы разложены по неколлинеарным векторам и . Разложите векторы по векторам .
3. Четырехугольник имеет вершины с координатами А (1;1), В (3;5), С (9;-1), D(7;-5). Определите вид четырехугольника (с обоснованием) и найдите его диагонали.
4. Напишите уравнение окружности с центром в точке С (-3;1), проходящей через точку А (2;3).
5. Прямая l проходит через точки А (-3;1) и В (1;-7). Напишите уравнение прямой m, проходящей через точку С(5;6) и перпендикулярной прямой l.
1. Установите связь между векторами
2. Векторы разложены по неколлинеарным векторам и . Разложите векторы по векторам .
3. Четырехугольник имеет вершины с координатами А (-6;1), В (2;5), С (4;-1), D(-4;-5). Определите вид четырехугольника (с обоснованием) и найдите его диагонали.
4. Напишите уравнение окружности с центром в точке С (2;-3), проходящей через точку А (-1;-2).
5. Прямая l проходит через точки А (2;-1) и В (-3;9). Напишите уравнение прямой m, проходящей через точку С(3;10) и перпендикулярной прямой l.
Контрольная работа №3.
Соотношение между сторонами и углами треугольника. Скалярное произведение векторов.
Контрольная работа №3.
Соотношение между сторонами и углами треугольника. Скалярное произведение векторов.
Вариант 1.
Вариант 2.
1. Упростите выражение
2. В треугольнике АВС . Найдите площадь треугольника и радиус окружности, описанной около него.
3. В параллелограмме ABCD даны стороны АВ=4 см, AD=5 см и угол Найдите диагонали параллелограмма и его площадь.
4. Найдите координаты вектора , если а угол между вектором и положительным направлением оси абсцисс острый.
5. Вычислите скалярное произведение векторов , если
1. Упростите выражение
2. В треугольнике АВС . Найдите площадь треугольника и радиус окружности, описанной около него.
3. В параллелограмме ABCD даны стороны АВ=8 см, AD=3 см и угол Найдите диагонали параллелограмма и его площадь.
4. Найдите координаты вектора , если а угол между вектором и положительным направлением оси абсцисс тупой.
5. Вычислите скалярное произведение векторов , если
Контрольная работа №4. Длина окружности и площадь круга.
Контрольная работа №4. Длина окружности и площадь круга.
Вариант 1.
Вариант 2.
1. Три последовательные стороны четырехугольника, описанного около окружности, относятся как 3:4:5. Периметр этого четырехугольника равен 48 см. Найдите длины его сторон.
2. Около правильного шестиугольника описана окружность и в него вписана окружность. Длина большей окружности равна 4π. Найдите площадь кольца и площадь шестиугольника.
3. Хорда окружности равна и стягивает дугу в 90. Найдите длину дуги и площадь соответствующего сектора.
4. Найдите радиус сектора, если площадь соответствующего сегмента равна
.
5. В треугольник вписана окружность радиуса 3 см. Найдите длины сторон треугольника, если одна из них разделена точкой касания на отрезки длиной 4 см и 3 см.
1. Три последовательные стороны четырехугольника, описанного около окружности, относятся как 4:5:6. Периметр этого четырехугольника равен 80 см. Найдите длины его сторон.
2. Около правильного треугольника описана окружность и в него вписана окружность. Длина меньшей окружности равна 8π. Найдите площадь кольца и площадь треугольника.
3. Хорда окружности равна 6 и стягивает дугу в 60. Найдите длину дуги и площадь соответствующего сектора.
4. Найдите радиус сектора, если площадь соответствующего сегмента равна
.
5. В треугольник вписана окружность радиуса 4 см. Найдите длины сторон треугольника, если одна из них разделена точкой касания на отрезки длиной 4 см и 5 см.
Контрольная работа №5. Движения.
Контрольная работа №5. Движения.
Вариант 1.
Вариант 2.
1. Точка А (-2;3) симметрична точке А1 (6;-9) относительно точки В. Найдите координаты точки В.
2. Дан треугольник АВС с вершинами А(2;1), В(-6;1), С(-1;5). Треугольник А1В1С1 симметричен треугольнику АВС относительно прямой, заданной уравнением х=1. Найдите координаты вершин А1, В1, С1.
3. Найдите вектор параллельного переноса, при котором прямая у=3х-2 переходит в прямую у=3х+4, а прямая 3х+2у=2 переходит в прямую 6х+4у=3.
4. В результате поворота вокруг точки В(1;2) на 60 против часовой стрелки точка А(4;2) перешла в точку А1. Найдите координаты этой точки.
5. Прямая m задана уравнением 3х+2у-5=0. Прямая n симметрична прямой m относительно точки В(2;3). Напишите уравнение прямой n.
1. Точка А (-3;1) симметрична точке А1 (9;-5) относительно точки В. Найдите координаты точки В.
2. Дан треугольник АВС с вершинами А(-4;5), В(1;5), С(-3;-1). Треугольник А1В1С1 симметричен треугольнику АВС относительно прямой, заданной уравнением у=1. Найдите координаты вершин А1, В1, С1.
3. Найдите вектор параллельного переноса, при котором прямая у=2х-1 переходит в прямую у=2х+3, а прямая 2х+3у=1 переходит в прямую 4х+6у=5.
4. В результате поворота вокруг точки В(2;1) на 30 против часовой стрелки точка А(6;1) перешла в точку А1. Найдите координаты этой точки.
5. Прямая m задана уравнением 2х+3у-7=0. Прямая n симметрична прямой m относительно точки В(3;2). Напишите уравнение прямой n.
Контрольная работа №6.
Итоговая по программе 9 класса.
Контрольная работа №6.
Итоговая по программе 9 класса.
Вариант 1.
Вариант 2.
1. В параллелограмме ABCD точка E, AE:EC=1:5. Разложите вектор по векторам
2. Найдите косинус угла между векторами , если и угол между векторами равен 30.
3. Около круга радиусом R описан правильный шестиугольник. Найдите разность между площадью шестиугольника и круга.
4. Напишите уравнение окружности, симметричной относительно точки А (-1;3) окружности, заданной уравнением х2+у2-4х+6у=0
5. Первая окружность радиуса 4 см касается трех сторон прямоугольника. Вторая окружность касается первой внешним образом, а также касается сторон прямого угла. Найдите максимальный радиус второй окружности, если стороны прямоугольника равны 8 см и 12 см.
1. В параллелограмме ABCD точка E, BE:ED=1:4. Разложите вектор по векторам
2. Найдите косинус угла между векторами , если и угол между векторами равен 30.
3. Около круга радиусом R описан правильный треугольник. Найдите разность между площадью треугольника и круга.
4. Напишите уравнение окружности, симметричной относительно точки А (-2;3) окружности, заданной уравнением х2+у2+6х-4у=0
5. Первая окружность радиуса 9 см касается трех сторон прямоугольника. Вторая окружность касается первой внешним образом, а также касается сторон прямого угла. Найдите максимальный радиус второй окружности, если стороны прямоугольника равны 18 см и 20 см.
Контрольная работа № 7. Итоговая по курсу геометрии (7-9 классы)
Контрольная работа № 7. Итоговая по курсу геометрии (7-9 классы)
Вариант 1.
Вариант 2.
1. В равнобедренный треугольник с основанием 10 см и боковой стороной 5 см вписан квадрат так, что две его вершины лежат на основании, а другие две вершины – на боковых сторонах. Найдите сторону квадрата.
2. Найдите площадь круга, вписанного в ромб с диагоналями, равными 12 см и 16 см.
3. Найдите длину медианы ВМ треугольника АВС, если координаты вершин треугольника А (2;5), В (0;0), С(4;3).
4. Точка М является серединой боковой стороны АВ трапеции ABCD. Найдите площадь трапеции, если площадь треугольника MCD равна 28 см2.
5. Окружность радиуса 2 см, центр О которой лежит на гипотенузе АС прямоугольного треугольника АВС, касается его катетов. Найдите площадь треугольника АВС, если ОА= см.
1. В равнобедренный треугольник с основанием 14 см и боковой стороной 7 см вписан квадрат так, что две его вершины лежат на основании, а другие две вершины – на боковых сторонах. Найдите сторону квадрата.
2. Найдите площадь круга, вписанного в ромб с диагоналями, равными 16 см и 30 см.
3. Найдите длину медианы СР треугольника АВС, если координаты вершин треугольника А (-3;-2), В (-13;14), С(0;0).
4. Точка М является серединой боковой стороны АВ трапеции ABCD. Найдите площадь треугольника MCD, если площадь трапеции равна 38 см2.
5. Окружность радиуса 3 см, центр О которой лежит на гипотенузе АС прямоугольного треугольника АВС, касается его катетов. Найдите площадь треугольника АВС, если ОА= см.
infourok.ru
Материал по геометрии (9 класс) по теме: Контрольные работы по геометрии (9 кл.)
К — 3
Вариант 1
• 1. В АВС, А = 45, В = 60, ВС = 3.
Найдите АС.
2. Две стороны треугольника равны 7 см и 8 см, а
угол между ними равен 120. Найдите третью
сторону треугольника.
3. В АВС, АВ = ВС, САВ = 30, АЕ – биссектриса,
ВЕ = 8 см. Найдите площадь треугольника АВС.
К — 3
Вариант 1
• 1. В АВС, А = 45, В = 60, ВС = 3.
Найдите АС.
2. Две стороны треугольника равны 7 см и 8 см, а
угол между ними равен 120. Найдите третью
сторону треугольника.
3. В АВС, АВ = ВС, САВ = 30, АЕ – биссектриса,
ВЕ = 8 см. Найдите площадь треугольника АВС.
К — 3
Вариант 1
• 1. В АВС, А = 45, В = 60, ВС = 3.
Найдите АС.
2. Две стороны треугольника равны 7 см и 8 см, а
угол между ними равен 120. Найдите третью
сторону треугольника.
3. В АВС, АВ = ВС, САВ = 30, АЕ – биссектриса,
ВЕ = 8 см. Найдите площадь треугольника АВС.
К — 3
Вариант 1
• 1. В АВС, А = 45, В = 60, ВС = 3.
Найдите АС.
2. Две стороны треугольника равны 7 см и 8 см, а
угол между ними равен 120. Найдите третью
сторону треугольника.
3. В АВС, АВ = ВС, САВ = 30, АЕ – биссектриса,
ВЕ = 8 см. Найдите площадь треугольника АВС.
К — 3
Вариант 1
• 1. В АВС, А = 45, В = 60, ВС = 3.
Найдите АС.
2. Две стороны треугольника равны 7 см и 8 см, а
угол между ними равен 120. Найдите третью
сторону треугольника.
3. В АВС, АВ = ВС, САВ = 30, АЕ – биссектриса,
ВЕ = 8 см. Найдите площадь треугольника АВС.
К – 3
Вариант 2
• 1. В СДЕ, С = 30, Д = 45, СЕ = 5.
Найдите ДЕ.
2. Две стороны треугольника равны 5 см и 7 см, а
угол между ними равен 60. Найдите третью
сторону треугольника.
3. В ромбе АВСД, АК – биссектрису угла САВ,
ВАД = 60, ВК = 12 см. Найдите площадь ромба.
К – 3
Вариант 2
• 1. В СДЕ, С = 30, Д = 45, СЕ = 5.
Найдите ДЕ.
2. Две стороны треугольника равны 5 см и 7 см, а
угол между ними равен 60. Найдите третью
сторону треугольника.
3. В ромбе АВСД, АК – биссектрису угла САВ,
ВАД = 60, ВК = 12 см. Найдите площадь ромба.
К – 3
Вариант 2
• 1. В СДЕ, С = 30, Д = 45, СЕ = 5.
Найдите ДЕ.
2. Две стороны треугольника равны 5 см и 7 см, а
угол между ними равен 60. Найдите третью
сторону треугольника.
3. В ромбе АВСД, АК – биссектрису угла САВ,
ВАД = 60, ВК = 12 см. Найдите площадь ромба.
К – 3
Вариант 2
• 1. В СДЕ, С = 30, Д = 45, СЕ = 5.
Найдите ДЕ.
2. Две стороны треугольника равны 5 см и 7 см, а
угол между ними равен 60. Найдите третью
сторону треугольника.
3. В ромбе АВСД, АК – биссектрису угла САВ,
ВАД = 60, ВК = 12 см. Найдите площадь ромба.
К – 3
Вариант 2
• 1. В СДЕ, С = 30, Д = 45, СЕ = 5.
Найдите ДЕ.
2. Две стороны треугольника равны 5 см и 7 см, а
угол между ними равен 60. Найдите третью
сторону треугольника.
3. В ромбе АВСД, АК – биссектрису угла САВ,
ВАД = 60, ВК = 12 см. Найдите площадь ромба.
nsportal.ru
ГДЗ по геометрии 9 класс самостоятельные и контрольные работы Иченская
ГДЗ > Геометрия > 9 класс > Самостоятельные и контрольные работы по геометрии 9 класс. ФГОС Иченская Просвещение
Изображения обложек учебников приведены на страницах данного сайта исключительно в качестве иллюстративного материала (ст. 1274 п. 1 части четвертой Гражданского кодекса Российской Федерации)
- Для планомерной и эффективной подготовки к сдаче итоговой аттестации в 9-м классе (ОГЭ по математике) важно глубоко и полно проработать все темы входящих в экзамен дисциплин. Особенно много трудностей вызывают задания по геометрии. Проводя регулярный самостоятельный контроль своих знаний в течение года, девятиклассники будут более уверены, успешно подготовятся к испытанию.
- Хорошее учебное пособие, способное помочь в достижении такого результата — самостоятельные и контрольные работы по геометрии для 9 класса, рекомендуемые многими учителями-предметниками. Автор сборника – Иченская М. А., подошла к его созданию творчески, сбалансировав глубокую проработку сложных тем и отработку до автоматизма заданий, связанных с использованием базовых аксиом и теорем по геометрии.
- Материалы позволяют понять, какие именно тематики вызывают наибольшие вопросы, проблемы и проработать их максимально подробно. Для тех, кто использует пособие в целях самостоятельной подготовки, необходим решебник к нему. День за днем отрабатывая решения по нему, девятиклассники поймут логику получения верных ответов. Также они научатся грамотно, правильно записывать их. От того, насколько верной будет запись, в немалой степени зависит итоговая оценка на ОГЭ.
КР-1. Глава X. Метод координат:
КР-2. Глава XI. Соотношения между сторонами и углами треугольника:
КР-3. Глава XII. Длина окружности и площадь круга:
КР-4. Глава XIII. Движения:
КР-5. Итоговая контрольная работа:
С-1. Координаты вектора:
С-2. Простейшие задачи в координатах:
С-3. Уравнения окружности и прямой:
С-4. Синус, косинус, тангенс угла:
С-5. Соотношения между сторонами и углами треугольника:
С-6. Скалярное произведение векторов:
С-7. Правильные многоугольники:
С-8. Длина окружности и площадь круга:
С-9. Понятие движения:
С-10. Параллельный перенос и поворот:
С-11. Решение задач:
С-12. Решение задач:
С-13. Решение задач:
1. Треугольники:
2. Четырехугольники:
3. Окружность. Правильные многоугольники:
www.euroki.org
Контрольные работы по геометрии 9 класс (Атанасян Л.С.)
Г- 9 Итоговая контрольная работа
Вариант 1
1. В треугольнике АВС точка D – середина стороны АВ, точка М – точка пересечения медиан.
а) Выразите вектор  через векторы
через векторы  и
и  и вектор
и вектор  через векторы
через векторы  и
и  .
.
б) Найдите скалярное произведение  , если
, если
2. Даны точки А(1; 1), В(4; 5), С(-3; 4).
а) Докажите, что треугольник АВС равнобедренный и прямоугольный.
б) Найдите длину медианы СМ.
3. В треугольнике АВС высота ВD равна h.
а) Найдите сторону АС и радиус R описанной окружности.
б) Вычислите значение R, если
4. Хорда окружности равна а и стягивает дугу в 120о. Найдите: а) длину дуги; б) площадь сектора, ограниченного этой дугой и двумя радиусами.
Итоговая контрольная работа
Вариант 2
1. В параллелограмме АВСD диагонали пересекаются в точке О.
а) Выразите вектор  через векторы
через векторы  и
и  и вектор
и вектор  через векторы
через векторы  и
и  .
.
б) Найдите скалярное произведение  , если
, если
2. Даны точки К(0; 1), М(-3; -3), N(1; -6).
а) Докажите, что треугольник KMN равнобедренный и прямоугольный.
б) Найдите длину медианы NL.
3. В треугольнике АВС высота ВD равна h.
а) Найдите сторону АD и радиус R описанной окружности.
б) Вычислите значение R, если
4. Хорда окружности равна а и стягивает дугу в 60о. Найдите: а) длину дуги; б) площадь сектора, ограниченного этой дугой и двумя радиусами.
infourok.ru
|
Контрольная работа № 1. Векторы |
|
|
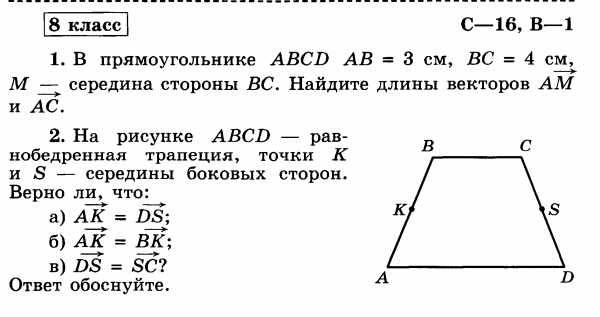
1 вариант. 1. Начертите два неколлинеарных вектора и . Постройте векторы, равные: а) ; б) 2. На стороне ВС ромба АВСD лежит точкаК такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы через векторы и . 3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции. 4.* В треугольнике АВС О – точка пересечения медиан. Выразите вектор через векторы и . |
2 вариант 1. Начертите два неколлинеарных вектора и . Постройте векторы, равные: а) ; б) 2. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы через векторы и 3. В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции. 4. * В треугольнике МNK О – точка пересечения медиан, . Найдите число k. |
|
Контрольная работа № 2. Метод координат. |
|
|
1 вариант. 1. Найдите координаты и длину вектора , если . 2. Напишите уравнение окружности с центром в точкеА (- 3;2), проходящей через точку В (0; — 2). 3. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N (2; 4), К (2; — 2). а) Докажите, что Δ- равнобедренный; б) Найдите высоту, проведённую из вершины М. 4. * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( — 1; 3 ) и К( 0; 2 ). |
2 вариант. 1). Найдите координаты и длину вектора , если . 2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ). 3). Треугольник СDЕ задан координатами своих вершин: С (2; 2), D (6; 5), Е (5; — 2). а) Докажите, что Δ- равнобедренный; б) Найдите биссектрису, проведённую из вершины С. 4. * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; — 3 ) и С( 2; 0 ). |
|
Контрольная работа № 3. Соотношения между сторонами и углами треугольника. |
|
|
1 вариант
В = 600, ВС = Найдите АС.
7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
|
2 вариант
D = 450, СЕ =Найдите DE.
5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
|
|
Контрольная работа № 4. Длина окружности и площадь круга. |
|
|
1 вариант 1. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 2. Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 1200. Чему равна площадь соответствующего данной дуге кругового сектора? 3. Периметр правильного треугольника, вписанного в окружность, равен Найдите периметр правильного шестиугольника, описанного около той же окружности. |
2 вариант 1. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см. 2. Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора? 3. Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность. |
|
Контрольная работа № 5. Движения. |
|
|
1 вариант 1. Начертите ромб АВСD. Постройте образ этого ромба: а) при симметрии относительно точки С; б) при симметрии относительно прямой АВ; в) при параллельном переносе на вектор ; г) при повороте вокруг точки D на 600 по часовой стрелке. 2. Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр. 3. * Начертите два параллельных отрезка, длины которых равны.начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой. |
2 вариант 1. Начертите параллелограмм АВСD. Постройте образ этого параллелограмма: а) при симметрии относительно точки D; б) при симметрии относительно прямой CD; в) при параллельном переносе на вектор ; г) при повороте вокруг точки А на 450 против часовой стрелки. 2. Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей. 3.* Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой. |
nsportal.ru
КР геометрия 9 класс (Атанасян)
Просмотр содержимого документа
«Итоговая контрольная работа НН»
Г- 9 Итоговая контрольная работа
Вариант 1
1. В треугольнике АВС точка D – середина стороны АВ, точка М – точка пересечения медиан.
а) Выразите вектор  через векторы
через векторы 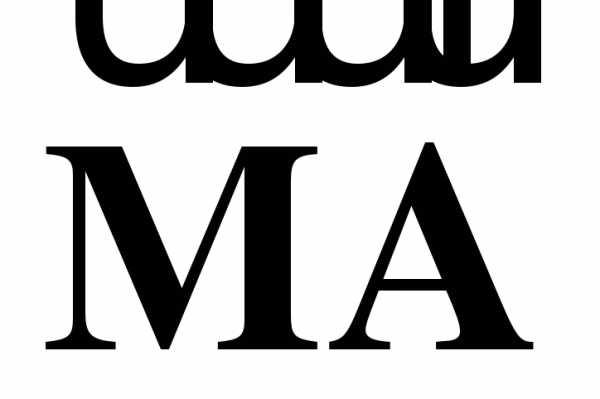 и
и 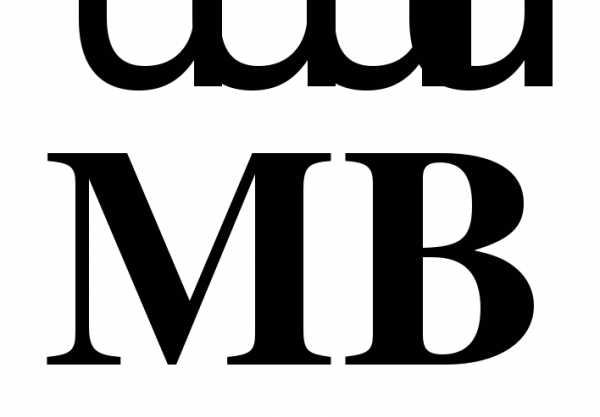 и вектор
и вектор 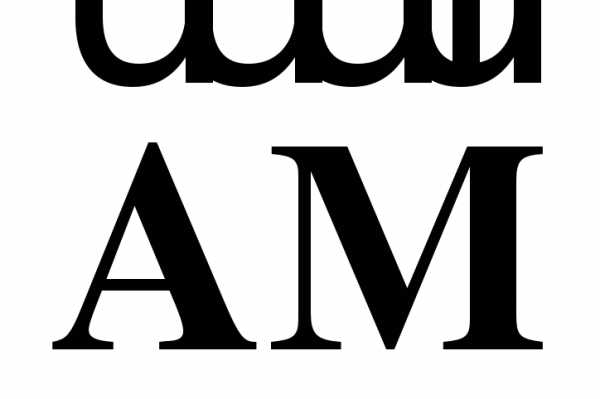 через векторы
через векторы  и
и  .
.
б) Найдите скалярное произведение  , если
, если
2. Даны точки А(1; 1), В(4; 5), С(-3; 4).
а) Докажите, что треугольник АВС равнобедренный и прямоугольный.
б) Найдите длину медианы СМ.
3. В треугольнике АВС высота ВD равна h.
а) Найдите сторону АС и радиус R описанной окружности.
б) Вычислите значение R, если
4. Хорда окружности равна а и стягивает дугу в 120о. Найдите: а) длину дуги; б) площадь сектора, ограниченного этой дугой и двумя радиусами.
Итоговая контрольная работа
Вариант 2
1. В параллелограмме АВСD диагонали пересекаются в точке О.
а) Выразите вектор 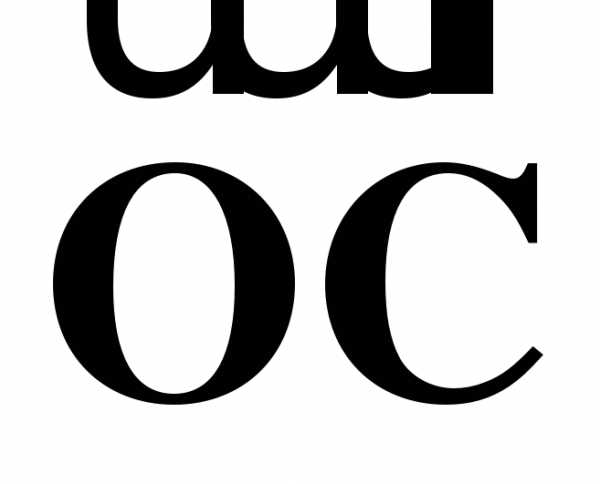 через векторы
через векторы  и
и  и вектор
и вектор  через векторы
через векторы  и
и  .
.
б) Найдите скалярное произведение 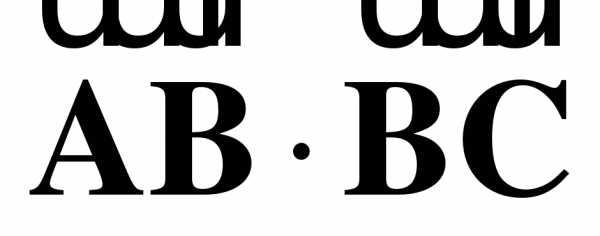 , если
, если
2. Даны точки К(0; 1), М(-3; -3), N(1; -6).
а) Докажите, что треугольник KMN равнобедренный и прямоугольный.
б) Найдите длину медианы NL.
3. В треугольнике АВС высота ВD равна h.
а) Найдите сторону АD и радиус R описанной окружности.
б) Вычислите значение R, если
4. Хорда окружности равна а и стягивает дугу в 60о. Найдите: а) длину дуги; б) площадь сектора, ограниченного этой дугой и двумя радиусами.
Просмотр содержимого документа
«Контрольная работа № 2 Соотношения между сторонами и углами треугольника НН»
Просмотр содержимого документа
«Контрольная работа №1 Метод координат НН»
Г — 9 Контрольная работа № 1
Метод координат
Вариант 1
1.Найдите координаты и длину вектора  если
если  , .
, .
2. Даны координаты вершин треугольника ABC: A (-6; 1), B (2; 4), С (2; -2).
Докажите, что треугольник ABC равнобедренный, и найдите высоту треугольника, проведенную из вершины A.
3. Окружность задана уравнением . Напишите уравнение прямой, проходящей через её центр и параллельной оси ординат
.4. Напишите уравнение окружности с центром в точке А (- 1;4), проходящей через точку
В (3; — 1).
5. * Найдите координаты точки F, лежащей на оси абсцисс и равноудалённой от точек N и M, если N( — 2; 1 ) и M( 0; 3 ).
Контрольная работа № 1
Метод координат
Вариант 2
1.Найдите координаты и длину вектора  если
если
2. Даны координаты вершин четырехугольника ABC D: A (-6; 1), B (0; 5), С (6; -4),D (0; -8).
Докажите, что ABCD – прямоугольник, и найдите координаты точки пересечения его диагоналей.
3. Окружность задана уравнением Напишите уравнение прямой, проходящей через её центр и параллельной оси абсцисс.
4. Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку
D ( 5; 5 ).
5. * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; — 3 ) и С( 2; 0 ).
Просмотр содержимого документа
«Контрольная работа №3 Длина окружности и площадь круга НН»
Просмотр содержимого документа
«Контрольная работа №4 Движения НН»
multiurok.ru
Контроль знаний и умений по геометрии 9 класс (УМК Л.С. Атанасян)
Самостоятельные и контрольные работы по геометрии для 9 класса (по УМК Л.С. Атанасян)
1 вариант
С.р №1 «Понятие вектора»
С.р. №2 «Сложение и вычитание векторов»

С.р. №3 «Умножение вектора на число»

С.р. №4 «Умножение вектора на число»

С.р.№5 «Координаты вектора»

С.р.№6 «Простейшие задачи в координатах»

С.р.№7 «Уравнение окружности и прямой»

С.р.№8 «Определение синуса, косинуса, тангенса»
С.р. №9 «Решение треугольников»
С.р.№10 «Косинус угла. Скалярное произведение»
С.р.№11 «Правильные многоугольники»

С.р.№12 «Длина окружности. Площадь круга»

С.р.№13 «Движение»
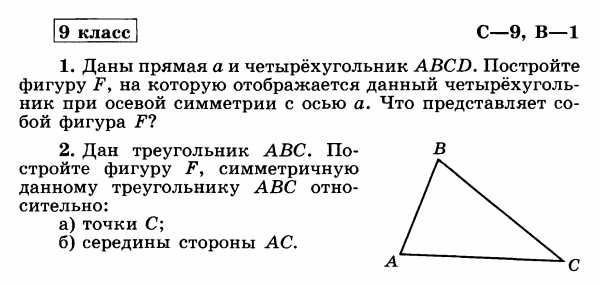
С.р.№14 «Параллельный перенос. Поворот»


С.р. №16 Решение задач

С.р. №17 Решение задач
Контрольные работы 1 вариант

К.р. №2

К.р.№3

К.р.№4

К.р №5

infourok.ru