9 класс самостоятельные и контрольные работы по геометрии: ГДЗ по геометрии 9 класс самостоятельные и контрольные работы Иченская Просвещение ответы и решения онлайн Самостоятельные работы, С-1. Координаты вектора. Задание: Вариант 2

Контрольные и самостоятельные работы по алгебре и геометрии 9 класс

АЛГЕБРА

САМОСТОЯТЕЛЬНЫЕ РАБОТЫ

KBАДРАТИЧНАЯ ФУНКЦИЯ

C1. Функции и их свойства

C2. Квадратный трехчлен

C3. График квадратичной функции

C4. Квадратичная функция: задачи с параметрами (домашняя самостоятельная работа)

C5. Решение квадратичных неравенств

C6. Решение неравенств методом интервалов

УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ

C7. Решение целых уравнений

C8. Уравнения высших степеней: методы решения, задачи с параметрами (домашняя самостоятельная работа)

C9. Решение систем уравнений второй степени

C10. Решение задач с помощью систем уравнений. Графическое решение систем

C11. Системы рациональных уравнений, (домашняя самостоятельная работа)

АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ

C12. Арифметическая прогрессия. Формула n-го члена

C13. Формула суммы n первых членов арифметической прогрессии

C14.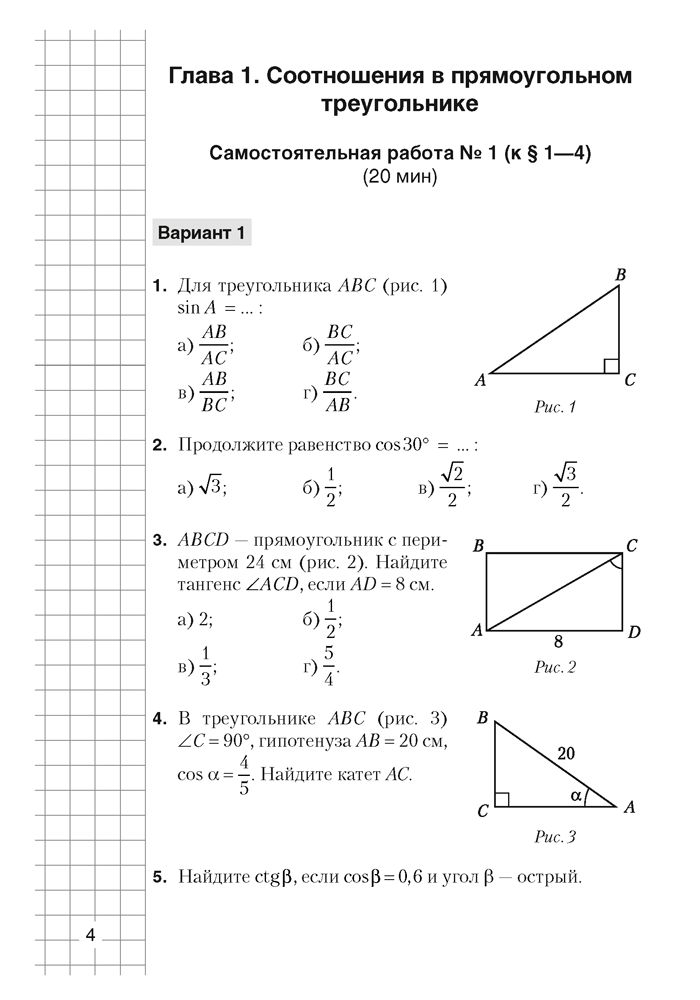 Геометрическая прогрессия. Формула n-го члена

C15. Формула суммы первых n членов геометрической прогрессии. Бесконечная геометрическая прогрессия

C16. Комбинированные задачи на прогрессии (домашняя самостоятельная работа)

СТЕПЕНЬ ЧИСЛА

C17. Четные и нечетные функции. Функция у = xn

C18. Корень n-й степени и его свойства

C19. Определение и свойства степени с дробным показателем

C20. Преобразование степенных выражений с рациональными показателями

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ

C21. Элементы комбинаторики

C22. Начальные сведения из теории вероятностей

C23. Элементы статистики и теории вероятностей

ТРИГОНОМЕТРИЧЕСКИЕ ВЫРАЖЕНИЯ И ИХ ПРЕОБРАЗОВАНИЯ

C24. Определение тригонометрических функций

C25. Свойства тригонометрических функций. Радианная мера угла

C26. Тригонометрические тождества и их применение

C27. Формулы приведения

C28. Формулы сложения

C29. Формулы двойного угла

C30. Формулы суммы и разности тригонометрических функций

C31. Дополнительные тригонометрические задачи (домашняя самостоятельная работа)

КОНТРОЛЬНЫЕ РАБОТЫ

К1. Квадратичная функция

К2. Решение неравенств

К3. Целые уравнения и системы уравнений

К4. Арифметическая прогрессия

К5. Геометрическая прогрессия

К6. Степень с рациональным показателем

К7. Элементы комбинаторики и теории вероятностей

К8. Свойства тригонометрических функций. Тригонометрические тождества. Формулы приведения

К9. Формулы сложения и их следствия

К10. Итоговая контрольная работа

ГЕОМЕТРИЯ

САМОСТОЯТЕЛЬНЫЕ РАБОТЫ (по учебнику Л.C. Атанасяна и др.)

МЕТОД КООРДИНАТ

C1. Координаты вектора

C2. Простейшие задачи в координатах

C3. Уравнение окружности

C4. Уравнение прямой

C5. Применение векторов и координат к решению задач (домашняя самостоятельная работа)

СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

C6. Синус, косинус, тангенс угла

C7. Теорема о площади треугольника. Теорема синусов

C8. Теорема косинусов. Решение треугольников

C9. Скалярное произведение векторов

C10. Решение треугольников. Скалярное произведение (домашняя самостоятельная работа)

ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА

C11. Правильные многоугольники

C12. Длина окружности, площадь круга, площадь кругового сектора

ДВИЖЕНИЯ

C13. Понятие движения

C14. Параллельный перенос и поворот

КОНТРОЛЬНЫЕ РАБОТЫ (по учебнику Л.С. Атанасяна и др.)

K1. Метод координат

K2. Соотношение между сторонами и углами треугольника

K3. Длина окружности й площадь круга

K4. Движение

K5. Итоговая контрольная работа

САМОСТОЯТЕЛЬНЫЕ РАБОТЫ (по учебнику А.В. Погорелова)

ПОДОБИЕ ФИГУР

C1. Преобразование подобия и его свойства

C2. Признаки подобия треугольников

C3. Подобие прямоугольных треугольников. Свойство биссектрисы угла треугольника

C4. Подобие треугольников (домашняя самостоятельная работа)

C5. Теорема о вписанных углах и ее следствия

C6. Применение теоремы о вписанных углах и ее следствий в задачах (домашняя самостоятельная работа)

РЕШЕНИЕ ТРЕУГОЛЬНИКОВ

C7. Теорема косинусов. Соотношение диагоналей и сторон параллелограмма

C8. Теорема синусов и ее следствия

C9. Теоремы косинусов и синусов (домашняя самостоятельная работа)

МНОГОУГОЛЬНИКИ

C10. Выпуклый многоугольник

C11. Правильные многоугольники. Формулы для радиусов вписанных и описанных окружностей правильных многоугольников

C12. Длина окружности. Радианная мера угла

ПЛОЩАДИ ФИГУР

C13. Площадь прямоугольника, квадрата, параллелограмма

C14. Площадь треугольника

C15. Площадь трапеции, площадь четырехугольника

C16. Окружность и многоугольники (домашняя самостоятельная работа)

C17. Площади подобных фигур. Площадь круга и его частей

C18. Площади фигур (домашняя самостоятельная работа)

КОНТРОЛЬНЫЕ РАБОТЫ (по учебнику А.В. Погорелова)

K1. Подобие фигур

K2. Решение треугольников

K3. Многоугольники

K4. Площади фигур

K5. Итоговая контрольная работа

ОТВЕТЫ

АЛГЕБРА

САМОСТОЯТЕЛЬНЫЕ РАБОТЫ

КОНТРОЛЬНЫЕ РАБОТЫ

ГЕОМЕТРИЯ

САМОСТОЯТЕЛЬНЫЕ РАБОТЫ (по учебнику Л.С. Атанасяна и др.)

КОНТРОЛЬНЫЕ РАБОТЫ (по учебнику Л.С. Атанасяна и др.)

САМОСТОЯТЕЛЬНЫЕ РАБОТЫ (по учебнику А.В. Погорелова)

КОНТРОЛЬНЫЕ РАБОТЫ (по учебнику А.В. Погорелова)

ГДЗ решебник к самостоятельным и контрольным работам по алгебре (геометрии) 9 класс Ершова, Голобородько

Предлагаются ответы к самостоятельным и контрольным работам по алгебре (геометрии) 9 класса по материалам учебника, написанного авторами Ершовой А.П. и Голобородько В.В.. Решебник содержит ГДЗ для девятиклассников по темам школьного курса. Ученики, используя пособие, найдут подробно расписанные решения и ответы на все интересующие их задания, которые даются для самостоятельного выполнения и для контроля знаний. Издание показывает различные варианты работ по двум родственным дисциплинам. Грамотно используя данную книгу, учащийся сумеет добиться хороших успехов в изучении этих сложных точных наук.

Алгебра

Квадратичная функция
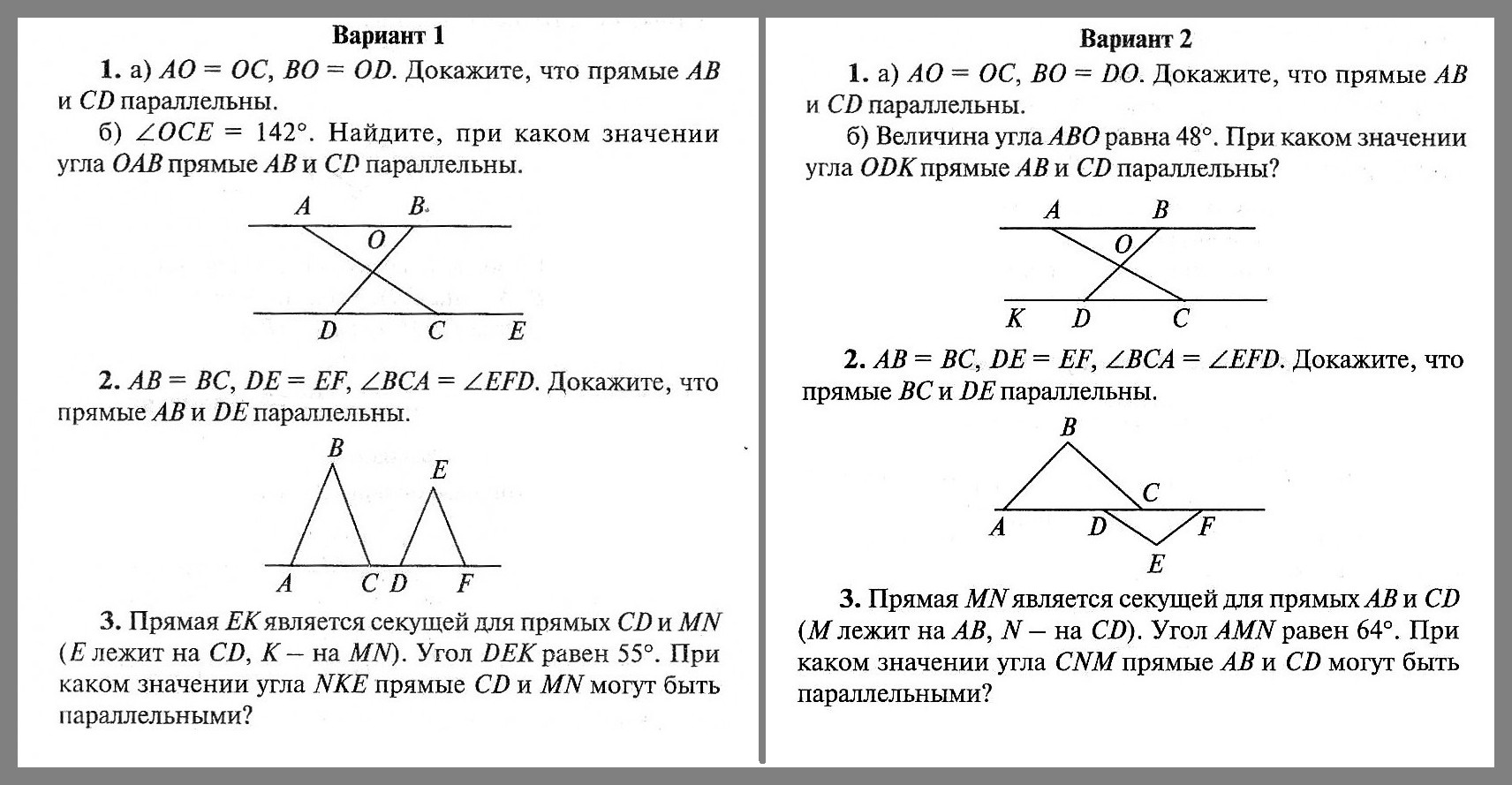
С-1. Функции и их свойства12345
С-2. Квадратный трехчлен1234567
С-3. График квадратичной функции123456789
С-4*. Квадратичная функция: задачи с параметрами (домашняя самостоятельная работа)
К-1. Квадратичная функция1234567891112131415
С-5. Решение квадратичных неравенств123456789101112
С-6. Решение неравенств методом интервалов12345678
К-2. Решение неравенств1234567891011121314151617181920212223
Уравнения и системы уравнений
С-7. Решение целых уравнений1234567891011
С-8*. Уравнения высших степеней: методы решения, задачи с параметрами (домашняя самостоятельная работа)
С-9. Решение систем уравнений второй степени1234567
С-10. Решение задач с помощью систем уравнений. Графическое решение систем1234567
С-11*. Системы рациональных уравнений (домашняя самостоятельная работа)
К-3. Целые уравнения и системы уравнений1234567891011
Арифметическая и геометрическая прогрессии
С-12. Арифметическая прогрессия. Формула n-ого члена123
С-13. Формула суммы п первых членов арифметической прогрессии1234
К-4. Арифметическая прогрессия123456
С-14. Геометрическая прогрессия. Формула n-ого члена1234
С-15. Формула суммы первых п членов геометрической прогрессии.1234
С-16*. Комбинированные задачи на прогрессии (домашняя самостоятельная работа)
К-5. Геометрическая прогрессия1234
Степень с рациональным показателем
С-17. Четные и нечетные функции. Функция У = *»123
С-18. Корень n-ой степени и его свойства123
С-19. Определение и свойства степени с дробным показателем123
С-20. Преобразование степенных выражений с рациональными показателями12
К-6. Степень с рациональным показателем12345
Тригонометрические выражения и их преобразования
С-21. Определение тригонометрических функций12
С-22. Свойства тригонометрических функций. Радианная мера угла12
С-23. Тригонометрические тождества и их применение123
С-24. Формулы приведения12
К-7. Свойства тригонометрических функций. 12345
С-25. Формулы сложения123
С-26. Формулы двойного угла123
С-27. Формулы суммы и разности тригонометрических функций12
К-8. Формулы сложения и их следствия12345
С-28*. Дополнительные тригонометрические задачи (домашняя самостоятельная работа)
К-9. Годовая контрольная работа12345678

Геометрия (по Погорелову)

Подобие фигур
СП-1. Преобразование подобия и его свойства123
СП-2. Признаки подобия треугольников123
СП-3. Подобие прямоугольных треугольников.123456
СП-4*. Подобие треугольников (домашняя самостоятельная работа)
КП-1. Подобие фигур1234567
СП-5. Теорема о вписанных углах и ее следствия1234567
СП-6*. Применение теоремы о вписанных углах и ее следствий в задачах (домашняя самостоятельная работа)
Решение треугольников
СП-7. Теорема косинусов. Соотношение диагоналей и сторон параллелограмма1234567
СП-8. Теорема синусов и ее следствия123456
СП-9*. Теоремы косинусов и синусов (домашняя самостоятельная работа)
КП-2. Решение треугольников1234567
Многоугольники
СП-10. Выпуклый многоугольник12345
СП-11. Правильные многоугольники.123456
СП-12. Длина окружности. Радианная мера угла1234567
КП-3. Многоугольники123456789101112
Площади фигур
СП-13. Площадь прямоугольника, квадрата, параллелограмма12345678910
СП-14. Площадь треугольника123456789
СП-15. Площадь трапеции. Площадь четырехугольника1234567891011
СП-16*. Окружность и многоугольник (домашняя самостоятельная работа)
СП-17. Площади подобных фигур. Площадь круга и его частей123456
СП-18*. Площади фигур (домашняя самостоятельная работа)
КП-4. Площади фигур1234567891011
КП-5. Годовая контрольная работа12345678910111213

ГЕОМЕТРИЯ (по Атанасяну)

Метод координат
СА-1. Координаты вектора12345
СА-2. Простейшие задачи в координатах123456
СА-3.Уравнение окружности1234567
СА-4.Уравнение прямой1234
С-5*. Применение векторов и координат к решению задач (домашняя самостоятельная работа)
КА-1. Метод координат123456789
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
СА-6.Синус, косинус, тангенс угла12345
СА-7.Теорема о площади треугольника.1234567
Теорема синусов
СА-8.Теорема косинусов. Решение треугольников12345678
СА-9.Скалярное произведение векторов1234567
СА-10*. Решение треугольников. Скалярное произведение (домашняя самостоятельная работа)
КА-2. Соотношение между сторонами и углами треугольника1234567891011
Длина окружности и площадь круга
СА-11. Правильные многоугольники123456
СА-12. Длина окружности, площадь круга, площадь кругового сектора123456789
КА-3. Длина окружности и площадь круга123456789
Движения
СА-13. Понятие движения12345
СА-14. Параллельный перенос и поворот123
КА-4. Движение123456
КА-5. Годовая контрольная работа1234567891011121314

Загрузка…

ГДЗ решебник по геометрии 7-9 класс Иченская, Атанасян Самостоятельные и контрольные работы

Геометрия 7-9 класс

Тип пособия: Самостоятельные и контрольные работы

Авторы: Иченская, Атанасян

Издательство: «Просвещение»

Когда нужен решебник

Применение «ГДЗ самостоятельные и контрольные работы по геометрии 7-9 класс Иченская (Просвещение)» зачастую не просто желательно, но даже необходимо. Например, если ученик пропустил одно или несколько занятий в классе, это вовсе не повод для беспокойства. Нужный материал можно наверстать дома с помощью ГДЗ. Пособие дает дополнительную возможность:

• лучше понять материал урока;
• выучить ключевые понятия;
• правильно выполнить задание;
• глубже познакомиться с изучаемым произведением.

Если ребенок регулярно проявляет невнимательность к словам учителя или плохо понимает тему, с помощью ГДЗ можно освоить упущенный материал без ущерба для успеваемости. Современный решебник это отличный шанс для ученика восполнить пробелы в знания.

Используйте ГДЗ правильно

Как нужно применять решебник, чтобы школьник смог извлечь из него максимальную пользу? Для этого необходимо пользоваться им наряду с учебником и тетрадью. Выполнив задание дома, ученик должен проверить его правильность по решебнику, вдумчиво исправить возможные ошибки, а затем уже переписать правильный вариант в чистовик. Только такая последовательность в выполнении домашних заданий воспитает в ребенке аккуратность и ответственность, а также поможет избежать бездумного списывания. Кроме того, пособие доступно в режиме онлайн, что соответствует формату дистанционного обучения. Это превращает Интернет из развлечения в мощный образовательный ресурс.

Эффективная подготовка к уроку

Школьные успехи напрямую зависят от качества домашней подготовки. «ГДЗ самостоятельные и контрольные работы по геометрии 7-9 класс Иченская М.А. (Просвещение)» поможет ученику справиться со всеми заданиями и полноценно подготовиться к уроку. Применяя решебник, ребенок получает возможность:

• самостоятельно проверить свои знания;
• усвоить главные моменты и повторить предыдущий материал;
• подтянуть оценки;
• чаще поднимать руку и активно участвовать в классной работе.

Издание содержит правильный ответ на каждое задание и упражнение. Сборник самостоятельных работ – один из дополнительных обучающих инструментов, который позволяет школьнику максимально погрузиться в предмет и запомнить как можно больше интересной и важной информации. Возникающие сложности можно легко преодолеть с помощью решебника. Онлайн ГДЗ всегда выручит в трудный момент.

Задачи с практическими содержанием по номерам

123456789101112

Итоговый зачет по курсу 7 класса

К-1К-2К-3К-4К-5К-6К-7К-8К-9К-10К-11К-12К-13К-14К-15К-16К-17К-18К-19К-20К-21

7 класс. Контрольная №1. Глава I. По теме: Начальные и геометрические сведения

В-1В-2

7 класс. Контрольная №2.

Глава II. По теме: Треугольники

В-1В-2

7 класс. Контрольная №3. Глава III. По теме: Параллельные прямые

В-1В-2

7 класс. Контрольная №4. Глава IV. По теме: Соотношения между сторонами и углами треугольника

В-1В-2

7 класс. Контрольная №5. Глава IV. По теме: Соотношения между сторонами и углами треугольника

В-1В-2

7 класс. Контрольная №6. Итог

В-1В-2

7 класс. Самостоятельная №1. По теме: Точка, прямые, отрезки

В-1В-2

7 класс. Самостоятельная №2. По теме: Луч и угол

В-1В-2

7 класс. Самостоятельная №3. По теме: Сравнение отрезков и углов

В-1В-2

7 класс. Самостоятельная №4. По теме: Измерение отрезков

В-1В-2

7 класс. Самостоятельная №5. По теме: Измерение углов

В-1В-2

7 класс. Самостоятельная №6. По теме: Перпендикулярные прямые. Смежные и вертикальные углы

В-1В-2

7 класс. Самостоятельная №7. По теме: Первый признак равенства треугольников

В-1В-2

7 класс.

Самостоятельная №8. По теме: Медианы, биссектрисы и высоты треугольника

В-1В-2

7 класс. Самостоятельная №9. По теме: Второй и третий признаки равенства треугольников

В-1В-2

7 класс. Самостоятельная №10. По теме: Задачи на построение

В-1В-2

7 класс. Самостоятельная №11. По теме: Признаки параллельности двух прямых

В-1В-2

7 класс. Самостоятельная №12. По теме: Аксиома параллельных прямых

В-1В-2

7 класс. Самостоятельная №13. По теме: Сумма углов треугольника

В-1В-2

7 класс. Самостоятельная №14. По теме: Соотношения между сторонами и углами треугольника

В-1В-2

7 класс. Самостоятельная №15. По теме: Прямоугольные треугольники

В-1В-2

7 класс. Самостоятельная №16. По теме: Построение треугольника по трем элементам

В-1В-2

7 класс. Самостоятельная №17. По теме: Решение задач

В-1В-2

Итоговый зачет по курсу 8 класса

К-1К-2К-3К-4К-5К-6К-7К-8К-9К-10К-11К-12К-13К-14К-15К-16К-17К-18К-19К-20К-21К-22К-23К-24К-25

8 класс.

Контрольная №1

В-1В-2

8 класс. Контрольная №2

В-1В-2

8 класс. Контрольная №3

В-1В-2

8 класс. Контрольная №4

В-1В-2

8 класс. Контрольная №5

В-1В-2

8 класс. Контрольная №6

В-1В-2

8 класс. Контрольная №7

В-1В-2

8 класс. Самостоятельная №1

В-1В-2

8 класс. Самостоятельная №2

В-1В-2

8 класс. Самостоятельная №3

В-1В-2

8 класс. Самостоятельная №4

В-1В-2

8 класс. Самостоятельная №5

В-1В-2

8 класс. Самостоятельная №6

В-1В-2

8 класс. Самостоятельная №7

В-1В-2

8 класс. Самостоятельная №8

В-1В-2

8 класс. Самостоятельная №9

В-1В-2

8 класс. Самостоятельная №10

В-1В-2

8 класс. Самостоятельная №11

В-1В-2

8 класс. Самостоятельная №12

В-1В-2

8 класс. Самостоятельная №13

В-1В-2

8 класс. Самостоятельная №14

В-1В-2

8 класс. Самостоятельная №15

В-1В-2

8 класс.

Самостоятельная №16

В-1В-2

8 класс. Самостоятельная №17

В-1В-2

8 класс. Самостоятельная №18

В-1В-2

8 класс. Самостоятельная №19

В-1В-2

8 класс. Самостоятельная №20

В-1В-2

8 класс. Самостоятельная №21

В-1В-2

Итоговый зачет по курсу 9 класса

К-1К-2К-3К-4К-5К-6К-7К-8К-9К-10К-11К-12К-13К-14К-15К-16К-17К-18К-19К-20К-21К-22К-23К-24К-25К-26

9 класс. Контрольная №1

В-1В-2

9 класс. Контрольная №2

В-1В-2

9 класс. Контрольная №3

В-1В-2

9 класс. Контрольная №4

В-1В-2

9 класс. Контрольная №5

В-1В-2

9 класс. Самостоятельная №1

В-1В-2

9 класс. Самостоятельная №2

В-1В-2

9 класс. Самостоятельная №3

В-1В-2

9 класс. Самостоятельная №4

В-1В-2

9 класс. Самостоятельная №5

В-1В-2

9 класс. Самостоятельная №6

В-1В-2

9 класс. Самостоятельная №7

В-1В-2

9 класс. Самостоятельная №8

В-1В-2

9 класс.

Самостоятельная №9

В-1В-2

9 класс. Самостоятельная №10

В-1В-2

9 класс. Самостоятельная №11

В-1В-2

9 класс. Самостоятельная №12

В-1В-2

9 класс. Самостоятельная №13

В-1В-2

Задачи с практическими содержанием по номерам: 1

Тревога первокурсников по математике предсказывает избегание STEM и низкую успеваемость в университете, независимо от математических способностей

Многие считают, что тревожность по математике является препятствием на пути к успеху в STEM ^1,2,3 . Однако предыдущие исследования, подтверждающие эту идею, на самом деле предоставили лишь ограниченные и косвенные доказательства того, что математическая тревожность связана с результатами STEM. Собирая показатели математической тревожности и математических способностей в начале учебы в университете, а также отслеживая объективные и всесторонние результаты STEM в течение четырех лет последующих данных стенограммы, мы показываем, что математическая тревожность, собранная у студентов первого семестра университета, проспективно предсказывает как реальный университет STEM участие и достижения в области STEM, даже с учетом индивидуальных различий в математических способностях. Эта работа демонстрирует четкую поддержку точки зрения о том, что математическая тревожность играет ключевую роль в подавлении результатов STEM. Эта работа также поддерживает и дополнительно информирует существующую теорию об академически значимых последствиях математической тревожности. Практические и теоретические последствия этих выводов, наряду с обсуждением их ограничений, подробно описаны ниже.

Насколько нам известно, текущие результаты предоставляют самые прямые и надежные доказательства на сегодняшний день, подтверждающие связь между математической тревожностью и двумя ее ранее предполагаемыми последствиями — избеганием и недостаточной успеваемостью в STEM.Ассоциации нулевого порядка показали устойчивые связи между математической тревожностью и математическими способностями, а также обоими результатами STEM (эффект нулевого порядка на рис. 1). Этот результат повторяет предыдущую работу, а также подчеркивает необходимость выявления уникального вклада математической тревожности и математических способностей в результаты STEM. Важно отметить, что мы выходим за пределы предыдущей работы, показывая связь между математической тревожностью и тем, что ни избегание STEM, ни неудовлетворительная успеваемость по STEM не могут быть просто отнесены к плохим математическим навыкам (уникальный эффект на рис. 1).Кроме того, сосредоточив внимание на исчерпывающем списке всех связанных с математикой курсов, которые студенты выбрали во время учебы в университете, а не на более узком наборе математических курсов, эта работа доказывает, что математическая тревожность связана как с избегание и неудовлетворительная успеваемость в STEM в более широком смысле. Другими словами, это поддерживает идею о том, что математическая тревожность может выступать в качестве барьера для результатов STEM , в отличие от просто математических результатов в более узком смысле.

Действительно, возможно неожиданно, мы обнаружили, что математические способности на самом деле не смогли предсказать уникальную дисперсию ни в участии, ни в достижениях STEM, когда учитывались индивидуальные различия в математической тревожности. Эти результаты показывают, что то, как учащиеся относятся к математике, помимо их объективных математических способностей, может быть особенно важно для принятия решений избегать или заниматься темами STEM, а также для академической успеваемости в этих областях. Таким образом, мы предполагаем, что будущие вмешательства, разработанные с целью улучшения результатов STEM, должны быть сосредоточены на математической тревожности как на ключевом рычаге воздействия.

Помимо практического значения, эти результаты также дают важную информацию для теории математической тревожности. Вывод о том, что математическая тревожность предсказывала индивидуальные различия в участии и достижениях в области STEM сверх математических способностей, предполагает, что математическая тревожность имеет отношение к результатам STEM независимо от уже хорошо задокументированных последствий математической тревожности для успеваемости по математике ^4,5,12,13 . Действительно, когда мы оценили, в какой степени связь между математической тревожностью и результатами STEM можно объяснить математическими способностями, мы обнаружили доказательства того, что математические способности составляют лишь относительно небольшую часть ассоциаций между математической тревожностью и результатами STEM (12. 6% за участие в STEM и 11,5% за достижение STEM; Рис. 2). И наоборот, математическая тревожность составляла 40,9% и 40,0% отношений между математическими способностями и участием в STEM и достижениями в STEM соответственно. Взятые вместе, эти результаты предполагают необходимость обновления наших представлений о конкретных способах и причинах, по которым математическая тревожность может негативно повлиять на результаты STEM.

Обычно считается, что избегание математики является следствием математической тревожности, но предыдущие данные, подтверждающие связь между математической тревожностью и избеганием связанного с математикой контента, были ограничены.Большая часть предыдущей работы, которая действительно существует, основана на ретроспективных ассоциациях между математической тревогой и избеганием STEM, где математическая тревога измеряется после поведения избегания, которое она призвана объяснить. Более того, в большинстве предыдущих работ не учитывались различия в математических способностях, так что было неясно, действительно ли тревога по отношению к математике связана с избеганием математики, или просто способность к математике приводит к избеганию математики. смежные области. Настоящая работа устраняет оба этих ограничения и показывает, что математическая тревожность предсказывает будущее избегание STEM сверх математических способностей.Объем настоящей работы также шире, чем предыдущая работа: мы показываем, что математическая тревожность предсказывает избегание курсов STEM, в широком смысле истолковываемых как курсы, связанные с математикой, выходя за рамки более ограниченного вывода предыдущей работы о том, что математическая тревожность связана с избеганием математики. курсы конкретно ⁵ . Таким образом, эти результаты являются одними из первых четких доказательств того, что люди с сильной математической тревожностью действительно избегают не только математических курсов, но и курсов STEM в целом. Кроме того, такое поведение избегания нельзя объяснить исключительно плохими математическими способностями.

Что касается достижений в области STEM (оценок), предыдущие исследователи предложили два основных способа воздействия математической тревожности на успеваемость. Согласно одному сообщению, боязнь математики со временем приводит к избеганию математики, и это избегание математики приводит к тому, что учащиеся не могут полностью развить свои математические навыки, что приводит к плохим математическим способностям ⁴ . Эти плохие математические способности затем наносят ущерб способности учащихся добиваться успеха в курсах, требующих математики. Однако этот отчет не может объяснить настоящие результаты — математическая тревожность предсказывала оценки STEM независимо от различий в математических способностях, что указывает на необходимость более прямой связи между математической тревожностью и достижениями в STEM.

Еще одна возможность, которая действует более прямым образом в режиме реального времени, заключается в том, что учащиеся с высоким уровнем математической тревожности испытывают усиление тревожности состояния в тот момент, когда им приходится выполнять математические задания. Это повышенное беспокойство затем кооптирует ресурсы рабочей памяти, которые необходимы для выполнения сложных математических задач ^1,4 , что приводит к снижению производительности. Чтобы это объяснение согласовывалось с нашим наблюдением о том, что математические способности не опосредовали связь между математической тревожностью и достижениями в области STEM, должно быть так, что онлайн-эффекты математической тревожности (т.э., вызывая повышенный уровень тревожности и беспокойства при столкновении с математикой) более выражены при реальной успеваемости, чем при лабораторных измерениях математических способностей. В противном случае онлайн-влияние математической тревожности на успеваемость по математике уже было бы зафиксировано в нашей лабораторной оценке математических способностей, которая, как мы уже отмечали, составляла лишь незначительную часть связи между математической тревожностью и оценками STEM (рис. 2). Таким образом, хотя наши данные не могут полностью исключить эту возможность, ниже мы предлагаем другое возможное объяснение нашего вывода о том, что тревожность по математике предсказывает оценки STEM независимо от математических способностей, которое фокусируется на избегании математики, но в другом масштабе, чем избегание математики. связанные курсы в целом.

Хотя наши результаты показывают, что тревожащиеся по математике учащиеся с большей вероятностью избегают курсов STEM, когда это возможно, важно отметить, что мы также показали, что это избегание курсов STEM не может объяснить наблюдаемую устойчивую связь между математической тревожностью и оценками STEM. Это связано с тем, что все модели с оценками STEM в качестве результата также включали % курсов STEM в качестве ковариации. Таким образом, решения высокого уровня избегать математических курсов — или то, что мы называем макроизбеганием математики — не могут объяснить плохие оценки по STEM.Вместо этого мы предлагаем, чтобы учащиеся с высоким уровнем математической тревожности могли принимать краткосрочные решения, чтобы избегать материалов, связанных с математикой, — случаи того, что мы называем микроизбеганием . Например, человек, сильно озабоченный математикой, может предпочесть уделять меньше усилий и внимания более связанным с математикой элементам курсов STEM, которые они изучают, что приводит к более низким оценкам по этим курсам. Важно отметить, что это объяснение не зависит от объективных математических способностей учащихся, а также от их долгосрочных решений записаться на большее или меньшее количество курсов STEM, что делает его согласующимся с наблюдаемой моделью результатов, демонстрирующей, что математическая тревожность предсказывает оценки STEM даже при контроле. за математические способности и количество курсов STEM, которые выбрали студенты.Вместо этого суть объяснения, сосредоточенного на «микроизбеганиях», больше фокусируется на том, как студенты предпочитают тратить свое ограниченное время и усилия на курсы, на которые они записываются. Эта идея имеет потенциально более широкое теоретическое значение, потому что в исследованиях математической тревожности часто обсуждается избегание математики как ее ключевое последствие, но исследователи редко дают более конкретную информацию о том, что на самом деле влечет за собой это избегание. В частности, решения высокого уровня избегать уроков или карьеры, связанных с математикой, и ежедневные (или даже ежеминутные) решения уделять меньше внимания на уроках математики или тратить меньше усилий на домашнее задание по математике часто обсуждаются взаимозаменяемо в разделе общий термин «избегание математики».

Мы должны отметить, что в прошлой работе Эшкрафта и его коллег было введено различие между типами уклонения от математики, которое похоже на различие между макро-избеганием и микро-избеганием, которое мы проводим здесь. В исследованиях Ashcraft and Faust ³¹ , например, исследователи обнаружили, что люди, озабоченные математикой, склонны жертвовать точностью в пользу скорости выполнения математических задач, что интерпретируется как форма «локального избегания математики» — компромисс между скоростью и точностью. предположительно отражает озабоченных математикой людей, решивших не тратить усилия на математическую задачу, которую их просят выполнить, вместо того, чтобы желать выполнить ее как можно скорее.Идея локального избегания математики (компромисс между скоростью и точностью при выполнении математических задач) в отличие от глобального избегания математики (полное избегание математических курсов и карьерного роста) также поднимается в некоторых более поздних работах Эшкрафта и его коллег ^{4, 31,32} . С одной стороны, мы считаем, что термины «макро-избегание», как описано здесь, и «глобальное избегание», как описано Эшкрафтом и его коллегами, в значительной степени являются синонимами. С другой стороны, в то время как «локальное избегание» математики до сих пор в литературе конкретно относилось к идее компромисса между скоростью и точностью при выполнении математических задач, здесь мы предлагаем идею «микроизбегания» математики, которая также включала бы релевантные академическое поведение, такое как уделение меньше внимания в классе, полный пропуск занятий, меньше учебы и т. д.Возвращаясь к нашей интерпретации связи между математической тревожностью и достижениями в области STEM (контроль математических способностей), если тревожно настроенные к математике люди склонны к микроизбеганию занятий на курсах, связанных с математикой, это снизит вероятность того, что они будут быть успешным в этих курсах.

Чтобы раскрыть эту гипотезу более подробно, отметим, что большая часть работ, связывающих математическую тревожность с избеганием математики (включая настоящую работу), была сосредоточена на поведении избегания высокого уровня (макроизбегании) — избегании занятий, специальностей и профессий, которые включить математику ^5,6,7,8,9 . Это можно противопоставить микроизбеганию математики, которое относится не к высокоуровневым решениям о том, следует ли следовать образовательным траекториям или карьере, связанным с математикой, а к мелкомасштабным решениям о том, сколько внимания уделять математике на уроках, как много усилий прикладывать к домашнему заданию по математике и так далее. Часто предполагается, что подобные микро-избегания поведения приводят к тому, что дети младшего возраста (которые, что важно, посещают математические курсы) не в состоянии полностью развить свои математические способности, заставляя учащихся меньше практиковаться (или менее эффективно практиковаться). ) с математикой со временем ^1,4,33,34 .Однако только недавно были проведены исследования, напрямую оценивающие, связана ли вообще математическая тревожность с микроизбеганием математики. Работа Пиззи и Кремера ³⁵ показала, что люди, озабоченные математикой, склонны отвлекать внимание от сложных математических формул, даже если от них не требуется никаких математических вычислений. Недавний набор исследований Choe, Jenifer et al. ³⁶ показали, что люди, озабоченные математикой, склонны избегать сложных математических вычислений, даже если это влечет за собой денежные затраты.В совокупности эти исследования предполагают, что математическая тревожность действительно может быть связана с микроизбеганием математики, но сами по себе они не предоставляют доказательств того, что такое микроизбегание может иметь место в реальном образовательном контексте. Одно недавнее исследование начало заполнять этот пробел, прямо задав вопрос, действительно ли страх перед математикой предсказывает количество внимания и усилий, которые учащиеся затрачивают на математических курсах ³⁷ . В этом исследовании исследователи обнаружили, что среди семиклассников тревожность по поводу математики предсказывала степень внимания учащихся на уроках математики, что, в свою очередь, предсказывало развитие их математических способностей.Умозрительно применяя этот вывод к настоящему исследованию, может случиться так, что математическая тревожность привела к тому, что студенты, зачисленные на курсы STEM, занимались или посещали субоптимально связанные с математикой материалы этих курсов, что, в свою очередь, может объяснить вариабельность оценок в этих курсах. курсы, помимо математических способностей и избегания содержания STEM на макроуровне. В целом, мы рассматриваем дальнейшее изучение микро-избегания математики как плодотворное направление для будущих исследований, которые пытаются понять возможные механизмы, с помощью которых математическая тревога влияет на академическую успеваемость.

В более широком смысле, при рассмотрении вопроса о том, почему тревожность по математике может предсказывать достижения в области STEM, а не математические способности, мы считаем полезным рассмотреть следующий вопрос: что определяет, насколько успешным будет студент в курсе STEM? Иногда существует тенденция предполагать, что успеваемость по курсу определяется просто тем, насколько «хорошо» учащийся усваивает материал курса, что делает акцент исключительно на способностях. Однако очевидно, что существует множество факторов, определяющих, насколько хорошо студент справляется с учебным курсом: как часто он посещает занятия, как часто он читает, как часто он учится, сколько внимания он уделяет каждой из этих вещей во время учебы. делать их.Эти типы поведения представляют собой то, что Экклс, Вигфилд и их коллеги называют «выборами, связанными с достижениями» ^38,39,40,41 . Конечно, существует гораздо больше факторов, определяющих успеваемость в рамках определенного класса, но ключевой момент здесь заключается в том, что то, что определяет окончательную оценку человека по курсу, возможно, определяется в такой же степени тем, сколько усилий он приложил к курсу, как и его существовавшие ранее способности в обучении. соответствующий домен. Здесь мы предполагаем, что математическая тревожность может предсказать достижение STEM помимо математических способностей, потому что математическая тревожность, скорее всего, будет напрямую связана с тенденцией избегать затрат усилий на курсах, связанных с математикой.

Следует отметить, что подход, использованный в этой статье, отличается от предыдущей работы по оценке степени, в которой тревожность по математике и оценки по математике в течение одного года обучения предсказывают тревожность по математике и оценки по математике в последующие годы (например, Meece, Wigfield и Eccles ⁶ ) в том смысле, что цель состояла не в том, чтобы оценить, как последние оценок по математическим курсам предсказывают достижения и уровни участия в будущих математических курсах наряду с математической тревожностью, а скорее как мера математических способностей предсказывает эти важные результаты наряду с математической тревогой. Предыдущая работа показала, что прошлые оценки, как правило, являются сильными предикторами будущих оценок ^6,38,39,40 . Тем не менее, важно спросить , почему прошлые успехи в учебе могут предсказать будущие успехи в учебе — в какой степени они обусловлены тем, что у учащихся есть установленный уровень способностей для такого рода курсов, и в какой степени это результат таких факторов, как усилие, которое студент решает потратить на этот курс? Собрав показатель математических способностей в начале университета вместе с нашим показателем математической тревожности, здесь мы смогли выделить ранее существовавшие различия в математических способностях как возможное объяснение различий в будущей успеваемости по STEM.Конечно, возможно, что прошлые трудности студентов, испытывающих тягу к математике, на математических курсах могут частично объяснить, почему они в первую очередь испытывают тягу к математике (обзор см. в Ramirez, Shaw, and Maloney ⁴² ). Важно, однако, то, что настоящие результаты показывают, что тревожность по математике была лучшим предиктором будущих достижений в области STEM, чем математические способности, предполагая, что, хотя тревожные по математике учащиеся в среднем имеют более низкие математические способности, чем их менее тревожные сверстники, эти существовавшие ранее различия в математические способности не могут объяснить, почему ученики, озабоченные математикой, в конечном итоге хуже учатся на курсах STEM. Это указывает на то, что действуют другие механизмы, и мы предполагаем, что описанные здесь виды поведения микроизбегания, относящиеся к классу, являются одним из таких механизмов.

В дополнение к оценке того, могут ли математические способности объяснить связь между математическими тревогой и результатами STEM, мы также исследовали противоположное: может ли математическая тревога объяснить ассоциации между математическими способностями и результатами STEM. Математические способности часто обсуждают как возможную путаницу для связи между математической тревожностью и реальными результатами, но противоположное — что математическая тревожность может на самом деле смешивать отношения между математическими способностями и реальными результатами — упоминается редко, но в принципе не менее вероятно.Наши результаты показали, что математическая тревожность составляет примерно 40% ассоциаций между математическими способностями и как участием, так и достижениями в области STEM (или примерно в 3-4 раза больше, чем математические способности могут объяснить ассоциации между математической тревожностью и результатами STEM). Эти результаты показывают, что, хотя математические способности действительно предсказывают различия в этих важных университетских результатах STEM, большую часть этих ассоциаций можно объяснить математической тревожностью. На практическом уровне это говорит о том, что вмешательства, направленные на повышение этих результатов STEM, возможно, игнорируют тревогу учащихся по поводу математики на свой страх и риск.

В более широком смысле, этот вывод имеет важное значение для предыдущей работы, связывающей различия в математических способностях с реальными результатами, такими как оценки, полученные на математических курсах ¹⁵ , карьера в STEM ^16,17,18 , а также уровень дохода и здоровье исходы ^19,20 . Точно так же, как мы указывали, что большая часть предыдущих работ, связывающих математическую тревожность с реальными результатами, не контролировала различия в математических способностях, подавляющее большинство работ, связывающих математические способности с этими важными реальными результатами, не учитывали различий. в математической тревоге.Хотя часть этих исследований контролировала другие математические установки, такие как математическая уверенность ¹⁹ , ни в одной из предыдущих работ не изучалась степень, в которой связь между математическими способностями и реальными результатами могла быть объяснена установками — положительными. или отрицательный — к математике. Наши нынешние результаты предполагают реальную возможность того, что многие ранее наблюдаемые связи между математическими способностями и реальными результатами могут быть, по крайней мере частично, объяснены негативным отношением к математике, а именно математической тревожностью.Таким образом, мы предлагаем будущим исследованиям пересмотреть некоторые из этих более ранних результатов, чтобы понять, в какой степени именно способности к математике, а не чувство беспокойства по отношению к математике, лучше объясняют эти различные результаты в реальном мире. Это не только проинформирует теорию о том, как математические способности и математическая тревожность формируют будущие результаты, но также позволит более целенаправленным вмешательствам больше сосредоточиться на математических способностях или тревожности в зависимости от того, на что указывают доказательства.

Настоящая работа также продемонстрировала, что математическая тревога независимо предсказала два ключевых академически значимых последствия — избегание математических курсов и неуспеваемость на них.Об этом свидетельствует обнаружение того факта, что тревожность по математике по-прежнему негативно предсказывала долю курсов STEM, которые студенты посещали, даже при контроле оценок STEM, и наоборот. Таким образом, прогностическое влияние математической тревожности на избегание STEM нельзя объяснить недавней низкой успеваемостью по STEM, и наоборот. Это говорит о том, что оба основных теоретизированных академических последствия математической тревожности — избегание курсовой работы по математике и неудовлетворительная успеваемость — действуют независимо друг от друга, формируя академические результаты, что указывает на необходимость постулировать отдельные потенциальные механизмы для объяснения этих несоизмеримых эффектов (как мы сделали в предыдущие разделы).Таким образом, с точки зрения вмешательства, может случиться так, что вмешательство, уменьшающее влияние математической тревожности на один результат (например, неудовлетворительная успеваемость по STEM), вряд ли уменьшит влияние математической тревожности на другой результат (избегание STEM). ). Несколько недавних вмешательств по поводу математической тревожности были сосредоточены не на непосредственном снижении уровня математической тревожности, а на смягчении негативного воздействия математической тревожности на успеваемость по математике. Например, экспрессивное письменное вмешательство, в котором учащиеся пишут о своих опасениях по поводу предстоящего теста по математике непосредственно перед его началом, направлено на то, чтобы помочь учащимся справиться с тревогой, вызванной математикой, перед тестом, и цель состоит в том, чтобы повысить результаты теста ^{. 43} .То же самое верно и для вмешательств, основанных на когнитивной переоценке, в которых участников просят думать о ситуации по-другому, чтобы снизить уровень сиюминутной тревоги ⁴⁴ . Даже если бы эти вмешательства были расширены и оказались эффективными для повышения оценок STEM, наш вывод о том, что математическая тревожность предсказывает избегание курсов STEM сверх оценок STEM, предполагает, что эти вмешательства вряд ли повлияют на решение учащихся записаться на большее количество курсов STEM. Настоящие результаты показывают, что для эффективного вмешательства, направленного на повышение как участия в STEM, так и достижений в области STEM у людей, испытывающих тревожность по математике, необходимо разработать меры, которые либо фокусируются отдельно на обоих этих результатах, либо пытаются напрямую снизить уровень математической тревожности.

Мы также обнаружили доказательства того, что отрицательная связь между математической тревожностью и оценками STEM была наиболее сильной среди учащихся с высокой успеваемостью по предметам, не связанным с STEM (рис. 3b). Этот результат подтверждает мнение о том, что математическая тревожность может помешать учащимся с высокими достижениями в реализации своего потенциала в STEM, предполагая, что математическая тревожность может быть особенно пагубным фактором «дырявого конвейера» в STEM, что, возможно, мешает талантливым учащимся добиться успеха на курсах STEM. .Одно из возможных объяснений этого вывода может заключаться в том, что для учащихся с высокой успеваемостью онлайн-негативное влияние математической тревожности на успеваемость может быть особенно заметным. Это согласуется с работой, показывающей, что учащиеся с высокими способностями чаще всего больше всего страдают от беспокойства и давления ²² . Другое возможное объяснение этого вывода связано с возможностью того, что математическая тревожность предсказывает оценки STEM в значительной степени за счет определения того, как учащиеся предпочитают тратить свое ограниченное время и ресурсы.Возможно, например, что учащиеся с высокими способностями, не связанными с STEM, и с высокой тревожностью по математике могут предпочесть посвящать больше своего ограниченного времени и усилий не-STEM и уделять меньше внимания предметам. курсы, на которые они зачислены, связаны с математикой.

Хотя это исследование направлено на устранение нескольких важных ограничений предыдущей работы, связывающей математическую тревожность с академическими результатами STEM, следует также отметить его собственные ограничения. В настоящем исследовании делается все возможное, чтобы исключить путаницу, контролируя несколько ковариат (включая математические способности, общую тревожность, рабочую память и оценки, отличные от STEM), а также решает предыдущие проблемы направленности, собирая нашу меру математической тревожности в начало пребывания студентов в университете до того, как были приняты решения о продолжении или отказе от STEM, и уровни успеваемости по курсам STEM (что делает невозможным, чтобы индивидуальные различия в результатах STEM на университетском уровне вызывали различия в математической тревожности). Тем не менее, дизайн по-прежнему принципиально корреляционный, что ограничивает нашу способность делать убедительные выводы о причинно-следственном влиянии математической тревожности на результаты STEM. Мы считаем, что эта работа убедительно свидетельствует о том, что математическая тревожность может играть причинную роль в определении результатов STEM, но необходима интервенционная работа, направленная на уменьшение влияния математической тревожности на эти результаты STEM, чтобы сделать окончательный вывод о том, что математическая тревожность может вызывать конкретные результаты. Результаты STEM мы рассмотрели здесь. Кроме того, это исследование было сосредоточено на студентах крупного государственного канадского университета, и в будущем необходимо будет провести работу, чтобы оценить, будут ли результаты обобщены на различные образовательные контексты.

Другим ограничением этой работы является то, что наша мера математических способностей — сложная ментальная арифметическая задача — не охватывает все возможные типы математических навыков (например, рассуждения о математике), которые могут повлиять на успех в курсах STEM. Как мы отметили в разделе «Методы», мы выбрали это в качестве критерия математических способностей, потому что все учащиеся, скорее всего, обладали необходимыми знаниями для выполнения задания (т. базового математического навыка, вероятно, будет широко применяться почти во всех типах специализированной математики, с которыми учащиеся могут столкнуться в любой дисциплине STEM.Более того, предыдущая работа показала, что способность к арифметике в уме является надежным предиктором способности к более сложной математике ^45,46 . Тем не менее, остается возможным, что способности к другим типам математических измерений могут частично объяснить связь между математической тревожностью и результатами STEM. Однако, учитывая связь между способностями к арифметике и более сложными математическими навыками, в этих более продвинутых математических навыках должно быть что-то конкретное, что объясняет связь между математической тревожностью и результатами STEM, которые не учитываются способностями к сложной ментальной арифметической задаче. мы использовали здесь.В будущем можно будет провести работу, чтобы выяснить, могут ли другие формы математических способностей объяснить прогностическую связь между математической тревожностью и результатами STEM, и такая работа улучшит наше теоретическое понимание связи между математической тревожностью и результатами STEM. Настоящая работа, однако, представляет собой важную демонстрацию того, что прогностическое влияние математической тревожности на университетские результаты STEM в значительной степени не зависит от ее влияния на трудный счет в уме.

В совокупности данные результаты представляют собой одно из самых убедительных на сегодняшний день доказательств того, что математическая тревожность, помимо математических способностей, служит барьером на пути к успеху в STEM по многим аспектам, подтверждая ключевые прогнозы, сделанные теорией математической тревожности.В частности, мы показываем, что прогностическое влияние на достижение STEM нельзя объяснить различиями в математических способностях, что побуждает к переоценке механизмов, с помощью которых математическая тревожность может привести к плохой успеваемости на курсах, связанных с математикой. Мы также приводим доказательства того, что математическая тревожность может фактически объяснить связь между математическими способностями и реальными результатами, предполагая, что математическая тревожность может спутать ранее наблюдаемые связи между математическими способностями и реальными результатами, которые в значительной степени игнорировали математическую тревожность.Более того, мы показываем, что математическая тревожность предсказывает достижение и участие в STEM независимо друг от друга, предполагая, что влияние математической тревожности на избегание и неудовлетворительную успеваемость в STEM может действовать через отдельные механизмы. Наконец, мы нашли доказательства того, что тревожность по математике особенно отрицательно влияет на достижения в области STEM у тех, у кого высокие оценки не по STEM. В целом, хотя это корреляционное исследование не может установить причинно-следственную роль математической тревожности в формировании участия и достижений в области STEM на университетском уровне, оно дает четкие теоретические основания для выделения ресурсов для проверки того, могут ли вмешательства, смягчающие негативные последствия математической тревожности при поступлении в университет, способствовать ее развитию. их результаты STEM.

Специальные службы VHHS, класс 9

АНГЛИЙСКИЙ — Академическая грамотность — Курс №: 9522L

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год ЗАЧЁТЫ: 1.0 ДРУГОЕ: Учащиеся могут продолжить развитие навыков чтения, повторно записавшись для получения оценок и зачётов.

Академическая грамотность предусматривает обучение в небольших группах и индивидуальное обучение для повышения уровня чтения учащихся. Программа предназначена для исправления навыков чтения и повышения уровня чтения учащихся, которые читают ниже уровня своего класса.Этот курс индивидуально структурирован, чтобы улучшить способность учащегося фонетически читать написанное слово, улучшить беглость чтения про себя, эффективно использовать стратегии понимания и улучшить словарный запас. Этот курс получает диплом об окончании, но не засчитывается в требования по английскому языку.
ПРЕДПОСЫЛКИ: Размещение

Академическая грамотность II — Курс №: 9529L

ОЦЕНКИ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год ЗАЧЕТ: 1.

0 ДРУГОЕ: Глобальный академический курс. Учащиеся могут продолжить развитие навыков чтения, повторно записавшись для получения оценок и зачетов.

Академическая грамотность предусматривает обучение в небольших группах и индивидуальное обучение для повышения уровня чтения учащихся. Программа предназначена для исправления навыков чтения и повышения уровня чтения учащихся, которые читают ниже уровня своего класса. Этот курс индивидуально структурирован, чтобы улучшить способность учащегося фонетически читать написанное слово, улучшить беглость чтения про себя, эффективно использовать стратегии понимания и улучшить словарный запас. Этот курс получает диплом об окончании, но не засчитывается в требования по английскому языку.

ПРЕДПОСЫЛКИ: Размещение

Академическая грамотность III — Курс №: 9533L

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год ЗАЧЁТЫ: 1.0 ДРУГОЕ: Учащиеся могут продолжить развитие навыков чтения, повторно записавшись для получения оценок и зачётов.

Академическая грамотность предусматривает обучение в небольших группах и индивидуальное обучение для повышения уровня чтения учащихся. Программа предназначена для исправления навыков чтения и повышения уровня чтения учащихся, которые читают ниже уровня своего класса.Этот курс индивидуально структурирован, чтобы улучшить способность учащегося фонетически читать написанное слово, улучшить беглость чтения про себя, эффективно использовать стратегии понимания и улучшить словарный запас. Этот курс получает диплом об окончании, но не засчитывается в требования по английскому языку.

ПРЕДПОСЫЛКИ: Размещение

АНГЛИЙСКИЙ – Лаборатория английского языка – Курс №: 9701R

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год КРЕДИТ: 1.0 ДРУГОЕ: Интенсивное письмо   

Лаборатория английского языка

предназначена для обучения четырем аспектам использования языка:  функциональным навыкам чтения, письма, разговорной речи и аудирования, и основана на предварительных знаниях каждого учащегося в области грамматики, словарного запаса, словоупотребления и механики письма. Журналистское письмо будет введено и включено в учебную программу. Студенты познакомятся с различными жанрами литературы с письменными упражнениями, связанными с чтением. Конкретные темы и цели могут варьироваться в зависимости от IEP учащегося.
ПРЕДПОСЫЛКИ: Размещение

АНГЛИЙСКИЙ — Литература и сочинение для первокурсников – Курс №: 9546L, 9646B

КЛАССЫ: 9 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год КРЕДИТ: 1.0 ДРУГОЕ: Интенсивное письмо    

Курс

«Литература и композиция для первокурсников» предназначен для улучшения навыков аудирования, чтения, разговорной речи, исследования и письма, а критическое мышление лежит в основе всех этих направлений.Студенты будут практиковать литературную интерпретацию через различные критические линзы. Особое внимание уделяется организации и корректуре письменной работы с помощью структуры предложений, абзацев и эссе, а также прямому обучению словарному запасу, грамматике и технике письма. Учащиеся также составят различные письменные работы, посвященные утверждениям и подкреплению этих утверждений текстовыми доказательствами. Курс «Литература и композиция для первокурсников» соответствует требованиям первого года обучения английскому языку.
ПРЕДПОСЫЛКИ: Размещение

ЗДОРОВЬЕ — Здоровье — Курс №: 9528LS

КЛАССЫ: 9, 10 ДЛИНА: 1 сем КРЕДИТ: 0,5

Здоровье — это семестровый курс, который студенты изучают вместо физического воспитания. Структура занятий делает упор на здоровье, ответственное принятие решений и планирование здорового образа жизни. Темы, которые изучают студенты, включают: психическое, эмоциональное и социальное благополучие, профилактическое образование, безопасность, просвещение по вопросам веществ, питание, контроль веса, сексуальное здоровье, стресс и управление стрессом.
ПРЕДПОСЫЛКИ: Размещение

ЗДОРОВЬЕ — Медицинские навыки — Курс №: 9702РФ, 9703РС

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: 1 сем (только 1-й семестр) КРЕДИТ: 0,5

Health Skills — это односеместровый курс, который студенты проходят вместо физического воспитания. Структура занятий делает упор на здоровье, ответственное принятие решений и планирование здорового образа жизни. Темы, которые изучают студенты, включают: психическое, эмоциональное и социальное благополучие, профилактическое образование, безопасность, просвещение по вопросам веществ, питание, контроль веса, сексуальное здоровье, стресс и управление стрессом.
ПРЕДПОСЫЛКИ: Размещение

МАТЕМАТИКА — Алгебра I, вариант 2 периода – курс №: 9502L

ОЦЕНКИ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год ЗАЧЕТ: 1.0 ДРУГОЕ: Соответствует 2 последовательным периодам. Требуется графический калькулятор TI-84+.

Algebra I 2 Period Option — это курс, предназначенный для студентов, не готовых к темпу однопериодного курса Algebra I. Темы включают свойства действительных чисел, решение уравнений и неравенств, линейные функции, системы уравнений, свойства показателей и экспоненциальных функций, многочлены и факторинг, квадратичные функции и уравнения, радикальные выражения и уравнения, рациональные выражения и функции, а также анализ данных и вероятность. .Акцент делается на решении проблем и построении математических аргументов. Этот курс соответствует компоненту алгебры I требований по математике для выпускников штата Иллинойс.
ПРЕДПОСЫЛКИ: Размещение

МАТЕМАТИКА — Алгебраические понятия — Курс №: 9594L

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год КРЕДИТ: 1.0

Курс

Algebraic Concepts предназначен для повторения основ математики и продолжения учебной программы, предшествующей алгебре, которая полностью подготовит учащихся к алгебре I в следующем году.Темы курса обычно включают линейные уравнения и системы уравнений, квадратичные уравнения и радикалы, вероятность и статистику, а также блок геометрии.
ПРЕДПОСЫЛКИ: Размещение

МАТЕМАТИКА — Математические приложения — Курс №: 9599L

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год КРЕДИТ: 1.0

Математические приложения будут рассматривать основы математики и продолжать развивать общие математические навыки в связи с навыками повседневной жизни взрослых, используя базовые математические навыки, понятия алгебры и геометрии. Примеры таких тем могут включать прошедшее время, деньги, составление бюджета, путешествия, навыки работы с календарем и другие ежедневные приложения.
ПРЕДПОСЫЛКИ: Размещение

МАТЕМАТИКА — Основы математики — Курс №: 9597L

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год КРЕДИТ: 1.0

Math Foundations предназначен для обучения общим математическим навыкам, расширения этих навыков за счет включения некоторых тем предварительной алгебры, алгебры и геометрии и использования этих навыков в различных практических, потребительских, деловых и профессиональных приложениях.Темы курса обычно включают числовую прямую, дроби, числовые операции, выражения и базовую геометрию.
ПРЕДПОСЫЛКИ: Размещение

НАУКА – Науки о Земле и космосе – Курс №: 9535L

ОЦЕНКИ: 9 или размещение ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год КРЕДИТ: 1.0

Науки о Земле и космосе — это лабораторный курс, посвященный наукам о Земле и космосе. Введение в курс расширяет базовые научные навыки учащихся (измерение, научный метод, построение графиков, структура материи) и сопровождается разделами по геологии, метеорологии и астрономии. Курс использует практический подход для развития правильной лабораторной техники и критического мышления, а также для подготовки студентов к будущим занятиям по естественным наукам.
ПРЕДПОСЫЛКИ: Размещение

СОЦИАЛЬНЫЕ ИССЛЕДОВАНИЯ — География — Курс №: 9506L, 9662B

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год КРЕДИТ: 1.0 ДРУГОЕ: Глобальный академический курс

География — введение в изучение людей мира и их образа жизни. Вводный раздел посвящен практическому использованию карт и глобусов, а также чтению, включая определение местоположения и географические данные.Оставшаяся часть курса посвящена изучению различных физических и культурных регионов мира. Каждый семестр требуется картографический/письменный исследовательский проект.
ПРЕДПОСЫЛКИ: Размещение

СОЦИАЛЬНЫЕ ИССЛЕДОВАНИЯ — Навыки географии — Курс №: 9707R

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год КРЕДИТ: 1.0

Навыки географии — это введение в изучение людей мира и их образа жизни. Вводный раздел посвящен практическому использованию карт и глобусов, а также чтению, включая определение местоположения и географические данные.Оставшаяся часть курса посвящена изучению различных физических и культурных регионов мира. Каждый семестр требуется картографический/письменный исследовательский проект.
ПРЕДПОСЫЛКИ: Размещение

СОЦИАЛЬНЫЕ ИССЛЕДОВАНИЯ – Навыки работы в правительстве США – Курс №: 9704RF, 9705RS 

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: 1 сем (только 1-й семестр) КРЕДИТ: 0,5

Навыки государственного управления США включают в себя основы Конституции Соединенных Штатов, управления штатами и местными органами власти, эволюционного развития политического процесса, а также прав и обязанностей граждан Соединенных Штатов.Для успешного завершения этого курса требуется завершение компонента обучения государственной обязательной службе.
ПРЕДПОСЫЛКИ: Размещение

СОЦИАЛЬНЫЕ ИССЛЕДОВАНИЯ — Навыки изучения истории США — Курс №: 9706R

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год КРЕДИТ: 1.

0

United States History Skills — это широкий обзор основных социальных, экономических, политических и культурных событий, концепций и тем, которые были в центре внимания в развитии Соединенных Штатов.Этот курс также включает акцент на грамотность и навыки письма за счет использования основных и дополнительных ресурсов. Исследовательская работа обязательна каждый семестр.
ПРЕДПОСЫЛКИ: Размещение

TUTORIAL — Учебное пособие — № курса: 9510L, 9600L, 9601L, 9602L

ОЦЕНКИ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год ЗАЧЕТ: 1.0 ДРУГОЕ: Оценки будут выставляться на кредитной/без кредитной основе. Студенты, получающие поддержку на основе непрямой регистрации/регистрации, не получают кредита.

Учебные курсы

предназначены для удовлетворения индивидуальных потребностей учащихся в IEP в академической, функциональной, социальной и / или поведенческой областях.Курс делает упор на развитие навыков самозащиты и решения проблем, а также оказывает академическую поддержку в выявленных областях дефицита. Учебные курсы предназначены для помощи учащимся, зачисленным на курсы общего и/или специального образования, и различаются по уровню поддержки, предоставляемой в зависимости от уровня самостоятельности учащегося.
ПРЕДПОСЫЛКИ: Размещение

ДОПОЛНИТЕЛЬНЫЕ КУРСЫ ПО СПЕЦИАЛЬНЫМ УСЛУГАМ — Стаж работы в школе — Курс №: 9595L

КЛАССЫ: 9, 10, 11, 12 ПРОДОЛЖИТЕЛЬНОСТЬ: Полный год КРЕДИТ: 0.5 за семестр /ДРУГОЕ: У студентов должна быть хорошая посещаемость.

Программа

In School Work Experience обеспечивает структурированный опыт работы в школе для соответствующих критериям учащихся со специальными услугами. Учащиеся работают в школьных офисах или над школьными проектами в классе. Акцент делается на следовании указаниям, соответствующем социальном взаимодействии с различными взрослыми и сверстниками, а также на развитии навыков до трудоустройства.
ПРЕДПОСЫЛКИ: Размещение

Регистрация | RPI INFO

Будучи студентом здесь, в Rensselaer, вам выдается «билет времени», который назначает вам определенное время, в течение которого вы можете зарегистрироваться на следующий семестр. Билет на время будет отправлен на ваш адрес электронной почты RPI за 2-3 недели до регистрации.

Время регистрации назначается на основе количества кредитных часов, которые вы заработали в качестве студента. Обратите внимание, что классы, которые все еще продолжаются, или курсы, которые были оценены как «незавершенные», засчитываются , а не  в счет заработанных кредитов.

Вы должны получить свой талон по электронной почте примерно за четыре недели до запланированного периода регистрации.В дополнение к назначению регистрации это сообщение электронной почты уведомляет вас о любых существующих задержках, которые могут помешать вам зарегистрироваться, если вы не разрешите их. Мы включили образец табеля ниже, чтобы дать вам лучший пример того, что вы можете увидеть в своем уведомлении по электронной почте.

Если вы не получили свой талон по электронной почте или потеряли его, вы можете найти идентичную информацию через Информационную систему для студентов (SIS). После входа в систему сначала выберите параметр  Меню студента  , затем  Просмотр статуса моей регистрации .

Табель учета рабочего времени указан по стандартному восточному времени США и отображается в военном/24-часовом формате. Вы можете зарегистрироваться в любое время после назначенного вам временного интервала в течение периода регистрации.

• Если вы не знакомы с представлением военного времени, время от 00:00 до 12:00 эквивалентно времени AM. Для времени между 12:01 и 23:59 вычтите 12, чтобы получить эквивалент времени PM (например, время 16:00 соответствует 16:00, время 19:30 соответствует 19:30).

Обязательно перепроверьте свою специальность, указанную в вашем расписании.Если ваша специальность не обновлена, вы должны подать форму изменения специальности в офис регистратора до регистрации!

• Обратите внимание, что некоторые студенты инженерных специальностей указаны как необъявленные инженеры до тех пор, пока они официально не заявят о своей специальности.

Математические обороты Любимое время дня

Я использовал математических оборотов в течение многих лет. После первых двух месяцев тревожных экспериментов это стало самым ожидаемым временем нашего дня.Каждый год я организовывал ротацию немного по-разному, в зависимости от потребностей и индивидуальности класса, но общий формат оставался неизменным. Эта система управления настолько проста, что мне не терпится поделиться ею с вами! Давайте сделаем математические вращения любимым временем дня!

Прежде чем я поделюсь с вами секретом, позвольте мне вернуться на несколько шагов назад…

На самом деле не существует «правильного» способа управлять математическими ротациями. Мне нравится делиться тем, что работает для меня, но я один человек! Вы эксперт в своем классе! Математические ротации должны и должны быть адаптированы к конкретным потребностям учителя в классе.Однако иногда я видел учителей, настолько увязших в «стратегиях» ротации, что их система могла соперничать с футбольной игрой. Мы все были здесь, верно?

Упростить

Мы можем упростить управление математическими ротациями с помощью двух мелочей:  Первая — это согласованность . Если вы понаблюдаете за каким-нибудь учителем в школе, то, скорее всего, если ротация по математике пройдет хорошо, у учеников будет последовательный распорядок .

Выбор системы управления ротацией и ее соблюдение является ключевым моментом.Помните, что может потребоваться пара дней недель, чтобы освоиться. Когда я представляю ротацию с учителями во время семинаров, первые несколько секунд каждой ротации немного сбивают с толку, и возникают вопросы. Это нормально. После того, как у нас есть пара вращений за плечами, мы переходим, как уверенная Бейонсе, когда ветер развевает наши волосы. Как только ваш распорядок установлен, контент становится фокусом.

Регулировка времени приращения ваших вращений , количества раундов и того, какие варианты выбора есть у учащихся, создает основу вашей системы. Я был полон решимости упростить эту задачу, поэтому создал редактируемую систему управления математическими ротациями! Просто перетащите свой выбор в круги группы, выберите приращение времени и количество раундов. Тогда нажмите играть! Учащиеся, которые борются с переходами, которым нужна визуальная подсказка или у которых есть трудности с управлением временем, могут извлечь выгоду из этой системы! Лично все трое описывают меня, учителя, несколько дней! Мне это нужно так же, как и студентам!

Найдите редактируемую доску для вращения по математике ЗДЕСЬ.Он также включает настенную версию, если технические вещи не являются вашим другом.

Посмотрите видео ниже, как легко его настроить! (В этом видео показана версия для управляемого чтения, но повороты настроены так же!)

Обычный

Напомним, первый шаг , согласованность формата. Используете ли вы мою систему ротации или другую, не важно. Найдите систему, которая соответствует вашему характеру и стилю обучения!

Давайте поговорим о приращениях времени и количестве оборотов.При выборе времени, затрачиваемого на каждое вращение, вы должны следить за своим классом. Тот факт, что вы хотели бы, чтобы ваши ротации длились 15 минут, не означает, что это подходит для этого класса, который находится перед вами в этом году. Основывайте время на естественной выносливости учащихся. Если день за днем ​​ученики беспокойны после 15 минут самостоятельности, значит, пора ужесточить темп. Сократите количество минут, чтобы увидеть повышенную срочность и лучшее качество работы. Вообще говоря, чем моложе студенты, тем короче ротации.Эта общность зависит от множества факторов, поэтому не переживайте, если у вас долгая ротация и молодые студенты. Не чини то, что не сломано!

Выбор вращения

(СПОЙ ЭТО со мной) «Давай поговорим о выборе, малышка , давай поговорим о ты и я . Давайте поговорим обо всех хороших и плохих вещах, которые могут быть… Давайте поговорим о ВЫБОР А-Б-О-У-Т!»

Шаг второй выбор и материалы .Я думал, что я замечательный учитель математики, когда в моем классе было 18 послушных и кротких учеников. У меня был выбор в изобилии и игры с одной стороны комнаты на другую. Когда в нашу комнату приходили гости, я была им рада. Затем, в следующем учебном году, у меня было 24 ученика со смесью личностей, которые варьировались от 90 253 беспокойных 90 254 до 90 253 бешеных 90 254 . Я использовал те же варианты и систему, что и годом ранее, и моим временем математической ротации была сцена из Экзорцизм .Мой счастливый мир управляемой математики был потрясен. (Не плачь, у этой истории счастливый конец)

Именно этот класс заставил меня вернуться к книгам и провести больше исследований. (Во время еды и питья ужасные вещи #пожиратель стресса) Это было либо изменить это, либо бросить это. Я знал, насколько удивительным это может быть, поэтому я был полон решимости найти решение этому безумию.

Математический СТЕК

Вместо того, чтобы собирать группы по всей комнате для одновременного участия в математических играх, пришло время определить для этих групп разные виды деятельности.Это должно было помочь уменьшить количество шума и хаоса в нашей комнате. Я придумал 5 заданий для своих учеников. Я придумал АБКРОНИМ для этих вариантов, потому что это то, что делают учителя. Аббревиатура STACK была для меня способом варьировать типы ресурсов, которые я использовал. Это свело к минимуму шум и хаос и позволило мне помочь своим ученикам развить более всесторонний математический опыт.

Независимо от того, нужно ли вам 3, 4 или 5 вращений, вы можете уменьшить количество шума и хаоса, выбирая действия из разных модальностей обучения.Вот наглядный пример различных вариантов, которые я могу выбрать для математического блока.

В этом посте я пропущу ротацию столов в малых группах. Вы можете посмотреть пост о малой группе ЗДЕСЬ.

Вращение технологий
В недавнем посте я поделился играми для каждой математической нити, в которые можно играть на любом устройстве. Несмотря на то, что есть несколько замечательных сайтов, которые укрепляют обучение с помощью технологий, я хотел найти проверенные и настоящие игры, которые напрямую соответствовали бы стандартам, которые я преподавал на уроках математики с гидом.Я создал 5 игр для каждого направления математики за год! Чтобы проверить сообщение об этих играх, вы можете прочитать ЗДЕСЬ. Ниже вы можете увидеть две игры по разрядности.

Применение

Станция приложений — это способ для учителя получить оценку или самостоятельное практическое занятие во время ротации. Как правило, вы обнаружите, что здесь происходит некоторая независимая практика. Для этой ротации я создал страницы практики навыков для каждой математической нити.

Если вы ищете печатные формы для математических навыков, у меня есть отдельные наборы из 20 страниц для практики навыков для каждой математической нити или комплект на год!

Ниже этот ученик заполняет ежедневную математическую страницу, на которой по спирали просматриваются навыки каждый день в течение года. Их можно найти ЗДЕСЬ.

Создать

Станция создания — это станция математического журнала! Дневник каждого ученика — это окно в его мышление и навыки! Математические журналы не должны быть повторяющимися или тусклыми! Я люблю разнообразить деятельность студентов в своих журналах.Учащиеся от детского сада могут извлечь пользу из математического журнала. У меня есть много сообщений в блогах о математических журналах, а также много ресурсов по математическим журналам K-3!

Ниже приведены ссылки на комплекты журналов для каждого класса (также продаются отдельными томами)

Набор журналов по математике для детского сада

Набор журналов по математике для первого класса 

Второй комплект математических журналов 

Комплект третьего математического журнала

 Набор математических журналов для четвертого класса

Кинестетик

Кинестетическое вращение — это практический математический центр! Это то, что обычно думают большинство учителей, когда вы говорите математический центр. Это способ для учащихся использовать конкретные объекты и взаимодействовать с материалами для дальнейшего понимания математических концепций. Ниже у меня есть фотографии некоторых моих математических центров в действии от друзей-учителей из нашей группы в Facebook!

Я разработал математические центры для К-3 классов! Найдите ссылки ниже на пакеты за год, если это то, что вам нужно. (также в месячных комплектах)

Комплект математических центров для детского сада

Комплект математических центров для первоклассников

Комплект математических центров для второго класса

Комплект математических центров третьего класса

Комплект математических центров для четвертого класса

Вот оно! Секрет ротации раскрыт! Вы можете начать математические вращения в любое время учебного года! Прервите свою рутину и попробуйте что-то новое или просто настройте то, что у вас уже есть! Я всегда надеюсь поделиться чем-то, что может сделать вашу школьную жизнь немного проще. Я надеюсь, что некоторые из моих любимых практик могут помочь!

Потерянный и забытый

Происходят одни из самых ценных математических минут, а также начало и закрытие математического блока. Поэтому я хочу обязательно поделиться некоторыми полезными ресурсами, чтобы начать и закончить ваши ежедневные занятия по математике!

Математическая разминка

Числовой чат — отличный способ начать свой математический блок! Цель числового чата — побудить учащихся поделиться стратегиями и математическим мышлением. Вместо того, чтобы сосредотачиваться на ответах, позвольте учащимся сосредоточиться на осмыслении.

Спроектируйте и обдумайте или распечатайте буклеты на поллиста!

Мой B набор математических чатов в течение года покрывает все математические направления со скидкой!

Выходные билеты

Эти билета на выход служат быстрой проверкой или математическим размышлением, чтобы подвести итоги вашего обучения! Как и числовые чаты, вы можете спроецировать их или создать небольшую половину листа для краткой оценки обучения. На каждую математическую ветвь есть 20 выходных билетов.

Вот новое видео, которое я добавил на этой неделе, чтобы немного лучше объяснить числовые чаты и билеты на выход!

Если у вас уже есть серия пошаговых инструкций по математике, серия дополнений даст вам больше практики для закрепления понятий!

Хорошей недели! Попробуйте новую технику или ресурс и дайте мне знать, как это работает, в комментариях ниже или в нашей группе на Facebook!

.