Окружность. Видеоурок. Геометрия 8 Класс
На данном уроке мы рассмотрим такую геометрическую фигуру, как окружность, и простейшую конструкцию – окружность и точка на окружности. Мы рассмотрим несколько теорем и их следствий, некоторые теоремы докажем.
Тема: Повторение курса геометрии 8 класса
Урок: Окружность
Дадим определение окружности, допустив типовую ошибку.
Определение
Окружность – это множество точек плоскости, равноудаленных от одной заданной – от центра.
Например, под это определение подходит следующее множество точек: четыре вершины квадрата, равноудаленные от центра квадрата, но данные четыре точки А, В, С и D не являются окружностью (см. Рис. 1).
Рис. 1
Таким образом, в определении пропущено ключевое слово: множество всех точек.
Определение
Окружность – это множество всех точек плоскости, равноудаленных от одной заданной – от центра.
Если известно, что точка В лежит на окружности, то расстояние от центра окружности до точки В равно радиусу окружности: (см. Рис. 2).
И наоборот, если не известно, лежит ли точка М на окружности, но известно, что расстояние от нее до центра окружности равно радиусу (), то можно утверждать, что точка М принадлежит окружности.
Рис. 2
Соотношение окружности и прямой. Возможны три варианта взаимного расположения окружности и прямой: они могут не пересекаться вообще, пересекаться в одной точке или в двух точках. Особое место занимает случай, когда окружность и прямая имеют единственную общую точку (см. Рис. 3).
Каким образом можно доказать, что общая точка единственная? Около точки А расположено множество точек, и возможно, найдется еще одна, общая для окружности и прямой. Но если радиус, проведенный в точку касания, перпендикулярен прямой, то точка касания – единственная общая точка окружности и прямой. В таком случае прямая называется касательной к окружности.
Рис. 3
Возьмем точку на окружности и изучим конструкции, которые определяются только окружностью и точкой на окружности (см. Рис. 4).
Если провести из точки А два луча, пересекающих окружность, мы получим вписанный треугольник.
Рис. 4
Свойства треугольника и окружности в данном случае взаимосвязаны. Для окружности здесь важна теорема о вписанном угле.
Определение
Угол , вершина которого А находится на окружности, а стороны пересекают окружность, называется вписанным в окружность углом (см. Рис. 5).
Вписанный угол опирается на дугу, в нашем случае на дугу . Вписанному углу соответствует центральный угол , .
Рис. 5
Вписанный угол измеряется половиной дуги, на которую он опирается (см. Рис. 6).
Напомним, что угловое измерение дуги равно угловому измерению соответствующего ей центрального угла.
Если обозначим угол за , то
interneturok.ru
Решение базовых задач. Видеоурок. Геометрия 8 Класс
В ходе данного урока мы рассмотрим решение базовых задач с применением теоремы Пифагора, научимся находить стороны прямоугольного треугольника и доказывать, что данный треугольник является (либо не является) прямоугольным.
Найти гипотенузу прямоугольного треугольника с катетами и .
Дано: ; . , .
Найти: .
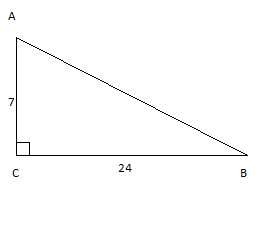
Рис. 1. Прямоугольный треугольник
Решение
Поскольку – прямоугольный, можем воспользоваться теоремой Пифагора.
Так как существует вариант, что , то берем во внимание, что длина стороны – число положительное.
Ответ: .
Является ли прямоугольным треугольник со сторонами , , ?
Дано: . , , .
Определить: – прямоугольный треугольник?
Решение
Обратим внимание, что если является прямоугольным, то прямой угол будет самым большим углом этого треугольника. А значит, напротив него будет лежать самая большая сторона. А сторона, которая лежит напротив большого угла называется гипотенузой. Допустим, что – гипотенуза. И пусть предположительно прямоугольный. Тогда сможем применить теорему Пифагора.
25 = 4 + 16
25 ¹ 20
А это значит, что не является прямоугольным.
Ответ: не является прямоугольным.
interneturok.ru
Конспекты уроков Геометрия 8 класс
Данный урок посвящен одному из видов выпуклых четырехугольников, а именно – параллелограмму. Параллелограмм – один из частных видов четырехугольников, который включает в себя такие подвиды, как прямоугольник, ромб, квадрат – фигуры, с которыми каждый из нас знаком еще с детства. Мы рассмотрим определение и свойства параллелограмма, а также решим несколько примеров с использованием этих свойств.
Тема: Четырехугольники
Урок: Параллелограмм
1. Определение параллелограмма
На прошлом уроке мы рассмотрели понятие выпуклого многоугольника. Теперь изучим частный случай многоугольника – четырехугольник, а точнее – частный случай четырехугольника – параллелограмм.
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны (см. Рис. 1).
Рис. 1. Параллелограмм
То есть, если даны две параллельные прямые, которые пересекают еще две параллельные прямые, то они образуют фигуру, которая называется параллелограммом .
Из того, что – параллелограмм, можно сделать следующие выводы: . Верно и обратное утверждение: если , то четырёхугольник – параллелограмм.
Помимо данного определения, можно дать ещё несколько эквивалентных, однако мы остановимся именно на таком, классическом определении параллелограмма, и сформулируем свойства данной фигуры, пользуясь параллельностью её противоположных сторон.
2. Первое свойство параллелограмма и его доказательство
Свойство 1. В параллелограмме противоположные стороны и углы попарно равны.
Дано:
– параллелограмм ().
Доказать: ; .
Доказательство:
Поскольку нам ничего не известно, кроме того, что – параллелограмм, то при доказательстве данного свойства мы будем пользоваться определением параллелограмма, то есть параллельностью его противоположных сторон.
Проведем диагональ и рассмотрим два полученных треугольника (см. Рис. 2.).
Они имеют общую сторону . Эта сторона является секущей при параллельных прямых .
Рис. 2
Воспользуемся свойством параллельных прямых, а именно: внутренние накрест лежащие углы при параллельных прямых равны. В нашем случае в роли внутренних накрест лежащих углов при параллельных прямых и секущей выступают углы . Аналогичное равенство можно получить и для внутренних накрест лежащих углов при параллельных прямых и секущей : .
Если теперь сложить полученные равенства, то получим, что: . Или: . Таким образом, мы доказали равенство двух противоположных углов параллелограмма. Осталось доказать равенство второй пары углов и равенство противоположных сторон.
Для этого рассмотрим треугольники: . Они имеют общую сторону . К стороне примыкают углы и в одном треугольнике, углы и в другом треугольнике. Значит, треугольники равны по стороне и двум прилегающим к ней углам (второй признак равенства треугольников).
Если записывать строго, то получаем следующую цепочку логических преобразований:
(по 2-му признаку равенства треугольников)
Примечание: при записи факта равенства треугольников необходимо учитывать порядок расстановки букв – буквы, означающие равные углы треугольника, должны идти на одинаковых порядковых местах в обозначении треугольников (в нашем примере: вторая буква в названии соответствует углу , как и вторая буква ).
Из равенства треугольников следует равенство всех соответствующих элементов этих треугольников. Значит:
. Таким образом, мы доказали, что если четырёхугольник – параллелограмм, то его противоположные углы и стороны попарно равны.
Доказано.
3. Второе свойство параллелограмма
Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.
Дано:
– параллелограмм ().
Доказать: (см. Рис. 3).
Доказательство:
Проведем диагонали и и отметим их точку пересечения: . Рассмотрим треугольники и .
Рис. 3
Они равны по второму признаку равенства треугольников (стороне и двум прилежащим к ней углам). Действительно:
(по 2-му признаку равенства треугольников)
Равенство углов вновь следует из того, что они являются внутренними накрест лежащими при соответствующей секущей и параллельных прямых (которыми являются противоположные стороны параллелограмма по определению). Противоположные стороны равны по доказанному выше свойству 1.
Из равенства треугольников следует равенство соответствующих элементов. Значит: .
Доказано.
Доказанные свойства параллелограмма позволяют решать многочисленный класс задач. Разберём несколько примеров.
4. Примеры задач на свойство параллелограмма
Пример 1.
Периметр параллелограмма равен 48 см. Найти его стороны, если одна сторона на 3 сантиметра больше другой (см. Рис. 4).
Дано:
– параллелограмм, . .
Найти:
Решение:
Рис. 4
Обозначим меньшую сторону параллелограмма . Учитывая свойство 1 для параллелограмма, запишем следующее равенство: . Из условия: .
Напомним, что периметр многоугольника – это сумма всех его сторон. Поэтому можем записать следующее равенство: .
Или: .
Получаем, что стороны параллелограмма: , .
Ответ: .
Пример 2
Биссектриса угла параллелограмма пересекает сторону в точке . . Найдите периметр параллелограмма.
Дано:
– параллелограмм, – биссектриса. . .
Найти:
Решение:
Рис. 5
Вспомним определение биссектрисы: биссектриса делит угол пополам. Это значит, что: . Кроме того, является секущей при параллельных прямых . А это значит, что внутренние накрест лежащие углы равны: .
Из этого получается:
.
Так как , то . Откуда: .
Периметр – сумма всех сторон, у параллелограмма противоположные стороны равны. Получаем: .
Ответ: .
Итак, мы рассмотрели определение и свойства параллелограмма, в частности: равенство противоположных сторон и углов, а также то, что диагонали параллелограмма точкой пересечения делятся пополам, и использовали эти свойства при решении задач.
В дальнейшем мы изучим признаки параллелограмма, а также научимся применять свойства и признаки параллелограмма при решении более сложных примеров.
nsportal.ru