Теория по геометрия 8 класс
Геометрия 8 класс. Теория.
Свойства параллелограмма. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны.
1. стороны. Противолежащие стороны параллельны и равны
2.Углы.
Противолежащие углы равны.
Сумма углов, прилежащих к одной стороне равна 1800
3.Диагонали. Диагонали точкой пересечения делятся пополам.
Дополнительные свойства.
1. Биссектриса угла отсекает от параллелограмма равнобедренный треугольник
2. Биссектрисы углов, прилежащих к одной стороне, пересекаются под прямым углом
3. Биссектрисы противолежащих углов параллельны.
4. Связь сторон и диагоналей: d12+d22=2a2+2b2Свойства прямоугольника. Прямоугольник — это параллелограмм, у которого все углы прямые.
1. Сохраняет все свойства параллелограмма
2. Свое свойство. Диагонали прямоугольника равны
Свойства ромба. Ромб – это параллелограмм, у которого все стороны равны
1. Сохраняет все свойства параллелограмма
2. Свое свойство. Диагонали ромба перпендикулярны и являются биссектрисами углов
Свойства квадрата. Квадрат – это прямоугольник, у которого все стороны равны.
1. Сохраняет все свойства прямоугольника.
2. Диагонали квадрата равны, перпендикулярны и являются биссектрисами углов
Свойства равнобедренной трапеции
1.Боковые стороны равны.
2.Углы, прилежащие к основаниям равны ( два острых и два тупых)
3. Сумма углов, прилежащих к боковой стороне равна 1800
4.Бисектрисы углов, прилежащих к боковой стороне, пересекаются под прямым углом
5. Длина средней линии трапеции равна большему отрезку на большем основании, если провести одну высоту
6. При решении задач всегда проводят две высоты. (равные отрезки на большем основании)
7. Средняя линия трапеции параллельна ее основаниям и равна а+в2 (полусумме оснований – параллельных сторон.)
8.При решении задач. Если диагонали трапеции перпендикулярны, тогда вторую диагональ перенести параллельно к первой. Получим прямоугольный треугольник, гипотенуза = сумме оснований
Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон.
Средняя линия треугольника параллельна одной из сторон и равна ее половине.
Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов.
Гипотенуза = Катет2+Катет2 Катет = Гипотенуза2-Катет2 Гипотенуза больше катета.
Как определить вид треугольника по углам
Большая сторона2 = сторона2 + сторона2 — треугольник прямоугольный
Большая сторона2
Большая сторона2 > сторона2 + сторона2 — треугольник тупоугольный
сИнус острого угла прямоугольного треугольника равен отношению прОтиволежащего катета к гипотенузе sin∝=прОтив. катетгипотенузакОсинус острого угла прямоугольного треугольника равен отношению прИлежащего катета к гипотенузе сOs∝=прИлеж.катетгипотенузаТангенс острого угла прямоугольного треуго
educontest.net
Основные определения за курс геометрии 8 класса
Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны
Сумма длин всех сторон многоугольника называется периметром многоугольника.
Две вершины многоугольника, принадлежащие одной стороне, называются соседними.
Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Сумма углов выпуклого n-угольника равна (n–2)·180°.
Четырёхугольник – это многоугольник у которого четыре вершины и четыре стороны.
Две несмежные стороны четырёхугольника называются противоположными.
Две вершины, не являющиеся соседними, называются противоположными.
Сумма углов выпуклого четырехугольника равна 360°.
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
(Свойства параллелограмма) В параллелограмме противоположные стороны равны и противоположные углы равны. Диагонали параллелограмма точкой пересечения делятся пополам.
(Признак параллелограмма) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
(Признак параллелограмма) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
(Признак параллелограмма) Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
Трапеция называется равнобедренной, если её боковые стороны равны.
Трапеция называется прямоугольной, если один из её углов прямой.
(Т. Фалеса) Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Прямоугольником называется параллелограмм, у которого все углы прямые.
(Особое свойство прямоугольника) Диагонали прямоугольника равны.
(Признак прямоугольника) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Ромбом называется параллелограмм, у которого все стороны равны.
(Особое свойство ромба) Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадратом называется прямоугольник, у которого все стороны равны.
(Основные свойства квадрата) Все углы квадрата прямые. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1.
(Основные свойства площадей) Равные многоугольники имеют равные площади.
Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Площадь квадрата равна квадрату его стороны ( S=a2).
(Т.)Площадь прямоугольника равна произведению его смежных сторон (S=ab).
(Т.)Площадь параллелограмма равна произведению его основания на высоту (S=ah).
(Т.)Площадь треугольника равна половине произведения его основания на высоту (S= ah).
Площадь прямоугольного треугольника равна половине произведения его катетов (S= ab).
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Площадь трапеции равна произведению полусуммы её оснований на высоту ( S= (AD+BC)·h ).
(Теорема Пифагора) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. (с2=a2+b2)
(Теорема, обратная теореме Пифагора) Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
(Формула Герона) Площадь треугольника со сторонами a, b, c выражается формулой S=, где p = (a+b+c) — полупериметр треугольника.
Говорят, что отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1 , если =.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
(Т.)Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
(Т. Первый признак подобия треугольников) Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
(Т. Второй признак подобия треугольников) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
(Т. Третий признак подобия треугольников) Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.
(Т. о средней линии треугольника) Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков АВ и CD, если XY=
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
Средняя линия трапеции — это отрезок, соединяющий середины ее боковых сторон.
(Т. о средней линии трапеции) Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Тангенс угла равен отношению синуса к косинусу этого угла.
sin2A+cos2A=1 – основное тригонометрическое тождество.
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
(Т. о свойстве касательной к окружности) Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
(Свойство отрезков касательных, проведённых из одной точки) Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
(Т. Признак касательной) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром окружности.
Угол с вершиной в центре окружности называется её центральным углом.
Центральный угол измеряется дугой, на которую он опирается.
Сумма градусных мер двух дуг окружности с общими концами равна 360°.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
(Т.) Вписанный угол измеряется половиной дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность – прямой.
(Теорема о произведении отрезков пересекающихся хорд) Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
Биссектрисы треугольника пересекаются в одной точке.
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
(Теорема о серединном перпендикуляре к отрезку) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Высоты треугольника (или их продолжения) пересекаются в одной точке.
Четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот(или их продолжений) называются замечательными точками треугольника.
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
(Теорема об окружности, вписанной в треугольник) В любой треугольник можно вписать окружность.
В треугольник можно вписать только одну окружность.
Не во всякий четырёхугольник можно вписать окружность.
В любом описанном четырёхугольнике суммы противоположных сторон равны.
Если суммы противоположных сторон выпуклого четырёхугольника равны то в него можно вписать окружность.
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
(Теорема об окружности, описанной около треугольника) Около любого треугольника можно описать окружность.
Около треугольника можно описать только одну окружность.
Около четырёхугольника не всегда можно описать окружность.
В любом вписанном четырёхугольнике сумма противоположных углов равна 180°.
Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.
infourok.ru
Геометрия 8 класс (теория и практика) 1 четверть
В данной презентации дано 25 заданий, состоящих из теории и практики за 1 четверть. Ученик выбирает по одному вопросу из пяти разделов и отвечает. Правильность овета проверяется, после каждого ответа ученика. Если ученик ответил неправильно, то учитель может спросить любого ученика из класса. Ученикам нравится такой способ опроса. Они заранее готовятся к повторению, повторяя весь пройденный материал за 1 четверть. Проявляют огромный интерес к ожидаемому вопросу. Задачи, включенные в задания , являются частью к подготовке к ОГЭ. Нам хорошо известно, как тяжело заинтересовать учеников геометрией, так как в большенстве из них очень тяжело понимают как найти правильное решение к поставленной задаче. В данной презентации учитель може самостоятельно изменить задания и ответы и таким образом получит новую презентацию, например по геометрии за 2 четверть или подобрать материал по алгебре.
Просмотр содержимого документа
«Геометрия 8 класс (теория и практика) 1 четверть »

Повторение геометрия 8 класс
Параллелограмм
Трапеция
Прямоугольник
Квадрат
Ромб
1
5
2
3
4
3
1
5
4
2
1
2
3
4
5
2
4
1
3
5
4
5
2
3
1

1
Дайте определение
параллелограмма
Четырехугольник, у которого стороны
попарно параллельны называется
параллелограммом

2
Чему равна сумма
углов выпуклого
многоугольника?
180°(n-2)

3
10,5; 10,5; 13,5; 13,5

4
12, 12, 24, 24

5
84°,96°, 96°

1
Дайте определение
прямоугольника
Параллелограмм, у которого все углы прямые называется прямоугольником
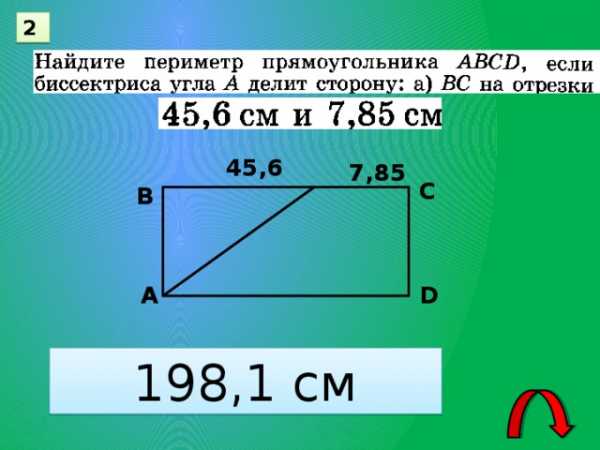
2
45,6
7,85
С
В
А
D
198,1 см
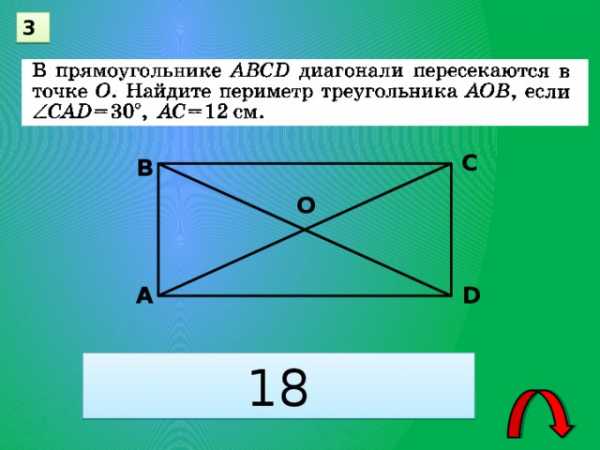
3
С
В
О
А
D
18
10
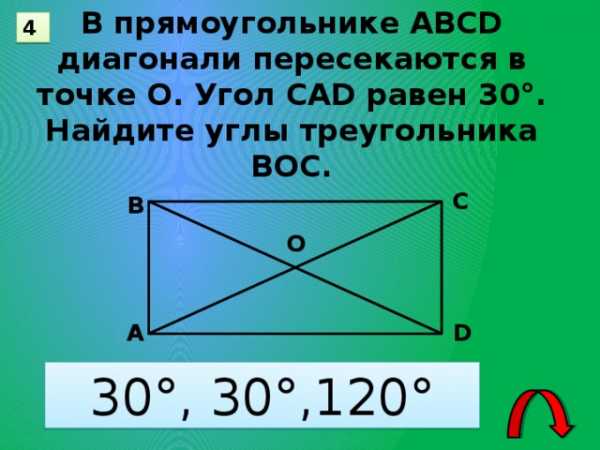
В прямоугольнике АВСD
диагонали пересекаются в
точке О. Угол САD равен 30°.
Найдите углы треугольника
ВОС.
4
С
В
О
А
D
30°, 30°,120°
11
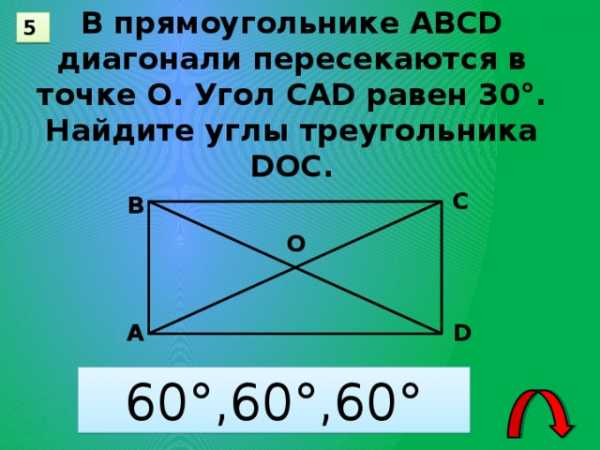
В прямоугольнике АВСD
диагонали пересекаются в
точке О. Угол САD равен 30°.
Найдите углы треугольника
DОС.
5
С
В
О
А
D
60°,60°,60°
12

1
Дайте определение
РОМБА
Параллелограмм, у которого
все стороны равны
называется ромбом
12
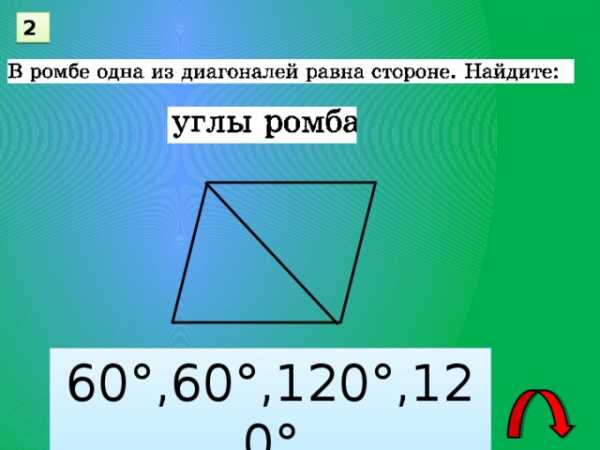
2
60°,60°,120°,120°
12

3
80°
40°,50°
12
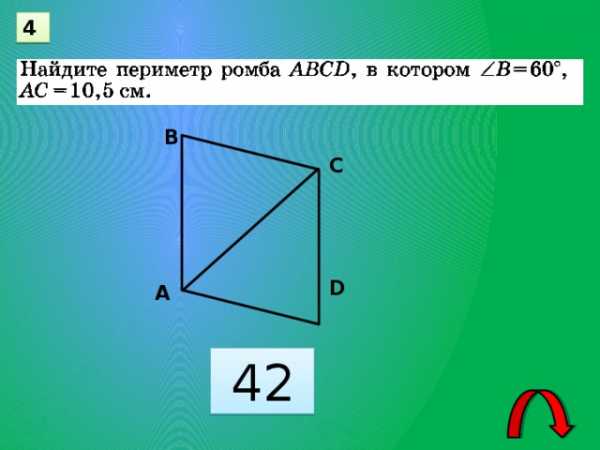
4
В
С
D
А
42
12

5
Сформулируйте свойство
диагоналей ромба
Диагонали ромба являются биссектрисами углов и пересекаются под прямым углом
12

1
Дайте определение
квадрата
Прямоугольник, у которого все стороны равны называется квадратом
12

2
нет
12

3
нет
12

4
да
12

5
Сформулируйте
свойство
диагоналей
квадрата
Диагонали квадрата
Равны и перпендикулярны
12
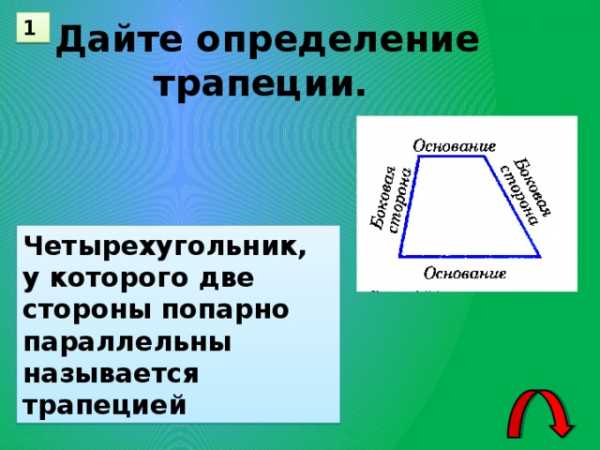
1
Дайте определение
трапеции.
Четырехугольник, у которого две стороны попарно параллельны называется трапецией
12
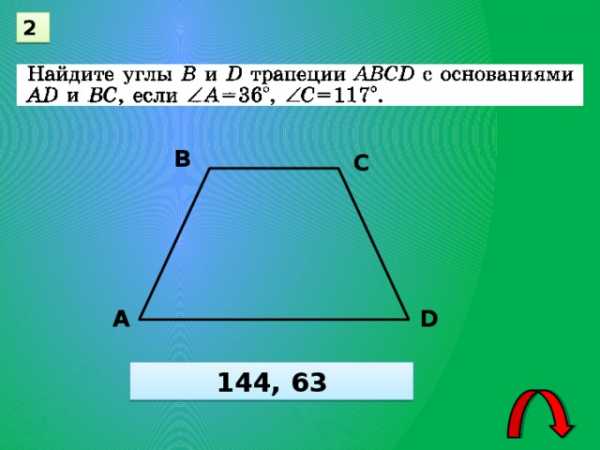
2
В
С
А
D
144, 63
24
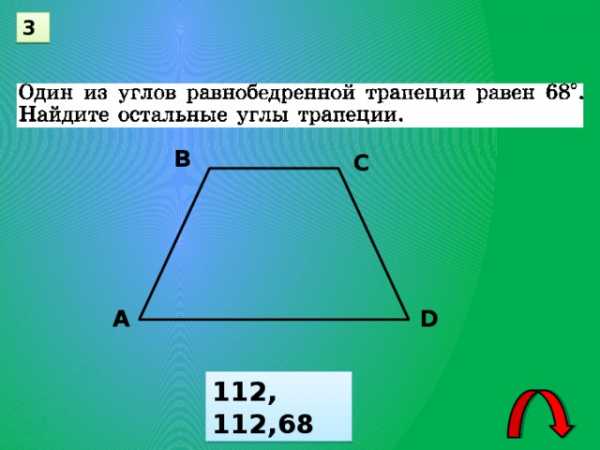
3
В
С
А
D
112, 112,68
25
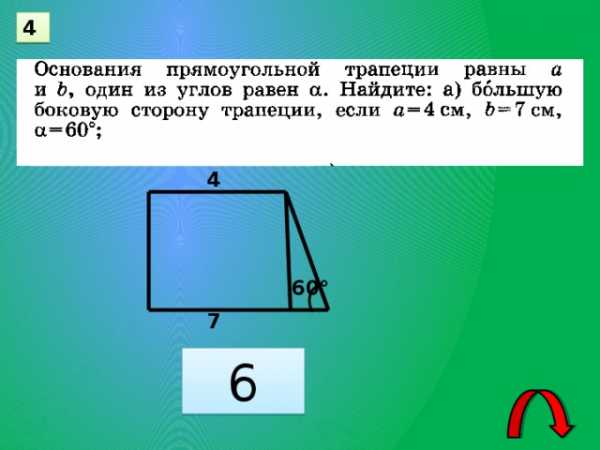
4
4
60°
7
6
26
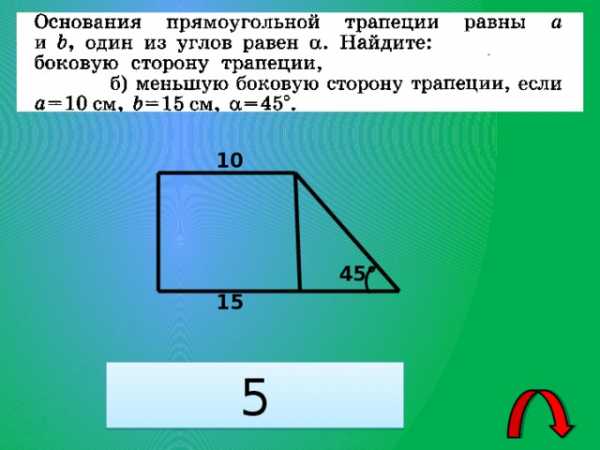
5
10
45°
15
5
26
kopilkaurokov.ru
Зачеты по теории геометрии (8 класс)
Зачеты по геометрии. 8 класс.
В варианты Основного государственного экзамена по математике входят отдельным разделом задачи и теоретические вопросы по геометрии. Поэтому при изучении курса геометрии очень важно уделять внимание и умению решать задачи, и знанию теоретического материала.
Как известно, без знания теории невозможно успешное выполнение практической части. Поэтому в своей работе я использую такую форму проведения промежуточной аттестации учащихся, как теоретические зачеты.
В разработке представлены материалы для проведения теоретических зачетов по геометрии в 8 классе по учебнику Л.С. Атанасяна. Темы зачетов: «Четырехугольники», «Площади фигур», «Подобие треугольников», «Окружность». Каждый зачет проводится после изучения всей теории по теме. Затем — блок отработки практических навыков. И в конце – контрольная работа.
Поясню на примере зачета № 1 технологию подготовки и проведения контрольного мероприятия в форме зачета.
В начале изучения темы учащиеся получают список вопросов зачета, который включает в себя определения, свойства, формулы, признаки и т.д.
Вопросы зачета № 1 «Четырехугольники»
-
Определение многоугольника.
-
Сумма углов выпуклого п-угольника.
-
Четырехугольник.
-
Определение параллелограмма.
-
Свойство сторон и углов параллелограмма (с доказательством).
-
Свойства диагоналей параллелограмма (с доказательством).
-
Первый признак параллелограмма (с доказательством).
-
Второй признак параллелограмма (с доказательством).
-
Третий признак параллелограмма (с доказательством).
-
Четвертый признак параллелограмма (с доказательством).
-
Определение и виды трапеций.
-
Свойства трапеций.
-
Определение прямоугольника.
-
Свойства прямоугольника (с доказательством).
-
Признак прямоугольника (с доказательством).
-
Определение ромба.
-
Свойства ромба (с доказательством).
-
Определение квадрата.
-
Свойства квадрата.
По окончании изучения теории проводится сам зачет. При этом все вопросы разбиваются на билеты. В каждый билет входят определения, свойства, теоремы для разных фигур.
Билеты зачета № 1 «Четырехугольники»
Вариант 1.
-
Определение многоугольника
-
Свойство прямоугольника
-
Свойство сторон и углов параллелограмма
Вариант 2.
-
Определения трапеции
-
Сумма углов n—угольника.
-
Первый признак параллелограмма
Вариант 3.
-
Определение прямоугольника
-
Свойство диагоналей параллелограмма
-
Свойства ромба
Вариант 4.
-
Определение параллелограмма
-
Свойства трапеции
-
Признак прямоугольника
Вариант 5.
-
Определение ромба
-
Свойства квадрата
-
Второй признак параллелограмма
Вариант 6.
-
Определение квадрата
-
Свойства четырехугольника
-
Третий признак параллелограмма
Учащиеся приглашаются по 6 человек (по количеству билетов). Время подготовки 3-6 минут (может быть и больше – в зависимости от уровня подготовки класса). Далее ученики подсаживаются к проверяющим учащимся и отвечают на вопросы своего варианта.
Проверяющие – это ученики того же класса (или параллельного, или старшеклассники), которые сдают зачет заранее непосредственно учителю.
Все этапы ответа фиксируются в бланке («+» верно, «-» неверно, «V» с недочетом и т.п. ). Выставляется общая оценка.
Геометрия. 8 класс. Зачет № 1 по теме «Четырехугольники».
Ф.И. ____________________________________________
Дата ___________________ Вариант _________________
Х
Ф.И. принимающего теорию ____________________________
В зависимости от уровня подготовки детей допускается использование тетрадей для теории, которые ученики ведут во время уроков и дома. В таком случае оценка за зачет снижается.
В случае получения учеником отметки «2», зачет пересдается во внеурочное время непосредственно учителю.
Зачет № 2 по теме «Площади фигур»
-
Свойства площадей. Площадь квадрата.
-
Площадь прямоугольника (с выводом).
-
Площадь параллелограмма (с выводом).
-
Площадь треугольника (с выводом).
-
Площадь прямоугольного треугольника (с выводом).
-
Площадь трапеции (с выводом).
-
Теорема Пифагора (с выводом).
-
Теорема, обратная теореме Пифагора (с выводом).
-
Площадь ромба через диагонали (с выводом).
-
Свойство равновеликих треугольников.
-
Площадь равностороннего треугольника (с выводом).
Билеты зачета № 2 по теме «Площади фигур»
Вариант 1.
-
Площадь прямоугольника (с выводом).
-
Площадь равностороннего треугольника.
Вариант 2.
-
Площадь параллелограмма (с выводом).
-
Теорема, обратная теореме Пифагора.
Вариант 3.
-
Площадь треугольника (с выводом).
-
Свойства площадей. Площадь квадрата.
Вариант 4.
-
Площадь трапеции (с выводом).
-
Площадь прямоугольного треугольника.
Вариант 5.
-
Теорема Пифагора (с выводом).
-
Площадь ромба через диагонали.
Геометрия. 8 класс. Зачет № 2 по теме «Площади».
Ф.И. ____________________________________________
Дата ___________________ Вариант _________________
Ф.И. принимающего теорию ____________________________
Зачет № 3 по теме «Подобие треугольников»
-
Пропорциональные отрезки.
-
Определение подобных треугольников.
-
Отношение площадей подобных треугольников (с выводом).
-
Первый признак подобия треугольников (с выводом).
-
Второй признак подобия треугольников (с выводом).
-
Третий признак подобия треугольников (с выводом).
-
Средняя линия треугольника (с выводом).
-
Свойство медиан треугольника (с выводом).
-
Пропорциональные отрезки в прямоугольном треугольнике (с выводом).
-
Применение подобия для практических задач: нахождение высоты предмета, расстояния до недоступной точки.
Билеты зачета № 3 по теме «Подобие треугольников»
Вариант 1
-
Средняя линия треугольника (с выводом).
-
Второй признак подобия треугольников.
Вариант 2
-
Свойство медиан треугольника (с выводом).
-
Третий признак подобия треугольников.
Вариант 3
-
Пропорциональные отрезки в прямоугольном треугольнике: выражение высоты через проекции катетов (с выводом).
-
Отношение площадей подобных треугольников.
Вариант 4
-
Первый признак подобия треугольников (с выводом).
-
Применение подобия для практических задач: нахождение расстояния до недоступной точки.
Вариант 5
-
Пропорциональные отрезки в прямоугольном треугольнике: выражение катета через проекцию и гипотенузу (с выводом).
-
Применение подобия для практических задач: нахождение высоты предмета.
Геометрия. 8 класс. Зачет № 3 по теме «Подобные треугольники».
Ф.И. ____________________________________________
Дата ___________________ Вариант _________________
Ф.И. принимающего теорию ____________________________
Зачет № 4 по теме «Окружность»
-
Взаимное расположение прямой и окружности.
-
Определение касательной к окружности.
-
Свойство касательной к окружности. Обратная теорема.
-
Свойство отрезков касательных.
-
Градусная мера дуги окружности.
-
Определение вписанного угла.
-
Свойство вписанного угла.
-
Следствия из теоремы о свойстве вписанного угла.
-
Теорема о свойстве двух пересекающихся хорд окружности.
-
Свойство биссектрис угла треугольника. Следствие.
-
Свойство серединных перпендикуляров треугольника. Следствие.
-
Свойства высот и медиан треугольника.
-
Вписанная окружность: определение, теорема о вписанной окружности в треугольник.
-
Теоремы (прямая и обратная) о вписанной окружности в четырехугольник.
-
Описанная окружность: определение, теорема об описанной окружности вокруг треугольника.
-
Теоремы (прямая и обратная) об описанной окружности вокруг четырехугольника.
Билеты зачета № 4 по теме «Окружность»
Вариант 1
-
Взаимное расположение прямой и окружности.
-
Свойство вписанного угла.
-
Вписанная окружность: определение, теорема о вписанной окружности в треугольник.
Вариант 2
-
Определение касательной к окружности.
-
Градусная мера дуги окружности.
-
Теоремы (прямая и обратная) о вписанной окружности в четырехугольник.
Вариант 3
-
Свойство касательной к окружности. Обратная теорема.
-
Следствия из теоремы о свойстве вписанного угла.
-
Описанная окружность: определение, теорема об описанной о
окружности вокруг треугольника.
Вариант 4
-
Свойство отрезков касательных.
-
Свойство серединных перпендикуляров треугольника. Следствие.
-
Теоремы (прямая и обратная) об описанной окружности вокруг четырехугольника.
Вариант 5
-
Определение вписанного угла.
-
Теорема о свойстве двух пересекающихся хорд окружности.
-
Свойство биссектрис угла треугольника. Следствие.
Геометрия. 8 класс. Зачет № 4 по теме «Окружность».
Ф.И. ____________________________________________
Дата ___________________ Вариант _________________
Ф.И. принимающего теорию ____________________________
infourok.ru
Опрос теории по геометрии 8 класс (по теме многоугольники)
____ _____ __ ___ ______ ______________________
Вариант 1
Напишите определение параллелограмма.
Напишите свойства прямоугольника с вершинами в точках LKJH
____ ____ ______ _____ ____ ___
Вариант 2
Напишите определение трапеции.
Напишите свойства для параллелограмма с вершинами в точках CNHD.
___ ____ ____ ____ ____ _____ ___
Вариант 3
Напишите определение прямоугольника.
Напишите свойства ромба с вершинами в точках GHJK
_____ _____ __ ______ ___________ ___
Вариант 4
Напишите определение ромба.
Напишите свойства квадрата с вершинами в точках SDFG
__ ___ ___ ____ ____ ____ _
Вариант 5
Напишите определение квадрата.
Напишите признаки параллелограмма с вершинами в точках MNBV
___ ____ ____ ____ ___ __
____ _____ __ ___ ______ ______________________
Вариант 6
Напишите определение параллелограмма.
Напишите свойства прямоугольника с вершинами в точках LSDE
____ ____ ______ _____ ____ ___
Вариант 7
Напишите определение трапеции.
Напишите свойства для параллелограмма с вершинами в точках ASPD.
___ ____ ____ ____ ____ _____ ___
Вариант 8
Напишите определение прямоугольника.
Напишите свойства ромба с вершинами в точках GMRE
_____ _____ __ ______ ___________ ___
Вариант 9
Напишите определение ромба.
Напишите свойства квадрата с вершинами в точках SMHQ
__ ___ ___ ____ ____ ____ _
Вариант 10
Напишите определение квадрата.
Напишите признаки параллелограмма с вершинами в точках PQBV
____ _____ __ ___ ______ ______________________
Вариант 11
Напишите определение параллелограмма.
Напишите свойства прямоугольника с вершинами в точках LTYU
____ ____ ______ _____ ____ ___
Вариант 12
Напишите определение трапеции.
Напишите свойства для параллелограмма с вершинами в точках BVKJ.
___ ____ ____ ____ ____ _____ ___
Вариант 13
Напишите определение прямоугольника.
Напишите свойства ромба с вершинами в точках KJZX
_____ _____ __ ______ ___________ ___
Вариант 14
Напишите определение ромба.
Напишите свойства квадрата с вершинами в точках SDZX
__ ___ ___ ____ ____ ____ _
Вариант 15
Напишите определение квадрата.
Напишите признаки параллелограмма с вершинами в точках JFYT
____ _____ __ ___ ______ ______________________
Вариант 16
Напишите определение параллелограмма.
Напишите свойства прямоугольника с вершинами в точках KQNM
____ ____ ______ _____ ____ ___
Вариант 17
Напишите определение трапеции.
Напишите свойства для параллелограмма с вершинами в точках GKAR.
___ ____ ____ ____ ____ _____ ___
Вариант 18
Напишите определение прямоугольника.
Напишите свойства ромба с вершинами в точках KEIV
_____ _____ __ ______ ___________ ___
Вариант 19
Напишите определение ромба.
Напишите свойства квадрата с вершинами в точках QMIY
__ ___ ___ ____ ____ ____ _
Вариант 20
Напишите определение квадрата.
Напишите признаки параллелограмма с вершинами в точках APBV
____ _____ __ ___ ______ ______________________
Вариант 21
Напишите определение параллелограмма.
Напишите свойства прямоугольника с вершинами в точках UNYV
____ ____ ______ _____ ____ ___
Вариант 22
Напишите определение трапеции.
Напишите свойства для параллелограмма с вершинами в точках GJKL.
___ ____ ____ ____ ____ _____ ___
Вариант 23
Напишите определение прямоугольника.
Напишите свойства ромба с вершинами в точках XGUI
_____ _____ __ ______ ___________ ___
Вариант 24
Напишите определение ромба.
Напишите свойства квадрата с вершинами в точках XDER
__ ___ ___ ____ ____ ____ _
Вариант 25
Напишите определение квадрата.
Напишите признаки параллелограмма с вершинами в точках KLFD
____ _____ __ ___ ______ ______________________
Вариант 26
Напишите определение параллелограмма.
Напишите свойства прямоугольника с вершинами в точках KHTY
____ ____ ______ _____ ____ ___
Вариант 27
Напишите определение трапеции.
Напишите свойства для параллелограмма с вершинами в точках LKGF
___ ____ ____ ____ ____ _____ ___
Вариант 28
Напишите определение прямоугольника.
Напишите свойства ромба с вершинами в точках CDEW
_____ _____ __ ______ ___________ ___
Вариант 29
Напишите определение ромба.
Напишите свойства квадрата с вершинами в точках IUTR
__ ___ ___ ____ ____ ____ _
Вариант 30
Напишите определение квадрата.
Напишите признаки параллелограмма с вершинами в точках KHFS
infourok.ru
Тест по геометрии тема «Четырехугольники» (теория, 8 класс).
Тест по геометрии. 8 класс
Тема: «Четырехугольники».
Вариант №1.
В заданиях 1 – 4 вставьте пропущенные слова.
1. *** называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков.
а) прямоугольник б) трапеция
в) ромб г) четырехугольник
2. Диагонали ромба являются *** его углов.
а) медианами б) высотами в) средними линиями г) биссектрисами
3. У параллелограмма противолежащие стороны равны, противолежащие *** равны.
а) вершины б) углы в) прямые г) отрезки
4. Ромб – это ***, у которого все стороны равны.
а) четырехугольник б) прямоугольник
в) квадрат г) параллелограмм
5. Найдите на рисунке параллелограмм.
а)
б)
в) г)
6. Назовите боковые стороны трапеции КМNЕ.
А) КЕ и МN Б) МN и ЕN В) КМ и NЕ Г) МN и МК
Вариант №2.
В заданиях 1-5 вставьте пропущенные.
1.Прямоугольник – это ***, у которого все углы прямые.
а) трапеция б) параллелограмм
в) ромб г) четырехугольник
2. *** называется четырехугольник, у которого только две противолежащие стороны параллельны.
а) прямоугольник б) трапеция
в) параллелограмм г) ромб
3. *** параллелограмма пересекаются и точкой пересечения делятся пополам.
а) вершины б) диагонали в) углы г) стороны
4. Диагонали *** равны.
а) четырехугольника б) прямоугольника
в) ромба г) трапеции
5. Средняя линия трапеции параллельна основаниям и равна их ***.
а) сумме б) полуразности в) полупроизведению г) полусумме
6. Найдите на рисунке трапецию.
а)
б)
в) г)
7. Назовите основания трапеции КМNЕ.
А) КЕ и МN Б) КМ и NЕ В) МN и ЕN Г) МN и МК
infourok.ru
Теория по геометрии 7-9 класс
Поиск Лекций
Виды углов:
· острый угол – от 0 до 90 градусов;
· прямой угол – равен 90 градусам;
· тупой угол – от 90 до 180 градусов;
· развернутый угол (прямая) – равен 180 градусам.
Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжением друг друга.
Свойство смежных углов:
· сумма смежных углов равна 180 градусам.
Вертикальные углы – два угла, у которых стороны являются продолжением друг друга.
Свойство вертикальных углов:
· вертикальные углы равны.
Перпендикулярные прямые – прямые пересекающиеся под углом 90 градусов.
Перпендикуляр – отрезок, проведенный из точки к прямой под углом 90 градусов.
Теорема о перпендикуляре: из точки, не лежащей на прямой можно провести перпендикуляр к этой прямой и при том только один.
Периметр многоугольника – сумма длин всех его сторон.
Треугольник – это геометрическая фигура, состоящая из трех сторон и трех углов.
Виды треугольников:
· остроугольный треугольник – все три угла острые;
· прямоугольный треугольник – один угол прямой и два угла острые;
· тупоугольный треугольник – один угол тупой и два угла острые.
Равные треугольники – треугольники, которые можно совместить наложением.
Свойства равных треугольников:
· если два треугольника равны, то их элементы (углы и стороны) попарно равны;
· в равных треугольниках напротив равных сторон лежат равные углы и наоборот, напротив равных углов лежат равные стороны.
Признаки равенства треугольников:
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны;
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны;
3. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Биссектриса – отрезок, выходящий из вершины треугольника к противоположной стороне и делящий угол пополам.
Медиана – отрезок, выходящий из вершины треугольника к противоположной стороне и делящий эту сторону пополам.
Высота – отрезок, выходящий из вершины треугольника к прямой, содержащей противоположную сторону, под углом 90 градусов.
Равнобедренный треугольник – треугольник, у которого две стороны равны, а третья является основанием.
Свойства равнобедренного треугольника:
· углы при основании равны;
· биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
Равносторонний треугольник – треугольник, у которого все стороны равны.
Свойства равностороннего треугольника:
· углы равны по 60 градусов;
· биссектриса равностороннего треугольника, проведенная к любой стороне, является медианой и высотой.
Параллельные прямые – прямые, которые не пересекаются.
Секущая – прямая, пересекающая параллельные прямые.
Виды углов, образованных при пересечении параллельных прямых секущей:
· накрест-лежащие;
· соответственные;
· односторонние.
Свойства параллельных прямых:
· при пересечении параллельных прямых секущей накрест-лежащие углы равны;
· при пересечении параллельных прямых секущей соответственные углы равны;
· при пересечении параллельных прямых секущей сумма односторонних углов равна 180 градусам.
Признаки параллельности прямых:
· если при пересечении двух прямых секущей накрест-лежащие углы равны, то прямые параллельны;
· если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
· если при пересечении двух прямых секущей сумма односторонних углов равна 180 градусам, то прямые параллельны.
Аксиома о параллельных прямых: через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и при том только одну.
Следствия из аксиомы:
· если секущая пересекает одну из параллельных прямых, то она пересечет и вторую параллельную прямую;
· если каждая из двух прямых параллельна третьей, то они параллельны между собой.
Теорема о сумме углов треугольника: сумма углов треугольника равна 180 градусам.
Внешний угол треугольника – угол, смежный с одним из углов треугольника.
Свойство внешнего угла треугольника:
· внешний угол треугольника равен сумме двух углов треугольника не смежных с ним.
Теорема о соотношении между сторонами и углами треугольника: в треугольнике напротив бОльшей стороны лежит бОльший угол и наоборот, напротив бОльшего угла лежит бОльшая сторона.
Теорема о сторонах треугольника: каждая сторона треугольника меньше суммы двух других сторон.
Прямоугольный треугольник – треугольник, у которого один угол равен 90 градусам.
Свойства прямоугольного треугольника:
· сумма острых углов треугольника равна 90 градусам;
· в прямоугольном треугольнике катет, лежащий на против угла 30 градусов, равен половине гипотенузы;
· если в прямоугольном треугольнике катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 градусов.
Признаки равенства прямоугольных треугольников:
1. если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны;
2. если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны;
3. если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны;
4. если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Расстояние от точки до прямой – перпендикуляр, проведенный от этой точки к данной прямой.
Расстояние между параллельными прямыми – перпендикуляр, проведенный от произвольной точки на одной прямой ко второй прямой.
Четырехугольник – геометрическая фигура, состоящая из 4 сторон и 4 углов.
Сумма углов выпуклого многоугольника равна (n-2)*180, где n – количество углов.
Сумма углов любого четырехугольника равна 360 градусов.
Параллелограмм – четырехугольник, у которого стороны попарно параллельны.
Свойства параллелограмма:
· противоположные углы и стороны равны;
· диагонали пересекаются и точкой пересечения делятся пополам.
Диагональ – отрезок, соединяющий две противоположные вершины четырехугольника.
Признаки параллелограмма:
· если в четырехугольнике стороны попарно равны, то данный четырехугольник – параллелограмм;
· если в четырехугольнике две стороны равны и параллельны, то данный четырехугольник параллелограмм;
· если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то данный четырехугольник параллелограмм.
Трапеция – четырехугольник, у которого две стороны параллельны (основания) а две другие – нет (боковые стороны).
Виды трапеций:
· произвольная;
· прямоугольная – трапеция, у которой два прямых угла;
· равнобедренная – трапеция, у которой боковые стороны равны.
Свойства равнобедренной трапеции:
· углы при основаниях равны;
· диагонали равны.
Ромб – частный случай параллелограмма, у которого все стороны равны.
Свойство ромба:
· у ромба диагонали перпендикулярны и делят углы, из которых они исходят, пополам.
Прямоугольник – частный случай параллелограмма, у которого все углы по 90 градусов.
Свойство прямоугольника:
· у прямоугольника диагонали равны
Признак прямоугольника:
· если в параллелограмме диагонали равны, то этот параллелограмм прямоугольник.
Квадрат – частный случай прямоугольника, у которого все стороны равны.
Теорема Фалеса – если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
Площадь многоугольника – часть плоскости, ограниченная сторонами многоугольника.
Свойство площадей:
· равные многоугольники имеют равные площади;
· если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей многоугольников, из которых он состоит.
Площадь квадрата равна квадрату его стороны: S =
Площадь прямоугольника равна произведению двух его смежных сторон: S =
Площадь трапеции равна половине произведения основания на высоту: S =
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне: S =
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними: S =
Площадь ромба равна половине произведения его диагоналей: S =
Площадь ромба равна произведению стороны на высоту, проведенную к этой стороне: S =
Площадь ромба равна произведению двух его смежных сторон на синус угла между ними:
S =
Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне: S =
Площадь треугольника равна половине произведения двух его смежных сторон на синус угла между ними: S =
Площадь треугольника равна произведению его сторон, деленное на 4 радиуса описанной окружности: S =
Формула Герона, где р – полупериметр: S =
Площадь прямоугольного треугольника равна половине произведения его катетов: S =
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе из вершины прямого угла: S =
Площадь равностороннего треугольника, где а – сторона треугольник: S =
Высота, медиана, биссектриса равностороннего треугольника, где а – сторона треугольника: h =
Площадь круга, где r – радиус: S =
Длина окружности, где r – радиус: C = 2
Длина дуги окружности, где r – радиус, α – грудасная мера дуги:
Площадь кругового сектора, где r – радиус, α – грудасная мера дуги:
Площадь правильного шестиугольника, где а – сторона шестиугольника: S =
Если в многоугольник можно вписать окружность, то его площадь можно найти как половина произведения периметра на радиус этой окружности: S =
Свойства площадей треугольников:
· если два треугольника имеют равные высоты, то их площади относятся как основания;
· если два треугольника имеют пару равных углов, то их площади относятся как произведение сторон, заключающих эти углы.
Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Обратная теорема Пифагора: если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то данный треугольник – прямоугольный.
Формула для нахождения гипотенузы равнобедренного прямоугольного треугольника: , где х – катет равнобедренного прямоугольного треугольника.
Формула для нахождения диагонали квадрата: , где х – сторона квадрата.
Отношение двух величин – деление одной величины на другую (дробь).
Пропорция – равенство нескольких дробей.
Основное свойство пропорции: *d = c*b
Подобные треугольники – треугольники, у которых углы равны, а стороны одного треугольника пропорциональны сходственным сторонам другого.
Сходственные стороны – стороны двух подобных треугольников, расположенные напротив равных углов.
Коэффициент подобия – отношение двух сходственных сторон подобных треугольников.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Коэффициент подобия равных треугольников равен единице.
Теорема о биссектрисе треугольника: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Признаки подобия треугольников:
1. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны;
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, заключенные между этими сторонами, равны, то такие треугольники подобны;
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Теорема о средней линии треугольника: средняя линия треугольника параллельна противоположной стороне и равна ее половине.
Среднее арифметическое для нескольких величин равно сумме этих величин, деленной на их количество.
Среднее геометрическое (пропорциональное) для нескольких величин равно квадратному корню из их произведения.
Свойства среднего геометрического в прямоугольных треугольниках:
· высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое для отрезков, на которые гипотенуза делится этой высотой;
· катет прямоугольного треугольника есть среднее геометрическое для гипотенузы и отрезка гипотенузы, заключенного между этим катетом и высотой, проведенной к гипотенузе.
Синус острого угла прямоугольного треугольника – отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника – отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника – отношение противолежащего катета к прилежащему.
Котангенс острого угла прямоугольного треугольника – отношение прилежащего катета к прилежащему.
Основное тригонометрическое тождество: sin2(a) + cos2(a) = 1
Тригонометрические формулы:
·
·
Табличные углы:
В прямоугольном треугольнике синус одного острого угла равен косинусу другого
В прямоугольном треугольнике косинус одного острого угла равен синусу другого
В прямоугольном треугольнике тангенс одного острого угла равен котангенсу другого
В прямоугольном треугольнике котангенс одного острого угла равен тангенсу другого
Синусы смежных углов равны
Косинусы смежных углов равны с противоположными знаками
Тангенсы смежных углов равны с противоположными знаками
Котангенсы смежных углов равны с противоположными знаками
Окружность – множество точек, равноудаленных от одной точки (центр окружности).
Радиус – отрезок, соединяющий центр окружности с любой точкой на окружности.
Хорда – отрезок, соединяющий любые две точки на окружности.
Диаметр – хорда, проходящая через центр окружности.
Соотношение диаметра и радиуса – диаметр равен двум радиусам.
Секущая – прямая, имеющая с окружностью две общих точки.
Касательная – прямая, имеющая с окружностью одну общую точку.
Теоремы о касательных:
1) Радиус, проведенный в точку касания, перпендикулярен касательной.
2) Отрезки касательных, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Теорема о хордах:
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Вписанный угол – угол, вершина которого лежит на окружности, а его стороны пересекают окружность.
Центральный угол – угол, вершина которого лежит в центре окружности, а его стороны пересекают окружность.
Дуга – часть окружности, ограниченная с двух сторон.
Вписанный угол равен половине дуги, на которую он опирается.
Центральный угол равен дуге, на которую он опирается.
Следствия из измерений центрального и вписанного углов:
1) вписанный угол равен половине центрального угла, опирающегося на ту же дугу;
2) если вписанные углы опираются на одну и ту же дугу, то они равны;
3) вписанный угол, опирающийся на диаметр равен 90 градусов.
Серединный перпендикуляр – прямая, проходящая через середину отрезка под углом 90 градусов.
Четыре замечательные точки треугольника:
· биссектрисы треугольника пересекаются в одной точке;
· медианы треугольника пересекаются в одной точке;
· высоты треугольника пересекаются в одной точке;
· серединные перпендикуляры треугольника пересекаются в одной точке.
Теорема о биссектрисе:
Любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.
Теорема о медианах:
Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1, считая от вершины.
Теорема о серединном перпендикуляре:
Любая точка, лежащая на серединном перпендикуляре, проведенному к отрезку, равноудалена от концов этого отрезка.
Вписанная окружность – окружность, касающаяся всех сторон фигуры.
Описанная окружность – окружность, проходящая через каждую вершину фигуры.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru