Методическая разработка (алгебра, 8 класс) по теме: таблицы — шпоргалки по алгебре и геометрии 8 класс
Алгоритм выделения полного квадрата
Сперва рассматриваем приведённое квадратное уравнение, одновременно выделяя алгоритм решения квадратных уравнений данным приёмом.
х2 – 6х – 7 = 0.
1-й ш а г. Записываем второй коэффициент в виде произведения двойки и некоторого числа: b = 2п.
х2 – 6х – 7 = х2 – 2 · 3х – 7.
2-й ш а г. Число п представляет собой второе слагаемое в искомом квадрате двучлена: п = 3. Для того чтобы получить искомый квадрат двучлена (х – n)2 = х2 – 2 · х · п + n2, необходимо прибавить п2 и одновременно вычесть его:
х2 – 2 · 3х – 7 = х2 – 2 · 3х + 9 – 9 – 7.
3-й ш а г. Выделяем квадрат двучлена:
х2 – 6х – 7 = х2 – 2 · 3х + 9 – 16 = (х – 3)2 – 16.
4-й ш а г. Решаем полученное уравнение, равносильное исходному:
(х – 3)2 – 16 = 0;
(х – 3)2 = 16;
х – 3 = 4 или х – 3 = –4;
х = 7 или х = –1.
О т в е т: –1; 7.
Алгоритм выделения полного квадрата
Сперва рассматриваем приведённое квадратное уравнение, одновременно выделяя алгоритм решения квадратных уравнений данным приёмом.
х2 – 6х – 7 = 0.
1-й ш а г. Записываем второй коэффициент в виде произведения двойки и некоторого числа: b = 2п.
х2 – 6х – 7 = х2 – 2 · 3х – 7.
2-й ш а г. Число п представляет собой второе слагаемое в искомом квадрате двучлена: п = 3. Для того чтобы получить искомый квадрат двучлена (х – n)2 = х2 – 2 · х · п + n2, необходимо прибавить п2 и одновременно вычесть его:
х2 – 2 · 3х – 7 = х2 – 2 · 3х + 9 – 9 – 7.
3-й ш а г. Выделяем квадрат двучлена:
х2 – 6х – 7 = х2 – 2 · 3х + 9 – 16 = (х – 3)2 – 16.
4-й ш а г. Решаем полученное уравнение, равносильное исходному:
(х – 3)2 – 16 = 0;
(х – 3)2 = 16;
х – 3 = 4 или х – 3 = –4;
х = 7 или х = –1.
О т в е т: –1; 7.
nsportal.ru
|
1. Произвольный треугольник (длины сторон, лежащих против вершин A, B и C, равны a, b, c соответственно; , , — величины углов A, B и C; p — полупериметр; R — радиус описанной окружности;r — радиус вписанной окружности; S — площадь; hA — высота, проведенная из вершины A): |
|
|
2. Прямоугольный треугольник (a, b — катеты; c — гипотенуза; ac, bc — проекции катетов на гипотенузу): |
|
|
3. Равносторонний треугольник: |
|
|
4. Произвольный четырехугольник (d1 и d2 — диагонали; — угол между ними; S — площадь): |
|
|
5. Параллелограмм (a и b — смежные стороны; — угол между ними;ha — высота, проведенная к стороне a): |
|
|
6. Ромб: |
|
|
7. Прямоугольник: |
|
|
8. Квадрат (d — диагональ): |
|
|
9. Трапеция (a и b — основания; h — расстояние между ними; l — средняя линия): |
|
|
10. Описанный многоугольник (p — периметр; r — радиус вписанной окружности): |
|
|
11. Правильный многоугольник (an — сторона правильного n-угольника; R — радиус описанной окружности; r — радиус вписанной окружности): |
|
|
12. Окружность, круг (r — радиус; c — длина окружности; S — площадь круга): |
|
|
13. Сектор (l — длина дуги, ограничивающей сектор; no — градусная мера соответствующего центрального угла; — радианная мера центрального угла): |
nsportal.ru
Формулы геометрии. Площади фигур. — материалы для подготовки к ЕГЭ по Математике
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
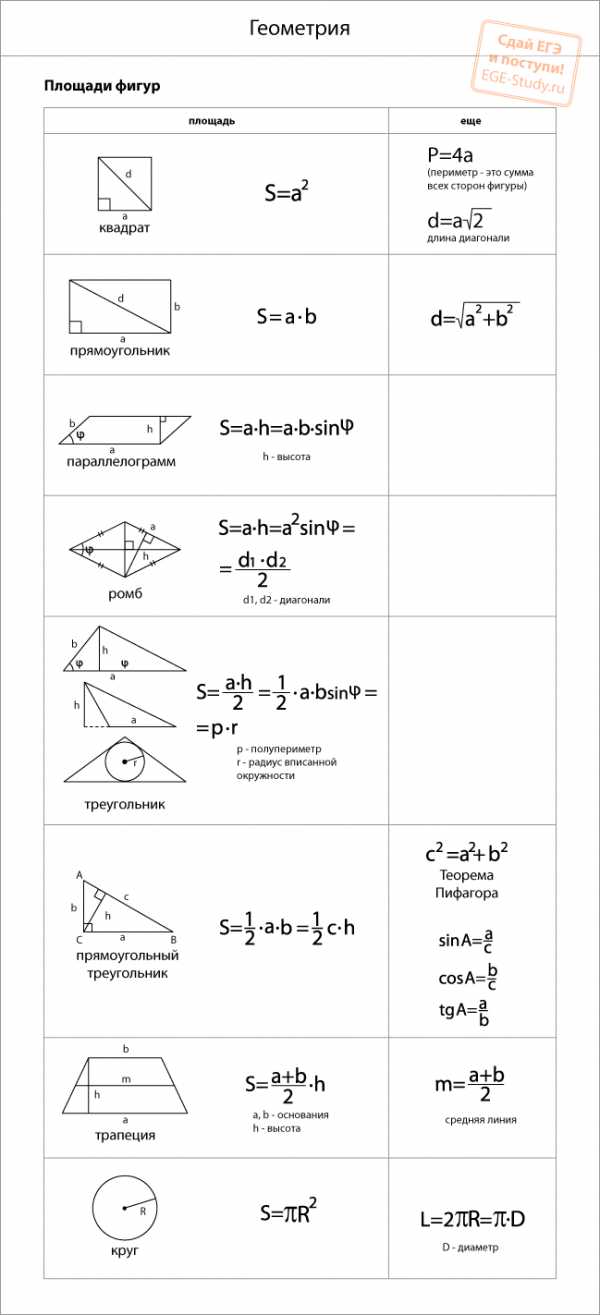
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
Ты нашел то, что искал? Поделись с друзьями!
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
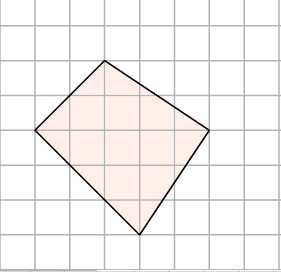
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
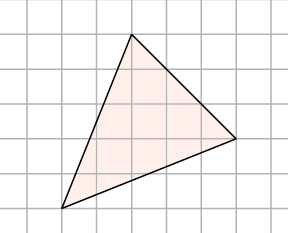
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
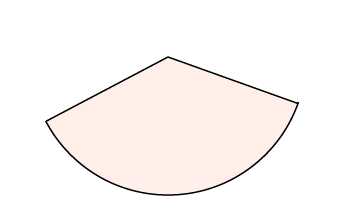
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: .
Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.
Звоните нам:
8 (800) 775-06-82 (бесплатный звонок по России)
+7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
8 класс. Геометрия. Площадь. Площадь треугольника и трапеции. — Повторение темы «Площадь». Решение задач.
Комментарии преподавателя
Повторение темы «Площадь». Решение задач
1. Повторение теоретической части главы «Площадь»
Вначале уделим внимание тому, что вспомним все основные теоремы, формулы и факты, полученные нами при изучении главы «Площадь», и акцентируем внимание на их особенностях. Затем рассмотрим сложный пример на комплексное применение нескольких из упомянутых фактов, касающихся площадей фигур.
1. Площадь квадрата равна квадрату его стороны (см. Рис. 1). .
Рис. 1. Квадрат
2. Площадь прямоугольника равна произведению его сторон (см. Рис. 2). .
Рис. 2. Прямоугольник
3. Площадь параллелограмма равна произведению основания на опущенную на него высоту (см. Рис. 3). .
Рис. 3. Параллелограмм
4. Площадь произвольного треугольника равна половине произведения основания на опущенную на него высоту (см. Рис. 4). .
Рис. 4. Произвольный треугольник
5. Площадь прямоугольного треугольника равна половине произведения катетов (см. Рис. 5). .
Рис. 5. Прямоугольный треугольник
6. Если у двух треугольников высоты равны (), то их площади относятся, как основания (см. Рис. 6). .
www.kursoteka.ru