Контроль знаний и умений по геометрии 8 класс (УМК Л.С. Атанасян)
Самостоятельные и контрольные работы по геометрии для 8 класса (по УМК Л.С. Атанасян)
1 вариант
Самостоятельные работы

С.р. №2 Параллелограмм и трапеция

С.р. №3 Параллелограмм и трапеция

С.р. №4 Прямоугольник. Ромб. Квадрат.
С.р. №5 Площадь многоугольника, прямоугольника, квадрата.
С.р. №6 Площадь параллелограмма, треугольника, трапеции

С.р. №7 Теорема Пифагора
С.р. №8 Определение подобных треугольников

С.р. №9 Признаки подобия треугольников
С.р. №10 Применение подобия к решению задач

С.р. №11 Соотношения между сторонами и углами в прямоугольном треугольнике

С.р. №12 Касательная к окружности


С.р. №14 Четыре замечательные точки треугольника
С.р. №15 Вписанная и описанная окружности
С.р. №16 Решение задач
С.р. №17 Решение задач
Контрольные работы

К.р. №2 по теме «Площадь»

К.р. №3 по теме «Подобные треугольники»
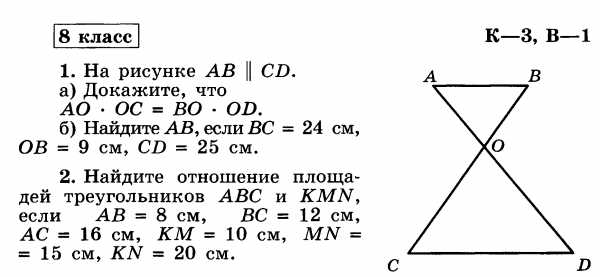
К.р. №4 по теме «Подобные треугольники»

К.р.№5 по теме «Окружность»

infourok.ru
Материал по геометрии (8 класс) на тему: Самостоятельная работа по геометрии 8 класс (Л.С. Атанасян) «Площади многоугольников «
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 1 1.Пусть а- основание, h – высота, S – площадь параллелограмма. Найдите : а) S, если а = 1,5 м, h = 1,2 м; б) а, если S = 34 см2 , h = 8,5 см. 2.Периметр прямоугольника равен 26 см, а одна из его сторон равна 9 см. Найдите сторону квадрата, имеющего такую же площадь, как этот прямоугольник. 3.Сторона ромба равна 8,6 см, а один из углов ромба равен 300. Найдите площадь ромба. |
Вариант — 2 1.Найдите площадь трапеции АВСD с основаниями АВ и СD, если: а)АВ = 2,1 м, СD =1,7м, высота DH = 0,7 м, б)h, если S = 77см2, СD = 13 см, а другое основание AB на 4 см меньше CD. 2.Диагональ параллелограмма, равная 24,2см, перпендикулярна к стороне параллелограмма, равной 38 см. Найдите площадь параллелограмма. 3.Дан ∆АВС, сторона АВ =11,4 см, АС = 17,6 см и угол между ними равен 300. Найдите площадь треугольника. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 3 1.Найдите площадь прямоугольного треугольника, если его катеты равны: а)6,2 см и 8,7 см; б) найти катет, если S = 30,78 см2 и другой катет равен 7,6см. 2.Найти площадь равнобедренной трапеции ABCD, если высота BH = 9см, основание ВС =9см, а отрезок AH = 3 см. 3.В параллелограмме диагональ BD=18,8см и она равна стороне АВ, а А = 300. Найдите площадь параллелограмма, если сторона AD = 20, 7 см. |
Вариант — 4 1.Пусть а- основание, h – высота, S – площадь треугольника. Найдите : а) S, если а = 7, 5 м, h = 11,2 м; б) а, если S = 21 см2 , h = 3,5 см. 2. Смежные стороны параллелограмма равны1,2м и 1,4м, а его острый угол равен 300. Найдите площадь параллелограмма. 3. Известно, что площадь ромба равна половине произведения его диагоналей. Найдите диагонали ромба, если одна из них в 1,5 раза меньше другой, а площадь ромба равна 37,5 см2. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 5 1.Пусть а- основание, h – высота, S – площадь параллелограмма. Найдите : а) S, если а = 3,5 м, h = 1,8 м; б) а, если S = 54 см2 , h = 4,5 см. 2.Периметр прямоугольника равен 40 см, а одна из его сторон равна 4 см. Найдите сторону квадрата, имеющего такую же площадь, как этот прямоугольник. 3.Сторона ромба равна 5,8 см, а один из углов ромба равен 300. Найдите площадь ромба. |
Вариант — 6 1.Найдите площадь трапеции АВСD с основаниями АВ и СD, если: а)АВ = 3,2 м, СD =2,6м, высота DH = 1,2 м, б)h, если S = 64,8см2, СD = 15 см, а другое основание AB на 3 см меньше CD. 2.Диагональ параллелограмма, равная 29,4см, перпендикулярна к стороне параллелограмма, равной 42 см. Найдите площадь параллелограмма. 3.Дан ∆АВС, сторона АВ =21,6 см, АС = 27,3 см и угол между ними равен 300. Найдите площадь треугольника. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 7 1.Найдите площадь прямоугольного треугольника, если его катеты равны: а)7,4 см и 6,4 см; б) найти катет, если S = 34,2 см2 и другой катет равен 7,2 см. 2.Найти площадь равнобедренной трапеции ABCD, если высота BH = 11см, основание ВС =12см, а отрезок AH = 4 см. 3.В параллелограмме диагональ BD = 22,6 см и она равна стороне АВ, а А = 300. Найдите площадь параллелограмма, если сторона AD = 28, 3 см. |
Вариант — 8 1.Пусть а- основание, h – высота, S – площадь треугольника. Найдите : а) S, если а = 4, 6 м, h = 2,8 м; б) а, если S = 46,17 см2 , h = 5,4 см. 2. Смежные стороны параллелограмма равны7,8м и 8,2м, а его острый угол равен 300. Найдите площадь параллелограмма. 3. Известно, что площадь ромба равна половине произведения его диагоналей. Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 168,75 см2. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 9 1.Пусть а- основание, h – высота, S – площадь параллелограмма. Найдите : а) S, если а = 9,1 м, h = 5,5 м; б) а, если S = 36,27 см2 , h = 3,9 см. 2.Периметр прямоугольника равен 32,8 см, а одна из его сторон равна 6,4 см. Найдите сторону квадрата, имеющего такую же площадь, как этот прямоугольник. 3.Сторона ромба равна 18,6 см, а один из углов ромба равен 300. Найдите площадь ромба. |
Вариант — 10 1.Найдите площадь трапеции АВСD с основаниями АВ и СD, если: а)АВ = 5,8 м, СD =2,4м, высота DH = 0,8 м, б)h, если S = 101,7см2, СD = 12,8см, а другое основание AB на 3 см меньше CD. 2.Диагональ параллелограмма, равная 24,4см, перпендикулярна к стороне параллелограмма, равной 47 см. Найдите площадь параллелограмма. 3.Дан ∆АВС, сторона АВ =18,4 см, АС = 21,3 см и угол между ними равен 300. Найдите площадь треугольника. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 11 1.Найдите площадь прямоугольного треугольника, если его катеты равны: а)9,2 см и 7,7 см; б) найти катет, если S = 106,5 см2 и другой катет равен 14,2 см. 2.Найти площадь равнобедренной трапеции ABCD, если высота BH = 11см, основание ВС =18см, а отрезок AH = 2,5 см. 3.В параллелограмме диагональ BD = 14,8 см и она равна стороне АВ, а А = 300. Найдите площадь параллелограмма, если сторона AD = 22, 3 см. |
Вариант — 12 1.Пусть а- основание, h – высота, S – площадь треугольника. Найдите : а) S, если а = 2, 3 м, h = 2,2 м; б) а, если S = 51,48 см2 , h = 7,8 см. 2. Смежные стороны параллелограмма равны 4,2м и 8,2м, а его острый угол равен 300. Найдите площадь параллелограмма. 3. Известно, что площадь ромба равна половине произведения его диагоналей. Найдите диагонали ромба, если одна из них в 1,5 раза меньше другой, а площадь ромба равна 216,75см2. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 13 1.Пусть а- основание, h – высота, S – площадь параллелограмма. Найдите : а) S, если а = 4,4 м, h = 8,9 м; б) а, если S = 157,78 см2 , h = 16,1 см. 2.Периметр прямоугольника равен 52 см, а одна из его сторон равна 8 см. Найдите сторону квадрата, имеющего такую же площадь, как этот прямоугольник. 3.Сторона ромба равна 23,4 см, а один из углов ромба равен 300. Найдите площадь ромба. |
Вариант — 14 1.Найдите площадь трапеции АВСD с основаниями АВ и СD, если: а)АВ = 5,6 м, СD =9,2м, высота DH = 1,4 м, б)h, если S = 136,4см2, СD = 19 см, а другое основание AB на 7 см меньше CD. 2.Диагональ параллелограмма, равная 29,7см, перпендикулярна к стороне параллелограмма, равной 43 см. Найдите площадь параллелограмма. 3.Дан ∆АВС, сторона АВ =13,2см, АС = 12,9 см и угол между ними равен 300. Найдите площадь треугольника. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 15 1.Найдите площадь прямоугольного треугольника, если его катеты равны: а)2,8 см и 6,5 см; б) найти катет, если S = 84,32 см2 и другой катет равен 13,6см. 2.Найти площадь равнобедренной трапеции ABCD, если высота BH = 10,5см, основание ВС =13см, а отрезок AH = 2 см. 3.В параллелограмме диагональ BD=19,4см и она равна стороне АВ, а А = 300. Найдите площадь параллелограмма, если сторона AD = 15, 3 см. |
Вариант — 16 1.Пусть а- основание, h – высота, S – площадь треугольника. Найдите : а) S, если а = 13, 4 м, h = 21,1 м; б) а, если S = 44,66 см2 , h = 7,7 см. 2. Смежные стороны параллелограмма равны4,8м и 5,9м, а его острый угол равен 300. Найдите площадь параллелограмма. 3. Известно, что площадь ромба равна половине произведения его диагоналей. Найдите диагонали ромба, если одна из них в 1,6 раза меньше другой, а площадь ромба равна 51,2 см2. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 17 1.Пусть а- основание, h – высота, S – площадь параллелограмма. Найдите : а) S, если а = 11,5 м, h = 8,2 м; б) а, если S = 112,56 см2 , h = 6,7 см. 2.Периметр прямоугольника равен 80 см, а одна из его сторон равна 32 см. Найдите сторону квадрата, имеющего такую же площадь, как этот прямоугольник. 3.Сторона ромба равна 12,6 см, а один из углов ромба равен 300. Найдите площадь ромба. |
Вариант — 18 1.Найдите площадь трапеции АВСD с основаниями АВ и СD, если: а)АВ = 8,3 м, СD =3,7м, высота DH = 0,9 м, б)h, если S = 165см2, СD = 15,5 см, а другое основание AB на 3,5 см меньше CD. 2.Диагональ параллелограмма, равная 34,4см, перпендикулярна к стороне параллелограмма, равной 42 см. Найдите площадь параллелограмма. 3.Дан ∆АВС, сторона АВ =15,8 см, АС = 12,6 см и угол между ними равен 300. Найдите площадь треугольника. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 19 1.Найдите площадь прямоугольного треугольника, если его катеты равны: а)3,6 см и 7,5 см; б) найти катет, если S = 88,2 см2 и другой катет равен 12,6см. 2.Найти площадь равнобедренной трапеции ABCD, если высота BH = 18см, основание ВС =19см, а отрезок AH = 5 см. 3.В параллелограмме диагональ BD=10,6см, и она равна стороне АВ, а А = 300. Найдите площадь параллелограмма, если сторона AD = 16, 3 см. |
Вариант — 20 1.Пусть а- основание, h – высота, S – площадь треугольника. Найдите : а) S, если а = 10, 8 м, h = 12,3 м; б) а, если S = 40,74 см2 , h = 8,4 см. 2. Смежные стороны параллелограмма равны6,3м и 4,6м, а его острый угол равен 300. Найдите площадь параллелограмма. 3. Известно, что площадь ромба равна половине произведения его диагоналей. Найдите диагонали ромба, если одна из них в 1,4 раза меньше другой, а площадь ромба равна 25,2 см2. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 21 1.Пусть а- основание, h – высота, S – площадь параллелограмма. Найдите : а) S, если а = 1,5 м, h = 1,2 м; б) а, если S = 34 см2 , h = 8,5 см. 2.Периметр прямоугольника равен 26 см, а одна из его сторон равна 9 см. Найдите сторону квадрата, имеющего такую же площадь, как этот прямоугольник. 3.Сторона ромба равна 8,6 см, а один из углов ромба равен 300. Найдите площадь ромба. |
Вариант — 22 1.Найдите площадь трапеции АВСD с основаниями АВ и СD, если: а)АВ = 2,1 м, СD =1,7м, высота DH = 0,7 м, б)h, если S = 77см2, СD = 13 см, а другое основание AB на 4 см меньше CD. 2.Диагональ параллелограмма, равная 24,2см, перпендикулярна к стороне параллелограмма, равной 38 см. Найдите площадь параллелограмма. 3.Дан ∆АВС, сторона АВ =11,4 см, АС = 17,6 см и угол между ними равен 300. Найдите площадь треугольника. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 23 1.Найдите площадь прямоугольного треугольника, если его катеты равны: а)6,2 см и 8,7 см; б) найти катет, если S = 30,78 см2 и другой катет равен 7,6см. 2.Найти площадь равнобедренной трапеции ABCD, если высота BH = 9см, основание ВС =9см, а отрезок AH = 3 см. 3.В параллелограмме диагональ BD=18,8см и она равна стороне АВ, а А = 300. Найдите площадь параллелограмма, если сторона AD = 20, 7 см. |
Вариант — 24 1.Пусть а- основание, h – высота, S – площадь треугольника. Найдите : а) S, если а = 7, 5 м, h = 11,2 м; б) а, если S = 21 см2 , h = 3,5 см. 2. Смежные стороны параллелограмма равны1,2м и 1,4м, а его острый угол равен 300. Найдите площадь параллелограмма. 3. Известно, что площадь ромба равна половине произведения его диагоналей. Найдите диагонали ромба, если одна из них в 1,5 раза меньше другой, а площадь ромба равна 37,5 см2. |
|
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
Самостоятельная работа по геометрии (40-45 мин) Глава VI 8 класс «Площади многоугольников» |
|
Вариант — 25 1.Пусть а- основание, h – высота, S – площадь параллелограмма. Найдите : а) S, если а = 3,5 м, h = 1,8 м; б) а, если S = 54 см2 , h = 4,5 см. 2.Периметр прямоугольника равен 40 см, а одна из его сторон равна 4 см. Найдите сторону квадрата, имеющего такую же площадь, как этот прямоугольник. 3.Сторона ромба равна 5,8 см, а один из углов ромба равен 300. Найдите площадь ромба. |
Вариант — 26 1.Найдите площадь трапеции АВСD с основаниями АВ и СD, если: а)АВ = 3,2 м, СD =2,6м, высота DH = 1,2 м, б)h, если S = 64,8см2, СD = 15 см, а другое основание AB на 3 см меньше CD. 2.Диагональ параллелограмма, равная 29,4см, перпендикулярна к стороне параллелограмма, равной 42 см. Найдите площадь параллелограмма. 3.Дан ∆АВС, сторона АВ =21,6 см, АС = 27,3 см и угол между ними равен 300. Найдите площадь треугольника. |
Ответы:
В-1 (В-21) 1) а) S=1,8м2 , б) а=4см. 2) а=6см. 3) S=36,98см2;
В-2 (В-22) 1) а) S=1,33м2 , б) h=7см. 2) S=919,6см2. 3) S=50,16см2;
В-3 (В-23) 1) а) S=26,97см2 , б) а=8,1см. 2) S=108см2. 3) S=194,58см2;
В-4 (В-24) 1) а) S=42м2 , б) а=12см. 2) S =0,84м2. 3) d1=5см, d2=7,5см;
В-5 (В-25) 1) а) S=6,3м2 , б) а=12см. 2) а=8см. 3) S=16,82см2;
В-6 (В-26) 1) а) S=3,48м2 , б) h=4,8см. 2) S =1234,8см2. 3) S=147,42см2;
В-7 1) а) S=23,68см2 , б) а=9,5см. 2) S=176см2. 3) S=319,79см2;
В-8 1) а) S=6,44м2 , б) а=17,1см. 2) S=31,98м2. 3) d1=15см, d2=22,5см;
В-9 1) а) S=50,05м2 , б) а=9,3см. 2) а=8см. 3) S=172,98см2;
В-10 1) а) S=3,28м2 , б) h=9см. 2) S =1146,8см2. 3) S=97,98см2;
В-11 1) а) S=35,42см2 , б) а=15см. 2) S =225,5см2 3) S=165,02см2;
В-12 1) а) S=2,53м2 , б) а=13,2см. 2) S =17,22м2 3) d1=17см, d2=25,5см;
В-13 1) а) S=39,16м2 , б) а=9,8см. 2) а=12см. 3) S=273,78см2;
В-14 1) а) S=10,36м2 , б) h =8,8см. 2). S =1277,1см2 3) S=42,57см2;
В-15 1) а) S=9,1см2 , б) а=12,4см. 2). S =157,5см2 3) S=148,41см2;
В-16 1) а) S=141,37м2 ,б) а=11,6см. 2) S =14,16м2 3) d1=8см, d2=12,8см;
В-17 1) а) S=94,3м2 , б) а=16,8см. 2) а=16см. 3) S=79,38см2;
В-18 1) а) S=5,4м2 , б) h=12см. 2). S =1444,8см2 3) S=49,77см2;
В-19 1) а) S=13,5см2 , б) а=14см. 2). S =432см2 3) S=86,39см2;
В-20 1) а) S=66,42м2 , б) а=9,7см. 2) S =14,49см2 3) d1=6см, d2=8,4см;
nsportal.ru
Самостоятельные работы по геометрии для 8 класса.
Просмотр содержимого документа
«1. Самостоятельная работа — Многоугольники»
Самостоятельная работа по геометрии в 8 классе по теме «Многоугольники»
Вариант 1
1.Найти сумму углов выпуклого двенадцатиугольника.
2.Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 2160 градусов?
3.Каждый угол выпуклого многоугольника равен 162 градуса. Найдите число сторон этого многоугольника.
4.В выпуклом пятиугольнике две стороны равны, третья сторона на 3 см больше, а четвертая в 2 раза больше первой стороны, пятая – на 4 см меньше четвертой. Найдите стороны пятиугольника, если известно, что его периметр равен 34 см.
Самостоятельная работа по геометрии в 8 классе по теме «Многоугольники»
Вариант 2
1.Найти сумму углов выпуклого тринадцатиугольника.
2.Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 2520 градусов?
3.Каждый угол выпуклого многоугольника равен 165 градуов. Найдите число сторон этого многоугольника.
4.В выпуклом шестиугольнике три стороны равны, четвертая в два раза больше первой стороны, пятая — на 3 см меньше четвертой, а шестая – на 1 см больше второй. Найдите стороны шестиугольника, если известно, что его периметр равен 30 см.
Самостоятельная работа по геометрии в 8 классе по теме «Многоугольники»
Вариант 1
1.Найти сумму углов выпуклого двенадцатиугольника.
2.Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 2160 градусов?
3.Каждый угол выпуклого многоугольника равен 162 градуса. Найдите число сторон этого многоугольника.
4.В выпуклом пятиугольнике две стороны равны, третья сторона на 3 см больше, а четвертая в 2 раза больше первой стороны, пятая – на 4 см меньше четвертой. Найдите стороны пятиугольника, если известно, что его периметр равен 34 см.
Самостоятельная работа по геометрии в 8 классе по теме «Многоугольники»
Вариант 2
1.Найти сумму углов выпуклого тринадцатиугольника.
2.Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 2520 градусов?
3.Каждый угол выпуклого многоугольника равен 165 градуов. Найдите число сторон этого многоугольника.
4.В выпуклом шестиугольнике три стороны равны, четвертая в два раза больше первой стороны, пятая — на 3 см меньше четвертой, а шестая – на 1 см больше второй. Найдите стороны шестиугольника, если известно, что его периметр равен 30 см.
Просмотр содержимого документа
«11. Самостоятельная работа — Подобные треугольники»
Просмотр содержимого документа
«15. Реальная математика — Подобие треугольников»
Просмотр содержимого документа
«17. Контрольная работа — Соотношение сторон и углов в пр треугольнике»
multiurok.ru
|
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
|
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
|
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
|
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
|
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
|
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
|
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
|
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
|
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
|
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
№1 Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45º. №2 Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МNР равен 80º. |
nsportal.ru
Промежуточные самостоятельные работы по геометрии 8 класс по учебнику Атанасяна
Самостоятельная работа по теме «Площади» 8 класс вариант№1
5)
.Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
6).Найдите площадь параллелограмма, изображённого на рисунке.
9).Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Решение.
Площадь трапеции вычисляется по формуле
где и — основания, а — высота трапеции. Найдём высоту: следовательно,
Ответ: 15.
Ответ: 15
10)Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
11) В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
12).В прямоугольнике одна сторона равна 10, периметр равен 44. Найдите площадь прямоугольника.
13).В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника
14).Найдите площадь ромба, если его диагонали равны 14 и 6.
Самостоятельная работа по теме «Площади» 8 класс вариант№2
|
.6). Найдите площадь параллелограмма, изображённого на рисунке |
|
|
9)В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции. Решение. Введём обозначения, как показано на рисунке. Тогда Треугольник прямоугольный и равнобедренный, тогда высота равна 3. Откуда
Ответ: Ответ: 18 |
|
|
10) Сторона ромба равна 8, а расстояние от центра ромба до неё равно 2. Найдите площадь ромба. |
|
|
11)В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC. |
|
|
12) В прямоугольнике одна сторона равна 15, периметр равен54. Найдите площадь прямоугольника. |
|
|
13) В прямоугольном треугольнике один из катетов равен 8, а прилежащий к нему угол, равен 45°. Найдите площадь треугольника |
14).Найдите площадь ромба, если его диагонали равны 27 и 4. |
Самостоятельная работа 8 класс по теме « Прямоугольные треугольники»
1)
В треугольнике угол равен 90°, . Найдите .
2) В треугольнике угол равен 90°, Найдите
2) Катеты прямоугольного треугольника равны и 1. Найдите синус наименьшего угла этого треугольника.
3) В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите
3) Площадь прямоугольного треугольника равна Один из острых углов равен 30°. Найдите длину гипотенузы.
4)
4)
5)
5) В прямоугольном треугольнике катет , а высота , опущенная на гипотенузу, равна Найдите
6) Высота равностороннего треугольника равна Найдите его периметр.
6) В треугольнике ABC AB = BC, а высота AH делит сторону BC на отрезки BH = 64 и CH = 16. Найдите cosB.
Самостоятельная работа по теме « Площади. Теорема Пифагора» 8 класс
Вариант №1 Вариант № 2
Самостоятельная работа по теме « Касательные и хорды» 8 класс
1) вариант №2
2)
2)
3)
3)
4)
4)
Домашняя самостоятельная работа по теме « Вписанная и описанная окружности»
1)
2)
2)
3)
3)
4)
4)
5)
5)
6)
6)
7)
7)
infourok.ru
Самостоятельные работы по геометрии (8 класс)
Самостоятельные работы по геометрии
(8 класс)
Самостоятельная работа обучающего характера № 1.
1 вариант.
-
Найдите сумму углов выпуклого одиннадцатиугольника.
-
Каждый угол выпуклого многоугольника равен 1350. Найти число сторон этого многоугольника.
2 вариант.
-
Найдите сумму углов выпуклого двенадцатиугольника.
-
Сумма углов выпуклого многоугольника равна 12600. Найти число сторон этого многоугольника.
Проверочная самостоятельная работа № 2.
1 вариант
-
ABCD – параллелограмм. Луч AN – биссектриса угла BAD; луч ВМ – биссектриса угла АВС. Докажите, что ABNM – параллелограмм.
2 вариант
-
ABCD – параллелограмм. Луч AM – биссектриса угла BAD; луч CN – биссектриса угла ВСD. Докажите, что ANCM – параллелограмм.
Проверочная самостоятельная работа № 3.
1 вариант
-
Найти боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 1200.
2 вариант
-
Найти меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая сторона — 10 см, а один из углов равен 600.
Самостоятельная работа обучающего характера № 4.
Прямоугольник, ромб, квадрат
1 вариант.
-
Найдите углы ромба, если его диагонали составляют с его стороной угол, равный 300 .
-
В квадрате АВСD проведена диагональ ВD. Найти углы треугольника ВСD.
2 вариант.
-
Угол между диагоналями прямоугольника равен 500. Найти углы между диагональю прямоугольника и его сторонами.
-
В ромбе АВСD проведены диагонали, которые пересекаются в точке О. Найти углы треугольника АОВ, если тупой угол ромба 1200 .
Проверочная самостоятельная работа № 5.
1 вариант
-
Через точку пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AD и ВС в точках Е и F соответственно. Найти стороны параллелограмма, если его периметр равен 28 см, АЕ = 5 см, BF = 3 см
-
Найти меньшую боковую сторону прямоугольной трапеции, основания которой равны 10 см и 6 см, а один из углов равен 450.
2 вариант
-
Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Найти стороны параллелограмма, если его периметр равен 36 см.
-
Найти боковую сторону равнобедренной трапеции, основания которой равны 12 см и 6 см, а один из углов равен 600.
Самостоятельная работа обучающего характера № 6.
1 вариант.
-
ABCD – прямоугольник, точка М – середина стороны ВС. Периметр прямоугольника равен 48 см, а сторона AD вдвое больше стороны АВ. Найти: а) площадь прямоугольника ABCD; б) площадь треугольника ADN;
2 вариант.
-
ABCD – прямоугольник, точка C – середина стороны ВF. Периметр прямоугольника равен 46 см, а сторона BC вдвое больше стороны АВ. Найти: а) площадь прямоугольника ABCD; б) площадь треугольника ABF;
Самостоятельная работа обучающего характера № 7.
1 вариант.
-
Стороны параллелограмма равны 10 см и 6 см, а угол между ними 1500. Найти площадь этого параллелограмма.
2 вариант.
-
Острый угол параллелограмма равен 300 , а высоты, проведенные из вершины тупого угла, равны 4 см и 3 см. Найти площадь этого параллелограмма.
Самостоятельная работа обучающего характера № 8.
1 вариант.
-
ОА = ОВ, ОС = 2ОD, SAOD = 12 см2. Найти площадь треугольника ВОС
2 вариант.
-
ОB = ОC, ОD = 3AО, SAOC = 16 см2. Найти площадь треугольника ВОD
Самостоятельная работа обучающего характера № 9.
1 вариант.
-
Высота и основания трапеции относятся как 5 : 6 : 4. Найдите меньшее основание трапеции, если ее площадь равна 88 см2.
2 вариант.
-
Высота трапеции равна меньшему основанию и в два раза меньше большего основания этой трапеции. Найдите высоту трапеции, если ее площадь равна 54 см2.
Проверочная самостоятельная работа № 10.
1 вариант
-
В прямоугольной трапеции основания равны 22 см и 6 см, а большая боковая сторона – 20 см. Найти площадь трапеции.
2 вариант
-
Боковые стороны прямоугольной трапеции равны 7 см и 25 см, а меньшее основание – 2 см. Найти площадь трапеции.
Итоговая самостоятельная работа № 11.
1 вариант
-
В треугольнике АВС угол А равен 450, ВС = 13 см, а высота BD отсекает на стороне АС отрезок DC, равный 12 см. Найти площадь треугольника АВС и высоту, проведенную к стороне ВС.
-
Одна из диагоналей ромба на 4 см больше другой, а площадь ромба равна 96 см2. Найти стороны ромба.
2 вариант
-
В треугольнике АВС угол В равен 450, высота AN делит сторону ВС на отрезки BN = 8 см, NC = 6 см. Найти площадь ∆ АВС и сторону АС.
-
Найдите площадь ромба, если его сторона равна 20 см, а диагонали относятся как 3 : 4.
Самостоятельная работа обучающего характера № 12.
1 вариант.
-
∆АВС ∞ ∆KMN, АС = 3 см, MN = 4 см, А = 300. Найти: а) ВС, MKN; б) SABC : SKMN ; в) отношение, в котором биссектриса угла С делит сторону АВ
2 вариант.
-
∆PQR ∞ ∆АВС , PQ = 3 см, PR = 4 см, А = 400. Найти: а) AС, QPR; б) SPQR : SABC ; в) отношение, в котором биссектриса угла P делит сторону RQ
Проверочная самостоятельная работа № 13.
1 вариант
-
Высота CD прямоугольного треугольника АВС делит гипотенузу АВ на части AD = 16 cм и BD = 9 см. Докажите, что ∆АСD ∞ ∆CBD и найдите высоту CD
-
Точки М и N лежат на сторонах АС и ВС треугольника АВС соответственно; АС = 16 см, ВС = 12 см, СМ = 12 см, CN = 9 см. Докажите, что MN || BC.
2 вариант
-
Высота CD прямоугольного треугольника АВС отсекает от гипотенузы АВ = 9 см отрезок AD = 4 cм. Докажите, что ∆АВС ∞ ∆АCD и найдите высоту АC
-
Диагонали АС и ВD четырехугольника АВСD пересекаются в точке О; АО = 18 см, ОВ = 15 см, ОС = 12 см, ОD = 10 см. Докажите, что ABCD – трапеция.
Проверочная самостоятельная работа № 14.
1 вариант
-
Площадь ромба равна 48 см2. Найдите площадь четырехугольника, вершинами которого являются середины сторон данного ромба.
2 вариант
-
Площадь прямоугольника равна 36 см2. Найдите площадь четырехугольника, вершинами которого являются середины сторон данного прямоугольника.
Проверочная самостоятельная работа № 15.
1 вариант
-
На рис. 197 в учебнике AD = 16 см, CD = 12 см. Найти АС, ВС, АВ, BD.
-
Начертите отрезок и разделите его в отношении 2 : 7.
2 вариант
-
На рис. 197 в учебнике ВС = 3 см, CD =
 см. Найти АВ, АС, AD, BD.
см. Найти АВ, АС, AD, BD. -
Начертите отрезок и разделите его в отношении 5 : 4.
Проверочная самостоятельная работа № 16.
1 вариант
-
Постройте прямоугольный треугольник по острому углу и медиане, проведенной из вершины этого угла.
2 вариант
-
Постройте прямоугольный треугольник по острому углу и биссектрисе прямого угла.
Проверочная самостоятельная работа № 17.
1 вариант
-
В равнобедренной трапеции меньшее основание равно 4 см, боковая сторона – 6 см, а один из углов – 1200. Найти площадь трапеции.
2 вариант
-
В прямоугольной трапеции меньшее основание равно 3 см, большая боковая сторона – 4 см, а один из углов – 1500. Найти площадь трапеции.
Проверочная самостоятельная работа № 18.
1 вариант
-
Из точки К к окружности с центром О проведены две прямые, касающиеся данной окружности в точках M и N. Найти КМ и КN, если ОК = 12 см, MON = 1200.
-
Диагонали ромба ABCD пересекаются в точке О. Докажите, что прямая BD касается окружности с центром А и радиусом, равным ОС.
2 вариант
-
Из точки К к окружности с центром О проведены две прямые, касающиеся данной окружности в точках M и N. Найти КМ и КN, если ОМ = 9 см, MКN = 1200.
-
BD – медиана равнобедренного треугольника АВС с основанием АС. Докажите, что прямая BD касается окружности с центром С и радиусом, равным AD.
Проверочная самостоятельная работа № 19.
1 вариант
-
Вершины треугольника АВС лежат на окружности с центром О, АOВ = 800, АС : ВС = 2 : 3. Найти углы треугольника АВС.
-
Хорды MN и KL окружности пересекаются в точке А, причем хорда MN делится точкой А на отрезки, равные 10 см и 6 см. На какие отрезки точка А делит хорду KL, если KL больше MN на 3 см.
2 вариант
-
Вершины треугольника АВС лежат на окружности с центром О, АВС = 800, ВС : АВ = 3 : 2. Найти углы треугольника ОАВ.
-
Хорды MN и KL окружности пересекаются в точке А, причем хорда MN делится точкой А на отрезки, равные 1 см и 15 см. На какие отрезки точка А делит хорду KL, если KL в два раза меньше MN.
Самостоятельная работа обучающего характера № 20.
1 вариант.
-
Радиус окружности, вписанной в прямоугольный треугольник, равен 2 см, гипотенуза этого треугольника равна 10 см. Найти периметр этого треугольника и его площадь.
-
вариант.
-
Радиус окружности, вписанной в прямоугольный треугольник, равен 2 см, сумма катетов — 17 см. Найти периметр этого треугольника и его площадь.
Проверочная самостоятельная работа № 21.
1 вариант
-
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, равные 5 см и 13 см. Найти площадь этого треугольника.
2 вариант
-
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, меньший из которых равен 8 см, основание треугольника – 12 см. Найти площадь этого треугольника.
Самостоятельная работа обучающего характера № 22.
1 вариант.
-
Перечертите рисунок в тетрадь. Постройте векторы
 и
и  такие, что
такие, что
-
ABCD – параллелограмм. Докажите, что

-
-
вариант.
-
-
Перечертите рисунок в тетрадь. Постройте векторы
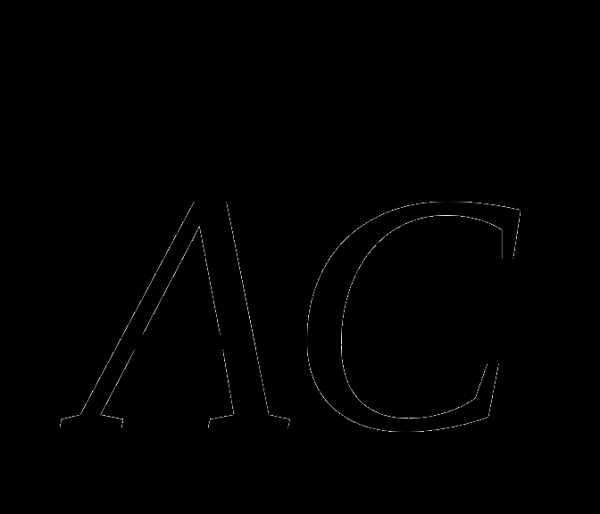 и
и  такие, что
такие, что
-
Точки M, K, N, P не лежат на одной прямой и
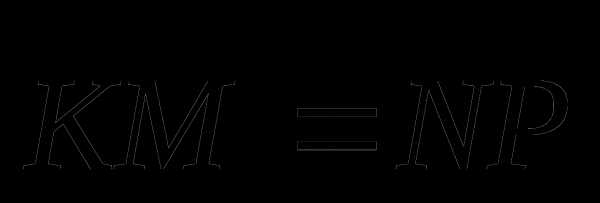 . Докажите, что KMNP – параллелограмм.
. Докажите, что KMNP – параллелограмм.
Самостоятельная работа обучающего характера № 23.
1 вариант.
-
Начертите четыре попарно неколлинеарных вектора . Постройте вектор
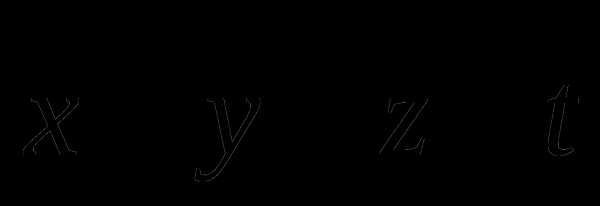
-
Упростите выражение:
2 вариант.
-
Начертите пять попарно неколлинеарных вектора . Постройте вектор
-
Упростите выражение:
Проверочная самостоятельная работа № 24.
1 вариант
-
Дан прямоугольный треугольник АВС с гипотенузой ВС. Постройте вектор и найдите
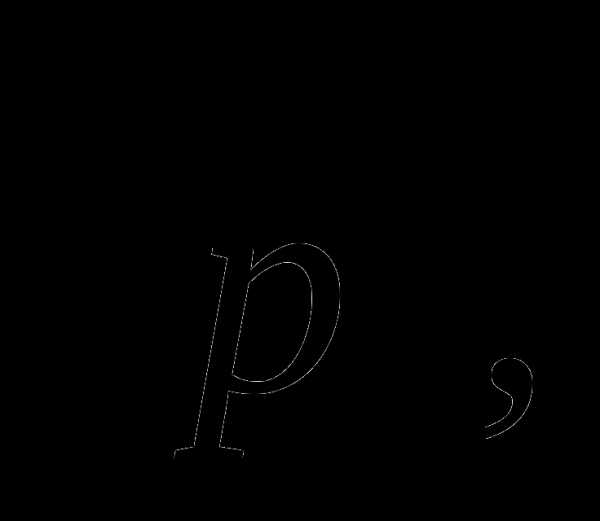 если АВ = 8 см.
если АВ = 8 см.
2 вариант
-
Дан прямоугольный треугольник АВС с гипотенузой АВ. Постройте вектор и найдите
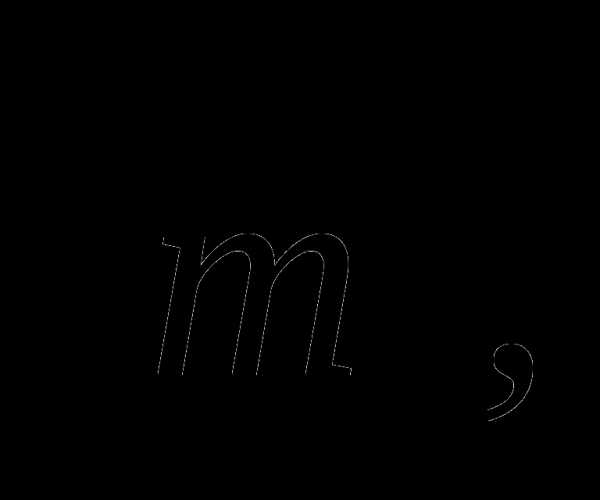 если ВС = 9 см.
если ВС = 9 см.
Практическое задание № 25
-
Начертите произвольный вектор
 и отметьте точки K, M, N, не лежащие на прямой АВ.
и отметьте точки K, M, N, не лежащие на прямой АВ.
Постройте: а) вектор  , равный вектору
, равный вектору  б) вектор
б) вектор  такой, что в) вектор
такой, что в) вектор  такой, что г) вектор
такой, что г) вектор 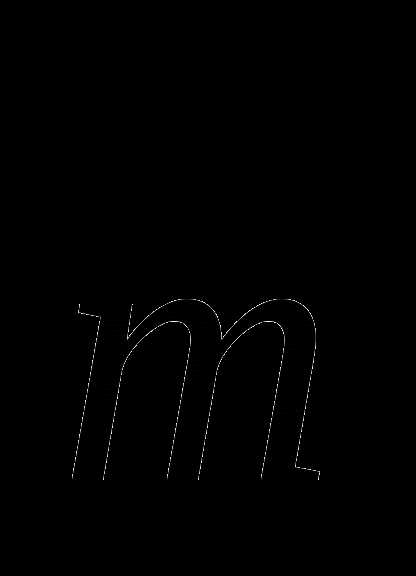 такой, что
такой, что
Проверочная самостоятельная работа № 26.
1 вариант
-
Начертите два неколлинеарных вектора
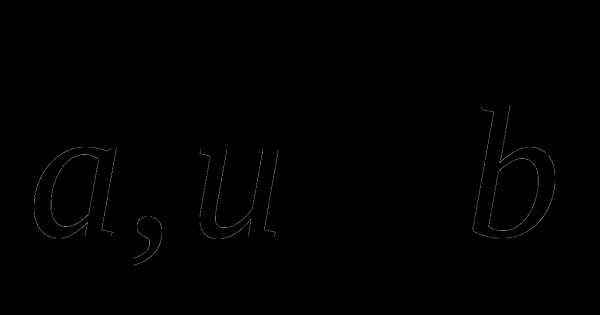 так, что . Постройте вектор
так, что . Постройте вектор 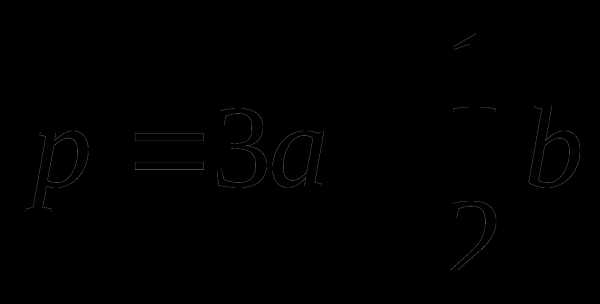
-
KMNP – параллелограмм. Выразите через векторы
 и
и 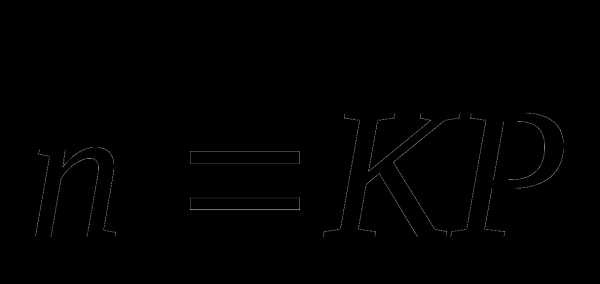 векторы
векторы  и
и  , где А – точка на отрезке PN такая, что PA : AN = 2 : 1, B – середина отрезка MN.
, где А – точка на отрезке PN такая, что PA : AN = 2 : 1, B – середина отрезка MN.
2 вариант
-
Начертите два неколлинеарных вектора
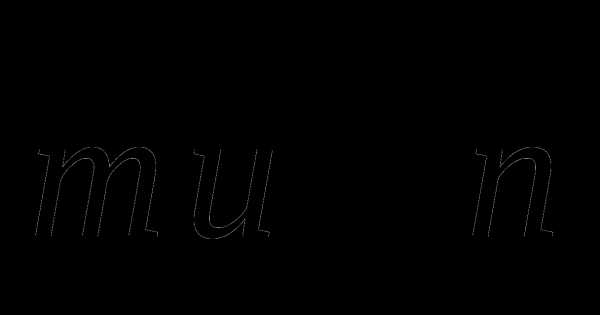 так, что . Постройте вектор
так, что . Постройте вектор 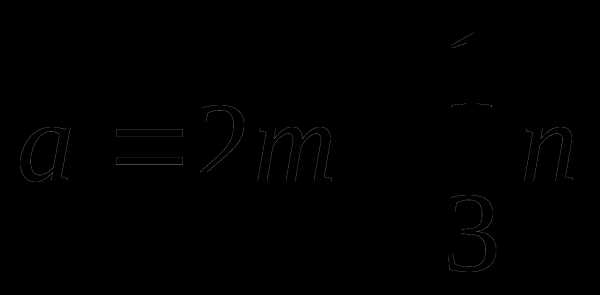
-
ABCD – параллелограмм. Точка М – середина стороны CD, N – точка на стороне AD такая, что AN : ND = 1 : 2. Выразите через векторы
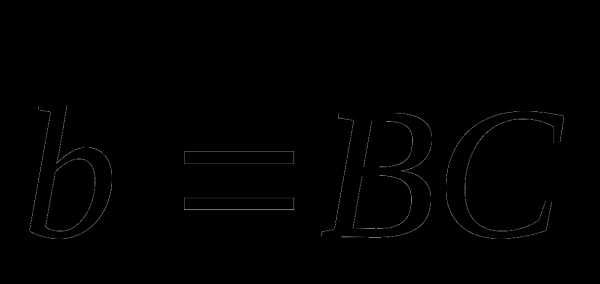 и
и 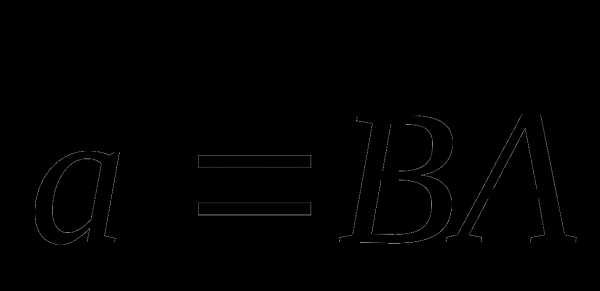 векторы
векторы  и
и  .
.
Проверочная самостоятельная работа № 27.
1 вариант
-
Точка К делит отрезок MN в отношении MK : KN = 3 : 4. Выразите через векторы
 и
и  вектор
вектор  , где А – произвольная точка
, где А – произвольная точка
2 вариант
1. Точка А делит отрезок EF в отношении ЕА : АF = 2 : 5. Выразите через векторы  и
и  вектор
вектор  , где К – произвольная точка
, где К – произвольная точка
Проверочная самостоятельная работа № 28.
1 вариант
-
Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит большее основание трапеции на два отрезка, меньший из которых равен 2 см. Найти большее основание трапеции, если ее средняя линия равна 8 см.
2 вариант
-
Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит среднюю линию трапеции на отрезки, равные 2 см и 6 см. Найти основания трапеции.
infourok.ru
Самостоятельные и контрольные работы по геометрии 8 класс
Самостоятельная работа по теме «Площадь квадрата и прямоугольника»
1 вариант
1. Найти сторону квадрата, если его площадь равна 64 см2.
1) 32 см 2) 4 см 3) 8 см 4) 12 см
2. Найти одну сторону прямоугольника, если его другая сторона равна 0,6 см и площадь равна 3 см2.
1) 5 см 2) 50 см 3) 18 см 4) 3,6 см
3. Сколько потребуется кафельных плиток квадратной формы со стороной 0,5 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 2 м и 4 м.
1) 16 2) 16 3) 13 4) 32
2 вариант
1. Найти сторону квадрата, если его площадь равна 36 см2.
1) 16 см 2) 4 см 3) 6 см 4) 12 см
2. Найти одну сторону прямоугольника, если его другая сторона равна 0,8 см и площадь равна 4 см2.
1) 5 см 2) 50 см 3) 3,2 см 4) 4,8 см
3. Сколько потребуется кафельных плиток квадратной формы со стороной 0,5 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 2 м и 4 м.
1) 16 2) 18 3) 13 4) 32
Самостоятельная работа по теме «Площадь квадрата и прямоугольника»
1 вариант
1. Найти сторону квадрата, если его площадь равна 64 см2.
1) 32 см 2) 4 см 3) 8 см 4) 12 см
2. Найти одну сторону прямоугольника, если его другая сторона равна 0,6 см и площадь равна 3 см2.
1) 5 см 2) 50 см 3) 18 см 4) 3,6 см
3. Сколько потребуется кафельных плиток квадратной формы со стороной 0,5 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 2 м и 4 м.
1) 16 2) 16 3) 13 4) 32
2 вариант
1. Найти сторону квадрата, если его площадь равна 36 см2.
1) 16 см 2) 4 см 3) 6 см 4) 12 см
2. Найти одну сторону прямоугольника, если его другая сторона равна 0,8 см и площадь равна 4 см2.
1) 5 см 2) 50 см 3) 3,2 см 4) 4,8 см
3. Сколько потребуется кафельных плиток квадратной формы со стороной 0,5 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 2 м и 4 м.
1) 16 2) 18 3) 13 4) 32
Самостоятельная работа по теме «Площадь квадрата и прямоугольника»
1 вариант
1. Найти сторону квадрата, если его площадь равна 64 см2.
1) 32 см 2) 4 см 3) 8 см 4) 12 см
2. Найти одну сторону прямоугольника, если его другая сторона равна 0,6 см и площадь равна 3 см2.
1) 5 см 2) 50 см 3) 18 см 4) 3,6 см
3. Сколько потребуется кафельных плиток квадратной формы со стороной 0,5 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 2 м и 4 м.
1) 16 2) 16 3) 13 4) 32
2 вариант
1. Найти сторону квадрата, если его площадь равна 36 см2.
1) 16 см 2) 4 см 3) 6 см 4) 12 см
2. Найти одну сторону прямоугольника, если его другая сторона равна 0,8 см и площадь равна 4 см2.
1) 5 см 2) 50 см 3) 3,2 см 4) 4,8 см
3. Сколько потребуется кафельных плиток квадратной формы со стороной 0,5 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 2 м и 4 м.
1) 16 2) 18 3) 13 4) 32
Самостоятельная работа по теме «Площадь квадрата и прямоугольника»
1 вариант
1. Найти стороны прямоугольника, если одна сторона больше другой в 4,5 раза и площадь равна 72 см2.
2. Сколько потребуется кафельных плиток квадратной формы со стороной 0,5 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 2 м и 4 м.
3. Два участка земли огорожены заборами одинаковой длины. Первый участок имеет форму прямоугольника со сторонами 12 м и 8 м, а второй имеет форму квадрата. Площадь какого участка больше и на сколько?
2 вариант
1. Найти стороны прямоугольника, если одна сторона больше другой в 5,5 раза и площадь равна 198 см2.
2. Сколько потребуется кафельных плиток квадратной формы со стороной 0,3 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 6 м и 9 м.
3. Два участка земли огорожены заборами одинаковой длины. Первый участок имеет форму прямоугольника со сторонами 2 м и 4 м, а второй имеет форму квадрата. Площадь какого участка больше и на сколько?
Самостоятельная работа по теме «Площадь квадрата и прямоугольника»
1 вариант
1. Найти стороны прямоугольника, если одна сторона больше другой в 4,5 раза и площадь равна 72 см2.
2. Сколько потребуется кафельных плиток квадратной формы со стороной 0,5 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 2 м и 4 м.
3. Два участка земли огорожены заборами одинаковой длины. Первый участок имеет форму прямоугольника со сторонами 12 м и 8 м, а второй имеет форму квадрата. Площадь какого участка больше и на сколько?
2 вариант
1. Найти стороны прямоугольника, если одна сторона больше другой в 5,5 раза и площадь равна 198 см2.
2. Сколько потребуется кафельных плиток квадратной формы со стороной 0,3 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 6 м и 9 м.
3. Два участка земли огорожены заборами одинаковой длины. Первый участок имеет форму прямоугольника со сторонами 2 м и 4 м, а второй имеет форму квадрата. Площадь какого участка больше и на сколько?
Самостоятельная работа по теме «Площадь квадрата и прямоугольника»
1 вариант
1. Найти стороны прямоугольника, если одна сторона больше другой в 4,5 раза и площадь равна 72 см2.
2. Сколько потребуется кафельных плиток квадратной формы со стороной 0,5 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 2 м и 4 м.
3. Два участка земли огорожены заборами одинаковой длины. Первый участок имеет форму прямоугольника со сторонами 12 м и 8 м, а второй имеет форму квадрата. Площадь какого участка больше и на сколько?
2 вариант
1. Найти стороны прямоугольника, если одна сторона больше другой в 5,5 раза и площадь равна 198 см2.
2. Сколько потребуется кафельных плиток квадратной формы со стороной 0,3 м, чтобы облицевать ими стену, имеющей форму прямоугольника со сторонами 6 м и 9 м.
3. Два участка земли огорожены заборами одинаковой длины. Первый участок имеет форму прямоугольника со сторонами 2 м и 4 м, а второй имеет форму квадрата. Площадь какого участка больше и на сколько?
infourok.ru