Функция алгебра 8 класс: Функция y = k/x — урок. Алгебра, 8 класс.

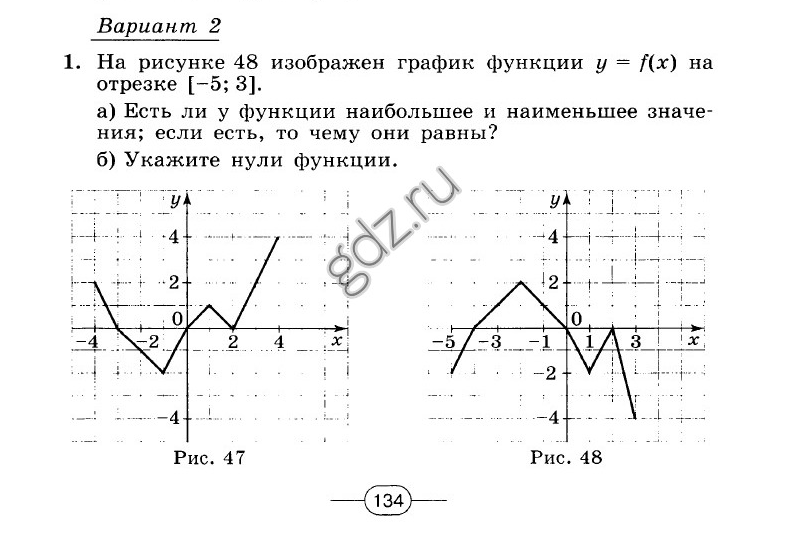
Алгебра 8 Мордкович (упр. 24.1

Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). § 24. Функция у = ах² + bх + с, её свойства и график. ОТВЕТЫ на упражнения 24.1 — 24.55. ГЛАВА 3. Квадратичная функция. Функция у = k/x. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.

§ 24. Функция у = ах² + bх + с, её свойства и график

Задание № 24.1. Какая из следующих функций является квадратичной:
а) у = 3x² + 5х + 6;   в) у = 5х² – 7х;
б) у = 3х – 1;   г) у = 9x ?

Смотреть ответы на № 24.1

Задание № 24.2. Назовите коэффициенты a, b и с квадратичной функции:
а) у = 7х² – 3x – 2;    в) у = 8x² – 2х;
б) y = x²/2 + 1;    г) y = 2x/5 + 1/7 – 3x²/10.

Смотреть ответы на № 24. 2

Задание № 24.3. Составьте квадратный трехчлен ах² + bх + с, у которого:
а) а = 2, b = –1, с = 4;    в) а = 9, b = –3, с = –1;
б) а = –1, b = 7, с = 0;    г) а = 1, b = 0, с = 5.

Смотреть ответы на № 24.3

Задание № 24.4.  Не выполняя построения, ответьте на вопрос, куда (вверх или вниз) направлены ветви параболы:
а) у = Зх² – 7х + 1;    в) у = –7х² + х – 2;
б) у = —5x² + 2x + 0,5;    г) y = 6х² + 9х + 1.

Смотреть ответы на № 24.4

Задание № 24.5. Запишите уравнение прямой, которая является осью симметрии параболы:
а) у = 2х² – х + 1;    в) у = 7х² + 12x + 4;
б) у = –5х² + 2х – 2;    г) у = –х² + 2x + 1.

Смотреть ответы на № 24.5

Задание № 24.6. Найдите координаты вершины параболы:
а) у = 4x² + 8x – 1;    в) у = –x² + х – 1;
б) у = –3х² – 6х + 2;    г) у = 5x² – 10x + 4.

Смотреть ответы на № 24.6

Задание № 24.7.

Смотреть ответы на № 24.7

Задание № 24.8.

Смотреть ответы на № 24.8

Задание № 24.9.

Смотреть ответы на № 24.9

Задание № 24.10.

Смотреть ответы на № 24.10

Задание № 24.11.

Смотреть ответы на № 24.11

Задание № 24.12.

Смотреть ответы на № 24.12

Задание № 24.13.

Смотреть ответы на № 24.13

Задание № 24.14.

Смотреть ответы на № 24.14

Задание № 24.15.

Смотреть ответы на № 24.15

Задание № 24.16.

Смотреть ответы на № 24.16

Задание № 24.17.

Смотреть ответы на № 24.17

Задание № 24.18. Постройте график функции у = х² + 4х – 5. С помощью графика определите:
а) значение функции при х = –3; 0; 1;
б) значения аргумента, если у = –8; –5; 0;
в) наименьшее значение функции;
г) промежутки возрастания и убывания функции;
д) значения аргумента, при которых у > 0, у < 0.

Смотреть ответы на № 24.18

Задание № 24.19. Постройте график функции у = –2x² + 4х + 6. С помощью графика определите:
а) значение функции при х = –2; 0; 3;
б) значения аргумента, если у = –10; 6; 0;
в) наибольшее значение функции;
г) промежутки возрастания и убывания функции;
д) значения аргумента, при которых у > 0, у < 0.

Смотреть ответы на № 24.19

Задание № 24.20.

Смотреть ответы на № 24.20

Задание № 24.21.

Смотреть ответы на № 24.21

Задание № 24.22.

Смотреть ответы на № 24.22

Задание № 24.23.

Смотреть ответы на № 24.23

Задание № 24.24.

Смотреть ответы на № 24.24

Задание № 24.25.

Смотреть ответы на № 24.25

Задание № 24.26.

Смотреть ответы на № 24.26

Задание № 24.27.

Смотреть ответы на № 24.27

Задание № 24.28. а) Найдите значение коэффициента с, если известно, что график функции у = х² + 4х + с пересекает ось ординат в точке А(0; 2).
б) Найдите значение коэффициента с, если известно, что график функции у = х² + 4х + с пересекает ось ординат в точке В(0; 4).

Смотреть ответы на № 24.28

Задание № 24.29. а) Найдите значение коэффициента а, если известно, что график функции у = ах² + 4х + 5 пересекает ось абсцисс в точке М(–10; 0).
б) Найдите значение коэффициента а, если известно, что график функции у = ах² + 4х – 8 пересекает ось абсцисс в точке N(4; 0).

Смотреть ответы на № 24.29

Задание № 24.30. ) Найдите значение коэффициента b, если известно, что осью симметрии графика функции у = х² + bх + 4 является прямая х = 1.
б) Найдите значение коэффициента b, если известно, что осью симметрии графика функции у = 2x² + bх – 3 является прямая х = –4.

Смотреть ответы на № 24.30

Задание № 24.31. Докажите, что функция у = х² – 4х + 5 является возрастающей на промежутке (3; 12).

Смотреть ответы на № 24. 31

Задание № 24.32. Докажите, что функция у = х² + 6х – 7 является убывающей на промежутке (–8; –5).

Смотреть ответы на № 24.32

Задание № 24.33.

Смотреть ответы на № 24.33

Задание № 24.34.

Смотреть ответы на № 24.34

Задание № 24.35.

Смотреть ответы на № 24.35

Задание № 24.36.

Смотреть ответы на № 24.36

Задание № 24.37.

Смотреть ответы на № 24.37

Задание № 24.38.

Смотреть ответы на № 24.38

Задание № 24.39.

Смотреть ответы на № 24.39

Задание № 24.40.

Смотреть ответы на № 24.40

Задание № 24.41.

Смотреть ответы на № 24.41

Задание № 24.42.

Смотреть ответы на № 24.42

Задание № 24.43.

Смотреть ответы на № 24.43

Задание № 24.44.

Смотреть ответы на № 24.44

Задание № 24.45.

Смотреть ответы на № 24.45

Задание № 24.46.

Смотреть ответы на № 24.46

Задание № 24.47.

Смотреть ответы на № 24.47

Задание № 24.48.

Смотреть ответы на № 24.48

Задание № 24.49.

Смотреть ответы на № 24.49

Задание № 24.50.

Смотреть ответы на № 24.50

Задание № 24.51.

Смотреть ответы на № 24.51

Задание № 24.52.

Смотреть ответы на № 24.52

Задание № 24.53.

Смотреть ответы на № 24.53

Задание № 24.54.

Смотреть ответы на № 24.54

Задание № 24.55.

Смотреть ответы на № 24.55

Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 3. Квадратичная функция. Функция у = k/x. § 24. Функция у = ах² + bх + с, её свойства и график. ОТВЕТЫ на упражнения 24.1 — 24.55. Вернуться в ОГЛАВЛЕНИЕ.

Просмотров:
56 495

Конспект урока по алгебре (8 класс) Тема:«Квадратичная функция, её виды и их графики»

Зябчук Виктория Валерьевна

учитель математики и физики,

КГУ «Общеобразовательная

средняя школа № 3 имени Ю. А.Гагарина»

отдела образования Шемонаихинского района»

Разработка урока по алгебре (8 класс)

Тема: «Квадратичная функция, её виды и их графики»

Глава ІІІ. Квадратичная функция

Математическое кафе “ФУНКЦИЯ”

“Чтобы переваривать знания,
их надо поглощать с аппетитом”
А.Франс

Цель урока: Систематизация теоретических и практических знаний по разделу «Квадратичная функция», через развитие самостоятельного мышление учащегося.

Ожидаемые результаты:

Тип урока: повторительно-обобщающий урок

Оборудование: меню для каждого столика, табличка с номером стола; цветные бланки заданий для каждого блюда меню ; “Хлеб”- бланки со справочными материалами, помогающими при построении графиков функции.

ПЛАН И ХОД УРОКА

1. Организационный момент (деление на группы; совместное определение целей и задач урока)

2. Историческая справка (творческое задание)

3. Теоретический тест (работа в группах)

4. Проверка “кредитоспособности”(парная работа)

5. Приём официантами заказов от каждого столика (5 учащихся старших классов)

6. Составление уравнения функций, частного случая квадратичной функции (Холодные закуски)

7. Выполнение заданий, на свойства квадратичной функции (Первые блюда)

8. Построение графиков квадратичной функции (Вторые блюда)

9. Задачка на смекалку (Напитки)- работа в группе

10. Подведение итогов урока (суммирование набранных баллов и занесение результатов урока в листы оценивания)

11. Обратная связь

Орг. момент

Деление на группы учащихся – метод «Цветы», распределение ролей в группе, знакомство с администрацией кафе- учащиеся 10 класса.

Сегодня мы с вами посетим необычное, математическое кафе , с названием «ФУНКЦИЯ». Почему такое название, как вы думаете?

— Да, именно потому, что на предыдущих уроках мы с вами изучили квадратичную функцию, её свойства и графики.

Надпись на доске- слово «ФУНКЦИЯ», прошу учеников назвать слова ассоциации. Составление кластера (фронтально), что способствует систематизации знаний об изученных понятиях и методах по данной теме. Учащиеся намечают задачи урока.

Историческая справка (творческое задание)- опережающая работа с одаренными учащимися: Матохиным Кириллом и Тюняевым Ильей.

Предлагаю просмотр презентации «Роль функции в познании реального мира», подготовленную вашими одноклассниками.

— Ну, а теперь перейдём к трапезе.

-На столы №1-4 администраторы-официанты приносят меню кафе, оценочный лист и «Хлеб». В меню предлагаются блюда изысканной кухни функции.

Первым делом проверим, а кредитоспособны ли вы? Хватит ли у вас знаний по теме ” Функция”, чтобы вкусить всю прелесть этих блюд? Ну что же, приступим.

Итак, отмечаем только ответы. Тест на время. 30 секунд на обдумывание.

Администраторы-официанты на столы разносят тесты соответствующего цвета.

Теоретический открытый тест на проверку кредитоспособности

«$» Задания выполняют всей группой. Ответы пишут на листах теста.

ТЕОРЕТИЧЕСКИЙ ТЕСТ

1. Если квадратный трехчлен раскладывается на множители, то он имеет корни.

2. Квадратный трехчлен называется приведенным, если его первый коэффициент равен единицы.

3. Квадратичной функцией называется функция вида у = ах² + bх + с, где a, b, c – любые действительные числа, а 0, х – независимая переменная.

4. Графиком функции у = а(х – m)² есть парабола, полученная из графика функции у = ах² в результате сдвига вправо вдоль оси абсцисс на m единиц при m0 или влево m 0.

5. Графиком функции у = ах² +n есть парабола, полученная из графика функции у = ах² в результате сдвига вдоль оси ординат вверх на n единиц при n0 или вниз 0.

6. Дискриминант D = b² – 4ac указывает на число точек пересечения графика параболы с осью абсцисс.

7. Точки пресечения графика функции с осью Ох называются нулями функции.

8. Прямая, проходящая через точку х = — и параллельная оси ординат, является осью симметрии параболы.

Администраторы- официанты собирают ответы на теоретические тесты, проверяют выполнение заданий.

Лидеры на каждом столе выставляют баллы в оценочный лист.

«$» Работа в парах ( цена ответа 1 бал)

1. Исправить ошибки в записи :

Координаты вершины графика функции у = х² – 2х -8, равны:

m = — = = ; n = ()² -2 -8= — 8 Ответ: а ≠ 8 а = 1, значит (1;-9)

2) Вычислить: — наименьшее значение функции у = х² – 2х + 7 (у_min = 6)

— наибольшее значение функции у = 3 — 2х — 2 х² (у_max = 3,5)

Администраторы-официанты принимают заказы.

— Перед вами на столах лежит меню (Приложение) сегодняшнего дня. Самостоятельно делайте заказ из любого набора блюд. Стоимость каждого блюда обозначена в баллах.

Официанты соберут ваши заказы и обеспечат своевременную доставку функциональных яств.

Холодные закуски (Составление уравнения функций, частного случая квадратичной функции )

— На ваших столах холодные закуски: — «Весенний» на зеленых тарелках и -«Функциональная рапсодия» на розовых тарелках

Решаете на этих же листах. Приступайте. Желаю вам приятного аппетита!

Салат «Весенний»: дана квадратичная функция, которую необходимо привести к виду у = а(х – m)² + n

1. у =2 х² +4х — 7 2) у = — 3х² + 12х — 5

Салат «Функциональная рапсодия»: составьте квадратный трехчлен..

1) х₁ = -5 и х₂ = 4 2) х₁ = 2,5 и х₂ = -3

Учащиеся выполняют задания.

— Вы так увлечены предлагаемыми блюдами нашей функциональной кухни, что даже забыли о “хлебе”! Сейчас вам ”хлеб” будет кстати. (Приложение ) Официанты разносят холодные закуски.

Первые блюда (Выполнение заданий, на свойства квадратичной функции)

— Проводится смена блюд. И сейчас на ваших столах появятся прекрасные функциональные первые блюда. Официанты разносят первые блюда.

Борщ с фукцией: переместите параболу у = — 3х²

1. вниз на 4 единицы;

2. влево на 7 единиц;

3. вправо на 2 единицы;

4. вверх на 5 единиц.

1. Для каждого случая напишите соответствующую функцию.

2. Cуп-пюре «Функциональное искусство»: определите направление ветвей параболы следующих функций

1. у = х² – 4х + 3

2. у = — х² – 12х + 1

3. у =3 – 8 х — х²

4. у = х² – 10х + 15

1. (Аналогичная работа тому, как осуществлялась проверка выполнения заданий по “холодным закускам”. Напоминать лидерам проставлять баллы в бланке результатов.) Официанты разносят вторые блюда.

2. Вторые блюда (Построение графиков квадратичной функции)

3. Блинчики с мясом «Разнообразие»: (задание выполняется на клетчатой бумаге)

   Дана функция у =2 х2 +4х – 7… 1.найдите координаты вершины параболы; 2.вычислите значения х, при которых функция обращается в нуль; 3.найдите наименьшее и наибольшее значения функции; 4.выясните , при каких значения х значения функции у 0; 5. постройте график функции.

   Дана функция у = — 3х2 + 12х — 5… 1.найдите координаты вершины параболы; 2.вычислите значения х, при которых функция обращается в нуль; 3.найдите наименьшее и наибольшее значения функции; 4. выясните , при каких значения х значения функции у 0; 5. постройте график функции.

5. Плов «Фэнтази»: установите соответствие между квадратичной функцией и координатами параболы…

   у = 3х2 – 12х + 10 (-4 ; -6) у = -х2 + 4х + 5 (2 ; -2) у = х2 + 8х + 10 (2 ; 9)

   у = х2 + 6х + 8 (-1 ; 6) у = -2х2 + 8х — 5 (2 ; 3) у = — 4х2 — 8х + 2 (-3 ; -1)

6. Напитки — работа в группе

7. *Коктейль «Смекалка»

8. — Для картины, размером которой 4 дм и 3 дм, делается прямоугольная рамка, имеющая со всех сторон одинаковую ширину Х. Выразите формулой площадь рамки в зависимости от Х.

9. -Чтобы изготовить емкость, из каждого угла металлического листа прямоугольной формы ра змером 2 м и 5 м отрезали квадрат со стороной Х. Выразите площадь оставшейся части металлического листа через Х.

10. *Кофе «Каппучино»

11. — Найдите значение коэффициента с функции у = 2х² + 4х + с,  если известно, что наименьшее значение функции равно  – 1. (с = 1)

12. — Найдите значение коэффициента  с функции у =  – 3х² + 6х + с, если известно, что наибольшее значение функции равно 4. (с = 1)

14. Подведение итогов.

15. Сейчас за каждым столиком необходимо просуммировать набранные баллы и занести результаты в таблицу. В соответствии с количеством набранных баллов каждый посетитель кафе получит “бонусы” в классный журнал.

17. Обратная связь

18. Каждому ученику предложено на стикере дописать предложения, метод «ЗПИ»

19. Как результат этого урока я:

20. Знаю…

21. Понимаю…

22. И могу использовать информацию в следующих ситуациях….

24. Ребята, также у вас на столах лежат стикеры-полоски, хочу попросить , чтоб каждый из вас уходя с сегодняшнего нашего урока, прикрепил его к воздушному шарику, который соответствует вашей работе на уроке.

    отлично по работал(а)	не всегда получалось	неудовлетворен(а) своей работой

27. Спасибо за урок!

29. ПРИЛОЖЕНИЕ

31. МЕНЮ

32. математического кафе «Ф У Н К Ц И Я»

36. Холодные закуски:

1. Салат «ВЕСЕННИЙ»__________________5 балл

2. Салат фруктовый “ФУНКЦИОНАЛЬНАЯ РАПСОДИЯ” ______ 2 балл

2. Первые блюда:

1. Борщ с ФУНКЦИЕЙ______________________2 балл

2. Суп – пюре из курицы(ФУНКЦИОНАЛЬНОЕ ИСКУССТВО)__________1 балла

2. Вторые блюда:

3. 1) Блинчики с мясом “РАЗНООБРАЗИЕ” _____________5 балл

4. 2) Плов “ФЭНТАЗИ”_____________1 балла

6. Напитки:

7. 1)Коктейль ”СМЕКАЛКА”_________________________2 балл

8. 2) Кофе “КАППУЧИНО”_____________2 балла

10. Зав. производством: АЛГЕБРА 8

12. Стол №___

13. математического кафе “ФУНКЦИЯ”

14. №

    Ф.И. учащегося

    Теоретический тест

    Работа в паре

    Холодные закуски

    Первые блюда

    Вторые блюда

    Напитки

    Итого

    «Весенний»

    «Функциональная рапсодия»

    борщ с функцией

    суп-пюре

    блинчики

    плов

    коктейль

    кофе

17. “Кредитоспособность” «$» ТЕОРЕТИЧЕСКИЙ ТЕСТ -Если квадратный трехчлен ………. ……………….., то он имеет корни. -Квадратный трехчлен ……………. ………………., если его первый коэффициент равен единицы. -Квадратичной функцией называется функция вида у = ах2 + bх + с, где a, b, c – …………. ……………. числа, а 0, х – независимая ……………… -Графиком функции у = а(х – m)2 есть парабола, полученная из …………. ………….. ……….. в результате сдвига ………. вдоль оси абсцисс на m единиц при m0 или …………. m 0. -Графиком функции у = ах2 +n есть парабола, полученная из ……………… ……………. ………в результате сдвига …….. ….. ……….. вверх на n единиц при n0 или ………… 0. -Дискриминант D = b2 – 4ac указывает на ………. ………. ………. графика параболы с осью абсцисс. -Точки пресечения графика функции с осью Ох называются ……. ……… . -Прямая, проходящая через точку х = — и параллельная оси ……. …, является осью ………….. параболы.

19. “Кредитоспособность” «$» ПАРНАЯ РАБОТА Исправить ошибки в записи : Координаты вершины графика функции у = х2 – 2х -8, равны: m = — = = ; n = ()2 -2 -8= — 8 2) Вычислить: — наименьшее значение функции у = х2 – 2х + 7 — наибольшее значение функции у = 3 — 2х — 2 х2

22. Салат «Весенний»: Холодные закуски Дана квадратичная функция у =2 х2 +4х — 7, которую необходимо привести к виду у = а(х – m)2 + n.

    Салат «Весенний»: Холодные закуски Дана квадратичная функция у = — 3х2 + 12х — 5, которую необходимо привести к виду у = а(х – m)2 + n .

    Салат «Функциональная рапсодия»: Холодные закуски Составьте квадратный трехчлен, если х1 = -5 и х2 = 4 .

    Салат «Функциональная рапсодия»: Холодные закуски Составьте квадратный трехчлен, если х1 = 2,5 и х2 = -3

25. Борщ с функцией: Первые блюда Переместите параболу у = — 3х2 вниз на 4 единицы; _____________ 3) влево на 7 единиц; ______________ вправо на 2 единицы; _____________ 4) вверх на 5 единиц. ______________ Для каждого случая напишите соответствующую функцию.

    Cуп-пюре «Функциональное искусство»: Первые блюда Определите направление ветвей параболы следующих функций: у = х2 – 4х + 3; ______________ у = — х2 – 12х + 1; ______________ у =3 – 8 х — х2 ; ______________ у = х2 – 10х + 15. ______________

28. Блинчики с мясом «Разнообразие»: Вторые блюда Дана функция у =2 х2 +4х – 7 … 1.найдите координаты вершины параболы; 2.вычислите значения х, при которых функция обращается в нуль; 3.найдите наименьшее и наибольшее значения функции; 4.выясните , при каких значения х значения функции у 0; 5. постройте график функции.

    Блинчики с мясом «Разнообразие»: Вторые блюда Дана функция у = — 3х2 + 12х – 5 … 1.найдите координаты вершины параболы; 2.вычислите значения х, при которых функция обращается в нуль; 3.найдите наименьшее и наибольшее значения функции; 4. выясните , при каких значения х значения функции у 0; 5. постройте график функции.

    Плов «Фэнтази»: Вторые блюда Установите соответствие между квадратичной функцией и координатами параболы… у = 3х2 – 12х + 10 (-4 ; -6) у = -х2 + 4х + 5 (2 ; -2) у = х2 + 8х + 10 (2 ; 9)

30. Коктейль «Смекалка» Напитки — Для картины, размером которой 4 дм и 3 дм, делается прямоугольная рамка, имеющая со всех сторон одинаковую ширину Х. Выразите формулой площадь рамки в зависимости от Х.

    Коктейль «Смекалка» Напитки -Чтобы изготовить емкость, из каждого угла металлического листа прямоугольной формы ра змером 2 м и 5 м отрезали квадрат со стороной Х. Выразите площадь оставшейся части металлического листа через Х.

    Кофе «Каппучино» Напитки — Найдите значение коэффициента с функции у = 2х2 + 4х + с,  если известно, что наименьшее значение функции равно  – 1.

31. ХЛЕБ Квадратичной функцией называется функция вида у = ах2 + bх + с, где a, b, c – любые действительные числа, а 0, х – независимая переменная.

    График: ПАРАБОЛА Ветви параболы направлены вверх (а0) или вниз (а 0).

32. ХЛЕБ Преобразования графика КФ:
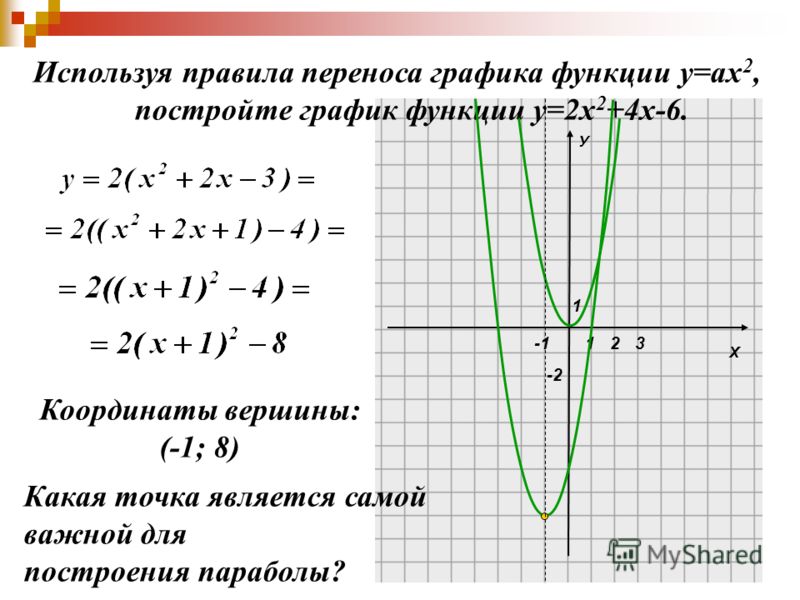
    Графиком функции у = ах2 +n есть парабола, полученная из графика функции у = ах2 в результате сдвига вдоль оси ординат вверх на n единиц при n0 или вниз при 0.	Графиком функции у = а(х – m)2 есть парабола, полученная из графика функции у = ах2 в результате сдвига вдоль оси абсцисс вправо на m единиц при m0 или влево m на единиц при m 0.

33. ХЛЕБ
    Координаты вершины параболы: (m; n) m = — ; n = —	Прямая, проходящая через точку х = — и параллельная оси ординат, является осью симметрии параболы.	Точки пресечения графика функции с осью Ох называются нулями функции.

34. ХЛЕБ Дискриминант D = b2 – 4ac указывает на число точек пересечения графика параболы с осью абсцисс.
    D 0 График пересекает Ох в точках: х1 = их2 =	D = 0 График пересекает Ох в точке: х1 = х2 = х = —	D0 Парабола не имеет общих точек с осью абсцисс

35. ХЛЕБ Наибольшее значение функции: m = — если а 0

    Наименьшее значение функции: n = — если а0

Что такое Функция в Алгебре?

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, функция у = 2х каждому действительному числу x ставит в соответствие число y, которое в два раза больше, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

• х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Рассмотрим другие типы соответствий между множествами.

Например, фрукты и цвет каждого:

У каждого фрукта есть свой цвет. Но такое соответствие нельзя назвать взаимно-однозначным. Например, яблоко может быть и красным, и желтым и даже зеленым.

Пример такого соответствия в математике — функция у = х2. Один и тот же элемент второго множества у = 4 соответствует двум разным элементам первого множества: х = 2 и х = -2.

Так на примере с фруктами можно показать соответствие, которое нельзя назвать функцией:

Видно, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества. Описать такое соответствие математически было бы сложнее.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Способы задания функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — самый наглядный. На графике сразу видно возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Задать функцию формулой

Через аналитический способ задания функции можно сразу по конкретному значению аргумента «x» найти значение функции «y».

Пример. Дана функция: y(x) = 32x + 5.

Найти: значения функции «y» при x = 0.

Как рассуждаем:

Подставим в формулу вместо «x» число «0». Запишем расчет.

y(0) = 32 * 0 + 5 = 5

Ответ: y = 5.

Учёба без слёз (бесплатный гайд для родителей)

Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Задать функцию таблицей

Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений «y» для произвольно выбранных значений «x».

Пример. Дана функция: y(x) = −x + 4.

Найти: значения «y» при x = -1, x = 0 и x = 1.

Как рассуждаем:

1. Подставим в функцию y(x) = −x + 4 вместо «x» первое число -1.

2. Продолжим подставлять в функцию y(x) = −x + 4 данные значения x (0 и 1).
y(0) = −0 + 4 = 4
y(1) = −1 + 4 = 3

Не путаем знаки!

Когда в функцию нужно подставить отрицательное число — включаем внимательность на максимум. Возьмите нужное число в скобки, чтобы точно не потерять знак минус.

3. Запишем полученные результаты в таблицу:

Так мы получили табличный способ задания функции y(x) = −x + 4.

Задать функцию графиком

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

График функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числовые значения вместо «x».

Пример. Дана функция: y(x) = −2x + 1.

Найти: значения «y» для произвольных «x», а именно −1, 0, 1.

Как рассуждаем:

1. Подставим данные значения х в функцию и запишем результаты:

2. Каждая пара значений «x» и «y» — это координаты точек по оси Ox (абсцисса точки) и Oy (ордината точки).

Дадим названия каждой точке и запишем их координаты:

3. Отметим точки А (-1; 3), B (0; 1) и С (1; -1) на прямоугольной системе координат.

4. Соединим отмеченные точки прямой.

Проведенная прямая будет графиком функции y(x) = −2x + 1.

Go Math, 8 класс, ключ к ответу, глава 6, функции – Go Math, ключ к ответу

Go Math, 8 класс, ключ к ответу, глава 6, функции PDF-файл предоставляется здесь для загрузки. Любимым экспертам по математике предоставляется простой способ решения математических вопросов вместе с объяснениями. Каждая проблема упрощается с четким объяснением с множеством трюков. Большие проблемы с высоким уровнем сложности также решаются простым способом. Обратитесь к главе 6 «Функции ответа на вопросы по математике для 8 класса», чтобы приступить к практике.

Предпочитаю учиться с помощью Go Math Class 8 Chapter 6 Functions Solution Key. Чтобы получить хорошие результаты на экзамене, вы должны подготовиться с помощью Ключа ответов к главе 6 Go Math Grade 8. Используйте ключ ответа HMH Go Math Grade 8 для лучшей практики математики. Пошаговое объяснение приведено ниже для каждого вопроса. Укрепите свою уверенность в решении математических задач, практикуясь с функциями Go Math 8 Class Answer Key Chapter 6.

Урок 1. Определение и представление функций

• Идентификация и представление функций — страница № 158
• Идентификация и представление функций — страница № 159
• Идентификация и представление функций — страница № 160

Урок 2: Описание функций

• Описание функций — страница № 164
• Описание функций — страница № 165
• Описание функций — страница № 166

Урок 3. Сравнение функций

• Функции сравнения — страница № 170
• Сравнение функций — страница № 171
• Сравнение функций — страница № 172

Урок 4: Анализ графиков

• Анализ графиков — страница № 176
• Анализ графиков — страница № 177
• Анализ графиков — страница № 178

Опрос по моделям 

• Опрос по моделям — страница № 179

Смешанный обзор

• Смешанный обзор — страница № 180

Практическое руководство – Идентификация и представление функций – Страница № 158

Заполните каждую таблицу. В строке с x в качестве входных данных запишите правило в виде алгебраического выражения для выходных данных. Затем заполните последнюю строку таблицы, используя правило.

Вопрос 1.

Введите ниже:
_______________

Ответ:

Объяснение:
Единица Стоимость билета = 40/2 = 20
Общая стоимость = 20x, где x — количество билетов.
x = 20x
10 = 20(100) = 200

Вопрос 2.

Введите ниже:
_______________

Ответ:

Объяснение:
Общее количество страниц = 7 0 0,5 стоимость 1/2 0,5x, где x — количество минут.
x = 0,5x
30 = 0,5(30) = 15

Вопрос 3.

Введите ниже:
_______________

Ответ:

Объяснение:

Общая стоимость маффинов = 9,2025 = 2,02525/шт. 2,25x, где x — количество кексов
x = 2,25x
12 = 2,25(12) = 27

Определите, является ли каждое отношение функцией.

Вопрос 4.

_______________

Ответ:
Функция

Объяснение:
Каждый вход назначается только одному выходу.

Вопрос 5.

_______________

Ответ:
Не функция

Объяснение:
Входное значение 4 связано с двумя выходами 25 и 35 пакеты и стоимость доставки для каждого пакета. Является ли отношение, представленное на графике, функцией? Объяснять.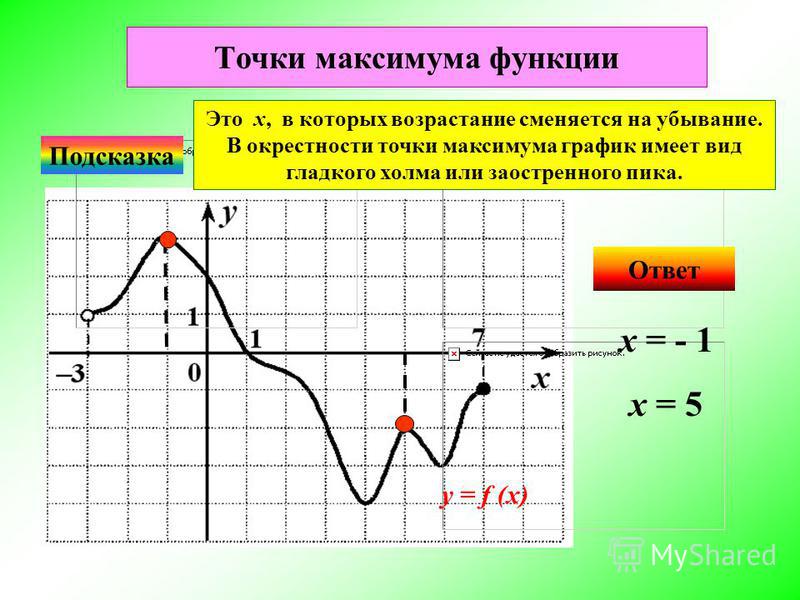

_______________

Ответ:
Функция

Объяснение:
Каждый вход назначается только одному выходу.

Основной вопрос Проверка

Вопрос 7.
Какие существуют четыре различных способа представления функций? Как определить, являются ли отношения функцией?
Введите ниже:
_______________

Ответ:
Функция может быть представлена ​​уравнением, таблицей, графиком и диаграммой Венна.
Если связь является функцией, каждый вход связан ровно с одним выходом.

Независимая практика — Идентификация и представление функций — № страницы 159

Определите, является ли каждое отношение, представленное упорядоченными парами, функцией. Объяснять.

Вопрос 8.
(2, 2), (3, 1), (5, 7), (8, 0), (9, 1)
_______________

Ответ:
Функция

Объяснение:
Каждый входное значение сочетается ровно с одним выходным значением.

Вопрос 9.
(0, 4), (5, 1), (2, 8), (6, 3), (5, 9)
_______________

Ответ:
Не функция

Объяснение:
Входное значение равно 5 в паре с двумя выходными значениями 1 и 9

Вопрос 10.
Подведем итоги
Хоакин получает 0,40 доллара за фунт за переработанные алюминиевые банки весом от 1 до 99 фунтов. . Он получает 0,50 доллара за фунт, если перерабатывает более 100 фунтов. Зависит ли сумма денег, которую получает Хоакин, от веса банок, которые он перерабатывает? Объясните свои рассуждения.
_______________

Ответ:
Да

Пояснение:
Сумма денег увеличивается с весом банок. Никакой вес не приведет к той же сумме заработанных денег.

Вопрос 11.
Биолог отследил рост штамма бактерий, как показано на графике.

а. Объясните, почему отношение, представленное на графике, является функцией.
Введите ниже:
_______________

Ответ:
Отношение является функцией, так как каждому входу соответствует ровно один выход. На каждое количество часов приходится только одно количество бактерий.

Вопрос 11.
b. Что если?
Предположим, что в течение двух часов подряд было одинаковое количество бактерий. Будет ли график по-прежнему представлять функцию? Объяснять.
Введите ниже:
_______________

Ответ:
Да. Если количество бактерий в течение двух последовательных часов одинаково, один вход по-прежнему будет совпадать с одним выходом, следовательно, связь по-прежнему является функцией.

Вопрос 12.
Множественные представления
Приведите пример функции из повседневной жизни и представьте ее в виде графика, таблицы и набора упорядоченных пар. Опишите, как вы узнали, что это функция.

Введите ниже:
_______________

Ответ:
Стоимость букета цветов и количество цветов в букете — это функция. Стоимость единицы цветов = 0,85 доллара США и x количество цветов. Следовательно, C = 0,85x

(2, 1,7), (4, 3,4), (6, 5,1), (8, 6,8), (10, 8,5)
. Каждое значение входа связано ровно с одним выходом .

Идентификация и представление функций — стр. № 160

На графике показано соотношение между весом шести ломтиков сыра и ценой каждого ломтика.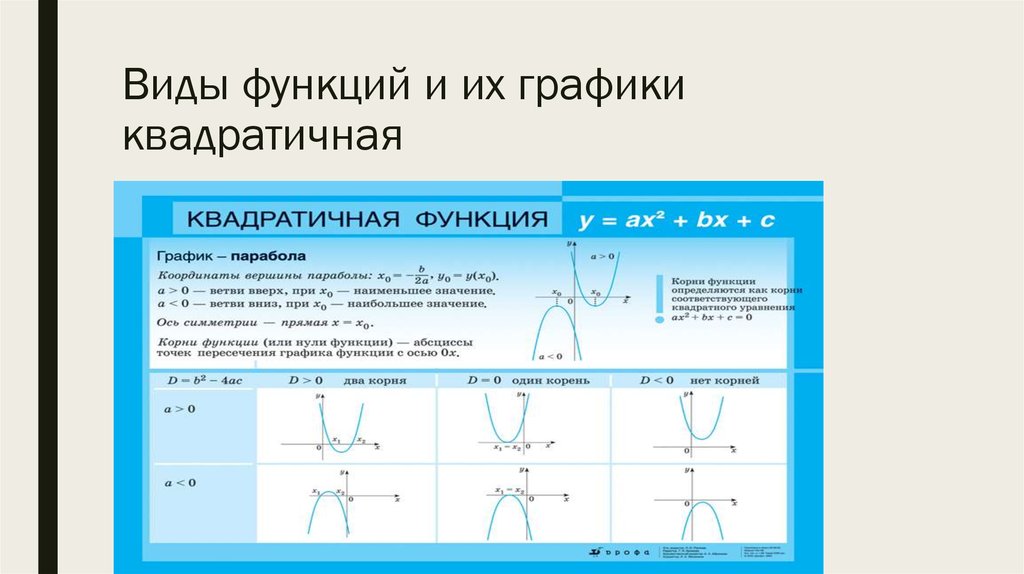

Вопрос 13.
Является ли отношение, представленное на графике, функцией? Обоснуйте свои рассуждения. Используйте слова «вход» и «выход» в своем объяснении и соедините их с контекстом, представленным на графике.
_______________

Ответ:
Да, отношение, представленное на графике, является функцией.
Каждому входу (весу) на графике соответствует ровно один выход (цена).

Вопрос 14.
Анализ взаимосвязей
Предположим, что на график нанесены веса и цены дополнительных кусков сыра. Может ли это изменить ваш ответ на вопрос 13? Объясните свои рассуждения.
Введите ниже:
_______________

Ответ:
Нет. По мере увеличения веса сыра стоимость ломтиков сыра также будет увеличиваться. Следовательно, для каждого входа (веса) будет ровно один выход (цена).

Г.О.Т.

Фокус на мышлении высшего порядка

Вопрос 15.
Обоснование рассуждений
Диаграмма сопоставления представляет отношение, которое содержит три различных входных значения и четыре различных выходных значения. Являются ли отношения функцией? Объясните свои рассуждения.
_______________

Ответ:
Нет. Поскольку имеется три входа и четыре выхода, один из входов будет иметь более одного выхода, следовательно, отношение не может быть функцией.

Вопрос 16.
Общение с математическими идеями
Фермер, выращивающий лук, нанимает рабочих для сбора урожая лука. Он знает, что количество дней, необходимое для сбора лука, зависит от количества нанятых им рабочих. Объясните употребление слова «функция» в данном контексте.
Введите ниже:
_______________

Ответ:
Количество дней = f(количество рабочих)

Пояснение:
Мы знаем, что чем больше рабочих будет задействовано в уборке лука, тем меньше дней потребуется на уборку лука.
Таким образом, количество рабочих становится независимой переменной, а количество дней становится зависимой переменной.
Здесь слово функция используется для описания того, что количество дней зависит от количества рабочих.
Количество дней = f(количество рабочих)

Практическое руководство — Описание функций — № страницы 164

Нанесите на график упорядоченные пары из таблицы. Затем постройте график функции, представленной упорядоченными парами, и скажите, является ли функция линейной или нелинейной.

Вопрос 1.
y = 5 − 2x

_______________

Ответ:

График линейной функции представляет собой прямую линию 2(-1) = 5 + 2 = 7 ·
у = 5 – 2(1) = 5 – 2 = 3
у = 5 – 2(3) = 5 – 6 = -1
у = 5 – 2(5) = 5 – 10 = -5

Вопрос 2.
y = 2 − x ²

_______________

Ответ:
y = 2 − x ²

Нарисуйте упорядоченные пары. Затем проведите линию через точки, чтобы представить решение.

График линейной функции не является прямой линией
Нелинейная зависимость

Объяснение:
y = 2 − x ²
y = 2 – 4 = -2
y = 2 – 1 = 1
y = 2 – 0 = 2
y = 2 – 1 = 1
y = 2 – 4 = -2

Объясните, является ли каждое уравнение линейным уравнением.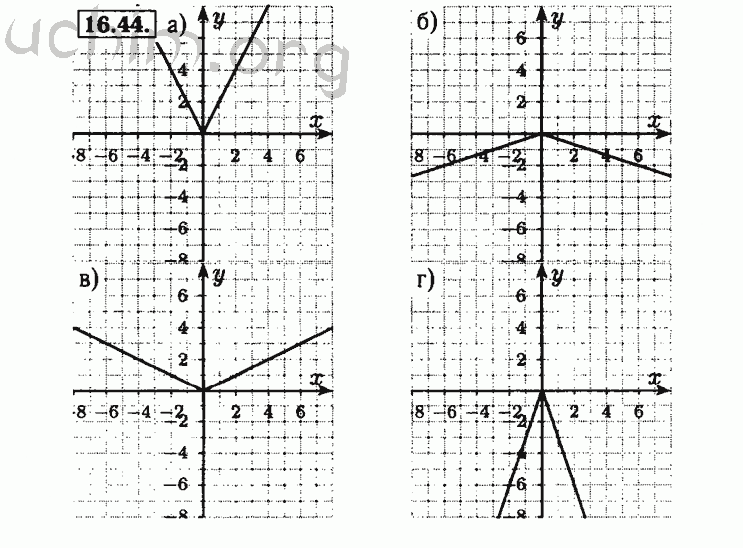

Вопрос 3.
y = x ² – 1
_______________

Ответ:
Уравнение не имеет форму линейного уравнения, следовательно, оно не является линейным уравнением.

Объяснение:
Сравните уравнение с общим линейным уравнением y = mx + b.
Уравнение не имеет формы линейного уравнения, следовательно, оно не является линейным уравнением.

Вопрос 4.
y = 1 – x
_______________

Ответ:
Уравнение имеет форму линейного уравнения, следовательно, является линейным уравнением.

Объяснение:
Сравните уравнение с общим линейным уравнением y = mx + b.
Уравнение имеет форму линейного уравнения, следовательно, является линейным уравнением.

Основной вопрос Проверка

Вопрос 5.
Объясните, как можно использовать таблицу значений, уравнение и график, чтобы определить, представляет ли функция пропорциональную зависимость.
Введите ниже:
_______________

Ответ:
Из таблицы определите отношение y/x. Если она постоянна, связь пропорциональна.
На графике обратите внимание, проходит ли график через начало координат. График пропорциональной зависимости должен проходить через начало координат (0, 0).
Из уравнения, сравните с общей линейной формой уравнения, y = mx + b. Если b = 0, отношение пропорциональное.

Независимая практика – Описание функций – Страница № 165

Вопрос 6.
Укажите, является ли связь между x и y в y = 4x – 5 пропорциональной или непропорциональной. Затем постройте график функции.

_______________

Ответ:

Объяснение:
Сначала сравним это уравнение с общим линейным уравнением y = mx + b. y = 4x – 5 имеет вид y = mx + b, где m = 4 и b = -5. Следовательно, уравнение является линейным уравнением. Поскольку b не равно 0, отношение непропорциональное.
Затем мы выбираем несколько значений для входа x. Мы подставляем эти значения x в уравнение, чтобы найти выход y.
y = 4x – 5
Если x = 0; у = 4(0) – 5 = -5; (0, -5)
Если х = 2; у = 4(2) – 5 = 3; (2, 3)
Если х = 4; у = 4(4) – 5 = 11; (4, 11)
Если х = 6; у = 4(6) – 5 = 19; (6, 19)
Нарисуем упорядоченные пары и проведем линию через точки, представляющие решения функции.

Вопрос 7.
Телескоп Форталеза в Бразилии — это радиотелескоп. Его форму можно аппроксимировать уравнением y = 0,013x ² . Является ли зависимость между x и y линейной? Это пропорционально? Объяснять.
____________
____________

Ответ:
Сравните уравнение с общим линейным уравнением y = mx + b.
Уравнение не имеет формы линейного уравнения, следовательно, оно не является линейным уравнением. Поскольку х в квадрате, он не пропорционален.

Вопрос 8.
Кайли потратила 20 долларов на аттракционы и закуски на государственной ярмарке. Если x — это сумма, которую она потратила на поездки, а y — это сумма, которую она потратила на закуски, общая сумма, которую она потратила, может быть представлена ​​уравнением x + y = 20. Является ли зависимость между x и y линейной? Это пропорционально? Объяснять.
____________
____________

Ответ:
x + y = 20
Переписать уравнение
y = 20 – x
Сравните уравнение с общим линейным уравнением y = mx + b.
Это линейно
Поскольку b не равно 0, соотношение не является пропорциональным.

Вопрос 9.
Представление реальных проблем
Бригада учений покупает новую форму. В таблице указаны y, общая стоимость в долларах, и x, количество купленной униформы.

а. Используйте данные, чтобы построить график. Является ли зависимость между x и y линейной? Объяснять.
____________

Ответ:

График линейной зависимости представляет собой прямую линию.
x и y линейны.

Вопрос 9.
б. Используйте свой график, чтобы предсказать стоимость покупки 12 униформ.
$ ________

Ответ:
$720

Объяснение:

Стоимость 12 комплектов одежды составляет $720

Вопрос 10.
Марту, детеныша кита в аквариуме, кормят специальной молочной смесью. Ее куратор использует график для отслеживания количества галлонов смеси y, которые теленок выпивает за x часов. Является ли зависимость между x и y линейной? Это пропорционально? Объяснять.

____________
____________

Ответ:
Связь линейная
Связь пропорциональная

Объяснение:
Поскольку данные лежат на прямой линии, связь линейная
Поскольку график проходит через начало координат, связь пропорциональна

Описание функций – страница № 166

Вопрос 11.
Критическое рассуждение
Учащийся утверждает, что уравнение y = 7 не является линейным уравнением, поскольку оно не имеет формы y=mx + b. Ты согласен или несогласен? Почему?

____________

Ответ:
Не согласен; Уравнение можно записать в виде y = mx + b, где m равно 0. График решений представляет собой горизонтальную линию.

Вопрос 12.
Сделайте прогноз
Пусть x представляет собой количество часов, в течение которых вы читали книгу, а y представляет собой общее количество прочитанных вами страниц. Вы уже прочитали 70 страниц и можете читать 30 страниц в час. Напишите уравнение, связывающее x часов и y страниц, которые вы прочитали. Затем предскажите общее количество страниц, которые вы прочитаете еще через 3 часа.
_______ страниц

Ответ:
160 страниц

Объяснение:
Пусть x представляет количество часов, в течение которых вы читали книгу, а y представляет общее количество прочитанных вами страниц. Вы уже прочитали 70 страниц и можете читать 30 страниц в час.
м = 30; b = 70 страниц
y = 30x + 70
x = 3 часа
y = 30(3) + 70 = 160

Г.О.Т.

Сосредоточьтесь на мышлении высшего порядка

Вопрос 13.
Подведите итоги
Ребекка рисует график реальных отношений, который оказывается набором не связанных между собой точек. Может ли зависимость быть линейной? Может ли оно быть пропорциональным? Объясните свои рассуждения.
Введите ниже:
______________

Ответ:
Зависимость является линейной, если все точки лежат на одной прямой. Если связь линейная и проходит через начало координат, она пропорциональна.

Вопрос 14.
Обмен математическими идеями
Напишите реальную задачу на пропорциональные отношения. Объясните, откуда вы знаете, что зависимость пропорциональна.
Введите ниже:
______________

Ответ:
Сумма денег, заработанная на автомойке, представляет собой пропорциональную зависимость. Когда помыто 0 машин, зарабатывается 0 долларов. Сумма заработанных денег увеличивается на удельную стоимость автомойки.

Вопрос 15.
Обоснуйте рассуждения
Покажите, что уравнение y + 3 = 3(2x + 1) является линейным и представляет собой пропорциональную зависимость между x и y.
Введите ниже:
______________

Ответ:
y + 3 = 3(2x + 1)
y +3 = 6x + 3
y = 6x
Поскольку b = 0, это пропорциональная зависимость.

Практика под руководством – Сравнение функций – № страницы 170

Врачи используют два метода расчета максимальной частоты сердечных сокращений. При использовании первого метода максимальная частота сердечных сокращений y в ударах в минуту равна y = 220 − x, где x — возраст человека. Максимальный пульс при втором способе показан в таблице.

Вопрос 1.
Какой метод дает большую максимальную частоту сердечных сокращений для 70-летнего человека?
____________ метод

Ответ:
Второй

Объяснение:
y = 220 – x
y = 220 – 70 = 150 – x1), где (x1, y1) = (20, 194) и (x2, y2) = (30, 187)
Наклон m = (y2 -y1)/(x2 – x1) = (187 – 194)/( 30 – 20) = -7/10 = -0,7
197 = -0,7(20) + b
точка пересечения с осью y b = 208
Подстановка значения наклона m и y-отрезка в форму наклона-отрезка. y = mx + b, где m = -0,7 и b = 208.
y = -0,7x +208
x = 70 лет
y = -0,7(70) + 208 = 159
150 < 159
Второй метод дает большее максимальная частота сердечных сокращений для 70-летних.

Вопрос 2.
Пропорциональны или непропорциональны частота сердечных сокращений и возраст для каждого метода?
____________

Ответ:
Для метода 1 зависимость не является пропорциональной.
Для метода 2 связь не является пропорциональной.

Объяснение:
Сравните уравнение с общим линейным уравнением y = mx + b.
Это линейно
Поскольку b не равно 0, соотношение не является пропорциональным.

Аиша занимается репетиторством. С планом 1 студенты могут платить 15 долларов в час. С Планом 2 они могут следовать плану, показанному на графике.

Вопрос 3.
Опишите план, изображенный на графике.
Введите ниже:
______________

Ответ:
Выберите две точки на графике, чтобы найти наклон.
Найдите уклон
м = (y2 -y1)/(x2 — x1)
м = (60 — 40)/(4 — 0) = 20/4 = 5
Прочтите точку пересечения оси y с графика: b = 40
Используйте значения наклона и точки пересечения с осью Y, чтобы написать уравнение в форме наклона и точки пересечения
.
y = 5x + 40
План 2 имеет начальную стоимость 40 долларов и ставку 5 долларов в час.

Вопрос 4.
Нарисуйте график, показывающий вариант $15 в час.
Введите ниже:
______________

Ответ:

Вопрос 5.
Что означает пересечение двух графиков?
Введите ниже:
______________

Ответ:
Пересечение двух графиков представляет количество часов, в течение которых оба плана будут стоить одинаково,

Вопрос 6.
Какой план дешевле за 10 часов обучения?
______________

Ответ:
План 1
y = 15x
x = 10 часов
y = 15(10) = 150 долл. $90
План 2 дешевле

Вопрос 7.
Являются ли затраты и время пропорциональными или непропорциональными для каждого плана?
Введите ниже:
______________

Ответ:
Сравнение с общей линейной формой уравнения y = mx + b. Поскольку b = 0, соотношение пропорционально
Стоимость и время пропорциональны для Плана 1
Сравнение с общей линейной формой уравнения y = mx + b. Поскольку b не равно 0, отношение является пропорциональным
Стоимость и время непропорциональны для Плана 2

Регистрация основного вопроса

Вопрос 8.
При использовании таблиц, графиков и уравнений для сравнения функций, почему вы находите уравнения для таблиц и графиков?
Введите ниже:
______________

Ответ:
Таблицы и графики представляют часть решения функции. Написав уравнение, любое значение можно заменить, чтобы оценить функцию и сравнить ее с уравнениями.

Независимая практика — сравнение функций — стр. № 171

В таблице и на графике показан пробег двух скутеров и расход топлива.

Вопрос 9.
Какой скутер потребляет меньше галлонов бензина при пробеге 1350 миль?
______________

Ответ:
Скутер B потребляет меньше галлонов бензина, когда проезжает 1350 миль

Пояснение:
Уравнение для скутера A Наклон m = m = (y2 -y1)/(x2 – x1), где (x1, y1) ) = (150, 2) и (x2, y2) = (300, 4)
Уклон m = (y2 -y1)/(x2 — x1) = (4 — 2)/(300 — 150) = 2/150 = 1/75
2 = 1/75(150) + b
y-отрезок b = 0
Подстановка значения наклона m и y-отрезка в форму наклона-отрезка. y = mx + b, где m = 1/75 и b = 0,
y = 1/75x
x = 1350 миль
y = 1/75(1,350)
y = 18 галлонов
Уравнение для скутера B Уклон m = m = (y2 -y1)/(x2 — x1), где (x1, y1) = (0, 0) и (x2, y2) = (90, 1)
Наклон m = (y2 -y1)/(x2 – x1) = (1 – 0)/(90 – 0) = 1/90
2 = 1/ 90(90) + b
y-отрезок b = 0
Подстановка значения наклона m и y-отрезка в форму наклона-отрезка. y = mx + b, где m = 1/90 и b = 0,
y = 1/90x
x = 1350 миль
y = 1/90(1350)
y = 15 галлонов
миль
18 > 15
Скутер B потребляет меньше галлонов бензина, когда проезжает 1350 миль.

Вопрос 10.
Расход топлива и количество миль пропорциональны или непропорциональны для каждого скутера?
______________

Ответ:
Расход бензина и пробег пропорциональны обоим скутерам.

Объяснение:
Сравните с общей линейной формой уравнения, y = mx + b. Если b = 0, отношение пропорциональное.
Используемый газ и пробег пропорциональны обоим скутерам.

Компания сотовой связи предлагает своим клиентам два плана текстовых сообщений. Ежемесячная стоимость, y долларов, одного плана составляет y = 0,10x + 5, где x — количество текстов. Стоимость другого плана указана в таблице.

Вопрос 11.
Какой тариф дешевле до 200 сообщений?
______________

Ответ:
План 1 дешевле

Объяснение:
План 1
y = 0,10x + 5
Подстановка x = 199
y = 0,10(199) + 5 = 24,90 $ 9007 Найдите наклон, используя две точки наклона. график по m = (y2 -y1)/(x2 — x1), где (x1, y1) = (100, 20), (x2, y2) = (200, 25)
Подставить значение m и (x1, y1) = (100, 20), (x2, y2) = (200, 25)
Наклон m = (y2 -y1)/(x2 — x1) = (25 — 20 )/(200 – 100) = 5/100 = 0,05
20 = 0,05(100) + b
точка пересечения по оси y b = 15
Подставляя значение уклона (м) и (x, y) в форму точки пересечения наклона к найти точку пересечения y (b):
y = 0,05x + 15
x = 199
y = 0,05(199) + 15 = 24,95 $
Сравните стоимость двух планов для текста < 200
24,90 $ < 24,95 $
Уровень 1 дешевле

Вопрос 12.
Граф первого плана не проходит через начало координат. Что это означает?
Введите ниже:
______________

Ответ:
План 1
y = 0,10x + 5
График, который не проходит через начало координат, показывает, что базовая цена плана составляет 5 долларов.

Вопрос 13.
Брианна хочет купить цифровую камеру для урока фотографии. Один магазин предлагает камеру за 50 долларов и план оплаты 20 долларов в месяц. План оплаты второго магазина описывается формулой y = 15x + 80, где y — общая стоимость в долларах, а x — количество месяцев. Какая камера дешевле, если камера окупится за 12 месяцев? Объяснять.
______________

Ответ:
Для первого магазина наклон пересекает форму y = mx + b, где m = 20 долларов в месяц и b = 50 долларов.
y = 20x + 50
x = 12 месяцев
y = 20(12) + 50 = 290 долларов
Второй магазин
y = 15x + 80
x = 12 месяцев стоимость камеры, если она окупится за 12 месяцев $290 > $260
Камера дешевле во втором магазине

Сравнение функций – страница № 172

Вопрос 14.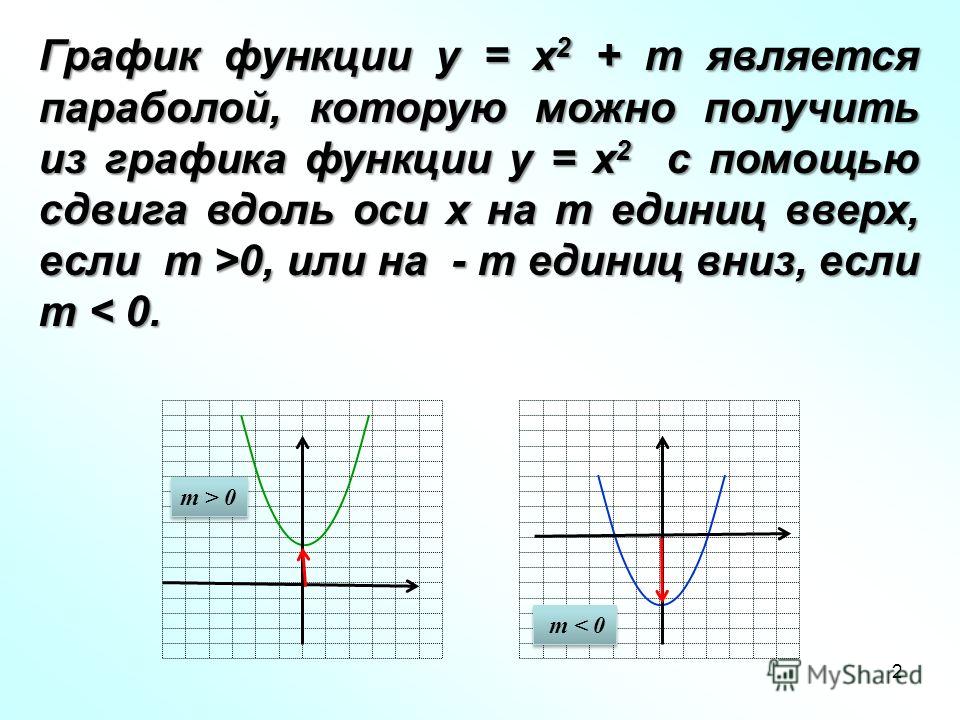
Французский клуб и футбольная команда моют машины, чтобы заработать денег. Сумма заработка, y долларов, за мойку x автомобилей является линейной функцией. Какая группа зарабатывает больше всего денег на машину? Объяснять.

______________

Ответ:

Объяснение:
Найдите наклон по двум точкам на графике по
Наклон m = (y2 -y1)/(x2 – x1), где (x1, y1) = (2, 10) и (x2, y2) = (4, 20)
Уклон m = (y2 -y1)/(x2 — x1) = (20 — 10)/(4 — 2) = 10/2 = 5
Французский клуб зарабатывает 5 долларов за автомобиль.
Найдите наклон по двум точкам на графике по
Наклон m = (y2 -y1)/(x2 — x1), где (x1, y1) = (0, 0) и (x2, y2) = (2, 16)
Наклон m = (y2 -y1)/(x2 — x1) = (16 — 0)/(2 — 0) = 16/2 = 8 9Футбольный клуб 0077 зарабатывает 8 долларов за машину.
Сравните деньги, заработанные на мойке одной машины $5 < $8
Футбольный клуб зарабатывает больше всех на машине

Сосредоточьтесь на мышлении высшего порядка

Вопрос 15.
Подведите итоги
Тренажерный зал А стоит 60 долларов в месяц плюс 5 долларов за посещение. Ежемесячные расходы в тренажерном зале B представлены как y = 5x + 40, где x — количество посещений в месяц. Какой вывод вы можете сделать о ежемесячных затратах на спортзалы?
__________ дороже

Ответ:
Тренажерный зал А дороже

Объяснение:
Поскольку ставка за посещение одинакова, месячная стоимость гинекологии А всегда больше, чем в тренажерном зале Б.

Вопрос 16.
Обоснуйте рассуждения
Почему значение y для функции y = 5x + 1 всегда будет больше, чем значение для функции y = 4x + 2, когда x > 1?
Введите ниже:
______________

Ответ:
y1 = 5x + 1 и y2 = 4x + 2 Вычитание y2 из y1
y1 – y2 = 5x + 1 – (4x + 2)
y1 – y2 = x -1
Для x>= 1 получаем x – 1 >= 0
Итак, y1 – y2 >= 0 или y1 >= y2

Вопрос 17.
Анализ отношений
Уравнения двух функций: y = −21x + 9 и y = −24x + 8. Какая функция меняется быстрее? Объяснять.
______________

Ответ:
y = -21x + 9
y = -24x + 8
y = -24x + 8 изменяется быстрее, поскольку абсолютное значение -24 больше, чем абсолютное значение -21.

Учебное пособие — Анализ графиков — № страницы 176

В лабораторных условиях колонии бактерий растут по предсказуемой схеме. График показывает этот рост с течением времени.

Вопрос 1.
Что происходит с населением во время Этапа 2?
______________

Ответ:
Для фазы 2 график быстро растет. Это свидетельствует о периоде быстрого роста.

Вопрос 2.
Что происходит с населением во время фазы 4?
______________

Ответ:
В фазе 4 график уменьшается, следовательно, количество бактерий уменьшается.

Графики показывают скорости трех человек, едущих на снегоходах. Скажите, какой график соответствует каждой ситуации.

Вопрос 3.
Чип медленно начинает свою поездку, но затем останавливается, чтобы поговорить с друзьями. Через несколько минут он продолжает свою езду, постепенно увеличивая скорость.
______________

Ответ:
График 2

Объяснение:
Наклон графика увеличивается, затем становится постоянным и снова начинает увеличиваться.
График 2

Вопрос 4.
Линда неуклонно увеличивает скорость на протяжении большей части поездки. Затем она замедляется, приближаясь к деревьям.
______________

Ответ:
График 3

Объяснение:
Наклон графика увеличивается, а затем уменьшается.
График 3

Вопрос 5.
Пауло стоял на вершине трамплина. Он подошел к концу доски, а затем нырнул в воду. Он погрузился под воду, а затем поплыл прямо под водой. Наконец, он поплыл вперед и вверх к поверхности воды. Нарисуйте график, отображающий высоту Пауло на разных расстояниях от края бассейна.

Введите ниже:
______________

Ответ:

Независимая практика – Анализ графиков – Страница № 177

Скажите, какой график соответствует каждой ситуации ниже.

Вопрос 6.
Арнольд вышел из дома и пошел к дому друга. Он остался со своим другом на некоторое время, а затем пошел в дом другого друга дальше от дома.
______________

Ответ:
График 3

Объяснение:
График увеличивается (по мере того, как Арнольд идет от дома к дому друга), затем становится постоянным (когда он остался со своим другом), а затем снова увеличивается (когда он идет к другому другу). дом подальше).
График 3

Вопрос 7.
Франциско вышел из дома и пошел в магазин. После покупок он вернулся домой.
______________

Ответ:
График 1

Объяснение:
График увеличивается (по мере того, как Франциско шел от дома до магазина), становится постоянным (когда он делал покупки), а затем уменьшался (по мере того, как он возвращался домой)
График 1

Вопрос 8.
Селия идет в библиотеку ровным шагом, не останавливаясь.
______________

Ответ:
График 2

Объяснение:
График увеличивается с постоянной скоростью (по мере того как Селия идет в библиотеку без остановок)
График 2

Регина арендовала мотороллер.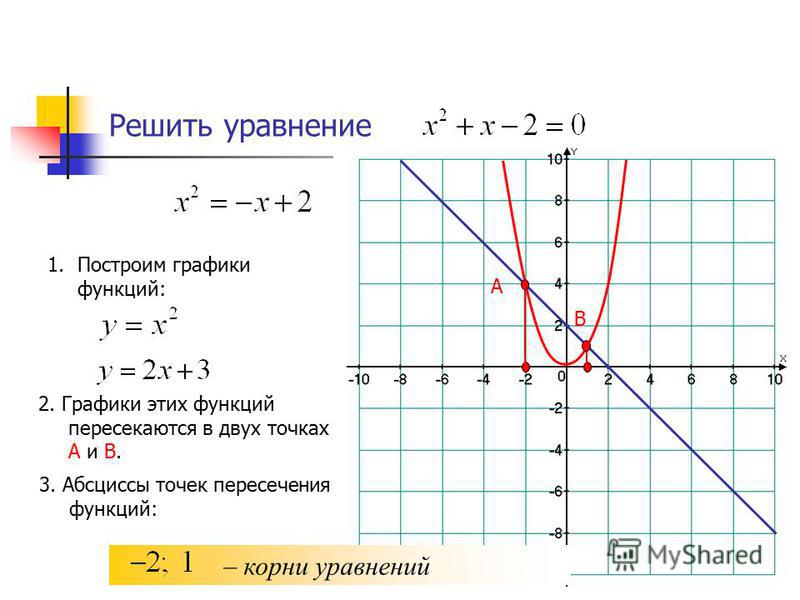 На графике показано, как далеко она от места проката через каждые полчаса катания.

Вопрос 9.
Представьте проблемы реального мира
Используйте график, чтобы описать путешествие Регины. Описание можно начать так: «Регина вышла из пункта проката и ехала час…»
Введите ниже:
______________

Ответ:
Регина вышла из пункта проката и ехала час. Она отдохнула полчаса, а затем пошла обратно. Через полчаса она передумала и каталась еще полчаса. Она отдыхает полчаса. Затем она начала обратно и заняла место проката за 2 часа.

Вопрос 10.
Анализ отношений
Определите, за какие полчаса Регина преодолела наибольшее расстояние.
Введите ниже:
______________

Ответ:
Регина преодолела наибольшее расстояние от 0,5 до 1 часа пути. Она преодолела 12 миль.

Анализ графиков – стр. № 178

Данные в таблице показывают скорость поездки в парке развлечений в разное время дня.

Вопрос 11.
Нарисуйте график, показывающий изменение скорости во времени.
Введите ниже:
______________

Ответ:

Вопрос 12.
Между какими моментами времени скорость движения увеличивается быстрее всего?
Введите ниже:
______________

Ответ:
Скорость увеличивается быстрее всего во время 3: 21 и 3: 22

Вопрос 13.
Между какими моментами скорость снижается быстрее всего?
Введите ниже:
______________

Ответ:
Скорость снижается быстрее всего во время 3: 23 и 3: 24

H.O.T.

Фокус на мышлении высшего порядка

Вопрос 14.
Обоснование рассуждений
Что происходит с популяцией лис до момента времени t? Объясните свои рассуждения.

Введите ниже:
______________

Ответ:
Население уменьшается, а затем увеличивается до времени t

Вопрос 15.
Что, если?
Предположим, что в момент времени t природоохранная организация перемещает на остров большую группу лисиц. Нарисуйте график, показывающий, как это действие может повлиять на население острова через время t.

Тип ниже:
______________

Ответ:

Объяснение:
Население сначала уменьшается, а затем быстро увеличивается.

Вопрос 16.
Сделайте прогноз
В какой-то момент времени t лесной пожар уничтожит часть лесного массива на острове. Опишите, как может измениться ваш график из задачи 15.
Введите ниже:
______________

Ответ:
Население резко уменьшится, если случится пожар из-за отсутствия продовольствия и хорошей земли.

6.1 Идентификация и представление функций — Тест по модели — Страница № 179

Определите, является ли каждое отношение функцией.

Вопрос 1.

__________

Ответ:
Не функция

Объяснение:
Связь представляет собой функцию, когда каждый вход связан ровно с одним выходом. Вход 5 имеет более одного выхода.
Не функция

Вопрос 2.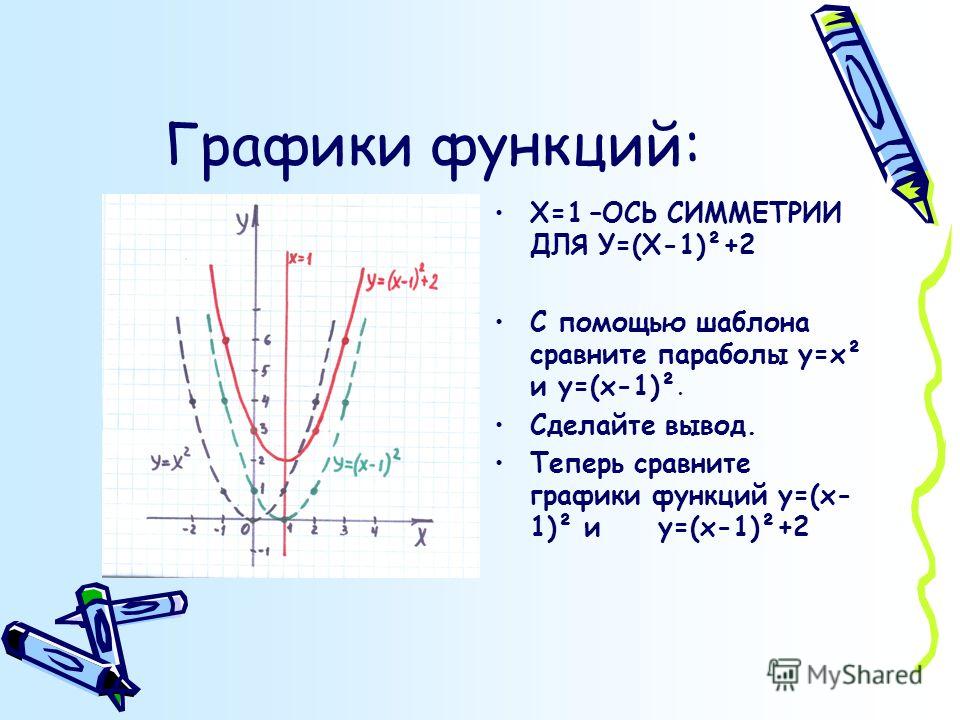

__________

Ответ:
Функция

Объяснение:
Связь представляет собой функцию, когда каждый вход связан ровно с одним выходом.
Каждый вход сопряжен только с одним выходом.
Функция

Вопрос 3.
(2, 5), (7, 2), (−3, 4), (2, 9), (1, 1)
__________

Ответ:
Не функция

Объяснение:
Связь – это функция, в которой каждому входу соответствует ровно один выход. Вход 2 имеет более одного выхода.
Не является функцией

6.2 Описание функций

Определите, является ли каждая ситуация линейной или нелинейной, пропорциональной или непропорциональной.

Вопрос 4.
Джоанне платят 14 долларов в час.
__________
__________

Ответ:
Линейная
Пропорциональная

Объяснение:
Запись ситуации в виде уравнения, где х — количество часов.
y = 14x
Сравните с общим линейным уравнением y = mx + b
Линейное
Поскольку b = 0, отношение пропорциональное.
Пропорциональный

Вопрос 5.
Альберто начал с жима лежа 50 фунтов. Затем он прибавлял по 5 фунтов каждую неделю.
__________
__________

Ответ:
Линейный
Непропорциональный

Объяснение:
Запись ситуации в виде уравнения, где х — количество часов.
y = 5x + 50
Сравните с общим линейным уравнением y = mx + b
Линейное
Поскольку b не равно 0, отношение непропорциональное.
Непропорциональное

6.3 Сравнение функций

Вопрос 6.
Какая функция меняется быстрее? Объяснять.

__________

Ответ:
Функция 2 меняется быстрее.

Объяснение:
Найдите скорость изменения для функции 1
Скорость изменения = (20 – 0)/(0 – 5) = -4
Найдите скорость изменения для функции 1
Скорость изменения = (6,5 – 11 )/(3 – 2) = -4,5
Хотя -4,5 < -4, абсолютное значение -4,5 с больше -4.
Функция 2 меняется быстрее.

6. 4 Анализ графиков

Вопрос 7.
Опишите график, на котором Сэм работает с постоянной скоростью.
Введите ниже:
______________

Ответ:
График будет прямой линией

Объяснение:
Поскольку Сэм бежит с постоянной скоростью, расстояние, пройденное за единицу времени, остается неизменным, а зависимость является линейной и пропорциональной.
График будет прямой линией

Основной вопрос

Вопрос 8.
Как можно использовать функции для решения реальных задач?
Введите ниже:
______________

Ответ:
Если в уравнении степень x равна 1, то оно линейно, в противном случае нелинейно.
На графике, если точки образуют линию, она является линейной, если они образуют кривую, это нелинейная функция.

Выбранный ответ – Смешанный обзор – № страницы 180

Вопрос 1.
В какой таблице показана пропорциональная функция?

Опции:
а. А
б. Б
с. С
д. D

Ответ:
c. C

Объяснение:
Содержит упорядоченную пару начала координат (0, 0)
Вариант C представляет пропорциональную зависимость.

Вопрос 2.
Каковы наклон и точка пересечения с координатой Y функции, показанной в таблице?

Опции:
а. м = -2; б = -4
б. м = -2; б = 4
в. м = 2; б = 4
д. м = 4; b = 2

Ответ:
c. м = 2; b = 4

Объяснение:
Найдите наклон, используя две точки на графике по
. Наклон m = (y2 -y1)/(x2 – x1), где (x1, y1) = (1, 6) и (x2, y2) ) = (4, 12)
Уклон m = (y2 -y1)/(x2 — x1) = (12 — 6)/(4 — 1) = 6/3 = 2
Подставляя значение наклона m и (x, y), чтобы найти форму пересечения наклона.
12 = 4(2) + b
y-отрезок b = 4

Вопрос 3.
В таблице ниже показаны некоторые входные и выходные значения функции.

Какое отсутствующее выходное значение?
Опции:
а. 20
б. 21
г. 22
д. 23

Ответ:
б. 21

Объяснение:
Найдите скорость изменения = (17,5 – 14)/(5 – 4) = 3,5
Так как отсутствующий выход соответствует x = 6 и 3,5 до 17,5 (для x = 5)
Результат = 17,5 + 3,5 = 21

Вопрос 4.
Том шел в школу ровным шагом, встретил свою сестру, и они ровным шагом пошли домой. Опишите этот график.
Опции:
а. V-образный
б. перевернутый V-образный
c. Прямая с уклоном вверх
d. Прямая с наклоном вниз

Ответ:
b. перевернутый V-образный

Объяснение:
График будет увеличиваться с постоянной скоростью и уменьшаться с постоянной скоростью.
График будет представлять собой перевернутую V-образную цифру 9.0003

Мини-задача

Вопрос 5.
Линейные функции можно использовать для определения цены здания на основе его площади. Ниже приведены две из этих функций.
у = 40х + 15000

а. Найдите и сравните наклоны.
Введите ниже:
____________

Ответ:
Сравните наклоны
Наклон первой функции меньше наклона второй функции.
y = 40x + 15000
Сравните с формой пересечения наклона y = mx + b, где m — уклон m = 40
Вторая функция находит наклон, используя заданные точки по наклону m = (y2 -y1)/(x2 — x1), где (x1, y1) = (7, 3) и (x2, y2) = (6, 4)
Уклон m = (y2 -y1)/(x2 — x1) = (56000 — 32000)/(700 — 400) = 24000/300 = 80
m = 80

Вопрос 5.
б. Найдите и сравните y-отрезки.
Введите ниже:
____________

Ответ:
y = 40x + 15 000
Сравните с формой пересечения наклона y = mx + b, где m — уклон b = 15000
Вторая функция находит уклон, используя заданные точки по Slope m и (x, y) в форме наклона-пересечения с ребрами y-пересечения b
y = mx + b, где (x, y) = (700, 56000) и m = 80
56000 = 80(700) + b
b = 0

Вопрос 5.
c. Опишите каждую функцию как пропорциональную или непропорциональную.
Введите ниже:
____________

Ответ:
Сопоставимо с формой пересечения наклона y = mx + b
Первая функция: y = 40x + 15000
Вторая функция: y = 80x
Поскольку b не равно 0
Первая функция непропорциональна
Так как b = 0
Вторая функция пропорциональна.

Заключение:

Скачать Go Math Class 8 Ключ к ответу Глава 6 Функции PDF бесплатно. Знаменитые и великие эксперты по математике работают над тем, чтобы обеспечить наилучший способ решения математических задач. Немедленно приступайте к практике и легко изучайте математику.

Иллюстративная математика

Иллюстративная математика

класс
8

8 класс

8.НС. 8 класс — Система счисления


8.Н.С.А. Знайте, что есть числа, которые не являются рациональными, и аппроксимируйте их рациональными числами.


• Аппроксимация пи
• Расчет и округление чисел
• Вычисление квадратного корня из 2
• Оценка квадратных корней

8.НС.А.1. Знайте, что числа, которые не являются рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число.


92$). Например, усекая десятичное представление $\sqrt{2}$, покажите, что $\sqrt{2}$ находится между $1$ и $2$, затем между $1,4$ и $1,5$, и объясните, как продолжить, чтобы получить лучшие приближения.


• Сравнение рациональных и иррациональных чисел
• Иррациональные числа на числовой прямой
• Помещение квадратного корня на числовую прямую

8.EE. 8 класс — Выражения и уравнения


8.Э.Э.А. Работа с радикалами и целочисленными показателями.
93 = p$, где $p$ — положительное рациональное число. Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что $\sqrt{2}$ иррационально.


• 
  Пока нет задач, иллюстрирующих этот стандарт.
  

8.EE.A.3. Используйте числа, выраженные в виде одной цифры, умноженной на целую степень числа 10, для оценки очень больших или очень малых величин и для выражения того, во сколько раз одно больше, чем другое.

9.$, и определите, что население мира более чем в $20$ раз больше.


• Муравей и слон
• Порядки величины
• Копейки в рай

8.EE.A.4. Выполнять операции с числами, выраженными в экспоненциальном представлении, включая задачи, в которых используется как десятичное, так и экспоненциальное представление. Используйте научные обозначения и выбирайте единицы соответствующего размера для измерения очень больших или очень малых величин (например, используйте миллиметры в год для распространения по морскому дну). Интерпретировать научную нотацию, созданную технологией.


• Муравьи против людей
• Выбор подходящих единиц
• Гигантбургеры
• Копейки в рай

8.Э.Э.Б. Понимать связи между пропорциональными отношениями, линиями и линейными уравнениями.


• Разные районы?
• Прибыль DVD, Вариант 1
• Уравнения линий
• Найдите изменение
• Складываем квадрат втрое
• Пропорциональные отношения, линии и линейные уравнения
• Набивка конвертов

8.

EE.B.5. Нарисуйте пропорциональные отношения, интерпретируя удельную скорость как наклон графика. Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график «расстояние-время» с уравнением «расстояние-время», чтобы определить, какой из двух движущихся объектов имеет большую скорость.


• Кофе на фунт
• Сравнение скоростей в графиках и уравнениях
• Персики и сливы
• Боль в горле, Вариант 2
• Набивка конвертов
• У кого лучшая работа?

8.EE.B.6. Используйте подобные треугольники, чтобы объяснить, почему наклон $m$ одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение $y = mx$ для прямой, проходящей через начало координат, и уравнение $y = mx + b$ для прямой, пересекающей вертикальную ось в точке $b$.


• Уклоны между точками на линии

8.EE.C. Анализируйте и решайте линейные уравнения и пары одновременных линейных уравнений.




• Две линии

8.ЕЕ.С.7. Решите линейные уравнения с одной переменной.


• Купон против скидки
• Наблюдения Сэмми за бурундуком и белкой
• Решение уравнений
• Знак решений

8.EE.C.7.а. Приведите примеры линейных уравнений от одной переменной с одним решением, бесконечным числом решений или отсутствием решений. Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данное уравнение в более простые формы, пока не получится эквивалентное уравнение вида $x = a$, $a = a$ или $a = b$ (где $a$ и $b$ — разные числа).


• 
  Пока нет задач, иллюстрирующих этот стандарт.
  

8.EE.C.7.b. Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием дистрибутивного свойства и сбора подобных членов.


• 
  Пока нет задач, иллюстрирующих этот стандарт.
  

8.ЕЕ.С.8. Анализируйте и решайте пары одновременных линейных уравнений.


• Тарифы на сотовый телефон
• Крепление печи
• Складываем квадрат втрое
• Сколько решений?
• Кими и Джордан

8.EE.C.8.а. Поймите, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, потому что точки пересечения удовлетворяют обоим уравнениям одновременно.


• Пересечение двух линий

8.EE.C.8.b. Решите системы двух линейных уравнений с двумя переменными алгебраически и оцените решения, построив уравнения в виде графика. Решите простые случаи путем проверки. Например, $3x + 2y = 5$ и $3x + 2y = 6$ не имеют решения, потому что $3x + 2y$ не может быть одновременно $5$ и $6$.


• 
  Пока нет задач, иллюстрирующих этот стандарт.
  

8.EE.C.8.c. Решайте реальные и математические задачи, приводящие к двум линейным уравнениям с двумя переменными.

Например, зная координаты двух пар точек, определите, пересекает ли прямая, проходящая через первую пару точек, прямую, проходящую через вторую пару.


• Паста с киноа 1
• Летнее плавание

8.Ф. 8 класс — Функции


8.Ф.А. Определите, оцените и сравните функции.


• Знакомство с функциями

8.Ф.А.1. Поймите, что функция — это правило, которое назначает каждому входу ровно один выход. График функции представляет собой набор упорядоченных пар, состоящих из входа и соответствующего выхода. Обозначение функции не требуется в 8 классе.


• Лисы и кролики
• Правила функций
• Знакомство с функциями
• Копейки в рай
• Покупатели
• Мусор США, версия 1

8.F.A.2. Сравните свойства двух функций, каждая из которых представлена ​​по-разному (алгебраически, графически, численно в таблицах или словесными описаниями).

Например, если дана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения.
92$, задающий площадь квадрата как функцию длины его стороны, не является линейным, поскольку его график содержит точки $(1,1)$, $(2,4)$ и $(3,9)$, которые не по прямой.


• Введение в линейные функции

8.Ф.Б. Используйте функции для моделирования отношений между величинами.


• Мониторинг сердечного ритма
• Моделирование с помощью линейной функции

8.Ф.Б.4. Создайте функцию, чтобы смоделировать линейную связь между двумя величинами. Определить скорость изменения и начальное значение функции по описанию зависимости или по двум значениям $(x, y)$, в том числе считывая их из таблицы или графика. Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.




• Бейсбольные карточки
• Курица и стейк, Вариант 1
• Курица и стейк, Вариант 2
• Доставка почты, вариант оценки
• Расстояние по каналу
• Скоростной спуск
• Выпускной
• Видео трансляция

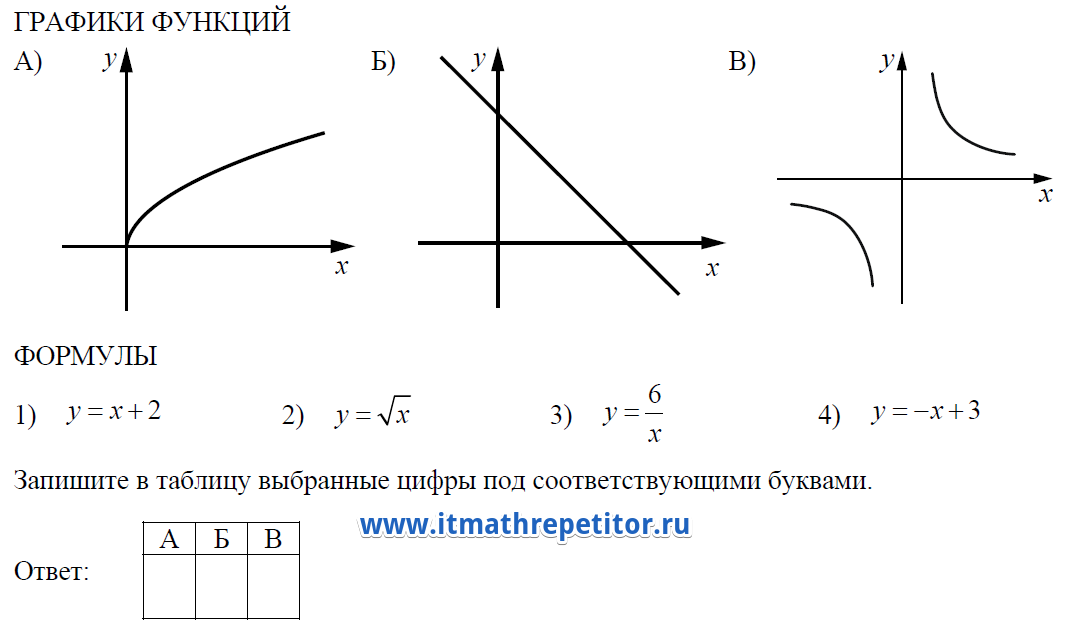
8.Ф.Б.5. Качественно опишите функциональную связь между двумя величинами, анализируя график (например, где функция возрастает или убывает, линейна или нелинейна). Нарисуйте график, демонстрирующий качественные характеристики функции, описанной словесно.


• Велосипедная гонка
• Расстояние
• Катание по библиотеке
• Приливы

8.Г. 8 класс — Геометрия


8.Г.А. Понимание конгруэнтности и сходства с помощью физических моделей, прозрачных пленок или программного обеспечения для создания геометрии.


• Масштабированная кривая
• Это прямоугольник?
• Разделение шестиугольника
• Отражение прямоугольника по диагонали
• Тот же размер, та же форма?
• Масштабирование углов и полигонов

8.

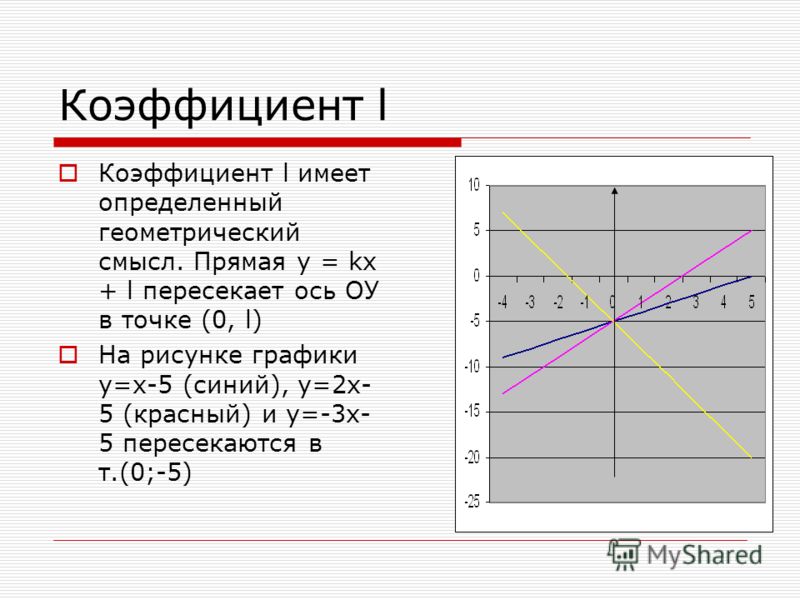Г.А.1. Экспериментально проверьте свойства поворотов, отражений и переводов:


• Серебряный прямоугольник оригами
• Отражения, вращения и переводы

8.G.A.1.а. Линии превращаются в прямые, а отрезки прямых в отрезки прямой одинаковой длины.


• 
  Пока нет задач, иллюстрирующих этот стандарт.
  

8.Г.А.2. Поймите, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.


• Круглый сэндвич
• Конгруэнтные прямоугольники
• Конгруэнтные сегменты
• Конгруэнтные треугольники
• Разрезание прямоугольника на два равных треугольника
• Конгруэнтность треугольника с координатами

8.Г.А.3. Опишите эффект расширения, перевода, поворота и отражения на двухмерных фигурах, используя координаты.




• Влияние дилатации на длину, площадь и углы
• Точечное отражение
• Отражающие отражения
• Конгруэнтность треугольника с координатами

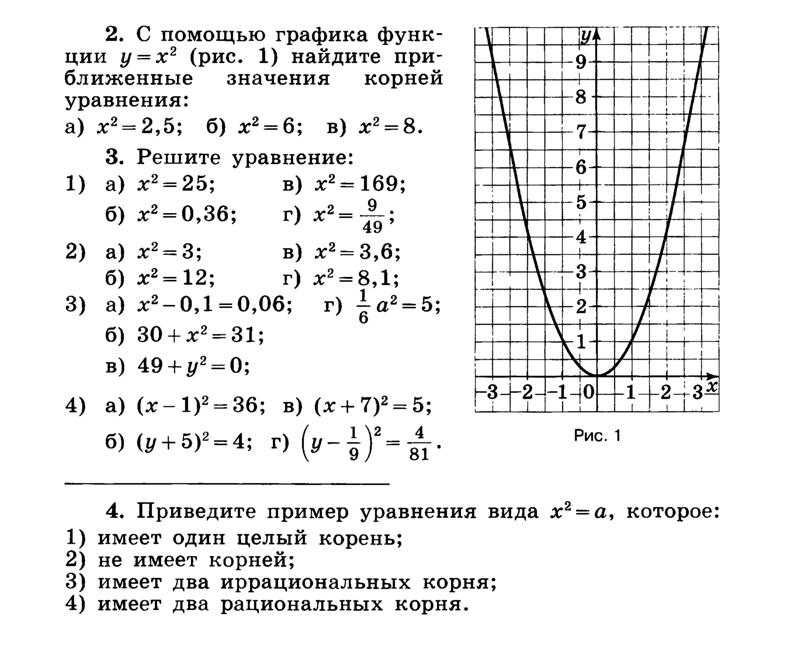
8.Г.А.4. Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними.


• Они похожи?
• Создание подобных треугольников
• Разные районы?

8.Г.А.5. Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образованных при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников. Например, расположите три копии одного и того же треугольника так, чтобы сумма трех углов представляла собой линию, и приведите аргумент в терминах секущей, почему это так.




• Внутренние углы треугольника
• Конгруэнтность альтернативных внутренних углов через повороты
• Найдите угол
• Найдите недостающий угол
• Жесткие движения и конгруэнтные углы
• Подобные треугольники I
• Подобные треугольники II
• Перекрестки улиц
• Шаблоны плитки II: шестиугольники
• Узоры плитки I: восьмиугольники и квадраты

8.Г.Б. Поймите и примените теорему Пифагора.


• Применение теоремы Пифагора в математическом контексте
• Прямоугольник в координатной плоскости
• Гонки птиц и собак
• Это прямоугольник?
• Измерение квадратов

8.GB.7. Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальном мире и математических задач в двух и трех измерениях.


• Площадь трапеции
• Площади геометрических фигур с одинаковым периметром
• Круглый сэндвич
• Очки
• Баллы от направлений
• Бег на футбольном поле
• Паукбокс
• Площадь двух треугольников

8.

GB.8. Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.


• Нахождение равнобедренных треугольников
• Нахождение расстояния между точками

8.G.C. Решайте реальные и математические задачи, связанные с объемом цилиндров, конусов и сфер.


8.G.C.9. Знать формулы объемов конусов, цилиндров и сфер и использовать их для решения реальных и математических задач.


• Сравнение снежных конусов
• Вазы для цветов
• Очки
• Доставка овсяных хлопьев

8.СП. 8 класс — Статистика и вероятность


8.СП.А. Исследуйте закономерности ассоциации в двумерных данных.


8.СП.А.1. Создавайте и интерпретируйте диаграммы рассеяния для данных двумерных измерений, чтобы исследовать закономерности связи между двумя величинами. Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная связь, линейная связь и нелинейная связь.




• Мозги животных
• Яйца птиц
• Размах рук и рост
• Текстовые сообщения и классы I

8.СП.А.2. Знайте, что прямые линии широко используются для моделирования отношений между двумя количественными переменными. Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии.


• Мозги животных
• Яйца птиц
• Зарядка аккумулятора ноутбука

8.СП.А.3. Используйте уравнение линейной модели для решения задач в контексте данных двумерных измерений, интерпретируя наклон и точку пересечения. Например, в линейной модели для биологического эксперимента интерпретируйте наклон 1,5 см/ч как означающий, что дополнительный час солнечного света каждый день связан с дополнительными 1,5 см высоты взрослого растения.


• Аэропорты США, вариант оценки

8.

СП.А.4. Поймите, что закономерности ассоциации также можно увидеть в двумерных категориальных данных, отображая частоты и относительные частоты в двусторонней таблице. Постройте и интерпретируйте двустороннюю таблицу, обобщающую данные по двум категориальным переменным, собранным у одних и тех же субъектов. Используйте относительные частоты, рассчитанные для строк или столбцов, чтобы описать возможную связь между двумя переменными. Например, соберите данные от учеников вашего класса о том, соблюдается ли у них комендантский час по вечерам в школе и есть ли у них работа по дому. Есть ли доказательства того, что те, у кого комендантский час, также, как правило, занимаются домашними делами?


• Музыка и спорт
• Какой твой любимый урок?

Класс 8A — RUSD Математика

Математика 8A

В этом сжатом курсе для 8-го класса учащиеся будут изучать эквивалент алгебры 1 вместе с некоторыми материалами для 8-го класса, которые не были охвачены в курсе 7C. Основные направления алгебры включают (1) видение структуры в выражениях, (2) арифметику с полиномами и рациональными функциями, (3) создание уравнений и (4) рассуждение с помощью уравнений и неравенств​.

​Посетите Concept Corner (ссылка) для получения дополнительных ресурсов.
​
​имя пользователя: студент
пароль: студент

Календарь домашних заданий и экзаменов

Объем и последовательность

Годовой объем и последовательность
Годовой обзор и руководство по темпам

8.1 Анализ графиков Обзор
​В этом разделе учащиеся создают, анализируют и оценивают графики. Цель состоит в том, чтобы сознательно перейти от конкретного к абстрактному и постепенно формализовать процесс построения графика.​

Ресурсы для домашних заданий Часть 1 Домашнее задание Часть 1 Домашнее задание — ключ ответа

Concept Corner Обзоры ​Concept 1 — Functions — Properties

8. 4 Линейные отношения
Линейные отношения окружают вас повсюду. Расстояние, которое вы пробегаете, зависит от количества времени, которое вы бегаете. Сколько воды вы используете в душе, зависит от того, как долго вы принимаете душ. В этом модуле вы рассмотрите примеры повседневных линейных отношений и научитесь отображать отношения как в виде уравнений, так и в виде графиков. Вы обнаружите, что постоянная скорость показана наклоном линии. Вы также узнаете, что означает «перевод линейного графика» и как он влияет на уравнение графика. Прежде чем вы это узнаете, вы будете видеть линейные уравнения везде, куда бы вы ни пошли!

Ресурсы для домашних заданий Домашнее задание по Разделу 4 Домашнее задание по Разделу 4 — ключ ответа

Обзор уголков понятий ​Концепция 1 — линия на плоскости Концепция 2 — линия на плоскости — пропорциональность

8. 5 Линейные уравнения
Учащиеся начинают этот модуль с решения уравнений с одной переменной, которые имеют переменные члены с обеих сторон. Затем они используют алгебраические преобразования, чтобы идентифицировать уравнения с одной переменной, которые имеют ровно одно, ни одного или бесконечно много решений. Эти навыки применяются для решения систем уравнений с двумя переменными с использованием как графических, так и алгебраических методов. В конце учащиеся используют эти методы для решения множества реальных и математических задач, связанных с числами, городами, такси и т. д.​

Ресурсы для домашних заданий ​Домашнее задание по Разделу 5 Домашнее задание по Разделу 5 — Ключ к ответу

Обзор уголка концепций Концепция 1 — Уравнения — Одна переменная Концепция 2 — Уравнения — Система линейных уравнений

8.7 Функции
В этом разделе учащиеся узнают, как графики отображают скорость изменения — как в линейных, так и в нелинейных ситуациях. Они изучат концепцию функций, домена и диапазона и применят ее к линейным функциям, представленным графиками, таблицами, уравнениями и словесными описаниями. Наконец, учащиеся будут моделировать реальные ситуации с помощью линейных и нелинейных функций.

Ресурсы для домашних заданий Домашнее задание по Разделу 7 Домашнее задание по Разделу 7 — Ключ к ответу

Обзор углов концепции ​Концепция 1 — функции — линейные ​Концепция 2 — функции — свойства Концепция 3 — функции — скорость изменения Концепция 4 — функции — представления

9.1 Моделирование с помощью функций

Домашнее задание, часть 1  Домашнее задание, часть 1 — ключ ответа

Обзор концепции в форме видео ​имя пользователя: student ​пароль: student

9.