Задачи с решениями 8класс( геометрия)
ЗАДАЧИ ДЛЯ УЧАЩИХСЯ 8 КЛАССА.( с решениями)
Задача № 1
Вычислите углы параллелограмма, если его углы, прилежащие к одной стороне, относятся как 2 : 3.
Д а н о: ABCD – параллелограмм; A: B = 2 : 3.
Н а й т и: A; B; C; D.
Задача №2
Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найти стороны параллелограмма.
Д а н о: ABCD – параллелограмм; ВС – АВ = 25 см; PАВСD = 122 см.
Н а й т и: АВ; ВС; CD; AD.
Задача № 3
Постройте параллелограмм со сторонами 4 см и 6 см и углом 50° между ними.
Д а н о: A = 50°; АВ = 4 см; AD = 6 см.
П о с т р о и т ь параллелограмм ABCD.
Задача № 4
Меньшая сторона прямоугольника равна 4 см и образует с диагональю угол в 60°. Найдите диагонали прямоугольника.
Д а н о: ABCD – прямоугольник; АВ = 4 см; BAC = 60°; АС – диагональ.
Н а й т и: АС.
Задача № 5
Биссектриса угла А прямоугольника ABCD делит сторону ВС на части 2 см и 6 см. Найдите периметр прямоугольника.
Д а н о: ABCD – прямоугольник; АЕ – биссектриса A; BE = 2 см; ЕС = 6 см; (или BE = 6 см, ЕС = 2 см).
Н а й т и: PАВСD.
Задача № 6
Д а н о: ABCD – четырехугольник; ОА = ОС; 1 = 2.
Д о к а з а т ь, что ABCD – параллелограмм.
Задача № 7
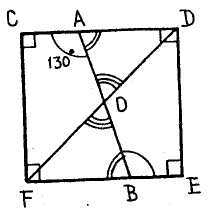
Д а н о: EFCD – квадрат; DO = OF; ACD; BEF; CAO = 130°.
Н а й т и все неизвестные углы.
Задача № 1
Р е ш е н и е.
Если ABCD – параллелограмм, то A = C, B = D, A + B = 180° – как внутренние односторонние при AD || BC и секущей АВ. Если A : B = 2 : 3, то A = 2х, B = 3х и 2х + 3х = 180°, 5х = 180°, х = 180° : 5 = 36°. A = C = 36° 2 = 72°, B = D = 36°3 = 108°.
О т в е т: 72°; 108°.
Задача №2
Р е ш е н и е.
Пусть АВ = х, тогда ВС = х + 25. Так как CD = АВ и ВС = AD, то CD = х и AD = х + 25. По условию PАВСD = 122 см, значит, 2х + (х + 25) 2 = 122, х + (х + 25) = 61. 2х + 25 = 61, 2х = 61 – 25, 2х = 36, х = 18, тогда АВ = CD = 18 см, ВС = AD = 18 + 25 = 43 (см).
О т в е т: 18 см; 43 см.
Задача № 3
А н а л и з:
П о с т р о е н и е:
1. Строим A = 50°.
2. На одной из сторон A откладываем отрезок АВ = 4 см, на другой – AD = 6 см.
3. Через точку В проводим прямую a || AD, через точку D прямую в || АВ. а || в = С. ABCD – искомый параллелограмм.
Д о к а з а т е л ь с т в о.
Задача № 4
Р е ш е н и е.
CBA = 90°, т. к. ABCD – прямоугольник. В ΔАВС CBA = 90°, BAC = 60°, тогда ACB = 180° – (60° + 90°) = 30°, т. к. сумма углов треугольника 180°. Катет, лежащий против угла в 30°, равен половине гипотенузы, значит, если АВ = 4 см, то АС = 42 = 8 (см).
О т в е т: 8 см.
Задача № 5
Р е ш е н и е.
PАВСD = АВ 2 + ВС 2; ВС = 2 + 6 = 8 см. В ΔАВЕ BAE = 90 : 2 = 45°, т. к. АЕ – биссектриса A, значит, BEA = 180° – (90° + 45°) = 180° – 135° = 45° и ΔАВЕ – прямоугольный и равнобедренный, т. е. АВ = BE = 2 см (или АВ = ВЕ = 6 см), тогда PАВСD = 2 8 + 2 2 = 16 + 4 = 20 (см) [или PАВСD = 2 8 + 2 6 = 16 + 12 = 28 (см)].
О т в е т: 20 см или 28 см.
Задача № 6
Р е ш е н и е.
1. 1 = 2, но эти углы накрест лежащие при пересечении прямых ВС и AD секущей BD, значит, ВС||АО.
2. BC||AD, AC – секущая, значит, BCO = DAO.
3. BOC = AOD как вертикальные.
4.
5.
Задача № 7
Р е ш е н и е.
C = D = E = F = 90°, т. к. EFCD – квадрат. DF – диагональ, и по свойству диагоналей квадрата CDF = EDF = DFE = DFC = 45°. DAO = 180° – 130° = 50°. так как DAO и CAO – смежные, ABF = DAO = 50°, т. к. CD || FE и АВ – секущая, ABF и DAO – внутренние накрест лежащие, аналогично ABE = ВАС = 130°. В ΔAOD DAO = 50°, ADO = 45°, значит, AOD = 180° – (50° + 45°) = 85°, т. к. сумма углов треугольника равна 180°. AOD = BOF = 85°, т. к. эти углы вертикальные.
О т в е т: 90°; 45°; 130°; 50°; 85°.
infourok.ru
Задачи по геометрии 8 класс
Задачи по геометрии для 8 класса для подготовки к итоговой контрольной работе
1. В прямоугольном треугольнике найдите гипотенузу с, если его катеты равны: а=5 см, b=12 см.
2. В равнобедренном треугольнике боковая сторона равна 10 дм и основание равно 12 см. Найдите: а)высоту треугольника, проведенную к основанию треугольника; б) площадь треугольника.
3. В прямоугольном треугольнике гипотенуза с=25 см, один из его катетов: а=24 см. Найдите другой катет b.
4. В равнобедренном треугольнике боковая сторона равна 13 дм и основание равно 10 см. Найдите: а)высоту этого треугольника, проведенную к основанию треугольника; б) площадь треугольника.
5. Высота равнобедренного треугольника, проведенная к основанию, равна 8 см, основание равно 12 см. Найдите боковую сторону.
6. Найдите площадь равнобедренной трапеции, если ее основания равны 4 и 10 см, а боковая сторона — 5 см.
7. Найдите сторону ромба, если его диагонали равны 24 и 32 см.
8. Найдите площадь равнобедренной трапеции, если одно из оснований равно 6 см, боковая сторона — 15 см, высота — 9 см.
9. Найдите длину основания АD, изображенной на рисунке трапеции ABCD, если BC=7, BO=3, OD=6.
4. В равнобедренном треугольнике, основание равно 14, угол между боковыми сторонами равен 60°. Найдите длину высоты, проведенной к основанию.
10. Найдите длину основания BC, изображенной на рисунке трапеции ABCD, если AD=15, BO=2, OD=6.
11. В равнобедренном треугольнике, основание равно 16, угол между основанием и боковой стороной 60°. Найдите длину высоты, проведенной к основанию.
Запишите ответ к заданиям 4 и 5.
12. В окружности с центром в точке О и радиусом равным 3 см, проведена касательная ВС (В — точка касания). Найдите длину отрезка ВС, если ОС=5.
13. На рисунке Р и Н середины сторон, ВК – высота треугольника. Найдите площадь треугольника, если РН=13см, ВК=8см.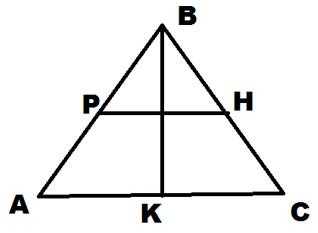
14. Используя данные рисунка, найдите площадь равнобедренной трапеции.
15. Найдите боковую сторону равнобедренного треугольника, если его высота равна 8, а угол при основании равен 30°.
16. В окружности с центром в точке О и радиусом равным 8 см, проведена касательная ВС (В — точка касания). Найдите длину отрезка OС, если BС=15.
17. На рисунке Р и Н середины сторон, ВК – высота треугольника. Найдите площадь треугольника, если РН=18см, ВК=17см.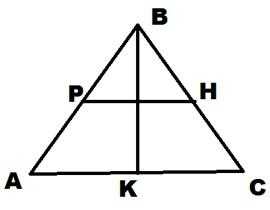
18. В квадрате ABCD диагональ АС пересекает отрезок ВM (МϵAD) в точке Р. Найдите длины отрезков ВР и РМ, если сторона квадрата равна 12 см, а отрезок АМ=5см.
multiurok.ru
Задачи КДР по геометрии с решениями. 8 класс.
Предлагаю решение пятого
варианта КДР по геометрии 2012 года, для
учащихся 8 классов. Варианты КДР по геометрии 2012 года можно посмотреть здесь
ЗАДАЧА 1. ABCD – прямоугольник. О — точка
пересечения АС и BD. Угол BOC=120º. Найдите угол DАО ( см. рис. 1 ).
| Рис.1 |
Решение.
Угол DAO
можно найти, рассмотрев треугольник DOA. Треугольник равнобедренный. Угол DOA равен углу BOC, так как они вертикальные. Сумма
углов при основании треугольника DOA равна 180-120=60.
Так как углы при основании равнобедренного треугольника равны, то искомый угол DAO равен 60/2=30. Ответ: 300.
ЗАДАЧА 2. Дан треугольник АВС. KF – средняя
линия треугольника АВС. АВ=10, ВС=8, АС=12. Найдите периметр треугольника BKF (см.
рис. 2).
| Рис.2 |
Решение. Для решения достаточно вспомнить, что
средняя линия треугольника равна половине его основания. Следовательно KF=12:2=6. Из определения средней линии
следует, что KB=10:2=5;
а BF=8:2=4. Находим
периметр треугольника BKF P=5+4+6=15.
ЗАДАЧА 3. АВС – прямоугольный треугольник со
сторонами 6, 8, 10. Найдите косинус угла треугольника АВС, лежащего против
меньшего катета.
| Рис. 3 |
Решение. Начертим
рисунок по заданному условию. Так как гипотенуза прямоугольного треугольника
всегда больше его катетов, то сторона, равная 10 – это гипотенуза. Катеты
расположим произвольно (см. рис. 3). На чертеже отметим искомый угол. Косинусом угла прямоугольного треугольника
называют отношение прилежащего катета к гипотенузе. Т.е. 8/10.
ЗАДАЧА 4. ABCD – параллелограмм. АС – его диагональ.
Угол BCА=35º, угол ADC=100º. Найдите угол АСD.
| Рис.4 |
Решение. Составляем чертеж по условию (см. рис.
4). При параллельных прямых BC и AD, и секущей AC, углы BCA и DAC являются внутренними накрест лежащими
углами. Эти углы равны, следовательно угол DAC=350. Рассмотрим
треугольник ADC.
Сумма углов треугольника равна 1800. Два угла нам известны, найдем
третий 180 — (100+35)=45. Ответ: 450.
ЗАДАЧА 5. В прямоугольной трапеции большая боковая
сторона и большее основание равны по 20 см, острый угол равен 60º. Найдите
меньшее основание.
| Рис.5 |
Решение. По условию задачи составим чертеж (см.
рис. 5). Проведем отрезок BK,
параллельный отрезку CD.
Рассмотрим получившийся прямоугольный треугольник ABK.
Теперь
осталось найти меньшее основание BC= AD-AK=20-10=10.
Задачу можно решить намного проще, если вспомнить, что в прямоугольном треугольнике катет, противолежащий углу 30º ( угол ABK) равен половине гипотенузы. Следовательно AK=10. Отсюда находим, что BC=10.
Ответ: 10 см.
ЗАДАЧА 6. Катеты прямоугольного треугольника
относятся как 8:15, гипотенуза равна 51. Найдите периметр этого треугольника.
Решение. Приведу решение без предварительного
составления чертежа. Катеты прямоугольного треугольника равны 8x и 15x. Используя теорему Пифагора, получим:
512=(8x)2+(15x)2. Решив данное уравнение,
получим, что x=3.
Следовательно стороны треугольника равны соответственно 24 и 45.
Если
у кого-то есть интересные задачи КДР по геометрии прошлых лет для
восьмиклассников, то просьба поделиться. Порешаем…
ЗАДАЧА 7. В параллелограмме большая сторона равна
25 . Меньшая высота равна 12. Меньшая
диагональ — 20. Найдите угол между этой диагональю и меньшей стороной.
| Рис.6 |
Решение. По условию составляем чертеж.
Рассмотрим треугольник BKD.
По теореме Пифагора находим KD:
202=122+x2. Откуда x=16. Отрезок AK=AD-KD=25-16=9. Теперь, рассмотрев
треугольник ABK,
по т. Пифагора найдем меньшую сторону AB=15. Для нахождения угла BDC перейдем к треугольнику BDC, где убеждаемся, что теорема
Пифагора, а именно 252=202+152, нам
показывает, что наш треугольник прямоугольный, следовательно, искомый угол
равен 900. Ответ: 900.
ЗАДАЧА 8. В параллелограмме ABCD диагонали пересекаются в точке О.
Угол AOD
равен 1100.
Угол DBC
равен 300. BD=2AB. Найти углы параллелограмма.
| Рис. 7 |
Решение. По условию составляем чертеж. Черным
на чертеже показаны исходные данные. Красным – то, что мы находим. Немного
поясню. 1. Угол BOC=1100
(свойство вертикальных углов). 2. Рассматриваем треугольник BOC и находим неизвестный угол BCO (400). 3. Угол DAO=BCO=400; угол CBO=ADO=300 (внутренние накрест
лежащие углы). 4. По условию AB=BO, следовательно треугольник ABO равнобедренный. Углы при основании равнобедренного
треугольника равны. Значит BAO=DCO=700. Осталось только
записать ответ. Ответ: Угол A=C=1100; угол B=D=700.
ЗАДАЧА, предложенная в комментариях к посту. На стороне АD параллелограмма АВСD взята точка Е так, что АЕ = 4, ЕD = 5, ВD = 13. Докажите, что треугольник ВЕD прямоугольный, и найдите площадь параллелограмма.
Решение: Рассмотрим этот чертеж с пояснениями (рисунок можно увеличить)

solodenkovagalina.blogspot.com