Алгебра 8 Класс Макарычев Дидактические Материалы ГДЗ – Telegraph
➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!
Алгебра 8 Класс Макарычев Дидактические Материалы ГДЗ
ГДЗ : готовые ответы по алгебре дидактические материалы за 8 класс, решебник Жохов, ФГОС, онлайн решения на GDZ .RU . Авторы : Жохов В .И ., Макарычев Ю .Н ., Миндюк Н .Г . Издательство: Просвещение . Тип книги: Дидактические материалы .
ГДЗ дидактические материалы по алгебре 8 класс Жохов, Макарычев , Миндюк Просвещение . Одной из главных дисциплин в восьмом классе является математика . Нужно отметить, что на этом этапе учебного процесса математика разделяется на алгебру и . .
Решебник к учебнику «Алгебра 8 класс Дидактические материалы Жохов, Макарычев, Миндюк Просвещение» помогает не только в усвоении ГДЗ выполняет именно такую работу – помогает исправить отставание в предмете ребятам, не очень знающих предмет, а любителей . .
Жохов В .И ., Макарычев Ю . Н ., Миндюк Н .Г . Решебник (ГДЗ ) по Алгебре за 8 (восьмой ) класс дидактические материалы авторы: Жохов, Макарычев, Миндюк издательство Просвещение, год .
Н ., Миндюк Н .Г . Решебник (ГДЗ ) по Алгебре за 8 (восьмой ) класс дидактические материалы авторы: Жохов, Макарычев, Миндюк издательство Просвещение, год .
Как помочь восьмикласснику с выполнением упражнений по алгебре ? Если у вас нет денег на репетиторов, не хватает времени, сил или компетенции для помощи своему чаду с уроками, лучшим вариантом будет воспользоваться онлайн-пособием ГДЗ по алгебре за 8 класс . .
Учебник «Алгебра 8 класс дидактические материалы Жохов, Макарычев, Миндюк» издательства «Просвещение», по мнению Благодаря детальному изложению материала в «ГДЗ по Алгебре 8 класс дидактические материалы Жохов» восьмиклассники быстро . .
• материал из этого сборника ГДЗ по алгебре за 8 класс дидактические материалы Жохов подобран в соответствии с Ведь здесь не меньше внимания уделяется и на решения усложненных заданий . ГДЗ по алгебре 8 класс Макарычев можно посмотреть здесь .
Ответы к дидактическим материалам по алгебре для 8 класса Жохов . Добавить книги в список » По зосу «» не найдено ни одной книги . Дидактические материалы по алгебре . 8 класс . 2005
Дидактические материалы по алгебре . 8 класс . 2005
Отправь задание и получи ответ . Получить решение . Алгебра Дидактические материалы Жохов В .И ., Макарычев Ю .Н ., Миндюк Н .Г . 8 класс .
Дидактические материалы по Алгебре 8 класс В .И . Жохов, Ю .Н . Макарычев . Просвещение, 2008 год . Перед учениками восьмых классов ставится ответственная задача изучения нового материала и подготовки к предстоящим выпускным экзаменам, которые состоятся в . .
Дидактические материалы 8 класс » Жохов, Макарычев , Миндюк, которые в полном объеме охватывают материал . Кроме того, ГДЗ по алгебре 8 класс заключает в себя досконально продуманные ответы по весенней и осенней олимпиадам .
Главная » Решебники, ГДЗ » ГДЗ (решебник) по алгебре 8 класс дидактические материалы — Жохов Макарычев . «Решебник» содержит ответы ко всем заданиям и упражнениям из «Дидактических материалов по алгебре 8 класс»; подробно разобраны методы и способы их . .
Дидактические материалы » Жохов, Макарычев , Миндюк с решениями (ГДЗ) . Алгебра 8 Контрольные Макарычев Ю .Н . + ОТВЕТЫ . Задачи контрольных работ из учебного пособия: «Алгебра 8 класс .
Алгебра 8 Контрольные Макарычев Ю .Н . + ОТВЕТЫ . Задачи контрольных работ из учебного пособия: «Алгебра 8 класс .
Избранное / Решебники (ГДЗ ) для школьников . ГДЗ к дидактическим материалам по алгебре для 8 класса Ю .Н . Макарычева ОНЛАЙН . 16 .11 .10 .11 .2020 . Все домашние работы к дидактическим материалам В .И . Жохова, Ю .Н . Макарычева , Н .Г . Миндюк . Алгебра 8 класс .
Пособие содержит упражнения для самостоятельных и контрольных работ по основным темам учебника «Алгебра , 8 » Ю . Н . Макарычева и др . Самостоятельные раб .
ГДЗ : готовые ответы по алгебре дидактические материалы за 8 класс, решебник Жохов, ФГОС, онлайн решения на GDZ .RU . Авторы : Жохов В .И ., Макарычев Ю .Н ., Миндюк Н .Г . Издательство: Просвещение . Тип книги: Дидактические материалы .
ГДЗ дидактические материалы по алгебре 8 класс Жохов, Макарычев , Миндюк Просвещение . Одной из главных дисциплин в восьмом классе является математика . Нужно отметить, что на этом этапе учебного процесса математика разделяется на алгебру и . .
.
Решебник к учебнику «Алгебра 8 класс Дидактические материалы Жохов, Макарычев, Миндюк Просвещение» помогает не только в усвоении ГДЗ выполняет именно такую работу – помогает исправить отставание в предмете ребятам, не очень знающих предмет, а любителей . .
Жохов В .И ., Макарычев Ю .Н ., Миндюк Н .Г . Решебник (ГДЗ ) по Алгебре за 8 (восьмой ) класс дидактические материалы авторы: Жохов, Макарычев, Миндюк издательство Просвещение, год .
Как помочь восьмикласснику с выполнением упражнений по алгебре ? Если у вас нет денег на репетиторов, не хватает времени, сил или компетенции для помощи своему чаду с уроками, лучшим вариантом будет воспользоваться онлайн-пособием ГДЗ по алгебре за 8 класс . .
Учебник «Алгебра 8 класс дидактические материалы Жохов, Макарычев, Миндюк» издательства «Просвещение», по мнению Благодаря детальному изложению материала в «ГДЗ по Алгебре 8 класс дидактические материалы Жохов» восьмиклассники быстро . .
• материал из этого сборника ГДЗ по алгебре за 8 класс дидактические материалы Жохов подобран в соответствии с Ведь здесь не меньше внимания уделяется и на решения усложненных заданий . ГДЗ по алгебре 8 класс Макарычев можно посмотреть здесь .
ГДЗ по алгебре 8 класс Макарычев можно посмотреть здесь .
Ответы к дидактическим материалам по алгебре для 8 класса Жохов . Добавить книги в список » По зосу «» не найдено ни одной книги . Дидактические материалы по алгебре . 8 класс . 2005
Отправь задание и получи ответ . Получить решение . Алгебра Дидактические материалы Жохов В .И ., Макарычев Ю .Н ., Миндюк Н .Г . 8 класс .
Дидактические материалы по Алгебре 8 класс В .И . Жохов, Ю .Н . Макарычев . Просвещение, 2008 год . Перед учениками восьмых классов ставится ответственная задача изучения нового материала и подготовки к предстоящим выпускным экзаменам, которые состоятся в . .
Дидактические материалы 8 класс » Жохов, Макарычев , Миндюк, которые в полном объеме охватывают материал . Кроме того, ГДЗ по алгебре 8 класс заключает в себя досконально продуманные ответы по весенней и осенней олимпиадам .
Главная » Решебники, ГДЗ » ГДЗ (решебник) по алгебре 8 класс дидактические материалы — Жохов Макарычев . «Решебник» содержит ответы ко всем заданиям и упражнениям из «Дидактических материалов по алгебре 8 класс»; подробно разобраны методы и способы их . .
«Решебник» содержит ответы ко всем заданиям и упражнениям из «Дидактических материалов по алгебре 8 класс»; подробно разобраны методы и способы их . .
Дидактические материалы » Жохов, Макарычев , Миндюк с решениями (ГДЗ) . Алгебра 8 Контрольные Макарычев Ю .Н . + ОТВЕТЫ . Задачи контрольных работ из учебного пособия: «Алгебра 8 класс .
Избранное / Решебники (ГДЗ ) для школьников . ГДЗ к дидактическим материалам по алгебре для 8 класса Ю .Н . Макарычева ОНЛАЙН . 16 .11 .10 .11 .2020 . Все домашние работы к дидактическим материалам В .И . Жохова, Ю .Н . Макарычева , Н .Г . Миндюк . Алгебра 8 класс .
Пособие содержит упражнения для самостоятельных и контрольных работ по основным темам учебника «Алгебра , 8 » Ю . Н . Макарычева и др . Самостоятельные раб .
ГДЗ Немецкий 2 Бим
ГДЗ По Физике 10 Класс Орлова
ГДЗ По Литературе 1 Часть Полухина
Гуревич Естествознание 5 6 ГДЗ
ГДЗ Английски Перевод Ваулина
ГДЗ Математика 6 Класс Великина
ГДЗ Тесты По Английскому 5 Класса
Решебник 8 Класс Скачать Pdf
Портфолио 6 Класс Английский Язык Spotlight ГДЗ
Разумовская 8 Класс ГДЗ 2009
Решебник По Гольцовой 11 Класс
Готовые Домашние Задания Математика Первый Класс
ГДЗ По Английскому 6 Класс Активити
ГДЗ Английский 2 Афанасьева Михеева
ГДЗ Решебники Английский Язык 1 Класс
ГДЗ П Геометрии 8 Класс Мерзляк
ГДЗ Алгебра 7 Класс Петерсон 1 Часть
Тихомирова 10 Класс ГДЗ
Решебник По Математике 9 Класса Автор Антропова
ГДЗ По Матике 5 Класс Бунимович
ГДЗ Математика 5 Рабочая Тетрадь Бунимович
ГДЗ Русский Язык 2 Класс Упр 14
ГДЗ По 5 Класс Афанасьева Михеева
ГДЗ 2 Класса Русский Малаховская
ГДЗ Косовцева Окружающий Мир 3
ГДЗ По Математике Страница 7 4 Класс
Решебник По Математике Дорофеева Шарыгина 6
ГДЗ По Английскому Языку Стьюдент Бук
Английский Язык ГДЗ 8 Класс Афанасьева Михеева
ГДЗ По Физике 9 Класс Упражнение 3
ГДЗ По Физике 8 Класс Пурышева Важеевская
ГДЗ По Английскому Языку 5 Класс Рыбченкова
ГДЗ По Английскому Языку 5 Класс Виргиния
Решебник По Математике Мерзляк
ГДЗ По Русскому Языку 6 Класс Разумская
ГДЗ Решебник Математика 2 Учебник Чекин
ГДЗ По Алгебре Фгос Учебник
Родной Русский Язык 5 Класс Александрова ГДЗ
Тест По Биологии ГДЗ
Решебник По Математике 11 Класс Алгебра Мордкович
ГДЗ По Матем Кл Мерзляк
ГДЗ Биология 7 Кл
ГДЗ Биболетова Трубанева
ГДЗ Кузовлев 9 Ридер
Решебник Разумовская 5
ГДЗ По Русскому 5 Класс Упражнение 10
ГДЗ Математика Н Класс
ГДЗ Английский Язык 9 Гроза
Решебник По Математике 1 Часть Герасимова
Виленкин ГДЗ Математика Онлайн
Гдз Иванов Учебник 4 Класса
ГДЗ Путина По Русскому 3 Класс Канакина
ГДЗ История России 6 Класс Пчелов Лукин
ГДЗ По Русскому Яз 7 Кл
ГДЗ По Физике 11 Класс Громов
ГДЗ решебник Алгебра за 8 класс Потапов (Дидактические материалы) «Просвещение»
Самостоятельная работа №1.
 Вариант 1
Вариант 1
123456
Самостоятельная работа №1. Вариант 2
123456
Самостоятельная работа №1. Вариант 3
123456
Самостоятельная работа №1. Вариант 4
123456
Самостоятельная работа №2. Вариант 1
1234
Самостоятельная работа №2. Вариант 2
1234
Самостоятельная работа №2. Вариант 3
1234
Самостоятельная работа №2. Вариант 4
1234
Самостоятельная работа №3. Вариант 1
123456
Самостоятельная работа №3. Вариант 2
123456
Самостоятельная работа №3. Вариант 3
123456
Самостоятельная работа №3. Вариант 4
123456
Самостоятельная работа №4. Вариант 1
123456
Самостоятельная работа №4. Вариант 2
123456
Самостоятельная работа №4. Вариант 3
123456
Самостоятельная работа №4. Вариант 4
123456
Самостоятельная работа №5. Вариант 1
12345
Самостоятельная работа №5. Вариант 2
12345
Самостоятельная работа №5. Вариант 3
12345
Самостоятельная работа №5. Вариант 4
12345
Самостоятельная работа №6.
 Вариант 1
Вариант 1
12345
Самостоятельная работа №6. Вариант 2
12345
Самостоятельная работа №6. Вариант 3
12345
Самостоятельная работа №6. Вариант 4
12345
Самостоятельная работа №7. Вариант 1
1234
Самостоятельная работа №7. Вариант 2
1234
Самостоятельная работа №7. Вариант 3
1234
Самостоятельная работа №7. Вариант 4
1234
Самостоятельная работа №8. Вариант 1
1234
Самостоятельная работа №8. Вариант 2
1234
Самостоятельная работа №8. Вариант 3
1234
Самостоятельная работа №8. Вариант 4
1234
Самостоятельная работа №9. Вариант 1
123
Самостоятельная работа №9. Вариант 2
123
Самостоятельная работа №9. Вариант 3
123
Самостоятельная работа №9. Вариант 4
123
Самостоятельная работа №10. Вариант 1
1234
Самостоятельная работа №10. Вариант 2
1234
Самостоятельная работа №10. Вариант 3
1234
Самостоятельная работа №10. Вариант 4
1234
Самостоятельная работа №11. Вариант 1
12345
Самостоятельная работа №11.
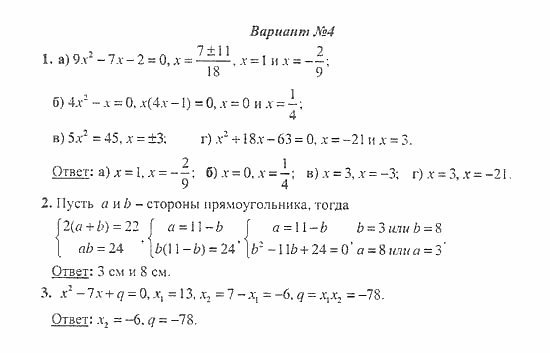 Вариант 2
Вариант 2
12345
Самостоятельная работа №11. Вариант 3
12345
Самостоятельная работа №11. Вариант 4
12345
Самостоятельная работа №12. Вариант 1
1234
Самостоятельная работа №12. Вариант 2
1234
Самостоятельная работа №12. Вариант 3
1234
Самостоятельная работа №12. Вариант 4
1234
Самостоятельная работа №13. Вариант 1
1234
Самостоятельная работа №13. Вариант 2
1234
Самостоятельная работа №13. Вариант 3
1234
Самостоятельная работа №13. Вариант 4
1234
Самостоятельная работа №14. Вариант 1
123456
Самостоятельная работа №14. Вариант 2
123456
Самостоятельная работа №14. Вариант 3
123456
Самостоятельная работа №14. Вариант 4
123456
Самостоятельная работа №15. Вариант 1
12345
Самостоятельная работа №15. Вариант 2
12345
Самостоятельная работа №15. Вариант 3
12345
Самостоятельная работа №15. Вариант 4
12345
Самостоятельная работа №16. Вариант 1
1234
Самостоятельная работа №16.
 Вариант 2
Вариант 2
1234
Самостоятельная работа №16. Вариант 3
1234
Самостоятельная работа №16. Вариант 4
1234
Самостоятельная работа №17. Вариант 1
12345
Самостоятельная работа №17. Вариант 2
12345
Самостоятельная работа №17. Вариант 3
12345
Самостоятельная работа №17. Вариант 4
12345
Самостоятельная работа №18. Вариант 1
123
Самостоятельная работа №18. Вариант 2
123
Самостоятельная работа №18. Вариант 3
123
Самостоятельная работа №18. Вариант 4
123
Самостоятельная работа №19. Вариант 1
1234
Самостоятельная работа №19. Вариант 2
1234
Самостоятельная работа №19. Вариант 3
1234
Самостоятельная работа №19. Вариант 4
1234
Самостоятельная работа №20. Вариант 1
12345
Самостоятельная работа №20. Вариант 2
12345
Самостоятельная работа №20. Вариант 3
12345
Самостоятельная работа №20. Вариант 4
12345
Самостоятельная работа №21. Вариант 1
123
Самостоятельная работа №21.
 Вариант 2
Вариант 2
123
Самостоятельная работа №21. Вариант 3
123
Самостоятельная работа №21. Вариант 4
123
Самостоятельная работа №22. Вариант 1
12
Самостоятельная работа №22. Вариант 2
12
Самостоятельная работа №22. Вариант 3
12
Самостоятельная работа №22. Вариант 4
12
Самостоятельная работа №23. Вариант 1
12
Самостоятельная работа №23. Вариант 2
12
Самостоятельная работа №23. Вариант 3
12
Самостоятельная работа №23. Вариант 4
12
Самостоятельная работа №24. Вариант 1
1234
Самостоятельная работа №24. Вариант 2
1234
Самостоятельная работа №24. Вариант 3
1234
Самостоятельная работа №24. Вариант 4
1234
Самостоятельная работа №25. Вариант 1
123
Самостоятельная работа №25. Вариант 2
123
Самостоятельная работа №25. Вариант 3
123
Самостоятельная работа №25. Вариант 4
123
Самостоятельная работа №26. Вариант 1
12345
Самостоятельная работа №26. Вариант 2
12345
Самостоятельная работа №26.
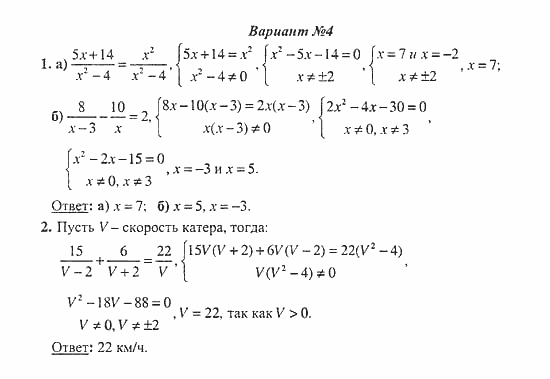 Вариант 3
Вариант 3
12345
Самостоятельная работа №26. Вариант 4
12345
Самостоятельная работа №27. Вариант 1
1234
Самостоятельная работа №27. Вариант 2
1234
Самостоятельная работа №27. Вариант 3
1234
Самостоятельная работа №27. Вариант 4
1234
Самостоятельная работа №28. Вариант 1
1234
Самостоятельная работа №28. Вариант 2
1234
Самостоятельная работа №28. Вариант 3
1234
Самостоятельная работа №28. Вариант 4
1234
Контрольная работа №1. Вариант 1
12345
Контрольная работа №1. Вариант 2
12345
Контрольная работа №1. Вариант 3
12345
Контрольная работа №1. Вариант 4
12345
Контрольная работа №2. Вариант 1
123456
Контрольная работа №2. Вариант 2
123456
Контрольная работа №2. Вариант 3
123456
Контрольная работа №2. Вариант 4
123456
Контрольная работа №3. Вариант 1
12345
Контрольная работа №3. Вариант 2
12345
Контрольная работа №3. Вариант 3
12345
Контрольная работа №3.
 Вариант 4
Вариант 4
12345
Контрольная работа №4. Вариант 1
12345
Контрольная работа №4. Вариант 2
12345
Контрольная работа №4. Вариант 3
12345
Контрольная работа №4. Вариант 4
12345
Контрольная работа №5. Вариант 1
12345
Контрольная работа №5. Вариант 2
12345
Контрольная работа №5. Вариант 3
12345
Контрольная работа №5. Вариант 4
12345
Контрольная работа №6. Вариант 1
12345
Контрольная работа №6. Вариант 2
12345
Контрольная работа №6. Вариант 3
12345
Контрольная работа №6. Вариант 4
12345
Контрольная работа №7. Вариант 1
123456
Контрольная работа №7. Вариант 2
123456
Контрольная работа №7. Вариант 3
123456
Контрольная работа №7. Вариант 4
123456
Похожие ГДЗ Алгебра 8 класс
Алгебра 8 классУчебникНикольский, Потапов«Просвещение»
Алгебра 8 классТематические тестыМГУ — школеЧулков, Струков«Просвещение»
Самостоятельная работа №1. Вариант 1: 1
◄ Предыдущий
Следующий ►
Условие
Решение
◄ Предыдущий
Следующий ►
закрыть
ГДЗ и решебники
Числовые неравенства оценивают значение выражения.
 Как оценить значение выражения? Методика получения сметы, примеры
Как оценить значение выражения? Методика получения сметы, примеры
М.: 2014 — 288с. М.: 2012 — 256с.
«Решебник» содержит ответы на все задания и упражнения из «Дидактических материалов по алгебре 8 класс»; подробно разобраны приемы и способы их решения. «Решебник» адресован исключительно родителям учащихся, для проверки домашних заданий и помощи в решение проблем.За короткое время родители могут стать весьма эффективными домашними воспитателями.
Формат: pdf
( 201
4
, 28 8с., Ерин В.К.)
Размер: 3.5 МБ
Смотреть, скачать:
диск.гугл
Формат: pdf
( 2012 г.
, 256 стр., Морозов А.В.)
Размер: 2.1 МБ
Смотреть, скачать:
ссылки удалены (см. примечание!!)
Формат: pdf( 2005
, 224с., Федоскина Н.С.)
Размер: 1,7 МБ
Смотреть, скачать:
диск.гугл
Содержание
Самостоятельная работа 4
Вариант 1 4
к многочлену (повторение) 4
С-2. Факторинг (обзор) 5
Факторинг (обзор) 5
C-3. Целочисленные и дробные выражения 6
C-4. Основное свойство дроби. Сокращение фракции 7
C-5. Сокращение дробей (продолжение) 9
С одинаковыми знаменателями 10
С разными знаменателями 12
Знаменатели (продолжение) 14
С-9. Умножение дробей 16
C-10. Разделение фракций 17
С-11. Все действия с дробями 18
С-12. Артикул 19
C-13. Рациональные и иррациональные числа 22
C-14. Арифметический квадратный корень 23
C-15. Решение уравнений вида x2=a 27
квадратный корень 29
C-17. Функция y=\/x 30
Корневой продукт 31
Частные корни 33
S-20. Квадратный корень из 34
Ввод множителя под знаком корня 37
, содержащий квадратные корни 39
C-23. Уравнения и их корни 42
Неполные квадратные уравнения 43
S-25. Решение квадратных уравнений 45
(продолжение) 47
C-27. Теорема Виета 49
квадратные уравнения 50
коэффициенты. Биквадратные уравнения 51
Биквадратные уравнения 51
S-30. Дробные рациональные уравнения 53
рациональные уравнения 58
S-32. Сравнение номеров (обзор) 59
С-33. Свойства числовых неравенств 60
С-34. Сложение и умножение неравенств 62
S-35. Доказательство неравенств 63
S-36. Оценка значения выражения 65
C-37. Оценка погрешности аппроксимации 66
S-38. Округление чисел 67
S-39. Относительная ошибка 68
S-40. Пересечение и объединение наборов 68
C-41. Номер пробела 69
С-42. Решение неравенств 74
C-43. Решение неравенств (продолжение) 76
C-44. Системы решения неравенств 78
С-45. Решение неравенств 81
переменная под знаком модуля 83
C-47. Степень с целым показателем 87
Степень с целым показателем 88
C-49. Стандартная форма номера 91
S-50. Запись ориентировочных значений 92
S-51. Элементы статистики 93
(повтор) 95
С-53. Определение квадратичной функции 99
S-54. Функция y=ax2 100
S-55. График функции y = ax2 + bx + c 101
График функции y = ax2 + bx + c 101
S-56. Решение квадратных неравенств 102
S-57. Метод интервала 105
Вариант 2 108
C-1. Преобразование целочисленного выражения
в полиномиальное (повторение) 108
C-2. Факторинг (обзор) 109
C-3. Целочисленные и дробные программные выражения
C-4. Основное свойство дроби.
Сокращение фракции 111
C-5. Сокращение фракции (продолжение) 112
C-6. Сложение и вычитание дробей
с одинаковыми знаменателями 114
С-7. Сложение и вычитание дробей
с разными знаменателями 116
С-8. Сложение и вычитание дробей с разными
знаменателями (продолжение) 117
C-9. Умножение дробей 118
C-10. Разделение фракций 119
С-11. Все действия с дробями 120
С-12. Артикул 121
C-13. Рациональные и иррациональные числа 123
C-14. Арифметический квадратный корень 124
C-15. Решение уравнений вида x2=a 127
C-16. Нахождение приблизительных значений
квадратный корень 129
C-17. Функция y=Vx 130
Функция y=Vx 130
С-18. Квадратный корень произведения.
Корневой продукт 131
C-19. Квадратный корень дроби.
Частные корни 133
S-20. Квадратный корень из 134
C-21. Вынесение множителя из-под знака корня
Ввод множителя под знаком корня 137
C-22. Преобразование выражений,
, содержащих квадратные корни 138
C-23. Уравнения и их корни 141
S-24. Определение квадратного уравнения.
Неполные квадратные уравнения 142
С-25. Решение квадратных уравнений 144
C-26. Решение квадратных уравнений
(продолжение) 146
C-27. Теорема Виета 148
C-28. Решение задач с
квадратными уравнениями 149
C-29. Разложение квадратного трехчлена на
множителя. Биквадратные уравнения 150
S-30. Дробные рациональные уравнения 152
C-31. Решение задач с
рациональными уравнениями 157
S-32. Сравнение номеров (обзор) 158
С-33. Свойства числовых неравенств 160
С-34. Сложение и умножение неравенств 161
S-35. Доказательство неравенств 162
Доказательство неравенств 162
S-36. Оценка значения выражения 163
C-37. Оценка ошибки аппроксимации 165
S-38. Округление номеров 165
S-39. Относительная ошибка 166
S-40. Пересечение и объединение наборов 166
C-41. Номер пробела 167
С-42. Решение неравенств 172
C-43. Решение неравенств (продолжение) 174
C-44. Системы решения неравенств 176
С-45. Решение неравенств 179
С-46. Уравнения и неравенства, содержащие
переменных под знаком по модулю 181
C-47. Степень с целым показателем 185
C-48. Преобразование выражений, содержащих
градуса, с целочисленным показателем степени 187
C-49. Стандартная форма номера 189
S-50. Запись ориентировочных значений 190
S-51. Элементы статистики 192
С-52. Понятие функции. График функций
(повторяющийся) 193
S-53. Определение квадратичной функции 197
S-54. Функция у=ах2 199
С-55. График функции y=ax2+txr+c 200
S-56. Решение квадратных неравенств 201
С-57. Метод интервалирования 203
Метод интервалирования 203
Исследования 206
Вариант 1 206
К-1 206
К-2 208
К-3 212
К-4 215
К-5 218
К-0 2521 9 8 226
К-9 229
К-10 (окончательная) 232
Вариант 2 236
К-1А 236
К-2А 238
К-ЗА 242
К-4А 243 К-9052 249
К-7А 252
К-8А 255
К-9А (финал) 257
Итоговое повторение по теме 263
Осенняя олимпиада 274
Весенняя олимпиада 275
35 соединяет знаки чисел 3 и 5. Тройка резонирует с вибрациями вдохновения и радости, энтузиазма и самовыражение. Это триединство прошлого, настоящего и будущего; тело, ум и дух. Человек под знаком тройки энергичен, талантлив, честен, горд и независим.
Пятерка добавляет в копилку общей вибрации долю эмоциональности и свободы выбора. Среди минусов — излишняя обидчивость и частые перепады настроения, негативное влияние которых компенсируется оптимизмом тройки. 35 в общих чертах олицетворяет творческую энергию, благоприятные возможности, желание поменяться местами.
Связь между числом и символом
Что означает число 35 в судьбе человека, если оно определяется датой рождения? Это придает ему особую харизму, привлекающую к нему друзей и последователей. Таких людей всегда окружают поклонники, которые выбирают их на роль публичного деятеля или неформального лидера.
Отрицательная сторона этой числовой комбинации в том, что человек использует свой авторитет для личного обогащения. У представителей числа 35 слабо развита духовная сфера. Зараженные прагматизмом и тщеславием, они способны, невзирая на лица, «идти по головам» к намеченной цели.
магические свойства
Мистическое значение числа 35 связано с тем, что оно предсказывает встречу со смертельным искушением. Избежать серьезных ошибок такого испытания можно только сохраняя спокойствие и благоразумие.
Сакральные сопоставления числа можно найти в Библии, где оно упоминается 5 раз. На тридцать пятый день поста в пустыне Люцифер подошел к Иисусу, чтобы искусить его.
Что означает число 35, если оно встречается часто
Если ангелы-хранители постоянно заставляют вас видеть цифру 35, они показывают, что вы не достигаете своих целей. Вы честны и старательны, но удача обходит вас стороной.
Вы сталкиваетесь с бесчисленными препятствиями и озадачены своим будущим. Это влияние на вашу жизнь оказывает управитель числа 35 — планета Сатурн. Его скрытое действие проявляется через число 8, которое получается при сложении 3 и 5. Возможно, вы отклоняетесь от своей судьбы и играете чужую роль. Чтобы найти свое истинное призвание, прислушайтесь к тому, о чем просит ваша душа, и следуйте ее невысказанному зову.
В этой статье мы разберем, во-первых, что понимается под вычислением значений выражения или функции, и, во-вторых, как оцениваются значения выражений и функций. Сначала введем необходимые определения и понятия. После этого подробно опишем основные методы получения оценок. Попутно будем давать решения на типичных примерах.
Что означает вычисление значения выражения?
Мы не смогли найти в школьных учебниках явного ответа на вопрос, что понимается под вычислением значения выражения. Попробуем разобраться с этим сами, отталкиваясь от тех крупиц информации по этой теме, которые все-таки содержатся в учебниках и в сборниках заданий для подготовки к ЕГЭ и поступления в вузы.
Попробуем разобраться с этим сами, отталкиваясь от тех крупиц информации по этой теме, которые все-таки содержатся в учебниках и в сборниках заданий для подготовки к ЕГЭ и поступления в вузы.
Посмотрим, что можно найти по интересующей нас теме в книгах. Вот некоторые цитаты:
Первые два примера включают вычисления чисел и числовых выражений. Здесь мы имеем дело с оценкой одного значения выражения. В остальных примерах используются вычисления, связанные с выражениями с переменными. Каждое значение переменной из ОДЗ для выражения или из некоторого интересующего нас множества X (которое, разумеется, является подмножеством допустимых значений области) соответствует своему значению выражения. То есть, если ОДЗ (или множество Х) не состоит из одного числа, то множеству значений выражения соответствует выражение с переменной. В этом случае приходится говорить об оценке не одного отдельного значения, а об оценке всех значений выражения на ОДЗ (или множестве X). Такая оценка имеет место для любого значения выражения, соответствующего некоторому значению переменной из ОДЗ (или множества X).
Для рассуждений немного отвлечемся от поиска ответа на вопрос, что значит вычислить значение выражения. Приведенные выше примеры продвигают нас в этом вопросе и позволяют нам принять следующие два определения:
Определение
Вычислить значение числового выражения — это означает указать числовой набор, содержащий значение, подлежащее оценке. В этом случае указанный числовой набор будет оценкой значения числового выражения.
Определение
Вычислить значения выражения с переменной на ОДЗ (или на множестве X) — это означает задание числового набора, содержащего все значения, которые выражение принимает на ОДЗ (или на множестве X) на множестве X). В этом случае указанный набор будет оценкой значений выражения.
Легко видеть, что для одного выражения можно задать более одной оценки. Например, числовое выражение может быть оценено как , или , или , или и т. д. То же самое относится и к выражениям с переменными. Например, выражение на ОДЗ может быть оценено как , или , или и т. д. В связи с этим стоит добавить к записанным определениям уточнение относительно указанного числового набора, являющегося оценкой: оценка не должна быть абы как, он должен соответствовать целям, для которых он найден. Например, для решения уравнения подойдет счет. Но эта оценка уже не годится для решения уравнения, здесь значения выражения следует оценивать иначе, например: .
д. В связи с этим стоит добавить к записанным определениям уточнение относительно указанного числового набора, являющегося оценкой: оценка не должна быть абы как, он должен соответствовать целям, для которых он найден. Например, для решения уравнения подойдет счет. Но эта оценка уже не годится для решения уравнения, здесь значения выражения следует оценивать иначе, например: .
Отдельно стоит отметить, что одной из оценок значений выражения f(x) является диапазон соответствующей функции y=f(x) .
В заключение этого абзаца обратим внимание на форму записи смет. Обычно оценки записывают с помощью неравенств. Вы, должно быть, заметили это.
Оценка значений выражения и оценка значений функции
По аналогии с оценкой значений выражения можно говорить об оценке значений функции. Это выглядит вполне естественно, особенно если мы имеем в виду функции, определяемые формулами, поскольку оценка значений выражения f(x) и оценка значений функции y=f(x) по существу совпадают вещь, которая очевидна. Более того, часто процесс получения оценок удобно описывать в терминах оценивания значений функции. В частности, в определенных случаях получение оценки выражения осуществляется путем нахождения наибольшего и наименьшего значений соответствующей функции.
Более того, часто процесс получения оценок удобно описывать в терминах оценивания значений функции. В частности, в определенных случаях получение оценки выражения осуществляется путем нахождения наибольшего и наименьшего значений соответствующей функции.
О точности оценок
В первом абзаце этой статьи мы сказали, что для выражения может иметь место множество оценок его значений. Являются ли некоторые из них лучше, чем другие? Это зависит от решаемой проблемы. Поясним на примере.
Например, используя методы оценки значений выражений, которые описаны в следующих пунктах, можно получить две оценки значений выражения: первая есть , вторая есть . Трудозатраты на получение этих оценок существенно различаются. Первая из них практически очевидна, а получение второй оценки связано с нахождением корневого выражения наименьшего значения и дальнейшим использованием свойства монотонности функции извлечения квадратного корня. В некоторых случаях любая из оценок может справиться с решением задачи. Например, любая наша оценка позволяет решить уравнение . Понятно, что в этом случае мы ограничились бы нахождением первой очевидной оценки и, конечно, не стали бы напрягаться в нахождении второй оценки. Но в других случаях может оказаться, что одна из оценок не подходит для решения задачи. Например, наша первая оценка не решает уравнение , а оценка позволяет это сделать. То есть в этом случае первой очевидной оценки нам бы не хватило, и пришлось бы искать вторую оценку.
Например, любая наша оценка позволяет решить уравнение . Понятно, что в этом случае мы ограничились бы нахождением первой очевидной оценки и, конечно, не стали бы напрягаться в нахождении второй оценки. Но в других случаях может оказаться, что одна из оценок не подходит для решения задачи. Например, наша первая оценка не решает уравнение , а оценка позволяет это сделать. То есть в этом случае первой очевидной оценки нам бы не хватило, и пришлось бы искать вторую оценку.
Итак, мы подошли к вопросу о точности оценок. Можно подробно определить, что подразумевается под точностью оценки. Но для наших нужд в этом нет особой необходимости; нам будет достаточно упрощенного представления о точности оценки. Условимся воспринимать точность оценки как некоторый аналог аппроксимации точности . То есть из двух оценок значений некоторого выражения f(x) будем считать более точной ту, которая находится «ближе» к области значений функции y=f(x). В этом смысле оценка является наиболее точной из всех возможных оценок значений выражения, так как совпадает с диапазоном соответствующей функции. Понятно, что оценка точнее оценки. Другими словами, оценка более грубая оценка.
Понятно, что оценка точнее оценки. Другими словами, оценка более грубая оценка.
Имеет ли смысл всегда искать наиболее точные оценки? Нет. И дело здесь в том, что сравнительно грубых оценок часто бывает достаточно для решения задач. И главное преимущество таких оценок перед точными оценками состоит в том, что зачастую их гораздо проще получить.
Основные методы получения оценок
Оценки значений основных элементарных функций
Оценки значений функций y=|x|
Помимо основных элементарных функций, хорошо изученными и полезными с точки зрения получения оценок являются функция у=|х| . Мы знаем диапазон этой функции: ; изд. С. А. Теляковский. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : больной. — ISBN 978-5-09-019243-9.
 Жижченко. — 3-е изд. — М.: Просвещение, 2010.- 368 с.: ил.-ISBN 978-5-09-022771-1.
Жижченко. — 3-е изд. — М.: Просвещение, 2010.- 368 с.: ил.-ISBN 978-5-09-022771-1. резюме других презентаций
«Сложение и вычитание алгебраических дробей» — Алгебраические дроби. 4а?б. Изучение новой темы. Цели: Помните! Кравченко Г. М. Примеры:
«Градусы с целым показателем» — Феоктистов Илья Евгеньевич Москва. 3. Степень с целым показателем (5 часов) стр.43. Преподавание алгебры в 8 классе с углубленным изучением математики. Отсроченное введение показателя степени с целым отрицательным показателем… Знайте определение показателя степени с целым отрицательным показателем. 2.
Отсроченное введение показателя степени с целым отрицательным показателем… Знайте определение показателя степени с целым отрицательным показателем. 2.
«Типы квадратных уравнений» — Неполные квадратные уравнения. Вопросы… Полные квадратные уравнения. Квадратные уравнения. Определение квадратного уравнения Виды квадратных уравнений Решение квадратных уравнений. Методы решения квадратных уравнений. Группа «Дискриминант»: Миронов А., Мигунов Д., Зайцев Д., Сидоров Е., Иванов Н., Петров Г. Редуцированное квадратное уравнение. Выполнено: учащиеся 8-го «в» класса. Метод полноквадратичного отбора. Типы квадратных уравнений. Позволять. Графический способ.
«Численные неравенства 8 класса» — A-c>0. Неравенства. НО= «Больше или равно.» б>в. Напишите a>b или 0. B-c>0. Числовые неравенства. Нестрогий. Свойства числовых неравенств. Примеры: Если a b, то a-5>b-5. А>0 означает, что а — положительное число;
«Решение квадратных уравнений по теореме Виета» — Один из корней уравнения равен 5. Задание №1. МОУ «Кисловская СОШ». Научный руководитель: учитель математики Баранникова Е.А. Кисловка — 2008 г. (Презентация к уроку алгебры в 8 классе). Найдите x2 и k. Работу выполнил: ученик 8 класса Слинько В. Решение квадратных уравнений с помощью теоремы Виета.
Задание №1. МОУ «Кисловская СОШ». Научный руководитель: учитель математики Баранникова Е.А. Кисловка — 2008 г. (Презентация к уроку алгебры в 8 классе). Найдите x2 и k. Работу выполнил: ученик 8 класса Слинько В. Решение квадратных уравнений с помощью теоремы Виета.
Наш «Решебник» содержит ответы на все задания и упражнения из «Дидактических материалов для алгебры 8 класса»; подробно анализируются методы и методы их решения. «Решебник» адресован исключительно родителям учеников, для проверки домашних заданий и помощи в решении задач.
За короткое время родители могут стать весьма эффективными домашними репетиторами.
Вариант 1 4
до полинома (повторение) 4
С-2. Факторинг (обзор) 5
С-3. Целочисленные и дробные выражения 6
С-4. Основное свойство дроби. Сокращение фракции. 7
С-5; Сокращение дробей (продолжение) 9
с теми же знаменателями 10
с разными знаменателями 12
знаменатели (продолжение) 14
C-9.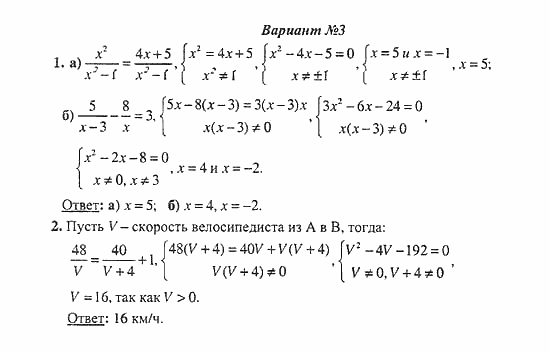 Умножение дробей 16
Умножение дробей 16
С-10. Разделение фракций 17
С-11. Все действия с дробями 18
С-12. Функция 19
C-13. Рациональные и иррациональные числа 22
C-14. Арифметический квадратный корень 23
С-15. Решение уравнений вида x2=a 27
C-16. Нахождение приблизительных значений
квадратный корень 29
C-17. Функция y=d/x 30
Корневой продукт 31
Частные корни 33
S-20. Квадратный корень из 34
C-21. Вынесение на множители корневого знака Вынесение на множитель корневого знака 37
C-23. Уравнения и их корни 42
Неполные квадратные уравнения 43
С-25. Решение квадратных уравнений 45
(продолжение) 47
C-27. Теорема Виета 49
C-28. Решение задач с
квадратными уравнениями 50
коэффициентами. Биквадратные уравнения 51
S-30. Дробные рациональные уравнения 53
C-31. Решение задач с
рациональными уравнениями 58
S-32. Сравнение номеров (обзор) 59
Сравнение номеров (обзор) 59
С-33. Свойства числовых неравенств 60
С-34. Сложение и умножение неравенств 62
С-35. Доказательство неравенств 63
С-36. Оценка значения выражения 65
C-37. Оценка погрешности аппроксимации 66
S-38. Округление чисел 67
S-39. Относительная ошибка 68
С-40. Пересечение и объединение множеств 68
C-41. Количество пробелов 69
С-42. Решение неравенств 74
C-43. Решение неравенств (продолжение) 76
C-44. Системы решения неравенств 78
С-45. Решение неравенств 81
переменная по модулю 83
С-47. Степень с целым показателем 87
Степень с целым показателем 88
C-49. Стандартная форма номера 91
S-50. Запись ориентировочных значений 92
S-51. Элементы статистики 93
(повторно) 95
С-53. Определение квадратичной функции 99
S-54. Функция y=ax2 100
S-55. График функции y = ax2 + bx + c 101
S-56. Решение квадратных неравенств 102
Решение квадратных неравенств 102
С-57. Метод интервалирования 105
Вариант 2 108
C-1. Преобразование целочисленного выражения
в полиномиальное (повторение) 108
C-2. Факторинг (обзор) 109
С-3. Целочисленные и дробные выражения 110
C-4. Основное свойство дроби.
Сокращение фракции 111
C-5. Сокращение фракции (продолжение) 112
C-6. Сложение и вычитание дробей
с одинаковыми знаменателями 114
С-7. Сложение и вычитание дробей
e разные знаменатели 116
C-8. Сложение и вычитание дробей с разными
знаменателями (продолжение) 117
C-9. Умножение дробей, 118
С-10. Разделение фракций 119
С-11. Все действия с дробями 120
С-12. Артикул 121
C-13. Рациональные и иррациональные числа 123
C-14. Арифметический квадратный корень 124
C-15. Решение уравнений вида x2-a 127
С-16. Нахождение приближенных квадратных корней 129
C-17. Функция y=\/x» 130
Функция y=\/x» 130
C-18. Корень квадратный из произведения.
Произведение корней 131
C-19. Корень квадратный из дроби.
Частные корни 133
S-20. Квадратный корень из 134
C-21.Вынесение множителя из-под знака корня
Ввод множителя под знаком корня 137
C-22.Преобразование выражений,
C-23.Уравнения и их корни 141
С-24. Определение квадратного уравнения.
Неполные квадратные уравнения 142
S-25. Решение квадратных уравнений 144
C-26. Решение квадратных уравнений
(продолжение) 146
C-27. Теорема Виета 148
C-28. Решение задач с
квадратными уравнениями 149
C-29. Разложение квадратного трехчлена на
сомножителей. Биквадратные уравнения 150
S-30. Дробные рациональные уравнения 152
С-31. Решение задач с
рациональными уравнениями 157
S-32. Сравнение номеров (обзор) 158
С-33. Свойства числовых неравенств 160
С-34. Сложение и умножение неравенств 161
Сложение и умножение неравенств 161
С-35. Доказательство неравенств 162
S-36. Оценка значения выражения 163
C-37. Оценка погрешности аппроксимации 165
S-38. Округление чисел 165
S-39. Относительная ошибка 166
S-40. Пересечение и объединение множеств 166
С-41. Номер пробела 167
С-42. Решение неравенств 172
С-43. Решение неравенств (продолжение) 174
C-44. Системы решения неравенств 176
С-45. Решение неравенств 179
С-46. Уравнения и неравенства, содержащие
переменных под знаком модуля 181
C-47. Степень с целым показателем 185
C-48. Преобразование выражений, содержащих
градуса с целым показателем степени 187
C-49. Стандартная форма номера 189
S-50. Запись ориентировочных значений 190
S-51. Элементы статистики 192
С-52. Понятие функции. График функций
(повтор) 193
S-53. Определение квадратичной функции 197
S-54. Функция y=ax2 199
Функция y=ax2 199
S-55. График функции у = ах24-бж + с 200
С-56. Решение квадратных неравенств 201
С-57. Метод интервалирования 203
Обследования 206
Опция 1 206
K-10 (финал) 232
Опция 2 236
K-2A 238
K-ZA 242
K-9A (Final) 257
Финальное повторение по теме 263
Олимпийцы. 274
Весенняя Олимпиада 275
|
УРОК №5 Тема. Почленное сложение и умножение неравенств. Применение свойств числовых неравенств для оценки значений выражений Цель занятия: добиться усвоения учащимися содержания понятия «сложить неравенства почленно» и «перемножить неравенства почленно», а также содержания свойств числовых неравенств, выраженных теоремы о почленном сложении и почленном умножении числовых неравенств и следствия из них. Тип урока: закрепление знаний, развитие начальных навыков. Обзорность и оборудование: реферат № 5. Во время занятий I. Организационный этап Учитель проверяет готовность учащихся к уроку, настраивает их на работу. II. Проверка домашнего задания Студенты выполняют тестовые задания с последующей проверкой. III. Формулировка цели и задач урока. Для сознательного участия учащихся в постановке цели урока можно предложить им практические задачи геометрического содержания (например, на оценку периметра и площади прямоугольника, длин смежных сторон которые оцениваются в виде двойных неравенств). Результатом проделанной работы является формулировка цели урока: изучить вопрос о таких свойствах неравенств, которые можно применять в случаях, аналогичных описанным в предложенной задаче для учащихся; для чего необходимо четко сформулировать математическим языком и в словесной форме, а затем привести соответствующие свойства числовых неравенств и научиться использовать их в сочетании с ранее изученными свойствами числовых неравенств для решения типовых задач. IV. Обновление базовых знаний и навыков учащихся устные упражнения 1. 1) а — б = -0,2; 2) а — б = 0,002; 3) а = б — 3; 4) а — б = м 2 ; 5) а = б — м 2 . 3. Сравните значения выражений а+b и abif a=3, b=2. Обоснуйте свой ответ. Полученное соотношение будет выполнено, если: 1) а = -3, б = -2; 2) а = -3, б = 2? V. Формирование знаний План изучения нового материала 1. Свойство почленного сложения числовых неравенств (с тонкой настройкой). 2. Свойство почленного умножения числовых неравенств (с тонкой настройкой). 3. Последствия. Свойство почленного умножения числовых неравенств (с тонкой настройкой). 4. Примеры применения проверенных свойств. Справочная записка № 5
Методический комментарий Для осознанного восприятия нового материала преподаватель может на этапе актуализации основных знаний и умений учащихся предложить решения устных упражнений с воспроизведением соответственно определения сравнения чисел и свойств числовых неравенств, изученных на предыдущих уроки (см. Обычно студенты хорошо усваивают содержание теорем о почленном сложении и умножении числовых неравенств, однако опыт работы показывает, что студенты склонны к некоторым ложным обобщениям. Поэтому, чтобы не допустить ошибок в формировании знаний учащихся по данному вопросу путем демонстрации примеров и контрпримеров, учителю следует акцентировать внимание на следующих моментах: Сознательное применение свойств числовых неравенств невозможно без умения записывать эти свойства как на математическом языке, так и в словесной форме; · теоремы почленного сложения и умножения числовых неравенств выполняются только для неправильностей одного знака; Свойство почленного сложения числовых неравенств выполняется при определенном условии (см. выше) для любых чисел, а теорема о почленном умножении (в форме, изложенной в справочном реферате № 5) только для положительных чисел; теоремы о почленном вычитании и почленном делении числовых неравенств не изучены, поэтому в тех случаях, когда необходимо оценить разность или пропорцию выражений, эти выражения представляют в виде суммы или произведения, соответственно, а затем при определенных условиях использовать свойства почленного сложения и умножения числовых неравенств. VI. Формирование навыков устные упражнения 1. Сложить почленные неравенства: 1) а > 2, б > 3; 2) с-2, д 4. Или одни и те же неравенства можно почленно умножать? Обоснуйте ответ. 2. Умножить неравенства почленно: 1) а > 2, б > 0,3; 2) в > 2, г > 4. Или можно такие же неровности добавить? Обоснуйте ответ. 3. Определите и обоснуйте, верно ли утверждение, что если 2 а 3, 1 б 2, то: 1) 3 а + б 5; 2) 2 аб 6; 3) 2 — 1 а — б 3 — 2; Письменные упражнения Для достижения дидактической цели урока следует решить упражнения следующего содержания: 1) сложить и умножить почленно эти числовые неравенства; 2) оценивает значение суммы, разности, произведения и частного двух выражений по заданным оценкам каждого из этих чисел; 3) оценивают значение выражений, содержащих эти буквы, по оценкам каждой из этих букв; 4) доказывает неравенство, используя теоремы почленного сложения и умножения для числовых неравенств и используя классические неравенства; 5) повторить изученные на предыдущих уроках свойства числовых неравенств. Методический комментарий Письменные упражнения, которые предлагаются для решения на данном этапе урока, должны способствовать выработке устойчивых навыков почленного сложения и умножения неравенств в простых случаях. (При этом очень важный момент: проверка соответствия записи неравенств в условии теоремы и правильности записи суммы и произведения левой и правой частей неравенств. Подготовительная работа проводится в ходе выполнение устных упражнений.) Для лучшего усвоения материала необходимо требовать от учащихся воспроизведения изученных теорем при комментировании действий. После того, как учащиеся успешно проработали теоремы в простых случаях, они могут постепенно переходить к более сложным случаям (для вычисления разности и частного двух выражений и более сложных выражений). На этом этапе работы учитель должен внимательно следить за тем, чтобы учащиеся не допускали типичных ошибок, пробуя разницу и оценивая долю за собственными ложными правилами. Также на уроке (разумеется, если позволяет время и уровень усвоения содержания материала учащимися) следует уделить внимание упражнениям по применению изученных теорем для доказательства более сложных неравенств. VII. Краткое содержание урока Известно, что 4 на 5; 6 б 8. Найдите неверные неравенства и исправьте ошибки. Обоснуйте ответ. 1) 10 а + б 13; 2) -4 а — б -1; 3) 24 аб 13; 4) ; 5) ; 7) 100 а2 + Ь 2 169? VIII. Домашнее задание 1. Изучить теоремы почленного сложения и умножения числовых неравенств (с уточнением). 2. Выполнять упражнения репродуктивного характера, аналогичные тем, что выполняются на уроках. 3. Для повторения: упражнения на применение определения сравнения чисел (на приведение неправильностей и на сравнение выражений).
|
||||||
 Развивать умение воспроизводить названные свойства числовых неравенств и использовать эти свойства для оценки значений выражений, а также продолжать работу по развитию навыков доказывания неравенств, сравнения выражений с использованием определения и свойств числовых неравенств
Развивать умение воспроизводить названные свойства числовых неравенств и использовать эти свойства для оценки значений выражений, а также продолжать работу по развитию навыков доказывания неравенств, сравнения выражений с использованием определения и свойств числовых неравенств  В ходе беседы учитель должен направить мысли учащихся на то, что хотя задачи и аналогичны тем, которые решались на предыдущем уроке (см. урок № 4, оценить значение выражений), однако, в отличие от названных, они не может быть решена теми же средствами, так как необходимо вычислять значения выражений, содержащих две (а в дальнейшем и больше) буквы. Таким образом, учащиеся осознают наличие противоречия между полученными ими к этому моменту знаниями и необходимостью решения определенной задачи.
В ходе беседы учитель должен направить мысли учащихся на то, что хотя задачи и аналогичны тем, которые решались на предыдущем уроке (см. урок № 4, оценить значение выражений), однако, в отличие от названных, они не может быть решена теми же средствами, так как необходимо вычислять значения выражений, содержащих две (а в дальнейшем и больше) буквы. Таким образом, учащиеся осознают наличие противоречия между полученными ими к этому моменту знаниями и необходимостью решения определенной задачи.  Сравните числа a и b, если:
Сравните числа a и b, если: 
 Докажем неравенство (m + n )(mn + 1) > 4mn, если m > 0, n > 0.
Докажем неравенство (m + n )(mn + 1) > 4mn, если m > 0, n > 0.  выше), а также рассмотрение соответствующих свойств числовых неравенств.
выше), а также рассмотрение соответствующих свойств числовых неравенств. 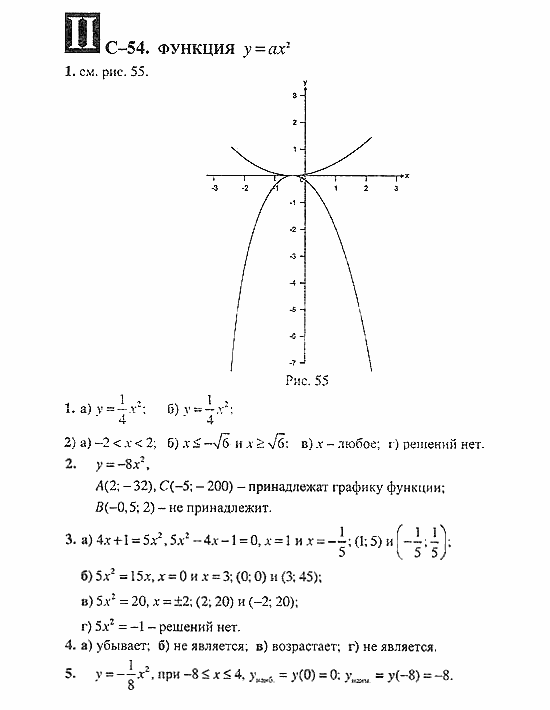


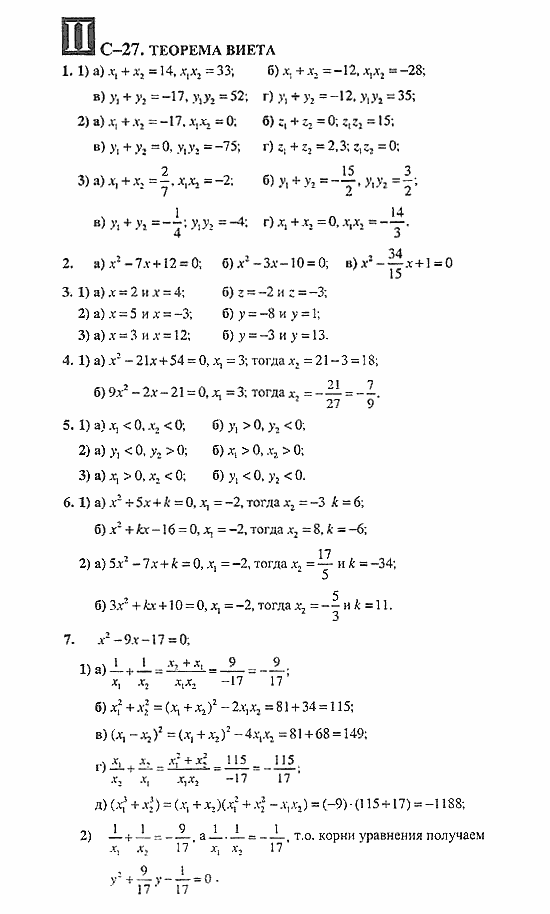 Среди минусов — излишняя обидчивость и частые перепады настроения, негативное влияние которых компенсируется оптимизмом тройки. 35 в общих чертах олицетворяет творческую энергию, благоприятные возможности, стремление перемениться местами.
Среди минусов — излишняя обидчивость и частые перепады настроения, негативное влияние которых компенсируется оптимизмом тройки. 35 в общих чертах олицетворяет творческую энергию, благоприятные возможности, стремление перемениться местами. 
 Цели: Помните! Кравченко Г. М. Примеры:
Цели: Помните! Кравченко Г. М. Примеры:  B-c>0. Числовые неравенства. Нестрогий. Свойства числовых неравенств. Примеры: Если a b, то a-5>b-5. A>0 означает, что a — положительное число;
B-c>0. Числовые неравенства. Нестрогий. Свойства числовых неравенств. Примеры: Если a b, то a-5>b-5. A>0 означает, что a — положительное число;  Основное свойство дроби. Сокращение фракции. 7
Основное свойство дроби. Сокращение фракции. 7  Решение задач с
Решение задач с  Запись ориентировочных значений 92
Запись ориентировочных значений 92  Артикул 121
Артикул 121  Биквадратные уравнения 150
Биквадратные уравнения 150 