Математические диктанты по геометрии 8 класс
МАТЕМАТИЧЕСКИЕ ДИКТАНТЫ
Геометрия 8 класс
Диктант 1. Четырехугольник. Параллелограмм.
- Дан четырехугольник ABCD [MKPE]. Назовите его диагонали.
- Как называется отрезок, соединяющий две противолежащие вершины четырехугольника? [Чем являются в четырехугольнике концы его диагоналей?]
- Какие вершины четырехугольника АМОР являются соседними для вершины А? [Какие стороны четырехугольника ВСКМ являются соседними для КМ?]
- Четырехугольник КЕРМ – параллелограмм. Сколько общих точек имеют прямые КЕ и РМ? [В четырехугольнике ВСОЕ стороны ВС и ОЕ параллельны, а углы В и С равны 90ْ. Являются ли четырехугольник ВСОЕ параллелограммом?]
- Диагонали четырехугольника АВКМ пересекаются. Обязательно ли этот четырехугольник параллелограмм? [Точка пересечения диагоналей четырехугольника ВСКМ не является серединой одной из них. Может ли этот четырехугольник быть параллелограммом?]
- Точка пересечения диагоналей четырехугольника является серединой каждой из них. Как называется такой четырехугольник? [Точка М служит серединой отрезков КО и ВD. Как называется четырехугольник ВКDО?]
- Диагонали параллелограмма равны 7 дм и 5 дм. На отрезки какой длины делит их точка пересечения? [Точка С – точка пересечения диагоналей параллелограмма ОВКМ. Какова длина диагоналей, если отрезки СО и СВ равны соответственно 3,5 см и 2,5 см?]
- Один из углов параллелограмма равен 35˚. Чему равны остальные углы? [Периметр параллелограмма равен 20 см, а одна из сторон равна 3 см. Найдите длины остальных сторон.]
- Периметр параллелограмма равен 26 м, а одна из сторон равна 5 м. Найдите длины остальных сторон. [Один из углов параллелограмма равен 45˚. Чему равны остальные его углы?].
Диктант 2. Прямоугольник. Ромб. Квадрат.
- Является ли прямоугольником параллелограмм, у которого есть прямой угол? [Обязательно ли является прямоугольником четырехугольник, у которого есть прямой угол?]
- Верно ли, что каждый прямоугольник является параллелограммом? [Верно ли, что каждый параллелограмм является прямоугольником?]
- Диагонали прямоугольника АЕКМ пересекаются в точке О. Отрезок АО равен 3 дм. Найдите длину диагонали ЕМ. [Диагонали параллелограмма равны 3 и 5 дм. Является ли этот параллелограмм прямоугольником?]
- Диагонали четырехугольника равны. Обязательно ли этот четырехугольник – прямоугольник? [Сумма длин диагоналей прямоугольника равна 13 см. Найдите длину каждой диагонали.]
- Периметр ромба равен 12 см. Найдите длины его сторон. [Верно ли, что каждый ромб является параллелограммом?].
- Верно ли, что каждый параллелограмм является ромбом? [Периметр ромба равен 30 см. Найдите его стороны.]
- Диагонали ромба делят его на четыре треугольника. Найдите углы каждого треугольника, если один из углов ромба равен 30˚. [Ромб АВСD имеет прямой угол. Является ли этот ромб квадратом?]
- Две соседние стороны параллелограмма равны и образуют прямой угол. Как называется такой параллелограмм? [Диагонали квадрата делят его на четыре треугольника. Найдите углы каждого треугольника.]
Диктант 3. Теорема Фалеса.
- Стороны угла пересечены тремя параллельными прямыми так, что на одной из сторон образовалось три отрезка по 3 см каждый. Один из образовавшихся отрезков на второй стороне равен 4 см. Чему равна сумма длин всех трех отрезков, образовавшихся на второй стороне? [Стороны угла пересечены тремя параллельными прямыми так, что на одной стороне образовалось три отрезка по 5 см каждый. Один из отрезков, образовавшихся на второй стороне, равен 2 см. Чему равна сумма длин всех отрезков, образовавшихся на второй стороне?].
- Две стороны треугольника соединили отрезком, непараллельным третьей стороне. Служит ли этот отрезок средней линией данного треугольника? [Точки А и В являются серединами двух сторон треугольника. Как называется отрезок АВ?].
- Сторона АВ треугольника АВС равна 6 м. Чему равна средняя линия треугольника, параллельная этой стороне? [Средняя линия треугольника АВD, параллельная стороне ВD, равна 4 см. Чему равна сторона ВD?].
- Точки М, Р и О – середины сторон треугольника АВС. Найдите периметр треугольника АВС, если стороны треугольника МРО равны 3 см, 4 см, 5 см. [Точки А, В, и С – середины сторон треугольника МРО. Найдите периметр треугольника АВС, если отрезки МР, МО и РО равны 3 дм, 4 дм и 5 дм.].
- Концы отрезка АВ лежат на двух сторонах треугольника, а длина этого отрезка равна половине третьей стороны. Обязательно ли отрезок АВ – средняя линия этого треугольника? [Концы отрезка КL лежат на двух сторонах треугольника. Отрезок КL параллелен третьей стороне этого треугольника и равен одной четвертой части ее длины. Служит ли отрезок КL средней линией этого треугольника?].
Диктант 4. Трапеция.
1. Всякий ли четырехугольник, у которого есть две параллельные стороны, является трапецией? [У четырехугольника ABCD и стороны АВ и СD не параллельны. Обязательно ли этот четырехугольник – трапеция?].
2. Стороны угла пересечены двумя параллельными прямыми. Как называется получившийся при этом четырехугольник? [Две параллельные прямые пересечены двумя прямыми, имеющими общую точку. Как называется получившийся при этом четырехугольник?].
3. Как называются параллельные [непараллельные] стороны трапеции?
4. Точки М и С делят боковые стороны трапеции пополам. Как называется отрезок МС? [Точки А и В лежат на боковых сторонах трапеции. Отрезок АВ параллелен основаниям трапеции. Обязательно ли АВ – средняя линия трапеции?]
5. Концы средней линии трапеции лежат на ее сторонах СЕ и МР. Как называются стороны СЕ и МР [РС и МЕ]?
6. Стороны трапеции равны 3 см, 5 см, 3 см и 7 см. Как называется такая трапеция? [Две противолежащие стороны равнобокой трапеции равны 5 см и 7 см, третья сторона равна 5 см. Вычислите периметр трапеции.].
7. Периметр равнобокой трапеции равен 26 см, а ее боковая сторона равна 5 см. Найдите длину средней линии этой трапеции. [Длина средней линии трапеции равна 3 см, а сумма длин ее боковых сторон равна 4 см. Чему равен периметр этой трапеции?].
Диктант 5. Синус, косинус, тангенс угла. Соотношения между сторонами и углами прямоугольного треугольника. Значения синуса, косинуса и тангенса
углов 30˚,45˚ и 60˚.
- Закончите предложение: «Косинусом острого угла прямоугольного треугольника называется отношение …». [Запишите, используя обозначение: косинус 60˚ равен 1/2.].
- Запишите, используя обозначение: косинус 45˚ приближенно равен 7/9. [Закончите предложение: «Косинусом острого угла прямоугольного треугольника называется отношение …»].
- Вычислите косинус острого угла В [M] прямоугольного треугольника, у которого катет АС равен 11 см [РО равен 21 м], второй катет равен 60 см [20 м], а гипотенуза равна 61 см [29 м].
- Постройте угол, косинус которого равен 0,6 [0,3].
- Вычислите синус угла М прямоугольного треугольника, если его катет МК равен 45 см, второй равен 28 см, а гипотенуза равна 53 см. [Вычислите тангенс угла F прямоугольного треугольника, если его гипотенуза равна 29 дм, катет ЕА равен 20 дм, а второй катет равен 21 дм.].
- Может ли синус острого угла равняться 1,01? [Тангенс острого угла прямоугольного треугольника равен единице. Какого вида этот треугольник?].
- Вычислите тангенс острого угла равнобедренного прямоугольного треугольника. [Может ли синус острого угла равняться 1,2?].
- Один из катетов треугольника равен 18 м, а тангенс противолежащего угла равен 9/4. Найдите длину второго катета. [Один из катетов треугольника равен 24 см, а тангенс прилежащего угла равен 5/12. Найдите длину второго катета.].
- Тангенс одного из углов прямоугольного треугольника равен ⅝, а прилежащий катет равен 16 м. Найдите длину второго катета. [Тангенс одного из углов прямоугольного треугольника равен 4/3, а противолежащий ему катет равен 8 см.Найдите длину второго катета.].
- Вычислите тангенс угла В прямоугольного треугольника, если его катет АВ равен 8 см, второй катет равен 6 см, а гипотенуза равна 10 см. [Вычислите синус угла D прямоугольного треугольника, если его катет DЕ равен 5 см, второй катет равен 12 см, а гипотенуза равна 13 см.].
- Закончите предложение: «Катет прямоугольного треугольника есть среднее пропорциональное между…» [«Высота прямоугольного треугольника, опущенная из вершины прямого угла, есть среднее пропорциональное между …»].
- Проекция катетов на гипотенузу равны 3 см и 12 см. Вычислите высоту, опущенную из вершины прямого угла. [Гипотенуза треугольника равна 27 мм, а проекция на нее одного из катетов равна 3 мм. Чему равна длина этого катета?].
- Запишите, чему равен тангенс 30˚ [синус 60˚] .
- Запишите, чему равен синус 45˚ [косинус 30˚].
- Запишите, чему равен косинус 60˚ [тангенс 45˚].
Диктант 6. Теорема Пифагора. Расстояние между точками. Уравнение окружности.
- Найдите длину гипотенузы прямоугольного треугольника, если катеты равны 5 и 12 м. [Найдите длину катета прямоугольного треугольника, если другой катет и гипотенуза равны соответственно 40 и 41 см.].
- Запишите теорему Пифагора для ∆ АВС, у которого Ð А [ÐВ] – прямой.
- Найдите длину катета прямоугольного треугольника, если другой катет и гипотенуза равны соответственно 60 и 61 дм. [Найдите длину гипотенузы прямоугольного, если катеты равны 6 и 8 мм.].
- Запишите, чему равно расстояние от точки В1 [М1] с координатами 0и y [х и 0] до точки В2 [M2] с координатами х и 0 [0 и y].
- Найдите длину отрезка СD [AB], если координаты точки С [A] – 1 и 3 [2 и 4], а координаты точки D[B] – 5 и 6 [7 и 16].
- Составьте уравнение окружности с центром в точке А (9,-4) [(3,-5)] и с радиусом 3 [7].
- Дано уравнение окружности (х+5)2+(у-1)2=144 [(х-7)2+(у+3)2=121]. Чему равен радиус этой окружности и в какой точке находится ее центр?
- Начертите окружность, имеющую уравнение (х-2)2+у2=4 [х2+(у-3)2=9].
Диктант 7. Уравнение прямой.
- Является ли уравнение 3+4у=0 [2х-5=0] уравнением прямой?
- Начертите прямую, заданную уравнением у-2х+3=0 [3х-у-1=0.].
- Составьте уравнение прямой, проходящей через точку с координатами (-2;1) [(-1;2)] и через начало координат.
- Как расположена относительно осей координат прямая 3х+7=0 [2у-6=0]?
- Чему равен угловой коэффициент прямой 2х+5у-8=0 [3х-6у+7=0]?
- Напишите уравнение какой-нибудь прямой, параллельной оси абсцисс [ординат].
- Сколько общих точек имеют прямая х=10 и окружность с центром в начале координат и радиусом, равным 3 [окружность х2+у2=9 и прямая, удаленная от начала координат на 2 единицы]?
- Сколько общих точек имеют окружность х2+у2=16 и прямая, удаленная от начала координат на 3 единицы [прямая у=5 и окружность с центром в начале координат и радиусом, равным 4]?
- Каково взаимное расположение прямой у=7 и окружности х2+у2=49 [окружности х2+у2=64 и прямой х=8]?
infourok.ru
Математические диктанты по геометрии (8 класс)
МНОГОУГОЛЬНИКИ.
-
У многоугольника стороны могут пересекаться, а могут не пересекаться.
-
Смежные отрезки многоугольника лежат на одной прямой.
-
Две смежные стороны многоугольника имеют одну общую вершину.
-
Название многоугольника зависит от количества вершин.
-
Количество сторон многоугольника не зависит от количества его вершин.
-
Периметр многоугольника – это сумма длин всех его сторон.
-
Соседние вершины многоугольника лежат на разных сторонах.
-
Отрезок, соединяющий любые две соседние вершины, называют диагональю многоугольника.
-
Любой многоугольник разделяет плоскость на внешнюю и внутреннюю области.
-
Многоугольник состоит из сторон многоугольника и его внутренней области.
-
Верно ли, что многоугольники бывают выпуклые и невыпуклые.
-
Прямая, проходящая через любую сторону выпуклого многоугольника разделяет его на две части.
-
Невыпуклый многоугольник находится по одну строну от прямой, проходящей через любую его сторону.
-
Верно ли, что у многоугольника углов столько же, сколько и сторон.
-
У четырехугольника и сторон, и углов, и вершин – четыре.
-
Соседние стороны четырехугольника называют противоположными.
-
Противоположные вершины четырехугольника не являются соседними.
-
Четырехугольники бывают только выпуклые.
-
У четырехугольника можно провести четыре диагонали.
-
Каждая диагональ разбивает четырехугольник на два треугольника.
-
Сумма углов любого выпуклого четырехугольника, параллелограмма и трапеции равна 3600.
-
У параллелограмма соседние стороны параллельны и равны.
-
У параллелограмма противоположные углы равны.
-
Диагонали параллелограмма точкой пересечения не делятся пополам.
-
У трапеции противоположные стороны параллельны.
-
Основания трапеции между собой равны.
-
Боковые стороны равнобедренной трапеции между собой равны.
-
У прямоугольной трапеции три угла прямые.
КЛЮЧ:
«+» — 3; 4; 6; 9; 10; 11; 14; 15; 17; 20; 21; 23; 27;
«-» — 1; 2; 5; 7; 8; 12; 13; 16; 18; 19; 22; 24; 25; 26; 28
ОЦЕНКИ:
«3» — 15 – 19
«4» — 20 – 25
«»5 – 26 – 28
ТЕМА: «ПЛОЩАДЬ»
-
Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
-
За единицу измерения площадей принимают только квадрат со стороной 1 см.
-
Площадь многоугольника выражается только положительной величиной.
-
Верно ли, что равные многоугольники имеют равные площади?
-
Если многоугольник разбит на части, то его площадь равна сумме площадей этих частей.
-
Площадь квадрата равна кубу его стороны.
-
Площадь прямоугольника равна половине произведения его противоположных сторон.
-
Площадь прямоугольника равна произведению его соседних сторон.
-
Основание – это одна из сторон параллелограмма.
-
Высота треугольника – это перпендикуляр, опущенный из любой точки противоположной стороны к прямой, содержащей основание.
-
Площадь параллелограмма равна половине произведения высоты на основание.
-
Одну из сторон треугольника называют основанием.
-
Площадь треугольника равна половине произведения его основания на высоту.
-
Площадь прямоугольного треугольника равна произведению его катетов.
-
Если основания двух треугольников равны, то их площади относятся как высоты.
-
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
-
Высота трапеции – это перпендикуляр, проведенный к боковой стороне.
-
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
-
Площадь ромба равна произведению его диагоналей.
-
Площадь ромба можно найти по той же формуле, что и параллелограмм.
-
Теорема Пифагора используется в любых треугольниках.
-
В прямоугольном треугольнике квадрат любого катета равен сумме квадратов гипотенузы и другого катета.
-
Пифагоровы треугольники те, у которых длины сторон выражаются целыми числами.
-
Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
КЛЮЧ:
«+» — 1; 3; 4; 5; 8; 9; 10; 12; 13; 16; 18; 20; 23; 24
«-» — 2; 6; 7; 11; 14; 15; 17; 19; 21; 22;
ОЦЕНКИ:
«3» — 12 – 16
«4» — 17 – 21
«5»– 22 – 24
ТЕМА: «Определение подобных треугольников. Признаки подобия треугольников»
-
Верно ли, что отношение двух отрезков – это деление одного отрезка на другой?
-
Если одна пара отрезков пропорциональна другой паре отрезков, то их отношения не равны.
-
Понятие пропорциональность рассматривается только на примере двух отрезков.
-
В геометрии фигуры одинаковой формы принято называть подобными.
-
Если у двух треугольников MNK и M1N1K1 соответствующие углы равны, то стороны MK и N1K1 называют сходственными.
-
Два треугольника называют подобными, если их углы соответственно равны, а стороны одного треугольника соответственно пропорциональны сторонам другого.
-
Коэффициент подобия – это число, равное отношению сходственных сторон подобных треугольников.
-
Подобие треугольников нельзя установить, если известно, что некоторые углы соответственно равны или некоторые стороны пропорциональны.
-
Площади двух подобных треугольников относятся как коэффициент подобия в квадрате.
-
Отношение периметров двух подобных треугольников равно коэффициенту подобия в квадрате.
-
По первому признаку подобия треугольников необходимо указать две пропорциональные стороны и угол между ними.
-
По второму признаку подобия треугольников необходимо указать два равных угла в каждом треугольнике.
-
По третьему признаку подобия треугольников необходимо указать пропорциональность трех сторон.
-
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
КЛЮЧ:
«+» — 1; 4; 6; 7; 9; 13; 14
«-» — 2; 3; 5; 8; 10; 11; 12
ОЦЕНКИ:
«3» — 7 – 9
«4» — 10 – 12
«5»– 13 – 14
ТЕМА : «Применение подобия к доказательству теорем и решению задач»
1) Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
2) В любом треугольнике можно провести только одну среднюю линию.
3) Средняя линия треугольника параллельна одной из его сторон и равна ее половине.
4) Средняя линия треугольника отсекает от первоначального треугольника подобный ему треугольник.
5) Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от конца медианы.
6) Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет его на два прямоугольных треугольника не подобных данному треугольнику.
7) Отрезок MN называют средним пропорциональным для двух отрезков АВ и CD, если он равен квадратному корню из суммы этих отрезков.
8) Высота прямоугольного треугольника, проведенная из любой вершины, есть среднее пропорциональное для отрезков, на которые делится катет.
9) Катет прямоугольного треугольника, проведенный из вершины прямого угла, есть среднее пропорциональное для гипотенузы и проекции этого катета на гипотенузу.
10) Метод подобия нельзя применить для решения задач на построение треугольников.
11) Измерительные работы на местности можно провести с помощью подобия двух прямоугольных треугольников.
12) Фигуры F и F1 называют подобными, если для любых двух точек этих фигур выполняется равенство .
13) Коэффициент подобия – это число, равное отношению сходственных сторон подобных фигур.
14) Верно ли, что если ширина одного прямоугольника больше в 2 раза ширины подобного ему прямоугольника, то длина может быть в 3 раза.
КЛЮЧ:
«+» — 1; 3; 4; 9; 11; 12: 13;
«-» — 2; 5; 6; 7; 8; 10; 14
ОЦЕНКИ:
«3» — 7 – 9
«4» — 10 – 12
«5»– 13 – 14
ТЕМА: «Окружность»
1) Верно ли, что возможны три случая взаимного расположения прямой и окружности.
2) Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность имеют две общих точки.
3) Прямая называется касательной, если расстояние от центра окружности до прямой равно радиусу окружности.
4) По свойству: радиус окружности, проведенный в точку касания перпендикулярен к касательной.
5) Отрезки касательных к окружности, проведенные из одной точки равны.
6) Верно ли, что прямая проходящая через конец диаметра, лежащий на окружности и перпендикулярна к этому диаметру, то она является касательной.
7) На окружности можно построить дугу любой градусной меры.
8) Центральный угол – это угол, одна сторона которого является диаметром.
9) Если центральный угол развернутый, то его соответствующая дуга называется полуокружностью.
10) Если центральный угол больше развернутого, то соответствующая дуга меньше полуокружности.
11) Градусная мера дуги – это градусная мера соответствующего центрального угла.
12) Вписанный угол – это угол, вершиной которого является центр окружности.
13) Говорят, что вписанный угол опирается на дугу, если она не лежит внутри вписанного угла.
14) Вписанный угол равен половине дуги, на которую он опирается.
15) Вписанный угол равен центральному углу.
16) Вписанные углы, опирающиеся на одну и ту же дугу не равны.
17) Вписанный угол, опирающийся на диаметр – прямой.
18) Каждая точка биссектрисы неразвернутого угла находится на разном расстоянии от его сторон.
19) Всего существует четыре замечательных точки треугольника.
20) Вписанная окружность касается всех сторон многоугольника.
21) Все вершины вписанного многоугольника лежат внутри окружности.
22) В любой четырехугольник можно вписать окружность и описать около него окружность.
23) Центры вписанной и описанной окружности треугольника не являются замечательными точками.
Ключ:
«+»: 1; 3; 4; 5; 6; 7; 9; 11; 13; 14; 17; 19; 20;
«-»: 2; 8; 10; 12; 15; 16; 18; 21; 22; 23.
Оценки:
«3» — 11 – 14;
«4» — 15 – 21;
«5» — 22 — 23
ТЕМА: «Понятие вектора. Сложение и вычитание векторов»
1) Величины, которые задаются не только числовым значением, но и направлением называют векторными величинами.
2) Вектор – это направленный отрезок.
3) У вектора неважно, какая точка является началом, а какая концом.
4) Любую точку можно назвать вектором.
5) Длина вектора – это обязательно расстояние от начала до конца вектора.
6) У нулевого вектора нельзя найти длину.
7) Коллинеарные векторы лежат только на параллельных прямых.
8) Нулевой вектор не может быть коллинеарен произвольному вектору.
9) Коллинеарные векторы делятся на сонаправленные и противоположно направленные.
10) Нулевой вектор имеет любое направление.
11) Векторы называют равными, если их длины равны.
12) От любой точки можно отложить несколько векторов, равных данному.
13) При сложении двух векторов по правилу треугольника необходимо, чтобы начало одного вектора, совпадало с началом другого.
14) При сложении векторов можно пользоваться сочетательным или переместительным законом.
15) При сложении векторов по правилу параллелограмма суммой будет являться диагональ, исходящая из их общего начала.
16) При вычитании векторов результатом будет вектор с началом в конце первого и концом в конце второго.
17) По правилу многоугольника можно сложить любое количество векторов.
18) При сложении по правилу многоугольника все векторы должны иметь общее начало.
Ключ:
«+»: 1; 2; 4; 9; 10; 14; 15; 17
«-»: 3; 5; 6; 7; 8; 11; 12; 13; 16; 18
Оценки:
«3» — 8 – 11;
«4» — 12 – 16;
«5» — 17 — 18
infourok.ru
Учебно-методический материал по геометрии (8 класс) на тему: Математические диктанты по геометрии для 8 класса (12.01.2016)
Геометрия 8 класс
Математические диктанты
- Многоугольники
- Постройте выпуклый шестиугольник ABCDEF.
- Проведите все диагонали, выходящие из точки В.
- Запишите какие-нибудь две смежные стороны.
- Найдите сумму внутренних углов данного шестиугольника.
- Сколько диагоналей можно провести в четырёхугольнике?
- Постройте параллелограмм КМСВ. Запишите параллельные стороны
- Один из углов параллелограмма равен 110 градусов . Найдите остальные углы.
- Периметр параллелограмма равен 28см. Одна его сторона равна 4 см. Найти остальные стороны.
- Противоположные стороны четырёхугольники попарно равны. Является ли этот четырёхугольник параллелограммом?
- Прямоугольник. Ромб. Квадрат .
- Верно ли , что каждый прямоугольник является параллелограммом?
- Запишите особое свойство прямоугольника.
- Всегда ли квадрат является прямоугольником?
- Всегда ли квадрат является ромбом?
- Сторона ромба равна 12см. Найдите его периметр.
- Верно ли, что каждый параллелограмм является ромбом?
- Как называется параллелограмм, у которого смежные стороны перпендикулярны?
- Постройте отрезок АВ = 7см и разделите его на 4 равные части с помощью циркуля и линейки.
- Сумма противоположных углов ромба равна 90 градусов. Найти углы ромба
- Площади. Теорема Пифагора
- Закончите предложения : а) Равные фигуры имеют… б) площадь квадрата равна …
- Найдите площадь параллелограмма с основанием 4см и высотой 3,6см
- Запишите формулу площади прямоугольного треугольника
- Запишите теорему Пифагора для треугольника с прямым углом В
- Найдите гипотенузу прямоугольного треугольника с катетами 12см и 5см
- Является ли треугольник прямоугольным, если его стороны равны 10см, 24см, 26см?
- Запишите формулу площади трапеции.
- Подобные треугольники
- Закончите предложение: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника…
- Закончите предложение: Отношение площадей двух подобных треугольников равно…
- Подобны ли треугольники, если два угла одного треугольника равны двум углам другого?
- Подобны ли равнобедренные треугольники, если они имеют по равному тупому углу?
- Подобны ли треугольники АВС и А1В1С1 , если АВ = 8, ВС = 5, АС = 10, А1В1 =12, В1С1 = 7,5, А1С1 = 15 ?
- Стороны треугольник равны 6см, 7см, 9см. Найдите длину меньшей средней линии треугольника.
- В каком отношении делятся медианы треугольника в точке пересечения?
5.Соотношения между сторонами и углами прямоугольного треугольника
- Закончите предложение: Синусом острого угла прямоугольного треугольника называется…
- Катеты реугольника равны 3см и 4см.Чему равны косинусы его острых углов?
- Может ли косинус острого угла равняться 1,2? А тангенс?
- Чему равен синус угла 30 градусов?
- Запишите основное тригонометрическое тождество
- Гипотенуза треугольника равна 10см, а меньший катет 6см. найдите тангенс большего острого угла треугольника
- Треугольник АВС – прямоугольный с прямым углом С и гипотенузой АВ = 8см. Косинус угла А равен 0,5. Найти катет ВС.
- Центральные и вписанные углы.
- Закончите предложение: центральным углом называется…
- Чему равна величина вписанного угла?
- Закончите предложение: вписанные углы, опирающиеся на одну дугу…
- Постройте вписанный угол, величина которого равна 90 градусов.
- Найдите величину вписаного угла, если он опирается на четвёртую часть окружности
nsportal.ru
Методическая разработка (геометрия, 8 класс) по теме: Терминологические диктанты по геометрии для 8 класса
МНОГОУГОЛЬНИКИ.
- У многоугольника стороны могут пересекаться, а могут не пересекаться.
- Смежные отрезки многоугольника лежат на одной прямой.
- Две смежные стороны многоугольника имеют одну общую вершину.
- Название многоугольника зависит от количества вершин.
- Количество сторон многоугольника не зависит от количества его вершин.
- Периметр многоугольника – это сумма длин всех его сторон.
- Соседние вершины многоугольника лежат на разных сторонах.
- Отрезок, соединяющий любые две соседние вершины, называют диагональю многоугольника.
- Любой многоугольник разделяет плоскость на внешнюю и внутреннюю области.
- Многоугольник состоит из сторон многоугольника и его внутренней области.
- Верно ли, что многоугольники бывают выпуклые и невыпуклые.
- Прямая, проходящая через любую сторону выпуклого многоугольника разделяет его на две части.
- Невыпуклый многоугольник находится по одну строну от прямой, проходящей через любую его сторону.
- Верно ли, что у многоугольника углов столько же, сколько и сторон.
- У четырехугольника и сторон, и углов, и вершин – четыре.
- Соседние стороны четырехугольника называют противоположными.
- Противоположные вершины четырехугольника не являются соседними.
- Четырехугольники бывают только выпуклые.
- У четырехугольника можно провести четыре диагонали.
- Каждая диагональ разбивает четырехугольник на два треугольника.
- Сумма углов любого выпуклого четырехугольника, параллелограмма и трапеции равна 3600.
- У параллелограмма соседние стороны параллельны и равны.
- У параллелограмма противоположные углы равны.
- Диагонали параллелограмма точкой пересечения не делятся пополам.
- У трапеции противоположные стороны параллельны.
- Основания трапеции между собой равны.
- Боковые стороны равнобедренной трапеции между собой равны.
- У прямоугольной трапеции три угла прямые.
КЛЮЧ:
«+» — 3; 4; 6; 9; 10; 11; 14; 15; 17; 20; 21; 23; 27;
«-» — 1; 2; 5; 7; 8; 12; 13; 16; 18; 19; 22; 24; 25; 26; 28
ОЦЕНКИ:
«3» — 15 – 19
«4» — 20 – 25
«»5 – 26 – 28
ТЕМА: Площадь.
- Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
- За единицу измерения площадей принимают только квадрат со стороной 1 см.
- Площадь многоугольника выражается только положительной величиной.
- Верно ли, что равные многоугольники имеют равные площади?
- Если многоугольник разбит на части, то его площадь равна сумме площадей этих частей.
- Площадь квадрата равна кубу его стороны.
- Площадь прямоугольника равна половине произведения его противоположных сторон.
- Площадь прямоугольника равна произведению его соседних сторон.
- Основание – это одна из сторон параллелограмма.
- Высота треугольника – это перпендикуляр, опущенный из любой точки противоположной стороны к прямой, содержащей основание.
- Площадь параллелограмма равна половине произведения высоты на основание.
- Одну из сторон треугольника называют основанием.
- Площадь треугольника равна половине произведения его основания на высоту.
- Площадь прямоугольного треугольника равна произведению его катетов.
- Если основания двух треугольников равны, то их площади относятся как высоты.
- Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
- Высота трапеции – это перпендикуляр, проведенный к боковой стороне.
- Площадь трапеции равна произведению полусуммы ее оснований на высоту.
- Площадь ромба равна произведению его диагоналей.
- Площадь ромба можно найти по той же формуле, что и параллелограмм.
- Теорема Пифагора используется в любых треугольниках.
- В прямоугольном треугольнике квадрат любого катета равен сумме квадратов гипотенузы и другого катета.
- Пифагоровы треугольники те, у которых длины сторон выражаются целыми числами.
- Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
КЛЮЧ:
«+» — 1; 3; 4; 5; 8; 9; 10; 12; 13; 16; 18; 20; 23; 24
«-» — 2; 6; 7; 11; 14; 15; 17; 19; 21; 22;
ОЦЕНКИ:
«3» — 12 – 16
«4» — 17 – 21
«5»– 22 – 24
ТЕМА: «Определение подобных треугольников. Признаки подобия треугольников»
- Верно ли, что отношение двух отрезков – это деление одного отрезка на другой?
- Если одна пара отрезков пропорциональна другой паре отрезков, то их отношения не равны.
- Понятие пропорциональность рассматривается только на примере двух отрезков.
- В геометрии фигуры одинаковой формы принято называть подобными.
- Если у двух треугольников MNK и M1N1K1 соответствующие углы равны, то стороны MK и N1K1 называют сходственными.
- Два треугольника называют подобными, если их углы соответственно равны, а стороны одного треугольника соответственно пропорциональны сторонам другого.
- Коэффициент подобия – это число, равное отношению сходственных сторон подобных треугольников.
- Подобие треугольников нельзя установить, если известно, что некоторые углы соответственно равны или некоторые стороны пропорциональны.
- Площади двух подобных треугольников относятся как коэффициент подобия в квадрате.
- Отношение периметров двух подобных треугольников равно коэффициенту подобия в квадрате.
- По первому признаку подобия треугольников необходимо указать две пропорциональные стороны и угол между ними.
- По второму признаку подобия треугольников необходимо указать два равных угла в каждом треугольнике.
- По третьему признаку подобия треугольников необходимо указать пропорциональность трех сторон.
- Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
КЛЮЧ:
«+» — 1; 4; 6; 7; 9; 13; 14
«-» — 2; 3; 5; 8; 10; 11; 12
ОЦЕНКИ:
«3» — 7 – 9
«4» — 10 – 12
«5»– 13 – 14
ТЕМА : «Применение подобия к доказательству теорем и решению задач»
1) Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
2) В любом треугольнике можно провести только одну среднюю линию.
3) Средняя линия треугольника параллельна одной из его сторон и равна ее половине.
4) Средняя линия треугольника отсекает от первоначального треугольника подобный ему треугольник.
5) Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от конца медианы.
6) Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет его на два прямоугольных треугольника не подобных данному треугольнику.
7) Отрезок MN называют средним пропорциональным для двух отрезков АВ и CD, если он равен квадратному корню из суммы этих отрезков.
8) Высота прямоугольного треугольника, проведенная из любой вершины, есть среднее пропорциональное для отрезков, на которые делится катет.
9) Катет прямоугольного треугольника, проведенный из вершины прямого угла, есть среднее пропорциональное для гипотенузы и проекции этого катета на гипотенузу.
10) Метод подобия нельзя применить для решения задач на построение треугольников.
11) Измерительные работы на местности можно провести с помощью подобия двух прямоугольных треугольников.
12) Фигуры F и F1 называют подобными, если для любых двух точек этих фигур выполняется равенство .
13) Коэффициент подобия – это число, равное отношению сходственных сторон подобных фигур.
14) Верно ли, что если ширина одного прямоугольника больше в 2 раза ширины подобного ему прямоугольника, то длина может быть в 3 раза.
КЛЮЧ:
«+» — 1; 3; 4; 9; 11; 12: 13;
«-» — 2; 5; 6; 7; 8; 10; 14
ОЦЕНКИ:
«3» — 7 – 9
«4» — 10 – 12
«5»– 13 – 14
ТЕМА: «Окружность»
1) Верно ли, что возможны три случая взаимного расположения прямой и окружности.
2) Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность имеют две общих точки.
3) Прямая называется касательной, если расстояние от центра окружности до прямой равно радиусу окружности.
4) По свойству: радиус окружности, проведенный в точку касания перпендикулярен к касательной.
5) Отрезки касательных к окружности, проведенные из одной точки равны.
6) Верно ли, что прямая проходящая через конец диаметра, лежащий на окружности и перпендикулярна к этому диаметру, то она является касательной.
7) На окружности можно построить дугу любой градусной меры.
8) Центральный угол – это угол, одна сторона которого является диаметром.
9) Если центральный угол развернутый, то его соответствующая дуга называется полуокружностью.
10) Если центральный угол больше развернутого, то соответствующая дуга меньше полуокружности.
11) Градусная мера дуги – это градусная мера соответствующего центрального угла.
12) Вписанный угол – это угол, вершиной которого является центр окружности.
13) Говорят, что вписанный угол опирается на дугу, если она не лежит внутри вписанного угла.
14) Вписанный угол равен половине дуги, на которую он опирается.
15) Вписанный угол равен центральному углу.
16) Вписанные углы, опирающиеся на одну и ту же дугу не равны.
17) Вписанный угол, опирающийся на диаметр – прямой.
18) Каждая точка биссектрисы неразвернутого угла находится на разном расстоянии от его сторон.
19) Всего существует четыре замечательных точки треугольника.
20) Вписанная окружность касается всех сторон многоугольника.
21) Все вершины вписанного многоугольника лежат внутри окружности.
22) В любой четырехугольник можно вписать окружность и описать около него окружность.
23) Центры вписанной и описанной окружности треугольника не являются замечательными точками.
Ключ:
«+»: 1; 3; 4; 5; 6; 7; 9; 11; 13; 14; 17; 19; 20;
«-»: 2; 8; 10; 12; 15; 16; 18; 21; 22; 23.
Оценки:
«3» — 11 – 14;
«4» — 15 – 21;
«5» — 22 — 23
ТЕМА: «Понятие вектора. Сложение и вычитание векторов»
1) Величины, которые задаются не только числовым значением, но и направлением называют векторными величинами.
2) Вектор – это направленный отрезок.
3) У вектора неважно, какая точка является началом, а какая концом.
4) Любую точку можно назвать вектором.
5) Длина вектора – это обязательно расстояние от начала до конца вектора.
6) У нулевого вектора нельзя найти длину.
7) Коллинеарные векторы лежат только на параллельных прямых.
8) Нулевой вектор не может быть коллинеарен произвольному вектору.
9) Коллинеарные векторы делятся на сонаправленные и противоположно направленные.
10) Нулевой вектор имеет любое направление.
11) Векторы называют равными, если их длины равны.
12) От любой точки можно отложить несколько векторов, равных данному.
13) При сложении двух векторов по правилу треугольника необходимо, чтобы начало одного вектора, совпадало с началом другого.
14) При сложении векторов можно пользоваться сочетательным или переместительным законом.
15) При сложении векторов по правилу параллелограмма суммой будет являться диагональ, исходящая из их общего начала.
16) При вычитании векторов результатом будет вектор с началом в конце первого и концом в конце второго.
17) По правилу многоугольника можно сложить любое количество векторов.
18) При сложении по правилу многоугольника все векторы должны иметь общее начало.
Ключ:
«+»: 1; 2; 4; 9; 10; 14; 15; 17
«-»: 3; 5; 6; 7; 8; 11; 12; 13; 16; 18
Оценки:
«3» — 8 – 11;
«4» — 12 – 16;
«5» — 17 — 18
nsportal.ru
|
1. Фигура, смежные отрезки которой не лежат на одной прямой, а несмежные отрезки не имеют общих точек, называется …. МНОГОУГОЛЬНИК 2. Две несмежные стороны четырехугольника называются….. ПРОТИВОПОЛОЖНЫМИ 3. Две вершины многоугольника, принадлежащие одной стороне, называются… СОСЕДНИМИ 4. На какие две части разделяет многоугольник любую плоскость? ВНУТРЕННЮЮ И ВНЕШНЮЮ 5. По какой формуле можно вычислить количество сторон правильного многоугольника, если задан один из его углов? 6. Верно ли утверждение, что каждая диагональ выпуклого четырехугольника разделяет его на два треугольника? ДА 7. Что такое периметр многоугольника? СУММА ВСЕХ СТОРОН 8. Чему равна сумма углов выпуклого шестиугольника? 720º |
1. Фигура, имеющая n вершин и n сторон, причем из каждой вершины выходят только по 2 стороны называется…. n-УГОЛЬНИКОМ 2. Две вершины, не являющиеся соседними, называются … ПРОТИВОПОЛОЖНЫМИ 3. Отрезок, соединяющий две не соседние вершины, называется… ДИАГОНАЛЬЮ 4. Какие существуют 2 вида многоугольников на плоскости? ВЫПУКЛЫЙ И НЕВЫПУКЛЫЙ 5. По какой формуле можно вычислить величину угла правильного многоугольника, если задано количество его сторон? 6. Верно ли утверждение, что одна из диагоналей невыпуклого четырехугольника разделяет его на два треугольника? ДА 7. По какой формуле вычисляется периметр четырехугольника АВСД? P=АВ+ВС+СД+АД 8. Сколько сторон имеет выпуклый многоугольник с углом 108º? 5 |
nsportal.ru
Математический диктант по геометрии 8 класс.
Просмотр содержимого документа
«Математический диктант по геометрии 8 класс.»
-
Параллелограмм – это _______________________________________________________________
-
Сумма углов параллелограмма равна___________________
-
Свойства параллелограмма: А)__________________________________________________
Б)________________________________________ В)________________________________________
Г)________________________________________________________________________
4. У параллелограмма один из углов равен 280. Найдите остальные углы. _________________________
5. У параллелограмма одна сторона на 8 см больше другой, периметр равен 80 см. Найдите все стороны параллелограмма. __________________________________________________________________________
6. У параллелограмма один угол на 460 больше другого. Найдите все углы параллелограмма.
__________________________________________________________________________________________
7. Найдите углы прямоугольного равнобедренного треугольника.__________________________________
8. Найдите сумму углов выпуклого восьмиугольника. ___________________________________________
-
Параллелограмм – это _______________________________________________________________
-
Сумма углов параллелограмма равна___________________
-
Свойства параллелограмма: А)__________________________________________________
Б)________________________________________ В)________________________________________
Г)________________________________________________________________________
4. У параллелограмма один из углов равен 280. Найдите остальные углы. _________________________
5. У параллелограмма одна сторона на 8 см больше другой, периметр равен 80 см. Найдите все стороны параллелограмма. __________________________________________________________________________
6. У параллелограмма один угол на 460 больше другого. Найдите все углы параллелограмма.
__________________________________________________________________________________________
7. Найдите углы прямоугольного равнобедренного треугольника.__________________________________
8. Найдите сумму углов выпуклого восьмиугольника. ___________________________________________
-
Параллелограмм – это _______________________________________________________________
-
Сумма углов параллелограмма равна___________________
-
Свойства параллелограмма: А)__________________________________________________
Б)________________________________________ В)________________________________________
Г)________________________________________________________________________
4. У параллелограмма один из углов равен 280. Найдите остальные углы. _________________________
5. У параллелограмма одна сторона на 8 см больше другой, периметр равен 80 см. Найдите все стороны параллелограмма. __________________________________________________________________________
6. У параллелограмма один угол на 460 больше другого. Найдите все углы параллелограмма.
__________________________________________________________________________________________
7. Найдите углы прямоугольного равнобедренного треугольника.__________________________________
8. Найдите сумму углов выпуклого восьмиугольника. ___________________________________________
-
Параллелограмм – это _______________________________________________________________
-
Сумма углов параллелограмма равна___________________
-
Свойства параллелограмма: А)__________________________________________________
Б)________________________________________ В)________________________________________
Г)________________________________________________________________________
4. У параллелограмма один из углов равен 280. Найдите остальные углы. _________________________
5. У параллелограмма одна сторона на 8 см больше другой, периметр равен 80 см. Найдите все стороны параллелограмма. __________________________________________________________________________
6. У параллелограмма один угол на 460 больше другого. Найдите все углы параллелограмма.
__________________________________________________________________________________________
7. Найдите углы прямоугольного равнобедренного треугольника.__________________________________
8. Найдите сумму углов выпуклого восьмиугольника. ___________________________________________
multiurok.ru
|
1. Вставьте пропущенные слова, чтобы получилось верное высказывание: В … треугольнике сумма квадратов катетов равна… 2. Укажите, истинно или ложно данное утверждение: В прямоугольном треугольнике одна из его сторон является проекцией другой стороны. 3. Найдите расстояние до окна, а) 8; б) 4; в) не знаю.
4. Найдите AD. Укажите верный ответ: а) 20; б) 10; в) не знаю.
|
1. Вставьте пропущенные слова, чтобы получилось верное высказывание: Если в прямоугольном АВС () АВ2 = АС2 – ВС2, то 2. Укажите, истинно или ложно данное утверждение: Если к прямой из одной точки проведены перпендикуляр и наклонная, то наклонная меньше перпендикуляра. 3. Определите неизвестный элемент. Укажите верный ответ: а)
4. Определите катет АВ, если AD = 9 см, AC = 16 см. Укажите верный ответ: а) 12; б) 18; в) 9.
|
multiurok.ru
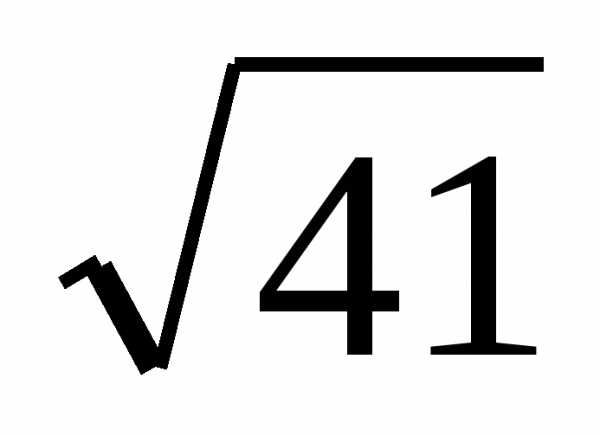 ; б) 7; в) 5.
; б) 7; в) 5.