Контрольная 8 класс по алгебре мордкович: ГДЗ Алгебра Мордкович 8 класс Контрольные работы

ГДЗ Алгебра Мордкович 8 класс Контрольные работы

Подробные решения по алгебре за 8 класс авторы Мордкович

Для того, чтобы результат от работы с гдз по алгебре за 8 класс контрольные работы Мордкович полностью оправдал ожидания, а еще лучше — превзошел их, необходимо начинать такую подготовку заблаговременно. Специалисты называют оптимальным временем старта момент, когда в классе только перешли к изучению той темы, параграфа или раздела, по которому представлена контрольная с решением. Минимальным же сроком, позволяющим адекватно подготовиться к проверочной, считается одна-две недели по предстоящей проверки. Многие восьмиклассники следуют этим советам и отмечают высокую эффективность подготовительных занятий.

Для кого предназначены онлайн решения для контрольных работ по алгебре 8 класс Мордкович

Среди тех, кто пользуется сборниками при подготовке к контрольным и проверочным, чаще всего встречаются:

• восьмиклассники, заинтересованные в математических знаниях, принимающие участие в разнообразных конкурсных программах, научных мероприятиях по предмету. Если в школе они изучают дисциплину по другим программам, УМК, учебным пособиям-практикумам, то эти источники позволят расширить, углубить свои знания, рассмотреть задания, которые не включены в те материалы, по которым алгебра изучается школьниками в классе;
• подростки, уже решившие после 9-го класса поступать в ССУЗы, поэтому заинтересованные в получении высокой оценки, среднего балла в аттестате для успешного прохождения конкурса аттестатов в техникумы и колледжи по выбранному направлению;
• школьники по уважительной причине часто пропускающие школьные занятия. Например, болеющие, проходящие реабилитацию, уезжающие на конкурсы, спортивные состязания. Для них площадка станет источником знаний, альтернативой учительскому объяснению материала, позволит написать проверочные на хорошую оценку;
• сами школьные учителя, которым надо оперативно проверить большое количество выполненных учениками контрольных в кратчайшие сроки. При помощи этих материалов они успешно решат эту задачу в условиях загруженности иной срочной работой, будучи уверенными в качестве результата;
• родители восьмиклассников, желающие оценить степень подготовленности своего ребенка к предстоящему контролю, не вдаваясь в программу предмета.

Почему так здорово заниматься по справочнику?

Хотя не все учителя и родители оценили полезность еуроки ГДЗ, скептики встречаются все реже и реже. Аргументы тех, кто понял преимущества этой площадки:

• доступность — круглосуточная и для всех;
• экономическая выгода, возможность сократить семейные расходы на репетиторскую помощь, математические курсы;
• соответствие информации нормативам Стандартов образования, включая требования к оформлению ответов.

Регулярно применяя подробные ответы на контрольные работы по алгебре за 8 класс Мордкович, восьмиклассники научатся ориентироваться в непростых математических вопросах, быстро находить и использовать справочные данные.

Алгебра 8. Контрольные Мордкович (ДМ Попов)

20/11/201806/06/2021 Администратор

Алгебра 8. Контрольные Мордкович (ДМ Попов). Цитаты контрольных работ и ответы на задачи контрольных работ из учебного пособия: «Дидактические материалы по алгебре к учебнику А.Г. Мордковича Алгебра 8 класс/ М.А. Попов — М.: Издательство Экзамен». Вопросы и ответы представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

При постоянном использовании данных контрольных работ (в 4-х вариантах) рекомендуем КУПИТЬ книгу:  Алгебра. 8 класс. Дидактические материалы к учебнику А.Г. Мордковича. ФГОС (переход по ссылке в интернет-магазин «Лабиринт.Ру»). Пособие содержит 36 самостоятельных работ, каждая в двух вариантах, так что при необходимости можно проверить полноту знаний учащихся после каждой пройденной темы; 7 контрольных работ, представленных в четырех вариантах, в том числе итоговая контрольная работа, дают возможность максимально точно оценить знания каждого ученика. В конце книги приведены олимпиадные задания и задания повышенной трудности.

Алгебра 8 класс (УМК Мордкович)

Контрольные работы (Попов):

КОНТРОЛЬНАЯ № 1. Основные понятия. Основное свойство алгебраической дроби. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Сложение и вычитание алгебраических дробей с разными знаменателями. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. Преобразование рациональных выражений. Первые представления о рациональных уравнениях. Степень с отрицательным целым показателем.

Контрольная работа № 1 КР-1 + ответы

КОНТРОЛЬНАЯ № 2. Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел. Функция у = √х, ее свойства и график. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Модуль действительного числа.

Контрольная работа № 2 КР-2 + ответы

КОНТРОЛЬНАЯ № 3. Функция у = kx², ее свойства и график. Функция у = k/x, ее свойства и график. Как построить график функции у = f(х + l), если известен график функции у = f(x). Как построить график функции у = f(x) + m если известен график функции у = f(х). Как построить график функции у = f(x + l) + m, если известен график функции у = f(x). Функция y = ах² + bx + с, ее свойства и график. Графическое решение квадратных уравнений.

Контрольная работа № 3 КР-3 + ответы

КОНТРОЛЬНАЯ № 4. Основные понятия. Формулы корней квадратных уравнений. Рациональные уравнения. Рациональные уравнения как математические модели реальных ситуаций. Еще одна формула корней квадратного уравнения. Теорема Виета. Иррациональные уравнения.

Контрольная работа № 4 КР-4 + ответы

КОНТРОЛЬНАЯ № 5. Свойства числовых неравенств. Исследование функций на монотонность. Решение линейных неравенств. Решение квадратных неравенств.

Контрольная работа № 5 КР-5 + ответы

КОНТРОЛЬНАЯ № 6. Множество рациональных чисел. Иррациональные числа. Множество действительных чисел. Модуль действительного числа. Приближенные значения действительных чисел. Стандартный вид положительного числа.

Контрольная работа № 6 КР-6 + ответы

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА за курс 8 класса.

Итоговая контрольная работа КР-7 + ответы

Вы смотрели страницу Алгебра 8. Контрольные Мордкович (ДМ Попов). Цитаты контрольных работ и ответы на задачи контрольных работ из учебного пособия: «Дидактические материалы по алгебре к учебнику А.Г. Мордковича Алгебра 8 класс/ М.А. Попов». Вернуться на страницу «Алгебра 8 класс»

Если Вы считаете, что какой-то пример решен неправильно обязательно напишите нам в поле для Комментариев (ниже) с указанием № контрольной работы, № варианта и № задачи.

Математика КР, Оглавление8 класс, Мордкович

Вас могут заинтересовать…

Математический факультет — 8 класс

Алгебра: что такое алгебра?

Математика изучается через вопросы, которые возникают при решении хорошо построенных задач. Наши ученики начинают с проблем, они используют стратегии для решения проблем и попутно изучают необходимую математику. Многие исследования в классе разработаны таким образом, чтобы учащиеся совместно или индивидуально открывали математические свойства. Затем свойства обсуждаются в классе, обобщаются и становятся частью математических знаний учащихся, которые можно применить к будущим задачам.

Открытие математики является важной частью развития уверенности каждого ученика как математика. Знания, полученные в ходе исследования, с большей вероятностью запомнятся на долгий срок. Учителя и родители работают вместе, чтобы продвигать это открытие математики посредством исследований, решения проблем и рассуждений. Наша цель состоит в том, чтобы учащиеся государственных школ Гластонбери поняли, что математика имеет смысл.

В течение этого года, посредством исследования и решения задач, учащиеся разовьют концептуальное понимание многих тем алгебры и подготовятся к формальному изучению алгебры в последующие годы.

Часть 1: Объем и иррациональные числа

В течение части 1 задачи на объем создают потребность в понимании иррациональных чисел.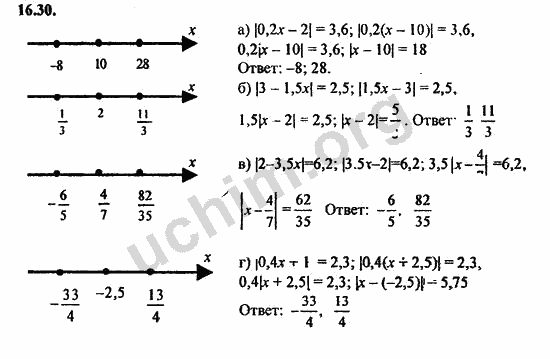 Учащиеся строят и понимают формулы объема цилиндров, конусов и сфер и используют их для нахождения объемов и недостающих размеров. Таким образом создается потребность понимать иррациональные числа. Студенты узнают, как найти рациональные приближения для иррациональных чисел и когда решение должно быть записано точно или приблизительно.

Стандарты Common Core State: 8.NS.A.1, 8.NS.A.2, 8.G.C.9, 8.EE.A.2,

Раздел 2: Теорема Пифагора

Студенты откроет теорему Пифагора через наблюдения закономерностей. Они будут использовать теорему для решения множества задач, включая расстояние на координатной плоскости. Затем учащиеся испытают и объяснят различные геометрические доказательства теоремы и разовьют общее понимание доказательства.

Общие основные государственные стандарты: 8.GB.6 , 8. GB.7 , 8.GB.8 9.2.EEA 9.00014, 8.0.EEA 9.00014, 8.0014 1, 8.НС.А2.

Раздел 3: Использование мер угла (уравнения с одной переменной)

В начале урока 3 учащиеся столкнутся с проблемой, которая, похоже, не имеет решения. Учащиеся обнаруживают взаимосвязь между углами, образованными параллельными прямыми и секущей, а также взаимосвязь между углами треугольников, как внутренних, так и внешних. Алгебра используется для решения отсутствующих углов, и учащиеся сталкиваются с проблемами, не имеющими реальных решений.

Общие основные государственные стандарты: 8.GB.6 , 8.GB.7 , 8.GB.8 9.2.EEA 9.00014, 8.0.EEA 9.00014, 8.0014 1, 8.NS.A.2

Раздел 4: Функции и линейные уравнения

Учащиеся начинают Раздел 4 с построения графиков зависимости между изменением радиуса цилиндра и изменением объемов. «Студенты понимают концепцию функции как правило, которое назначает каждому входу ровно один выход. Они понимают, что функции описывают ситуации, когда одна величина определяет другую. Они могут переводить между таблицами, уравнениями, графиками и словесными представлениями, а также частичными представлениями функций».

Стандарты общего ядра: 8.F.A.1 , 8.F.A.2 , 8.F.A.3 , 8.F.B.4 , 8.F.B.4 , 8.F.B.4 , 8.F.B.4 , 8.F.B.4 , 8.F.B.4 , 8.F. , 8.EE.B.5 , 8.EE.B.6 ,

Раздел 5: Системы линейных уравнений

900 уравнений с использованием задачи, которая создает необходимость одновременного анализа двух отношений. Преимущество использования графа становится очевидным через характер проблемы. Они строят понимание смысла решения системы сначала графически, затем аналитически. Затем используются различные методы для решения простых систем уравнений: проверка, замена с y = ax + b и y = cx + d и, наконец, замена с одним уравнением в стандартной форме. Графический калькулятор вводится как метод решения систем, а затем и решения уравнений с одной переменной.

Общие основные государственные стандарты: 8.EE.C.8A , 8.EE.C.8B , 8.EE.C.8C 8. .7a, 8.EE.C.7b

Раздел 6: Научная запись и свойства показателей степени

Учащиеся узнают о необходимости эффективного способа записи и работы с очень большими и очень маленькими числами. Работа с экспоненциальной записью приведет к артикуляции закономерностей, обнаруженных в экспоненциальных выражениях, ведущих к степенным свойствам. Хотя шаблоны с показателями (свойствами) будут передаваться через алгебраические символы, учащиеся поймут, что запоминание правил не требуется. Вместо этого шаблоны имеют смысл и всегда могут быть логически обоснованы путем расширения и сжатия выражения.

Общие базовые государственные стандарты: 8.EE.A.1 , 8.EE.A.3 , 8.EE.A.4 9004 Единица преобразования: 9004

9004

Ученики будут выражать ранее изученные переводы алгебраически, используя сопоставление. Они обнаружат связь между жесткими преобразованиями (изометриями) и конгруэнтностью. Затем работа будет сосредоточена на расширении и сходстве. Учащиеся обнаружат, что, хотя определение сходства включает в себя пропорциональность сторон подобных фигур и конгруэнтность углов, учащиеся делают вывод, что сходство треугольников можно определить, используя только 2 пары конгруэнтных углов.

Стандарты общего ядра: 8. G.A.1A , 8.G.A.1.B , 8.G.A.1.C , 8.G.A.1.C , 8.G.A.1.1.C , 8.G.A.1.C , 8.G.A.1.C , 8.G.A.1.C , 8. 8.G.A.3 , 8.G.A.4 , 8G.A.5

Модуль 8: Двумерные данные

В разделе 8 учащиеся изучают связи между наборами данных. Учащиеся также используют линейное уравнение для описания связи между двумя величинами в двумерных данных (например, между размахом рук и ростом учащихся в классе). На этом уровне подгонка модели и оценка ее соответствия данным выполняются неформально. Интерпретация модели в контексте данных требует, чтобы учащиеся выражали взаимосвязь между двумя рассматриваемыми величинами и интерпретировали компоненты взаимосвязи (такие как наклон и пересечение оси Y) с точки зрения ситуации. Ассоциация также исследуется с помощью представлений в двусторонних таблицах с использованием процентов и отношений.

Общие основные государственные стандарты: 8.SP.A.1 , 8.SP.A.2 , 8.SP.A.3 9.0015 , A.4

8 класс / 8 класс Математика

• Список поставок 8 класса

• 2022 Летнее чтение

• 8 класс ЭЛА

• 8 класс Математика

• Обществознание 8 класс

• 8 класс Наука

• 8 класс Мировые языки

• 8 класс физкультура/здоровье

• Цель школьной программы по математике округа состоит в том, чтобы дать учащимся опыт, который позволит им развить математическое мышление и приобрести основные математические понятия и навыки. В начальной учебной программе широко используются манипуляторы (конкретные объекты) для более глубокого понимания.

  Учебная программа предназначена для развития у учащихся компетенций, необходимых для математического развития. По мере прохождения курсовой работы у них будут развиваться все более сложные способности решения задач, ряд математических «привычек ума» и набор высокоразвитых навыков математического мышления. Кроме того, учащиеся будут все больше и больше владеть устными и письменными математическими выражениями, поскольку они будут свободно говорить на языке математики и смогут устанавливать связи в математике.

  Оценка: 8

  Типы оценок: Конец единичных тестов, викторины в середине единицы и кумулятивные квартавры

  Пререквизиты: математика 7 или математика 700044

  92 Кэтч: или математика 1,1,1,1,1,1,1, ОПИСАНИЕ

  Математика восьмого класса продолжается с пропорциональными рассуждениями и рациональными числами. Студенты также начнут изучать более сложные алгебраические понятия и геометрические отношения. В течение года учащиеся будут продолжать работать над упорством в решении задач, имея возможность понимать и использовать математические методы.

  1. Рациональные числа
  2. Экспоненты и научная нотация
  3. Алгебраические уравнения
  1. Линейные уравнения
  2. Буквенные уравнения
  3. Системы уравнений
  4. Измерение и геометрия
  1. Круги
  2. Объем трехмерных фигур
  5. Угловые измерения
  1. Углы, образованные пересекающимися линиями
  2. Параллельные линии, пересекаемые секущей
  3. Треугольники
  6. Пропорциональные отношения
  1. Соотношения, ставки, удельные ставки
  2. Похожие фигурки
  7. Трансформационная геометрия
  1. Переводы
  2. Отражения
  3. оборотов
  4. Расширения 
  8. Графики линейных уравнений
  9. Функции
  10. Квадратные корни и кубические корни
  11. Теорема Пифагора

  ТЕКСТ и другие материалы

  Ready New York Mathematics Practice and Problem Solving — Curriculum Associates
  Учитель предоставил заметки и раздаточные материалы

  ОЖИДАНИЯ РАБОТЫ
  Приходить вовремя на занятия Принесите необходимые материалы и будьте готовы (сделайте домашнюю работу и готовьтесь к любым оценкам).