Олимпиадные задания по алгебре (7 класс) по теме: сборник олимпиад для 7 класса по математике
Олимпиадные задачи для 7 класса
Сумма двух чисел равна 13,5927. Если в большем из них перенести запятую на один знак влево, то получим меньшее число. Чему равны эти числа?
Вычислите: 2379 • 23782378 — 2378 • 23792379.
Один из четырёх гангстеров украл чемодан с деньгами. На допросе Алекс сказал, что чемодан украл Луи, Луи утверждал, что виновник Том, Том заверял следователя, что Луи лжёт. Жорж настаивал только на том, что он не виноват. В ходе следствия выяснилось, что только один из гангстеров сказал правду. Кто украл чемодан?
Найдите площадь закрашенной фигуры:
В каждой клетке шахматной доски 5×5 сидит жук. В некоторый момент по команде все жуки переползают на соседние (по горизонтали или по вертикали) клетки. Докажите, что при этом одна из клеток обязательно останется пустой.
Леспромхоз решил вырубить сосновый лес, но экологи запротестовали. Тогда директор леспромхоза всех успокоил, сказав: «В нашем лесу 99 % сосен. Мы будем рубить только сосны. После их вырубки останется 98 % от всех деревьев». Какая часть леса будет вырублена?
Коза и корова съедают воз сена за 45 дней, корова и овца — за 60 дней, овца и коза — за 90 дней. За сколько дней съедят воз сена коза, овца и корова вместе?
Делится ли число 44444…44 на 8?
2005штук
Докажите, что число 2 делится на 9.
Два поезда движутся навстречу друг другу по параллельным путям — один со скоростью 60 км\ч, а другой со скоростью 80 км\ч. Пассажир, сидящий во втором поезде, заметил, что первый поезд шел мимо него в течение 6 с. Какова длина первого поезда?
Магазин продал третью часть полученных апельсин и ещё 32 кг, третью часть остатка и ещё 32 кг отпустил школьной столовой, третью часть нового остатка и ещё 32 кг передали детскому саду, после чего осталась третья часть нового остатка и ещё 32 кг. Сколько кг апельсин было в магазине первоначально?
Имеется 9 пластинок и двухчашечные весы без гирь. По виду все пластинки одинаковые, но одна из них легче других. Как с помощью двух взвешиваний найти более лёгкую пластинку?
В приёмной 10 кресел. Сколькими способами в них могут разместиться 4 посетителей?
У звезды ACFBD равны углы при вершинах А и В, углы при вершинах F и С, а также длины отрезков АС и ВF. Докажите, что AD = BD.
Малыш и Карлсон поочерёдно берут конфеты из одного пакета. Малыш берёт одну конфету, Карлсон — две, затем Малыш берёт 3 конфеты, Карлсон — 4, и так далее. Когда количество оставшихся в пакете конфет станет меньше необходимого, тот, чья очередь наступила, заберёт все оставшиеся конфеты. Сколько конфет было в пакете первоначально, если у Малыша в итоге оказалось 101 конфета?
Вычислите: ;
Два джентльмена одновременно отправились на прогулку по аллее длиной 100 метров. Мистер Смит за час проходит 1 км, мистер Джонс идёт помедленнее — всего 600 метров в час. Дойдя до конца аллеи, каждый поворачивает и с прежней скоростью идёт обратно. Встречаясь, они каждый раз раскланиваются. Сколько раз они раскланиваются на протяжении первых 25 минут? Сколько времени из этих 25 минут они шли в одном направлении?
В бутылке, стакане, кувшине и банке находится молоко, лимонад, квас, вода. Известно, что вода и молоко находятся не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. Куда налита каждая жидкость?
Сколько белых грибов надо собрать для получения 1 кг сушеных, если при переработке свежих грибов остаётся 50 % их массы, а при сушке остаётся 10 % массы обработанных грибов?
Углы 60° и 40° имеют общую сторону. Найдите отношение меры угла, образованного не общей стороной угла 40° и биссектрисой большего угла, к мере большего угла.
Сколько рыб в пруду? Некий ихтиолог хотел определить, сколько в пруду рыб, годных для улова. Для этого он забросил сеть с заранее выбранным размером ячеек и, вытащив её, обнаружил 30 рыб, отметил каждую из них меткой и бросил в пруд. На другой день забросил ту же самую сеть и поймал 40 рыб, на 2 из которых были его метки. Как по этим данным он приблизительно вычислил сколько рыб в пруду?
Найти все такие целые числа х и у, такие что (1 +у)(ху — 1) = 3.
Число х при делении на 10 даёт в остатке 3, а число у при делении на 10 даёт в остатке 2. Доказать, что сумма (х + у) делится нацело на 5.
Среднее арифметическое шести чисел равно 345, а среднее арифметическое четырёх других чисел равно 555. Чему равно среднее арифметическое всех десяти чисел?
В комнате стоят табуретки и стулья, у каждой табуретки 3 ножки, у каждого стула 4 ножки. Когда на всех табуретках и стульях сидят люди, в комнате 39 ног. Сколько стульев и табуреток в комнате?
Теплоход проходит путь от А до В по течению за 3 часа, а возвращается обратно за 4 часа. За какое время путь от А до В преодолевает плот?
Решите уравнение: || х — 674| -1| = 4.
В классе учатся 40 человек. Из них по русскому языку имеют «3» 19 человек, по математике — 17 человек и по физике — 22 человека. Только по одному предмету имеют «3»: по русскому языку — 4 человека, по математике — 4 человека и по физике 11 человек. Семь человек имеют «3» и по математике, и по физике, из них пятеро имеют «3» и по русскому языку. Сколько человек учатся без троек?
В шестизначном числе первая цифра совпадает с четвёртой, вторая — с пятой, третья — с шестой. Докажите, что это число кратно 7, 11, 13.
Докажите, что если треугольники АВМ и АВМ равны, то треугольники CDMи CDM тоже равны.
nsportal.ru
Подборка занимательных задач для 6
Занимательные задачи по математике 6 — 7 класс. Переправы и разъезды
Автор: Колпаков А.Н. on 10 августа 2011
Предлагаю небольшую подборку задач на реки и мосты, переправы и разъезды. Они не привязаны к программам 6 и 7 класса, поэтому репетитор по математике может использовать их в 5-ом и даже в 4-oм классе. Но все-таки совсем маленьким ученикам (даже олимпиадникам) большинство задач покажутся слишком трудными (из-за большого перебора вариантов). Я ориентировался на уровень развития среднестатистического шести — семиклассника с математическим и логическим складом ума. Для него задачи репетитора по математике покажутся и не только интересными, но и более доступными. Тренируйте мозги у своих учеников!
1) Знаменитая задача про волка, козу и капусту:
Фермеру необходимо переправить через широкую реку капусту, козу и волка. Но беда в том, что в лодке с человеком есть одно место или для капусты или для козу или для волка. Если фермер оставит козу с волком, то волк может съесть козу, а если оставить капусту с козой, то она съесть капусту. В присутствии фермера никто никого не ест. Подскажите ему способ переправы на другой берег?
2) Отряд солдат подошел к реке и задумал через нее переправиться. Однако мост оказался сломанным, а река очень глубокой. Рядом с берегом в лодке сидят 2 мальчика, но их лодка настолько маленькая, что на ней можно переправиться на другой берег или только одиному солдату или только двум мальчикам — не больше. Как им переправиться?
3) Три рыцаря у каждого из которых был свой оруженосец съехались на берегу реки, к которому была привязана двухместная лодка. Их лошади переправились вплавь, а людей ждала лодка. Но оруженосцы, словно сговорившись, не захотели оставаться на берегу в компании незнакомых рыцарей. Иговоры и угрозы не помогли. Тогда оруженосцы подумали и нашли способ переправиться не нарушая требование оруженосцев. Как они это сделали?
4) Можно ли рыцарям переправиться при этих же условиях, если съедутся 4 рыцаря и 4 оруженосца?
5) К реке подошли 4 рыцаря и 4 оруженосца, но лодка оказалась трехместной. Можно ли осуществить переправу с теми же условиями оруженосцев?
6) К берегу реки подошли 3 контрабандиста с двумя мешками золота каждый. У берега нашлась трехместная лодка в которую помещались любые три мешка, или контрабандист + 2 мешка, или 2 контрабандиста + 1 мешок или 3 контрабандиста. Каждый из преступников не может оставить ни один из своих мешков наедине с другими преступниками, но может их оставить на безлюдном берегу. Могут ли все они переправиться через реку?
7) Четыре рыцаря с оруженосцами хотят переправиться через глубокую реку на лодке без гребца, вмешающая не более двух человек. Недалеко от места переправы есть островок, на котором можно высаживаться. Как можно переправиться с условием, что нигде (ни на берегах, ни в лодке, ни на острове) ни один оруженосец не находился в компании чужих для него рыцарей?
8) Поезд M приближается к железнодорожной станции и его обгоняет быстро едущий поезд из города N, который нужно пропустить вперед. От главного пути, около станции, отходит боковая ветка — тупик, на которую временно можно оттащить вагоны с главного пути, но она так мала, что может вместить весь поезд M. Как можно пропустить поезд N вперед?
9) По речному каналу один за другим плывут три парохода: M;N и K. Навстречу им плывут еще три парохода, идущие также один за другим: P;H и E. Канал такой ширины, что два парохода не могут в нем разъехаться, но в конце одной из сторон канала есть карман в виде залива. В него можно отвести только один из пароходов. Могут ли эти пароходы разъехаться около этого кармана?
Дети с удовольствием решаю задачи предложенные репетитором математики, над которыми можно «думать рисунком». Объяснительные тексты к ним писать нет смысла, так как не хватит тетрадного листа. Достаточно нарисовать. К олимпиадным задачам они не относятся, а больше рассчитаны на развлечение и тренировку памяти, внимания и смекалки. Рисуйте и думайте на здоровье!
Колпаков Александр Николаевич. Репетитор по математике, Строгино
Задачи на разъезды прислал мой коллега Александров Григорий Павлович репетитор по математике. Москва, Митино.
Автор: Колпаков А.Н. on 18 декабря 2010
На этой странице сайта «профессиональный репетитор по математике» вы найдете подборку задач на логику высказываний, на перебор и сортировку вариантов, на доказательство и на рассуждение. Такие задачи учат ребенка анализировать условия и делать выводы, обосновывать факты и явления. Репетитор по математике может использовать эти материалы в своей работе с учениками не младше 5-6 класса. Список задач будет постепенно пополняться.
1) Имеется 25 городов. Известно, что из каждого города в другие города ведут как минимум 12 дорог. Докажите, что из каждого города можно проехать в каждый.
2) В марсианском метро 101 станция и 5000 перегонов между ними. Докажите, что можно добраться с любой станции до любой станции.
3) В соревнованиях по лыжным гонкам участвовали 3 лыжника: Антонов, Володин и Степанов. Перед дистанцией один зритель сказал, что первым придет Антонов, второй зритель сказал, что Степанов не будет последним, а третий зритель предсказал, что Володин не будет последним. После забега выяснилось, что угадал всего лишь один зритель, а другие ошиблись. В каком порядке лыжники пришли к финишу?
4) Варя сказала, что на ее день рождения пришли больше шести подруг. А ее сестра сказала, что подруг было больше пяти. Сколько подруг пришло к Варе, если из двух этих утверждений одно истинное, а другое ложное?
Здесь представлены примеры логических задач для 5-го, 6-го и 7-го класса. Это рекомендуемый возраст для знакомства с приемами их решения, так как в более ранний период жизни ребенок чаще всего еще не способен ни анализировать информацию на несколько шагов вперед, ни мыслить абстрактно. Вместе с этим критический вид деятельности у него не является основным средством познания. В 8-ом классе и старше я бы не советовал репетиторам увлекаться такими задачами из-за их очевидного отклонения от содержания программы. Есть куда более важные направления для развития ученика.
Колпаков Александр Николаевич, репетитор по математике Москва, Строгино.
Автор: Колпаков А.Н. on 15 ноября 2010
Репетиторам по математике, а также ученикам, проявляющим интерес к математике, предлагается подборка задач олимпиадного уровня на часы, даты и календарь. Список задач регулярно пополняется. Большинство из этих задач отобрано мной именно для работы с шести-семиклассниками, однако некоторые из них репетитор по математике может предложить ученикам уже 5-ом классе. У задач нет четкой возрастной принадлежности и единственным требованием к пониманию их решения, кроме способностей удерживать в голове все расуждения, является умение выполнять действия с дробями. Уровень задач соответствует уровню малого мехмата МГУ, второй математической школы, Курчатовской школы и др.
1) Найдите самое большое количество пятниц в году?
2) Может ли в каком-либо месяце быть 5 понедельников и 5 четвергов?
3) В одном месяце три сестры пришлись на четные числа. Какого числа в этом будет второе воскресенья?
4) Какой сегодня день недели, если известно, что когда послезавтра станет вчера, то сегодня будет также далеко от воскресенья, как тот день, который был сегодня, когда вчера было завтра?
5) Человек родился 7 января 40 года до нашей эры, а умер 7 января 50 года нашей эры. Сколько лет он прожил?
6) Найдите угол в градусах между минутной и часовой стрелкой в 8ч 30мин.
7) Найдите угол в градусах между минутной и часовой стрелкой в 18ч 15мин.
8)*Совешание у директора завода началось между 6 и 7 часами вечера, завершилось между 9 и 10 часами. Требуется найти точное время начала и окончания этого совещания, если за его время часовая и минутная стрелки
поменялись местами.
9)*Дима начал выполнять домашнее задание репетитора по математике между 4 и 5 часами вечера, когда его часов совпадали, а закончил работу, когда часовая стрелка оказалась напротив минутной (по одной прямой). Надите сколько минут Дима выполнял задание репетитора и в котором часу он его сделал?
Автор: Колпаков А.Н. on 7 ноября 2010
Вашему вниманию предлагается подборка задач на определение фальшивых монет путем взвешивания на чашечных весах без гирь. Данный тип задач очень распространен и обычно используется репетиторами по математике на развивающих занятиях со способными школьниками разного возраста. Никакой математической нагрузки задачи на взвешивание не несут. Их назначение — развитие абстрактного мышления, тренировка памяти, внимания, обучение построению алгоритмов и планов решений не отягощенных математикой. Учитывая оторванность задач от программ учебников, репетитор по математике может предлагать работать с монетами произвольно и в любой период учебы ребенка. Единственный критерий их отбора — количество взвешиваний, необходимых репетитору для демонстрации решений. В данном списке большинство задач требует более двух взвешиваний и поэтому редко доступны для самых маленьких.
1) Имеется 6 одинаковых настоящих монет и еще одна фальшивая, которая легче остальных. Как на чашечных весах без гирь найти эту фальшивую менету? Опишите порядок взвешиваний.
2) Теперь у нас 7 настоящих монет и еще одна фальшивая, также более легкая остальных. Как найти фальшивую монету за два взвешивания ?
3) Как из 10 монет, среди которой тоже есть фальшивая определить ее за три взвешивания?
4) А теперь попробуйте из 16 монет обнаружить фальшивую не более чем за 3 взвешивания.
5) Задача усложняется и теперь перед нами 17 монет, а количество взвешиваний опять не более чем три.
6) А вот у нас уже 20 монет вместе с фальшивой, как всегда более легкой. Нужно потратить не более 3-х взвешиваний для ее вывления. Как надо их выполнить?
7) Монет 26 штук, одна фальшивая. Взвешиваний опять не более трех. Как найти эту фальшивую монету?
8) Из 27 монет одна фальшивая. как ее найти снова за три взвешивания?
9) Теперь у нас всего 28 монет вместе с одной фальшивой. Как ее найти за 4 взвешивания?
10) Имеется 40 монет среди которых какие-то две монеты фальшивые. Определите за 2 взвешивания 20 настоящих монеты.
11) А сможете ли вы из 82 монет среди которых одна более легкая (фальшивая) найти наименьшее число взвешиваний, которое потребуется для ее определения?
12) И наконец перед нами 11 настоящих монет и еще одна фальшивая. Надо потратить не более четырех взвешиваний.
infourok.ru
Задачи, решаемые с помощью уравнения. 7-й класс
Цели урока:
- Проверка практических умений и навыков решения задач на составление
уравнения. - Активизация учебной деятельности учащихся путём общения в динамических
парах, когда каждый учит каждого. - Воспитывать ответственное отношение к учебному труду, развивать
логическое мышление, любознательность, умение проверять и оценивать
выполненную работу.
Коллективным способом обучения (А. Г. Ривин и В.К. Дьяченко) является такая
его организация, при которой обучение осуществляется путём общения в
динамических парах, когда каждый учит каждого.
Ход урока
I. Работа начинается с ввода или так называемого “запуска” раздела.
Обобщение и систематизация знаний по теме “ Задачи, решаемые с помощью
уравнения”.
Примеры задач:
1. За 9 ч по течению реки теплоход проходит тот же путь, что за 11 ч против
течения. Найдите собственную скорость теплохода, если скорость течения реки 2
км/ч.
Пусть собственная скорость теплохода – Х км/ч. Заполним таблицу значений трёх
величин.
| Скорость (км/ч) | Время (ч) | Расстояние (км) | |
| По течению | Х + 2 | 9 | 9(Х + 2) |
| Против течения | Х – 2 | 11 | 11(Х – 2) |
На основании условия задачи составим уравнение:
9(Х + 2) = 11(Х – 2), которое имеет единственный корень 20.
Собственная скорость теплохода 20 км/ч.
2. Увеличив среднюю скорость с 250 до300 м/мин, спортсменка стала пробегать
дистанцию на 1 мин быстрее. Какова длина дистанции?
Пусть Х мин – время, за которое спортсменка пробегала дистанцию со скоростью 300
м/мин, тогда Х +1 мин – время, за которое спортсменка пробегала дистанцию со
скоростью 250 м/мин. Составим уравнение:
250(Х + 1) = 300Х , которое имеет единственный корень 5.Найдём длину дистанции
300Х = 300×5 = 1500 м.
3. В первую бригаду привезли раствора цемента на 50 кг меньше, чем во вторую.
Каждый час работы первая бригада расходовала 150 кг раствора, а вторая – 200кг.
Через 3 ч работы в первой бригаде осталось раствора в 1,5 раза больше, чем во
второй. Сколько раствора привезли в каждую бригаду?
Пусть в первую бригаду привезли Х кг раствора, тогда во вторую – Х + 50 кг.
Заполним таблицу значений величин для двух бригад:
| Привезли(кг) | Расход(кг)за 1 час | Время (ч) | Осталось раствора(кг) | |
| 1-я бригада | Х | 150 | 3 | Х – 450 |
| 2-я бригада | Х + 50 | 200 | 3 | Х + 50 – 600 |
По условию задачи в первой бригаде осталось раствора в 1,5 раза больше, чем
во второй. Составим уравнение:
Х – 450 = (Х + 50 – 600)×1,5 , имеющее единственный корень 750. 750 кг
раствора привезли в первую бригаду, а во вторую привезли 750 + 50 = 800 кг.
4. (Задача Э.Безу) По контракту работникам причитается 48 франков за каждый
отработанный день, а за каждый неотработанный день с них вычитается по 12
франков. Через 30 дней выяснилось, что работникам ничего не причитается. Сколько
дней они отработали в течение этих 30 дней?
Пусть работники отработали Х дней, тогда они не работали (30 – Х) дней. Составим
уравнение:
48Х – 12 (30 – Х) = 0.
Решив это уравнение, получим Х = 6, то есть они отработали 6 дней.
5. Книгу в 296 страниц ученик прочитал за три дня. Во второй день он прочитал
на 20% больше, чем в первый, а в третий – на 24 страницы больше, чем во второй.
Сколько страниц прочитал ученик в первый день?
Пусть в первый день ученик прочитал Х страниц, тогда во второй день ученик
прочитал Х + 0,2Х = 1,2Х страниц, а в третий день прочитал 1,2Х + 24. Составим
уравнение:
Х + 1,2Х +1,2Х + 24 = 296. Решив это уравнение, получим Х = 80, то есть ученик
прочитал в первый день 80 страниц.
6. На солнышке грелось несколько кошек. У них лап на 10 больше, чем ушей.
Сколько кошек грелось на солнышке?
Пусть грелось Х кошек, тогда у этих кошек 2Х ушей и 4Х лап. Составим уравнение:
4Х – 2Х = 10. Решив это уравнение, получим Х = 5,то есть 5 кошек грелось на
солнышке.
II. Самостоятельная работа учащихся.
Каждый ученик получает индивидуальную карточку с задачами. Правильность
решения проверяет преподаватель, при необходимости он оказывает помощь в
решении. После проверки ученику выставляется в оценочный лист плюс или оценка.
Примеры карточек для первой группы:
Карточка № 1.
1. (Старинная задача.) Послан человек из Москвы в Вологду и велено ему
проходить во всякий день по 40 вёрст. На следующий день вслед ему был послан
другой человек и велено ему проходить по 45 вёрст в день. Через сколько дней
второй догонит первого?
2. Чтобы сделать вовремя заказ, артель стеклодувов должна была изготовлять в
день по 40 изделий. Однако она изготовляла ежедневно на 20 изделий больше и
выполнила заказ на 3 дня раньше срока. Каков был срок выполнения заказа?
Ответ: № 1 – 8 дней, № 2 – 9 дней.
Карточка № 2.
1. Кооператив наметил изготовить партию мужских сорочек за 8 дней. Выпуская в
день на 10 сорочек больше, чем предполагалось, он выполнил план за один день до
срока. Сколько сорочек в день должен был выпускать кооператив?
2. На ферме 1000 кроликов и кур, у них 3150 ног. Сколько кроликов и сколько
кур на ферме?
Ответ: № 1 – 70 сорочек, № 2 – 575 кроликов и 425 кур..
Карточка № 3.
1. Из пункта А вышла грузовая машина со скоростью 60км/ч. Через 2 ч вслед за
ней из пункта А вышла легковая машина со скоростью 90 км/ч. На каком расстоянии
от пункта А легковая машина догонит грузовую?
2. Чтобы выполнить задание в срок, токарь должен изготавливать по 24 детали в
день. Однако он ежедневно перевыполнял норму на 15 деталей и уже за 6дней до
срока изготовил 21 деталь сверх плана. Сколько деталей изготовил токарь?
Ответ: № 1 – 360 км, № 2 – 408 деталей.
Карточка № 4.
1. От турбазы до привала туристы шли со скоростью 4,5км/ч, а возвращались на
турбазу со скоростью 4км/ч, затратив на обратный путь на 15 мин больше. На каком
расстоянии от турбазы был сделан привал?
2. На одном складе было 185 т угля, а на другом – 237 т. Первый склад стал
отпускать ежедневно по 15 т угля, а второй – по 18 т. Через сколько дней на
втором складе угля будет в полтора раза больше, чем на первом?
Ответ: № 1 – 9 км, № 2 – 9 дней.
Примеры карточек для второй группы:
Карточка № 5.
1. Из пункта А выехал велосипедист. Одновременно вслед за ним из пункта В ,
отстоящего от пункта А на расстоянии 60 км/ч, выехал мотоциклист. Велосипедист
ехал со скоростью 12 км/ч, а мотоциклист – со скоростью 30 км/ч. На каком
расстоянии от пункта А мотоциклист догонит велосипедиста?
2. Три бригады изготовили 65 деталей. Первая бригада изготовила на 10 деталей
меньше, чем вторая, а третья – 30% того числа деталей, которые изготовили первая
и вторая детали вместе. Сколько деталей изготовила каждая бригада?
Ответ: № 1 – 40 км, № 2 – 20, 30, 15 деталей.
Карточка № 6.
1. Расстояние между пристанями М и N равно 162 км. От пристани М отошёл
теплоход со скоростью 45 км/ч. Через 45 мин от пристани N навстречу ему отошёл
другой теплоход, скорость которого 36 км/ч. Через сколько часов после
отправления первого теплохода они встретятся?
2. Бригада рабочих должна была изготовить определённое количество деталей за
20 дней. Однако она ежедневно изготавливала на 70 деталей больше, чем
планировалось первоначально. Поэтому уже за 7 дней до срока ей осталось
изготовить 140 деталей. Сколько деталей должна была изготовить бригада?
Ответ: № 1 – 2
ч, № 2 –
3000 деталей.
Карточка № 7.
1. От пристани А отошел теплоход со скоростью 40 км/ч. Через 1
ч вслед за
ним отошёл другой теплоход со скоростью 60 км/ч. Через сколько часов после
своего отправления и на каком расстоянии от А второй теплоход догонит первый?
2. В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе
19 голов и 46 ног?
Ответ: № 1 – 2 ,5 ч; 150 км, № 2 – 4 овцы и15 кур.
Карточка № 8.
1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было
монет по 2 р.?
2. За 4 ч катер проходит по течению расстояние, в 2,4 раза большее, чем за 2
ч против течения. Какова скорость катера в стоячей воде, если скорость течения
1,5 км/ч?
Ответ: № 1 – 7 монет, № 2 – 16,5 км/ч.
Примеры карточек для третьей группы:
Карточка № 9.
1. Со станции М и N, расстояние между которыми 380 км, одновременно навстречу
друг другу вышли два поезда. Скорость поезда, отправившегося со станции N, была
больше скорости другого поезда на 5 км/ч. Через 2 ч после отправления поездам
оставалось пройти до встречи 30 км. Найдите скорость поездов.
2. В одном резервуаре 380 м³ воды, а в другом 1500 м³. В первый резервуар
каждый час поступает 80 м³ воды, а из второго каждый час выкачивают 60 м³. Через
сколько часов воды в резервуаре станет поровну?
Ответ: № 1 – 85 и 90км/ч, № 2 – 56 ч.
Карточка № 10.
1. Сумму в 74 р. заплатили девятнадцатью монетами по 2 р. и 5 р. Сколько было
монет по 2 р.?
2. Скашивая ежедневно по 60 га вместо 50 га, бригада сумела скосить луг на
один день быстрее, чем планировалось. Какова площадь луга?
Ответ: № 1 – 7 монет, № 2 – 300 га.
Карточка № 11.
1. (Старинная задача.) Летели галки, сели на палки: по две сядут – одна палка
лишняя, по одной сядут – одна галка лишняя. Сколько было галок и сколько палок?
2. Турист рассчитал, что если он будет идти к железнодорожной станции со
скоростью 4км/ч, то опоздает к поезду на полчаса, а если он будет идти со
скоростью 5км/ч, то придёт на станцию за 6 мин до отправления поезда. Какое
расстояние должен пройти турист?
Ответ: № 1 – 4 галки и 3 палки, № 2 – 12 км.
Карточка № 12.
1. (Задача С.А. Рачинского.) Я дал одному ученику 3 ореха, а всем остальным
по 5 . Если бы я всем дал по 4 ореха, у меня осталось бы 15. Сколько было
орехов?
2. К числу приписали справа нуль. Число увеличилось на 405. Найдите первое
число.
Ответ: № 1 – 83 ореха, № 2 – 45.
Раздел считается введённым в работу, если каждая карточка с заданиями
выполнена хотя бы одним учеником.
III. Работа в группах.
Затем работа классного коллектива выглядит так: организуется 3–4 группы по 4
человека (можно до 7 человек). В группе у каждого ученика своя карточка, за
которую ученик уже получил плюс или оценку в оценочный лист. Каждый в группе
выбирает партнёра, и они меняются карточками. Школьники работают в парах (решают
карточку своего партнера полностью), затем пары в группе меняются. Если
необходима помощь, то происходит взаимообучение. Если помощь не нужна, то после
выполнения задания происходит взаимопроверка и делается отметка в оценочный
лист. Потом пары меняются, и процесс продолжается до тех пор, пока каждый ученик
не выполнит задания других учеников группы. Затем подводится итог, и
выставляется общая оценка.
Оценочный лист.
| №1 | №2 | №3 | №4 | Итоговая оценка | |
| Лаптева Алина | 5 | ||||
| Борзенков Егор | 3 | ||||
| Мартышин Сергей | 4 | ||||
| Казакова Виктория | 3 |
По диагонали оценка выставлена учителем. За выполнение карточки № 1оценка
выставляется Лаптевой А., № 2 – Борзенковым Е., № 3 – Мартышиным С., № 4 –
Казаковой В..
urok.1sept.ru
Как решать задачи за 7 класс по алгебре
В 7 классе курс алгебры усложняется. В программе возникает много увлекательных тем. В 7 классе решают задачи на различные темы, скажем: «на скорость (на движение)», «движение по реке», «на дроби», «на сопоставление величин». Мастерство с легкостью решать задачи указывает на высокий ярус математического и логичного мышления. Абсолютно,с удовольствием решаются только те, которые легко поддаются и получаются.

Инструкция
1. Разберем, как решать больше распространенные задачи.При решении задач на скорость нужно знать несколько формул и уметь верно составить уравнение.Формулы для решения :S=V*t – формула пути;V=S/t – формула скорости;t =S/V – формула времени, где S – расстояние, V – скорость, t – время.На примере разберем, как решать задания такого типа.Условие: Грузовой автомобиль на путь из города «А» в город «Б» потратил 1,5часа. 2-й грузовой автомобиль потратил 1,2 часа. Скорость второго автомобиля огромнее на 15 км/ч., чем скорость первого. Обнаружить расстояние между двумя городами.Решение: Для комфорта применяйте следующую таблицу. В ней укажите то, что вестимо по условию: 1 авто 2 автоS X XV X/1,5 X/1,2t 1,5 1,2За Х примите то, что нужно обнаружить, т.е. расстояние. При составлении уравнения будьте внимательнее, обратите внимание, дабы все величины были в идентичном измерении (время – в часах, скорость в км/ч). По условию скорость 2-го авто огромнее скорости 1-го на 15 км/ч, т.е. V1 – V2=15. Зная это, составим, и решим уравнение:X/1,2 – X/1,5=151,5Х – 1,2Х – 27=00,3Х=27Х=90(км) – расстояние между городами.Результат: Расстояние между городами 90 км.
2. При решении задач на “движение по воде” нужно знать, что существуют несколько видов скоростей: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость вопреки течения (Vпр. теч.), скорость течения (Vтеч.).Запомните следующие формулы:Vпо теч=Vс+Vтеч.Vпр. теч.=Vс-Vтеч.Vпр. теч=Vпо теч. – 2Vтеч.Vпо теч.=Vпр. теч+2Vтеч.Vс=(Vпо теч.+Vпр теч.)/2 либо Vс=Vпо теч.+Vтеч.Vтеч.=(Vпо теч. – Vпр. теч)/2На примере, разберем, как их решать.Условие: Скорость катера по течению 21,8км/ч, а супротив течения 17,2 км/ч. Обнаружить собственную скорость катера и скорость течения реки.Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. – Vпр. теч)/2, обнаружим:Vтеч = (21,8 – 17,2)/2=4,6\2=2,3 (км/ч)Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)Результат: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
3. Задачи на сопоставление величинУсловие: Масса 9 кирпичей на 20 кг огромнее, чем масса одного кирпича. Обнаружить массу одного кирпича.Решение: Обозначим за Х (кг), тогда масса 9 кирпичей 9Х (кг). Из данные следует, что:9Х – Х=208х=20Х=2,5Ответ: Масса одного кирпича 2,5 кг.
4. Задачи на дроби. Основное правило при решении таких такого типа задач: Дабы обнаружить дробь от числа, нужно это число умножить на данную дробь.Условие: Путешественник был в пути 3 дня. В 1-й день он прошел? каждого пути, во 2-й 5/9 оставшегося пути, а в 3-й день – последние 16 км. Обнаружить каждый путь путешественника.Решение: Пускай каждый путь путешественника равен Х (км). Тогда в 1-й день он прошел? х (км), во 2-й день – 5/9(х -?) = 5/9*3/4х = 5/12х. Потому что в 3-й день он прошел 16 км, то:1/4х+5/12х+16=х1/4х+5/12х-х= – 16- 1/3х=-16Х=- 16:(-1/3)Х=48Ответ: Каждый путь путешественника равен 48 км.
Решить задачу на движение относительно примитивно. Довольно знать каждого одну формулу: S=V*t.

Инструкция
1. При решении задач на движение основными параметрами считаются:пройденный путь, обозначаемый традиционно как S,скорость – V ивремя – t.Связанность между этими параметрами выражается следующими формулами:S=Vt, V=S/t и t=S/VЧтобы не запутаться в единицах измерения, перечисленные параметры обязаны быть заданы в одной системе. Скажем, если время измеряется в часах, а пройденный путь в километрах, то скорость, соответственно, должна измеряться в километр/час.При решении задач этого типа традиционно производятся следующие действия:1. Выбирается один из незнакомых параметров и обозначается буквой х (у, z и т.п.)2. Уточняется, какой из 3 основных параметров вестим.3. 3-й из оставшихся параметров с подмогой приведенных выше формул выражается через два других.4. Исходя из условий задачи , составляют уравнение, которое объединяет неведомое значение с знаменитыми параметрами.5. Решают полученное уравнение.6. Проверяют обнаруженные корни уравнения на соответствие условиям задачи .В некоторых случаях решить задачу помогает чертеж (самостоятельно от качества рисунка).
2. Пример 1.Решить задачу:Лыжник проезжает 5 км за то же время, за которое пешеход поспевает пройти 2 км.Обнаружить это время, если знаменито, что скорость лыжника огромнее скорости пешехода на 6 км/ч. Определить скорости пешехода и лыжника.Обозначим желанное время (в часах) через t.Тогда, по формуле V=S/t, скорость лыжника равна 5/t км/ч, а скорость пешехода равна 2/t км/ч.Применяя данные задачи дозволено составить уравнение:5/t – 2/t = 6Откуда определяем, что: t=0,5Следовательно: скорость пешехода равна 4 км/ч, а лыжника – 10 км/ч.Результат: 0,5 часа; 4 км/ч; 10 км/ч.
3. Пример 2.Решим вышеприведенную задачу иным методом:Обозначим скорость пешехода через V (км/ч).Тогда скорость лыжника составит (V+6) км/ч.В соответствии с формулой: t=S/V, время дозволено определить согласно дальнейшему выражению:t=5/(V+6)=2/VОткуда элементарно находится:V=4,t=0,5.
В задачах на сложение скоростей движение тел бывает, как водится, равномерным и откровенным и описывается примитивными уравнениями. Тем не менее, эти задачи дозволено отнести к сложнейшим задачам механики. При решении таких задач пользуются правилом сложения классических скоростей. Дабы осознать правило решения, отменнее разглядеть его на определенных примерах задач.

Инструкция
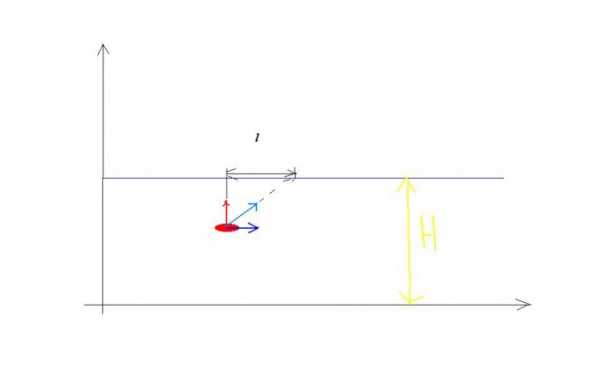
1. Пример на правило сложения скоростей. Пускай скорость течения реки v0, а скорость лодки, переплывающей эту реку, касательно воды равна v1 и направлена перпендикулярно храню (см рисунок 1). Лодка единовременно участвует в 2-х самостоятельных движениях: она за некоторое время t переплывает реку шириной Н со скорость ю v1 касательно воды и за это же время ее сносит вниз по течению реки на расстояние l. В итоге лодка проплывает путь S со скорость ю v касательно берега, равной по модулю: v равно корень квардратный из выражения v1 в квадрате + v0 в квадрате за это же самое время t. Следственно дозволено записать уравнения, которые решают сходственные задачи: H=v1t, l = v0t? S= корень квадратный из выражения: v1 в квадрате + v0 в квадрате, умноженный на t.
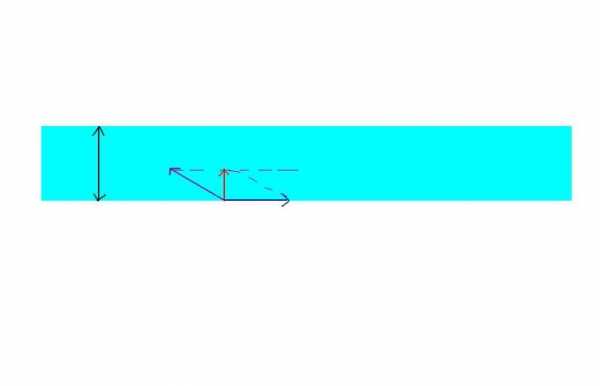
2. Иной тип таких задач задает вопросы: под каким углом к храню должне грести гребец в лодке, дабы оказаться на противоположном храню, пройдя во время переправы наименьший путь? За какое время данный путь будет пройден? С какой скорость ю лодка пройдет данный путь?Дабы ответить на эти вопросы следует сделать рисунок (см рис 2). Видимо, что наименьший путь, тот, что может пройти лодка, пересекая реку, равен ширине реки Н. Дабы проплыть данный путь, гребец должен направить лодку под таким углом а к брегу, при которм вектор безусловной скорости лодки v будет направлен перпендикулярно храню. Тогда из прямоугольного треугольника дозволено обнаружить: cos a=v0/v1. Отсель дозволено извлечь угол а. Скорость определить из этого же треугольника по теореме Пифагора: v= корень квадратный из выражения: v1 в квадрате – v0 в квадрате.И наконец время t, за которое лодка пересечет реку шириной Н, двигаясь со скорость ю v, будет t=H/v.
Видео по теме
Алгебра – это раздел математики, направленный на постижение операций над элементами произвольного множества, тот, что обобщает обыкновенные операции по сложению и умножению чисел.
Вам понадобится
- – условие задачи;
- – формулы.
Инструкция
1. Элементарная алгебраИзучает свойства операций с вещественными числами, правила реформирования математических выражений и уравнений. Именно элементарную алгебру преподают в школах. Для решения задачи требуются следующие умения:Правила записи символов элементов и операций, скажем, присутствие скобок в выражении указывает на приоритетность заключенного в них действия. Свойства операций (при перегруппировке мест слагаемых сумма не меняется). Свойства равенства (если a=b, то b=a).Другие законы (если a поменьше b, то b огромнее a).
2. Тригонометрия – часть элементарной алгебры, постигающая тригонометрические функции, скажем, синус, косинус, тангенс, котангенс и т.д. Задачи на тригонометрические функции решают с поддержкой особых формул: тригонометрических тождеств, формул сложения, формул приведения тригонометрических функций, формул двойного довода, двойного угла и т.п. Основное тождество тригонометрии: сумма квадратов синуса и косинуса угла равна 1.
3. Производные функции и их применениеВ этом разделе для решения используются основные правила дифференцирования, скажем, производная суммы равна сумме производных. Область использования производных функций – физика, скажем, производная координаты по времени равна скорости, это механический толк производной функции.
4. Первообразная и интегралОбласть использования – физика, а вернее, механика. Скажем, первообразная (интеграл) от расстояния есть скорость. для нахождения первообразной функции существуют определенные правила, скажем, если F – первообразная для f, а G – для g, то F+G – первообразная для f+g.
5. Показательная и логарифмическая функцииПоказательная функция – это функция возведения в степень. Число, возводимое в степень, именуется основанием функции, а степень – показателем функции. Подчиняется правилам, скажем, всякое основание в нулевой степени равно 1.В логарифмической функции основанием именуется степень, в которую необходимо построить основание, дабы получить итоговое значение. Некоторые примитивные правила: логарифм, у которого основание и показатель идентичны, равен 1; логарифм по основанию 1 с любым показателем будет равен 0.
Видео по теме
Полезный совет
Главно осознать область, к которой относится ваша задача, остальное – дело техники.Немыслимо запомнить все формулы, следственно имейте под рукой математический справочник.
Дабы решить задачу с дробями , необходимо обучиться делать с ними арифметические действия. Они могут быть десятичные, но почаще каждого применяются естественные дроби с числителем и знаменателем. Только позже этого дозволено переходить на решения математических задач с дробными величинами.

Вам понадобится
- – калькулятор;
- – познания свойств дробей;
- – знание изготавливать действия с дробями.
Инструкция
1. Дробью называют запись деления одного числа на другое. Нередко это сделать нацело невозможно, следственно и оставляют это действие «неоконченным . Число, которое является делимым (оно стоит над либо перед знаком дроби), именуются числителем, а второе число (под знаком дроби либо позже него) – знаменателем. Если числитель огромнее знаменателя, дробь именуется неправильной, и из нее дозволено выделить целую часть. Если числитель поменьше знаменателя, то такая дробь именуется положительной, и ее целая часть равна 0.
2. Задачи с дробями делятся на несколько видов. Определите, к какому из них относится задача. Примитивный вариант – нахождение доли числа, выраженной дробью. Для решения этой задачи довольно умножить это число на дробь. Скажем, на склад завезли 8 т картошки. В первую неделю было продано 3/4 от ее всеобщего числа. Сколько картошки осталось? Дабы решить эту задачу, число 8 умножьте на 3/4. Получится 8?3/4=6 т.
3. Если необходимо обнаружить число по его части, умножьте знаменитую часть числа на дробь, обратную той, которая показывает какова доля данной части в числе. Скажем, 8 человек из класса составляют 1/3 от всеобщего числа учеников. Сколько детей учится в классе? От того что 8 человек это часть, которая представляет 1/3 от каждого числа, то обнаружьте обратную дробь, которая равна 3/1 либо примитивно 3. После этого для приобретения числа учеников в классе 8?3=24 ученика.
4. Когда надобно обнаружить какую часть числа составляет одно число от иного, поделите число, которое представляет часть на то, которое является целым. К примеру, если расстояние между городами 300 км, а автомобиль проехал 200 км, какую часть данный составит от каждого пути? Поделите часть пути 200 на полный путь 300, позже сокращения дроби получите итог. 200/300=2/3.
5. Дабы обнаружить часть незнакомую долю от числа, когда есть знаменитая, возьмите целое число за условную единицу, и отнимите от нее знаменитую долю. Скажем, если теснее прошло 4/7 части урока, сколько еще осталось? Возьмите каждый урок как условную единицу и отнимите от нее 4/7. Получите 1-4/7=7/7-4/7=3/7.
Дроби – это математическая форма записи простого разумного числа. Она представляет собой число, которое состоит из одной либо нескольких долей единицы, может быть как в десятичном, так и в обыкновенном виде. Сегодня операции по реформированию дробей имеют громадное значение не только в математике, но и в иных областях познаний.
Инструкция
1. Как водится, множество обычных дробей бывают неправильными, и в таком случае они требуют определенных действий со стороны того, кто решает примеры и задачи с данной дробью.
2. Возьмите учебник со своей задачей. Наблюдательно ознакомьтесь с условием, прочитав его несколько раз, и перейдите к решению. Посмотрите, какие дроби имеются в решаемых вами действиях. Это могут быть неправильные, положительные либо десятичные дроби. Переведите верные дроби в неправильные, но при этом помните, что для записи результата все действия придется исполнить обратно, преобразовав теснее неправильную дробь в положительную. У неправильной дроби число над дробной чертой (числитель) неизменно огромнее числа под чертой – знаменателя. Для того дабы сделать перевод из верной дроби в неправильную нужно исполнить следующие шаги.
3. Умножьте знаменатель на целое число и прибавьте к полученному итогу числитель. К примеру, если дробь вида 2 целых 7/9, нужно 9 умножить на 2 и потом к 18 прибавить 7 – финальным итогом будет 25/9.
4. Произведите все нужные действия по своей задаче (сложения, вычитания, деления, умножения), применяя преобразованные дроби.Возьмите свой результат, его нужно будет представить в обычной дроби. Для этого поделите числитель на знаменатель. К примеру, если нужно перевести число 25/9 в положительную дробь, поделите 25 на 9. Потому что 25 на 9 нацело не делится, в результате получается 2 целых и семь (числитель) девятых (знаменатель). Сейчас получена верная дробь, где числитель огромнее знаменателя и имеется целая часть.
5. Запишите результат задачи положительной дробью. Проведите проверку своим действиям, в случае если ее требует сделать условие задачи либо преподаватель.
Полезный совет
Дабы с легкостью решать задачи, нужно обучиться переводить их на “язык чисел”, применяя некоторые хитрости. Составление таблиц и схем максимально помогает осознать условие задачи, отношения величин. Так же облегчает процесс составления уравнений. Абсолютно, нужно знать нужны формулы.
jprosto.ru