Математика 7 класс Мерзляк, Полонский, Якир Номер 1067
Учебник по математике 7 класс Мерзляк
авторы: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
издательство: Вентана-Граф, 2018 г.
Решите уравнение:
1)
(x+y)2+(x−3)2=0
;
2)
(x+2y−3)2+x2−4xy+4y2=0
;
3)
|x−3y−6|+(9x+6y−32)2=0
;
4)
x2+y2+10x−12y+61=0
;
5)
25×2+10y2−30xy+8y+16=0
.
2)
3)
4)
5)
Решение 1
(x+y)2+(x−3)2=0
(x+y)2=−(x−3)2
(x+y)2⩾0
и
(x−3)2⩾0
, тогда уравнение будет верно при:
(x+y)2=0
и
(x−3)2=0
(x−3)2=0
x − 3 = 0
x = 3;
(3+y)2=0
3 + y = 0
y = −3.
Ответ: (3;−3).
Решение 2
(x+2y−3)2+x2−4xy+4y2=0
(x+2y−3)2+(x−2y)2
(x+2y−3)2=−(x−2y)2
(x+2y−3)2⩾0
и
(x−2y)2⩾0
, тогда уравнение будет верно при:
(x+2y−3)2=0
и
(x−2y)2=0
{x+2y−3=0x−2y=0
x + 2y − 3 + x − 2y = 0
2x = 3
x = 3 : 2
x = 1,5;
1,5 − 2y = 0
−2y = −1,5
y = −1,5 : −2
y = 0,75.
Ответ: (1,5;0,75).
Решение 3
|x−3y−6|+(9x+6y−32)2=0
|x−3y−6|=−(9x+6y−32)2
|x−3y−6|⩾0
и
(9x+6y−32)2⩾0
, тогда уравнение будет верно при:
|x−3y−6|=0
и
(9x+6y−32)2=0
{x−3y−6=0|∗29x+6y−32=0
{2x−6y−12=09x+6y−32=0
2x − 6y − 12 + 9x + 6y − 32 = 0
11x = 44
x = 44 : 11
x = 4;
4 − 3y − 6 = 0
−3y = 6 − 4
y=−23
Ответ:
(4;−23)
.
Решение 4
x2+y2+10x−12y+61=0
x2+y2+10x−12y+25+36=0
(x2+10x+25)+(y2−12y+36)=0
(x+5)2+(y−6)2=0
(x+5)2=−(y−6)2
(x+5)2⩾0
и
(y−6)2⩾0
, тогда уравнение будет верно при:
(x+5)2=0
и
(y−6)2=0
x + 5 = 0
x = −5;
y − 6 = 0
y = 6.
Ответ: (−5;6).
Решение 5
25×2+10y2−30xy+8y+16=0
25×2+9y2+y2−30xy+8y+16=0
(25×2−30xy+9y2)+(y2+8y+16)=0
(5x−3y)2+(y+4)2=0
(5x−3y)2⩾0
и
(y+4)2⩾0
, тогда уравнение будет верно при:
(5x−3y)2=0
и
(y+4)2=0
y + 4 = 0
y = −4;
5x − 3 * (−4) = 0
5x = −12
x = −12 : 5
x = −2,4.
Ответ: (−2,4;−4).
×
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Отправить
reshalka.com
учебник для 7 класса (авт. А.Г. Мерзляк и др. ) ОНЛАЙН
Мерзляк А.Г. Алгебра : 7 класс : учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М., 2015. — 272 с.
Учебник предназначен для изучения алгебры в 7 классе общеобразовательных организаций. В нём предусмотрена уровневая дифференциация, позволяющая формировать у школьников познавательный интерес к алгебре.
Учебник входит в систему учебно-методических комплектов «Алгоритм успеха».
Содержание учебника соответствует федеральному государственному образовательному стандарту основного общего образования (2010 г.).
Учебник разделён на четыре главы, каждая из которых состоит из параграфов. В параграфах изложен теоретический материал. Особое внимание обращайте на текст, выделенный жирным шрифтом. Также обращайте внимание на слова, выделенные курсивом.
Как правило, изложение теоретического материала завершается примерами решения задач. Эти записи можно рассматривать как один из возможных образцов оформления решения.
К каждому параграфу подобраны задачи для самостоятельного решения, к которым мы советуем приступать только после усвоения теоретического материала. Среди заданий есть как простые и средние по сложности упражнения, так и трудные задачи (особенно те, которые обозначены звёздочкой
Каждый параграф завершает особая рубрика, которую мы назвали «Учимся делать нестандартные шаги». В ней собраны задачи, для решения которых нужны не специальные алгебраические знания, а лишь здравый смысл, изобретательность и сообразительность. Они помогут вам научиться принимать неожиданные и нестандартные решения не только в математике, но и в жизни.
Кроме того, в учебнике вы сможете прочитать рассказы по истории алгебры.
СОДЕРЖАНИЕ
От авторов ……………………………………………3
§ 1. Введение в алгебру ………………………………..5
Книга о восстановлении и противопоставлении ……………..11
Глава 1. Линейное уравнение с одной переменной
§ 2. Линейное уравнение с одной переменной ………………13
§ 3. Решение задач с помощью уравнений ………………….19
Задание «Проверьте себя» № 1 в тестовой форме ……………27
Итоги главы 1 ………………………………………..28
Глава 2. Целые выражения
§ 4. Тождественно равные выражения. Тождества ……………30
§ 5. Степень с натуральным показателем ………………….35
§ 6. Свойства степени с натуральным показателем ………….43
§ 7. Одночлены ……………………………………….51
§ 8. Многочлены ………………………………………57
§ 9. Сложение и вычитание многочленов …………………..61
Задание «Проверьте себя» № 2 в тестовой форме ……………68
§ 10. Умножение одночлена на многочлен ………………….69
§ 11. Умножение многочлена на многочлен …………………74
§ 12. Разложение многочленов на множители.
Вынесение общего множителя за скобки ……………………80
§ 13. Разложение многочленов на множители. Метод группировки .87
Задание «Проверьте себя» № 3 в тестовой форме ……………91
§ 14. Произведение разности и суммы двух выражений ……….92
§ 15. Разность квадратов двух выражений …………………97
§ 16. Квадрат суммы и квадрат разности двух выражений ……102
§ 17. Преобразование многочлена в квадрат суммы или разности двух выражений ..109
Задание «Проверьте себя» № 4 в тестовой форме …………..116
§ 18. Сумма и разность кубов двух выражений……………..117
§ 19. Применение различных способов разложения многочлена на множители ..122
Задание «Проверьте себя» № 5 в тестовой форме …………..129
Язык, понятный всем ………………………………….130
Итоги главы 2 ………………………………………..132
Глава 3. ФУНКЦИИ
§ 20. Связи между величинами. Функция …………………..135
§ 21. Способы задания функции ………………………….147
§ 22. График функции ………………………………….153
§ 23. Линейная функция, её график и свойства …………….163
Задание «Проверьте себя» № 6 в тестовой форме ……………175
Итоги главы 3…………………………………………177
Глава 4. Системы линейных уравнений с двумя переменными
§ 24. Уравнения с двумя переменными …………………….178
§ 25. Линейное уравнение с двумя переменными и его график …186
Как строили мост между геометрией и алгеброй …………….195
§ 26. Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными ………………….195
§ 27. Решение систем линейных уравнений методом подстановки .203
§ 28. Решение систем линейных уравнений методом сложения ….207
§ 29. Решение задач с помощью систем линейных уравнений …..214
Задание «Проверьте себя» № 7 в тестовой форме ……………223
Итоги главы 4 ………………………………………..225
Упражнения для повторения курса 7 класса ………………..227
Сведения из курса математики 5-6 классов ………………..237
Проектная работа ……………………………………..250
Дружим с компьютером ………………………………….254
Ответы и указания …………………………………….259
Ответы к заданиям «Проверьте себя» в тестовой форме ………266
Предметный указатель ………………………………….268
uch-lit.ru
Математика 7 класс Мерзляк, Полонский, Якир Номер 978
Учебник по математике 7 класс Мерзляк
авторы: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
издательство: Вентана-Граф, 2018 г.
Графиком каких уравнений является та же прямая, что и график уравнения 2x − 5y = 3:
1) 4x − 10y = 6;
2) 4x − 10y = 3;
3) 2x − 5y = 6;
4) 5y − 2x = −3;
5) x − 2,5y = 1,5;
6) −0,4x − y = 0,6?
Решение 1
4x−10y=62x−5y=3=4x2x=−10y−5y=63=21
, следовательно графиком данного уравнения является та же прямая, что и график уравнения 2x − 5y = 3.
Решение 2
4x−10y=32x−5y=3=4x2x=−10y−5y≠33
, следовательно графиком данного уравнения НЕ является та же прямая, что и график уравнения 2x − 5y = 3.
Решение 3
2x−5y=62x−5y=3=2x2x=−5y−5y≠63
, следовательно графиком данного уравнения НЕ является та же прямая, что и график уравнения 2x − 5y = 3.
Решение 4
5y − 2x = −3, умножаем обе части уравнения на одно и тоже число −1, тогда оно примет вид:
2x − 5y = 3, следовательно, следовательно графиком данного уравнения является та же прямая, что и график уравнения 2x − 5y = 3.
Решение 5
x−2,5y=1,52x−5y=3=x2x=−2,5y−5y=1,53=12
, следовательно графиком данного уравнения является та же прямая, что и график уравнения 2x − 5y = 3.
Решение 6
−0,4x−y=0,62x−5y=3=−y−5y=0,63≠−0,4x2x
, следовательно графиком данного уравнения НЕ является та же прямая, что и график уравнения 2x − 5y = 3.
×
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Отправить
reshalka.com
Математика 7 класс Мерзляк, Полонский, Якир Номер 1050
Учебник по математике 7 класс Мерзляк
авторы: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
издательство: Вентана-Граф, 2018 г.
Решите систему уравнений методом сложения:
1)
{5x+y=7,7x−4y=−1;
2)
{6x−5y=23,2x−7y=13;
3)
{5x−2y=16,8x+3y=38;
4)
{5x−4y=10,2x−3y=−3;
5)
{4a+6b=9,3a−5b=2;
6)
{9m−13n=22,2m+3n=−1.
Решение 1
{5x+y=7,7x−4y=−1;
Чтобы исключить переменную y, умножим обе части первого уравнения на 4:
{20x+4y=28,7x−4y=−1;
20x + 4y + 7x − 4y = 28 − 1
27x = 27
x = 27 : 27
x = 1;
7 * 1 − 4y = −1
−4y = −1 − 7
−4y = −8
y = −8 : −4
y = 2.
Пара чисел (1;2) − решение данной системы уравнений.
Решение 2
{6x−5y=23,2x−7y=13;
Чтобы исключить переменную x, умножим обе части второго уравнения на −3:
{6x−5y=23,−6x+21y=−39;
6x − 5y − 6x + 21y = 23 − 39
16y = −16
y = −16 : 16
y = −1,
6x − 5 * (−1) = 23
6x = 23 − 5
x = 18 : 6
x = 3.
Пара чисел (3;−1) − решение данной системы уравнений.
Решение 3
{5x−2y=16,8x+3y=38;
Чтобы исключить переменную y, умножим обе части первого уравнения на 3, а второго на 2:
{15x−6y=48,16x+6y=76;
15x − 6y + 16x + 6y = 48 + 76
31x = 124
x = 124 : 31
x = 4;
15 * 4 − 6y = 48
60 − 6y = 48
−6y = 48 − 60
y = −12 : −6
y = 2.
Пара чисел (4;2) − решение данной системы уравнений.
Решение 4
{5x−4y=10,2x−3y=−3;
Чтобы исключить переменную y, умножим обе части первого уравнения на 3, а второго на −4:
{15x−12y=30,−8x+12y=12;
15x − 12y − 8x + 12y = 30 + 12
7x = 42
x = 42 : 7
x = 6;
−8 * 6 + 12y = 12
−48 + 12y = 12
12y = 12 + 48
y = 60 : 12
y = 5.
Пара чисел (6;5) − решение данной системы уравнений.
Решение 5
{4a+6b=9,3a−5b=2;
Чтобы исключить переменную b, умножим обе части первого уравнения на 5, а второго на 6:
{20a+30b=45,18a−30b=12;
20a + 30b + 18a − 30b = 45 + 12
38a = 57
a = 57 : 38
a = 1,5;
18 * 1,5 − 30b = 12
27 − 30b = 12
−30b = 12 − 27
−30b = −15
b = −15 : −30
b = 0,5.
Пара чисел (1,5;0,5) − решение данной системы уравнений.
Решение 6
{9m−13n=22,2m+3n=−1.
Чтобы исключить переменную m, умножим обе части второго уравнения на −4,5:
{9m−13n=22,−9m−13,5n=4,5.
9m − 13n − 9m − 13,5n = 22 + 4,5
−26,5n = 26,5
n = 26,5 : −26,5
n = −1,
9m − 13 * (−1) = 22
9m = 22 − 13
9m = 9
m = 9 : 9
m = 1
Пара чисел (1;−1) − решение данной системы уравнений.
×
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Отправить
reshalka.com
Математика 7 класс Мерзляк, Полонский, Якир Номер 1026
Учебник по математике 7 класс Мерзляк
авторы: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
издательство: Вентана-Граф, 2018 г.
Решите графически систему уравнений:
1)
{x2−y2=0,x+2y=3;
2)
{|y−2x|=3,x−2y=0;
3)
{x2−2xy+y2=4,|x+y|=2.
Решение 1
{x2−y2=0,x+2y=3;
x2−y2=0
(x − y)(x + y) = 0
x − y = 0
y = x
x + y = 0
y = −x
x + 2y = 3
x = 3 − 2y
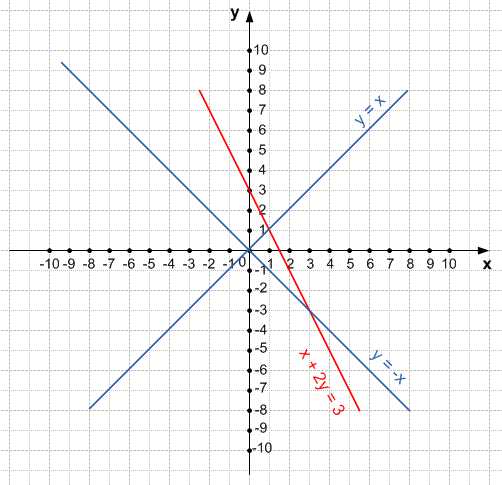
Графики уравнений пересекаются в точках (1;1) и (−3;3), следовательно данные пары чисел являются решением данной системы уравнения.
Решение 2
{|y−2x|=3,x−2y=0;
y − 2x = 3
y = 3 + 2x
y − 2x = −3
y = 2x − 3
x − 2y = 0
x = 2y

Графики уравнений пересекаются в точках (−2;−1) и (2;1), следовательно данные пары чисел являются решением данной системы уравнения.
Решение 3
×
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Отправить
reshalka.com